Remarkably Efficient [4+4] Dimerization of [n]-Cyclacenes
Abstract
1. Introduction
2. Methods
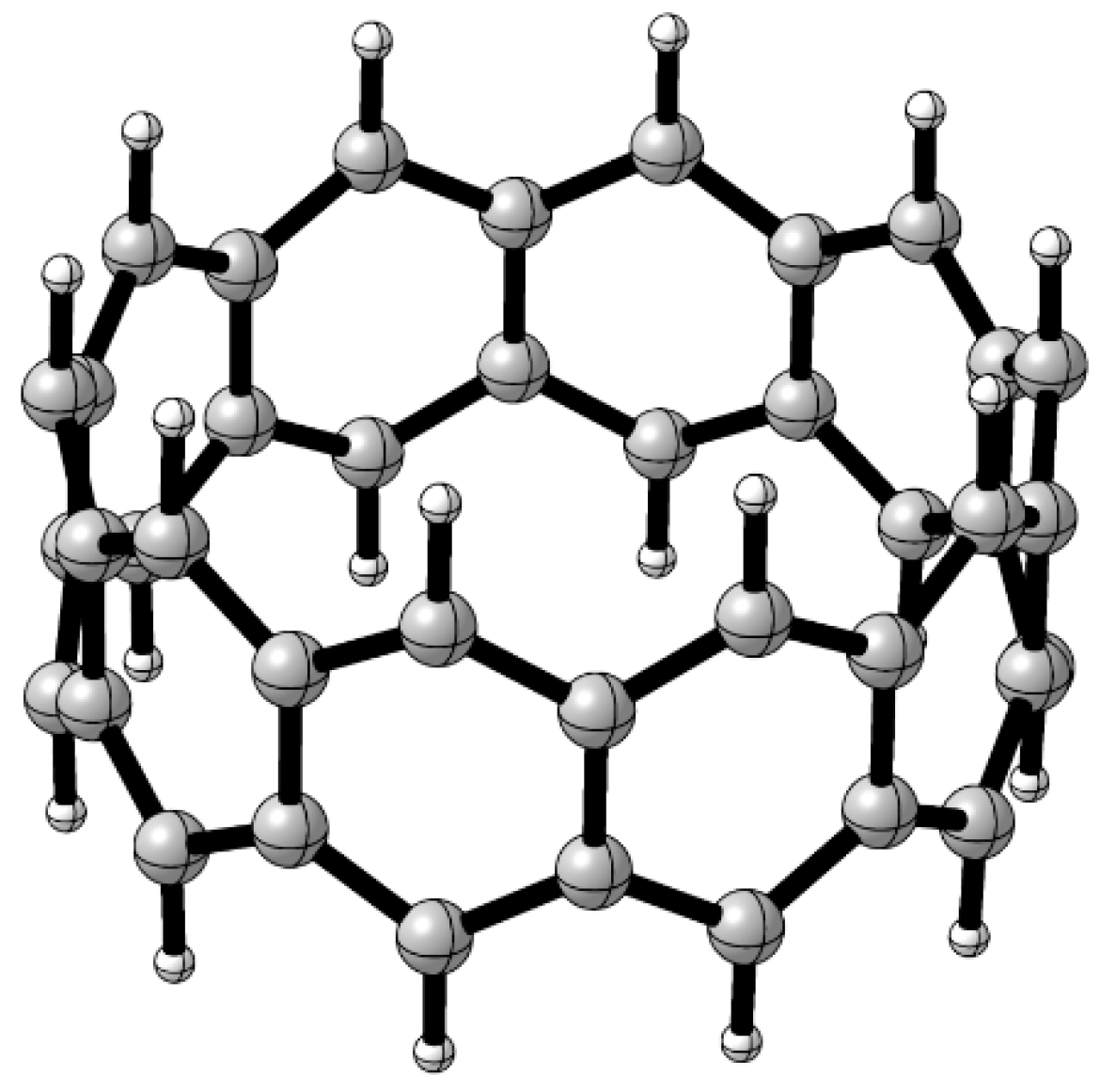
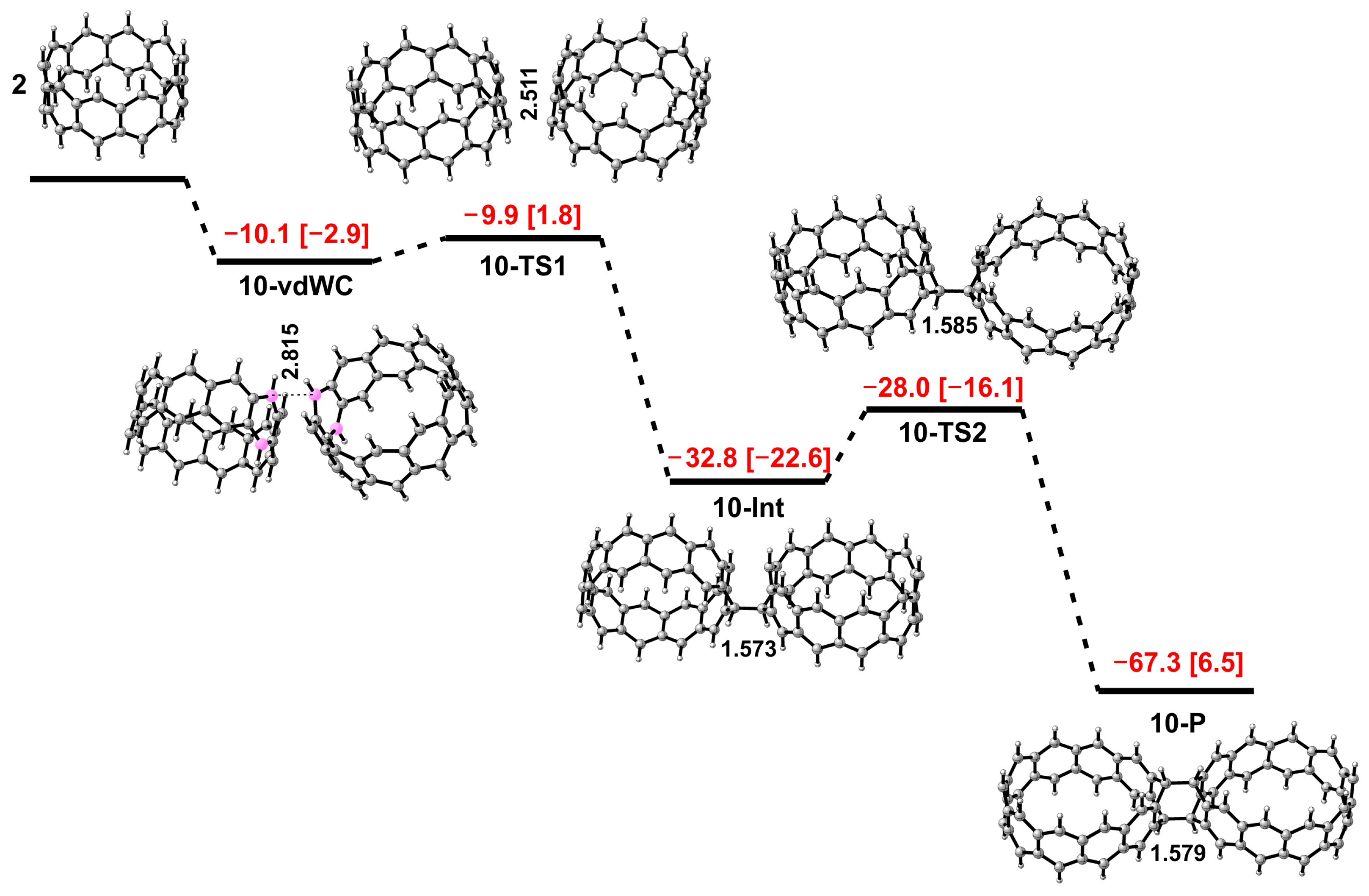
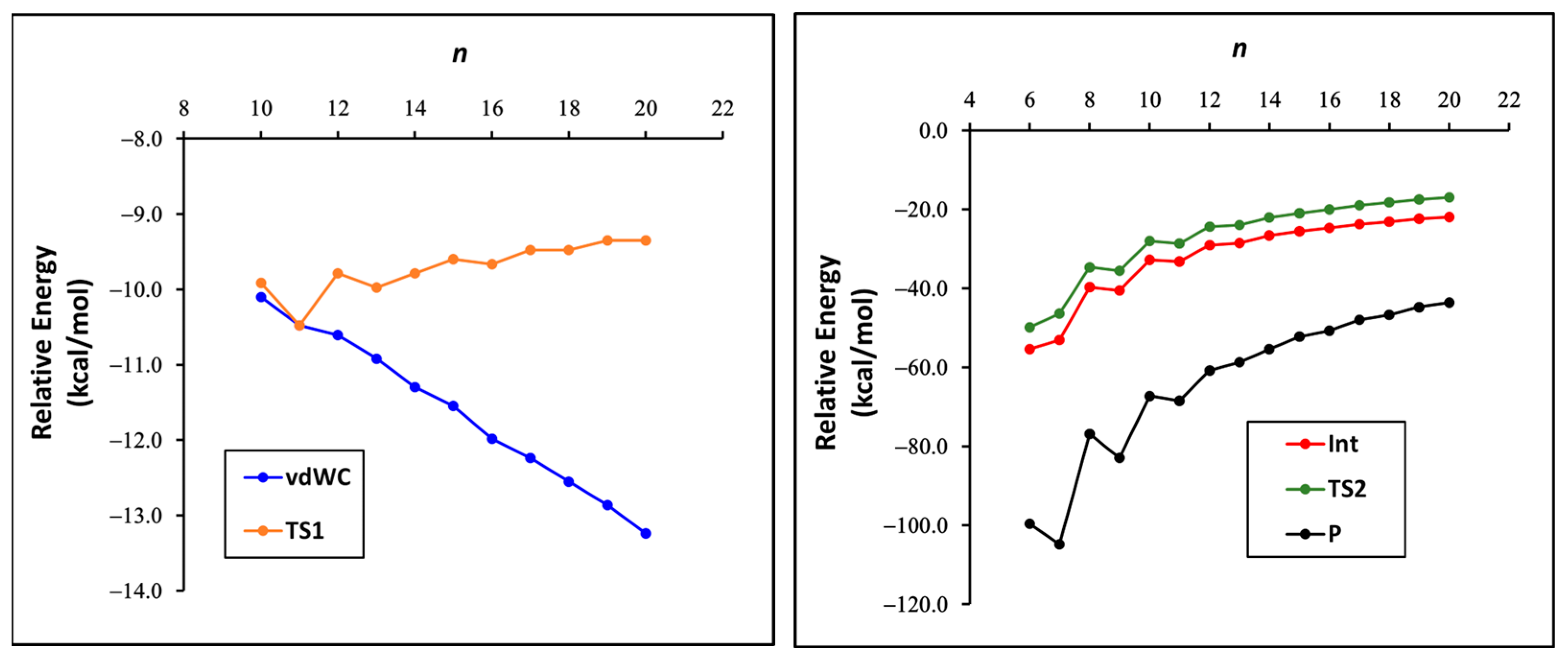
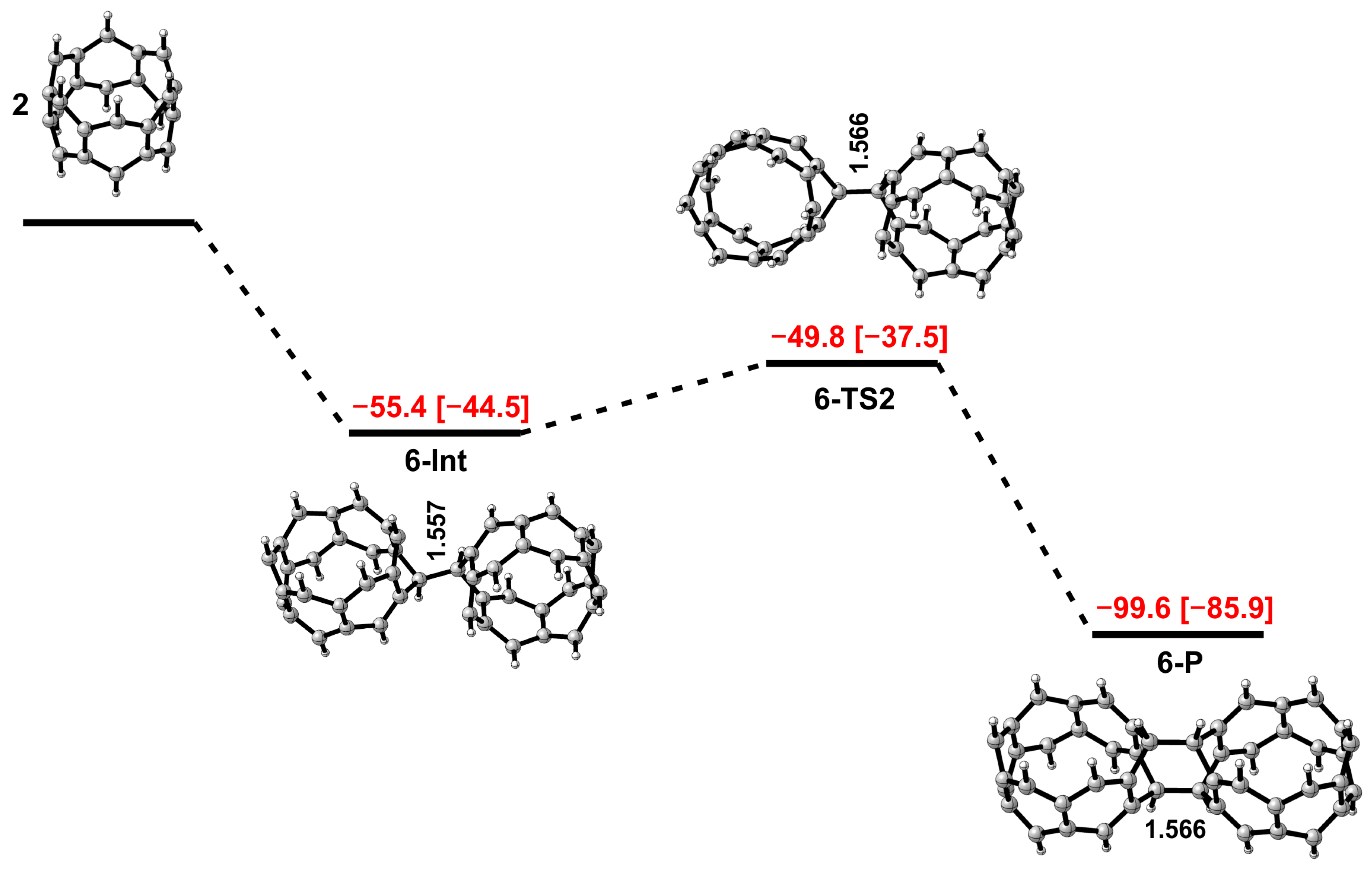
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Türker, L.; Gümüş, S. Cyclacenes. J. Mol. Struct. THEOCHEM 2004, 685, 1–33. [Google Scholar] [CrossRef]
- Gleiter, R.; Esser, B.; Kornmayer, S.C. Cyclacenes: Hoop-Shaped Systems Composed of Conjugated Rings. Acc. Chem. Res. 2009, 42, 1108–1116. [Google Scholar] [CrossRef] [PubMed]
- Shi, T.-H.; Wang, M.-X. Zigzag Hydrocarbon Belts. CCS Chem. 2021, 3, 916–931. [Google Scholar] [CrossRef]
- Bendikov, M.; Duong, H.M.; Starkey, K.; Houk, K.N.; Carter, E.A.; Wudl, F. Oligoacenes: Theoretical Prediction of Open-Shell Singlet Diradical Ground States. J. Am. Chem. Soc. 2004, 126, 7416–7417. [Google Scholar] [CrossRef]
- Hachmann, J.; Dorando, J.J.; Avilés, M.; Chan, G.K.-L. The radical character of the acenes: A density matrix renormalization group study. J. Chem. Phys. 2007, 127, 13. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.-e.; Dai, S. Electronic Ground State of Higher Acenes. J. Phys. Chem. A 2008, 112, 332–335. [Google Scholar] [CrossRef]
- Bettinger, H.F. Electronic structure of higher acenes and polyacene: The perspective developed by theoretical analyses. Pure Appl. Chem. 2010, 82, 905–915. [Google Scholar] [CrossRef]
- Yang, Y.; Davidson, E.R.; Yang, W. Nature of ground and electronic excited states of higher acenes. Proc. Natl. Acad. Sci. USA 2016, 113, E5098–E5107. [Google Scholar] [CrossRef]
- Urgel, J.I.; Mishra, S.; Hayashi, H.; Wilhelm, J.; Pignedoli, C.A.; Di Giovannantonio, M.; Widmer, R.; Yamashita, M.; Hieda, N.; Ruffieux, P.; et al. On-surface light-induced generation of higher acenes and elucidation of their open-shell character. Nat. Commun. 2019, 10, 861. [Google Scholar] [CrossRef]
- Tönshoff, C.; Bettinger, H.F. Pushing the limits of acene chemistry: The recent surge of large acenes. Chem. Eur. J. 2021, 27, 3193–3212. [Google Scholar] [CrossRef]
- Lerena, L.; Zuzak, R.; Godlewski, S.; Echavarren, A.M. The Journey for the Synthesis of Large Acenes. Chem. Eur. J. 2024, 30, e202402122. [Google Scholar] [CrossRef] [PubMed]
- Ruan, Z.; Schramm, J.; Bauer, J.B.; Naumann, T.; Bettinger, H.F.; Tonner-Zech, R.; Gottfried, J.M. Synthesis of Tridecacene by Multistep Single-Molecule Manipulation. J. Am. Chem. Soc. 2024, 146, 3700–3709. [Google Scholar] [CrossRef] [PubMed]
- Zuzak, R.; Kumar, M.; Stoica, O.; Soler-Polo, D.; Brabec, J.; Pernal, K.; Veis, L.; Blieck, R.; Echavarren, A.M.; Jelinek, P.; et al. On-Surface Synthesis and Determination of the Open-Shell Singlet Ground State of Tridecacene. Angew. Chem. Int. Ed. 2024, 63, e202317091. [Google Scholar] [CrossRef] [PubMed]
- Ruan, Z.; Schramm, J.; Bauer, J.B.; Naumann, T.; Müller, L.V.; Sättele, F.; Bettinger, H.F.; Tonner-Zech, R.; Gottfried, J.M. On-Surface Synthesis and Characterization of Pentadecacene and Its Gold Complexes. J. Am. Chem. Soc. 2025, 147, 4862–4870. [Google Scholar] [CrossRef]
- Türker, L. The Possibility of Superaromatic Cyclacenes. Polycyclic Aromat. Compd. 1995, 4, 231–236. [Google Scholar] [CrossRef]
- Choi, H.S.; Kim, K.S. Structures, Magnetic Properties, and Aromaticity of Cyclacenes. Angew. Chem. Int. Ed. 1999, 38, 2256–2258. [Google Scholar] [CrossRef]
- Chen, Z.; Jiang, D.-e.; Lu, X.; Bettinger, H.F.; Dai, S.; Schleyer, P.v.R.; Houk, K.N. Open-Shell Singlet Character of Cyclacenes and Short Zigzag Nanotubes. Org. Lett. 2007, 9, 5449–5452. [Google Scholar] [CrossRef]
- Wu, C.-S.; Lee, P.-Y.; Chai, J.-D. Electronic Properties of Cyclacenes from TAO-DFT. Sci. Rep. 2016, 6, 37249. [Google Scholar] [CrossRef]
- Chung, J.-H.; Chai, J.-D. Electronic Properties of Möbius Cyclacenes Studied by Thermally-Assisted-Occupation Density Functional Theory. Sci. Rep. 2019, 9, 2907. [Google Scholar] [CrossRef]
- Huang, X.; Gan, P.-y.; Gao, F.-w.; Su, Z.-m. Tuning optical properties of π-conjugated double nanohoops under external electric field stimuli-responsiveness. Phys. Chem. Chem. Phys. 2024, 26, 8716–8723. [Google Scholar] [CrossRef]
- Heilbronner, E. Molecular Orbitals in homologen Reihen mehrkerniger aromatischer Kohlenwasserstoffe: I. Die Eigenwerte yon LCAO-MO’s in homologen Reihen. Helv. Chim. Acta 1954, 37, 921–935. [Google Scholar] [CrossRef]
- Clar, E. The Aromatic Sextet. In Mobile Source Emissions Including Policyclic Organic Species; Rondia, D., Cooke, M., Haroz, R.K., Eds.; Springer: Dordrecht, The Netherlands, 1983; pp. 49–58. [Google Scholar]
- Solà, M. Forty years of Clar’s aromatic π-sextet rule. Front. Chem. 2013, 1, 22. [Google Scholar] [CrossRef]
- Chai, J.-D. Thermally-assisted-occupation density functional theory with generalized-gradient approximations. J. Chem. Phys. 2014, 140. [Google Scholar] [CrossRef]
- Guo, Q.-H.; Qiu, Y.; Wang, M.-X.; Fraser Stoddart, J. Aromatic hydrocarbon belts. Nat. Chem. 2021, 13, 402–419. [Google Scholar] [CrossRef]
- Povie, G.; Segawa, Y.; Nishihara, T.; Miyauchi, Y.; Itami, K. Synthesis of a carbon nanobelt. Science 2017, 356, 172–175. [Google Scholar] [CrossRef] [PubMed]
- Povie, G.; Segawa, Y.; Nishihara, T.; Miyauchi, Y.; Itami, K. Synthesis and Size-Dependent Properties of [12], [16], and [24]Carbon Nanobelts. J. Am. Chem. Soc. 2018, 140, 10054–10059. [Google Scholar] [CrossRef]
- Bauer, J.B.; Diab, F.; Maichle-Mössmer, C.; Schubert, H.; Bettinger, H.F. Synthesis of the [11]Cyclacene Framework by Repetitive Diels–Alder Cycloadditions. Molecules 2021, 26, 3047. [Google Scholar] [CrossRef] [PubMed]
- Eisenberg, D.; Shenhar, R.; Rabinovitz, M. Synthetic approaches to aromatic belts: Building up strain in macrocyclic polyarenes. Chem. Soc. Rev. 2010, 39, 2879–2890. [Google Scholar] [CrossRef]
- Chen, H.; Gui, S.; Zhang, Y.; Liu, Z.; Miao, Q. Synthesis of a Hydrogenated Zigzag Carbon Nanobelt. CCS Chem. 2021, 3, 613–619. [Google Scholar] [CrossRef]
- Kohnke, F.H.; Slawin, A.M.; Stoddart, J.F.; Williams, D.J. Molecular belts and collars in the making: A hexaepoxyoctacosahydro [12] cyclacene derivative. Angew. Chem. Int. Ed. 1987, 26, 892–894. [Google Scholar] [CrossRef]
- Ashton, P.R.; Isaacs, N.S.; Kohnke, F.H.; Slawin, A.M.; Spencer, C.M.; Stoddart, J.F.; Williams, D.J. Towards the making of [12] collarene. Angew. Chem. Int. Ed. 1988, 27, 966–969. [Google Scholar] [CrossRef]
- Ashton, P.R.; Brown, G.R.; Isaacs, N.S.; Giuffrida, D.; Kohnke, F.H.; Mathias, J.P.; Slawin, A.M.Z.; Smith, D.R.; Stoddart, J.F.; Williams, D.J. Molecular LEGO. 1. Substrate-directed synthesis via stereoregular Diels-Alder oligomerizations. J. Am. Chem. Soc. 1992, 114, 6330–6353. [Google Scholar] [CrossRef]
- Ashton, P.R.; Girreser, U.; Giuffrida, D.; Kohnke, F.H.; Mathias, J.P.; Raymo, F.M.; Slawin, A.M.; Stoddart, J.F.; Williams, D.J. Molecular belts. 2. Substrate-directed syntheses of belt-type and cage-type structures. J. Am. Chem. Soc. 1993, 115, 5422–5429. [Google Scholar] [CrossRef]
- Cory, R.M.; McPhail, C.L. Transformations of a macrocyclic cyclophane belt into advanced [8] cyclacene and [8] cyclacene triquinone precursors. Tetrahedron Lett. 1996, 37, 1987–1990. [Google Scholar] [CrossRef]
- Cory, R.M.; McPhail, C.L.; Dikmans, A.J.; Vittal, J.J. Macrocyclic cyclophane belts via double Diels-Alder cycloadditions: Macroannulation of bisdienes by bisdienophiles. Synthesis of a key precursor to an [8] cyclacene. Tetrahedron Lett. 1996, 37, 1983–1986. [Google Scholar] [CrossRef]
- Godt, A.; Enkelmann, V.; Schlüter, A.D. Double-Stranded Molecules: A [6] Beltene Derivative and the Corresponding Open-Chain Polymer. Angew. Chem. Int. Ed. 1989, 28, 1680–1682. [Google Scholar] [CrossRef]
- Kintzel, O.; Luger, P.; Weber, M.; Schlüter, A.-D. Ring-Chain Equilibrium between an [18]Cyclacene Derivative and a Ladder Oligomer. Eur. J. Org. Chem. 1998, 1998, 99–105. [Google Scholar] [CrossRef]
- Shi, T.-H.; Guo, Q.-H.; Tong, S.; Wang, M.-X. Toward the Synthesis of a Highly Strained Hydrocarbon Belt. J. Am. Chem. Soc. 2020, 142, 4576–4580. [Google Scholar] [CrossRef]
- Schulz, F.; García, F.; Kaiser, K.; Pérez, D.; Guitián, E.; Gross, L.; Peña, D. Exploring a Route to Cyclic Acenes by On-Surface Synthesis. Angew. Chem. Int. Ed. 2019, 58, 9038–9042. [Google Scholar] [CrossRef]
- Somani, A.; Gupta, D.; Bettinger, H.F. Computational Studies of Dimerization of [n]-Cyclacenes. J. Phys. Chem. A 2024, 128, 6847–6852. [Google Scholar] [CrossRef]
- Türker, L. Cryptoannulenic Behavior of Cyclacenes. Polycyclic Aromat. Compd. 1994, 4, 191–197. [Google Scholar] [CrossRef]
- Türker, L. AM1 treatment of Hückel type cyclacenes. J. Mol. Struct. 1997, 407, 217–220. [Google Scholar] [CrossRef]
- Türker, L. MNDO treatment of the Hückel and Möbius types of cyclacenes. J. Mol. Struct. THEOCHEM 1998, 454, 83–86. [Google Scholar] [CrossRef]
- Türker, L. The Effect of Peripheral Circuits on the Total\pi-Electron Energies of Cyclacenes. Turk. J. Chem. 2000, 24, 217–222. [Google Scholar]
- Sadowsky, D.; McNeill, K.; Cramer, C.J. Electronic structures of [n]-cyclacenes (n = 6–12) and short, hydrogen-capped, carbon nanotubes. Faraday Discuss. 2010, 145, 507–521. [Google Scholar] [CrossRef]
- Christoph, H.; Grunenberg, J.; Hopf, H.; Dix, I.; Jones, P.G.; Scholtissek, M.; Maier, G. MP2 and DFT Calculations on Circulenes and an Attempt to Prepare the Second Lowest Benzolog, [4]Circulene. Chem. Eur. J. 2008, 14, 5604–5616. [Google Scholar] [CrossRef]
- Gupta, D.; Omont, A.; Bettinger, H.F. Energetics of Formation of Cyclacenes from 2,3-Didehydroacenes and Implications for Astrochemistry. Chem. Eur. J. 2021, 27, 4605–4616. [Google Scholar] [CrossRef]
- Segawa, Y.; Omachi, H.; Itami, K. Theoretical Studies on the Structures and Strain Energies of Cycloparaphenylenes. Org. Lett. 2010, 12, 2262–2265. [Google Scholar] [CrossRef]
- Segawa, Y.; Yagi, A.; Ito, H.; Itami, K. A Theoretical Study on the Strain Energy of Carbon Nanobelts. Org. Lett. 2016, 18, 1430–1433. [Google Scholar] [CrossRef]
- Smith, P.J.; Liebman, J.F.; Hopf, H.; Starý, I.; Stará, I.G.; Halton, B. Strained Aromatic Molecules. In Strained Hydrocarbons; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2009; pp. 147–204. [Google Scholar]
- Zade, S.S.; Zamoshchik, N.; Reddy, A.R.; Fridman-Marueli, G.; Sheberla, D.; Bendikov, M. Products and mechanism of acene dimerization. A computational study. J. Am. Chem. Soc. 2011, 133, 10803–10816. [Google Scholar] [CrossRef]
- Battaglia, S.; Faginas-Lago, N.; Andrae, D.; Evangelisti, S.; Leininger, T. Increasing Radical Character of Large [n]cyclacenes Unveiled by Wave Function Theory. J. Phys. Chem. A 2017, 121, 3746–3756. [Google Scholar] [CrossRef]
- Pérez-Guardiola, A.; Sandoval-Salinas, M.E.; Casanova, D.; San-Fabián, E.; Pérez-Jiménez, A.J.; Sancho-García, J.C. The role of topology in organic molecules: Origin and comparison of the radical character in linear and cyclic oligoacenes and related oligomers. Phys. Chem. Chem. Phys. 2018, 20, 7112–7124. [Google Scholar] [CrossRef] [PubMed]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Challenges for Density Functional Theory. Chem. Rev. 2012, 112, 289–320. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Chai, J.-D. Role of exact exchange in thermally-assisted-occupation density functional theory: A proposal of new hybrid schemes. J. Chem. Phys. 2017, 146. [Google Scholar] [CrossRef]
- Chen, B.-J.; Chai, J.-D. TAO-DFT fictitious temperature made simple. RSC Adv. 2022, 12, 12193–12210. [Google Scholar] [CrossRef]
- Koch, W.; Holthausen, M.C. A Chemist’s Guide to Density Functional Theory; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Parr, R.G. Density functional theory. Annu. Rev. Phys. Chem. 1983, 34, 631–656. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Grimme, S. Density functional theory with London dispersion corrections. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Hratchian, H.P.; Schlegel, H.B. Accurate reaction paths using a Hessian based predictor–corrector integrator. J. Chem. Phys. 2004, 120, 9918–9924. [Google Scholar] [CrossRef]
- Hratchian, H.; Schlegel, H. Using Hessian updating to increase the efficiency of a Hessian based predictor-corrector reaction path following method. J. Chem. Theory Comput. 2005, 1, 61–69. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C. 01, 2016; Gaussian Inc.: Wallingford, CT, USA, 2016; Volume 1, p. 572. [Google Scholar]
- Epifanovsky, E.; Gilbert, A.T.; Feng, X.; Lee, J.; Mao, Y.; Mardirossian, N.; Pokhilko, P.; White, A.F.; Coons, M.P.; Dempwolff, A.L. Software for the frontiers of quantum chemistry: An overview of developments in the Q-Chem 5 package. J. Chem. Phys. 2021, 155, 084801. [Google Scholar]
- Grimme, S.; Hansen, A. A Practicable Real-Space Measure and Visualization of Static Electron-Correlation Effects. Angew. Chem. Int. Ed. 2015, 54, 12308–12313. [Google Scholar] [CrossRef]
- Bauer, C.A.; Hansen, A.; Grimme, S. The Fractional Occupation Number Weighted Density as a Versatile Analysis Tool for Molecules with a Complicated Electronic Structure. Chem. Eur. J. 2017, 23, 6150–6164. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta--Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Xu, H.-L.; Su, Z.-M. NICS values scan in three-dimensional space of the hoop-shaped π-conjugated molecules [6]8cyclacene and [16]trannulene. New J. Chem. 2018, 42, 1987–1994. [Google Scholar] [CrossRef]
- Zamoshchik, N.; Zade, S.S.; Bendikov, M. Formation of Acene-Based Polymers: Mechanistic Computational Study. J. Org. Chem. 2013, 78, 10058–10068. [Google Scholar] [CrossRef]
- Einholz, R.; Fang, T.; Berger, R.; Grüninger, P.; Fruh, A.; Chasse, T.; Fink, R.F.; Bettinger, H.F. Heptacene: Characterization in solution, in the solid state, and in films. J. Am. Chem. Soc. 2017, 139, 4435–4442. [Google Scholar] [CrossRef] [PubMed]
- Jančařík, A.; Holec, J.; Nagata, Y.; Šámal, M.; Gourdon, A. Preparative-scale synthesis of nonacene. Nat. Commun. 2022, 13, 223. [Google Scholar] [CrossRef]
- Wagner, M.S.; Peisert, H.; Chassé, T.; Bettinger, H.F. Detection of diheptacendiyl diradical intermediate in the cycloreversion of diheptacene to heptacene. Chem. Commun. 2024, 60, 8451–8453. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Somani, A.; Gupta, D.; Bettinger, H.F. Remarkably Efficient [4+4] Dimerization of [n]-Cyclacenes. Chemistry 2025, 7, 62. https://doi.org/10.3390/chemistry7020062
Somani A, Gupta D, Bettinger HF. Remarkably Efficient [4+4] Dimerization of [n]-Cyclacenes. Chemistry. 2025; 7(2):62. https://doi.org/10.3390/chemistry7020062
Chicago/Turabian StyleSomani, Ankit, Divanshu Gupta, and Holger F. Bettinger. 2025. "Remarkably Efficient [4+4] Dimerization of [n]-Cyclacenes" Chemistry 7, no. 2: 62. https://doi.org/10.3390/chemistry7020062
APA StyleSomani, A., Gupta, D., & Bettinger, H. F. (2025). Remarkably Efficient [4+4] Dimerization of [n]-Cyclacenes. Chemistry, 7(2), 62. https://doi.org/10.3390/chemistry7020062







