Abstract
The structure, bonding, and properties of diradicals, triradicals, and polyradicals have been investigated using broken symmetry (BS) molecular orbital (MO) and BS density functional theory (DFT) methods, which are regarded as the first steps in the mean-field approach toward strongly correlated electron systems (SCES). The natural orbital (NO) analyses of the BS MO and BS DFT solutions were performed to elucidate the natural orbitals of their occupation numbers, which are used for derivations of the diradical character (y) and several chemical indices for the open-shell molecules under investigation. These chemical indices are also obtained using SCES, the next theoretical step, which uses symmetry-recovered resonating BS (RBS) and multi-determinant methods such as multi-reference (MR) configuration interaction (CI) and MR-coupled cluster (CC) methods that employ the NOs generated in the first step. The nonlinear optical response properties of organic open-shell species were theoretically investigated with several procedures, such as MR CI (CC), the numerical Liouville, and Monte Carlo wavefunction methods, as the third step to SCES. The second-order hyperpolarizability (γ) of diradicals such as a phenalenyl radical dimer were mainly investigated in relation to the generation of quantum squeezed lights, which are used for the construction of the quantum entangled states for quantum optical devices such as quantum sensing and quantum computation. Basic quantum mechanical concepts, such as the Pegg–Barnett quantum phase operator, were also revisited in relation to the design and chemical synthesis of stable diradicals and polyradicals such as optical quantum molecular materials and future molecular qubits materials.
1. Introduction
One hundred years have passed since the establishment of quantum mechanics (QM) [1,2,3,4,5,6,7,8,9,10,11,12,13] between 1924 and 1927. Quantum mechanics provides fundamental equations to solve chemical problems at the atomic and electron levels in whole fields of chemistry. Indeed, quantum chemistry based on quantum mechanics has been developed to provide fundamental principles, basic concepts, and computational methods to gain an understanding and explanation of the nature of the chemical bonds of molecules [14,15,16,17,18,19]. In the 1980s, new quantum physics emerged due to experimental discoveries of quantum Hall effects [20,21,22], high-Tc superconductivity [23], etc., on strongly correlated electron systems (SCES). Open-shell systems, such as diradicals and polyradicals, have also been accepted as examples of SCES in chemistry, opening a new field of molecular magnetism. In 2004, a quantum chemistry group at Osaka University published a monograph entitled “Introduction to Quantum Chemistry of Mesoscopic Molecular Systems (in Japanese; Bussei Ryoshi-kagaku Nyumon)” [24], consisting of fourteen chapters that introduce interesting subjects regarding SCES investigations. The key common concepts in the book are strong electron correlation, spin, photon, Bose condensation, quantum phase, and quantum computation. The latter two concepts in quantum information science [25,26,27,28] were a favorite theme of Prof. Masayoshi Nakano. The book’s last chapter, Chapter 14 [24], highlights future prospects relating to (i) bio-molecular spin, (ii) organic photo devices, (iii) quantum computation, (iv) the quantum brain, and (v) quantum chaos. Nowadays, quantum computation [27,28] is an interesting topic in the field of chemical and material sciences.
In this memorial issue attributed to Prof. Masayoshi Nakano at Osaka University, the basic concepts, theoretical methods, and computational procedures developed for open-shell molecules and clusters [29] are revisited in relation to his varied and distinguished work on quantum chemistry for molecular optical materials. He was born in Osaka in 1966 and graduated from Osaka University in 1991 with a PhD in quantum chemistry and chemical engineering. After his post-doctoral studies in the group of Prof. Nasu, focusing on theoretical optics at the Institute for Molecular Science (IMS), Okazaki, Japan, he joined our quantum chemistry group at Osaka University in 1992. In 2005, he was promoted to Full Professor at the Department of Material Engineering Science, Osaka University, performing theoretical investigations of nonlinear optical responses and quantum optics on open-shell molecules such as diradicals, which are under discussion in this issue. However, in 2022, Prof. Masayoshi Nakano suddenly passed away, only partially completing his goals for quantum optical sciences and engineering.
During his high school years (in 1981), Prof. Kenichi Fukui [30], at Kyoto University, won the Nobel Prize in Chemistry for his great contribution to chemical reactions, and particularly, concerted reactions. During his undergraduate course at Osaka University, young Nakano had a great interest in quantum physics and chemistry. Historically, the concepts of orbital symmetry conservation by Woodward and Hoffmann [31,32] and frontier orbital theory [33] by Fukui were the guiding principles for the theoretical investigations of chemical reactions in the late 1960s and early 1970s. The orbital correlation diagrams by Longuet–Higgins [34] and the concept of aromaticity by Dewar [35] were also guiding principles for the greater understanding of concerted reactions. These theoretical models that were used for derivations of the selection rules are applicable to molecules with closed-shell orbitals, indicating a weak electron correlation with the field of modern theoretical science. Therefore, in the 1970s, Prof. Nakano’s interest steered toward open-shell molecules for theoretical investigations in SCES.
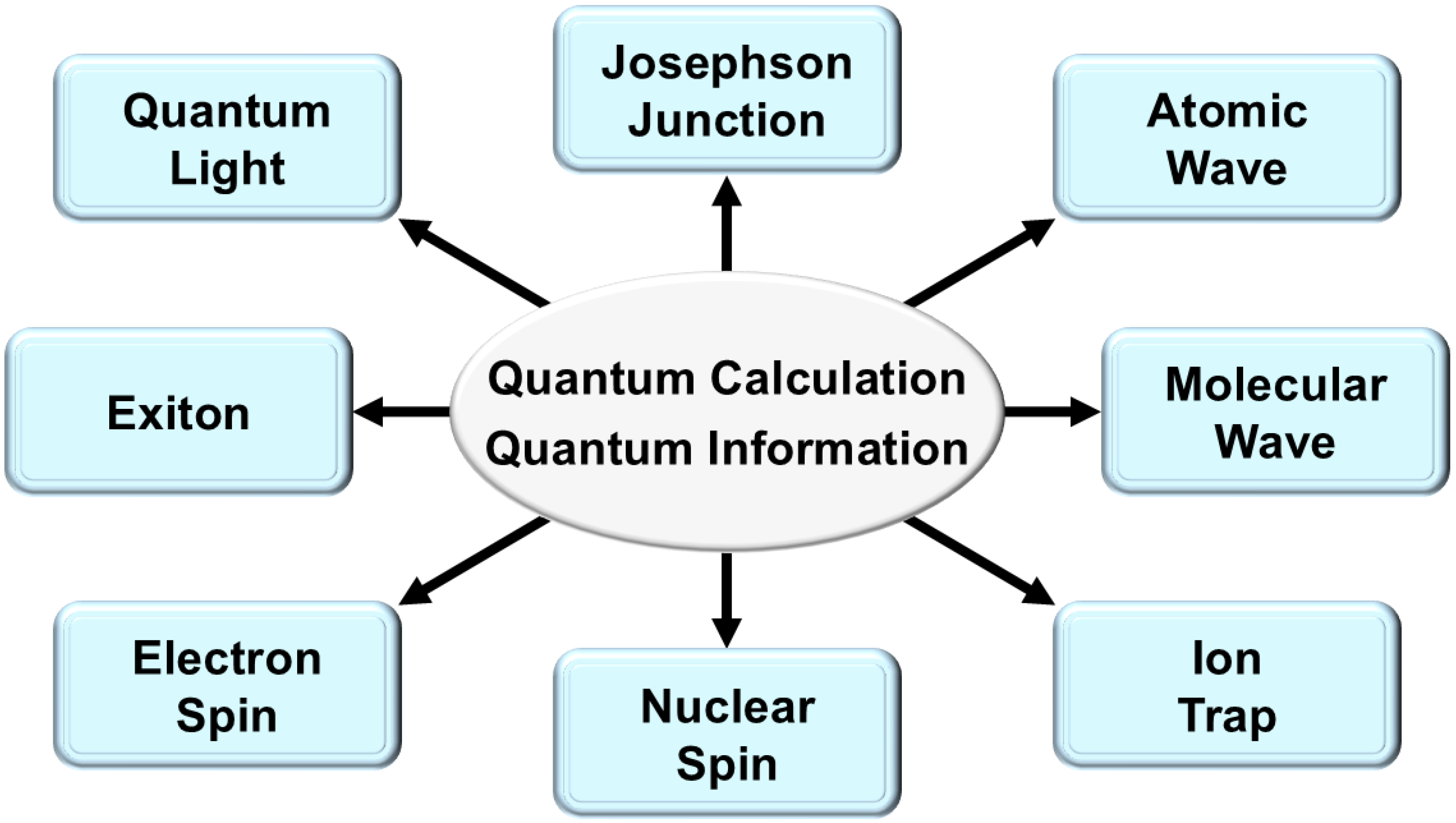
In the 1970s, Prof. Nagamiya, Prof. Kanamori, and Prof. Yoshimori developed the theory of magnetism in the Department of Solid-State Physics at Osaka University, providing a theoretical foundation and influence for quantum chemical approaches to open-shell systems, which were different from those of the Fukui school at Kyoto University. The Kanamori–Goodenough rule [36,37] for super-exchange interactions between spins in open-shell systems is now well known, even among experimental chemists. The theoretical chemistry group at Osaka University was also interested in another direction of quantum chemistry from the Kyoto school [30], namely the theoretical study of structure, bonding, and properties of open-shell molecules, such as homolytic diradicals and electron-transfer diradicals, at that time. Since then, we have been performing theoretical investigations on open-shell molecules, which are now regarded as SCES, in general. Interestingly, the quantum theory of SCES is now closely related to the theory of quantum information (QI) [25,26,38] and quantum biology (QB) [39], as illustrated in Figure 1. In 2019, Osaka University opened a new center of QIQB at the Toyonaka Campus for research and education of the young generation.
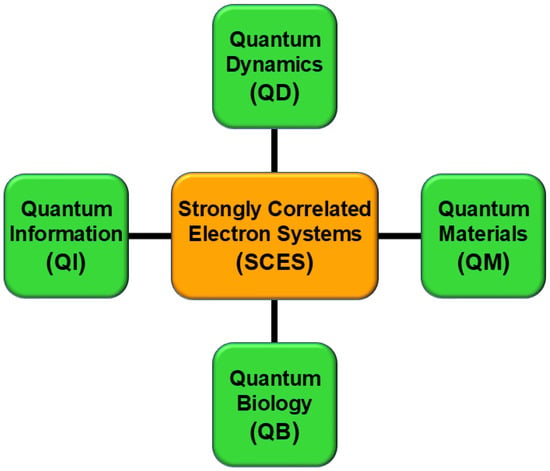
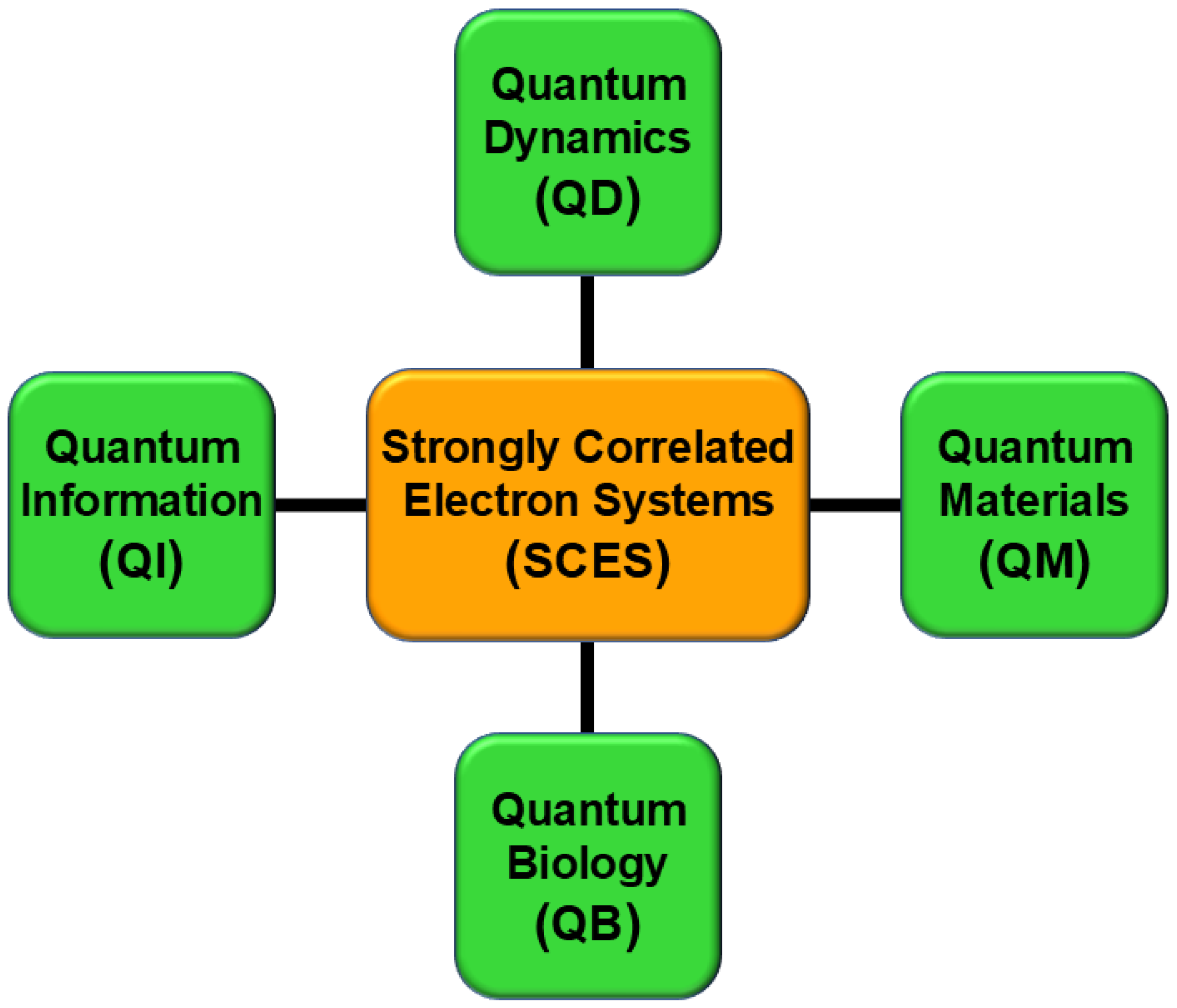
Figure 1.
Strongly correlated electrons (SCES) such as the di-, tri-, and polyradicals. These have been attractive target molecules for quantum materials (QM), quantum information (QI), quantum dynamics (QD), and quantum biology (QB) [24].
Over the past five decades, theoretical interests in our quantum chemistry group have been classified into (i) theory-oriented (TO) quantum chemistry (QC), (ii) reaction-oriented (RO) QC, (iii) material-oriented (MO) QC, and (iv) biology-oriented (BO) QC. Therefore, first of all, historical developments of the computational methods in TO QC for SCES [40] are briefly summarized in Section 2, Section 3 and Section 4. Early applications of these to radical reactions of active oxygen and oxy-radicals via the RO QC approach have already been summarized in several review articles [41,42,43]. Molecular magnetism and spin-mediated superconductivity [24,44,45] are our interest in MO QC. The broken symmetry (BS) and post-BS methods, developed in the 1980s [40], have been used as convenient and practical theoretical procedures to investigate metalloenzymes such as P450 for mono-oxygenations [41] and CaMn4O5 cluster catalysts for water oxidation, namely in the field of BO QC [46,47].
Prof. Nakano and his research groups have been mainly interested in TO QC and MO QC, performing a number of theoretical investigations in these fields. He and his collaborators have investigated the nature of chemical bonds of open-shell systems, such as diradicals, in relation to quantum optics and optical devices, as summarized in Section 5, Section 6 and Section 7 [48,49,50,51,52,53,54,55,56,57,58,59]. In the 1980s, he was interested in the second- and third-order nonlinear response properties of molecular materials [60,61], which are indispensable for the generation of squeezed states of quantum light [57,58,59] with squeezed and anti-squeezed components, namely broken symmetry but in a coherent (minimum uncertainty) state. The squeezed lights have been used to generate the so-called entangled state of light for several quantum devices [62,63,64,65]. For example, the entangled state is now essential for the construction of new optical computers based on a loop-based approach [65]. He has also investigated the interaction between quantum light and molecular material [66,67]. He also had an interest in the fundamental problems of quantum mechanics and the Pegg–Barnett phase operator [68,69,70,71] in relation to a well-defined Hermitian phase operator in quantum mechanics and collapse-revival phenomena [72] in the Jaynes–Cummings model [73]. In this review, the philosophical background and basic interest in quantum optics of Prof. Nakano are briefly revisited in relation to the theoretical modeling and design of quantum materials such as diradicals and polyradicals for qubits of quantum devices [52,62,65].
2. Symmetry Breaking and Its Recovery via Quantum Resonance
2.1. Cultural Background and Symmetry Breaking in Japan
First of all, we would like to touch on the cultural background of our review article in this special issue for Prof. Nakano. In the 1960s, a new faculty of Engineering Science was opened at Osaka University for investigations and developments of future materials in Science and Engineering. In the early 1970s, Prof. Tsubomura, in the Chemistry Department of our Faculty of Engineering Science, was a founder of the Institute of Artificial Photosynthesis (1981) located near the faculty, and kindly recommended that we read the essay of Prof. San-ichiro Mizushima entitled “A History of Physical Chemistry in Japan” [74]. Prof. Mizushima had been a great leader in the field of physical chemistry in Japan. Prof. Mizushima initiated his essay [74] by pointing out that it is fairly difficult to explain the Japanese mentality appropriately for English-speaking people.
According to his essay, “In Japan, the traditional method of introducing new culture has not been substitution, but putting things side by side, i.e., instead of wiping out the old and putting a new thing in its place, we have preserved what was already there. One of the reasons is a long history of Japanese culture developed in the nature of the island surrounded by sea”. Prof. Mizushima has deeply considered the beauty of our Japanese culture and symmetry breaking: the subtle symmetry breaking in flower arrangements, symmetry breaking in Japanese gardens, etc. [74]. Our introduction of quantum mechanics into chemistry [40,41,42,43] is in accordance with a traditional way of thinking. From such a perspective, we may imagine the similarity of a flower arrangement to the unsymmetrical structure of a water oxidation site of photosystem II (PSII) for subtle biological function, as illustrated in Figure 2. According to the essay by Prof. Mizushima [74], such philosophical backgrounds come partly from our natural environment. Therefore, our mind is open to the philosophy written in the essay by Prof. P. W. Anderson [75] entitled “More is Different: Broken Symmetry and the Nature of the Hierarchical Structure of Science”. Anderson’s essay in 1972 provided a cultural influence on our theoretical investigation of “diradical” molecular magnetism [40,45] and magneto-optics [60,61].
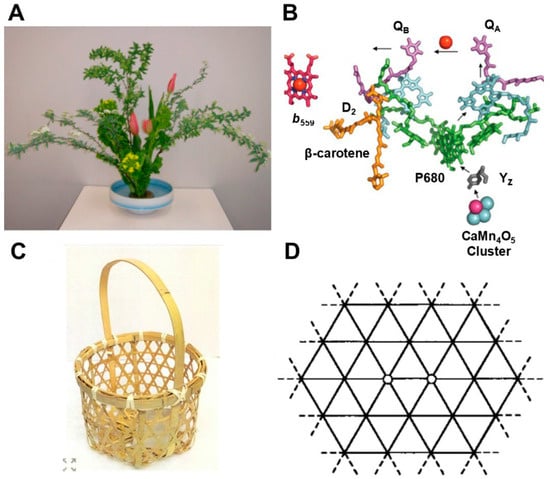
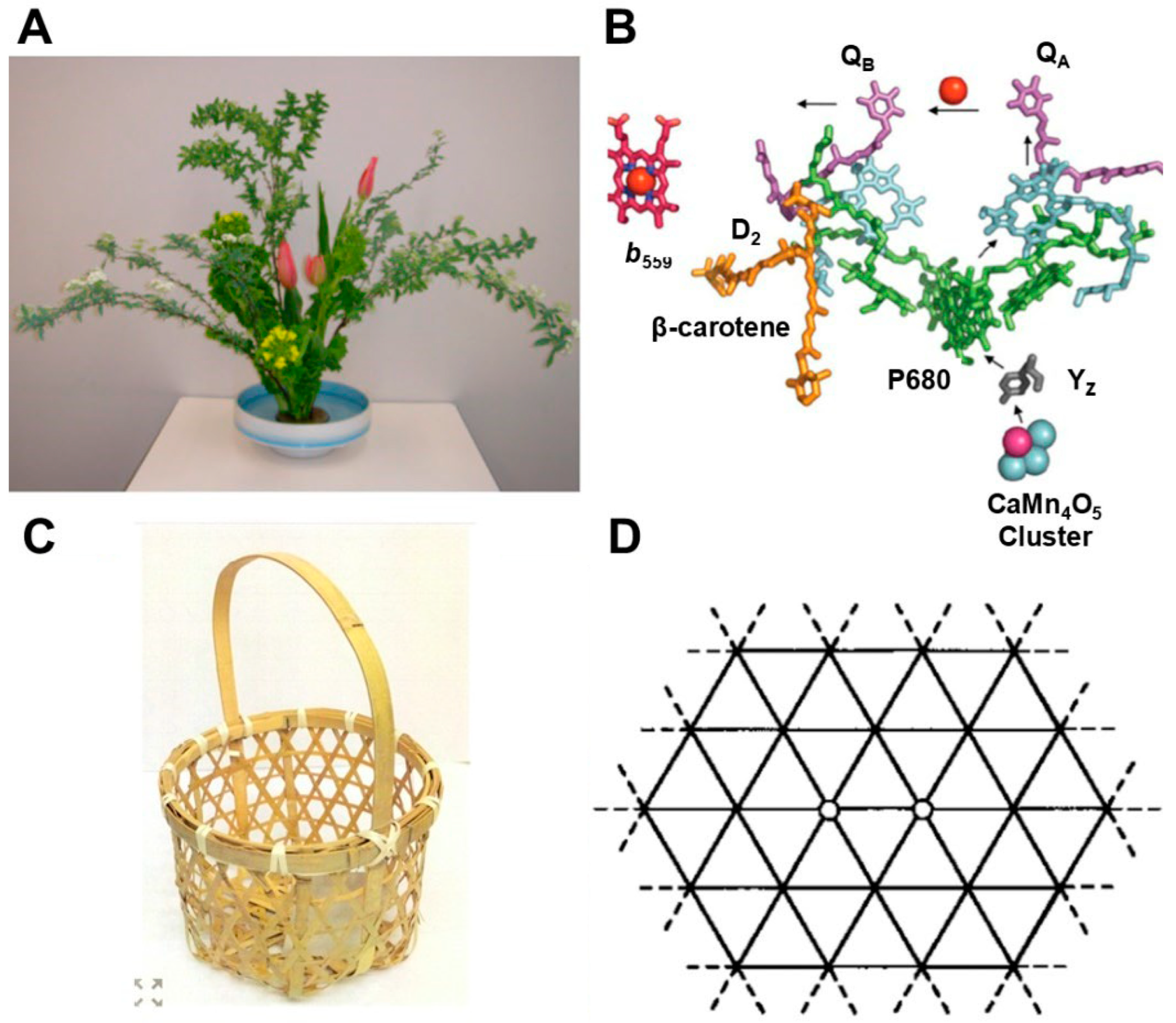
Figure 2.
(A) Subtle symmetry breaking of flower arrangements in Japan and (B) an unsymmetrical geometric structure of the water oxidation system in photosystem II (PSII), indicating the common symmetry breaking [24], (C) Japanese Kagome basket, and (D) Triangular lattice.
Our theoretical group can also remember the great influence of the concept of “spontaneous symmetry breaking” [76,77], discovered by Prof. Nambu, who was a Japanese American at the house of his family in Toyonaka City in Japan. Nambu’s philosophy [76,77] has helped us to understand why the chemical world is so complex, even though the basic quantum laws [78] that govern it are simple. Thus, the concept of symmetry breaking is common in several fields of science [75,76,77,78,79,80,81,82,83,84]. This review is really related to the explanation of the concept of orbital symmetry breaking in an independent particle model with a single Slater determinant and its recovery via quantum resonance and multi-determinant models for diradicals and polyradicals [24,40].
In 1980, Klitzing et al. [20] experimentally discovered the quantum Hall effect for two-dimensional electronic systems. Thouless et al. [22] have investigated this effect on the theoretical ground, discovering the topological quantum number for the understanding and explanation of the quantum Hall effect. Since then, topology has also been one of the fundamental concepts in physics. Kosterlitz–Thouless theory for two-dimensional (XY model) systems [85,86] and Haldane conjecture for one-dimensional systems [87,88], as well as the Berry phase [89,90], have been presented in solid-state physics, indicating the concept of topological symmetry for an understanding of these discoveries.
In quantum chemistry, the resonating valence bond (RVB) model [16,17] was proposed to describe the quantum resonance of the VB structures of molecules. Therefore, in an analogy of RVB, the resonating BS (RBS) model has resulted because of the quantum effect in diradicals and polyradicals. The RBS concept has also been applied to explain the quantum spin frustrations in triangle lattices. The Japanese can easily imagine the old Kagome basket in Figure 2C and the triangular lattice in the spin-frustration system in Figure 2D for topological beauty. Thus, the concept of topology is also a guiding principle in quantum chemistry.
2.2. Equivalence Transformation in Material Sciences
Equivalence transformations have been used for understanding similarity, as shown in Figure 2. They have been investigated in relation to the emergence and derivations of new ideas for problems under investigation from well-known ideas in other fields [91,92,93,94]. In Japan, Prof. Ichikawa presented equivalence transformation thinking for a creative purpose [91]. Prof. Hoffmann presented a well-known paper entitled “Building Bridges Between Inorganic and Organic Chemistry (Nobel Lecture)” [95], showing the isolobal concept for equivalence transformation between organic and inorganic chemical bonding on the basis of the molecular orbital (MO) model. On the other hand, we have presented the isolobal and isospin analogies between open-shell organic molecules and inorganic molecules on the basis of broken symmetry orbitals with both orbital and spin degrees of freedom [96]. Thus, the concept of equivalence transformation is effective for creative purposes.
As mentioned above, the concept of broken symmetry has emerged in solid-state physics [75], nuclear physics [79], elementary particle physics [80,81], and molecular physics [82,83,84]. A quantum squeezed state in this review also exhibits unsymmetrical quantum fluctuations (symmetry breaking) (see Figure 3 later). On the other hand, the concept of topology [22,87] provides an analogy between quantum spins in several lattices.
Here, we briefly revisit the fundamental concepts illustrated in Figure 1 as an example of equivalence transformation. The general quantum state of the quantum bit (qubit) for quantum information science in Figure 1 can be represented as a linear superposition of two orthonormal basis states (or basis vectors) [38,52,53]. These vectors are usually expressed with the ket notation of Dirac [78] as and , respectively. A pure qubit state is a coherent superposition of the basis sets, providing the following expression:
where α and β are the probability amplitudes [38], and they are constrained as
Two vectors in Equation (1) are realized with several physical units in Figure 1. For example, two units (levels) for electrons can be taken as the up- and down-spins. The levels for photons are the left-handed and right-handed circular polarizations, and they are measured as the horizontal (H) and vertical (V) linear polarizations [38,52]. Therefore, equivalence transformations are feasible for qubits under the same mathematical equation, depending on the materials employed in Figure 1.
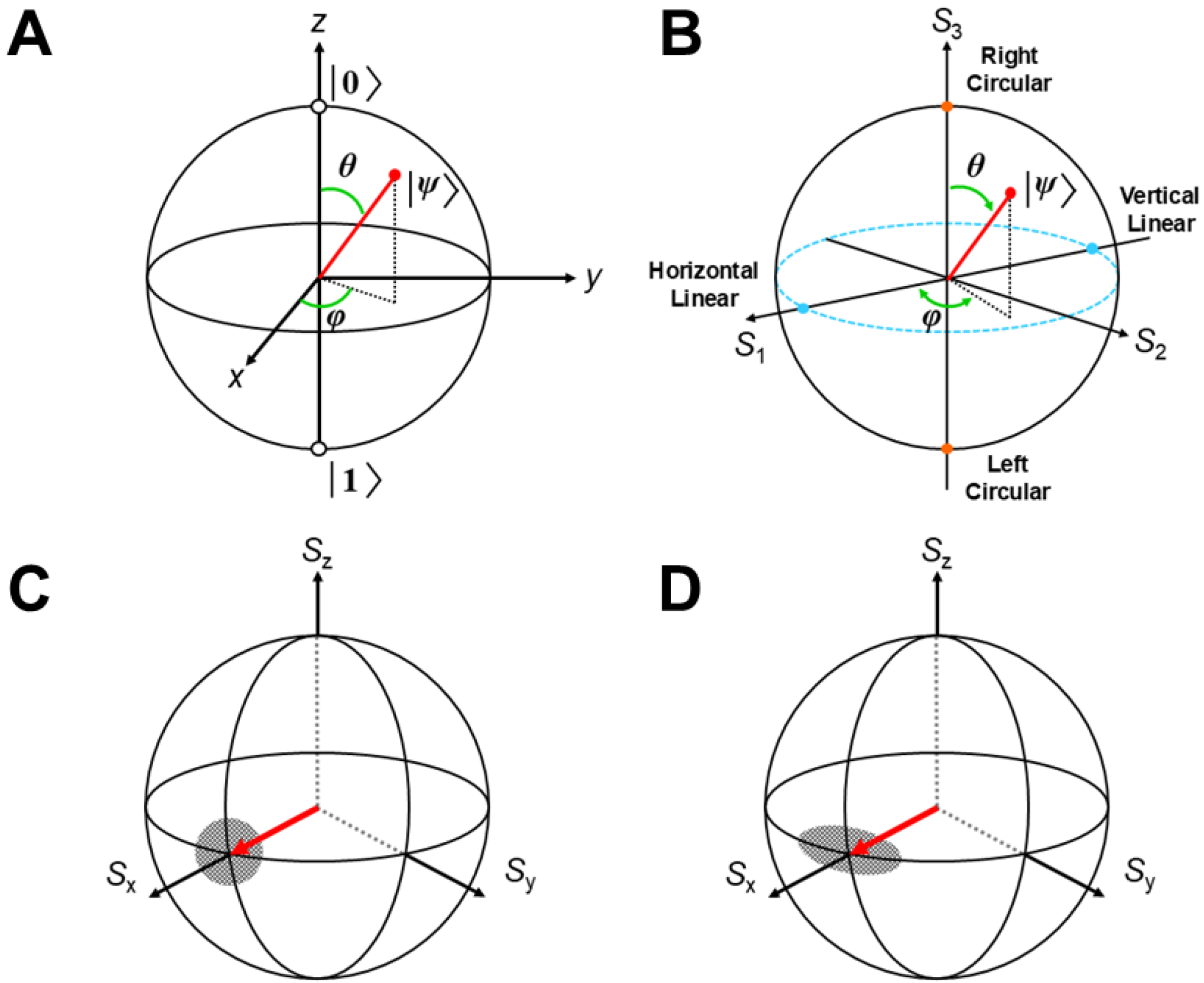
The possible quantum states for a single spin qubit can be visualized using a Bloch sphere, as illustrated in Figure 3A [52]. A classical bit for digital computers is only at the North Pole or South Pole for or . On the other hand, a pure qubit state can be represented with any point on the surface. For example, the pure qubit state lies on the equator of the sphere at the positive X-axis. The α and β for any qubit are expressed by the two degrees of freedom in the Bloch sphere [38,52,53]
where is the physically significant relative phase [38,68,69,70,71,72,73].
The and points in the Bloch sphere correspond to the right-circular (S3 = 1) and left-circular points (S3 = −1) in the Poincaré sphere for light, respectively, as shown in Figure 3B [38,52,53]. The horizontal linear (S1 = 1) and vertical linear (S1 = −1) correspond to the points on the equator of the sphere at the X-axis, respectively. A pure qubit state for quantum light is expressed with any point on the Poincaré (Bloch) square, indicating the concept of equivalence transformation between the quantum spin state and the quantum light state. Any quantum state of the qubit, constituted of quantum materials such as the Josephson junction of superconductors [97,98], is expressed by the same sphere. Therefore, we have been interested in the structure, bonding, and properties of molecular materials relating to spin, photons, and superconductivity [23,99,100] in a unified manner [24,98]. Anderson has presented a “pseudo spin” model for superconductivity [99]. Prof. Nakano and his collaborators have mainly been interested in the photon modes among the three directions in material science and engineering. They have investigated the second hyperpolarizability (γ) of molecular materials, which is related to the generation of the coherent state of light and squeezed light [52,53,57,58,59] in Figure 1.
Schrödinger investigated the coherent state of the quantum harmonic oscillator [13]. The coherent state [13] was considered the minimum quantum fluctuation state of the uncertainty principle of Heisenberg [12]. In the 1960s, Klauder [48], Glauber [49,50], and Sudarshan [51] have reformulated the coherent state [13], providing the following relation.
where ΔX and ΔP are the quantum fluctuations of the position operator (X) and momentum operator (P).
The concept of the coherent state [52] was also extended to other fields, such as quantum computing [62]. Photon is a Bose particle with the spin S = 1, indicating the three following components: SZ = 1, 0, −1 [52]. However, a photon in the vacuum has no longitudinal (SZ = 0) component, exhibiting the transverse (SZ = 1, −1) components, which are regarded as the two-level “pseudo” spin state [52,99,100,101]. Therefore, as mentioned above, quantum light and quantum spin are under the equivalence transformation, as illustrated in Figure 3. In a previous paper [98], we also examined the “pseudo” spin models for quantum spin, quantum light, and the Cooper pair for superconductivity [98,99,100,101,102] for understanding, explaining, and designing molecular materials, as shown in Figure 1.
Kitagawa and Ueda [103] first investigated the coherent state in Figure 3C and another coherent state in Figure 3D, namely the squeezed state of spin, where the magnitude between <ΔX>2 and <ΔP>2 is not equivalent, indicating the possibility of symmetry breaking (a reduction in the quantum fluctuation of X or P). Recently, experimental works for the spin-squeezed state are in progress in relation to the development of spin quantum devices [104,105,106,107]. Similarly, the squeezed states of quantum light are also investigated by both theoretical and experimental methods in relation to the generation of the entangled state of quantum light [48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73]. As is well known, Einstein–Podolsky–Rosen (EPR) [108] entangled light is the resource for a high-quality level of quantum key distribution (QKD). However, the squeezed states are sensitive to environmental conditions, indicating that quantum dynamic simulations to elucidate decoherence processes [52,53] are indispensable, as illustrated in Figure 1. Nakano et al. [70,71] have performed quantum dynamics simulations in this regard.
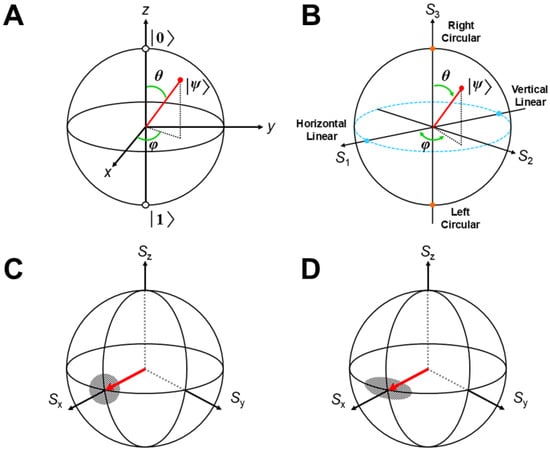
Figure 3.
(A) Schematic illustrations of a possible quantum state of spin qubit in the Bloch sphere, (B) the Poincaré sphere for quantum light and the optical qubit; (C) uncertainties of the spin components (symmetry) in the coherent state, and (D) uncertainties of the spin components (broken symmetry) in the squeezed state [98].
Figure 3.
(A) Schematic illustrations of a possible quantum state of spin qubit in the Bloch sphere, (B) the Poincaré sphere for quantum light and the optical qubit; (C) uncertainties of the spin components (symmetry) in the coherent state, and (D) uncertainties of the spin components (broken symmetry) in the squeezed state [98].
2.3. Theoretical Models for Strongly Correlated Electron Systems
In this section, fundamental concepts and basic theories for the strongly correlated electron systems (SCES) in Figure 1 are revisited briefly [24]. In the 1970s, the Hückel [109] and extended Hückel [110] methods were used for the elucidation of spatially symmetry-adapted molecular orbitals (MO). The Woodward–Hoffmann (WH) rule [31,32], based on the Hückel MO (HMO) [109] and extended Hückel MO (EHMO) [110], has been applied for the elucidation and predictions of various types of concerted reactions. HMO and EHMO were obtained by neglecting the electron repulsion to provide symmetry-adapted orbitals, which are characterized by spatial symmetry, which is expressed with the spatial symmetry group PN. Therefore, these MO models work well for derivations of the WH rules and isolobal modeling [95], providing the famous words: there are none for violation of this rule. However, these MO models are not sufficient for the MO-theoretical descriptions of symmetry-forbidden diradical reactions by the WH rule [31,32] because of the lack of orbital bifurcation to reduce the electron repulsion effect and the emergence of local spins [24,40].
In the early 1970s, we searched the appropriate MO models, including this repulsion effect, explicitly for diradicals with the singlet- and triplet-spin states, and found that Hubbard [111], Kanamori [112], and Gutzwiller [113] already proposed effective model Hamiltonians involving the electron repulsion effects () with different spins in the singlet diradical. The Hubbard Hamiltonian for di-radicals, tri-radicals, etc., was written in the second quantization notation, including electron spin σ in the quantum chemistry
where denotes the operator that creates an electron with σ = ↑, ↓ at site i, and tij is the transfer integral, and denotes the on-site repulsion integral, which is neglected in the Hückel model [109,110]. The corresponding annihilation operator is , and the is the spin-density operator for spin σ on the i-th site. These fermion operators obey the canonical anticommutation relations.
The Hubbard model [111] is closely related to the local spin-density (LSD)-type density functional theory (DFT) + model [114]. These simple models are practically useful for theoretical investigations of SCES. The transfer integrals of the on-site (tii) and nearest sites (tij) are chemically referred to as the Coulomb integral (−αii) and resonance integral (−βij) in the HMO model [109]. Therefore, the Hubbard model [111] in physics was often referred to as the Hückel–Hubbard (HH) or Hückel–Hubbard–Hund (HHH) model with the exchange integral (Kij) in our chemistry papers [24,40].
Recently, as mentioned above, quantum mechanics is closely related to quantum information science, as shown in Figure 1. For example, the fermion relations in Equation (6) are mapped into those of Pauli matrices [9,115] with Jordan–Wigner [116] and/or Bravyi–Kitaev [117] transformations for the quantum information and computations [52,53] of large radical systems using quantum bits (qubits), as touched in the final Section 7. From recent developments, we feel nostalgia for the past five decades: we analytically solved the HH models for the di-, tri, and tetra-radicals to examine the fundamental concepts and basic theories for open-shell systems under investigation in this special issue. Nowadays, we may expect to obtain exact solutions of any quantum system by such quantum devices, as touched in Section 7 [53,62].
2.4. Instability of Chemical Bonds and HOMO-LUMO Mixing for Diradicals
The Hückel–Hubbard model [24,40] may be regarded as a simplified version of the Hartree–Fock (HF) independent particle model [118,119] that provides the symmetry-adapted molecular orbitals (MO) used for the MO-modeling of concerted reactions of organic molecules. To this end, the spatial symmetries of the highest occupied MO (HOMO) and the lowest unoccupied MO (LUMO) [33] play important roles in the theoretical elucidation of the symmetry-allowed concerted reactions for which the HOMO-LUMO energy gap is sufficiently large to prevent the singlet and triplet instability for the symmetry breaking revealed by the classic papers [120,121,122,123,124,125].
On the other hand, the HOMO-LUMO energy gap (Δε) becomes small for symmetry-forbidden diradical reactions, indicating the triplet instability of the HH and HF MO solutions [126,127,128]
where the εX (X = HOMO, LUMO) denotes the orbital energy of X. The instability condition indicates that the closed-shell bond is reorganized into the more stable spin-polarized (SP) bond given by the unrestricted (U) Hubbard, Hartree–Fock (UHF), and Hartree–Fock–Slater (UHFS) [128] solutions. UHFS is a precursor for unrestricted density functional theory (DFT). The HOMO-LUMO mixing of the spin-restricted (R) HF (RHF, RHFS) solution [126,127,128] was indeed found to be effective and convenient to obtain spin-polarized (SP) molecular orbitals (MO) for 1,3-diradicals [129,130,131] at the Hubbard and UHF level of theory as follows:
where θ denotes the orbital mixing parameter determined by the UHF (UHFS) computations [126,127,128]. Since HOMO and LUMO by RHF are symmetry-adapted and usually belong to different spatial symmetries (PN), UHF MOs, and , obtained by the HOMO-LUMO mixing, are often spatially symmetry-broken, as shown in Figure 4. The “broken symmetry (BS)” orbitals respond to local electrons with up- or down-spins (↑ or ↓), which are often represented with the dot (•↑ or ↓•) for local spin in radical reactions [132].
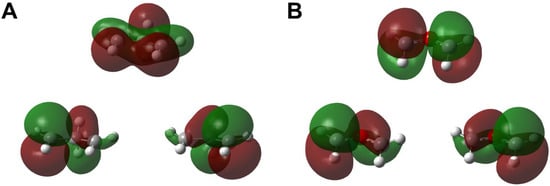
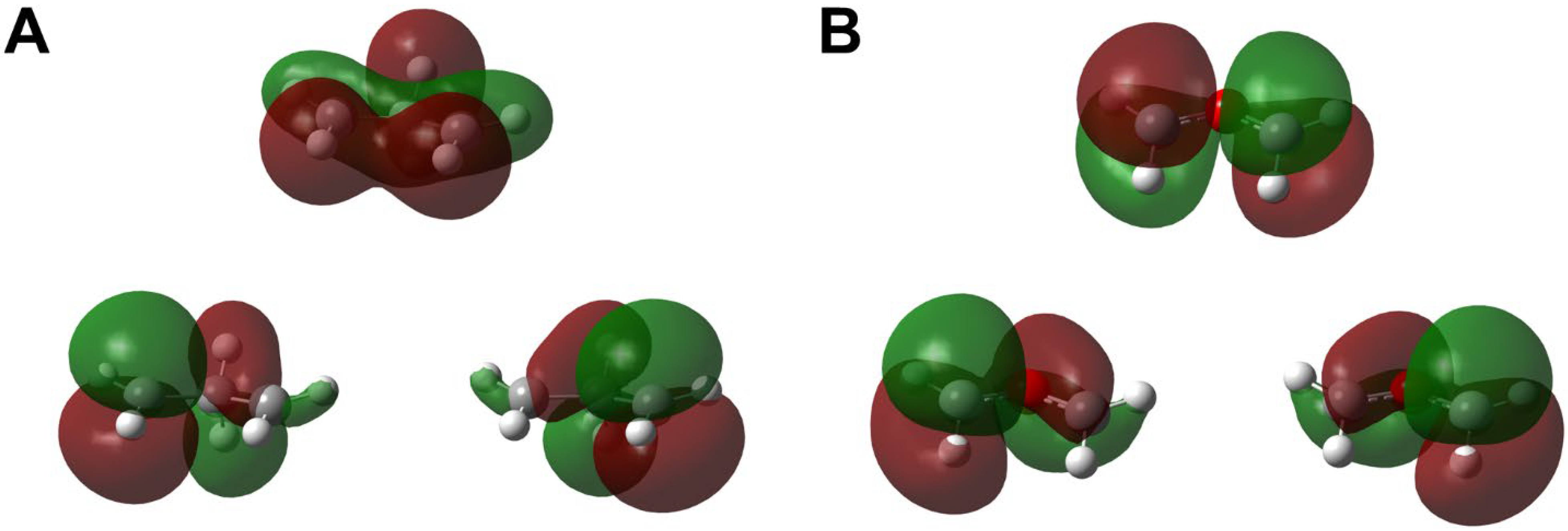
Figure 4.
Bifurcations of the molecular orbitals from the symmetric closed-shell orbitals into the right- and left-localized broken symmetry (BS) orbitals (different orbitals for different spins (DODS)) in the course of the C-C dissociation of cyclopropane (A) and oxirane (B). The σ-σ diradical orbitals of (A) are almost localized at the 1,3-radical sites, respectively. On the other hand, the σ-σ and π-π diradical orbitals of (B) exhibit small delocalization over the C-O-C skeleton, indicating a moderate orbital overlap (T) responding to a reduction in the diradical character (y) [40,132].
In the 1970s, the stereospecific ring-opening reaction was investigated in relation to a typical example of the WH rule [31,32]. As an example, the dissociation of the C-C bond of cyclopropane into the ring-opened form is examined, as shown in Figure 4 [129,130]. The C2v-symmetry-adapted closed-shell molecular orbital is obtained for cyclopropane before ring-opening, as shown in Figure 4A. However, it bifurcates into BS MOs localized mainly at the C1 and C3 sites, indicating the loss of the C2v-orbital symmetry responding to the σ-σ 1,3-diradical structure (↑•H2C-CH2-CH2•↓). The internal rotation of the terminal CH2 group is facile because of the non-exsistant C-C bond, providing π-π 1,3-diradical. Thus, the stereo-specificity of the ring-opening reaction of the three-membered rings is lost because of its strong diradical character, indicating radical reactions. The BS orbitals obtained by Equation (8) are often referred to as the different orbitals for different spins (DODS) in quantum chemistry. Introductions of polar substituents at 1,3-carbon sites have been investigated to reduce the diradical character of the ring-opened 1,3-radicals. The HOMO-LUMO energy gap for such large π-electron systems by HMO is a useful index for estimation of the diradical character because of Equations (7) and (8).
Huisgen [131] investigated the stereochemical reactions of α-cyano-cis-stilbene oxide, finding that apart from the normal symmetry-allowed conrotatory mode of ring-opening, predicted by the WH rule [32], the disrotatory process, forbidden by the WH rule [32], also appeared to occur in this reaction. The diradical character [132] was considered to remain for the ring-opened oxirane. We will revisit the Huisgen–Firestone debate on the 1,3-diradicals after a detailed examination of the computational models employed (see later).
2.5. Structure, Bonding, and Potential Energy Structure for Homolytic Diradicals
In the early 1970s, the elucidation of the scope and reliability of the BS method for mono-, di-, tri-, and tetra-radicals was an important theoretical problem. Analytical solutions for [n electrons, n orbitals] references (n = 2–4) have been obtained to elucidate the functional behaviors of the BS solutions [126,127,128]. For example, methylene (CH2) and carbene molecules (CR1R2) are typical examples of mono-centric species with a two-orbital two-electron model [2o, 2e], as shown in Figure 5. Hoffmann et al. [133] performed the EHMO calculations of the σ-type MO with two electrons (σ)2 and π-type MO with two electrons (π)2 and (σ)1(π)1 MO configurations of methylene and many carbene molecules, elucidating potential curves against the R1CR2 angle. Judging from their potential curves, the σ and π orbital energy gaps in Equation (7) are small for some methylene analogs, indicating instability [126]. For example, the energy gap between the σ-type HOMO and π-type HOMO of CH2 (Figure 5a) is small. Therefore, the HOMO-LUMO mixing in Equation (8) occurs, providing the DODS’ orbitals responding to a mono-centric singlet diradical state (Figure 5b) [126]. The relative stability between the singlet (Figure 5b and triplet (Figure 5c) diradicals was also estimated at the EHMO level of theory. On the other hand, the energy gaps between the σ-type HOMO and π-type LUMO are variable for carbene molecules CR1R2, depending on the types of substituents R1 and R2 introduced. The mixing parameters θ in Equation (8) are also variable with the energy gaps, indicating variations of diradical configuration (θ > 0) (Figure 5b) between two closed-shell limits [126]: the closed-shell σ-orbital (Figure 5d) with θ =0 and the closed-shell π-orbital (Figure 5e) with θ = 90 degrees, as shown in Figure 5.
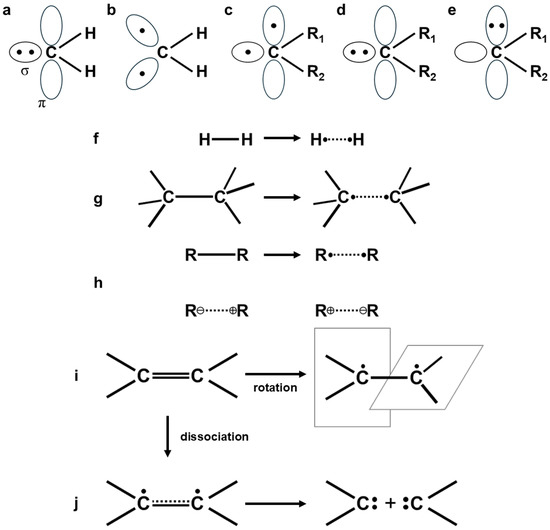
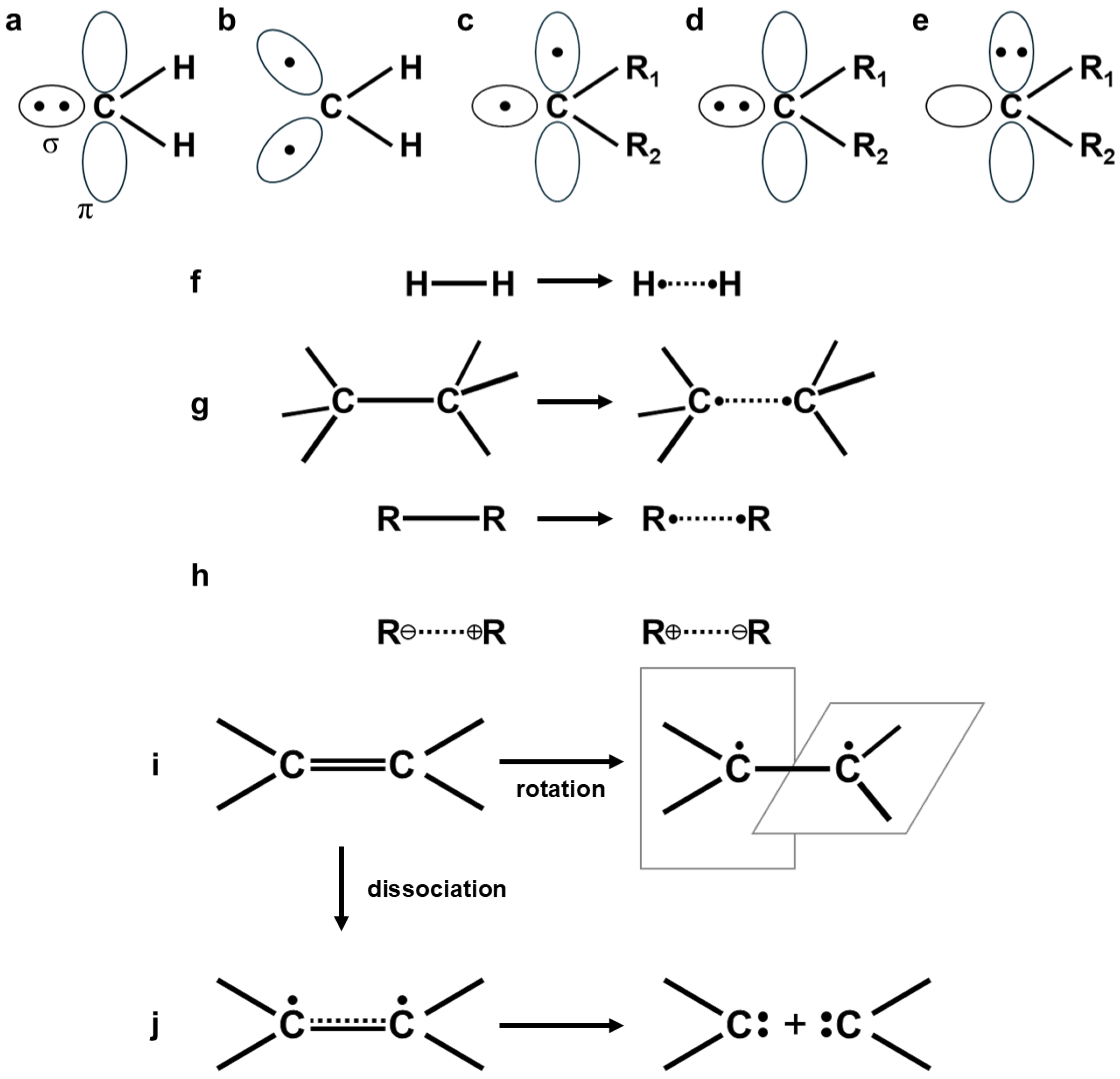
Figure 5.
Closed-shell σ-orbital of singlet methylene (a), different orbitals for different spin (DODS) orbitals of singlet (b) and triplet (c) diradical states of methylene and σ-type (d) and π-type (e) closed-shell orbitals of carbenes with R1 and R2 substituents. The radical dissociation of the covalent bonds of the hydrogen molecule (f), ethane (g), and others (h), for which ionic dissociation products are also depicted. The internal rotation of the CH2 group of the C-C double bond proves the perpendicular conformation with strong diradical character (i). The dissociation of the C=C double bond provides two triplet methylene molecules (j).
Methylene (CH2) and related small carbenes have been target molecules for the examination of the scope and reliability of ab initio computations such as small-scale CI [134,135] and two- and multi-configuration (MC) self-consistent-fields (SCFs) [136,137]. The relative stability between singlet and triplet states was found to be highly sensitive to the types of substituents (R1, R2), such as hetero atoms. On the other hand, Tomioka and his group have synthesized persistent triplet carbenes by introducing balky substituents [138,139]. Nowadays, a number of experimental results have been reported for triplet carbene (Figure 5c) and singlet carbenes (Figure 5b,d,e), as summarized in the review articles [134,135,136,137,138,139,140].
In the early 1970s, orbital bifurcations (symmetry breaking) were not familiar with the dissociation reactions of singlet covalent bonds into two doublet radicals, as illustrated in Figure 5. However, the dissociation of hydrogen molecules into two hydrogen atoms was chemically well known (Figure 5f). The dissociation of the C-C covalent bond of ethane (H3C-CH3) into two methyl radicals (2CH3) (Figure 5g) was also one of the typical processes. The situation was the same for the ring-opening of unsubstituted cyclopropane, as shown in Figure 5. The dissociation of the C-C double (triple) bond of ethylene (acetylene) into two triplet methylene (Figure 5c) (quartet C-H tri-radical) was one of the theoretically interesting processes (Figure 5j). Thus, orbital bifurcations in the dissociation reactions entailed unfamiliar spin-coupling problems at that time; for example, the singlet state consisted of the exchange coupling of two triplet (quartet) states, namely the reverse process of singlet fission [24,40].
In the 1970s, the orbital bifurcation process [40,126] of the two-center two-electron model [2e, 2o] for dissociation of the R-R covalent bond into two radicals (2R•) was first solved to understand the essential roles of electron delocalization (t) and electron repulsion () in chemical bonding. To this end, the covalent bonding parameter (x) is defined to express the magnitude of chemical bonding.
The normalized total energy of the spin-restricted HF (RHF) solution (ERHF) [24] for the closed-shell bond of the [2e, 2o] system is given by [40]
where α denotes the aforementioned Coulomb integral for the HMO model. Half of the one-center repulsion () remains at the dissociation limit (x = 0) by the RHF model, indicating instability because of the half inclusion of the closed-shell zwitterionic (ZW) structure (R−…+R or R+…−R) in Figure 5. This, in turn, indicates an important role for the introduction of polar substituents to stabilize the ZW states [119]. On the other hand, the broken symmetry (BS) UHF solution responding to the generation of radical fragments (R•…•R) (Figure 5h) emerges in the weak covalent bonding region as follows.
The orbital bifurcation point from the RHF to UHF is given by x = 1/2, where the HOMO-LUMO energy gap (2β) becomes equivalent to the on-site repulsion integral . The UHF orbital bifurcation model provides the exact dissociation limit because of no term in the mono-centric free radical at the dissociation limit.
The above theoretical modeling means, chemically, a conversion from a closed-shell bond, for example, H3C-CH3, to a homolytic singlet diradical; H3C•↑…↓•CH3 is obtained by the C-C bond dissociation [40,126]. The situation is the same for the conversion from the closed-shell HO-OH bond to the open-shell singlet HO…OH bond with the HO•↑…↓•OH diradical character [24,40,43]. Therefore, as mentioned above, the narrow HOMO-LUMO energy gap (Δε) obtained by the EHMO model [110] is also regarded as a chemical index for conversion from the non-radical to the diradical (magnetic) bond. Active oxygen and oxy-radicals with reactive local spin often undergo toxic reactions in biological systems [43].
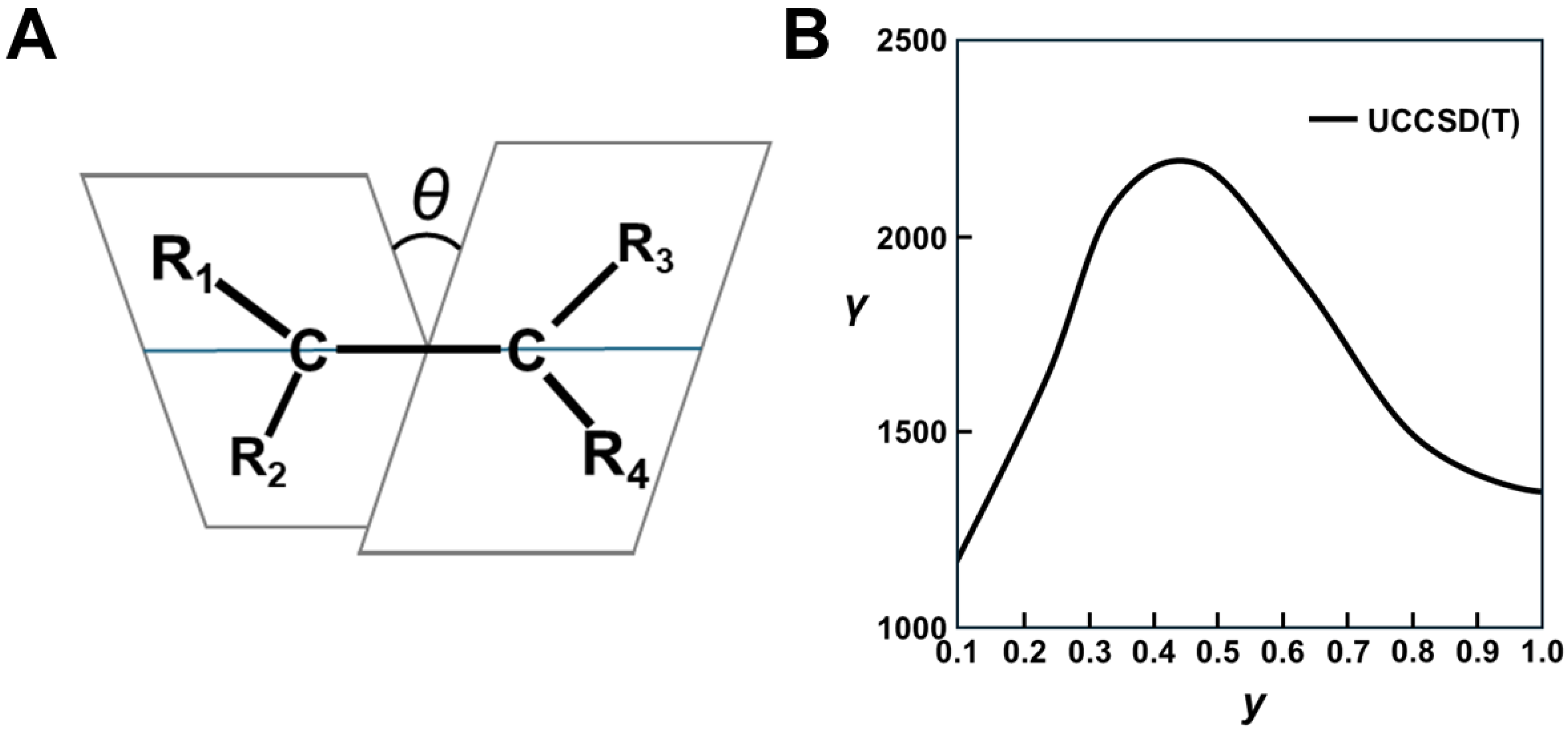
The thermal cis-trans isomerization of the C-C (C-N) double bonds has been accepted as a great interest in relation to the chemical and biological processes [141,142,143]. This process is also expressed with the above BS Hubbard model [40]. The diradical character of the C-C double bond was induced with the internal rotation of one of the CH2 groups, as shown in Figure 5h [144]. We have examined this internal rotational process for ethylene with several substituents, indicating the utility of the BS MO model and CI using the natural orbitals (DODS-NO) of the BS solution [144], where DODS-NO is often referred to as UNO [40]. On the other hand, EPR spectroscopy has been used for the experimental study of diradical species [142]. The HOMO-LUMO mixing procedure [126] was applicable to obtain the BS-UHF MOs for systems with moderate diradical character [144]. The orbital bifurcation occurs in the case of the hybrid density functional models (HUDFT) obtained by the mixing of the UHF and unrestricted DFT (UDFT) models for large organic molecules [144], although the bifurcation points are variable with the weight of the UHF component.
2.6. Resonating Broken Symmetry for Recovery of Symmetry Breaking
The orbital symmetry breaking by the HOMO-LUMO mixing in Figure 4 and Figure 5 does not imply the broken symmetry-ordered (Néel) state obtained by the true magnetic phase transition in solid-state physics. P. W. Anderson has pointed out the misunderstanding of the concept of symmetry breaking by quantum chemists in his famous book [145,146,147]. The DODS solution (UHF) I (R•↑…•↓R) in Figure 6, obtained by HOMO-LUMO mixing, degenerates in energy with the DODS solution II (R•↓…•↑R) obtained by the HOMO-LUMO mixing with a different phase (− and + mixing instead of + and − mixing in Equation (8)). The overlap between these DODS solutions is not zero, entailing the quantum resonance [146] between two diradical configurations, as illustrated in Figure 6. Indeed, the quantum mechanical resonance occurs in di-, tri-, and polyradicals [145,146,147,148,149,150,151,152], affording the resonating BS (RBS) states, which are true eigenfunctions of the total spin operator S2, namely the pure singlet and triplet states of diradicals [126,127,128]. The normalized energy for the pure singlet diradical state given by the out-of-phase mixing of two diradical configurations is given by
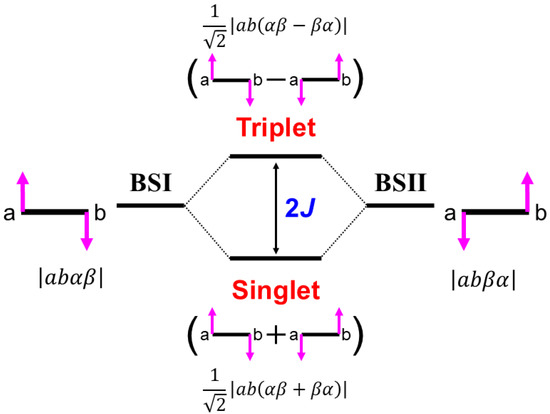
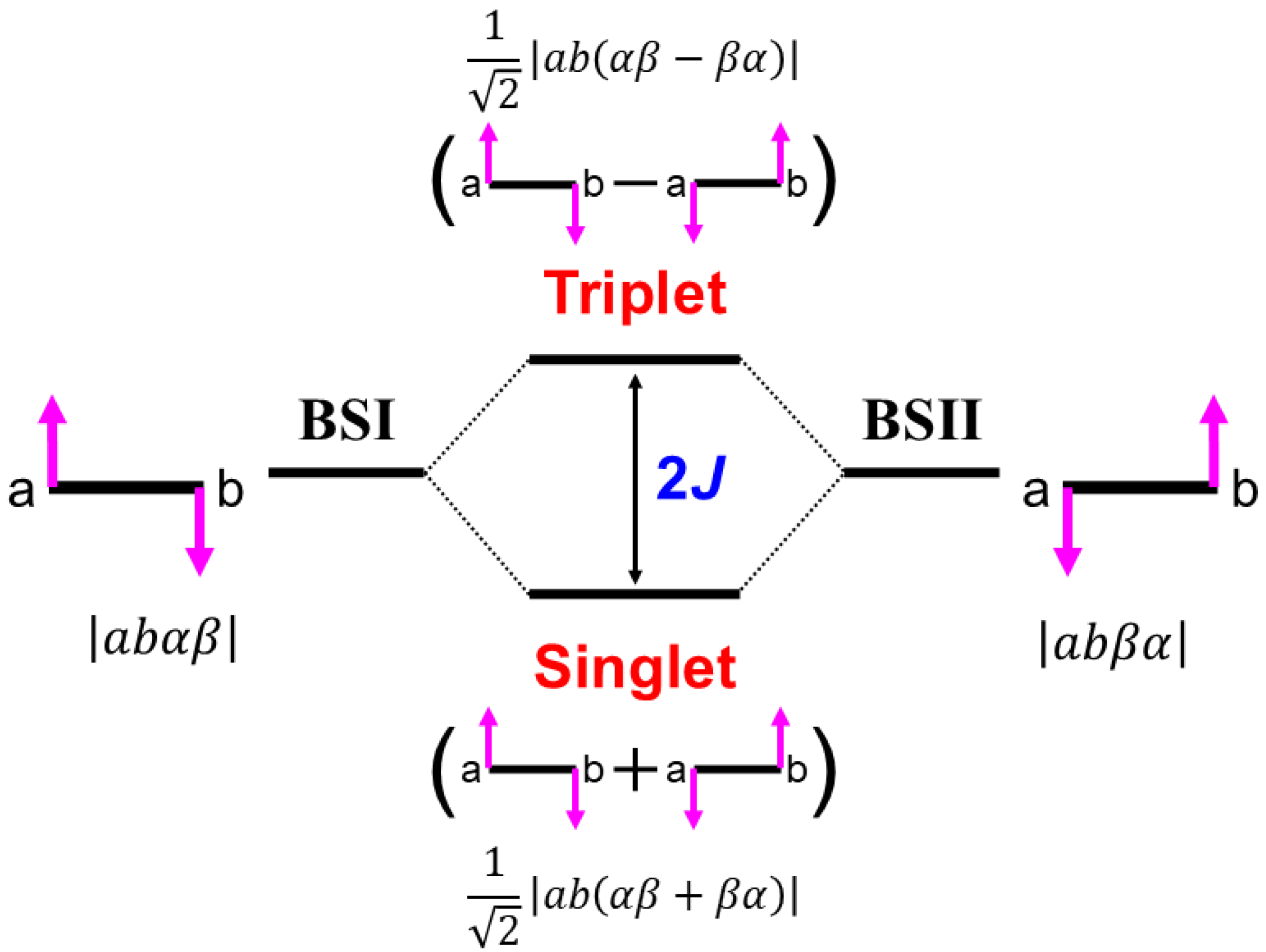
Figure 6.
Quantum resonance of the broken symmetry (BS) configurations, BS-I and BS-II, provide resonating BS (RBS) states, which are singlet and triplet-spin states of diradicals. The energy gap between them is given by 2J (chemist’s notation) in the Heisenberg model [40].
The normalized pure triplet energy obtained by the in-phase mixing of them is zero, Etriplet = 0, indicating the no bond state, as illustrated in Figure 7.
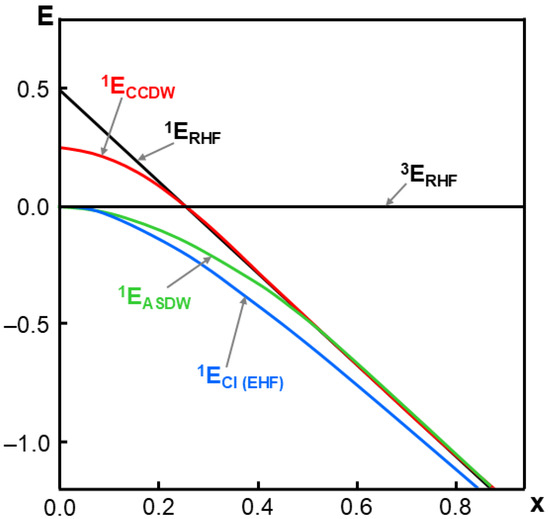
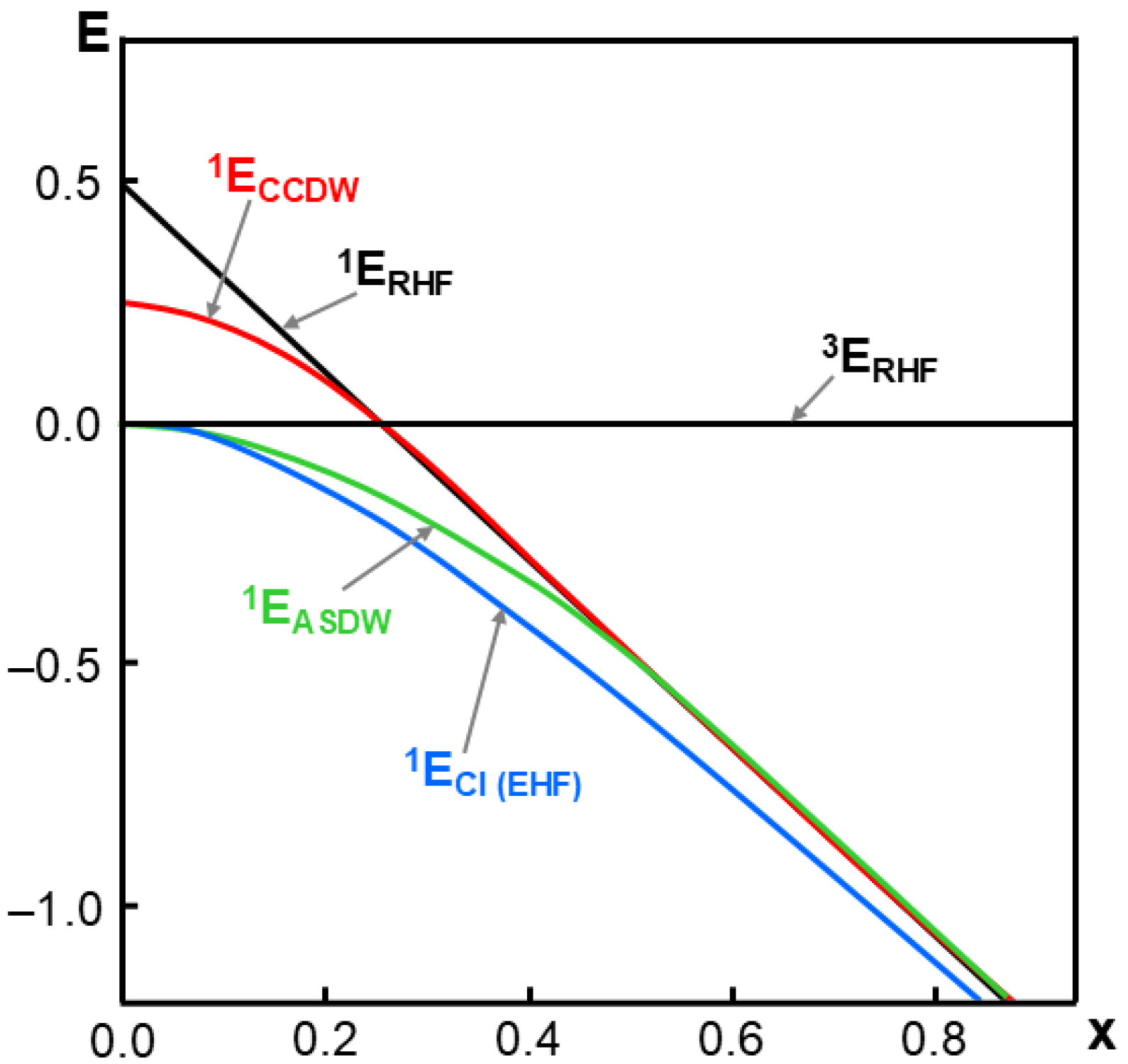
Figure 7.
The renormalized total energy curves by the RHF, UHF, EHF, and CI solutions on the basis of the Hubbard model for two-center two-electron (2e, 2o) [40,149] systems. The HOMO-LUMO mixing occurs in the region (x < 1/2). The complex charge density wave (CCDW) denotes the singlet bond-order broken solution in chemistry [123,124]. The axial-spin-density wave (ASDW) solution [84,124] is a UHF (collinear spin) solution [121,126]. The Extended Hartree–Fock (EHF) [144] provides the same energy by the CI (2e, 2o).
The configuration interaction (CI) is often used for a symmetry-adapted approach to diradicals. The 2 × 2 CI corresponds to the full CI for the [2e, 2o] model [40,126,127,128]. The normalized total energy for the singlet state is given by
Therefore, the resonating (Res) broken symmetry (RBS) energy is almost equivalent to that of the exact 2 × 2 CI in the weak bond region, namely the diradical region.
The magnitude of the BS-UHF energy in Eq. (10b) is reduced to one half of the Res-UHF (RBS) energy because of the contamination of the triplet configuration with Etriplet = 0, indicating the necessity of spin projection (SP) and approximate SP (AP) using the triplet (high-spin) energy [40]. This is the reason why we perform the SP (AP) for the broken symmetry (BS) solution by removing the energy contribution arising from the triplet contamination for quantitative purposes. Thus, the simple Hubbard model has been useful for the elucidation and understanding of characteristic behaviors of the RHF (RDFT), UHF (UHDFT), Res-UHF (UHDFT), AP-UHF (HUDFT), and CI (UNO) descriptions of the chemical bond for [2e, 2o] systems, as shown in Figure 7.
The DODS orbitals in Equation (8) correspond to the atomic orbitals (AO) localized at two sites, a and b, respectively, in the well-known VB (RVB) model, and the out-of-phase singlet spin state is often expressed by Dirac notation [78]: with Sz = 0 [40]. On the other hand, the in-phase triplet-spin state is given by with Sz = 0. Two other triplet-spin states are expressed by and . Therefore, in- and out-of-phase mixing provides the and . These four quantum resonating spin configurations are often referred to as the Bell states [153,154,155] and/or entangled states [156,157,158] in the field of quantum information [38,52,53]. The Bell states are used for derivation of Bell’s inequality [153] for examination of the Einstein–Podolsky–Rosen (EPR) paradox [108]. Aspect et al. [158] have demonstrated the breakdown of the EPR paradox [108]. The entanglement state is now an important state for quantum teleportation and quantum computation [38,52,53], as touched on in the previous Section 2.2. Recently, organic radicals, diradicals, and polyradicals have attracted great interest as quantum bits for quantum devices. However, the decoherence problem is known to be serious for such systems, indicating further investigations (see Section 7).
2.7. Chemical Indices for Diradicals by Broken Symmetry (BS) and Resonating BS (RBS) Methods
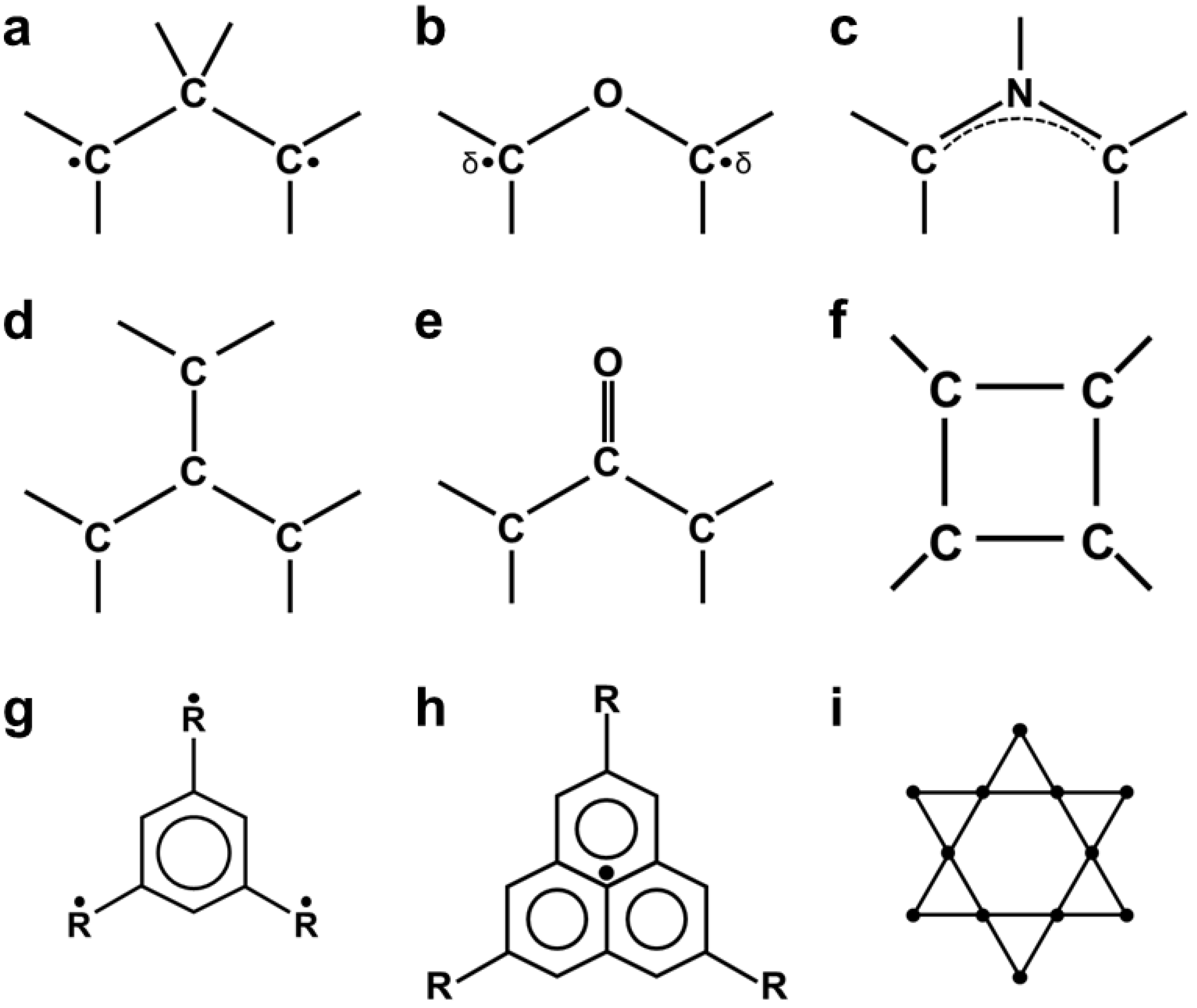
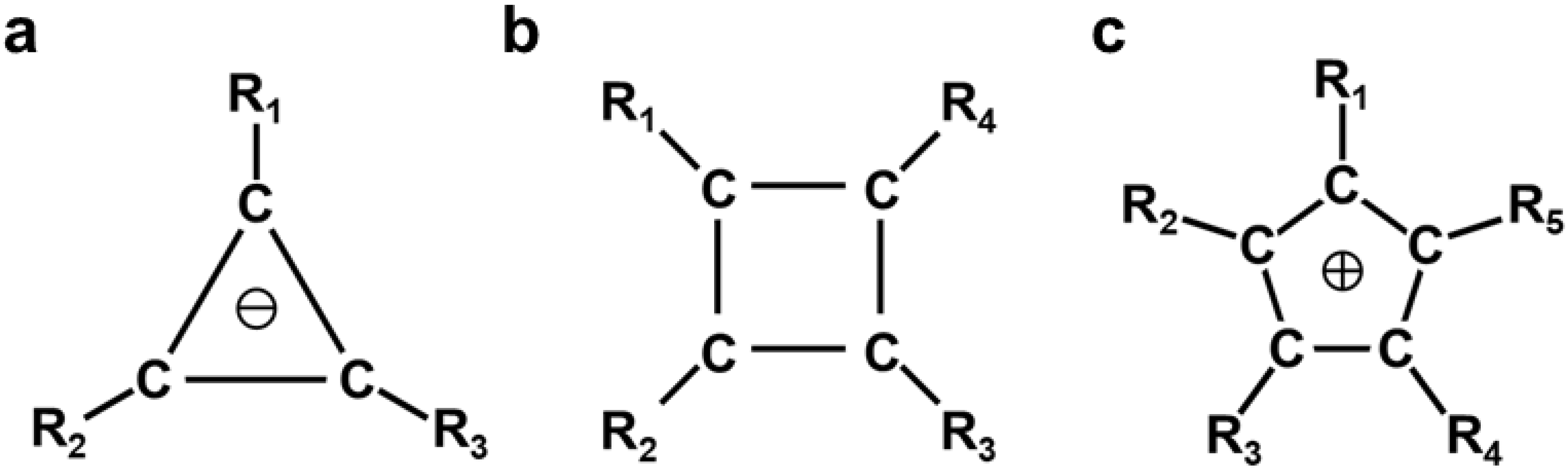
Simple VB models using atomic orbitals [146] are hardly applicable for large-scale stable organic diradicals, which are of current interest for material sciences and the development of molecular devices. In 1975, we proposed the use of BS-UHF MO methods for organic diradicals [126] such as 1,3-diradicals (Figure 8a), carbonyl ylides (Figure 8b) with intermediate diradical character, and azomethine ylides (Figure 8c) with a weak 1,3-diradical character. The diradical character (see y below), defined by 2 × 2 CI by the natural orbitals (UNO) by UHF [126,130,132], are 80–90, 40–50, and 10–20% for Figure 8a, Figure 8b, and Figure 8c, respectively, indicating the high dependence of types of central atoms or groups. Therefore, the diradical character of parent azomethine ylide (Figure 8c) was reduced with the introduction of appropriate substituents, providing stable 1,3-dipole structures, which responded to the concerted (3+2) cycloaddition [159]. Similarly, carbonyl ylide (Figure 8b) derivatives with the reduced diradical character undergo the concerted 1,3-dipolar cycloadditions [132,159]. Abe et al. [160] also synthesized the 1,3-diradical (Figure 8a) derivatives, for which the central CH2 was replaced with the CX2 group: X = electron-withdrawing group (type I) and X = electron-donating group (type II). Type I and II compounds were found to be regarded as a resonant state between singlet diradical and zwitterionic (or π-bonded) structures [160], indicating a reduction in the strong diradical character of the parent 1,3-diradical (Figure 8a). BS MO and DFT models are applicable to investigate the reduction in the diradical characters by the introduction of polar substituents.
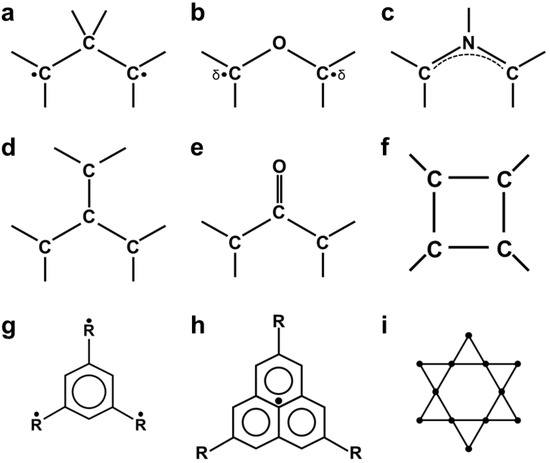
Figure 8.
Schematic illustrations of 1,3-diradical (a), 1,3-diradicaloid (b), and 1,3-dipole (c) for three-center systems; trimethylenemethane (d) and its analog (oxyallyl) (e), and cyclobutadiene (f) for the four-center systems; benzene with substituted with triradicals (g), and the phenalenyl radical (h) with delocalized SOMO, as well as the Kagome radical cluster (i).
Trimethylenemethane analogs (Figure 8d,e) [161,162,163] were calculated to be the ground triplet state [126]. In the late 1970s, several theoretical investigations [164,165,166] were performed for parent trimethylenemethane, showing the triplet ground state. On the other hand, cyclobutadiene (Figure 8f) was the singlet anti-aromatic molecule [127], as illustrated in Figure 8. The singlet ground state of Figure 8f was explained with dynamic spin polarization [167] and the pseudo-Jahn–Teller effect [168], indicating further investigations (see later). Over the past five decades, the independent particle model [157,158] based on the single Slater determinant has provided several BS models, such as UDFT, hybrid UDFT, etc., for the theoretical modeling of tri-diradical (Figure 8g) dimer and clusters of phenalenyl radical (Figure 8h). Therefore, common chemical indices between BS and CI models have also been employed to investigate the nature of chemical bonds of the open-shell systems expressed by Equation (8).
The orbital overlap Ti between the BS MOs obtained by the HOMO-LUMO mixing in Equation (8) is defined as [40,126,127,128]:
Therefore, Ti becomes 1.0 in the case of the closed-shell (restricted) case; = = , whereas Ti is 0.0 for the complete mixing case (θ = π/4): complete the SP split pair in accordance with the order parameter in the phase transition. In order to express the decrease in chemical bonding via orbital symmetry breaking, Coulson’s (first order) effective bond order [169] is defined by [126]:
where and denote the occupation numbers of the bonding (HOMO; HONO) and antibonding (LUMO; LUNO) orbitals, respectively, and they are expressed by using the orbital overlap; ni = 1 + Ti and ni* = 1 − Ti [126]. The effective bond order (b) is nothing but the orbital overlap between the BS MOs under the BS approximations.
Salem and his collaborators [170] performed 3 × 3 CI using the ground, singlet excited, and doubly excited configurations for a diradical pair. On the other hand, we have defined a 2 × 2 CI scheme to define the diradical character by the ground and doubly excited configurations [126,127,128]. To this end, the natural orbital (NO) analyses of several types of BS solutions have been performed for the BS solutions to elucidate their canonical natural orbitals (UNO) and their occupation numbers (ni and ni*). The UNO provides the pure singlet diradical state, which is expressed by two configurations:
where Ti (= cos 2θ in Equation (14)) is the orbital overlap between the up- and down-spin orbitals in Equation (14), and the first and second terms denote the ground and doubly excited configurations, respectively. The single excitation triplet configuration is removed in the case of the spin-projected BS, 2 × 2 CI (UNO), and MCSCF solutions. As mentioned above, the single singlet excited configuration usually appears if the RHF and other MOs are used for the diradical [170]. On the other hand, the effective bond order (B) for in our scheme is given by:
The B value after spin correction, namely after the elimination of the triplet state, is larger than b in Equation (13). Therefore, the B value in Equation (15a) is also applicable to the 2 × 2 MCSCF wave function [40].
The spin density (ρ) appears in the BS solution by the independent particle model [171,172], even for singlet diradicals, since its functional behavior is given by the orbital overlap Ti and the occupation number ni as follows:
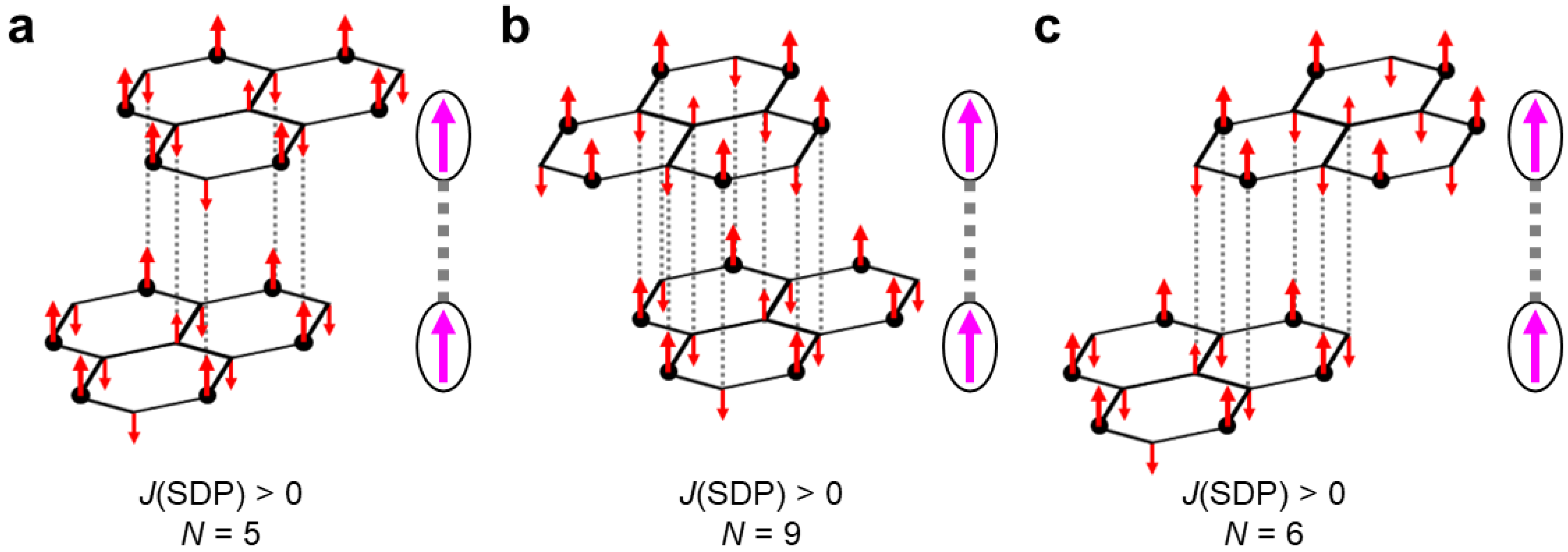
We have examined the physical meaning of the spin density for strongly correlated electron systems (SCES) [40,173,174] from the spin correlation functions for magnetic materials [175] and large open-shell species, which are observed by the neutron diffraction methods [176]. The spin correlation function for SCES by the BS model is approximately expressed with the product of spin densities ρi and ρj at the i and j magnetic sites [173,174]. This means that the parallel and anti-parallel spin alignments with the positive and negative spin-density products (SDP; ρiρj) are considered as the ferromagnetic and antiferromagnetic spin correlations (not spin order) for finite open-shell species such as diradicals and polyradicals.
Therefore, the spin density is a useful chemical index, even for singlet diradicals, and the magnitude increases sharply in the weak diradical regime, indicating the overestimation of the diradical character. On the other hand, the diradical character (y) is defined as twice the weight of the doubly excited configuration (WD) under the canonical delocalized NO (UNO) approximation as
The y value is also obtained by the multi-determinant approaches, such as complete active space (CAS) UNO CI, CASSCF, CASPT2, MR UNO CI, and the MR-coupled cluster (CC) [24,40]. It is directly related to the decrease in the effective bond order B, indicating a moderate increase with the decrease in the orbital overlap, as shown in Equation (17b). Thus, the y value is a common chemical index between the AP BS and MR methods.
Information entropy (−n ln n) is introduced in the field of quantum information science [22,38,70,71,87,90] in Figure 1. It is also used as an index of the effective bond orders [177,178] defined by the occupation numbers [40,46,47] as:
where the denominator in Equation (18) denotes the information entropy for the closed-shell bond with no fluctuability [70,71]. The information entropy is also obtained by the occupation numbers of natural orbitals by MR methods such as MCSCF, MR CI (CC) etc.
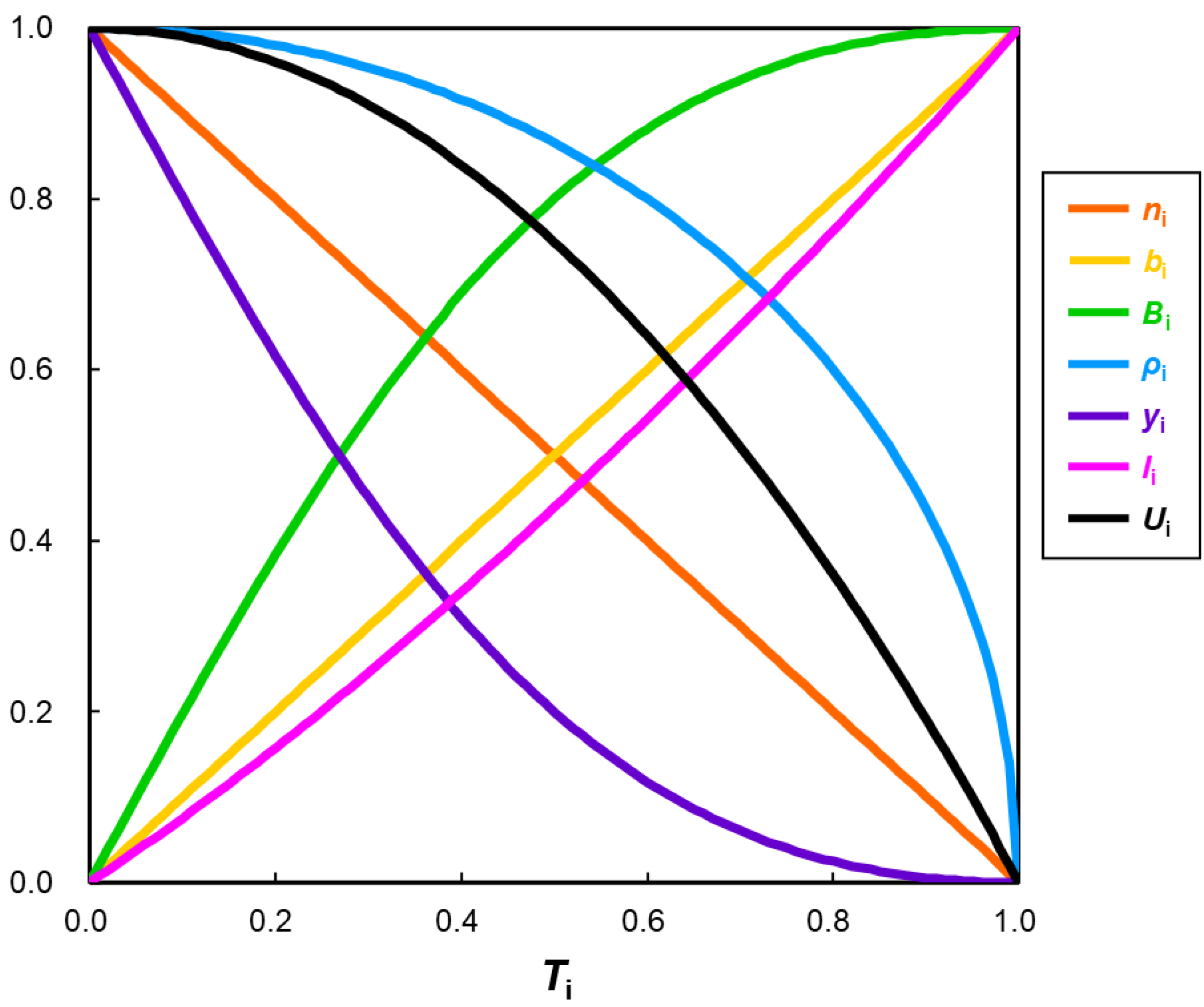
In summary, the functional dependence of the chemical indices against the orbital overlap (T) is illustrated in Figure 9. The spin density (ρi) by BS increases sharply, even in the strong orbital overlap region, where the diradical character (yi) is relatively small. This characteristic feature is partly ascribed to the triplet-spin contamination of the BS solution. The effective bond order (bi) and information entropy (Ii) linearly decrease with the decrease in the orbital overlap (Ti). On the other hand, the diradical character (yi) increases sharply in the small orbital overlap region, whereas the effective bond (Bi = 1 − yi) after spin projection indicates the reverse tendency. Thus, functional dependence indicates the characteristic behaviors of the chemical indices for the diradical species by the BS and beyond BS methods.
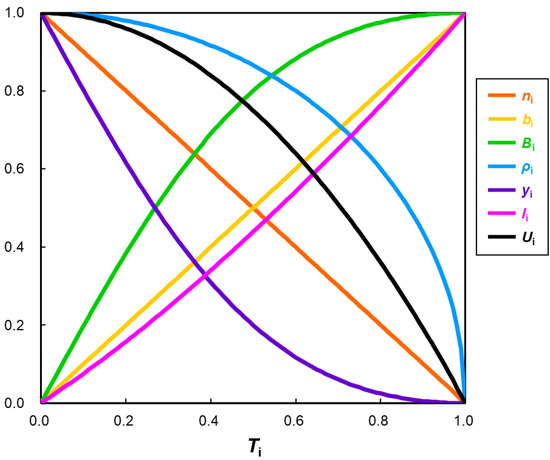
Figure 9.
Schematic illustration of the variations in the chemical indices against the orbital overlap (Ti) between broken symmetry (BS) orbitals in the BS methods coupled with spin projections. Spin density (ρi; blue line) increases sharply, even in the large orbital overlap region (Ti = 0.7–0.8), indicating the overestimation of the diradical property. The unpaired electron density (i; black line) exhibits a similar tendency. The diradical character (yi; violet line) increases sharply in the weak overlap region [40,45,126].
2.8. Interrelationship Between VB and Localized MO Models
Here, the interrelationship between the VB and MO methods is revisited briefly. G. N. Lewis [179] proposed the octet model for the chemical bonds of organic molecules. The Heitler–London quantum mechanical theory [14] for chemical bonds provided a quantum-theoretical foundation of the concept of the electron-pair bond [179] for the two-center two-electron systems in Figure 5. The 1,3-dipole compounds in Figure 8 are essentially regarded as the three-center four-electron systems, which have two electron-pair bonds based on the Lewis model [179]. In fact, Linnett and collaborators [180,181,182] have presented the double-quartet theory, providing a four-dot representation to avoid electron repulsions in 1,3-dipoles. However, the Linnett model may entail a misunderstanding of the tetra-radical structure of 1,3-dipoles [132]. The Linnett model indeed requires a detailed analysis of the static and dynamic electron correlations in SECS [40] (see later).
Firestone [183] applied the Linnett model for organic molecules. He presented the Linnett model for the 1,3-dipoles and 1,3-dipolar cycloaddition reactions [184], proposing the diradical mechanism in sharp contrast to the concerted mechanism proposed by Huisgen [185] on the basis of the stereochemical results for the 1,3-dipolar reactions. Firestone’s proposal [183], based on the Linnett model [182], entailed serious debates with Prof. Huisgen [186] based on the closed-shell (RHF) MO model. However, their debates were not on the same wavelength because of different theoretical models. Therefore, a common basis was necessary for understanding and explaining the nature of the chemical bonds of 1,3-dipoles.
We performed a natural orbital analysis [126,127,128,187] of the complex wavefunctions obtained for the 1,3-dipoles by several Linnett-type models to elucidate the natural orbitals and their occupation numbers [40]. It was found that the occupation number of the HOMO obtained by the diagonalization of the first-order density matrix of the Linnett wavefunctions was largely reduced from 2.0 (closed-shell) and the occupation number of LUMO was larger than zero (open-shell), indicating a strongly correlated pair responding to the diradical state, whereas the occupation number of the next HOMO was near 2.0, responding to a weak (spin polarization) correlation [40]. Thus, two electrons exhibit static (strong) electron correlation, and the remaining two electrons present a dynamic (weak) electron correlation in conformity with the classification of the electron correlations by Sinanoğlu [188]. Thus, the NO analysis [126,127,128,187] supported a diradical picture [132] instead of the tetra-radical picture of 1,3-dipol compounds [180,181,182,183,184]. Recently, Saito et al. [189] have performed extensive theoretical modeling of the 1,3-dipolar cycloadditions by the MR-coupled cluster (CC) level of computations, supporting the concerted mechanism [132,186].
We have performed a NO analysis of the BS solutions for the 1,3-dipolar compounds in Figure 8, showing that the HOMO-LUMO pair indicates a radical character (y < 1.0), whereas the other pairs are regarded as almost closed shells with a small dynamical correlation. Therefore, the HOMO-LUMO pair is considered for elucidation of the interrelationship between the MO and VB models within the static (non-dynamical) level of electron correlation instead of the Linnett model [170]. To this end, the canonical HOMO-LUMO pair is transformed into the localized MO (LMO) picture for the VB explanation of diradical and diradicaloid species. More generally, the localized natural orbitals (LNO) are obtained by the localization of natural orbitals (ULO) of the BS solutions [190].
The LMOs are defined as the complete mixing limit (θ = π/4) in Equation (4): p = θ = π/4 for bi-centric diradicals. The BS MOs in Equation (8) are indeed re-expressed with LMOs (LNOs) in Equation (19), as follows:
where the mixing parameter ω is given by θ + π/4. Therefore, the BS MO configuration can be expanded by using LMO (LNO) as
where the no-bar and bar denote the alpha (α) and beta (β) spins, respectively, and the pure singlet diradical (SD) and triplet diradical (TD) covalent terms in the VB concept are therefore given by
where the SD and TD terms are expressed by and , respectively. On the other hand, the zwitterionic (ZW) configurations result from the charge transfer from to (vice versa) as follows:
The low-spin (LS) BSI MO configuration involves the pure triplet covalent term, showing the spin-symmetry breaking property. Similarly, the LS BS-II MO configuration is expressed by
The LS BSII MO solution also involves the pure triplet term. Thus, spin-symmetry breaking is inevitable in the case of the single-determinant (reference) BS solution for diradical species. However, both the orbital and spin symmetries are conserved in finite quantum systems [40,145,146]; for example, the error arising from the triplet term in Equations (20b) and (22b) i easily eliminated by the AP procedure that eliminates the pure triplet term.
Indeed, as shown in Equations (20b) and (22b), the BSI and BSII solutions are degenerate in energy. Then, the quantum resonance of them is required, providing the VB CI-type solution as follows [24,40]:
where the normalizing factor is neglected for simplicity; thus, the in- (+) and out-of-phase (−) resonating LMO (or localized natural orbitals (LNO)) BS (RBS) solutions are nothing but the pure singlet- and triplet-state wave functions, respectively; the broken symmetries are recovered via the quantum resonance. The chemical bonding of the diracaloids is expressed with the configuration mixing of the covalent singlet term and two ZW terms under the LMO (LNO) approximation in conformity with the VB concept. The singlet diradicaloid state is expressed by the 3 × 3 CI of the VB configurations in Equation (23) instead of the 2 × 2 MO scheme in Equation (14).
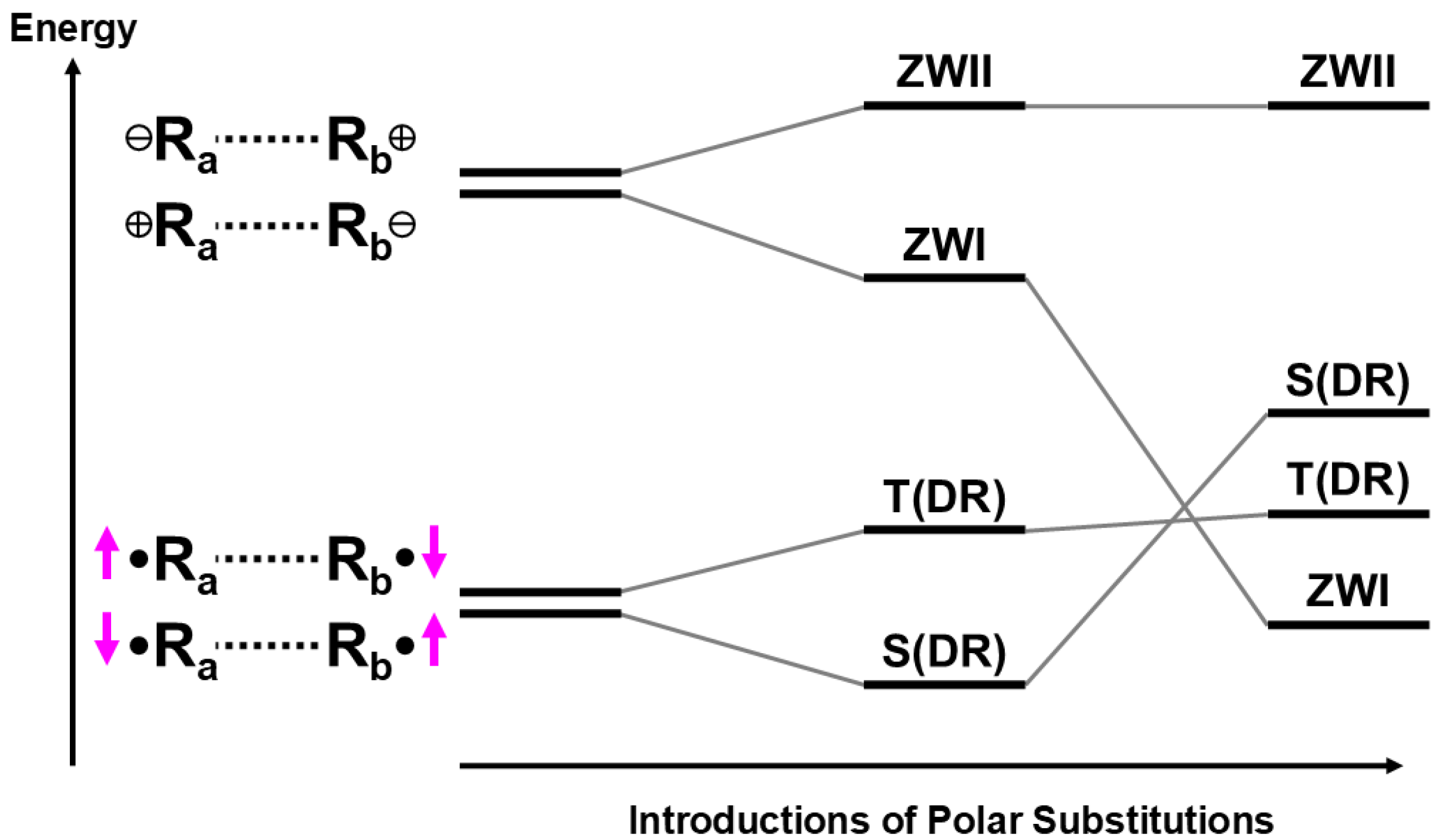
The VB-type explanation of the electronic structures becomes feasible under the LMO (LNO) model [40,190]. For example, the effective bond order becomes zero for the pure covalent term (diradical configuration in the VB term), but it increases with the increase in mixing with the ZW term until the ZW/SD ratio becomes 1.0, namely the closed-shell MO limit. The LMO (LNO) CI descriptions of both the ground diradical and excited ZW states are examined for bi-centric and tetra-centric diradicals, as illustrated in Figure 10 [191]. The ZW state becomes the ground state under an introduction of donor (push)-acceptor (pull) substituents into the diradicals, as shown in Figure 10.
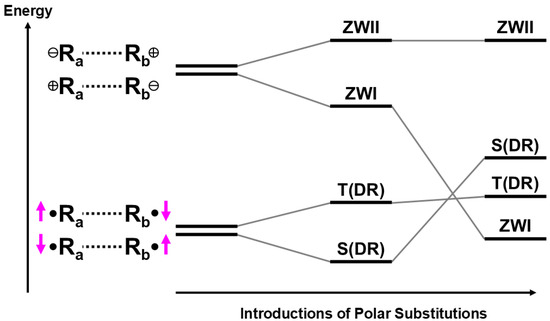
Figure 10.
Energy diagrams obtained by the localized NO (ULO) CI [190,191], providing the VB CI-type pictures for singlet (S) and triplet (T) diradical (DR) and singlet zwitterionic (ZW) states. The introduction of the push–pull polar substituents a radical states stabilizes the ZW ionic state, inducing the conversion from S(DR) to ZW in the ground state [40,144].
3. Collinear and Non-Collinear Spin Structures and Spin Frustrations in Tri- and Polyradicals
3.1. Collinear and Non-Collinear Spin Structures for Tri- and Polyradicals
In the 1960s–1970s, theoretical groups of Prof. Nagamiya [175] and Prof. Yoshimori [192] in the Solid-State Physics Department extensively investigated the helical spin structures of magnetic solids such as manganese oxides. In 1975, because of the strong influence of magnetic materials, we also examined the possible general spin structures of organic radicals and radical clusters, as shown in Figure 11 [193]. For example, three collinear (axial) solutions (↑↑↓, ↓↑↑, ↑↓↑) are available for the equilateral triangular conformation, indicating spin degeneracy. A two-dimensional (2D) triangular spin structure is also feasible for the triangular conformation and related Kagome-type cluster (Figure 8i) [194,195], as illustrated in Figure 2D.
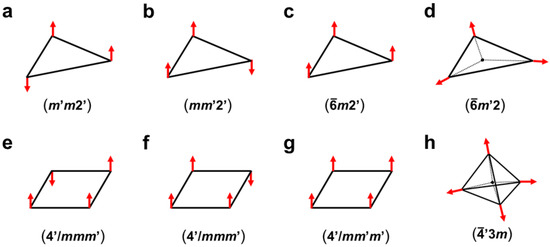
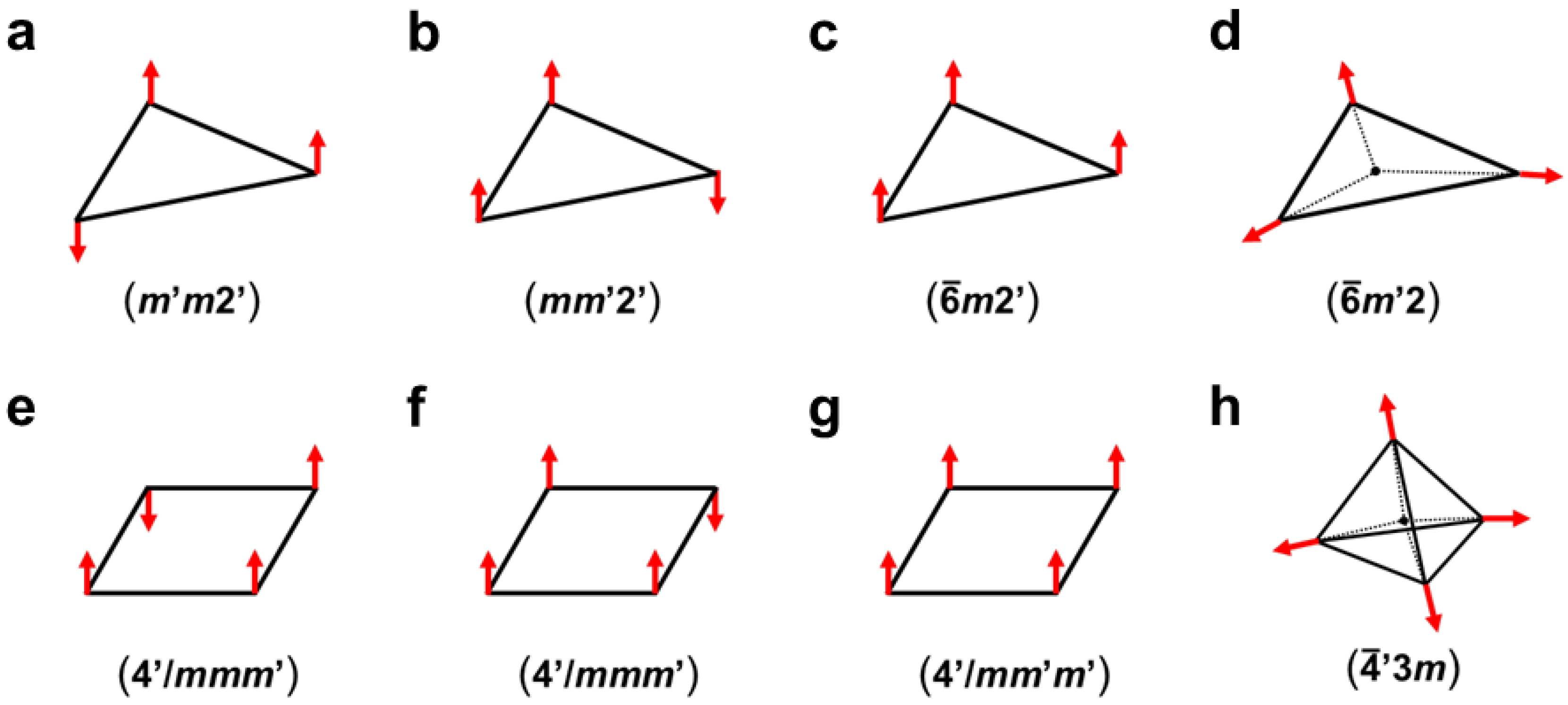
Figure 11.
Magnetic group theoretical notations of two axial-spin structures (a,b); high-spin structure (c); and the helical (triangular)-spin structure (d) for the equilateral triangular conformation. Magnetic group theoretical notations of two axial-spin structures (e,f); high-spin structure (g) for the square planar conformation and the tetrahedral-spin structure (h) for tetrahedral conformation [40,193,195].
According to the theory of magnetic materials [175,192], magnetic group theory [196] has been used to characterize the spin structures of radical clusters, as shown in Figure 11, where the time-reversal operation (T) denoted by ‘ is necessary for spin inversion because spin angular momentum is an axial vector instead of polar vector: the axial vector is different from the quantum spin described by Equation (1). Therefore, the magnetic group (G) is defined for spin structures by both spatial symmetry (PN) and time-reversal (T) symmetry, as follows [40,196,197]
where H denotes the subgroup of PN, and the second term is the remaining group with the time-reversal operation (T). Figure 11 illustrates the magnetic group symmetry of the spin structures consisting of local classical spin vectors for tri- and multi-centric radical clusters. The magnetic symmetries have been used for characterizations of spin correlation diagrams for exchange-allowed and -forbidden radical reactions. The details are given in references [40,197].
G = H + T (PN − H)
The two collinear (axial) spin structures for the equilateral triangle geometry (Figure 11a,b) have C2-type magnetic symmetry. Figure 11a,b become the ground states for acute and obtuse triangles after the Jahn–Teller distortion, respectively. On the other hand, the ferromagnetic (Figure 11c) and non-collinear (helical or triangular: Figure 11d) spin structures exhibit the full C3 magnetic symmetry at the equilateral triangle geometry, as illustrated in Figure 11. For example, the 1,3,5-triradical benzenes (Figure 8g) in Figure 8 are regarded as triradicals with ferromagnetic (↑↑↑) or triangular antiferromagnetic (helical) spin structures. The odd-membered rings consisting of organic radicals (•R)n (n = 3, 5, 7, …), such as the phenalenyl radical (Figure 8h), are also expected to exhibit non-collinear spin structures [193]. The magnetic group is also useful for the characterizations of the tetra-radical spin structures (Figure 11e–g) of the square planar radical clusters. Theoretically, the cone- and tetrahedral-type spin structures (Figure 11h) are also feasible for putative tetrahedral- and cubane-type radicals and radical clusters [193].
The triangular- and tetrahedral-type multi-center radicals in Figure 11 have been realized, respectively, in the cases of the triangular transition metal M3O4 (M = Mn(III) with S = 4/2, etc.) clusters and cubane-type transition metal M4O4 and M4S4 clusters, as examined in references [198,199]. The CaMn4O5 cluster with the cubane-type CaMn3O4 has been found to be the catalytic site of the water oxidation reaction in photosystem II (PSII) [47]. Therefore, many third transition metal (M = Cu, Mn, Co, …) clusters have been synthesized as model catalysts for water oxidation [46,47]. On the other hand, triangular and Kagome (Figure 8i) lattices consisting of transition metal ions have been investigated extensively in the field of solid-state physics [192,194,195].
3.2. Instability of the UHF Solution and General Spin Orbitals for Non-Collinear Spin Structures
In 1972, Prof. Fukutome [84] developed a generalized Hartree–Fock (GHF) theory responding to the collinear and non-collinear spin structures [193] in Figure 11. He has elucidated eight types of GHF solutions [84], including the RHF, UHF with a collinear (axial) spin-density wave (SDW) in solid-state physics, and the GHF with a non-collinear SDW: two-dimensional (2D) spin structures, such as a helical SDW, and 3D spin structures, such as the cone and tetrahedral SDWs in Figure 11. According to the Fukutome GHF theory [84], electronic structures are variable depending on the type of spin correlation: RHF (no spin density) → UHF with a 1D SDW → GHF (HSDW) with a 2D SDW → GHF (helical spin wave (HSW)) with a 3D SDW.
The triradical species in Figure 8 and Figure 11 are interesting examples of non-collinear spin structures in quantum chemistry. Indeed, the equilateral triangle H3 radical is one of the best molecules for the explanation and understanding of these spin structures in Figure 12 [148,149]. The doublet open-shell 2RHF solution is always doublet unstable because of the spin polarization (SP) effect, providing the axial (one-dimensional (1D)) spin-density wave (2ASDW) [84], which is the conventional UHF solution with collinear spins (Figure 11a,b) in chemistry. The 2ASDW solution can be obtained by the HOMO–LUMO mixing in Equation (8). However, 2ASDW is spin-flip (SF) unstable because of the degeneracy between HOMO and SOMO in the equilateral triangle geometry, reorganizing into the more stable helical SDW(GHF) (2HSDW) solution with the triangular spin structure illustrated in Figure 12. The 2HSDW solution is obtained by the HOMO–SOMO–LUMO mixing procedure [198]. 2HSDW is often referred to as a general Hartree–Fock (GHF) with a non-collinear spin structure, which is generally expressed by a two-component spinor, namely general spin orbitals (GSO).
where GSO involves both α- and β-spin components for 2D spin structures.
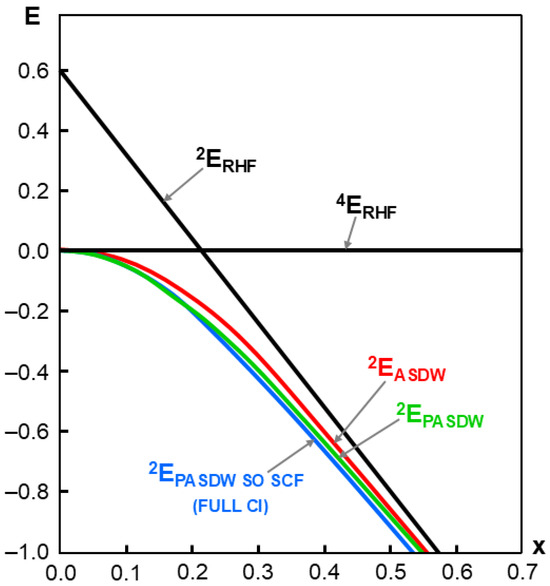
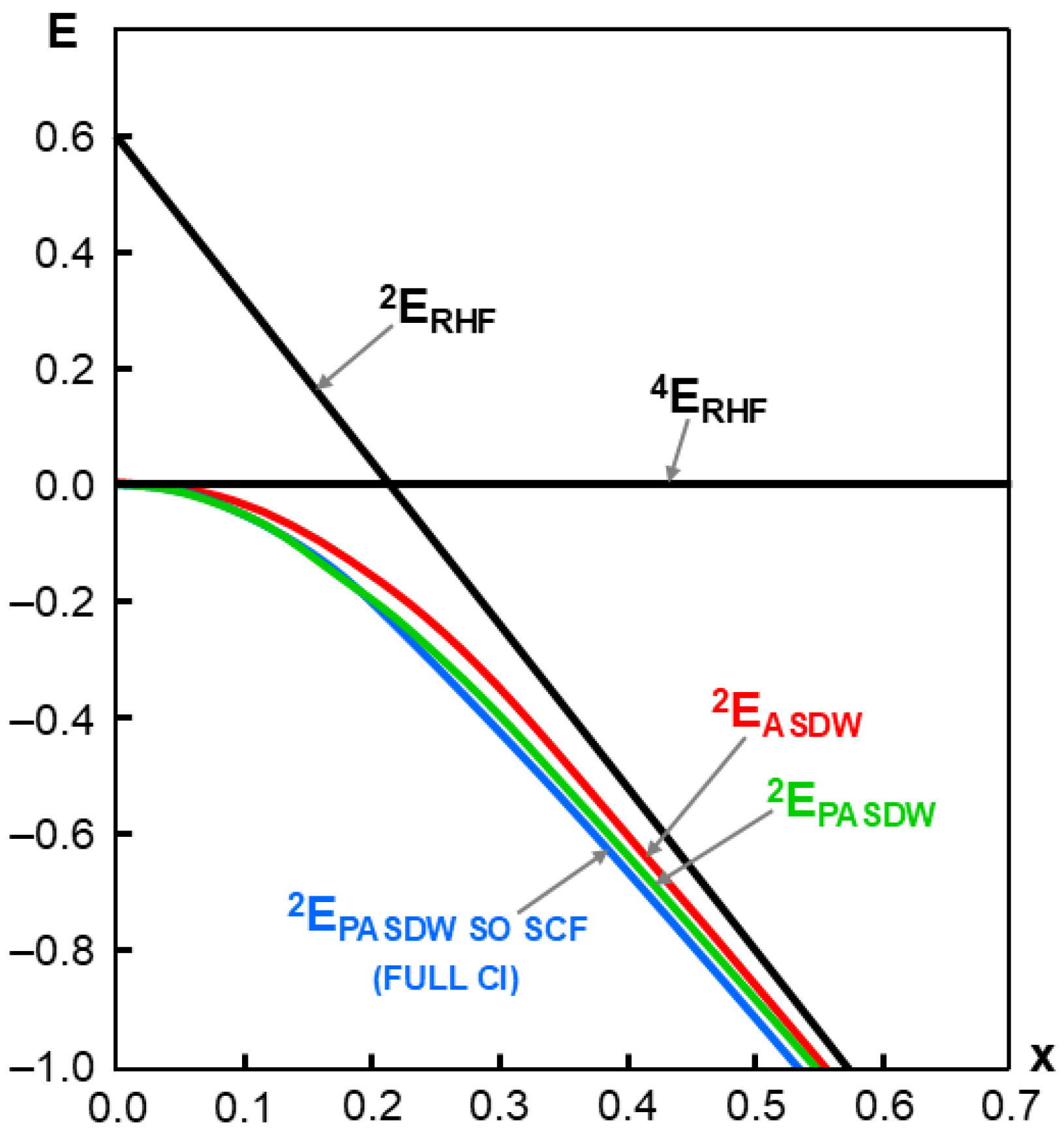
Figure 12.
Potential energy curves against the covalent bonding parameter (x) of the Hubbard models for the equilateral conformation with (3o, 3e) by the doublet RHF (2RHF), UHF (2ASDW), spin-projected (P) ASDW (PASDW), and spin-optimized (SO) self-consistent-field (SCF) PASDW, which are equivalent to the full CI (3o, 3e) of the Hubbard model [148,149].
As mentioned above, the UHF (2ASDW) solution is not an eigenfunction of the total spin angular momentum operator S2, and the GHF (2HSDW) solution is not an eigenfunction of the S2 and Sz operators [148,149]. Therefore, spin projections for them are necessary for the elimination of spin contamination errors, providing more stable projected PUHF (2PASDW) and PGHF (2PHSDW) solutions, as shown in Figure 12. The SCF computation after the S2 and Sz projections provides the most general extended Hartree–Fock (EHF) solutions responsible for the spin degeneracies. There are two different spin functions for the three electron systems [148,149], namely the total doublet functions obtained by the doublet (D) and singlet (S) coupling 2[D•S] and doublet and triplet (T) coupling 2[D•T]. For example, doublet H3 and HO2 radicals dissociate into doublet H radical-singlet H2 and doublet H radical-triplet O2 in accordance with these coupling schemes. Therefore, the doublet spin state is generally expressed by the linear combination of these two spin-coupling schemes, providing the so-called spin-optimized (SO) HSDW solution [40,200].
The Hubbard model for the equilateral triangular systems with [3o, 3e] was solved analytically to confirm the above theoretical predictions, as shown in Figure 12 [148]. The normalized total energies for the unprojected and projected (P) UHF(ASDW) and GHF(HSDW) solutions indeed confirmed the theoretical conclusions. The hybrid DFT solutions obtained by the mixing of GHF and general DFT (GDFT) are handy and useful for the theoretical investigations of triangular- and cubane-type clusters, as shown previously [198,199].
3.3. Developments of BS GSO-X (X = HF, DFT, and Hybrid DFT) Program Systems
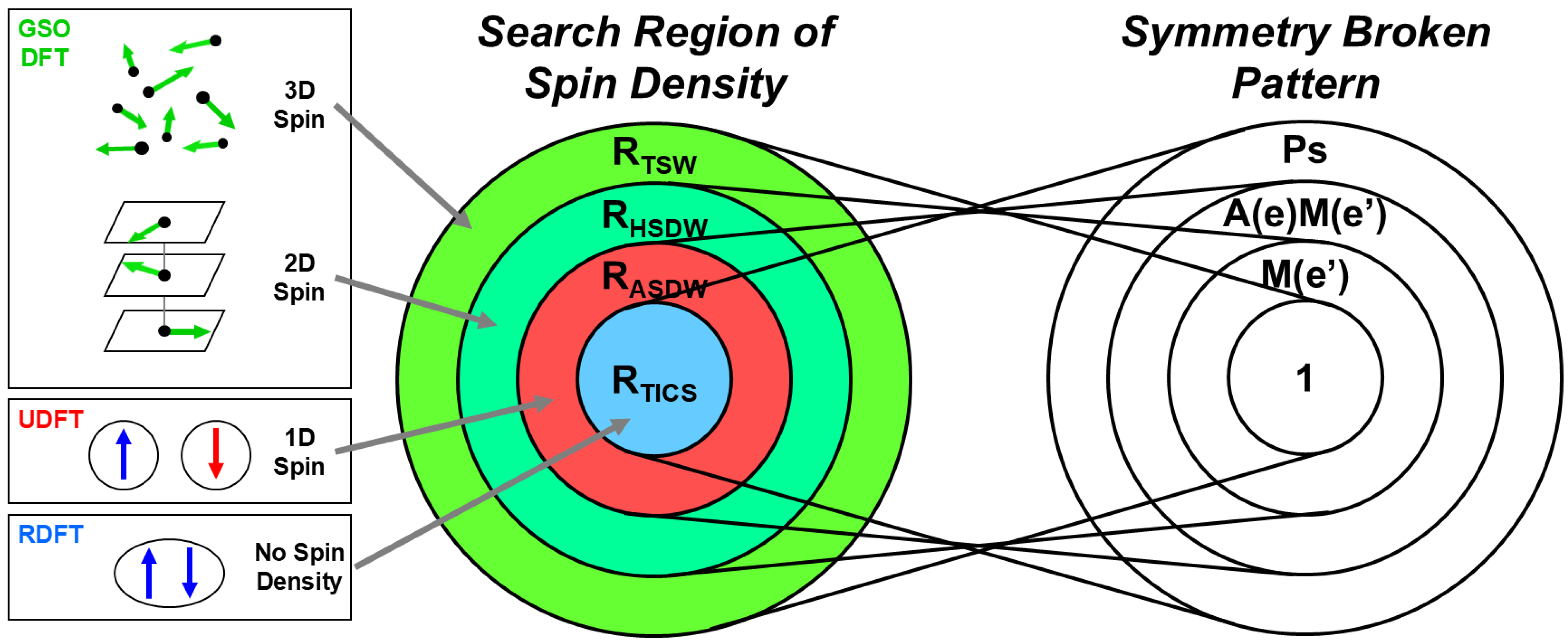
In the 1980s–1990s, the chemical synthesis of multi-center-transition metal clusters with spin frustrations was performed to obtain artificial catalysts for an oxygen-evolving center (OEC) of photosystem II (PSII): XMn3O4 and Mn4O4 [198,199], and artificial iron-sulfur (Fe-S) [201] catalysts for the nitrogen fixation center of FeMoco [202,203,204]. However, complex clusters with spin frustration could not be investigated by conventional program packages. Therefore, Yamanaka et al. [198] have newly developed ab initio program packages for GSO-X (X = HF, DFT, hybrid DFT) for theoretical elucidations of the structure and bonding of large transition metal complexes with spin frustrations, as illustrated in Figure 13. The closed-shell state is described by the restricted Hartree–Fock (RHF) or restricted DFT (RDFT) solution. On the other hand, one (1D)-, two (2D)-, and three (3D)-dimensional spin structures are generally described by the 1D UHF(UDFT), 2D Helical SDW(HSDW), and 3D torsional DFT(TSDW) (GDFT) solutions, respectively [198,199], where the corresponding DFT solutions are given in Figure 13.
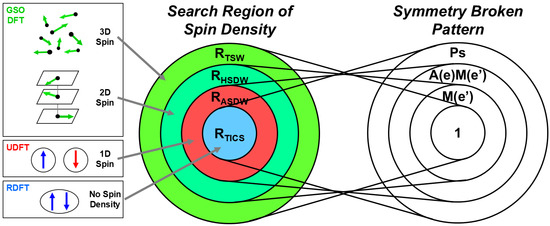
Figure 13.
Collinear and non-collinear broken symmetry (BS) solutions are classified by the magnetic double groups of M(e’) and A(e)M(e’) [84,205]. These solutions are obtained by using the GSO-X (X = HF, DFT, and hybrid DFT) program system developed by Yamanaka et al. [198,199,206].
The general spin structures for the systems under consideration are first obtained by the spin vector model in Figure 11 [193], which is characterized by the magnetic group (spin rotation (S) × time-reversal (T) symmetry) [196], as illustrated in Figure 11. On the other hand, spatial symmetry-adapted (PN) molecular orbitals (MO) for systems such as Fe4S4 clusters were obtained with the EHMO model. Therefore, trial general spin orbitals (GSO) for them are constructed by HOMO-SOMO-LUMO mixing using the magnetic double group theory (PN × S × T) [84,205]. Therefore, the spin structures obtained by the magnetic group (see Figure 11) [193] are useful for the construction of possible GSO solutions. The SCF calculations, starting from the trial GSO obtained, were performed to obtain GHF solutions with the desired magnetic double group theory [198,205]. The GSO HDFT is applicable to elucidate the structure and bonding of multi-center clusters with spin frustrations, such as the cubane-type Mn4O4 cluster [199]. Details of the program packages are given in reference [186].
Yamanaka et al. [206,207] have further performed GDFT computations of triangular-type and related Co-model clusters, whose 2D lattices in Figure 2D exhibit low-temperature superconductivity. They have also performed the GDFT computations of triangular ladder models consisting of (H)n clusters (n = 3–7) [207]. Total energy and total spin angular momentums for low-spin and high-spin states by GDFT have been utilized to obtain the effective exchange interactions (J) between the local spins, even in these spin-frustration systems. The calculated J values are used for the construction of quantum Heisenberg models for spin-frustration systems, which are diagonalized by several methods to elucidate the quantum energy levels in relation to the RVB model for superconductivity [14,146].
3.4. Spin Frustration and Resonating Broken Symmetry Method
Spin vector models in Figure 11 and Figure 13 are conveniently used for a pictorial understanding of local spins in molecular magnetic materials. However, we should be very careful with the quantum effects of molecular spins [22,40,44,87]. Here, we revisit the quantum spin in Equation (1). The spin quantum number of local electron spins in organic radicals is S = 1/2 with two states in Equation (1), indicating opportunities of the spin-frustrated quantum systems in the triangular-type and Kagome-type geometries [195] in Figure 2D. Therefore, we come back to the RVB and related quantum spin models, such as RBS, for these systems [145,146,147,148,149,200,207]. For example, the triradicals consisting of a half-integer spin (S = 1/2) in Figure 11 are indeed quantum spin systems that are described by the three different VB structures with one singlet-pair bond plus one unpaired spin, indicating the so-called spin-frustrated state [200,207]. The three VB structures are degenerated in energy in the equilateral conformation, entailing the quantum resonance states, which are expressed with a total of two degenerated doublet states in energy and one total quartet state [199,200,201]. Three BS structures are also degenerated in energy, providing the RBS states for the doublets and quintet states.
The RVB states investigated by Pauling–Anderson [208,209] have been employed to rationalize the high-Tc superconductivity of cuprates with essentially a two-dimensional lattice [146,147,208,210]. Recently, the RVB concept has also been applicable to specific electronic behaviors of one-dimensional radical chains and frustrated radical clusters of organic radicals (see later). In this review, we do not enter the new topological materials investigated in solid-state physics. We do not touch the exact DFT model instead of the Kohn–Sham-type DFT model, which provides the broken symmetry (BS) solution: we may expect no symmetry breaking for the exact DFT.
The spin-frustrated clusters consisting of quantum spin (S = 1/2) in Figure 11 are certainly described with RVB models because of the strong spin frustrations. However, the RVB model is not applicable to complex organic radical clusters since the SOMO of component radicals are often delocalized over molecular skeletons. Therefore, we can use the SOMO of the BS for the molecular q-bit in the analogy of the RVB, providing the resonating states of the BS solutions with the same energy, namely the RBS state. Indeed, the RBS state consisted of three triangular (2D) spin structures [200], proving two double and one quintet quantum states, as illustrated in Figure 12.
The resonating BS (RBS) models [200,207] are applicable for theoretical investigations of such complex molecular systems. For example, the hole-doped BEDT-TTF dimer derivatives have a quantum spin S = 1/2, which is required for new quantum materials from the original RVB models [146,147]. The 2D lattices of BEDT-TTF with nearly a triangular lattice in Figure 2D have been indeed investigated in relation to several magnetic phases, such as superconductivity, etc. Recently, triangular lattices constituted of these derivatives, such as κ-(BEDT-TTF)2Cu2(CN)3, have attracted great interest in relation to the quantum spin liquid (QSL) state of the spin-frustration system [211,212,213,214,215,216]. The QSL state is a phase of matter with long-range quantum entanglement but has an absence of the ordinary magnetic order in spite of the non-negligible effective exchange interaction [211,212,213,214,215,216]. The design [215,216] and synthesis of appropriate organic radicals, such as (Figure 8g) for QSL, remain a challenge for chemists.
3.5. Dirac Identity for Permutation Operator and Heisenberg Spin Hamiltonian Model
Quantum spin systems consisting of S = 1/2 spin are now re-accepted and are of great interest for quantum spin materials, which is in sharp contrast with local classical spins of transition metals ions such as Fe (III) (S = 5/2) and Mn (III) (S = 4/2). In the early 1970s, both spin-free [217,218,219] and spin-dependent models [193,197,201] were proposed for the theoretical modeling of radical reactions. In many electron systems, the exchange of electron spin is a fundamental concept for understanding the nature of chemical bonding [14,15,16,17]. Indeed, the magnetism and chemical bonds [37,39,40,82,83,84,85,86,87,88,89,90] are classic problems in quantum chemistry.
Prof. Matsen’s group [217] performed the spin-free approach to investigate radical reactions, where the permutation group (SN) [220,221] is used for the quantum mechanical description of the exchange interactions between quantum spins. On the other hand, over the past decades, we have used a spin-dependent approach, namely the quantum Heisenberg model, to open-shell systems because of several reasons [222]. For example, the spin Hamiltonian models have been used for the theoretical analysis of experimental results for metalloenzymes [41,42,43] by EPR and several magnetic experiments. In fact, spin Hamiltonian models [40,45] have also been employed to elucidate the effective exchange interactions of SCES [210] in material science [44,45]. The computational results by ab initio methods in Figure 13 are often used to determine the bonding parameters of the BS Hubbard models [111], which are often mapped into the Heisenberg spin Hamiltonian model [40,45] through transformation from the canonical orbital to localized orbitals [190] for exchange-coupled open-shell species [40].
The permutation operator in the quantum VB model [220,221] is closely related to spin exchange in the spin Hamiltonian [78]. The scalar product of local spins is expressed by the squares of the total spin (Si + Sj) and local spin operators as follows [40,222]:
The expectation value of the spin scalar product is given by the singlet and triplet diradicals as follows:
Therefore, the permutation operator Pij [221,222] can be defined by the spin scalar product.
The above relationship is called the Dirac identity [79], indicating the direct relation between the permutation operator (SN) in the valence bond (VB) model [217,218,219] and the spin operators in the spin Hamiltonian model. Dirac identity [78] is the theoretical foundation for the spin-free approach to radical reactions by Matsen and his collaborators [217,218,219,223], which is in sharp contrast to our spin-dependent approach to open-shell systems [40,206,207]. The equivalence transformation between spin-free [219] and spin-dependent [197] models is feasible by using Equation (29).
The BS MO model, such as the Hubbard model in Equation (6), is often transformed into the spin Hamiltonian model [40,197,222] based on the second quantization formula of the spin operator Si in the weak bond region as follows:
where Jij is the effective exchange integral. The total energies of the singlet and triplet states of the binuclear open-shell systems on the Heisenberg model [40,45,46,222] are given by
The energy gap between the singlet and triplet states is given by (see also Figure 6)
where Equation (31b) for the J value is often referred to as the chemist’s notation where the signs of J are negative and positive for the antiferromagnetic and ferromagnetic exchange interactions.
The above two spin models can be generalized in the case of the multi-electrons A and B at the sites a and b, where the A (B) electrons are parallel at the a (b) site, namely the local high-spin configurations. The effective exchange integrals, defined by each orbital (i, j), are approximated by the orbital-averaged exchange integrals as follows [40,45,46,222]:
where
Therefore, the Heisenberg models for the polyradical species [46,47,222] are generally given by
where Jab is the orbital-averaged effective exchange integral between the spin sites a and b with the total spin operators Sa and Sb. The Jab-values are calculated by using the total energy and total spin angular momentums (S2) of the BS solutions [40,222]
where YEX and HS<S2>X denote the total energy and total angular momentums obtained by the X-computational method (BS = UHF, UDFT, HUDFT) for the Y-spin state (Y = HS or LS), respectively. The total energy of the spin-projected (SPBS) is given by the following equation [40,222].
where S(S + 1) denotes the exact eigenvalue of the total spin-density operator; therefore, the second term in Equation (35) corresponds to the spin correction term for spin contamination in the BS model [40]. The computational scheme in Equations (34) and (35) is also applicable to the symmetry-adapted multi-determinant methods such as CASSCF, MR CI, and MR CC [40].
The exact diagonalizations of the spin Hamiltonians consisting of the ab initio calculated Jab are necessary to elucidate the quantum energy levels and projection factors for the molecular quantum spins [44,45], which are used for the explanation and understanding of the EPR experimental results [224,225,226]. The diagonalizations of the quantum spin Hamiltonian for the radical clusters are performed by the density matrix renormalized group (DMRG) [227,228], matrix product state (MPS) [229], and quantum Monte Carlo (QMC) [221] methods. The large-scale spin Hamiltonian for large magnetic clusters is mapped into the quantum spin Hamiltonians with the Jordan–Wigner transformation [116] of the Pauli matrix into qubits for diagonalization by the phase estimation procedures [38,52,230] of quantum computations in the future.
4. Beyond BS Methods for Quantitative Computations of Open-Shell Systems
4.1. Early MR CI and MR CC Methods as Direct Extensions of BS Methods for Radicals
Strongly correlated electron systems (SCES) in Figure 1 have been investigated by many body theories developed in the late 1950s and 1960s, as shown in a review article [231]. As mentioned in the above Section 1, Section 2 and Section 3, we have been interested in BS unrestricted HF (UHF) and unrestricted HF-Slater (UHFS) models by the use of different orbitals for different spins (DODS) and the more generalized HF (GHF) and generalized HFS (GHFS) based on the general spin orbitals (GSO) in Equation (26)—the two-component spinors that arise from the static electron and spin correlations. These models under the mean-field approximation are regarded as a first step to SCES, being applicable to the ground and lower-layer states. However, well-balanced descriptions of both the ground and excited states are necessary for the theoretical investigations of quantum optics, as shown in Figure 1.
In the 1970s, as the second step, the MR CI methods [232,233,234,235,236,237] were examined regarding theoretical investigations of the ground and excited states of SCES. Several basis orbitals were examined for effective CI calculations [233,234,235]. To this end, we have performed the NO analysis [236,237,238] of BS solutions [126,127,128] for SCES to obtain the UNOs and their occupation numbers [40]. The NO analysis has indeed elucidated the active orbitals that are closely related to the non-dynamical correlation corrections for SCES [188,189,236,237]; the partitioning of active orbitals has entailed the necessity of using the genuine MR approach to SCES, as illustrated in Figure 14.
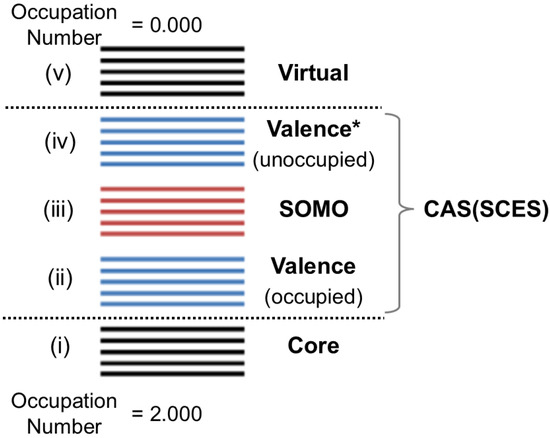
Figure 14.
Classification of natural orbitals (UNO) on the basis of their occupation numbers obtained by the natural orbital analysis of BS solutions for open-shell systems. The SOMO (iii) and CAS (SCES; ii and vi) are the minimum CAS for strongly correlated electron systems (SCES), where occupied and unoccupied (*) valence orbitals were responsible for non-dynamical correlations. Core (i) and virtual (v) orbitals are responding to the dynamical electron correlations [40,236,237].
Öksüz and Sinanoğlu [239] classified the electron correlation effects into (i) internal, (ii) semi-internal, and (iii) external correlations on the basis of the decomposition of orbital space in Figure 14. We have performed the full CI within the SOMOs and strongly correlated the occupied and unoccupied (*) valence orbitals responsible for non-dynamical correlations, which were referred to as active reaction natural orbitals (RNO) [240,241], which is now referred to as complete active space (CAS) [242]. We have performed the second-order (SO) MRCISD [236] in which the references are chosen as all possible distributions of electrons within CAS. However, the SO-type MRSDCI is too heavy for open-shell molecules, and perturbation selections were necessary [233,234]. The second-order type MR CI was necessary for well-balanced descriptions of low- and high-spin states of open-shell species. The SO-type MRCI schemes using UNO in Figure 14 are the most natural extensions of the BS and RBS methods, namely the independent particle model, because the reference MR space can be constructed so as to describe the quasi-degenerated electronic systems related to the BS solutions, as illustrated in Figure 15. We presented our MRCI(CC) scheme at Sanibel 1980 [236]. Roos [242] proposed CASSCF by the use of complete active space (CAS) at the same Sanibel conference.
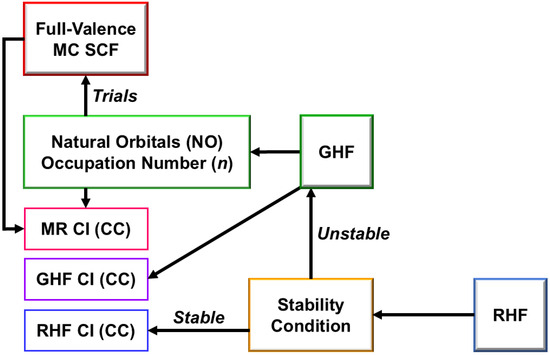
Figure 15.
Early computational schemes started from the instability of RHF, providing generalized HF (GHF) including UHF, as a first step to SCES. As the next step, the natural orbital analysis of the GHF solution was performed to elucidate the natural orbitals (UNO) and occupation numbers (n). The active spaces of SCES for the MR references were selected for MR CI and MR CC with n values. Full valence (FV) multi-configuration (MC) SCF was a dream at that time (1980) [40,236,237].
Čížek has presented the size-consistent coupled cluster (CC) methods for atoms and molecules [243] instead of the CI approach [232,233,234,235]. The CC method was found to be effective in nuclear physics [244]. The MR reference version of the CC method was also presented for the degenerated systems [245,246]. Therefore, from the equivalence transformation, MRCI into MRCC for atoms and molecules was also a natural new approach to SCES [247]. However, for our natural extension of the BS to MR CI (CC) [236,237], the active space in our scheme was limited so as to include non-dynamical (static) correlations that are origins of the instabilities in the RHF solution at that time. Under this approximation, only the minimum reaction (R) NO (Mini-RNO) = principal active space (PAS), namely CAS in our definition in Figure 14, was considered instead of the maximum RNO (Max-RNO) = PAS + SAS (secondary active space). Therefore, the reference function in Min-RNO was taken to be UNO (= UHF-NO) and GNO (= GHF-NO) CASCI in our MR CI and MR CC schemes for both non-dynamical and dynamical correlations. Nevertheless, perturbation selections of the main configurations [234] were inevitable, performing the MR CI [236,237] followed by Davison correction [248] instead of MRCC [247]. Later, Roos et al. developed CASPT2 [249] and related PT theories to include higher-order excitations.
The CC excitation operator [236,243,244] was considered for the reference state to obtain the UNO (GNO) CASCC as
where T = Σ Ti (i = 1–4). A uniform excitation operator formalism had been considered in the MRCC approach before Jeziorski and Monkhorst [250] proposed their CC scheme in 1981. UNO (GNO) CASCC-single (S) was formally equivalent to UNO (GNO) CASSCF after the convergence of the CC-S equation since we considered only the one-electron excitation operator responsible for semi-internal correlation for active (or full valence active space) NO space,
where the generalized Hartree–Fock–Slater (GHFS) solutions were feasible for transition metal complexes [40,237] since the UHF computations were often time-consuming or divergent for such materials [47]. The situation for UHF is the same, even for CaMn4Ox clusters [47], indicating the utility of the UNO obtained by hybrid DFT computations [46,47,241,251].
The inclusion of the external correlations was crucial for quantitative computations of binding energies for open-shell species. To this end, the inclusion of the double excitation operator (D) in UNO (GNO) CASCCS is essential for dynamical correlation correction, namely UNO (GNO) CASCCSD, as
.
The UNO (GNO) CASCCSD approach, starting from UNO (GNO) CASCI, was our chemical picture. However, MR CC calculations for diradicals were not practical at that time. Alternatively, UNO MR CI with Davidson’s correction [248] was used as an approximate method for UNO MR CC [236,237].
4.2. Potential Curves for Dissociation of the Covalent Bond: Fluorine Molecule
The MRCC approach to SCES, such as open-shell molecules [236], was our dream for a long time. Nowadays, ab initio coupled cluster (CC) computations, in Figure 15, are feasible for relatively small molecules. We are extremely grateful for the theoretical efforts toward MRCC [247,248,249,250,251,252] by the Mukherjee group and many related developers (see Ref. [253]). As an example of open-shell molecules, the potential energy (PE) curve of the fluorine molecule is examined by the CC methods since the UHF and UMP methods do not provide quantitative PE curves because of the strong electron repulsion effects between lone pairs [254]. Figure 16 shows the PE curves of F2 by several CC-type computations using the [2o, 2e] CAS CI reference for diradicals. From Figure 16A, BS UCCSD, using a cc-pVTZ basis set, provides a reasonable PE curve for dissociation from the F2 molecule to two fluorine atoms. However, its depth near the equilibrium region is shallow as compared with the PE curve of APCCSD, indicating the necessity of AP for quantitative purposes [254].
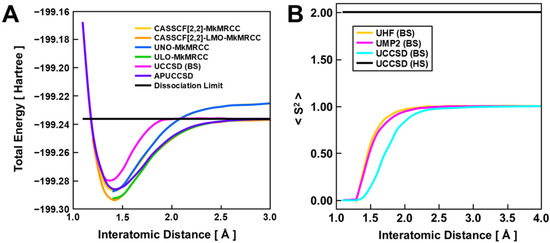
Figure 16.
(A) Potential energy curves for the dissociation reaction of the fluorine molecule by UCCSD, AP-UCCSD, and MkMRCC [2o, 2e] with canonical molecular orbitals (MO) and localized MO (LMO) by CASSCF [2o, 2e] and UNO (ULO) by UCCSD [253]. (B) The calculated total spin quantum <S2> number against the F-F distance by the UHF, UMP, and UCCSD methods [254].
Figure 16B shows the variations in the total spin quantum <S2> numbers against the F-F distance. The <S2> value by the UHF and UMP2 methods for a low-spin BS state increases sharply with the elongation from the equilibrium distance, indicating the necessity of the spin-projected (SP) AP-UHF and APUMP2 [253]. The <S2> value by UCCSD also increases with the increase in the F-F distance, requiring the AP, even at the CCSD level, providing AP-UCCSD [253] for quantitative purposes.
Size consistency is essential for the quantitative descriptions of the dissociation reactions of the covalent bonds. UCCSD and AP-UCCSD satisfy the size consistency condition, as shown in Figure 16A. On the other hand, the PE curves by Mukherjee (Mk)-type MRCC (MkMRCCSD) do not provide the exact energies near the dissociation region because of this type of error, as shown in Figure 16, where the canonical delocalized orbitals by CASSCF [2o,2e] and delocalized UNO by UCCSD are employed. The size-consistent error is indeed a serious problem in the MkMRCCSD method. On the other hand, the MkMRCCSD computations by using the localized orbitals of the CASSCF [2o, 2e] [253] and localized natural orbital (LNO) [254] by UCCSD, provide the exact PE curves for the dissociation reaction of F2, as shown in Figure 16. Thus, LNOs are often necessary for the elimination of size-consistent errors for MR-type computations in Figure 16.
4.3. Geometry Optimization of Open-Shell Molecules: Methylene
Carbene molecules have been investigated extensively [133,134,135,136,137,138,139,140]. The bonding and reactivity of these molecules are highly dependent on structures, as revealed on experimental grounds. Here, geometry optimizations [255] are briefly revisited for investigations of the structure and bonding of open-shell molecules. Kitagawa and Saito et al. [256] have developed an energy gradient optimization procedure under the approximate spin (AP) projection scheme to eliminate the geometric errors arising from spin contamination in the singlet BS solution. Methylene, in Figure 5, is a typical mono-centric diradical [126], for which the observed geometries are considerably different between the singlet (S) and triplet (T) states; for example, the observed HCH angles are 102.4 and 134 degrees for the S and T states, respectively. Therefore, the singlet BS solution is supposed to provide an intermediate angle between them because of the triplet contaminations.
Kitagawa et al. [257] have performed the full geometry optimizations of CH2 by using their AP geometry optimization procedure. They examined the basis set dependencies by setting the STO-3G, 6–31G*, and 6–311++G** basis sets. The BS methods employed were UHF, UMP2, UMP3, UMP4(SDQ), and UB3LYP for Figure 5b. The optimized HCH angles by these BS methods with 6–311++G** were in the range of 115–121 (100–104) degrees, where the corresponding values after AP were given in parentheses. The singlet (low-spin; LS) BS methods have indeed overestimated the HCH angle because of the triplet contamination, whereas the AP BS provided reasonable values because of the elimination of the error term. On the other hand, the optimized HCH angles for the triplet (high-spin; HS) state by these methods were in the range of 132–136 degrees, indicating no contamination error from the higher spin states.
Kitagawa et al. [257] performed the coupled cluster (CC) level computations of CH2, reporting that the optimized HCH angles are 122, 101, and 102 degrees by UCCSD, AP-UCCSD, and MkMRCCSD, respectively. The spin contamination error remains at the UCCSD level of theory, indicating the necessity of the AP correction. The corrected value by AP-UCCSD is compatible with that of MkMRCC and the observed value. Kitagawa et al. [257] have depicted the potential energy (PE) curves of both the singlet and triplet states of CH2 against the HCH angle, as shown in Figure 17.
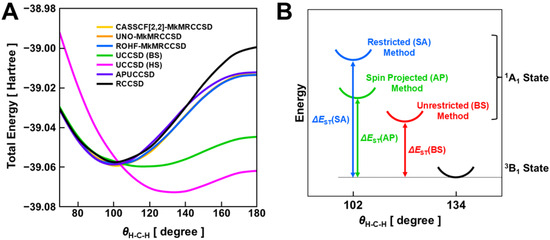
Figure 17.
(A) Potential energy curves [256] against the HCH angles of the singlet (BS) and triplet (HS) states of methylene by RCCSD, ROCCSD, UCCSD, AP-UCCSD, and MkMRCC with canonical molecular orbitals (MO) by CASSCF [2o, 2e] and UNO of UCCSD [257]. (B) Relative energies between the singlet and triplet states of methylene by the symmetry-adapted (SA), broken symmetry (BS), and symmetry projected (AP) methods [257].
From Figure 17, the PE curves for the singlet state are almost the same between MkMRCCSD based on the canonical natural orbital by CASSCF [2o, 2e] and UNO-MkMRCCSD, indicating that the PE curve by APUCCSD is compatible with those of them, although the RHF CCSD (RCCSD) indicates the wrong behavior near the linear H-C-H geometry. The UCCSD calculations provide the wrong PE curve in the region of the larger HCH angle than 100 degrees because of the triplet contamination error. Thus, the AP procedure is necessary when optimized geometries of open-shell systems exhibit non-negligible differences between the LS and HS states. Indeed, Kitagawa et al. [257] have shown several such examples in both organic and inorganic systems. The computational results at the CC level of theory are found to be useful for examining the scope and reliability of hybrid DFT computational methods for open-shell systems, as shown later.
4.4. Trimethylenemethane Analogs: Heteroatom Effect
Historically, trimethyelemethane (TMM) (Figure 8d) has been extensively investigated as a typical ground triplet diradical [161,162,163,164,165,166]. Iminoallyl (IA) and oxyallyl (OXA) (Figure 8e) are heteroatom analogs, obtained by the substitutions of one of the CH2 groups of TMM with NH and O. The spectroscopic experiments [258] have revealed that 8e is the ground singlet diradical species, indicating stabilization of the singlet configuration with the heteroatom substitution. As an extension of our early BS computation [126], Saito et al. [259] performed the full geometry optimizations of TMM (Figure 8d), IA, and OXA(Figure 8e). The diradical characters (y) of the singlet state for these species are 99 (98), 61 (70), and 31 (46) % by AP-UB3LYP, where the corresponding values by UNO-MkMRCCSD(2e, 2o) are given in parentheses. The calculated y values indicate a reduction in the diradical characters by the heteroatom substitutions.
The singlet-triplet (ST) energy gaps (2J) at the optimized geometries are calculated by the AP-UHF, AP-UCCSD(T), unrestricted Brueckner double (UBD), AP-UBD(T), and MkMRCCCD methods. Table 1 summarizes the calculated 2J values for TMM, IA, and OXA. From Table 1, all the computational methods examined predicted the triplet ground states for TMM and IA in accordance with the experiments [258]. On the other hand, the relative stability between the S and T states of OXA is variable, depending on the computational methods. For example, AP-UCCSD(T), AP-UBD(T), UNO-MkMRCCSD(2e, 2o), and CASPT2 predicted the triplet ground state in contradiction to the experimental result [259]. On the other hand, ULO-MkMRCCSD(2e, 2o) reproduced the experimental result for OXA [259], indicating the importance of the elimination of the size-consistent error. The MRCI(2e, 2o) [260] also reproduced the negative J value for OXA.

Table 1.
The singlet-triplet energy gap (2J kcal/mol) for parent anti-aromatic compounds by AP-UHF- and UHF-based computational methods [259].
The pure DFT (UBLYP) provided the large negative J value for OXA, whereas the hybrid DFT (UB3LYP, CAM-UB3LYP) predicted a positive J value, indicating the variation with the weight (w) of the Hartree–Fock exchange term. This indicates the importance of the examination of the DFT results beyond the DFT results, such as MR CI. Practically, the w value of the hybrid DFT is modified to reproduce the MRCI result before its use for large open-shell systems under examination.
Nowadays, the RHF and BS MO methods, such as UHF and GHF, are used as hybrid DFT methods to obtain the corresponding DFT models: RDFT, UDFT, and GDFT for a first-step approach to large molecules. The natural orbital (NO) analysis of the BS solutions, UHF(HDFT) and GHF(HGDFT), for these systems are performed to elucidate the canonical natural orbitals (UNO) and their occupation numbers, which are used for selections of active orbital space for the non-dynamical (static) correlations. UNO CASSCF is also feasible for organic open-shell systems with relatively small CAS space. The localized natural orbitals (LNO) are also obtained by RHF (HRDFT), UHF (HDFT), GHF (HGDFT), and CASSCF. The MR CI (CC), MR DFT, and DMRG computations are performed on open-shell systems by using LNOs obtained by these methods. We can construct LNO by appropriate computational methods, such as the Pipek–Mezey localization method [261], depending on the systems under examination. These methods are applicable to large open-shell systems. Figure 18 illustrates several MR methods using UNO (ULO) for SCES, which are important as molecular quantum materials, as illustrated in Figure 1.
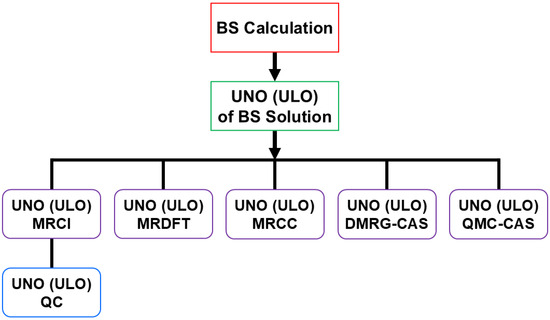
Figure 18.
Modern computational schemes of open-shell systems start from a first-step BS approach to beyond BS methods. The natural orbital analysis of the BS solution provides the natural orbitals UNO (ULO) and their occupation numbers (n) to select CAS in Figure 14. CAS CI references are used for the recent MR CI, MRDFT, MRCC, density matrix renormalization group (DMRG)-CAS, quantum Monte Carlo (QMC)-CAS, and UNO (ULO) quantum computation (QC) methods for SCES [24,40,47,235,236,240,241,251].
5. Theoretical and Computational Studies of Diradical Species
5.1. Anti-Aromatic Compounds with 4π Electrons
After the explanation of the theoretical foundations for SCES in Figure 18, we come back to open-shell organic molecules, such as the diradicals and anti-aromatic molecules in Figure 19. In 1973, Breslow [262] wrote an account of the structure, bonding, and reactivity of the anti-aromatic compounds with 4π electrons, such as the cyclopropenyl anion [263], cyclobutadiene [264], and cyclopentadienyl cation [265]. More generally, 4nπ electron systems [266] are known as anti-aromatic molecules, as shown in Figure 8 and Figure 11. According to the Lewis pair bond theory [179,180], two singlet-pair bonds are feasible for a square planer 4π system, providing two VB structures, which exhibit quantum resonance in the sense of the RVB model [145,146]. Therefore, the examination of the RVB model was necessary for the square planer 4π system.
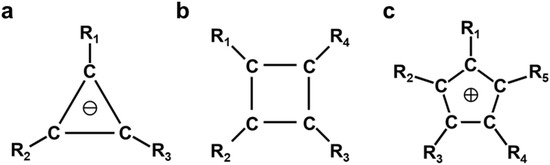
Figure 19.
Antiaromatic molecules: cyclopropenyl anion (a) [261], cyclobudadiene (b) [262,263], and cyclopropenyl cation (c) [262,265]. Relative stabilities between the singlet (S) and triplet (T) states of parent molecules were calculated by the AP UCCSD, AP-UCCSD(T), and MkMRCC methods, as shown in Table 1. The SR gaps for the derivatives of these anti-aromatic compounds were variable, depending on the substituents (Ri) introduced, as shown in the experimental papers in parentheses.
We have performed BS (UHF) calculations of the square planer cyclobutadiene (CBD) [267], followed by the natural orbitals (NO) analysis of the BS solution. From the BS analysis, the occupation numbers of the HOMO and LUMO were nearly 1.0, but the next HOMO was almost the closed-shell orbital (n ~ 2.0), indicating the diradical nature of CBD-like 1,3-dipoles [132]. The NO analysis indicated that the HOMO-LUMO mixing scheme in Equation (8) is applicable for CBD, providing that the BS-A (DODS) orbital for the up-spin is delocalized on the C1 and C3 atoms, whereas the BS-B (DODS) orbital for the down-spin is delocalized on the C2 and C4 atoms. Therefore, this type of BS-I solution provides the spin structure 11e in Figure 11. On the other hand, the other type of HOMO-LUMO mixing provides BS-B orbital for the up-spin and BS-A orbital for the down-spin, showing the BS-II solution with the spin structure Figure 11f. The BS-I and BS-II solutions are degenerated in energy, giving the resonating BS (RBS) states responsible for the singlet and triplet states with a 2J energy gap, as shown in Figure 6. Thus, the two-configuration RBS model is sufficient enough for a first step to CBD since the stable C-C bonds are retained near the equilibrium geometry in sharp contrast to the four radical clusters without the intermolecular bonds.
For stabilizations of anti-aromatic molecules [266], several substituents are introduced to the cyclopropenyl anion (Figure 19a), cyclobutadiene (Figure 19b), and cyclopentadienyl cation (Figure 19c), and are illustrated in Figure 19. Saito et al. [267] have performed theoretical computations of the effective exchange integrals (J) for these diradicals. Table 2 summarizes the calculated J values. From Table 2, the J values by all the computational methods are positive in the sign for Figure 19a, indicating the ferromagnetic (triplet) ground state [127,258]. However, the RHF-based methods have overestimated the magnitude of the positive J values. On the other hand, the J values by AP UCCSD and AP UCCSD(T) are 15.5 and 12.7 kcal/mol, respectively. The latter value is compatible with those of the MkMRCCSD calculations, indicating the important contribution of the triple excitation correction in the so-called gold standard CCSD(T) method.

Table 2.
The singlet-triplet energy gap (2J kcal/mol) for parent anti-aromatic compounds by RHF- and UHF-based computational methods [267].
The calculated J values for cyclobutadiene (Figure 19b) by the RHF-based methods are positive in sign, indicating the ferromagnetic (triplet) ground state. On the other hand, the calculated J values for cyclobutadiene (Figure 19b) by the UHF-based methods are negative in sign, indicating the anti-aromatic (singlet) ground state. Kollmar and Staemmler [167] have performed theoretical investigations of Figure 19b, indicating the important role of dynamic spin polarization for the stabilization of the singlet diradical state rather than the triplet diradical state. All the MkMRCCSD computations examined are also negative in sign, supporting the UHF-based computational results. Interestingly, the J value by AP UCCSD is rather compatible with that of the MkMRCCSD calculation. The AP CCSD(T) provided a smaller magnitude J value than that of MkMRCCSD, suggesting the necessary of MkMRCCSD(T) or MkMRCCSDT for Figure 19b.
In 1980, Bally and Masamune [266] summarized the experimental results for the cyclobutadiene derivatives stabilized by bulky groups, together with theoretical investigations at that time. Automerization from the D2h → D4h → D2h structure was discussed in relation to the Jahn–Teller effect [168]. Recently, Saito et al. [267] have investigated the barrier height for the automerization of CBD by both the BS DFT and coupled cluster (CC) methods, providing about 8 kcal/mol by the MkMRCC. The Brueckner doubles, including perturbative triple excitation (UBD(T)) with AP, which is effective in reproducing this barrier at the DFT level. Therefore, AP-UBD(T) [267] is considered to be applicable for cyclobutadiene with bulky groups [266].
From Table 2, the J values by all the computational methods are positive in sign for cyclopentadienyl cation (19c), indicating the ferromagnetic (triplet) ground state. However, the RHF-based methods have overestimated the magnitude of the positive J values. On the other hand, the J values by AP UHF are negative in sign, whereas it is largely positive by AP UMP2, indicating the necessity of the CC level of theory. In fact, AP UCCSD and AP UCCSD(T) provide reasonable J values that are compatible with those of MkMRCCSD.
Saito et al. [267] have examined the scope and applicability of several types of DFT computational methods for the anti-aromatic molecules (Figure 19a,c,d). The J values for Figure 19a by these DFT methods are positive in sign and are in the range of 6.7–17.7 kcal/mol, indicating a ferromagnetic interaction. This means that the appropriate DFT method can be selected to reproduce the J value of the cyclopropenyl parent structure (Figure 19a) of MkMRCCSD before the DFT computations of many large cyclopropenyl anions with stabilizing substituents Figure 19a (Ri; i = 1–3).
The J values for Figure 19b by several DFT methods are negative in sign in the broad range: −4.2–−24.3 kcal/mol, indicating an antiferromagnetic interaction. This, in turn, means that the appropriate DFT method can be selected to reproduce the J value of the parent structure (Figure 19b) by MkMRCCSD before the DFT computations of many large cyclobutadiene with stabilizing substituents Figure 19b (Ri; i = 1–4) [266]. As mentioned above, Saito et al. [267] have performed DFT computations of the substituted Figure 19b (Ri; i = 1–4), showing reliable computational results.
The J values for Figure 19c by these DFT methods are positive in sign in the range of 1.5–9.3 kcal/mol, indicating a ferromagnetic interaction in accordance with the experiment [266]. This also means that the appropriate DFT method can be selected to reproduce the J value of the parent structure (Figure 19c) of MkMRCCSD before the DFT computations of many large cyclopentadienyl cations with stabilizing substituents Figure 19c (Ri; i = 1–5) [268,269,270,271]. Many experimental [272] and theoretical [273,274,275,276,277] studies have been performed for Figure 19c. From these papers, we can learn the scope and limitations of several computational methods for the anti-aromatic compounds with large bulky substituents.
5.2. Through-Bond Interactions Between Phenalenyl Radicals
As shown in the preceding section, organic chemists can synthesize target molecules, such as organic molecules with diradical characters [160,161,162,163,185,186,214]. Open-shell diradicals can be constructed with through-bond (L) interactions of free radicals. Kubo and his collaborators [278,279,280,281] have synthesized diradical compounds (Figure 20) consisting of two stable phenalenyl radicals (Figure 8h) [282] linked with several types of ligands, as shown in Figure 20. For example, Kubo et al. [283] have synthesized tetra-tert-butyldicyclopenta[b;d [thieno [1,2,3-cd; 5,6,7-c’d’]diphenalene (TTB-TDPL) (Figure 20a), for which the HOMO and LUNO are obtained by the linear combinations of SOMOs of phenalenyl groups (Figure 8h). The HOMO-LUMO energy gap for TTB-TDPL is small, indicating the triplet instability in Equation (3). This entails the HOMO-LUMO mixing in Equation (4), providing the BS orbitals, which are mainly localized on the left and right phenalenyl groups. However, the BS orbitals are delocalized over the thieno linker group (L) Figure 20a, providing a large orbital overlap (T) on Equation (9). Therefore, the diradical character (y) Equation (14) is expected to be small. In fact, Kubo et al. [266] have performed the CASSCF [2o, 2e] calculations, showing the 4% contribution of the doubly excited configuration, namely the 8% diradical character in our definition.
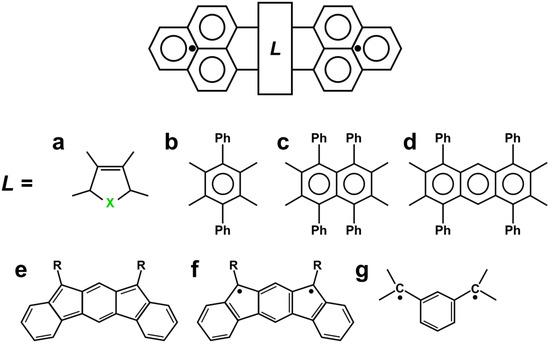
Figure 20.
Schematic illustrations of large organic diradicals formed with through-bond interactions via the linking group (L) of phenalenyl radicals. Linking groups are denoted as (a–d). Indeno [2, 1-b]fluorene: 20π-electron hydrocarbon with Kekulé (e) and diradical (f) structures, and meta-xylene with the triplet ground state (g) [278,279,280,281,282,283,284,285,286,287,288,289].
Kubo et al. [284] and Shimizu et al. [285] have synthesized the biphenalenyl biradicaloid compound linked with the phenyl ring [BBCP] (Figure 20b). The diradical character by UB3LYP was not reduced for BBCP because of the weak through-bond interaction via the phenyl group. The moderate diradical character (y) was also calculated for the biphenalenyl biradicaloid compound linked with the bi- and tri-phenyl rings in Figure 20c,d. Kamada et al. [286] have derived the diradical character of the biphenalenyl compounds in Figure 20 from the experimental results. To this end, they have also observed strong two-photon absorptions of singlet diradical hydrocarbons in Figure 19 [287]. Konishi et al. [288] have synthesized tetracene with the Kekulé structure in addition to the biradical character.
Shimizu et al. [289] have synthesized indeno [2, 1-b] fluorene with the anti-aromatic 20π electrons in Figure 20. This compound has a small HOMO-LUMO energy gap in Equation (7) in accordance with a calculated moderate singlet diradical character (y = 0.68; 68%) because of the meta-quinodimethan subunit, indicating the resonance for the Kekulé (Figure 20e) and diradical (Figure 20f) structures in Figure 20. The singlet and triplet energy gaps (ΔEST = 2J) observed by temperature-dependent EPR were about −4.2 kcal/mole for fluorene with R = mesityl group, which is in sharp contrast to the m-xylene (Figure 20g) with the triplet ground state, which has been proposed as a unit of ferromagnetic polymers [289]. The y values were estimated to be 68 and 83% for the biphenalenes with Ph and no Ph(H) substitutions in Figure 20c [285,289], indicating a reduction by Ph substitution [282,283,284,285,286,287,288,289]. The APDFT and MCSCF [2o, 2e] have been successively applied to estimate the diradical characters of large π-electron systems.
The one-dimensional (1D) chain of BBCP (Figure 20b) was observed with X-ray experiments [285]. It exhibits characteristic behaviors of 1D chains. Kubo et al. [279,280] have proposed the resonating valence bond (RVB) picture [145,146] for the conductive behavior of the 1D chain. Pal et al. [290] have also proposed the RVB model [145,146] for crystals of a phenalenyl-based neutral radical conductor, for which the electron-accepting boron compound BO2(NR)2 is used as the linker L in Figure 20. On the other hand, Huang and Kertesz [291] have proposed the t-J model for the explanation of the 1D chain of BBCP (Figure 20c). Thus, further chemical syntheses of molecular materials with phenalenyl radical groups are expected for the elucidation of the electronic and magnetic properties in their crystal states.
5.3. Through-Space Interactions Between Phenalenyl Radicals
The phenalenyl radical (Figure 8h) in Figure 8 has a delocalized SOMO, which is responsible for the magnetic properties of its dimer and clusters with through-space interactions such the 1D chain mentioned above. However, the unsubstituted phenalenyl radical (Figure 8h) is highly reactive, requiring protection by the introduction of bulky substituents, indicating the necessity of crystal engineering. In fact, Figure 8h stabilized with introductions of three tertiary (t) butyl groups at 2, 5, and 8 positions, as illustrated by Figure 8h with the R = t-butyl group [282], which has been used for the purpose. In fact, the dimer of Figure 8h was isolated in a crystalline state. The X-ray diffraction experiments have elucidated the packing structure, as illustrated in Figure 21. The SQUID experiments by Fukui et al. [292] have elucidated a large negative value (J = −659 cm−1), indicating an almost diamagnetic diradicaloids state because of a strong SOMO-SOMO interaction.
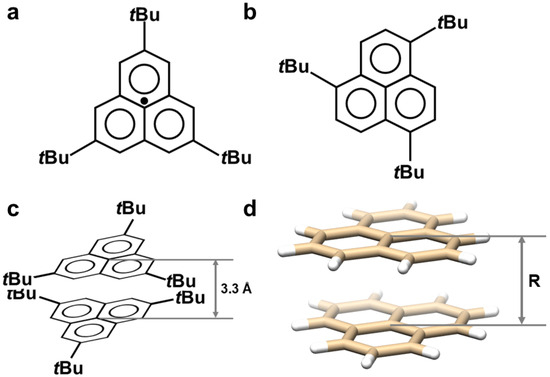
Figure 21.
Structures of the phenalenyl radical with the 2, 5, and 8 t-butyl groups (a) and 1, 4, and 7 t-butyl groups (b), and the stacking dimer structure (c) of a and a simplified dimer structure (d) of c with the same inter plane distance (3.3 Å) [293].
Takano et al. [293] have performed hybrid DFT and CASSCF computations of the dimer model (Figure 21d) of an unsubstituted phenalenyl radical (Figure 21a), as shown in Figure 21. The calculated chemical indices and J values for Figure 21d are summarized in Table 3. The diradical characters (y) were calculated to be about 3 (0.78), 5 (0.72), and 6 (0.70) % for Figure 21d by UB3LYP, CASCF [2o, 2e], and CASSCF [6o, 6e], respectively, where the SOMO-SOMO orbital overlaps are given in parentheses. These chemical indices indicate the characteristics of the nature of chemical bonds of diradicaloids Figure 21d. The calculated J values for Figure 21d are largely negative in sign, indicating −1470 (−1505) and −1729 (−1984) cm−1, where the corresponding values for Figure 21c are given in parentheses. Similar J values between Figure 21c,d indicate that the t-butyl group does not contribute to the SOMO-SOMO interaction.

Table 3.
The effective exchange integrals and chemical indices for the stacking dimer of the parent phenalenyl radical by UHF-based methods and CASSCF methods.
Takano et al. [293] have investigated the slide-type packing structure in Figure 22a–c in addition to the face-to-face packing structures (21d in Figure 21), as illustrated in Figure 22. The calculated J values by UB2LYP were 133 (−4), 346 (72), and 87 (−16) cm−1 for Figure 22a, Figure 22b, and Figure 22c, respectively, where the corresponding values by CASSCF [2o, 2e] are given in parentheses. Interestingly, the calculated J values for Figure 22b by both methods are positive in sign, indicating the conversion of the sign of the J value with the sliding conformation change in the staggered packing: CASSCF [2o, 2e] indicates that the SOMO-SOMO interaction provides a ferromagnetic intermolecular Hund (ferromagnetic) term, which is in sharp contrast to the large intermolecular antiferromagnetic interaction before the sliding, and the nearest intermolecular spin-density product terms (SDP) [45] arising from the spin polarization effect are also ferromagnetic. The numbers of the SDP are given in Figure 22. This means that the ferromagnetic state is realized by controlling the stacking structure of Figure 21a. Kodama et al. [294,295] have reported the through-space antiferromagnetic interactions between phenalenyl radicals.
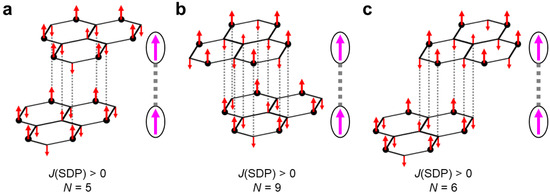
Figure 22.
Dislocated dimer structures of phenalenyl radicals (a–c), indicating the possibility of ferromagnetic interactions (b) between phenalenyl radicals via dynamic spin polarization effects [293]. N denotes the numbers of the nearest intermolecular magnetic couplings via the spin polarization effect obtained by UB2KYP.
Mou et al. [296] have investigated the σ- and π-type stacking modes of the phenalenyl radical. Kubo et al. [280,281] have synthesized the 1,4,7-t-butyl substituted phenalenyl radical (Figure 21b). Interestingly, they have elucidated that the dimer of Figure 21b exhibits a ferromagnetic interaction because of a specific stacking structure in accordance with the calculated results in Figure 21. The experimental results for the phenalenyl radical solids have indicated the necessity of RBS computations using three different BS configurations for triangular radical clusters without covalent bonds in Figure 12, where the delocalized SOMO of a component radical (for example, biphenalenyl radical) is regarded as the localized MO. In fact, Takeda, Kawakami Yamanaka, and their collaborators [200] have developed the ab initio RBS CI scheme for spin-frustrated radical clusters instead of the RVB model [145,146].
Research groups of Prof. Kubo and Prof. Nakano have performed both extensive experimental and theoretical investigations of the dimers and solids of several phenalenyl-type free radicals to develop material sciences of stable radical species. Nowadays, many experimental and theoretical results for phenalenyl derivatives and other stable free radicals have been published in many papers cited in excellent review articles [297,298,299,300,301,302,303]. For example, Abe has reported a review article summarizing a number of experimental and theoretical results [297]. Therefore, citations of all the papers in these reviews are not performed in this theory-oriented review.
6. Nonlinear Optical Properties of Diradical Materials
6.1. Linear and Nonlinear Responses of Materials for Electronic Field
The optical properties of diradicals and clusters of diradicals have attracted great interest for several reasons [52,303]. Nakano and his collaborators focused on the academic interest of fundamental problems of quantum optics [66,67,68,69,70,71]. They are also interested in the nonlinear optical properties of open-shell molecules, such as diradicals, for optical applications. First of all, linear and nonlinear responses of materials for an electronic field are briefly revisited to understand their workings and underlying basic concepts and computational procedures [55,56]. The energy change of molecular materials under the electromagnetic field (F) is generally expanded as follows:
where i, j, k denote the x, y, and z coordinates, and μi, αij, βijk, and γijkl are referred to as dipole moment, polarizability, first hyperpolarizability, and second hyperpolarizability, respectively. The magnetic responses are neglected in Equation (39) for brevity. The first hyperpolarizability βijk (−2ω, ω, ω) is the origin of second-harmonic generation (SHG) [303,304]. The second hyperpolarizability γijkl (−3ω, ω, ω, ω) is the origin of third-harmonic generation (THG). SHG and THG are applicable for investigating the optical responses of molecular materials [305,306].
Polarization Pi at the microscopic level is also defined by the difference of the dipole moment with and without an electronic field as
where Fi denotes the local electronic field for the molecule. On the other hand, macroscopic polarizability is defined by
where I denotes the I-th component of polarizability at the experimental coordinate, and χIJ(1), χIJK(2), and χIJKL(3) are referred to as linear, second-order, and third-order susceptibilities, respectively. Macroscopic second-order χIJK(2) susceptibility disappears in the case of crystals with the inversion center, even if the microscopic βijk is not zero. This, in turn, indicates the utility of the SHG method for the investigation of the structure and bonding of molecules on the surface, etc. [306,307,308]. The third-order susceptibility χIJKL(3) is directly related to γijklf (the local field correction coefficient). Details of f are not touched on in this review [303].
6.2. Theoretical Computational Methods of Linear and Nonlinear Responses of Materials
Response properties of molecules and molecular clusters are highly sensitive to the computational methods and basis sets employed. Theoretically, computational schemes of linear and nonlinear optical responses are generally classified into four methods as follows: (i) sum-over-states (SOS), (ii) response theoretical methods, (iii) the finite field (FF) method, and (iv) the numerical quantum Liouville equation method [55,56]. Time-dependent (TD) perturbation (PT) methods are used for the SOS approach. On the other hand, TD variation principle (VP) methods based on the semi-classical method using the classical electromagnetic field and quantum electronic states of molecules are used for several types of response theories. Sasagane et al. [309] have derived response properties (ii) by the Taylor expansion forms of quasi-energy derivatives (QED). The QED formula at the Hartree–Fock (HF) level of theory is reduced to the TD HF (TDCHF, TDCPHF, RPA) method [310,311]. Kobayashi et al. [312] have used the MP2 method for the QED computations, indicating the importance of correlation correction.
The finite field (FF) method is practically used for the theoretical computations of static polarizability and hyperpolarizability of molecules [313,314]. Several computational methods, such as size-consistent HF, MP2, CC, etc., which are examined in Section 2, Section 3 and Section 4, are indeed applicable to the FF computations of molecular optical properties. The second hyperpolarizability (γ) is given by the fourth derivatives of energy with the electronic field, for example:
where E(Fi) denotes the energy under the electronic field with the i direction.
The computational methods based on the perturbation approaches are not applicable for the higher-order nonlinear responses induced by a strong electronic field. The numerical quantum Liouville equation method [315,316] is one of the computational methods that is useful for such experimental conditions, as illustrated in Figure 23.

Figure 23.
Interrelationships between microscopic (p) and macroscopic (P) polarizations of nonlinear optical materials for the conversion of an incident electric field (FI) to output electronic field (FO) [55,56]. Magnetic response terms are neglected here.
6.3. Functional Behaviors of Nonlinear γ Value with Diradical Character: Exact Models
The electromagnetic properties of diradicals have been investigated extensively in relation to the development of molecular-based materials and devices. Over the past decades, the third-order optical susceptibility, namely the second hyperpolarizability (γ) of molecular materials, has attracted great interest in relation to the generation of squeezed light, which is essential for the formation of the entanglement state for quantum teleportation and optical computation [48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65]. Research groups of Prof. Nakano, Prof. Kubo, and Prof. Champagne [317,318,319,320,321] have performed international collaborative work for the elucidation of fundamental aspects of optical properties of the following open-shell systems: spin, charge, and orbital degrees of freedom of SCES in Figure 1.
To this end, Nakano et al. [315,316] have derived a perturbation expansions formula of γ, elucidating the three following contributions: Type I (0-n-n-n-0), Type II (0-n-0-m-0), Type III-1 (0-n-n-m-0), and Type III-2 (0-n-m-n’-0), where 0, n, n’, and m denote the ground state, virtual n, n’, and m transition states, respectively, as illustrated in Figure 24. Nakano et al. [316,317,318,319,320,321,322] have investigated the functional dependence of γ on the diradical character (y) in Equation (17). They have performed the valence bond (VB) and VB CI exact diagonalization of the Hückel–Hubbard–Hund (HHH) Hamiltonian involving the exchange integral (KAB) for two centers A and B in the two-electron model (2o, 2e) [321].
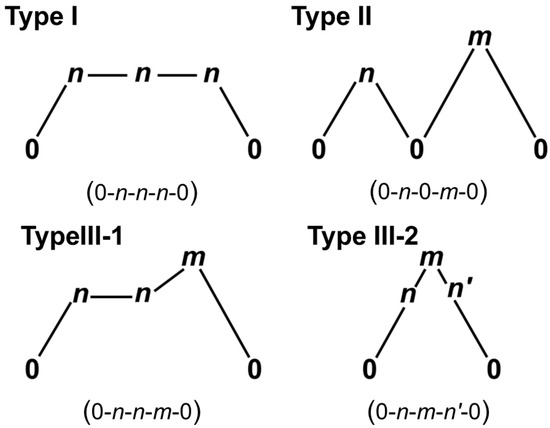
Figure 24.
Classifications of the virtual excitation processes into four types (Type I, Type II, Type III-1, and Type III-2) for the second-order hyperpolarizability (γ) by the perturbation methods [315,316,317].
From the above theoretical modeling, it has been found that the γ values of type II and type III-2, defined by the perturbation expansion formula [321,322], are drastically enhanced in the symmetric open-shell diradical systems with intermediate diradical character (y), as shown in Figure 25. They have also elucidated the interrelationships between γ and the diradical character (y) of molecular materials [321,322]. Thus, theoretical modeling by the above theoretical groups has provided a guiding principle for the development of molecular materials with large γ values for experimental chemists. Judging from their results, diradicals consisting of phenalenyl radicals, in Figure 20, are promising nonlinear optical materials with large γ values.
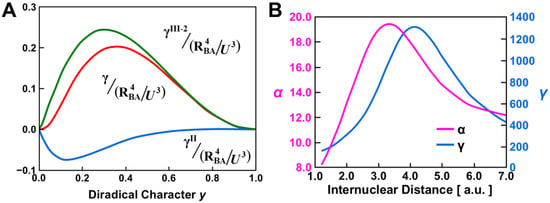
Figure 25.
(A) The enhancement of two types of γ values of molecular materials with the intermediate diradical character (y) was revealed by the valence bond (VB) and full VB CI modeling [321]. (B) Variations in the polarizability (α) and second hyperpolarizability (γ), along with the interatomic distance of the hydrogen molecule by the wave packet method [322].
In order to confirm the above guiding principle, Nakano et al. [322] have developed the finite field (FF) many-electron wave packet (MEWP) method, which provides the exact solution of simple molecules under the Born–Oppenheimer approximation. The FF MEWP method was applied to elucidate the variations in the polarizability (α) and second hyperpolarizability (γ) with the elongation (ΔX) of the H-H distance of the hydrogen molecule with [2o, 2e], as shown in Figure 25B. From Figure 25B, the α and γ values indeed increase in the intermediate dissociation region with the intermediate diradical character, and these values decrease in the dissociation region with the strong radical character. This means an important contribution of the ZW configuration in the VB CI model for enhancement of the linear and nonlinear polarizabilities, supporting the guiding principle for a large γ [318,319,320,321,322,323].
6.4. Variations in the Nonlinear γ Value with Diradical Character: ab Initio Computations
The internal cis-trans rotation of the C=C double bond in Figure 26 has been regarded as a diradical process [141,142], for which the potential curve is qualitatively described by the Hubbard model, as shown in Figure 7. Very recently, a highly twisted C=C double bond (θ = 57.33 degree) of bianthrone derivative substituted with long-chain alkoxy groups in the intermediate π-bond dissociation region was isolated, indicating the elongated C-C distance (1.429 Å), which was revealed with X-ray diffraction [324]. Judging from the intermediate twisted angle, an intermediate diradical character is expected for this compound. On the other hand, a perpendicularly twisted double of ethylene exhibited strong (y = 1.0) diradical character, which is in sharp contrast to the planer ethylene with a C-C double bond, as shown in Figure 5h [142].
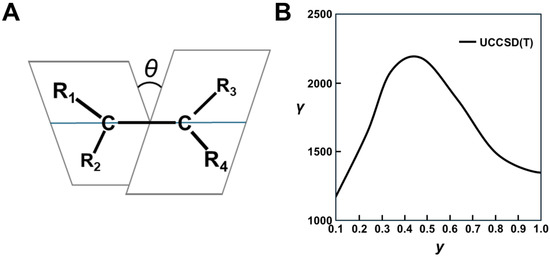
Figure 26.
(A) The optimized geometry of the internal rotation of ethylene with diradical character (y); (B) variations in the second hyperpolarizability (γ) against the diradical character (y) by the UCCSD(T) method, indicating the maximum value in the intermediate diradical region [142,325,326].
Yamada and Nakano et al. [325,326] have examined the variations in γ with the twisted angle (θ) of the CH2 group, as illustrated in Figure 26A. The FF UCCSD(T) method was applied to elucidate the variations in γ against the diradical character (y), as shown in Figure 26B. The γ value was found to be maximum near the diradicaloids conformation with the intermediate diradical character (y = 0.4–0.5). Thus, the above newly synthesized ethylene derivative [324] is indeed expected as such a desired example [325,326]. Similar conclusions for the γ value have been derived for twisted ethylene by the MRCISD and AP DFT methods [327,328].
The γ value is supposed to be sensitive to the elongation of the C-C distance of the planer conformation of π-electron compounds [329,330,331,332]. The para-quinodimethane (PQM) molecule [333] in Figure 27A is a typical example among them since the electronic structure of PQM is regarded as the quinoid (B) structure (y = 0–10%) with a short R1 distance and a diradical (C) structure (y = 80–90%) with an elongated R1 distance. Therefore, the diradical character (y) of POM increases with the elongation of R1. The γ values of POM [330,333] were calculated by both the RHF and UHF MP(CC) methods, as shown in Figure 25B. From 25B, the γ value by the RHF-dependent CCSD(T) decreases suddenly in the 50–60% diradical region, indicating its breakdown in the strong diradical conformation (y > 0.5). On the other hand, UCCSD(T) provides the maximum γ value of POM in the intermediate radical region (y = 0.5), supporting the general tendency.
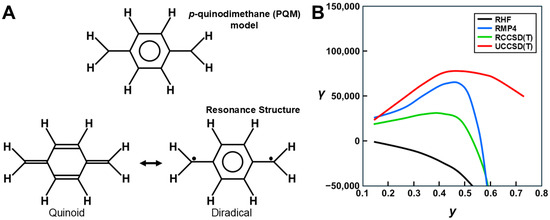
Figure 27.
(A) The resonating state between the quinoid and diradical structures of para-quinodimethane (PQM); (B) the second hyperpolarizability (γ) of PQM by the RHF- and UHF-based CCSD(T) methods [330,331,332,333].
6.5. γ Values of 1,3-Diradical and 1,3- Dipole: ab Initio Computations
Abe et al. have synthesized 1,3-diradicals with several substituents and related diradicals and have elucidated the structure, bonding, and reactivity, as shown in their review article [160]. The diradical characters (y) of 1,3-dipoles: H2C-X-CH2 are variable with types of the center group: X = CH2 (Figure 8a), O(Figure 8b), and NH (Figure 8c), as shown in Figure 5 [131,132]. The contribution of the zwitterionic (ZW) configurations in the LNO CI (VB CI) contributes to a reduction in the y value, as illustrated in Figure 9 and Figure 28A. Kishi and Nakano have developed the quantum Master equation combined with the BS time-dependent DFT with the Tamm–Dankoff approximation (BS DFTQME) [334]. They have applied the BS DFTQME method for the investigation of dynamic polarizability (α) of 1,3-dipoles in relation to many experimental investigations. Kishi et al. [335] have examined the γ values of 1,3-dipoles by using the long-range corrected (LC) UBLYP methods with and without spin projection (SP), as shown in Figure 28B. The natural orbital analysis of the LC UBLYP has also been performed for elucidation of its spin contamination. From Figure 28B, the γ values of these species by the SP UBLYP and UCCSD(T) methods are found to become maximum in the intermediate region (y = 0.4), indicating that the SP procedure is effective in removing the spin contamination error of the broken symmetry (BS) DFT method. The ZW configuration in Figure 28A plays an important role in the enhancement of γ in the 1,3-diradicaloids compounds.
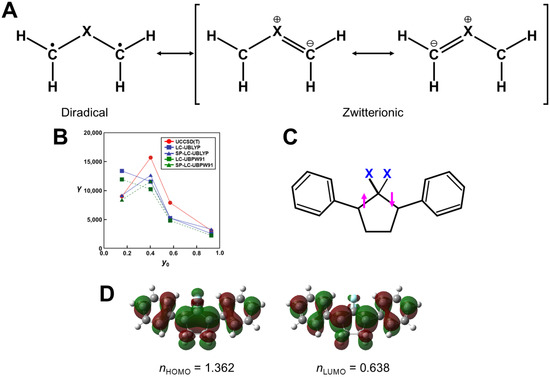
Figure 28.
(A) Diradical and zwitterionic structures of 1,3-dipole species, (B) variations in the γ of 1,4-dipoles by UCCSD(T) and UBLYP with and without spin projection (SP); (C) 1,3-dipenylcyclopentane 1,3-diyl derivatives (DPCP), and (D) occupation numbers (n) of HOMO and LUMO of DPCP with X = F [335].
Kishi et al. [335] have investigated the nonlinear optical properties of several 1,3-dipenylcyclopentane 1,3-diyl derivatives (DPCP) by BS DFT methods, as shown in Figure 28. The unsubstituted DPCP (X = H) indicated a strong diradical character. On the other hand, the introduction of electron-donating (X = OH) and -withdrawing (X = F) substituents for DPCP have induced a reduction in the y value because of the push–pull effects. In fact, the orbital overlaps (Ti) (diradical character (y)) are calculated to be 0.033 (97%), 0.280 (72%), and 0.362 (64%), respectively, for the DPCP with X = H, OH, and F. Therefore, the magnitudes of the γ value are enhanced by factors of 4.5 for DPCP with X = OH and 6.4 for DPCP with X = F, as compared with that of DPCP with X = H.
Kishi et al. [335] have examined DPCP with phenyl-substituted analogs. They calculated several chemical indices (see Figure 9) based on the occupation numbers of the canonical natural orbitals obtained by the natural orbital analysis of BS DFT solutions for complex DPCP. Their procedures are useful for theoretical investigations of linear and nonlinear properties of many other large organic systems, such as biphenalene systems with t-butyl substituents [289] and 20π electron systems with a small HOMO-LUMO gap responding to a radical character (see Equation (1)).
The Kubo and Nakano groups have elucidated the diradical characters (y) of two biphenalenyl linked π-electron systems in Figure 20, indicating the nonlinear correlations between y and the second hyperpolarizability (γ) of the biphenalenyl compound in Figure 20a with hetero atoms X: for example, γ = 1349 × 103 a.u. (X = S; y = 77%), 1934 × 103 a.u. (X = O; y = 73%), 415 × 103 a.u. (X = BH; y = 37%), and 98 × 103 a.u. (X = C = S; y = 0%), supporting the selection rules in Figure 24, Figure 25 and Figure 26. Many experimental and theoretical results summarized in their papers indicate the constructive collaboration of theory and experiments for the structure, bonding, and properties of molecular materials with open-shell characters.
6.6. Nonlinear Optical Materials: γ Values of Nitronyl Niroxide
Inorganic materials such as BaTiO3 have been used for nonlinear optical materials. In the 1990s, Prasad, Kana, and Bredas and their collaborators [313,336,337,338,339] were challenged to open the door for both experimental and theoretical investigations of organic and polymeric compounds as nonlinear optical materials. They examined the nonlinear optical properties of polyene derivatives, aromatic compounds, polymers, etc. Contributions of charge transfer (CT) excitations induced with the introduction of donor-accepter substituents have also been examined for enhancements of optical responses of these materials with closed-shell ground states [336,337,338,339]. On the other hand, the use of open-shell molecules for such materials was limited at that time.
Yamada, Shigemoto, and Nakano [340,341,342] began to examine the opportunities to use open-shell organic molecules as nonlinear optical materials. To this end, they examined the nonlinear optical properties of simple nitroxide radical (H2N=O•) in comparison with formaldehyde (H2C=O) using ab initio HF, MPn (n = 2–4), CCSD, CCSD(T), QCI, and DFT methods. The basis set effects were also examined to elucidate the nature of the chemical bond of the nitroxide group. They used the FF methods for theoretical computations of the γ values. They have found that the extended basis sets, including both diffuse p and d functions, were reliable for the estimation of the second hyperpolarizability, such as the γzzzz value of H2NO. They examined variations in the γzzzz value of H2NO with the above computational methods, indicating the utility of the CCSD and CCSD(T) methods for quantitative purposes. The BLYP method was also effective for this purpose. Yamada et al. [341] performed the computations of the first hyperpolarizability, the βzzz value of H2NO, proving the same conclusion: the importance of the CCSD method.
Bulky groups were introduced for the stabilization of organic nitroxides with the N=O radical reactive group. Para-nitrophenyl nitronyl nitroxide (p-NPNN) was an interesting nitroxide among them since the β-phase crystal of p-NPNN was found to be an organic ferromagnet (see later). According to the perturbation selection rule in Figure 24, p-NPNN was expected to exhibit the negative γxxxx (χ(3)XXXX) in the X-direction of the bond axis of the nitronyl nitroide group, as illustrated in Figure 29. There are two intermolecular interacting modes, (A) and (B), in the β-phase crystal of p-NPNN. Yamada et al. [342] have performed the FF field computation χ(3) based on the oriented gas model for crystal [343]. They found that the χ(3)xxxx for the X-direction of Figure 28A was negative in accordance with the theoretical prediction, and χ(3)zzzz for the Z-direction was positive. The magnitude of χ(3)XXXX was larger than χ(3)ZZZZ, indicating the net negative χ(3) value for the β-phase crystal of p-NPNN.
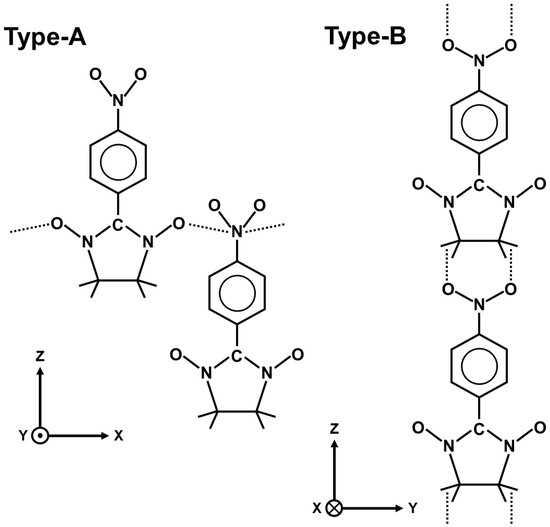
Figure 29.
Intermolecular interactions between p-NPNN in the β-phase crystal: (Type-A) the X-Z plane with negative χ(3) XXXX, and (Type-B) the X-Y plane with positive χ(3) ZZZZ. The magnitude of χ(3) XXXX is larger than that of χ(3) ZZZZ [342].
Yamada et al. [344] further examined the nonlinear optical properties of radical species, elucidating a new opportunity. Since then, a number of diradicals with two nitroxide radicals and triradicals with three nitroxide radicals have been synthesized, as summarized in a recent review article [345]. As shown in a recent paper [346], an appropriately selected DFT functional is effective for the investigations of structure and nonlinear optical properties of very large molecules, for which UCCSD with extended basis sets is impossible. In this review, we do not discuss the applications of SHG and THG for the many spectroscopic experiments summarized in recent review articles [305,306,307,308,347,348].
7. Discussions, Conclusions, and Future Prospects
7.1. A New Direction for Molecular Magnetism
In the 1980s, one of the important targets in the field of molecular magnetism was the generation and construction of pure organic ferromagnets without strong spin-orbit interactions. Several theoretical models and experimental efforts [40,45,224,225,226,349,350] were performed to search for the appropriate organic radicals, such as nitroxide radicals with a quantum spin S = 1/2. In 1991, genuine long-range ferromagnetism was realized for the β-phase crystal of the p-NPNN radical with S = 1/2 [351]. Since then, many nitroxide compounds have been synthesized to achieve pure organic ferromagnets, and organic ferromagnetism was realized in well-organized packing forms with a ferromagnetic exchange interaction [351,352]. The AP BS method was successfully applied to elucidate the origin of the ferromagnetic exchange interaction (J) between p-NPNN [353].
After the great discovery of pure organic ferromagnet (long-range order) by the Kinoshita group [351,352], Gatteschi and Yamaguchi discussed opportunities for new physics in molecular magnetism [44]. In the 1980s, macroscopic quantum tunneling (MQT) and macroscopic quantum coherence (MQC) [354,355,356,357,358,359,360,361,362,363,364,365,366,367,368] in mesoscopic systems were considered new physics [44]. In 1983, Caldeira and Leggett examined quantum tunneling (MQT) in a dissipative system [354]. Leggett and Garg discussed the possibility of the observation of MQC in a realistic experiment [355]. Leggett and collaborators presented the results of a functional-integral approach to the dynamics of a two-state system coupled to a dissipative environment [356]. Chudnovsky and Gunther performed theoretical computations of the probability of MQT of several model clusters with magnetic anisotropy, indicating such a possibility [357]. In the 1990s, we changed the scientific paradigm from 4M to 4Q for our quantum chemistry group, namely molecular (M) to quantum (Q) X: X = magnetism (MM → QM), X = dynamics (MD → QD), X = information (MI → QI), and X = biology (MB → QB) [98]. Quantum effects such as MQT and MQC [358,359,360,361,362,363] were considered possible new directions of molecular magnetism. Sessoli, Gatteschi, and their collaborators have reported the MQT for a mesoscopic Mn cluster: Mn12O12Ln [358,359]. Nishino et al. have examined the antiferromagnetic exchange interaction between Cr atoms, proposing an MQT for Cr atom clusters [360]. Many inorganic complexes have been synthesized for the examination of MQT [358,359]. Nagao et al. [361] have performed the path-integral formulations of the spin structures of several Mn clusters, presenting the expressions of tunneling rates for cluster spins. Nagao, Nakano, and Shigeta [362] have discussed the relationships between quantum light and spin (see Figure 3). Wernsdorfer and Sessoli [363] derived the selection rules for MQT, emphasizing the Berry phase [89,90,364]. The transition metal complexes toward MQT are summarized in review articles [365,366]. However, the MQC materials [354,356] were not so developed for molecular systems, although Nakamura et al. [97] discovered MQC for superconducting materials. Nagao et al. [367] and Leuenberger and Loss [368] proposed the potential use of Mn12O12Ln for quantum computing.
7.2. NMR Computer and Other Candidates for Quantum Bits
In the 1980s–1990s, fundamental theories were published in relation to quantum computing [154,369,370,371,372,373,374,375]. Researchers of IBM [376] constructed the NMR computer using the two nuclear spins as quantum (q) bits, demonstrating the quantum algorithm of fast quantum searching by Grover [377]. They also constructed the NMR computer with seven qubits [378], demonstrating the polynomial-time algorithm for prime factorization [379]. These successes have caused scientific interest in searching qubits for quantum computing, quantum teleportation, and quantum sensing. As mentioned above, Nagao et al. [367] were interested in the use of electron spin instead of nuclear spin, proposing manganese complexes as a possible candidate for quantum qubits. On the other hand, Nakano et al. had an interest in the fundamental sciences of quantum optics [60,61], performing quantum dynamics simulations [66,67]. We have found several proposals for the purpose, as summarized in Figure 30 in our book (Chapter 14.4) [24].
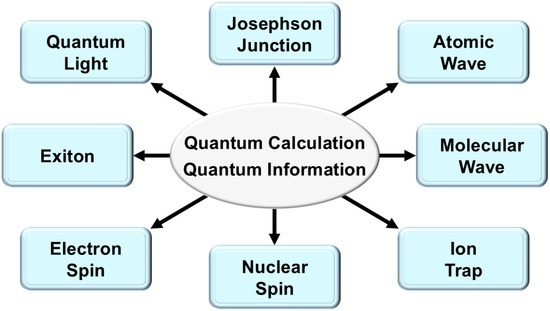
Figure 30.
Possible candidates for qubits for quantum information (QI) and quantum computation (QC) [24]: nuclear spin, electron spin, exciton, quantum light, Josephson junction (superconductor), atomic wave, molecular wave, and ion trap (Figure 14.4 of the book [24]).
In the 2000s, several groups presented proposals for molecule-based q-bits. Recently, open-shell inorganic and organic molecular materials have attracted renewed interest from quantum information science as molecular qubits for quantum devices (see later). Topological materials [20,22,85,86,87,88,89,90,380] are also expected to protect the topological order from environmental effects. Quantum optics are also expected to offer protection for topological materials against defects [381]. However, such recent topics are not touched upon in this review article.
7.3. Opportunities of Inorganic Open-Shell Species as Quantum Materials
Inorganic open-shell species are considered as possible candidates of qubits in Figure 30. Ishikawa and his group have synthesized phthalocyanito-lanthanide complexes [382,383,384]. They derived the selection rules for the MQT of the f-electron of lanthanide compounds on both experimental and theoretical grounds. Ishikawa, Sugita, and Wernsdorfer indeed observed the nuclear spin-driven quantum tunneling of magnetization in the new lanthanide single-molecule magnet [385]. Ishikawa and his group [385,386] also synthesized binuclear lanthanide complexes, elucidating similar MQTs for the binuclear f-f complex. Kato et al. [387] synthesized the multiple-decker phthalocyanine dinuclear lanthanide (III) single molecular magnets. They elucidated the magnetic behaviors of the complex.
Molecular spins were expected as qubits in Figure 30 [362,363,365,380,388,389]. Recently, Ruben and Wernsdorfer’s group demonstrated the utility of the above phthalocyanine-lanthanide complexes (TbPc2) for quantum computations [390,391,392]. Their achievements are summarized in a review article [392]. Atzori et al. [393] performed a search of spin systems with long-lived quantum coherence, finding the vanadium (IV) complex as a potential inorganic molecule for the purpose [394]. Atzori and Sessoli presented a perspective review article for the second quantum revolution in molecular materials [395]. The decoherence [396], temperature [397], etc., remain future issues for molecular quantum materials.
7.4. Early and Recent Investigations of Organic Radicals and Diradicals as Quantum Materials
Stable organic radicals, diradicals, and polyradicals are considered as challenging molecules for quantum and optical devices in Figure 30. Basic mathematical and physical concepts for quantum computations and quantum optics have been published in well-known papers [47,57,60,356,357,358,359,360,361,362,363,364]. First of all, dynamic spin polarizations of open-shell molecules have been investigated by using the EPR and ENDOR methods [398,399,400,401,402]. The organic chemists’ group [403,404] synthesized open-shell systems with nitroxide groups, which were investigated as possible quantum materials by using pulsed ENDOR [405]. The same magnetic experiments were performed for many nitroxide molecules synthesized; too many molecular structures are omitted in this review.
According to the Lloyd theory [373], packing structures of nitroxide molecules are also important for the construction of quantum devices [406]. Therefore, crystal engineering [407,408] was crucial for the realization of the desired packing structure of organic radicals [409]. We have considered the magnetic modifications of DNA with an introduction of stable radical groups for the formation of 1D, 2D, and 3D magnetic materials [410]. Maekawa et al. [411] synthesized the programmed assembly of organic radicals on DNA. Mujica-Martinez investigated the possibility of π-conjugated copolymers as molecular-charge qubits on the theoretical ground [412]. Recently, experimental and theoretical investigations have been extensively performed on the structure, bonding, and properties of organic radicals for quantum devices [413,414,415,416,417,418,419,420,421,422]. Probably, a design of topologically stable molecular q-bits will be important in the future [85,86,87,88,89,90,380].
7.5. A New Direction for Optical Molecular Materials for Quantum Optics
Nonlinear optical materials have been used for SHG and THG procedures, which are applicable to laser formations from IR to UV lasers [53] and several types of optical experiments for molecular and biological materials [307]. Nakano and his collaborators searched for a new direction of quantum optical materials [60,61], finding an interesting application to optical quantum computing [52,62]. To this end, basic notions of the coherent state [48,49,50,51,52,53,54,55,56], squeezed quantum light [57,58,59], quantum phase [66,67,68,69,70,71], and entanglement state [63,64] were found to be essential for opening a new direction of theoretical chemistry at Osaka [98]. Historically, the quantum phase in quantum mechanics has been an important but difficult problem [423,424,425,426]. The phase operator by Pegg–Barnett [68,69] is now accepted [427], providing a fundamental concept and procedure for quantum optics. Nakano and his collaborators were deeply involved in quantum physics, such as quantum collapse and revival phenomena [72], performing a quantum dynamic simulation for two- and three-level models of molecular systems [70] and two-component Bose–Einstein condensates [71]. Nowadays, entanglement states [63,65] generated with two squeezed quantum lights are important for quantum teleportation [428,429,430,431,432,433,434,435], optical quantum computing [52,62,65,436,437,438], and quantum sensing [439].
However, the decoherence of the quantum state [355,356,357] remains serious for dissipative quantum molecular systems, such as single molecular magnets with quantum spin, seen in Figure 3 and Figure 30. The same is true for the squeezed quantum light generated by using nonlinear optical materials and the quantum entangled state. Therefore, Nakano et al. [440] investigated dissipative quantum molecular systems [355,356,357,381] with interactions with two different reservoirs using the Monte Carlo wavefunction approach [441], which is similar to the related quantum dynamics methods for dissipative systems [442,443], as illustrated in Figure 31B, proving fundamental information on the relaxation processes of optical quantum systems [440,444]. Such dynamic information is important for understanding, designing, and constructing optical quantum devices based on molecules: quantum sensing, quantum teleportation, and optical computation [62].
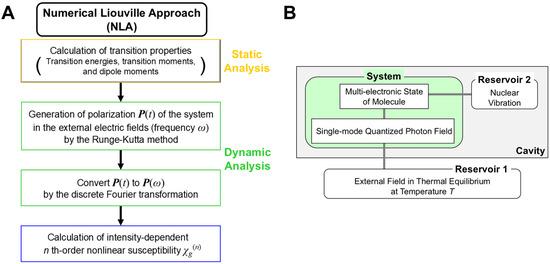
Figure 31.
(A) The numerical Liouville approach to calculate the time (t)- and frequency (ω)-dependent n-th order nonlinear susceptibilities of the strongly correlated molecular materials [440]. (B) The Monte Carlo wave function (or master equation) approaches to quantum dissipative photon fields, such as squeezed light interacting with an external field (reservoir 1) and nuclear vibration (reservoir 2) [440].
7.6. Concluding Remarks and Future Prospects
In this review article, basic concepts and approaches of chemical sciences in the Osaka group (see Figure 2) are briefly touched on in relation to our early efforts for theoretical investigations of strongly correlated electron systems (SCES), which are now receiving great interest in the field of material and biological sciences, as illustrated in Figure 1 (see Section 1). Symmetry breaking [76,77] and topological symmetry [22,87] are guiding principles for SCES. In the 1970s, a diradical, one of the SCESs, was regarded as an unstable, reactive intermediate of forbidden reactions [160] of the Woodward–Hoffman (WH) rule [31,32]. The basic concept of the WH rule for concerted reactions is “the orbital symmetry conservation”. Numerous significant non-mechanistic reactions, previously unexplained, are now understood through application of the Woodward–Hoffmann rule. Therefore, the concept of “the orbital symmetry breaking” and the resulting local spins [126] was not a familiar one in the early days. However, during such a period, basic theories and computational methods were developed to elucidate the nature of the chemical bonds of diradicals and chemical indices, such as the diradical character (see Section 2, Section 3 and Section 4) of open-shell molecules. Great efforts by organic chemists realized that stable diradicals were protected by bulky groups [138,139,160,266], which were detected and characterized with several magnetic and optical experiments. Nowadays, such stable diradicals have been synthesized, as shown in this Special Issue for diradicals. The concept of the orbital-symmetry-breaking and the recovery of the spin symmetry via quantum resonance is also a guiding principle for understanding and explanation of the chemical bonds of diradicals.
In the 1980s, stable radicals, such as nitroxide radicals, were regarded as the building blocks of spin-dependent materials, such as organic ferromagnets [224,351,352,353]. Pure organic ferromagnetism was realized for a three-dimensional (3D) crystal of para-nitrophenyl nitroxide (p-NPNN) [352]. Organic ferromagnets were found for crystals of other nitroxide molecules [352], indicating that a classical long-range order is feasible with 3D crystals of a spin S = 1/2 organic molecules. Phenalenyl radicals, stabilized by bulky groups, are also used as building blocks for large π-diradicals and π-polyradicals via the through-bond and through-space exchange interactions. Antiferromagnetic exchange interactions between phenalenyl radicals were found to have origins of the so-called spin frustrations and resonating VB (RVB) states of specific clusters and solid structures [278,290], indicating the quantum nature of a molecular spin S = 1/2. Recently, organic diradicals, triradicals, and polyradicals have been focused on as quantum bits for the construction of optical quantum devices, such as quantum sensing, for which quantum dynamic simulations of open-shell materials interacting with quantum lights are essential, as shown in many papers by Prof. Nakano and his group [440,444].
Prof. Masayoshi Nakano has written a comprehensive review article entitled the “Diradical Character-Based Design of Functional Molecular Systems” [445], summarizing the fundamental concepts, theoretical and computational methods, and important conclusions obtained by himself, his group (Dr. Yamada, Dr. Shigemoto, and Dr. Kishi, in particular) and from collaborations with the Prof. Kubo group., while Prof. Nakano and Prof. Champagne have participated in international collaborations on the nonlinear optics of open-shell molecules. Nakano and his collaborators have elucidated the structure, bonding, and properties (mainly optical) of open-shell systems with a diradical character and excited states of π-electron systems. To this end, they developed the numerical Liouville, Monte Carlo wave function and quantum aster equation methods for theoretical investigations of both static and dynamical optical properties, as illustrated in Figure 31A. These methods have been successfully applied to elucidate the optical properties of open-shell molecules and molecular clusters. Some of their results are revisited in this review article. Unfortunately, the late Prof. Nakano could not continue the quantum dynamic simulations of dissipative quantum systems, such as open-shell molecules interacting with quantum lights [440,444], which provide indispensable information for the development of quantum optical devices. However, his successors are now performing such quantum dynamic computations in the Center of Quantum Information and Quantum Biology (QIQB). Finally, we would like to express our sincere thanks for all of the efforts of the late Prof. Nakano, who opened a new door for quantum chemistry on quantum optics, quantum optical materials, and devices.
Author Contributions
Conceptualization, S.Y., I.S. and K.Y.; methodology, S.Y., I.S. and K.M.; software, S.Y., I.S. and T.K.; investigation, S.Y., I.S., H.I., M.S., T.K., K.M. and K.Y.; writing—original draft preparation, K.Y.; writing—review and editing, K.Y., T.K. and K.M.; visualization, K.M.; supervision, K.Y.; project administration, K.Y.; funding acquisition, H.I., M.S. and K.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by JP20H05453 (M.S.), JP22K05317 (H.I.), and JP22H04916 (M.S. and K.Y.).
Data Availability Statement
The dataset is available on request from the corresponding author.
Acknowledgments
We thank all the members of our published manuscripts in this review article. One of the authors (K.Y.) would like to thank J. Paldus and H. Fukutome for their guidance, suggestions, and discussions regarding the scope and applicability of broken symmetry (BS) and beyond BS methods. We also thank Y. Yoshioka, H. Nagao, Y. Takano, and Y. Shigeta for their collaboration and support. We would like to thank B. Champagne for the helpful international collaborations. Numerical calculations were carried out with the support of the Research Center for Computational Science, Okazaki, Japan.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- De Broglie, L. Recherches sur la théorie des Quanta. Ann. Phys. 1925, 10, 22–128. [Google Scholar] [CrossRef]
- Heisenberg, W. Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Z. Phys. 1925, 33, 879–893. [Google Scholar] [CrossRef]
- Heisenberg, W. Zur Quantentheorie der Multiplettstruktur und der anomalen Zeemaneffekte. Z. Phys. 1925, 32, 841–860. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The fundamental equations of quantum mechanics. Proc. R. Soc. Lond. A 1925, 109, 642–653. [Google Scholar] [CrossRef]
- Born, M.; Heisenberg, W.; Jordan, P. Zur Quantenmechanik. II. Z. Phys. 1926, 35, 557–615. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem. Ann. Phys. 1926, 384, 361–376. [Google Scholar] [CrossRef]
- Schrödinger, E. Der stetige Übergang von der Mikro- zur Makromechanik. Naturwissenschaften 1926, 14, 664–666. [Google Scholar] [CrossRef]
- Born, M.; Jordan, P. Zur Quantenmechanik. Z. Phys. 1925, 34, 858–888. [Google Scholar] [CrossRef]
- Pauli, W. Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik. Z. Phys. 1926, 36, 336–363. [Google Scholar] [CrossRef]
- Born, M. Zur Quantenmechanik der Stoßvorgänge. Z. Phys. 1926, 37, 863–867. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The physical interpretation of the quantum dynamics. Proc. R. Soc. Lond. A 1927, 113, 621–641. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Schrödinger, E. Über den Comptoneffekt. Ann. Phys. 1927, 387, 257–264. [Google Scholar] [CrossRef]
- Heitler, W.; London, F. Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik. Z. Phys. 1927, 44, 455–472. [Google Scholar] [CrossRef]
- Born, M.; Oppenheimer, R. Zur Quantentheorie der Molekeln. Ann. Phys. 1927, 389, 457–484. [Google Scholar] [CrossRef]
- Lewis, G.N. Valence and the Structure of Atoms and Molecules; American Chemical Monograph Series; Chemical Catalog Company: New York, NY, USA, 1923. [Google Scholar]
- Pauling, L. The Shared-Electron Chemical Bond. Proc. Natl. Acad. Sci. USA 1928, 14, 359–362. [Google Scholar] [CrossRef] [PubMed]
- Hund, F. Zur Deutung einiger Erscheinungen in den Molekelspektren. Z. Phys. 1926, 36, 657–674. [Google Scholar] [CrossRef]
- Mulliken, R.S. The Assignment of Quantum Numbers for Electrons in Molecules. I. Phys. Rev. 1928, 32, 186–222. [Google Scholar] [CrossRef]
- Klitzing, K.V.; Dorda, G.; Pepper, M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 1980, 45, 494–497. [Google Scholar] [CrossRef]
- Laughlin, R.B. Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations. Phys. Rev. Lett. 1983, 50, 1395–1398. [Google Scholar] [CrossRef]
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys. Rev. Lett. 1982, 49, 405–408. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Possible highTc superconductivity in the Ba−La−Cu−O system. Z. Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yoshioka, Y.; Nakano, M.; Nagao, H.; Okumura, M. Bussei Ryoshikagaku Nyumon; Kodansha Scientific: Tokyo, Japan, 2004. [Google Scholar]
- Vedral, V. Introduction to Quantum Information Science; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Alfieri, A.; Anantharaman, S.B.; Zhang, H.; Jariwala, D. Nanomaterials for Quantum Information Science and Engineering. Adv. Mater. 2023, 35, 2109621. [Google Scholar] [CrossRef]
- Benioff, P. The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines. J. Stat. Phys. 1980, 22, 563–591. [Google Scholar] [CrossRef]
- Buluta, I.; Nori, F. Quantum Simulators. Science 2009, 326, 108–111. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.; Li, Z. Recent progress in open-shell organic conjugated materials and their aggregated states. J. Mater. Chem. C 2022, 10, 2431–2449. [Google Scholar] [CrossRef]
- Fukui, K. The role of frontier orbitals in chemical reactions (Nobel lecture). Angew. Chem. Int. Ed. 1982, 21, 801–809. [Google Scholar] [CrossRef]
- Hoffmann, R.; Woodward, R.B. Selection Rules for Concerted Cycloaddition Reactions. J. Am. Chem. Soc. 1965, 84, 2046–2048. [Google Scholar] [CrossRef]
- Woodward, R.B.; Hoffmann, R. The Conservation of Orbital Symmetry. Angew. Chem. Int. Ed. 1969, 8, 781–853. [Google Scholar] [CrossRef]
- Fukui, K.; Yonezawa, T.; Nagata, C.; Shingu, H. Molecular Orbital Theory of Orientation in Aromatic, Heteroaromatic, and Other Conjugated Molecules. J. Chem. Phys. 1954, 22, 1433–1442. [Google Scholar] [CrossRef]
- Longuet-Higgins, H.C.; Abrahamson, E.W. The Electronic Mechanism of Electrocyclic Reactions. J. Am. Chem. Soc. 1965, 87, 2045–2046. [Google Scholar] [CrossRef]
- Dewar, M.J.S. Aromaticity and Pericyclic Reactions. Angew. Chem. Int. Ed. 1971, 10, 761–776. [Google Scholar] [CrossRef]
- Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids 1959, 10, 87–98. [Google Scholar] [CrossRef]
- Goodenough, J.B. Magnetism and The Chemical Bond; John Wiley & Sons: Chichester, UK, 1963. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Löwdin, P.-O. Quantum Genetics and the Aperiodic Solid: Some Aspects on the Biological Problems of Heredity, Mutations, Aging, and Tumors in View of the Quantum Theory of the DNA Molecule. In Advances in Quantum Chemistry; Löwdin, P.-O., Ed.; Elsevier: Amsterdam, The Netherlands, 1966; Volume 2, pp. 213–360. [Google Scholar] [CrossRef]
- Yamaguchi, K. Instability in Chemical Bonds—SCF, APUMP, APUCC, MR-CI and MR- CC Approaches. In Self-Consistent Field: Theory and Applications; Carbó, R., Klobukowski, M., Eds.; Elsevier: Amsterdam, The Netherlands, 1990; pp. 727–823. [Google Scholar]
- Yamaguchi, K. Symmetry and broken symmetry in molecular orbital (MO) descriptions of unstable molecules. Generalized MO theoretical studies on 1,3-dipolar species. J. Mol. Struct. THEOCHEM 1983, 103, 101–120. [Google Scholar] [CrossRef]
- Yamaguchi, K. Theoretical calculations of singlet oxygen reactions. In Singlet O2; Frimer, A.A., Ed.; CRC Press: Boca Raton, FL, USA, 1985; Volume III, Chapter 2; pp. 119–250. [Google Scholar]
- Yamaguchi, K.; Takada, K.; Otsuji, Y.; Mizuno, K. Theoretical and general aspects of organic peroxides. In Organic Peroxides; Ando, W., Ed.; John Wiley & Sons: Chichester, UK, 1992; pp. 1–100. [Google Scholar]
- Gatteschi, D.; Yamaguchi, K. Opportunities for New Physics in Molecular Magnetism. In Molecular Magnetism: From Molecular Assemblies to the Devices NATO ASI Series; Coronado, E., Delhaès, P., Gatteschi, D., Miller, J.S., Eds.; Springer: Dordrecht, The Netherlands, 1996; Volume 321, pp. 561–570. [Google Scholar] [CrossRef]
- Yamaguchi, K. Electrons in Specific Molecular Systems. In From Molecules to Molecular Systems; Nagakura, S., Ed.; Springer: Tokyo, Japan, 1998; pp. 67–91. [Google Scholar]
- Yamaguchi, K.; Isobe, H.; Shoji, M.; Kawakami, T.; Miyagawa, K. The Nature of the Chemical Bonds of High-Valent Transition–Metal Oxo (M=O) and Peroxo (MOO) Compounds: A Historical Perspective of the Metal Oxyl–Radical Character by the Classical to Quantum Computations. Molecules 2023, 28, 7119. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Miyagawa, K.; Shoji, M.; Kawakami, T.; Isobe, H.; Yamanaka, S.; Nakajima, T. Theoretical elucidation of the structure, bonding, and reactivity of the CaMn4Ox clusters in the whole Kok cycle for water oxidation embedded in the oxygen evolving center of photosystem II. New molecular and quantum insights into the mechanism of the O–O bond formation. Photosynth. Res. 2024, 162, 291–330. [Google Scholar] [CrossRef]
- Klauder, J.R. The action option and a Feynman quantization of spinor fields in terms of ordinary c-numbers. Ann. Phys. 1960, 11, 123–168. [Google Scholar] [CrossRef]
- Glauber, R.J. The Quantum Theory of Optical Coherence. Phys. Rev. 1963, 130, 2529–2539. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766–2788. [Google Scholar] [CrossRef]
- Sudarshan, E.C.G. Equivalence of Semiclassical and Quantum Mechanical Descriptions of Statistical Light Beams. Phys. Rev. Lett. 1963, 10, 277–279. [Google Scholar] [CrossRef]
- Walls, D.F.; Milburn, G.J. Quantum Optics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Mandel, L.; Wolf, E. Coherence Properties of Optical Fields. Rev. Mod. Phys. 1965, 37, 231–287. [Google Scholar] [CrossRef]
- Perelomov, A.M. Coherent states for arbitrary Lie group. Commun. Math. Phys. 1972, 26, 222–236. [Google Scholar] [CrossRef]
- Kimble, H.J.; Mandel, L. Theory of resonance fluorescence. Phys. Rev. A 1976, 13, 2123–2144. [Google Scholar] [CrossRef]
- Walls, D.F.; Zoller, P. Reduced Quantum Fluctuations in Resonance Fluorescence. Phys. Rev. Lett. 1981, 47, 709–711. [Google Scholar] [CrossRef]
- Walls, D.F. Squeezed states of light. Nature 1983, 306, 141–146. [Google Scholar] [CrossRef]
- Slusher, R.E.; Hollberg, L.W.; Yurke, B.; Mertz, J.C.; Valley, J.F. Observation of Squeezed States Generated by Four-Wave Mixing in an Optical Cavity. Phys. Rev. Lett. 1985, 55, 2409–2412. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.-A.; Kimble, H.J.; Hall, J.L.; Wu, H. Generation of Squeezed States by Parametric Down Conversion. Phys. Rev. Lett. 1986, 57, 2520–2523. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Analysis of nonlinear optical processes for molecular systems. In Trends in Chemical Physics; Research Trends: Trivandrum, India, 1997; Volume 5, pp. 87–237. [Google Scholar]
- Nakano, M.; Yamaguchi, K. Polarizabilities and Hyperpolarizabilities of Dendritic Systems. In Advances in Multi-Photon Processes and Spectroscopy; Lin, S.H., Villaeys, A.A., Fujimura, Y., Eds.; World Scientific: Singapore, 2003; Volume 15, pp. 3–146. [Google Scholar]
- Knill, E.; Laflamme, R.; Milburn, G. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Moreau, P.-A.; Toninelli, E.; Gregory, T.; Padgett, M.J. Imaging with quantum states of light. Nat. Rev. Phys. 2019, 1, 367–380. [Google Scholar] [CrossRef]
- Asavanant, W.; Shiozawa, Y.; Yokoyama, S.; Charoensombutamon, B.; Emura, H.; Alexander, R.N.; Takeda, S.; Yoshikawa, J.; Menicucci, N.C.; Yonezawa, H.; et al. Generation of time-domain-multiplexed two-dimensional cluster state. Science 2019, 366, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Yamaguchi, K. Quantum-phase and information-entropy dynamics of a two-state molecular system interacting with strongly amplitude- and phase-squeezed fields. J. Chem. Phys. 2000, 112, 2769–2780. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Quantum-phase and information-entropy dynamics of a molecular system interacting with a two-mode squeezed coherent field. Phys. Rev. A 2001, 64, 033415. [Google Scholar] [CrossRef]
- Pegg, D.T.; Barnett, S.M. Phase properties of the quantized single-mode electromagnetic field. Phys. Rev. A 1989, 39, 1665–1675. [Google Scholar] [CrossRef] [PubMed]
- Barnett, S.M.; Pegg, D.T. Quantum theory of optical phase correlations. Phys. Rev. A 1990, 42, 6713–6720. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Yamada, S.; Yamaguchi, K. Quantum phase dynamics: Collapse and revival behavior in a two- and a three-state molecule systems interacting with an initially one-mode coherent field. Synth. Met. 1999, 102, 1540–1541. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Ohta, S.; Takahashi, H.; Furukawa, S.; Yamaguchi, K. Quantum-phase dynamics of two-component Bose–Einstein condensates: Collapse–revival of macroscopic superposition states. Phys. B Condens. Matter 2005, 370, 110–120. [Google Scholar] [CrossRef]
- Rempe, G.; Walther, H.; Klein, N. Observation of quantum collapse and revival in a one-atom maser. Phys. Rev. Lett. 1987, 58, 353–356. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Mizushima, S. A History of Physical Chemistry in Japan. Annu. Rev. Phys. Chem. 1972, 23, 1–14. [Google Scholar] [CrossRef]
- Anderson, P.W. More Is Different. Science 1972, 177, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y. Nobel Lecture: Spontaneous symmetry breaking in particle physics: A case of cross fertilization. Rev. Mod. Phys. 2009, 81, 1015–1018. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Quantum mechanics of many-electron systems. Proc. R. Soc. Lond. A 1929, 123, 714–733. [Google Scholar] [CrossRef]
- Rainwater, J. Nuclear Energy Level Argument for a Spheroidal Nuclear Model. Phys. Rev. 1950, 79, 432–434. [Google Scholar] [CrossRef]
- Higgs, P.W. Spontaneous Symmetry Breakdown without Massless Bosons. Phys. Rev. 1966, 145, 1156–1163. [Google Scholar] [CrossRef]
- Kobayashi, M.; Maskawa, T. CP-Violation in the Renormalizable Theory of Weak Interaction. Prog. Theor. Phys. 1973, 49, 652–657. [Google Scholar] [CrossRef]
- Slater, J.C. Ferromagnetism and the Band Theory. Rev. Mod. Phys. 1953, 25, 199–210. [Google Scholar] [CrossRef]
- Nesbet, R.K. Approximate Methods in the Quantum Theory of Many-Fermion Systems. Rev. Mod. Phys. 1961, 33, 28–36. [Google Scholar] [CrossRef]
- Fukutome, H. The Unrestricted Hartree-Fock Theory of Chemical Reactions. I: The Electronic Instabilities in the Chemical Reactions and the Solutions of the Unrestricted SCF LCAO MO Equation for the Homopolar Two-Center Two-Electron System. Prog. Theor. Phys. 1972, 47, 1156–1180. [Google Scholar] [CrossRef]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 1973, 6, 1181–1203. [Google Scholar] [CrossRef]
- Kosterlitz, J.M. Kosterlitz–Thouless physics: A review of key issues. Rep. Prog. Phys. 2016, 79, 026001. [Google Scholar] [CrossRef] [PubMed]
- Haldane, F.D.M. Nonlinear Field Theory of Large-Spin Heisenberg Antiferromagnets: Semiclassically Quantized Solitons of the One-Dimensional Easy-Axis Néel State. Phys. Rev. Lett. 1983, 50, 1153–1156. [Google Scholar] [CrossRef]
- Affleck, I.; Kennedy, T.; Lieb, E.H.; Tasaki, H. Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev. Lett. 1987, 59, 799–802. [Google Scholar] [CrossRef]
- Longuet-Higgins, H.C.; Öpik, U.; Pryce, M.H.L.; Sack, R.A. Studies of the Jahn-Teller effect II. The dynamical problem. Proc. R. Soc. Lond. A 1958, 244, 1–16. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 1984, 392, 45–57. [Google Scholar] [CrossRef]
- Ichikawa, K. Souzousei No Kagaku; NHK Publishing: Tokyo, Japan, 1970. [Google Scholar]
- Magri, F. Equivalence transformations for nonlinear evolution equations. J. Math. Phys. 1977, 18, 1405–1411. [Google Scholar] [CrossRef]
- Bellucci, S.; Ivanov, E.; Krivonos, S. AdS/CFT equivalence transformation. Phys. Rev. D 2002, 66, 086001. [Google Scholar] [CrossRef]
- Ganghoffer, J.F.; Rahouadj, R.; Cheviakov, A. Symmetry analysis and equivalence transformations for the construction and reduction of constitutive models. Adv. Model. Simul. Eng. Sci. 2021, 8, 1. [Google Scholar] [CrossRef]
- Hoffmann, R. Building Bridges Between Inorganic and Organic Chemistry (Nobel Lecture). Angew. Chem. Int. Ed. 1982, 21, 711–724. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Miyagawa, K.; Isobe, H.; Shoji, M.; Kawakami, T.; Yamanaka, S. Isolobal and isospin analogy between organic and inorganic open-shell molecules—Application to oxygenation reactions by active oxygen and oxy-radicals and water oxidation in the native and artificial photosynthesis. In Advances in Quantum Chemistry; Brändas, E.J., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Volume 84, pp. 425–564. [Google Scholar] [CrossRef]
- Nakamura, Y.; Pashkin, Y.A.; Tsai, J.S. Coherent control of macroscopic quantum states in a single-Cooper-pair box. Nature 1999, 398, 786–788. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Nakano, M.; Nagao, H.; Okumura, M.; Yamanaka, S.; Kawakami, T.; Yamaki, D.; Nishino, M.; Shigeta, Y.; Kitagawa, Y.; et al. Spin and Pseudo Spins in Theoretical Chemistry. A Unified View for Superposed and Entangled Quantum Systems. Bull. Korean Chem. Soc. 2003, 24, 864–880. [Google Scholar] [CrossRef]
- Anderson, P.W. Random-Phase Approximation in the Theory of Superconductivity. Phys. Rev. 1958, 112, 1900–1916. [Google Scholar] [CrossRef]
- Leggett, A.J. A theoretical description of the new phases of liquid 3He. Rev. Mod. Phys. 1975, 47, 331–414. [Google Scholar] [CrossRef]
- Matsunaga, R.; Tsuji, N.; Fujita, H.; Sugioka, A.; Makise, K.; Uzawa, Y.; Terai, H.; Wang, Z.; Aoki, H.; Shimano, R. Light-induced collective pseudospin precession resonating with Higgs mode in a superconductor. Science 2014, 345, 1145–1149. [Google Scholar] [CrossRef]
- Aoki, H.; Tsuji, N.; Eckstein, M.; Kollar, M.; Oka, T.; Werner, P. Nonequilibrium dynamical mean-field theory and its applications. Rev. Mod. Phys. 2014, 86, 779–837. [Google Scholar] [CrossRef]
- Kitagawa, M.; Ueda, M. Squeezed spin states. Phys. Rev. A 1993, 47, 5138–5143. [Google Scholar] [CrossRef] [PubMed]
- Perlin, M.A.; Qu, C.; Rey, A.M. Spin Squeezing with Short-Range Spin-Exchange Interactions. Phys. Rev. Lett. 2020, 125, 223401. [Google Scholar] [CrossRef]
- Comparin, T.; Mezzacapo, F.; Roscilde, T. Robust spin squeezing from the tower of states of U(1)-symmetric spin Hamiltonians. Phys. Rev. A 2022, 105, 022625. [Google Scholar] [CrossRef]
- Bornet, G.; Emperauger, G.; Chen, C.; Ye, B.; Block, M.; Bintz, M.; Boyd, J.A.; Barredo, D.; Comparin, T.; Mezzacapo, F.; et al. Scalable spin squeezing in a dipolar Rydberg atom array. Nature 2023, 621, 728–733. [Google Scholar] [CrossRef]
- Block, M.; Ye, B.; Roberts, B.; Chern, S.; Wu, W.; Wang, Z.; Pollet, L.; Davis, E.J.; Halperin, B.I.; Yao, N.Y. Scalable spin squeezing from finite-temperature easy-plane magnetism. Nat. Phys. 2024, 20, 1575–1581. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 48, 777–780. [Google Scholar] [CrossRef]
- Hückel, E. Quantentheoretische Beiträge zum Benzolproblem, I. Die Elektronenkonfiguration des Benzols und verwandter Verbindungen. Z. Phys. 1931, 70, 204–286. [Google Scholar] [CrossRef]
- Hoffmann, R. An Extended Hückel Theory. I. Hydrocarbons. J. Chem. Phys. 1963, 39, 1397–1412. [Google Scholar] [CrossRef]
- Hubbard, J. Electron correlations in narrow energy bands. Proc. R. Soc. Lond. A 1963, 276, 238–257. [Google Scholar] [CrossRef]
- Kanamori, J. Electron Correlation and Ferromagnetism of Transition Metals. Prog. Theor. Phys. 1963, 30, 275–289. [Google Scholar] [CrossRef]
- Gutzwiller, M.C. Effect of Correlation on the Ferromagnetism of Transition Metals. Phys. Rev. Lett. 1963, 10, 159–162. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Floris, A.; de Gironcoli, S.; Cococcioni, M. Hubbard-corrected DFT energy functionals: The LDA+U description of correlated systems. Int. J. Quant. Chem. 2014, 114, 14–49. [Google Scholar] [CrossRef]
- Pauli, W., Jr. Zur Quantenmechanik des magnetischen Elektrons. Z. Phys. 1927, 43, 601–623. [Google Scholar] [CrossRef]
- Jordan, P.; Wigner, E. Über das Paulische Äquivalenzverbot. Z. Phys. 1928, 47, 631–651. [Google Scholar] [CrossRef]
- Bravyi, S.B.; Kitaev, A.Y. Fermionic Quantum Computation. Ann. Phys. 2002, 298, 210–226. [Google Scholar] [CrossRef]
- Hartree, D.R. The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part I. Theory and Methods. Math. Proc. Camb. Philos. Soc. 1928, 24, 89–110. [Google Scholar] [CrossRef]
- Fock, V. Näherungsmethode zur Lösung des quantenmechanischen Mehrkörperproblems. Z. Phys. 1930, 61, 126–148. [Google Scholar] [CrossRef]
- Overhauser, A.W. Giant Spin Density Waves. Phys. Rev. Lett. 1960, 4, 462–465. [Google Scholar] [CrossRef]
- Thouless, D.J. Stability conditions and nuclear rotations in the Hartree-Fock theory. Nucl. Phys. 1960, 21, 225–232. [Google Scholar] [CrossRef]
- Sawada, K.; Fukuda, N. On the Stability of the Hartree-Fock Solution in Many-Body Problem. Prog. Theor. Phys. 1961, 25, 653–666. [Google Scholar] [CrossRef]
- Čížek, J.; Paldus, J. Stability conditions for the solutions of the Hartree-Fock equations for atomic and molecular systems. Application to the pi-electron model of cyclic polyenes. J. Chem. Phys. 1967, 47, 3976–3985. [Google Scholar] [CrossRef]
- Fukutome, H. Spin density wave and charge transfer wave in long conjugated molecules. Prog. Theor. Phys. 1968, 40, 998–1012. [Google Scholar] [CrossRef]
- Slater, J.C. Magnetic Effects and the Hartree-Fock Equation. Phys. Rev. 1951, 82, 538–541. [Google Scholar] [CrossRef]
- Yamaguchi, K. The electronic structures of biradicals in the unrestricted Hartree-Fock approximation. Chem. Phys. Lett. 1975, 33, 330–335. [Google Scholar] [CrossRef]
- Yamaguchi, K. Electronic structures of antiaromatic molecules. Chem. Phys. Lett. 1975, 35, 230–235. [Google Scholar] [CrossRef]
- Yamaguchi, K. Singlet unrestricted Hartree-Fock Slater (UHFS) model for unstable metal-metal bonds. Chem. Phys. Lett. 1979, 66, 395–399. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fueno, T. Mechanistic characterization of the thermal ring-opening of three-membered cyclic compounds. Chem. Phys. Lett. 1973, 22, 471–475. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Ohta, K.; Yabushita, S.; Fueno, T. Generalized Hartree-Fock natural-orbital configuration-interaction (GHF NO CI) approach to unstable molecules: Trimethylene. Chem. Phys. Lett. 1977, 49, 555–559. [Google Scholar] [CrossRef]
- Huisgen, R. Electrocyclic Ring Opening Reactions of Ethylene Oxides. Angew. Chem. Int. Ed. 1977, 16, 572–585. [Google Scholar] [CrossRef]
- Houk, K.N.; Yamaguchi, K. Theory of 1,3-Dipolar Cycloadditions. In 1,3-Dipolar Cycloaddition Chemistry; Padwa, A., Ed.; Wiley: New York, NY, USA, 1984; Volume 2, Chapter 13; pp. 407–448. [Google Scholar]
- Hoffmann, R.; Zeiss, G.D.; van Dine, G.W. The electronic structure of methylenes. J. Am. Chem. Soc. 1968, 90, 1485–1499. [Google Scholar] [CrossRef]
- Harrison, J.F. Electronic structure of carbenes. I. Methylene, fluoromethylene, and difluoromethylene. J. Am. Chem. Soc. 1971, 93, 4112–4119. [Google Scholar] [CrossRef]
- Harrison, J.F.; Liedtke, R.C.; Liebman, J.F. The multiplicity of substituted acyclic carbenes and related molecules. J. Am. Chem. Soc. 1979, 101, 7162–7168. [Google Scholar] [CrossRef]
- Bauschlicher, C.W., Jr.; Schaefer, H.F., III; Bagus, P.S. Structure and energetics of simple carbenes methylene, fluoromethylene, chloromethylene, bromomethylene, difluoromethylene, and dichloromethylene. J. Am. Chem. Soc. 1977, 99, 7106–7110. [Google Scholar] [CrossRef]
- Feller, D.; Borden, W.T.; Davidson, E.R. Dependence of the singlet-triplet splitting in heterosubstituted carbenes on the heteroatom electronegativity and conformation. Chem. Phys. Lett. 1980, 71, 22–26. [Google Scholar] [CrossRef]
- Tomioka, H. Persistent Triplet Carbenes. Acc. Chem. Res. 1997, 30, 315–321. [Google Scholar] [CrossRef]
- Hirai, K.; Itoh, T.; Tomioka, H. Persistent Triplet Carbenes. Chem. Rev. 2009, 109, 3275–3332. [Google Scholar] [CrossRef] [PubMed]
- Bourissou, D.; Guerret, O.; Gabbaï, F.P.; Bertrand, G. Stable Carbenes. Chem. Rev. 2000, 100, 39–92. [Google Scholar] [CrossRef] [PubMed]
- Wyman, G.M. The Cis-Trans Isomerization of Conjugated compounds. Chem. Rev. 1955, 55, 625–657. [Google Scholar] [CrossRef]
- Dugave, C.; Demange, L. Cis−Trans Isomerization of Organic Molecules and Biomolecules: Implications and Applications. Chem. Rev. 2003, 103, 2475–2532. [Google Scholar] [CrossRef] [PubMed]
- Oka, T.; Maeda, T.; Sakamaki, D.; Suzuki, N.; Yagi, S.; Kodama, S.; Fujiwara, H. Intermediate diradical character and thermal cis–trans isomerization of near-infrared absorbing thionated squaraine dyes. Org. Chem. Front. 2025, 12, 42–47. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yabushita, S.; Minokawa, O.; Fueno, T. DODS natural-orbital CI (DODS-NO CI) approach to the excited states of unstable molecules: Twisted substituted ethyelenes. Chem. Phys. Lett. 1978, 59, 303–307. [Google Scholar] [CrossRef]
- Anderson, P.W. Basic Notations of Condensed Matter Physics; Benjamin/Cummings Publishing Co.: Menio Park, CA, USA, 1984. [Google Scholar]
- Anderson, P.W. Resonating valence bonds: A new kind of insulator? Mater. Res. Bull. 1973, 8, 153–160. [Google Scholar] [CrossRef]
- Anderson, P.W. The Resonating Valence Bond State in La2CuO4 and Superconductivity. Science 1987, 235, 1196–1198. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yoshioka, Y.; Fueno, T. Interrelationships between the effective Hamiltonians for the H3 radical. Chem. Phys. Lett. 1977, 46, 360–365. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yoshioka, Y.; Takatsuka, T.; Fueno, T. Extended Hartree-Fock (EHF) theory in chemical reactions II. Symmetry properties of the EHF wavefunctions constructed by the magnetically ordered general spin orbitals. Theoret. Chim. Acta 1978, 48, 185–206. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fukui, H.; Fueno, T. Molecular orbital (MO) theory for magnetically interacting organic compounds. ab-initio MO calculations of the effective exchange integrals for cyclophane-type carbene dimers. Chem. Lett. 1986, 15, 625–628. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Tsunekawa, T.; Toyoda, Y.; Fueno, T. Ab initio molecular orbital calculations of effective exchange integrals between transition metal ions. Chem. Phys. Lett. 1988, 143, 371–376. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Jensen, F.; Dorigo, A.; Houk, K.N. A spin correction procedure for unrestricted Hartree-Fock and Møller-Plesset wavefunctions for singlet diradicals and polyradicals. Chem. Phys. Lett. 1988, 149, 537–542. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419–478. [Google Scholar] [CrossRef]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef]
- Schrödinger, E. Discussion of Probability Relations between Separated Systems. Math. Proc. Camb. Philos. Soc. 1936, 31, 555–563. [Google Scholar] [CrossRef]
- Freedman, S.J.; Clauser, J.F. Experimental Test of Local Hidden-Variable Theories. Phys. Rev. Lett. 1972, 28, 938–941. [Google Scholar] [CrossRef]
- Aspect, A.; Grangier, P.; Roger, G. Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities. Phys. Rev. Lett. 1982, 49, 91–94. [Google Scholar] [CrossRef]
- Breugst, M.; Reissig, H.-U. The Huisgen Reaction: Milestones of the 1,3-Dipolar Cycloaddition. Angew. Chem. Int. Ed. 2020, 59, 12293–12307. [Google Scholar] [CrossRef] [PubMed]
- Abe, M.; Ye, J.; Mishima, M. The chemistry of localized singlet 1,3-diradicals (biradicals): From putative intermediates to persistent species and unusual molecules with a π-single bonded character. Chem. Soc. Rev. 2012, 41, 3808–3820. [Google Scholar] [CrossRef] [PubMed]
- Skell, P.S.; Doerr, R.G. Trimethylenemethane. J. Am. Chem. Soc. 1967, 89, 4688–4692. [Google Scholar] [CrossRef]
- Dowd, P. Trimethylenemethane. Acc. Chem. Res. 1972, 5, 242–248. [Google Scholar] [CrossRef]
- Berson, J.A. The chemistry of trimethylenemethanes, a new class of biradical reactive intermediates. Acc. Chem. Res. 1978, 11, 446–453. [Google Scholar] [CrossRef]
- Davidson, E.R.; Borden, W.T. Some aspects of the potential surface for singlet trimethylenemethane. J. Am. Chem. Soc. 1977, 99, 2053–2060. [Google Scholar] [CrossRef]
- Davis, J.H.; Goddard, W.A., III. Electronic states of trimethylenemethane. J. Am. Chem. Soc. 1977, 99, 4242–4247. [Google Scholar] [CrossRef]
- Hood, D.M.; Pitzer, R.M.; Schaefer, H.F., III. Equilibrium geometry of trimethylenemethane and the absence of an adjacent secondary minimum on the triplet potential energy surface. J. Am. Chem. Soc. 1978, 100, 2227–2228. [Google Scholar] [CrossRef]
- Kollmar, H.; Staemmler, V. A theoretical study of the structure of cyclobutadiene. J. Am. Chem. Soc. 1977, 99, 3583–3587. [Google Scholar] [CrossRef]
- Borden, W.T. Can a square or effectively square singlet be the ground state of cyclobutadiene? J. Am. Chem. Soc. 1975, 97, 5968–5970. [Google Scholar] [CrossRef]
- Coulson, C.A.; Rushbrooke, G.S. Note on the method of molecular orbitals. Math. Proc. Camb. Philos. Soc. 1940, 36, 193–200. [Google Scholar] [CrossRef]
- Salem, L.; Rowland, C. The Electronic Properties of Diradicals. Angew. Chem. Int. Ed. 1972, 11, 92–111. [Google Scholar] [CrossRef]
- Lykos, P.; Pratt, G.W. Discussion on the Hartree-Fock approximation. Rev. Mod. Phys. 1963, 35, 496–501. [Google Scholar] [CrossRef]
- Löwdin, P.-O. Some Aspects on the Correlation Problem and Possible Extensions of the Independent-Particle Model. In Advances in Chemical Physics; LeFebvre, R., Moser, C., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1969; Volume 14, pp. 283–340. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fueno, T. Correlation effects in singlet biradical species. Chem. Phys. 1977, 19, 35–42. [Google Scholar] [CrossRef]
- Yamaguchi, K. Generalized molecular orbital (GMO) theories of organic reaction mechanisms. Orbital symmetry, orbital stability and orbital pairing rules. Chem. Phys. 1978, 29, 117–139. [Google Scholar] [CrossRef]
- Nagamiya, T. Helical Spin Ordering—1 Theory of Helical Spin Configurations. Solid State Phys. 1968, 20, 305–411. [Google Scholar] [CrossRef]
- Shirane, G.; Chikazumi, S.; Akimitsu, J.; Chiba, K.; Matsui, M.; Fujii, Y. Neutron Scattering from Low-Temperature Phase of Magnetite. J. Phys. Soc. Jpn. 1975, 39, 949–957. [Google Scholar] [CrossRef]
- Nalewajski, R.F. Entropic Measures of Bond Multiplicity from the Information Theory. J. Phys. Chem. A 2000, 104, 11940–11951. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Shepelevich, I.S. Information Entropy in Chemistry: An Overview. Entropy 2021, 23, 1240. [Google Scholar] [CrossRef]
- Lewis, G.N. The atom and the molecule. J. Am. Chem. Soc. 1916, 38, 762–785. [Google Scholar] [CrossRef]
- Linnett, J.W. A Modification of the Lewis-Langmuir Octet Rule. J. Am. Chem. Soc. 1961, 83, 2643–2653. [Google Scholar] [CrossRef]
- Linnett, J.W.; Poë, A.J. Directed valency in elements of the first short period. Trans. Faraday Soc. 1951, 47, 1033–1041. [Google Scholar] [CrossRef]
- Linnett, J.W. Valency and the chemical bond. Am. Sci. 1964, 52, 459–475. [Google Scholar]
- Firestone, R.A. Application of the Linnett electronic theory to organic chemistry. IV. SN2 transition state. J. Org. Chem. 1971, 36, 702–711. [Google Scholar] [CrossRef]
- Firestone, R.A. Application of the Linnett electronic theory to organic chemistry. V. Orientation in 1,3-dipolar cycloadditions according to the diradical mechanism. Partial formal charges in the Linnett structures of the diradical intermediate. J. Org. Chem. 1972, 37, 2181–2191. [Google Scholar] [CrossRef]
- Huisgen, R. 1,3-Dipolar Cycloadditions. Past and Future. Angew. Chem. Int. Ed. 1963, 2, 565–598. [Google Scholar] [CrossRef]
- Huisgen, R. 1,3-Dipolar cycloadditions. 76. Concerted nature of 1,3-dipolar cycloadditions and the question of diradical intermediates. J. Org. Chem. 1976, 41, 403–419. [Google Scholar] [CrossRef]
- Löwdin, P.-O.; Shull, H. Natural Orbitals in the Quantum Theory of Two-Electron Systems. Phys. Rev. 1956, 101, 1730–1739. [Google Scholar] [CrossRef]
- Sinanoğlu, O. Many-Electron Theory of Atoms and Molecules. I. Shells, Electron Pairs vs Many-Electron Correlations. J. Chem. Phys. 1962, 36, 706–717. [Google Scholar] [CrossRef]
- Saito, T.; Nishihara, S.; Kataoka, Y.; Nakanishi, Y.; Kitagawa, Y.; Kawakami, T.; Yamanaka, S.; Okumura, M.; Yamaguchi, K. Multireference Character of 1,3-Dipolar Cycloaddition of Ozone with Ethylene and Acrylonitrile. J. Phys. Chem A 2010, 114, 12116–12123. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Ohta, K.; Fueno, T. Localized natural orbitals of unstable molecules: Ozone. Chem. Phys. Lett. 1977, 50, 266–270. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fueno, T. Diradical and zwitterionic intermediates in the excited state. Chem. Phys. 1977, 23, 375–386. [Google Scholar] [CrossRef]
- Yoshimori, A. A New Type of Antiferromagnetic Structure in the Rutile Type Crystal. J. Phys. Soc. Jpn. 1959, 14, 807–821. [Google Scholar] [CrossRef]
- Yamaguchi, K. General spin structures of organic radicals. Chem. Phys. Lett. 1975, 30, 288–292. [Google Scholar] [CrossRef]
- Husimi, K.; Syôzi, I. The Statistics of Honeycomb and Triangular Lattice. I. Prog. Theor. Phys. 1950, 5, 177–186. [Google Scholar] [CrossRef]
- Syozi, I. The Statistics of Honeycomb and Triangular Lattice. II. Prog. Theor. Phys. 1950, 5, 341–351. [Google Scholar] [CrossRef]
- Bradley, C.J.; Cracknell, A.P. The Mathematical Theory of Symmetry in Solids: Representation Theory for Point Groups and Space Groups; Oxford University Press: Oxford, UK, 1972; Chapter 7; pp. 569–683. [Google Scholar]
- Yamaguchi, K.; Yoshioka, Y.; Fueno, F. Heisenberg models of radical reactions: Local spin (magnetic) symmetry conservations of biradical species. Chem. Phys. 1977, 20, 171–181. [Google Scholar] [CrossRef]
- Yamanaka, S.; Yamaki, D.; Shigeta, Y.; Nagao, H.; Yoshioka, Y.; Suzuki, N.; Yamaguchi, K. Generalized spin density functional theory for noncollinear molecular magnetism. Int. J. Quant. Chem. 2000, 80, 664–671. [Google Scholar] [CrossRef]
- Yamanaka, S.; Takeda, R.; Yamaguchi, K. Density functional study of tetrahedral manganese clusters. Polyhedron 2003, 22, 2013–2017. [Google Scholar] [CrossRef]
- Takeda, R.; Yamanaka, S.; Yamaguchi, K. Spin-optimized resonating Hartree-Fock configuration interaction. Int. J. Quant. Chem. 2007, 107, 3219–3227. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yamanaka, S.; Nishino, M.; Takano, Y.; Kitagawa, Y.; Nagao, H.; Yoshioka, Y. Symmetry and broken symmetries in molecular orbital descriptions of unstable molecules II. Alignment, flustration and tunneling of spins in mesoscopic molecular magnets. Theoret. Chem. Acc. 1999, 102, 328–345. [Google Scholar] [CrossRef]
- Einsle, O.; Rees, D.C. Structural Enzymology of Nitrogenase Enzymes. Chem. Rev. 2020, 120, 4969–5004. [Google Scholar] [CrossRef]
- Reiher, M.; Wiebe, N.; Svore, K.M.; Wecker, D.; Troyer, M. Elucidating reaction mechanisms on quantum computers. Proc. Natl. Acad. Sci. USA 2017, 114, 7555–7560. [Google Scholar] [CrossRef]
- Miyagawa, K.; Shoji, M.; Isobe, H.; Yamanaka, S.; Kawakami, T.; Okumura, M.; Yamaguchi, K. Theory of chemical bonds in metalloenzymes XXIV electronic and spin structures of FeMoco and Fe-S clusters by classical and quantum computing. Mol. Phys. 2020, 118, e1760388. [Google Scholar] [CrossRef]
- Ozaki, M.; Fukutome, H. Group Theoretical Classification of Solutions of the Unrestricted Hartree-Fock Equation in Molecular Systems with a Spatial Point Symmetry. Prog. Theor. Phys. 1978, 60, 1322–1336. [Google Scholar] [CrossRef]
- Yamanaka, S.; Takeda, R.; Kawakami, T.; Nakano, S.; Yamaki, D.; Yamada, S.; Nakata, K.; Sakuma, T.; Takada, T.; Yamaguchi, K. Spin correlation functions by generalized spin orbital density functional and multireference approaches. Int. J. Quant. Chem. 2003, 95, 512–520. [Google Scholar] [CrossRef]
- Yamanaka, S.; Yamaki, D.; Takeda, R.; Nagao, H.; Yamaguchi, K. J-model for magnetism and superconductivity of triangular, kagome, and related spin lattice systems. Int. J. Quant. Chem. 2004, 100, 1179–1196. [Google Scholar] [CrossRef]
- Pauling, L. The Nature of The Chemical Bond, 3rd ed.; Cornell University Press: Ithaca, NY, USA, 1960; p. 204. [Google Scholar]
- Fazekas, P.; Anderson, P.W. On the ground state properties of the anisotropic triangular antiferromagnet. Philos. Mag. 1974, 30, 423–440. [Google Scholar] [CrossRef]
- Kivelson, S.A.; Rokhsar, D.S.; Sethna, J.P. Topology of the resonating valence-bond state: Solitons and high-Tc superconductivity. Phys. Rev. B 1987, 35, 8865–8868. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yamanaka, S.; Isobe, H.; Kawakami, K.; Kitagawa, Y.; Takeda, R.; Saito, T.; Nishihara, M.; Okumura, M. Instability in Chemical Bonds from Broken-Symmetry Single-Reference to Symmetry-Adapted Multireference Approaches to Strongly Correlated Electron Systems. AIP Conf. Proc. 2009, 1108, 20–29. [Google Scholar] [CrossRef]
- Kawakami, T.; Takeda, R.; Nishihara, S.; Saito, T.; Shoji, M.; Yamada, S.; Yamanaka, S.; Kitagawa, Y.; Okumura, M.; Yamaguchi, K. Symmetry and Broken-Symmetry in Molecular Orbital Descriptions of Unstable Molecules. 3. The Nature of Chemical Bonds of Spin Frustrated Systems. J. Phys. Chem. A 2009, 113, 15281–15297. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.; Wang, X. Spin Frustration in Organic Radicals. Angew. Chem. Int. Ed. 2024, 63, e202310147. [Google Scholar] [CrossRef]
- Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Maesato, M.; Saito, G. Spin Liquid State in an Organic Mott Insulator with a Triangular Lattice. Phys. Rev. Lett. 2003, 91, 107001. [Google Scholar] [CrossRef] [PubMed]
- Broholm, C.; Cava, R.J.; Kivelson, S.A.; Nocera, D.G.; Norman, M.R.; Senthil, T. Quantum spin liquids. Science 2020, 367, eaay0668. [Google Scholar] [CrossRef]
- Zhou, Y.; Kanoda, K.; Ng, T.-K. Quantum spin liquid states. Rev. Mod. Phys. 2017, 89, 025003. [Google Scholar] [CrossRef]
- Matsen, F.A. Spin-Free Quantum Chemistry. In Advances in Quantum Chemistry; Löwdin, P.-O., Ed.; Elsevier: Amsterdam, The Netherlands, 1964; Volume 1, pp. 59–114. [Google Scholar] [CrossRef]
- Klein, D.J.; Junker, B.R. Spin-Free Computation of Matrix Elements. I. Group-Theoretical Computation of Pauling Numbers. J. Chem. Phys. 1971, 54, 4290–4296. [Google Scholar] [CrossRef]
- Yoshioka, Y.; Yamaguchi, K.; Fueno, T. Heisenberg models of radical reactions II. Conservation of the local spin-permutation symmetry in reactions of biradical species. Theoret. Chim. Acta 1977, 45, 1–20. [Google Scholar] [CrossRef]
- Pauncz, R. The Construction of Spin Eigenfunctions: An Exercise Book; Springer: New York, NY, USA, 2000. [Google Scholar]
- Song, M.; Alavi, A.; Li Manni, G. Permutation symmetry in spin-adapted many-body wave functions. Faraday Discuss. 2024, 254, 261–294. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Takahara, Y.; Fueno, T. Ab-initio molecular orbital studies of structure and reactivity of transition metal-oxo compounds. In Applied Quantum Chemistry; Smith, V.H., Jr., Schaefer, H.F., III, Morokuma, K., Eds.; D. Reidel Publishing Company: Lancaster, UK, 1986; pp. 155–184. [Google Scholar] [CrossRef]
- Matsen, F.A. Correlation of molecular orbital and valence bond states in π systems. Acc. Chem. Res. 1978, 11, 387–392. [Google Scholar] [CrossRef]
- Itoh, K. Electron spin resonance of an aromatic hydrocarbon in its quintet ground state. Chem. Phys. Lett. 1967, 1, 235–238. [Google Scholar] [CrossRef]
- Wasserman, E.; Murray, R.W.; Yager, W.A.; Trozzolo, A.M.; Smolinsky, G. Quintet ground states of m-dicarbene and m-dinitrene compounds. J. Am. Chem. Soc. 1967, 89, 5076–5078. [Google Scholar] [CrossRef]
- Breslow, R.; Chang, H.W.; Hill, R.; Wasserman, E. Stable Triplet States of Some Cyclopentadienyl Cations. J. Am. Chem. Soc. 1967, 89, 1112–1119. [Google Scholar] [CrossRef]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. [Google Scholar] [CrossRef] [PubMed]
- Chan, G.K.-L.; Sharma, S. The Density Matrix Renormalization Group in Quantum Chemistry. Annu. Rev. Phys. Chem. 2011, 62, 465–481. [Google Scholar] [CrossRef]
- Cirac, J.I.; Pérez-García, D.; Schuch, N.; Verstraete, F. Matrix product states and projected entangled pair states: Concepts, symmetries, theorems. Rev. Mod. Phys. 2021, 93, 045003. [Google Scholar] [CrossRef]
- Aspuru-Guzik, A.; Dutoi, A.D.; Love, P.J.; Head-Gordon, M. Simulated quantum computation of molecular energies. Science 2005, 309, 1704–1707. [Google Scholar] [CrossRef]
- Dagotto, E. Complexity in Strongly Correlated Electronic Systems. Science 2005, 309, 257–262. [Google Scholar] [CrossRef]
- Buenker, R.J.; Peyerimhoff, S.D. Individualized configuration selection in CI calculations with subsequent energy extrapolation. Theoret. Chim. Acta 1974, 35, 33–58. [Google Scholar] [CrossRef]
- Shavitt, I.; Rosenberg, B.J.; Palalikit, S. Comparison of configuration interaction expansions based on different orbital transformations. Int. J. Quant. Chem. 1976, 10, 33–46. [Google Scholar] [CrossRef]
- Iwata, S. Potential energy curves of several excited states of the Ne2* excimer: Assignment of the transient absorption spectra of the excimer. Chem. Phys. 1979, 37, 251–257. [Google Scholar] [CrossRef]
- Buenker, R.J.; Peyerimhoff, S.D.; Butscher, W. Applicability of the multi-reference double-excitation CI (MRD-CI) method to the calculation of electronic wavefunctions and comparison with related techniques. Mol. Phys. 1978, 35, 771–791. [Google Scholar] [CrossRef]
- Yamaguchi, K. Multireference (MR) configuration interaction (CI) approach for quasidegenerate systems. Int. J. Quant. Chem. 1980, 18, 269–284. [Google Scholar] [CrossRef]
- Yamaguchi, K. Configuration interaction (CI), coupled-cluster (CC) and many-body perturbation (MBPT) approaches in the unrestricted Hartree—Fock—Slater (UHFS) model. Chem. Phys. Lett. 1979, 68, 477–482. [Google Scholar] [CrossRef]
- Löwdin, P.-O. Quantum Theory of Many-Particle Systems. III. Extension of the Hartree-Fock Scheme to Include Degenerate Systems and Correlation Effects. Phys. Rev. 1955, 97, 1509–1520. [Google Scholar] [CrossRef]
- Öksüz, İ.; Sinanoğlu, O. Theory of Atomic Structure Including Electron Correlation. I. Three Kinds of Correlation in Ground and Excited Configurations. Phys. Rev. 1969, 181, 42–53. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Ohta, K.; Yabushita, S.; Fueno, T. DODS natural orbital (NO) CI investigations of 1,3-diradicals: CH2NHO, CH2OO, and CH2CH2O. J. Chem. Phys. 1978, 68, 4323–4325. [Google Scholar] [CrossRef]
- Yamaguchi, K. Ab initio unrestricted Hartree–Fock (UHF) and UHF–natural orbital CI studies of ozone. Int. J. Quant. Chem. 1980, 18, 101–106. [Google Scholar] [CrossRef]
- Roos, B.O. The complete active space SCF method in a fock-matrix-based super-CI formulation. Int. J. Quant. Chem. 1980, 18, 175–189. [Google Scholar] [CrossRef]
- Čížek, J. On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods. J. Chem. Phys. 1966, 45, 4256–4266. [Google Scholar] [CrossRef]
- Coester, F.; Kümmel, H. Short-range correlations in nuclear wave functions. Nucl. Phys. 1960, 17, 477–485. [Google Scholar] [CrossRef]
- Offermann, R.; Ey, W.; Kümmel, H. Degenerate many fermion theory in expS form: (I). General formalism. Nucl. Phys. A 1976, 273, 349–367. [Google Scholar] [CrossRef]
- Dean, D.J.; Hjorth-Jensen, M. Coupled-cluster approach to nuclear physics. Phys. Rev. C 2004, 69, 054320. [Google Scholar] [CrossRef]
- Mukherjee, D.; Moitra, R.K.; Mukhopadhyay, A. Correlation problem in open-shell atoms and molecules. Mol. Phys. 1975, 30, 1861–1888. [Google Scholar] [CrossRef]
- Langhoff, S.R.; Davidson, E.R. Configuration interaction calculations on the nitrogen molecule. Int. J. Quant. Chem. 1974, 8, 61–72. [Google Scholar] [CrossRef]
- Roos, B.O.; Andersson, K. Multiconfigurational perturbation theory with level shift—The Cr2 potential revisited. Chem. Phys. Lett. 1995, 245, 215–223. [Google Scholar] [CrossRef]
- Jeziorski, B.; Monkhorst, H.J. Coupled-cluster method for multideterminantal reference states. Phys. Rev. A 1981, 24, 1668–1681. [Google Scholar] [CrossRef]
- Bofill, J.M.; Pulay, P. The unrestricted natural orbital–complete active space (UNO–CAS) method: An inexpensive alternative to the complete active space–self-consistent-field (CAS–SCF) method. J. Chem. Phys. 1989, 90, 3637–3646. [Google Scholar] [CrossRef]
- Mahapatra, U.S.; Datta, B.; Bandyopadhyay, B.; Mukherjee, M. State-Specific Multi-Reference Coupled Cluster Formulations: Two Paradigms. In Advances in Quantum Chemistry; Löwdin, P.-O., Ed.; Elsevier: Amsterdam, The Netherlands, 1998; Volume 30, pp. 163–193. [Google Scholar] [CrossRef]
- Demel, O.; Pittner, J.; Neese, F. A Local Pair Natural Orbital-Based Multireference Mukherjee’s Coupled Cluster Method. J. Chem. Theory Comput. 2015, 11, 3104–3114. [Google Scholar] [CrossRef]
- Nishihara, S.; Yamanaka, S.; Saito, T.; Kitagawa, Y.; Kawakami, T.; Okumura, M.; Yamaguchi, K. UNO- and ULO-MRCC(Mk), AP-UCC and AP-UBD approaches to diradical systems. Int. J. Quant. Chem. 2010, 110, 3015–3026. [Google Scholar] [CrossRef]
- Paizs, B.; Fogarasi, G.; Pulay, P. An efficient direct method for geometry optimization of large molecules in internal coordinates. J. Chem. Phys. 1998, 109, 6571–6576. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Saito, T.; Ito, M.; Shoji, M.; Koizumi, K.; Yamanaka, S.; Kawakami, T.; Okumura, M.; Yamaguchi, K. Approximately spin-projected geometry optimization method and its application to di-chromium systems. Chem. Phys. Lett. 2007, 442, 445–450. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Saito, T.; Nakanishi, Y.; Kataoka, Y.; Matsui, T.; Kawakami, T.; Okumura, M.; Yamaguchi, K. Spin Contamination Error in Optimized Geometry of Singlet Carbene (1A1) by Broken-Symmetry Method. J. Phys. Chem. A 2009, 113, 15041–15046. [Google Scholar] [CrossRef]
- Ichino, T.; Villano, S.M.; Gianola, A.J.; Goebbert, D.J.; Velarde, L.; Sanov, A.; Blanksby, S.J.; Zhou, X.; Hrovat, D.A.; Borden, W.T.; et al. The Lowest Singlet and Triplet States of the Oxyallyl Diradical. Angew. Chem. Int. Ed. 2009, 48, 8509–8511. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Nishihara, S.; Yamanaka, S.; Kitagawa, Y.; Kawakami, T.; Yamada, S.; Isobe, H.; Okumura, M.; Yamaguchi, K. Singlet–triplet energy gap for trimethylenemethane, oxyallyl diradical, and related species: Single- and multireference computational results. Theoret. Chem. Acc. 2011, 130, 739–748. [Google Scholar] [CrossRef]
- Shen, J.; Fang, T.; Li, S.; Jiang, Y. Performance of Block Correlated Coupled Cluster Method with the CASSCF Reference Function for the Prediction of Activation Barriers, Spectroscopic Constants in Diatomic Molecules, and Singlet−Triplet Gaps in Diradicals. J. Phys. Chem. A 2008, 112, 12518–12525. [Google Scholar] [CrossRef]
- Pipek, J.; Mezey, P.G. A fast intrinsic localization procedure applicable for ab initio and semiempirical linear combination of atomic orbital wave functions. J. Chem. Phys. 1989, 90, 4916–4926. [Google Scholar] [CrossRef]
- Breslow, R. Antiaromaticity. Acc. Chem. Res. 1973, 6, 393–398. [Google Scholar] [CrossRef]
- Breslow, R.; Brown, J.; Gajewski, J.J. Antiaromaticity of cyclopropenyl anions. J. Am. Chem. Soc. 1967, 89, 4383–4390. [Google Scholar] [CrossRef]
- Breslow, R.; Grubbs, R.; Murahashi, S. Electrochemical evidence for the antiaromaticity of cyclobutadiene. J. Am. Chem. Soc. 1970, 92, 4139–4140. [Google Scholar] [CrossRef]
- Fujii, S.; Marqués-González, S.; Shin, J.-Y.; Shinokubo, H.; Masuda, T.; Nishino, T.; Arasu, N.P.; Vázquez, H.; Kiguchi, M. Highly-conducting molecular circuits based on antiaromaticity. Nat. Commun. 2017, 8, 15984. [Google Scholar] [CrossRef]
- Bally, T.; Masamune, S. Cyclobutadiene. Tetrahedron 1980, 36, 343–370. [Google Scholar] [CrossRef]
- Saito, T.; Nishihara, S.; Kitagawa, Y.; Kawakami, T.; Yamanaka, S.; Okumura, M.; Yamaguchi, K. A broken-symmetry study on the automerization of cyclobutadiene. Comparison with UNO- and DNO-MRCC methods. Chem. Phys. Lett. 2010, 498, 253–258. [Google Scholar] [CrossRef]
- Saunders, M.; Berger, R.; Jaffe, A.; McBride, J.M.; O’Neill, J.; Breslow, R.; Hoffman, J.M., Jr.; Perchonock, C.; Wasserman, E.; Hutton, R.S.; et al. Unsubstituted cyclopentadienyl cation, a ground-state triplet. J. Am. Chem. Soc. 1973, 95, 3017–3018. [Google Scholar] [CrossRef]
- Lambert, J.B.; Lin, L.; Rassolov, V. The Stable Pentamethylcyclopentadienyl Cation. Angew. Chem. Int. Ed. 2002, 41, 1429–1431. [Google Scholar] [CrossRef]
- Costa, P.; Trosien, I.; Mieres-Perez, J.; Sander, W. Isolation of an Antiaromatic Singlet Cyclopentadienyl Zwitterion. J. Am. Chem. Soc. 2017, 139, 13024–13030. [Google Scholar] [CrossRef]
- Schulte, Y.; Wölper, C.; Rupf, S.M.; Malischewski, M.; SantaLucia, D.J.; Neese, F.; Haberhauser, G.; Schulz, S. Structural characterization and reactivity of a room-temperature-stable, antiaromatic cyclopentadienyl cation salt. Nat. Chem. 2024, 16, 651–657. [Google Scholar] [CrossRef]
- Wörner, H.J.; Merkt, F. Diradicals, antiaromaticity, and the pseudo-Jahn-Teller effect: Electronic and rovibronic structures of the cyclopentadienyl cation. J. Chem. Phys. 2007, 127, 034303. [Google Scholar] [CrossRef]
- Phillips, D.H.; Schug, J.C. Projected States of Open Shell Molecules: The Pi-Electron States of the Cyclopentadienyl Cation. J. Chem. Phys. 1972, 57, 3498–3503. [Google Scholar] [CrossRef]
- Hehre, W.J.; Schleyer, P.v.R. Cyclopentadienyl and related (CH)5+ cations. J. Am. Chem. Soc. 1973, 95, 5837–5839. [Google Scholar] [CrossRef]
- Borden, W.T.; Davidson, E.R. Potential surfaces for the planar cyclopentadienyl radical and cation. J. Am. Chem. Soc. 1979, 101, 3771–3775. [Google Scholar] [CrossRef]
- Reindl, B.; Schleyer, P.V.R. Molecular mechanics and ab initio calculations on cyclopentadienyl cations. J. Comput. Chem. 1998, 19, 1402–1420. [Google Scholar] [CrossRef]
- Ranasinghe, S.; Martin, C.D.; Dutton, J.L. Cyclopentadienyl cations. Chem. Sci. 2025, 16, 2083–2088. [Google Scholar] [CrossRef] [PubMed]
- Kubo, T. Recent Progress in Quinoidal Singlet Biradical Molecules. Chem. Lett. 2015, 44, 111–122. [Google Scholar] [CrossRef]
- Kubo, T. Phenalenyl-Based Open-Shell Polycyclic Aromatic Hydrocarbons. Chem. Rec. 2015, 15, 218–232. [Google Scholar] [CrossRef]
- Kubo, T. Syntheses and Properties of Open-Shell π-Conjugated Molecules. Bull. Chem. Soc. Jpn. 2021, 94, 2235–2244. [Google Scholar] [CrossRef]
- Kubo, T. Closed-shell and open-shell dual nature of singlet diradical compounds. Pure Appl. Chem. 2023, 95, 363–375. [Google Scholar] [CrossRef]
- Goto, K.; Kubo, T.; Yamamoto, K.; Nakasuji, K.; Sato, K.; Shiomi, D.; Takui, T.; Kubota, M.; Kobayashi, T.; Yakusi, K.; et al. A Stable Neutral Hydrocarbon Radical: Synthesis, Crystal Structure, and Physical Properties of 2,5,8-Tri-tert-butyl-phenalenyl. J. Am. Chem. Soc. 1999, 121, 1619–1620. [Google Scholar] [CrossRef]
- Kubo, T.; Sakamoto, M.; Akabane, M.; Fujiwara, Y.; Yamamoto, K.; Akita, M.; Inoue, K.; Takui, T.; Nakasuji, K. Four-Stage Amphoteric Redox Properties and Biradicaloid Character of Tetra-tert-butyldicyclopenta[b;d]thieno[1,2,3-cd;5,6,7-c′d′]diphenalene. Angew. Chem. Int. Ed. 2004, 43, 6474–6479. [Google Scholar] [CrossRef]
- Kubo, T.; Shimizu, A.; Sakamoto, M.; Uruichi, M.; Yakushi, K.; Nakano, M.; Shiomi, D.; Sato, K.; Takui, T.; Morita, Y.; et al. Synthesis, Intermolecular Interaction, and Semiconductive Behavior of a Delocalized Singlet Biradical Hydrocarbon. Angew. Chem. Int. Ed. 2005, 44, 6564–6568. [Google Scholar] [CrossRef]
- Shimizu, A.; Uruichi, M.; Yakushi, K.; Matsuzaki, H.; Okamoto, H.; Nakano, M.; Hirao, Y.; Matsumoto, K.; Kurata, H.; Kubo, T. Resonance Balance Shift in Stacks of Delocalized Singlet Biradicals. Angew. Chem. Int. Ed. 2009, 48, 5482–5486. [Google Scholar] [CrossRef]
- Kamada, K.; Ohta, K.; Shimizu, A.; Kubo, T.; Kishi, R.; Takahashi, H.; Botek, E.; Champagne, B.; Nakano, M. Singlet Diradical Character from Experiment. J. Chem. Phys. Lett. 2010, 1, 937–940. [Google Scholar] [CrossRef]
- Kamada, K.; Ohta, K.; Kubo, T.; Shimizu, A.; Morita, Y.; Nakasuji, K.; Kishi, R.; Ohta, S.; Furukawa, S.; Takahashi, H.; et al. Strong Two-Photon Absorption of Singlet Diradical Hydrocarbons. Angew. Chem. Int. Ed. 2007, 46, 3544–3546. [Google Scholar] [CrossRef] [PubMed]
- Konishi, A.; Hirao, Y.; Nakano, M.; Shimizu, A.; Botek, E.; Champagne, B.; Shiomi, D.; Sato, K.; Takui, T.; Matsumoto, K.; et al. Synthesis and Characterization of Teranthene: A Singlet Biradical Polycyclic Aromatic Hydrocarbon Having Kekulé Structures. J. Am. Chem. Soc. 2010, 132, 11021–11023. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, A.; Kishi, R.; Nakano, M.; Shiomi, D.; Sato, K.; Takui, T.; Hisaki, I.; Miyata, M.; Tobe, Y. Indeno[2,1-b]fluorene: A 20-π-Electron Hydrocarbon with Very Low-Energy Light Absorption. Angew. Chem. Int. Ed. 2013, 52, 6076–6079. [Google Scholar] [CrossRef] [PubMed]
- Pal, S.K.; Itkis, M.E.; Tham, F.S.; Reed, R.W.; Oakley, R.T.; Haddon, R.C. Resonating Valence-Bond Ground State in a Phenalenyl-Based Neutral Radical Conductor. Science 2005, 309, 281–284. [Google Scholar] [CrossRef]
- Huang, J.; Kertesz, M. Intermolecular Covalent π−π Bonding Interaction Indicated by Bond Distances, Energy Bands, and Magnetism in Biphenalenyl Biradicaloid Molecular Crystal. J. Am. Chem. Soc. 2007, 129, 1634–1643. [Google Scholar] [CrossRef]
- Fukui, K.; Sato, K.; Shiomi, D.; Takui, T.; Itoh, K.; Gotoh, K.; Kubo, T.; Yamamoto, K.; Nakasuji, K.; Naito, A. Electronic structure of a stable phenalenyl radical in crystalline state as studied by SQUID measurements, cw-ESR, and 13C CP/MAS NMR spectroscopy. Synth. Met. 1999, 103, 2257–2258. [Google Scholar] [CrossRef]
- Takano, Y.; Taniguchi, T.; Isobe, H.; Kubo, T.; Morita, Y.; Yamamoto, K.; Nakasuji, K.; Takui, T.; Yamaguchi, K. Hybrid Density Functional Theory Studies on the Magnetic Interactions and the Weak Covalent Bonding for the Phenalenyl Radical Dimeric Pair. J. Am. Chem. Soc. 2002, 124, 11122–11130. [Google Scholar] [CrossRef]
- Kodama, T.; Aoba, M.; Hirao, Y.; Rivero, S.M.; Casado, J.; Kubo, T. Molecular and Spin Structures of a Through-Space Conjugated Triradical System. Angew. Chem. Int. Ed. 2022, 61, e202200688. [Google Scholar] [CrossRef]
- Kodama, T.; Hirao, Y.; Kubo, T. Synthesis and Properties of a Through-Space Interacting Diradicaloid. Precis. Chem. 2023, 1, 183–191. [Google Scholar] [CrossRef]
- Mou, Z.; Uchida, K.; Kubo, T.; Kertesz, M. Evidence of σ- and π-Dimerization in a Series of Phenalenyls. J. Am. Chem. Soc. 2014, 136, 18009–18022. [Google Scholar] [CrossRef] [PubMed]
- Abe, M. Diradicals. Chem. Rev. 2013, 113, 7011–7088. [Google Scholar] [CrossRef] [PubMed]
- Konishi, A.; Kubo, T. Benzenoid Quinodimethanes. In Physical Organic Chemistry of Quinodimethanes. Topics in Current Chemistry Collections; Tobe, Y., Kubo, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Chapter 2; pp. 69–105. [Google Scholar] [CrossRef]
- Stuyver, T.; Chen, B.; Zeng, T.; Geerling, P.; De Proft, F.; Hoffmann, R. Do Diradicals Behave Like Radicals? Chem. Rev. 2019, 119, 11291–11351. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; Tang, S.; Su, Y.; Wang, X. Recent advances in stable main group element radicals: Preparation and characterization. Chem. Soc. Rev. 2022, 51, 5930–5973. [Google Scholar] [CrossRef]
- Hinz, A.; Bresien, J.; Breher, F.; Schulz, A. Heteroatom-Based Diradical(oid)s. Chem. Rev. 2023, 123, 10468–10526. [Google Scholar] [CrossRef]
- Zhang, H.; Miao, F.; Liu, X.; Wang, D.; Zheng, Y. Recent Advances of Stable Phenoxyl Diradicals. Chem. Res. Chin. Univ. 2023, 39, 170–175. [Google Scholar] [CrossRef]
- Prasad, P.N.; Williams, D.J. Introduction to Nonlinear Optical Effects in Molecules and Polymers; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Franken, P.A.; Hill, A.E.; Peters, C.W.; Weinreich, G. Generation of Optical Harmonics. Phys. Rev. Lett. 1961, 7, 118–119. [Google Scholar] [CrossRef]
- Tsang, T.Y.F. Optical third-harmonic generation at interfaces. Phys. Rev. A 1995, 52, 4116–4125. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Dadap, J.I.; Petrone, N.; Yeh, P.-C.; Hone, J.; Osgood, R.M., Jr. Optical Third-Harmonic Generation in Graphene. Phys. Rev. X 2013, 3, 021014. [Google Scholar] [CrossRef]
- Roy, S.; Covert, P.A.; FitzGerald, W.R.; Hore, D.K. Biomolecular Structure at Solid–Liquid Interfaces As Revealed by Nonlinear Optical Spectroscopy. Chem. Rev. 2014, 114, 8388–8415. [Google Scholar] [CrossRef]
- Johansson, P.K.; Schmüser, L.; Castner, D.G. Nonlinear Optical Methods for Characterization of Molecular Structure and Surface Chemistry. Top. Catal. 2018, 61, 1101–1124. [Google Scholar] [CrossRef] [PubMed]
- Sasagane, K.; Aiga, F.; Itoh, R. Higher-order response theory based on the quasienergy derivatives: The derivation of the frequency-dependent polarizabilities and hyperpolarizabilities. J. Chem. Phys. 1993, 99, 3738–3778. [Google Scholar] [CrossRef]
- Sekino, H.; Bartlett, R.J. Frequency dependent nonlinear optical properties of molecules. J. Chem. Phys. 1986, 85, 976–989. [Google Scholar] [CrossRef]
- Karna, S.P. Spin-unrestricted time-dependent Hartree–Fock theory of frequency-dependent linear and nonlinear optical properties. J. Chem. Phys. 1996, 104, 6590–6605. [Google Scholar] [CrossRef]
- Kobayashi, T.; Sasagane, K.; Aiga, F.; Yamaguchi, K. Calculation of frequency-dependent first hyperpolarizabilities using the second-order Møller–Plesset perturbation theory. J. Chem. Phys. 1999, 110, 11720–11733. [Google Scholar] [CrossRef]
- Bredas, J.L.; Adant, C.; Tackx, P.; Persoons, A.; Pierce, B.M. Third-Order Nonlinear Optical Response in Organic Materials: Theoretical and Experimental Aspects. Chem. Rev. 1994, 94, 243–278. [Google Scholar] [CrossRef]
- Nakano, M.; Yamada, S.; Shigemoto, I.; Yamaguchi, K. Dynamic (hyper)polarizability density analysis based on virtual excitation processes: Visualization of the dynamic electron fluctuatability of systems under time-dependent external electric fields. Chem. Phys. Lett. 1996, 250, 247–254. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Numerical Liouville approach: A calculation method for nonlinear optical susceptibilities of N-state systems. Phys. Rev. A 1994, 50, 2989–3004. [Google Scholar] [CrossRef]
- Nakano, M.; Yamada, S.; Shigemoto, I.; Yamaguchi, K. Theoretical study on the geometry dependence of the second hyperpolarizability of the allyl cation based on a numerical Liouville three-type analysis. Chem. Phys. Lett. 1996, 251, 381–386. [Google Scholar] [CrossRef]
- Nakano, M.; Nitta, T.; Yamaguchi, K.; Champagne, B.; Botek, E. Spin Multiplicity Effects on the Second Hyperpolarizability of an Open-Shell Neutral π-Conjugated System. J. Phys. Chem. A 2004, 108, 4105–4111. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Nakagawa, N.; Ohta, S.; Takahashi, H.; Furukawa, S.; Kamada, K.; Ohta, K.; Champagne, B.; Botek, E.; et al. Second Hyperpolarizabilities (γ) of Bisimidazole and Bistriazole Benzenes: Diradical Character, Charged State, and Spin State Dependences. J. Phys. Chem. A 2006, 110, 4238–4243. [Google Scholar] [CrossRef] [PubMed]
- Champagne, B.; Botek, E.; Nakano, M.; Nitta, T.; Yamaguchi, K. Basis set and electron correlation effects on the polarizability and second hyperpolarizability of model open-shell π-conjugated systems. J. Chem. Phys. 2005, 122, 114315. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Kishi, R.; Ohta, S.; Takebe, A.; Takahashi, H.; Furukawa, S.; Kubo, T.; Morita, Y.; Nakasuji, K.; Yamaguchi, K.; et al. Origin of the enhancement of the second hyperpolarizability of singlet diradical systems with intermediate diradical character. J. Chem. Phys. 2006, 125, 074113. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Ohta, S.; Takahashi, H.; Kubo, T.; Kamada, K.; Ohta, K.; Botek, E.; Champagne, B. Relationship between Third-Order Nonlinear Optical Properties and Magnetic Interactions in Open-Shell Systems: A New Paradigm for Nonlinear Optics. Phys. Rev. Lett. 2007, 99, 033001. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Nagao, H.; Yamaguchi, K. Many-electron hyperpolarizability density analysis: Application to the dissociation processof one-dimensional H2s. Phys. Rev. A 1997, 55, 1503–1513. [Google Scholar] [CrossRef]
- Nakano, M.; Yamada, S.; Yamaguchi, K. Third-order nonlinear optical responses of molecules in the intermediate and strong correlation regime: Variation of second hyperpolarizability in the bond dissociation. J. Comput. Methods Sci. Eng. 2004, 4, 677–701. [Google Scholar] [CrossRef]
- Hamamoto, Y.; Hirao, Y.; Kubo, T. Biradicaloid Behavior of a Twisted Double Bond. J. Phys. Chem. Lett. 2021, 12, 4729–4734. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Nagao, H.; Yamaguchi, K. Electron correlation and structure dependencies of the second hyperpolarizability of ethylene. Int. J. Quant. Chem. 1999, 71, 177–183. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Nitta, T.; Kubo, T.; Nakasuji, K.; Kamada, K.; Ohta, K.; Champagne, B.; Botek, E.; Yamaguchi, K. Second Hyperpolarizability (γ) of Singlet Diradical System: Dependence of γ on the Diradical Character. J. Phys. Chem. A 2005, 109, 885–891. [Google Scholar] [CrossRef]
- Mondal, A.; Hatua, K.; Nandi, P.K. Static second hyperpolarizability of twisted ethylene: A comprehensive computational study. J. Theoret. Comput. Chem. 2015, 14, 1550060. [Google Scholar] [CrossRef]
- De Wergifosse, M. Approximate Spin-Projected Density-Based Romberg Differentiation Procedure to Evaluate the Second-Hyperpolarizability of p-Quinodimethane and Twisted Ethylene and Their Diradical Character Dependence. J. Phys. Chem. A 2016, 120, 2727–2736. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Takahata, M.; Kishi, R.; Nitta, T.; Yamaguchi, K. Theoretical Study on Static Second Hyperpolarizabilities for Several π-Conjugated Systems Including Nitrogen Atoms: Effects of Charged Defects and Extension of π-Conjugation. J. Phys. Chem. A 2004, 108, 4151–4155. [Google Scholar] [CrossRef]
- Sun, Z.; Zeng, Z.; Wu, J. Zethrenes, Extended p-Quinodimethanes, and Periacenes with a Singlet Biradical Ground State. Acc. Chem. Res. 2014, 47, 2582–2591. [Google Scholar] [CrossRef]
- Zeng, Z.; Shi, X.; Chi, C.; Navarrete, J.T.L.; Casado, J.; Wu, J. Pro-aromatic and anti-aromatic π-conjugated molecules: An irresistible wish to be diradicals. Chem. Soc. Rev. 2015, 44, 6578–6596. [Google Scholar] [CrossRef]
- Casado, J. Para-Quinodimethanes: A Unified Review of the Quinoidal-Versus-Aromatic Competition and its Implications. In Physical Organic Chemistry of Quinodimethanes. Topics in Current Chemistry Collections; Tobe, Y., Kubo, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 209–248. [Google Scholar] [CrossRef]
- Nakano, M.; Fukui, H.; Minami, T.; Yoneda, K.; Shigeta, Y.; Kishi, R.; Champagne, B.; Botek, E.; Kubo, T.; Ohta, K.; et al. (Hyper)polarizability density analysis for open-shell molecular systems based on natural orbitals and occupation numbers. Theor. Chem. Acc. 2011, 130, 711–724. [Google Scholar] [CrossRef]
- Kishi, R.; Nakano, M. Quantum Master Equation Method Based on the Broken-Symmetry Time-Dependent Density Functional Theory: Application to Dynamic Polarizability of Open-Shell Molecular Systems. J. Phys. Chem. A 2011, 115, 3565–3575. [Google Scholar] [CrossRef]
- Kishi, R.; Murata, Y.; Saito, M.; Morita, K.; Abe, M.; Nakano, M. Theoretical Study on Diradical Characters and Nonlinear Optical Properties of 1,3-Diradical Compounds. J. Phys. Chem. A 2014, 118, 10837–10848. [Google Scholar] [CrossRef]
- Prasad, P.N.; Reinhardt, B.A. Is there a role for organic materials chemistry in nonlinear optics and photonics? Chem. Mater. 1990, 2, 660–669. [Google Scholar] [CrossRef]
- Prasad, P.N.; Karna, S.P. Nonlinear optical effects in molecules and polymers: Issues and opportunities. Int. J. Quant. Chem. 1994, 52, 395–410. [Google Scholar] [CrossRef]
- Marder, S.T.; Gorman, C.B.; Meyers, F.; Perry, J.W.; Bourhill, G.; Brédas, J.-L.; Pierce, B.M. A Unified Description of Linear and Nonlinear Polarization in Organic Polymethine Dyes. Science 1994, 265, 632–635. [Google Scholar] [CrossRef]
- Bhawalkar, J.D.; He, G.S.; Prasad, P.N. Nonlinear multiphoton processes in organic and polymeric materials. Rep. Prog. Phys. 1996, 59, 1041–1071. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Shigemoto, I.; Yamaguchi, K. Static second hyperpolarizabilities γ of nitroxide radical and formaldehyde: Evaluation of spatial contributions to γ by a hyperpolarizability density analysis. Chem. Phys. Lett. 1996, 254, 158–164. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Shigemoto, I.; Kiribayashi, S.; Yamaguchi, K. Intense electron correlation dependence of the first hyperpolarizabilities β of a nitroxide radical and formaldehyde. Chem. Phys. Lett. 1997, 267, 445–451. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Shigemoto, I.; Kiribayashi, S.; Yamaguchi, K. Theoretical study of the third-order nonlinear optical susceptibilities for the β-phase crystal of p-NPNN. Chem. Phys. Lett. 1997, 267, 438–444. [Google Scholar] [CrossRef]
- Oudar, J.L.; Zyss, J. Structural dependence of nonlinear-optical properties of methyl-(2,4-dinitrophenyl)-aminopropanoate crystals. Phys. Rev. A 1982, 26, 2016–2027. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Nishino, M.; Yamaguchi, K. Theoretical Study on the Second Hyperpolarizabilities for Small Radical Systems. Opt. Rev. 1999, 6, 237–241. [Google Scholar] [CrossRef]
- Shu, C.; Yang, Z.; Rajca, A. From Stable Radicals to Thermally Robust High-Spin Diradicals and Triradicals. Chem. Rev. 2023, 123, 11954–12003. [Google Scholar] [CrossRef]
- Khalid, M.; Khan, M.; Mahmood, K.; Arshad, M.; Imran, M.; Braga, A.A.C.; Hussain, R. Theoretical designing of non-fullerene derived organic heterocyclic compounds with enhanced nonlinear optical amplitude: A DFT based prediction. Sci. Rep. 2022, 12, 20220. [Google Scholar] [CrossRef]
- Mingabudinova, L.R.; Vinogradov, V.V.; Milichko, V.A.; Hey-Hawkins, E.; Vinogradov, A.V. Metal–organic frameworks as competitive materials for non-linear optics. Chem. Soc. Rev. 2016, 45, 5408–5431. [Google Scholar] [CrossRef]
- Li, C.; Qian, G.; Cui, Y. Metal–organic frameworks for nonlinear optics and lasing. Inf. Funct. Mater. 2024, 1, 125–159. [Google Scholar] [CrossRef]
- Iwamura, H.; Koga, N. Studies of organic di-, oligo-, and polyradicals by means of their bulk magnetic properties. Acc. Chem. Res. 1993, 26, 346–351. [Google Scholar] [CrossRef]
- Rajca, A. Organic Diradicals and Polyradicals: From Spin Coupling to Magnetism? Chem. Rev. 1994, 94, 871–893. [Google Scholar] [CrossRef]
- Kinoshita, M.; Turek, P.; Tamura, M.; Nozawa, K.; Shiomi, D.; Nakazawa, Y.; Ishikawa, M.; Takahashi, M.; Awaga, K.; Inabe, T.; et al. An Organic Radical Ferromagnet. Chem. Lett. 1991, 20, 1225–1228. [Google Scholar] [CrossRef]
- Kinoshita, M. Ferromagnetism of Organic Radical Crystals. Jpn. J. Appl. Phys. 1994, 33, 5718–5733. [Google Scholar] [CrossRef]
- Okumura, M.; Yamaguchi, K.; Nakano, M.; Mori, W. A theoretical explanation of the organic ferromagnetism in the β-phase of para-nitrophenyl nitronyl nitroxide. Chem. Phys. Lett. 1993, 207, 1–8. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Leggett, A.J. Quantum tunnelling in a dissipative system. Ann. Phys. 1983, 149, 374–456. [Google Scholar] [CrossRef]
- Leggett, A.J.; Garg, A. Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 1985, 54, 857–860. [Google Scholar] [CrossRef]
- Leggett, A.J.; Chakravarty, S.; Dorsey, A.T.; Fisher, M.P.A.; Grag, A.; Zwerger, W. Dynamics of the dissipative two-state system. Rev. Mod. Phys. 1987, 59, 1–85. [Google Scholar] [CrossRef]
- Chudnovsky, E.M.; Gunther, L. Quantum Tunneling of Magnetization in Small Ferromagnetic Particles. Phys. Rev. Lett. 1988, 60, 661–664. [Google Scholar] [CrossRef]
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Thomas, L.; Lionti, F.; Ballou, R.; Gatteschi, D.; Sessoli, R.; Barbara, B. Macroscopic quantum tunnelling of magnetization in a single crystal of nanomagnets. Nature 1996, 383, 145–147. [Google Scholar] [CrossRef]
- Nishino, M.; Yamanaka, S.; Yoshioka, Y.; Yamaguchi, K. Theoretical Approaches to Direct Exchange Couplings between Divalent Chromium Ions in Naked Dimers, Tetramers, and Clusters. J. Phys. Chem. A 1997, 101, 705–712. [Google Scholar] [CrossRef]
- Nagao, H.; Yamanaka, S.; Nishino, M.; Yoshioka, Y.; Yamaguchi, K. Theoretical studies on the magnetic quantum tunneling rates in Mn clusters by the path integral method. Chem. Phys. Lett. 1999, 302, 418–424. [Google Scholar] [CrossRef]
- Nagao, H.; Nakano, M.; Shigeta, Y.; Yamaguchi, K. Quantum Phase Dynamics of Interaction between Photon Field and Magnetic System: Effects of Magnetic Quantum Tunnelling. Opt. Rev. 1999, 6, 227–231. [Google Scholar] [CrossRef]
- Wernsdorfer, W.; Sessoli, R. Quantum Phase Interference and Parity Effects in Magnetic Molecular Clusters. Science 1999, 284, 133–135. [Google Scholar] [CrossRef]
- Nagao, H.; Nishino, M.; Shigeta, Y.; Soda, T.; Kitagawa, Y.; Onishi, T.; Yoshioka, Y.; Yamaguchi, K. Theoretical studies on effective spin interactions, spin alignments and macroscopic spin tunneling in polynuclear manganese and related complexes and their mesoscopic clusters. Coord. Chem. Rev. 2000, 198, 265–295. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R. Quantum Tunneling of Magnetization and Related Phenomena in Molecular Materials. Angew. Chem. Int. Ed. 2003, 42, 268–297. [Google Scholar] [CrossRef]
- Leggett, A.J. Some Thought-Experiments Involving Macrosystems as Illustrations of Various Interpretations of Quantum Mechanics. Found. Phys. 1999, 29, 445–456. [Google Scholar] [CrossRef]
- Nagao, H.; Kinugawa, K.; Shigeta, Y.; Ohta, K.; Yamaguchi, K. Quantum spin dynamics in solution applicable to quantum computing. J. Mol. Liq. 2001, 90, 63–68. [Google Scholar] [CrossRef]
- Leuenberger, M.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef]
- Fredkin, E.; Toffoli, T. Conservative logic. Int. J. Theor. Phys. 1982, 21, 219–253. [Google Scholar] [CrossRef]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum theory, the Church–Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A 1985, 400, 97–117. [Google Scholar] [CrossRef]
- Feynman, R.P. Quantum mechanical computers. Found. Phys. 1986, 16, 507–531. [Google Scholar] [CrossRef]
- Lloyd, S. A Potentially Realizable Quantum Computer. Science 1993, 261, 1569–1571. [Google Scholar] [CrossRef]
- Ozawa, M. Phase Operator Problem and Macroscopic Extension of Quantum Mechanics. Ann. Phys. 1997, 257, 65–83. [Google Scholar] [CrossRef]
- DiVincenzo, D.P. The Physical Implementation of Quantum Computation. Prog. Phys. 2000, 48, 771–783. [Google Scholar] [CrossRef]
- Chuang, I.L.; Gershenfeld, N.; Kubinec, M. Experimental Implementation of Fast Quantum Searching. Phys. Rev. Lett. 1998, 80, 3408–3411. [Google Scholar] [CrossRef]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the STOC ’96: Proceedings of the 28th Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar] [CrossRef]
- Vandersypen, L.M.K.; Steffen, M.; Breyta, G.; Yannoni, C.S.; Sherwood, M.H.; Chuang, I.L. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 2001, 414, 883–887. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 2006, 321, 2–111. [Google Scholar] [CrossRef]
- Nie, W.; Antezza, M.; Liu, Y.; Nori, F. Dissipative Topological Phase Transition with Strong System-Environment Coupling. Phys. Rev. Lett. 2021, 127, 250402. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Okubo, T.; Tanaka, N.; Iino, T.; Kaizu, Y. Determination of Ligand-Field Parameters and f-Electronic Structures of Double-Decker Bis(phthalocyaninato)lanthanide Complexes. Inorg. Chem. 2003, 42, 2440–2446. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Tanaka, N.; Ishikawa, T.; Koshihara, S.; Kaizu, Y. Upward Temperature Shift of the Intrinsic Phase Lag of the Magnetization of Bis(phthalocyaninato)terbium by Ligand Oxidation Creating an S = 1/2 Spin. Inorg. Chem. 2004, 43, 5498–5500. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Wernsdorfer, W. Quantum Tunneling of Magnetization in Lanthanide Single-Molecule Magnets: Bis(phthalocyaninato)terbium and Bis(phthalocyaninato)dysprosium Anions. Angew. Chem. Int. Ed. 2005, 44, 2931–2935. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Wernsdorfer, W. Nuclear Spin Driven Quantum Tunneling of Magnetization in a New Lanthanide Single-Molecule Magnet: Bis(Phthalocyaninato)holmium Anion. J. Am. Chem. Soc. 2005, 127, 3650–3651. [Google Scholar] [CrossRef]
- Fukuda, T.; Matsumura, K.; Ishikawa, N. Influence of Intramolecular f-f Interactions on Nuclear Spin Driven Quantum Tunneling of Magnetizations in Quadruple-Decker Phthalocyanine Complexes Containing Two Terbium or Dysprosium Magnetic Centers. J. Phys. Chem. A 2013, 117, 10447–10454. [Google Scholar] [CrossRef]
- Katoh, K.; Horii, Y.; Yasuda, N.; Wernsdorfer, W.; Toriumi, K.; Breedlove, B.K.; Yamashita, M. Multiple-decker phthalocyaninato dinuclear lanthanoid(iii) single-molecule magnets with dual-magnetic relaxation processes. Dalton Trans. 2012, 41, 13582–13600. [Google Scholar] [CrossRef]
- Meier, F.; Levy, J.; Loss, D. Quantum Computing with Spin Cluster Qubits. Phys. Rev. Lett. 2003, 90, 047901. [Google Scholar] [CrossRef]
- Lehmann, J.; Gaita-Ariño, A.; Coronado, E.; Loss, D. Quantum computing with molecular spin systems. J. Mater. Chem. 2009, 19, 1672–1677. [Google Scholar] [CrossRef]
- Godfrin, C.; Ferhat, A.; Ballou, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W.; Balestro, F. Operating Quantum States in Single Magnetic Molecules: Implementation of Grover’s Quantum Algorithm. Phys. Rev. Lett. 2017, 119, 187702. [Google Scholar] [CrossRef]
- Moreno-Pineda, E.; Klyatskaya, S.; Du, P.; Damjanović, M.; Taran, G.; Wernsdorfer, W.; Ruben, M. Observation of Cooperative Electronic Quantum Tunneling: Increasing Accessible Nuclear States in a Molecular Qudit. Inorg. Chem. 2018, 57, 9873–9879. [Google Scholar] [CrossRef]
- Moreno-Pineda, E.; Godfrin, C.; Balestro, F.; Wernsdorfer, W.; Ruben, M. Molecular spin qudits for quantum algorithms. Chem. Soc. Rev. 2018, 47, 501–513. [Google Scholar] [CrossRef]
- Atzori, M.; Tesi, L.; Morra, E.; Chiesa, M.; Sorace, L.; Sessoli, R. Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits. J. Am. Chem. Soc. 2016, 138, 2154–2157. [Google Scholar] [CrossRef]
- Atzori, M.; Chiesa, A.; Morra, E.; Chiesa, M.; Sorace, L.; Carretta, S.; Sessoli, R. A two-qubit molecular architecture for electron-mediated nuclear quantum simulation. Chem. Sci. 2018, 9, 6183–6192. [Google Scholar] [CrossRef]
- Atzori, M.; Sessoli, R. The Second Quantum Revolution: Role and Challenges of Molecular Chemistry. J. Am. Chem. Soc. 2019, 141, 11339–11352. [Google Scholar] [CrossRef]
- Takahashi, S.; Tupitsyn, I.S.; van Tol, J.; Beedle, C.C.; Hendrickson, D.N.; Stamp, P.C.E. Decoherence in crystals of quantum molecular magnets. Nature 2011, 476, 76–79. [Google Scholar] [CrossRef]
- Bader, K.; Dengler, D.; Lenz, S.; Endeward, B.; Jiang, S.-D.; Neugebauer, P.; van Slageren, J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014, 5, 5304. [Google Scholar] [CrossRef] [PubMed]
- Teki, Y.; Miyamoto, S.; Nakatsuji, M.; Miura, Y. π-Topology and Spin Alignment Utilizing the Excited Molecular Field: Observation of the Excited High-Spin Quartet (S = 3/2) and Quintet (S = 2) States on Purely Organic π-Conjugated Spin Systems. J. Am. Chem. Soc. 2001, 123, 294–305. [Google Scholar] [CrossRef] [PubMed]
- Takeda, K.; Takegoshi, K.; Terao, T. Dynamic nuclear polarization by photoexcited-triplet electron spins in polycrystalline samples. Chem. Phys. Lett. 2001, 345, 166–170. [Google Scholar] [CrossRef]
- Rahimi, R.; Sato, K.; Furukawa, K.; Toyota, K.; Shiomi, D.; Nakamura, T.; Kitagawa, M.; Takui, T. Pulsed ENDOR-based quantum information processing. Int. J. Quant. Inf. 2005, 3, 197–204. [Google Scholar] [CrossRef]
- Kagawa, A.; Murokawa, Y.; Takeda, K.; Kitagawa, M. Optimization of 1H spin density for dynamic nuclear polarization using photo-excited triplet electron spins. J. Magn. Reson. 2009, 197, 9–13. [Google Scholar] [CrossRef] [PubMed]
- Negoro, M.; Nakayama, K.; Tateishi, K.; Kagawa, A.; Takeda, K.; Kitagawa, M. 2H-decoupling-accelerated 1H spin diffusion in dynamic nuclear polarization with photoexcited triplet electrons. J. Chem. Phys. 2010, 133, 154504. [Google Scholar] [CrossRef]
- Kanzaki, Y.; Shiomi, D.; Kaneda, C.; Ise, T.; Sato, K.; Takui, T. Clustering of molecular spins in the crystals of nitronylnitroxide and iminonitroxide triradicals based on benzene-1,3,5-triyl frameworks. J. Mater. Chem. 2006, 16, 2064–2073. [Google Scholar] [CrossRef]
- Suzuki, S.; Morita, Y.; Fukui, K.; Sato, K.; Shiomi, D.; Takui, T.; Nakasuji, K. Aromaticity on the Pancake-Bonded Dimer of Neutral Phenalenyl Radical as Studied by MS and NMR Spectroscopies and NICS Analysis. J. Am. Chem. Soc. 2006, 128, 2530–2531. [Google Scholar] [CrossRef]
- Sato, K.; Rahimi, R.; Mori, N.; Nishida, S.; Toyota, K.; Shiomi, D.; Morita, Y.; Ueda, A.; Suzuki, S.; Furukawa, K.; et al. Implementation of molecular spin quantum computing by pulsed ENDOR technique: Direct observation of quantum entanglement and spinor. Phys. E Low-Dimens. Syst. Nanostruct. 2007, 40, 363–366. [Google Scholar] [CrossRef]
- Kawano, Y.; Yamashita, S.; Kitagawa, M. Explicit implementation of quantum circuits on a quantum-cellular-automata-like architecture. Phys. Rev. A 2005, 72, 012301. [Google Scholar] [CrossRef]
- Beer, L.; Mandal, S.K.; Reed, R.W.; Oakley, R.T.; Tham, F.S.; Donnadieu, B.; Haddon, R.C. The First Electronically Stabilized Phenalenyl Radical: Effect of Substituents on Solution Chemistry and Solid-State Structure. Cryst. Growth Des. 2007, 7, 802–809. [Google Scholar] [CrossRef]
- Morita, Y.; Ueda, A.; Nishida, S.; Fukui, K.; Ise, T.; Shiomi, D.; Sato, K.; Takui, T.; Nakasuji, K. Curved Aromaticity of a Corannulene-Based Neutral Radical: Crystal Structure and 3 D Unbalanced Delocalization of Spin. Angew. Chem. Int. Ed. 2008, 47, 2035–2038. [Google Scholar] [CrossRef]
- Morita, Y.; Suzuki, S.; Sato, K.; Takui, T. Synthetic organic spin chemistry for structurally well-defined open-shell graphene fragments. Nat. Chem. 2011, 3, 197–204. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Taniguchi, T.; Kawakami, T.; Hamamoto, T.; Okumura, M. Possibilities of magnetic modifications of DNA wires, sheets and related materials. Polyhedron 2005, 24, 2758–2766. [Google Scholar] [CrossRef]
- Maekawa, K.; Nakazawa, S.; Atsumi, H.; Shiomi, D.; Sato, K.; Kitagawa, M.; Takui, T.; Nakatani, K. Programmed assembly of organic radicals on DNA. Chem. Commun. 2010, 46, 1247–1249. [Google Scholar] [CrossRef] [PubMed]
- Mujica-Martinez, C.A.; Nalbach, P.; Thorwart, M. Organic π-Conjugated Copolymers as Molecular Charge Qubits. Phys. Rev. Lett. 2013, 111, 016802. [Google Scholar] [CrossRef]
- Barone, V.; Cacelli, I.; Ferretti, A.; Prampolini, G. Magnetic gaps in organic tri-radicals: From a simple model to accurate estimates. J. Chem. Phys. 2017, 146, 104103. [Google Scholar] [CrossRef]
- Zhang, H.; Pink, M.; Wang, Y.; Rajca, S.; Rajca, A. High-Spin S = 3/2 Ground-State Aminyl Triradicals: Toward High-Spin Oligo-Aza Nanographenes. J. Am. Chem. Soc. 2022, 144, 19576–19591. [Google Scholar] [CrossRef] [PubMed]
- Boudalis, A.K.; Constantinides, C.P.; Chrysochos, N.; Carmieli, R.; Leitus, G.; Kourtellaris, A.; Lawson, D.B.; Koutentis, P.A. Deciphering the ground state of a C3-symmetrical Blatter-type triradical by CW and pulse EPR spectroscopy. J. Magn. Reson. 2023, 349, 107406. [Google Scholar] [CrossRef]
- Zhang, D.; Zhu, Z.; Xiao, X.; Fang, Y.-H.; Xiao, T.; Wang, X.; Jiang, S.-D.; Zhao, D. An Air-Stable Carbon-Centered Triradical with a Well-Addressable Quartet Ground State. J. Am. Chem. Soc. 2024, 146, 21752–21761. [Google Scholar] [CrossRef]
- Gorgon, S.; Lv, K.; Grüne, J.; Drummond, B.H.; Myers, W.K.; Londi, G.; Ricci, G.; Valverde, D.; Tonnelé, C.; Murto, P.; et al. Reversible spin-optical interface in luminescent organic radicals. Nature 2023, 620, 538–544. [Google Scholar] [CrossRef]
- Poh, Y.R.; Morozov, D.; Kazmierczak, N.P.; Hadt, R.G.; Groenhof, G.; Yuen-Zhou, J. Alternant Hydrocarbon Diradicals as Optically Addressable Molecular Qubits. J. Am. Chem. Soc. 2024, 146, 15549–15561. [Google Scholar] [CrossRef]
- Kopp, S.M.; Nakamura, S.; Phelan, B.T.; Poh, Y.R.; Tyndall, S.B.; Brown, P.J.; Huang, Y.; Yuen-Zhou, J.; Krzyaniak, M.D.; Wasielewski, M.R. Luminescent Organic Triplet Diradicals as Optically Addressable Molecular Qubits. J. Am. Chem. Soc. 2024, 146, 27935–27945. [Google Scholar] [CrossRef]
- Inoue, M.; Yamauchi, A.; Parmar, B.; Orihashi, K.; Singh, M.; Asada, M.; Nakamura, T.; Yanai, N. Guest-responsive coherence time of radical qubits in a metal–organic framework. Chem. Commun. 2024, 60, 6130–6133. [Google Scholar] [CrossRef] [PubMed]
- Zhou, A.; Sun, Z.; Sun, L. Stable organic radical qubits and their applications in quantum information science. Innovation 2024, 5, 100662. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Fujiwara, S.; Kimizuka, N.; Asada, M.; Fujiwara, M.; Nakamura, T.; Pirillo, J.; Hijikata, Y.; Yanai, N. Modulation of triplet quantum coherence by guest-induced structural changes in a flexible metal-organic framework. Nat. Commun. 2024, 15, 7622. [Google Scholar] [CrossRef] [PubMed]
- Dirac, P.A.M. The quantum theory of the emission and absorption of radiation. Proc. R. Soc. Lond. A 1927, 114, 243–265. [Google Scholar] [CrossRef]
- Susskind, L.; Glogower, J. Quantum mechanical phase and time operator. Phys. Phys. Fiz. 1964, 1, 49–61. [Google Scholar] [CrossRef]
- Loudon, R. The Quantum Theory of Light; Oxford university Press: Oxford, UK, 1973. [Google Scholar]
- Pegg, D.T.; Barnett, S.M. Unitary Phase Operator in Quantum Mechanics. Europhys. Lett. 1988, 6, 483–487. [Google Scholar] [CrossRef]
- Mendaš, I.; Popović, D.B. Number-phase uncertainty product for generalized squeezed states arising from the Pegg-Barnett Hermitian phase operator formalism. Phys. Rev. A 1995, 52, 4356–4364. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef]
- Bergmann, K.; Theuer, H.; Shore, B.W. Coherent population transfer among quantum states of atoms and molecules. Rev. Mod. Phys. 1998, 70, 1003–1025. [Google Scholar] [CrossRef]
- Furusawa, A.; Sørensen, J.L.; Braunstein, S.L.; Fuchs, C.A.; Kimble, H.J.; Polzik, E.S. Unconditional Quantum Teleportation. Science 1998, 282, 706–709. [Google Scholar] [CrossRef]
- Chou, C.W.; de Riedmatten, H.; Felinto, D.; Polyakov, S.V.; van Enk, S.J.; Kimble, H.J. Measurement-induced entanglement for excitation stored in remote atomic ensembles. Nature 2005, 438, 828–832. [Google Scholar] [CrossRef] [PubMed]
- Proos, J.; Zalka, C. Shor’s discrete logarithm quantum algorithm for elliptic curves. Quant. Inf. Comput. 2003, 3, 317–344. [Google Scholar] [CrossRef]
- Sherson, J.F.; Krauter, H.; Olsson, R.K.; Julsgaard, B.; Hammerer, K.; Cirac, I.; Polzik, E.S. Quantum teleportation between light and matter. Nature 2006, 443, 557–560. [Google Scholar] [CrossRef]
- Kimble, H. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- Dakir, Y.; Slaoui, A.; Mohamed, A.-B.A.; Laamara, R.A.; Eleuch, H. Quantum teleportation and dynamics of quantum coherence and metrological non-classical correlations for open two-qubit systems. Sci. Rep. 2023, 13, 20526. [Google Scholar] [CrossRef] [PubMed]
- Kok, P.; Munro, W.J.; Nemoto, K.; Ralph, T.C.; Dowling, J.P.; Milburn, G.J. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 2007, 79, 135–174. [Google Scholar] [CrossRef]
- Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O’Brien, J.L. Quantum computers. Nature 2010, 464, 45–53. [Google Scholar] [CrossRef]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Nitta, T.; Yamaguchi, K. Monte Carlo wave-function approach to the quantum-phase dynamics of a dissipative molecular system interacting with a single-mode amplitude-squeezed field. J. Chem. Phys. 2003, 119, 12106–12118. [Google Scholar] [CrossRef]
- Mølmer, K.; Castin, Y.; Dalibard, J. Monte Carlo wave-function method in quantum optics. J. Opt. Soc. Am. B 1993, 10, 524–538. [Google Scholar] [CrossRef]
- Dum, R.; Zoller, P.; Ritsch, H. Monte Carlo simulation of the atomic master equation for spontaneous emission. Phys. Rev. A 1992, 45, 4879–4887. [Google Scholar] [CrossRef] [PubMed]
- Dalibard, J.; Castin, Y.; Mølmer, K. Wave-function approach to dissipative processes in quantum optics. Phys. Rev. Lett. 1992, 68, 580–583. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Kishi, R.; Nitta, T.; Yamaguchi, K. Second-order Monte Carlo wave-function approach to the relaxation effects on ringing revivals in a molecular system interacting with a strongly squeezed coherent field. Phys. Rev. A 2004, 70, 033407. [Google Scholar] [CrossRef]
- Nakano, M. Open-Shell-Character-Based Molecular Design Principles: Applications to Nonlinear Optics and Singlet Fission. Chem. Rec. 2017, 17, 27–62. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).