Quantum Mechanical Approaches to Strongly Correlated Electron Systems: Structure, Bonding, and Properties of Diradicals, Triradicals, and Polyradicals
Abstract
1. Introduction
2. Symmetry Breaking and Its Recovery via Quantum Resonance
2.1. Cultural Background and Symmetry Breaking in Japan
2.2. Equivalence Transformation in Material Sciences
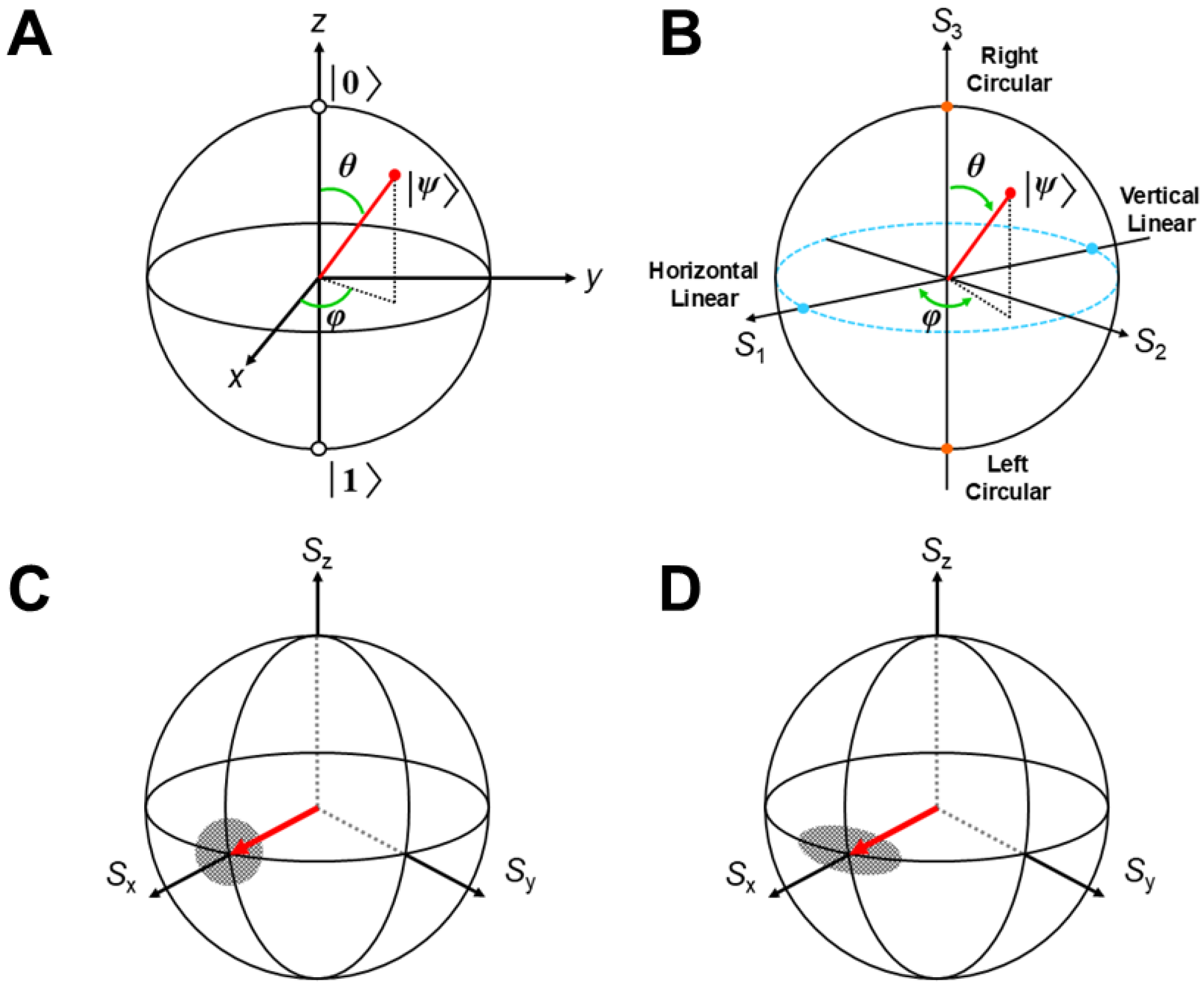
2.3. Theoretical Models for Strongly Correlated Electron Systems
2.4. Instability of Chemical Bonds and HOMO-LUMO Mixing for Diradicals
2.5. Structure, Bonding, and Potential Energy Structure for Homolytic Diradicals
2.6. Resonating Broken Symmetry for Recovery of Symmetry Breaking
2.7. Chemical Indices for Diradicals by Broken Symmetry (BS) and Resonating BS (RBS) Methods
2.8. Interrelationship Between VB and Localized MO Models
3. Collinear and Non-Collinear Spin Structures and Spin Frustrations in Tri- and Polyradicals
3.1. Collinear and Non-Collinear Spin Structures for Tri- and Polyradicals
3.2. Instability of the UHF Solution and General Spin Orbitals for Non-Collinear Spin Structures
3.3. Developments of BS GSO-X (X = HF, DFT, and Hybrid DFT) Program Systems
3.4. Spin Frustration and Resonating Broken Symmetry Method
3.5. Dirac Identity for Permutation Operator and Heisenberg Spin Hamiltonian Model
4. Beyond BS Methods for Quantitative Computations of Open-Shell Systems
4.1. Early MR CI and MR CC Methods as Direct Extensions of BS Methods for Radicals
4.2. Potential Curves for Dissociation of the Covalent Bond: Fluorine Molecule
4.3. Geometry Optimization of Open-Shell Molecules: Methylene
4.4. Trimethylenemethane Analogs: Heteroatom Effect
5. Theoretical and Computational Studies of Diradical Species
5.1. Anti-Aromatic Compounds with 4π Electrons
5.2. Through-Bond Interactions Between Phenalenyl Radicals
5.3. Through-Space Interactions Between Phenalenyl Radicals
6. Nonlinear Optical Properties of Diradical Materials
6.1. Linear and Nonlinear Responses of Materials for Electronic Field
6.2. Theoretical Computational Methods of Linear and Nonlinear Responses of Materials
6.3. Functional Behaviors of Nonlinear γ Value with Diradical Character: Exact Models
6.4. Variations in the Nonlinear γ Value with Diradical Character: ab Initio Computations
6.5. γ Values of 1,3-Diradical and 1,3- Dipole: ab Initio Computations
6.6. Nonlinear Optical Materials: γ Values of Nitronyl Niroxide
7. Discussions, Conclusions, and Future Prospects
7.1. A New Direction for Molecular Magnetism
7.2. NMR Computer and Other Candidates for Quantum Bits
7.3. Opportunities of Inorganic Open-Shell Species as Quantum Materials
7.4. Early and Recent Investigations of Organic Radicals and Diradicals as Quantum Materials
7.5. A New Direction for Optical Molecular Materials for Quantum Optics
7.6. Concluding Remarks and Future Prospects
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Broglie, L. Recherches sur la théorie des Quanta. Ann. Phys. 1925, 10, 22–128. [Google Scholar] [CrossRef]
- Heisenberg, W. Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen. Z. Phys. 1925, 33, 879–893. [Google Scholar] [CrossRef]
- Heisenberg, W. Zur Quantentheorie der Multiplettstruktur und der anomalen Zeemaneffekte. Z. Phys. 1925, 32, 841–860. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The fundamental equations of quantum mechanics. Proc. R. Soc. Lond. A 1925, 109, 642–653. [Google Scholar] [CrossRef]
- Born, M.; Heisenberg, W.; Jordan, P. Zur Quantenmechanik. II. Z. Phys. 1926, 35, 557–615. [Google Scholar] [CrossRef]
- Schrödinger, E. Quantisierung als Eigenwertproblem. Ann. Phys. 1926, 384, 361–376. [Google Scholar] [CrossRef]
- Schrödinger, E. Der stetige Übergang von der Mikro- zur Makromechanik. Naturwissenschaften 1926, 14, 664–666. [Google Scholar] [CrossRef]
- Born, M.; Jordan, P. Zur Quantenmechanik. Z. Phys. 1925, 34, 858–888. [Google Scholar] [CrossRef]
- Pauli, W. Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik. Z. Phys. 1926, 36, 336–363. [Google Scholar] [CrossRef]
- Born, M. Zur Quantenmechanik der Stoßvorgänge. Z. Phys. 1926, 37, 863–867. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The physical interpretation of the quantum dynamics. Proc. R. Soc. Lond. A 1927, 113, 621–641. [Google Scholar] [CrossRef]
- Heisenberg, W. Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Z. Phys. 1927, 43, 172–198. [Google Scholar] [CrossRef]
- Schrödinger, E. Über den Comptoneffekt. Ann. Phys. 1927, 387, 257–264. [Google Scholar] [CrossRef]
- Heitler, W.; London, F. Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik. Z. Phys. 1927, 44, 455–472. [Google Scholar] [CrossRef]
- Born, M.; Oppenheimer, R. Zur Quantentheorie der Molekeln. Ann. Phys. 1927, 389, 457–484. [Google Scholar] [CrossRef]
- Lewis, G.N. Valence and the Structure of Atoms and Molecules; American Chemical Monograph Series; Chemical Catalog Company: New York, NY, USA, 1923. [Google Scholar]
- Pauling, L. The Shared-Electron Chemical Bond. Proc. Natl. Acad. Sci. USA 1928, 14, 359–362. [Google Scholar] [CrossRef] [PubMed]
- Hund, F. Zur Deutung einiger Erscheinungen in den Molekelspektren. Z. Phys. 1926, 36, 657–674. [Google Scholar] [CrossRef]
- Mulliken, R.S. The Assignment of Quantum Numbers for Electrons in Molecules. I. Phys. Rev. 1928, 32, 186–222. [Google Scholar] [CrossRef]
- Klitzing, K.V.; Dorda, G.; Pepper, M. New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance. Phys. Rev. Lett. 1980, 45, 494–497. [Google Scholar] [CrossRef]
- Laughlin, R.B. Anomalous Quantum Hall Effect: An Incompressible Quantum Fluid with Fractionally Charged Excitations. Phys. Rev. Lett. 1983, 50, 1395–1398. [Google Scholar] [CrossRef]
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys. Rev. Lett. 1982, 49, 405–408. [Google Scholar] [CrossRef]
- Bednorz, J.G.; Müller, K.A. Possible highTc superconductivity in the Ba−La−Cu−O system. Z. Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yoshioka, Y.; Nakano, M.; Nagao, H.; Okumura, M. Bussei Ryoshikagaku Nyumon; Kodansha Scientific: Tokyo, Japan, 2004. [Google Scholar]
- Vedral, V. Introduction to Quantum Information Science; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Alfieri, A.; Anantharaman, S.B.; Zhang, H.; Jariwala, D. Nanomaterials for Quantum Information Science and Engineering. Adv. Mater. 2023, 35, 2109621. [Google Scholar] [CrossRef]
- Benioff, P. The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines. J. Stat. Phys. 1980, 22, 563–591. [Google Scholar] [CrossRef]
- Buluta, I.; Nori, F. Quantum Simulators. Science 2009, 326, 108–111. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.; Li, Z. Recent progress in open-shell organic conjugated materials and their aggregated states. J. Mater. Chem. C 2022, 10, 2431–2449. [Google Scholar] [CrossRef]
- Fukui, K. The role of frontier orbitals in chemical reactions (Nobel lecture). Angew. Chem. Int. Ed. 1982, 21, 801–809. [Google Scholar] [CrossRef]
- Hoffmann, R.; Woodward, R.B. Selection Rules for Concerted Cycloaddition Reactions. J. Am. Chem. Soc. 1965, 84, 2046–2048. [Google Scholar] [CrossRef]
- Woodward, R.B.; Hoffmann, R. The Conservation of Orbital Symmetry. Angew. Chem. Int. Ed. 1969, 8, 781–853. [Google Scholar] [CrossRef]
- Fukui, K.; Yonezawa, T.; Nagata, C.; Shingu, H. Molecular Orbital Theory of Orientation in Aromatic, Heteroaromatic, and Other Conjugated Molecules. J. Chem. Phys. 1954, 22, 1433–1442. [Google Scholar] [CrossRef]
- Longuet-Higgins, H.C.; Abrahamson, E.W. The Electronic Mechanism of Electrocyclic Reactions. J. Am. Chem. Soc. 1965, 87, 2045–2046. [Google Scholar] [CrossRef]
- Dewar, M.J.S. Aromaticity and Pericyclic Reactions. Angew. Chem. Int. Ed. 1971, 10, 761–776. [Google Scholar] [CrossRef]
- Kanamori, J. Superexchange interaction and symmetry properties of electron orbitals. J. Phys. Chem. Solids 1959, 10, 87–98. [Google Scholar] [CrossRef]
- Goodenough, J.B. Magnetism and The Chemical Bond; John Wiley & Sons: Chichester, UK, 1963. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Löwdin, P.-O. Quantum Genetics and the Aperiodic Solid: Some Aspects on the Biological Problems of Heredity, Mutations, Aging, and Tumors in View of the Quantum Theory of the DNA Molecule. In Advances in Quantum Chemistry; Löwdin, P.-O., Ed.; Elsevier: Amsterdam, The Netherlands, 1966; Volume 2, pp. 213–360. [Google Scholar] [CrossRef]
- Yamaguchi, K. Instability in Chemical Bonds—SCF, APUMP, APUCC, MR-CI and MR- CC Approaches. In Self-Consistent Field: Theory and Applications; Carbó, R., Klobukowski, M., Eds.; Elsevier: Amsterdam, The Netherlands, 1990; pp. 727–823. [Google Scholar]
- Yamaguchi, K. Symmetry and broken symmetry in molecular orbital (MO) descriptions of unstable molecules. Generalized MO theoretical studies on 1,3-dipolar species. J. Mol. Struct. THEOCHEM 1983, 103, 101–120. [Google Scholar] [CrossRef]
- Yamaguchi, K. Theoretical calculations of singlet oxygen reactions. In Singlet O2; Frimer, A.A., Ed.; CRC Press: Boca Raton, FL, USA, 1985; Volume III, Chapter 2; pp. 119–250. [Google Scholar]
- Yamaguchi, K.; Takada, K.; Otsuji, Y.; Mizuno, K. Theoretical and general aspects of organic peroxides. In Organic Peroxides; Ando, W., Ed.; John Wiley & Sons: Chichester, UK, 1992; pp. 1–100. [Google Scholar]
- Gatteschi, D.; Yamaguchi, K. Opportunities for New Physics in Molecular Magnetism. In Molecular Magnetism: From Molecular Assemblies to the Devices NATO ASI Series; Coronado, E., Delhaès, P., Gatteschi, D., Miller, J.S., Eds.; Springer: Dordrecht, The Netherlands, 1996; Volume 321, pp. 561–570. [Google Scholar] [CrossRef]
- Yamaguchi, K. Electrons in Specific Molecular Systems. In From Molecules to Molecular Systems; Nagakura, S., Ed.; Springer: Tokyo, Japan, 1998; pp. 67–91. [Google Scholar]
- Yamaguchi, K.; Isobe, H.; Shoji, M.; Kawakami, T.; Miyagawa, K. The Nature of the Chemical Bonds of High-Valent Transition–Metal Oxo (M=O) and Peroxo (MOO) Compounds: A Historical Perspective of the Metal Oxyl–Radical Character by the Classical to Quantum Computations. Molecules 2023, 28, 7119. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Miyagawa, K.; Shoji, M.; Kawakami, T.; Isobe, H.; Yamanaka, S.; Nakajima, T. Theoretical elucidation of the structure, bonding, and reactivity of the CaMn4Ox clusters in the whole Kok cycle for water oxidation embedded in the oxygen evolving center of photosystem II. New molecular and quantum insights into the mechanism of the O–O bond formation. Photosynth. Res. 2024, 162, 291–330. [Google Scholar] [CrossRef]
- Klauder, J.R. The action option and a Feynman quantization of spinor fields in terms of ordinary c-numbers. Ann. Phys. 1960, 11, 123–168. [Google Scholar] [CrossRef]
- Glauber, R.J. The Quantum Theory of Optical Coherence. Phys. Rev. 1963, 130, 2529–2539. [Google Scholar] [CrossRef]
- Glauber, R.J. Coherent and Incoherent States of the Radiation Field. Phys. Rev. 1963, 131, 2766–2788. [Google Scholar] [CrossRef]
- Sudarshan, E.C.G. Equivalence of Semiclassical and Quantum Mechanical Descriptions of Statistical Light Beams. Phys. Rev. Lett. 1963, 10, 277–279. [Google Scholar] [CrossRef]
- Walls, D.F.; Milburn, G.J. Quantum Optics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Mandel, L.; Wolf, E. Coherence Properties of Optical Fields. Rev. Mod. Phys. 1965, 37, 231–287. [Google Scholar] [CrossRef]
- Perelomov, A.M. Coherent states for arbitrary Lie group. Commun. Math. Phys. 1972, 26, 222–236. [Google Scholar] [CrossRef]
- Kimble, H.J.; Mandel, L. Theory of resonance fluorescence. Phys. Rev. A 1976, 13, 2123–2144. [Google Scholar] [CrossRef]
- Walls, D.F.; Zoller, P. Reduced Quantum Fluctuations in Resonance Fluorescence. Phys. Rev. Lett. 1981, 47, 709–711. [Google Scholar] [CrossRef]
- Walls, D.F. Squeezed states of light. Nature 1983, 306, 141–146. [Google Scholar] [CrossRef]
- Slusher, R.E.; Hollberg, L.W.; Yurke, B.; Mertz, J.C.; Valley, J.F. Observation of Squeezed States Generated by Four-Wave Mixing in an Optical Cavity. Phys. Rev. Lett. 1985, 55, 2409–2412. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.-A.; Kimble, H.J.; Hall, J.L.; Wu, H. Generation of Squeezed States by Parametric Down Conversion. Phys. Rev. Lett. 1986, 57, 2520–2523. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Analysis of nonlinear optical processes for molecular systems. In Trends in Chemical Physics; Research Trends: Trivandrum, India, 1997; Volume 5, pp. 87–237. [Google Scholar]
- Nakano, M.; Yamaguchi, K. Polarizabilities and Hyperpolarizabilities of Dendritic Systems. In Advances in Multi-Photon Processes and Spectroscopy; Lin, S.H., Villaeys, A.A., Fujimura, Y., Eds.; World Scientific: Singapore, 2003; Volume 15, pp. 3–146. [Google Scholar]
- Knill, E.; Laflamme, R.; Milburn, G. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46–52. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865–942. [Google Scholar] [CrossRef]
- Moreau, P.-A.; Toninelli, E.; Gregory, T.; Padgett, M.J. Imaging with quantum states of light. Nat. Rev. Phys. 2019, 1, 367–380. [Google Scholar] [CrossRef]
- Asavanant, W.; Shiozawa, Y.; Yokoyama, S.; Charoensombutamon, B.; Emura, H.; Alexander, R.N.; Takeda, S.; Yoshikawa, J.; Menicucci, N.C.; Yonezawa, H.; et al. Generation of time-domain-multiplexed two-dimensional cluster state. Science 2019, 366, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Yamaguchi, K. Quantum-phase and information-entropy dynamics of a two-state molecular system interacting with strongly amplitude- and phase-squeezed fields. J. Chem. Phys. 2000, 112, 2769–2780. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Quantum-phase and information-entropy dynamics of a molecular system interacting with a two-mode squeezed coherent field. Phys. Rev. A 2001, 64, 033415. [Google Scholar] [CrossRef]
- Pegg, D.T.; Barnett, S.M. Phase properties of the quantized single-mode electromagnetic field. Phys. Rev. A 1989, 39, 1665–1675. [Google Scholar] [CrossRef] [PubMed]
- Barnett, S.M.; Pegg, D.T. Quantum theory of optical phase correlations. Phys. Rev. A 1990, 42, 6713–6720. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Yamada, S.; Yamaguchi, K. Quantum phase dynamics: Collapse and revival behavior in a two- and a three-state molecule systems interacting with an initially one-mode coherent field. Synth. Met. 1999, 102, 1540–1541. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Ohta, S.; Takahashi, H.; Furukawa, S.; Yamaguchi, K. Quantum-phase dynamics of two-component Bose–Einstein condensates: Collapse–revival of macroscopic superposition states. Phys. B Condens. Matter 2005, 370, 110–120. [Google Scholar] [CrossRef]
- Rempe, G.; Walther, H.; Klein, N. Observation of quantum collapse and revival in a one-atom maser. Phys. Rev. Lett. 1987, 58, 353–356. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Mizushima, S. A History of Physical Chemistry in Japan. Annu. Rev. Phys. Chem. 1972, 23, 1–14. [Google Scholar] [CrossRef]
- Anderson, P.W. More Is Different. Science 1972, 177, 393–396. [Google Scholar] [CrossRef] [PubMed]
- Nambu, Y.; Jona-Lasinio, G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y. Nobel Lecture: Spontaneous symmetry breaking in particle physics: A case of cross fertilization. Rev. Mod. Phys. 2009, 81, 1015–1018. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Quantum mechanics of many-electron systems. Proc. R. Soc. Lond. A 1929, 123, 714–733. [Google Scholar] [CrossRef]
- Rainwater, J. Nuclear Energy Level Argument for a Spheroidal Nuclear Model. Phys. Rev. 1950, 79, 432–434. [Google Scholar] [CrossRef]
- Higgs, P.W. Spontaneous Symmetry Breakdown without Massless Bosons. Phys. Rev. 1966, 145, 1156–1163. [Google Scholar] [CrossRef]
- Kobayashi, M.; Maskawa, T. CP-Violation in the Renormalizable Theory of Weak Interaction. Prog. Theor. Phys. 1973, 49, 652–657. [Google Scholar] [CrossRef]
- Slater, J.C. Ferromagnetism and the Band Theory. Rev. Mod. Phys. 1953, 25, 199–210. [Google Scholar] [CrossRef]
- Nesbet, R.K. Approximate Methods in the Quantum Theory of Many-Fermion Systems. Rev. Mod. Phys. 1961, 33, 28–36. [Google Scholar] [CrossRef]
- Fukutome, H. The Unrestricted Hartree-Fock Theory of Chemical Reactions. I: The Electronic Instabilities in the Chemical Reactions and the Solutions of the Unrestricted SCF LCAO MO Equation for the Homopolar Two-Center Two-Electron System. Prog. Theor. Phys. 1972, 47, 1156–1180. [Google Scholar] [CrossRef]
- Kosterlitz, J.M.; Thouless, D.J. Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C Solid State Phys. 1973, 6, 1181–1203. [Google Scholar] [CrossRef]
- Kosterlitz, J.M. Kosterlitz–Thouless physics: A review of key issues. Rep. Prog. Phys. 2016, 79, 026001. [Google Scholar] [CrossRef] [PubMed]
- Haldane, F.D.M. Nonlinear Field Theory of Large-Spin Heisenberg Antiferromagnets: Semiclassically Quantized Solitons of the One-Dimensional Easy-Axis Néel State. Phys. Rev. Lett. 1983, 50, 1153–1156. [Google Scholar] [CrossRef]
- Affleck, I.; Kennedy, T.; Lieb, E.H.; Tasaki, H. Rigorous results on valence-bond ground states in antiferromagnets. Phys. Rev. Lett. 1987, 59, 799–802. [Google Scholar] [CrossRef]
- Longuet-Higgins, H.C.; Öpik, U.; Pryce, M.H.L.; Sack, R.A. Studies of the Jahn-Teller effect II. The dynamical problem. Proc. R. Soc. Lond. A 1958, 244, 1–16. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 1984, 392, 45–57. [Google Scholar] [CrossRef]
- Ichikawa, K. Souzousei No Kagaku; NHK Publishing: Tokyo, Japan, 1970. [Google Scholar]
- Magri, F. Equivalence transformations for nonlinear evolution equations. J. Math. Phys. 1977, 18, 1405–1411. [Google Scholar] [CrossRef]
- Bellucci, S.; Ivanov, E.; Krivonos, S. AdS/CFT equivalence transformation. Phys. Rev. D 2002, 66, 086001. [Google Scholar] [CrossRef]
- Ganghoffer, J.F.; Rahouadj, R.; Cheviakov, A. Symmetry analysis and equivalence transformations for the construction and reduction of constitutive models. Adv. Model. Simul. Eng. Sci. 2021, 8, 1. [Google Scholar] [CrossRef]
- Hoffmann, R. Building Bridges Between Inorganic and Organic Chemistry (Nobel Lecture). Angew. Chem. Int. Ed. 1982, 21, 711–724. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Miyagawa, K.; Isobe, H.; Shoji, M.; Kawakami, T.; Yamanaka, S. Isolobal and isospin analogy between organic and inorganic open-shell molecules—Application to oxygenation reactions by active oxygen and oxy-radicals and water oxidation in the native and artificial photosynthesis. In Advances in Quantum Chemistry; Brändas, E.J., Ed.; Elsevier: Amsterdam, The Netherlands, 2021; Volume 84, pp. 425–564. [Google Scholar] [CrossRef]
- Nakamura, Y.; Pashkin, Y.A.; Tsai, J.S. Coherent control of macroscopic quantum states in a single-Cooper-pair box. Nature 1999, 398, 786–788. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Nakano, M.; Nagao, H.; Okumura, M.; Yamanaka, S.; Kawakami, T.; Yamaki, D.; Nishino, M.; Shigeta, Y.; Kitagawa, Y.; et al. Spin and Pseudo Spins in Theoretical Chemistry. A Unified View for Superposed and Entangled Quantum Systems. Bull. Korean Chem. Soc. 2003, 24, 864–880. [Google Scholar] [CrossRef]
- Anderson, P.W. Random-Phase Approximation in the Theory of Superconductivity. Phys. Rev. 1958, 112, 1900–1916. [Google Scholar] [CrossRef]
- Leggett, A.J. A theoretical description of the new phases of liquid 3He. Rev. Mod. Phys. 1975, 47, 331–414. [Google Scholar] [CrossRef]
- Matsunaga, R.; Tsuji, N.; Fujita, H.; Sugioka, A.; Makise, K.; Uzawa, Y.; Terai, H.; Wang, Z.; Aoki, H.; Shimano, R. Light-induced collective pseudospin precession resonating with Higgs mode in a superconductor. Science 2014, 345, 1145–1149. [Google Scholar] [CrossRef]
- Aoki, H.; Tsuji, N.; Eckstein, M.; Kollar, M.; Oka, T.; Werner, P. Nonequilibrium dynamical mean-field theory and its applications. Rev. Mod. Phys. 2014, 86, 779–837. [Google Scholar] [CrossRef]
- Kitagawa, M.; Ueda, M. Squeezed spin states. Phys. Rev. A 1993, 47, 5138–5143. [Google Scholar] [CrossRef] [PubMed]
- Perlin, M.A.; Qu, C.; Rey, A.M. Spin Squeezing with Short-Range Spin-Exchange Interactions. Phys. Rev. Lett. 2020, 125, 223401. [Google Scholar] [CrossRef]
- Comparin, T.; Mezzacapo, F.; Roscilde, T. Robust spin squeezing from the tower of states of U(1)-symmetric spin Hamiltonians. Phys. Rev. A 2022, 105, 022625. [Google Scholar] [CrossRef]
- Bornet, G.; Emperauger, G.; Chen, C.; Ye, B.; Block, M.; Bintz, M.; Boyd, J.A.; Barredo, D.; Comparin, T.; Mezzacapo, F.; et al. Scalable spin squeezing in a dipolar Rydberg atom array. Nature 2023, 621, 728–733. [Google Scholar] [CrossRef]
- Block, M.; Ye, B.; Roberts, B.; Chern, S.; Wu, W.; Wang, Z.; Pollet, L.; Davis, E.J.; Halperin, B.I.; Yao, N.Y. Scalable spin squeezing from finite-temperature easy-plane magnetism. Nat. Phys. 2024, 20, 1575–1581. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 48, 777–780. [Google Scholar] [CrossRef]
- Hückel, E. Quantentheoretische Beiträge zum Benzolproblem, I. Die Elektronenkonfiguration des Benzols und verwandter Verbindungen. Z. Phys. 1931, 70, 204–286. [Google Scholar] [CrossRef]
- Hoffmann, R. An Extended Hückel Theory. I. Hydrocarbons. J. Chem. Phys. 1963, 39, 1397–1412. [Google Scholar] [CrossRef]
- Hubbard, J. Electron correlations in narrow energy bands. Proc. R. Soc. Lond. A 1963, 276, 238–257. [Google Scholar] [CrossRef]
- Kanamori, J. Electron Correlation and Ferromagnetism of Transition Metals. Prog. Theor. Phys. 1963, 30, 275–289. [Google Scholar] [CrossRef]
- Gutzwiller, M.C. Effect of Correlation on the Ferromagnetism of Transition Metals. Phys. Rev. Lett. 1963, 10, 159–162. [Google Scholar] [CrossRef]
- Himmetoglu, B.; Floris, A.; de Gironcoli, S.; Cococcioni, M. Hubbard-corrected DFT energy functionals: The LDA+U description of correlated systems. Int. J. Quant. Chem. 2014, 114, 14–49. [Google Scholar] [CrossRef]
- Pauli, W., Jr. Zur Quantenmechanik des magnetischen Elektrons. Z. Phys. 1927, 43, 601–623. [Google Scholar] [CrossRef]
- Jordan, P.; Wigner, E. Über das Paulische Äquivalenzverbot. Z. Phys. 1928, 47, 631–651. [Google Scholar] [CrossRef]
- Bravyi, S.B.; Kitaev, A.Y. Fermionic Quantum Computation. Ann. Phys. 2002, 298, 210–226. [Google Scholar] [CrossRef]
- Hartree, D.R. The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part I. Theory and Methods. Math. Proc. Camb. Philos. Soc. 1928, 24, 89–110. [Google Scholar] [CrossRef]
- Fock, V. Näherungsmethode zur Lösung des quantenmechanischen Mehrkörperproblems. Z. Phys. 1930, 61, 126–148. [Google Scholar] [CrossRef]
- Overhauser, A.W. Giant Spin Density Waves. Phys. Rev. Lett. 1960, 4, 462–465. [Google Scholar] [CrossRef]
- Thouless, D.J. Stability conditions and nuclear rotations in the Hartree-Fock theory. Nucl. Phys. 1960, 21, 225–232. [Google Scholar] [CrossRef]
- Sawada, K.; Fukuda, N. On the Stability of the Hartree-Fock Solution in Many-Body Problem. Prog. Theor. Phys. 1961, 25, 653–666. [Google Scholar] [CrossRef]
- Čížek, J.; Paldus, J. Stability conditions for the solutions of the Hartree-Fock equations for atomic and molecular systems. Application to the pi-electron model of cyclic polyenes. J. Chem. Phys. 1967, 47, 3976–3985. [Google Scholar] [CrossRef]
- Fukutome, H. Spin density wave and charge transfer wave in long conjugated molecules. Prog. Theor. Phys. 1968, 40, 998–1012. [Google Scholar] [CrossRef]
- Slater, J.C. Magnetic Effects and the Hartree-Fock Equation. Phys. Rev. 1951, 82, 538–541. [Google Scholar] [CrossRef]
- Yamaguchi, K. The electronic structures of biradicals in the unrestricted Hartree-Fock approximation. Chem. Phys. Lett. 1975, 33, 330–335. [Google Scholar] [CrossRef]
- Yamaguchi, K. Electronic structures of antiaromatic molecules. Chem. Phys. Lett. 1975, 35, 230–235. [Google Scholar] [CrossRef]
- Yamaguchi, K. Singlet unrestricted Hartree-Fock Slater (UHFS) model for unstable metal-metal bonds. Chem. Phys. Lett. 1979, 66, 395–399. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fueno, T. Mechanistic characterization of the thermal ring-opening of three-membered cyclic compounds. Chem. Phys. Lett. 1973, 22, 471–475. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Ohta, K.; Yabushita, S.; Fueno, T. Generalized Hartree-Fock natural-orbital configuration-interaction (GHF NO CI) approach to unstable molecules: Trimethylene. Chem. Phys. Lett. 1977, 49, 555–559. [Google Scholar] [CrossRef]
- Huisgen, R. Electrocyclic Ring Opening Reactions of Ethylene Oxides. Angew. Chem. Int. Ed. 1977, 16, 572–585. [Google Scholar] [CrossRef]
- Houk, K.N.; Yamaguchi, K. Theory of 1,3-Dipolar Cycloadditions. In 1,3-Dipolar Cycloaddition Chemistry; Padwa, A., Ed.; Wiley: New York, NY, USA, 1984; Volume 2, Chapter 13; pp. 407–448. [Google Scholar]
- Hoffmann, R.; Zeiss, G.D.; van Dine, G.W. The electronic structure of methylenes. J. Am. Chem. Soc. 1968, 90, 1485–1499. [Google Scholar] [CrossRef]
- Harrison, J.F. Electronic structure of carbenes. I. Methylene, fluoromethylene, and difluoromethylene. J. Am. Chem. Soc. 1971, 93, 4112–4119. [Google Scholar] [CrossRef]
- Harrison, J.F.; Liedtke, R.C.; Liebman, J.F. The multiplicity of substituted acyclic carbenes and related molecules. J. Am. Chem. Soc. 1979, 101, 7162–7168. [Google Scholar] [CrossRef]
- Bauschlicher, C.W., Jr.; Schaefer, H.F., III; Bagus, P.S. Structure and energetics of simple carbenes methylene, fluoromethylene, chloromethylene, bromomethylene, difluoromethylene, and dichloromethylene. J. Am. Chem. Soc. 1977, 99, 7106–7110. [Google Scholar] [CrossRef]
- Feller, D.; Borden, W.T.; Davidson, E.R. Dependence of the singlet-triplet splitting in heterosubstituted carbenes on the heteroatom electronegativity and conformation. Chem. Phys. Lett. 1980, 71, 22–26. [Google Scholar] [CrossRef]
- Tomioka, H. Persistent Triplet Carbenes. Acc. Chem. Res. 1997, 30, 315–321. [Google Scholar] [CrossRef]
- Hirai, K.; Itoh, T.; Tomioka, H. Persistent Triplet Carbenes. Chem. Rev. 2009, 109, 3275–3332. [Google Scholar] [CrossRef] [PubMed]
- Bourissou, D.; Guerret, O.; Gabbaï, F.P.; Bertrand, G. Stable Carbenes. Chem. Rev. 2000, 100, 39–92. [Google Scholar] [CrossRef] [PubMed]
- Wyman, G.M. The Cis-Trans Isomerization of Conjugated compounds. Chem. Rev. 1955, 55, 625–657. [Google Scholar] [CrossRef]
- Dugave, C.; Demange, L. Cis−Trans Isomerization of Organic Molecules and Biomolecules: Implications and Applications. Chem. Rev. 2003, 103, 2475–2532. [Google Scholar] [CrossRef] [PubMed]
- Oka, T.; Maeda, T.; Sakamaki, D.; Suzuki, N.; Yagi, S.; Kodama, S.; Fujiwara, H. Intermediate diradical character and thermal cis–trans isomerization of near-infrared absorbing thionated squaraine dyes. Org. Chem. Front. 2025, 12, 42–47. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yabushita, S.; Minokawa, O.; Fueno, T. DODS natural-orbital CI (DODS-NO CI) approach to the excited states of unstable molecules: Twisted substituted ethyelenes. Chem. Phys. Lett. 1978, 59, 303–307. [Google Scholar] [CrossRef]
- Anderson, P.W. Basic Notations of Condensed Matter Physics; Benjamin/Cummings Publishing Co.: Menio Park, CA, USA, 1984. [Google Scholar]
- Anderson, P.W. Resonating valence bonds: A new kind of insulator? Mater. Res. Bull. 1973, 8, 153–160. [Google Scholar] [CrossRef]
- Anderson, P.W. The Resonating Valence Bond State in La2CuO4 and Superconductivity. Science 1987, 235, 1196–1198. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yoshioka, Y.; Fueno, T. Interrelationships between the effective Hamiltonians for the H3 radical. Chem. Phys. Lett. 1977, 46, 360–365. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yoshioka, Y.; Takatsuka, T.; Fueno, T. Extended Hartree-Fock (EHF) theory in chemical reactions II. Symmetry properties of the EHF wavefunctions constructed by the magnetically ordered general spin orbitals. Theoret. Chim. Acta 1978, 48, 185–206. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fukui, H.; Fueno, T. Molecular orbital (MO) theory for magnetically interacting organic compounds. ab-initio MO calculations of the effective exchange integrals for cyclophane-type carbene dimers. Chem. Lett. 1986, 15, 625–628. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Tsunekawa, T.; Toyoda, Y.; Fueno, T. Ab initio molecular orbital calculations of effective exchange integrals between transition metal ions. Chem. Phys. Lett. 1988, 143, 371–376. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Jensen, F.; Dorigo, A.; Houk, K.N. A spin correction procedure for unrestricted Hartree-Fock and Møller-Plesset wavefunctions for singlet diradicals and polyradicals. Chem. Phys. Lett. 1988, 149, 537–542. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Brunner, N.; Cavalcanti, D.; Pironio, S.; Scarani, V.; Wehner, S. Bell nonlocality. Rev. Mod. Phys. 2014, 86, 419–478. [Google Scholar] [CrossRef]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682–686. [Google Scholar] [CrossRef]
- Schrödinger, E. Discussion of Probability Relations between Separated Systems. Math. Proc. Camb. Philos. Soc. 1936, 31, 555–563. [Google Scholar] [CrossRef]
- Freedman, S.J.; Clauser, J.F. Experimental Test of Local Hidden-Variable Theories. Phys. Rev. Lett. 1972, 28, 938–941. [Google Scholar] [CrossRef]
- Aspect, A.; Grangier, P.; Roger, G. Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities. Phys. Rev. Lett. 1982, 49, 91–94. [Google Scholar] [CrossRef]
- Breugst, M.; Reissig, H.-U. The Huisgen Reaction: Milestones of the 1,3-Dipolar Cycloaddition. Angew. Chem. Int. Ed. 2020, 59, 12293–12307. [Google Scholar] [CrossRef] [PubMed]
- Abe, M.; Ye, J.; Mishima, M. The chemistry of localized singlet 1,3-diradicals (biradicals): From putative intermediates to persistent species and unusual molecules with a π-single bonded character. Chem. Soc. Rev. 2012, 41, 3808–3820. [Google Scholar] [CrossRef] [PubMed]
- Skell, P.S.; Doerr, R.G. Trimethylenemethane. J. Am. Chem. Soc. 1967, 89, 4688–4692. [Google Scholar] [CrossRef]
- Dowd, P. Trimethylenemethane. Acc. Chem. Res. 1972, 5, 242–248. [Google Scholar] [CrossRef]
- Berson, J.A. The chemistry of trimethylenemethanes, a new class of biradical reactive intermediates. Acc. Chem. Res. 1978, 11, 446–453. [Google Scholar] [CrossRef]
- Davidson, E.R.; Borden, W.T. Some aspects of the potential surface for singlet trimethylenemethane. J. Am. Chem. Soc. 1977, 99, 2053–2060. [Google Scholar] [CrossRef]
- Davis, J.H.; Goddard, W.A., III. Electronic states of trimethylenemethane. J. Am. Chem. Soc. 1977, 99, 4242–4247. [Google Scholar] [CrossRef]
- Hood, D.M.; Pitzer, R.M.; Schaefer, H.F., III. Equilibrium geometry of trimethylenemethane and the absence of an adjacent secondary minimum on the triplet potential energy surface. J. Am. Chem. Soc. 1978, 100, 2227–2228. [Google Scholar] [CrossRef]
- Kollmar, H.; Staemmler, V. A theoretical study of the structure of cyclobutadiene. J. Am. Chem. Soc. 1977, 99, 3583–3587. [Google Scholar] [CrossRef]
- Borden, W.T. Can a square or effectively square singlet be the ground state of cyclobutadiene? J. Am. Chem. Soc. 1975, 97, 5968–5970. [Google Scholar] [CrossRef]
- Coulson, C.A.; Rushbrooke, G.S. Note on the method of molecular orbitals. Math. Proc. Camb. Philos. Soc. 1940, 36, 193–200. [Google Scholar] [CrossRef]
- Salem, L.; Rowland, C. The Electronic Properties of Diradicals. Angew. Chem. Int. Ed. 1972, 11, 92–111. [Google Scholar] [CrossRef]
- Lykos, P.; Pratt, G.W. Discussion on the Hartree-Fock approximation. Rev. Mod. Phys. 1963, 35, 496–501. [Google Scholar] [CrossRef]
- Löwdin, P.-O. Some Aspects on the Correlation Problem and Possible Extensions of the Independent-Particle Model. In Advances in Chemical Physics; LeFebvre, R., Moser, C., Eds.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1969; Volume 14, pp. 283–340. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fueno, T. Correlation effects in singlet biradical species. Chem. Phys. 1977, 19, 35–42. [Google Scholar] [CrossRef]
- Yamaguchi, K. Generalized molecular orbital (GMO) theories of organic reaction mechanisms. Orbital symmetry, orbital stability and orbital pairing rules. Chem. Phys. 1978, 29, 117–139. [Google Scholar] [CrossRef]
- Nagamiya, T. Helical Spin Ordering—1 Theory of Helical Spin Configurations. Solid State Phys. 1968, 20, 305–411. [Google Scholar] [CrossRef]
- Shirane, G.; Chikazumi, S.; Akimitsu, J.; Chiba, K.; Matsui, M.; Fujii, Y. Neutron Scattering from Low-Temperature Phase of Magnetite. J. Phys. Soc. Jpn. 1975, 39, 949–957. [Google Scholar] [CrossRef]
- Nalewajski, R.F. Entropic Measures of Bond Multiplicity from the Information Theory. J. Phys. Chem. A 2000, 104, 11940–11951. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Shepelevich, I.S. Information Entropy in Chemistry: An Overview. Entropy 2021, 23, 1240. [Google Scholar] [CrossRef]
- Lewis, G.N. The atom and the molecule. J. Am. Chem. Soc. 1916, 38, 762–785. [Google Scholar] [CrossRef]
- Linnett, J.W. A Modification of the Lewis-Langmuir Octet Rule. J. Am. Chem. Soc. 1961, 83, 2643–2653. [Google Scholar] [CrossRef]
- Linnett, J.W.; Poë, A.J. Directed valency in elements of the first short period. Trans. Faraday Soc. 1951, 47, 1033–1041. [Google Scholar] [CrossRef]
- Linnett, J.W. Valency and the chemical bond. Am. Sci. 1964, 52, 459–475. [Google Scholar]
- Firestone, R.A. Application of the Linnett electronic theory to organic chemistry. IV. SN2 transition state. J. Org. Chem. 1971, 36, 702–711. [Google Scholar] [CrossRef]
- Firestone, R.A. Application of the Linnett electronic theory to organic chemistry. V. Orientation in 1,3-dipolar cycloadditions according to the diradical mechanism. Partial formal charges in the Linnett structures of the diradical intermediate. J. Org. Chem. 1972, 37, 2181–2191. [Google Scholar] [CrossRef]
- Huisgen, R. 1,3-Dipolar Cycloadditions. Past and Future. Angew. Chem. Int. Ed. 1963, 2, 565–598. [Google Scholar] [CrossRef]
- Huisgen, R. 1,3-Dipolar cycloadditions. 76. Concerted nature of 1,3-dipolar cycloadditions and the question of diradical intermediates. J. Org. Chem. 1976, 41, 403–419. [Google Scholar] [CrossRef]
- Löwdin, P.-O.; Shull, H. Natural Orbitals in the Quantum Theory of Two-Electron Systems. Phys. Rev. 1956, 101, 1730–1739. [Google Scholar] [CrossRef]
- Sinanoğlu, O. Many-Electron Theory of Atoms and Molecules. I. Shells, Electron Pairs vs Many-Electron Correlations. J. Chem. Phys. 1962, 36, 706–717. [Google Scholar] [CrossRef]
- Saito, T.; Nishihara, S.; Kataoka, Y.; Nakanishi, Y.; Kitagawa, Y.; Kawakami, T.; Yamanaka, S.; Okumura, M.; Yamaguchi, K. Multireference Character of 1,3-Dipolar Cycloaddition of Ozone with Ethylene and Acrylonitrile. J. Phys. Chem A 2010, 114, 12116–12123. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Ohta, K.; Fueno, T. Localized natural orbitals of unstable molecules: Ozone. Chem. Phys. Lett. 1977, 50, 266–270. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fueno, T. Diradical and zwitterionic intermediates in the excited state. Chem. Phys. 1977, 23, 375–386. [Google Scholar] [CrossRef]
- Yoshimori, A. A New Type of Antiferromagnetic Structure in the Rutile Type Crystal. J. Phys. Soc. Jpn. 1959, 14, 807–821. [Google Scholar] [CrossRef]
- Yamaguchi, K. General spin structures of organic radicals. Chem. Phys. Lett. 1975, 30, 288–292. [Google Scholar] [CrossRef]
- Husimi, K.; Syôzi, I. The Statistics of Honeycomb and Triangular Lattice. I. Prog. Theor. Phys. 1950, 5, 177–186. [Google Scholar] [CrossRef]
- Syozi, I. The Statistics of Honeycomb and Triangular Lattice. II. Prog. Theor. Phys. 1950, 5, 341–351. [Google Scholar] [CrossRef]
- Bradley, C.J.; Cracknell, A.P. The Mathematical Theory of Symmetry in Solids: Representation Theory for Point Groups and Space Groups; Oxford University Press: Oxford, UK, 1972; Chapter 7; pp. 569–683. [Google Scholar]
- Yamaguchi, K.; Yoshioka, Y.; Fueno, F. Heisenberg models of radical reactions: Local spin (magnetic) symmetry conservations of biradical species. Chem. Phys. 1977, 20, 171–181. [Google Scholar] [CrossRef]
- Yamanaka, S.; Yamaki, D.; Shigeta, Y.; Nagao, H.; Yoshioka, Y.; Suzuki, N.; Yamaguchi, K. Generalized spin density functional theory for noncollinear molecular magnetism. Int. J. Quant. Chem. 2000, 80, 664–671. [Google Scholar] [CrossRef]
- Yamanaka, S.; Takeda, R.; Yamaguchi, K. Density functional study of tetrahedral manganese clusters. Polyhedron 2003, 22, 2013–2017. [Google Scholar] [CrossRef]
- Takeda, R.; Yamanaka, S.; Yamaguchi, K. Spin-optimized resonating Hartree-Fock configuration interaction. Int. J. Quant. Chem. 2007, 107, 3219–3227. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yamanaka, S.; Nishino, M.; Takano, Y.; Kitagawa, Y.; Nagao, H.; Yoshioka, Y. Symmetry and broken symmetries in molecular orbital descriptions of unstable molecules II. Alignment, flustration and tunneling of spins in mesoscopic molecular magnets. Theoret. Chem. Acc. 1999, 102, 328–345. [Google Scholar] [CrossRef]
- Einsle, O.; Rees, D.C. Structural Enzymology of Nitrogenase Enzymes. Chem. Rev. 2020, 120, 4969–5004. [Google Scholar] [CrossRef]
- Reiher, M.; Wiebe, N.; Svore, K.M.; Wecker, D.; Troyer, M. Elucidating reaction mechanisms on quantum computers. Proc. Natl. Acad. Sci. USA 2017, 114, 7555–7560. [Google Scholar] [CrossRef]
- Miyagawa, K.; Shoji, M.; Isobe, H.; Yamanaka, S.; Kawakami, T.; Okumura, M.; Yamaguchi, K. Theory of chemical bonds in metalloenzymes XXIV electronic and spin structures of FeMoco and Fe-S clusters by classical and quantum computing. Mol. Phys. 2020, 118, e1760388. [Google Scholar] [CrossRef]
- Ozaki, M.; Fukutome, H. Group Theoretical Classification of Solutions of the Unrestricted Hartree-Fock Equation in Molecular Systems with a Spatial Point Symmetry. Prog. Theor. Phys. 1978, 60, 1322–1336. [Google Scholar] [CrossRef]
- Yamanaka, S.; Takeda, R.; Kawakami, T.; Nakano, S.; Yamaki, D.; Yamada, S.; Nakata, K.; Sakuma, T.; Takada, T.; Yamaguchi, K. Spin correlation functions by generalized spin orbital density functional and multireference approaches. Int. J. Quant. Chem. 2003, 95, 512–520. [Google Scholar] [CrossRef]
- Yamanaka, S.; Yamaki, D.; Takeda, R.; Nagao, H.; Yamaguchi, K. J-model for magnetism and superconductivity of triangular, kagome, and related spin lattice systems. Int. J. Quant. Chem. 2004, 100, 1179–1196. [Google Scholar] [CrossRef]
- Pauling, L. The Nature of The Chemical Bond, 3rd ed.; Cornell University Press: Ithaca, NY, USA, 1960; p. 204. [Google Scholar]
- Fazekas, P.; Anderson, P.W. On the ground state properties of the anisotropic triangular antiferromagnet. Philos. Mag. 1974, 30, 423–440. [Google Scholar] [CrossRef]
- Kivelson, S.A.; Rokhsar, D.S.; Sethna, J.P. Topology of the resonating valence-bond state: Solitons and high-Tc superconductivity. Phys. Rev. B 1987, 35, 8865–8868. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Yamanaka, S.; Isobe, H.; Kawakami, K.; Kitagawa, Y.; Takeda, R.; Saito, T.; Nishihara, M.; Okumura, M. Instability in Chemical Bonds from Broken-Symmetry Single-Reference to Symmetry-Adapted Multireference Approaches to Strongly Correlated Electron Systems. AIP Conf. Proc. 2009, 1108, 20–29. [Google Scholar] [CrossRef]
- Kawakami, T.; Takeda, R.; Nishihara, S.; Saito, T.; Shoji, M.; Yamada, S.; Yamanaka, S.; Kitagawa, Y.; Okumura, M.; Yamaguchi, K. Symmetry and Broken-Symmetry in Molecular Orbital Descriptions of Unstable Molecules. 3. The Nature of Chemical Bonds of Spin Frustrated Systems. J. Phys. Chem. A 2009, 113, 15281–15297. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.; Wang, X. Spin Frustration in Organic Radicals. Angew. Chem. Int. Ed. 2024, 63, e202310147. [Google Scholar] [CrossRef]
- Shimizu, Y.; Miyagawa, K.; Kanoda, K.; Maesato, M.; Saito, G. Spin Liquid State in an Organic Mott Insulator with a Triangular Lattice. Phys. Rev. Lett. 2003, 91, 107001. [Google Scholar] [CrossRef] [PubMed]
- Broholm, C.; Cava, R.J.; Kivelson, S.A.; Nocera, D.G.; Norman, M.R.; Senthil, T. Quantum spin liquids. Science 2020, 367, eaay0668. [Google Scholar] [CrossRef]
- Zhou, Y.; Kanoda, K.; Ng, T.-K. Quantum spin liquid states. Rev. Mod. Phys. 2017, 89, 025003. [Google Scholar] [CrossRef]
- Matsen, F.A. Spin-Free Quantum Chemistry. In Advances in Quantum Chemistry; Löwdin, P.-O., Ed.; Elsevier: Amsterdam, The Netherlands, 1964; Volume 1, pp. 59–114. [Google Scholar] [CrossRef]
- Klein, D.J.; Junker, B.R. Spin-Free Computation of Matrix Elements. I. Group-Theoretical Computation of Pauling Numbers. J. Chem. Phys. 1971, 54, 4290–4296. [Google Scholar] [CrossRef]
- Yoshioka, Y.; Yamaguchi, K.; Fueno, T. Heisenberg models of radical reactions II. Conservation of the local spin-permutation symmetry in reactions of biradical species. Theoret. Chim. Acta 1977, 45, 1–20. [Google Scholar] [CrossRef]
- Pauncz, R. The Construction of Spin Eigenfunctions: An Exercise Book; Springer: New York, NY, USA, 2000. [Google Scholar]
- Song, M.; Alavi, A.; Li Manni, G. Permutation symmetry in spin-adapted many-body wave functions. Faraday Discuss. 2024, 254, 261–294. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Takahara, Y.; Fueno, T. Ab-initio molecular orbital studies of structure and reactivity of transition metal-oxo compounds. In Applied Quantum Chemistry; Smith, V.H., Jr., Schaefer, H.F., III, Morokuma, K., Eds.; D. Reidel Publishing Company: Lancaster, UK, 1986; pp. 155–184. [Google Scholar] [CrossRef]
- Matsen, F.A. Correlation of molecular orbital and valence bond states in π systems. Acc. Chem. Res. 1978, 11, 387–392. [Google Scholar] [CrossRef]
- Itoh, K. Electron spin resonance of an aromatic hydrocarbon in its quintet ground state. Chem. Phys. Lett. 1967, 1, 235–238. [Google Scholar] [CrossRef]
- Wasserman, E.; Murray, R.W.; Yager, W.A.; Trozzolo, A.M.; Smolinsky, G. Quintet ground states of m-dicarbene and m-dinitrene compounds. J. Am. Chem. Soc. 1967, 89, 5076–5078. [Google Scholar] [CrossRef]
- Breslow, R.; Chang, H.W.; Hill, R.; Wasserman, E. Stable Triplet States of Some Cyclopentadienyl Cations. J. Am. Chem. Soc. 1967, 89, 1112–1119. [Google Scholar] [CrossRef]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. [Google Scholar] [CrossRef] [PubMed]
- Chan, G.K.-L.; Sharma, S. The Density Matrix Renormalization Group in Quantum Chemistry. Annu. Rev. Phys. Chem. 2011, 62, 465–481. [Google Scholar] [CrossRef]
- Cirac, J.I.; Pérez-García, D.; Schuch, N.; Verstraete, F. Matrix product states and projected entangled pair states: Concepts, symmetries, theorems. Rev. Mod. Phys. 2021, 93, 045003. [Google Scholar] [CrossRef]
- Aspuru-Guzik, A.; Dutoi, A.D.; Love, P.J.; Head-Gordon, M. Simulated quantum computation of molecular energies. Science 2005, 309, 1704–1707. [Google Scholar] [CrossRef]
- Dagotto, E. Complexity in Strongly Correlated Electronic Systems. Science 2005, 309, 257–262. [Google Scholar] [CrossRef]
- Buenker, R.J.; Peyerimhoff, S.D. Individualized configuration selection in CI calculations with subsequent energy extrapolation. Theoret. Chim. Acta 1974, 35, 33–58. [Google Scholar] [CrossRef]
- Shavitt, I.; Rosenberg, B.J.; Palalikit, S. Comparison of configuration interaction expansions based on different orbital transformations. Int. J. Quant. Chem. 1976, 10, 33–46. [Google Scholar] [CrossRef]
- Iwata, S. Potential energy curves of several excited states of the Ne2* excimer: Assignment of the transient absorption spectra of the excimer. Chem. Phys. 1979, 37, 251–257. [Google Scholar] [CrossRef]
- Buenker, R.J.; Peyerimhoff, S.D.; Butscher, W. Applicability of the multi-reference double-excitation CI (MRD-CI) method to the calculation of electronic wavefunctions and comparison with related techniques. Mol. Phys. 1978, 35, 771–791. [Google Scholar] [CrossRef]
- Yamaguchi, K. Multireference (MR) configuration interaction (CI) approach for quasidegenerate systems. Int. J. Quant. Chem. 1980, 18, 269–284. [Google Scholar] [CrossRef]
- Yamaguchi, K. Configuration interaction (CI), coupled-cluster (CC) and many-body perturbation (MBPT) approaches in the unrestricted Hartree—Fock—Slater (UHFS) model. Chem. Phys. Lett. 1979, 68, 477–482. [Google Scholar] [CrossRef]
- Löwdin, P.-O. Quantum Theory of Many-Particle Systems. III. Extension of the Hartree-Fock Scheme to Include Degenerate Systems and Correlation Effects. Phys. Rev. 1955, 97, 1509–1520. [Google Scholar] [CrossRef]
- Öksüz, İ.; Sinanoğlu, O. Theory of Atomic Structure Including Electron Correlation. I. Three Kinds of Correlation in Ground and Excited Configurations. Phys. Rev. 1969, 181, 42–53. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Ohta, K.; Yabushita, S.; Fueno, T. DODS natural orbital (NO) CI investigations of 1,3-diradicals: CH2NHO, CH2OO, and CH2CH2O. J. Chem. Phys. 1978, 68, 4323–4325. [Google Scholar] [CrossRef]
- Yamaguchi, K. Ab initio unrestricted Hartree–Fock (UHF) and UHF–natural orbital CI studies of ozone. Int. J. Quant. Chem. 1980, 18, 101–106. [Google Scholar] [CrossRef]
- Roos, B.O. The complete active space SCF method in a fock-matrix-based super-CI formulation. Int. J. Quant. Chem. 1980, 18, 175–189. [Google Scholar] [CrossRef]
- Čížek, J. On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods. J. Chem. Phys. 1966, 45, 4256–4266. [Google Scholar] [CrossRef]
- Coester, F.; Kümmel, H. Short-range correlations in nuclear wave functions. Nucl. Phys. 1960, 17, 477–485. [Google Scholar] [CrossRef]
- Offermann, R.; Ey, W.; Kümmel, H. Degenerate many fermion theory in expS form: (I). General formalism. Nucl. Phys. A 1976, 273, 349–367. [Google Scholar] [CrossRef]
- Dean, D.J.; Hjorth-Jensen, M. Coupled-cluster approach to nuclear physics. Phys. Rev. C 2004, 69, 054320. [Google Scholar] [CrossRef]
- Mukherjee, D.; Moitra, R.K.; Mukhopadhyay, A. Correlation problem in open-shell atoms and molecules. Mol. Phys. 1975, 30, 1861–1888. [Google Scholar] [CrossRef]
- Langhoff, S.R.; Davidson, E.R. Configuration interaction calculations on the nitrogen molecule. Int. J. Quant. Chem. 1974, 8, 61–72. [Google Scholar] [CrossRef]
- Roos, B.O.; Andersson, K. Multiconfigurational perturbation theory with level shift—The Cr2 potential revisited. Chem. Phys. Lett. 1995, 245, 215–223. [Google Scholar] [CrossRef]
- Jeziorski, B.; Monkhorst, H.J. Coupled-cluster method for multideterminantal reference states. Phys. Rev. A 1981, 24, 1668–1681. [Google Scholar] [CrossRef]
- Bofill, J.M.; Pulay, P. The unrestricted natural orbital–complete active space (UNO–CAS) method: An inexpensive alternative to the complete active space–self-consistent-field (CAS–SCF) method. J. Chem. Phys. 1989, 90, 3637–3646. [Google Scholar] [CrossRef]
- Mahapatra, U.S.; Datta, B.; Bandyopadhyay, B.; Mukherjee, M. State-Specific Multi-Reference Coupled Cluster Formulations: Two Paradigms. In Advances in Quantum Chemistry; Löwdin, P.-O., Ed.; Elsevier: Amsterdam, The Netherlands, 1998; Volume 30, pp. 163–193. [Google Scholar] [CrossRef]
- Demel, O.; Pittner, J.; Neese, F. A Local Pair Natural Orbital-Based Multireference Mukherjee’s Coupled Cluster Method. J. Chem. Theory Comput. 2015, 11, 3104–3114. [Google Scholar] [CrossRef]
- Nishihara, S.; Yamanaka, S.; Saito, T.; Kitagawa, Y.; Kawakami, T.; Okumura, M.; Yamaguchi, K. UNO- and ULO-MRCC(Mk), AP-UCC and AP-UBD approaches to diradical systems. Int. J. Quant. Chem. 2010, 110, 3015–3026. [Google Scholar] [CrossRef]
- Paizs, B.; Fogarasi, G.; Pulay, P. An efficient direct method for geometry optimization of large molecules in internal coordinates. J. Chem. Phys. 1998, 109, 6571–6576. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Saito, T.; Ito, M.; Shoji, M.; Koizumi, K.; Yamanaka, S.; Kawakami, T.; Okumura, M.; Yamaguchi, K. Approximately spin-projected geometry optimization method and its application to di-chromium systems. Chem. Phys. Lett. 2007, 442, 445–450. [Google Scholar] [CrossRef]
- Kitagawa, Y.; Saito, T.; Nakanishi, Y.; Kataoka, Y.; Matsui, T.; Kawakami, T.; Okumura, M.; Yamaguchi, K. Spin Contamination Error in Optimized Geometry of Singlet Carbene (1A1) by Broken-Symmetry Method. J. Phys. Chem. A 2009, 113, 15041–15046. [Google Scholar] [CrossRef]
- Ichino, T.; Villano, S.M.; Gianola, A.J.; Goebbert, D.J.; Velarde, L.; Sanov, A.; Blanksby, S.J.; Zhou, X.; Hrovat, D.A.; Borden, W.T.; et al. The Lowest Singlet and Triplet States of the Oxyallyl Diradical. Angew. Chem. Int. Ed. 2009, 48, 8509–8511. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Nishihara, S.; Yamanaka, S.; Kitagawa, Y.; Kawakami, T.; Yamada, S.; Isobe, H.; Okumura, M.; Yamaguchi, K. Singlet–triplet energy gap for trimethylenemethane, oxyallyl diradical, and related species: Single- and multireference computational results. Theoret. Chem. Acc. 2011, 130, 739–748. [Google Scholar] [CrossRef]
- Shen, J.; Fang, T.; Li, S.; Jiang, Y. Performance of Block Correlated Coupled Cluster Method with the CASSCF Reference Function for the Prediction of Activation Barriers, Spectroscopic Constants in Diatomic Molecules, and Singlet−Triplet Gaps in Diradicals. J. Phys. Chem. A 2008, 112, 12518–12525. [Google Scholar] [CrossRef]
- Pipek, J.; Mezey, P.G. A fast intrinsic localization procedure applicable for ab initio and semiempirical linear combination of atomic orbital wave functions. J. Chem. Phys. 1989, 90, 4916–4926. [Google Scholar] [CrossRef]
- Breslow, R. Antiaromaticity. Acc. Chem. Res. 1973, 6, 393–398. [Google Scholar] [CrossRef]
- Breslow, R.; Brown, J.; Gajewski, J.J. Antiaromaticity of cyclopropenyl anions. J. Am. Chem. Soc. 1967, 89, 4383–4390. [Google Scholar] [CrossRef]
- Breslow, R.; Grubbs, R.; Murahashi, S. Electrochemical evidence for the antiaromaticity of cyclobutadiene. J. Am. Chem. Soc. 1970, 92, 4139–4140. [Google Scholar] [CrossRef]
- Fujii, S.; Marqués-González, S.; Shin, J.-Y.; Shinokubo, H.; Masuda, T.; Nishino, T.; Arasu, N.P.; Vázquez, H.; Kiguchi, M. Highly-conducting molecular circuits based on antiaromaticity. Nat. Commun. 2017, 8, 15984. [Google Scholar] [CrossRef]
- Bally, T.; Masamune, S. Cyclobutadiene. Tetrahedron 1980, 36, 343–370. [Google Scholar] [CrossRef]
- Saito, T.; Nishihara, S.; Kitagawa, Y.; Kawakami, T.; Yamanaka, S.; Okumura, M.; Yamaguchi, K. A broken-symmetry study on the automerization of cyclobutadiene. Comparison with UNO- and DNO-MRCC methods. Chem. Phys. Lett. 2010, 498, 253–258. [Google Scholar] [CrossRef]
- Saunders, M.; Berger, R.; Jaffe, A.; McBride, J.M.; O’Neill, J.; Breslow, R.; Hoffman, J.M., Jr.; Perchonock, C.; Wasserman, E.; Hutton, R.S.; et al. Unsubstituted cyclopentadienyl cation, a ground-state triplet. J. Am. Chem. Soc. 1973, 95, 3017–3018. [Google Scholar] [CrossRef]
- Lambert, J.B.; Lin, L.; Rassolov, V. The Stable Pentamethylcyclopentadienyl Cation. Angew. Chem. Int. Ed. 2002, 41, 1429–1431. [Google Scholar] [CrossRef]
- Costa, P.; Trosien, I.; Mieres-Perez, J.; Sander, W. Isolation of an Antiaromatic Singlet Cyclopentadienyl Zwitterion. J. Am. Chem. Soc. 2017, 139, 13024–13030. [Google Scholar] [CrossRef]
- Schulte, Y.; Wölper, C.; Rupf, S.M.; Malischewski, M.; SantaLucia, D.J.; Neese, F.; Haberhauser, G.; Schulz, S. Structural characterization and reactivity of a room-temperature-stable, antiaromatic cyclopentadienyl cation salt. Nat. Chem. 2024, 16, 651–657. [Google Scholar] [CrossRef]
- Wörner, H.J.; Merkt, F. Diradicals, antiaromaticity, and the pseudo-Jahn-Teller effect: Electronic and rovibronic structures of the cyclopentadienyl cation. J. Chem. Phys. 2007, 127, 034303. [Google Scholar] [CrossRef]
- Phillips, D.H.; Schug, J.C. Projected States of Open Shell Molecules: The Pi-Electron States of the Cyclopentadienyl Cation. J. Chem. Phys. 1972, 57, 3498–3503. [Google Scholar] [CrossRef]
- Hehre, W.J.; Schleyer, P.v.R. Cyclopentadienyl and related (CH)5+ cations. J. Am. Chem. Soc. 1973, 95, 5837–5839. [Google Scholar] [CrossRef]
- Borden, W.T.; Davidson, E.R. Potential surfaces for the planar cyclopentadienyl radical and cation. J. Am. Chem. Soc. 1979, 101, 3771–3775. [Google Scholar] [CrossRef]
- Reindl, B.; Schleyer, P.V.R. Molecular mechanics and ab initio calculations on cyclopentadienyl cations. J. Comput. Chem. 1998, 19, 1402–1420. [Google Scholar] [CrossRef]
- Ranasinghe, S.; Martin, C.D.; Dutton, J.L. Cyclopentadienyl cations. Chem. Sci. 2025, 16, 2083–2088. [Google Scholar] [CrossRef] [PubMed]
- Kubo, T. Recent Progress in Quinoidal Singlet Biradical Molecules. Chem. Lett. 2015, 44, 111–122. [Google Scholar] [CrossRef]
- Kubo, T. Phenalenyl-Based Open-Shell Polycyclic Aromatic Hydrocarbons. Chem. Rec. 2015, 15, 218–232. [Google Scholar] [CrossRef]
- Kubo, T. Syntheses and Properties of Open-Shell π-Conjugated Molecules. Bull. Chem. Soc. Jpn. 2021, 94, 2235–2244. [Google Scholar] [CrossRef]
- Kubo, T. Closed-shell and open-shell dual nature of singlet diradical compounds. Pure Appl. Chem. 2023, 95, 363–375. [Google Scholar] [CrossRef]
- Goto, K.; Kubo, T.; Yamamoto, K.; Nakasuji, K.; Sato, K.; Shiomi, D.; Takui, T.; Kubota, M.; Kobayashi, T.; Yakusi, K.; et al. A Stable Neutral Hydrocarbon Radical: Synthesis, Crystal Structure, and Physical Properties of 2,5,8-Tri-tert-butyl-phenalenyl. J. Am. Chem. Soc. 1999, 121, 1619–1620. [Google Scholar] [CrossRef]
- Kubo, T.; Sakamoto, M.; Akabane, M.; Fujiwara, Y.; Yamamoto, K.; Akita, M.; Inoue, K.; Takui, T.; Nakasuji, K. Four-Stage Amphoteric Redox Properties and Biradicaloid Character of Tetra-tert-butyldicyclopenta[b;d]thieno[1,2,3-cd;5,6,7-c′d′]diphenalene. Angew. Chem. Int. Ed. 2004, 43, 6474–6479. [Google Scholar] [CrossRef]
- Kubo, T.; Shimizu, A.; Sakamoto, M.; Uruichi, M.; Yakushi, K.; Nakano, M.; Shiomi, D.; Sato, K.; Takui, T.; Morita, Y.; et al. Synthesis, Intermolecular Interaction, and Semiconductive Behavior of a Delocalized Singlet Biradical Hydrocarbon. Angew. Chem. Int. Ed. 2005, 44, 6564–6568. [Google Scholar] [CrossRef]
- Shimizu, A.; Uruichi, M.; Yakushi, K.; Matsuzaki, H.; Okamoto, H.; Nakano, M.; Hirao, Y.; Matsumoto, K.; Kurata, H.; Kubo, T. Resonance Balance Shift in Stacks of Delocalized Singlet Biradicals. Angew. Chem. Int. Ed. 2009, 48, 5482–5486. [Google Scholar] [CrossRef]
- Kamada, K.; Ohta, K.; Shimizu, A.; Kubo, T.; Kishi, R.; Takahashi, H.; Botek, E.; Champagne, B.; Nakano, M. Singlet Diradical Character from Experiment. J. Chem. Phys. Lett. 2010, 1, 937–940. [Google Scholar] [CrossRef]
- Kamada, K.; Ohta, K.; Kubo, T.; Shimizu, A.; Morita, Y.; Nakasuji, K.; Kishi, R.; Ohta, S.; Furukawa, S.; Takahashi, H.; et al. Strong Two-Photon Absorption of Singlet Diradical Hydrocarbons. Angew. Chem. Int. Ed. 2007, 46, 3544–3546. [Google Scholar] [CrossRef] [PubMed]
- Konishi, A.; Hirao, Y.; Nakano, M.; Shimizu, A.; Botek, E.; Champagne, B.; Shiomi, D.; Sato, K.; Takui, T.; Matsumoto, K.; et al. Synthesis and Characterization of Teranthene: A Singlet Biradical Polycyclic Aromatic Hydrocarbon Having Kekulé Structures. J. Am. Chem. Soc. 2010, 132, 11021–11023. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, A.; Kishi, R.; Nakano, M.; Shiomi, D.; Sato, K.; Takui, T.; Hisaki, I.; Miyata, M.; Tobe, Y. Indeno[2,1-b]fluorene: A 20-π-Electron Hydrocarbon with Very Low-Energy Light Absorption. Angew. Chem. Int. Ed. 2013, 52, 6076–6079. [Google Scholar] [CrossRef] [PubMed]
- Pal, S.K.; Itkis, M.E.; Tham, F.S.; Reed, R.W.; Oakley, R.T.; Haddon, R.C. Resonating Valence-Bond Ground State in a Phenalenyl-Based Neutral Radical Conductor. Science 2005, 309, 281–284. [Google Scholar] [CrossRef]
- Huang, J.; Kertesz, M. Intermolecular Covalent π−π Bonding Interaction Indicated by Bond Distances, Energy Bands, and Magnetism in Biphenalenyl Biradicaloid Molecular Crystal. J. Am. Chem. Soc. 2007, 129, 1634–1643. [Google Scholar] [CrossRef]
- Fukui, K.; Sato, K.; Shiomi, D.; Takui, T.; Itoh, K.; Gotoh, K.; Kubo, T.; Yamamoto, K.; Nakasuji, K.; Naito, A. Electronic structure of a stable phenalenyl radical in crystalline state as studied by SQUID measurements, cw-ESR, and 13C CP/MAS NMR spectroscopy. Synth. Met. 1999, 103, 2257–2258. [Google Scholar] [CrossRef]
- Takano, Y.; Taniguchi, T.; Isobe, H.; Kubo, T.; Morita, Y.; Yamamoto, K.; Nakasuji, K.; Takui, T.; Yamaguchi, K. Hybrid Density Functional Theory Studies on the Magnetic Interactions and the Weak Covalent Bonding for the Phenalenyl Radical Dimeric Pair. J. Am. Chem. Soc. 2002, 124, 11122–11130. [Google Scholar] [CrossRef]
- Kodama, T.; Aoba, M.; Hirao, Y.; Rivero, S.M.; Casado, J.; Kubo, T. Molecular and Spin Structures of a Through-Space Conjugated Triradical System. Angew. Chem. Int. Ed. 2022, 61, e202200688. [Google Scholar] [CrossRef]
- Kodama, T.; Hirao, Y.; Kubo, T. Synthesis and Properties of a Through-Space Interacting Diradicaloid. Precis. Chem. 2023, 1, 183–191. [Google Scholar] [CrossRef]
- Mou, Z.; Uchida, K.; Kubo, T.; Kertesz, M. Evidence of σ- and π-Dimerization in a Series of Phenalenyls. J. Am. Chem. Soc. 2014, 136, 18009–18022. [Google Scholar] [CrossRef] [PubMed]
- Abe, M. Diradicals. Chem. Rev. 2013, 113, 7011–7088. [Google Scholar] [CrossRef] [PubMed]
- Konishi, A.; Kubo, T. Benzenoid Quinodimethanes. In Physical Organic Chemistry of Quinodimethanes. Topics in Current Chemistry Collections; Tobe, Y., Kubo, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Chapter 2; pp. 69–105. [Google Scholar] [CrossRef]
- Stuyver, T.; Chen, B.; Zeng, T.; Geerling, P.; De Proft, F.; Hoffmann, R. Do Diradicals Behave Like Radicals? Chem. Rev. 2019, 119, 11291–11351. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; Tang, S.; Su, Y.; Wang, X. Recent advances in stable main group element radicals: Preparation and characterization. Chem. Soc. Rev. 2022, 51, 5930–5973. [Google Scholar] [CrossRef]
- Hinz, A.; Bresien, J.; Breher, F.; Schulz, A. Heteroatom-Based Diradical(oid)s. Chem. Rev. 2023, 123, 10468–10526. [Google Scholar] [CrossRef]
- Zhang, H.; Miao, F.; Liu, X.; Wang, D.; Zheng, Y. Recent Advances of Stable Phenoxyl Diradicals. Chem. Res. Chin. Univ. 2023, 39, 170–175. [Google Scholar] [CrossRef]
- Prasad, P.N.; Williams, D.J. Introduction to Nonlinear Optical Effects in Molecules and Polymers; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Franken, P.A.; Hill, A.E.; Peters, C.W.; Weinreich, G. Generation of Optical Harmonics. Phys. Rev. Lett. 1961, 7, 118–119. [Google Scholar] [CrossRef]
- Tsang, T.Y.F. Optical third-harmonic generation at interfaces. Phys. Rev. A 1995, 52, 4116–4125. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Dadap, J.I.; Petrone, N.; Yeh, P.-C.; Hone, J.; Osgood, R.M., Jr. Optical Third-Harmonic Generation in Graphene. Phys. Rev. X 2013, 3, 021014. [Google Scholar] [CrossRef]
- Roy, S.; Covert, P.A.; FitzGerald, W.R.; Hore, D.K. Biomolecular Structure at Solid–Liquid Interfaces As Revealed by Nonlinear Optical Spectroscopy. Chem. Rev. 2014, 114, 8388–8415. [Google Scholar] [CrossRef]
- Johansson, P.K.; Schmüser, L.; Castner, D.G. Nonlinear Optical Methods for Characterization of Molecular Structure and Surface Chemistry. Top. Catal. 2018, 61, 1101–1124. [Google Scholar] [CrossRef] [PubMed]
- Sasagane, K.; Aiga, F.; Itoh, R. Higher-order response theory based on the quasienergy derivatives: The derivation of the frequency-dependent polarizabilities and hyperpolarizabilities. J. Chem. Phys. 1993, 99, 3738–3778. [Google Scholar] [CrossRef]
- Sekino, H.; Bartlett, R.J. Frequency dependent nonlinear optical properties of molecules. J. Chem. Phys. 1986, 85, 976–989. [Google Scholar] [CrossRef]
- Karna, S.P. Spin-unrestricted time-dependent Hartree–Fock theory of frequency-dependent linear and nonlinear optical properties. J. Chem. Phys. 1996, 104, 6590–6605. [Google Scholar] [CrossRef]
- Kobayashi, T.; Sasagane, K.; Aiga, F.; Yamaguchi, K. Calculation of frequency-dependent first hyperpolarizabilities using the second-order Møller–Plesset perturbation theory. J. Chem. Phys. 1999, 110, 11720–11733. [Google Scholar] [CrossRef]
- Bredas, J.L.; Adant, C.; Tackx, P.; Persoons, A.; Pierce, B.M. Third-Order Nonlinear Optical Response in Organic Materials: Theoretical and Experimental Aspects. Chem. Rev. 1994, 94, 243–278. [Google Scholar] [CrossRef]
- Nakano, M.; Yamada, S.; Shigemoto, I.; Yamaguchi, K. Dynamic (hyper)polarizability density analysis based on virtual excitation processes: Visualization of the dynamic electron fluctuatability of systems under time-dependent external electric fields. Chem. Phys. Lett. 1996, 250, 247–254. [Google Scholar] [CrossRef]
- Nakano, M.; Yamaguchi, K. Numerical Liouville approach: A calculation method for nonlinear optical susceptibilities of N-state systems. Phys. Rev. A 1994, 50, 2989–3004. [Google Scholar] [CrossRef]
- Nakano, M.; Yamada, S.; Shigemoto, I.; Yamaguchi, K. Theoretical study on the geometry dependence of the second hyperpolarizability of the allyl cation based on a numerical Liouville three-type analysis. Chem. Phys. Lett. 1996, 251, 381–386. [Google Scholar] [CrossRef]
- Nakano, M.; Nitta, T.; Yamaguchi, K.; Champagne, B.; Botek, E. Spin Multiplicity Effects on the Second Hyperpolarizability of an Open-Shell Neutral π-Conjugated System. J. Phys. Chem. A 2004, 108, 4105–4111. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Nakagawa, N.; Ohta, S.; Takahashi, H.; Furukawa, S.; Kamada, K.; Ohta, K.; Champagne, B.; Botek, E.; et al. Second Hyperpolarizabilities (γ) of Bisimidazole and Bistriazole Benzenes: Diradical Character, Charged State, and Spin State Dependences. J. Phys. Chem. A 2006, 110, 4238–4243. [Google Scholar] [CrossRef] [PubMed]
- Champagne, B.; Botek, E.; Nakano, M.; Nitta, T.; Yamaguchi, K. Basis set and electron correlation effects on the polarizability and second hyperpolarizability of model open-shell π-conjugated systems. J. Chem. Phys. 2005, 122, 114315. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Kishi, R.; Ohta, S.; Takebe, A.; Takahashi, H.; Furukawa, S.; Kubo, T.; Morita, Y.; Nakasuji, K.; Yamaguchi, K.; et al. Origin of the enhancement of the second hyperpolarizability of singlet diradical systems with intermediate diradical character. J. Chem. Phys. 2006, 125, 074113. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Ohta, S.; Takahashi, H.; Kubo, T.; Kamada, K.; Ohta, K.; Botek, E.; Champagne, B. Relationship between Third-Order Nonlinear Optical Properties and Magnetic Interactions in Open-Shell Systems: A New Paradigm for Nonlinear Optics. Phys. Rev. Lett. 2007, 99, 033001. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Nagao, H.; Yamaguchi, K. Many-electron hyperpolarizability density analysis: Application to the dissociation processof one-dimensional H2s. Phys. Rev. A 1997, 55, 1503–1513. [Google Scholar] [CrossRef]
- Nakano, M.; Yamada, S.; Yamaguchi, K. Third-order nonlinear optical responses of molecules in the intermediate and strong correlation regime: Variation of second hyperpolarizability in the bond dissociation. J. Comput. Methods Sci. Eng. 2004, 4, 677–701. [Google Scholar] [CrossRef]
- Hamamoto, Y.; Hirao, Y.; Kubo, T. Biradicaloid Behavior of a Twisted Double Bond. J. Phys. Chem. Lett. 2021, 12, 4729–4734. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Nagao, H.; Yamaguchi, K. Electron correlation and structure dependencies of the second hyperpolarizability of ethylene. Int. J. Quant. Chem. 1999, 71, 177–183. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Nitta, T.; Kubo, T.; Nakasuji, K.; Kamada, K.; Ohta, K.; Champagne, B.; Botek, E.; Yamaguchi, K. Second Hyperpolarizability (γ) of Singlet Diradical System: Dependence of γ on the Diradical Character. J. Phys. Chem. A 2005, 109, 885–891. [Google Scholar] [CrossRef]
- Mondal, A.; Hatua, K.; Nandi, P.K. Static second hyperpolarizability of twisted ethylene: A comprehensive computational study. J. Theoret. Comput. Chem. 2015, 14, 1550060. [Google Scholar] [CrossRef]
- De Wergifosse, M. Approximate Spin-Projected Density-Based Romberg Differentiation Procedure to Evaluate the Second-Hyperpolarizability of p-Quinodimethane and Twisted Ethylene and Their Diradical Character Dependence. J. Phys. Chem. A 2016, 120, 2727–2736. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Takahata, M.; Kishi, R.; Nitta, T.; Yamaguchi, K. Theoretical Study on Static Second Hyperpolarizabilities for Several π-Conjugated Systems Including Nitrogen Atoms: Effects of Charged Defects and Extension of π-Conjugation. J. Phys. Chem. A 2004, 108, 4151–4155. [Google Scholar] [CrossRef]
- Sun, Z.; Zeng, Z.; Wu, J. Zethrenes, Extended p-Quinodimethanes, and Periacenes with a Singlet Biradical Ground State. Acc. Chem. Res. 2014, 47, 2582–2591. [Google Scholar] [CrossRef]
- Zeng, Z.; Shi, X.; Chi, C.; Navarrete, J.T.L.; Casado, J.; Wu, J. Pro-aromatic and anti-aromatic π-conjugated molecules: An irresistible wish to be diradicals. Chem. Soc. Rev. 2015, 44, 6578–6596. [Google Scholar] [CrossRef]
- Casado, J. Para-Quinodimethanes: A Unified Review of the Quinoidal-Versus-Aromatic Competition and its Implications. In Physical Organic Chemistry of Quinodimethanes. Topics in Current Chemistry Collections; Tobe, Y., Kubo, T., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; pp. 209–248. [Google Scholar] [CrossRef]
- Nakano, M.; Fukui, H.; Minami, T.; Yoneda, K.; Shigeta, Y.; Kishi, R.; Champagne, B.; Botek, E.; Kubo, T.; Ohta, K.; et al. (Hyper)polarizability density analysis for open-shell molecular systems based on natural orbitals and occupation numbers. Theor. Chem. Acc. 2011, 130, 711–724. [Google Scholar] [CrossRef]
- Kishi, R.; Nakano, M. Quantum Master Equation Method Based on the Broken-Symmetry Time-Dependent Density Functional Theory: Application to Dynamic Polarizability of Open-Shell Molecular Systems. J. Phys. Chem. A 2011, 115, 3565–3575. [Google Scholar] [CrossRef]
- Kishi, R.; Murata, Y.; Saito, M.; Morita, K.; Abe, M.; Nakano, M. Theoretical Study on Diradical Characters and Nonlinear Optical Properties of 1,3-Diradical Compounds. J. Phys. Chem. A 2014, 118, 10837–10848. [Google Scholar] [CrossRef]
- Prasad, P.N.; Reinhardt, B.A. Is there a role for organic materials chemistry in nonlinear optics and photonics? Chem. Mater. 1990, 2, 660–669. [Google Scholar] [CrossRef]
- Prasad, P.N.; Karna, S.P. Nonlinear optical effects in molecules and polymers: Issues and opportunities. Int. J. Quant. Chem. 1994, 52, 395–410. [Google Scholar] [CrossRef]
- Marder, S.T.; Gorman, C.B.; Meyers, F.; Perry, J.W.; Bourhill, G.; Brédas, J.-L.; Pierce, B.M. A Unified Description of Linear and Nonlinear Polarization in Organic Polymethine Dyes. Science 1994, 265, 632–635. [Google Scholar] [CrossRef]
- Bhawalkar, J.D.; He, G.S.; Prasad, P.N. Nonlinear multiphoton processes in organic and polymeric materials. Rep. Prog. Phys. 1996, 59, 1041–1071. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Shigemoto, I.; Yamaguchi, K. Static second hyperpolarizabilities γ of nitroxide radical and formaldehyde: Evaluation of spatial contributions to γ by a hyperpolarizability density analysis. Chem. Phys. Lett. 1996, 254, 158–164. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Shigemoto, I.; Kiribayashi, S.; Yamaguchi, K. Intense electron correlation dependence of the first hyperpolarizabilities β of a nitroxide radical and formaldehyde. Chem. Phys. Lett. 1997, 267, 445–451. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Shigemoto, I.; Kiribayashi, S.; Yamaguchi, K. Theoretical study of the third-order nonlinear optical susceptibilities for the β-phase crystal of p-NPNN. Chem. Phys. Lett. 1997, 267, 438–444. [Google Scholar] [CrossRef]
- Oudar, J.L.; Zyss, J. Structural dependence of nonlinear-optical properties of methyl-(2,4-dinitrophenyl)-aminopropanoate crystals. Phys. Rev. A 1982, 26, 2016–2027. [Google Scholar] [CrossRef]
- Yamada, S.; Nakano, M.; Nishino, M.; Yamaguchi, K. Theoretical Study on the Second Hyperpolarizabilities for Small Radical Systems. Opt. Rev. 1999, 6, 237–241. [Google Scholar] [CrossRef]
- Shu, C.; Yang, Z.; Rajca, A. From Stable Radicals to Thermally Robust High-Spin Diradicals and Triradicals. Chem. Rev. 2023, 123, 11954–12003. [Google Scholar] [CrossRef]
- Khalid, M.; Khan, M.; Mahmood, K.; Arshad, M.; Imran, M.; Braga, A.A.C.; Hussain, R. Theoretical designing of non-fullerene derived organic heterocyclic compounds with enhanced nonlinear optical amplitude: A DFT based prediction. Sci. Rep. 2022, 12, 20220. [Google Scholar] [CrossRef]
- Mingabudinova, L.R.; Vinogradov, V.V.; Milichko, V.A.; Hey-Hawkins, E.; Vinogradov, A.V. Metal–organic frameworks as competitive materials for non-linear optics. Chem. Soc. Rev. 2016, 45, 5408–5431. [Google Scholar] [CrossRef]
- Li, C.; Qian, G.; Cui, Y. Metal–organic frameworks for nonlinear optics and lasing. Inf. Funct. Mater. 2024, 1, 125–159. [Google Scholar] [CrossRef]
- Iwamura, H.; Koga, N. Studies of organic di-, oligo-, and polyradicals by means of their bulk magnetic properties. Acc. Chem. Res. 1993, 26, 346–351. [Google Scholar] [CrossRef]
- Rajca, A. Organic Diradicals and Polyradicals: From Spin Coupling to Magnetism? Chem. Rev. 1994, 94, 871–893. [Google Scholar] [CrossRef]
- Kinoshita, M.; Turek, P.; Tamura, M.; Nozawa, K.; Shiomi, D.; Nakazawa, Y.; Ishikawa, M.; Takahashi, M.; Awaga, K.; Inabe, T.; et al. An Organic Radical Ferromagnet. Chem. Lett. 1991, 20, 1225–1228. [Google Scholar] [CrossRef]
- Kinoshita, M. Ferromagnetism of Organic Radical Crystals. Jpn. J. Appl. Phys. 1994, 33, 5718–5733. [Google Scholar] [CrossRef]
- Okumura, M.; Yamaguchi, K.; Nakano, M.; Mori, W. A theoretical explanation of the organic ferromagnetism in the β-phase of para-nitrophenyl nitronyl nitroxide. Chem. Phys. Lett. 1993, 207, 1–8. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Leggett, A.J. Quantum tunnelling in a dissipative system. Ann. Phys. 1983, 149, 374–456. [Google Scholar] [CrossRef]
- Leggett, A.J.; Garg, A. Quantum mechanics versus macroscopic realism: Is the flux there when nobody looks? Phys. Rev. Lett. 1985, 54, 857–860. [Google Scholar] [CrossRef]
- Leggett, A.J.; Chakravarty, S.; Dorsey, A.T.; Fisher, M.P.A.; Grag, A.; Zwerger, W. Dynamics of the dissipative two-state system. Rev. Mod. Phys. 1987, 59, 1–85. [Google Scholar] [CrossRef]
- Chudnovsky, E.M.; Gunther, L. Quantum Tunneling of Magnetization in Small Ferromagnetic Particles. Phys. Rev. Lett. 1988, 60, 661–664. [Google Scholar] [CrossRef]
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic bistability in a metal-ion cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Thomas, L.; Lionti, F.; Ballou, R.; Gatteschi, D.; Sessoli, R.; Barbara, B. Macroscopic quantum tunnelling of magnetization in a single crystal of nanomagnets. Nature 1996, 383, 145–147. [Google Scholar] [CrossRef]
- Nishino, M.; Yamanaka, S.; Yoshioka, Y.; Yamaguchi, K. Theoretical Approaches to Direct Exchange Couplings between Divalent Chromium Ions in Naked Dimers, Tetramers, and Clusters. J. Phys. Chem. A 1997, 101, 705–712. [Google Scholar] [CrossRef]
- Nagao, H.; Yamanaka, S.; Nishino, M.; Yoshioka, Y.; Yamaguchi, K. Theoretical studies on the magnetic quantum tunneling rates in Mn clusters by the path integral method. Chem. Phys. Lett. 1999, 302, 418–424. [Google Scholar] [CrossRef]
- Nagao, H.; Nakano, M.; Shigeta, Y.; Yamaguchi, K. Quantum Phase Dynamics of Interaction between Photon Field and Magnetic System: Effects of Magnetic Quantum Tunnelling. Opt. Rev. 1999, 6, 227–231. [Google Scholar] [CrossRef]
- Wernsdorfer, W.; Sessoli, R. Quantum Phase Interference and Parity Effects in Magnetic Molecular Clusters. Science 1999, 284, 133–135. [Google Scholar] [CrossRef]
- Nagao, H.; Nishino, M.; Shigeta, Y.; Soda, T.; Kitagawa, Y.; Onishi, T.; Yoshioka, Y.; Yamaguchi, K. Theoretical studies on effective spin interactions, spin alignments and macroscopic spin tunneling in polynuclear manganese and related complexes and their mesoscopic clusters. Coord. Chem. Rev. 2000, 198, 265–295. [Google Scholar] [CrossRef]
- Gatteschi, D.; Sessoli, R. Quantum Tunneling of Magnetization and Related Phenomena in Molecular Materials. Angew. Chem. Int. Ed. 2003, 42, 268–297. [Google Scholar] [CrossRef]
- Leggett, A.J. Some Thought-Experiments Involving Macrosystems as Illustrations of Various Interpretations of Quantum Mechanics. Found. Phys. 1999, 29, 445–456. [Google Scholar] [CrossRef]
- Nagao, H.; Kinugawa, K.; Shigeta, Y.; Ohta, K.; Yamaguchi, K. Quantum spin dynamics in solution applicable to quantum computing. J. Mol. Liq. 2001, 90, 63–68. [Google Scholar] [CrossRef]
- Leuenberger, M.; Loss, D. Quantum computing in molecular magnets. Nature 2001, 410, 789–793. [Google Scholar] [CrossRef]
- Fredkin, E.; Toffoli, T. Conservative logic. Int. J. Theor. Phys. 1982, 21, 219–253. [Google Scholar] [CrossRef]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Deutsch, D. Quantum theory, the Church–Turing principle and the universal quantum computer. Proc. R. Soc. Lond. A 1985, 400, 97–117. [Google Scholar] [CrossRef]
- Feynman, R.P. Quantum mechanical computers. Found. Phys. 1986, 16, 507–531. [Google Scholar] [CrossRef]
- Lloyd, S. A Potentially Realizable Quantum Computer. Science 1993, 261, 1569–1571. [Google Scholar] [CrossRef]
- Ozawa, M. Phase Operator Problem and Macroscopic Extension of Quantum Mechanics. Ann. Phys. 1997, 257, 65–83. [Google Scholar] [CrossRef]
- DiVincenzo, D.P. The Physical Implementation of Quantum Computation. Prog. Phys. 2000, 48, 771–783. [Google Scholar] [CrossRef]
- Chuang, I.L.; Gershenfeld, N.; Kubinec, M. Experimental Implementation of Fast Quantum Searching. Phys. Rev. Lett. 1998, 80, 3408–3411. [Google Scholar] [CrossRef]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the STOC ’96: Proceedings of the 28th Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar] [CrossRef]
- Vandersypen, L.M.K.; Steffen, M.; Breyta, G.; Yannoni, C.S.; Sherwood, M.H.; Chuang, I.L. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 2001, 414, 883–887. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Kitaev, A. Anyons in an exactly solved model and beyond. Ann. Phys. 2006, 321, 2–111. [Google Scholar] [CrossRef]
- Nie, W.; Antezza, M.; Liu, Y.; Nori, F. Dissipative Topological Phase Transition with Strong System-Environment Coupling. Phys. Rev. Lett. 2021, 127, 250402. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Okubo, T.; Tanaka, N.; Iino, T.; Kaizu, Y. Determination of Ligand-Field Parameters and f-Electronic Structures of Double-Decker Bis(phthalocyaninato)lanthanide Complexes. Inorg. Chem. 2003, 42, 2440–2446. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Tanaka, N.; Ishikawa, T.; Koshihara, S.; Kaizu, Y. Upward Temperature Shift of the Intrinsic Phase Lag of the Magnetization of Bis(phthalocyaninato)terbium by Ligand Oxidation Creating an S = 1/2 Spin. Inorg. Chem. 2004, 43, 5498–5500. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Wernsdorfer, W. Quantum Tunneling of Magnetization in Lanthanide Single-Molecule Magnets: Bis(phthalocyaninato)terbium and Bis(phthalocyaninato)dysprosium Anions. Angew. Chem. Int. Ed. 2005, 44, 2931–2935. [Google Scholar] [CrossRef]
- Ishikawa, N.; Sugita, M.; Wernsdorfer, W. Nuclear Spin Driven Quantum Tunneling of Magnetization in a New Lanthanide Single-Molecule Magnet: Bis(Phthalocyaninato)holmium Anion. J. Am. Chem. Soc. 2005, 127, 3650–3651. [Google Scholar] [CrossRef]
- Fukuda, T.; Matsumura, K.; Ishikawa, N. Influence of Intramolecular f-f Interactions on Nuclear Spin Driven Quantum Tunneling of Magnetizations in Quadruple-Decker Phthalocyanine Complexes Containing Two Terbium or Dysprosium Magnetic Centers. J. Phys. Chem. A 2013, 117, 10447–10454. [Google Scholar] [CrossRef]
- Katoh, K.; Horii, Y.; Yasuda, N.; Wernsdorfer, W.; Toriumi, K.; Breedlove, B.K.; Yamashita, M. Multiple-decker phthalocyaninato dinuclear lanthanoid(iii) single-molecule magnets with dual-magnetic relaxation processes. Dalton Trans. 2012, 41, 13582–13600. [Google Scholar] [CrossRef]
- Meier, F.; Levy, J.; Loss, D. Quantum Computing with Spin Cluster Qubits. Phys. Rev. Lett. 2003, 90, 047901. [Google Scholar] [CrossRef]
- Lehmann, J.; Gaita-Ariño, A.; Coronado, E.; Loss, D. Quantum computing with molecular spin systems. J. Mater. Chem. 2009, 19, 1672–1677. [Google Scholar] [CrossRef]
- Godfrin, C.; Ferhat, A.; Ballou, R.; Klyatskaya, S.; Ruben, M.; Wernsdorfer, W.; Balestro, F. Operating Quantum States in Single Magnetic Molecules: Implementation of Grover’s Quantum Algorithm. Phys. Rev. Lett. 2017, 119, 187702. [Google Scholar] [CrossRef]
- Moreno-Pineda, E.; Klyatskaya, S.; Du, P.; Damjanović, M.; Taran, G.; Wernsdorfer, W.; Ruben, M. Observation of Cooperative Electronic Quantum Tunneling: Increasing Accessible Nuclear States in a Molecular Qudit. Inorg. Chem. 2018, 57, 9873–9879. [Google Scholar] [CrossRef]
- Moreno-Pineda, E.; Godfrin, C.; Balestro, F.; Wernsdorfer, W.; Ruben, M. Molecular spin qudits for quantum algorithms. Chem. Soc. Rev. 2018, 47, 501–513. [Google Scholar] [CrossRef]
- Atzori, M.; Tesi, L.; Morra, E.; Chiesa, M.; Sorace, L.; Sessoli, R. Room-Temperature Quantum Coherence and Rabi Oscillations in Vanadyl Phthalocyanine: Toward Multifunctional Molecular Spin Qubits. J. Am. Chem. Soc. 2016, 138, 2154–2157. [Google Scholar] [CrossRef]
- Atzori, M.; Chiesa, A.; Morra, E.; Chiesa, M.; Sorace, L.; Carretta, S.; Sessoli, R. A two-qubit molecular architecture for electron-mediated nuclear quantum simulation. Chem. Sci. 2018, 9, 6183–6192. [Google Scholar] [CrossRef]
- Atzori, M.; Sessoli, R. The Second Quantum Revolution: Role and Challenges of Molecular Chemistry. J. Am. Chem. Soc. 2019, 141, 11339–11352. [Google Scholar] [CrossRef]
- Takahashi, S.; Tupitsyn, I.S.; van Tol, J.; Beedle, C.C.; Hendrickson, D.N.; Stamp, P.C.E. Decoherence in crystals of quantum molecular magnets. Nature 2011, 476, 76–79. [Google Scholar] [CrossRef]
- Bader, K.; Dengler, D.; Lenz, S.; Endeward, B.; Jiang, S.-D.; Neugebauer, P.; van Slageren, J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014, 5, 5304. [Google Scholar] [CrossRef] [PubMed]
- Teki, Y.; Miyamoto, S.; Nakatsuji, M.; Miura, Y. π-Topology and Spin Alignment Utilizing the Excited Molecular Field: Observation of the Excited High-Spin Quartet (S = 3/2) and Quintet (S = 2) States on Purely Organic π-Conjugated Spin Systems. J. Am. Chem. Soc. 2001, 123, 294–305. [Google Scholar] [CrossRef] [PubMed]
- Takeda, K.; Takegoshi, K.; Terao, T. Dynamic nuclear polarization by photoexcited-triplet electron spins in polycrystalline samples. Chem. Phys. Lett. 2001, 345, 166–170. [Google Scholar] [CrossRef]
- Rahimi, R.; Sato, K.; Furukawa, K.; Toyota, K.; Shiomi, D.; Nakamura, T.; Kitagawa, M.; Takui, T. Pulsed ENDOR-based quantum information processing. Int. J. Quant. Inf. 2005, 3, 197–204. [Google Scholar] [CrossRef]
- Kagawa, A.; Murokawa, Y.; Takeda, K.; Kitagawa, M. Optimization of 1H spin density for dynamic nuclear polarization using photo-excited triplet electron spins. J. Magn. Reson. 2009, 197, 9–13. [Google Scholar] [CrossRef] [PubMed]
- Negoro, M.; Nakayama, K.; Tateishi, K.; Kagawa, A.; Takeda, K.; Kitagawa, M. 2H-decoupling-accelerated 1H spin diffusion in dynamic nuclear polarization with photoexcited triplet electrons. J. Chem. Phys. 2010, 133, 154504. [Google Scholar] [CrossRef]
- Kanzaki, Y.; Shiomi, D.; Kaneda, C.; Ise, T.; Sato, K.; Takui, T. Clustering of molecular spins in the crystals of nitronylnitroxide and iminonitroxide triradicals based on benzene-1,3,5-triyl frameworks. J. Mater. Chem. 2006, 16, 2064–2073. [Google Scholar] [CrossRef]
- Suzuki, S.; Morita, Y.; Fukui, K.; Sato, K.; Shiomi, D.; Takui, T.; Nakasuji, K. Aromaticity on the Pancake-Bonded Dimer of Neutral Phenalenyl Radical as Studied by MS and NMR Spectroscopies and NICS Analysis. J. Am. Chem. Soc. 2006, 128, 2530–2531. [Google Scholar] [CrossRef]
- Sato, K.; Rahimi, R.; Mori, N.; Nishida, S.; Toyota, K.; Shiomi, D.; Morita, Y.; Ueda, A.; Suzuki, S.; Furukawa, K.; et al. Implementation of molecular spin quantum computing by pulsed ENDOR technique: Direct observation of quantum entanglement and spinor. Phys. E Low-Dimens. Syst. Nanostruct. 2007, 40, 363–366. [Google Scholar] [CrossRef]
- Kawano, Y.; Yamashita, S.; Kitagawa, M. Explicit implementation of quantum circuits on a quantum-cellular-automata-like architecture. Phys. Rev. A 2005, 72, 012301. [Google Scholar] [CrossRef]
- Beer, L.; Mandal, S.K.; Reed, R.W.; Oakley, R.T.; Tham, F.S.; Donnadieu, B.; Haddon, R.C. The First Electronically Stabilized Phenalenyl Radical: Effect of Substituents on Solution Chemistry and Solid-State Structure. Cryst. Growth Des. 2007, 7, 802–809. [Google Scholar] [CrossRef]
- Morita, Y.; Ueda, A.; Nishida, S.; Fukui, K.; Ise, T.; Shiomi, D.; Sato, K.; Takui, T.; Nakasuji, K. Curved Aromaticity of a Corannulene-Based Neutral Radical: Crystal Structure and 3 D Unbalanced Delocalization of Spin. Angew. Chem. Int. Ed. 2008, 47, 2035–2038. [Google Scholar] [CrossRef]
- Morita, Y.; Suzuki, S.; Sato, K.; Takui, T. Synthetic organic spin chemistry for structurally well-defined open-shell graphene fragments. Nat. Chem. 2011, 3, 197–204. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Taniguchi, T.; Kawakami, T.; Hamamoto, T.; Okumura, M. Possibilities of magnetic modifications of DNA wires, sheets and related materials. Polyhedron 2005, 24, 2758–2766. [Google Scholar] [CrossRef]
- Maekawa, K.; Nakazawa, S.; Atsumi, H.; Shiomi, D.; Sato, K.; Kitagawa, M.; Takui, T.; Nakatani, K. Programmed assembly of organic radicals on DNA. Chem. Commun. 2010, 46, 1247–1249. [Google Scholar] [CrossRef] [PubMed]
- Mujica-Martinez, C.A.; Nalbach, P.; Thorwart, M. Organic π-Conjugated Copolymers as Molecular Charge Qubits. Phys. Rev. Lett. 2013, 111, 016802. [Google Scholar] [CrossRef]
- Barone, V.; Cacelli, I.; Ferretti, A.; Prampolini, G. Magnetic gaps in organic tri-radicals: From a simple model to accurate estimates. J. Chem. Phys. 2017, 146, 104103. [Google Scholar] [CrossRef]
- Zhang, H.; Pink, M.; Wang, Y.; Rajca, S.; Rajca, A. High-Spin S = 3/2 Ground-State Aminyl Triradicals: Toward High-Spin Oligo-Aza Nanographenes. J. Am. Chem. Soc. 2022, 144, 19576–19591. [Google Scholar] [CrossRef] [PubMed]
- Boudalis, A.K.; Constantinides, C.P.; Chrysochos, N.; Carmieli, R.; Leitus, G.; Kourtellaris, A.; Lawson, D.B.; Koutentis, P.A. Deciphering the ground state of a C3-symmetrical Blatter-type triradical by CW and pulse EPR spectroscopy. J. Magn. Reson. 2023, 349, 107406. [Google Scholar] [CrossRef]
- Zhang, D.; Zhu, Z.; Xiao, X.; Fang, Y.-H.; Xiao, T.; Wang, X.; Jiang, S.-D.; Zhao, D. An Air-Stable Carbon-Centered Triradical with a Well-Addressable Quartet Ground State. J. Am. Chem. Soc. 2024, 146, 21752–21761. [Google Scholar] [CrossRef]
- Gorgon, S.; Lv, K.; Grüne, J.; Drummond, B.H.; Myers, W.K.; Londi, G.; Ricci, G.; Valverde, D.; Tonnelé, C.; Murto, P.; et al. Reversible spin-optical interface in luminescent organic radicals. Nature 2023, 620, 538–544. [Google Scholar] [CrossRef]
- Poh, Y.R.; Morozov, D.; Kazmierczak, N.P.; Hadt, R.G.; Groenhof, G.; Yuen-Zhou, J. Alternant Hydrocarbon Diradicals as Optically Addressable Molecular Qubits. J. Am. Chem. Soc. 2024, 146, 15549–15561. [Google Scholar] [CrossRef]
- Kopp, S.M.; Nakamura, S.; Phelan, B.T.; Poh, Y.R.; Tyndall, S.B.; Brown, P.J.; Huang, Y.; Yuen-Zhou, J.; Krzyaniak, M.D.; Wasielewski, M.R. Luminescent Organic Triplet Diradicals as Optically Addressable Molecular Qubits. J. Am. Chem. Soc. 2024, 146, 27935–27945. [Google Scholar] [CrossRef]
- Inoue, M.; Yamauchi, A.; Parmar, B.; Orihashi, K.; Singh, M.; Asada, M.; Nakamura, T.; Yanai, N. Guest-responsive coherence time of radical qubits in a metal–organic framework. Chem. Commun. 2024, 60, 6130–6133. [Google Scholar] [CrossRef] [PubMed]
- Zhou, A.; Sun, Z.; Sun, L. Stable organic radical qubits and their applications in quantum information science. Innovation 2024, 5, 100662. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Fujiwara, S.; Kimizuka, N.; Asada, M.; Fujiwara, M.; Nakamura, T.; Pirillo, J.; Hijikata, Y.; Yanai, N. Modulation of triplet quantum coherence by guest-induced structural changes in a flexible metal-organic framework. Nat. Commun. 2024, 15, 7622. [Google Scholar] [CrossRef] [PubMed]
- Dirac, P.A.M. The quantum theory of the emission and absorption of radiation. Proc. R. Soc. Lond. A 1927, 114, 243–265. [Google Scholar] [CrossRef]
- Susskind, L.; Glogower, J. Quantum mechanical phase and time operator. Phys. Phys. Fiz. 1964, 1, 49–61. [Google Scholar] [CrossRef]
- Loudon, R. The Quantum Theory of Light; Oxford university Press: Oxford, UK, 1973. [Google Scholar]
- Pegg, D.T.; Barnett, S.M. Unitary Phase Operator in Quantum Mechanics. Europhys. Lett. 1988, 6, 483–487. [Google Scholar] [CrossRef]
- Mendaš, I.; Popović, D.B. Number-phase uncertainty product for generalized squeezed states arising from the Pegg-Barnett Hermitian phase operator formalism. Phys. Rev. A 1995, 52, 4356–4364. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef]
- Bergmann, K.; Theuer, H.; Shore, B.W. Coherent population transfer among quantum states of atoms and molecules. Rev. Mod. Phys. 1998, 70, 1003–1025. [Google Scholar] [CrossRef]
- Furusawa, A.; Sørensen, J.L.; Braunstein, S.L.; Fuchs, C.A.; Kimble, H.J.; Polzik, E.S. Unconditional Quantum Teleportation. Science 1998, 282, 706–709. [Google Scholar] [CrossRef]
- Chou, C.W.; de Riedmatten, H.; Felinto, D.; Polyakov, S.V.; van Enk, S.J.; Kimble, H.J. Measurement-induced entanglement for excitation stored in remote atomic ensembles. Nature 2005, 438, 828–832. [Google Scholar] [CrossRef] [PubMed]
- Proos, J.; Zalka, C. Shor’s discrete logarithm quantum algorithm for elliptic curves. Quant. Inf. Comput. 2003, 3, 317–344. [Google Scholar] [CrossRef]
- Sherson, J.F.; Krauter, H.; Olsson, R.K.; Julsgaard, B.; Hammerer, K.; Cirac, I.; Polzik, E.S. Quantum teleportation between light and matter. Nature 2006, 443, 557–560. [Google Scholar] [CrossRef]
- Kimble, H. The quantum internet. Nature 2008, 453, 1023–1030. [Google Scholar] [CrossRef] [PubMed]
- Dakir, Y.; Slaoui, A.; Mohamed, A.-B.A.; Laamara, R.A.; Eleuch, H. Quantum teleportation and dynamics of quantum coherence and metrological non-classical correlations for open two-qubit systems. Sci. Rep. 2023, 13, 20526. [Google Scholar] [CrossRef] [PubMed]
- Kok, P.; Munro, W.J.; Nemoto, K.; Ralph, T.C.; Dowling, J.P.; Milburn, G.J. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 2007, 79, 135–174. [Google Scholar] [CrossRef]
- Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O’Brien, J.L. Quantum computers. Nature 2010, 464, 45–53. [Google Scholar] [CrossRef]
- Peruzzo, A.; McClean, J.; Shadbolt, P.; Yung, M.H.; Zhou, X.Q.; Love, P.J.; Aspuru-Guzik, A.; O’brien, J.L. A variational eigenvalue solver on a photonic quantum processor. Nat. Commun. 2014, 5, 4213. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Nitta, T.; Yamaguchi, K. Monte Carlo wave-function approach to the quantum-phase dynamics of a dissipative molecular system interacting with a single-mode amplitude-squeezed field. J. Chem. Phys. 2003, 119, 12106–12118. [Google Scholar] [CrossRef]
- Mølmer, K.; Castin, Y.; Dalibard, J. Monte Carlo wave-function method in quantum optics. J. Opt. Soc. Am. B 1993, 10, 524–538. [Google Scholar] [CrossRef]
- Dum, R.; Zoller, P.; Ritsch, H. Monte Carlo simulation of the atomic master equation for spontaneous emission. Phys. Rev. A 1992, 45, 4879–4887. [Google Scholar] [CrossRef] [PubMed]
- Dalibard, J.; Castin, Y.; Mølmer, K. Wave-function approach to dissipative processes in quantum optics. Phys. Rev. Lett. 1992, 68, 580–583. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Kishi, R.; Nitta, T.; Yamaguchi, K. Second-order Monte Carlo wave-function approach to the relaxation effects on ringing revivals in a molecular system interacting with a strongly squeezed coherent field. Phys. Rev. A 2004, 70, 033407. [Google Scholar] [CrossRef]
- Nakano, M. Open-Shell-Character-Based Molecular Design Principles: Applications to Nonlinear Optics and Singlet Fission. Chem. Rec. 2017, 17, 27–62. [Google Scholar] [CrossRef]

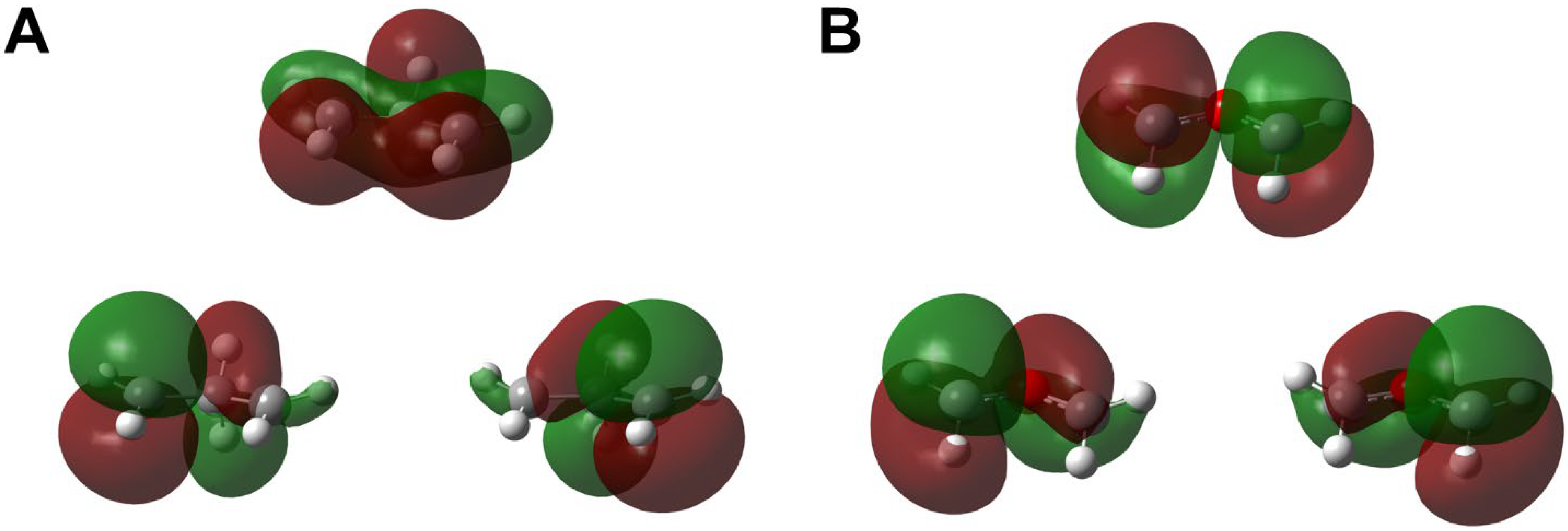
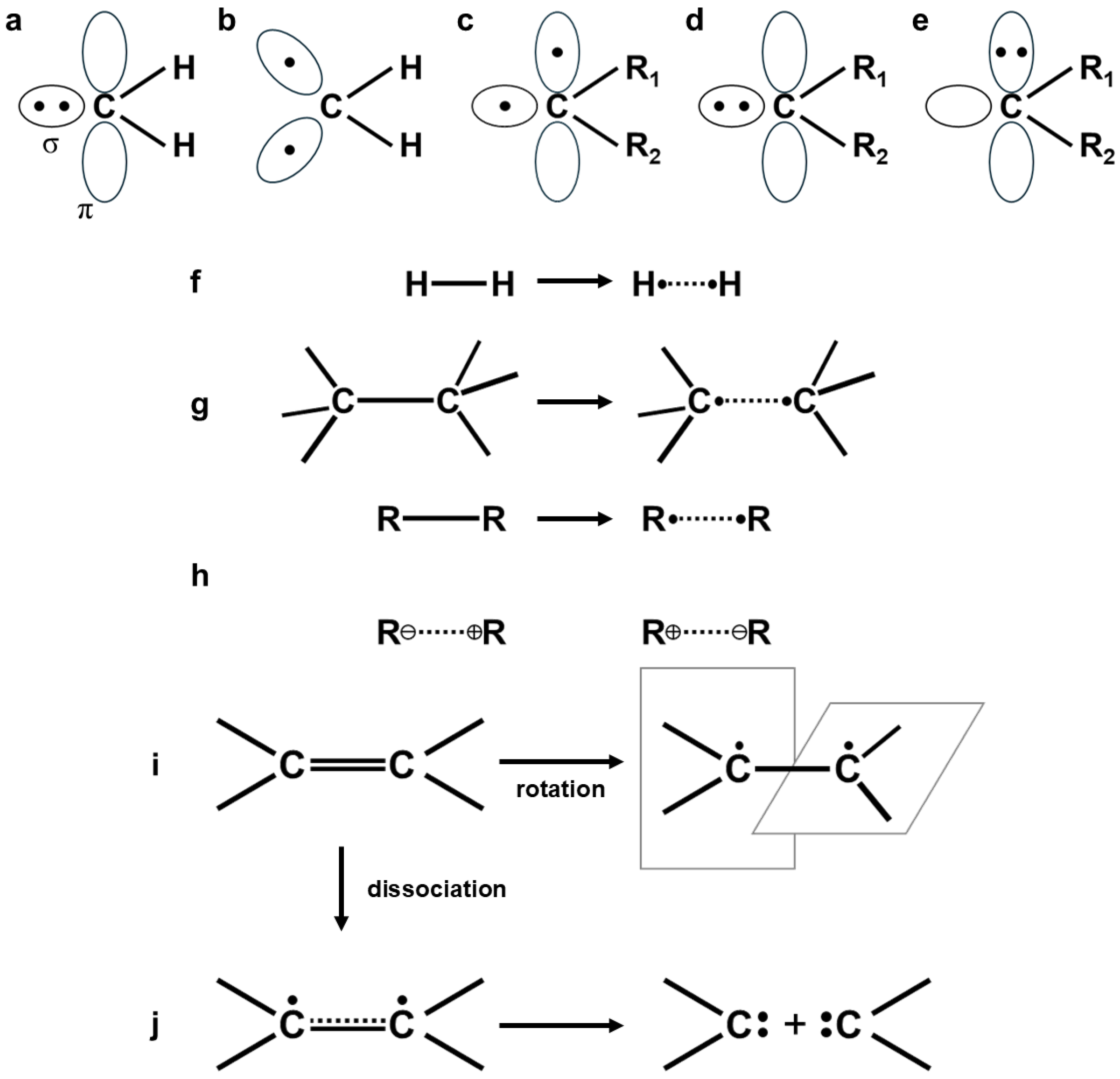

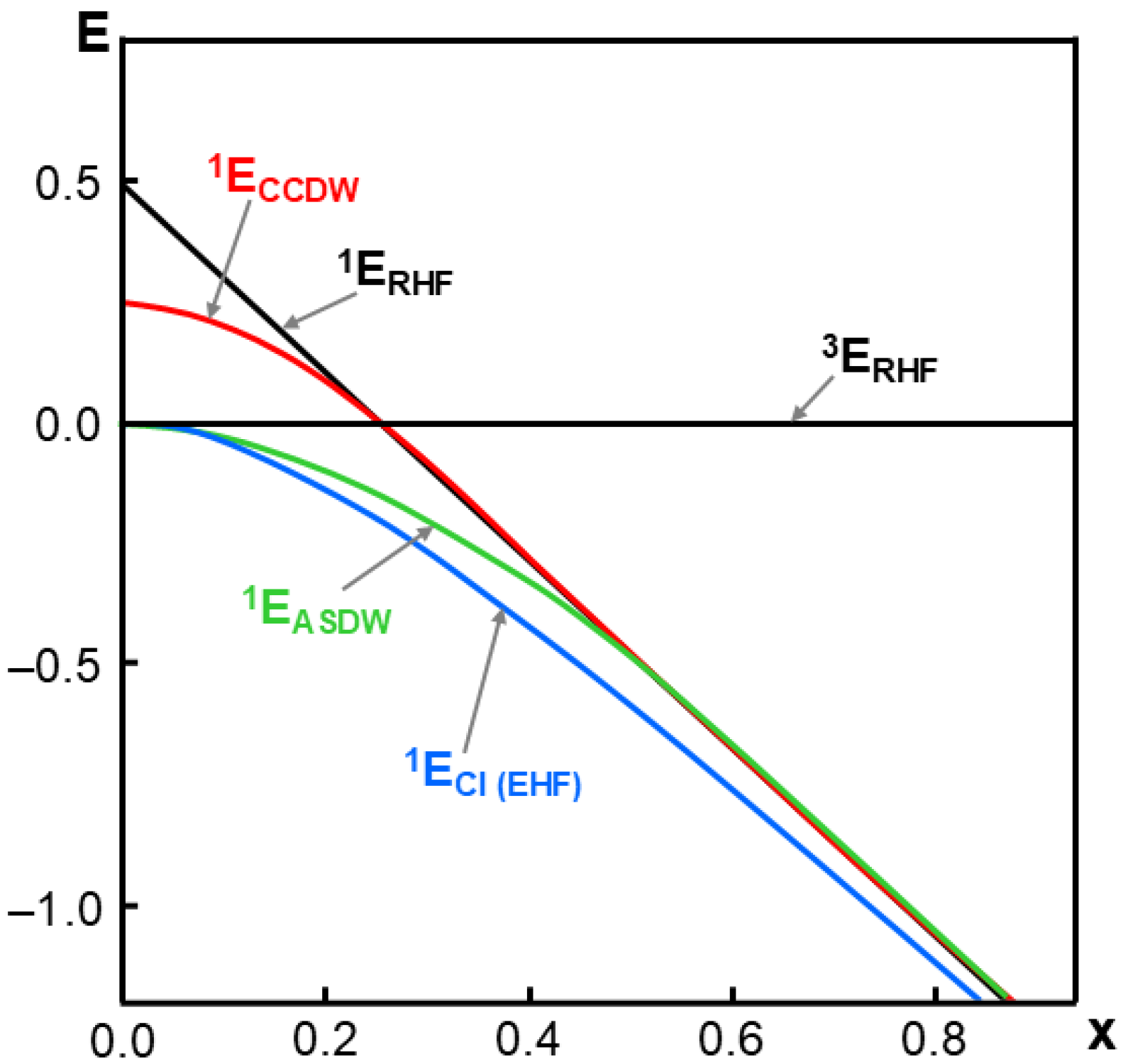
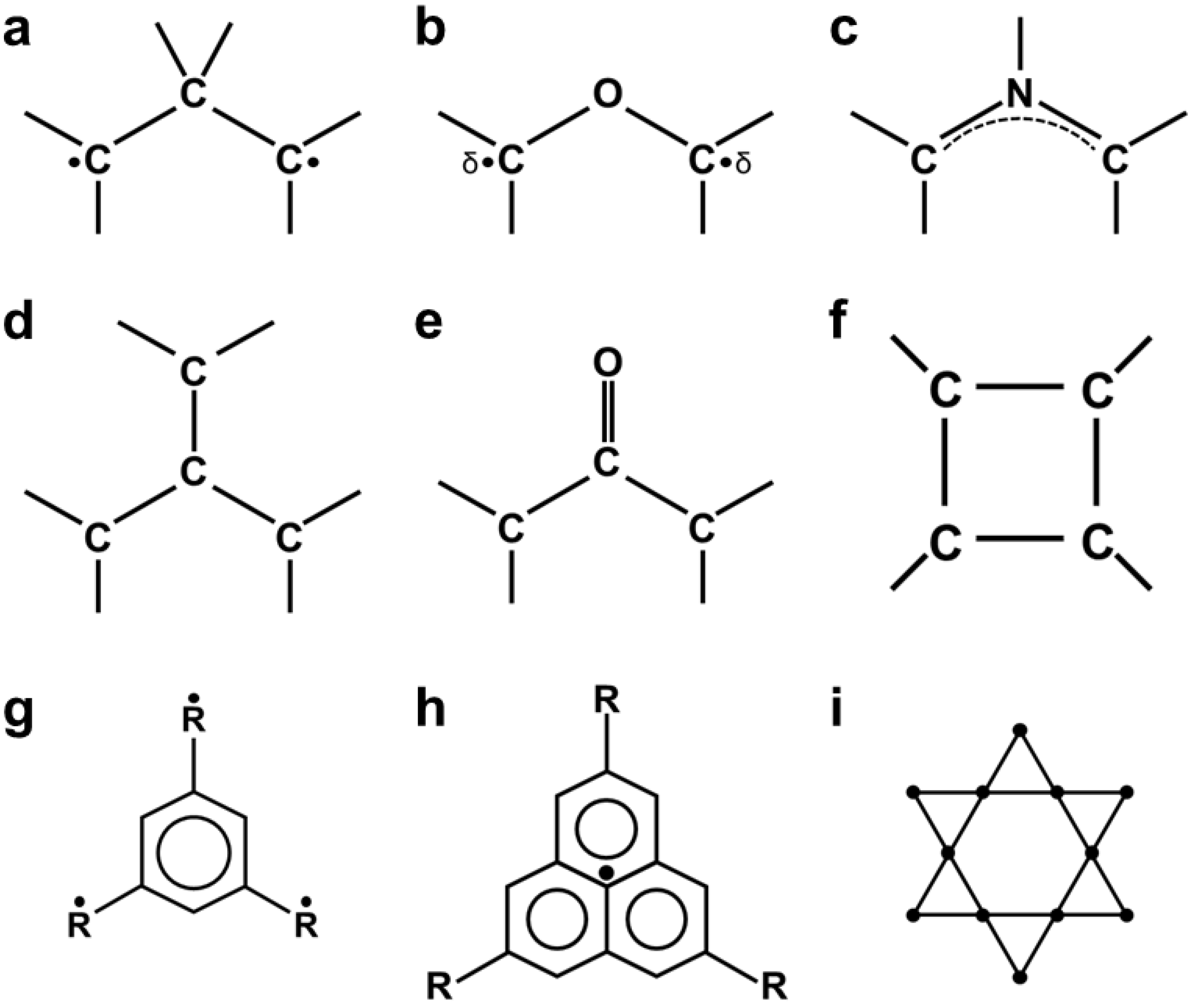

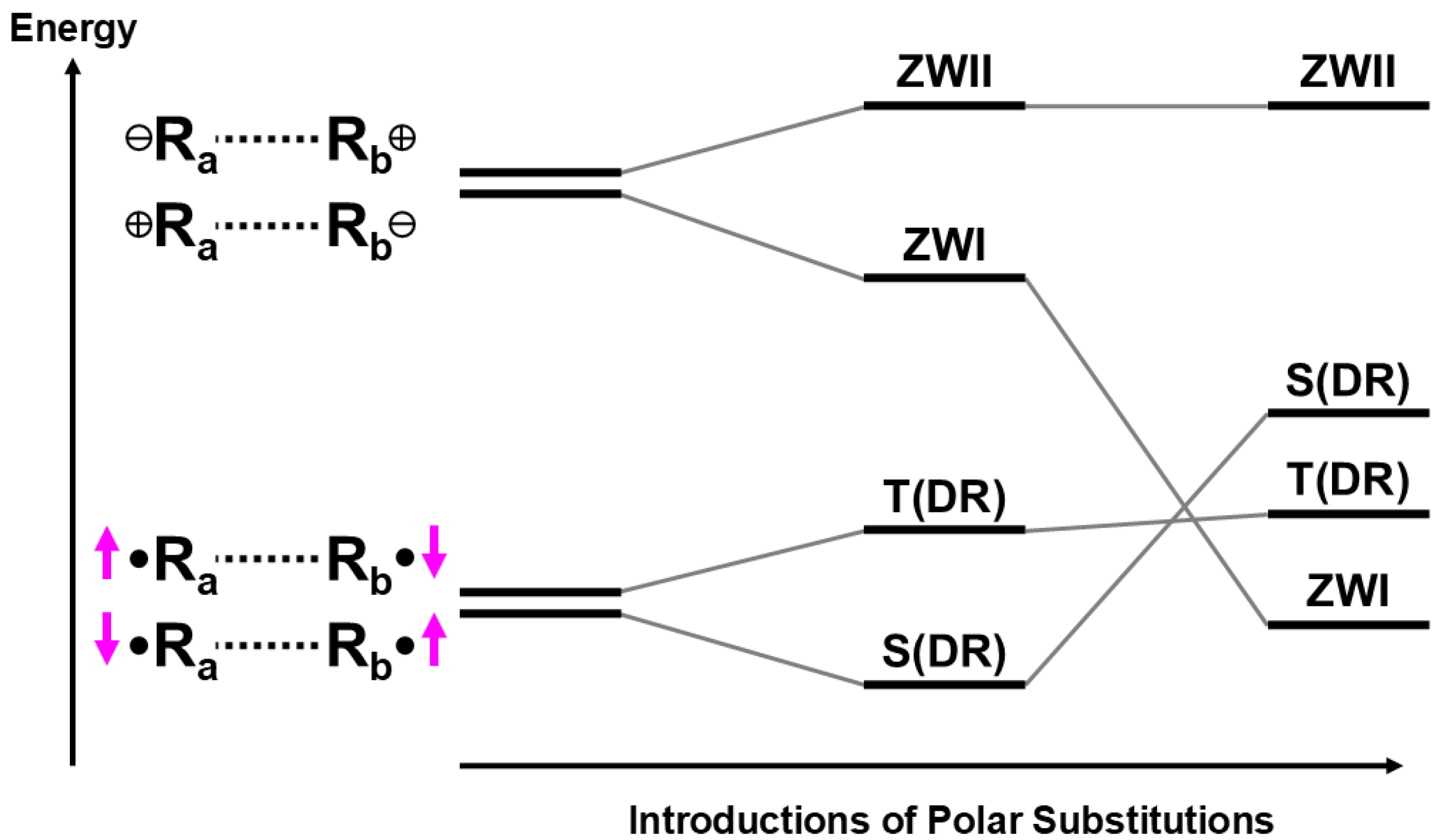
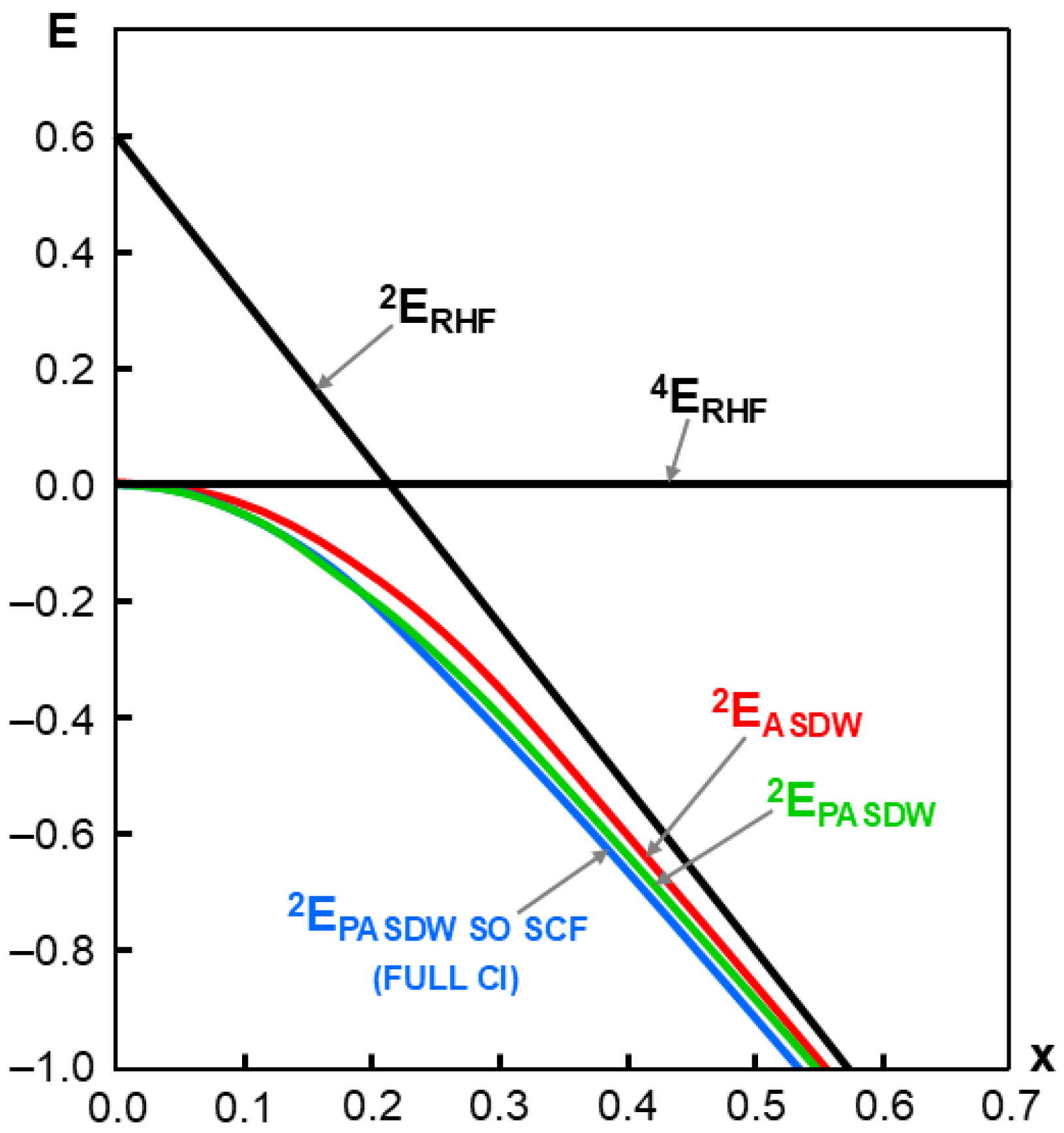
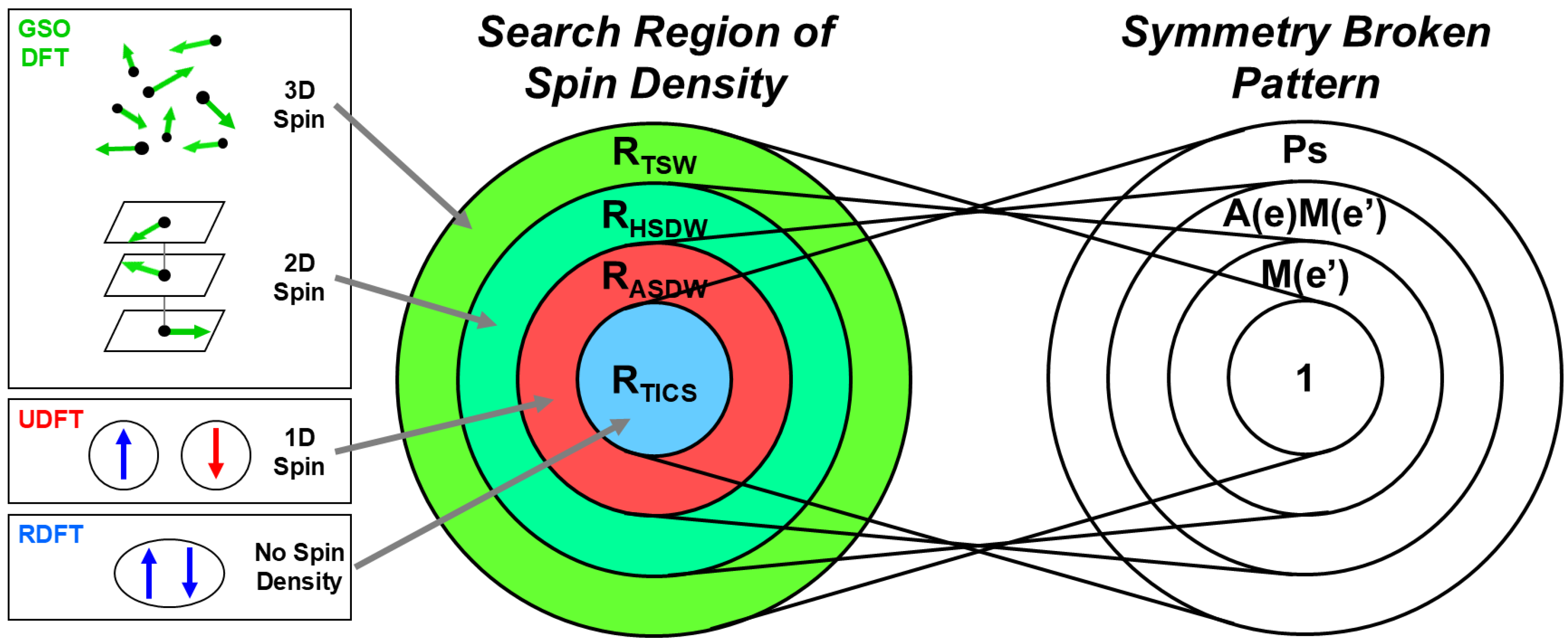

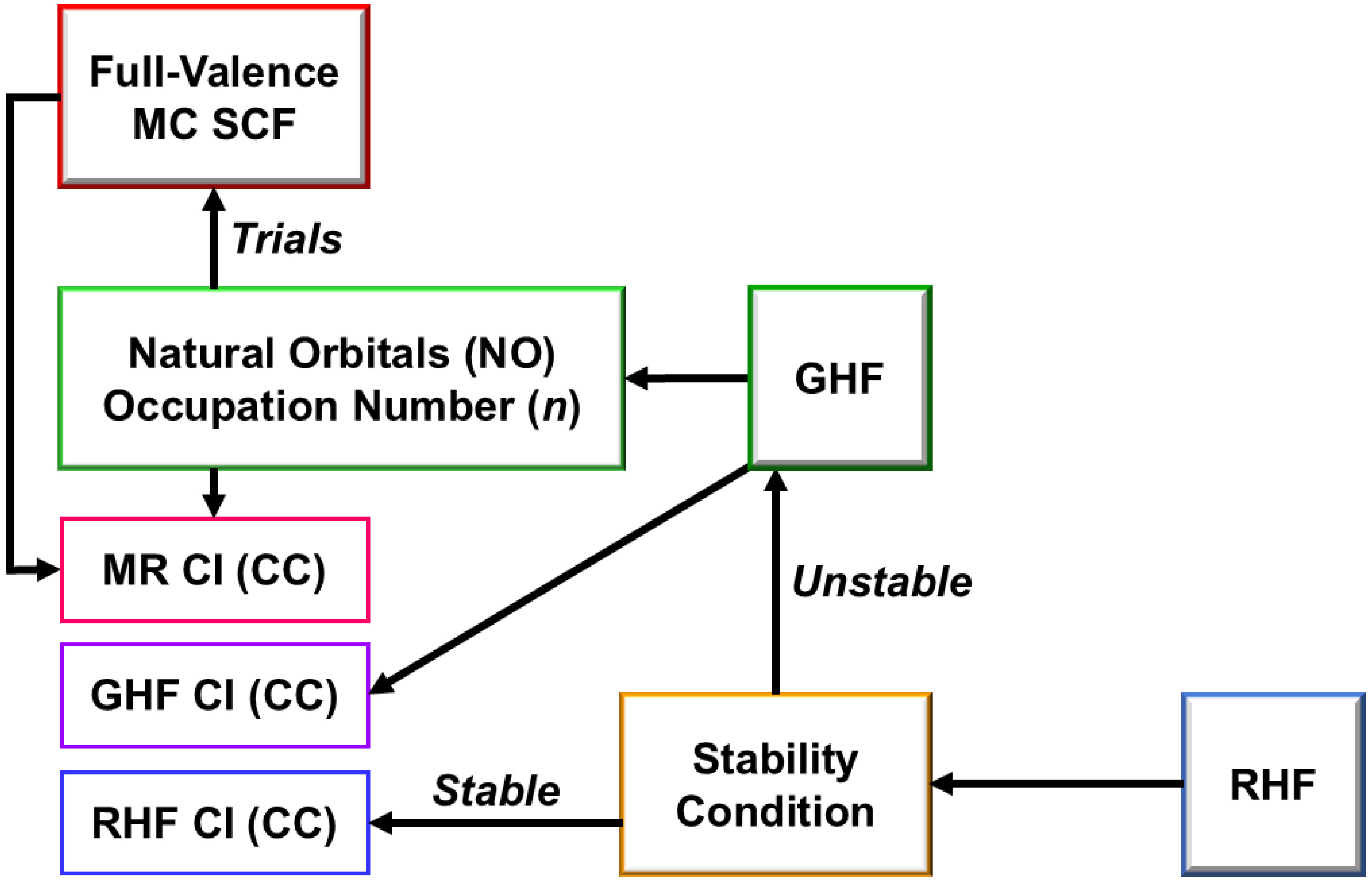

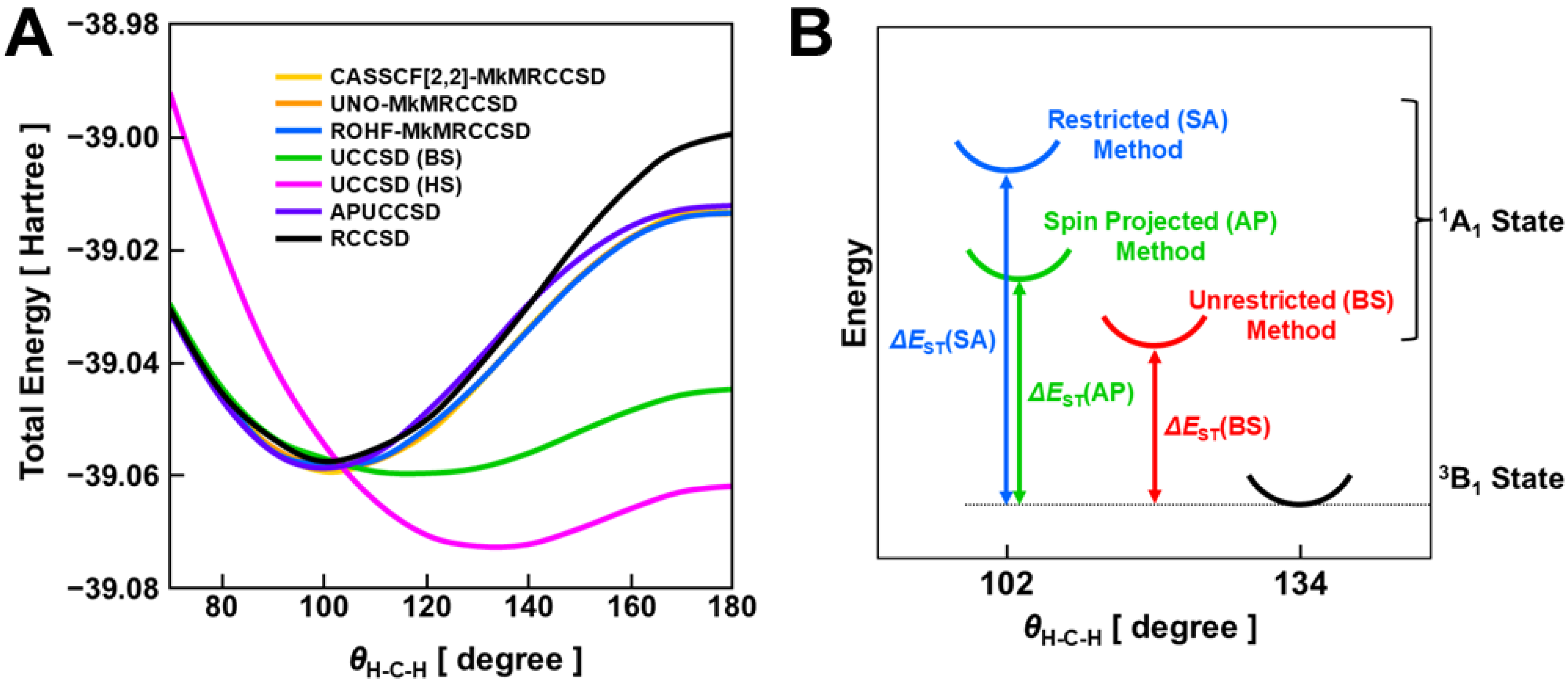
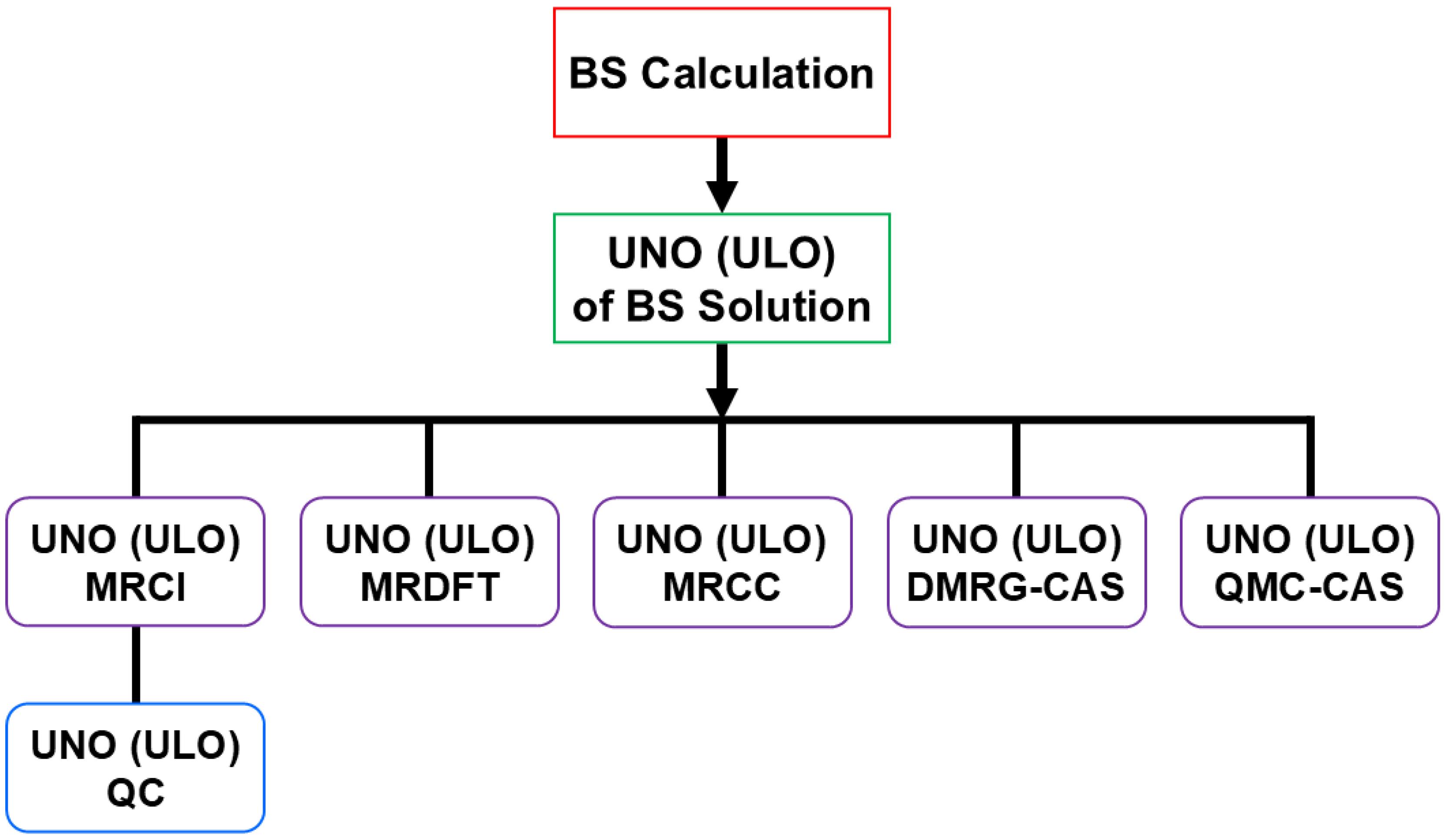

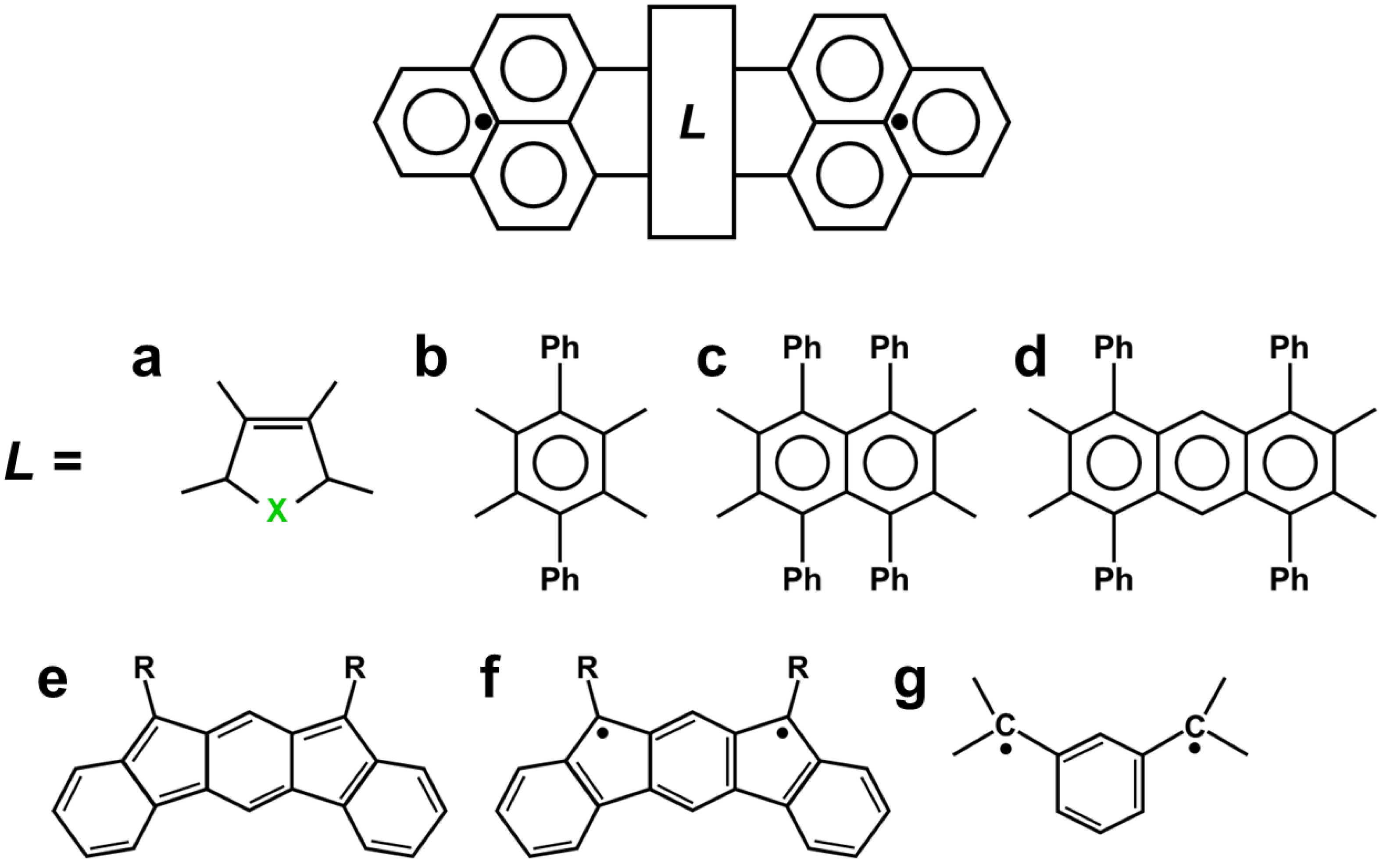
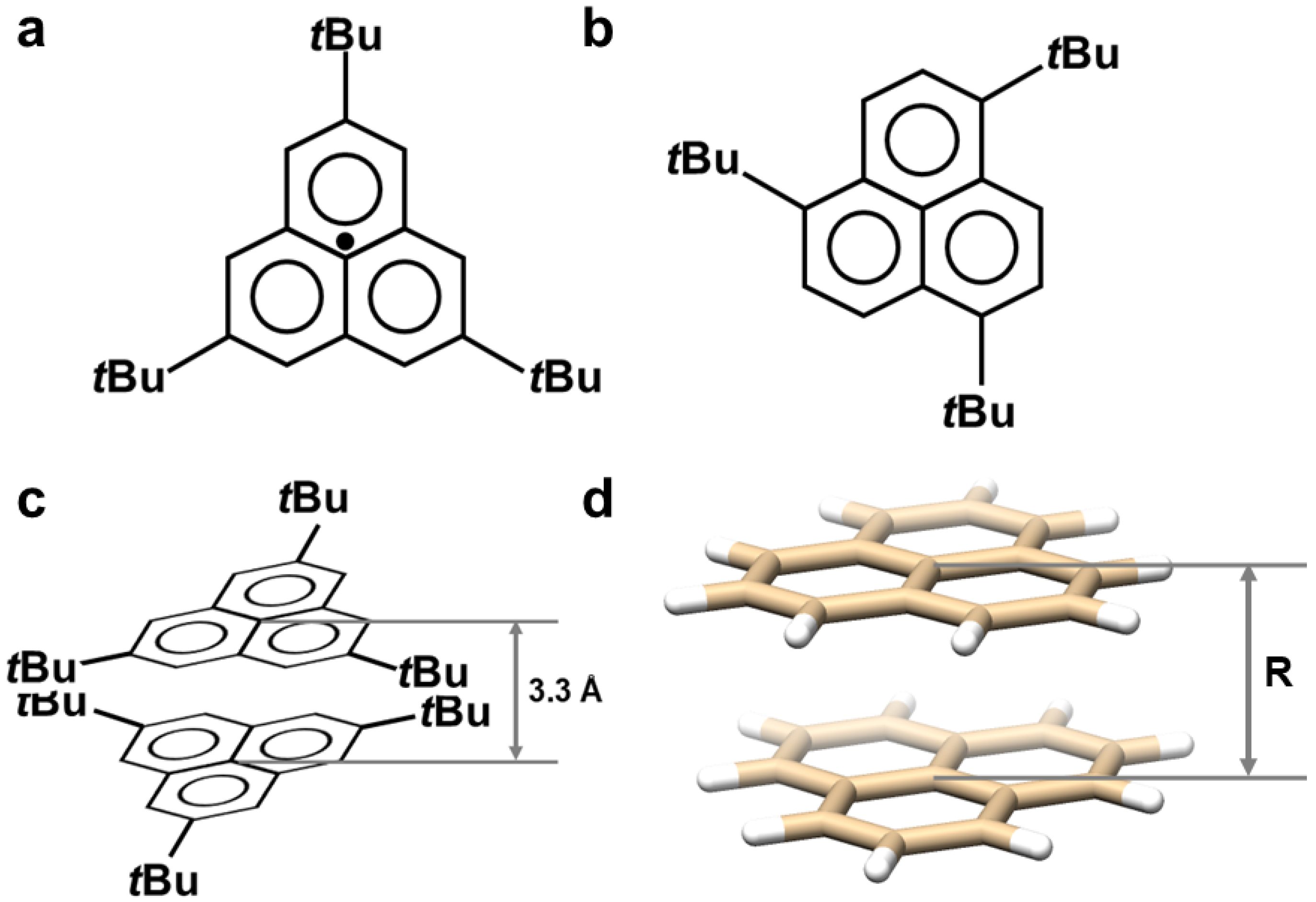






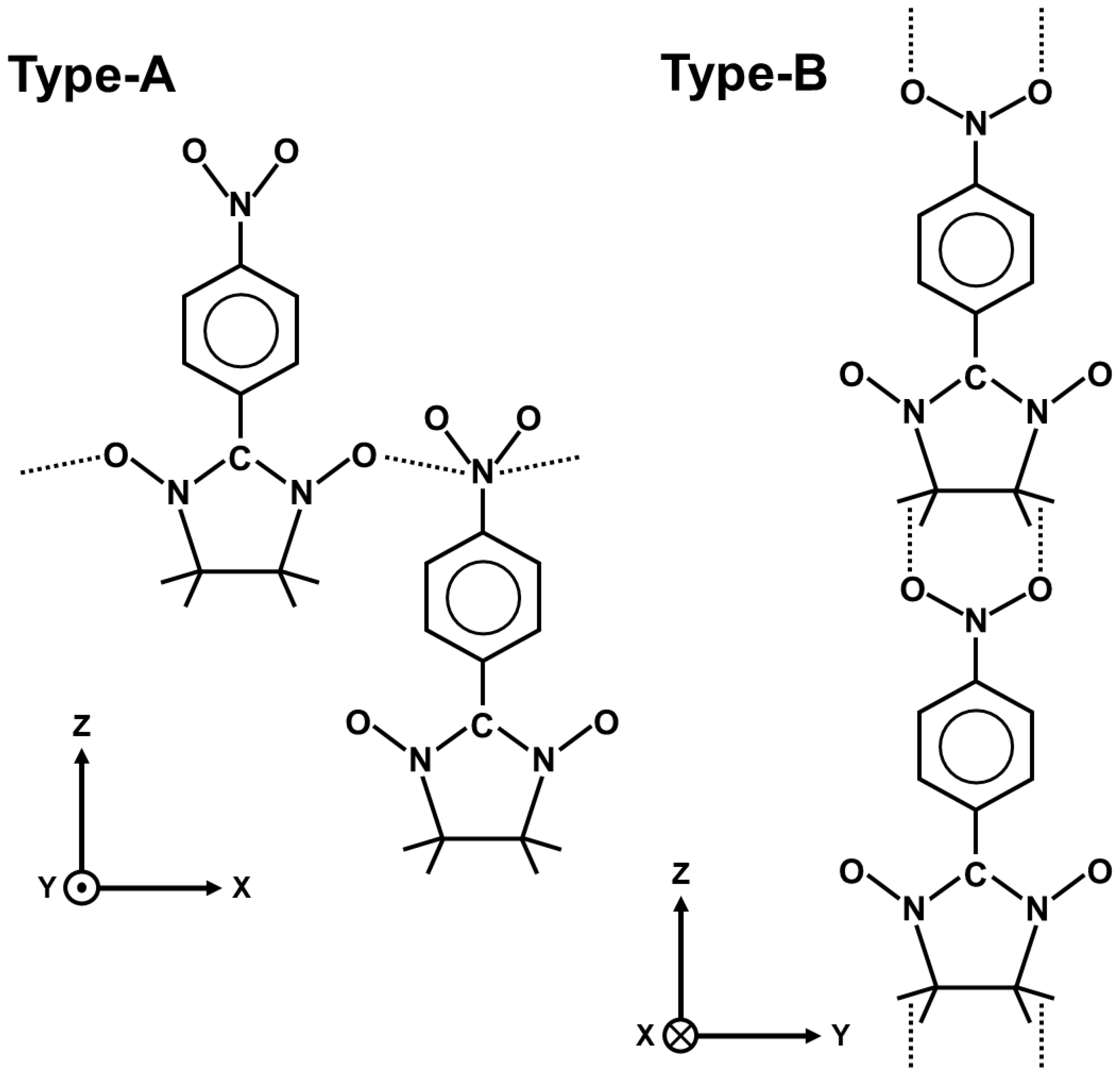
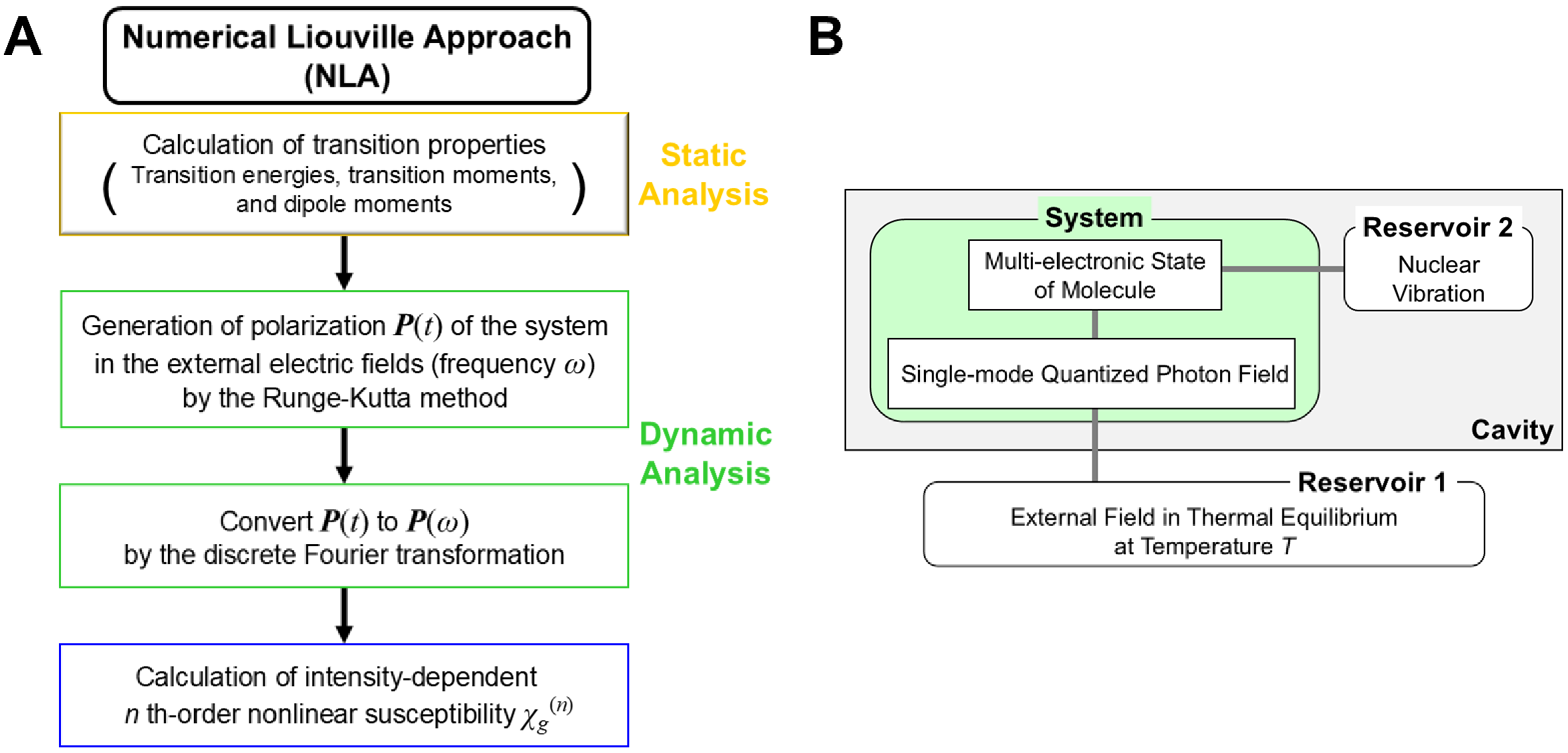
| Method | TMM | IA | OXA |
|---|---|---|---|
| AP-UHF | 44.3 | 39.6 | 22.3 |
| AP-UCCSD | 25.0 | 18.3 | 4.7 |
| AP-UCCSD(T) | 17.9 | 13.5 | 1.8 |
| AP-UBD | 26.1 | 18.3 | 4.9 |
| AP-UBD(T) | 18.3 | 13.3 | 2.2 |
| AP-UBLYP | 5.8 | 9.5 | −3.5 |
| AP-UB3LYP | 21.6 | 15.2 | 1.2 |
| AP-UCAM-B3LYP | 25.6 | 18.4 | 3.9 |
| CASSCF(2e,2o) | 11.6 | 4.3 | −5.2 |
| ROHF-MkMRCCSD(2e, 2o) | 20.6 | 14.6 | 1.6 |
| UNO-MkMRCCSD(2e, 2o) | 21.3 | 13.5 | 1.7 |
| ULO-MkMRCCSD(2e, 2o) | 15.8 | 9.1 | −1.6 |
| CASPT2(2e, 2o)/6–31G(d) [260] | 3.4 | ||
| MRCISD(2e, 2o) [260] | −1.5 | ||
| Exp. [258] | 16.1 | −1.3 |
| Method | C3H3− | C4H4 | C5H5+ |
|---|---|---|---|
| R(O)HF | 49.7 | 33.1 | 34.0 |
| R(O)MP2 | 760 | 14.2 | 26.5 |
| R(O)CCSD | 72.8 | 10.5 | 22.9 |
| R(O)CCSD(T) | 73.0 | 4.0 | 20.3 |
| UHF | 20.9 | −62.2 | −9.2 |
| UHF-MP2 | 19.3 | 14.8 | 39.2 |
| UHF-CCSD | 15.5 | −9.9 | 11.1 |
| UHF-CCSD(T) | 12.7 | −4.8 | 14.8 |
| ROHF-MkCCSD | 12.0 | −8.6 | 13.5 |
| CASSCF-MkCCSD | 13.0 | −8.1 | 9.4 |
| UNO-MkCCSD | 12.3 | −8.9 | 13.8 |
| U(D)NO-MkCCSD | 12.3 | −9.0 | 13.7 |
| Methods | Ti | In | y (%) | B | J (cm−1) |
|---|---|---|---|---|---|
| AP-UB2LYP | 0.41 | 0.35 | 30 | 0.70 | −1470 |
| APUB2’LYP | 0.56 | 0.50 | 15 | 0.85 | −1731 |
| AP-UB3LYP | 0.78 | 0.74 | 3 | 0.97 | −1729 |
| CAS SCF [2o, 2e] | 0.72 | 0.67 | 5 | 0.95 | −2266 |
| CAS SCF [6o, 6e] | 0.70 | 0.65 | 6 | 0.94 | −3417 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, S.; Shigemoto, I.; Kawakami, T.; Isobe, H.; Shoji, M.; Miyagawa, K.; Yamaguchi, K. Quantum Mechanical Approaches to Strongly Correlated Electron Systems: Structure, Bonding, and Properties of Diradicals, Triradicals, and Polyradicals. Chemistry 2025, 7, 38. https://doi.org/10.3390/chemistry7020038
Yamada S, Shigemoto I, Kawakami T, Isobe H, Shoji M, Miyagawa K, Yamaguchi K. Quantum Mechanical Approaches to Strongly Correlated Electron Systems: Structure, Bonding, and Properties of Diradicals, Triradicals, and Polyradicals. Chemistry. 2025; 7(2):38. https://doi.org/10.3390/chemistry7020038
Chicago/Turabian StyleYamada, Satoru, Isamu Shigemoto, Takashi Kawakami, Hiroshi Isobe, Mitsuo Shoji, Koichi Miyagawa, and Kizashi Yamaguchi. 2025. "Quantum Mechanical Approaches to Strongly Correlated Electron Systems: Structure, Bonding, and Properties of Diradicals, Triradicals, and Polyradicals" Chemistry 7, no. 2: 38. https://doi.org/10.3390/chemistry7020038
APA StyleYamada, S., Shigemoto, I., Kawakami, T., Isobe, H., Shoji, M., Miyagawa, K., & Yamaguchi, K. (2025). Quantum Mechanical Approaches to Strongly Correlated Electron Systems: Structure, Bonding, and Properties of Diradicals, Triradicals, and Polyradicals. Chemistry, 7(2), 38. https://doi.org/10.3390/chemistry7020038






