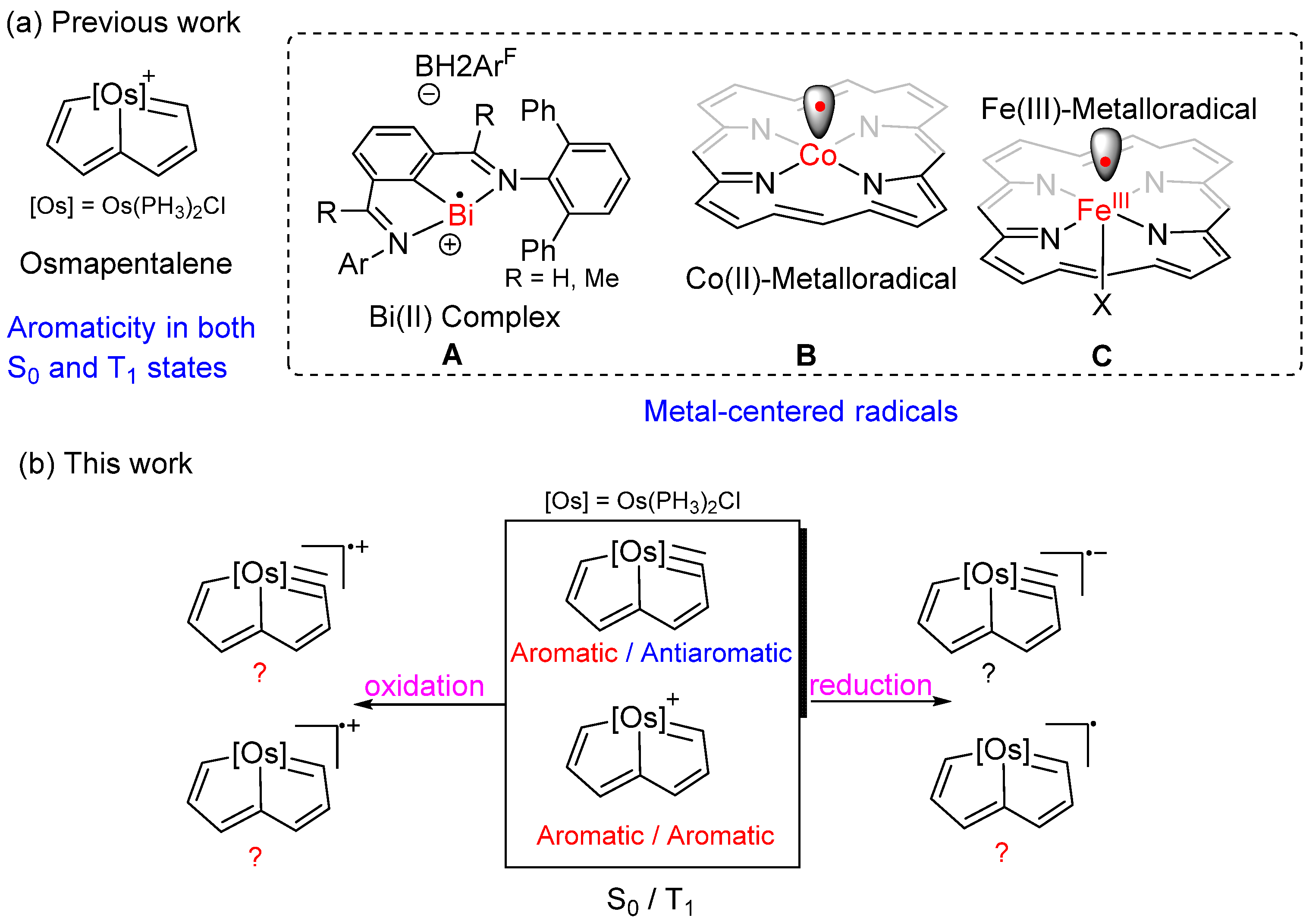
Too Persistent to Resist: Aromaticity in 16e Osmapentalene Radicals Survives Regardless of Redox
Abstract
1. Introduction
2. Methods
3. Results and Discussion
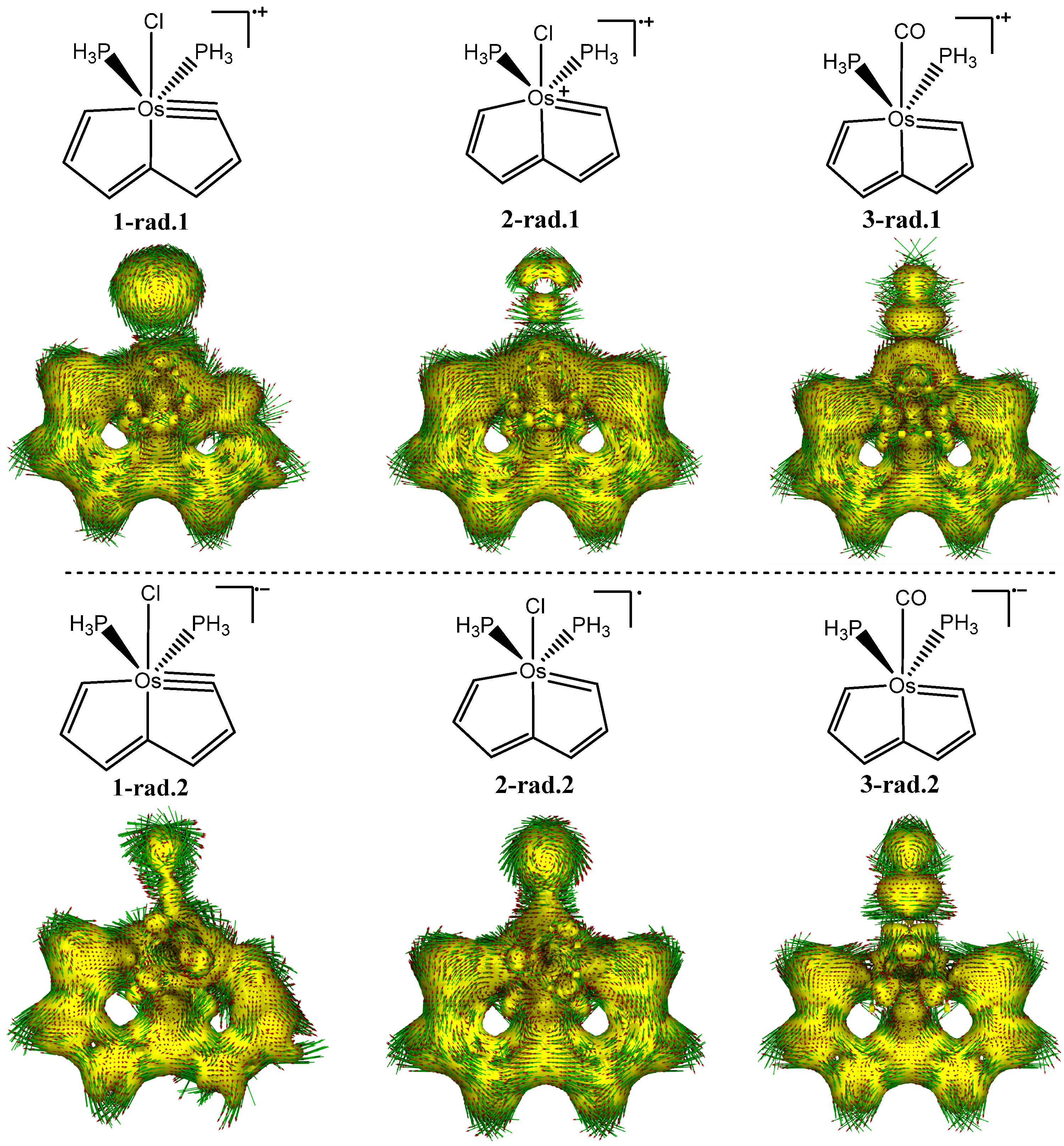
3.1. The Geometries of the Corresponding Radicals from Complexes 1 to 3
3.2. Aromaticity Analyses Based on Magnetic Properties
3.3. Electron Density of Delocalized Bonds (EDDB) Analysis
3.4. Aromaticity Analyses Based on Electron Localization Function
3.5. Aromaticity Analyses Based on Frontier Molecular Orbitals and Spin Populations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hückel, E. Quantentheoretische Beiträge zum Benzolproblem. Z. Phys. 1931, 70, 204–286. [Google Scholar] [CrossRef]
- Dewar, M.J.S. A molecular orbital theory of organic chemistry-VIII: Aromaticity and electrocyclic reactions. Tetrahedron 1966, 22, 75–92. [Google Scholar] [CrossRef]
- Heilbronner, E. Hückel molecular orbitals of Möbius-type conformations of annulenes. Tetrahedron Lett. 1964, 5, 1923–1928. [Google Scholar] [CrossRef]
- Zimmerman, H.E. On molecular orbital correlation diagrams, the occurrence of Möbius systems in cyclization reactions, and factors controlling ground-and excited-state reactions. I. J. Am. Chem. Soc. 1966, 88, 1564–1565. [Google Scholar] [CrossRef]
- Zimmerman, H.E. Möbius-Hückel concept in organic chemistry. Application of organic molecules and reactions. Acc. Chem. Res. 1971, 4, 272–280. [Google Scholar] [CrossRef]
- Thorn, D.L.; Hoffmann, R. Delocalization in metallocycles. Nouv. J. Chem. 1979, 3, 39–45. [Google Scholar]
- Elliott, G.P.; Roper, W.R.; Waters, J.M. Metallacyclohexatrienes or ‘Metallabenzenes’ Synthesis of Osmabenzene Derivatives and X-Ray Crystal-Structure of [Os(CsCHCHCHCH)(Co)(PPh3)2]. J. Chem. Soc. Chem. Commun. 1982, 14, 811–813. [Google Scholar] [CrossRef]
- Bleeke, J.R. Metallabenzenes. Chem. Rev. 2001, 101, 1205–1228. [Google Scholar] [CrossRef] [PubMed]
- He, G.; Xia, H.; Jia, G. Progress in the synthesis and reactivity studies of metallabenzenes. Chin. Sci. Bull. 2004, 49, 1543–1553. [Google Scholar] [CrossRef]
- Landorf, C.W.; Haley, M.M. Recent Advances in Metallabenzene Chemistry. Angew. Chem. Int. Ed. 2006, 45, 3914–3936. [Google Scholar] [CrossRef] [PubMed]
- Bleeke, J.R. Aromatic Iridacycles. Acc. Chem. Res. 2007, 40, 1035–1047. [Google Scholar] [CrossRef]
- Paneque, M.; Poveda, M.L.; Rendón, N. Synthesis and Reactivity of Iridacycles Containing the TpMe2Ir Moiety. Eur. J. Inorg. Chem. 2011, 2011, 19–33. [Google Scholar] [CrossRef]
- Zhu, C.; Cao, X.; Xia, H. Double Stabilization of Highly Strained Six-Membered Rings by Phosphonium and Transition Metal. Chin. J. Org. Chem. 2013, 33, 657–662. [Google Scholar] [CrossRef]
- Cao, X.Y.; Zhao, Q.; Lin, Z.; Xia, H. The Chemistry of Aromatic Osmacycles. Acc. Chem. Res. 2014, 47, 341–354. [Google Scholar] [CrossRef] [PubMed]
- Wen, T.B.; Zhou, Z.Y.; Jia, G. Synthesis and Characterization of a Metallabenzyne. Angew. Chem. Int. Ed. 2001, 40, 1951–1954. [Google Scholar] [CrossRef]
- Jia, G. Recent progress in the chemistry of osmium carbyne and metallabenzyne complexes. Coord. Chem. Rev. 2007, 251, 2167–2187. [Google Scholar] [CrossRef]
- Chen, J.; Jia, G. Recent development in the chemistry of transition metal-containing metallabenzenes and metallabenzynes. Coord. Chem. Rev. 2013, 257, 2491–2521. [Google Scholar] [CrossRef]
- He, G.; Zhu, J.; Hung, W.Y.; Wen, T.B.; Sung HH, Y.; Williams, I.D.; Lin, Z.; Jia, G. A Metallanaphthalyne Complex from Zinc Reduction of a Vinylcarbyne Complex. Angew. Chem. Int. Ed. 2007, 46, 9065–9068. [Google Scholar] [CrossRef]
- Zhang, M.-X.; Zhang, J.; Jin, X.; Sun, X.; Yin, J.; Hartl, F.; Liu, S.H. Diphenylamine-Substituted Osmanaphthalyne Complexes: Structural, Bonding, and Redox Properties of Unusual Donor–Bridge–Acceptor Systems. Chem. Eur. J. 2018, 24, 18998–19009. [Google Scholar] [CrossRef]
- Zhang, M.-X.; Xu, Z.; Lu, T.; Yin, J.; Liu, S.H. A Visible-Light-Induced Strategy To Construct Osmanaphthalynes, Osmaanthracyne, and Osmaphenanthryne. Chem. Eur. J. 2018, 24, 14891–14895. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Yang, Y.; Wu, J.; Luo, M.; Fan, J.; Zhu, J.; Xia, H. Five-Membered Cyclic Metal Carbyne: Synthesis of Osmapentalynes by the Reactions of Osmapentalene with Allene, Alkyne, and Alkene. Angew. Chem. Int. Ed. 2015, 54, 7189–7192. [Google Scholar] [CrossRef] [PubMed]
- Zhuo, Q.; Lin, J.; Hua, Y.; Zhou, X.; Shao, Y.; Chen, S.; Chen, Z.; Zhu, J.; Zhang, H.; Xia, H. Multiyne chains chelating osmium via three metal-carbon σ bonds. Nat. Commun. 2017, 8, 1912. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Xia, H. Carbolong Chemistry: A Story of Carbon Chain Ligands and Transition Metals. Acc. Chem. Res. 2018, 51, 1691–1700. [Google Scholar] [CrossRef]
- Zhu, C.; Luo, M.; Zhu, Q.; Zhu, J.; Schleyer, P.v.R.; Wu, J.I.-C.; Lu, X.; Xia, H. Planar Möbius aromatic pentalenes incorporating 16 and 18 valence electron osmiums. Nat. Commun. 2014, 5, 3265. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Yang, C.; Wang, Y.; Lin, G.; Yang, Y.; Wang, X.; Zhu, J.; Chen, X.; Lu, X.; Liu, G.; et al. CCCCC pentadentate chelates with planar Möbiusaromaticity and unique properties. Sci. Adv. 2016, 2, e1601031. [Google Scholar] [CrossRef]
- Grotjahn, D.B.; Hoerter, J.M.; Hubbard, J.L. Double C-H Activation during Functionalization of Phenyl(methyl)ketene on Iridium(I) Using Alkynes. Synthesis of 1,4-Dien-3-ones. J. Am. Chem. Soc. 2004, 126, 8866–8867. [Google Scholar] [CrossRef]
- Weller, K.J.; Filippov, I.; Briggs, P.M.; Wigley, D.E. Pyridine Degradation Intermediates as Models for Hydrodenitrogenation Catalysis: Preparation and Properties of a Metallapyridine Complex. Organometallics 1998, 17, 322–329. [Google Scholar] [CrossRef]
- Wang, T.; Han, F.; Huang, H.; Li, J.; Zhang, H.; Zhu, J.; Lin, Z.; Xia, H. Synthesis of Aromatic Aza-metallapentalenes from Metallabenzene via Sequential Ring Contraction/Annulation. Sci. Rep. 2015, 5, 9584. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zhu, C.; Li, S.; Luo, M.; Zhou, X.; Niu, Y.; Lin, M.; Zhu, J.; Cao, Z.; Lu, X.; Wen, T.; et al. Stabilization of anti-aromatic and strained five-membered rings with a transition metal. Nat. Chem. 2013, 5, 698–703. [Google Scholar] [CrossRef]
- Baird, N.C. Quantum Organic Photochemistry. II. Resonance and Aromaticity in the Lowest ππ* State of Cyclic Hydrocarbons. J. Am. Chem. Soc. 1972, 94, 4941–4948. [Google Scholar] [CrossRef]
- Chen, D.; Shen, T.; An, K.; Zhu, J. Adaptive aromaticity in S0 and T1 states of pentalene incorporating 16 valence electron osmium. Commun. Chem. 2018, 1, 18. [Google Scholar] [CrossRef]
- Chen, D.; Qiu, R.; Dong SZhu, J. Adaptive aromaticity in ruthenacycles. Theor. Chem. Acc. 2020, 139, 21. [Google Scholar] [CrossRef]
- Dai, C.; Chen, D.; Zhu, J. Achieving Adaptive Aromaticity in Cyclo[10]carbon by Screening Cyclo[n]carbon (n=8-24). Chem. Asian J. 2020, 15, 2187–2191. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Chen, D.; Zhu, J. Adaptive Aromaticity in Metallasilapentalynes. Organometallics 2021, 40, 899–906. [Google Scholar] [CrossRef]
- Xu, F.; Chen, D.; Zeng, J.; Zhu, J. Osmapentalyne and Osmapentalene Complexes Containing Boron Monofluoride Ligands: Structure, Bonding and Adaptive Aromaticity. New J. Chem. 2021, 45, 15294–15302. [Google Scholar] [CrossRef]
- Qiu, R.; Zhu, J. Adaptive Aromaticity in 16-valence-electron Metallazapentalenes. Dalton Trans. 2021, 50, 16842–16848. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Zhang, Y.; Chi, Y.; Liu, L.; Zhang, W.-X.; Xi, Z. Aromatic Dicupra[10]Annulenes. J. Am. Chem. Soc. 2016, 138, 60–63. [Google Scholar] [CrossRef]
- An, K.; Shen, T.; Zhu, J. Craig-Type Möbius Aromaticity and Antiaromaticity in Dimetalla[10]Annulenes: A Metal-Induced Yin-and-Yang Pair. Organometallics 2017, 36, 3199–3204. [Google Scholar] [CrossRef]
- Miwa, K.; Yokota, T.; Wang, Q.; Sakurai, T.; Fliegl, H.; Sundholm, D.; Shinokubo, H. Metallaantiaromaticity of 10-Platinacorrole Complexes. J. Am. Chem. Soc. 2024, 146, 1396–1402. [Google Scholar] [CrossRef] [PubMed]
- Merino, G.; Solà, M.; Fernández, I.; Foroutan-Nejad, C.; Lazzeretti, P.; Frenking, G.; Anderson, H.L.; Sundholm, D.; Cossío, F.P.; Petrukhina, M.A.; et al. Aromaticity: Quo Vadis. Chem. Sci. 2023, 14, 5569–5576. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves, T.P.; Dutta, I.; Huang, K.-W. Aromaticity in catalysis: Metal ligand cooperation via ligand dearomatization and rearomatization. Chem. Commun. 2021, 57, 3070–3082. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves, T.P.; Huang, K.-W. Metal–Ligand Cooperative Reactivity in the (Pseudo)-Dearomatized PNx(P) Systems: The Influence of the Zwitterionic Form in Dearomatized Pincer Complexes. J. Am. Chem. Soc. 2017, 139, 13442–13449. [Google Scholar] [CrossRef] [PubMed]
- Chatgilialoglu, C.; Studer, A. Encyclopedia of Radicals in Chemistry, Biology and Materials; Wiley: Chichester, UK, 2012. [Google Scholar]
- Tang, S.; Liu, K.; Liu, C.; Lei, A. Olefinic C–H functionalization through radical alkenylation. Chem. Soc. Rev. 2015, 44, 1070. [Google Scholar] [CrossRef]
- Hammer, S.G.; Heinrich, M.R. Carbon-Carbon Bond-Forming Reactions Involving Aryl Radicals. In Comprehensive Organic Synthesis, 2nd ed.; Molander, G.A., Knochel, P., Eds.; Elsevier: Oxford, UK, 2014; Volume 4, pp. 495–516. [Google Scholar]
- Subramanian, H.; Landais, Y.; Sibi, M.P. Radical Addition Reactions. In Comprehensive Organic Synthesis, 2nd ed.; Molander, G.A., Knochel, P., Eds.; Elsevier: Oxford, UK, 2014; Volume 4, pp. 699–741. [Google Scholar]
- Loertscher, B.M.; Castle, S.L. Radical Cyclizations and Sequential Radical Reactions. In Comprehensive Organic Synthesis, 2nd ed.; Molander, G.A., Knochel, P., Eds.; Elsevier: Oxford, UK, 2014; Volume 4, pp. 742–809. [Google Scholar]
- Yoshioka, E.; Kohtani, S.; Jichu, T.; Fukazawa, T.; Nagai, T.; Takemoto, Y.; Miyabe, H. Direct Photoinduced Electron Transfer from Excited State of Rhodamine B for Carbon-Radical Generation. Synlett 2015, 26, 265–270. [Google Scholar] [CrossRef]
- Majumdar, K.C.; Basu, P.K.; Chattopadhyay, S.K. Formation of five- and six-membered heterocyclic rings under radical cyclisation conditions. Tetrahedron 2007, 63, 793–826. [Google Scholar] [CrossRef]
- Gansäuer, A. (Ed.) Radicals in Synthesis I: Methods and Mechanisms; Springer: Berlin, Germany, 2006. [Google Scholar]
- Gansäuer, A. (Ed.) Radicals in Synthesis II: Complex Molecules; Springer: Berlin, Germany, 2006. [Google Scholar]
- Taniguchi, T. Recent Advances in Reactions of Heteroatom-Centered Radicals. Synthesis 2017, 49, 3511–3534. [Google Scholar] [CrossRef]
- Lynch, D.M.; Scanlan, E.M. Thiyl Radicals: Versatile Reactive Intermediates for Cyclization of Unsaturated Substrates. Molecules 2020, 25, 3094. [Google Scholar] [CrossRef]
- Poater, J.; Viñas, C.; Bennour, I.; Escayola, S.; Solà, M.; Teixidor, F. Too Persistent to Give Up: Aromaticity in Boron Clusters Survives Radical Structural Changes. J. Am. Chem. Soc. 2020, 142, 9396–9407. [Google Scholar] [CrossRef]
- Goulin, C.A.; Huber, T.A.; Nelson, J.M.; Macartney, D.H.; Baird, M.C. Atom Transfer Reactions Involving the Metal-centred Radical [(η5-C5H5)Cr(CO)3]. J. Chem. Soc. Chem. Commun. 1991, 798–799. [Google Scholar] [CrossRef]
- Gao, D.Z.; Liao, D.Z.; Jiang, Z.H.; Yan, S.P. Two hetero-spin metal–radical complexes exhibiting strong antiferromagnetic interactions between the metal ions and nitroxide radicals. Transition Met. Chem. 2008, 33, 107–112. [Google Scholar] [CrossRef]
- Bai, W.; Li, L.; Fu, Y.; Tang, J.; Zhao, Y.; Wang, Y.; Li, Y. Radical metallacyclopropene: Synthesis, structure and aromaticity. Dalton Trans. 2023, 52, 9731–9736. [Google Scholar] [CrossRef]
- Shao, X.; Wu, X.; Wu, S.; Zhu, C. Metal-Free Radical-Mediated C(sp3)-H Heteroarylation of Alkanes. Org. Lett. 2020, 22, 7450–7454. [Google Scholar] [CrossRef]
- Ganesamoorthy, C.; Helling, C.; Wölper, C.; Frank, W.; Bill, E.; Cutsail, G.E., III; Schulz, S. From stable Sb- and Bi-centered radicals to a compound with a Ga=Sb double bond. Nat. Commun. 2018, 9, 87. [Google Scholar] [CrossRef]
- Neidlinger, A.; Kienz, T.; Heinze, K. Spin Trapping of Carbon-Centered Ferrocenyl Radicals with Nitrosobenzene. Organometallics 2015, 34, 5310–5320. [Google Scholar] [CrossRef]
- Yang, X.; Reijerse, E.J.; Nöthling, N.; SantaLucia, D.J.; Leutzsch, M.; Schnegg, A.; Cornella, J. Synthesis, Isolation, and Characterization of Two CationicOrganobismuth(II) Pincer Complexes Relevant in Radical RedoxChemistry. J. Am. Chem. Soc. 2023, 145, 5618–5623. [Google Scholar] [CrossRef] [PubMed]
- Ke, J.; Lee, W.-C.C.; Wang, X.; Wang, Y.; Wen, X.; Zhang, X.P. Metalloradical Activation of In Situ-Generated α-Alkynyldiazomethanes for Asymmetric Radical Cyclopropanation of Alkenes. J. Am. Chem. Soc. 2022, 144, 2368–2378. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.-C.C.; Wang, D.-S.; Zhu, Y.; Zhang, X.P. Iron(III)-based metalloradical catalysis for asymmetric cyclopropanation via a stepwise radical mechanism. Nat. Chem. 2023, 15, 1569–1580. [Google Scholar] [CrossRef] [PubMed]
- Xu, P.; Xie, J.; Wang, D.-S.; Zhang, X.P. Metalloradical approach for concurrent control in intermolecular radical allylic C−H amination. Nat. Chem. 2023, 15, 498–507. [Google Scholar] [CrossRef]
- Shi, J.; Xu, W.; Yu, H.; Wang, X.; Jin, F.; Zhang, Q.; Zhang, H.; Peng, Q.; Abdurahman, A.; Wang, M. A Highly Luminescent Metallo-Supramolecular Radical Cage. J. Am. Chem. Soc. 2023, 145, 24081–24088. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16. Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Hay, P.J.; Wadt, W.R. Ab initio effective core potentials for molecular calculations. Potentials for potassium to gold including the outermost core orbitals. J. Chem. Phys. 1985, 82, 299–310. [Google Scholar] [CrossRef]
- Huzinaga, S. Basis sets for molecular calculations. Comput. Phys. Rep. 1985, 2, 281–339. [Google Scholar] [CrossRef]
- Legault, C.Y. CYLview, 1.0 b; Université de Sherbrooke Sherbrooke: Sherbrooke, QC, Canada, 2009. [Google Scholar]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; Hommes, N.J.R.v.E. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef] [PubMed]
- Szczepanik, D.W.; Andrzejak, M.; Dyduch, K.; Żak, E.; Makowski, M.; Mazur, G.; Mrozek, J. A uniform approach to the description of multicenter bonding. Phys. Chem. Chem. Phys. 2014, 16, 20514–20523. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Andrzejak, M.; Dominikowska, J.; Pawełek, B.; Krygowski, T.M.; Szatylowicz, H.; Solà, M. The electron density of delocalized bonds (EDDB) applied for quantifying aromaticity. Phys. Chem. Chem. Phys. 2017, 19, 28970–28981. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Manoharan, M.; Wang, Z.X.; Kiran, B.; Jiao, H.; Puchta, R.; Hommes, N.J.R.v.E. Dissected nucleus-independent chemical shift analysis of pi-aromaticity and antiaromaticity. Org. Lett. 2001, 3, 2465–2468. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Nucleus-independent chemical shifts (NICS) as an aromaticity criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef] [PubMed]
- Fallah-Bagher-Shaidaei, H.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.V.R. Which NICS aromaticity index for planar π rings is best? Org. Lett. 2006, 8, 863–866. [Google Scholar] [CrossRef] [PubMed]
- Gershoni-Poranne, R.; Stanger, A. The NICS-XY-scan: Identification of local and global ring currents in multi-ring systems. Chem. Eur. J. 2014, 20, 5673–5688. [Google Scholar] [CrossRef]
- Peeks, M.D.; Claridge, T.D.; Anderson, H.L. Aromatic and antiaromatic ring currents in a molecular nanoring. Nature 2017, 541, 200–203. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; An, K.; Zhu, J. Triplet State Aromaticity: NICS Criterion, Hyperconjugation, and Charge Effects. Chem. Asian J. 2016, 11, 234–240. [Google Scholar] [CrossRef] [PubMed]
- Herges, R.; Geuenich, D. Delocalization of electrons in molecules. J. Phys. Chem. A 2001, 105, 3214–3220. [Google Scholar] [CrossRef]
- Geuenich, D.; Hess, K.; Köhler, F.; Herges, R. Anisotropy of the induced current density (ACID), a general method to quantify and visualize electronic delocalization. Chem. Rev. 2005, 105, 3758–3772. [Google Scholar] [CrossRef]
- Zhu, Q.; Chen, S.; Chen, D.; Lin, L.; Xiao, K.; Zhao, L.; Solà, M.; Zhu, J. The application of aromaticity and antiaromaticity to reaction mechanisms. Fundam. Res. 2023, 3, 926–938. [Google Scholar] [CrossRef]
- Orozco-Ic, M.; Soriano-Agueda, L.; Escayola, S.; Sundholm, D.; Merino, G.; Matito, E. Understanding Aromaticity in [5] Helicene-Bridged Cyclophanes: A Comprehensive Study. J. Org. Chem. 2024, 89, 2459–2466. [Google Scholar] [CrossRef] [PubMed]





| Compounds | ΔES-T | ΔES-D1 | ΔES-D2 |
|---|---|---|---|
| 1 | −44.2 | −168.8 | 23.6 |
| 2 | −21.6 | −269.3 | 140.2 |
| 3 | −36.0 | −155.1 | 24.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, S.; Yan, J.; Li, W.; Shuai, Z.; Zhu, J. Too Persistent to Resist: Aromaticity in 16e Osmapentalene Radicals Survives Regardless of Redox. Chemistry 2025, 7, 22. https://doi.org/10.3390/chemistry7010022
Pan S, Yan J, Li W, Shuai Z, Zhu J. Too Persistent to Resist: Aromaticity in 16e Osmapentalene Radicals Survives Regardless of Redox. Chemistry. 2025; 7(1):22. https://doi.org/10.3390/chemistry7010022
Chicago/Turabian StylePan, Shijie, Jun Yan, Weitang Li, Zhigang Shuai, and Jun Zhu. 2025. "Too Persistent to Resist: Aromaticity in 16e Osmapentalene Radicals Survives Regardless of Redox" Chemistry 7, no. 1: 22. https://doi.org/10.3390/chemistry7010022
APA StylePan, S., Yan, J., Li, W., Shuai, Z., & Zhu, J. (2025). Too Persistent to Resist: Aromaticity in 16e Osmapentalene Radicals Survives Regardless of Redox. Chemistry, 7(1), 22. https://doi.org/10.3390/chemistry7010022








