Electron Transfer Rates in Solution: Toward a Predictive First Principle Approach
Abstract
1. Introduction
2. Theory
2.1. The Kinetic Model
2.2. Solvent Reorganization Energy
3. Computational Details
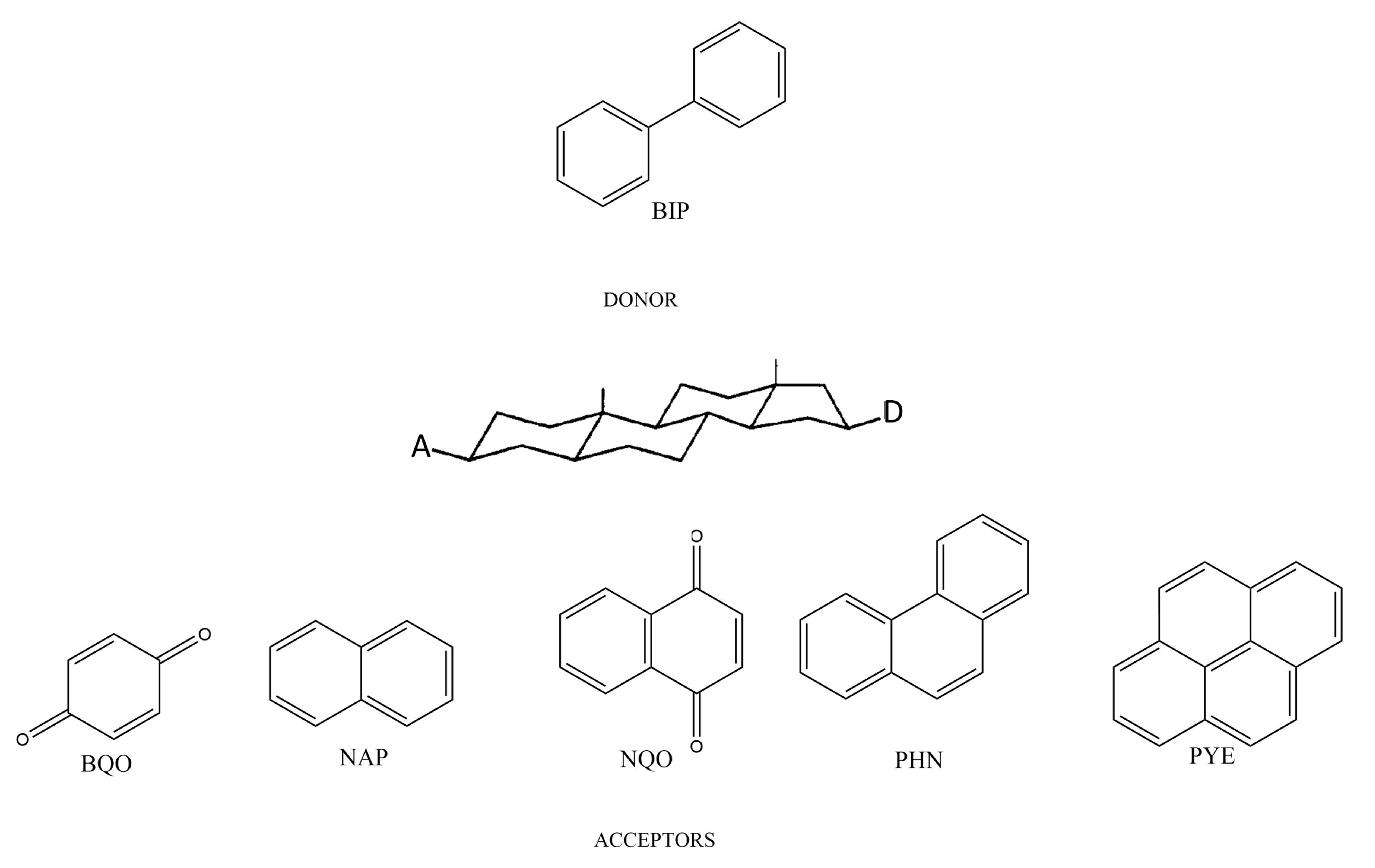
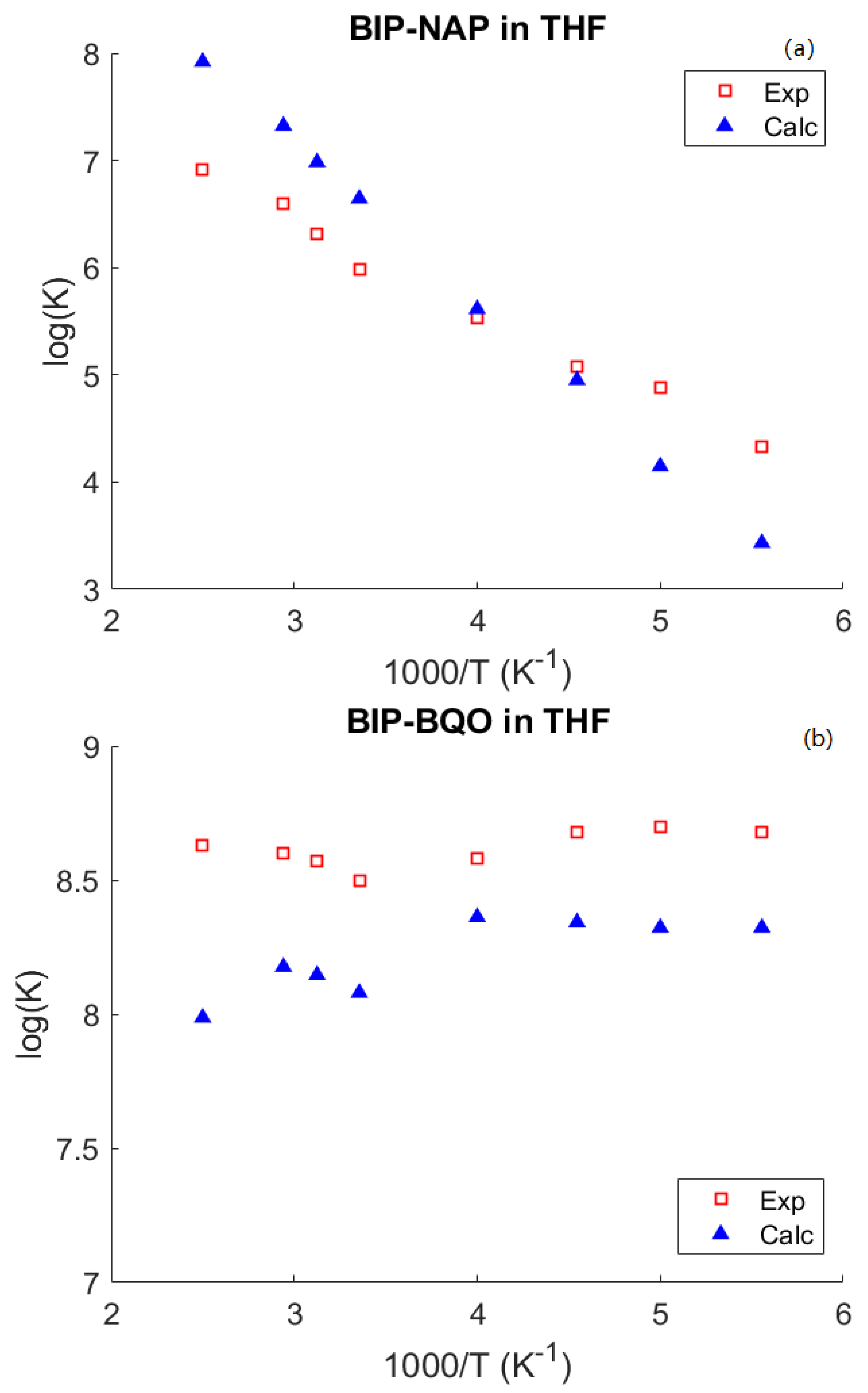
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Marcus, R.A. On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. I. J. Chem. Phys. 1956, 24, 966–978. [Google Scholar] [CrossRef]
- Marcus, R.A. Chemical and Electrochemical Electron-Transfer Theory. Annu. Rev. Phys. Chem. 1964, 15, 155–196. [Google Scholar] [CrossRef]
- Sumi, H.; Marcus, R.A. Dinamical Effects in Electron Transfer Reactions. J. Chem. Phys. 1986, 84, 4894. [Google Scholar] [CrossRef]
- Landi, A.; Borrelli, R.; Capobianco, A.; Velardo, A.; Peluso, A. Hole Hopping Rates in Organic Semiconductors: A Second-Order Cumulant Approach. J. Chem. Theory Comput. 2018, 14, 1594–1601. [Google Scholar] [CrossRef] [PubMed]
- Landi, A. Charge Mobility Prediction in Organic Semiconductors: Comparison of Second-Order Cumulant Approximation and Transient Localization Theory. J. Phys. Chem. C 2019, 123, 18804–18812. [Google Scholar] [CrossRef]
- Landi, A.; Borrelli, R.; Capobianco, A.; Velardo, A.; Peluso, A. Second-Order Cumulant Approach for the Evaluation of Anisotropic Hole Mobility in Organic Semiconductors. J. Phys. Chem. C 2018, 122, 25849–25857. [Google Scholar] [CrossRef]
- Akesson, E.; Walker, G.C.; Barbara, P.F. Dinamical Solvent Effects on Electron Transfer Rates in the Inverted Regime: Ultrafast Studies on the Betaines. J. Chem. Phys. 1991, 95, 4188. [Google Scholar] [CrossRef]
- Formosinho, S.J.; Arnaut, L.G.; Fausto, R. A Critical Assessment of Classical and Semi-classical Models for Electron Transfer Reactions in Solution. Prog. React. Kinet 1998, 23, 1–90. [Google Scholar]
- Levich, V.G. Present State of the Theory of Oxidation-Reduction in Solution; Interscience: New York, NY, USA, 1965; Volume 4. [Google Scholar]
- Dogonadze, R.; Kuznetsov, A.; Margishvili, T. The Present State of the Theory of Charge Transfer Processes in Condensed Phase. Electrochim. Acta 1980, 25, 1–28. [Google Scholar] [CrossRef]
- Kestner, N.; Logan, J.; Jortner, J. Thermal Electron Transfer Reactions in Polar Solvents. J. Phys. Chem. 1974, 78, 2148. [Google Scholar] [CrossRef]
- Jortner, J.; Bixon, M. Intramolecular Vibrational Excitations Accompanying Solvent-Controlled Electron Transfer Reactions. J. Chem. Phys. 1988, 88, 167. [Google Scholar] [CrossRef]
- Bixon, M.; Jortner, J. Electron Transfer—From Isolated Molecules to Biomolecules, Part One; John Wiley & Sons: New York, NY, USA, 1999; Volume 106. [Google Scholar]
- Zusman, L.D. Outer-Sphere Electron Transfer in Polar Solvents. Chem. Phys. 1980, 49, 295. [Google Scholar] [CrossRef]
- Sparpaglione, M.; Mukamel, S. Adiabatic vs. Nonadiabatic Electron Transfer and Longitudinal Solvent Dielectric Relaxation: Beyond the Debye Model. J. Phys. Chem. 1987, 91, 15. [Google Scholar] [CrossRef]
- Ovchinnikova, M.Y. Teor. Eksp. Kim. Theor. Exper. Chem. 1982, 17, 507. [Google Scholar] [CrossRef]
- Borrelli, R.; Peluso, A. The Temperature Dependence of Radiationless Transition Rates from Ab Initio Computations. Phys. Chem. Chem. Phys. 2011, 13, 4420–4426. [Google Scholar] [CrossRef]
- Schenck, C.; Parson, W.; Holten, D.; Windsor, M.W.; Sarai, A. Temperature Dependence of Electron Transfer Between Bacteriopheophytin and Ubiquinone in Protonated and Deuterated Reaction Centers of Rhodopseudomonas shaeroides. Biophys. J. 1981, 36, 479–489. [Google Scholar] [CrossRef]
- Kirmaier, C.; Holten, D.; Parson, W.W. Temperature and Detection-Wevelenght Dependence of the Picosecond Electron-Transfer Kinetics Mesured in Rhodopseudomonas shaeroides Reaction Centers. Resolution of New Spectral and Kinetic Components in the Primary Charge-Separation Process. Biochim. Biophys. Acta Bioenerg. 1985, 810, 33–48. [Google Scholar] [CrossRef]
- Leo, A.; Peluso, A. Electron Transfer Rate in Polar and Non-Polar Environments: A Generalization of Marcus’ Theory to Include an Effective Treatment of Tunneling Effects. J. Phys. Chem. Lett. 2022, 13, 9148–9155. [Google Scholar] [CrossRef]
- Landi, A.; Borrelli, R.; Capobianco, A.; Peluso, A. Transient and Enduring Electronic Resonances Drive Coherent Long Distance Charge Transport in Molecular Wires. J. Phys. Chem. Lett. 2019, 10, 1845–1851. [Google Scholar] [CrossRef]
- Landi, A.; Capobianco, A.; Peluso, A. Coherent Effects in Charge Transport in Molecular Wires: Toward a Unifying Picture of Long-Range Hole Transfer in DNA. J. Phys. Chem. Lett. 2020, 11, 7769–7775. [Google Scholar] [CrossRef]
- Peluso, A.; Caruso, T.; Landi, A.; Capobianco, A. The Dynamics of Hole Transfer in DNA. Molecules 2019, 24, 4044. [Google Scholar] [CrossRef]
- Landi, A.; Capobianco, A.; Peluso, A. The Time Scale of Electronic Resonance in Oxidized DNA as Modulated by Solvent Response: An MD/QM-MM Study. Molecules 2021, 26, 5497. [Google Scholar] [CrossRef]
- Kubo, R.; Toyozawa, Y. Application of the Method of Generating Function to Radiative and Non-Radiative Transitions of a Trapped Electron in a Crystal. Prog. Theor. Phys. 1955, 13, 160–182. [Google Scholar] [CrossRef]
- Lax, M. The Franck-Condon Principle and Its Application to Crystals. J. Chem. Phys. 1952, 20, 1752–1760. [Google Scholar] [CrossRef]
- Closs, G.L.; Calcaterra, L.T.; Green, N.J.; Penfield, K.W.; Miller, J.R. Distance, Stereoelectronic Effects, and the Marcus Inverted Region in Intramolecular Electron Transfer in Organic Radical Anions. J. Chem. Phys. 1989, 90, 3673–3683. [Google Scholar] [CrossRef]
- Liang, N.; Miller, J.R.; Closs, G.L. Correlating Temperature Dependence to Free Energy Dependence of Intramolecular Long-Range Electron Transfer. J. Am. Chem. Soc. 1989, 11, 8740–8741. [Google Scholar] [CrossRef]
- Parson, W.W. Effects of Free Energy and Solvent on Rates of Intramolecular Electron Transfer in Organic Radical Anions. J. Phys. Chem. A 2017, 121, 7297–7306. [Google Scholar] [CrossRef]
- Parson, W.W. Vibrational Relaxations and Dephasing in Electron-Transfer Reactions. J. Phys. Chem. 2016, 120, 11412–11418. [Google Scholar] [CrossRef]
- Parson, W.W. Electron-Transfer Dynamics in a Zn-Porphyrin-Quinone Cyclophane: Effects of Solvent, Vibrational Relaxations, and Conical Intersections. J. Phys. Chem. B 2018, 122, 3854–3863. [Google Scholar] [CrossRef]
- Parson, W.W. Temperature Dependence of the Rate of Intramolecular Electron Transfer. J. Phys. Chem. B 2018, 122, 8824–8833. [Google Scholar] [CrossRef]
- Mahan, B.H. Microscopic Reversibility and Detailed Balance. J. Chem. Educ. 1975, 52, 299–302. [Google Scholar] [CrossRef]
- Hopfield, J.J. Electron transfer between biological molecules by thermal activated tunneling. Proc. Natl. Acad. Sci. USA 1974, 71, 3640–3644. [Google Scholar] [CrossRef] [PubMed]
- Borrelli, R.; Peluso, A. Elementary Electron Transfer Reactions: From Basic Concepts to Recent Computational Advances. WIREs: Comput. Mol. Sci. 2013, 3, 542–559. [Google Scholar] [CrossRef]
- Rabalais, J.W.; Karlsson, L.; Werme, L.O.; Bergmark, T.; Siegbahn, K. Analysis of Vibrational Structure and Jahn-Teller Effects in the Electron Spectrum of Ammonia. J. Chem. Phys. 1973, 58, 3370–3372. [Google Scholar] [CrossRef]
- Wang, X.B.; Woo, H.K.; Wang, L.S. Vibrational Cooling in a Cold Ion Trap: Vibrationally Resolved Photoelectron Spectroscopy of Cold C60− Anions. J. Chem. Phys. 2005, 123, 051106. [Google Scholar] [CrossRef]
- Capobianco, A.; Carotenuto, M.; Caruso, T.; Peluso, A. The Charge-Transfer Band of an Oxidized Watson-Crick Guanosine-Cytidine Complex. Angew. Chem. Int. Ed. 2009, 48, 9526–9528. [Google Scholar] [CrossRef]
- Niu, Y.; Peng, Q.; Deng, C.; Gao, X.; Shuai, Z. Theory of Excited State Decays and Optical Spectra: Application to Polyatomic Molecules. J. Phys. Chem. A 2010, 114, 7817–7831. [Google Scholar] [CrossRef] [PubMed]
- Santoro, F.; Lami, A.; Improta, R.; Bloino, J.; Barone, V. Effective Method for the Computation of Optical Spectra of Large Molecules at Finite Temperature Including the Duschinsky and Herzberg-Teller Effect: The Qx Band of Porphyrin as A Case Study. J. Chem. Phys. 2008, 128, 224311. [Google Scholar] [CrossRef]
- Capobianco, A.; Borrelli, R.; Landi, A.; Velardo, A.; Peluso, A. Absorption Band Shapes of a Push-Pull Dye Approaching the Cyanine Limit: A Challenging Case for First Principle Calculations. J. Phys. Chem. A 2016, 120, 5581–5589. [Google Scholar] [CrossRef]
- Peluso, A.; Borrelli, R.; Capobianco, A. Photoelectron Spectrum of Ammonia, a Test Case for the Calculation of Franck–Condon Factors in Molecules Undergoing Large Geometrical Displacements upon Photoionization. J. Phys. Chem. A 2009, 113, 14831–14837. [Google Scholar] [CrossRef]
- Landi, A.; Landi, A.; Velardo, A.; Peluso, A. Efficient Charge Dissociation of Triplet Excitons in Bulk Heterojunction Solar Cells. ACS Appl. Energy Mater. 2022, 5, 10815–10824. [Google Scholar] [CrossRef]
- Landi, A.; Padula, D. Multiple Charge Separation Pathways in New-Generation Non-Fullerene Acceptors: A Computational Study. J. Mater. Chem. A 2021, 9, 24849–24856. [Google Scholar] [CrossRef]
- Velardo, A.; Borrelli, R.; Capobianco, A.; Landi, A.; Peluso, A. Disentangling Electronic and Vibrational Effects in the Prediction of Band Shapes for Singlet-Triplet Transitions. J. Phys. Chem. C 2019, 123, 14173–14179. [Google Scholar] [CrossRef]
- Marcus, R.A. Electrostatic Free Energy and Other Properties of States Having Nonequilibrium Polarization. II. J. Chem. Phys. 1956, 24, 979–989. [Google Scholar] [CrossRef]
- Matyushov, V.D. Solvent Reorganization Energy of Electron-Transfer Reactions in Polar Solvent. J. Chem. Phys. 2004, 120, 7532–7556. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Kim, K.; Jordan, K.D. Comparison of Density Functional and MP2 Calculations on the Water Monomer and Dimer. J. Phys. Chem. 1994, 98, 10089–10094. [Google Scholar] [CrossRef]
- Stephens, P.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Cramer, C.J. Essentials of Computational Chemistry: Theories and Models, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Miertiuš, S.; Scrocco, E.; Tomasi, J. Electrostatic Interaction of a Solute with a Continuum. A Direct Utilization of Ab Initio Molecular Potentials for the Prevision of Solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Matyushov, D. Software Package for the Solvation Thermodynamics of Biomolecules. 2007. Available online: https://skysonginnovations.com/technology/software-package-for-the-solvation-thermodynamics-of-biomolecules/ (accessed on 16 December 2022).
- Singh, U.C.; Kollman, P.A. An Approach to Computing Electrostatic Charges for Molecules. J. Comput. Chem. 1984, 5, 129–145. [Google Scholar] [CrossRef]
- Capobianco, A.; Borrelli, R.; Noce, C.; Peluso, A. Franck-Condon Factors in Curvilinear Coordinates: The Photoelectron Spectrum of Ammonia. Theor. Chem. Acc. 2012, 131, 1181. [Google Scholar] [CrossRef]
- Dormand, J.R.; Prince, P.J. A Family of Embedded Runge-Kutta Formulae. J. Comput. Appl. Math. 1980, 6, 19–26. [Google Scholar] [CrossRef]
- Simon, J.D. Time-Resolved Studies of Solvation in Polar Media. Res. Chem. Acc. 1988, 21, 128–134. [Google Scholar] [CrossRef]
- Liang, N.; Miller, J.R.; Closs, G.L. Temperature-Independent Long-Range Electron Transfer Reactions in the Marcus Inverted Region. J. Am. Chem. Soc. 1990, 112, 5353–5354. [Google Scholar] [CrossRef]
- Metz, D.J.; Glines, A. Density, Viscosity and Dielectric Constant of Tetrahydrofuran Between -78 and 30. J. Chem. Phys. 1966, 11973. [Google Scholar] [CrossRef]

| k(s) | ||||||
|---|---|---|---|---|---|---|
| Acceptor | Equation (8) | SolvMol | Theo | Exp | ||
| BQO | −2.4 | 0.78 | 0.71 | - | 1.2 × 10 | (2.5 ± 0.3) × 10 |
| NAP | −0.03 | 0.74 | 0.71 | 0.2 | 4.4 × 10 | (1.5 ± 0.5) × 10 |
| NQO | −2.1 | 0.73 | 0.64 | - | 6.7 × 10 | (3.8 ± 1) × 10 |
| PHN | −0.1 | 0.71 | 0.68 | 0.2 | 1.3 × 10 | (1.2 ± 0.2) × 10 |
| PYE | −0.5 | 0.66 | 0.68 | 0.01 | 4.0 × 10 | (1.5 ± 0.5) × 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leo, A.; Ambrosio, F.; Landi, A.; Peluso, A. Electron Transfer Rates in Solution: Toward a Predictive First Principle Approach. Chemistry 2023, 5, 97-105. https://doi.org/10.3390/chemistry5010008
Leo A, Ambrosio F, Landi A, Peluso A. Electron Transfer Rates in Solution: Toward a Predictive First Principle Approach. Chemistry. 2023; 5(1):97-105. https://doi.org/10.3390/chemistry5010008
Chicago/Turabian StyleLeo, Anna, Francesco Ambrosio, Alessandro Landi, and Andrea Peluso. 2023. "Electron Transfer Rates in Solution: Toward a Predictive First Principle Approach" Chemistry 5, no. 1: 97-105. https://doi.org/10.3390/chemistry5010008
APA StyleLeo, A., Ambrosio, F., Landi, A., & Peluso, A. (2023). Electron Transfer Rates in Solution: Toward a Predictive First Principle Approach. Chemistry, 5(1), 97-105. https://doi.org/10.3390/chemistry5010008






