Abstract
Molecular motors convert light and thermal energies into mechanical work, offering good opportunities to design novel molecular devices. Among them, molecular motors alternate a photoisomerization and a thermal helix inversion to achieve unidirectional rotation. The rotational speed is limited by the helix inversion step, which in turn is governed by a barrier in the electronic ground state. In this work, we systematically study the solvation effect on the thermal process of selected molecular motors, comparing reaction barriers obtained from both density functional theory (DFT) in the isolated system and umbrella sampling within a hybrid quantum mechanics/molecular mechanics (QM/MM) model in solution. We find more prominent solvation effects on those molecular motors with larger dipole moments. The results could provide insight into how to functionalize molecular motors to speed up their rotation.
1. Introduction
Molecular machines have been extensively studied in recent decades due to their broad applicability in fields as diverse as drug delivery, electronic devices, and photoswitchable catalysis [1,2,3,4,5]. Such molecules process at least two configurations that are switchable under external stimuli. In the so-called molecular motors [6], the external energy can be converted into mechanical movement, similar to some fiber-based [7,8] or nanoparticle-based artificial muscles [9]. The group of the Nobel laurate Feringa has successfully synthesized a large number of molecular motors, aiming at finding mechanically more efficient transformations; the last two decades saw already three generations of molecular systems with increasingly rotational speedup [10,11,12,13,14,15]. Such molecular motors combine a photoisomerization and a thermal helix inversion step in an alternate fashion, so that unidirectional motion is achieved (see Figure 1). The thermal step, in which two configurations convert each other by the inversion of the central C=C bond when the molecule is heated, is slower than the photochemical one by a few orders of magnitude. Thus, different functional groups have been suggested to reduce the reaction barrier of this thermal inversion process, both experimentally [11,16] as well as theoretically [17,18,19].
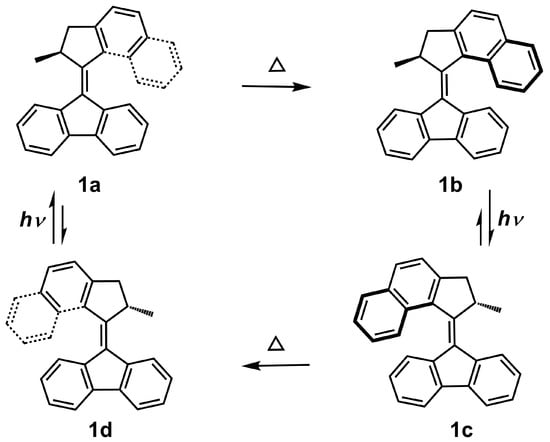
Figure 1.
Schematic illustration of unidirectional rotation in 1, consisting of two thermal helix inversion processes and two photoisomerizations, thus giving four configurations (1a)–(1d).
Remarkably, not only the molecular properties but also the solvent employed can play an important role on the speed of the unidirectional motion [20,21,22,23]. Thus, it would be interesting to investigate how the solvent affects the helix inversion step of molecular motors. Theoretically, solvation effects can be investigated with both implicit and explicit models. In implicit models, the solvation effect is calculated as electrostatic interactions between the dipoles with low cost, but the intermolecular interactions (e.g., hydrogen bonds) are missing [24]. Explicit models instead treat all the molecules in the calculation on the same footing; therefore, intermolecular interactions can be accurately treated. However, treating solvent and solute at the same quantum mechanical level of theory is computationally demanding. Therefore, divide-and-conquered approaches, such as the combination of quantum mechanical with molecular mechanical calculations (QM/MM) [25], have been introduced. Within the framework of a QM/MM model, a reaction barrier could be determined by comparing the energy difference between different configurations and the transition state, but the search for a transition state is not straightforward. A powerful method to simulate the reaction barrier between the reactant and the product, avoiding explicit transition state optimizations, is umbrella sampling (US) [26,27]. Here, a bias potential is applied to reach the coordinates of different states along the reaction space, which is split into different windows to sample the reaction path individually [28], thus mimicking a reaction path. In each of the windows, molecular dynamics simulations can be performed within a constraint bias potential until sufficient overlap between the probability distributions along the reaction coordinates is reached [28].
In the present contribution, we investigate the solvation effect on the helix inversion step between the two involved states of molecular motors using US within a QM/MM framework. The systems under investigation are shown in Figure 2. Considering the solubility in all motors, dimethyl sulfoxide (DMSO) is selected as the solvent due to its good solvation properties reported in a previous experimental study [29]. Here, we study the role of DMSO in several motors with different dipole moments, achieved as a result of placing different functional groups in either the stator (lower half) or the rotator (upper half). The suggested motors are derivatives of the parent second-generation molecular structure 1a (recall Figure 1), for which the photoisomerization step has been investigated by us recently [30].
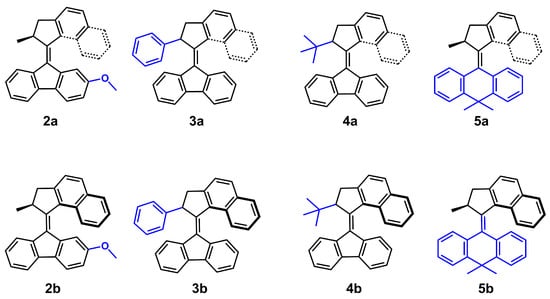
Figure 2.
Structures of selected molecular motors, 2–4 in their different configurations, noted as a and b, respectively.
2. Computational Methods
2.1. Quantum Chemical Calculations
The initial geometry of the transition state 1ts between 1a and 1b in the gas phase was obtained using the Nudged Elastic Band (NEB) approach [31,32], at the BP86/def2-SVP level of theory [33,34,35] using TURBOMOLE 7.2 [36]. The structures of 1a, 1b, and 1ts were optimized in the gas phase at the B3LYP/cc-pVDZ level with Grimme’s dispersion correction [37] using a Gaussian 16, Revision A.03 software package [38], followed by a frequency calculation to confirm the nature of the critical point (Tables S1–S15). The same protocol was applied in the geometry optimizations of the other molecular motors, 2–5. The Gibbs free energies at B3LYP-D3/cc-pVDZ level were used to predict the thermal reaction barrier in comparison with their speed of thermal isomerization. The desired level of accuracy in the reaction barrier of the helix inversion depends on the selection of the functionals in DFT, which had been discussed extensively by Head-Gordon and his coworker [39]. Therefore, in this study, we validated the accuracy of the DFT calculations by the comparison with the domain-based local pair natural orbital coupled-cluster method with single and double excitations (DLPNO-CCSD) [40,41,42,43] with the cc-pVDZ basis set using ORCA program, version 4.2.1 [44,45] on the relative energies of the different configurations of 1.
2.2. Molecular Dynamics Simulations
The general AMBER force field (GAFF) [46] was used to perform molecular dynamics (MD) simulations of the systems solvated by DMSO with the force field adopted from Ref. [47] in a 25 Å truncated box. The system was heated to 300 K during the 100 ps simulations in an NVT ensemble after it was converged in the optimization. The equilibrium step was performed in 1 ns in an NPT ensemble when the pressure was set to 1 bar before the production calculations were carried out. The production calculations were simulated in the NPT ensemble with the Berendsen thermostat for 10 ns after the equilibrium was reached. The time step was 0.5 fs in all MD simulations using the AMBER17 suite [48].
2.3. QM/MM Calculations
US was employed to simulate the thermal helix inversion process in the framework of QM/MM. The solvent molecules were treated classically, coming from the MD simulations, while the molecular motors were simulated quantum mechanically, with the self-consistent-charge density-functional tight-binding method (SCC-DFTB) within the DFTB3 formulation [49,50]. The time step was set as 0.5 fs in the NPT ensemble, and the snapshots were collected every 50 fs during the 2ps-steered QM/MM MD dynamics. The cut-off in describing the electrostatic interaction between QM and MM regions was set as 10 Å. The reaction coordinates in the US were the dihedral angles of the inversion in C=C bond, which were used in the MD simulations with a harmonic restraint constant of 200 kcal mol degrees. The time step was 0.1 fs in each window for 20 ps simulations with the force constant of 500 kcal mol degrees. The variational free energy profile (VFEP) method implemented with the maximum likelihood principle [51,52] was employed to simulate the energy profile. All calculations were performed using the AMBER:DFTB3 scheme implemented in AMBER17 [48].
3. Results and Discussion
The speed of the helix inversion in molecular motors depends on the reaction barrier. This could be calculated either by QM in the gas phase or by QM/MM with the solvent included explicitly. We shall use both approaches to compare the geometries obtained and understand the effect of the solvents on the helix inversion of the chosen molecular motors.
3.1. Helix Inversion in the Gas Phase
Different structures with various functional groups were selected based on a parental molecular motor (1). The dipole moments of the selected motors are listed in Table S16 calculated at the B3LYP-D3/cc-pVDZ level in the gas phase. The accurate DLPNO-CCSD method is used to calculate a reference inversion barrier to be compared with values from DFT. Depicted in Figure 3 are the inversion barriers of 22.2 and 21.1 kcal/mol obtained with DFT and DLPNO-CCSD, respectively. Both calculations reproduce satisfactorily the experimentally measured barrier of 20.3 kcal/mol [12]. The 1b configuration is 3.1 or 4.3 kcal/mol more stable than 1a configuration at B3LYP-D3 or DLPNO-CCSD levels, respectively. We conclude that both methods provide similar reaction barriers and relative energies between the two configurations and thus justify that we shall employ the B3LYP functional to determine the reaction barriers of the other motors in solution, expecting similar accuracy to what DLPNO-CCSD would provide.
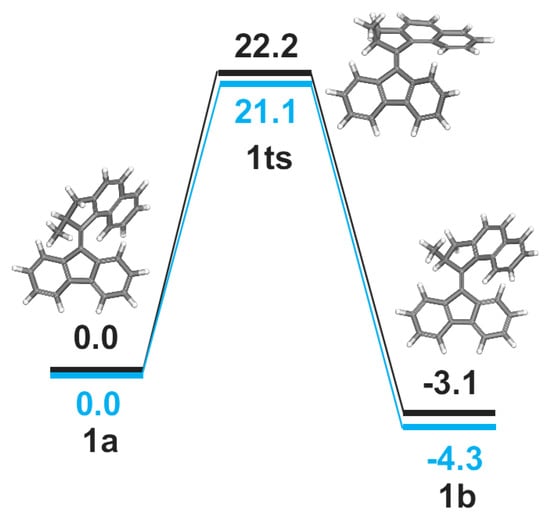
Figure 3.
The activation energy of the helix inversion between 1a and 1b configurations calculated at B3LYP-D3/cc-pVDZ (in black) and DLPNO-CCSD/cc-pVDZ (in blue) levels.
The rotational speed is expected to be faster when the inversion barrier is reduced—-as observed in some molecular motors [11]. The B3LYP-D3 calculated reaction barriers of the other molecular motors (2–5) are depicted in Figure 4. The reaction barrier of 2 is similar to that of 1, demonstrating that the methoxy group in the stator part (lower half of 2) does not substantially affect the thermal reaction. The inversion barrier of 3 is 23.5 kcal/mol, which is slightly higher than that of 1, in line with the observed slower rotation in 3 [53], caused by the sterically demanding phenyl group in 3.
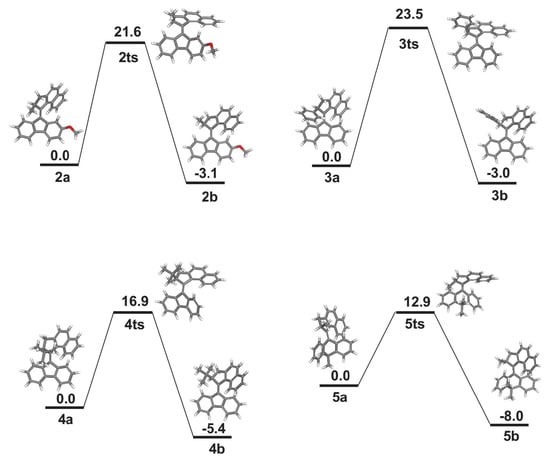
Figure 4.
Activation energies of the helix inversion between a and b configurations in 2–5 calculated at the B3LYP-D3/cc-pVDZ level.
The inversion barriers of 4 and 5 are 16.9 and 12.9 kcal/mol, which are much lower than that of 1, in agreement with the observed half-life of 5.7 ms and 8.0 ns, respectively [13,54]. It means that the rotational speed of 5 is increased tremendously when the inversion barrier is reduced by about 4 kcal/mol from 4. This indicates that the reduction of the reaction barrier could improve the rotational process significantly. The energy difference between the two stable configurations 5a and 5b is 8.0 kcal/mol, which is larger than that in the other molecular motors. The larger energy difference between the two configurations could be another factor that makes 5 rotate much faster. These results indicate that the performance of the unidirectional motion of the molecular motor is expected to be improved by both reducing the inversion barrier and stabilizing the b configuration.
3.2. Helix Inversion in Solution
As it is expensive to include the solvent explicitly in the simulation, we treat the molecular motor and the solvent molecules separately. Umbrella sampling is carried out based on trajectories from classical MD simulations, which are performed to locate the orientation of the solvents around the molecular motors in the equilibrium state. The radial distribution and orientation of the solvent molecules are then analyzed, as it will be discussed next.
3.2.1. Dihedral Angle Distributions
The evolution of the dihedral angles in the two configurations 1a and 1b as obtained from classical MD simulations can be found in Figure 5. Black lines indicate the dihedral angle values of 1a and 1b obtained from the DFT optimized geometries in the gas phase. This value lies in the center of the oscillation of 1a but is slightly above the center of the distribution oscillation in 1b by about 5 degrees. The oscillations are between 30 and 60 degrees (1a) and between −60 to −30 degrees (1b), which are symmetric at 0 degrees.
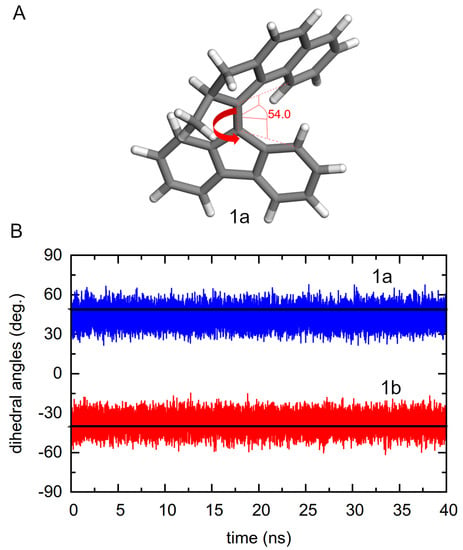
Figure 5.
Definition of the C=C dihedral angles (A) and its evolution in 1a (in blue) and 1b (in red) from the MD simulations (B). Values from the DFT optimized geometries in the gas phase are shown with black lines.
The evolution of the torsion distributions for the other molecular motors 2–5 during 40 ns is presented in Figure 6, with a and b configurations in blue and red, respectively. The symmetric character in 2–4 is similar to 1 in DMSO solution. Exceptions are found in 5a and 5b configurations in the gas phase, whose values are smaller than that in the other motors, as shown by the closer black lines in Figure 6D. This can be explained by the fact that the stators are rigid in the 2–4 motors, while the six-membered ring in the middle of the stator of 5 makes it bend more than the other motors. This indicates that the planarity in the stator could affect the stability of the molecular motors in the gas phase. The dihedral evolution in 2–4 motors is similar to 1 even with different rotators. This means that the flexibility in the rotator part does not seem to affect the torsion in a and b configurations.
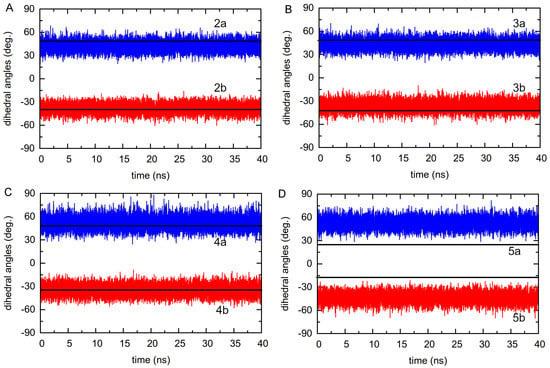
Figure 6.
The evolution of the dihedral angles of a (in blue) and b (in red) configurations for (A) 2, (B) 3, (C) 4, and (D) 5 in MD simulations with the optimized geometries in the gas phase illustrated with black lines.
In the classical MD simulations in solution, the dihedral angles of the a and b configurations are stable, oscillating between 30 to 60 and −20 to −50 degrees, respectively. In the US simulations, we convert the a into b configuration gradually in different windows, in which dihedral angles change from 40 to −40 degrees.
3.2.2. Solvent Distributions
Next, we will analyze the distribution of the solvent molecules around the molecular motors. To that aim, the radial distribution of the solvent DMSO is presented as the distance from sulfur or oxygen atoms of DMSO to C atoms of the molecular motors, noted as R(S-C) or R(O-C), respectively. The radial distribution functions in these five motors g(S-C) and g(O-C) are presented in Figure 7. One can see that the a and b configurations have similar distributions of R(S-C) in all five molecules, within the first and second solvation shells at 5.0 and 9.4 Å, respectively, due to the low polarizability of the system. Comparing between the radial distributions g(S-C) and g(O-C) in the two configurations, we find a broader distribution in the first solvation shell with a shoulder around 3.8 Å in g(O-C). This indicates that the O atoms are less ordered than the S atoms in DMSO around the motors, since S atoms of DMSO and the molecular motors are weakly interacting due to dispersion interactions. The radial distribution functions are quite similar in 1–5, which implies that there is a small difference in the short-range interactions between DMSO and molecular motors.
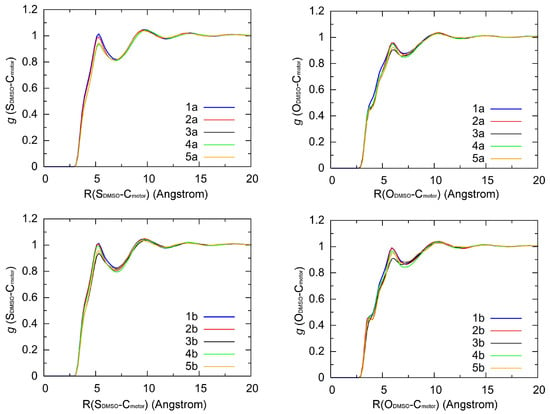
Figure 7.
Radial distribution functions of R(S-C) and R(O-C) as obtained from MD simulations of motors 1–5 in DMSO.
3.2.3. Inversion Reaction Paths
As the analysis of the C=C central bond of Figure 5B shows, the inversion angles change from 45 to −45 degrees during the helix inversion from 1a to 1b. Therefore, we have constrained the torsion angles to change from 45 to −45 degrees in 40 windows gradually during the US simulations within the QM/MM model. The obtained free energy profile along the inversion path as a function of the dihedral angles is shown in Figure 8 in black for motor 1. The reaction barrier is about 25 kcal/mol at the US-QM/MM level of theory, which is about 3 kcal/mol higher than that calculated by DFT method in the gas phase. The agreement shows that our models are robust; however, the small difference stems from the employed solvation model and the computational method. Within the QM/MM, the intermolecular interactions between the molecular motor and DMSO are included correctly, as opposed to the gas phase. In contrast, the energy barrier is calculated with a semi-empirical method, DFTB3, in the QM/MM model, which is less accurate than DFT. The reaction barrier could be made more accurate if the DFT method is used in the QM part in QM/MM MD simulations, at the expense of computational time. However, based on the US-QM/MM simulations, we consider DFTB3 a good compromise between the cost and the accuracy.
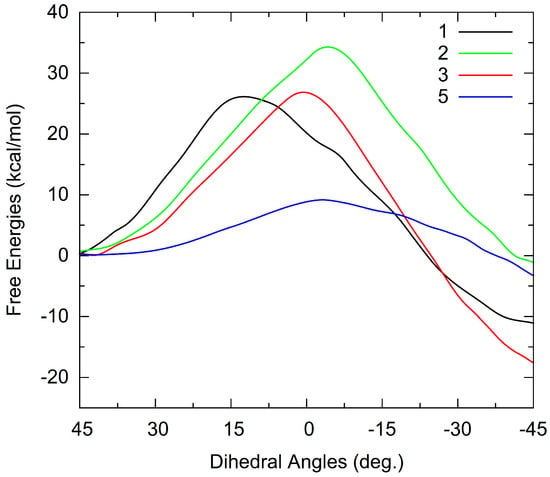
Figure 8.
Reaction paths of the helix inversion of 1 (in black), 2 (in green), 3 (in red), and 5 (in blue) simulated by umbrella sampling within a QM/MM model.
The product, 1b, is predicted to be 10 kcal/mol more stable than 1a within the US-QM/MM simulations—in comparison with 3 kcal/mol from the DFT calculations in the gas phase. This indicates that the solvent stabilizes the product. The higher stability obtained from the US-QM/MM simulations in the solution is also observed in 3b, but not in 2 and 5. The energy difference between a and b configurations of 2 and 5 in QM/MM calculations is similar to that obtained by DFT calculations because of their small dipole moments. The motors 2 and 5 are less affected by the polarization of DMSO in the US-QM/MM model, resulting in a negligible solvation effect. In contrast, the motors 1 and 3 are more polarized by DMSO, thus stabilizing the product b configuration more in the solution.
The reaction barriers for the motors 1 and 3 are about 25 kcal/mol, slightly smaller than that in 2 by about 8 kcal/mol. For 5, the barrier is about 10 kcal/mol, about 3 kcal/mol smaller than that obtained in the gas phase by DFT calculations. In general, we conclude that the reaction barriers obtained from US-QM/MM simulations resemble that obtained from the DFT calculations in the gas phase.
4. Conclusions
The helix inversion process of some selected molecular motors with different dipole moments has been simulated in solution using a hybrid QM/MM approach and compared with values in the gas phase obtained from DFT calculations. We note that dihedral angles of two configurations (a and b) are symmetrical about the central C=C bond in both gas phase and solution. Calculated reaction barriers of the helix inversion process obtained with DFT in the gas phase and umbrella sampling in the solution are comparable, indicating that the solvation effect on this reaction is negligible for the solvent employed, DMSO, particularly for the motors with small dipole moments. The solvation effect is more significant for molecular motors displaying larger dipole moments, providing slightly larger differences in the reaction barrier between the gas phase and solution. Based on the analysis of the solvent orientation in the first solvation shell of the motors by radial distribution functions, it is found that S atoms of the solvent point to the motors due to the weak dispersion interactions between the aromatic rings of the motors and S atoms of DMSO. In conclusion, we expect that the computational simulations of the thermal reaction highlighting the solvation effect on the helix inversion provide insight into how to design molecular motors with faster rotational speed.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/chemistry4010016/s1: Tables S1–S16: optimized coordinates and dipole moments of motors in a and b configurations and their transition state.
Author Contributions
Methodology, J.W. and L.G.; formal analysis, J.W.; investigation, J.W.; resources, J.W.; data curation, J.W.; writing—original draft preparation, J.W.; writing—review and editing, L.G. and M.Z.; visualization, J.W.; supervision, L.G. and M.Z.; project administration, J.W.; funding acquisition, J.W. and L.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China (22173017), the Austrian Science Fund (M2709), and the Fundamental Research Funds for the Central Universities (2232021A-06).
Data Availability Statement
Data is available upon reasonable request.
Acknowledgments
We thank Pedro A. Sánchez Murcia and Boris Maryasin for fruitful discussions and the Vienna Scientific Cluster (VSC) for allocation of computer resources.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DFT | Density Functional Theory |
| QM/MM | Quantum Mechanics/Molecular Mechanics |
| US | Umbrella Sampling |
References
- García-López, V.; Liu, D.; Tour, J.M. Light-Activated Organic Molecular Motors and Their Applications. Chem. Rev. 2019, 120, 79–124. [Google Scholar] [CrossRef] [PubMed]
- van Dijk, L.; Tilby, M.J.; Szpera, R.; Smith, O.A.; Bunce, H.A.P.; Fletcher, S.P. Molecular machines for catalysis. Nat. Rev. Chem. 2018, 2, 1–18. [Google Scholar] [CrossRef]
- Lancia, F.; Ryabchun, A.; Katsonis, N. Life-like motion driven by artificial molecular machines. Nat. Rev. Chem. 2019, 3, 536–551. [Google Scholar] [CrossRef]
- Song, T.J.; Liang, H.J. Capability of DNA-fueled molecular machine in tuning association rate of DNA-functionalized gold nanoparticles. Chin. J. Polym. Sci. 2013, 31, 1183–1189. [Google Scholar] [CrossRef]
- Feng, Y.; Ovalle, M.; Seale, J.S.W.; Lee, C.K.; Kim, D.J.; Astumian, R.D.; Stoddart, J.F. Molecular Pumps and Motors. J. Am. Chem. Soc. 2021, 143, 5569–5591. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Leung, F.K.C.C.; Stuart, M.C.A.; Kajitani, T.; Fukushima, T.; Van Der Giessen, E.; Feringa, B.L. Artificial muscle-like function from hierarchical supramolecular assembly of photoresponsive molecular motors. Nat. Chem. 2018, 10, 132–138. [Google Scholar] [CrossRef]
- Gao, P.; Li, J.; Shi, Q. A Hollow Polyethylene Fiber-Based Artificial Muscle. Adv. Fiber Mater. 2019, 1, 214–221. [Google Scholar] [CrossRef]
- Li, L.; Wang, H. Unipolar-stroke Electrochemical Artificial Muscles. Adv. Fiber Mater. 2021, 3, 147–148. [Google Scholar] [CrossRef]
- Zhang, Q.; Rao, S.J.; Xie, T.; Li, X.; Xu, T.Y.; Li, D.W.; Qu, D.H.; Long, Y.T.; Tian, H. Muscle-like Artificial Molecular Actuators for Nanoparticles. Chem 2018, 4, 2670–2684. [Google Scholar] [CrossRef]
- Koumura, N.; Zijlstra, R.W.J.; van Delden, R.A.; Harada, N.; Feringa, B.L. Light-driven monodirectional molecular rotor. Nature 1999, 401, 152–155. [Google Scholar] [CrossRef]
- Pijper, D.; van Delden, R.A.; Meetsma, A.; Feringa, B.L. Acceleration of a Nanomotor: Electronic Control of the Rotary Speed of a Light-Driven Molecular Rotor. J. Am. Chem. Soc. 2005, 127, 17612–17613. [Google Scholar] [CrossRef] [PubMed]
- Vicario, J.; Meetsma, A.; Feringa, B.L. Controlling the speed of rotation in molecular motors. Dramatic acceleration of the rotary motion by structural modification. Chem. Commun. 2005, 2005, 5910–5912. [Google Scholar] [CrossRef] [PubMed]
- Bauer, J.; Hou, L.; Kistemaker, J.C.; Feringa, B.L. Tuning the rotation rate of light-driven molecular motors. J. Org. Chem. 2014, 79, 4446–4455. [Google Scholar] [CrossRef]
- Kistemaker, J.C.; Štacko, P.; Roke, D.; Wolters, A.T.; Heideman, G.H.; Chang, M.C.; Van Der Meulen, P.; Visser, J.; Otten, E.; Feringa, B.L. Third-Generation Light-Driven Symmetric Molecular Motors. J. Am. Chem. Soc. 2017, 139, 9650–9661. [Google Scholar] [CrossRef]
- Pfeifer, L.; Scherübl, M.; Fellert, M.; Danowski, W.; Cheng, J.; Pol, J.; Feringa, B.L. Photoefficient 2nd generation molecular motors responsive to visible light. Chem. Sci. 2019, 10, 8768–8773. [Google Scholar] [CrossRef]
- Štacko, P.; Kistemaker, J.C.M.; van Leeuwen, T.; Chang, M.C.; Otten, E.; Feringa, B.L. Locked synchronous rotor motion in a molecular motor. Science 2017, 356, 964–968. [Google Scholar] [CrossRef]
- Nikiforov, A.; Gamez, J.A.; Thiel, W.; Filatov, M. Computational Design of a Family of Light-Driven Rotary Molecular Motors with Improved Quantum Efficiency. J. Phys. Chem. Lett. 2016, 7, 105–110. [Google Scholar] [CrossRef] [PubMed]
- Filatov, M.; Paolino, M.; Min, S.K.; Choi, C.H. Design and photoisomerization dynamics of a new family of synthetic 2-stroke light driven molecular rotary motors. Chem. Commun. 2019, 55, 5247–5250. [Google Scholar] [CrossRef]
- Feng, M.; Gilson, M.K. Mechanistic analysis of light-driven overcrowded alkene-based molecular motors by multiscale molecular simulations. Phys. Chem. Phys. Chem. 2021, 23, 8525–8540. [Google Scholar] [CrossRef]
- Klok, M.; Janssen, L.P.; Browne, W.R.; Feringa, B.L. The influence of viscosity on the functioning of molecular motors. Faraday Discuss. 2009, 143, 319–334. [Google Scholar] [CrossRef]
- Lubbe, A.S.; Kistemaker, J.C.; Smits, E.J.; Feringa, B.L. Solvent effects on the thermal isomerization of a rotary molecular motor. Phys. Chem. Phys. Chem. 2016, 18, 26725–26735. [Google Scholar] [CrossRef] [PubMed]
- Conyard, J.; Stacko, P.; Chen, J.; McDonagh, S.; Hall, C.R.; Laptenok, S.P.; Browne, W.R.; Feringa, B.L.; Meech, S.R. Ultrafast Excited State Dynamics in Molecular Motors: Coupling of Motor Length to Medium Viscosity. J. Phys. Chem. A 2017, 121, 2138–2150. [Google Scholar] [CrossRef] [PubMed]
- Lubbe, A.S.; Böhmer, C.; Tosi, F.; Szymanski, W.; Feringa, B.L. Molecular Motors in Aqueous Environment. J. Org. Chem. 2018, 83, 11008–11018. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, H.; Wu, T.; Wang, Q.; Van Der Spoel, D. Comparison of Implicit and Explicit Solvent Models for the Calculation of Solvation Free Energy in Organic Solvents. J. Chem. Theory Comput. 2017, 13, 1034–1043. [Google Scholar] [CrossRef] [PubMed]
- Monard, G.; Merz, K.M. Combined Quantum Mechanical/Molecular Mechanical Methodologies Applied to Biomolecular Systems. Acc. Chem. Res. 1999, 32, 904–911. [Google Scholar] [CrossRef]
- Noh, S.Y.; Notman, R. Comparison of umbrella sampling and steered molecular dynamics methods for computing free energy profiles of aromatic substrates through phospholipid bilayers. J. Chem. Phys. 2020, 153, 034115. [Google Scholar] [CrossRef]
- Zhang, Y.; Voth, G.A. Combined Metadynamics and Umbrella Sampling Method for the Calculation of Ion Permeation Free Energy Profiles. J. Chem. Theory Comput. 2011, 7, 2277–2283. [Google Scholar] [CrossRef][Green Version]
- Kästner, J. Umbrella sampling. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 932–942. [Google Scholar] [CrossRef]
- Wezenberg, S.J.; Feringa, B.L. Supramolecularly Directed Rotary Motion in a Photoresponsive Receptor. Nat. Commun. 2018, 9, 1984. [Google Scholar] [CrossRef]
- Wen, J.; Mai, S.; Gonzalez, L. Non-Adiabatic Dynamics Simulations of a Light-Driven Molecular Motor in Solution. ChemRxiv 2021. [Google Scholar] [CrossRef]
- Mills, G.; Jónsson, H. Quantum and thermal effects in H2 dissociative adsorption: Evaluation of free energy barriers in multidimensional quantum systems. Phys. Rev. Lett. 1994, 72, 1124–1127. [Google Scholar] [CrossRef] [PubMed]
- Henkelman, G.; Jónsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822–8824. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Phys. Chem. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- TURBOMOLE V7.2 2017, a Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007. TURBOMOLE GmbH, Since 2007. Available online: http://www.turbomole.com (accessed on 30 June 2017).
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision A.03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Guo, Y.; Riplinger, C.; Becker, U.; Liakos, D.G.; Minenkov, Y.; Cavallo, L.; Neese, F. Communication: An improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method [DLPNO-CCSD(T)]. J. Chem. Phys. 2018, 148, 011101. [Google Scholar] [CrossRef]
- Riplinger, C.; Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 2013, 138, 034106. [Google Scholar] [CrossRef]
- Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef]
- Saitow, M.; Becker, U.; Riplinger, C.; Valeev, E.F.; Neese, F. A new near-linear scaling, efficient and accurate, open-shell domain-based local pair natural orbital coupled cluster singles and doubles theory. J. Chem. Phys. 2017, 146, 164105. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Software update: The ORCA program system, version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Wang, B.; Merz, K.M. A fast QM/MM (quantum mechanical/molecular mechanical) approach to calculate nuclear magnetic resonance chemical shifts for macromolecules. J. Chem. Theory Comput. 2006, 2, 209–215. [Google Scholar] [CrossRef]
- Fox, T.; Kollman, P.A. Application of the RESP methodology in the parametrization of organic solvents. J. Phys. Chem. B 1998, 102, 8070–8079. [Google Scholar] [CrossRef]
- Case, D.; Cerutti, D.; Cheatham, T., III; Darden, T.; Duke, R.; Giese, T.; Gohlke, H.; Goetz, A.; Greene, D. AMBER 2017; University of California: San Francisco, CA, USA, 2017. [Google Scholar]
- Seabra, G.D.M.; Walker, R.C.; Elstner, M.; Case, D.A.; Roitberg, A.E. Implementation of the SCC-DFTB method for hybrid QM/MM simulations within the Amber molecular dynamics package. J. Phys. Chem. A 2007, 111, 5655–5664. [Google Scholar] [CrossRef]
- Gaus, M.; Cui, Q.; Elstner, M. DFTB3: Extension of the self-consistent-charge density-functional tight-binding method (SCC-DFTB). J. Chem. Theory Comput. 2011, 7, 931–948. [Google Scholar] [CrossRef]
- Lee, T.S.; Radak, B.K.; Pabis, A.; York, D.M. A new maximum likelihood approach for free energy profile construction from molecular simulations. J. Chem. Theory Comput. 2013, 9, 153–164. [Google Scholar] [CrossRef]
- Lee, T.S.; Radak, B.K.; Huang, M.; Wong, K.Y.; York, D.M. Roadmaps through Free Energy Landscapes Calculated Using the Multidimensional vFEP Approach. J. Chem. Theory Comput. 2014, 10, 24–34. [Google Scholar] [CrossRef]
- Pollard, M.M.; Klok, M.; Pijper, D.; Feringa, B.L. Rate Acceleration of Light-Driven Rotary Molecular Motors. Adv. Func. Mater. 2007, 17, 718–729. [Google Scholar] [CrossRef]
- Feringa, B.L. In Control of Motion: From Molecular Switches to Molecular Motors. Acc. Chem. Res. 2001, 34, 504–513. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).