The Magnetic Response of Starphenes †
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
3.1. [4]Starphene
3.2. [7]Starphene
3.3. [10]Starphene
3.4. [13]Starphene
3.5. [16]Starphene
3.6. [19]Dendriphene
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pozo, I.; Guitián, E.; Pérez, D.; Peña, D. Synthesis of Nanographenes, Starphenes, and Sterically Congested Polyarenes by Aryne Cyclotrimerization. Acc. Chem. Res. 2019, 52, 2472–2481. [Google Scholar] [CrossRef] [PubMed]
- Rüdiger, E.C.; Müller, M.; Freudenberg, J.; Bunz, U.H.F. Starphenes and Phenes: Structures and Properties. Org. Mater. 2019, 01, 001–018. [Google Scholar] [CrossRef]
- Müllen, K.; Rabe, J.P. Nanographenes as Active Components of Single-Molecule Electronics and How a Scanning Tunneling Microscope Puts Them to Work. Acc. Chem. Res. 2008, 41, 511–520. [Google Scholar] [CrossRef] [PubMed]
- Holec, J.; Cogliati, B.; Lawrence, J.; Berdonces-Layunta, A.; Herrero, P.; Nagata, Y.; Banasiewicz, M.; Kozankiewicz, B.; Corso, M.; de Oteyza, D.G.; et al. A Large Starphene Comprising Pentacene Branches. Angew. Chem. Int. Ed. Engl. 2021, 60, 7752–7758. [Google Scholar] [CrossRef]
- Alonso, J.M.; Díaz-Álvarez, A.E.; Criado, A.; Pérez, D.; Peña, D.; Guitián, E. [16]Cloverphene: A Clover-Shaped Cata-Condensed Nanographene with Sixteen Fused Benzene Rings. Angew. Chem. Int. Ed. Engl. 2012, 51, 173–177. [Google Scholar] [CrossRef]
- Vilas-Varela, M.; Fatayer, S.; Majzik, Z.; Pérez, D.; Guitián, E.; Gross, L.; Peña, D. [19]Dendriphene: A 19-Ring Dendritic Nanographene. Chem. Eur. J. 2018, 24, 17697–17700. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.; Stuyver, T.; Rong, C.; Alonso, M.; Lu, T.; De Proft, F.; Geerlings, P.; Liu, S. Global and Local Aromaticity of Acenes from the Information-Theoretic Approach in Density Functional Reactivity Theory. Phys. Chem. Chem. Phys. 2019, 21, 18195–18210. [Google Scholar] [CrossRef] [PubMed]
- Portella, G.; Poater, J.; Bofill, J.M.; Alemany, P.; Solà, M. Local Aromaticity of [n]acenes, [n]phenacenes, and [n]helicenes (n = 1-9). J. Org. Chem. 2005, 70, 2509–2521. [Google Scholar] [CrossRef] [PubMed]
- Pino-Rios, R.; Báez-Grez, R.; Solà, M. Acenes and Phenacenes in Their Lowest-Lying Triplet States. Does Kinked Remain More Stable than Straight? Phys. Chem. Chem. Phys. 2021, 23, 13574–13582. [Google Scholar] [CrossRef]
- Orozco-Ic, M.; Dimitrova, M.; Barroso, J.; Sundholm, D.; Merino, G. Magnetically Induced Ring-Current Strengths of Planar and Nonplanar Molecules: New Insights from the Pseudo-π Model. J. Phys. Chem. A 2021, 125, 5753–5764. [Google Scholar] [CrossRef]
- Orozco-Ic, M.; Restrepo, A.; Muñoz-Castro, A.; Merino, G. Molecular Helmholtz Coils. J. Chem. Phys. 2019, 151, 014102. [Google Scholar] [CrossRef]
- Jusélius, J.; Sundholm, D.; Gauss, J. Calculation of Current Densities Using Gauge-Including Atomic Orbitals. J. Chem. Phys. 2004, 121, 3952–3963. [Google Scholar] [CrossRef]
- Fliegl, H.; Taubert, S.; Lehtonen, O.; Sundholm, D. The Gauge Including Magnetically Induced Current Method. Phys. Chem. Chem. Phys. 2011, 13, 20500–20518. [Google Scholar] [CrossRef] [PubMed]
- Sundholm, D.; Fliegl, H.; Berger, R.J.F. Calculations of Magnetically Induced Current Densities: Theory and Applications. WIREs Comput. Mol. Sci. 2016, 6, 639–678. [Google Scholar] [CrossRef]
- Steiner, E.; Fowler, P.W. Patterns of Ring Currents in Conjugated Molecules: A Few-Electron Model Based on Orbital Contributions. J. Phys. Chem. A 2001, 105, 9553–9562. [Google Scholar] [CrossRef]
- Steiner, E.; Fowler, P.W.; Havenith, R.W.A. Current Densities of Localized and Delocalized Electrons in Molecules. J. Phys. Chem. A 2002, 106, 7048–7056. [Google Scholar] [CrossRef]
- Fowler, P.W.; Steiner, E. Pseudo-π Currents: Rapid and Accurate Visualisation of Ring Currents in Conjugated Hydrocarbons. Chem. Phys. Lett. 2002, 364, 259–266. [Google Scholar] [CrossRef]
- Charistos, N.D.; Muñoz-Castro, A.; Sigalas, M.P. The Pseudo-π Model of the Induced Magnetic Field: Fast and Accurate Visualization of Shielding and Deshielding Cones in Planar Conjugated Hydrocarbons and Spherical Fullerenes. Phys. Chem. Chem. Phys. 2019, 21, 6150–6159. [Google Scholar] [CrossRef] [PubMed]
- Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange–correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Lehtola, S.; Dimitrova, M.; Fliegl, H.; Sundholm, D. Benchmarking Magnetizabilities with Recent Density Functionals. J. Chem. Theory Comput. 2021, 17, 1457–1468. [Google Scholar] [CrossRef] [PubMed]
- Valiev, R.R.; Benkyi, I.; Konyshev, Y.V.; Fliegl, H.; Sundholm, D. Computational Studies of Aromatic and Photophysical Properties of Expanded Porphyrins. J. Phys. Chem. A 2018, 122, 4756–4767. [Google Scholar] [CrossRef]
- Ditchfield, R. Self-Consistent Perturbation Theory of Diamagnetism. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Merino, G.; Heine, T.; Seifert, G. The Induced Magnetic Field in Cyclic Molecules. Chem. Eur. J. 2004, 10, 4367–4371. [Google Scholar] [CrossRef]
- Heine, T.; Islas, R.; Merino, G. Sigma and Pi Contributions to the Induced Magnetic Field: Indicators for the Mobility of Electrons in Molecules. J. Comput. Chem. 2007, 28, 302–309. [Google Scholar] [CrossRef] [PubMed]
- Islas, R.; Heine, T.; Merino, G. The Induced Magnetic Field. Acc. Chem. Res. 2012, 45, 215–228. [Google Scholar] [CrossRef]
- Orozco-Ic, M.; Cabellos, J.L.; Merino, G. Aromagnetic; Cinvestav-Mérida: Mérida, Mexico, 2016. [Google Scholar]
- von Ragué Schleyer, P.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; von Rague Schleyer, P. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef]
- Fallah-Bagher-Shaidaei, H.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Which NICS Aromaticity Index for Planar Pi Rings Is Best? Org. Lett. 2006, 8, 863–866. [Google Scholar] [CrossRef]
- Radenković, S.; Đorđević, S. Relating Nucleus Independent Chemical Shifts with Integrated Current Density Strengths. Phys. Chem. Chem. Phys. 2021, 23, 11240–11250. [Google Scholar] [CrossRef] [PubMed]
- Monaco, G.; Zanasi, R.; Pelloni, S.; Lazzeretti, P. Relative Weights of σ and π Ring Currents in a Few Simple Monocycles. J. Chem. Theory Comput. 2010, 6, 3343–3351. [Google Scholar] [CrossRef] [PubMed]
- Papadopoulos, A.G.; Charistos, N.D.; Sigalas, M.P. Aromaticity Variation in BN Substituted Triphenylene: A Theoretical Study. AIP Conf. Proc. 2012, 1504, 1223–1226. [Google Scholar]
- Lampkin, B.J.; Karadakov, P.B.; VanVeller, B. Detailed Visualization of Aromaticity Using Isotropic Magnetic Shielding. Angew. Chem. Int. Ed. Engl. 2020, 59, 19275–19281. [Google Scholar] [CrossRef] [PubMed]
- Sundholm, D.; Berger, R.J.F.; Fliegl, H. Analysis of the Magnetically Induced Current Density of Molecules Consisting of Annelated Aromatic and Antiaromatic Hydrocarbon Rings. Phys. Chem. Chem. Phys. 2016, 18, 15934–15942. [Google Scholar] [CrossRef][Green Version]
- Solà, M. Forty Years of Clar’s Aromatic π-Sextet Rule. Front. Chem. 2013, 1, 22. [Google Scholar] [CrossRef]
- von Ragué Schleyer, P.; Manoharan, M.; Jiao, H.; Stahl, F. The Acenes: Is There a Relationship between Aromatic Stabilization and Reactivity? Org. Lett. 2001, 3, 3643–3646. [Google Scholar] [CrossRef]
- Fias, S.; Van Damme, S.; Bultinck, P. Multidimensionality of Delocalization Indices and Nucleus Independent Chemical Shifts in Polycyclic Aromatic Hydrocarbons. J. Comput. Chem. 2008, 29, 358–366. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Solà, M.; Krygowski, T.M.; Szatylowicz, H.; Andrzejak, M.; Pawełek, B.; Dominikowska, J.; Kukułka, M.; Dyduch, K. Aromaticity of Acenes: The Model of Migrating π-Circuits. Phys. Chem. Chem. Phys. 2018, 20, 13430–13436. [Google Scholar] [CrossRef]
- Aihara, J.-I. Circuit Resonance Energy: A Key Quantity That Links Energetic and Magnetic Criteria of Aromaticity. J. Am. Chem. Soc. 2006, 128, 2873–2879. [Google Scholar] [CrossRef] [PubMed]
- Gershoni-Poranne, R. Piecing It Together: An Additivity Scheme for Aromaticity Using NICS-XY Scans. Chem. Eur. J. 2018, 24, 4165–4172. [Google Scholar] [CrossRef] [PubMed]
- Bendikov, M.; Duong, H.M.; Starkey, K.; Houk, K.N.; Carter, E.K.; Wudl, F. Oligoacenes: Theoretical Prediction of Open-Shell Singlet Diradical Ground States. J. Am. Chem. Soc. 2004, 126, 7416–7417. [Google Scholar] [CrossRef] [PubMed]
- Poater, J.; Bofill, J.M.; Alemany, P.; Solà, M. Local Aromaticity of the Lowest-Lying Singlet States of [n]Acenes (n = 6-9). J. Phys. Chem. A 2005, 109, 10629–10632. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Dai, S. Electronic Ground State of Higher Acenes. J. Phys. Chem. A 2008, 112, 332–335. [Google Scholar] [CrossRef]
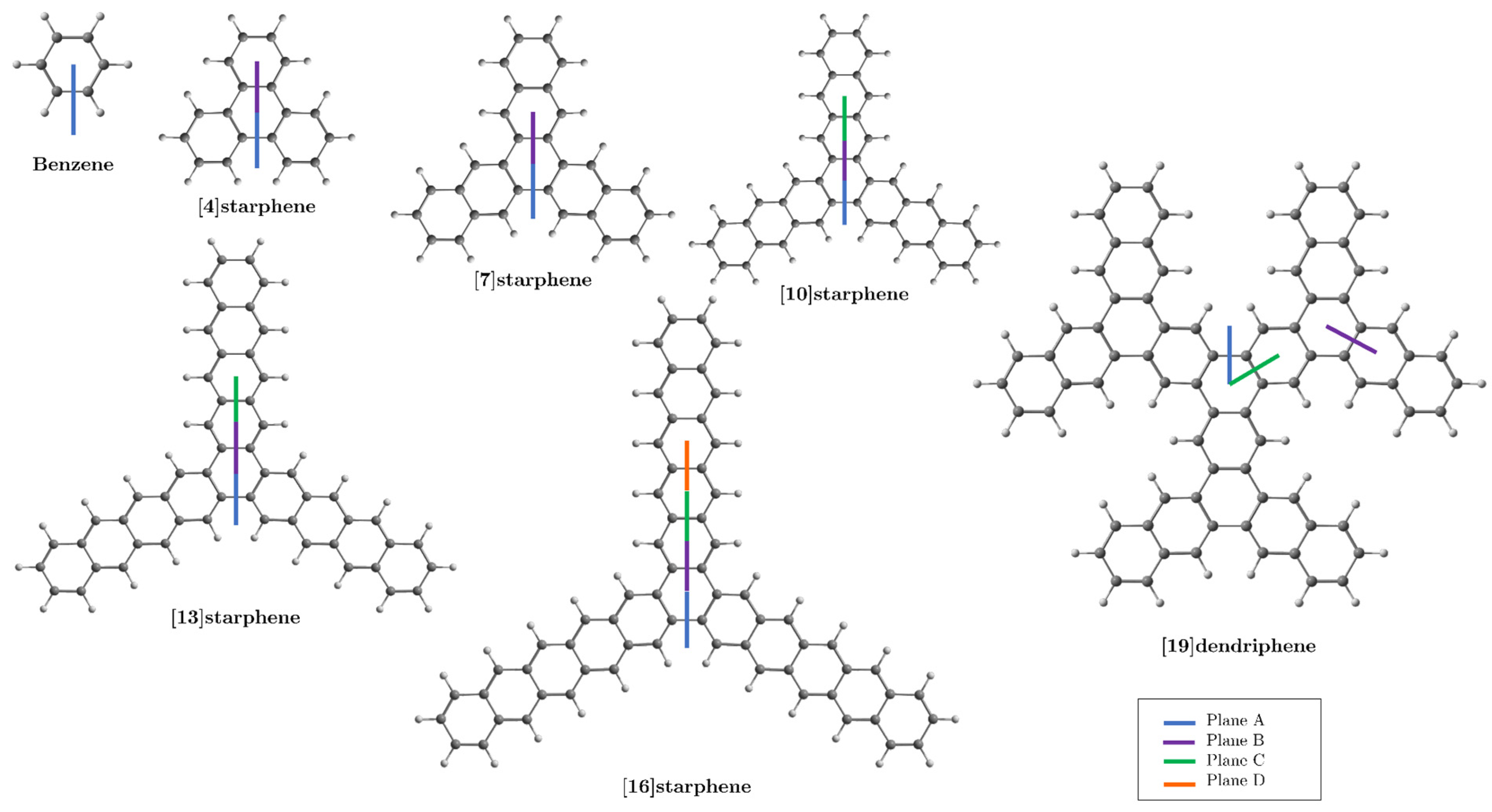

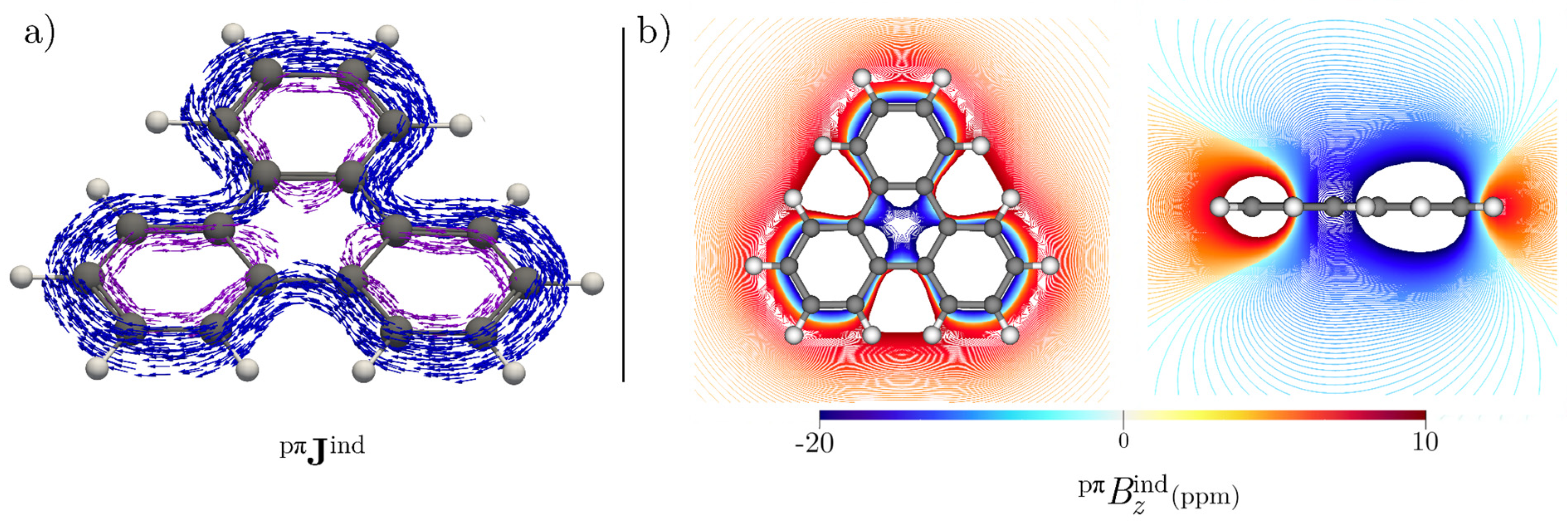



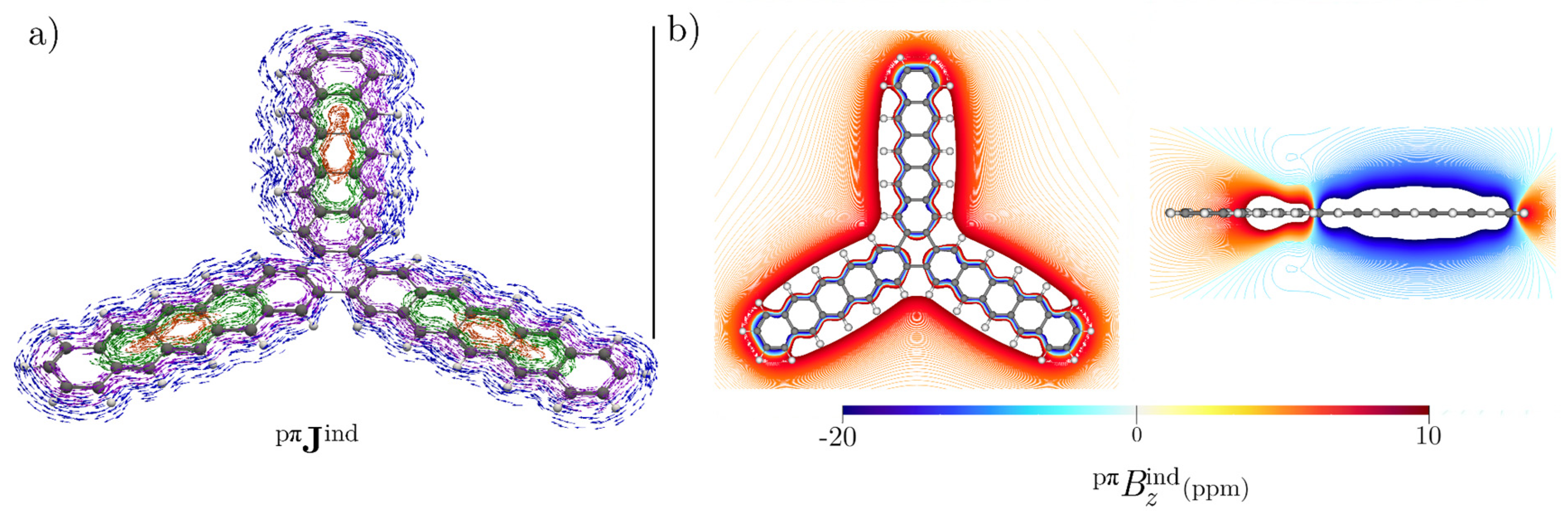

| Molecule | Plane | Diatropic | Paratropic | Net |
|---|---|---|---|---|
| Benzene | A | 12.52 | 0.0 | 12.52 |
| [4]starphene | A (peripheral) | 8.99 | −0.71 | 8.28 |
| B (local 6-MR) | 4.12 | 0.0 | 4.12 | |
| [7]starphene | A (peripheral) | 5.20 | −1.40 | 3.80 |
| B (naphthalene-like) | 9.41 | 0.0 | 9.41 | |
| [10]starphene | A (peripheral) | 3.79 | −1.81 | 1.98 |
| B (anthracene-like) | 10.46 | 0.0 | 10.46 | |
| C (local 6-MR) | 3.62 | 0.0 | 3.62 | |
| [13]starphene | A (peripheral) | 3.22 | −0.01 | 1.30 |
| B (tetracene-like) | 10.27 | 0.0 | 10.27 | |
| C (naphthalene-like) | 5.53 | 0.0 | 5.05 | |
| [16]starphene | A (peripheral) | 2.98 | −1.87 | 1.11 |
| B (pentacene-like) | 9.77 | 0.0 | 9.77 | |
| C (anthracene-like) | 5.61 | 0.0 | 5.61 | |
| D (local 6-MR) | 1.73 | 0.0 | 1.73 | |
| [19]dendriphene | A (peripheral) | 6.63 | 0.0 | 6.63 |
| B (naphthalene-like) | 9.09 | 0.0 | 9.09 | |
| C (local 6-MR) | 4.74 | 0.0 | 4.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Orozco-Ic, M.; Merino, G. The Magnetic Response of Starphenes. Chemistry 2021, 3, 1381-1391. https://doi.org/10.3390/chemistry3040099
Orozco-Ic M, Merino G. The Magnetic Response of Starphenes. Chemistry. 2021; 3(4):1381-1391. https://doi.org/10.3390/chemistry3040099
Chicago/Turabian StyleOrozco-Ic, Mesías, and Gabriel Merino. 2021. "The Magnetic Response of Starphenes" Chemistry 3, no. 4: 1381-1391. https://doi.org/10.3390/chemistry3040099
APA StyleOrozco-Ic, M., & Merino, G. (2021). The Magnetic Response of Starphenes. Chemistry, 3(4), 1381-1391. https://doi.org/10.3390/chemistry3040099







