Abstract
Ring-current maps give a direct pictorial representation of molecular aromaticity. They can be computed at levels ranging from empirical to full ab initio and DFT. For benzenoid hydrocarbons, Hückel–London (HL) theory gives a remarkably good qualitative picture of overall current patterns, and a useful basis for their interpretation. This paper describes an implemention of Aihara’s algorithm for computing HL currents for a benzenoid (for example) by partitioning total current into its constituent cycle currents. The Aihara approach can be used as an alternative way of calculating Hückel–London current maps, but more significantly as a tool for analysing other empirical models of induced current based on conjugated circuits. We outline an application where examination of cycle contributions to HL total current led to a simple graph-theoretical approach for cycle currents, which gives a better approximation to the HL currents for Kekulean benzenoids than any of the existing conjugated-circuit models, and unlike these models it also gives predictions of the HL currents in non-Kekulean benzenoids that are of similar quality.
1. Introduction
Benzene was first isolated almost 200 years ago [1] and the term ‘aromatic’ came into use as a description for this and similar compounds soon afterwards [2]. Since Kekulé’s famous identification of the special structure of benzene [3], the importance, meaning and even existence of ‘aromaticity’ have been hotly debated, and these discussions show no sign of reaching a universally accepted conclusion [4,5,6,7,8,9,10,11,12]. However, one widely accepted working criterion for aromaticity is the manifestation in a cyclic system of global currents (ring currents) induced by application of an external magnetic field [13,14,15,16,17,18,19,20]. This definition of aromaticity appeals to the community of theoretical chemists who calculate molecular electric and magnetic response properties, and it has featured extensively in the scientific career of Riccardo Zanasi, from their early work with Paolo Lazzeretti in Modena, to their work over several decades with colleagues in Salerno. As a definition, it also has the desirable feature that the criterion is, at least in principle, clearcut: either there is a global current or not, and if there is one, it has a sense of circulation with respect to the axis of the external field, which leads to a natural division of (monocyclic) ring systems into disjoint aromatic, non-aromatic and anti-aromatic classes. This criterion is ideally suited to probing by theoretical methods that calculate induced current either directly, or via other response magnetic properties as proxies. The ring-current picture has a close connection to experiment, through ring-current effects on H NMR chemical shifts [16,17] and ‘exaltation of diamagnetism’ [13,14,15,21].
Over the last quarter of a century, the field has gained impetus from new possibilities for plotting physically realistic ab initio maps of the current density induced by an external magnetic field [22,23,24,25], and for interpreting these maps in terms of chemical concepts such as orbital energy, symmetry and nodal character [20,25]. Riccardo Zanasi has participated in all of these developments [26]. One paper from the Salerno group of particular relevance to the present topic is [27], where quantities from the Aihara model, to be discussed below, are used to aid interpretation of ab initio current maps.
In this paper, we concentrate on the oldest model for mapping induced currents in benzenoids and similar systems: Hückel–London (HL) theory [14,28], which can be formulated in several equivalent ways: as a finite-field method [29], a perturbation method based on bond-bond polarisabilities [30,31,32,33], or a treatment of current as the formal superposition of cycle contributions [34,35]. The purpose of the present paper is to draw attention to this third version of HL theory, which is associated with the name of the late Professor Jun-Ichi Aihara. His innovative reformulation of the HL problem has not always received the attention from other chemists that it deserves. Although the concepts that it generated, such as Topological Resonance Energy, Bond Resonance Energy and Magnetic Resonance Energy (TRE, BRE and MRE), are influential, it is rare to find examples of direct use by other chemists of the specifics of the method itself. This may be because the Aihara formalism employs a number of concepts from graph theory that are unfamiliar to most chemists, or because the defining equations are scattered over a long series of interlocking papers, so that their conversion to a workable algorithm has not always appeared straightforward.
Our aim here is to remedy this situation, by giving an explicit implementation. Our main motivation was not to calculate HL current maps (for which several easily implemented algorithms already exist), but to exploit the defining feature of Aihara’s approach: the emphasis on cycle contributions to current, where every cycle within the molecular graph, be it a chemical ring or larger, is taken into account. This feature has assumed new relevance over the last decade with the revival of interest in conjugated-circuit (CC) models [36,37,38,39,40,41]. A cycle C in a graph G is a conjugated circuit if both G and (the graph where all vertices of C and their associated edges have been deleted) have a perfect matching. In a CC model, each conjugated circuit contributes currents along its edges, with weights specific to the model [42].
Conjugated-circuit models have an attractive simplicity, but have crucial drawbacks for non-Kekulean systems, where they predict zero current, and for Kekulean systems with fixed bonds, where they predict ‘dead zones’ of vanishing current [43,44,45]. The current maps from conjugated-circuit models can be seen as approximate versions of HL current maps in which only certain ‘important’ cycles have been selected and given model-dependent weightings. The Aihara approach can be used as a toolkit to test these approximations, and to design better models.
Comparison of HL and CC currents in benzenoids by cycle size has allowed us to evaluate these selection and weighting schemes, and to propose a new model, also based on matchings, that gives an approximation to HL currents for both Kekulean and non-Kekulean benzenoids that is better than any of the published CC models [43]. The dual nature of HL theory as a graph theoretical method based on molecular-orbital theory, makes it interesting to compare HL results with conjugated-circuit models on the one hand, and with more sophisticated wavefunction and density functional approaches to electronic structure on the other. The relevance of the present graph-theoretical investigation to ab initio calculation is that HL currents already typically mimic pseudo- currents [43], which in turn are usually excellent mimics for current maps derived from full ab initio and density functional calculations. Some systematic exceptions to this statement are discussed in [43].
The symmetries and energies of HL molecular orbitals provide a useful basis for rationalising the frontier-orbital analysis of current maps obtained from ipsocentric calculations at these higher levels [20,25], even though HL and ipsocentric definitions of molecular-orbital contributions are markedly different. In delocalised systems, current maps calculated within the ipsocentric approach are dominated by the frontier orbitals. In contrast, as usually formulated, HL currents in these systems have significant contributions from lower-lying molecular orbitals.
Graph Theoretical Background
An undirected graph G consists of a set V of vertices and a set E of edges where each edge corresponds to an unordered pair of vertices from V. We use n to denote the number of vertices of a graph and m to denote the number of edges. A graph is planar if it can be drawn in the plane with no crossing edges. When traversing the faces of a graph, each edge is treated as the two arcs and . A traversal of each face of the graph uses each arc exactly once.
The graphs considered in this paper are benzenoids. Benzenoids may be defined as simply connected subgraphs of the hexagonal lattice composed of edge-fused hexagons. Hence, they correspond to connected planar graphs having all internal faces of size 6. The vertices on the interior have degree 3. The vertices on the perimeter (external face) either have degree 2 or degree 3. As is well known, the systems of benzenoids support circulations of electrons induced by an external magnetic field with consequences for magnetic susceptibilities and H NMR chemical shifts [13,14,15,16,17,21]. The calculation of this magnetic response in HL theory requires an embedding of the molecular graph, with explicit coordinates for the atomic positions. The embedding used here for benzenoids idealises each carbon framework as planar and composed of regular hexagons of side Å, embedded without overlap in the hexagonal tessellation of the plane.
When representing current, the graph is converted to a directed graph. If there is a current of magnitude k on arc and a current of magnitude r on arc then the net current on arc is equal to . A current of magnitude k on arc is equivalent to a current of magnitude on arc . In our depictions of currents, the current contributions and arc directions are shown so that all magnitudes are greater than or equal to zero. In our maps, diatropic currents, representing aromatic currents, are those in a counter-clockwise direction, and conversely paratropic currents, representing anti-aromatic currents, are those in a clockwise direction.
By convention, the ‘absolute’ currents obtained from HL theory are often reported on a scale where unit current is equal to the HL current along an edge of an isolated, neutral benzene ring with side length Å [46]. When comparing different models, it is more useful to consider scaled current, as empirical methods for approximating currents give relative and not absolute results. A scaled current is obtained from the current picture by dividing the current value of each edge by the maximum current value. Scaled currents have a current of one on each arc that bears maximum current.
2. The Hückel–London Model as a Superposition of Cycle Contributions
The Aihara formulation of Hückel–London theory was refined over a series of papers, and here we give the working equations needed for its implementation. As a practical check, our implementation was run on all the small benzenoids (both Kekulean and non-Kekulean) having up to ten hexagons and the computed results matched against HL currents from the standard finite-perturbation approach, giving computational verification that our interpretation of the equations is correct. Aihara’s basic formalism was presented in two papers from 1979 [34,35] in which the relationship to London’s approximations [14] was established. In London theory, the effect of an external magnetic field is to perturb the original Hückel secular matrix of the molecule, effectively converting the entries in the adjacency matrix into exponentials that reduce to in the limit of vanishing applied magnetic field. This gives an easily implemented finite-field version of HL theory, e.g., [29]. In contrast, the Aihara formalism is an analytic perturbation theory and hence the calculated current densities are simple functions of field-free characteristic polynomials [47].
The first step is to find the eigenvalues of the adjacency matrix of the graph G. The number of times that a value appears as an eigenvalue is the multiplicity of , denoted by . The multiplicity of the zero eigenvalue is the nullity of the graph, . The characteristic polynomial, , for a graph G is equal to
where is the identity matrix. If a graph has no vertices, then the characteristic polynomial is 1.
In the Hückel model, eigenvectors of the adjacency matrix correspond to molecular orbitals, and eigenvalues correspond to orbital energies. It is usual to choose for the origin of the energy scale and for the energy unit, where and are the (negative) Coulomb and Resonance integrals from Hückel theory. The energy of an electron occupying one of the shell of degenerate orbitals that have eigenvalue in the field-free -system is then , giving the correspondence between values , , and and the bonding, non-bonding or antibonding character of the shell, respectively. Electrons are assigned to orbitals using the Aufbau and Pauli Principles and Hund’s Rule of Maximum Multiplicity. In brief: orbitals are filled sequentially in non-increasing order of eigenvalues (Aufbau), each orbital has a maximum occupancy of two electrons (Pauli), and where , no orbital receives a second electron until each of the orbitals in the given shell contains at least one (Hund).
In practice, for calculations of HL currents the fractional occupation approximation is used, where the average number of electrons per orbital over a given shell is taken as the occupation number for every orbital in that shell. For the shell with eigenvalue , this occupation number is denoted by . In cases where all are equal to 2 or 0, we have a closed shell; otherwise there is partial occupation of some orbital or orbitals and we have an open shell.
As benzenoids have bipartite molecular graphs, their Hückel eigenvalues and eigenvectors are subject to the Coulson-Rushbrooke Pairing Theorem [48]. If a bipartite graph has an eigenvalue satisfying , then the spectrum of the graph includes shells with eigenvalues and , with the same multiplicity. Moreover, to each of the orthonormal eigenvectors for the shell there is an eigenvector in the shell derived by swapping the signs of all entries for vertices belonging to one partite set. Hence, a bipartite molecular graph has equal numbers of bonding and anti-bonding molecular orbitals, and the number of non-bonding orbitals () has the same parity as n, the number of conjugated carbon centres. Application of Aufbau, Pauli and Hund rules for the neutral molecule leads to an electron configuration with all bonding orbitals full (), all anti-bonding orbitals empty (), and any non-bonding orbitals half full ().
We can simplify the calculation of HL current for a benzenoid by noting that an electron in a non-bonding orbital of a bipartite system makes no contribution to the total current (see Section 3), so we may deal with the equivalent closed-shell system where any non-bonding occupancies have been set to zero. This closed shell corresponds to the neutral molecule for a Kekulean benzenoid, and otherwise to the cation of charge . This simplification is specific to bipartite systems treated within the HL model. In ipsocentric ab initio approaches [20,25,49], non-bonding orbitals may contribute current, whether or not the molecular graph is bipartite. Consideration of the nearest closed-shell for a non-Kekulean benzenoid has a direct chemical application in the study of benzenoid cations; a modified CC approach has been used to give an account of the current maps for these species [50].
Characteristic polynomials are manipulated in order to calculate a resonance energy for each cycle C. The fundamental quantities in the Aihara analysis are Circuit Resonance Energies (CRE), denoted by the symbol (originally RE [51]) where C is any cycle in G, conjugated or not. The CRE represents a partition of the Topological Resonance Energy into cycle contributions, interpretable as a gain or loss in energy arising from conjugation along a cycle C [52,53]. It is defined in dimensionless form as [54]:
where is the (shell average) number of electrons in the orbital with eigenvalue , is the function described below, and the sum in (2) runs over distinct values (each eigenvalue counted once, irrespective of multiplicity). The value can be compared to the standard case of neutral benzene, for which (see Section 5.1).
The function is defined in terms of the characteristic polynomials of graphs G and , and is described in different ways for cases with and . In the simple case where = 1, the function is
where the polynomial is defined as
For , is equal to the first derivative of evaluated at , i.e.,
In systems with degenerate orbitals, the contribution from these orbitals to the CRE must account for the splitting induced by the external magnetic field [55]. To do so, the function is defined as
If is taken to be the identity, (3) is the formal limit of (6) for .
The value for a given cycle can be converted into a Hückel–London cycle current, , by accounting for the area of the cycle [56]. The cycle contribution to the total current-density map is defined, again in dimensionless form, as
Written in this way, the equation gives the cycle contribution as a multiple of the unit HL current for neutral benzene [47]. The quantity is the area of cycle C in terms of benzene rings. In benzenoids, is therefore simply the number of hexagons enclosed by the cycle. In non-benzenoids, is the area of the cycle normalised to that of a hexagon, i.e., the faces inside the cycle are considered to be regular polygons and their areas are summed and divided by the area of a regular hexagon with the same side length. Hence, each polygonal ring of size p that is enclosed by cycle C contributes to .
The HL current-density map for a benzenoid is obtained edge by edge by summing contributions from all cycles that pass through the given edge to assign the bond current. A more compact representation uses ring currents assigned to the faces; current on a perimeter edge equates to the ring current for the face containing it; current on an interior edge is the vector sum of the ring currents flowing in the two faces that meet along that edge.
We denote the ring current of a face F by . Note that the ring current on a face in a polycyclic system is not in general equal to the current contribution for that same cycle as given by the Aihara formula (7). The two are of course equal for benzene, and unscaled ring currents in dimensionless form are therefore also specified as ratios to the benzene value.
The sum of values over all cycles is used to define as a proposed aromaticity index, the magnetic resonance energy (MRE) of G [57]:
Aihara has argued that this index has a physical advantage over raw ring current as it is independent of cycle area, whereas ring currents are not. One of their most recent papers [58] is an encyclopaedic survey of the magnetic criteria of aromaticity, in which he concludes that MRE is for many purposes an ideal aromaticity index. This paper also gives a good working summary of all the basic equations of the Aihara approach.
A third cycle property related to aromaticity on the magnetic definition is the magnetic susceptibility of a cycle C, , which has an even stronger dependence on cycle area and is defined, again in dimensionless form referred to the susceptibility of benzene (which is diamagnetic and therefore negative) as [35]:
The -electron contribution to the molecular magnetic susceptibility, , is obtained by summing over all cycles.
Thus, the three quantities of circuit resonance energy (), cycle current, (), and cycle magnetic susceptibility () all contain the same information, weighted differently. Aihara’s objection to the use of ring currents as a measure of aromaticity also applies to the magnetic susceptibility. A related point was made by Estrada [59], who argued that correlations between magnetic and energetic criteria of aromaticity for some molecules could simply be a result of underlying separate correlations of susceptibility and resonance energy with molecular weight.
3. A Pairing Theorem for HL Currents
As noted above, bipartite graphs obey the Pairing Theorem [48]. The theorem implies that when the eigenvalues of a bipartite graph are arranged in non-increasing order from to , positive and negative eigenvalues are paired, with
where is shorthand for . If is the number of zero eigenvalues of the graph, is even. Zero eigenvalues occur at positions ranging from to . HL currents for benzenoids and other bipartite molecular graphs also obey a pairing theorem, as is easily proved using the Aihara Formulas (2)–(7),
We consider arbitrary elctron counts and occupations of the shells. Each electron in an occupied orbital with eigenvalue makes a contribution to the Circuit Resonance Energy of cycle C (Equation (2)). The function depends on the multiplicity : it is given by Equation (3) for non-degenerate and Equation (6) for degenerate .
Theorem 1.
For a benzenoid graph, the contributions per electron of paired occupied shells to the Circuit Resonance Energy of cycle C, , are equal and opposite, i.e.,
Proof.
Some straightforward corollaries are:
The result follows from parity of the polynomials used to construct . The characteristic polynomial for a bipartite graph has well defined parity, as
On differentiation the parity reverses:
A benzenoid graph is bipartite, so all cycles C are of even size and has the same parity as :
Therefore, for ,
The argument for the case for is similar. For a bipartite graph, the parity of can equally be stated in terms of order or nullity:
Functions and are therefore related by
as and and are formed by cancelling factors and , respectively, from . Hence, the quotient function behaves as
Each differentiation flips the parity, and the pairing result for is therefore
□
Corollary 1.
In the fractional occupation model, where all orbitals of a shell are assigned equal occupation, paired shells of a bipartite graph that contain the same number of electrons make cancelling contributions of current for every cycle C, and hence no net contribution to the HL current map.
Corollary 2.
In the fractional occupation model, all electrons in a non-bonding shell of a bipartite graph () make no contribution to any cycle current and hence make no net contribution to the HL current map.
It should be noted that if a graph is non-bipartite, the non-bonding shell may contribute a significant current in the HL model. Furthermore, if G is bipartite but subject to first-order Jahn-Teller distortion, current may arise from the occupied part of an originally non-bonding shell; this can be treated by using the form of the Aihara model appropriate to edge-weighted graphs [58]. Corollary (2) also highlights a significant difference between HL and ipsocentric ab initio methods. In the latter, an occupied non-bonding molecular orbital of an alternant hydrocarbon can make a significant contribution to total current through low-energy virtual excitations to nearby shells, and can be a source of differential and currents.
Corollary 3.
In the fractional occupation model, the HL current maps for the cation and anion of a π system that has a bipartite molecular graph are identical.
We can also note that in the extreme case of the cation/anion pair where the neutral system has gained or lost a total of n electrons, the HL current map has zero current everywhere. For bipartite graphs, this follows from Corollary (3), but it is true for all graphs, as a consequence of the perturbational nature of the HL model, where currents arise from field-induced mixing of unoccupied into occupied orbitals: when either set is empty, there is no mixing.
4. Implementation of the Aihara Method
4.1. Generating All Cycles of a Planar Graph
By definition, conjugated-circuit models consider only the conjugated circuits of the graph. In contrast, the Aihara formalism considers all cycles of the graph. A catafused benzenoid (or catafusene) has no vertex belonging to more than two hexagons. Catafusenes are Kekulean. For catafusenes, all cycles are conjugated circuits. All other benzenoids have at least one vertex in three hexagons, and have some cycles that are not conjugated circuits.
The size of a cycle is the number of vertices in the cycle. The area of a cycle C of a benzenoid is the number of hexagons enclosed by the cycle. One way to represent a cycle of the graph is with a vector which has one entry for each edge of the graph where is set to one if edge i is in the cycle, and is set to 0 otherwise. When we add these vectors together, the addition is done modulo two. The addition of two cycles of the graph can either result in another cycle, or a disconnected graph whose components are all cycles.
A cycle basis B of a graph G is a set of linearly independent cycles (none of the cycles in B is equal to a linear combination of the other cycles in B) such that every cycle of the graph G is a linear combination of the cycles in B. It is well known that the set of faces of a planar graph G is a cycle basis for G [60]. The approach that we use for generating all the cycles starts with this cycle basis and finds the remaining cycles by taking linear combinations.
The cycles of a benzenoid that have unit area are the faces. The cycles that have area are generated from those of area r by considering the cycles that result from adding each cycle of area one to each of the cycles of area r. If the result is connected and is a cycle that is not yet on the list, then this new cycle is added to the list.
For the Aihara approach, a counterclockwise representation of each cycle of the graph is computed. It is easy to compute these as the cycles are generated. A face traversal algorithm [61] first provides the internal faces as traversed in counterclockwise order. If a new cycle is a linear combination of and then arcs that are in both and disappear and the remaining arcs should be oriented in the same way as they are in the cycle from which they came.
4.2. Efficient Computation of Necessary Derivatives
The derivative of a function f with respect to x is denoted here as . We first recall some elementary properties of the derivative. For a polynomial of degree n that is equal to , the derivative is equal to . The product rule for a function states that . The quotient rule for a function states that .
In the set of small benzenoids we used for initial testing (Kekuléan benzenoids with at most seven hexagons) the maximum multiplicity of an eigenvalue is four (implying that the differentiation in the formula for (Equation (6)) has to be applied three times). If the quotient rule is applied directly without additional simplification, then the degree of the denominator polynomial doubles. For example, starting with a polynomial of degree 30, results of one of degree 60. Differentiating a second time gives degree 120, and the third differentiation gives degree 240. Polynomials of such large degree resulted in numerical instability in the computations. In order to correct this problem, we changed the way that the differentiation was implemented. The new approach is as follows.
In the formula for the two polynomials can each be expressed in the form . For the numerator, , the values are just the eigenvalues of . For the denominator, , they correspond to the eigenvalues of G with each of the occurrences of an eigenvalue equal to excluded. For a polynomial we use the notation to denote the polynomial or in equivalent product form, with the terms of the form crossed out. (Eigenvalues are not to be confused with the Hückel integrals , .)
Suppose that the function that we want to differentiate is for polynomials p and q with degrees and , and . Applying quotient and product rules and cancelling out common terms in numerator and denominator gives this formula for :
Note that, with this approach, the maximum degree increases by one each time instead of doubling. This results in better numerical stability.
For computing , it is not necessary to use a data structure that represents polynomials. Instead, vectors can be used. The recursive algorithm given below evaluates at . The vectors (indexed starting from 0) are p[i] and q[i]. These are used to compute derivatives instead of computing characteristic polynomials explicitly.
The function eval_deriv differentiates power times, where the argument x at which to evaluate the derivative has already been chosen and the vectors have been pre-computed. If power is 0 then the answer is the product of the values p[0] to p[-1] divided by the product of the values q[0] to q[-1]. Otherwise the answer is computed from: . MAX_DEG is the maximum degree of any polynomial.
double eval_deriv(int power, int dp, double p[MAX_DEG], int dq, double q[MAX_DEG])
{
double r[MAX_DEG];
double ans, top, bottom;
int limit, pos, i, j;
// When power is 0, stop taking derivatives and evaluate.
if (power == 0)
{
if (dp < dq) limit = dq;
else limit = dp;
ans = 1;
// The answer is the product of the p values divided by the product of the q values.
for (i = 0; i < limit; i++)
{
if (i < dp) top = p[i];
else top = 1;
if (i < dq) bottom = q[i];
else bottom = 1;
ans* = (top/bottom);
}
return(ans);
}
ans = 0;
// Compute qp’ / q^2 = p’/q.
// Ignore if dp = 0 since a polynomial of degree 0 has a derivative of 0.
if (dp > 0)
{
// If dp = 1 then the polynomial is x-a0 and the derivative of this is 1.
if (dp == 1)
{
r[0] = 1;
ans+ = eval_deriv(power-1, dp-1, r, dq, q);
}
else // dp > 1.
{
for (i = 0; i < dp; i++)
{
// Compute p(x)[-i]:
pos = 0;
for (j=0; j < dp; j++)
{
if (i != j)
{
r[pos] = p[j];
pos++;
}
}
ans+ = eval_deriv(power-1, dp-1, r, dq, q);
}
}
}
// Now subtract off p q’ / q^2
for (i = 0; i < dq; i++)
r[i] = q[i];
for (i = 0; i < dq; i++)
{
r[dq] = q[i];
ans -= eval_deriv(power-1, dp, p, dq+1, r);
}
return(ans);
}
5. Some Examples of the Aihara Model
5.1. The Basic Case: Benzene
Benzene is the standard against which aromaticity of other molecules is judged, and is invoked in the dimensionless formulation of the Aihara Equations (2)–(9). For benzene, the characteristic polynomial and its derivative are
As benzene is a monocycle, . The eigenvalues are , with occupation numbers in the neutral system of . Hence, the first shell has and and, by (3),
and the second shell and and, by (6),
Therefore, by (2), . As , the cycle contribution to current, which in this case is also the ring current, is 1 (by (7), and the (diamagnetic) susceptibility is . The value of for benzene is the reason for the factors of in the other Aihara equations.
Notice that in the HL model half of the ring current arises from the LOMO and half from the HOMO, in contrast to the ipsocentric picture where essentially the whole of the current arises from the HOMO [20].
5.2. An Analytical Example: The HL Current in Anthracene
Our approach is computational, but it is also interesting for interpretation purposes to see how the various quantities in the Aihara cycle decomposition of HL current can be worked out fully analytically in a simple case. The characteristic polynomial for anthracene is
the roots of which are the eigenvalues of the adjacency matrix of the graph, split equally between bonding and anti-bonding shells. As anthracene is a catafusene, the graph is Kekulean and there are no non-bonding orbitals. The occupied orbitals of neutral anthracene correspond to eigenvalues . The unoccupied orbitals correspond to eigenvalues . Thus, anthracene has doubly degenerate pairs of orbitals at and . In the Aihara formalism, every cycle within the graph is considered. For anthracene there are six possible cycles. Three are the individual hexagonal faces, two result from the naphthalene-like fusion of two hexagonal faces, and the final cycle is the result of the fusion of all three hexagonal faces. The cycles and corresponding polynomials are displayed in Table 1.

Table 1.
Cycles and corresponding polynomials in anthracene. Bold lines represent edges in C; removal of bold and dashed lines yields the graph .
Individual circuit resonance energies, , can now be calculated using Equation (2). For all occupied orbitals, . Calculations can be reduced by accounting for symmetry-equivalent cycles. For anthracene, six calculations of reduce to four as = and = .
First, the functions must be calculated for each cycle. For those eigenvalues with , is calculated using Equation (3), where the appropriate form of can be deduced from the factorised characteristic polynomial in Equation (25). For those occupied eigenvalues with , is calculated using a single differentiation in Equation (6). This procedure yields the values in Table 2.

Table 2.
Circuit resonance energy (CRE) values, , calculated using Equation (2) for cycles of anthracene. Cycles are labelled as shown in Table 1.
Circuit resonance energies, , are converted to cycle current contributions, , by Equation (7). These results are summarised in Table 3.

The significance of these quantities for interpretation is that they allow us to rank the contributions to the total HL current, and see that even in this simple case there are different factors in play. Notice that the contributions and are not equal. The two cycles have the same area, and correspond to graphs with the same number of perfect matchings, so would contribute equally in a CC model. In the Aihara partition of the HL current, the largest contribution from a cycle is from a face ( for the terminal hexagon), but so is the smallest ( for the central hexagon). The contributions of the cycles that enclose two and three faces are boosted by the area factors , in accord with Aihara’s ideas on the difference in weighting between energetic and magnetic criteria of aromaticity [57].
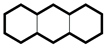
Finally, the ring currents in the terminal and central hexagonal faces of anthracene are calculated. They are listed in Table 4 and displayed in maps of ring and bond currents in Figure 1. As they must, the currents correspond exactly to the results of the finite-field numerical Hückel–London approach. Note that now the largest bond and ring currents appear in the central hexagon, not in the terminal hexagons. Although the local cycle contribution is larger than , the ring current in the central hexagon has contributions from more of the large cycles. The same effect is seen in CC models. The profile of increasing ring current from the ends to the middle of a linear polyacene chain is also seen in ab initio calculations. It has given rise to the so-called ‘anthracene problem’ [42,62], which is seen as a difficulty for theories of local aromaticity, in itself a contentious concept.

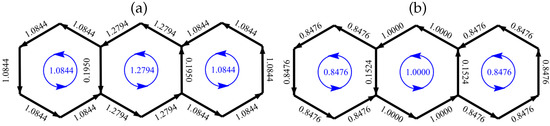
Figure 1.
Hückel London ring-current maps for anthracene: (a) raw and (b) scaled currents.
5.3. A Numerical Example: An Non-Kekulean Case
As an illustration of how the Aihara version of the HL model deals with non-Kekulean benzenoids, we take the 5-ring dibenzo-derivative of phenalenyl that is shown as (I) in Figure 2a.
Figure 2.
A non-Kekulean benzenoid, I. (a) Labelling of faces. (b) Distribution of coefficients in the unique non-bonding Hückel molecular orbital. For the normalised orbital, multiply all entries by .
The graph (though not necessarily the molecule) has symmetry, and three symmetry-distinct hexagons, , , and , where the last two are related by symmetry to their images and . The five hexagonal faces generate 19 cycles, which give 12 distinct cases, up to isomorphism, as listed in Table 5 along with their respective contributions to current.

Table 5.
Cycle contributions to HL current in the non-Kekulean benzenoid I. D and P stand for diatropic and paratropic contributions, respectively.
Collecting contributions, the ring currents in the unscaled map are , and . Scaled to the maximum bond current, the ring currents are , and . All are positive and hence diatropic, but arise from different balances of three terms: (i) the local contribution from the face itself (strongest for ), (ii) the diatropic contribution from the other cycles of size 2 mod 4 (strongest for face ) (iii) the summed paratropic contribution from the cycles of size 0 mod 4 (weakest for ). As Figure 2b shows, the terminal faces and , which support the largest ring current, have the smallest contributions to local spin density in the neutral radical from the single electron in the non-bonding Hückel molecular orbital.
6. A New Cycle Current Model
The implementation of the Aihara version of the HL model described in Section 4 was used in our investigation of the possibility of improving existing conjugated-circuit models of induced current. This stage of the work has been described in detail in [43], and here we give only a brief sketch of the strategy and and an even shorter summary of the results.
6.1. Conjugated-Circuit Models of Current
As noted earlier, the conjugated-circuit (CC) model of aromaticity is based on the idea that the important cycles in a -system are those cycles C for which both G and have perfect matchings. By analogy with aromatic benzene and anti-aromatic cyclooctatetraene, cycles of size 2 mod 4 or 0 mod 4 are taken to have positive or negative effects on aromaticity. Initially, this idea was used as a way of correlating resonance energy with counts of cyclic substructures [36,63,64]. The idea was extended to the magnetic criterion of aromaticity by associating contributions from conjugated circuits with paratropicity (antiaromaticity)/diatropicity (aromaticity), according to the divisibility of the cycle size [37,39,40,41]. This is in effect an importation of monocycle results from HL theory, in that Kekulé structures in themselves do not have an obvious connection to the direction of current induced in ring by a perpendicular external magnetic field.
In the chemical literature, a popular approach to calculation of energetics and currents was to construct all conjugated circuits by making pairwise unions of Kekulé structures (perfect matchings) of the molecular graph G [39]. The union consists of a set of disjoint units where these edges are in both matchings, and a collection of even cycles where the edges in each cycle come alternately from the first and second matching. Some chemical models distinguish between cases where the union of two Kekulé structures contains only one cycle and where it contains a set of two or more disjoint cycles; with opinion divided over whether the latter case should be included in CC models of current.
A simpler way to look at the array of different CC models, which leads to a framework for classifying the various models is given in [42]. All the published CC models of current are covered by a formula for the contribution of a cycle C to bond currents. Each CC model attributes a bond current of [43]
to each edge of the cycle, where the ∓ sign allows for the diatropic/paratropic sense of the current and the factor of 2 arises from the two perfect matchings of an even cycle. The parameter a (equal to , or 1) defines the weighting by cycle area in the particular model. The parameter b (equal to 1 or 2) defines how the weights in the model depend on . The factor is usually unity but allows for the extra parameters that are introduced in some CC models. This factor has also been used to normalise CC currents in various ways, though this is not relevant for our comparisons of scaled current maps. The published CC models and their parameters are [43]:
Model R, [39], Model CKCDA, [40], Model M, [41], and Model GM, originally with , later used with [37]. The models that include non-trivial parameters are M and GM, as noted in [43]:
From the viewpoint of HL theory and the possibility of partitioning currents into cycle contributions, all CC models are approximations in which the true HL cycle current from Equation (7) has been replaced either by when C is conjugated, and zero otherwise. In fact, despite the different physical rationales for the choices of a, b and , all CC models give qualitatively similar accounts of the current maps of most benzenoids.
However, as noted in the Introduction, the CC model maps diverge widely from HL maps for benzenoids in two cases. The first is for the benzenoids with fixed bonds. These are either perylenoids (Kekulean with fixed single bonds) or zethrenoids (Kekulean with both fixed single and fixed double bonds). All fixed bonds carry zero current in the CC current maps, as a fixed bond cannot appear in a cycle in the union of two perfect matchings. In HL maps, however, such edges may carry significant current.
In the second case, the CC maps diverge from their HL counterparts in a more dramatic way. This is for the non-Kekulean benzenoids. All CC models necessarily predict zero current on all bonds of a non-Kekulean benzenoid, whereas the HL model gives a non-zero current map for all benzenoid species with electron counts between 1 and .
6.2. A Cycle-Current Model for All Benzenoids
Figure 3 gives an example of how CC and HL current maps can show major qualitative differences. The example is zethrene, the smallest of the zethrenoid family. In this case, the scaled map is identical for all CC models. This graph has five fixed single bonds and two fixed double bonds in the bridge region, and hence vanishing CC current in all bonds outside the terminal naphthalenoid units. However, the HL map shows currents on the bridge with of the maximum strength, and zero current in only one bond, where it is forced by symmetry. Our goal was to find a cycle current model that would be simple, give good current approximations overall, and avoids this ‘dead-zone’ limitation of conjugated-circuit models.
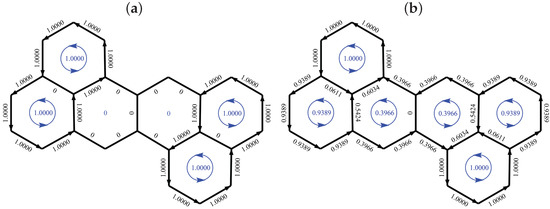
Figure 3.
Current maps of zethrene. (a) Scaled CC current; (b) scaled HL current.
We use the notation for the coefficient of in the characteristic polynomial of G. Note that for a benzenoid G, is 0 for odd n, and otherwise . The value of is also equal to the determinant of the adjacency matrix of G.
The new model was inspired by the Aihara partition of current, and the best form for the first term turned out to be identical with that of the CKCDA model, which itself was designed to have the same dependence on area as the Aihara expression (7) for cycle current. The CKCDA model [40] can be thought of as assigning a current of weight to each conjugated cycle C, with clockwise/anticlockwise sense for cycles of length or , respectively. We took this as the first term of the new approximation formula.
In order to ensure that some current is predicted in the non-conjugated cycles, a second term was included. Experimentation suggested adding a term proportional to . This term is analogous to the first term, but involves the next () coefficients in the characteristic polynomials for the bipartite graphs G and .
For a nonsingular matrix A, the classical adjoint matrix for A, denoted Adj is equal to Det. Application of Jacobi’s theorem allows the value of to be computed in time given the classical adjoint matrix.
The relative weight of first and second terms gives a disposable parameter in the new model, and after further experimentation it was decided to settle for a weighting of 4. This gives a formula for cycle contributions in Kekulean benzenoids that depends on the tail coefficients (i.e., those of and ) in and :
As a last step, to ensure that some current is predicted for non-Kekulean benzenoids, we rewrite this formula in a more general way, replacing by c and by , where is the nullity of the benzenoid graph G, so that in this case too we are using the tail coefficients of the characteristic polynomials. Thus, in final form the new model (Model W in [43]), has cycle contributions to current given by
Whatever the number of non-bonding orbitals in the benzenoid, the cycle contribution is specified in terms of the lowest and next-to-lowest powers of x that occur in . The result of this change is that the formula now gives currents for both Kekulean and non-Kekulean benzenoids, offering a unified solution to the two problems of fixed bonds and open shells that beset CC models.
6.3. Testing the Model
An evaluation of Model W is reported in [43], where its ability to track HL current maps was compared to that of the four published CC models and four hypothetical variants. For this comparison, the test set of benzenoids on up to 10 hexagonal rings was used: it comprises 18,360 Kekulean benzenoids (of which 2388 are perylenoids and 2184 are zethrenoids) and 20,112 non-Kekulean benzenoids.
Two types of comparison were made. Overall statistical measures of model quality were based on the bond-current error function for an edge of G, . This function is calculated for two sets of scaled currents, from the model under test and from the HL reference, using the formula , where each current is taken in the sense of the arc from u to v. Qualititative incorrectness of some maps is detected by counting misdirected graphs. A graph G is misdirected if at least one edge of G carries currents in and that are both non-negligible (magnitude ), run in opposite directions and give rise to . Error norms , and are computed for the set of bond-current errors for each model. ( is the mean absolute error, is the root mean square error, and is the maximum absolute error, all averaged over the molecules in the given test set). For misdirected graphs, a simple count is made.
Extensive tabulations of the relative performances of eight CC models and Model W for the test set and various subsets are given in [43]. The main conclusions are as follows.
First, Model W performs better than the best CC model for the set of Kekulean benzenoids. The errors calculated with , and norms are all reduced by factors of two or more compared to the best CC model. Model W has , and , expressed as percentages of the maximum scaled current in each molecule. This good performance is maintained when the test set is restricted to zethrenoids. Every CC model gives at least 2247 misdirected Kekulean benzenoid graphs, including at least 952 zethrenoids, whereas the new model gives only 110 in total, all of which are zethrenoids.
Secondly, the new model performs even better for non-Kekulean benzenoids. For the non-Kekulean benzenoids, Model W gives errors of , and , and no misdirected graphs at all.
7. Conclusions
The design of this useful effective new model of current maps in benzenoids benefitted considerably from the availability of an implementation of the Aihara cycle partition of HL theory. Other applications are planned.
Author Contributions
Conceptualization, W.M. and P.W.F.; methodology, W.M., P.W.F. and J.C.; software, W.M., P.W.F. and J.C.; validation, W.M., P.W.F. and J.C.; formal analysis, W.M., P.W.F. and J.C.; investigation, W.M., P.W.F. and J.C.; resources, W.M. and P.W.F.; data curation, W.M. and P.W.F.; writing—original draft preparation, W.M., P.W.F. and J.C.; writing—review and editing, W.M., P.W.F. and J.C.; visualization, P.W.F. and J.C.; supervision, P.W.F.; project administration, W.M. and P.W.F.; funding acquisition, W.M. and P.W.F.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Faraday, M. On New Compounds of Carbon and Hydrogen, and on Certain Other Products Obtained during the Decomposition of Oil by Heat. Philos. Trans. R. Soc. Lond. 1825, 115, 440–446. [Google Scholar] [CrossRef][Green Version]
- Rocke, A.J. It Began with a Daydream: The 150th Anniversary of the Kekulé Benzene Structure. Angew. Chem. Int. Ed. 2015, 54, 46–50. [Google Scholar] [CrossRef]
- Kekulé, A. Sur la constitution des substances aromatiques. Bulletin de la Société Chimique de Paris 1865, 3, 98–110. [Google Scholar]
- Aromaticity: An International Symposium Held at Sheffield on 6th–8th July 1966; The Chemical Society: London, UK, 1966.
- Bergmann, E.D.; Pullman, B. Aromaticity, Pseudo-Aromaticity, Anti-Aromaticity, The Jerusalem Symposium on Quantum Chemistry and Biochemistry III; Academic Press Inc.: New York, NY, USA, 1971. [Google Scholar]
- Schleyer, P.V.R.; Jiao, H. What is aromaticity? Pure Appl. Chem. 1996, 68, 209–218. [Google Scholar] [CrossRef]
- Special Issue on ‘Aromaticity’. Chem. Rev. 2001, 101, 1115–1566.
- Lazzeretti, P. Assessment of aromaticity via molecular response properties. PCCP 2004, 6, 217–223. [Google Scholar] [CrossRef]
- Special Issue on ‘Delocalisation- Pi and Sigma’. Chem. Rev. 2005, 105, 3433–3947.
- Themed Collection on ‘Challenges in Aromaticity: 150 Years after Kekulé’s Benzene’. Chem. Soc. Rev. 2015, 44, 6397–6643. [CrossRef] [PubMed]
- Hoffmann, R. The many guises of aromaticity. Am. Sci. 2015, 103, 18–22. [Google Scholar] [CrossRef]
- Zhao, L.; Grande-Aztatzi, R.; Foroutan-Nejad, C.; Ugalde, J.M.; Frenking, G. Aromaticity, the Hückel 4n + 2 Rule and Magnetic Current. Chem. Sel. 2017, 2, 863–870. [Google Scholar]
- Pauling, L. The Diamagnetic Anisotropy of Aromatic Molecules. J. Chem. Phys. 1936, 4, 673–677. [Google Scholar] [CrossRef]
- London, F. Théorie quantique des courants interatomiques dans les combinaisons aromatiques. J. Phys. Radium 1937, 8, 397–409. [Google Scholar] [CrossRef]
- Lonsdale, K. Diamagnetic anisotropy of conjugated compounds. J. Chem. Soc. 1937, 364–368. [Google Scholar] [CrossRef]
- Pople, J.A. Molecular orbital theory of aromatic ring currents. Mol. Phys. 1958, 1, 175–180. [Google Scholar] [CrossRef]
- McWeeny, R. Ring currents and proton magnetic resonance in aromatic molecules. Mol. Phys. 1958, 1, 311–321. [Google Scholar] [CrossRef]
- Elvidge, J.A.; Jackman, L.M. Studies of aromaticity by nuclear magnetic resonance spectroscopy. Part 1. 2-pyridones and related systems. J. Chem. Soc. 1961, 859–866. [Google Scholar] [CrossRef]
- Schleyer, P.V.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-independent chemical shifts: A simple and efficient aromaticity probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef] [PubMed]
- Steiner, E.; Fowler, P.W. Four- and two-electron rules for diatropic and paratropic ring currents in monocyclic π systems. Chem. Commun. 2001, 2220–2221. [Google Scholar] [CrossRef]
- Dauben, H.J.; Wilson, J.D.; Laity, J.L. Diamagnetic susceptibility exaltation as a criterion of aromaticity. J. Am. Chem. Soc. 1968, 90, 811–813. [Google Scholar] [CrossRef]
- Keith, T.A.; Bader, R.F.W. Calculation of magnetic response properties using a continuous set of gauge transformations. J. Am. Chem. Soc. 1993, 210, 223–231. [Google Scholar] [CrossRef]
- Lazzeretti, P.; Malagoli, M.; Zanasi, R. Computational approach to molecular magnetic properties by continuous transformation of the origin of the current density. Chem. Phys. Lett. 1994, 220, 299–304. [Google Scholar] [CrossRef]
- Coriani, S.; Lazzeretti, P.; Malagoli, M.; Zanasi, R. On CHF calculations of 2nd-order magnetic properties using the method of continuous transformation of origin of the current density. Theor. Chim. Acta 1994, 89, 181–192. [Google Scholar] [CrossRef]
- Steiner, E.; Fowler, P.W. Patterns of Ring Currents in Conjugated Molecules: A Few-Electron Model Based on Orbital Contributions. J. Phys. Chem. A 2001, 105, 9553–9562. [Google Scholar] [CrossRef]
- Monaco, G.; Summa, F.F.; Zanasi, R. Program Package for the Calculation of Origin-Independent Electron Current Density and Derived Magnetic Properties in Molecular Systems. J. Chem. Inf. Mod. 2021, 61, 270–283. [Google Scholar] [CrossRef]
- Monaco, G.; Zanasi, R. Three Contra-Rotating Currents from a Rational Design of Polycyclic Aromatic Hydrocarbons: altan-Corannulene and altan-Coronene. J. Phys. Chem. A 2012, 116, 9020–9026. [Google Scholar] [CrossRef]
- Salem, L. The Molecular Orbital Theory of Conjugated Systems; W.A. Benjamin: New York, NY, USA, 1966. [Google Scholar]
- Pasquarello, A.; Schlüter, M.; Haddon, R.C. Ring currents in topologically complex molecules: Application to C60, C70, and their hexa-anions. Phys. Rev. A 1993, 47, 1783–1789. [Google Scholar] [CrossRef]
- Haigh, C.W.; Mallion, R.B.; Armour, E.A.G. Proton magnetic resonance of planar condensed benzenoid hydrocarbons II. A critical evaluation of the McWeeny ‘ring current’ theory. Mol. Phys. 1970, 18, 751–766. [Google Scholar] [CrossRef]
- Haigh, C.W.; Mallion, R.B.; Armour, E.A.G. On the magnetic properties of conjugated molecules. Mol. Phys. 1973, 25, 1415–1432. [Google Scholar]
- Mallion, R.B. Some Graph-Theoretical Aspects of Simple Ring Current Calculations on Conjugated Systems. Proc. R. Soc. Lond. A 1975, 341, 429–449. [Google Scholar]
- Dickens, T.K.; Mallion, R.B. An analysis of topological ring currents and their use in assessing the annulene within an annulene model for super-ring conjugated systems. Croatica Chem. Acta 2013, 86, 387–406. [Google Scholar] [CrossRef]
- Aihara, J. Theoretical relationship between diamagnetic susceptibility exaltation and aromatic stabilization. J. Am. Chem. Soc. 1979, 101, 558–560. [Google Scholar] [CrossRef]
- Aihara, J. Graph-theoretical formulation of London diamagnetism. J. Am. Chem. Soc. 1979, 101, 5913–5917. [Google Scholar] [CrossRef]
- Randić, M. Conjugated circuits and resonance energies of benzenoid hydrocarbons. Chem. Phys. Lett. 1970, 38, 68–70. [Google Scholar] [CrossRef]
- Gomes, J.A.N.F.; Mallion, R.B. A Quasi-topological method for the calculation of relative ring current intensities in polycyclic, conjugated hydrocarbons. Rev. Port. Quim. 1979, 21, 82–89. [Google Scholar]
- Randić, M. Aromaticity of Polycyclic Conjugated Hydrocarbons. Chem. Rev. 2003, 103, 3449–3606. [Google Scholar] [CrossRef] [PubMed]
- Randić, M. Graph theoretical approach to π-electron currents in polycyclic conjugated hydrocarbons. Chem. Phys. Lett. 2010, 500, 123–127. [Google Scholar] [CrossRef]
- Ciesielski, A.; Krygowski, T.M.; Cyrański, M.K.; Dobrowolski, M.A.; Aihara, J. Graph-topological approach to magnetic properties of benzenoid hydrocarbons. PCCP 2009, 11, 11447–11455. [Google Scholar] [CrossRef]
- Mandado, M. Determination of London Susceptibilities and Ring Current Intensities using Conjugated Circuits. J. Chem. Theory Comput. 2009, 5, 2694–2701. [Google Scholar] [CrossRef]
- Fowler, P.W.; Myrvold, W. The ‘anthracene problem’: Closed-form conjugated-circuit models of ring currents in linear polyacenes. J. Phys. Chem. A 2011, 115, 13191–13200. [Google Scholar] [CrossRef]
- Fowler, P.W.; Myrvold, W.; Gibson, C.; Clarke, J.; Bird, W.H. Ring-current maps for benzenoids: Comparisons, contradictions, and a versatile combinatorial model. J. Phys. Chem. A 2020, 124, 4517–4533. [Google Scholar] [CrossRef]
- Gutman, I.; Radenković, S. Paradise Lost: π-Electron Conjugation in Homologs and Derivatives of Perylene. In Applications of Topological Methods in Molecular Chemistry; Springer International: Berlin, Germany, 2016; pp. 297–320. [Google Scholar]
- Radenković, S.; Bultinck, P.; Gutman, I.; Đurđević, J. On induced current density in the perylene/bisanthrene homologous series. Chem. Phys. Lett. 2012, 552, 151–155. [Google Scholar] [CrossRef]
- Mallion, R.B. Topological ring currents in condensed benzenoid hydrocarbons. Croat. Chem. Acta 2008, 81, 227–246. [Google Scholar]
- Aihara, J.; Horikawa, T. Graph-theoretical Formula for Ring Currents Induced in a Polycyclic Conjugated System. Bull. Chem. Soc. Jpn. 1983, 56, 1853–1854. [Google Scholar] [CrossRef]
- Coulson, C.A.; Rushbrooke, G.S. Note on the method of molecular orbitals. Proc. Camb. Philos. Soc. 1940, 36, 193–200. [Google Scholar] [CrossRef]
- Soncini, A.; Fowler, P.W. Ring-Current Aromaticity in Open-Shell Systems. Chem. Phys. Lett. 2008, 450, 431–436. [Google Scholar] [CrossRef]
- Ramos-Berdullas, N.; Radenković, S.; Bultinck, P.; Mandado, M. Aromaticity of Closed-Shell Charged Polybenzenoid Hydrocarbons. J. Phys. Chem. A 2013, 117, 4679–4687. [Google Scholar] [CrossRef]
- Aihara, J. Aromaticity and Diatropicity. Pure Appl. Chem. 1982, 54, 1115–1128. [Google Scholar] [CrossRef]
- Aihara, J. Circuit Resonance Energy: A Key Quantity That Links Energetic and Magnetic Criteria of Aromaticity. J. Am. Chem. Soc. 2006, 128, 2873–2879. [Google Scholar] [CrossRef]
- Aihara, J. Dimensionality of aromaticity. Bull. Chem. Soc. Jpn. 2008, 2, 241–247. [Google Scholar] [CrossRef]
- Aihara, J. Unified theory of aromaticity and London diamagnetism. J. Am. Chem. Soc. 1981, 103, 5704–5706. [Google Scholar] [CrossRef]
- Aihara, J.; Horikawa, T. General graph-theoretical formula for the London susceptibility of a cyclic conjugated system with highly degenerate orbitals. Chem. Phys. Lett. 1983, 95, 561–563. [Google Scholar] [CrossRef]
- Aihara, J. Magnetotropism of biphenylene and related hydrocarbons. A circuit current analysis. J. Am. Chem. Soc. 1985, 107, 298–302. [Google Scholar] [CrossRef]
- Aihara, J. Magnetic Resonance Energy and the Aromaticity of Polycyclic Aromatic Hydrocarbon Dianions/Dications. Bull. Chem. Soc. Jpn. 2004, 77, 651–659. [Google Scholar] [CrossRef]
- Aihara, J. Graph Theory of Ring-Current Diamagnetism. Bull. Chem. Soc. Jpn. 2018, 91, 274–303. [Google Scholar] [CrossRef]
- Estrada, E. On the dimensionality of aromaticity criteria. MATCH Commun. Math. Comput. Chem. 2006, 56, 331–344. [Google Scholar]
- Gibbons, A. Algorithmic Graph Theory; Cambridge University Press: Cambridge, UK, 1985; pp. 54–57. [Google Scholar]
- Gross, J.; Yellen, J. Graph Theory and Its Applications, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2005; pp. 652–656. [Google Scholar]
- Bultinck, P. Critical analysis of the local aromaticity concept in polyaromatic hydrocarbons. Faraday Discuss. 2007, 135, 347–365. [Google Scholar] [CrossRef] [PubMed]
- Gutman, I.; Polansky, O.E. Mathematical Concepts in Organic Chemistry; Springer: Berlin, Germany, 1986. [Google Scholar]
- Trinajstić, N. Chemical Graph Theory, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).