Next Article in Journal
Study on Adsorption Performance of Benzoic Acid in Cyclocarya paliurus Extract by Ethyl Cellulose Microspheres
Next Article in Special Issue
Partitioning Hückel–London Currents into Cycle Contributions
Previous Article in Journal / Special Issue
Chirality Transfer in a Calixarene-Based Directional Pseudorotaxane Complex
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Chemistry
Volume 3
Issue 4
10.3390/chemistry3040080
chemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

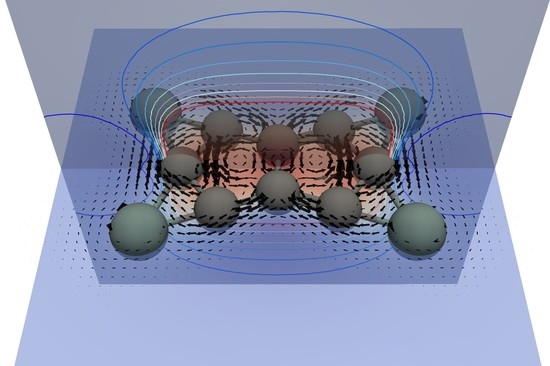
Analysis of Local and Global Aromaticity in Si3C5 and Si4C8 Clusters. Aromatic Species Containing Planar Tetracoordinate Carbon

by
Juan J. Torres-Vega
1,
Diego R. Alcoba
2,3,
Ofelia B. Oña
4,
Alejandro Vásquez-Espinal
5,
Rodrigo Báez-Grez
5,
Luis Lain
6,
Alicia Torre
6,
Víctor García
7,* and
William Tiznado
5,*
1
Centro de Investigaciones Tecnológicas, Biomédicas y Medioambientales, Calle José Santos Chocano 199, Urb. San Joaquín, Callao 07006, Peru
2
Departamento de Física, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, Ciudad Universitaria, Buenos Aires 1428, Argentina
3
Instituto de Física de Buenos Aires, Consejo Nacional de Investigaciones Científicas y Técnicas, Ciudad Universitaria, Buenos Aires 1428, Argentina
4
Instituto de Investigaciones Fisicoquímicas Teóricas y Aplicadas, Universidad Nacional de La Plata, CCT La Plata, Consejo Nacional de Investigaciones Científicas y Técnicas, Diag. 113 y 64 (S/N), Sucursal 4, CC 16, La Plata 1900, Argentina
5
Computational and Theoretical Chemistry Group, Departamento de Ciencias Químicas, Facultad de Ciencias Exactas, Universidad Andres Bello, República 498, Santiago 8370251, Chile
6
Departamento de Química Física, Facultad de Ciencia y Tecnología, Universidad del País Vasco, Apdo. 644, E-48080 Bilbao, Spain
7
Departamento Académico de Fisicoquímica, Facultad de Química e Ingeniería Química, Universidad Nacional Mayor de San Marcos, Lima 15004, Peru
*
Authors to whom correspondence should be addressed.
Chemistry 2021, 3(4), 1101-1112; https://doi.org/10.3390/chemistry3040080
Submission received: 20 August 2021 / Revised: 14 September 2021 / Accepted: 17 September 2021 / Published: 25 September 2021
(This article belongs to the Special Issue Current Density and Spectroscopy—A Themed Issue in Honor of Professor Riccardo Zanasi on the Occasion of His 70th Birthday)
Browse Figures
Review Reports Versions Notes

Abstract

:
The minimum energy structures of the Si3C5 and Si4C8 clusters are planar and contain planar tetracoordinate carbons (ptCs). These species have been classified, qualitatively, as global (π) and local (σ) aromatics according to the adaptive natural density partitioning (AdNDP) method, which is an orbital localization method. This work evaluates these species’ aromaticity, focusing on confirming and quantifying their global and local aromatic character. For this purpose, we use an orbital localization method based on the partitioning of the molecular space according to the topology of the electronic localization function (LOC-ELF). In addition, the magnetically induced current density is analyzed. The LOC-ELF-based analysis coincides with the AdNDP study (double aromaticity, global, and local). Moreover, the current density analysis detects global and local ring currents. The strength of the global and local current circuit is significant, involving 4n + 2 π- and σ-electrons, respectively. The latter implicates the Si-ptC-Si fragment, which would be related to the 3c-2e σ-bond detected by the orbital localization methods in this fragment.

Graphical Abstract

1. Introduction

The concept of aromaticity has been extended over time to coin new features that define a system as aromatic and address a diversity of organic and inorganic systems [1,2,3,4,5]. In this regard, nowadays the concept of aromaticity, π and σ, is used extensively to rationalize the stability of some atomic clusters [6]. Accordingly, the aromaticity well justifies the clusters’ highly symmetric and stable structures. So, numerous planar boron clusters [7,8,9], metal clusters [1,5,6,7,10,11,12,13,14], and metallabenzenes [15,16,17,18,19] fit well into the concept of aromaticity. Along with π- and σ-aromaticity, multiple local π-aromaticity shows to be a helpful concept for rationalizing complex conjugate systems, such as polycyclic hydrocarbons or graphene [20,21]. Moreover, it was indicated that the concept of multiple local σ-aromaticity is also applicable in the chemistry of nonagermanide clusters [22].
Chemists dedicate considerable effort to predicting new molecules with exotic non-classical structures. Planar hypercoordinate carbons, i.e., carbon linked to four or more ligands in the plane, are especially puzzling systems. With the modest goal of achieving a thermally accessible transition state for a classical racemization experiment, in 1970 Hoffman and coworkers introduced strategies to stabilize a planar tetracoordinate carbon (ptC) [23]. Notably, this study inspired many theoretical and experimental studies over the last 50 years culminating in numerous compounds with ptCs [24,25,26,27,28,29,30]. More recently, “planar hypercoordinate” chemistry expanded to include planar species where the central atom is not limited to carbon, and the coordination number is more than four. Species with planar pentacoordinate [31,32,33,34,35,36,37,38] and hexacoordinate [39,40,41,42] carbons (ppCs or phCs) have been designed in silico. Electronic delocalization (i.e., aromaticity, resonance) plays a determining role in the stability of many of these species. Consequently, a comprehensible chemical bonding analysis is fundamental for interpreting their stability. For instance, the 18-valence electron D4h-CAl42− cluster is a doubly σ- and π-aromatic cluster experimentally detected in the Na+[CAl42−] complex [29,30]. Of particular interest in this work is the concept of aromaticity (π, σ, local, global) and the role it plays in justifying the stability of systems with planar hypercoordinate carbons.
Aromaticity is not an observable property, yet it is generally assessed in terms of structural, energetic, and magnetic criteria [3,43,44,45,46,47,48]. Aromatic and antiaromatic species sustain diatropic and paratropic ring currents when exposed to a uniform magnetic field perpendicular to the molecular plane [49,50,51,52,53,54]. This magnetic response allows the interpretation of experimental NMR spectroscopy and magnetic anisotropy measurements on (anti) aromatic molecules [45,55]. The nucleus-independent chemical shift (NICS) is a very popular theoretical descriptor used for assessing aromaticity. Schleyer and coworkers defined the NICS as “the negative of the absolute magnetic shielding,” further suggesting to compute it at the molecular center [56]. Note that the Biot–Savart law connects the induced magnetic field at the ring center, and thus the chemical shift at this point, to the ring current density [57]. In particular, the out-of-plane component of the NICS measured above the molecular plane [i.e., NICSzz(1)] is well correlated with the intensity of the ring current flux (according to the ring current strength, RCS, values) [58,59]. However, some works reported significant discrepancies between the NICS-based and the current density-based analyses for systems with multiple (local and global) aromaticity (i.e., aromatic polycyclic hydrocarbons) [60,61]. These differences are because the NICS is affected by coupling contributions from local and global aromatic circuits, making it difficult to assign local, semilocal, and global ring current contributions.
Previously, some of the authors of this work designed a series of ptC global minima composed of carbon and heavier atoms of group 14 of the periodic table [62,63,64]. The design strategy consisted of replacing three consecutive protons from an aromatic hydrocarbon by one E24+ fragment (E = Si-Pb), favoring the preservation of the π-aromatic circuits of the parent aromatic hydrocarbons (see Scheme 1) [62]. Interestingly, the systems Si3C5, Ge3C5, Si4C8, and Ge4C8 (C5H5− and C8H62− derivatives) contain one or two ptCs in their lowest energy structures. The chemical bonding analysis—employing the adaptive natural density partitioning analysis (AdNDP)—suggests that these systems are globally π-aromatic and locally σ-aromatic. This aromatic character was supported by the analysis of the nucleus-independent chemical shift (NICS) [62].
Given the NICS problems mentioned above, in this work we analyze the local and global ring currents in the Si3C5 and Si4C8 systems. In addition, we analyzed the chemical bonding with the ELF-LOC method, an orbital localization scheme in the domains of the electronic localization function (ELF). The ELF-LOC, like AdNDP, provides information related to electronic delocalization, given its flexibility to identify orbitals distributed in more than two atomic centers. Our results confirm the presence of two delocalization circuits, one global (π) and one local (σ). More importantly, the global and local ring currents are diatropic and significant (according to the ring current strength, RCS, calculations). These results strongly support these systems’ double aromatic character (local and global) and their role in their stability.

2. Computational Methods

Geometry optimizations were performed at B3LYP [65]/6-311+G* [66,67] level. Vibrational frequencies were evaluated at the same level to confirm the optimized structures as true minima on their potential energy surface using the Gaussian16 program [68]. Cartesian coordinates of the optimized structures are shown in Table S1.
A detailed description of the ELF-LOC algorithm can be found elsewhere [69,70,71,72]. In this work, all numerical determinations were performed at the B3LYP level within density functional theory (DFT), using the atomic STO-3G basis sets. The overlap integrals over the ELF regions, required to calculate the localized natural orbitals, were obtained from the GAMESS computational package [73] and a modified version of the ToPMoD program [74]. The orbital localization was performed using our codes [69,70].
Current densities were computed with the GIMIC program [75,76] using the gauge- including atomic orbital (GIAO) [77] method. In the calculations, the magnetic field is directed along the z-axis, i.e., perpendicular to the molecular plane. The unit for current susceptibility is nA T−1 and the results are, therefore, independent of the magnitude of the magnetic field. For a qualitative analysis, vector plots of the current density in a plane placed 0.0 and 0.5 Å above the molecular plane were generated. Diatropic (aromatic) and paratropic (antiaromatic) currents are assumed to circle clockwise and counterclockwise, respectively. Current pathways are visualized using Paraview [78,79]. The ring current strengths (RCS), a measure of the net current intensity around the molecular ring, were obtained after considering different integration planes (see Figures S1–S3). The integration planes correspond to cut-off planes perpendicular to the chosen bonds of the molecule and extend horizontally along the ring’s plane in 3.6 Å, with 2.6 Å above and below the ring. The two-dimensional Gauss-Lobatto algorithm [76,80] was used to integrate the current passing through an integration plane.
Vector plot visualization of the current density in the plane of the molecule and 0.5Å above are reported in Figures S1–S5. It is essential to mention that the negative (diatropic) and the positive (paratropic) NICS at the center of the molecules are associated with aromaticity and anti-aromaticity. In contrast, for the RCS, a positive (diatropic) and negative (paratropic) sign correspond to aromatic and anti-aromatic molecules, respectively. For both the NICS and the RCS, values close to zero suggest non-aromatic behavior [81]. Both the NICS and the current density analysis were performed at B3LYP/6-311+G* level.
The NICS were computed using the gauge-including atomic orbital (GIAO) [77] method and dissected into their core, σ, and π contributions, using the natural chemical shielding (NCS) [82] analysis as implemented in the NBO 6.0 program [83]. To evaluate the NICS, we used NICSall, a simple program developed in our group, which is interfaced with the Gaussian program. NICSall helps to prepare the inputs and submits the calculations to generate the data according to the user’s requirements. In this work, we computed the NICS in 2D. To do this, we first estimated the box size, which in this case was defined by the sides equal to 1.5 times the length and width of the molecule (centered and placed in the XY plane) by the height (z-axis), taking their lowest value. NICSall prepares the inputs to fill the grid with a step size of 0.2 Å (this is a default value; it could be modified by the user). Finally, NICSall delivers the outputs: text files with the properties (scans, FiPC-NICS) or cube files to plot maps and isosurfaces. The NICS plots were performed with the VisIt 3.0.2 program [84].
It is essential to mention that both the ring currents analysis [76] and the ELF analysis [85,86] are not very dependent on the method or the basis set used in their calculation.

3. Results

For the sake of clarity, our analysis will be divided into two parts: the chemical bonding analysis according to the ELF-LOC method and the global and local aromaticity analysis according to magnetic criteria.

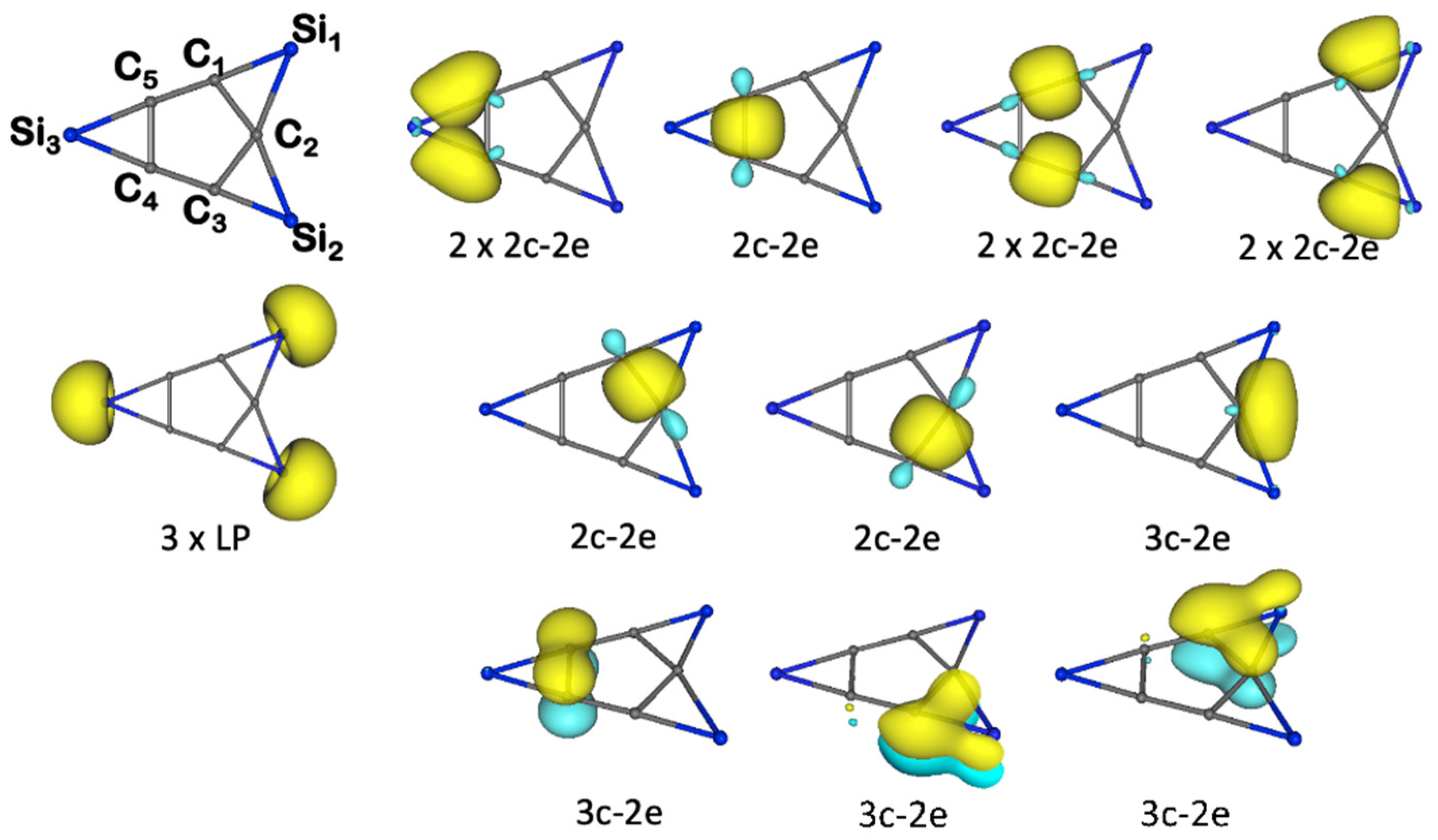
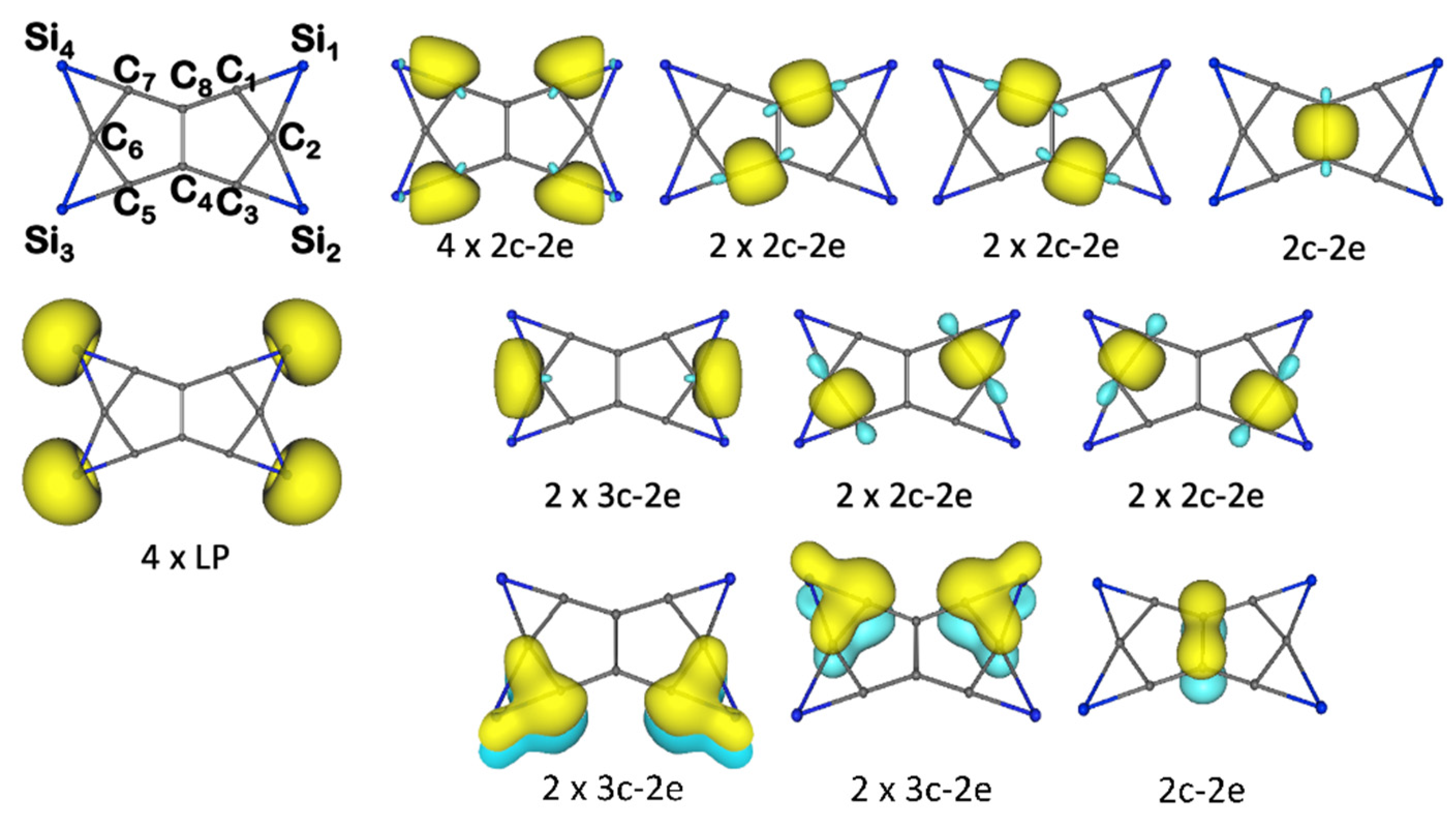
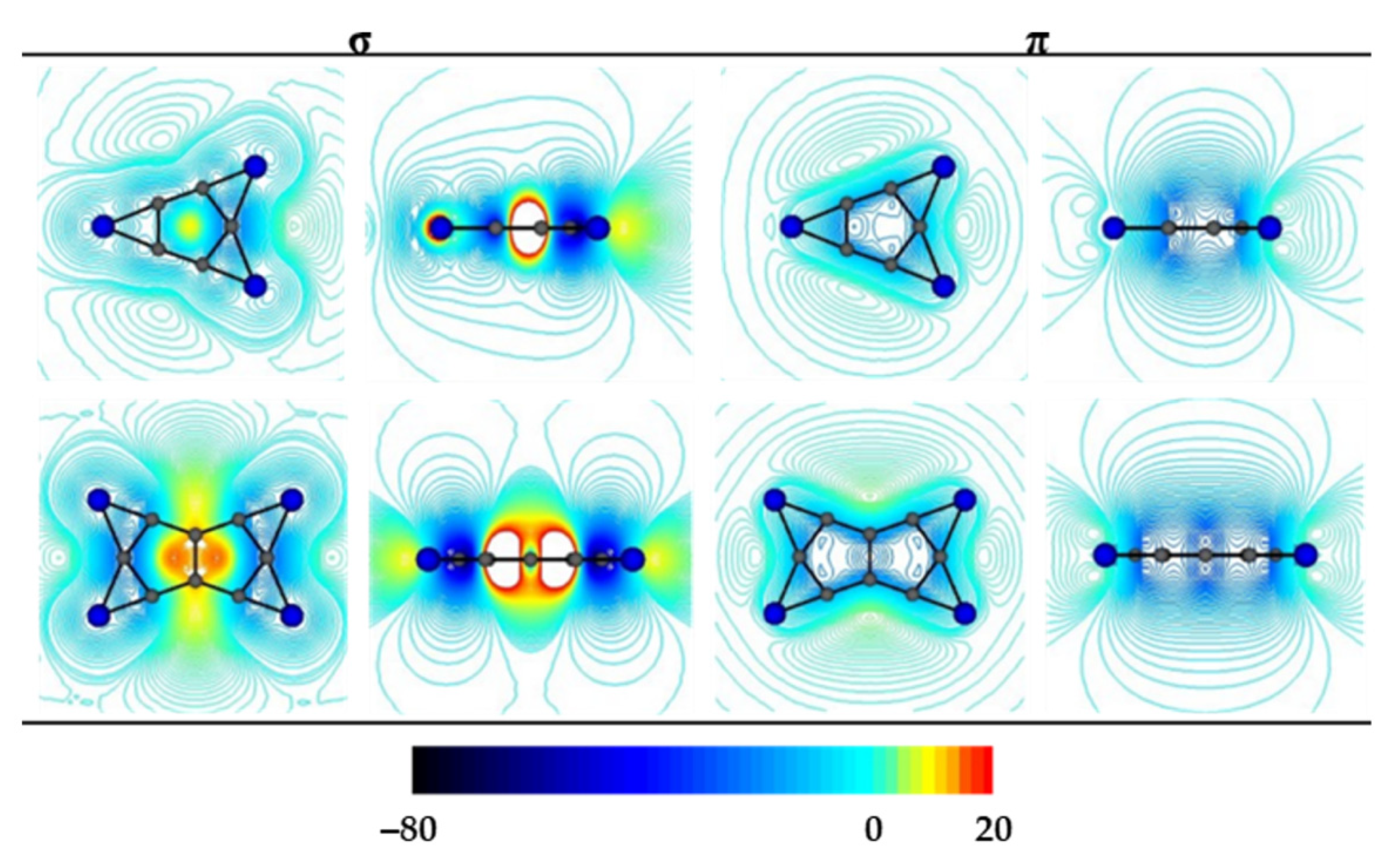
3.1. Chemical Bonding Analysis According to the ELF-LOC Method

The orbital localization provided by the ELF-LOC method reveals a chemical bonding pattern similar to that described by AdNDP, as shown in Figure 1 and Figure 2. In Si3C5 and Si4C8, the C5 and C8 rings are connected by 2-center 2-electron C-C σ-bonds (2c-2e). For Si4C8, one C-C σ-bond (2c-2e) that splits the C8 ring into two pentagons is also detected. Additionally, delocalized bonds are detected, three π-bonds in the case of Si3C5 and five in Si4C8. Note that in this set, the π-orbitals are distributed over the entire molecular structure. Moreover, delocalized σ-bonds (3c-2e) are also detected in each Si-ptC-Si triangular fragment. These results support global π- and local σ-delocalization, suggesting possible global and local aromaticity according to Hückel’s 4n + 2 rule [87,88,89].

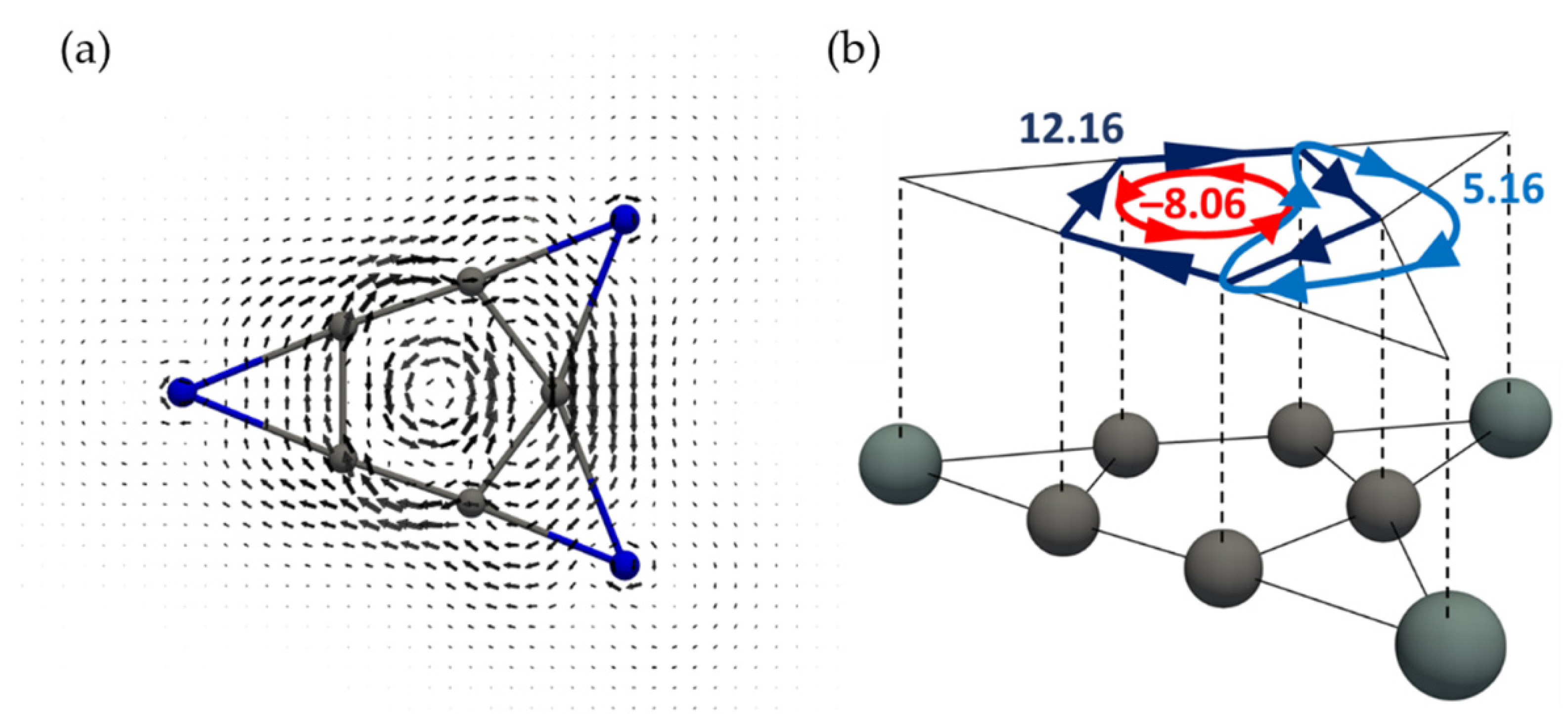
3.2. Current Density Analysis

According to the magnetic criteria, in the presence of an external magnetic field, aromatic (antiaromatic) molecules sustain diatropic (paratropic) currents. In contrast, in nonaromatic molecules, the currents in one direction or the other cancel out, giving a resultant current strength close to zero [53,54,55,76,81,90,91]. In this work, we define “local ring current” as the current circuits distributed in a local molecular ring. In contrast, we describe the “global ring current” circuit as distributed around the whole molecule. This assignment was introduced by Sundholm et al. [61] and recently used by our group to highlight the shortcomings of the NICS in assessing the aromaticity of polycyclic systems [92]. Note that Aihara introduced a similar concept to distinguish between different current density pathways [93].
We can glimpse the patterns of current flows by inspecting current density plots. Hence, the magnetically induced current density of Si3C5 and Si4C8 systems, calculated in a plane located 0.5 Å above the molecular plane, are shown in Figure 3 and Figure 4 (part a). These plots guide our selection of the integration planes. The different contributions (bond, atomic and ring currents) are defined and quantified by analyzing the integration profiles along the integration planes, see Figures S1 and S2. In this way, it is possible to computationally determine the local and global character of the induced currents. The strength of the local currents (diatropic) is computed and then subtracted from the strength of the diatropic current connecting the local rings to determine the global RCS [61,92]. Accordingly, it has been possible to identify the different delocalization circuits in the studied systems (part b of Figure 3 and Figure 4). In addition, the intensity of each current is also shown in these figures. For the Si3C5 system, an intense and paratropic current is detected inside the C5 (RCS = −8.06 nA/T). This ring current is more paratropic than that exhibited by the cyclopentadienyl anion (−3.5 nA T−1), the results of which are shown in Figure S3. A global diatropic ring current with a strength of 12.2 nA T−1 is also detected. The latter result is from the delocalization of the six π-electrons and is weaker than that of the cyclopentadienyl anion (14.5 nA T−1). The differences may be due to the effect of the polarization of the π-electron cloud toward the silicon atoms. This hypothesis is supported by analyzing the Si2C5H2 system, with one less bridged silicon atom exhibiting a paratropic (RCS = −3.6 nA T−1) and diatropic (RCS = 13.4 nA T−1) current intensity closer to those of the cyclopentadienyl anion (see Figures S3 and S5). Interestingly, a local diatropic ring current involving the Si-ptC-Si fragment is also detected, in complete agreement with that predicted by AdNDP and the ELF-LOC, which indicated the presence of a σ-delocalized 3c-2e bond. Moreover, the RCS value (5.2 nA/T) suggests that this species has a moderate local σ-aromatic character.
For the case of the Si4C8 system (Figure 4), the current density analysis detects two paratropic and local ring currents (within each C5 ring). Similar to Si3C5, these currents are more paratropic (RCS = −4.7 nA T−1) than those of the pentalene dianion (RCS = −4.4 nA T−1), whose current density analysis is shown in Figure S4. We also detect a weak global paratropic ring current (RCS = −1.6 nA T−1) distributed around the C8 fragment in addition to an intense global diatropic current (RCS = 10.4 A T−1). The global diatropic current is less intense than those of the pentalene dianion (RCS = 10.4 A T−1), presumably because of the polarization of the π-electron cloud toward the silicon. Finally, two local sigma currents are detected, involving the Si-ptC-Si circuits, similar to that exhibited by Si3C5 system. Moreover, these currents are of moderate intensity (RCS = 5.8 nA T−1), leaving in evidence the local sigma aromatic character of these species.

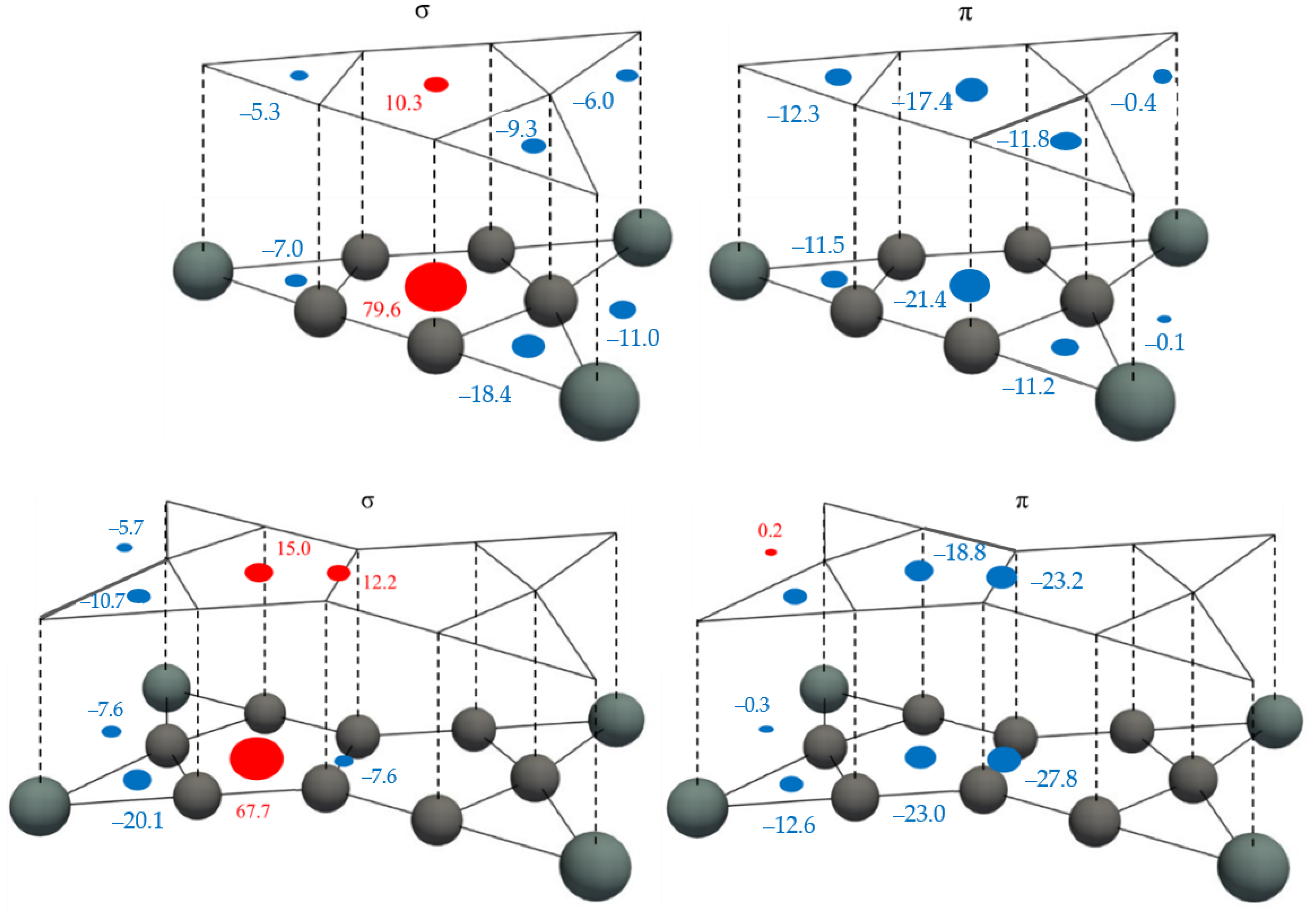
3.3. NICS Analysis

Figure 5 shows the σ- and π-components of the NICSzz computed in both the molecular plane and a plane perpendicular to the molecular plane for the Si3C5 and Si4C8 systems. These plots are in complete agreement with the ring current analysis. The σ-component clearly depicts paratropic regions at the center of the C5 rings in both Si3C5 and Si4C8, in accord with the presence of paratropic ring currents inside these rings. In addition, an intense diatropic region (long-range) centered on the local Si-ptC-Si ring is observed supporting the presence of a local diatropic current in this region. The π-component exhibits a strong diatropic region around the whole Si3C5 and Si4C8 ring (long-range), in agreement with the presence of a global diatropic ring current. As indicated previously [61,92], the NICS analysis does not allow the identification of all the ring current circuits. However, it is a suitable complement to understand the magnetic behavior of these species and the interpretation of their aromaticity under the magnetic criterion. Figure 6 shows a classical NICSzz analysis, i.e., discrete measurements at the center of the ring and 1.0 A above. The values measured in the molecular plane are pretty large (presumably because of the coupling of bond contributions). In contrast, the values above the plane agree with the current strength values measured in the induced current density analysis. In addition, Figures S6–S8 show an identical NICSzz analysis for Si2C5H2, the cyclopentadienyl anion (C5H5−), and the pentalene dianion (C8H62−). As seen with the current density analysis, diatropicity due to π-delocalization decreases for species with ptCs, presumably by the electron cloud polarization towards silicon atoms.

4. Conclusions

The global (π) and local (σ) aromaticity of Si3C5 and Si4C8 clusters have been reviewed, employing an orbital localization method (ELF-LOC) and magnetically induced current density analysis.
The ELF-LOC investigation leads to bond descriptions like those reported previously, based on the adaptive natural partitioning analysis (AdNDP) method. These systems show σ- and π-delocalization in agreement with Hückel’s rule of 4n + 2 electrons.
The induced current density analysis identifies global and local aromatic current circuits. In the case of Si3C5, a local paratropic current (of moderate-intensity, RCS = −8.1 nA T−1) is detected inside the C5 ring. However, a diatropic current of higher intensity (RCS = 12.16 nA T−1) is also present, which provides a global aromatic character to this species. A local σ-diatropic current involving the Si-ptC-Si fragment is also identified, with moderate intensity (RCS = 5.2 nA T−1). These results highlight the double aromatic character of this species. In the case of Si4C8, a weak global paratropic current (RCS = −1.5 nA T−1) and an intense global diatropic current (RCS = 10.4 nA T−1) are identified. In addition, two local diatropic currents around the Si-ptC-Si rings (RCS = 5.8 nA T−1) are also identified. This study highlights the double aromatic character of these clusters and the importance of this delocalization pattern in the stabilization of these species.
The ptC structures of the Si3C5 and Si4C8 clusters correspond to the global minima and, together with their double aromatic character, suggest that gas-phase experiments could detect these species.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/chemistry3040080/s1, Table S1: Cartesian coordinates of the studied systems, Figure S1: (a) Vector plot visualization of the current density of Si3C5 in a plane placed 0.5 Å above the molecular plane and top view of integration planes. (b) Integration profiles along the integration planes of Si3C5, Figure S2: (a) Vector plot visualization of the current density of Si4C8 in a plane placed 0.5 Å above the molecular plane and top view of integration planes. (b) Integration profiles along the integration planes of Si4C8, Figure S3: (a) Vector plot visualization of the current density of C5H5− in a plane placed 0.5 Å above the molecular plane and top view of integration planes (RCS are also reported in nA T−1). (c) Integration profiles along the integration planes of C5H5−, Figure S4: (a) Schematic representation of local and global currents. (b) Vector plot visualization of the current density of C8H62− in a plane placed 0.5 Å above the molecular plane and top view of integration planes. (c) Integration profiles along the integration planes of C8H62−, Figure S5: (a) Schematic representation of local and global currents. (b) Vector plot visualization of the current density of Si2C5H2 in a plane placed 0.5 Å above the molecular plane and top view of integration planes. (c) Integration profiles along the integration planes of Si2C5H2, Figure S6: (a) Computed values (in ppm) of σ- and π-components (left and right sides) of NICSzz at and above the ring centers (local and global) of Si2C5H2 (at the GIAO-B3LYP/6-311+G*//B3LYP/6-311+G* level). The blue/red dots denote diatropic/paratropic character, and the dot size is in line with the NICSzz magnitude. (b) Isolines of the σ- and π-components of NICSzz for Si2C5H2 (at the GIAO-B3LYP/6-311+G*//B3LYP/6-311+G* level). The isolines are plotted in both the molecular plane (left) and a plane perpendicular to the molecular plane (right). The color scale at the bottom is in ppm, Figure S7: Isolines of the σ- and π-components of NICSzz for both the cyclopentadienyl anion (C5H5−) and the pentalene dianion (C8H62−) (at the GIAO-B3LYP/6-311+G*//B3LYP/6-311+G* level). The isolines are plotted in both the molecular plane (left) and a plane perpendicular to the molecular plane (right). The color scale at the bottom is in ppm, Figure S8: Computed values (in ppm) of σ- and π-components (left and right sides) of NICSzz at and above the ring centers (local and global) of both the cyclopentadienyl anion (C5H5−) and the pentalene dianion (C8H62−) (at the GIAO-B3LYP/6-311+G*//B3LYP/6-311+G* level). The blue/red dots denote diatropic/paratropic character, and the dot size is in line with the NICSzz magnitude.

Author Contributions

Conceptualization, J.J.T.-V., V.G. and W.T.; methodology, J.J.T.-V., V.G., D.R.A., O.B.O. and R.B.-G.; computations, J.J.T.-V., V.G., A.V.-E., D.R.A., O.B.O. and R.B.-G.; validation, D.R.A., O.B.O., L.L. and A.T.; formal analysis, W.T., D.R.A., L.L. and A.T.; investigation, J.J.T.-V., V.G., D.R.A. and W.T.; resources, D.R.A., L.L. and W.T.; writing—original draft preparation, J.J.T.-V., W.T. and D.R.A.; writing—review and editing, O.B.O., V.G. and L.L.; supervision, D.R.A. and W.T.; project administration, V.G. and W.T.; funding acquisition, D.R.A., O.B.O. and W.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by FONDECYT, grant number 1211128, the Universidad de Buenos Aires (Argentina), grant number 20020150100157BA, the Consejo Nacional de Investigaciones Científicas y Técnicas (Argentina), grant numbers PIP 11220130100377CO and PIP 11220130100311CO, and the Agencia Nacional de Promoción Científica y Tecnológica (Argentina), grant number PICT201-0381.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

We thank the financial support of the National Agency for Research and Development (ANID) through FONDECYT project 1211128 (W.T.) R.B-G. acknowledge the financial support of FONDECYT Postdoctorado 3210037. Powered@NLHPC: This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02). D.R.A. acknowledges the financial support from the Universidad de Buenos Aires (Grant No. 20020150100157BA). D.R.A. and O.B.O. acknowledge the financial support from the Consejo Nacional de Investigaciones Científicas y Técnicas (Grant Nos. PIP 11220130100377CO and PIP 11220130100311CO), and the Agencia Nacional de Promoción Científica y Tecnológica (Grant No. PICT201-0381), Argentina.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. von Schleyer, P.R.; Jiao, H. What is aromaticity? Pure Appl. Chem. 1996, 68, 209–218. [Google Scholar] [CrossRef]
  2. Minkin, V.I.; Glukhovtsev, M.N.; Simkin, B.Y. Aromaticity and Antiaromaticity; John Wiley & Sons, Incorporated: Hoboken, NJ, USA, 1994; ISSN 0471593826. [Google Scholar]
  3. Krygowski, T.M.; Cyrański, M.K. Structural Aspects of Aromaticity. Chem. Rev. 2001, 101, 1385–1420. [Google Scholar] [CrossRef]
  4. Schleyer, P.V.R. Introduction: Aromaticity. Chem. Rev. 2001, 101, 1115–1118. [Google Scholar] [CrossRef] [Green Version]
  5. Boldyrev, A.I.; Wang, L.-S. All-Metal Aromaticity and Antiaromaticity. Chem. Rev. 2005, 105, 3716–3757. [Google Scholar] [CrossRef]
  6. Liu, C.; Popov, I.A.; Chen, Z.; Boldyrev, A.I.; Sun, Z. Aromaticity and antiaromaticity in Zintl clusters. Chem. Eur. J. 2018, 24, 14583–14597. [Google Scholar] [CrossRef]
  7. Boldyrev, A.I.; Wang, L.-S.S. Beyond organic chemistry: Aromaticity in atomic clusters. Phys. Chem. Chem. Phys. 2016, 18, 11589–11605. [Google Scholar] [CrossRef] [PubMed]
  8. Alexandrova, A.N.; Boldyrev, A.I.; Zhai, H.-J.J.; Wang, L.-S.S. All-boron aromatic clusters as potential new inorganic ligands and building blocks in chemistry. Coord. Chem. Rev. 2006, 250, 2811–2866. [Google Scholar] [CrossRef]
  9. Sergeeva, A.P.; Popov, I.A.; Piazza, Z.A.; Li, W.-L.; Romanescu, C.; Wang, L.-S.; Boldyrev, A.I. Understanding boron through size-selected clusters: Structure, chemical bonding, and fluxionality. Acc. Chem. Res. 2014, 47, 1349–1358. [Google Scholar] [CrossRef] [PubMed]
  10. Mercero, J.M.; Boldyrev, A.I.; Merino, G.; Ugalde, J.M. Recent developments and future prospects of all-metal aromatic compounds. Chem. Soc. Rev. 2015, 44, 6519–6534. [Google Scholar] [CrossRef]
  11. Huang, X.; Zhai, H.; Kiran, B.; Wang, L. Observation of d-orbital aromaticity. Angew. Chemie 2005, 117, 7417–7420. [Google Scholar] [CrossRef]
  12. Tsipis, C.A. DFT study of “all-metal” aromatic compounds. Coord. Chem. Rev. 2005, 249, 2740–2762. [Google Scholar] [CrossRef]
  13. Rabanal-León, W.; Vásquez-Espinal, A.; Yañez, O.; Pino-Rios, R.; Arratia-Pérez, R.; Alvarez-Thon, L.; Torres-Vega, J.; Tiznado, W. Aromaticity of [M3(µ-X)3X6] 0/2-(M= Re and Tc, X= Cl, Br, I) Clusters Confirmed by Ring Current Analysis and Induced Magnetic Field. Eur. J. Inorg. Chem. 2018, 2018, 3312–3319. [Google Scholar] [CrossRef]
  14. Vásquez-Espinal, A.; Pino-Rios, R.; Alvarez-Thon, L.; Rabanal-León, W.A.; Torres-Vega, J.J.; Arratia-Perez, R.; Tiznado, W. New Insights into Re3(μ-Cl)3Cl6 Aromaticity. Evidence of σ-and π-Diatropicity. J. Phys. Chem. Lett. 2015, 6, 4326–4330. [Google Scholar] [CrossRef]
  15. Bleeke, J.R.; Behm, R.; Xie, Y.-F.; Chiang, M.Y.; Robinson, K.D.; Beatty, A.M. Synthesis, Structure, Spectroscopy, and Reactivity of a Metallabenzene1. Organometallics 1997, 16, 606–623. [Google Scholar] [CrossRef]
  16. Bleeke, J.R.; Xie, Y.F.; Peng, W.J.; Chiang, M. Metallabenzene: Synthesis, structure, and spectroscopy of a 1-irida-3, 5-dimethylbenzene complex. J. Am. Chem. Soc. 1989, 111, 4118–4120. [Google Scholar] [CrossRef]
  17. Bleeke, J.R. Metallabenzenes. Chem. Rev. 2001, 101, 1205–1228. [Google Scholar] [CrossRef] [PubMed]
  18. Fernández, I.; Frenking, G.; Merino, G. Aromaticity of metallabenzenes and related compounds. Chem. Soc. Rev. 2015, 44, 6452–6463. [Google Scholar] [CrossRef] [PubMed]
  19. Vásquez-Espinal, A.; Poater, J.; Solà, M.; Tiznado, W.; Islas, R. Testing the effectiveness of the isoelectronic substitution principle through the transformation of aromatic osmathiophene derivatives into their inorganic analogues. New J. Chem. 2017, 41, 1168–1178. [Google Scholar] [CrossRef] [Green Version]
  20. Popov, I.A.; Bozhenko, K.V.; Boldyrev, A.I. Is graphene aromatic? Nano Res. 2012, 5, 117–123. [Google Scholar] [CrossRef]
  21. Zubarev, D.Y.; Boldyrev, A.I. Revealing intuitively assessable chemical bonding patterns in organic aromatic molecules via adaptive natural density partitioning. J. Org. Chem. 2008, 73, 9251–9258. [Google Scholar] [CrossRef]
  22. Tkachenko, N.V.; Boldyrev, A.I. Multiple local σ-aromaticity of nonagermanide clusters. Chem. Sci. 2019, 10, 5761–5765. [Google Scholar] [CrossRef] [Green Version]
  23. Hoffmann, R.; Alder, R.W.; Wilcox, C.F. Planar tetracoordinate carbon. J. Am. Chem. Soc. 1970, 92, 4992–4993. [Google Scholar] [CrossRef]
  24. Erker, G. Planar-Tetracoordinate Carbon: Making Stable Anti-van′ t Hoff/LeBel Compounds. Comments Inorg. Chem. 1992, 13, 111–131. [Google Scholar] [CrossRef]
  25. Röttger, D.; Erker, G. Compounds Containing Planar-Tetracoordinate Carbon. Angew. Chemie Int. Ed. English 1997, 36, 812–827. [Google Scholar] [CrossRef]
  26. Siebert, W.; Gunale, A. Compounds containing a planar-tetracoordinate carbon atom as analogues of planar methane. Chem. Soc. Rev. 1999, 28, 367–371. [Google Scholar] [CrossRef]
  27. Keese, R. Carbon flatland: Planar tetracoordinate carbon and fenestranes. Chem. Rev. 2006, 106, 4787–4808. [Google Scholar] [CrossRef] [PubMed]
  28. Merino, G.; Méndez-Rojas, M.A.; Vela, A.; Heine, T. Recent advances in planar tetracoordinate carbon chemistry. J. Comput. Chem. 2007, 28, 362–372. [Google Scholar] [CrossRef] [PubMed]
  29. Zhang, X.; Ding, Y. Computational prediction of a global planar penta-coordinate carbon structure CAl4Ga+. Comput. Theor. Chem. 2014, 1048, 18–24. [Google Scholar] [CrossRef]
  30. Li, X.; Zhang, H.; Wang, L.; Geske, G.D.; Boldyrev, A.I. Pentaatomic tetracoordinate planar carbon,[CAl4] 2−: A new structural unit and its salt complexes. Angew. Chemie Int. Ed. 2000, 39, 3630–3632. [Google Scholar] [CrossRef]
  31. Wang, Z.-X.; von Ragué Schleyer, P. Construction principles of ”hyparenes”: Families of molecules with planar pentacoordinate carbons. Science 2001, 292, 2465–2469. [Google Scholar] [CrossRef]
  32. Wang, Y.; Li, F.; Li, Y.; Chen, Z. Semi-metallic Be5C2 monolayer global minimum with quasi-planar pentacoordinate carbons and negative Poisson’s ratio. Nat. Commun. 2016, 7, 11488. [Google Scholar] [CrossRef] [Green Version]
  33. Pan, S.; Cabellos, J.L.; Orozco-Ic, M.; Chattaraj, P.K.; Zhao, L.; Merino, G. Planar pentacoordinate carbon in CGa5+ derivatives. Phys. Chem. Chem. Phys. 2018, 20, 12350–12355. [Google Scholar] [CrossRef] [PubMed]
  34. Pei, Y.; An, W.; Ito, K.; Schleyer, P.V.R.; Zeng, X.C. Planar pentacoordinate carbon in CAl5+: A global minimum. J. Am. Chem. Soc. 2008, 130, 10394–10400. [Google Scholar] [CrossRef] [PubMed]
  35. Vassilev-Galindo, V.; Pan, S.; Donald, K.J.; Merino, G. Planar pentacoordinate carbons. Nat. Rev. Chem. 2018, 2, 114. [Google Scholar] [CrossRef]
  36. Grande-Aztatzi, R.; Cabellos, J.L.; Islas, R.; Infante, I.; Mercero, J.M.; Restrepo, A.; Merino, G. Planar pentacoordinate carbons in CBe54− derivatives. Phys. Chem. Chem. Phys. 2015, 17, 4620–4624. [Google Scholar] [CrossRef]
  37. Zhao, X.-F.; Bian, J.-H.; Huang, F.; Yuan, C.; Wang, Q.; Liu, P.; Li, D.; Wang, X.; Wu, Y.-B. Stabilization of beryllium-containing planar pentacoordinate carbon species through attaching hydrogen atoms. RSC Adv. 2018, 8, 36521–36526. [Google Scholar] [CrossRef] [Green Version]
  38. Cui, Z.; Vassilev-Galindo, V.; Cabellos, J.L.; Osorio, E.; Orozco, M.; Pan, S.; Ding, Y.; Merino, G. Planar pentacoordinate carbon atoms embedded in a metallocene framework. Chem. Commun. 2017, 53, 138–141. [Google Scholar] [CrossRef]
  39. Wu, Y.-B.; Duan, Y.; Lu, G.; Lu, H.-G.; Yang, P.; von Rague Schleyer, P.; Merino, G.; Islas, R.; Wang, Z.-X. D3h CN3Be3+ and CO3Li3+: Viable planar hexacoordinate carbon prototypes. Phys. Chem. Chem. Phys. 2012, 14, 14760–14763. [Google Scholar] [CrossRef]
  40. Exner, K.; von Ragué Schleyer, P. Planar hexacoordinate carbon: A viable possibility. Science. 2000, 290, 1937–1940. [Google Scholar] [CrossRef]
  41. Parra, L.L.; Diego, L.; Yañez, O.; Inostroza, D.; Barroso, J.; Espinal, A.V.; Merino, G.; Tiznado, W. Planar Hexacoordinate Carbons: Half Covalent, Half Ionic. Angew. Chem. Int. Ed. Engl. 2021, 60, 8700–8704. [Google Scholar] [CrossRef]
  42. Li, Y.; Liao, Y.; Chen, Z. Be2C monolayer with quasi-planar hexacoordinate carbons: A global minimum structure. Angew. Chemie 2014, 126, 7376–7380. [Google Scholar] [CrossRef]
  43. Feixas, F.; Matito, E.; Poater, J.; Sola, M. Quantifying aromaticity with electron delocalisation measures. Chem. Soc. Rev. 2015, 44, 6434–6451. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  44. Gomes, J.; Mallion, R.B. Aromaticity and ring currents. Chem. Rev. 2001, 101, 1349–1384. [Google Scholar] [CrossRef]
  45. Mitchell, R.H. Measuring aromaticity by NMR. Chem. Rev. 2001, 101, 1301–1316. [Google Scholar] [CrossRef]
  46. Cyranski, M.K.; Krygowski, T.M.; Katritzky, A.R.; Schleyer, P.V.R. To what extent can aromaticity be defined uniquely? J. Org. Chem. 2002, 67, 1333–1338. [Google Scholar] [CrossRef] [PubMed]
  47. Randic, M. Aromaticity of polycyclic conjugated hydrocarbons. Chem. Rev. 2003, 103, 3449–3606. [Google Scholar] [CrossRef]
  48. Balaban, A.T.; Oniciu, D.C.; Katritzky, A.R. Aromaticity as a cornerstone of heterocyclic chemistry. Chem. Rev. 2004, 104, 2777–2812. [Google Scholar] [CrossRef]
  49. McWeeny, R. Ring currents and proton magnetic resonance in aromatic molecules. Mol. Phys. 1958, 1, 311–321. [Google Scholar] [CrossRef]
  50. Pople, J.A. Molecular orbital theory of aromatic ring currents. Mol. Phys. 1958, 1, 175–180. [Google Scholar] [CrossRef]
  51. Pauling, L. The diamagnetic anisotropy of aromatic molecules. J. Chem. Phys. 1936, 4, 673–677. [Google Scholar] [CrossRef] [Green Version]
  52. Kumar, C.; Fliegl, H.; Sundholm, D. Relation Between Ring Currents and Hydrogenation Enthalpies for Assessing the Degree of Aromaticity. J. Phys. Chem. A 2017, 121, 7282–7289. [Google Scholar] [CrossRef] [Green Version]
  53. Ligabue, A.; Pincelli, U.; Lazzeretti, P.; Zanasi, R. Current density maps, magnetizability, and nuclear magnetic shielding tensors for anthracene, phenanthrene, and triphenylene. J. Am. Chem. Soc. 1999, 121, 5513–5518. [Google Scholar] [CrossRef]
  54. Monaco, G.; Fowler, P.W.; Lillington, M.; Zanasi, R. Designing paramagnetic circulenes. Angew. Chemie 2007, 119, 1921–1924. [Google Scholar] [CrossRef]
  55. Lazzeretti, P. Assessment of aromaticity via molecular response properties. Phys. Chem. Chem. Phys. 2004, 6, 217–223. [Google Scholar] [CrossRef]
  56. Schleyer, P.V.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-independent chemical shifts: A simple and efficient aromaticity probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
  57. Haddon, R.C. The application of the Biot-Savart law to the ring current analysis of proton chemical shifts—II: An approach to aromatic character in the annulenes. Tetrahedron 1972, 28, 3635–3655. [Google Scholar] [CrossRef]
  58. Báez-Grez, R.; Rabanal-León, W.A.; Alvarez-Thon, L.; Ruiz, L.; Tiznado, W.; Pino-Rios, R. Aromaticity in heterocyclic analogues of benzene: Dissected NICS and current density analysis. J. Phys. Org. Chem. 2019, 32, e3823. [Google Scholar] [CrossRef]
  59. Báez-Grez, R.; Ruiz, L.; Pino-Rios, R.; Tiznado, W. Which NICS method is most consistent with ring current analysis? Assessment in simple monocycles. RSC Adv. 2018, 8, 13446–13453. [Google Scholar] [CrossRef] [Green Version]
  60. Poater, J.; Solà, M.; Viglione, R.G.; Zanasi, R. Local aromaticity of the six-membered rings in pyracylene. A difficult case for the NICS indicator of aromaticity. J. Org. Chem. 2004, 69, 7537–7542. [Google Scholar] [CrossRef] [PubMed]
  61. Sundholm, D.; Berger, R.J.F.; Fliegl, H. Analysis of the magnetically induced current density of molecules consisting of annelated aromatic and antiaromatic hydrocarbon rings. Phys. Chem. Chem. Phys. 2016, 18, 15934–15942. [Google Scholar] [CrossRef] [Green Version]
  62. Yañez, O.; Vásquez-Espinal, A.; Báez-Grez, R.; Rabanal-León, W.A.; Osorio, E.; Ruiz, L.; Tiznado, W. Carbon rings decorated with group 14 elements: New aromatic clusters containing planar tetracoordinate carbon. New J. Chem. 2019, 43, 6781–6785. [Google Scholar] [CrossRef]
  63. Yañez, O.; Báez-Grez, R.; Garza, J.; Pan, S.; Barroso, J.; Vásquez-Espinal, A.; Merino, G.; Tiznado, W. Embedding a Planar Hypercoordinate Carbon Atom into a [4n+ 2] π-System. ChemPhysChem 2020, 21, 145–148. [Google Scholar] [CrossRef] [PubMed]
  64. Yañez, O.; Vásquez-Espinal, A.; Pino-Rios, R.; Ferraro, F.; Pan, S.; Osorio, E.; Merino, G.; Tiznado, W. Exploiting electronic strategies to stabilize a planar tetracoordinate carbon in cyclic aromatic hydrocarbons. Chem. Commun. 2017, 53, 12112–12115. [Google Scholar] [CrossRef]
  65. Becke, A.D. Becke’s three parameter hybrid method using the LYP correlation functional. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
  66. Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-consistent molecular-orbital methods. IX. An extended Gaussian-type basis for molecular-orbital studies of organic molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
  67. Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self—consistent molecular orbital methods. XII. Further extensions of Gaussian—type basis sets for use in molecular orbital studies of organic molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
  68. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revis. C.01; Gaussian, Inc.: Wallingford, CT, USA.
  69. Oña, O.B.; Alcoba, D.R.; Tiznado, W.; Torre, A.; Lain, L. An orbital localization criterion based on the topological analysis of the electron localization function. Int. J. Quantum Chem. 2013, 113, 1401–1408. [Google Scholar] [CrossRef]
  70. Oña, O.B.; Alcoba, D.R.; Torre, A.; Lain, L.; Torres-Vega, J.J.; Tiznado, W. Orbital Localization Criterion as a Complementary Tool in the Bonding Analysis by Means of Electron Localization Function: Study of the Sin(BH)5-n2- (n = 0–5) Clusters. J. Phys. Chem. A 2013, 117, 12953–12958. [Google Scholar] [CrossRef]
  71. Alcoba, D.R.; Oña, O.B.; Torre, A.; Lain, L.; Tiznado, W. An orbital localization criterion based on the topological analysis of the electron localization function at correlated level. Int. J. Quantum Chem. 2018, 118, e25588. [Google Scholar] [CrossRef]
  72. Oña, O.B.; Torres-Vega, J.J.; Torre, A.; Lain, L.; Alcoba, D.R.; Vásquez-Espinal, A.; Tiznado, W. Chemical bonding analysis in boron clusters by means of localized orbitals according to the electron localization function topology. Theor. Chem. Acc. 2015, 134, 1–9. [Google Scholar] [CrossRef]
  73. Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
  74. Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. Computational tools for the electron localization function topological analysis. Comput. Chem. 1999, 23, 597–604. [Google Scholar] [CrossRef]
  75. Fliegl, H.; Taubert, S.; Lehtonen, O.; Sundholm, D. The gauge including magnetically induced current method. Phys. Chem. Chem. Phys. 2011, 13, 20500–20518. [Google Scholar] [CrossRef] [PubMed]
  76. Jusélius, J.; Sundholm, D.; Gauss, J. Calculation of current densities using gauge-including atomic orbitals. J. Chem. Phys. 2004, 121, 3952–3963. [Google Scholar] [CrossRef]
  77. Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
  78. Ahrens, J.; Geveci, B.; Law, C. Paraview: An end-user tool for large data visualization. Vis. Handb. 2005, 717. [Google Scholar] [CrossRef]
  79. Ayachit, U. The ParaView Guide: A Parallel Visualization Application; Kitware, Inc.: Saratoga County, NY, USA, 2015; ISBN 1930934300. [Google Scholar]
  80. Abramowitz, M. Handbook of Mathematical Functions, With Formulas, Graphs, and Mathematical Tables; Dover Publications, Inc.: New York, NY, USA, 1974; ISBN 0486612724. [Google Scholar]
  81. Sundholm, D.; Fliegl, H.; Berger, R.J.F. Calculations of magnetically induced current densities: Theory and applications. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2016, 6, 639–678. [Google Scholar] [CrossRef]
  82. Bohmann, J.A.; Weinhold, F.; Farrar, T.C. Natural chemical shielding analysis of nuclear magnetic resonance shielding tensors from gauge-including atomic orbital calculations. J. Chem. Phys. 1997, 107, 1173–1184. [Google Scholar] [CrossRef]
  83. Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Landis, C.R.; Weinhold, F. Natural Bond Orbital Analysis Program: NBO 6.0; Theoretical Chemistry Institute and Department of Chemistry, University of Wisconsin: Madison, WI, USA, 2013. [Google Scholar]
  84. Childs, H.; Brugger, E.; Whitlock, B.; Meredith, J.; Ahern, S.; Pugmire, D.; Biagas, K.; Miller, M.; Harrison, C.; Weber, G.H.; et al. VisIt: An End-User Tool For Visualizing and Analyzing Very Large Data. In High Performance Visualization—Enabling Extreme-Scale Scientific Insight; CRC Press: Boca Raton, FL, USA, 2012; pp. 357–372. [Google Scholar]
  85. Llusar, R.; Beltrán, A.; Andrés, J.; Noury, S.; Silvi, B. Topological analysis of electron density in depleted homopolar chemical bonds. J. Comput. Chem. 1999, 20, 1517–1526. [Google Scholar] [CrossRef]
  86. Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
  87. Hückel, E. Quantentheoretische Beiträge zum Benzolproblem. Zeitschrift Phys. 1931, 70, 204–286. [Google Scholar] [CrossRef]
  88. Hückel, E. Quanstentheoretische Beiträge zum Benzolproblem. Zeitschrift Phys. 1931, 72, 310–337. [Google Scholar] [CrossRef]
  89. Hückel, E. Zur Quantentheorie der Doppelbindung. Zeitschrift Phys. 1930, 60, 423–456. [Google Scholar] [CrossRef]
  90. Lazzeretti, P. Ring currents. Prog. Nucl. Magn. Reson. Spectrosc. 2000, 36, 1–88. [Google Scholar] [CrossRef]
  91. Juse, J.; Sundholm, D. Ab initio determination of the induced ring current in aromatic molecules. Phys. Chem. Chem. Phys. 1999, 1, 3429–3435. [Google Scholar]
  92. Inostroza, D.; García, V.; Yañez, O.; Torres-Vega, J.J.; Vásquez-Espinal, A.; Pino-Rios, R.; Báez-Grez, R.; Tiznado, W. On the NICS limitations to predict local and global current pathways in polycyclic systems. New J. Chem. 2021, 45, 8345–8351. [Google Scholar] [CrossRef]
  93. Aihara, J. Circuit resonance energy: A key quantity that links energetic and magnetic criteria of aromaticity. J. Am. Chem. Soc. 2006, 128, 2873–2879. [Google Scholar] [CrossRef] [PubMed]
Chemistry 03 00080 sch001 550
Scheme 1. Design strategy of aromatic ptC systems employed in reference [62].
Scheme 1. Design strategy of aromatic ptC systems employed in reference [62].
Chemistry 03 00080 sch001
Chemistry 03 00080 g001 550
Figure 1. Results of ELF-LOC for Si3C5 cluster.
Figure 1. Results of ELF-LOC for Si3C5 cluster.
Chemistry 03 00080 g001
Chemistry 03 00080 g002 550
Figure 2. Results of ELF-LOC for Si4C8 cluster.
Figure 2. Results of ELF-LOC for Si4C8 cluster.
Chemistry 03 00080 g002
Chemistry 03 00080 g003 550
Figure 3. (a) Vector plot visualization of the current density of Si3C5 in a plane placed 0.5 Å above the molecular plane; (b) schematic representation of local and global currents.
Figure 3. (a) Vector plot visualization of the current density of Si3C5 in a plane placed 0.5 Å above the molecular plane; (b) schematic representation of local and global currents.
Chemistry 03 00080 g003
Chemistry 03 00080 g004 550
Figure 4. (a) Vector plot visualization of the current density of Si4C8 in a plane placed 0.5 Å above the molecular plane; (b) schematic representation of local and global currents.
Figure 4. (a) Vector plot visualization of the current density of Si4C8 in a plane placed 0.5 Å above the molecular plane; (b) schematic representation of local and global currents.
Chemistry 03 00080 g004
Chemistry 03 00080 g005 550
Figure 5. Isolines of the σ- and π-components of NICSzz for the studied molecules (at the GIAO-B3LYP/6-311+G*//B3LYP/6-311+G* level). The isolines are plotted in both the molecular plane (left) and a plane perpendicular to the molecular plane (right). The color scale at the bottom is in ppm.
Figure 5. Isolines of the σ- and π-components of NICSzz for the studied molecules (at the GIAO-B3LYP/6-311+G*//B3LYP/6-311+G* level). The isolines are plotted in both the molecular plane (left) and a plane perpendicular to the molecular plane (right). The color scale at the bottom is in ppm.
Chemistry 03 00080 g005
Chemistry 03 00080 g006 550
Figure 6. Computed values (in ppm) of σ- and π-components (left and right sides) of NICSzz at and above the ring centers (local and global) of studied molecules (at the GIAO-B3LYP/6-311+G*//B3LYP/6-311+G* level). The blue/red dots denote diatropic/paratropic character, and the dot size is in line with the NICSzz magnitude.
Figure 6. Computed values (in ppm) of σ- and π-components (left and right sides) of NICSzz at and above the ring centers (local and global) of studied molecules (at the GIAO-B3LYP/6-311+G*//B3LYP/6-311+G* level). The blue/red dots denote diatropic/paratropic character, and the dot size is in line with the NICSzz magnitude.
Chemistry 03 00080 g006
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Torres-Vega, J.J.; Alcoba, D.R.; Oña, O.B.; Vásquez-Espinal, A.; Báez-Grez, R.; Lain, L.; Torre, A.; García, V.; Tiznado, W. Analysis of Local and Global Aromaticity in Si3C5 and Si4C8 Clusters. Aromatic Species Containing Planar Tetracoordinate Carbon. Chemistry 2021, 3, 1101-1112. https://doi.org/10.3390/chemistry3040080

AMA Style

Torres-Vega JJ, Alcoba DR, Oña OB, Vásquez-Espinal A, Báez-Grez R, Lain L, Torre A, García V, Tiznado W. Analysis of Local and Global Aromaticity in Si3C5 and Si4C8 Clusters. Aromatic Species Containing Planar Tetracoordinate Carbon. Chemistry. 2021; 3(4):1101-1112. https://doi.org/10.3390/chemistry3040080

Chicago/Turabian Style

Torres-Vega, Juan J., Diego R. Alcoba, Ofelia B. Oña, Alejandro Vásquez-Espinal, Rodrigo Báez-Grez, Luis Lain, Alicia Torre, Víctor García, and William Tiznado. 2021. "Analysis of Local and Global Aromaticity in Si3C5 and Si4C8 Clusters. Aromatic Species Containing Planar Tetracoordinate Carbon" Chemistry 3, no. 4: 1101-1112. https://doi.org/10.3390/chemistry3040080

APA Style

Torres-Vega, J. J., Alcoba, D. R., Oña, O. B., Vásquez-Espinal, A., Báez-Grez, R., Lain, L., Torre, A., García, V., & Tiznado, W. (2021). Analysis of Local and Global Aromaticity in Si3C5 and Si4C8 Clusters. Aromatic Species Containing Planar Tetracoordinate Carbon. Chemistry, 3(4), 1101-1112. https://doi.org/10.3390/chemistry3040080

Article Metrics

Back to TopTop