Abstract
Knowledge about the absolute configuration of small bioactive organic molecules is essential in pharmaceutical research because enantiomers can exhibit considerably different effects on living organisms. X-ray crystallography enables chemists to determine the absolute configuration of an enantiopure compound due to anomalous dispersion. Here, we present the determination of the absolute configuration of the flavoring agent (+)-γ-decalactone, which is liquid under ambient conditions. Single crystals were grown from the liquid in a glass capillary by in situ cryo-crystallization. Diffraction data collection was performed using Cu-Kα radiation. The absolute configuration was confirmed. The molecule consists of a linear aliphatic non-polar backbone and a polar lactone head. In the solid state, layers of polar and non-polar sections of the molecule alternating along the c-axis of the unit cell are observed. In favorable cases, this method of absolute configuration determination of pure liquid (bioactive) agents or liquid products from asymmetric catalysis is a convenient alternative to conventional methods of absolute structure determination, such as optical rotatory dispersion, vibrational circular dichroism, ultraviolet-visible spectroscopy, use of chiral shift reagents in proton NMR and Coulomb explosion imaging.
1. Introduction
Knowledge of the absolute configuration of small bioactive organic molecules is essential for understanding the significant different pharmacological effects of enantiomers on organisms [1,2]. The synthesis and characterization of chiral drug compounds is of considerable interest, especially in the pharmaceutical industry [3]. Additionally, enantiomers can differ in taste and smell perception [4,5]. This particularly applies to the natural compound discussed in this paper. γ-(+)-Decalactone [γ-lac], a compound that is liquid under ambient conditions, can be found in fruits, for example, strawberries or peaches and is suitable as a fruit flavoring agent [6,7]. In nature, the R-configuration of γ-lac is predominant. The absolute configuration of γ-lac has a significant influence on olfactory and taste perception. While the aroma of the R-enantiomer is reminiscent of peaches, the S-enantiomer smells of coconuts [8]. X-ray crystallography is able to determine the absolute configuration of enantiopure crystalline compounds by measuring intensity differences of Bijvoet pairs that are caused by anomalous dispersion [9]. One challenge is to determine the absolute configuration of organic drugs without atoms heavier than oxygen owing to the small anomalous scattering contribution of these elements [7]. For γ-lac, this is the case. The molecule contains solely carbon, oxygen, and hydrogen. The anomalous scattering contribution of an atom is not only dependent on the atom type but also on the wavelength of the radiation used. To get more accurate results, Cu-Kα radiation has an advantage in comparison with Ag-Kα or Mo-Kα radiation because of the enhanced anomalous scattering factor at this wavelength [10]. Currently, there exist several approaches to circumvent these difficulties of absolute configuration determination. For example, co-crystallization with compounds that contain heavy atoms or co-crystallization with a chiral compound with known configuration are possible solutions to obtain the absolute configuration of the target molecule [11]. Similarly, in case of an amine, the formation of a hydrochloride can serve this purpose [9]. The object of this study was to determine the absolute configuration of an enantiopure compound that is liquid under ambient conditions. We chose to look at γ-lac because of its industrial relevance. In situ crystallization is a powerful tool to grow crystals direct on the diffractometer from pure liquid compounds in a glass capillary [12,13]. In this paper, the determination of the absolute configuration of a liquid natural organic compound is presented, together with a further technique for in situ crystal growth. This procedure can easily be transferred to other liquid or gaseous organic compounds.
2. Materials and Methods
(+)-γ-Decalactone was purchased from Sigma-Aldrich (purity > 97%) and used as received = +41.6 (c 0.087, CHCl3). The liquid compound was crystallized in a capillary with a diameter of 0.3 mm directly (in situ) on the diffractometer (volume of approximately 0.5 µL). The low-temperature phase behavior was established beforehand by differential scanning calorimetry (DSC). Experiments were performed on a METTLER TOLEDO DSC 820 (Mettler-Toledo GmbH, Gießen, Germany). Two cycles with different cooling and heating rates were carried out in the range of −150–+20 °C. The first and second scan employed temperature gradients of 10 and 5 K per minute, respectively.
For single crystal growth, the compound was cooled below its liquid–solid phase transition temperature of 258 K (determined by LT-DSC) on the diffractometer using a stream of cold nitrogen gas delivered by an Oxford Cryosystems Cryostream 700 (Oxford Cryosystems, Long Hanborough, Oxford, UK). The crystalline powder thus obtained was used as starting material for crystal growth. By translation of the capillary through the cold nitrogen gas stream, a suitable single crystal was grown at the liquid–solid phase boundary (inverse zone melting) following a newly developed procedure [12].
For this purpose, a small attachment to a standard Huber goniometer head (model 1004) was constructed, in order to move the capillary along its axis at a controlled speed over a distance of several millimeters during a time period of several hours (Figure 1). Since there is a temperature gradient across the cold gas stream of the Cryostream 700, it is possible to slowly grow a single crystal at the solid–liquid interface and to continually transfer the crystallized portion of the compound into the colder part of the gas stream, until such time that a nearly perfect single crystal is located in the X-ray beam. The attachment comprises a bracket, which holds a miniaturized stepper motor equipped with a gear box and connected at one end to an indexer board and power supply. The motor axis is coupled to a square nut, which fits snugly over the height adjustment drive of the goniometer head. This attachment can be slid off after crystal growth has been accomplished, thus allowing subsequent free rotation of all goniometer axes.
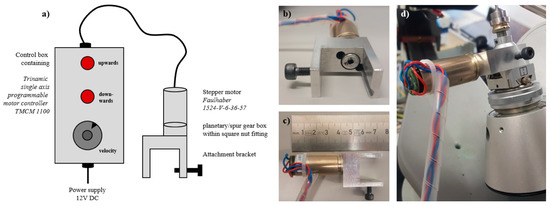
Figure 1.
(a) Sketch of the attachment showing its main components, (b) front view of attachment bracket with square nut fitting, (c) side view and size relations of attachment, (d) device attached to a Huber goniometer head (model 1004) mounted on the φ-axis of a Mach-III four circle goniometer.
Once crystal growth is completed, there are in some cases several crystals next to each other in the capillary. The procedure can be repeated and if the problem subsists, the major single crystal component can be selected, or the twinning identified in a three-dimensional representation of the reciprocal space.
X-ray intensity data were collected at 100(2) K on a Bruker-AXS Kappa Mach3 goniometer equipped with an APEX-II detector, using Cu-Kα radiation produced by a FR591 rotating anode X-ray source (BrukerNonius B. V., Delft, The Netherlands). Scaling and absorption correction were performed with SADABS (Bruker AXS Inc., Madison, WI, USA). The crystal structure was solved by SHELXT and refined using SHELXL-2018/3. No further constraints or restraints were applied. A summary of the crystallographic details is given in Table 1, while further structural details including bond lengths and angles can be found in the Supplementary Material. CCDC 2072278 contains the supplementary crystallographic data for this crystal structure. These data can be obtained free of charge from the Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/structures.

Table 1.
Crystal data and refinement details for (+)-γ-Decalactone.
3. Results
The absolute configuration of γ-lac was determined using anomalous dispersion effects. The derived Flack parameter calculated from 717 quotients of Bijvoet pairs according to Parsons’ method (SHELXL) is −0.019(60) and thus the R-configuration is verified (Figure 2). γ-lac consists of a non-polar alkyl chain and a more polar cyclic ester. The polar parts appear to interact via non-classical C-H···O hydrogen bonds involving the carbonyl group of the lactone. The supramolecular structure comprising these intermolecular hydrogen bonds between the polar groups is shown in Figure 3 (numerical values are given in Table 2). In the crystal layers consisting of the non-polar and the polar parts alternate along the c-axis of the unit cell. The structure in solid state appears to be governed by the polar ends of the molecule, since there are no short contacts between atoms in the non-polar region. The five-membered lactone ring adopts an envelope conformation with the apex at C3, which is 0.5 Å above the mean plane (r. m. s. 0.01 Å) formed by the other four atoms of the ring. The ring puckering parameter φ equals 291.8° (see Supplementary Material) [14]. The aliphatic alkyl chain adopts an all-trans conformation in the crystal structure (Figure 2) [15].
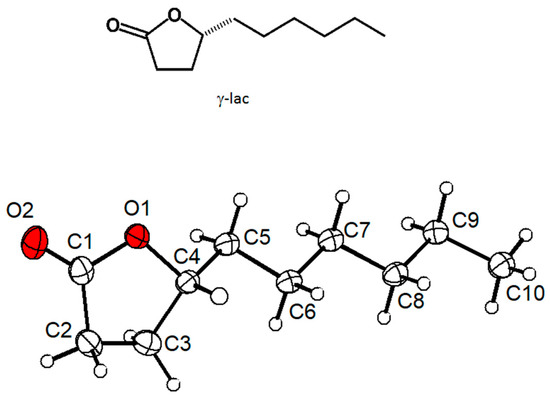
Figure 2.
Molecular structure of the chiral compound (+)-γ-decalactone ((R)-5-hexyloxolan-2-one) determined by single crystal X-ray crystallography. The probability level of the displacement ellipsoids is 50%. Hydrogen atoms are shown with arbitrary sizes.
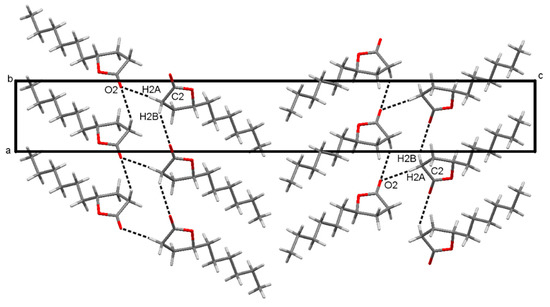
Figure 3.
Crystal structure of γ-lac, view along the b-axis, C-H···O hydrogen bonds marked with black dashed lines.

Table 2.
Distance/Å and angles/° of the hydrogen bonds in γ-lac.
4. Discussion
For molecules without atoms heavier than oxygen, the determination of the absolute structure becomes difficult due to the low anomalous scattering signal. Two strategies were pursued. First, Cu-Kα radiation was chosen because of the larger resonant scattering factors. This resulted in larger measured intensity differences of the Bijvoet pairs as compared with shorter wavelength radiation. Second, the diffracted intensities were measured with a high redundancy. This enabled outliers to be more easily identified and errors in the measured intensities to be reduced. Both techniques allowed the absolute structure parameters to be determined more accurately. The Flack parameter obtained from 718 quotients with its resultant standard deviation verifies the absolute configuration of the molecule and hence that of the structure (Table 1). The Flack parameter in absolute structure determination has to be evaluated carefully. There can be significant differences between the classical Flack parameter derived from fitting scale factors to the structure factors of both antipodes and the Flack parameter according to Parsons’ method, which uses quotients [18]. The Flack parameter determined by Parsons’ method usually has a smaller standard uncertainty than the classical Flack parameter and is implemented in standard crystallography programs like SHELXL [19,20]. A standard uncertainty for the Flack parameter smaller than 0.1 is necessary for accurate absolute structure determination in order to ensure that its value is zero within error and hence can be differentiated reliably from the configuration with the opposite hand, for which a value of one would be expected. Here, we report an example in which the Flack parameter is very sensitive to the measured intensity of just one outlier. By chance, we discovered that the reflection with Miller indices -5 2 14 and a d-spacing of 0.89 Å has a significant influence on the determination of the absolute configuration. The measured intensity was far too large (19 standard uncertainties from the expected value) and was subsequently attributed to a diffracted intensity of a second crystal in the capillary. If this reflection is included in the intensity data, the Flack parameter is −1.62(22) (determined from 733 Bijvoet pairs according to the procedure described in [18]). On omitting this reflection, the Flack parameter assumes a meaningful value of 0.02(6) (see Supplementary Material). In the capillary, multiple crystals cannot always be avoided when a crystal is grown by translation perpendicular to the nitrogen gas stream and extreme caution is advised, as this example illustrates.
To the best of our knowledge, there is no report in the Cambridge Structural Database of the crystal structure determination of a pure γ-lactone that has only an aliphatic substituent with no functional groups in the chain. The bipolar structure of γ-lac can be compared with non-ionic surfactants, which have a polar head and a non-polar backbone. The packing of the molecules in the crystal is likely to be a consequence of the polarity of the molecular structure of γ-lac. A layer structure or in more general a structure in which some parts of a molecule agglomerate may be expected when the molecule has a hydrophobic chain and polar head.
One of the advantages of the goniometer head attachment described above is the simplicity of operation. The set-up is initialized by retracting the height adjustment until the stall guard functionality of the stepper motor controller signals that the end of travel has been reached. A 10-turn potentiometer connected to the analogue input of the controller allows setting the speed of the translational movement over a time range between minutes and hours, while two illuminated push buttons allow the direction of travel to be input.
5. Conclusions
We have shown that in situ cryo-crystallization allows one to determine the absolute configuration of the enantiopure liquid compound γ-lac by using single crystal x-ray crystallography. Especially for medicinal and pharmaceutical research, in situ cryo-crystallization combined with X-ray crystallography promises to be a powerful and easy tool to determine the absolute configuration of drugs and small-molecule compounds that are liquid under ambient conditions. In addition, the technique allows intermolecular interactions to be studied in more detail. In this example, the polarity and molecular geometry of γ-lac leads to a layered structure. Intermolecular C-H···O hydrogen bonds between the lactone-part of γ-lac can be observed. This procedure can easily be transferred to other liquid organic drug compounds that crystallize at low temperature.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/chemistry3020040/s1, Figure S1: ORTEP-Plot of the molecular structure of (+)-γ-Decalactone. Figure S2: Screen shots of the capillary, face indexing and unit cell indexing. Figure S3: Recorded ambient to low temperature DSC curve of γ-lac. Figure S4: ATR-FT-IR spectra of γ-lac. Figure S5: Determination of the Flack-Parameter by Parsons’ method; (a) The full data-set of 733 Bijvoet-Pairs was used for determination of the Flack-Parameter (variable p in linear regression), the quotient with highest difference from theory is marked with a red circle; (b) Linear regression of 732 Bijvoet pairs, the red marked quotient in (a) was omitted. Figure S6: Excerpt from the HKLF4 file for γ-lac. Symmetry-equivalent reflections are marked with colored boxes (point group 2 2 2: h k l = -h-k l = -h k -l = h -k -l). The reflection (-5 -2 -14) in the blue box strongly deviates from its Bijvoet-pairs (red box). Table S1: Crystal data and structure refinement. Table S2: Bond lengths [Å] and angles [°]. Table S3: Anisotropic displacement parameters (Å2). Table S4: Hydrogen coordinates and isotropic displacement parameters (Å2). Table S5: Torsion angles [°]. Table S6: Hydrogen bonds [Å and °]. Table S7: Asymmetry Parameters of the Five Membering Ring (Puckering Coordinates Analysis).
Author Contributions
Conceptualization, N.N.; methodology, M.P., N.N., and C.W.L.; writing—original draft preparation, M.P.; writing—review and editing, all; visualization, M.P.; supervision, C.W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We are grateful to M. Felderhoff for providing access to low temperature DSC and A. Fürstner for access to ATR-IR spectroscopy and optical rotation measurements.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maher, T.J.; Johnson, D.A. Review of chirality and its importance in pharmacology. Drug Dev. Res. 1991, 24, 149–156. [Google Scholar] [CrossRef]
- Jayakumar, R.; Vadivel, R.; Ananthi, N. Role of Chirality in Drugs. Org. Med. Chem. Int. J. 2018, 5, 555661. [Google Scholar]
- Sheldon, R.A. Chirotechnology: Designing economic chiral syntheses. J. Chem. Technol. Biotechnol. Int. Res. Process Environ. AND Clean Technol. 1996, 67, 1–14. [Google Scholar]
- Bassoli, A.; Borgonovo, G.; Drew, M.G.B.; Merlini, L. Enantiodifferentiation in taste perception of isovanillic derivatives. Tetrahedron Asymmetry 2000, 11, 3177–3186. [Google Scholar] [CrossRef]
- Zawirska-Wojtasiak, R. Chirality and the Nature of Food Authenticity of Aroma. Acta Sci. Pol. Technol. Aliment. 2006, 5, 21–36. [Google Scholar]
- Ulrich, D.; Hoberg, E.; Rapp, A.; Kecke, S. Analysis of strawberry flavour—Discrimination of aroma types by quantification of volatile compounds. Z. Lebensm. Forsch. A 1997, 205, 218–223. [Google Scholar] [CrossRef]
- Guillot, S.; Peytavi, L.; Bureau, S.; Boulanger, R.; Lepoutre, J.-P.; Crouzet, J.; Schorr-Galindo, S. Aroma characterization of various apricot varieties using headspace–solid phase microextraction combined with gas chromatography–mass spectrometry and gas chromatography–olfactometry. Food Chem. 2006, 96, 147–155. [Google Scholar] [CrossRef]
- Ternes, W. Naturwissenschaftliche Grundlagen der Lebensmittelzubereitung. Behr: Santa Ana, CA, USA, 2008. [Google Scholar]
- Parsons, S. Determination of absolute configuration using X-ray diffraction. Tetrahedron Asymmetry 2017, 28, 1304–1313. [Google Scholar] [CrossRef]
- Linden, A. Best practice and pitfalls in absolute structure determination. Tetrahedron Asymmetry 2017, 28, 1314–1320. [Google Scholar] [CrossRef]
- Bhatt, P.M.; Desiraju, G.R. Co-crystal formation and the determination of absolute configuration. CrystEngComm 2008, 10, 1747–1749. [Google Scholar] [CrossRef]
- Boese, R. Special issue on In Situ Crystallization. Z. Krist. Cryst. Mater. 2014, 229, 595–601. [Google Scholar] [CrossRef]
- Veith, M.; Frank, W. Low-temperature x-ray structure techniques for the characterization of thermolabile molecules. Chem. Rev. 1988, 88, 81–92. [Google Scholar] [CrossRef]
- Cremer, D.; Pople, J.A. General definition of ring puckering coordinates. J. Am. Chem. Soc. 1975, 97, 1354–1358. [Google Scholar] [CrossRef]
- Thomas, S.A.; Agbaji, E.B. Molecular conformations of γ-lactone rings from crystal structure data. J. Crystallogr. Spectrosc. Res. 1989, 19, 3–23. [Google Scholar] [CrossRef]
- Torshin, I.Y.; Weber, I.T.; Harrison, R.W. Geometric criteria of hydrogen bonds in proteins and identification of ‘bifurcated’ hydrogen bonds. Protein Eng. Design Sel. 2002, 15, 359–363. [Google Scholar] [CrossRef] [PubMed]
- Wood, P.A.; Allen, F.H.; Pidcock, E. Hydrogen-bond directionality at the donor H atom—Analysis of interaction energies and database statistics. CrystEngComm 2009, 11, 1563–1571. [Google Scholar] [CrossRef]
- Parsons, S.; Flack, H.D.; Wagner, T. Use of intensity quotients and differences in absolute structure refinement. Acta Crystallogr. Sect. B 2013, 69, 249–259. [Google Scholar] [CrossRef] [PubMed]
- Escudero-Adan, E.C.; Benet-Buchholz, J.; Ballester, P. The use of Mo K[alpha] radiation in the assignment of the absolute configuration of light-atom molecules; the importance of high-resolution data. Acta Crystallogr. Sect. B 2014, 70, 660–668. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A 2015, C71, 3–8. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).