The Tyranny of Arm-Wrestling Methyls on Iron(II) Spin State in Pseudo-Octahedral [Fe(didentate)₃] Complexes ^†

Abstract

The connection of a sterically constrained 3-methyl-pyrazine ring to a N-methyl-benzimidazole unit to give the unsymmetrical α,α’-diimine ligand L5 has been programmed for the design of pseudo-octahedral spin-crossover [Fe(L5)₃]²⁺ units, the transition temperature (T_1/2) of which occurs in between those reported for related facial tris-didentate iron chromophores fitted with 3-methyl-pyridine-benzimidazole in a LaFe helicate (T_1/2 ~ 50 K) and with 5-methyl-pyrazine-benzimidazole L2 ligands (T_1/2 ~350 K). A thorough crystallographic analysis of [Fe(L5)₃](ClO₄)₂ (I), [Ni(L5)₃](ClO₄)₂ (II), [Ni(L5)₃](BF₄)₂∙H₂O (III), [Zn(L5)₃](ClO₄)₂ (IV), [Ni(L5)₃](BF₄)₂∙1.75CH₃CN (V), and [Zn(L5)₃](BF₄)₂∙1.5CH₃CN (VI) shows the selective formation of pure facial [M(L5)₃]²⁺ cations in the solvated crystals of the tetrafluoroborate salts and alternative meridional isomers in the perchlorate salts. Except for a slightly larger intra-strand interannular twist between the aromatic heterocycles in L5, the metric parameters measured in [Zn(L5)₃]²⁺ are comparable to those reported for [Zn(L2)₃]²⁺, where L2 is the related unconstrained ligand. This similitude is reinforced by comparable ligand-field strengths (∆_oct) and nephelauxetic effects (as measured by the Racah parameters B and C) extracted from the electronic absorption spectra recorded for [Ni(L5)₃]²⁺ and [Ni(L2)₃]²⁺. In this context, the strictly high-spin behavior observed for [Fe(L5)₃]²⁺ within the 5–300 K range contrasts with the close to room-temperature spin-crossover behavior of [Fe(L2)₃]²⁺ (T_1/2 = 349(5) K in acetonitrile). This can be unambiguously assigned to an intraligand arm wrestling match operating in bound L5, which prevents the contraction of the coordination sphere required for accommodating low-spin Fe^II. Since the analogous 3-methyl-pyridine ring in [Fe(L3)₃]²⁺ derivatives are sometimes compatible with spin-crossover properties, the consequences of repulsive intra-strand methyl–methyl interactions are found to be amplified in [Fe(L5)₃]²⁺ because of the much lower basicity of the 3-methyl-pyrazine ring and the resulting weaker thermodynamic compensation. The decrease of the stability constants by five orders of magnitude observed in going from [M(L2)₃]²⁺ to [M(L5)₃]²⁺ (M = Ni^II and Zn^II) is diagnostic for the operation of this effect, which had been not foreseen by the authors.

1. Introduction

In line with the formulation of the ligand field theory [1,2], or as it was originally called by Bethe, crystal-field theory [3], it was realized that an open-shell metal with at least two valence electrons in a specific chemical environment could exist with either high-spin or low-spin configuration [4]. Following van Vleck’s approach to magnetism [5], Pauling perceptively recognized that it would be feasible to obtain systems in which two spin states could be present simultaneously, while their ratio should depend on the energy difference between them [6,7]. The discovery of thermal spin-state equilibria operating in Fe^III dithiocarbamate by Cambi et al. [8,9,10] at the same period, indeed confirmed these predictions. Since then, a myriad of metal coordination complexes and polymeric materials have been shown to display spin transitions, often referred to as spin-crossover (SCO) materials. These have been studied in detail and extensively reviewed over the last two decades [11,12,13,14,15,16,17,18,19,20]. Due to the ‘on–off’ switching of the magnetic properties accompanying the spin transition from the low-spin diamagnetic configuration (¹A₁ label in octahedral symmetry) to the high-spin paramagnetic form (⁵T₂ label in octahedral symmetry) for d⁶ transition metals in pseudo-octahedral geometry (Scheme 1a), the ‘magic’ [Fe^IIN₆] chromophores, where N is a heterocyclic nitrogen donor atom, have been intensively investigated [11,12,13,14,15,16,17,18,19,20]. Various external stimulations such as changes in temperature [21,22], pressure [23,24], magnetic field [25] or light-irradiation [26,27] can be used for inducing the SCO processes, which makes these microscopic magneto-optical switches very attractive for their introduction into responsive macroscopic materials [12,13,16,28,29,30,31]. The most common and accepted approach for rationalizing the design of spin-crossover pseudo-octahedral Fe^II complexes relies on the energetic balance $\Delta E_{\mathrm{HL}}=E_{\mathrm{hs}}^0-E_{\mathrm{ls}}^0=2\left({\Delta }_{\mathrm{oct}}-P\right)$ between the ligand-field stabilization energy as measured by ∆_oct = 10 Dq and the spin pairing energy modeled with the Racah parameters B and C with P = 2B + 4C ≈ 19B (Scheme 1a) [31]. When ∆_oct >> P, $\Delta E_{\mathrm{HL}}=E_{\mathrm{hs}}^0-E_{\mathrm{ls}}^0=2\left({\Delta }_{\mathrm{oct}}-P\right)>>0$ and the pseudo-octahedral Fe^II complex adopts a low spin configuration with a diamagnetic ¹A₁ electronic ground state, as shown in the right part of the Tanabe–Sugano diagram built for the electronic d⁶ configuration (∆_oct/B > 20 in Scheme 1b). The reverse situation occurs when P >> ∆_oct, which leads to $\Delta E_{\mathrm{HL}}=E_{\mathrm{hs}}^0-E_{\mathrm{ls}}^0=2\left({\Delta }_{\mathrm{oct}}-P\right)<<0$ and the existence of the paramagnetic high-spin ⁵T₂ ground state (left part of Tanabe–Sugano diagram with ∆_oct/B < 10 in Scheme 1b). Finally, for intermediate values $0\le \left|\Delta E_{\mathrm{HL}}=2\left({\Delta }_{\mathrm{oct}}-P\right)\right|\le mRT$ (m ≤ 10), the two spin states coexist and are thermally populated at accessible temperatures. However, the latter statement is misleading and physically unsound since both ∆_oct and P change during the spin transition as a result of the population of the antibonding orbitals in the high-spin form. For pseudo-octahedral spin-crossover [Fe^IIN₆] complexes, the Fe–N bond lengths extend by approximately 10% upon the low-spin to high-spin transition and ∆_oct consequently decreases according to a 1/rⁿ dependence with n = 5–6 (Equation (1)) [31].

$$\frac{{\Delta }_{\mathrm{oct}}^{\mathrm{HS}}}{{\Delta }_{\mathrm{oct}}^{\mathrm{LS}}}={\left(\frac{r_{\mathrm{LS}}}{r_{\mathrm{HS}}}\right)}^n$$

(1)

Taking typical Fe–N bond distances of r_LS = 2.0 Å and r_HS = 2.2 Å [11,12,13,14,15,16,17,18,19,20] leads to ${\Delta }_{\mathrm{oct}}^{\mathrm{LS}}/{\Delta }_{\mathrm{oct}}^{\mathrm{HS}}$ ≈ 1.75 accompanying the spin transition, whereas P changes very little ($P^{\mathrm{HS}}:P^{\mathrm{LS}}\cong 19B$), except for a faint reduction of the nephelauxetic effect with larger bond lengths [32].

Taking into account the 10% bond length expansion accompanying the spin transition, the simplistic zero-point energy differences between the two states summarized in Scheme 1a (i.e., $\Delta E_{\mathrm{HL}}=E_{\mathrm{hs}}^0-E_{\mathrm{ls}}^0=2\left({\Delta }_{\mathrm{oct}}-P\right)$) should be replaced with Equation (2), which is transformed into Equations (3) and (4) upon introducing ${\Delta }_{\mathrm{oct}}^{\mathrm{LS}}/{\Delta }_{\mathrm{oct}}^{\mathrm{HS}}$ ≈ 1.75.

$$\Delta E_{\mathrm{HL}}=E_{\mathrm{hs}}^0-E_{\mathrm{ls}}^0=\frac{12}{5}{\Delta }_{\mathrm{oct}}^{\mathrm{LS}}-\frac{2}{5}{\Delta }_{\mathrm{oct}}^{\mathrm{HS}}-38B$$

(2)

$$\Delta E_{\mathrm{HL}}=E_{\mathrm{hs}}^0-E_{\mathrm{ls}}^0=3.8{\Delta }_{\mathrm{oct}}^{\mathrm{HS}}-38B$$

(3)

$$\Delta E_{\mathrm{HL}}=E_{\mathrm{hs}}^0-E_{\mathrm{ls}}^0=2.17{\Delta }_{\mathrm{oct}}^{\mathrm{LS}}-38B$$

(4)

Solving Equations (3) and (4) for ∆E_HL = 0 provides ${\Delta }_{\mathrm{oct}}^{\mathrm{HS}}/B=38/3.8=10$ and ${\Delta }_{\mathrm{oct}}^{\mathrm{LS}}/B=38/2.17=17.5$ as the lower limit of the existence of thermally accessible spin state equilibria, while the higher limits can be estimated for ∆E_HL = 2000 cm⁻¹, which gives ${\Delta }_{\mathrm{oct}}^{\mathrm{HS}}/B=10+\left[2000/\left(3.8B\right)\right]$ and ${\Delta }_{\mathrm{oct}}^{\mathrm{LS}}/B=17.5+\left[2000/\left(2.17B\right)\right]$ (red areas in Scheme 1b). More sophisticated calculations using Racah parameters B and C, reduced by 70–80% of their free ion values, predict narrow ranges of ligand field strengths 11,000 ≤ ${\Delta }_{\mathrm{oct}}^{\mathrm{HS}}$ ≤ 12,500 cm⁻¹ and 19,000 ≤ ${\Delta }_{\mathrm{oct}}^{\mathrm{LS}}$ ≤ 22,000 cm⁻¹, for which the phenomenon of a thermal spin transition can be expected in Fe^II coordination complexes [31]. Following this theoretical approach, the toolkit of coordination chemists for programming and tuning the thermodynamic spin transition parameters in molecular [Fe^IIN₆] complexes logically relied on the manipulation of ∆_oct and B via (i) some controlled distortions of the coordination geometry from a perfect octahedron by using chelating ligands with fixed bite angles [33] and (ii) specific programming of metal–ligand bonding interactions via ligand design [15,19,34]. Benefiting from the huge amount of experimental data collected during the last decades for [Fe(N^∩N)₃]²⁺ complexes, where N^∩N is an α,α’-diimine chelate ligand possessing two N-heterocyclic donor atoms, it was shown that the connection of a six-membered heterocycle to a five-membered heterocycle in N^∩N provides favorable ligand-field strengths around Fe^II for promoting spin-state equilibria (Equation (5)) with transition temperatures T_1/2 = ∆H_SCO/∆S_SCO (i.e., the temperature at which ∆G_SCO = 0 and x_hs = x_ls = 0.5) within the 30–500 K range [14,15,33].

$${\mathrm{Fe}}_{\mathrm{low}-\mathrm{spin}}^{\mathrm{II}}\stackrel{K_{\mathrm{SCO}}}{\rightleftharpoons }{\mathrm{Fe}}_{\mathrm{high}-\mathrm{spin}}^{\mathrm{II}}\hspace{1em}{K}_{\mathrm{SCO}}=x_{\mathrm{hs}}/x_{\mathrm{ls}}=e^{-\left(\Delta G_{\mathrm{SCO}}/RT\right)}=e^{\left(\Delta S_{\mathrm{SCO}}/R-\Delta H_{\mathrm{SCO}}/RT\right)}$$

(5)

The didentate ligands L1 and L2 match the latter criteria and the associated pseudo-octahedral complexes [Fe(Lk)₃]²⁺ indeed exhibit spin-crossover behaviors in acetonitrile solutions, the transition temperatures of which reveal the stronger Fe–N bonds induced by the strong-accepting pyrazine units in [Fe(L2)₃]²⁺ (T_1/2 ~350 K) compared with pyridine units in [Fe(L1)₃]²⁺ (T_1/2 ~310 K, Scheme 2) in the absence of sterical constraints [35].

Moving the methyl group bound to the pyridine ring from the 5-position in L1 to the 3-position in L3 and to the 6-position in L4 (Scheme 2) is well-known to stepwise decrease the ligand-field strengths in the resulting [Fe(Lk)₃]²⁺ complexes because the operation of additional sterical constraints, produced by intra-strand interactions in [Fe(L3)₃]²⁺ [37] and by inter-strand interactions in [Fe(L4)₃]²⁺, extends the Fe–N bond lengths (see Equation (1)) [38,39,40]. The associated trend ∆_oct(L1) ≈ ∆_oct(L2) > ∆_oct(L3) > ∆_oct(L4) observed for the isostructural [Ni(Lk)₃]²⁺ complexes (Scheme 2), for which the determination of ligand field ∆_oct and Racah B parameters are not complicated by any SCO behavior, are in line with the observation of pure high-spin configurations for the [Fe(L3)₃]²⁺ and [Fe(L4)₃]²⁺ complexes in solution (Scheme 2) [35]. Whereas the connection of methyl groups adjacent to the donor nitrogen atom in the bound 6-methyl-pyridine groups in [Fe(L4)₃]²⁺ produces such large inter-strand interactions that the contraction accompanying the high-spin to low-spin transition cannot be envisioned [41], the situation with the remote 3-methyl substituted pyridine units in [Fe(L3)₃]²⁺ is less clear and a sophisticated triple-stranded heterometallic LaFe helicate containing the facial [Fe(L3)₃]²⁺ chromophore has been shown to display partial SCO behavior at low temperature (T_1/2 ~50 K) [36]. Taking into account that (i) the replacement of a pyridine with a pyrazine ring in going from [Fe(L1)₃]²⁺ and [Fe(L2)₃]²⁺ stabilizes the low-spin state by T_1/2 = 40 K (Scheme 2) and (ii) moving the methyl group from the 5-position in [Fe(L1)₃]²⁺ to the 3-position in fac-[Fe(L3)₃]²⁺ (as found in the related LaFe helicate) produces an opposite trend with the stabilization of the high-spin form by T_1/2 ≈ 50–310 = −260 K [36], we thus ingenuously explored the possibility of combining both aspects in the didentate ligand L5 where the methyl group is now connected to the 3-position of a pyrazine ring (Scheme 3a) with the hope of pushing the transition temperature toward cryoscopic temperatures for [Fe(L5)₃]²⁺ around T_1/2 ~ T_1/2 ([Fe(L2)₃]²⁺) − 260 = 350 − 260 = 90 K (3-methyl-pyrazine). This effort is justified by our long-term quest for designing a pseudo-octahedral spin-crossover [Fe(Lk)₃]²⁺ unit that can modulate the luminescence of adjacent emissive lanthanides in (supra)molecular assemblies via energy transfers within a temperature domain (77–150 K) accessible to optical reading and addressing [36]. Finally, since minor structural variations may induce large changes in ligand-field strength, the systematic exploration of unpredictable intermolecular packing interactions [42,43] operating in crystalline samples of [Fe(L5)₃]X₂ complexes (X^- = monoanionic counter-ions) may contribute to the lucky search for some ‘ideal’ Fe^II complexes, which additionally exhibit hysteretic behavior and bistability [17,44,45].

2. Experimental

Chemicals were purchased from Sigma-Aldrich (Gmbh, Buchs) and Acros and used without further purification unless otherwise stated. Dichloromethane, 1,2-dichloroethane, tert-butylmethyl ether, and N,N-dimethylformamide were dried through an alumina cartridge. Silica-gel plates (Merck, 60 F₂₅₄) were used for thin-layer chromatography, SiliaFlash^® silica gel P60 (0.04–0.063 mm,) and Acros silica gel 60 (0.035–0.07 mm) were used for preparative column chromatography.

Preparation ofN-methyl-2-nitroaniline(4). 1-chloro-2-nitrobenzene (3, 31.75 g, 201.5 mmol, 1.0 eq) and methylamine (198 mL, 40% weight in H₂O, 2295.6 mmol, 11.4 eq) were introduced into a Carius tube equipped with a magnetic stirrer and heated at 120 °C for 48 h. Excess of methylamine was rotatory evaporated and the residual brown oil was partitioned between CH₂Cl₂ (300 mL) and half sat. aq. NH4Cl (300 mL). The organic layer was separated and the aq. phase was further extracted with CH₂Cl₂ (3 × 150 mL). The combined organic extracts were dried over anhydrous Na₂SO₄, filtered, and the solvent evaporated to dryness. The resulting red oil was purified by column chromatography (Silica, CH₂Cl₂) to give 28.99 g of N-methyl-2-nitroaniline (4, 190.5 mmol, yield 94%) as a deep red orange oil, which slowly crystallized within hours. ¹H NMR (CDCl₃, 400 MHz, 298 K) δ/ppm: 8.13 (1H, dd, ³J = 8.8 Hz, ⁴J = 1.6 Hz), 8.00 (1H, bs), 7.43 (1H, ddd, ³J = 8.8 Hz, ³J = 7.2 Hz, ⁴J = 1.6 Hz), 6.81 (1H, dd, ³J = 8.6 Hz, ⁴J = 1.0 Hz), 6.62 (1H, ddd, ³J = 8.4 Hz, ³J = 7.2 Hz, ⁴J = 1.2 Hz), 2.99 (3H, s).

Preparation of N,3-dimethyl-N-(2-nitrophenyl) pyrazine-2-carboxamide (2, left pathway in Scheme 3a). A suspension of 3-methyl-pyrazine-2-carboxylic acid (1, 5 g, 35.5 mmol, 1 eq) and di-isopropyl-ethylamine (7.2 mL, 5.5 g, 45 mmol, 1.26 eq) in CH₂Cl₂ (4 mL) was added dropwise into a two-necked flask containing isobutyl chloroformate (5.4 mL, 5.408 g, 45 mmol, 1.26 eq) dissolved in CH₂Cl₂ (1 mL). The mixture was stirred at −15 °C for 120 min, after which a solution of N-methyl-2-nitroaniline (4, 5.5 g, 0.0352 mol, 1 eq) in CH₂Cl₂ was added. After stirring for 15 h at room temperature, the solution was partitioned between CH₂Cl₂ (100 mL) and half-sat. aq. NH₄Cl (250 mL). The organic layer was separated and the aqueous phase was further extracted with CH₂Cl₂ (3 × 100 mL). The organic fractions were dried over anhydrous Na₂SO₄, concentrated under vacuum, and purified by column chromatography (Silica, CH₂Cl₂/MeOH 99.2:0.8) to yield N,3-dimethyl-N-(2-nitrophenyl) pyrazine-2-carboxamide (2, 8.22 mmol, yield 22%). ¹H NMR (CDCl₃, 400 MHz, 298 K) δ/ppm: mixture of two rotamers A (72.5%) and B (27.5 %): 2.67 (3H, s, A), 2.72 (3H, s, B), 3.58 (3H, s, A), 3.33 (3H, s, B), 7.37–7.80 (3H, m, A and B), 8.29 (1H, d, ³J = 2.5 Hz, A), 8.60 (1H, d, ³J = 2.5 Hz, B), 8.0 (1H, dd, ³J = 2.5 Hz, ⁵J = 0.6 Hz, A), 8.50 (1H, dd, ³J = 2.5 Hz, ⁵J = 0.6 Hz, B), 7.86 (1H, dd, ³J = 8.5 Hz, ⁴J = 1.5 Hz, A), 8.13 (1H, dd, ³J = 8.5 Hz, ⁴J = 1.5 Hz, B). ESI-MS (soft-positive mode; MeOH+CHCl₃+HCOOH): m/z =273.0 ([2 + H]⁺), 295.1 ([2 + Na]⁺).

Preparation of N,3-dimethyl-N-(2-nitrophenyl) pyrazine-2-carboxamide (2, right pathway in Scheme 3a). A suspension of 3-methyl-pyrazine-2-carboxylic acid (1, 0.2 g, 1.44 mmol, 1 eq) and di-isopropyl-ethylamine (0.37 mL, 0.28 g, 2.16 mmol, 1.5 eq) in 1,2-dichloroethane (4 mL) was added dropwise into a two-necked flask containing trimethylacetyl chloride (0.194 mL, 0.19 g, 1.58 mmol, 1.1 eq) in 1,2-dichloroethane (1 mL). The mixture was stirred at −20 °C for 60 min, after which a solution of N-methyl-2-nitroaniline (4, 0.329 g, 2.16 mmol, 1.5 eq) in 1,2-dichloroethane (5 mL) was added. After refluxing for 16 h, the solution was concentrated under vacuum and partitioned between CH₂Cl₂ (80 mL) and half-saturated aqueous solution of NH₄Cl (200 mL). The organic layer was separated and the aqueous phase was further extracted using CH₂Cl₂ (3 × 80 mL). The combined organic fractions were concentrated under vacuum after drying with anhydrous Na₂SO₄. Ultimate purification using column chromatography (Silica, CH₂Cl₂/MeOH 99.2:0.8) yielded 0.106 g of N, 3-dimethyl-N-(2-nitrophenyl) pyrazine-2-carboxamide (2, 0.387 mmol, yield 27%).

Preparation of 1-methyl-2-(3-methylpyrazin-2-yl)-1H-benzo[d]imidazole (L5). N,3-dimethyl-N-(2-nitrophenyl)pyrazine-2-carboxamide (2, 2.56 g, 7.58 mmol, 1 eq) was dissolved in EtOH:DMF (20 mL:25 mL). Sodium dithionite (8.0 g, 40 mmol, 5.2 eq) was added to the mixture and the temperature of the system was raised to 80 °C when 20 mL of water was added. After refluxing for 36 h, the mixture was neutralized using aqueous ammonia and the solvents were removed in vacuo. The concentrate was dissolved in CH₂Cl₂ (50 mL) and washed with water (3 × 200 mL). The aqueous layers were collectively further extracted with CH₂Cl₂ (3 × 50 mL). The combined organic fraction was then concentrated under vacuum and purified by column chromatography (silica, CH₂Cl₂/MeOH 98:2) to yield L5 (7.67 mmol, yield 60%). The compound was crystallized as needles by slow diffusion of n-hexane into a concentrated CH₂Cl₂ solution of L5. ¹H NMR (CDCl₃, 400 MHz, 298 K) δ/ppm: 2.91 (3H, s), 3.96 (3H, s), 7.35–7.44 (2H, m), 7.49 (1H, d, ³J = 7 Hz), 7.88 (1H, d, ³J = 7 Hz), 8.57 (1H-pz, dd, ³J = 2.4 Hz, ⁵J = 0.5 Hz), 8.60 (1H-pz, dd, ³J = 2.4 Hz). ¹³C NMR (CDCl₃, 101 MHz, 298K) δ/ppm: 155.68 (C_q), 149.12 (C_q), 144.54 (C_q), 143.84 (CH_pz), 142.45 (C_q), 140.86 (CH_pz), 136.15 (C_q), 123.85 (CH), 122.90 (CH), 120.45 (CH), 110.01 (CH), 31.83 (CH₃), 23.26 (CH₃). ESI-MS (soft-positive mode; MeOH+CHCl₃+HCOOH): m/z 225.1([L5 + H]⁺). Elemental analysis calculated for C₁₃H₁₂N₄ (%): C 69.62, H 5.39, N 24.98; Found (%): C 69.46, H 5.09, N 25.20.

Preparation of mononuclear Fe^II, Zn^II, and Ni^II complexes with 1-methyl-2-(3-methylpyrazin-2-yl)-1H-benzo[d]imidazole (L5). In a typical synthesis, 0.3 mmol (3 eq) of the ligand L5 dissolved in acetonitrile (2 mL) was added to 0.1 mmol (1 eq) of Fe(ClO₄)₂∙6H₂O or Fe(CF₃SO₃)₂ or Ni(BF₄)₂∙6H₂O or Zn(CF₃SO₃)₂ in acetonitrile (2 mL). The resulting mixture was stirred under an inert atmosphere for 3 h, then evaporated to dryness under vacuum to yield microcrystalline powders of the respective complexes. These powders were dissolved in acetonitrile and allowed to crystallize by evaporation or by slow diffusion of tert-butyl methyl ether to give 64–78% of primary [Fe(L5)₃](CF₃SO₃)₂∙1.5H₂O, [Ni(L5)₃](BF₄)₂∙1.5H₂O∙1.5CH₃CN and [Zn(L5)₃](BF₄)₂∙4H₂O complexes (Table S1). Single crystals suitable for characterization by X-ray diffraction could be obtained by slow evaporation of acetonitrile solution containing 10 eq of (ⁿBu)₄NClO₄ or (ⁿBu)₄NBF₄ to give [Fe(L5)₃](ClO₄)₂ (I), [Ni(L5)₃](ClO₄)₂ (II), [Ni(L5)₃](BF₄)₂∙H₂O (III), [Zn(L5)₃](ClO₄)₂ (IV), [Ni(L5)₃](BF₄)₂∙1.75CH₃CN (V) and [Zn(L5)₃](BF₄)₂∙1.5CH₃CN (VI).

Caution! Dry perchlorates may explode and should be handled in small quantities and with the necessary precautions [46,47].

2.1. Spectroscopic and Analytical Measurements

¹H and ¹³C NMR spectra were recorded at 298 K on a Bruker Avance 400 MHz spectrometer. Chemical shifts are given in ppm with respect to tetramethylsilane. Spectrophotometric titrations were performed with a J&M diode array spectrometer (Tidas series) connected to an external computer. In a typical experiment, 25 cm³ of ligand in acetonitrile (2 × 10⁻⁴ M) was titrated at 298 K with a solution of Fe(CF₃SO₃)₂ or Ni(BF₄)2∙6H₂O or Zn(CF₃SO₃)₂ (2 × 10⁻³ M) in acetonitrile under an inert atmosphere. After each addition of 33 μL, the absorbance was recorded using Hellma optrodes (optical path length 0.1 cm) immersed in the thermostated titration vessel and connected to the spectrometer. Mathematical treatment of the spectrophotometric titrations was performed with factor analysis [48,49,50] and with ReactLab^TM Equilibria (previously Specfit/32) [51,52,53]. Pneumatically-assisted electrospray (ESI-MS) mass spectra were recorded from 10⁻⁴ M (ligands) and 10⁻³ M (complexes) solutions on an Applied Biosystems API 150EX LC/MS System equipped with a Turbo Ionspray source. Elemental analyses were performed by K. L. Buchwalder from the Microchemical Laboratory of the University of Geneva. Elemental analysis was not conducted for perchlorate salts for security reasons, while crystals of the tetrafluoroborate salts lost their solvent upon separation from the mother liquor and were not further characterized. Electronic spectra in the UV–Vis region were recorded at 293 K from solutions in CH₃CN with a Perkin-Elmer Lambda 1050 using quartz cells of a 0.1 or 1.0 mm path length. Solid-state absorption spectra were recorded with a Perkin-Elmer Lambda 900 using capillaries. Solid-state magnetic data were recorded on a MPMS 3 or MPMS 5 QUANTUM DESIGN magnetometers using magnetic fields of 1000–5000 Oe at 1 K/min rates within the 5–300 K range. The magnetic susceptibilities were corrected for the magnetic response of the sample holder and for the diamagnetism of the compounds by using the approximation ${\chi }_{\mathrm{D}}=-\frac{\mathrm{MW}}{2}\cdot {10}^{-6}$ cm³·mol⁻¹ [54].

2.2. X-Ray Crystallography

Summary of crystal data, intensity measurements, and structure refinements for compounds L5, [Fe(L5)₃](ClO₄)₂ (I), [Ni(L5)₃](ClO₄)₂ (II), [Ni(L5)₃](BF₄)₂∙H₂O (III), and [Zn(L5)₃](ClO₄)₂ (IV) is presented in Tables S2–S4. Pertinent bond lengths, bond angles, and interplanar angles are collected in Tables S5–S14 together with ORTEP views and pertinent numbering schemes gathered in Figures S1–S5. The crystals were mounted on MiTeGen kapton cryoloops with protection oil. X-ray data collection was performed with an Agilent SuperNova Dual diffractometer equipped with a CCD Atlas detector (Cu[Kα] radiation). The structures were solved by using direct methods [55,56] or dual-space methods [57]. Full-matrix least-square refinements on F² were performed with SHELX2014 [58]. CCDC 1988655-1988659 contained the supplementary crystallographic data. These data can be obtained free of charge from the Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/. Single crystals of [Ni(L5)₃](BF₄)₂∙1.75CH₃CN (V) and [Zn(L5)₃](BF₄)₂∙1.5CH₃CN (VI) could also be obtained as inversion twins. The two complexes were isostructural and crystallized in the trigonal system (P3c1 space group) with five independent complexes in the asymmetric unit, all located on three-fold rotation axes (the metal content of the asymmetric unit is 5/3) and Z = 10 (Table S15). Although there is no doubt that the three ligands adopt facial arrangements around the metal to give exclusively fac-[M(L5)₃]²⁺ cations (Figures S6–S7), we were only able to locate unambiguously three BF₄^- counter-anions in the asymmetric unit. Despite numerous efforts, we were not able to obtain a satisfying model for the last third of a BF₄⁻ counter-anion and gave up to further discuss these structures and to deposit the cif files.

3. Results and Discussion

Synthesis, characterization, and solid-state structures were obtained for the didentate ligand L5 and its pseudo-octahedral complexes [M(L5)₃]X₂ (M = Fe, Ni, Zn and X = BF₄, ClO₄). Compared with pyridine-carboxylic acids, which are easily activated via their transformation into acyl chloride with the help of thionyl chloride or oxalyl chloride [59], the electron-rich pyrazine analogue 1 produced only negligible yield (<1%) of the target amide product 2 under these standard conditions [60]. The 3-methylpyrazine-2-carboxylic acid 1 was thus activated as its anhydride through reaction with either isobutyl chloroformate (left path in Scheme 3a) or pivaloyl chloride (right path in Scheme 3a). Subsequent nucleophilic attack with N-methyl-2-nitroaniline 4 yielded the ortho-nitroamide compound 2 in moderate yield. A subsequent reductive cyclisation reaction provided ligand L5, which was characterized by its ¹H-NMR spectrum (Scheme 3b). The lack of NOE effect observed between the methyl groups in positions 5 and 8 indicates an anti-conformation for the α,α’-diimine chelate unit, which was confirmed by (i) the crystal structure of L5 (Figure 1a) and (ii) gas-phase calculations predicting a global energy minimum for the planar anti-conformation (interplanar angle between the two aromatic rings α = 180°, Figure 1b) [61]. Given that the same anti-conformations are (i) found in the solid state (Figure S8) and (ii) predicted in the gas phase for the ligands L2 [60] and L5, their computed EHMO frontiers orbitals are comparable (Figure S9a) and lead to akin electronic absorption spectra dominated by intense π*←π covering the near UV range (Figure S9b).

Interestingly, the gas-phase energy of L5 displayed two additional local energy minima for α = ±16° (Figure 1b), which shifted from α = 0° previously reported for the second local minimum in L2 (Figure S10) [60]. The larger interplanar angle of 16° in the optimized syn-conformation of L5 was the result of the sterical crowding between the close methyl groups connected to the adjacent aromatic rings (positions 5 and 8 in the numbering of Scheme 3b). Taking the latter conformation as a limiting structural model when L5 is bound to a metal cation provides d_N∙∙∙N = 2.83 Å between the two nitrogen donor atoms of the α,α’-diimine chelate. According to Phan et al. [33], the latter separation matches the 2.78 ≤ d_N∙∙∙N ≤ 2.93 Å range for which a diimine ligand might be used to achieve spin-crossover behavior in tris-homoleptic Fe^II complexes.

Stoichiometric mixing of L5 (3 eq.) with Fe(CF₃SO₃)₂, Ni(BF₄)₂∙6H₂O or Zn(BF₄)₂∙6H₂O (1 eq,) in acetonitrile gave fair yields of microcrystalline primary precipitates of [Fe(L5)₃](CF₃SO₃)₂∙1.5H₂O, [Ni(L5)₃](BF₄)₂∙1.5H₂O∙1.5CH₃CN, and [Zn(L5)₃](BF₄)₂∙4H₂O complexes (Table S1). A series of isostructural complexes [Fe(L5)₃](ClO₄)₂ (I), [Ni(L5)₃](ClO₄)₂ (II), and [Zn(L5)₃](ClO₄)₂ (IV) could be obtained as single crystals by recrystallization in acetonitrile containing 10 eq of (ⁿBu)₄NClO₄.

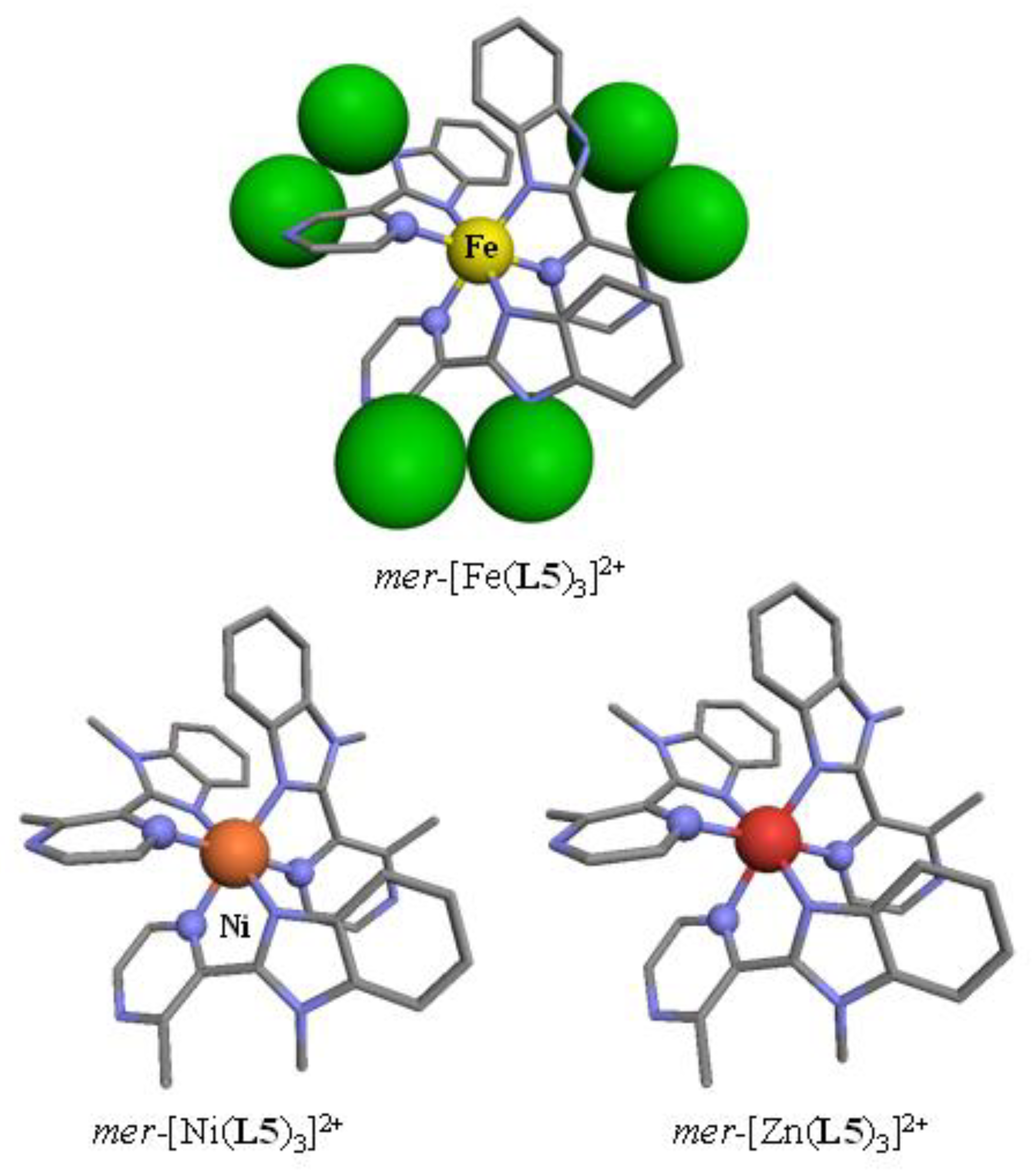
Monocrystals suitable for x-ray diffractions were also obtained for [Ni(L5)₃](BF₄)₂∙H₂O (III), [Ni(L5)₃](BF₄)₂∙1.75CH₃CN (V), and [Zn(L5)₃](BF₄)₂∙1.5CH₃CN (VI) using the same method except for the replacement of (ⁿBu)₄NClO₄ with (ⁿBu)₄NBF₄ (Tables S3 and S4). The crystal structures of the perchlorate salts systematically displayed the formation of mer-[M(L5)₃]²⁺ cations (Figure 2), in which the [MN₆] chromophores adopted a geometry close to the perfect octahedron as ascertained by SHAPE’s scores close to zero (

Table 1. Structural data for hexa-coordinate metallic centers (Fe^II, Ni^II or Zn^II) found in the crystal structures of [Fe(L5)₃](ClO₄)₂ (I), [Ni(L5)₃](ClO₄)₂ (II), [Ni(L5)₃](BF₄)₂∙H₂O (III), [Zn(L5)₃](ClO₄)₂ (IV), [Ni(L5)₃](BF₄)₂∙1.75CH₃CN (V), and [Zn(L5)₃](BF₄)₂∙1.5CH₃CN (VI) at 180 K collecting average bond lengths, interannular intraligand angles (α), interchelate angles (β), chelate bite angles (γ), and SHAPE’s scores.

	[Fe(L5)3](ClO4)2	[Ni(L5)3](ClO4)2	[Ni(L5)3](BF4)2	[Ni(L5)3](BF4)2	[Zn(L5)3](ClO4)2	[Zn(L5)3](BF4)2	[Zn(L2)3](CF3SO3)2
Crystal Structure	I	II	III	V	IV	VI
Configuration	meridional	meridional	facial	facial	meridional	facial	meridional
d(M-Nbz)/Å a	2.14 (1)	2.08 (2)	2.08 (2)	2.07 (2)	2.11 (2)	2.09 (1)	2.09 (7)
d(M-Npz)/Å b	2.24 (3)	2.14 (2)	2.12 (2)	2.12 (1)	2.25 (6)	2.26 (1)	2.27 (3)
α/°	39 (3)	37 (3)	39 (3)	36 (4)	39 (3)	38 (4)	21 (13)
β/°	85 (9)	86 (7)	88 (8)	83.4 (9)	85 (8)	84 (1)	81 (8)
γ/°	76.6 (7)	78.8 (4)	79.1 (5)	79.2 (7)	77 (1)	77.8 (8)	76.6 (1)
Octahedron c	1.85	1.41	1.25 (3) d	1.21 (8) d	1.74	1.5 (1) d	1.95
Trigonal Prism c	15.65	15.42	15.5 (1) d	16.0 (2) d	15.39	15.9 (2) d	12.99
Reference	This work	This work	This work	This work	This work	This work	[60]

^a bz = benzimidazole. ^b pz = pyrazine. ^c SHAPE’s scores calculated with reference to ideal octahedral and trigonal prismatic geometries [62,63,64,65,66]. ^d Average for more than one complex in the asymmetric unit.

) [62,63,64,65,66].

On the contrary, the crystal structures of the tetrafluoroborate salts showed the existence of fac-[M(L5)₃]²⁺, in which the three didentate ligands adopted the same orientation along the pseudo-threefold axis passing through the metal (Figure 3). Having previously established that the energy gap between the facial (C₃-symmetry) and meridional (C₁-symmetry) geometries in [Zn(L1)₃]²⁺ and [Zn(L2)₃]²⁺ roughly followed a pure statistical (i.e., entropic) trend and does not overcome thermal energy at room temperature [60], we concluded that packing forces, specific to the use of perchlorate or tetrafluoroborate counter anions, are more than enough for the quantitative and selective crystallization of pure meridional, respectively facial isomers. For the [Ni(L5)₃]²⁺ and [Zn(L5)₃]²⁺ chromophores, the M–N bonds are systematically shorter for the more basic benzimidazole nitrogen donor (Table 1, entry 4; pK_a(bzim) = 5.68) than with its pyrazine counterpart (Table 1, entry 5; pK_a(pyrazine) = 0.65) [67], a trend in complete agreement with that reported for the analogous complex [Zn(L2)₃]²⁺ (Table 1, column 8) [60]. Moreover, the shift of the methyl group bound to the pyrazine ring from the 5-position in L2 to the 3-position in L5 has globally no geometric influence on the [ZnN₆] coordination sphere, thus leading to Zn–N bond distances surrounding the standard value of Zn–N = 0.74 + 1.46 = 2.20 Å deduced from the effective ionic radii [68]. In other words, the close methyl groups found in the bound didentate ligand L5 do not induce major intramolecular steric constraints in [Zn(L5)₃]²⁺ and only a slight increase of the interannular intraligand angles can be detected in going from [Zn(L2)₃]²⁺ (α = 21(13)°) to [Zn(L5)₃]²⁺ (α = 38(4)°, entry 5 in Table 1). The molecular structures of [Ni(L5)₃]²⁺ were very similar to those observed for the Zn^II analogues (Figure 2 and Figure 3), except for the slightly shorter Ni–N bond distances, a trend in line with the contraction of Shannon’s effective ionic radii predicted to be 0.74 Å for six-coordinate Zn²⁺ and 0.69 Å for six-coordinate Ni²⁺ [68]. The detection of long Fe–N bond distances in [Fe(L5)₃]²⁺ (d(Fe-N_bz) = 2.14(1) Å and d(Fe-N_pz) = 2.24(3) Å, entries 3–4 in Table 1) is more remarkable since it suggests that the Fe^II metal center adopts a pure high spin configuration at 180 K as previously found for the analogous 3-methylpyridine-benzimidazole ligand in [Fe(L3)₃]²⁺ (d(Fe-N_bz) = 2.14(2) Å and d(Fe-N_py) = 2.26(5) Å) [35].

Spin-state, magnetic, and electronic properties of the pseudo-octahedral complexes [M(L5)₃]X₂ (M = Fe, Ni and X = BF₄, ClO₄) were obtained in the solid state. Molar magnetic susceptibilities (χ_M), corrected for diamagnetism of solid state samples of [Fe(L5)₃](ClO₄)₂ (I) were recorded at variable temperatures in a constant magnetic field of 5000 Oe. The χ_MT versus T plot shows a smooth and regular increase of the χ_MT product in the 50–300 K range (red trace in Figure 4), which can be fitted to Equation (6) using a high Curie constant C = 3.5708(9) cm³·K·mol⁻¹ and a non-negligible temperature independent paramagnetism TIP = 848(5) × 10⁻⁶ cm³·mol⁻¹, a behavior diagnostic for a high-spin Fe(II) complex [69].

$${\chi }_{\mathrm{M}}T=C_{}+T\cdot \mathrm{TIP}$$

(6)

The additional abrupt decrease in the magnetic susceptibility occurring at low temperature (T < 40 K) can be assigned to zero-field splitting (ZFS) of high-spin Fe(II), which was modeled with Equation (7), where D and E are the axial and rhombic ZFS parameters, respectively [70,71,72,73].

$$E_n^0=D\cdot \left(S_{\widehat{z}}^2-\frac{S(S+1)}{3}\right)+E\cdot \left(S_{\widehat{x}}^2-S_{\widehat{y}}^2\right)$$

(7)

The pseudo-threefold axis characterizing the [FeN₆] chromophore in [Fe(L5)₃](ClO₄)₂ implies that E can be neglected (E ~ 0). Consequently, the electron–electron interaction splits the S = 2 manifold at zero magnetic field into three energy levels located at $E_1^0=-2D$ (m_s = 0), $E_2^0=-D$ (m_s = ±1), and $E_3^0=2D$ (m_s = ±2). Application of the van Vleck Equation (8), where k_B = 0.695039 cm⁻¹∙K⁻¹ is the Boltzmann constant and N_A is Avogadro number, $E_n^1$ are first-order spin-only Zeeman effects given in Equation (9), where μ_B = −4.6686 × 10⁻⁵ cm⁻¹·G⁻¹ is the Bohr magneton, and $E_n^2$ stands for the second-order Zeeman effects, leads to a satisfying fit (dotted black trace in Figure 4 with agreement factor AF = 3.73 × 10⁻³) with Landé factor g = 2.20(1), D = 0.52(1) cm⁻¹ and $\mathrm{TIP}=-N_{\mathrm{A}}{E}_n^2$ = 319(4) × 10⁻⁶ cm³·mol⁻¹.

$${\chi }_{\mathrm{M}}T=T\cdot N_{\mathrm{A}}\cdot \frac{\underset{n}{\Sigma }\left[\left(\frac{{\left(E_n^1\right)}^2}{k_{\mathrm{B}}T}-2E_n^2\right)\cdot \exp \left(-\frac{E_n^0}{k_{\mathrm{B}}T}\right)\right]}{\underset{n}{\Sigma }\left[\exp \left(-\frac{E_n^0}{k_{\mathrm{B}}T}\right)\right]}$$

(8)

$$E_n^1=-g\cdot {\mu }_{\mathrm{B}}\cdot m_S$$

(9)

The latter magnetic data closely matched those reported for the analogous [Fe(L3)₃](CF₃SO₃)₂ complex (g = 2.20(2), D = 0.85(1) cm⁻¹ [36]), and demonstrate that our novel [Fe(L5)₃](ClO₄)₂ complex, in which the 3-methyl-pyridine group of L3 is replaced with a 3-methyl-pyrazine group in L5, is also purely high-spin within the 5–300 K range with no trace of SCO behavior. A careful inspection of the experimental curve around 80 K (Figure 4) showed a very minor deviation from the theoretical model, which could be tentatively assigned to traces of trapped low-spin form as previously reported for fac-[Fe(L3)₃]²⁺ when it is incorporated into a LaFe triple-stranded helicate [36].

The electronic absorption spectrum recorded for [Fe(L5)₃](ClO₄)₂ (I) in the solid state shows the expected Jahn–Teller split Fe^II(⁵E←⁵T₂) ligand-field transition (Figure 5a) [31]. A deconvolution using two Gaussian functions gives ${\tilde{\nu }}_{\max }$ = 8881 cm⁻¹ and 11,887 cm⁻¹, thus leading to a barycenter at 10,384 cm⁻¹, which provides a direct estimation of ${\Delta }_{\mathrm{oct}}^{\mathrm{HS}}({\mathrm{Fe}}^{\mathrm{II}})$ = 10 Dq, a value only 700 cm⁻¹ below the minimum of ${\Delta }_{\mathrm{oct}}^{\mathrm{HS}}$ ≈ 11,000 cm⁻¹ suggested to be the lower limit for inducing spin state equilibria [31]. However, the latter criterion strongly depends on the choice of the Racah parameter B, which is not easily extracted from the single intrashell d–d transition observed in the electronic spectra of high-spin Fe^II complexes. For this reason, we have recorded the electronic absorption spectrum of the analogous Ni^II complex [Ni(L5)₃](BF₄)₂∙H₂O (III), for which the combination of two spin-allowed d–d transitions Ni(³T₂←³A₂) and Ni(³T₁←³A₂) and one spin-forbidden transition Ni(¹E←³A₂) (Figure 5b) allows a complete characterization of the electronic parameters ${\Delta }_{\mathrm{oct}}^{}({\mathrm{Ni}}^{\mathrm{II}})$, B(Ni^II), and C(Ni^II) with the help of Equations (10)–(13) [74,75].

$$E\left({}^3{\mathrm{A}}_{2\mathrm{g}}\right)=0$$

(10)

$$E\left({}^1{\mathrm{E}}_{\mathrm{g}}\right)=8B+2C-\frac{6B^2}{{\Delta }_{\mathrm{oct}}}$$

(11)

$$E\left({}^3{\mathrm{T}}_{2\mathrm{g}}\right)={\Delta }_{\mathrm{otc}}$$

(12)

$$E\left({}^3{\mathrm{T}}_{1\mathrm{g}}\right)=1.5{\Delta }_{\mathrm{oct}}+7.5B-0.5\sqrt{225B^2+{\Delta }_{\mathrm{oct}}{}^2-18{\Delta }_{\mathrm{oct}}B}$$

(13)

A Gaussian deconvolution of the visible part of the absorption spectrum into three peaks yielded two broad bands, diagnostic for the spin-allowed, but parity-forbidden, transitions at 10,672 cm⁻¹ (³T₂←³A₂) and 16,763 cm⁻¹ (³T₁←³A₂; Table S16), together with a third weaker band at 12,584 cm⁻¹, which can be ascribed to the spin-forbidden ¹E←³A₂ component (Figure 5b). Subsequent non-linear least-squares fits of the energies of these transitions with Equations (10)–(13) provides a first rough set of ligand field strength Δ_oct = 10,672 cm⁻¹ and Racah parameters B = 760 cm⁻¹ and C = 3413 cm⁻¹ (Table S16). However, the mixing of the spin-allowed ³T₂←³A₂ transition with the spin-forbidden ¹E←³A₂ transition via spin-orbit coupling for apparent ligand field strengths around 11,000–12,000 cm⁻¹, as found for [Ni(L5)₃](BF₄)₂∙H₂O, requires further refinements [76]. A detailed analysis of a series of Ni^II complexes led Hancock and coworkers to propose three empirical Equations (14)–(16) to obtain more reliable ligand field strengths Δ_oct and Racah parameters B and C in cm⁻¹ units (ε₁ and ε₂ are the extinction coefficients at the observed frequencies of the ¹E←³A₂ transition and ³T₂←³A₂ transition, respectively) [76]. The analysis of the experimental absorption spectra using this model gives the corrected parameters gathered in

Table 2. Ligand-field strengths (_oct) and Racah parameters (B, C) computed with Equations (14)–(16) for [Ni(L5)₃](BF₄)₂∙H₂O (III) in the solid state and in 0.1 M acetonitrile solution at 298 K.

	[Ni(L5)3](BF4)2 (solid)	[Ni(L5)3]2+ (0.1 M CH3CN)	[Ni(L2)3]2+ (0.1 M CH3CN)
Δoct/cm−1	11,631	11,555	11,605
B/cm−1	864	866	865
C/cm−1	2986	3012	2995
Δoct/B	13.5	13.3	13.4
C/B	3.45	3.48	3.46
β a	0.83	0.83	0.83

^a Nephelauxetic parameter β = B/B^o using B^o = 1042 cm⁻¹ for free Ni²⁺ ion [77].

for the [Ni(L5)₃]²⁺ and [Ni(L2)₃]²⁺ chromophores.

$${\Delta }_{\mathrm{oct}}=10\mathrm{Dq}\hspace{0.17em}=10630\hspace{0.17em}+1370\left({\epsilon }_1/{\epsilon }_2\right)$$

(14)

$$B=1120\hspace{0.17em}-0.022\cdot {\Delta }_{\mathrm{oct}}$$

(15)

$$C=15B-9975$$

(16)

The refined ∆_oct, B and C parameters computed for [Ni(L5)₃]²⁺ (Table 2) almost exactly matched those previously reported for the unconstrained [Ni(L2)₃]²⁺ complex, for which the related [Fe(L2)₃]²⁺ complex displayed spin-crossover behavior above room temperature (T_1/2 ~400 K in the solid state, T_1/2 ~ 350 K in acetonitrile solution [35]). Moreover ∆_oct ([Ni(L5)₃]²⁺) = 11,630 cm−¹ is compatible with the ligand field range 11,200 ≤ ∆_oct (Ni^II) ≤ 12,400 cm⁻¹ established by Busch and coworkers [78] as a reliable and useful benchmark for predicting and rationalizing the spin-crossover of the related Fe^II complexes [40]. The absence of SCO behavior depicted by [Fe(L5)₃](ClO₄)₂ is thus difficult to assign to some inadequate electronic properties of the [FeN₆] chromophore, but more probably to the impossibility of the coordination sphere to shrink for adopting short-enough Fe–N bonds compatible with low-spin Fe^II. This pure sterical limitation can be tentatively assigned to the intraligand sterical constraints programmed to occur between the methyl groups bound to the pyrazine and benzimidazole rings in each coordinated syn-L5 ligand in [Fe(L5)₃]²⁺. However, packing forces operating in the solid state may be as important, or even much larger than intramolecular constraints and a definitive assessment requires the extension of our analysis to isolated complexes in solution, where intermolecular interactions are significantly reduced.

Stabilities and electronic properties of the pseudo-octahedral complexes [M(L5)₃]X₂ (M = Fe, Ni, Zn and X = BF₄, CF₃SO₃) were obtained in acetonitrile solutions. Following the procedure previously detailed for analogous [Zn(Lk)₃]²⁺ [60] and [Fe(Lk)₃]²⁺ [35] with the didentate ligands L1 and L2, spectrophotometric titrations of submillimolar concentrations of L5 with M(CF₃SO₃)₂ (M = Ni, Zn) in dry acetonitrile (Figure 6a,b and Figure S11a,b) showed the successive formation of two absorbing complexes [M(L5)_n]²⁺ (n = 2, 1; equilibria (17)–(18)) as ascertained by their independent eigenvectors found in the factor analyses (Figure 6c and Figures S11c–S12c) [48,49,50] and their satisfying re-constructed absorption spectra (Figure 6d and Figure S11d) [51,52,53].

$${\mathrm{M}}^{2+}+\mathbf{L}5 ⥨ {\left[\mathrm{M}\right(\mathbf{L}5\left)\right]}^{2+} {\beta }_{1,1}^{\mathrm{M},\mathbf{L}5}$$

(17)

$${\mathrm{M}}^{2+}+2 \mathbf{L}5 ⥨ {\left[\mathrm{M}\right(\mathbf{L}5{)}_2]}^{2+} {\beta }_{1,2}^{\mathrm{M},\mathbf{L}5}$$

(18)

$${\mathrm{M}}^{2+}+3 \mathbf{L}5 ⥨ {\left[\mathrm{M}\right(\mathbf{L}5{)}_3]}^{2+} {\beta }_{1,3}^{\mathrm{M},\mathbf{L}5}$$

(19)

The 4000 cm−1 red-shift of the ligand-centered π*←π transition observed upon complexation to M^II (Figure 6a and Figure S11a) is diagnostic for the anti→syn conformational change of the α,α’diimine unit accompanying the coordination of L5 to M^II [79,80]. Non-linear least-square fits [51,52,53] of the spectrophotometric data to equilibria (17)–(18) provide the macroscopic cumulative formation constants gathered in

Table 3. Cumulative stability constants ($\log \left({\beta }_{1,n}^{\mathrm{M},\mathbf{L}\mathit{k}}\right)$, Equations (17)–(19), intrinsic affinities ($\Delta G_{}^{\mathrm{M},\mathbf{L}\mathit{k}}=-RT\ln \left(f^{\mathrm{M},\mathbf{L}\mathit{k}}\right)$ ) and global interligand interactions ($\Delta E_{}^{\mathbf{L}\mathit{k},\mathbf{L}\mathit{k}}=-RT\ln \left(u^{\mathbf{L}\mathit{k},\mathbf{L}\mathit{k}}\right)$ ) estimated in acetonitrile at 298 K.

Ligand	L5		L2
Metal	Ni(II)	Zn(II)	Zn(II)	Fe(II)
$\log \left({\beta }_{1,1}^{\mathrm{M},\mathbf{L}\mathit{k}}\right)$	4.27 (1)	4.38 (1)	6.89 (3)	6.045 (9)
$\log \left({\beta }_{1,2}^{\mathrm{M},\mathbf{L}\mathit{k}}\right)$	8.73 (1)	8.73 (1)	12.76 (5)	11.49 (2)
$\log \left({\beta }_{1,3}^{\mathrm{M},\mathbf{L}\mathit{k}}\right)$	12.0 a	12.7 a	17.64 (5)	16.88 (2)
$\Delta G_{}^{\mathrm{M},\mathbf{L}\mathit{k}}$/kJ/mol	−16.5 (1)	−17.1 (7)	−31.1 (3)	−25.9 (8)
$\Delta E_{}^{\mathbf{L}\mathit{k},\mathbf{L}\mathit{k}}$/kJ/mol	−4.9 (1)	−3.6 (1)	1.1 (4)	−2.7 (9)
Reference	This work	This work	[60]	[35]

^a Computed with Equation (22).

(entries 3–4) together with speciation curves [81] showing a maximum formation of ca. 50% of the ligand speciation under the form of [M(L5)₂]²⁺ at submillimolar concentrations (Figure 6e and Figure S11e). Attempts to consider the formation of an additional [M(L5)₃]²⁺ complex according to equilibrium (19) only failed in our hands, which suggests that the ${\beta }_{1,3}^{\mathrm{M},\mathbf{L}5}$ constant is too low for providing significant quantities of the latter complex at this concentration.

According to the site-binding model [82,83], the first stability constant ${\beta }_{1,1}^{\mathrm{M},\mathbf{L}\mathit{k}}$ reflects the simple intermolecular affinity $f_{}^{\mathrm{M},\mathbf{L}\mathit{k}}$ between the didentate ligand Lk and the entering M^II cation (including the change in solvation, Equation (20)) modulated by a pure entropic contribution ω_1,1 = 24 [60] produced by the change in rotational entropies accompanying the transformation of the reactants into products, a parameter often referred to as the statistical factor [84,85].

$${\beta }_{1,1}^{\mathrm{M},\mathbf{L}\mathit{k}}=24f_{}^{\mathrm{M},\mathbf{L}\mathit{k}}$$

(20)

Applying Equation (20) to the stability constants ${\beta }_{1,1}^{\mathrm{M},\mathbf{L}\mathit{k}}$ collected in Table 3 (entry 3) leads to intrinsic free energy affinities $\Delta G_{}^{\mathrm{M},\mathbf{L}\mathit{k}}=-RT\ln \left(f^{\mathrm{M},\mathbf{L}\mathit{k}}\right)=-RT\ln \left({\beta }_{1,1}^{\mathrm{M},\mathbf{L}\mathit{k}}/24\right)$ (entry 6), which are roughly reduced by a factor two in going from the 5-methyl-pyrazine ligand L2 to the 3-methyl-pyrazine analogue L5, as illustrated for [Zn(L2)]²⁺ ($\Delta G_{}^{\mathrm{Zn},\mathbf{L}\mathbf{2}}$ = −31.1(3) kJ∙mol⁻¹) and [Zn(L5)]²⁺ ($\Delta G_{}^{\mathrm{Zn},\mathbf{L}\mathbf{5}}$ = −17.1(7) kJ∙mol⁻¹).

The fixation of two ligands to give [M(Lk)₂]²⁺ obeying equilibrium (18) requires twice the intermolecular metal-ligand affinity, a statistical factor of ω_1,2 = 120, which takes into account all the possible geometric isomers [60] and the operation of allosteric cooperativity factors $u_{}^{\mathbf{L}\mathit{k},\mathbf{L}\mathit{k}}$ measuring the extra energy cost ($u_{}^{\mathbf{L}\mathit{k},\mathbf{L}\mathit{k}}$ < 1), respectively, energy benefit ($u_{}^{\mathbf{L}\mathit{k},\mathbf{L}\mathit{k}}$ > 1) produced by the binding of two ligands to the same metal (Equation (21)) [82,83,86].

$${\beta }_{1,2}^{\mathrm{M},\mathbf{L}\mathit{k}}=120{\left(f_{}^{\mathrm{M},\mathbf{L}\mathit{k}}\right)}^2{u}_{}^{\mathbf{L}\mathit{k},\mathbf{L}\mathit{k}}$$

(21)

Applying Equation (21) to the stability constants ${\beta }_{1,2}^{\mathrm{M},\mathbf{L}\mathit{k}}$ (entry 4 in Table 3) with the help of the intrinsic affinities $f^{\mathrm{M},\mathbf{L}\mathit{k}}=\exp \left(-\Delta G_{}^{\mathrm{M},\mathbf{L}\mathit{k}}/RT\right)$ deduced from $\Delta G_{}^{\mathrm{M},\mathbf{L}\mathit{k}}$ (entry 6 in Table 3) provides interligand free energies interactions $\Delta E_{}^{\mathbf{L}\mathit{k},\mathbf{L}\mathit{k}}=-RT\ln \left(u^{\mathbf{L}\mathit{k},\mathbf{L}\mathit{k}}\right)=-RT\ln \left({\beta }_{1,2}^{\mathrm{M},\mathbf{L}\mathit{k}}/120\right)-2\Delta G_{}^{\mathrm{M},\mathbf{L}\mathit{k}}$ (entry 7 in Table 3) close to zero (non-cooperativity) for [M(L2)₂]²⁺ complexes, but negative (positive cooperativity) for [M(L5)₂]²⁺. However, the neglect of the expected [M(L5)₃]²⁺ for modeling the spectrophotometric titrations results in a slight overestimation of the second cumulative constant ${\beta }_{1,2}^{\mathrm{M},\mathbf{L}\mathit{k}}$, fully compatible with the apparent, but probably not pertinent, minor positive cooperativity observed for the successive binding of L5 ligands to M²⁺ centers. Finally, the introduction of the estimated intrinsic affinities and interligand interactions into Equation (22) allows some predictions concerning the inaccessible third cumulative stability constants [35].

$${\beta }_{1,3}^{\mathrm{M},\mathbf{L}\mathit{k}}=64{\left(f_{}^{\mathrm{M},\mathbf{L}\mathit{k}}\right)}^3{\left(u_{}^{\mathbf{L}\mathit{k},\mathbf{L}\mathit{k}}\right)}^3$$

(22)

The resulting values of $\log \left({\beta }_{1,3}^{\mathrm{M},\mathbf{L}\mathbf{5}}\right)$ ≈ 12.0 (Table 3, entry 5) correspond to a reduction by five orders of magnitude with respect to $\log \left({\beta }_{1,3}^{\mathrm{M},\mathbf{L}\mathbf{2}}\right)$ ≈ 17.0 experimentally found with the less constrained ligand L2. There is no doubt that the hindered planar arrangement of the two aromatic heterocycles in L5 has a deep impact on the strength of the M–N bonds because of the misalignment of the nitrogen lone pairs with metal d-orbitals in pseudo-octahedral geometry. Nevertheless, at 1 M concentration of L5 in acetonitrile, the ligand speciation curve computed [81] by using ${\beta }_{1,n}^{\mathrm{M},\mathbf{L}\mathbf{5}}$ (n = 1–3) gathered in Table 3 shows that [M(L5)₃]²⁺ (M = Ni, Zn) corresponds to more than 90% of the distribution at the stoichiometric M:L5 = 1/3 ratio (Figure S12). At a total ligand concentration of 0.1 M in acetonitrile, [Ni(L5)₃]²⁺ stands for 84% of the ligand speciation and its absorption spectrum closely matches that recorded for related solid state samples (Figure 5). Repeating the detailed analysis described in the previous section (Equations (10)–(16)) provides ligand-field strengths (∆_oct) and Racah parameters (B, C) similar to those found in the solid state (Table 2), especially for the crucial ratio ∆_oct/B = 13.3, which is identical for [Ni(L2)₃]²⁺ and [Ni(L5)₃]²⁺, both in solution and in the solid state. In other words, the moving of the methyl group connected to the pyrazine ring from the 5-position in L2 to the 3-position in L5 indeed strongly reduces the affinity of the didentate ligand for Ni(II) in solution, but only has a weak effect on the ligand field strengths and on the Ni–N (or Zn–N) bond length. Interestingly, the variable-temperature ¹H NMR spectra recorded for diamagnetic [Zn(L5)₃]²⁺ (>80% for a total concentration of 0.1 M in CD₃CN in the 233–333 K range, Figure S13) showed a single set of signals compatible with the exclusive formation of an averaged C₃-symmetrical species with no contribution from either blocked facial and meridional isomers or from partial decomplexation to give [Zn(L5)₂]²⁺ + L5 (equilibrium (19)). These observations are in contrast with the detection at low temperature in CD₃CN of two well-resolved spectra characteristics of a slow exchange operating between fac-[Zn(L2)₃]²⁺ and mer-[Zn(L2)₃]²⁺ [60], and suggests that the weaker stability constants are accompanied by faster ligand exchange processes around Zn²⁺ in [Zn(L5)₃]²⁺. This decrease in affinity reaches its paroxysm for the coordination of Fe²⁺ since the spectrophotometric titration of L5 with Fe(CF₃SO₃)2 conducted at submillimolar concentration displays only a minor drift of the absorption spectra with no pronounced end point (Figure 7).

Attempts to model these limited variations within the frame of equilibria (17)–(18) only failed. The amount of [Fe(L5)_n]²⁺ in solution is strongly limited by (very) low cumulative stability constants, a situation produced by the impossibility for Fe^II to adopt a compact low-spin configuration in the sterically constrained complex [35]. In the absence of a significant amount of [Fe(L5)₃]²⁺ complexes in solution, no spin state equilibria could be investigated for this system.

4. Conclusions

Having established that the shift of the methyl group connected to the pyridine ring in going from the didentate ligand L1 (5-position) to L3 (3-position) was accompanied by a drift of the transition temperature in the associated spin-crossover complexes from T_1/2 ~310 K in [Fe(L1)₃]²⁺ [34] to T_1/2 ~50 K in a pure facial version of the [Fe(L3)₃]2+ chromophore [36], we attempted in this work to transpose this trend for pyrazine analogues L2 and L5 with the preparation of the missing member of the series [Fe(L5)₃]²⁺ (3-methyl-pyrazine), for which an ideal T_1/2 ~ 90 K could be naively predicted since T_1/2 ~ 350 K in [Fe(L2)₃]2+ (5-methyl-pyrazine). At first sight, this approach appeared to be promising since the molecular structures of pseudo-octahedral [M(L2)₃]²⁺ and [M(L5)₃]²⁺ (M = Ni^II and Zn^II) were comparable, except for the expected larger interannular twist between the connected aromatic rings produced by the close methyl groups in bound L5. The diagnostic ratio ∆/B = 13.3 was identical for both Ni^II complexes, thus pointing to electronic properties also compatible with the induction of SCO behavior in the analogous Fe^II complexes. Surprisingly and disappointingly, [Fe(L5)₃]²⁺ exists as a pure high spin complex within the 5–300 K range with no trace of spin state equilibrium. A thorough analysis of its thermodynamic formation in solution highlights a huge decrease in affinity of the ligand L5, compared with L2, for its binding to M²⁺ cations despite the presence of the same nitrogen donor atoms. Compared with the pyridine analogues [M(L3)₃]²⁺, which possess similar intra-strand sterical constraints (3-methyl substituents), the much weaker σ-donating N-pyrazine donor atoms were unable to compensate for the additional interstrand constraints required for chelating L5 around M²⁺. This limiting factor, which can be compared to a sort of arm wrestling match, is amplified with small cations and low-spin Fe^II cannot be complexed to L5.