Study of Physical GUP-Influenced Properties of Regular Black Holes in the Context of
Abstract
1. Introduction
2. Introductory Review of Black Hole Spacetime in the Context of Gravity
3. GUP’s Influence on Tunneling Radiation
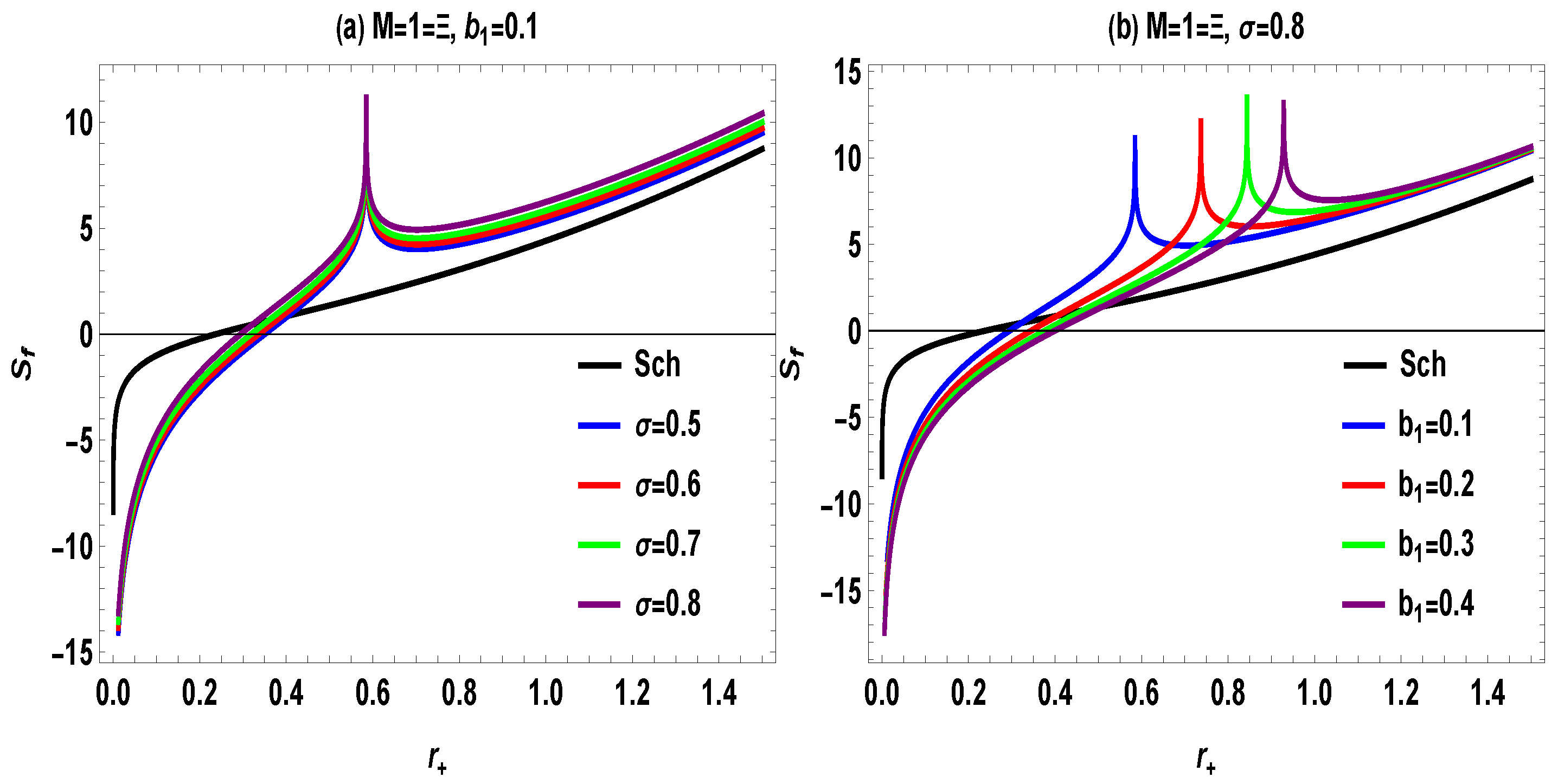
4. GUP-Influenced Entropy
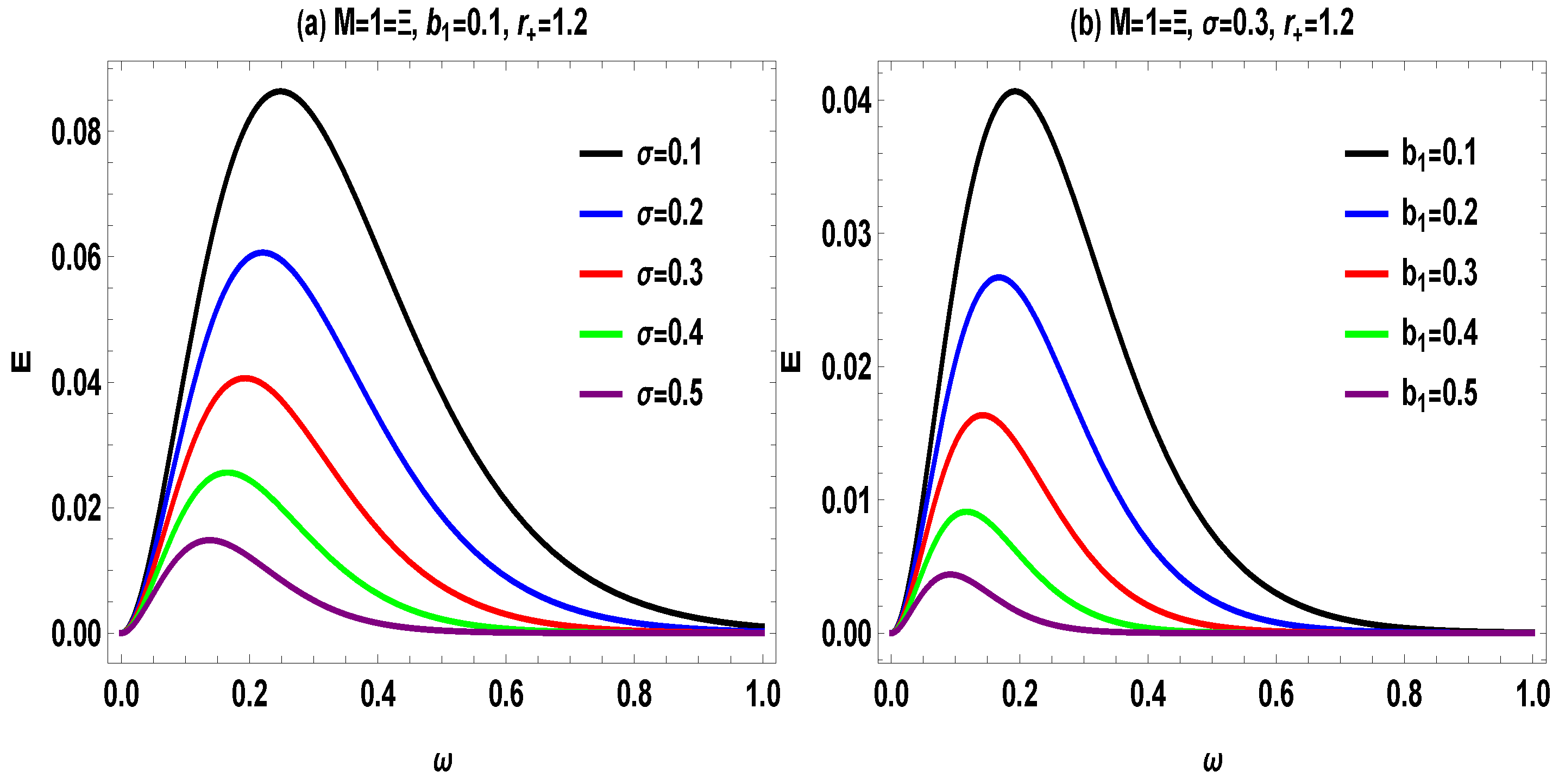
5. GUP-Influenced Emission Energy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bekenstein, J.D. Black holes and the second law. Lett. Nuovo Cim. 1972, 737–740. [Google Scholar] [CrossRef]
- Hawking, S.W. Black hole explosions? Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–200. [Google Scholar] [CrossRef]
- Ali, R.; Asgher, M. Tunneling analysis under the influences of Einstein Gauss Bonnet black holes gravity theory. New Astron. 2022, 93, 101759. [Google Scholar] [CrossRef]
- Gecim, G.; Sucu, Y. The GUP effect on Hawking radiation of the 2 + 1 dimensional black hole. Phys. Lett. B 2017, 773, 391–394. [Google Scholar] [CrossRef]
- Ali, R.; Babar, R.; Asgher, M. Gravitational analysis of rotating charged black hole-like solution in Einstein–Gauss–Bonnet gravity. Ann. Phys. 2022, 534, 2200074. [Google Scholar] [CrossRef]
- Babar, R.; Javed, W.; Övgün, A. Effect of the GUP on the Hawking radiation of black hole in 2+1 dimensions with quintessence and charged BTZ-like magnetic black hole. Mod. Phys. Lett. A 2020, 35, 2050104. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press, Inc.: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Das, S.; Vagenas, E.C. Universality of quantum gravity corrections. Phys. Rev. Lett. 2008, 101, 221301. [Google Scholar] [CrossRef]
- Amelino-Camelia, G.; Arzano, M.; Ling, Y.; Mandanici, G. Black-hole thermodynamics with modified dispersion relations and generalized uncertainty principles. Class. Quant. Grav. 2006, 23, 2585–2606. [Google Scholar] [CrossRef]
- Sakalli, I.; Kanzi, S. Physical properties of brane-world black hole solutions via a confining potential. Ann. Phys. 2022, 439, 168803. [Google Scholar] [CrossRef]
- Ali, R.; Tiecheng, X.; Babar, R. First-order quantum corrections of tunneling radiation in modified Schwarzschild–Rindler black hole. Gen. Relat. Gravit. 2024, 56, 13. [Google Scholar] [CrossRef]
- Ali, R.; Babar, R.; Asgher, M.; Shah, S.A.A. Gravity effects on Hawking radiation from charged black strings in Rastall theory. Ann. Phys. 2021, 432, 168572. [Google Scholar] [CrossRef]
- Dernek, M.; Tekincay, C.; Gecim, G.; Kucukakca, Y.; Sucu, Y. Hawking radiation of Euler–Heisenberg–adS black hole under the GUP effect. Eur. Phys. J. Plus 2023, 138, 369. [Google Scholar] [CrossRef]
- Ong, Y.C. A critique on some aspects of GUP effective metric. Eur. Phys. J. C 2023, 83, 209. [Google Scholar] [CrossRef]
- Ali, R.; Tiecheng, X.; Babar, R. First-order GUP corrections of black hole thermodynamics in the framework of f (R) gravity. Fortschr. Phys. 2025, 73, e70017. [Google Scholar] [CrossRef]
- Babar, R.; Akhtar, Z.; Asgher, M.; Ali, R. Study of thermodynamics for Dymnikova regular black hole under the influence of quantum gravity. Indian J. Phys. 2023, 97, 3155–3166. [Google Scholar] [CrossRef]
- Ali, R.; Bamba, K.; Shah, S.A.A. Effect of quantum gravity on the stability of black holes. Symmetry 2019, 11, 631. [Google Scholar] [CrossRef]
- Ali, R.; Babar, R.; Asgher, M.; Mustafa, G. Quantum gravity evolution of the Kalb–Ramond like black hole. Chin. J. Phys. 2023, 86, 269–279. [Google Scholar] [CrossRef]
- Sucu, E.; Sakalli, I. GUP-reinforced Hawking radiation in rotating linear dilaton black hole spacetime. Phys. Scr. 2023, 98, 105201. [Google Scholar] [CrossRef]
- D’Agostino, R.; Luongo, O.; Mancini, S. Geometric and topological corrections to Schwarzschild black hole. Eur. Phys. J. C 2024, 84, 1060. [Google Scholar] [CrossRef]
- Giambo, R.; Luongo, O. De Sitter-like configurations with asymptotic quintessence environment. Class. Quant. Grav. 2024, 41, 125005. [Google Scholar] [CrossRef]
- Corona, D.; Giambo, R.; Luongo, O. Motion of test particles in quasi anti-de Sitter regular black holes. Int. J. Geom. Methods Mod. Phys. 2024, 21, 2440019. [Google Scholar] [CrossRef]
- Kanzi, S.; Sakalli, I. GUP modified Hawking radiation in bumblebee gravity. Nucl. Phys. B 2019, 946, 114703. [Google Scholar] [CrossRef]
- Ali, R.; Tiecheng, X.; Babar, R. First-order correction of tunneling and entropy in the Horndeski gravity-like hairy black hole. Commun. Theor. Phys. 2025, 77, 075404. [Google Scholar] [CrossRef]
- Capozziello, S.; De Falco, V.; Ferrara, C. The role of the boundary term in f (Q, B) symmetric teleparallel gravity. Eur. Phys. J. C 2023, 83, 915. [Google Scholar] [CrossRef]
- De, A.; Loo, T.H.; Saridakis, E.N. Non-metricity with bounday terms: f (Q, C) gravity and cosmology. J. Cosmol. Astropart. Phys. 2024, 03, 050. [Google Scholar] [CrossRef]
- Junior, J.T.S.S.; Lobo, F.S.N.; Rodrigues, M.E. Black holes and regular black holes in coincident f (Q,BQ) gravity coupled to nonlinear electrodynamics. Eur. Phys. J. C 2024, 84, 332. [Google Scholar] [CrossRef]
- Dimakis, N.; Terzis, P.A.; Paliathanasis, A.; Christodoulakis, T. Static, spherically symmetric solutions in f (Q)-gravity and in nonmetricity scalar-tensor theory. J. High Energy Astrophys. 2025, 45, 273–289. [Google Scholar] [CrossRef]
- Yale, A. Exact Hawking radiation of scalars, fermions, and bosons using the tunneling method without back-reaction. Phys. Lett. B 2011, 697, 398–403. [Google Scholar] [CrossRef]
- Norte, R.A. Negative-temperature pressure in black holes. EPL (Europhys. Lett.) 2024, 145, 29001. [Google Scholar] [CrossRef]
- Bo, L.; Biao, L.W. Negative temperature of inner horizon and Planck absolute entropy of a Kerr–Newman black hole. Commun. Theor. Phys. 2010, 53, 83–86. [Google Scholar] [CrossRef]
- Park, M.-I. Thermodynamics of exotic black Holes, negative temperature, and Bekenstein–Hawking entropy. Phys. Lett. B 2007, 647, 472–476. [Google Scholar] [CrossRef]
- Ali, R.; Tiecheng, X.; Babar, R. Study of first-order quantum corrections of thermodynamics to a Dyonic black hole solution surrounded by a perfect fluid. Nucl. Phys. B 2024, 1008, 116710. [Google Scholar] [CrossRef]
- Ovgun, A.; Javed, W.; Ali, R. Tunneling Glashow-Weinberg-Salam Model Particles from Black Hole Solutions in Rastall Theory. Adv. High Energy Phys. 2018, 3131620, 11. [Google Scholar]
- Konishi, K.; Paffuti, G.; Provero, P. Minimum physical length and the generalized uncertainty principle in string theory. Phys. Lett. B 1990, 234, 276–284. [Google Scholar] [CrossRef]
- Maggiore, M. The algebraic structure of the generalized uncertainty principle. Phys. Lett. B 1993, 319, 83–86. [Google Scholar] [CrossRef]
- Garay, L.J. Quantum gravity and minimum length. Int. J. Mod. Phys. A 1995, 10, 145–165. [Google Scholar] [CrossRef]
- Amelino-Camelia, G. Doubly-special relativity: First results and key open problems. Int. J. Mod. Phys. D 2002, 11, 1643–1669. [Google Scholar] [CrossRef]
- Kempf, A.; Mangano, G.; Mann, R.B. Hilbert space representation of the minimal length uncertainty relation. Phys. Rev. D 1995, 52, 1108. [Google Scholar] [CrossRef]
- Scardigli, F. Generalized uncertainty principle in quantum gravity from micro-black hole gedanken experiment. Phys. Lett. B 1999, 452, 39–44. [Google Scholar] [CrossRef]
- Scardigli, F.; Casadio, R. Generalized uncertainty principle, extra-dimensions and holography. Class. Quant. Grav. 2003, 20, 3915–3926. [Google Scholar] [CrossRef]
- Hossenfelder, S.; Bleicher, M.; Hofmann, S.; Ruppert, J.; Scherer, S.; Stoecker, H. Signatures in the Planck regime. Phys. Lett. B 2003, 575, 85–89. [Google Scholar] [CrossRef]
- Chen, D.; Wu, H.; Yang, H.; Yang, S. Effects of quantum gravity on black holes. Int. J. Mod. Phys. A 2014, 29, 1430054. [Google Scholar] [CrossRef]
- Liberati, S.; Maccione, L.; Sotiriou, T.P. Scale hierarchy in Horava–Lifshitz gravity: Strong constraint from synchrotron radiation in the Crab Nebula. Phys. Rev. Lett. 2012, 109, 151602. [Google Scholar] [CrossRef]
- Nairz, O.; Arndt, M.; Zeilinger, A. Experimental verification of the Heisenberg uncertainty principle for fullerene molecules. Phys. Rev. A 2002, 65, 032109. [Google Scholar] [CrossRef]
- Pikovski, I.; Vanner, M.R.; Aspelmeyer, M.; Kim, M.S.; Brukner, C. Probing Planck-scale physics with quantum optics. Nat. Phys. 2012, 8, 393–397. [Google Scholar] [CrossRef]
- Li, X.-Q. Massive vector particles tunneling from black holes influenced by the generalized uncertainty principle. Phys. Lett. B 2016, 763, 80–86. [Google Scholar] [CrossRef]
- Kober, M. Gauge theories under incorporation of a generalized uncertainty principle. Phys. Rev. D 2010, 82, 085017. [Google Scholar] [CrossRef]
- Ali, R.; Tiecheng, X.; Babar, R. Evaluation of physical properties of Kiselev like AdS spacetime in the context of f (R, T) gravity under the impact of quantum gravity. Phys. Dark Universe 2025, 48, 101868. [Google Scholar] [CrossRef]
- Ali, R.; Babar, R.; Akhtar, Z.; Övgün, A. Thermodynamics and logarithmic corrections of symmergent black holes. Results Phys. 2023, 46, 106300. [Google Scholar] [CrossRef]
- Nozari, K.; Mehdipour, S.H. Quantum gravity and recovery of information in black hole evaporation. EPL (Europhys. Lett.) 2008, 84, 20008. [Google Scholar] [CrossRef]
- Ali, R.; Babar, R.; Aounallah, H.; Övgün, A. First-order quantum correction of thermodynamics in a charged accelerating AdS black hole with gauge potential. Int. J. Geom. Methods Mod. Phys. 2024, 21, 2450149. [Google Scholar] [CrossRef]
- Das, S.; Majumdar, P.; Bhaduri, R.K. General logarithmic corrections to black hole entropy. Class. Quant. Grav. 2001, 19, 2355–2367. [Google Scholar] [CrossRef]
- Sen, A. Logarithmic corrections to Schwarzschild and other non-extremal black hole entropy in different dimensions. J. High Energy Phys. 2013, 2013, 156. [Google Scholar] [CrossRef]
- Banerjee, R.; Majhi, B.R. Hawking black body spectrum from tunneling mechanism. Phys. Lett. B 2018, 675, 243–245. [Google Scholar] [CrossRef]
- Banerjee, R.; Majhi, B.R. Quantum tunneling beyond semiclassical approximation. J. High Energy Phys. 2008, 2008, 095. [Google Scholar] [CrossRef]
- Banerjee, R.; Majhi, B.R.; Samanta, S. Noncommutative black hole thermodynamics. Phys. Rev. D 2008, 77, 124035. [Google Scholar] [CrossRef]
- Pradhan, P. CFT and logarithmic corrections to the black hole entropy product formula. Adv. High Energy Phys. 2017, 2017, 2367387. [Google Scholar] [CrossRef]
- Papnoi, U.; Atamurotov, F.; Ghosh, S.G.; Ahmedov, B. Shadow of five-dimensional rotating Myers-Perry black hole. Phys. Rev. D 2014, 90, 024073. [Google Scholar] [CrossRef]
- Ali, R.; Tiecheng, X.; Babar, R.; Övgün, A. Exploring light deflection and black hole shadows in Rastall theory with plasma effects. Int. J. Theor. Phys. 2025, 64, 75. [Google Scholar] [CrossRef]
- Papnoi, U.; Atamurotov, F. Rotating charged black hole in 4D Einstein–Gauss–Bonnet gravity: Photon motion and its shadow. Phys. Dark Universe 2022, 35, 100916. [Google Scholar] [CrossRef]
- Ali, R.; Tiecheng, X.; Awais, M.; Babar, R. Study of light deflection and shadow from a hairy black hole under the influence of the non-magnetic plasma. Chin. J. Phys. 2025, 94, 416–430. [Google Scholar] [CrossRef]
- Wei, S.-W.; Liu, Y.-X. Observing the shadow of Einstein–Maxwell–Dilaton–Axion black hole. J. Cosmol. Astropart. Phys. 2013, 11, 063. [Google Scholar] [CrossRef]
- Li, X.-Q.; Chen, G.-R. Massive vector particles tunneling from Kerr and Kerr–Newman black holes. Phys. Lett. B 2015, 751, 34–38. [Google Scholar] [CrossRef]
- Javed, W.; Abbas, G.; Ali, R. Charged vector particle tunneling from a pair of accelerating and rotating and 5D gauged super-gravity black holes. Eur. Phys. J. C 2017, 77, 296. [Google Scholar] [CrossRef]
- Loustó, C.O.; Sánchez, N.G. Back reaction effects in black hole spacetimes. Phys. Lett. B 1988, 212, 411–414. [Google Scholar] [CrossRef]


| 1 | 0 | ≈0.03979 | 0.5 | ≈0.01989 | |
| 3 | 2 | 0.1 | ≈0.03523 | 0.2 | ≈0.02819 |
| 4 | 2.5 | 0.5 | ≈0.02472 | 0.3 | ≈0.017304 |
| 5 | 3 | 1 | ≈0.01899 | 0.4 | ≈0.01139 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, R.; Xia, T.; Babar, R.
Study of Physical GUP-Influenced Properties of Regular Black Holes in the Context of
Ali R, Xia T, Babar R.
Study of Physical GUP-Influenced Properties of Regular Black Holes in the Context of
Ali, Riasat, Tiecheng Xia, and Rimsha Babar.
2025. "Study of Physical GUP-Influenced Properties of Regular Black Holes in the Context of
Ali, R., Xia, T., & Babar, R.
(2025). Study of Physical GUP-Influenced Properties of Regular Black Holes in the Context of







