Nonlinear Dynamics of Cylindrical Waves in Isentropic Plasma

Abstract

Based on the hydrodynamic description, the dynamics of nonlinear cylindrical waves in an isentropic plasma are investigated. The problem is considered in an electrostatic formulation for a two-dimensional plasma medium where ions form a stationary background. Proceeding from the particular, exact solution of hydrodynamic equations, we obtain the system of differential equations which describes the electron’s dynamics, taking into account the finite temperature of electrons. Moreover, we find the conditions when this system is reduced to the generalized Ermakov–Pinney equation which was used for analyzing electron dynamics. In the present calculations, a parabolic-in-radius temperature profile was used, associated with an electron density varying only with time. In the framework of the model that worked out, the influence of initial conditions and thermal effects on the regular and singular dynamics of excited waves are discussed. It is shown that the development of singular behavior due to intrinsic nonlinearity is avoided by taking into account thermal effects and the initial rotation of the electron flow.

1. Introduction

The rotating plasma is one of the canonical physical systems exhibiting unexpected remarkable nonlinear wave properties that are of considerable fundamental and applied interest [1,2,3,4]. For example, when nonlinear plasma cylindrical waves were excited in cold plasma, the accumulations of energy/momentum in one of the macroscopic degrees of freedom of the rotating plasma flow were discovered. This process is fundamentally different from the ordinary mechanism of energy dissipation during the development of any instability that converts energy into thermal form [1,2]. Such behavior is caused by the interaction of nonlinear radial and axial plasma oscillations under the local violation of quasi-neutrality when the system is far from equilibrium and where non-inertial effects begin to manifest themselves. As a result, acceleration of the entire plasma flow in the axial or azimuthal direction may occur, which can be used, in particular, in the development of collective acceleration methods or the creation of effective radiation sources (see, e.g., [3,4,5,6] and references therein). Additionally, such type of studies are of interest for understanding the formation of coherent structures such as tornados, atmospheric and astrophysical plasmoids [7,8,9,10].

However, the above-discussed results were obtained for cold plasma flows only [11,12,13], where strongly nonlinear plasma waves are excited. raise some natural questions. How may the finite electron temperature affect such a mechanism of energy/momentum redistribution? How does the finite electron temperature affect the development of hydrodynamical singularities?

In this regard, it is worth mentioning the studies [14,15,16,17,18,19,20], where different aspects of the effects influencing electron oscillations, including the role of electron pressure, have been discussed. However, all the models proposed belong to a one-dimensional class, that is, the ones that are rather artificial in their physical nature because real systems are essentially higher dimensional. Nevertheless, from those studies, one may suggest the emergence of the formation of time-dependent structures in higher dimensions governed by hydrodynamic nonlinearities, especially since the last experimental works on Thomson scattering and related diagnostics [21,22,23,24,25,26] have shown the necessity take into account the real dimensionality of the problems under consideration.

In order to address these issues and following the earlier results [14,15,16,17,18], we consider the influence of electron pressure and the plasma’s own electrostatic field on the two-dimensional electron dynamics, assuming cold and motionless ions. Such an approximation to be valid at the initial stage of the development of Langmuir waves, when the mobility of the ion liquid may be ignored.

2. Model

In this paper, we examine the electron dynamics in a plasma cylinder of radius $R_0$ and height $d$ that is surrounded by vacuum (see Figure 1), in which the cold, positive ions form an immobile background with constant density $n_0$. In the case under examination, plasma is assumed to be a quasi-neutral medium, although in general, the system may not be a neutral one.

Herewith we consider that the electron fluid behaves like an ideal gas, i.e.,

$$p_e=T_e{n}_e,$$

(1)

where $p_e$, $T_e$, ${\mathrm{a}\mathrm{n}\mathrm{d} n}_e$ are the electron pressure, temperature and density, respectively. On the other hand, in the time scale of electron oscillation one can neglect the heat transport and dissipative processes. In this case, the electron pressure is described by the Poisson adiabat:

$$p_e=p_0{\left({\displaystyle \frac{n_e}{n_0}}\right)}^{\gamma },$$

(2)

where $\gamma$ is the adiabatic index, and $p_0$ and $n_0$ are some characteristic values of electron pressure and density, respectively, in undisturbed plasma.

In the electrostatic approximation, the governing equations are

$${\displaystyle \frac{\partial n_e}{\partial t}}+\nabla \left(n_e{\mathit{v}}_e\right)=0,$$

(3)

$${\displaystyle \frac{\partial {\mathit{v}}_e}{\partial t}}+\left({\mathit{v}}_e·\nabla \right){\mathit{v}}_e=-{\displaystyle \frac{1}{m_{e}n}}\nabla \left(p_e\right)-{\displaystyle \frac{e}{m_e}}\mathit{E},$$

(4)

$$\nabla ·\mathit{E}=4\pi e(n_0-n_e),$$

(5)

where ${\mathit{v}}_e$, $m_e$ and $e$ are the electron velocity, mass and charge, respectively; $\mathit{E}$ is the electrostatic field which may include an external field in the case of a non-neutral plasma.

It is convenient to rewrite the adiabatic Equation (2) in differential form. To do this, using Equations (1) and (2), one obtains the relationship between the electron density and temperature:

$$n_e=n_{e0}{\left({\displaystyle \frac{T_e}{T_0}}\right)}^{{\displaystyle \frac{1}{\gamma -1}}},$$

where $T_0$ is the characteristic electron temperature of undisturbed plasma. Substituting this expression into the continuity Equation (3) one finds

$${\displaystyle \frac{\partial T_e}{\partial t}}+\left({\mathit{v}}_e·\nabla \right)T_e=-\left(\gamma -1\right)T_e\nabla ·{\mathit{v}}_e.$$

(6)

Restricting ourselves to axially symmetric geometry in the limit $d\ll R_0$, when ${\partial }_{\phi }={\partial }_z=0$, with ${\partial }_a\equiv \partial /\partial a,$ one considers the dynamics of a cylindrical wave in the $r0\phi$ plane. In this two-dimensional case, Equations (3)–(6) in dimensionless, scalar form can be rewritten as

$${\displaystyle \frac{\partial n}{\partial t}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial \left(rn{v}_r\right)}{\partial r}}=0,$$

(7)

$${\displaystyle \frac{\partial v_r}{\partial t}}+v_r{\displaystyle \frac{\partial v_r}{\partial r}}-{\displaystyle \frac{v_{\phi }^2}{r}}=-{\beta }_T^2{\displaystyle \frac{1}{n}}{\displaystyle \frac{\partial \left(nT\right)}{\partial r}}-E,$$

(8)

$${\displaystyle \frac{\partial v_{\phi }}{\partial t}}+v_r{\displaystyle \frac{\partial v_{\phi }}{\partial r}}+{\displaystyle \frac{v_r{v}_{\phi }}{r}}=0,$$

(9)

$${\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial \left(rE\right)}{\partial r}}=1-n,$$

(10)

$${\displaystyle \frac{\partial T}{\partial t}}+v_r{\displaystyle \frac{\partial T}{\partial r}}=-\left(\gamma -1\right){\displaystyle \frac{T}{r}}{\displaystyle \frac{\partial \left(r{v}_r\right)}{\partial r}},$$

(11)

where the time, coordinates and electron temperature are normalized by the inverse Langmuir frequency ${\omega }_{pe}=\sqrt{4\pi n_0{e}^2/m_e}$, the radius of the plasma cylinder $R_0$ and $T_0$, respectively. The radial and azimuthal velocity components are normalized by $v_{\ast }={\omega }_{pe}{R}_0$, and the electric field is normalized by $E_{\ast }=4\pi e{n}_0{R}_0$. The dimensionless parameter

$${\beta }_T^2={\displaystyle \frac{a_T^2}{{\omega }_{pe}^2{R}_0^2}}$$

(12)

is the square of the ratio for thermal velocity $a_T=\sqrt{T_0/m_e}$ to characteristic velocity $v_{\ast }$. It is worth noting that this parameter determines the different physical scripta for the system under consideration. On the other hand, taking into account that the Debye length is defined by the relation ${\lambda }_D=a_T/{\omega }_{pe}$, one can rewrite Equation (12) in a better visible form as ${\beta }_T^2={\lambda }_T^2/R_0^2$, i.e., actually, the value ${\beta }_T^{-1}$ is the initial radius of plasma layer expressed in ${\lambda }_D$.

3. Hypothetical Solution Form

Proceeding from the earlier results [11,12], let us find some particular, exact solution of Equations (7)–(11) in the following form:

$$n=n\left(t\right),$$

(13)

$$\mathit{v}=rA\left(t\right){\mathit{e}}_r+rB\left(t\right){\mathit{e}}_{\phi },$$

(14)

$$T=C\left(t\right)\pm D\left(t\right)r^2,$$

(15)

$$E={\displaystyle \frac{\epsilon \left(t\right)}{2}}r.$$

(16)

This ansatz turns the partial differential Equations (7)–(11) into identities if the currently unknown functions $n\left(t\right)$, $A\left(t\right)$, $B\left(t\right),C\left(t\right),D\left(t\right)$ and $\epsilon \left(t\right)$ satisfy the system of ordinary differential equations obtained by substituting Equations (13)–(16) into Equations (7)–(11). We also adopt the following notations: the temperature profile is called a concave one if Equation (15) has a positive sign, but in the case of a negative sign Equation (15) describes a convex profile of temperature.

Substituting Equations (13) and (14) into Equation (7), one obtains

$${\displaystyle \frac{dn}{dt}}=-2An.$$

(17)

From Equation (10), taking into account Equations (13) and (16), it follows that

$$\epsilon =1-n.$$

(18)

Bearing in mind Equation (14), from Equation (9) one finds

$${\displaystyle \frac{dB}{dt}}=-2AB.$$

(19)

Inserting relations (14)–(16) and (18) into Equation (8), one obtains

$${\displaystyle \frac{dA}{dt}}=B^2-A^2\mp 2{\beta }_T^{2}D+{\displaystyle \frac{n-1}{2}}.$$

(20)

Finally, substitution of Equations (14) and (15) into Equation (11) gives

$$\left({\displaystyle \frac{dC}{dt}}+2\left(\gamma -1\right)AC\right)r^0\pm \left({\displaystyle \frac{dD}{dt}}+2\gamma AD\right)r^2=0.$$

Since this relation must be satisfied for any $r$, then by equating the terms at the corresponding powers of $r$ one finds

$${\displaystyle \frac{dC}{dt}}=-2\left(\gamma -1\right)AC$$

(21)

and

$${\displaystyle \frac{dD}{dt}}=-2\gamma AD.$$

(22)

Equations (17) and (19)–(22), together with relation (18), form a closed set. However, this system can be significantly simplified. To this end, from Equations (17) and (22) it follows that

$${\displaystyle \frac{d}{dt}}\ln \left(D\right)=\gamma {\displaystyle \frac{d}{dt}}\ln \left(n\right),$$

which can be integrated to obtain

$$D=D_0{n}^{\gamma },$$

(23)

where $D_0$ is the constant of integration determined by the initial conditions. Similarly, from Equations (17) and (22) one finds

$${\displaystyle \frac{d}{dt}}\ln \left(C\right)=\left(\gamma -1\right){\displaystyle \frac{d}{dt}}\ln \left(n\right).$$

By integrating this equation, one finds

$$C=C_0{n}^{\gamma -1}.$$

(24)

where constant $C_0$ is defined by the initial conditions. Finally, substituting of Equations (23) and (24) into Equations (20) and (15) gives

$${\displaystyle \frac{dA}{dt}}=B^2-A^2\mp 2D_0{\beta }_T^2{n}^{\gamma }+{\displaystyle \frac{n-1}{2}}$$

(25)

and

$$T=n^{\gamma -1}\left(C_0\pm D_{0}n{r}^2\right).$$

(26)

At this stage, it is worth pointing out the physical sense of the functions $C\left(t\right)$ and $D\left(t\right)$. If one considers the initial moment of time as $t=0$ and set as $r=0$, then $C_0=T(t=0)\equiv 1.$ That is, the function $C\left(t\right)$ plays role a characteristic temperature (for example, temperature in the center of system). In this case, one can treat $D\left(t\right)$ as a characteristic velocity of temperature change on $r$. Herein, the function $D\left(t\right)$ may take any value, which provides $T(t,r)>0$. It follows that this condition can be violated only for a convex profile.

In order to establish such condition, let us rewrite Equations (17), (19), (21) and (22) in integral form as

$$\begin{array}{c}n=\mathrm{e}\mathrm{x}\mathrm{p}(-\theta ), B=B_0\mathrm{e}\mathrm{x}\mathrm{p}(-\theta ),\\ C=\mathrm{e}\mathrm{x}\mathrm{p}\left(-\left(\gamma -1\right)\theta \right), D=D_0\mathrm{e}\mathrm{x}\mathrm{p}\left(-\gamma \theta \right),\end{array}$$

(27)

where

$$\theta =2{\int }_0^{t}A\left(x\right)dx.$$

(28)

Since $\gamma >0$ and 0$\le r\le 1$ are from the last two relations of Equation (27), it follows that in the case $\theta \ge 0$ it always holds that $T>0$ for $D_0\le 1.$ However, in the case $\theta <0,$ no conclusion can be made about the behavior of the temperature.

These entirely mathematical features allow us to define the initial conditions for the evolution equations relating to the physical formulation of the problem. Herein we proceed from the assumption that at the initial moment of time $t=0$, the plasma is quasi-neutral and there are no external fields but there is a nonequilibrium initial distribution of the velocity and temperature of electrons specified in the interval 0 ≤ r ≤ 1 by smooth, finite functions. That is, for the ansatz (13)–(16), these conditions are satisfied if one sets the following relations:

$$\begin{gathered} n\left(t=0\right)=1, \epsilon \left(t=0\right)=0, C\left(t=0\right)=1, A\left(t=0\right)=A_0, B\left(t=0\right)=B_0, \\ D\left(t=0\right)=D_0>0. \end{gathered}$$

(29)

Finally, it is constructive to touch upon the isothermal limit in which the relation (26) transforms for $\gamma$ = 1; see [13,16]. As seen from Equation (27), the temporal dependence for the first term of Equation (26) drops out automatically, but this expression admits a temporal and spatial dependence via the second term of Equation (26). The similar thermal contribution in electron oscillation was established in Ref. [16] for one-dimensional geometry where the change in the oscillation parameters (amplitude, frequency, etc.) is governed by the equation similar to Equation (25). However, in the case considered here, there is the effect of plasma rotation; therefore, the results may coincide with that from Ref. [16] only for $B\equiv 0$ (see Equation (25)); the case $B\ne 0$ to be considered separately.

4. Ermakov–Pinney Model

As seen from Equations (27) and (28), the dynamics of azimuthal velocity density and the components of electron temperature $C\left(t\right)$ and $D\left(t\right)$ are fully determined by the time evolution of the radial component for velocity via the nonlocal dependence of Equation (29). As a result, the oscillations in all values are smoothed out.

In this regard, a natural question immediately arises: is there an inverse influence of temperature profile (15) on radial velocity component $A\left(t\right)$? In order to analyze the behavior of the solution (26) depending on the sign in Equation (15), let us use substitution

$$W={\displaystyle \frac{1}{n^{1/2}}},$$

(30)

with the help of which from Equation (17) one finds

$$A={\displaystyle \frac{1}{W}}{\displaystyle \frac{dW}{dt}},$$

(31)

and from Equations (19) and (30) it follows that

$$B={\displaystyle \frac{B_0}{W^2}}.$$

(32)

Substituting Equations (30) and (31) into Equation (25), one obtains

$${\displaystyle \frac{d^{2}W}{d{t}^2}}-{\displaystyle \frac{B_0^2}{W^3}}\pm H_T{\displaystyle \frac{1}{W^{2\gamma -1}}}-{\displaystyle \frac{1}{2W}}+{\displaystyle \frac{W}{2}}=0$$

(33)

with initial conditions

$$W\left(t=0\right)=1,{\left.{\displaystyle \frac{dW}{dt}}\right|}_{t=0}=A_0,$$

(34)

where the parameter

$$H_T=2D_0{\beta }_T^2=2D_0{\displaystyle \frac{a_T^2}{v_{\ast }^2}}$$

(35)

reflects the influence of thermal effects and oscillatory processes on plasma dynamics.

At this stage, it is instructive to touch on the physical sense of the introduced variable W and some physical models associated with Equation (33). According to definition (30), Equation (33) describes some oscillations brought about by the electron density change in a cylindrical electron wave. Actually, Equation (33) is the generalized Ermakov–Pinney equation which differs from wave equations describing the linear or nonlinear oscillations of Langmuir type [17,21,22,23,24,25,26,27,28]. That is, the sequence of exact, transformations (13)–(16) and (31) makes it possible to identify one of the admissible but hidden wave structures allowed by Equations (3)–(5).

In order to reveal this dynamic structure of the Ermakov–Pinney model, let us write the first integral of Equation (33) as

$${\left({\displaystyle \frac{dW}{dt}}\right)}^2+\mathsf{\Phi }\left(W\right)=E_0,$$

(36)

where

$$\mathsf{\Phi }\left(W\right)={\displaystyle \frac{1}{2}}\left[{\displaystyle \frac{B_0^2}{W^2}}\mp {\displaystyle \frac{H_T}{{(\gamma -1)W}^{2\gamma -2}}}-\ln W+{\displaystyle \frac{1}{2}}{W}^2\right]$$

(37)

which is commonly termed a potential energy of a system, and

$$E_0\left(A_0,B_0\right){=A}_0^2+B_0^2\mp {\displaystyle \frac{H_T}{\gamma -1}}+{\displaystyle \frac{1}{2}}$$

(38)

is considered as the total energy of a system. Herein, it should be kept in mind that the condition $E_0\left(A_0,B_0\right)>0$ imposes some restrictions on the parameters $A_0,B_0$ and $H_T$.

Resolving Equation (36) with respect to the variable $dW/dt$, one obtains an explicit dependence

$${\displaystyle \frac{dW}{dt}}=\pm \sqrt{E_0-\mathsf{\Phi }\left(W\right)},$$

(39)

that provides with an analytical expression for the integral curves on the phase plane. In the case presented here, the type of function $\mathsf{\Phi }=\mathsf{\Phi }\left(W\right)$ determines the permissible oscillation types of solution for Equation (33). That is, depending on the number of zeros (the so-called fixed points) for

$${\displaystyle \frac{d\mathsf{\Phi }\left(W\right)}{dW}}=0,$$

(40)

one can obtain fundamentally different behaviors of the system.

Also, it is convenient to rewrite Equation (36) in the following form:

$$2{\left({\displaystyle \frac{dW}{dt}}\right)}^2+{\displaystyle \frac{B_0^2}{W^2}}+{\displaystyle \frac{1}{2}}{W}^2=2E_0+\ln W\pm {\displaystyle \frac{H_T}{{(\gamma -1)W}^{2\gamma -2}}}.$$

(41)

Since the left-hand side of Equation (41) is always positive, one can use this feature to determine the acceptable limits of the function $W$. For the convex temperature profile (minus sign in the relation (41)), the case $W\to 0$ is unfeasible since for any $E_0$ and $H_T$ there always is a value $W_{\ast }$ that for $W\le W_{\ast }$ the right-hand side of Equation (41) becomes a negative. This signifies that the variant $W\to 0$ is prohibited, i.e., in this case, the density is a finite function. Herein, for the convex temperature profile, Equation (40) has only one root, hence, the potential function is a concave function with one minimum. In this case, the phase portrait is a set of concentric curves centered around the origin that is a typical sample for finite, periodic oscillations. As an example of such behavior, in Figure 2, the phase portrait is sketched for $B_0=1.1$, $H_T=1$ and $\gamma =2.1$; the characteristic size of these closed paths is determined by the initial energy $E_0$.

In this regard, it is worth explaining the choice of value for adiabatic index $\gamma$ which actually is $\gamma =5/3$ for electron gas. However, the numerical simulation with this $\gamma$ for the selected energy range has given a family of phase trajectories that actually merge with each other. Herein it should be borne in mind that depending on the number of degrees of freedom, value $\gamma$ may be changed in limits $1\le \gamma \le 3$ (the value $\gamma =3$ corresponds to one-dimensional gas). To distinctly display the qualitative dependence of phase portraits on the parameters of the problem, we chose the appropriate value $\gamma$ from the acceptable range. Furthermore, this magnitude is close to the value of adiabatic index corresponding to a particle with two degrees of freedom, which correlates with the problem’s dimensionality. Therefore, the present results to be taken as preliminary: the finding is a qualitative, approximate picture indicating the direction for further studies.

Now, let us consider the concave temperature profile (plus sign in the relation (41)) where the option $W\to 0$ is not excluded since

$$\left|\ln W\right|<{\displaystyle \frac{H_T}{{(\gamma -1)W}^{2\gamma -2}}}$$

for $\gamma >1$ in the interval $0<W\le 1.$ In the present case, one can see a completely different picture when Equation (40) may have two roots, i.e., there are two extrema points in $\mathsf{\Phi }\left(W\right)$. The typical phase portrait is presented in Figure 3: one can observe the domain where there is a finite motion (${0.5\le E}_0\le 1.5$); above this domain the motion is unbounded which is separated by a separatrix for $E_0=1.5$. According to Equation (38), the ownership of trajectory to finite or infinite type is determined only by the initial conditions. Finally, it is noteworthy that the phase portrait of isothermal case ($\gamma =1$) coincides with the one presented in Figure 3.

However, it should be borne in mind that the phase analysis allows us to present a global picture of the system’s behavior only, the analysis of fixed points requires the use of other methods, for example, numerical simulation.

5. Regular Dynamics of Electrons

Let us now move to the consideration of numerical results with initial conditions (29) that ensure regular dynamics.

The numerical results presented below were obtained by integrating the system of ordinary differential Equations (17)–(22), which is equivalent to the Ermakov–Pinney Equation (33) with initial conditions (34). For numerical simulation, we have applied the Mathcad environment with the built-in Odesolve procedure which provides the numerical discretization error on the level [29].

In all calculations of this Section, we set $C_0$ = 1 and $\gamma =2.1$ which provides the positive value of electron temperature as defined by the relation (26), whereby the values $A_0$ and $B_0$ may be varied.

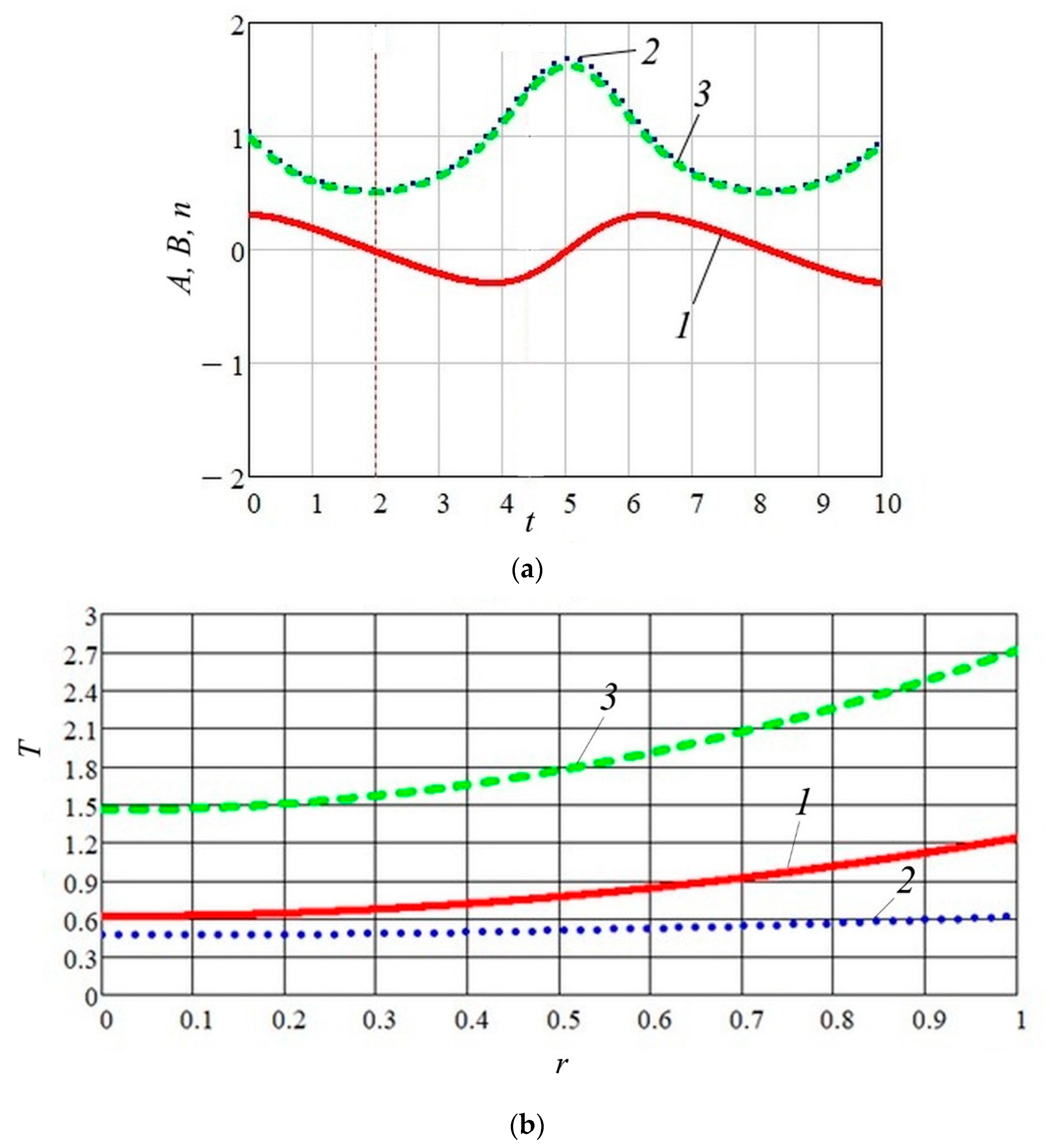
We start with the option of concave parabolic temperature profile when there is no initial perturbation in the electron velocity profile but there is an effect of non-zero thermal parameter $H_T(H_T=1)$. The initial azimuthal velocity was chosen as in the results above, $B_0=1.05.$ The remaining initial values were found from the expression for total energy (38). Herein, we take such appropriate values under which the nonlinear peculiarities considered here can be revealed to the best advantage as they are not obscured by other factors.

The corresponding dependencies of electron velocity and density on the dimensionless time are plotted in Figure 4a. As seen, the radial velocity and electron density experience regular, almost harmonic oscillations of Langmuir type due to the action of $H_T$ and the resulting electric field $\epsilon$. The temperature profiles shown in Figure 4b relate to some characteristic moments of time when the electron density $n\left(t\right)$ increases over the course of time (see Equations (23) and (24)). From these results relating to $E_0=$ 1.0, it follows that the system is stable and has periodic oscillations, which corresponds to the obtained analytical description (see Figure 3).

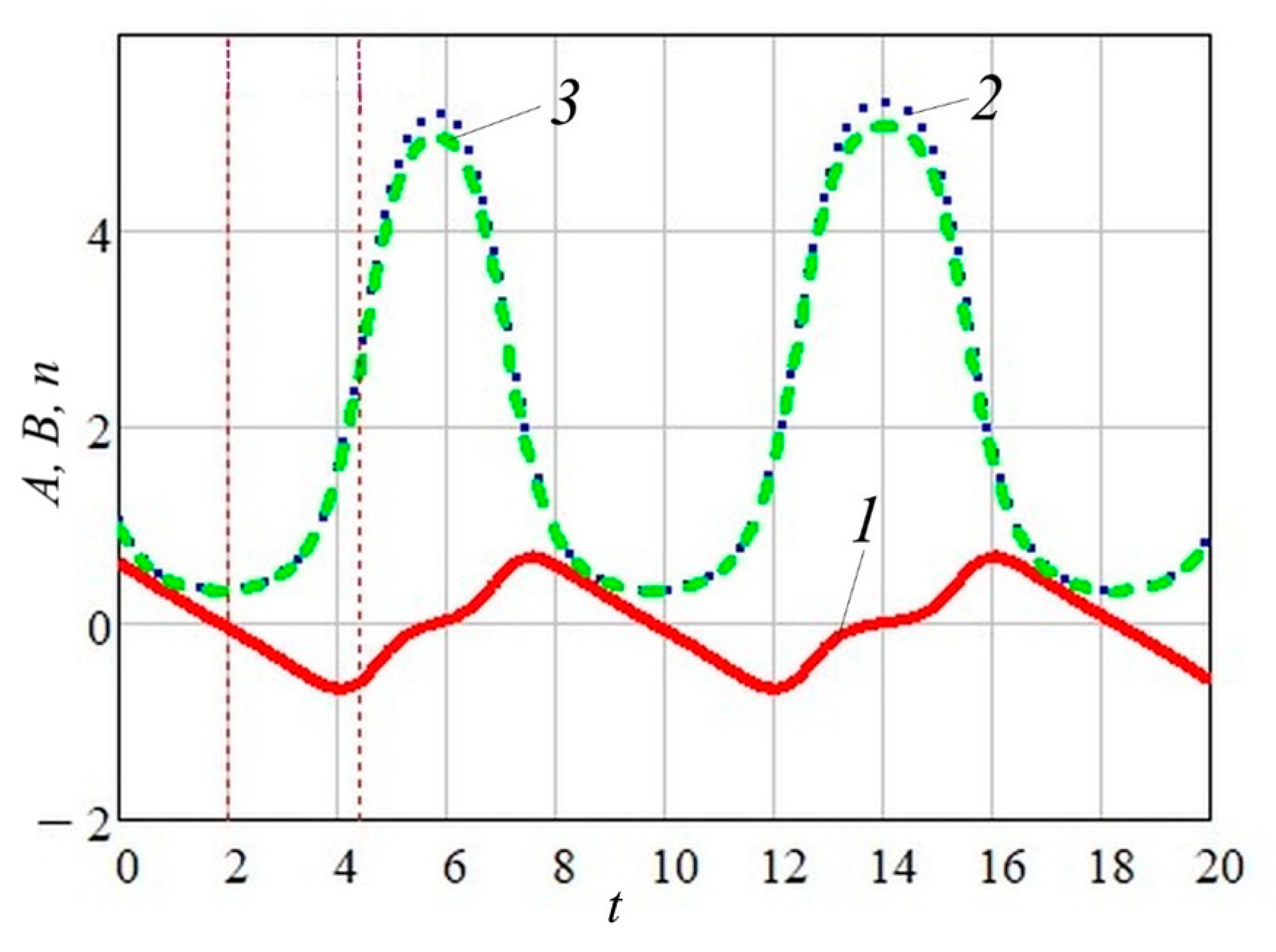
Herein, it is worth noting that a relatively small change in initial energy $E_0$ can significantly alter the oscillation pattern. To illustrate such a feature, Figure 5 presents the corresponding distributions for $E_0=1.065$. In this case, a pronounced increase in the amplitudes A and B is observed, along with a somewhat distorted profile of the radial component of velocity, while the temperature profile follows the dependence shown in Figure 4b.

Next, let us consider the behavior when the system has an open phase trajectory for $E_0$ = 2. As seen from the dependencies presented in Figure 6, here there are no periodic oscillations, the density begins to grow over time and tends to infinity, i.e., that is a singular regime.

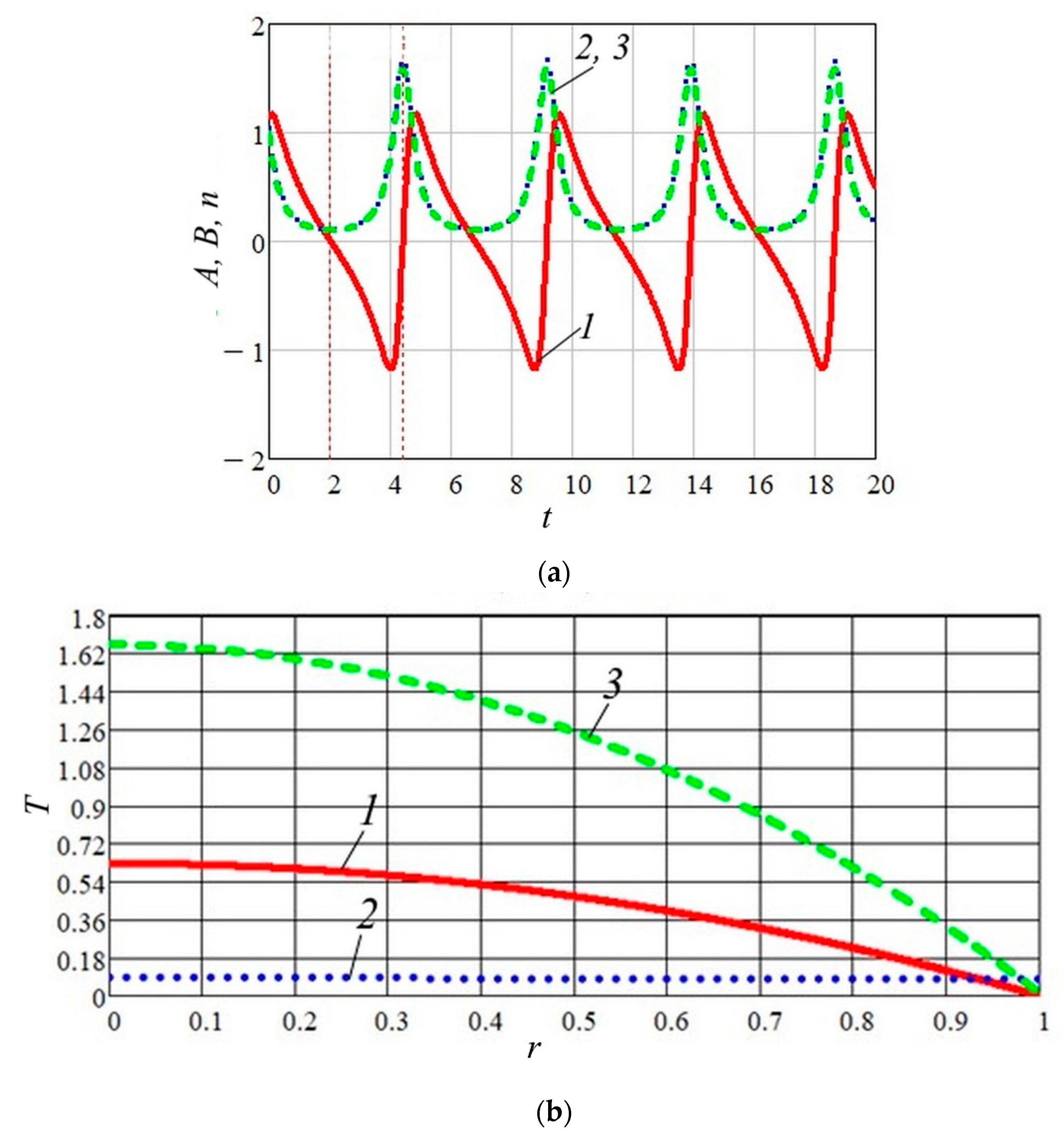
Finally, let us analyze the case of a convex temperature profile (see Equation (15)). The corresponding results for $E_0$ = 2 are sketched in Figure 7. As is seen, with the ones in Figure 4 and Figure 5, the oscillation dynamics are alike in general. However, there are some small differences: here, the amplitude and frequency of electron oscillations is larger than in the cases presented in Figure 4 and Figure 5. As is seen in Figure 7b, this feature results in temperature change in a narrower range than the temperature in Figure 4b. It seems that such features are caused by the nonlinearity of issues (i.e., the effect of initial conditions $A_0$ and $B_0$) and the intrinsic electrostatic field.

Thus, the present numerical results about regular electron oscillations confirm the analytical estimates for the system (17)–(22).

6. Cold Limit

Let us now consider the limit of $H_T\to 0$ that corresponds to ${\beta }_T\to 0$ or $D_0\to 0$. As seen from the relations (27) and (28), the dynamics of azimuthal velocity and electron density are fully determined by the time evolution of the radial component for velocity via nonlocal the dependence (28). That is, because the temporal dependencies of the values given by the relation (27) depend only on the time integrals of $A\left(t\right)$, the oscillations in the latter are smoothed out.

So, it is instructive to consider the evolution of $A\left(t\right)$ for small enough times. Taking into account the form of the relation (28) for $\left|\theta \right|\ll 1$, one can set $\mathrm{e}\mathrm{x}\mathrm{p}\left(\theta \right)\approx 1.$ As a result, Equation (25) reduces to

$${\displaystyle \frac{dA}{dt}}{+A}^2={\alpha }^2,$$

(42)

where for definiteness, we define a positive constant

$${\alpha }^2=B_0^2\mp H_T>0$$

(43)

linking the governing parameters $B_0$, $D_0$ and ${\beta }_T$ of the system.

The general solution of Equation (42) is

$$A=\alpha {\displaystyle \frac{A_0\left(1+\mathrm{e}\mathrm{x}\mathrm{p}\left(2\alpha t\right)\right)+\alpha \left(\exp \left(2\alpha t\right)-1\right)}{\alpha \left(1+\mathrm{e}\mathrm{x}\mathrm{p}\left(2\alpha t\right)\right)+A_0\left(\exp \left(2\alpha t\right)-1\right)}}.$$

(44)

As seen from Equation (44), there can be a formation of singularity at the moment of time $t=t_{\ast }$ if the denominator in Equation (44) becomes zero and the numerator takes on a finite value, i.e., the algebraic equation

$${\displaystyle \frac{A_0-\alpha }{A_0+\alpha }}=\exp \left(2\alpha t_{\ast }\right)$$

(45)

has a real solution that implies

$${\displaystyle \frac{A_0-\alpha }{A_0+\alpha }}>0.$$

(46)

In this case, one obtains

$$t_{\ast }={\displaystyle \frac{1}{2\alpha }}\ln {\displaystyle \frac{A_0-\alpha }{A_0+\alpha }}.$$

(47)

As seen, the relations (43) and (46) determine the necessary conditions for the development of hydrodynamic collapse even for $H_T\ne 0$. However, for $H_T=0$ the inequality (43) is always valid, and the condition (46) is fulfilled if $\left|A_0\right|>\left|B_0\right|$, i.e., this is the domain of initial data in which there may appear a singular behavior [30,31,32].

On the other hand, if the conditions (43) and (46) are violated, then one can expect regular behavior in the dynamics of the system under consideration. In particular, such dynamics is realized even for $H_T=0$ when $\left|A_0\right|<\left|B_0\right|$.

These estimates make it possible to draw a tentative conclusion about regular or singular dynamics brought about by initial conditions, magnetic field and thermal contribution. In this regard, it is worth noticing that the case ${\beta }_T=0$ belongs to the subclass of rotating cold plasma system with an immobile ion background. Such a feature distinguishes the present study from our earlier investigation [11,12,13], where both the electron and the ion components are mobile. Also, in Refs. [11,12,13], there is no external magnetic field considered but we took into account the magnetic and electric field which was caused by the electron and ion flows; as a result, Equation (5) was only used to find the connection between electron and ion densities. In the examined case, the electric field of the plasma layer has just an electrostatic nature, i.e., is defined by Equation (5) only. Thus, the features in the present study, again demonstrate that the correct description of evolution of nonequilibrium plasma for comparably large times have to take into account the mobility of electron and ionic components. We consider to discuss this point in the forthcoming studies.

7. Conclusions

In the present paper, based on the hydrodynamic description, we have considered the nonlinear dynamics of cylindrical plasma waves with finite electron pressure and stationary cold ions in a two-dimensional geometry. The results obtained are consistent with modern experimental data [33,34,35,36,37,38], where the influence of the final temperature on the dynamics of plasma waves and the development of instabilities are observed.

Our study was restricted to an adiabatic approximation where the electron pressure was described by the Poisson formula (2) or in differential form by the relation (6). Such formulation of the problem made it possible to use the substitution of Equations (13)–(16), which transforms the hydrodynamic equations into a system of ordinary differential equations, namely Equations (17)–(22). In turn, this set was reduced to the generalized Ermakov–Pinney equation with dimensionless parameter ${\beta }_T$ (see Equation (33)) which reflects the manifestation of the thermal effect in the system under consideration (see Equations (12) and (35)). This governing parameter ${\beta }_T$ actually allows to select the range of values where the thermal effect must define the dynamics of electron nonlinear waves, including the formation of hydrodynamic singularities. In particular, the present consideration shows that the evolution of singular behavior due to intrinsic nonlinearity can be avoided by taking into account thermal effects and the initial rotation of the electron flow (see Equation (35)). However, there is a domain of parameters $H_T$, $B_0$ and $A_0$ (see Equations (43) and (46)) where it is impossible to escape the collapse formation. On the other hand, the regular dynamics correspond not only to certain values of ${\beta }_T$, but the value of $B_0$ be also taken into account.

Herein it should be borne in mind that this model describes only an initial stage of evolution for the nonlinear electron waves of finite amplitude. On the other hand, this particular exact solution can be regarded as a majorizing estimate of the exact solution to the system (2)–(5), making it possible to establish the limits within which the general solution may vary. Such an approach allows us to identify the range of system parameters at which regular behavior that was performed in the present study can be realized.

In conclusion, we again would like to emphasize the role of problem dimension which can highly influence the wave processes occurring far from equilibrium. As was shown, in two-dimensional geometry one can obtain either regular behavior (see Figure 4, Figure 5 and Figure 7) or singular dynamics (see Figure 6). In the present case, in order to avoid the wave breaking, we had to maintain some ratio between initial velocity, magnetic field and electron temperature. However, in three-dimensional geometry there is another possibility where the oscillation energy of plasma cylinder in the radial mode tends to be transferred to the azimuthal and axial degrees of freedom [11,12,13]. It means that there may be some conditions under which the thermal mode might serve as a tank of “internal” energy, which can be transformed in one degree of freedom. So, one may venture a guess that the energy of chaotic degrees of freedom may be transferred into the rotation or axial mode of the plasma but this problem originates from the framework of this paper and we hope to discuss this question later.