Temperature Dependence of the Response Functions of Graphene: Impact on Casimir and Casimir–Polder Forces in and out of Thermal Equilibrium
Abstract
1. Introduction
2. Main Quantities: Polarization Tensor, Electric Conductivity, Dielectric Functions and Reflection Coefficients
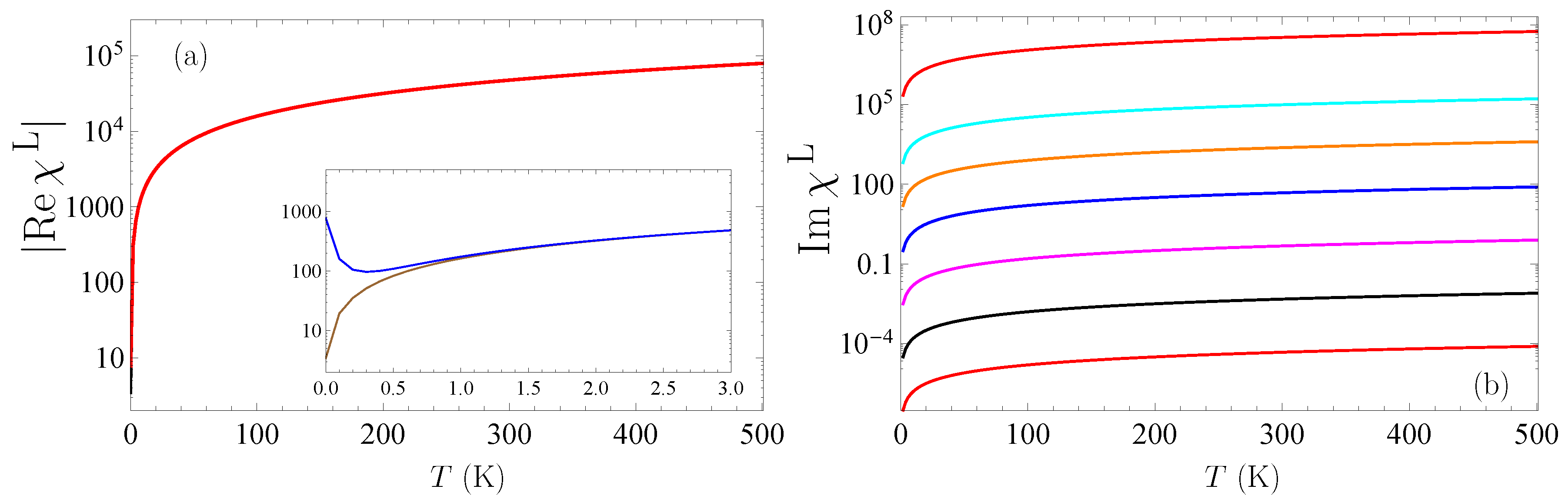
3. Temperature Dependence of the Dielectric Functions of Graphene Below the Threshold
4. Temperature Dependence of the Dielectric Functions of Graphene Above the Threshold
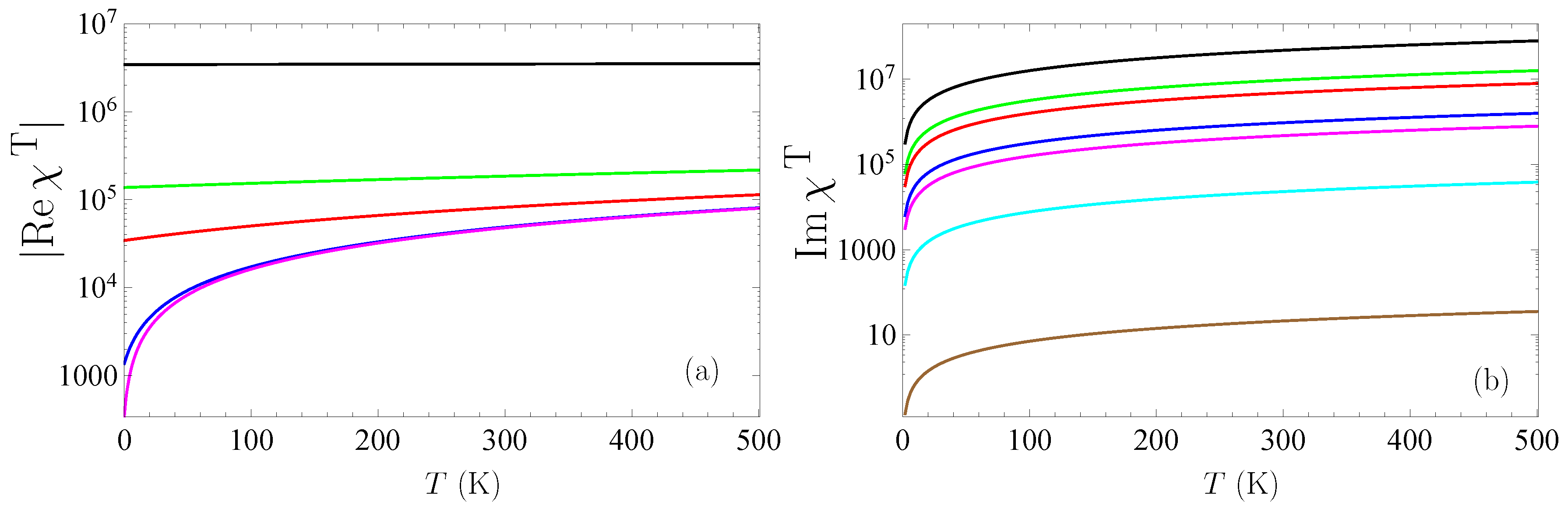
5. Thermal Effects in the Casimir Force Between Two Graphene Sheets
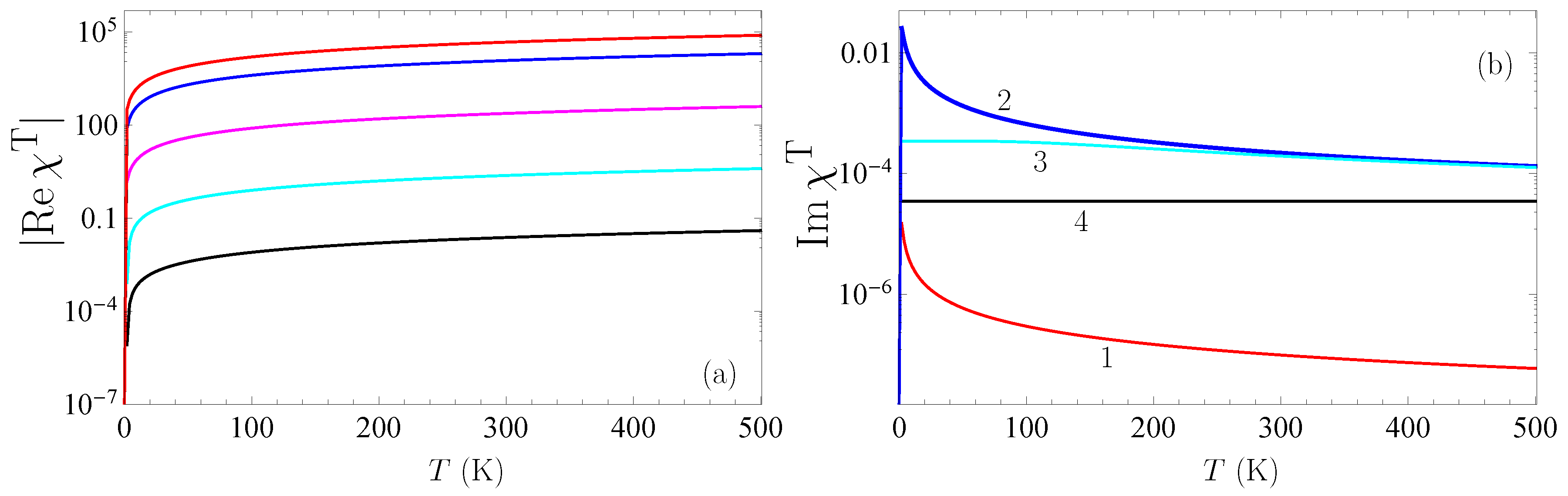
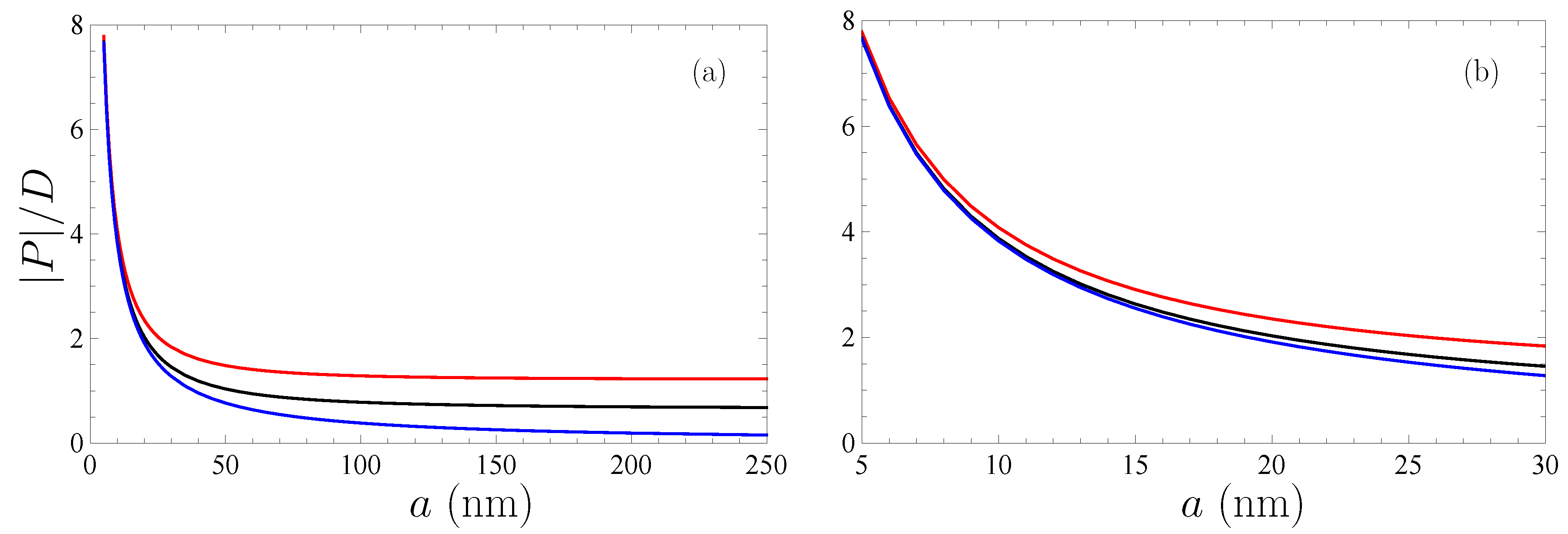
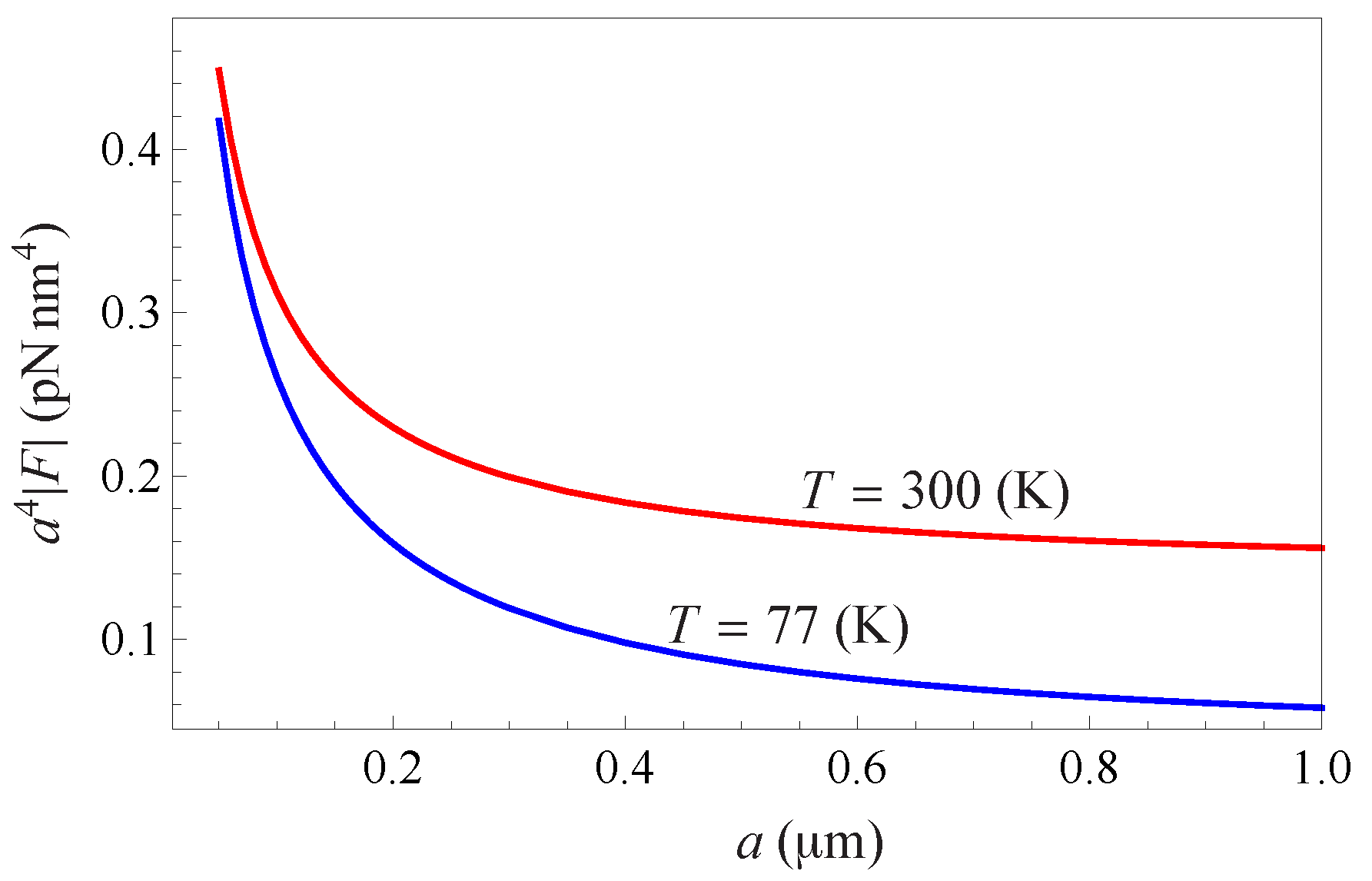
6. Thermal Effects in the Casimir–Polder Force Between a Nanoparticle and a Graphene Sheet
7. Thermal Effects in the Casimir and Casimir–Polder Forces from Graphene out of Thermal Equilibrium
8. Discussion
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Casimir, H.B.G. On the attraction between two perfectly conducting plates. Proc. Kon. Ned. Akad. Wetensch. 1948, 51, 793–795. [Google Scholar]
- Casimir, H.B.G.; Polder, D. The influence of retardation on the London-van der Waals forces. Phys. Rev. 1948, 73, 360–372. [Google Scholar] [CrossRef]
- Milton, K.A. The Casimir Effect: Physical Manifestations of Zero-Point Energy; World Scientific Co. Pte. Ltd.: Singapore, 2001. [Google Scholar]
- Buhmann, S.Y. Disperson Forces I: Macroscopic Quantum Electrodynamics and Ground-State Casimir, Casimir–Polder and van der Waals Forces; Springer: Berlin/Heidelberg, Germany, 2012; Volumes 1–2. [Google Scholar] [CrossRef]
- Buhmann, S.Y. Disperson Forces II: Many-Body Effects, Excited Atoms, Finite Temperature and Quantum Friction; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press: Oxford, UK, 2015. [Google Scholar] [CrossRef]
- Sernelius, B.E. Fundamentals of van der Waals and Casimir Interactions; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Lifshitz, E.M. The theory of molecular attractive forces between solids. Zh. Eksp. Teor. Fiz. 1955, 29, 94–110. (In Russian); English Translation: Sov. Phys. JETP 1956, 2, 73–83. [Google Scholar]
- Dzyaloshinskii, I.E.; Lifshitz, E.M.; Pitaevskii, L.P. The general theory of van der Waals forces. Usp. Fiz. Nauk 1961, 73, 381–422. (In Russian); English Translation: Sov. Phys. Uspekhi 1961, 4, 153–176. [Google Scholar] [CrossRef]
- Lifshitz, E.M.; Pitaevskii, L.P. Statistical Physics, Part 2; Pergamon: Oxford, UK, 1980; Available online: https://haidinh89.files.wordpress.com/2015/08/landau-l-d-lifshitz-e-m-course-of-theoretical-physics-vol-09-statistical-physics-part-2-3455.pdf (accessed on 24 August 2025).
- Decca, R.S.; López, D.; Osquiguil, E. New results for the Casimir interaction: Sample characterization and low temperature measurements. Int. J. Mod. Phys. A 2010, 25, 2223–2230. [Google Scholar] [CrossRef]
- Castillo-Garza, R.; Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M. Mohideen, U. Casimir interaction at liquid nitrogen temperature: Comparison between experiment and theory. Phys. Rev. B 2013, 88, 075402. [Google Scholar] [CrossRef]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Warner, J.H.; Schäffel, F.; Bachmatiuk, A.; Rümmeli, M.H. Graphene: Fundamentals and Emergent Applications; Elsevier Inc.: Oxford, UK, 2013. [Google Scholar] [CrossRef]
- Aoki, H.; Dresselhaus, M.S. (Eds.) Physics of Graphene; Springer International Publishing Switzerland: Cham, Switzerland, 2014. [Google Scholar]
- Sharon, M.; Sharon, M. Graphene: An Introduction to the Fundamentals and Industrial Applications; Scrivener Publishing LLC: Salem, MA, USA; John Wiley and Sons: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Proctor, J.E.; Melendrez Armada, D.A.; Vijayaraghavan, A. An Introduction to Graphene and Carbon Nanotubes; CRC Press/Taylor Francis Group: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Johnson, L.; Meany, J.E. Graphene: The Superstrong, Superthin, and Superversatile Material That Will Revolutionize the World; Prometheus Books: Amherst, NY, USA, 2018; Available online: https://archive.org/details/GrapheneTheSuperhard/ (accessed on 24 August 2025).
- Katsnelson, M.I. The Physics of Graphene; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar] [CrossRef]
- Gómez-Santos, G. Thermal van der Waals interaction between graphene layers. Phys. Rev. B 2009, 80, 245424. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Origin of large thermal effect in the Casimir interaction between two graphene sheets. Phys. Rev. B 2015, 91, 174501. [Google Scholar] [CrossRef]
- Cahangirov, S.; Topsakal, M.; Aktürk, E.; Sahin, H.; Ciraci, S. Two- and one-dimensional honeycomb structures of silicon and germanium. Phys. Rev. Lett. 2009, 102, 236804. [Google Scholar] [CrossRef]
- Xu, M.; Liang, T.; Shi, M.; Chen, H. Graphene-like two-dimensional materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef]
- Küchle, J.T.; Baklanov, A.; Seitsonen, A.P.; Ryan, P.T.P.; Feulner, P.; Pendem, P.; Lee, T.L.; Muntwiler, M.; Schwarz, M.; Haag, F.; et al. Silicene’s pervasive surface alloy on Ag(111): A scaffold for two-dimensional growth. 2D Mater. 2022, 9, 045021. [Google Scholar] [CrossRef]
- Bianco, E.; Butler, S.; Jiang, S.; Restrepo, O.D.; Windl, W.; Goldberger, J.E. Stability and exfoliation of germanane: A germanium graphane analogue. ACS Nano 2013, 7, 4414–4421. [Google Scholar] [CrossRef] [PubMed]
- Bampoulis, P.; Zhang, L.; Safaei, A.; van Gastel, R.; Poelsema, B.; Zandvliet, H.J.W. Germanene termination of Ge2Pt crystals on Ge(110). J. Phys. Condens. Matter 2014, 26, 442001. [Google Scholar] [CrossRef] [PubMed]
- Yuhara, J.; Shimazu, H.; Ito, K.; Ohta, A.; Kurosawa, M.; Nakatake, M.; Le Lay, G. Germanene epitaxial growth by segregation through Ag(111) thin films on Ge(111). ACS Nano 2018, 12, 11632–11637. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, L.; Takahashi, K. Low temperature pollutant trapping and dissociation over two-dimensional tin. Phys. Chem. Chem. Phys. 2015, 17, 21394–21396. [Google Scholar] [CrossRef]
- Yuhara, J.; Fujii, Y.; Isobe, N.; Nakatake, M.; Lede, X.; Rubio, A.; Le Lay, G. Large Area Planar Stanene Epitaxially Grown on Ag(111). 2D Mater. 2018, 5, 025002. [Google Scholar] [CrossRef]
- Ahmed, R.; Nakagawa, T.; Mizuno, S. Structure determination of ultra-flat stanene on Cu(111) using low energy electron diffraction. Surf. Sci. 2020, 691, 121498. [Google Scholar] [CrossRef]
- Li, L.; Yu, Y.; Ye, G.J.; Ge, Q.; Ou, X.; Wu, H.; Feng, D.; Chen, X.H.; Zhang, Y. Black phosphorus field-effect transistors. Nat. Nanotech. 2016, 9, 372–377. [Google Scholar] [CrossRef]
- Ritu, H. Large area fabrication of semiconducting phosphorene by Langmuir–Blodgett assembly. Sci. Rep. 2016, 6, 34095. [Google Scholar]
- Liu, N.; Hong, J.; Pidaparti, R.; Wang, X. Fracture patterns and the energy release rate of phosphorene. Nanoscale 2016, 8, 5728–5736. [Google Scholar] [CrossRef] [PubMed]
- Barton, G. Casimir energies of spherical plasma shells. J. Phys. A Math. Gen. 2004, 37, 1011–1050. [Google Scholar] [CrossRef]
- Barton, G. Casimir effect for a flat plasma sheet. I. Energies. J. Phys. A Math. Gen. 2005, 38, 2997–3020. [Google Scholar] [CrossRef]
- Bordag, M. The Casimir effect for thin plasma sheets and the role of the surface plasmons. J. Phys. A Math. Gen. 2006, 39, 6173–6185. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G. Transport of Dirac quasiparticles in graphene: Hall and optical conductivities. Phys. Rev. B 2006, 73, 245411. [Google Scholar] [CrossRef]
- Katsnelson, M.I. Zitterbewegung, chirality, and minimal conductivity in graphene. Eur. Phys. J. B 2006, 51, 157–160. [Google Scholar] [CrossRef]
- Peres, N.M.R.; Guinea, F.; Castro Neto, A.H. Electronic properties of disordered two-dimensional carbon. Phys. Rev. B 2006, 73, 125411. [Google Scholar] [CrossRef]
- Ziegler, K. Robust Transport Properties in Graphene. Phys. Rev. Lett. 2006, 97, 266802. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. Magneto-optical conductivity in graphene. J. Phys. Condens. Matter 2007, 19, 026222. [Google Scholar] [CrossRef]
- Bordag, M. Generalized Lifshitz formula for a cylindrical plasma sheet in front of a plane beyond proximity force approximation. Phys. Rev. D 2007, 75, 065003. [Google Scholar] [CrossRef]
- Ziegler, K. Minimal conductivity of graphene: Nonuniversal values from the Kubo formula. Phys. Rev. B 2007, 75, 233407. [Google Scholar] [CrossRef]
- Peres, N.M.R.; Lopes dos Santos, J.M.B.; Stauber, T. Phenomenological study of the electronic transport coefficients of graphene. Phys. Rev. B 2007, 76, 073412. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. Anomalous absorption line in the magneto-optical response of graphene. Phys. Rev. Lett. 2007, 98, 157402. [Google Scholar] [CrossRef] [PubMed]
- Stauber, T.; Peres, N.M.R.; Guinea, F. Electronic transport in graphene: A semiclassical approach including midgap states. Phys. Rev. B 2007, 76, 205423. [Google Scholar] [CrossRef]
- Falkovsky, L.A.; Varlamov, A.A. Space-time dispersion of graphene conductivity. Eur. Phys. J. B 2007, 56, 281–284. [Google Scholar] [CrossRef]
- Falkovsky, L.A.; Pershoguba, S.S. Optical far-infrared properties of a graphene monolayer and multilayer. Phys. Rev. B 2007, 76, 153410. [Google Scholar] [CrossRef]
- Stauber, T.; Peres, N.M.R.; Geim, A.K. Optical conductivity of graphene in the visible region of the spectrum. Phys. Rev. B 2008, 78, 085432. [Google Scholar] [CrossRef]
- Peres, N.M.R.; Stauber, T. Transport in a clean graphene sheet at finite temperature and frequency. Int. J. Mod. Phys. B 2008, 22, 2529–2536. [Google Scholar] [CrossRef]
- Falkovsky, L.A. Optical properties of graphene. J. Phys. Conf. Series 2008, 129, 012004. [Google Scholar] [CrossRef]
- Qaiumzadeh, A.; Asgari, R. Ground-state properties of gapped graphene using the random phase approximation. Phys. Rev. B 2009, 79, 075414. [Google Scholar] [CrossRef]
- Pedersen, T.G.; Jauho, A.P.; Pedersen, K. Optical response and excitons in gapped graphene. Phys. Rev. B 2009, 79, 113406. [Google Scholar] [CrossRef]
- Lewkowicz, M.; Rosenstein, B. Dynamics of particle–hole Pair creation in graphene. Phys. Rev. Lett. 2009, 102, 106802. [Google Scholar] [CrossRef]
- Beneventano, C.G.; Giacconi, P.; Santangelo, E.M.; Soldati, R. Planar QED at finite temperature and density: Hall conductivity, Berry’s phases and minimal conductivity of graphene. J. Phys. A Math. Theor. 2009, 42, 275401. [Google Scholar] [CrossRef]
- Palacios, J.J. Origin of the quasiuniversality of the minimal conductivity of graphene. Phys. Rev. B 2010, 82, 165439. [Google Scholar] [CrossRef]
- Scholz, A.; Schliemann, J. Dynamical current-current susceptibility of gapped graphene. Phys. Rev. B 2011, 83, 235409. [Google Scholar] [CrossRef]
- Moriconi, L.; Niemeyer, D. Graphene conductivity near the charge neutral point. Phys. Rev. B 2011, 84, 193401. [Google Scholar] [CrossRef]
- Horng, J.; Chen, C.F.; Geng, B.; Girit, C.; Zhang, Y.; Hao, Z.; Bechtel, H.A.; Martin, M.; Zettl, A.; Crommie, M.F.; et al. Drude conductivity of Dirac fermions in graphene. Phys. Rev. B 2011, 83, 165113. [Google Scholar] [CrossRef]
- Koppens, F.H.L.; Chang, D.E.; García de Abajo, F.J. Graphene Plasmonics: A platform for strong light–matter interactions. Nano Lett. 2011, 11, 3370–3377. [Google Scholar] [CrossRef]
- Drosdoff, D.; Woods, L.M. Casimir interaction between graphene sheets and metamaterials. Phys. Rev. A 2011, 84, 062501. [Google Scholar] [CrossRef]
- Svetovoy, V.; Moktadir, Z.; Elwenspoek, M.; Mizuta, H. Tailoring the thermal Casimir force with graphene. Europhys. Lett. 2011, 96, 14006. [Google Scholar] [CrossRef]
- Sernelius, B.E. Casimir interactions in graphene systems. Europhys. Lett. 2011, 95, 57003. [Google Scholar] [CrossRef]
- Drosdoff, D.; Phan, A.D.; Woods, L.M.; Bondarev, I.V.; Dobson, J.F. Effects of spatial dispersion on the Casimir force between graphene sheets. Eur. Phys. J. B 2012, 85, 365. [Google Scholar] [CrossRef]
- Sernelius, B.E. Retarded interactions in graphene systems. Phys. Rev. B 2012, 85, 195427. [Google Scholar] [CrossRef]
- Phan, A.D.; Woods, L.M.; Drosdoff, D.; Bondarev, I.V.; Viet, N.A. Temperature dependent graphene suspension due to thermal Casimir interaction. Appl. Phys. Lett. 2012, 101, 113118. [Google Scholar] [CrossRef]
- Buividovich, P.V.; Luschevskaya, E.V.; Pavlovsky, O.V.; Polikarpov, M.I.; Ulybyshev, M.V. Numerical study of the conductivity of graphene monolayer within the effective field theory approach. Phys. Rev. B 2012, 86, 045107. [Google Scholar] [CrossRef]
- Bácsi, Á.; Virosztek, A. Low-frequency optical conductivity in graphene and in other scale-invariant two-band systems. Phys. Rev. B 2013, 87, 125425. [Google Scholar] [CrossRef]
- Dartora, C.A.; Cabrera, G.G. U(1) × SU(2) gauge invariance leading to charge and spin conductivity of Dirac fermions in graphene. Phys. Rev. B 2013, 87, 165416. [Google Scholar] [CrossRef]
- Louvet, T.; Delplace, P.; Fedorenko, A.A.; Carpentier, D. On the origin of minimal conductivity at a band crossing. Phys. Rev. B 2015, 92, 155116. [Google Scholar] [CrossRef]
- Patel, D.K.; Sharma, A.C.; Ashraf, S.S.Z. Temperature dependent screened electronic transport in gapped graphene. Phys. Status Solidi 2015, 252, 282. [Google Scholar] [CrossRef]
- Merano, M. Fresnel coefficients of a two-dimensional atomic crystal. Phys. Rev. A 2016, 93, 013832. [Google Scholar] [CrossRef]
- Rani, L.; Singh, N. Dynamical electrical conductivity of graphene. J. Phys. Condens. Matter 2017, 29, 255602. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.; Antezza, M.; Wang, J.-S. Dynamical polarizability of graphene with spatial dispersion. Phys. Rev. B 2021, 103, 125421. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. AC conductivity of graphene: From tight-binding model to 2+1-dimensional quantum electrodynamics. Int. J. Mod. Phys. B 2007, 21, 4611–4658. [Google Scholar] [CrossRef]
- Peres, N.M.R. The transport properties of graphene: An introduction. Rev. Mod. Phys. 2010, 82, 2673–2700. [Google Scholar] [CrossRef]
- Das Sarma, S.; Adam, S.; Hwang, E.H.; Rossi, E. Electronic transport in two-dimensional graphene. Rev. Mod. Phys. 2011, 83, 407–470. [Google Scholar] [CrossRef]
- Pisarski, R.D. Chiral symmetry breaking in three-dimensional electrodynamics. Phys. Rev. D 1984, 29, 2423–2426. [Google Scholar] [CrossRef]
- Appelquist, T.W.; Bowick, M.J.; Karabali, D.; Wijewardhana, L.C.R. Spontaneous chiral-symmetry breaking in three-dimensional QED. Phys. Rev. D 1986, 33, 3704–3713. [Google Scholar] [CrossRef]
- Dorey, N.; Mavromatos, N.E. QED3 and two-dimensional superconductivity without parity violation. Nucl. Phys. B 1992, 386, 614–680. [Google Scholar] [CrossRef]
- Zeitlin, V. QED2+1 with nonzero fermion density and quantum Hall effect. Phys. Lett. B 1995, 352, 422–427. [Google Scholar] [CrossRef]
- Pyatkovsky, P.K. Dynamical polarization, screening, and plasmons in gapped graphene. J. Phys. Condens. Matter 2009, 21, 025506. [Google Scholar] [CrossRef]
- Bordag, M.; Fialkovsky, I.V.; Gitman, D.M.; Vassilevich, D.V. Casimir interaction between a perfect conductor and graphene described by the Dirac model. Phys. Rev. B 2009, 80, 245406. [Google Scholar] [CrossRef]
- Fialkovsky, I.V.; Marachevsky, V.N.; Vassilevich, D.V. Finite-temperature Casimir effect for graphene. Phys. Rev. B 2011, 84, 035446. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Petrov, V.M. Quantum field theoretical description for the reflectivity of graphene. Phys. Rev. D 2015, 91, 045037, Erratum in: Phys. Rev. D 2016, 93, 089907.. [Google Scholar] [CrossRef]
- Bordag, M.; Fialkovskiy, I.; Vassilevich, D. Enhanced Casimir effect for doped graphene. Phys. Rev. B 2016, 93, 075414, Erratum in: Phys. Rev. B 2017, 95, 119905.. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Sernelius, B.E. Two approaches for describing the Casimir interaction with graphene: Density-density correlation function versus polarization tensor. Phys. Rev. B 2014, 89, 125407. [Google Scholar] [CrossRef]
- Bordag, M.; Pirozhenko, I.G. Transverse-electric surface plasmon for graphene in the Dirac equation model. Phys. Rev. B 2014, 89, 035421. [Google Scholar] [CrossRef]
- Bordag, M.; Pirozhenko, I.G. Surface plasmons for doped graphene. Phys. Rev. D 2015, 91, 085038. [Google Scholar] [CrossRef]
- Bordag, M.; Pirozhenko, I.G. QED and surface plasmons on graphene. Int. J. Mod. Phys. A 2016, 31, 1641027. [Google Scholar] [CrossRef]
- Bordag, M.; Pirozhenko, I.G. Surface plasmon on graphene at finite T. Int. J. Mod. Phys. B 2016, 30, 1650120. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Tsybin, O.Y. Casimir–Polder attraction and repulsion between nanoparticles and graphene in out-of-thermal-equilibrium conditions. Phys. Rev. B 2022, 105, 195430, Erratum in: Phys. Rev. B 2024, 109, 079901.. [Google Scholar] [CrossRef]
- Fialkovskiy, I.V.; Vassilevich, D.V. Quantum field theory in graphene. Int. J. Mod. Phys. A 2012, 27, 1260007. [Google Scholar] [CrossRef]
- Fialkovskiy, I.V.; Vassilevich, D.V. Graphene through the looking glass of QFT. Mod. Phys. Lett. A 2016, 31, 1630047. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M.; Pitaevskii, L.P. Electrodynamics of Continuous Media; Pergamon Press Ltd./Elsevier: Amsterdam, The Netherlands, 1984; Available online: https://www.sciencedirect.com/book/9780080302751/electrodynamics-of-continuous-media (accessed on 24 August 2025).
- Klimchitskaya, G.L.; Mostepanenko, V.M. Conductivity of pure graphene: Theoretical approach using the polarization tensor. Phys. Rev. B 2016, 93, 245419. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Quantum electrodynamic approach to the conductivity of gapped graphene. Phys. Rev. B 2016, 94, 195405. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Petrov, V.M. Conductivity of graphene in the framework of Dirac model: Interplay between nonzero mass gap and chemical potential. Phys. Rev. B 2017, 96, 235432. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Kramers-Kronig relations and causality conditions for graphene in the framework of Dirac model. Phys. Rev. D 2018, 97, 085001. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. The Casimir force between two graphene sheets: 2D Fresnel reflection coefficients, contributions of different polarizations, and the role of evanescent waves. Physics 2023, 5, 1013–1030. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Theory of the Casimir interaction from graphene-coated substrates and comparison with experiment. Phys. Rev. B 2014, 89, 115419. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys. 2009, 81, 1827–1885. [Google Scholar] [CrossRef]
- Mostepanenko, V.M. Casimir Puzzle and Conundrum: Discovery and Search for Resolution. Universe 2021, 7, 84. [Google Scholar] [CrossRef]
- Bimonte, G.; Spreng, B.; Maia Neto, P.A.; Ingold, G.-L.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Decca, R.S. Measurement of the Casimir force between 0.2 and 8 μm: Experimental procedures and comparison with theory. Universe 2021, 7, 93. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Current status of the problem of thermal Casimir force. Int. J. Mod. Phys. A 2022, 37, 2241002. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Y.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Demonstration of unusual thermal effect in the Casimir force from graphene. Phys. Rev. Lett. 2021, 126, 206802. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Zhang, Y.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Experimental and theoretical investigation of the thermal effect in the Casimir interaction from graphene. Phys. Rev. B 2021, 104, 085436. [Google Scholar] [CrossRef]
- Rodriguez-Lopez, P.; Wang, J.-S.; Antezza, M. Electric conductivity in graphene: Kubo model versus a nonlocal quantum field theory model. Phys. Rev. B 2025, 111, 115428. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mostepanenko, V.M. Convergence of the polarization tensor in spacetime of three dimensions. Phys. Rev. D 2024, 109, 125014. [Google Scholar] [CrossRef]
- Bordag, M.; Khusnutdinov, N.; Klimchitskaya, G.L.; Mostepanenko, V.M. Comment on “Electric conductivity in graphene: Kubo model versus a nonlocal quantum field theory model”. arXiv 2025, arXiv:2506.10792. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Quantum field theoretical framework for the electromagnetic response of graphene and dispersion relations with implications to the Casimir effect. Phys. Rev. D 2023, 107, 105007. [Google Scholar] [CrossRef]
- Sarabadani, J.; Naji, A.; Asgari, R.; Podgornik, R. Many-body effects in the van der Waals–Casimir interaction between graphene layers. Phys. Rev. B 2011, 84, 155407, Erratum in: Phys. Rev. B 2013, 87, 239905.. [Google Scholar] [CrossRef]
- Drosdoff, D.; Woods, L.M. Casimir forces and graphene sheets. Phys. Rev. B 2010, 82, 155459. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Van der Waals and Casimir interactions between two graphene sheets. Phys. Rev. B 2013, 87, 075439. [Google Scholar] [CrossRef]
- Bimonte, G.; Klimchitskaya, G.L.; Mostepanenko, V.M. Thermal effect in the Casimir force for graphene and graphene-coated substrates: Impact of nonzero mass gap and chemical potential. Phys. Rev. B 2017, 96, 115430. [Google Scholar] [CrossRef]
- Khusnutdinov, N.; Kashapov, R.; Woods, L.M. Thermal Casimir and Casimir–Polder interactions in N parallel 2D Dirac materials. 2D Mater. 2018, 5, 035032. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Observability of thermal effects in the Casimir interaction from graphene-coated substrates. Phys. Rev. A 2014, 89, 052512. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mostepanenko, V.M. Thermal Casimir effect in the interaction of graphene with dielectrics and metals. Phys. Rev. B 2012, 86, 165429. [Google Scholar] [CrossRef]
- Judd, T.E.; Scott, R.G.; Martin, A.M.; Kaczmarek, B.; Fromhold, T.M. Quantum reflection of ultracold atoms from thin films, graphene and semiconductor heterostructures. New J. Phys. 2011, 13, 083020. [Google Scholar] [CrossRef]
- Eizner, E.; Horovitz, B.; Henkel, C. Van der Waals–Casimir–Polder interaction of an atom with a composite surface. Eur. Phys. J. D 2012, 66, 321. [Google Scholar] [CrossRef]
- Ribeiro, S.; Scheel, S. Shielding vacuum fluctuations with graphene. Phys. Rev. A 2013, 88, 042519, Erratum in: Phys. Rev. A 2014, 89, 039904.. [Google Scholar] [CrossRef]
- Cysne, T.; Kort-Kamp, W.J.M.; Oliver, D.; Pinheiro, F.A.; Rosa, F.S.S.; Farina, C. Tuning the Casimir–Polder interaction via magneto-optical effects in graphene. Phys. Rev. A 2014, 90, 052511. [Google Scholar] [CrossRef]
- Khusnutdinov, N.; Kashapov, R.; Woods, L.M. Casimir–Polder effect for a stack of conductive planes. Phys. Rev. A 2016, 94, 012513. [Google Scholar] [CrossRef]
- Cysne, T.P.; Rapoport, T.G.; Ferreira, A.; Viana Parente Lopes, J.M.; Peres, N.M.R. Numerical calculation of the Casimir–Polder interaction between a graphene sheet with vacancies and an atom. Phys. Rev. B 2016, 94, 235405. [Google Scholar] [CrossRef]
- Nichols, N.S.; Del Maestro, A.; Wexler, C.; Kotov, V.N. Adsorption by design: Tuning atom-graphene van der Waals interactions via mechanical strain. Phys. Rev. B 2016, 93, 205412. [Google Scholar] [CrossRef]
- Khusnutdinov, N.; Emelianova, N. The low-temperature expansion of the Casimir–Polder free energy of an atom with graphene. Universe 2021, 7, 70. [Google Scholar] [CrossRef]
- Chaichian, M.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Tureanu, A. Thermal Casimir–Polder interaction of different atoms with graphene. Phys. Rev. A 2012, 86, 012515. [Google Scholar] [CrossRef]
- Henkel, C.; Klimchitskaya, G.L.; Mostepanenko, V.M. Influence of the chemical potential on the Casimir–Polder interaction between an atom and gapped graphene or a graphene-coated substrate. Phys. Rev. A 2018, 97, 032504. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Classical Casimir–Polder force between polarizable microparticles and thin films including graphene. Phys. Rev. A 2014, 89, 012516. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir–-Polder force on atoms or nanoparticles from gapped and doped graphene: Asymptotic behavior at large separations. C 2023, 9, 64. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Large-separation behavior of the Casimir–Polder force from real graphene sheet deposited on a dielectric substrate. C 2023, 9, 84. [Google Scholar] [CrossRef]
- Polder, D.; Van Hove, M. Theory of radiative heat transfer between closely spaced bodies. Phys. Rev. B 1971, 4, 3303–3314. [Google Scholar] [CrossRef]
- Dorofeyev, I.A. The force of attraction between two solids with different temperatures. J. Phys. A Math. Gen. 1998, 31, 4369–4380. [Google Scholar] [CrossRef]
- Bimonte, G. A Theory of electromagnetic fluctuations for metallic surfaces and van der Waals interactions between metallic bodies. Phys. Rev. Lett. 2006, 96, 160401. [Google Scholar] [CrossRef]
- Antezza, M.; Pitaevskii, L.P.; Stringari, S.; Svetovoy, V.B. Casimir–Lifshitz force out of thermal equilibrium and asymptotic nonadditivity. Phys. Rev. Lett. 2006, 97, 223203. [Google Scholar] [CrossRef] [PubMed]
- Antezza, M.; Pitaevskii, L.P.; Stringari, S.; Svetovoy, V.B. Casimir–Lifshitz force out of thermal equilibrium. Phys. Rev. A 2008, 77, 022901. [Google Scholar] [CrossRef]
- Bimonte, G. Scattering approach to Casimir forces and radiative heat transfer for nanostructured surfaces out of thermal equilibrium. Phys. Rev. A 2009, 80, 042102. [Google Scholar] [CrossRef]
- Messina, R.; Antezza, M. Scattering-matrix approach to Casimir–Lifshitz force and heat transfer out of thermal equilibrium between arbitrary bodies. Phys. Rev. A 2011, 84, 042102. [Google Scholar] [CrossRef]
- Messina, R.; Antezza, M. Non-equilibrium fluctuational quantum electrodynamics: Heat radiation, heat transfer, and force. Europhys. Lett. 2011, 95, 61002. [Google Scholar] [CrossRef]
- Bimonte, G.; Emig, T.; Krüger, M.; Kardar, M. Dilution and resonance-enhanced repulsion in nonequilibrium fluctuation forces. Phys. Rev. A 2011, 84, 042503. [Google Scholar] [CrossRef]
- Krüger, M.; Emig, T.; Kardar, M. Nonequilibrium electromagnetic fluctuations: Heat transfer and interactions. Phys. Rev. Lett. 2011, 106, 210404. [Google Scholar] [CrossRef]
- Krüger, M.; Emig, T.; Bimonte, G.; Kardar, M. Non-equilibrium Casimir forces: Spheres and sphere-plate. Europhys. Lett. 2011, 95, 21002. [Google Scholar] [CrossRef]
- Krüger, M.; Bimonte, G.; Emig, T.; Kardar, M. Trace formulas for nonequilibrium Casimir interactions, heat radiation, and heat transfer for arbitrary bodies. Phys. Rev. B 2012, 86, 115423. [Google Scholar] [CrossRef]
- Ingold, G.-L.; Klimchitskaya, G.L.; Mostepanenko, V.M. Nonequilibrium effects in the Casimir force between two similar metallic plates kept at different temperatures. Phys. Rev. A 2020, 101, 032506. [Google Scholar] [CrossRef]
- Castillo-López, S.G.; Esquivel-Sirvent, R.; Pirruccio, G.; Villarreal, C. Casimir forces out of thermal equilibrium near a superconducting transition. Sci. Rep. 2022, 12, 2905. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Korikov, C.C.; Mostepanenko, V.M. Nonequilibrium Casimir pressure for two graphene-coated plates: Quantum field theoretical approach. Int. J. Mod. Phys. A 2025, 40, 2543003. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Korikov, C.C.; Mostepanenko, V.M. Polarization tensor in spacetime of three dimensions and a quantum field-theoretical description of the nonequilibrium Casimir force in graphene systems. Phys. Rev. A 2025, 111, 012812. [Google Scholar] [CrossRef]
- Henkel, C.; Joulain, K.; Mulet, J.P.; Greffet, J.J. Radiation forces on small particles in thermal near fields. J. Opt. A Pure Appl. Opt. 2002, 4, S109–S114. [Google Scholar] [CrossRef]
- Antezza, M.; Pitaevskii, L.P.; Stringari, S. New asymptotic behavior of the surface-atom force out of thermal equilibrium. Phys. Rev. Lett. 2005, 95, 113202. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Korikov, C.C.; Mostepanenko, V.M.; Tsybin, O.Y. Impact of mass-gap on the dispersion interaction of nanoparticles with graphene out of thermal equilibrium. Appl. Sci. 2023, 13, 7511. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Korikov, C.C.; Mostepanenko, V.M.; Tsybin, O.Y. Nonequilibrium Casimir–Polder interaction between nanoparticles and substrates coated with gapped graphene. Symmetry 2023, 15, 1580, Erratum in: Symmetry 2024, 16, 274.. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Korikov, C.C.; Mostepanenko, V.M. Nonequilibrium Casimir–Polder force between nanoparticles and graphene-coated silica plate: Combined effect of the chemical potential and mass gap. Symmetry 2024, 16, 320. [Google Scholar] [CrossRef]
- Arora, B.; Kaur, H.; Sahoo, B.K. C3 coefficients for the alkali atoms interacting with a graphene and carbon nanotube. J. Phys. B Atom. Molec. Opt. Phys. 2014, 47, 155002. [Google Scholar] [CrossRef]
- Kaur, K.; Kaur, J.; Arora, B.; Sahoo, B.K. Emending thermal dispersion interaction of Li, Na, K and Rb alkali-metal atoms with graphene in the Dirac model. Phys. Rev. B 2014, 90, 245405. [Google Scholar] [CrossRef]
- Arora, B.; Sahoo, B.K. van der Waals coefficients for alkali-metal atoms in material media. Phys. Rev. A 2014, 89, 022511. [Google Scholar] [CrossRef]
- Kaur, K.; Arora, B.; Sahoo, B.K. Dispersion coefficients for the interactions of the alkali-metal and alkaline-earth-metal ions and inert-gas atoms with a graphene layer. Phys. Rev. A 2015, 92, 032704. [Google Scholar] [CrossRef]
- Kaur, H.; Shukla, N.; Srivastava, R.; Arora, B. Dispersion C3 coefficients for physisorption of heavy ions and atoms with graphene and carbon nanotubes. Phys. Rev. A 2021, 104, 012806. [Google Scholar] [CrossRef]
- Pereira, V.M.; Castro Neto, A.H.; Peres, N.M.R. Tight-binding approach to uniaxial strain in graphene. Phys. Rev. B 2009, 80, 045401. [Google Scholar] [CrossRef]
- Guinea, F. Strain engineering in graphene. Solid State Commun. 2012, 152, 1437–1441. [Google Scholar] [CrossRef]
- de Juan, F.; Sturla, M.; Vozmediano, M.A.H. Space dependent Fermi velocity in strained graphene. Phys. Rev. Lett. 2012, 108, 227205. [Google Scholar] [CrossRef] [PubMed]
- de Juan, F.; Mañes, J.L.; Vozmediano, M.A.H. Gauge fields from strain in graphene. Phys. Rev. B 2013, 87, 165131. [Google Scholar] [CrossRef]
- Sharma, A.; Harnish, P.; Sylvester, A.; Kotov, V.N.; Castro Neto, A.H. van der Waals forces and electron–electron interactions in two strained graphene layers. Phys. Rev. B 2014, 89, 235425. [Google Scholar] [CrossRef]
- Phan, A.D.; Phan, T.-L. Casimir interactions in strained graphene systems. Phys. Status Solidi RRL 2014, 8, 1003–1006. [Google Scholar] [CrossRef]
- Amorim, B.; Cortijo, A.; De Juan, F.; Grushin, A.G.; Guinea, F.; Gutiérrez-Rubio, A.; Ochoa, H.; Parente, V.; Roldán, R.; San-Jose, P.; et al. Novel effects of strains in graphene and other two dimensional materials. Phys. Rep. 2016, 617, 1–54. [Google Scholar] [CrossRef]
- Chudnovsky, E.M.; Zarzuela, R. Stability of suspended graphene under Casimir force. Phys. Rev. B 2016, 94, 085424. [Google Scholar] [CrossRef]
- Bordag, M.; Fialkovsky, I.; Vassilevich, D. Casimir interaction of strained graphene. Phys. Lett. A 2017, 381, 2439–2443. [Google Scholar] [CrossRef]
- Svetovoy, V.B.; van Zwol, P.J.; Chevrier, J. Plasmon enhanced near-field radiative heat transfer for graphene covered dielectrics. Phys. Rev. B 2012, 85, 155418. [Google Scholar] [CrossRef]
- Drosdoff, D.; Phan, A.D.; Woods, L.M. Transverse electric mode for near-field radiative heat transfer in graphene–metamaterial systems. Adv. Opt. Mater. 2014, 2, 1038–1042. [Google Scholar] [CrossRef]
- Yu, R.; Manjavacas, A.; García de Abajo, F.J. Ultrafast radiative heat transfer. Nature Commun. 2017, 8, 2. [Google Scholar] [CrossRef]
- Zhong, L.-Y.; Zhao, Q.-M.; Wang, T.-B.; Yu, T.-B.; Liao, Q.-H.; Liu, N.-H. Near-field radiative heat transfer between graphene/silicon carbide multilayers. J. Heat Transf. 2018, 140, 072701. [Google Scholar] [CrossRef]
- Thomas, N.H.; Sherrott, M.C.; Broulliet, J.; Atwater, H.A.; Minnich, A.J. Electronic modulation of near-field radiative transfer in graphene field effect heterostructures. Nano Lett. 2019, 19, 3898–3904. [Google Scholar] [CrossRef]
- Landrieux, S.; Ben-Abdallah, P.; Messina, R. Graphene-based enhancement of near-field radiative-heat-transfer rectification. Appl. Phys. Lett. 2022, 120, 143502. [Google Scholar] [CrossRef]
- Lu, L.; Zhang, B.; Ou, H.; Li, B.; Zhou, K.; Song, J.; Luo, Z.; Cheng, Q. Enhanced near-field radiative heat transfer between graphene/hBN systems. Nano-Micro Small 2022, 18, 2108032. [Google Scholar] [CrossRef]
- Habibzadeh, M.; Lin, H.; Edalatpour, H. Near-field radiative heat transfer between on-substrate graphene sheets. J. Quant. Spectrosc. Rad. Transf. 2023, 307, 108662. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, K.; Lu, L.; Song, J.; Luo, Z.; Cheng, Q. Tunable near-field radiative heat transfer between graphene-coated magneto-optical metasurfaces. Langmuir 2024, 40, 15541–15549. [Google Scholar] [CrossRef]
- Castillo-López, S.G.; Cortés-López, S.; Castillo-López, D.N. Control of the near-field radiative heat transfer between graphene-coated nanoparticle metasurfaces. Sci. Rep. 2024, 14, 18316. [Google Scholar] [CrossRef] [PubMed]
- He, Q.; Wu, S.; Yin, Z.; Zhang, H. Graphene-based electronic sensors. Chem. Sci. 2012, 3, 1764–1772. [Google Scholar] [CrossRef]
- Sun, Y.; Sun, M.; Xie, D. Graphene electronic devices. In Graphene: Fabrication, Characterizations, Properties and Applications; Zhu, H., Xu, Z., Xie, D., Fang, Y., Eds.; Tsinghua University Press Limited, Academic Press/Elsevier Inc.: London, UK,, 2018; pp. 103–155. [Google Scholar] [CrossRef]
- Donnelly, M.; Mao, D.; Park, J.; Xu, G. Graphene field-effect transistors: The road to bioelectronics. J. Phys. D 2018, 51, 493001. [Google Scholar] [CrossRef]
- Dehmiwal, S.; Bahuguna, M. Graphene—Properties, production and rising applications: A review. J. Mater. NanoSci. 2021, 8, 51–63. Available online: https://pubs.iscience.in/journal/index.php/jmns/article/view/1258 (accessed on 24 August 2025).
- Kogan, E. Graphene for electronics. Nanomaterials 2022, 12, 4359. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimchitskaya, G.L.; Mostepanenko, V.M. Temperature Dependence of the Response Functions of Graphene: Impact on Casimir and Casimir–Polder Forces in and out of Thermal Equilibrium. Physics 2025, 7, 44. https://doi.org/10.3390/physics7040044
Klimchitskaya GL, Mostepanenko VM. Temperature Dependence of the Response Functions of Graphene: Impact on Casimir and Casimir–Polder Forces in and out of Thermal Equilibrium. Physics. 2025; 7(4):44. https://doi.org/10.3390/physics7040044
Chicago/Turabian StyleKlimchitskaya, Galina L., and Vladimir M. Mostepanenko. 2025. "Temperature Dependence of the Response Functions of Graphene: Impact on Casimir and Casimir–Polder Forces in and out of Thermal Equilibrium" Physics 7, no. 4: 44. https://doi.org/10.3390/physics7040044
APA StyleKlimchitskaya, G. L., & Mostepanenko, V. M. (2025). Temperature Dependence of the Response Functions of Graphene: Impact on Casimir and Casimir–Polder Forces in and out of Thermal Equilibrium. Physics, 7(4), 44. https://doi.org/10.3390/physics7040044





