Applicability of Hydrodynamics in the Hadronic Phase of Heavy-Ion Collisions
Abstract
1. Introduction
2. Expanding Hadronic Phase
2.1. Statistical Hadronization
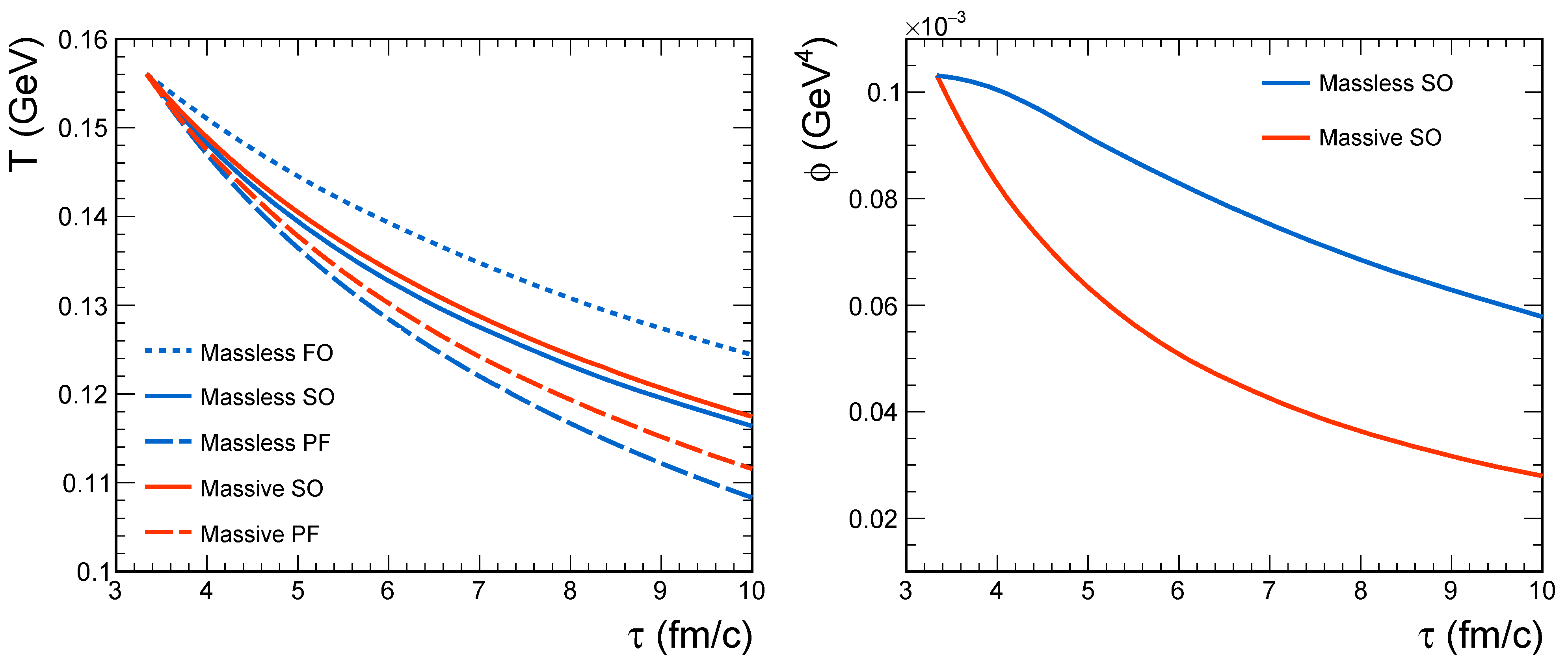
2.2. Temperature Evolution of the Hadronic Medium
2.3. Cooling Law for Massive Pionic Medium
2.4. Transverse Correction to the Cooling Law
3. Kinetic Formation Model for Resonance Particles
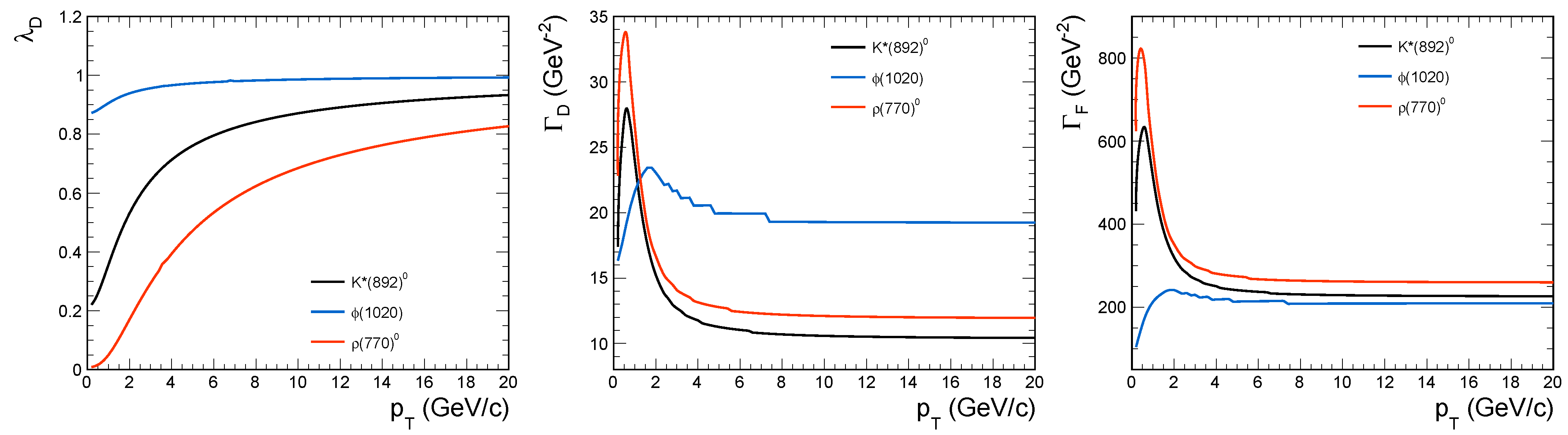
3.1. Regeneration
3.2. Decay
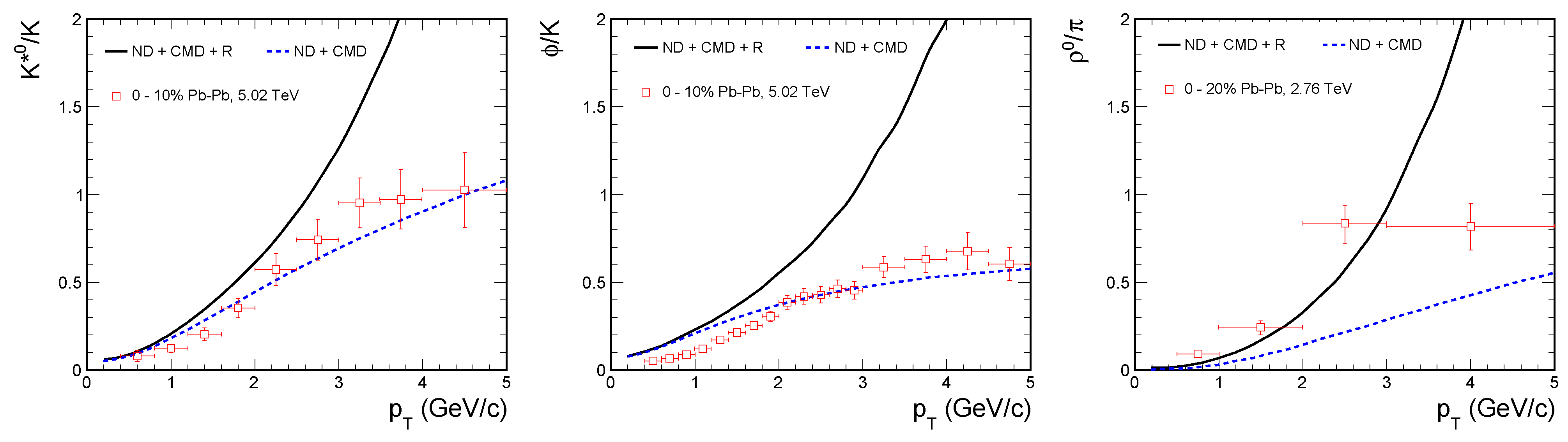
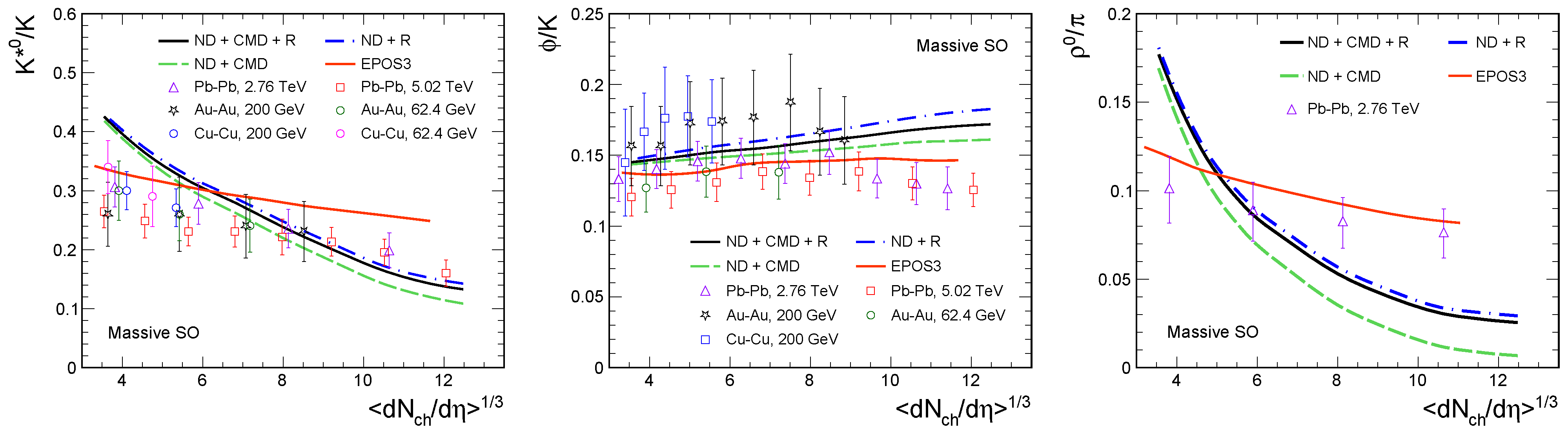
4. Results and Discussion
5. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AdS | anti-de Sitter |
| ALICE | A Large Ion Collider Experiment |
| AMPT | A Multi-Phase Transport |
| BTE | Boltzmann transport equation |
| CFT | Conformal field theory |
| EPOS | Energy conserving quantum mechanical approach, based on Partons, parton ladders, strings, |
| Off-shell remnants, and Saturation of parton ladders | |
| EV | excluded volume |
| HRG | hadron resonance gas |
| FO | first-order |
| LHC | Large Hadron Collider |
| LQCD | Lattice QCD |
| MC | Monte Carlo |
| PCE | partial chemical equilibrium |
| PF | perfect fluid |
| QCD | quantum chromodynamics |
| QGP | quark–gluon plasma |
| RHIC | Relativistic Heavy-Ion Collider |
| SO | second-order |
| UrQMD | Ultra-relativistic Quantum Molecular Dynamics (model) |
| vdW | van der Waals |
| 0+1D | temporal one-dimensional |
| 3+1D | three-spatial and temporal dimensional |
References
- Arsene, I. et al. [BRAHMS Collaboration] Quark–gluon plasma and color glass condensate at RHIC? The perspective from the BRAHMS experiment. Nucl. Phys. A 2005, 757, 1–27. [Google Scholar] [CrossRef]
- Back, B.B. et al. [PHOBOS Collaboration] The PHOBOS perspective on discoveries at RHIC. Nucl. Phys. A 2005, 757, 28–101. [Google Scholar] [CrossRef]
- Adams, J. et al. [STAR Collaboration] Experimental and theoretical challenges in the search for the quark gluon plasma: The STAR Collaboration’s critical assessment of the evidence from RHIC collision. Nucl. Phys. A 2005, 757, 102–183. [Google Scholar] [CrossRef]
- Adcox, K. et al. [PHENIX Collaboration] Formation of dense partonic matter in relativistic nucleus-nucleus collisions at RHIC: Experimental evaluation by the PHENIX collaboration. Nucl. Phys. A 2005, 757, 184–283. [Google Scholar] [CrossRef]
- Kovtun, P.; Son, D.T.; Starinets, A.O. Viscosity in strongly interacting quantum field theories from black hole physics. Phys. Rev. Lett. 2005, 94, 111601. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Redlich, K.; Stachel, J. Decoding the phase structure of QCD via particle production at high energy. Nature 2018, 561, 321–330. [Google Scholar] [CrossRef]
- Singh, C.R.; Ganesh, S.; Mishra, M. Centrality and transverse momentum dependent suppression of Υ(1S) and Υ(2S) in p-Pband Pb-Pb collisions at the CERN Large Hadron Collider. Eur. Phys. J. C 2019, 79, 147. [Google Scholar] [CrossRef]
- Singh, C.R.; Deb, S.; Sahoo, R.; Alam, J. Charmonium suppression in ultra-relativistic proton–proton collisions at LHC energies: A hint for QGP in small systems. Eur. Phys. J. C 2022, 82, 542. [Google Scholar] [CrossRef]
- Bebie, H.; Gerber, P.; Goity, J.L.; Leutwyler, H. The role of the entropy in an expanding hadronic gas. Nucl. Phys. B 1992, 378, 95–128. [Google Scholar] [CrossRef]
- Becattini, F. Universality of thermal hadron production in pp, and e+ e− collisions. arXiv 1996. [Google Scholar] [CrossRef]
- Motornenko, A.; Vovchenko, V.; Greiner, C.; Stoecker, H. Kinetic freeze-out temperature from yields of short-lived resonances. Phys. Rev. C 2020, 102, 024909. [Google Scholar] [CrossRef]
- Bernhard, J.E.; Moreland, J.S.; Bass, S.A. Bayesian estimation of the specific shear and bulk viscosity of quark–gluon plasma. Nat. Phys. 2019, 15, 1113–1117. [Google Scholar] [CrossRef]
- Parkkila, J.E.; Onnerstad, A.; Taghavi, S.F.; Mordasini, C.; Bilandzic, A.; Virta, M.; Kim, D.J. New constraints for QCD matter from improved Bayesian parameter estimation in heavy-ion collisions at LHC. Phys. Lett. B 2022, 835, 137485. [Google Scholar] [CrossRef]
- Bernhard, J.E.; Moreland, J.S.; Bass, S.A.; Liu, J.; Heinz, U. Applying Bayesian parameter estimation to relativistic heavy-ion collisions: Simultaneous characterization of the initial state and quark–gluon plasma medium. Phys. Rev. C 2016, 94, 024907. [Google Scholar] [CrossRef]
- Parkkila, J.E.; Onnerstad, A.; Kim, D.J. Bayesian estimation of the specific shear and bulk viscosity of the quark–gluon plasma with additional flow harmonic observables. Phys. Rev. C 2021, 104, 054904. [Google Scholar] [CrossRef]
- Petersen, H.; Steinheimer, J.; Burau, G.; Bleicher, M.; Stöcker, H. Fully integrated transport approach to heavy ion reactions with an intermediate hydrodynamic stage. Phys. Rev. C 2008, 78, 044901. [Google Scholar] [CrossRef]
- Lin, Z.-W.; Ko, C.M.; Li, B.-A.; Zhang, B.; Pal, S. A Multiphase transport model for relativistic heavy ion collisions. Phys. Rev. C 2005, 72, 064901. [Google Scholar] [CrossRef]
- Steinheimer, J.; Aichelin, J.; Bleicher, M.; Stöcker, H. Influence of the hadronic phase on observables in ultrarelativistic heavy ion collisions. Phys. Rev. C 2017, 95, 064902. [Google Scholar] [CrossRef]
- Knospe, A.G.; Markert, C.; Werner, K.; Steinheimer, J.; Bleicher, M. Hadronic resonance production and interaction in partonic and hadronic matter in the EPOS3 model with and without the hadronic afterburner UrQMD. Phys. Rev. C 2016, 93, 014911. [Google Scholar] [CrossRef]
- Song, H.; Bass, S.A.; Heinz, U. Viscous QCD matter in a hybrid hydrodynamic+Boltzmann approach. Phys. Rev. C 2011, 83, 024912. [Google Scholar] [CrossRef]
- Demir, N.; Bass, S.A. Shear-viscosity to entropy-density ratio of a relativistic hadron gas. Phys. Rev. Lett. 2009, 102, 172302. [Google Scholar] [CrossRef] [PubMed]
- Romatschke, P. Collective flow without hydrodynamics: Simulation results for relativistic ion collisions. Eur. Phys. J. C 2015, 75, 429. [Google Scholar] [CrossRef]
- Berges, J.; Borsányi, S.; Wetterich, C. Prethermalization. Phys. Rev. Lett. 2004, 93, 142002. [Google Scholar] [CrossRef] [PubMed]
- Romatschke, P. Relativistic fluid dynamics far from local equilibrium. Phys. Rev. Lett. 2018, 120, 012301. [Google Scholar] [CrossRef]
- Romatschke, P.; Romatschke, U. Relativistic Fluid Dynamics In and Out of Equilibrium (and Applications to Relativistic Nuclear Collisions); Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Gallmeister, K.; Niemi, H.; Greiner, C.; Rischke, D.H. Exploring the applicability of dissipative fluid dynamics to small systems by comparison to the Boltzmann equation. Phys. Rev. C 2018, 98, 024912. [Google Scholar] [CrossRef]
- Scaria, R.; Sahu, D.; Singh, C.R.; Sahoo, R.; Alam, J.-e. Fluidity of the system produced in relativistic pp and heavy-ion collisions: Hadron resonance gas model approach. Eur. Phys. J. A 2023, 59, 140. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Evidence of rescattering effect in Pb–Pb collisions at the LHC through production of K*(892)0 and ϕ(1020) mesons. Phys. Lett. B 2020, 802, 135225. [Google Scholar] [CrossRef]
- Singha, S.; Mohanty, B.; Lin, Z.-W. Studying re-scattering effect in heavy-ion collision through K* production. Int. J. Mod. Phys. E 2015, 24, 1550041. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Thermal hadron production in relativistic nuclear collisions: The Hadron mass spectrum, the horn, and the QCD phase transition. Phys. Lett. B 2009, 673, 142–145. [Google Scholar] [CrossRef]
- Cleymans, J.; Redlich, K. Chemical and thermal freeze-out parameters from 1A GeV to 200A GeV. Phys. Rev. C 1999, 60, 054908. [Google Scholar] [CrossRef]
- Chatterjee, S.; Das, S.; Kumar, L.; Mishra, D.; Mohanty, B.; Sahoo, R.; Sharma, N. Freeze-out parameters in heavy-ion collisions at AGS, SPS, RHIC, and LHC energies. Adv. High Energy Phys. 2015, 2015, 349013. [Google Scholar] [CrossRef]
- Cho, S.; Lee, S.H. Reduction of the K* meson abundance in heavy ion collisions. Phys. Rev. C 2018, 97, 034908. [Google Scholar] [CrossRef]
- Sahu, D.; Tripathy, S.; Pradhan, G.S.; Sahoo, R. Role of event multiplicity on hadronic phase lifetime and QCD phase boundary in ultrarelativistic collisions at energies available at the BNL Relativistic Heavy Ion Collider and CERN Large Hadron Collider. Phys. Rev. C 2020, 101, 014902. [Google Scholar] [CrossRef]
- Karsch, F. Lattice QCD at high temperature and density. In Lectures on Quark Matter; Plessas, W., Mathelitsch, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 209–249. [Google Scholar] [CrossRef]
- Aoki, Y.; Endrodi, G.; Fodor, Z.; Katz, S.; Szabo, K. The order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef]
- Bazavov, A. et al. [HotQCD Collaboration] Equation of state in (2+1)-flavor QCD. Phys. Rev. D 2014, 90, 094503. [Google Scholar] [CrossRef]
- Borsányi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Ratti, C.; Szabó, K.K. Is there still any Tc mystery in lattice QCD? Results with physical masses in the continuum limit III. J. High Energy Phys. 2010, 2010, 73. [Google Scholar] [CrossRef]
- Borsányi, S.; Fodor, Z.; Hoelbling, C.; Katz, S.D.; Krieg, S.; Szabó, K.K. Full result for the QCD equation of state with 2+1 flavors. Phys. Lett. B 2014, 730, 99–104. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J.; Winn, M. Interacting hadron resonance gas meets lattice QCD. Phys. Lett. B 2012, 718, 80–85. [Google Scholar] [CrossRef]
- Vovchenko, V.; Anchishkin, D.V.; Gorenstein, M.I. Hadron resonance gas equation of state from lattice QCD. Phys. Rev. C 2015, 91, 024905. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Hadron production in central nucleus-nucleus collisions at chemical freeze-out. Nucl. Phys. A 2006, 772, 167–199. [Google Scholar] [CrossRef]
- Stachel, J.; Andronic, A.; Braun-Munzinger, P.; Redlich, K. Confronting LHC data with the statistical hadronization model. J. Phys. Conf. Ser. 2014, 509, 012019. [Google Scholar] [CrossRef]
- Muronga, A. Causal theories of dissipative relativistic fluid dynamics for nuclear collisions. Phys. Rev. C 2004, 69, 034903. [Google Scholar] [CrossRef]
- Kouno, H.; Maruyama, M.; Takagi, F.; Saito, K. Relativistic hydrodynamics of quark–gluon plasma and stability of scaling solutions. Phys. Rev. D 1990, 41, 2903–2911. [Google Scholar] [CrossRef] [PubMed]
- Muronga, A. Second order dissipative fluid dynamics for ultrarelativistic nuclear collisions. Phys. Rev. Lett. 2002, 88, 062302. [Google Scholar] [CrossRef]
- Israel, W. Nonstationary irreversible thermodynamics: A causal relativistic theory. Ann. Phys. 1976, 100, 310–331. [Google Scholar] [CrossRef]
- Stewart, J.M. On transient relativistic thermodynamics and kinetic theory. Proc. R. Soc. Lond. A Math. Phys. Sci. 1977, 357, 59–75. Available online: https://www.jstor.org/stable/79453 (accessed on 22 March 2025).
- Israel, W.; Stewart, J.M. Transient relativistic thermodynamics and kinetic theory. Ann. Phys. (N.Y.) 1979, 118, 341–372. [Google Scholar] [CrossRef]
- Prakash, M.; Prakash, M.; Venugopalan, R.; Welke, G. Nonequilibrium properties of hadronic mixtures. Phys. Rep. 1993, 227, 321–366. [Google Scholar] [CrossRef]
- Kadam, G.P.; Mishra, H. Dissipative properties of hot and dense hadronic matter in an excluded-volume hadron resonance gas model. Phys. Rev. C 2015, 92, 035203. [Google Scholar] [CrossRef]
- Tiwari, S.K.; Tripathy, S.; Sahoo, R.; Kakati, N. Dissipative properties and isothermal compressibility of hot and dense hadron gas using non-extensive statistics. Eur. Phys. J. C 2018, 78, 938. [Google Scholar] [CrossRef]
- Lokhtin, I.P.; Snigirev, A.M. A model of transverse expansion of the quark gluon fluid with phase transition and hadron spectra in heavy ion collisions. Phys. Lett. B 1996, 378, 247–254. [Google Scholar] [CrossRef]
- Hanus, P.; Mazeliauskas, A.; Reygers, K. Entropy production in pp and Pb–Pb collisions at energies available at the CERN Large Hadron Collider. Phys. Rev. C 2019, 100, 064903. [Google Scholar] [CrossRef]
- Loizides, C.; Kamin, J.; d’Enterria, D. Improved Monte Carlo Glauber predictions at present and future nuclear colliders. Phys. Rev. C 2018, 97, 054910. [Google Scholar] [CrossRef]
- Bleicher, M.; Aichelin, J. Strange resonance production: Probing chemical and thermal freeze-out in relativistic heavy ion collisions. Phys. Lett. B 2002, 530, 81–87. [Google Scholar] [CrossRef]
- Torrieri, G.; Rafelski, J. Strange hadron resonances as a signature of freeze-out dynamics. Phys. Lett. B 2001, 509, 239–245. [Google Scholar] [CrossRef]
- Johnson, S.C.; Jacak, B.V.; Drees, A. Rescattering of vector meson daughters in high-energy heavy ion collisions. Eur. Phys. J. C 2001, 18, 645–649. [Google Scholar] [CrossRef]
- Ilner, A.; Blair, J.; Cabrera, D.; Markert, C.; Bratkovskaya, E. Probing the hot and dense nuclear matter with K*, vector mesons. Phys. Rev. C 2019, 99, 024914. [Google Scholar] [CrossRef]
- Thews, R.L. Quarkonium formation at high energy. Nucl. Phys. A 2002, 702, 341–345. [Google Scholar] [CrossRef]
- Thews, R.L.; Schroedter, M.; Rafelski, J. Enhanced J/ψ production in deconfined quark matter. Phys. Rev. C 2001, 63, 054905. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J.; Stocker, H. Production of light nuclei, hypernuclei and their antiparticles in relativistic nuclear collisions. Phys. Lett. B 2011, 697, 203–207. [Google Scholar] [CrossRef]
- Yang, K.; Xu, X.-M.; Weber, H.J. Cross sections for inelastic meson–meson scattering. Phys. Rev. D 2017, 96, 114025. [Google Scholar] [CrossRef]
- Li, W.-X.; Xu, X.-M.; Weber, H.J. Cross sections for 2-to-1 meson–meson scattering. Eur. Phys. J. C 2021, 81, 225. [Google Scholar] [CrossRef]
- Nendzig, F.; Wolschin, G. Bottomium suppression in PbPb collisions at LHC energies. J. Phys. G 2014, 41, 095003. [Google Scholar] [CrossRef][Green Version]
- Hoelck, J.; Nendzig, F.; Wolschin, G. In-medium Υ suppression and feed-down in UU and PbPb collisions. Phys. Rev. C 2017, 95, 024905. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Production of charged pions, kaons, and (anti-)protons in Pb–Pb and inelastic pp collisions at = 5.02 TeV. Phys. Rev. C 2020, 101, 044907. [Google Scholar] [CrossRef]
- Navas, S. et al. [Particle Data Group] Review of Particle Physics. Phys Rev D 2024, 110, 030001. [Google Scholar] [CrossRef]
- Aggarwal, M.M. et al. [STAR Collaboration] K*0 production in Cu+Cu and Au+Au collisions at = 62.4 GeV and 200 GeV. Phys. Rev. C 2011, 84, 034909. [Google Scholar] [CrossRef]
- Acharya, S. et al. [ALICE Collaboration] Production of the ρ(770)0 meson in pp and Pb–Pb collisions at = 2.76 TeV. Phys. Rev. C 2019, 99, 064901. [Google Scholar] [CrossRef]
- Abelev, B.I. et al. [STAR Collaboration] Measurements of ϕ meson production in relativistic heavy-ion collisions at the BNL Realtivistic Heavy Ion Collider (RHIC). Phys. Rev. C 2009, 79, 064903. [Google Scholar] [CrossRef]
- Abelev, B.B. et al. [ALICE Collaboration] K*(892)0 and ϕ(1020) production in Pb–Pb collisions at = 2.76 TeV. Phys. Rev. C 2015, 91, 024609. [Google Scholar] [CrossRef]
- Pradhan, G.S.; Rath, R.; Scaria, R.; Sahoo, R. Exploring the effect of hadron cascade time on particle production in Xe + Xe collisions at =5.44 TeV using a multiphase transport model. Phys. Rev. C 2022, 105, 054905. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scaria, R.; Singh, C.R.; Sahoo, R. Applicability of Hydrodynamics in the Hadronic Phase of Heavy-Ion Collisions. Physics 2025, 7, 13. https://doi.org/10.3390/physics7020013
Scaria R, Singh CR, Sahoo R. Applicability of Hydrodynamics in the Hadronic Phase of Heavy-Ion Collisions. Physics. 2025; 7(2):13. https://doi.org/10.3390/physics7020013
Chicago/Turabian StyleScaria, Ronald, Captain R. Singh, and Raghunath Sahoo. 2025. "Applicability of Hydrodynamics in the Hadronic Phase of Heavy-Ion Collisions" Physics 7, no. 2: 13. https://doi.org/10.3390/physics7020013
APA StyleScaria, R., Singh, C. R., & Sahoo, R. (2025). Applicability of Hydrodynamics in the Hadronic Phase of Heavy-Ion Collisions. Physics, 7(2), 13. https://doi.org/10.3390/physics7020013