SU(2)-Symmetric Exactly Solvable Models of Two Interacting Qubits
Abstract
1. Introduction
2. The Model
2.1. SU(2) Symmetry
2.2. SU(2) Two-Qubit Model
3. Dynamical Scenarios
3.1. Time-Independent Case
3.2. Rabi Scenario
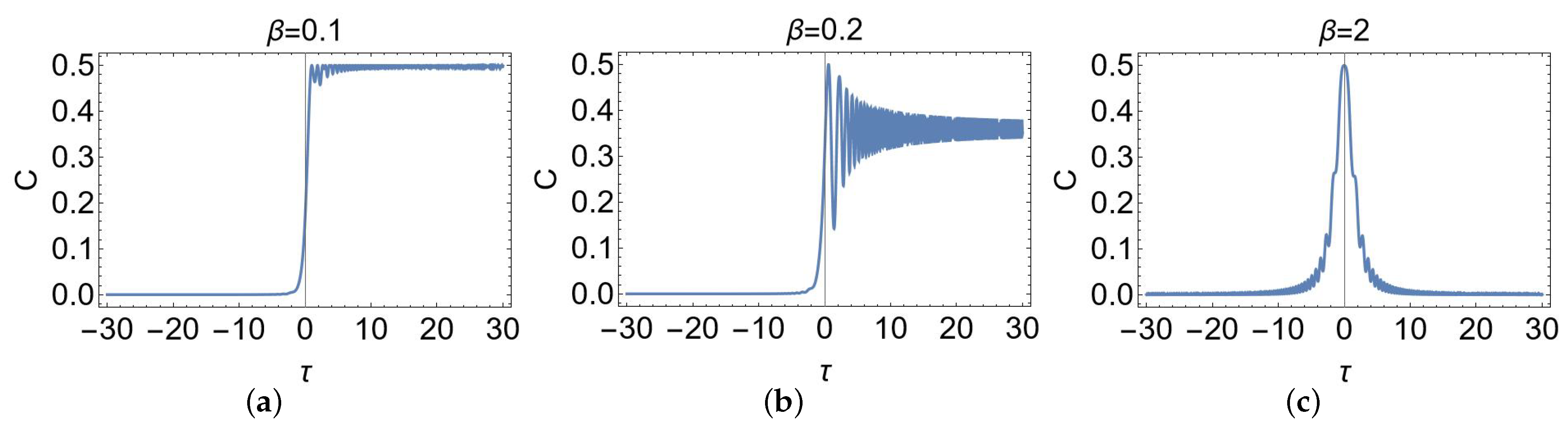
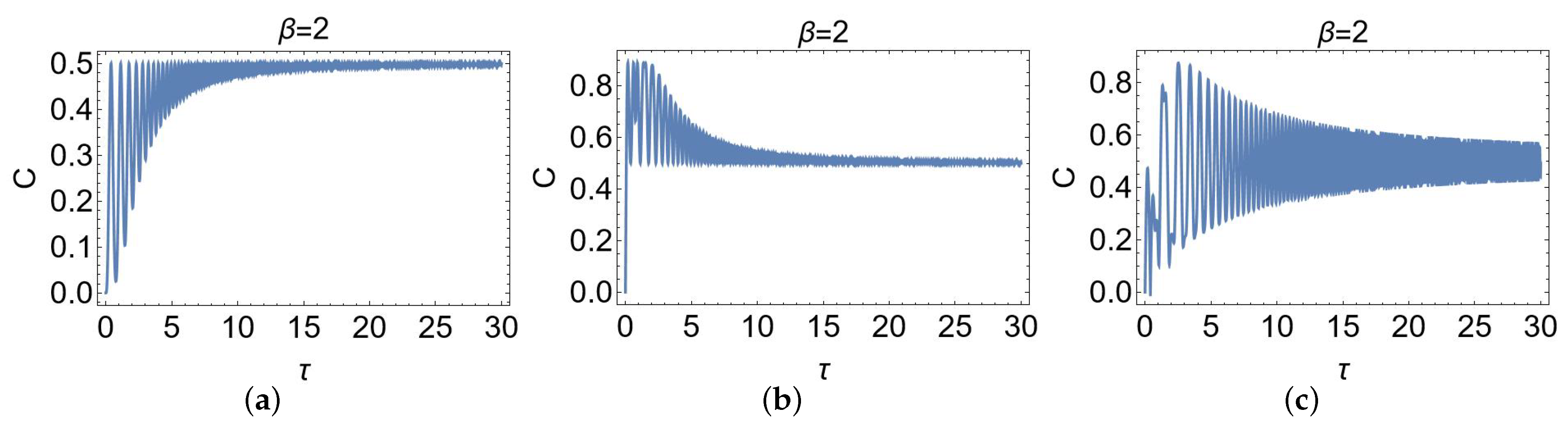
3.3. Landau–Majorana-Stückelberg–Zener Scenario
3.4. Two-Qubit Spin–Flip and Phase Gate Realization
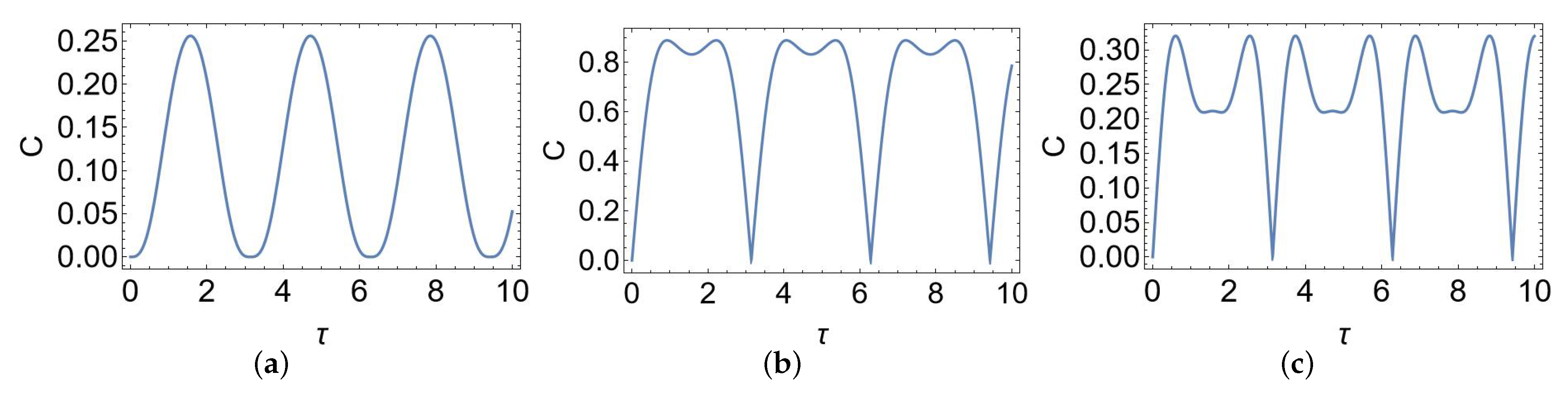
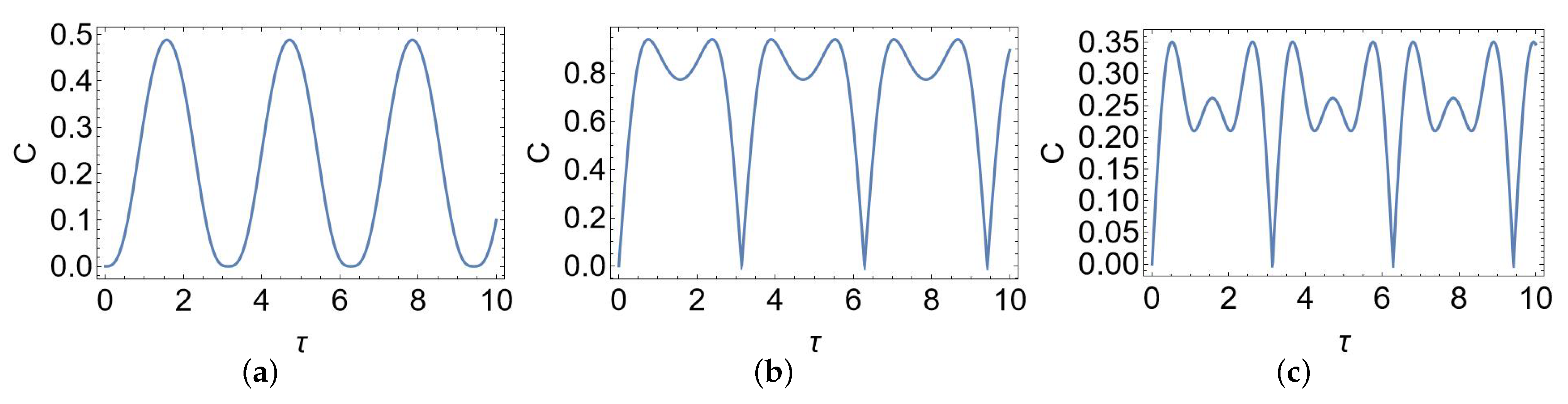
4. Concurrence Dynamics
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the SU(2) Two-Qubit Model
References
- Dell’Anno, F.; De Siena, S.; Illuminati, F. Multiphoton quantum optics and quantum state engineering. Phys. Rep. 2006, 428, 53–168. [Google Scholar] [CrossRef]
- Shevchenko, S.; Ashhab, S.; Nori, F. Landau–Zener–Stückelberg interferometry. Phys. Rep. 2010, 492, 1–30. [Google Scholar] [CrossRef]
- Ivakhnenko, O.V.; Shevchenko, S.N.; Nori, F. Nonadiabatic Landau–Zener–Stückelberg–Majorana transitions, dynamics, and interference. Phys. Rep. 2023, 995, 1–89. [Google Scholar] [CrossRef]
- Newton, M.D. Quantum chemical probes of electron-transfer kinetics: The nature of donor-acceptor interactions. Chem. Rev. 1991, 91, 767–792. [Google Scholar] [CrossRef]
- Gupta, S.; Yang, J.H.; Yakobson, B.I. Two-level quantum systems in two-dimensional materials for single photon emission. Nano Lett. 2018, 19, 408–414. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Kelkar, H.; Martin-Cano, D.; Rattenbacher, D.; Shkarin, A.; Utikal, T.; Götzinger, S.; Sandoghdar, V. Turning a molecule into a coherent two-level quantum system. Nat. Phys. 2019, 15, 483–489. [Google Scholar]
- Migliore, A. Nonorthogonality problem and effective electronic coupling calculation: Application to charge transfer in π-stacks relevant to biochemistry and molecular electronics. J. Chem. Theo. Comput. 2011, 7, 1712–1725. [Google Scholar] [CrossRef] [PubMed]
- Migliore, A.; Messina, A. Controlling the charge-transfer dynamics of two-level systems around avoided crossings. J. Chem. Phys. 2024, 160, 084112. [Google Scholar] [CrossRef]
- McArdle, S.; Endo, S.; Aspuru-Guzik, A.; Benjamin, S.C.; Yuan, X. Quantum computational chemistry. Rev. Mod. Phys. 2020, 92, 015003. [Google Scholar] [CrossRef]
- Koch, C.P.; Boscain, U.; Calarco, T.; Dirr, G.; Filipp, S.; Glaser, S.J.; Kosloff, R.; Montangero, S.; Schulte-Herbrüggen, T.; Sugny, D.; et al. Quantum optimal control in quantum technologies. Strategic report on current status, visions and goals for research in Europe. EPJ Quant. Technol. 2022, 9, 19. [Google Scholar] [CrossRef]
- Chiavazzo, S.; Sørensen, A.S.; Kyriienko, O.; Dellantonio, L. Quantum manipulation of a two-level mechanical system. Quantum 2023, 7, 943. [Google Scholar] [CrossRef]
- Chu, Y.; Liu, Y.; Liu, H.; Cai, J. Quantum sensing with a single-qubit pseudo-Hermitian system. Phys. Rev. Lett. 2020, 124, 020501. [Google Scholar] [CrossRef]
- Hönigl-Decrinis, T.; Shaikhaidarov, R.; de Graaf, S.; Antonov, V.; Astafiev, O. Two-level system as a quantum sensor for absolute calibration of power. Phys. Rev. Appl. 2020, 13, 024066. [Google Scholar] [CrossRef]
- Jafarizadeh, M.; Naghdi, F.; Bazrafkan, M. Time optimal control of two-level quantum systems. Phys. Lett. A 2020, 384, 126743. [Google Scholar] [CrossRef]
- Feng, T.; Xu, Q.; Zhou, L.; Luo, M.; Zhang, W.; Zhou, X. Quantum information transfer between a two-level and a four-level quantum systems. Photonics Res. 2022, 10, 2854–2865. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, X.; Wang, J.; Jing, J. Quantum metrology of phase for accelerated two-level atom coupled with electromagnetic field with and without boundary. Quant. Inf. Process. 2018, 17, 54. [Google Scholar] [CrossRef]
- Pezzè, L.; Smerzi, A.; Oberthaler, M.K.; Schmied, R.; Treutlein, P. Quantum metrology with nonclassical states of atomic ensembles. Rev. Mod. Phys. 2018, 90, 035005. [Google Scholar] [CrossRef]
- Bagrov, V.G.; Gitman, D.M.; Baldiotti, M.C.; Levin, A.D. Spin equation and its solutions. Ann. Phys. 2005, 517, 764–789. [Google Scholar] [CrossRef]
- Kuna, M.; Naudts, J. General solutions of quantum mechanical equations of motion with time-dependent hamiltonians: A lie algebraic approach. Rep. Math. Phys. 2010, 65, 77–108. [Google Scholar] [CrossRef]
- Barnes, E.; Sarma, S.D. Analytically solvable driven time-dependent two-level quantum systems. Phys. Rev. Lett. 2012, 109, 060401. [Google Scholar] [CrossRef]
- Messina, A.; Nakazato, H. Analytically solvable Hamiltonians for quantum two-level systems and their dynamics. J. Phys. A Math. Theor. 2014, 47, 445302. [Google Scholar] [CrossRef]
- Markovich, L.; Grimaudo, R.; Messina, A.; Nakazato, H. An example of interplay between physics and mathematics: Exact resolution of a new class of Riccati equations. Ann. Phys. 2017, 385, 522–531. [Google Scholar] [CrossRef]
- Liang, H. Generating arbitrary analytically solvable two-level systems. J. Phys. A Math. Theor. 2024, 57, 095301. [Google Scholar] [CrossRef]
- Castaños, L. Simple, analytic solutions of the semiclassical Rabi model. Opt. Commun. 2019, 430, 176–188. [Google Scholar] [CrossRef]
- Castaños, L. A simple, analytic solution of the semiclassical Rabi model in the red-detuned regime. Phys. Lett. A 2019, 383, 1997–2003. [Google Scholar] [CrossRef]
- Rabi, I.I. Space quantization in a gyrating magnetic field. Phys. Rev. 1937, 51, 652–654. [Google Scholar] [CrossRef]
- Landau, L.D. A theory of energy transfer II. Phys. Z. Sowjetun. 1932, 2, 46–51, Reprinted in Collected Papers of L.D. Landau; Ter Haar, D., Ed.; Pergamon Press Ltd.: Oxford, UK; Gordon and Breach, Science Publishers Inc.: New York, NY, USA, 1965; pp. 63–66. [Google Scholar] [CrossRef]
- Majorana, E. Atomi orientati in campo magnetico variabile. Nuovo Cim. 1932, 9, 43–50. [Google Scholar] [CrossRef]
- Stückelberg, E.C.G. Theorie der unelastischen Stösse zwischen Atomen. Helv. Phys. Acta 1932, 5, 369–422. Available online: https://www.e-periodica.ch/digbib/view?pid=hpa-001%3A1932%3A5%3A%3A5#373 (accessed on 10 August 2024).
- Stückelberg, E.C.G. Theory of Inelastic Collisions between Atoms; Report NASA TT F-13,970; National Aerounatics Space Administration: Washington, DC, USA, 1971; Available online: https://archive.org/details/nasa_techdoc_19720003957 (accessed on 10 August 2024).
- Zener, C. Non-adiabatic crossing of energy levels. Proc. R. Soc. London. A Math. Phys. Engin. Sci. 1932, 137, 696–702. [Google Scholar] [CrossRef]
- Grimaudo, R.; Man’ko, V.I.; Man’ko, M.A.; Messina, A. Dynamics of a harmonic oscillator coupled with a Glauber amplifier. Phys. Scr. 2019, 95, 024004. [Google Scholar] [CrossRef]
- Grimaudo, R.; de Castro, A.S.M.; Nakazato, H.; Messina, A. Analytically solvable 2×2 PT-symmetry dynamics from su(1,1)-symmetry problems. Phys. Rev. A 2019, 99, 052103. [Google Scholar] [CrossRef]
- Calvo, R.; Abud, J.E.; Sartoris, R.P.; Santana, R.C. Collapse of the EPR fine structure of a one-dimensional array of weakly interacting binuclear units: A dimensional quantum phase transition. Phys. Rev. B 2011, 84, 104433. [Google Scholar] [CrossRef]
- Napolitano, L.M.B.; Nascimento, O.R.; Cabaleiro, S.; Castro, J.; Calvo, R. Isotropic and anisotropic spin-spin interactions and a quantum phase transition in a dinuclear Cu(II) compound. Phys. Rev. B 2008, 77, 214423. [Google Scholar] [CrossRef]
- Kang, Y.-H.; Chen, Y.-H.; Wu, Q.-C.; Huang, B.-H.; Song, J.; Xia, Y. Fast generation of W states of superconducting qubits with multiple Schrödinger dynamics. Sci. Rep. 2016, 6, 36737. [Google Scholar] [CrossRef]
- Lu, M.; Xia, Y.; Song, J.; An, N.B. Generation of N-atom W-class states in spatially separated cavities. J. Opt. Soc. Am. B 2013, 30, 2142–2147. [Google Scholar] [CrossRef]
- Li, J.; Paraoanu, G.S. Generation and propagation of entanglement in driven coupled-qubit systems. New J. Phys. 2009, 11, 113020. [Google Scholar] [CrossRef]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517–576. [Google Scholar] [CrossRef]
- Morzhin, O.V.; Pechen, A.N. Optimal state manipulation for a two-qubit system driven by coherent and incoherent controls. Quant. Inf. Process. 2023, 22, 241. [Google Scholar] [CrossRef]
- Ding, L.; Hays, M.; Sung, Y.; Kannan, B.; An, J.; Di Paolo, A.; Karamlou, A.H.; Hazard, T.M.; Azar, K.; Kim, D.K.; et al. High-fidelity, frequency-flexible two-qubit fluxonium gates with a transmon coupler. Phys. Rev. X 2023, 13, 031035. [Google Scholar] [CrossRef]
- Schäfter, D.; Wischnat, J.; Tesi, L.; De Sousa, J.A.; Little, E.; McGuire, J.; Mas-Torrent, M.; Rovira, C.; Veciana, J.; Tuna, F.; et al. Molecular one-and two-qubit systems with very long coherence times. Adv. Mater. 2023, 35, 2302114. [Google Scholar] [CrossRef] [PubMed]
- Mills, A.R.; Guinn, C.R.; Gullans, M.J.; Sigillito, A.J.; Feldman, M.M.; Nielsen, E.; Petta, J.R. Two-qubit silicon quantum processor with operation fidelity exceeding 99%. Sci. Adv. 2022, 8, eabn5130. [Google Scholar] [CrossRef]
- Petit, L.; Russ, M.; Eenink, G.H.; Lawrie, W.I.; Clarke, J.S.; Vandersypen, L.M.; Veldhorst, M. Design and integration of single-qubit rotations and two-qubit gates in silicon above one kelvin. Commun. Mater. 2022, 3, 82. [Google Scholar] [CrossRef]
- Noiri, A.; Takeda, K.; Nakajima, T.; Kobayashi, T.; Sammak, A.; Scappucci, G.; Tarucha, S. A shuttling-based two-qubit logic gate for linking distant silicon quantum processors. Nat. Commun. 2022, 13, 5740. [Google Scholar] [CrossRef] [PubMed]
- Moskalenko, I.N.; Simakov, I.A.; Abramov, N.N.; Grigorev, A.A.; Moskalev, D.O.; Pishchimova, A.A.; Smirnov, N.S.; Zikiy, E.V.; Rodionov, I.A.; Besedin, I.S. High fidelity two-qubit gates on fluxoniums using a tunable coupler. NPJ Quant. Inf. 2022, 8, 130. [Google Scholar] [CrossRef]
- Bresque, L.; Camati, P.A.; Rogers, S.; Murch, K.; Jordan, A.N.; Auffèves, A. Two-qubit engine fueled by entanglement and local measurements. Phys. Rev. Lett. 2021, 126, 120605. [Google Scholar] [CrossRef]
- Cai, T.Q.; Han, X.Y.; Wu, Y.K.; Ma, Y.L.; Wang, J.H.; Wang, Z.L.; Zhang, H.Y.; Wang, H.Y.; Song, Y.P.; Duan, L.M. Impact of spectators on a two-qubit gate in a tunable coupling superconducting circuit. Phys. Rev. Lett. 2021, 127, 060505. [Google Scholar] [CrossRef]
- Blümel, R.; Grzesiak, N.; Nguyen, N.H.; Green, A.M.; Li, M.; Maksymov, A.; Linke, N.M.; Nam, Y. Efficient stabilized two-qubit gates on a trapped-ion quantum computer. Phys. Rev. Lett. 2021, 126, 220503. [Google Scholar] [CrossRef]
- Gu, X.; Fernández-Pendás, J.; Vikstål, P.; Abad, T.; Warren, C.; Bengtsson, A.; Tancredi, G.; Shumeiko, V.; Bylander, J.; Johansson, G.; et al. Fast multiqubit gates through simultaneous two-qubit gates. PRX Quantum 2021, 2, 040348. [Google Scholar] [CrossRef]
- Foxen, B.; Neill, C.; Dunsworth, A.; Roushan, P.; Chiaro, B.; Megrant, A.; Kelly, J.; Chen, Z.; Satzinger, K.; Barends, R.; et al. Demonstrating a continuous set of two-qubit gates for near-term quantum algorithms. Phys. Rev. Lett. 2020, 125, 120504. [Google Scholar] [CrossRef]
- Xu, Y.; Chu, J.; Yuan, J.; Qiu, J.; Zhou, Y.; Zhang, L.; Tan, X.; Yu, Y.; Liu, S.; Li, J.; et al. High-fidelity, high-scalability two-qubit gate scheme for superconducting qubits. Phys. Rev. Lett. 2020, 125, 240503. [Google Scholar] [CrossRef]
- von Lüpke, U.; Beaudoin, F.; Norris, L.M.; Sung, Y.; Winik, R.; Qiu, J.Y.; Kjaergaard, M.; Kim, D.; Yoder, J.; Gustavsson, S.; et al. Two-qubit spectroscopy of spatiotemporally correlated quantum noise in superconducting qubits. PRX Quantum 2020, 1, 010305. [Google Scholar] [CrossRef]
- Hendrickx, N.; Franke, D.; Sammak, A.; Scappucci, G.; Veldhorst, M. Fast two-qubit logic with holes in germanium. Nature 2020, 577, 487–491. [Google Scholar] [CrossRef]
- Wie, C.R. Two-qubit bloch sphere. Physics 2020, 2, 383–396. [Google Scholar] [CrossRef]
- Watson, T.; Philips, S.; Kawakami, E.; Ward, D.; Scarlino, P.; Veldhorst, M.; Savage, D.; Lagally, M.; Friesen, M.; Coppersmith, S.; et al. A programmable two-qubit quantum processor in silicon. Nature 2018, 555, 633–637. [Google Scholar] [CrossRef] [PubMed]
- Veldhorst, M.; Yang, C.; Hwang, J.; Huang, W.; Dehollain, J.; Muhonen, J.; Simmons, S.; Laucht, A.; Hudson, F.; Itoh, K.M.; et al. A two-qubit logic gate in silicon. Nature 2015, 526, 410–414. [Google Scholar] [CrossRef] [PubMed]
- DiCarlo, L.; Chow, J.M.; Gambetta, J.M.; Bishop, L.S.; Johnson, B.R.; Schuster, D.; Majer, J.; Blais, A.; Frunzio, L.; Girvin, S.; et al. Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 2009, 460, 240–244. [Google Scholar] [CrossRef] [PubMed]
- Grimaudo, R.; Messina, A.; Nakazato, H. Exactly solvable time-dependent models of two interacting two-level systems. Phys. Rev. A 2016, 94, 022108. [Google Scholar] [CrossRef]
- Grimaudo, R.; Vitanov, N.V.; Messina, A. Coupling-assisted Landau-Majorana-Stückelberg-Zener transition in a system of two interacting spin qubits. Phys. Rev. B 2019, 99, 174416. [Google Scholar] [CrossRef]
- Ghiu, I.; Grimaudo, R.; Mihaescu, T.; Isar, A.; Messina, A. Quantum correlation dynamics in controlled two-coupled-qubit systems. Entropy 2020, 22, 785. [Google Scholar] [CrossRef]
- Grimaudo, R.; Isar, A.; Mihaescu, T.; Ghiu, I.; Messina, A. Dynamics of quantum discord of two coupled spin-1/2’s subjected to time-dependent magnetic fields. Res. Phys. 2019, 13, 102147. [Google Scholar] [CrossRef]
- Grimaudo, R.; de Castro, A.S.M.d.; Messina, A.; Solano, E.; Valenti, D. Quantum phase transitions for an integrable quantum Rabi-like model with two interacting qubits. Phys. Rev. Lett. 2023, 130, 043602. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Sol. 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91–98. [Google Scholar] [CrossRef]
- Weil, J.A.; Bolton, J.R. Electron Paramagnetic Resonance: Elementary Theory and Practical Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Krantz, P.; Kjaergaard, M.; Yan, F.; Orlando, T.P.; Gustavsson, S.; Oliver, W.D. A quantum engineer’s guide to superconducting qubits. Appl. Phys. Rev. 2019, 6, 021318. [Google Scholar] [CrossRef]
- Vitanov, N.V.; Garraway, B.M. Landau–Zener model: Effects of finite coupling duration. Phys. Rev. A 1996, 53, 4288–4304. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions. With Formulas, Graphs, and Mathematical Tables; Dover Publications, Inc.: New York, NY, USA, 1972; Available online: https://archive.org/details/handbookofmathe000abra/ (accessed on 10 August 2024).
- Grimaudo, R.; Vitanov, N.V.; Messina, A. Landau-Majorana-Stückelberg-Zener dynamics driven by coupling for two interacting qutrit systems. Phys. Rev. B 2019, 99, 214406. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80, 2245–2248. [Google Scholar] [CrossRef]
- Cafaro, C.; Alsing, P.M. Continuous-time quantum search and time-dependent two-level quantum systems. Int. J. Quant. Inf. 2019, 17, 1950025. [Google Scholar] [CrossRef]
- Cafaro, C.; Gassner, S.; Alsing, P.M. Information geometric perspective on off-resonance effects in driven two-level quantum systems. Quant. Rep. 2020, 2, 166–188. [Google Scholar] [CrossRef]
- Cafaro, C.; Alsing, P.M. Information geometry aspects of minimum entropy production paths from quantum mechanical evolutions. Phys. Rev. E 2020, 101, 022110. [Google Scholar] [CrossRef] [PubMed]
- Gassner, S.; Cafaro, C.; Ali, S.A.; Alsing, P.M. Information geometric aspects of probability paths with minimum entropy production for quantum state evolution. Int. J. Geom. Meth. Mod. Phys. 2021, 18, 2150127. [Google Scholar] [CrossRef]
- Casado-Pascual, J.; Lamata, L.; Reynoso, A.A. Spin dynamics under the influence of elliptically rotating fields: Extracting the field topology from time-averaged quantities. Phys. Rev. E 2021, 103, 052139. [Google Scholar] [CrossRef]
- Cafaro, C.; Ray, S.; Alsing, P.M. Complexity and efficiency of minimum entropy production probability paths from quantum dynamical evolutions. Phys. Rev. E 2022, 105, 034143. [Google Scholar] [CrossRef] [PubMed]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grimaudo, R. SU(2)-Symmetric Exactly Solvable Models of Two Interacting Qubits. Physics 2024, 6, 1111-1123. https://doi.org/10.3390/physics6030069
Grimaudo R. SU(2)-Symmetric Exactly Solvable Models of Two Interacting Qubits. Physics. 2024; 6(3):1111-1123. https://doi.org/10.3390/physics6030069
Chicago/Turabian StyleGrimaudo, Roberto. 2024. "SU(2)-Symmetric Exactly Solvable Models of Two Interacting Qubits" Physics 6, no. 3: 1111-1123. https://doi.org/10.3390/physics6030069
APA StyleGrimaudo, R. (2024). SU(2)-Symmetric Exactly Solvable Models of Two Interacting Qubits. Physics, 6(3), 1111-1123. https://doi.org/10.3390/physics6030069




