Discovering Bohr’s Yin-Yang Diagram in Quantum Tunneling Dynamics

Abstract

On 17 October 1947, Niels Bohr was made a knight of the Order of the Elephant by the King of Denmark in view of his outstanding achievements and contributions to science. Bohr designed his own coat of arms that featured a pattern of Yin and Yang (Tai Chi symbol) to symbolize the wave–particle complementarity. However, Bohr’s Yin-Yang diagram (YYD) was neither drawn based on the principles of quantum mechanics, nor did it originate from the traditional Taoist YYD. Scientists still have doubts about the legitimacy of using YYD as the icon of the wave–particle complementarity, because the YYD belonging to quantum mechanics itself is unknown so far. This paper reports the YYDs existing in quantum mechanics and justifies the role of YYD in the wave–particle duality by showing that any system, whether classical or quantum, has an ideal YYD as long as it satisfies Bohr’s principle of complementarity (BPC). The deviation of a deformed YYD from the ideal YYD indicates the extent to which a real system satisfies BPC. This paper constructs the quantum YYD by the complex quantum trajectory of a particle tunneling via a step barrier, which displays the continuous transition between the wave behavior and the particle behavior. It appears that the YYD designed by Bohr in his coat of arms resembles the YYD generated by tunneling motion, not only in appearance but also in the governing equation.

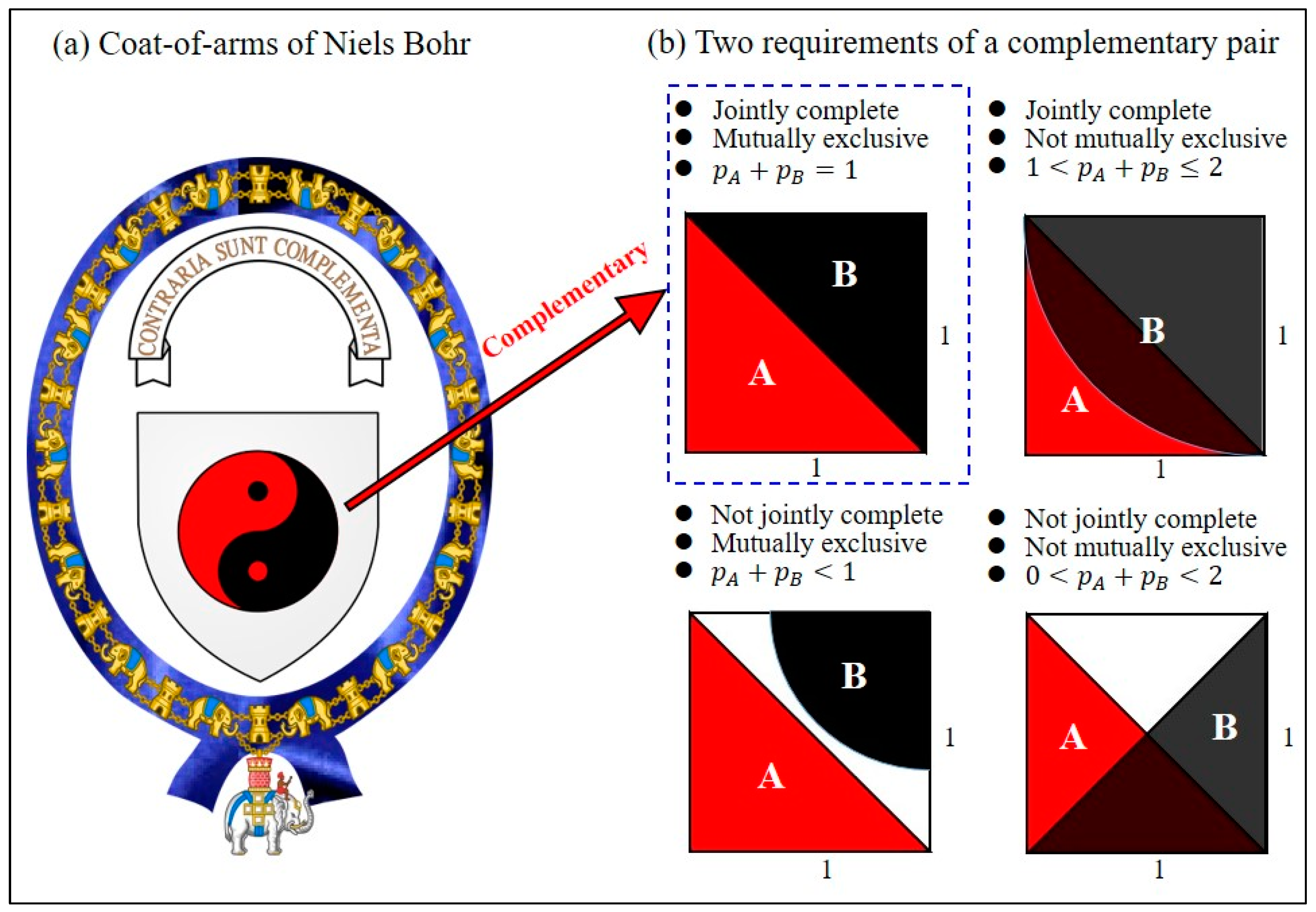
1. Introduction

Before Niels Bohr, the principle of complementarity had appeared in many intellectual disciplines, dating as far back as Yin-Yang thought in ancient China more than 3000 years ago. Yin and Yang elements appear in pairs, called the complementary pairs, such as the moon and the sun, female and male, dark and bright, cold and hot, passive and active, and so on. Complementary elements are opposite in nature yet rely on each other to exist. Bohr was the first person to introduce the principle of complementarity into the world of physics and regarded it as a universal principle. Bohr’s principle of complementarity (BPC) holds that objects have certain pairs of complementary properties which cannot all be observed or measured simultaneously. Using one particular piece of apparatus, only one of the features could be made manifest at the expense of the other.

Taoist Yin-Yang diagram (YYD), which is also known as Tai Chi symbol in China [1,2], is a graphical demonstration of the complementary Yin-Yang pair by means of areas in black and red to display their interlaced changes within a period (see Figure 1a). Why Bohr used this ancient symbol to represent his principle of complementarity [3] has remained a mystery for nearly eighty years. Except for philosophical or even religious connections, physicists have so far found no scientific clues to substantiate Bohr’s original ideas [4]. The key reason why this mystery has not been solved for many years is because physicists and even Bohr himself have no idea how to create the YYD from the principle of complementarity. Taoist YYD is a graphic representation of the ancient Chinese version of the principle of complementarity [5]. However, Taoist YYD has no unified form, and Chinese scholars of various dynasties have proposed different methods for the drawing of Taoist YYD. Different complementary pairs will derive different forms of YYD, so there is indeed no YYD that can uniquely represent BPC. Although the forms of YYD are quite diverse, these different forms of YYD have common characteristics. This paper proposes the common rules in the construction of various YYDs. The ancient Taoist YYD and the quantum YYDs of wave–particle duality and tunneling effect can all be constructed by the proposed common rules. The resulting YYDs are all concrete realizations of the idea of complementarity, and any one of them can be used as a symbol of BPC.

As shown in Figure 1, the areas occupied by red and black in Taoist YYD serve as the quantitative indices $p_A$ and $p_B$ for the state A (Yang) and state B (Yin), respectively. Using the two indices $p_A$ and $p_B$, the two properties of BPC, i.e., joint completeness and mutual exclusion, can be expressed quantitatively.

YYD is a graphical indicator that reflects the degree to which a system satisfies the principle of complementarity, and it is present in almost every system in nature, whether classical or quantum. What Bohr could not have imagined was that he did not need to borrow Taoist YYD to convey his principle of complementarity, because the principle of complementarity is the theoretical foundation of Taoist YYD. This study reverses Bohr’s idea by applying the definition of YYD to reproduce Taoist YYD, which is an ideal YYD satisfying BPC, and using the same definition to construct the YYDs belonging to quantum mechanics itself. The results obtained here reveal that the YYD designed by Bohr in his coat of arms is different from Taoist YYD but is close to the quantum YYD based on tunneling effect.

Taoist YYD contains two states: Yin and Yang, whose magnitudes wax and wane over time, but their sum remains constant, hence forming a pattern like two fish rotating around each other within a circle. The Yin-Yang states in Taoist YYD are a complementary pair possessing three properties. The first property is that they are jointly complete, that is, the two states constitute the entire system. The second property is that they are mutually exclusive, that is, there is no intersection or interference between the two states. The combination of the above two properties indicates that the Yin-Yang states satisfy BPC [7], which can be expressed as $p_A+p_B=1$ in terms of the quantitative measures $p_A$ and $p_B$ (see Figure 1b). The third property of the Yin-Yang pair is that the pair remains complementary over a complete period, i.e., $p_A\left(t\right)+p_B\left(t\right)=1$, $0\le t\le T$. The YYD composed of the Yin-Yang states having the above three properties is said to be an ideal YYD. The traditional Taoist YYD is a typical example of ideal YYDs, and this paper reveals two ideal YYDs emerging from quantum mechanics, one from two-path interference experiments and the other from quantum tunneling dynamics.

The complementary pair $(A,B)$ that Bohr considered includes: (i) position and momentum, (ii) spin on different axes, (iii) wave nature and particle nature of a quanton, (iv) value of a field and its change, (v) entanglement and coherence, and (vi) photon polarization. Among these complementary pairs, the most discussed is the particle nature and the wave nature of a quanton, whose relationship with BPC has been tested by many experiments in recent decades. In these experiments, the quantitative measures for the complementary pair are given by $\left(p_A,p_B\right)=(D^2,V^2)$, where $D$ is the distinguishability of the which-way information, and $V$ is visibility of wave fringe measured by the Mach–Zehnder interferometer (MZI) [8,9]. The manifested wave and/or particle property of the tested quantons depend on the detecting devices used in the experiments. In the all-or-nothing cases [10,11,12], quantons behave as a particle ($p_A=1$ and $p_B=0$) or as a wave ($p_A=0$ and $p_B=1$), while in the intermediate cases [13,14,15,16], quantons behave simultaneously as a particle and as a wave, whose quantitative measures satisfy the inequality $p_A+p_B\le 1$. It was further verified [17] that the equality $p_A+p_B=1$ holds if the tested quantons have no internal degree of freedom, for which the conditions of joint completeness and mutual exclusion are both met.

In recent years, the advancement of quantum beam splitters [18] has allowed the MZI to be set in a state of quantum superposition of “on” and “off” such that the wave and particle behaviors of a single photon can coexist simultaneously, with a continuous morphing between them. Unlike the classical MZI, where the wave nature and the particle nature are treated independently, the wave and particle natures of a single quanton in the setup of quantum MZI become quantum states [19,20] so that there can be interference between them. The interference between the wave state and the particle state in the quantum MZI implies that they are not mutually exclusive and cannot form a qualified complementary pair $(A,B)$, for which the violation of the complementarity, $1<p_A+p_B\le 2$, has been experimentally observed [21,22].

Although BPC has been tested by numerous experiments, these experiments still cannot tell us why Bohr used the YYD to symbolize his principle. As a first point, this paper constructs the ideal YYD and the deformed YYD from the experimental data $\left(p_A,p_B\right)=(D^2,V^2)$. According to the difference between the ideal YYD and the deformed YYD, one can judge the extent to which the experimental results satisfy the principle of complementarity. Interestingly, the ideal YYD constructed by the two-path interference experiment is closer to the traditional Taoist YYD but different from the YYD designed by Bohr in his coat of arms. This finding prompts us to explore another complementary pair in order to more closer represent Bohr’s YYD.

The finding of a more suitable complementary pair is inspired by the quantum tunneling motion of a quanton via a step barrier, wherein one finds that the changes in the quanton’s real velocity ${\dot{x}}_R$ and imaginary velocity ${\dot{x}}_I$ synchronously reflect the alternating changes in its particle nature and wave nature. It was pointed out that the wave–particle duality is a direct result of quantum motion occurring in complex space [23,24,25]. The validity of the complex-trajectory interpretation of wave–particle duality is further supported by the recent findings of weak measurements, which reveal that every physical observable has a real part as well as an imaginary part [26,27]. Similar to the entanglement, the imaginarity has been recognized as an indispensable resource responsible for quantum advantages [28,29,30], which has ruled out the real-valued standard formalism of quantum theory [31]. When a quanton exhibits particle behavior, the real component $x_R$ alone is sufficient to describe its motion, as treated in classical mechanics. But when a quanton’s motion exhibits wave behavior, the imaginary component $x_I$ is also needed to describe its motion. The results obtained reveal that the quantum YYD constructed by the complementary pair $\left(p_A,p_B\right)=({\dot{x}}_R^2,{\dot{x}}_I^2)$ is closer to Bohr’s YYD than the YYD constructed by the complementary pair $\left(p_A,p_B\right)=(D^2,V^2)$.

In what follows, first the general YYD and the ideal YYD are defined in Section 2 and it is shown that the traditional Taoist YYD is the oldest example of the ideal YYD satisfying BPC. With $\left(p_A,p_B\right)=(D^2,V^2)$, Section 3 constructs the quantum YYD by the data of the two-path interference experiments, from which the similarity between Taoist YYD and the interference-based YYD is shown. Section 4 introduces the mapping between the complex tunneling trajectory and the quantum YYD for a particle’s tunneling motion via a step barrier. The particle’s tunneling trajectories are solved by quantum Hamilton mechanics [32] in Section 5 to yield the particle’s complex position $x_R+\mathrm{i}{x}_I$ and complex velocity ${\dot{x}}_R+\mathrm{i}{\dot{x}}_I$ by which the tunneling-based YYD is then generated. The obtained tunneling-based YYD is a graphical recorder of the particle’s tunneling dynamics, which moves together with the particle, recording the velocity of the particle, and presenting it graphically, as demonstrated in Section 6. The tunneling-based YYD is not always an ideal YYD, and how its shape evolves with the intensity of the tunneling effect is discussed in Section 7. Section 8 compares the four different YYDs considered in this paper and clarifies their relationship with BPC, which brings to the following conclusions: complementarity is a universal principle, as Bohr said, and the YYD constructed in this paper is a universal image found all over in the nature.

2. Definitions for General YYD and Ideal YYD

Traditional Taoist YYD is an ideal YYD satisfying BPC, which is a special case of the general YYD. In this Section, the general YYD is defined first and then it is explained under what conditions the ideal YYD can be induced. A general YYD is defined for any periodic system, which is composed of state A (Yang) and state B (Yin) with quantitative measures $p_A$ and $p_B$ normalized between 0 and 1. The growth and decline of the Yin-Yang states are conveyed through the interlacing changes of $p_A$ (in red) and $p_B$ (in black). 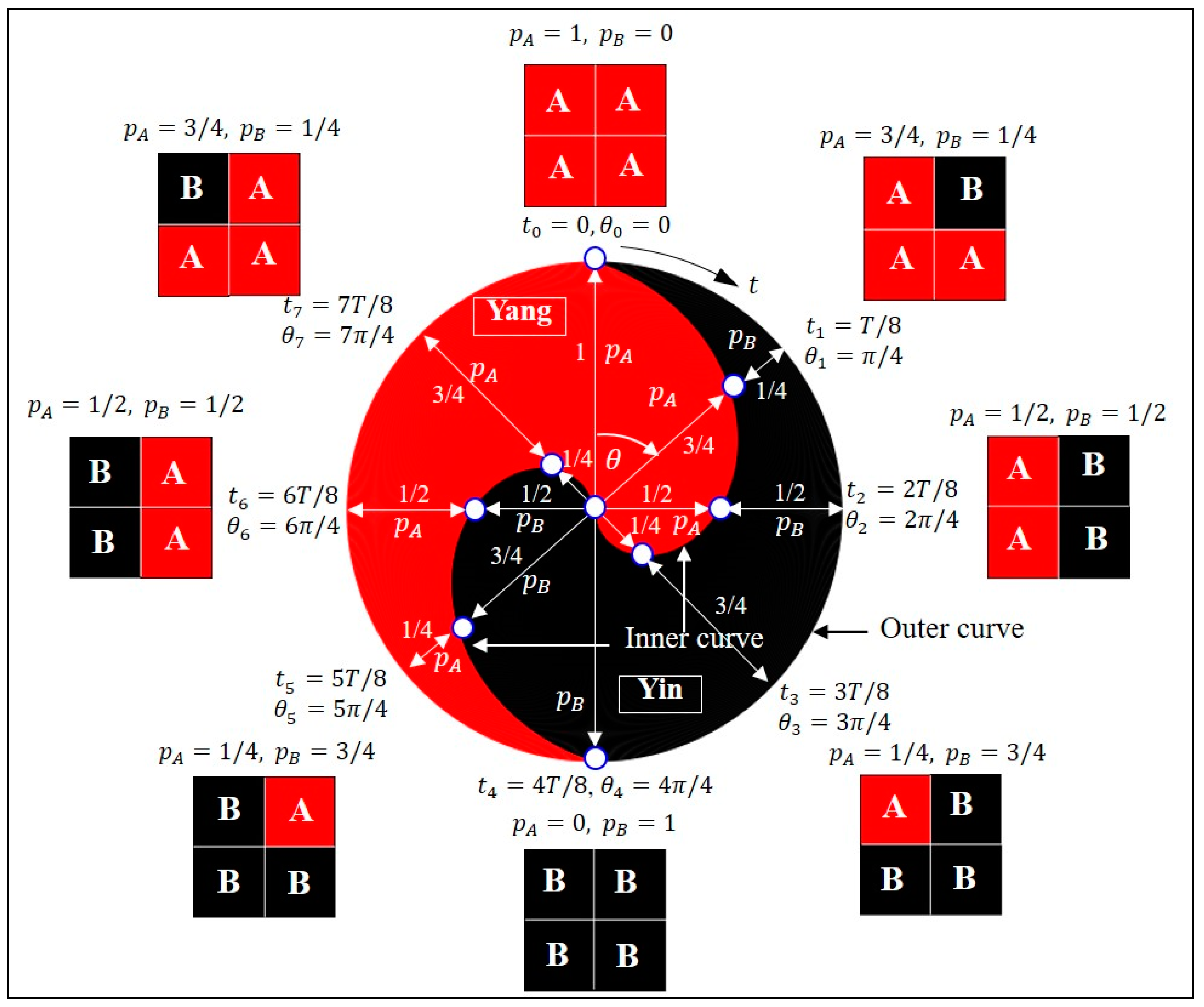As shown in Figure 2, the shape of YYD is uniquely determined by its inner and outer curves.

The radial coordinates of the inner and outer curves are called inner and outer radii, respectively. In terms of the quantitative measures $p_A\left(t\right)$ and $p_B\left(t\right)$ recorded at each moment $t$, the inner radius of a general YYD is defined by

$$r=\left\{\begin{array}{cc}{p}_A\left(t\right),& 0\le t\le T/2\\ p_B\left(t\right),& T/2\le t\le T\end{array}\right.=\left\{\begin{array}{cc}{p}_A\left(\theta \right),& 0\le \theta \le \pi ,\\ p_B\left(\theta \right),& \pi \le \theta \le 2\pi ,\end{array}\right.$$

(1)

and its outer radius is defined by $r=p_A\left(\theta \right)+p_B\left(\theta \right)$, where the azimuth angle $\theta =2\pi t/T$ is measured clockwise from the vertical axis and $T$ is the period of time, as shown in Figure 2. It is noted that the periodic property of the system implies $p_A\left(0\right)=p_A\left(2\pi \right)$ and $p_B\left(0\right)=p_B\left(2\pi \right)$.

The ideal YYD is a special case of the general YYD, which further meets the continuity condition and the complementarity condition. The continuity condition requires that the two sections of the inner curve defined by Equation (1) must be continuous at the origin, i.e., $p_A\left(\pi \right)=p_B\left(2\pi \right)=0$, or equivalently, the state A must occupy the whole system at $\theta =2\pi \left(\theta =0\right),$ and the state B must occupy the whole system at $\theta =\pi$. The complementarity condition requires that the states A and B must satisfy BPC: $p_A\left(\theta \right)+p_B\left(\theta \right)=1$ over the entire interval, or equivalently, the outer curve has to be a unit circle, $r=p_A\left(\theta \right)+p_B\left(\theta \right)=1$, $0\le \theta \le 2\pi$.

In ancient China, the most representative complementary pair $(A,B)$ was day and night. In this case, $p_A$ represents the proportion of daytime in a day, and $p_B$ represents the proportion of night. These two proportions vary on different days of the year, but they always meet the complementarity condition $p_A+p_B=1$. By recording the proportions of day and night for each day of the year in the polar coordinates, with white area denoting the daytime and black area denoting the nighttime, the original YYD in ancient China was then formed [5]. However, the original YYD determined by sunshine time is not an ideal YYD, because it does not necessarily satisfy the continuity condition. The continuity condition requires that in the year there be exactly one day with 24 h daytime (at the summer solstice, $\theta =0$) and exactly one another day with 24 h nighttime (at the winter solstice, $\theta =\pi$). Except for those who live at a certain latitude on the earth, people cannot actually draw an ideal YYD based on local sunshine hours.

The first ideal YYD, called Taoist YYD, was constructed by Chen Tuan (871AC–989AC), a philosopher in the early Song Dynasty of China. He drew the YYD according to the sequence of the sixty-four hexagrams appeared in the Book of Changes [10] (also called Yijing or I Ching), which is the oldest Chinese classics formed around the ninth century BC. Here, the Taoist YYD is reproduced by the BPC. Figure 2 shows a schematic diagram of constructing Taoist YYD from the measured $p_A\left(t\right)$ and $p_B\left(t\right)$ under the situation that the system is divided into four parts, and one period is divided into eight intervals. In Taoist YYD, the quantitative measures $p_A\left(t_k\right)$ and $p_B\left(t_k\right)$, $k=0,1,\cdots ,8$, represent the proportions of the states A and B in the entire system at time $t_k$. For example, at time $t_1$, state A occupies three-quarters of the system, and state B occupies one-quarter of the system, so one gets $p_A=3/4$ and $p_B=1/4$. The situation considered in Figure 2 can be extended to the general case, where the system has $N/2$ partitions and the period has $N$ partitions. Now, the measure $p_A$ ($p_B$) represents the ratio of the number of partitions containing A (B) state to the total $N/2$ partitions of the system. Therefore,

$$p_A\left(t_k\right)=\left\{\begin{array}{cc}1-k/(N/2),& k=\mathrm{0,1},\dots ,N/2,\\ k/(N/2)-1,& k=N/2,\dots ,N.\end{array}\right.$$

(2)

In order to satisfy the complementarity condition, the measure of B is set to $p_B\left(t_k\right)=1-p_A\left(t_k\right)$. Substituting the $p_A\left(t_k\right)$ and $p_B\left(t_k\right)$ defined by Equation (2) into Equation (1) yields the polar coordinates $(r_k,{\theta }_k)$ describing the inner curve of Taoist YYD:

$$r_k=\left\{\begin{array}{cc}1-k/(N/2),& k=\mathrm{0,1},\dots ,N/2\\ 2-k/(N/2),& k=N/2,\dots ,N\end{array}\right.=\left\{\begin{array}{cc}1-{\theta }_k/\pi ,& 0\le {\theta }_k\le \pi ,\\ 2-{\theta }_k/\pi ,& \pi \le {\theta }_k\le 2\pi ,\end{array}\right.$$

(3)

where the index $k$ and the azimuth angle ${\theta }_k$ have the linear relation $k/(N/2)={\theta }_k/\pi$; by noting that when the integer $k$ increases sequentially from $0$ to $N/2$, the azimuth angle ${\theta }_k$ increases linearly from 0 to $\pi$. It is noted that the continuity condition $p_A\left(\pi \right)=p_B\left(2\pi \right)=0$ is also satisfied by $p_A$ and $p_B$ defined by Equation (2). When $N$ is set to 8, the eight points $(r_k,{\theta }_k)$ defined by Equation (3) are just those shown in Figure 2. When $N$ is set to 64, the curve formed by connecting the sixty four coordinate points $(r_k,{\theta }_k)$ defined in Equation (3) recovers the traditional Taoist YYD, which was first constructed according to the order of the sixty four hexagrams in the Book of Changes. The ancient Taoist YYD is reproduced here by the principle of complementarity, i.e., by requiring that the complementary pair $\left(A,B\right)$ must be jointly complete and mutually exclusive.

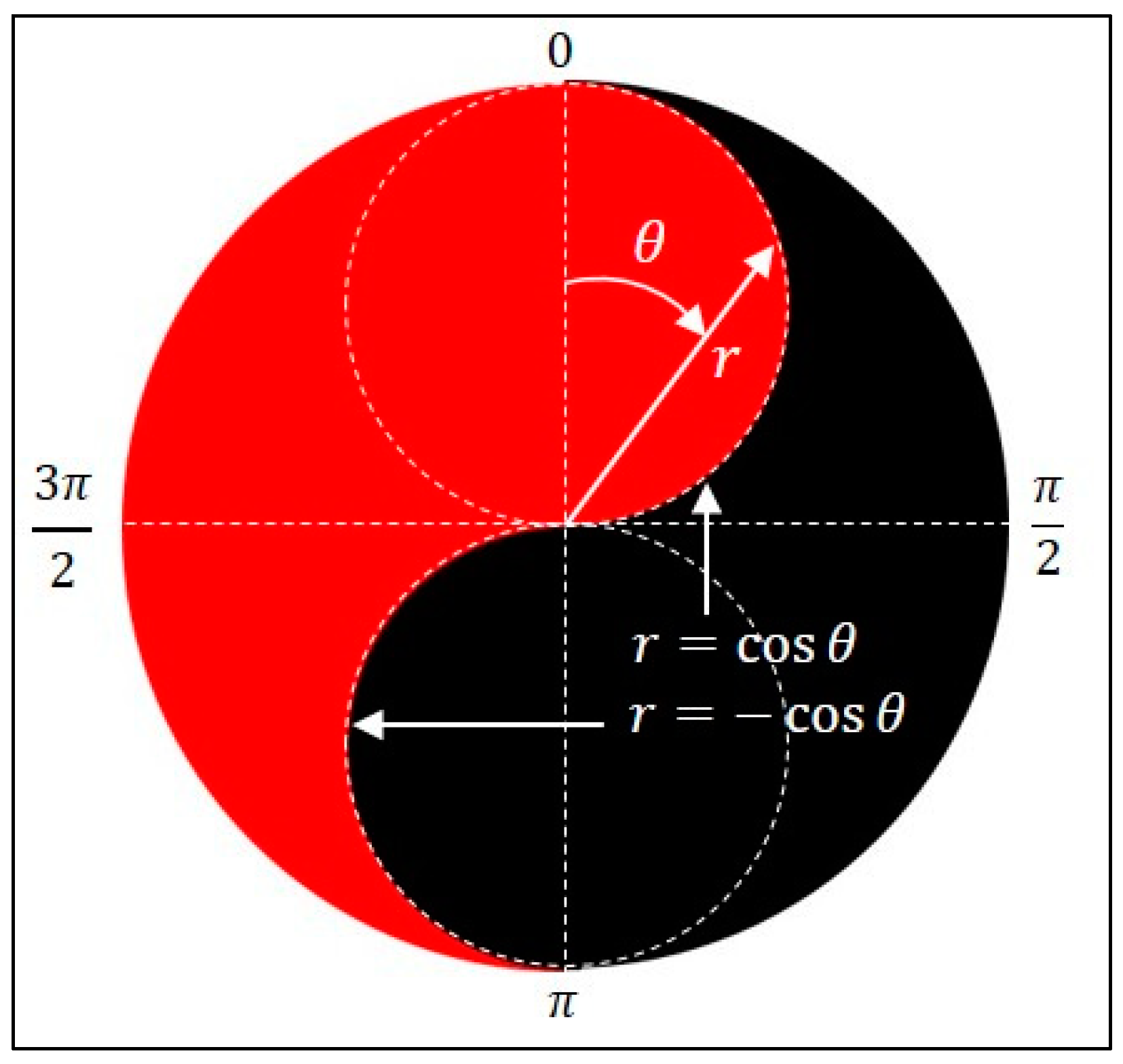
As the number of partitions $N$ approaches infinity, the discrete points defined by Equation (3) become a continuous polar curve

$$r=\left\{\begin{array}{cc}1-\theta /\pi ,& 0\le \theta \le \pi ,\\ 2-\theta /\pi ,& \pi \le \theta \le 2\pi ,\end{array}\right.$$

(4)

This is the inner curve of the ideal Taoist YYD formed by two sections of Archimedean spiral, which has a general expression $r=a+b\theta$. If Bohr’s original intention was to use Taoist YYD to convey his principle of complementarity, his correct choice should be the pattern in Figure 2, which is Taoist YYD drawn exactly according to his principle of complementarity. However, the YYD designed by Bohr in his coat of arms, as shown in Figure 3, is based on a popular drawing method, which is composed of a unit circle and two inscribed circles with polar equation given by

$$r=\left\{\begin{array}{cc}\cos \theta ,& 0\le \theta \le \pi /2,\\ -\cos \theta ,& \pi \le \theta \le 3\pi /2.\end{array}\right.$$

(5)

Apparently, the inner curve of Bohr’s YYD only passes through the first and third quadrants and is significantly different from Taoist YYD defined by Equation (4). In what follows, the definition (1) of the general YYD to derive the YYDs belonging to quantum mechanics itself.

3. Constructing Quantum YYD by Two-Path Interference Experiments

Among various natural phenomena, wave–particle duality best embodies the complementary relationship. In the past several decades, many experiments have been proposed to test whether the wave–particle duality satisfies BPC. However, all experiments on wave–particle duality so far still cannot explain the relationship between Bohr’s YYD and wave–particle duality. In this Section, it is shown that regardless of the test results of BPC, a YYD can always be constructed according to Equation (1) by the experimental data $\left(p_A,p_B\right)=(D^2,V^2)$ from the MZI, where $p_A=D^2$ is a measure of the particle nature regarding the distinguishability of the which-way information, and $p_B=V^2$ is a measure of the wave nature regarding the visibility of wave fringe.

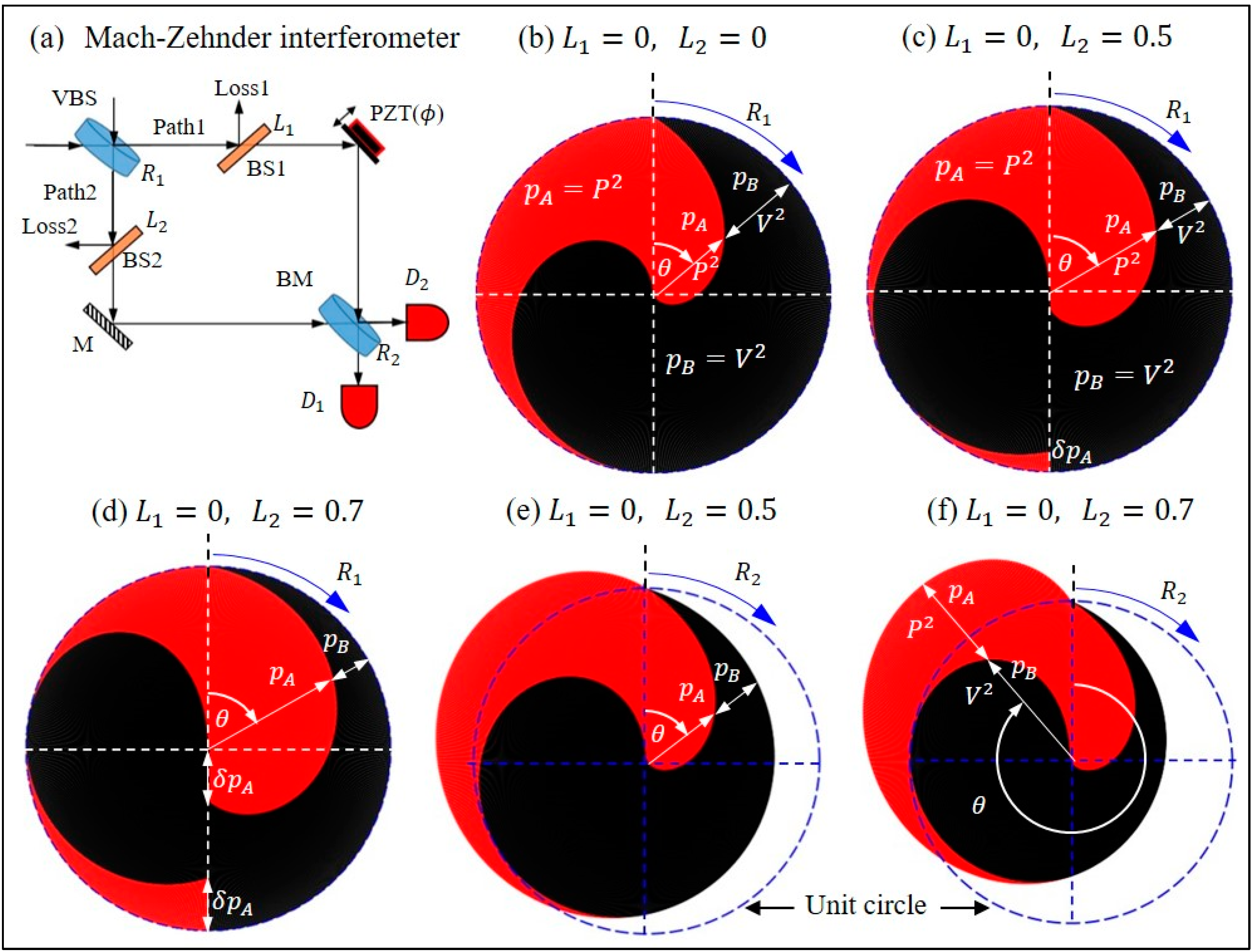
An experimental setup to construct the YYD for wave–particle duality is shown in Figure 4a [16,33], wherein a single photon pulse is split by a variable beam splitter (VBS) with adjustable reflectivity in the range $0\le R_1\le 1$, and a piezoelectric transducer (PZT) is employed to adjust the relative phase $\varphi$ between the two paths. The two paths of photon are recombined at the beam merger (BM), which is a fixed equal-probability beam splitter, and finally the photon is detected by the detectors $D_1$ and $D_2$. The measured values of $D$ and $V$ depend on the reflectivity $R_1$ of the VBS. If $R_1=0$ or $R_1=1$, the which-path information is known deterministically, and the photon manifests the property of a pure particle with $D=1$ and $V=0$. If $0<R_1<1$, the interference fringe appears behind the beam merger and yields a nonzero wave visibility $V$, which achieves its maximum value $V=1$ at $R_1=1/2$.

Following Berthold-Georg Englert [9], the distinguishability $D$ has two different notions: a-priori distinguishability and a-posteriori distinguishability, where the former is also called predictability $P$, which refers to a which-way information obtained using an unbalanced interferometer with different particle flux along the two paths. The a-priori distinguishability and visibility are especially useful in the construction of the ideal YYD, because it requires analytical expressions for the distinguishability and the visibility. In the case of a MZI without path loss, the a-priori distinguishability, $P$, and the a-priori visibility, $V,$ can be expressed analytically as a function of $R_1$ [33]:

$$P\left(R_1\right)=\left|1-2R_1\right|,V\left(R_1\right)=2\sqrt{R_1\left(1-R_1\right)},0\le R_1\le 1.$$

(6)

Substituting $p_A=P^2$ and $p_B=V^2$ into Equation (1), the polar equation of the YYD corresponding to the two-path interference experiment reads

$$r=\left\{\begin{array}{cc}{(1-2R_1)}^2,& 0\le R_1\le 1/2\\ 4R_1(1-R_1),& 1/2\le R_1\le 1\end{array}\right.=\left\{\begin{array}{cc}{(1-\theta /\pi )}^2,& 0\le \theta \le \pi ,\\ (\theta /\pi )(2-\theta /\pi ),& \pi \le \theta \le 2\pi ,\end{array}\right.$$

(7)

where the azimuth angle, $\theta ,$ is related to the reflectivity, $R_1,$ as $\theta =2\pi R_1$. The continuity condition $p_A\left(\pi \right)=p_{\mathit{B}}\left(2\pi \right)=0$ and the complementarity condition $p_A\left(\theta \right)+p_B\left(\theta \right)=P^2+V^2=1$ are satisfied so that the resulting YYD is an ideal YYD as shown in Figure 4b.

There are visible differences in the mathematical form between Taoist YYD (4) and the interference-based YYD (7) in that the former is a linear function of $\theta /\pi$, while the latter is a quadratic function of $\theta /\pi$. The quadratic form of the interference-based YYD comes from the feature that quantum probability is the squared magnitude of the wave function. Despite of their difference, both Taoist YYD and the interference-based YYD satisfy the condition of BPC: $p_A\left(\theta \right)+p_B\left(\theta \right)=1,0\le \theta \le 2\pi$, so both can be regarded as representative symbols of BPC.

The ideal YYD shown in Figure 4b is constructed from a perfect MZI without path loss; however, path loss in a MZI is inevitable, which causes the actual YYD to deviate from the ideal YYD. In what follows in this Section, the two kinds of nonideal YYDs are considered, one from the violation of the continuity condition and the other from the violation of the complementarity condition. When path loss occurs, the measured values of $V$ and $P$ are different from their ideal values (6) and read [33]

$$V(R_1)={\displaystyle \frac{2\sqrt{R_1(1-R_1)(1-L_1)(1-L_2)}}{\left(1-R_1\right)\left(1-L_1\right)+R_1(1-L_2)}}\mathrm{and}P(R_1)={\displaystyle \frac{\left|\left(1-R_1\right)\left(1-L_1\right)-R_1(1-L_2)\right|}{\left(1-R_1\right)\left(1-L_1\right)+R_1(1-L_2)}},$$

(8)

respectively, where $L_1$ and $L_2$ with values between 0 and 1 are the losses of the two paths and are simulated in the experiment by the two beam splitters BS1 and BS2 with reflectivity equal to $L_1$ and $L_2$, as shown in Figure 4a. Again by substituting $p_A=P^2$ and $p_B=V^2$ from Equation (8) into Equation (1), one obtains the deformed YYD caused by the path loss as shown in Figure 4c,d. It can be seen that this type of path loss does not produce the deformation of the outer curve of the YYD, that is, the complementarity condition $p_A+p_B=P^2+V^2=1$ is still satisfied, but the inner curve of the YYD is not continuous. The continuity condition requires $p_A\left(\pi \right)=p_B\left(2\pi \right)=0$, but for this case, $p_A\left(\pi \right)=P^2(1/2)={(L_2/2)}^2/{(1-L_2/2)}^2\ne 0$ and $p_B\left(2\pi \right)=V^2\left(1\right)=0$. The discrepancy between $p_A\left(\pi \right)$ and $p_B\left(2\pi \right)$ denoted by $\delta p_A$ increases with the path loss $L_2$ as shown in Figure 4c,d.

Figure 4e,f demonstrates the YYD deformation caused by the path loss under another configuration of the experiment, where the setups in the input and output ports are interchanged such that the input port is a fixed equal-probability beam splitter, while the output port is a variable beam splitter with adjustable reflectivity in the range $0\le R_2\le 1$. The predictability $P$ and the visibility $V$ for this configuration can be expressed by [33]

$$P\left(R_1\right)=\left|1-2R_2\right|, V\left(R_1\right)={\displaystyle \frac{2\sqrt{R_2\left(1-R_2\right)\left(1-L_1\right)\left(1-L_2\right)}}{\left(1-R_2\right)\left(1-L_1\right)+R_2\left(1-L_2\right)}}, 0\le R_2\le 1.$$

(9)

Opposite to the case (8), as can be seen from Figure 4e,f, the type (9) of path loss causes the outer curve of the YYD to deviate from the unit circle, i.e., the complementarity condition $p_A+p_B=1$ is not satisfied over the entire interval, but the continuity conditions $p_A\left(\pi \right)=P^2(1/2)=0$ and $p_B\left(2\pi \right)=V^2\left(1\right)=0$ still hold. As the path loss increases, the deformation of YYD intensifies and deviates further from the ideal YYD. In short, both the violation of the continuity condition (Figure 4c,d) and the violation of complementarity condition (Figure 4e,f) can deform the ideal YYD (Figure 4b), and the deformation tells us graphically the extent to which BPC is violated.

4. The Mapping between Quantum YYD and Complex Tunneling Velocity

The YYD generated by the two-path interference experiments shows a static picture of YYD, as found in Section 3. This Section considers a complementary pair $(A,B)$, whose quantitative measures $\left(p_A\left(t\right),p_B\left(t\right)\right)$ are time dependent so that the pattern of YYD changes with time. This dynamic picture of the YYD can be visualized by the quantum tunneling process, where the particle’s real and imaginary velocity components $({\dot{x}}_R\left(t\right),{\dot{x}}_I\left(t\right))$ constitute a time-dependent complementary pair. 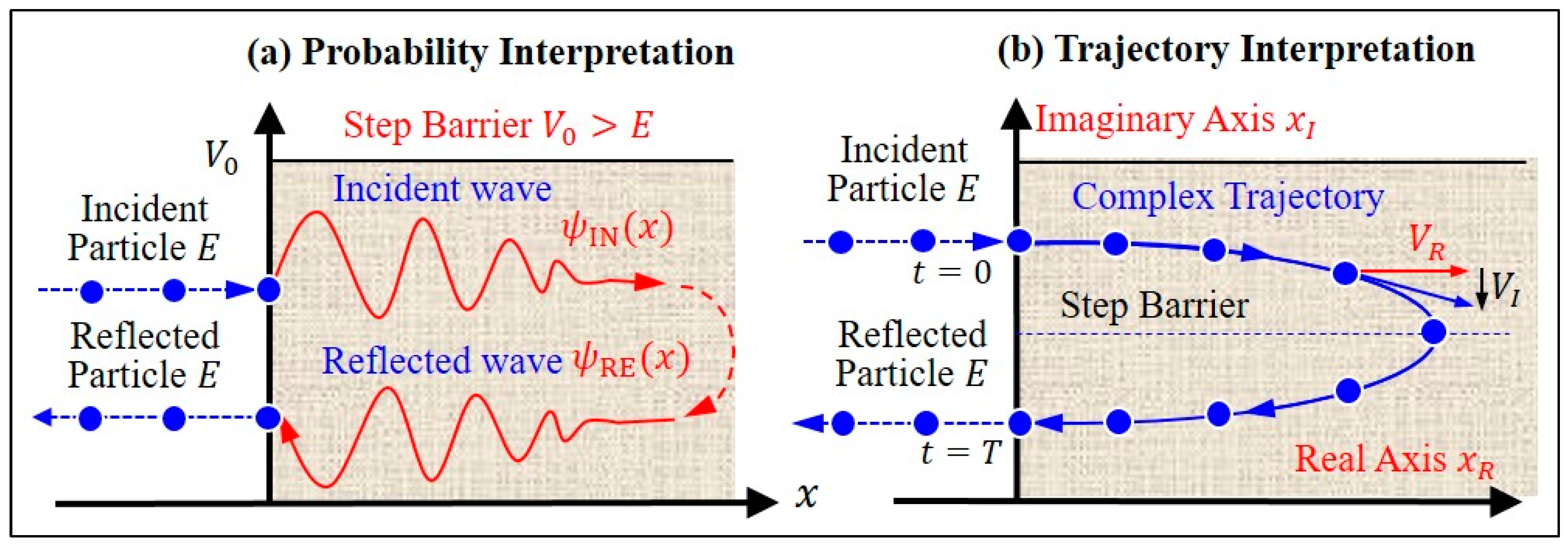The concepts of trajectory and velocity given to a tunneling particle are derived from the complex trajectory interpretation of quantum mechanics [32,34,35,36,37,38,39,40], which is different from the probability interpretation, as compared in Figure 5, but they have a common source: the wavefunction $\psi \left(x\right)$. Probability interpretation treats the particle’s position $x\in \mathbb{R}$ as a real variable and employs ${\left|\psi \left(x\right)\right|}^2$ as the probability of finding the particle at the position $x$. On the other hand, the complex trajectory interpretation uses the same wavefunction, $\psi \left(x\right)$ but with $x\in \mathbb{C}$ to generate the complex quantum trajectory $x\left(t\right)=x_R\left(t\right)+\mathrm{i}{x}_I\left(t\right)$.

Here, the wavefunction is considered describing a particle’s tunneling motion via a step barrier with height, $V_0$ greater than the particle’s energy, $E$. Such a wavefunction $\psi \left(x\right)$ can be found analytically from the Schrödinger equation and then used in the quantum Hamilton mechanics [32] to produce the particle’s complex position, $x\left(t\right)=x_R\left(t\right)+\mathrm{i}{x}_I\left(t\right),$ and complex velocity, $\dot{x}\left(t\right)={\dot{x}}_R\left(t\right)+\mathrm{i}{\dot{x}}_I\left(t\right),$ during the tunneling process. As soon as $x\left(t\right)$ and $\dot{x}\left(t\right)$ are determined, the quantitative measures $\left(p_A,p_B\right)=\left(x_R^2,x_I^2\right)$ and $\left(p_A,p_B\right)=\left({\dot{x}}_R^2,{\dot{x}}_I^2\right)$ can be used in Equation (1) to construct the tunneling-based YYDs.

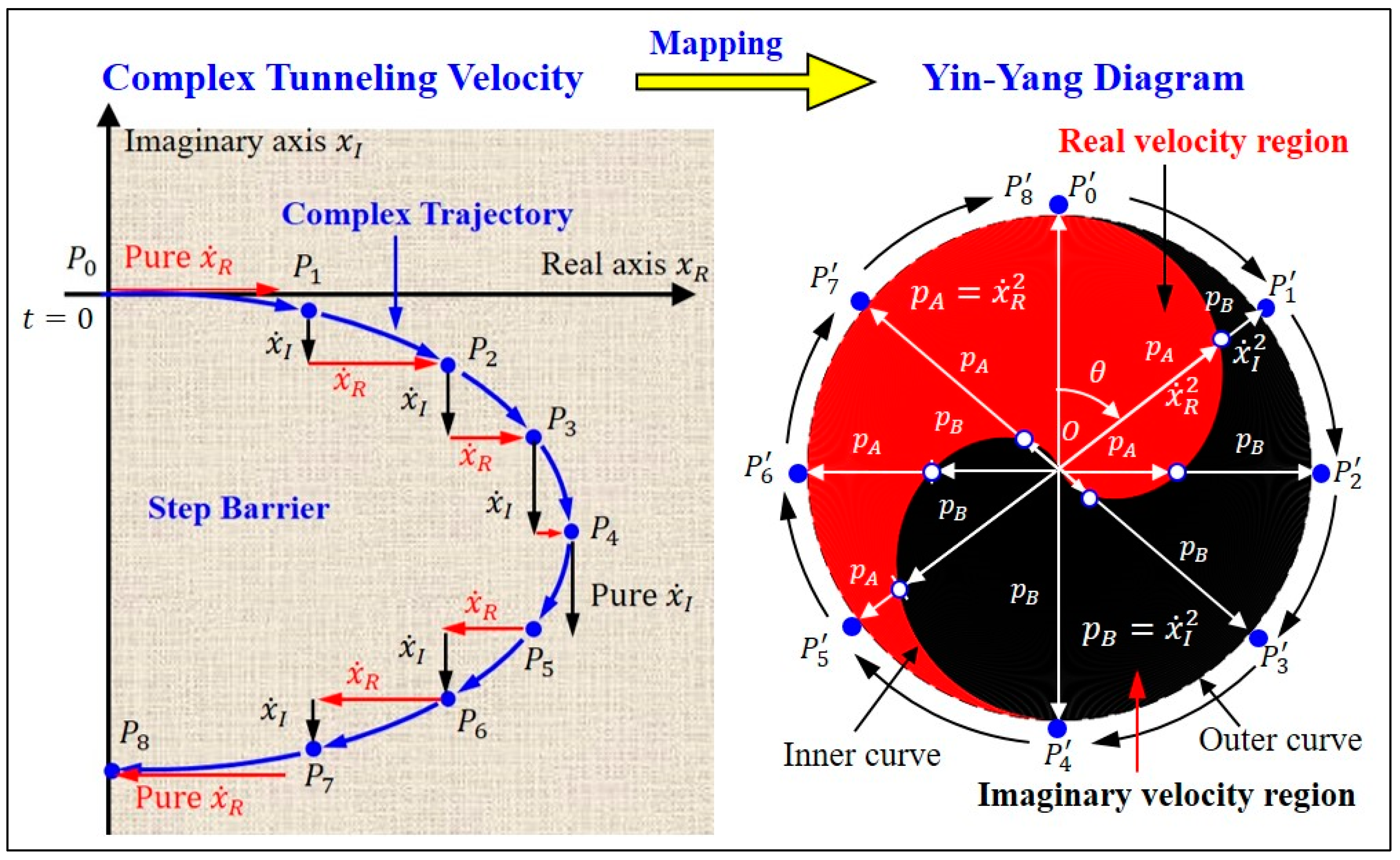
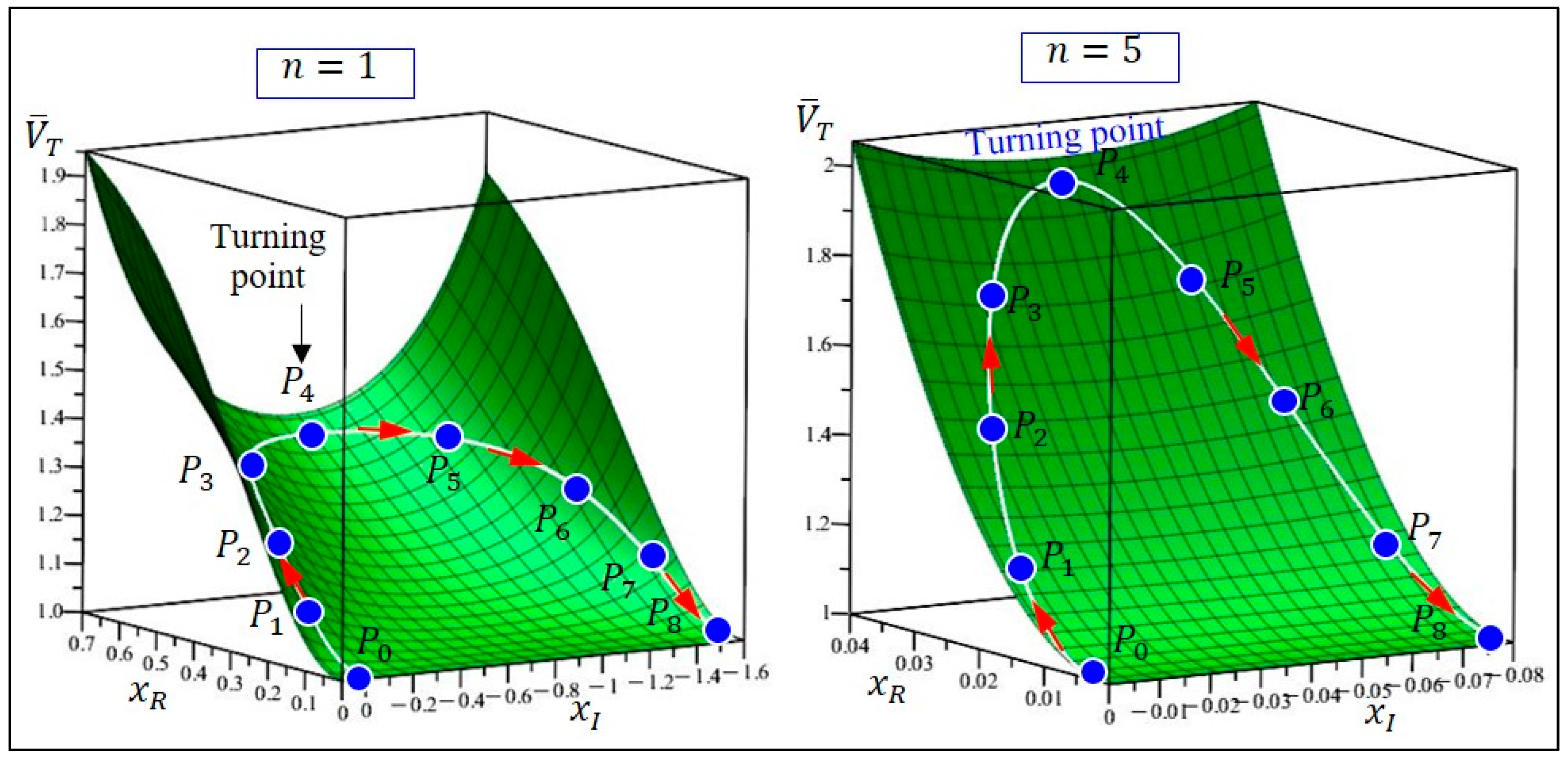
Figure 6 shows how the complex tunneling velocities are mapped into the quantum YYD. The Figure 6, left, shows the positions $P_i$ of the particle on the tunneling trajectory at nine moments $t_i$, $i=0,1,\dots ,8$. A trajectory point $P_i$ with velocity ${\dot{x}}_R\left(t_i\right)+\mathrm{i}{\dot{x}}_I\left(t_i\right)$ is mapped into the point $P_i^{\prime }$ on the YYD with radial coordinate $r_i={\dot{x}}_R^2\left(t_i\right)+{\dot{x}}_I^2\left(t_i\right)$ and azimuth coordinate ${\theta }_i=2\pi t_i/T$, where $T$ is the total tunneling time. As time $t_i$ increases from 0 to $T$, the area swept by the radial line segment ${\dot{x}}_R^2$ forms the Yang region (in red) of the YYD, while the area swept by the radial line segment ${\dot{x}}_I^2$ forms the Yin region (in black) of the YYD.

Among the nine trajectory points, $P_0$ is the entry point whose velocity ${\dot{x}}_0$ is pure real, $P_4$ is the turning point whose velocity ${\dot{x}}_4$ is pure imaginary, and $P_8$ is the exit point whose velocity is opposite to the entrance velocity ${\dot{x}}_8=-{\dot{x}}_0$. Given the trajectory point $P_i$ with the accompanying velocity $\dot{x}\left(t_i\right)={\dot{x}}_R\left(t_i\right)+\mathrm{i}{\dot{x}}_I\left(t_i\right)$, the inner and outer curves of the YYD can be determined as shown in the Figure 6, right. As time $t$ evolves continuously, the tunneling particle follows a continuous complex trajectory $x\left(t\right)=x_R\left(t\right)+\mathrm{i}{x}_I\left(t\right)$ and, according to Equation (1), the inner curve of the velocity-based quantum YYD can be expressed in polar coordinates:

$$r=\left\{\begin{array}{cc}{\dot{x}}_R^2\left(t\right),& 0\le t\le T/2\\ {\dot{x}}_I^2\left(t\right),& T/2\le t\le T\end{array}\right.=\left\{\begin{array}{cc}{p}_A\left(\theta \right),& 0\le \theta \le \pi ,\\ p_B\left(\theta \right),& \pi \le \theta \le 2\pi ,\end{array}\right.$$

(10)

and the outer curve is given by $r=p_A+p_B={\dot{x}}_R^2\left(t\right)+{\dot{x}}_I^2\left(t\right)$. The azimuth coordinate $\theta$ is related to time $t$ as $\theta =2\pi t/T$, $0\le t\le T$. In the time range of $0\le t<T/2$, the inner radius of the YYD is given by the squared real velocity $r=p_A={\dot{x}}_R^2$, while in the time range of $T/2\le t<T$, the inter radius is given by the squared imaginary velocity $r=p_B={\dot{x}}_I^2$.

5. Computing Complex Tunneling Trajectory

To construct the YYD by Equation (10), one needs the particle’s tunneling velocity $\dot{x}\left(t\right)={\dot{x}}_R\left(t\right)+\mathrm{i}{\dot{x}}_I\left(t\right)$, which can be derived from the complex-extended Schrödinger equation,

$$\mathrm{i}\hslash {\displaystyle \frac{\partial \Psi \left(t,x\right)}{\partial t}}=-{\displaystyle \frac{{\hslash }^2}{2m}}{\displaystyle \frac{{\partial }^2}{\partial x^2}}\Psi \left(t,x\right)+V\left(x\right)\Psi \left(t,x\right),$$

(11)

where $\hslash$ is the reduced Planck constant, $m$ is the particle mass, and the coordinate $x$ is defined on the complex plane $x=x_R+\mathrm{i}{x}_I\in \mathbb{C}$. Using the transformation $\Psi \left(t,x\right)=e^{\mathrm{i}S\left(t,x\right)/\hslash }$, one transforms the Schrödinger Equation (11) into the quantum Hamilton–Jacobi equation (QHJE):

$${\displaystyle \frac{\partial S\left(t,x\right)}{\partial t}}+{\left[{\displaystyle \frac{1}{2m}}{p}^2+V\left(t,x\right)+{\displaystyle \frac{1}{2m\mathrm{i}}}{\displaystyle \frac{\partial p}{\partial x}}\right]}_{p=\partial S/\partial x}={\displaystyle \frac{\partial S\left(t,x\right)}{\partial t}}+{\left.H\left(t,x,p\right)\right|}_{p=\partial S/\partial x}=0,$$

(12)

where $p=\partial S/\partial x$ is the canonical momentum conjugate to $x$, $S\left(t,x\right)$ is the quantum action function, and $H\left(t,x,p\right)$ is the quantum Hamiltonian defined as

$$H\left(t,x,p\right)={\displaystyle \frac{1}{2m}}{p}^2+V\left(t,x\right)+Q\left(t,x\right).$$

(13)

The quantum Hamiltonian $H\left(t,x,p\right)$ (13) contains three items: (i) the particle’s kinetic energy $p^2/2m$, (ii) the applied potential $V\left(t,x\right)$, and (iii) the internal quantum potential $Q\left(t,x\right)$, defined as:

$$Q\left(t,x\right)={\left.{\displaystyle \frac{1}{2m\mathrm{i}}}{\displaystyle \frac{\partial p}{\partial x}}\right|}_{\mathit{p}=\partial S/\partial x}={\displaystyle \frac{\hslash }{2m\mathrm{i}}}{\displaystyle \frac{{\partial }^{2}S\left(t,x\right)}{\partial x^2}}=-{\displaystyle \frac{{\hslash }^2}{2m}}{\displaystyle \frac{{\partial }^2\ln \Psi \left(t,x\right)}{\partial x^2}}.$$

(14)

It can be seen that the quantum potential is state-dependent and is uniquely determined by the wavefunction $\Psi \left(t,x\right)$. If the applied potential $V\left(t,x\right)$ is independent of time, that is, $V\left(t,x\right)=V\left(x\right)$, then the wavefunction $\Psi \left(t,x\right)$ can be further separated as

$$\Psi \left(t,x\right)=\psi \left(x\right)e^{-\mathrm{i}\left(E/\hslash \right)t}⟹S\left(t,x\right)=-\mathrm{i}\hslash \ln \psi \left(x\right)-Et.$$

(15)

The particle’s momentum, $p$, according to the momentum definition in QHJE, is then given by

$$p={\displaystyle \frac{\partial S}{\partial x}}={\displaystyle \frac{\hslash }{\mathrm{i}}}{\displaystyle \frac{\mathrm{d}\ln \psi \left(x\right)}{\mathrm{d}x}}={\displaystyle \frac{\hslash }{\mathrm{i}}}{\displaystyle \frac{\psi \prime \left(x\right)}{\psi \left(x\right)}}.$$

(16)

Substituting the separated form of $S\left(t,x\right)$ into QHJE (12) yields

$$H\left(t,x,p\right)={\displaystyle \frac{p^2}{2m}}+V\left(x\right)+Q\left(x\right)=-{\displaystyle \frac{\partial S}{\partial t}}=E=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.$$

(17)

Equation (17) expresses the law of energy conservation, indicating that the total energy, E, of the particle represented by the Hamiltonian $H\left(t,x,p\right)$ is a constant. The energy conservation law (17) is actually an alternative expression of the time-independent Schrödinger equation,

$${\displaystyle \frac{{\hslash }^2}{2m}}{\displaystyle \frac{{\mathrm{d}}^2\psi }{\mathrm{d}{x}^2}}+\left(E-V\left(x\right)\right)\psi =0,$$

(18)

as can be shown by substituting the momentum $p$ (16) and the quantum potential $Q$ (14) into Equation (17).

According to the Hamiltonian $H\left(t,x,p\right)$ (17), the quantum Hamilton equations of motion read

$$\dot{x}={\displaystyle \frac{\partial H}{\partial p}}={\displaystyle \frac{p}{m}},x\left(t_0\right)=x_0\in \mathbb{C},$$

(19)

$$\dot{p}=-{\displaystyle \frac{\partial H}{\partial x}}=-{\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}}\left(V+Q\right),p\left(t_0\right)=p_0\in \mathbb{C},$$

(20)

where the sum of $V$ and $Q$ is defined as the total potential,

$$V_{\mathrm{T}}=V+Q=E-{\displaystyle \frac{p^2}{2m}}=E+{\displaystyle \frac{{\hslash }^2}{2m}}{\left({\displaystyle \frac{{\psi }^{\prime \left(x\right)}}{\psi \left(x\right)}}\right)}^2.$$

(21)

The wave behavior of the particle is attributed to the quantum potential $Q$. If $Q$ is constant, Equations (19) and (20) become classical equations of motion and the particle exhibits particle behavior. The quantum potential $Q$ has a close relationship with the quantum probability. From Equation (21), one can see that except for a constant bias $E$, the magnitude of the total potential, $\left|V_{\mathrm{T}}\right|=\left|V+Q\right|$, is inversely proportional to the probability density function, ${\left|\psi \left(x\right)\right|}^2$. Therefore, the smaller the probability density function ${\left|\psi \left(x\right)\right|}^2$ the higher the corresponding total potential is. Where $\psi \left(x\right)$ is equal to zero, the total potential is infinitely high, so a particle with limited energy cannot reach it, and the probability of finding the particle there is zero.

For a given quantum state $\psi \left(x\right)$, the velocity and acceleration of a particle moving in this state are computed by Equations (19) and (20), respectively:

$$\dot{x}={\displaystyle \frac{p}{m}}={\displaystyle \frac{\hslash }{im}}{\displaystyle \frac{1}{\psi \left(x\right)}}{\displaystyle \frac{\mathrm{d}\psi \left(x\right)}{\mathrm{d}x}},x\left(t_0\right)=x_0\in \mathbb{C},$$

(22)

$$\ddot{x}=-{\displaystyle \frac{1}{m}}{\displaystyle \frac{\mathrm{d}{V}_{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}{\mathrm{d}x}}=-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}}{\left({\displaystyle \frac{\hslash }{m}}{\displaystyle \frac{{\psi }^{\prime }\left(x\right)}{\psi \left(x\right)}}\right)}^2,\dot{x}\left(t_0\right)={\dot{x}}_0\in \mathbb{C}.$$

(23)

The particle’s trajectory $x\left(t\right)$ in the state $\psi \left(x\right)$ is obtained by integrating Equation (22) and the quantum force exerted on the particle at different positions is given by Equation (23).

The applied potential $V\left(x\right)$ in Equation (18) to be considered here is the step barrier:

$$V\left(x\right)=\left\{\begin{array}{cc}{V}_0,& x_R>0,\\ 0,& x_R<0,\end{array}\right.$$

(24)

where the height, $V_0,$ of the step barrier is greater than the energy, $E$, of the incident particle in order to explore quantum tunneling motion. The solution of the Schrödinger Equation (18) with $V\left(x\right)$ (24) is obtained readily as

$$\psi \left(x\right)=\left\{\begin{array}{cc}C{e}^{k_{2}x}+D{e}^{-k_{2}x},& x_R\ge 0,\\ A{e}^{\mathrm{i}{k}_{1}x}+B{e}^{-\mathrm{i}{k}_{1}x},& x_R<0,\end{array}\right.$$

(25)

where $k_1=\sqrt{2mE}/\hslash$ and $k_2=\sqrt{2m(V_0-E)}/\hslash$. The range $x_R<0$ is the region of free motion, while $x_R\ge 0$ is the region where quantum tunneling motion takes place to generate the associated YYD. With the wavefunction $\psi \left(x\right)$ given by Equation (25), the particle’s velocity in the region $x_R\ge 0$ is obtained by Equation (22) as

$${\displaystyle \frac{dx}{dt}}={\displaystyle \frac{\hslash k_2}{\mathrm{i}m}}{\displaystyle \frac{\mathcal{C}{e}^{k_{2}x}-\mathcal{D}{e}^{-k_{2}x}}{\mathcal{C}{e}^{k_{2}x}+\mathcal{D}{e}^{-k_{2}x}}},\mathrm{R}\mathrm{e}\left(x\right)\ge 0,$$

(26)

$${\displaystyle \frac{dx}{dt}}={\displaystyle \frac{\hslash k_1}{m}}{\displaystyle \frac{\mathcal{A}{e}^{i{k}_{1}x}-\mathcal{B}{e}^{{-ik}_{1}x}}{\mathcal{A}{e}^{i{k}_{1}x}+\mathcal{B}{e}^{-i{k}_{1}x}}},\mathrm{R}\mathrm{e}\left(x\right)<0,$$

(27)

where the four constants $\mathcal{A}$, $\mathcal{B}$, $\mathcal{C}$, and $\mathcal{D}$ are to be determined from the given initial conditions. To avoid the influence of physical units on the shape of the quantum YYD, the dimensionless variables $(\sqrt{2mE}/\hslash )x\to x$ and $(2E/\hslash )t\to t$ are adopted here to rewrite Equations (26) and (27) as

$${\displaystyle \frac{dx}{dt}}={\displaystyle \frac{n}{\mathrm{i}}}{\displaystyle \frac{\mathcal{C}{e}^{nx}-\mathcal{D}{e}^{-nx}}{\mathcal{C}{e}^{nx}+\mathcal{D}{e}^{-nx}}},\mathrm{R}\mathrm{e}\left(x\right)\ge 0,$$

(28)

$${\displaystyle \frac{dx}{dt}}={\displaystyle \frac{\mathcal{A}{e}^{nx}-\mathcal{B}{e}^{-nx}}{\mathcal{A}{e}^{nx}+\mathcal{B}{e}^{-nx}}},\mathrm{R}\mathrm{e}\left(x\right)<0,$$

(29)

where the parameter $n=\sqrt{V_0/E-1}$ is a measure of the tunneling intensity. When $n=0$, i.e., $V_0=E$, the tunneling effect disappears completely. The four constants in Equations (28) and (29) are determined by the given initial conditions $x\left(0^{+}\right)=x\left(0^{-}\right)=0$ and $\dot{x}\left(0^{+}\right)=\dot{x}\left(0^{-}\right)=1$, from which

$$\mathcal{B}=0,{\displaystyle \frac{\mathcal{C}}{\mathcal{D}}}={\displaystyle \frac{n+\mathrm{i}}{n-\mathrm{i}}}.$$

(30)

In the region $\mathrm{R}\mathrm{e}\left(x\right)<0$, the particle is free from the action of the applied potential and has a constant velocity, $\dot{x}=1$ given by Equation (29) with $\mathcal{B}=0$. By substituting $\psi \left(x\right)=A{e}^{\mathrm{i}{k}_{1}x}$ for $\mathrm{R}\mathrm{e}\left(x\right)<0$ into Equation (21), one obtains $V_{\mathrm{T}}=V+Q=0$, which together with Equation (30) shows that the particle exhibits particle behavior with constant velocity, as shown in the region outside the step potential in Figure 5.

In the region $\mathrm{R}\mathrm{e}\left(x\right)\ge 0$, the particle undergoes tunneling process with wave behavior caused by the quantum potential, $Q$. Once a particle enters the tunneling process, its motion extends from the real axis to the complex plane, and its complex trajectory can be solved analytically from Equation (28) as

$$\alpha e^{nx}-e^{-nx}=\beta e^{-\mathrm{i}{n}^{2}t},$$

(31)

where the two constants $\alpha$ and $\beta$ are determined from the given initial conditions as

$$\alpha ={\displaystyle \frac{\mathcal{C}}{\mathcal{D}}}={\displaystyle \frac{n+\mathrm{i}}{n-\mathrm{i}}}, \beta ={\displaystyle \frac{2\mathrm{i}}{n-\mathrm{i}}}.$$

(32)

Due to $\left|\alpha \right|=1$, the constant $\alpha$ can be expressed as $\alpha =e^{\mathrm{i}{\theta }_{\alpha }}$ with ${\theta }_{\alpha }=2{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}(1/n)$. In terms of ${\theta }_{\alpha }$ and $n$, the particle’s complex trajectory $x\left(t\right)$ can be solved from Equation (31) as an explicit function of time

$$x\left(t\right)={\displaystyle \frac{1}{n}}\left[-\mathrm{i}{\displaystyle \frac{{\theta }_{\alpha }}{2}}+{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{h}}^{-1}\left({\displaystyle \frac{\beta }{2}}{e}^{-\mathrm{i}\left(n^{2}t+{\theta }_{\alpha }/2\right)}\right)\right]=x_R\left(t\right)+\mathrm{i}{x}_I\left(t\right).$$

(33)

Regarding the particle’s velocity, Equation (31) is substituted into Equation (28) to yield an analytical expression for $\dot{x}\left(t\right)$:

$${\displaystyle \frac{dx}{dt}}=\pm {\displaystyle \frac{n}{\mathrm{i}}}{\displaystyle \frac{\beta e^{-\mathrm{i}{n}^{2}t}}{\sqrt{{\beta }^2{e}^{-2\mathrm{i}{n}^{2}t}+4\alpha }}}={\dot{x}}_R\left(t\right)+\mathrm{i}{\dot{x}}_I\left(t\right).$$

(34)

where the plus sign is taken for the time interval $0\le t<T/2$, and the minus sign is for $T/2\le t<T$, where $T$ is the total tunneling time to be determined. The quantum YYD shown in Figure 6 is drawn using ${\dot{x}}_R\left(t\right)$ and ${\dot{x}}_I\left(t\right)$ computed from Equation (33). 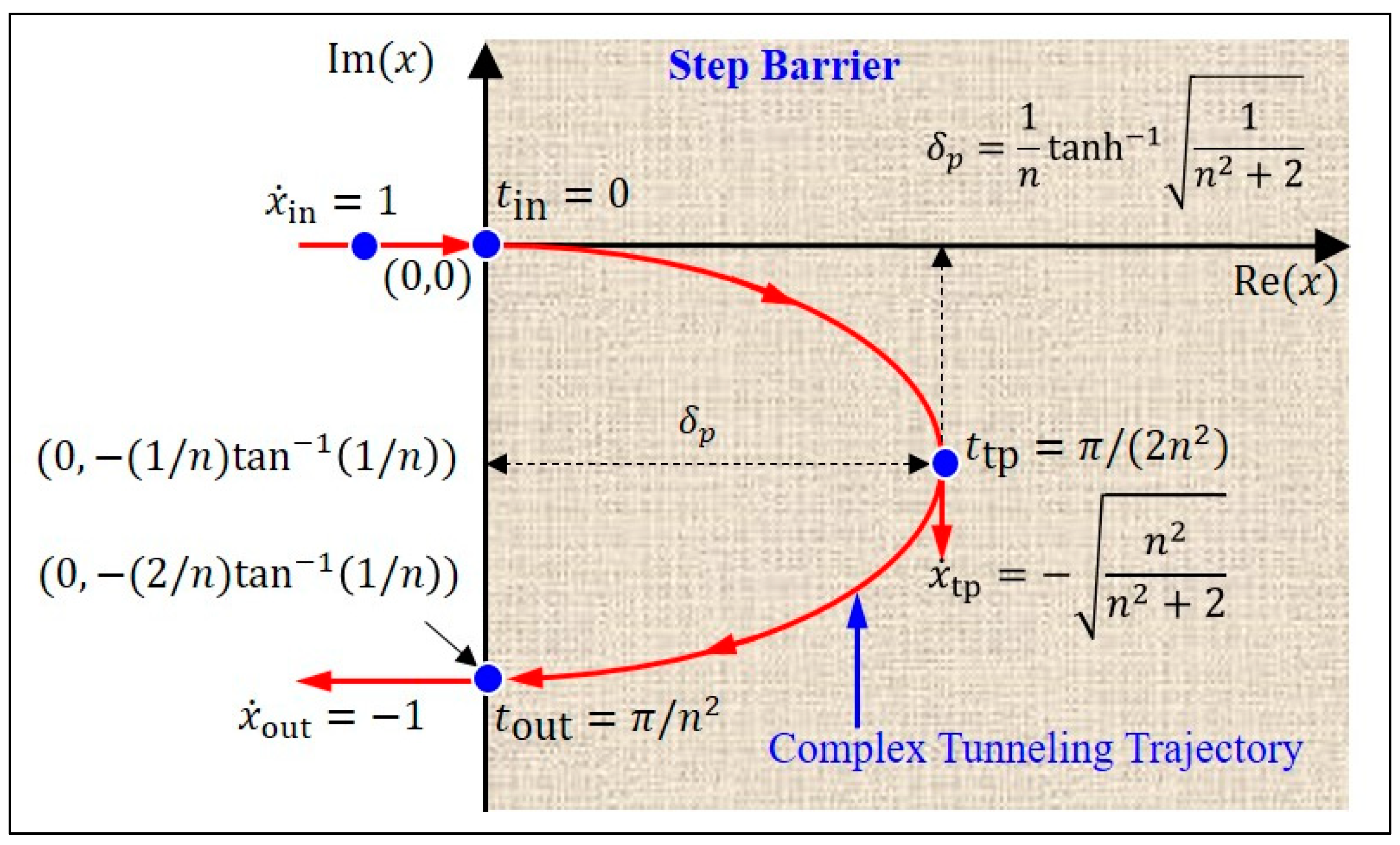The remaining task is to determine the tunneling time $T=t_{\mathrm{o}\mathrm{u}\mathrm{t}}$, the turning point $x_{\mathrm{t}\mathrm{p}}$, and the exit point $x_{\mathrm{o}\mathrm{u}\mathrm{t}}$ of the tunneling trajectory, as shown in Figure 7.

The turning point $x_{\mathrm{t}\mathrm{p}}$ is the position where the particle reaches the maximum depth of penetration. Taking the absolute values of both sides of Equation (31), the relationship between $x_R$ and $x_I$ is obtained as follows:

$$\cosh \left(2n{x}_R\right)=\cos \left({\theta }_{\alpha }+2n{x}_I\right)+{\displaystyle \frac{{\left|\beta \right|}^2}{2}}.$$

(35)

The maximum value of $x_R$ occurs at $\cos \left({\theta }_{\alpha }+2n{x}_I\right)=1$, and the related coordinate $x_I$ solution is

$$x_I=-{\displaystyle \frac{{\theta }_{\alpha }}{2n}}=-{\displaystyle \frac{1}{n}}{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left({\displaystyle \frac{1}{n}}\right).$$

(36)

Substituting the above $x_I$ (36) into Equation (35) yields the maximum penetration depth:

$${\delta }_p={\displaystyle \frac{1}{2n}}{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}}^{-1}\left(10+{\displaystyle \frac{2}{n^2+1}}\right)={\displaystyle \frac{1}{n}}{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}}^{-1}{\left({\displaystyle \frac{1}{n^2+2}}\right)}^{1/2}.$$

(37)

When the particle reaches the maximum penetration depth, its position is the turning point $x_{\mathrm{t}\mathrm{p}}$, so the complex coordinates of $x_{\mathrm{t}\mathrm{p}}$ can be expressed as

$$x_{\mathrm{t}\mathrm{p}}={\delta }_p+i{x}_I={\delta }_p-\mathrm{i}{\displaystyle \frac{{\theta }_{\alpha }}{2n}}={\displaystyle \frac{1}{n}}{\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}}^{-1}{\left({\displaystyle \frac{1}{n^2+2}}\right)}^{{\displaystyle \frac{1}{2}}}-{\displaystyle \frac{\mathrm{i}}{n}}{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left({\displaystyle \frac{1}{n}}\right).$$

(38)

Next, let us compute the time $t_{\mathrm{t}\mathrm{p}}$ and the velocity ${\dot{x}}_{\mathrm{t}\mathrm{p}}$ when the particle reaches the turning point $t_{\mathrm{t}\mathrm{p}}$. Squaring both sides of Equation (31) and using the turning condition, ${\theta }_{\alpha }+2n{x}_I=0$, one obtains $t_{\mathrm{t}\mathrm{p}}$ as

$$t_{\mathrm{t}\mathrm{p}}={\displaystyle \frac{\pi }{\left(2n^2\right)}}.$$

(39)

The velocity ${\dot{x}}_{\mathrm{t}\mathrm{p}}$ at the turning point is then determined by substituting the position $x_{\mathrm{t}\mathrm{p}}$ (39) into Equation (28) to give

$${\dot{x}}_{\mathrm{t}\mathrm{p}}={\displaystyle \frac{n}{\mathrm{i}}}{\displaystyle \frac{e^{2n{\delta }_p}-1}{e^{2n{\delta }_p}+1}}={\displaystyle \frac{n}{\mathrm{i}}}\tanh \left(n{\delta }_p\right)=-\mathrm{i}{\left({\displaystyle \frac{n^2}{n^2+2}}\right)}^{1/2}.$$

(40)

This result verifies what Figure 5 and Figure 7 show, that the particle has only imaginary velocity component at the turning point.

Finally, let us calculate the position $x_{\mathrm{o}\mathrm{u}\mathrm{t}}$ and time $t_{\mathrm{o}\mathrm{u}\mathrm{t}}$ at the exit point. From Figure 7, one observes that the real coordinates $x_R$ of the entry point and exit point are both zero. By using this condition in Equation (35), one obtains

$$\cos \left({\theta }_{\alpha }+2n{x}_I\right)={\displaystyle \frac{n^2-1}{n^2+1}}=\cos \left({\theta }_{\alpha }\right).$$

(41)

from which $x_I=0$ or $x_I=-{\theta }_{\alpha }/n$, where the former corresponds to the position of the entrance, and the latter corresponds to the position of the exit. Therefore, the position coordinate of the particle at the exit is

$$x_{\mathrm{o}\mathrm{u}\mathrm{t}}=0-{\displaystyle \frac{\mathrm{i}{\theta }_{\alpha }}{n}}=-\mathrm{i}{\displaystyle \frac{2}{n}}{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left({\displaystyle \frac{1}{n}}\right).$$

(42)

Comparing Equation (42) with Equation (38), one has $\mathrm{I}\mathrm{m}\left(x_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)=2\mathrm{I}\mathrm{m}\left(x_{\mathrm{t}\mathrm{p}}\right)=-{\theta }_{\alpha }/n$, that is, the imaginary coordinate of the exit point is twice that of the turning point. Furthermore, the time for the particle to reach the exit point can be obtained by substituting $x_{\mathrm{o}\mathrm{u}\mathrm{t}}$ (42) into Equation (31) as

$$T=t_{\mathrm{o}\mathrm{u}\mathrm{t}}={\displaystyle \frac{\pi }{n^2}}.$$

(43)

Comparing $T$ with $t_{\mathrm{t}\mathrm{p}}$ (35), one finds that the time for the particle to reach the turning point is exactly half of the overall tunneling $T$. This result explains why in Figure 6, when the YYD is drawn halfway at $P_4^{\prime }$, the particle just reaches the turning point $P_4$. The particle’s velocity at the exit point is found by substituting $x_{\mathrm{o}\mathrm{u}\mathrm{t}}=\mathrm{i}{\theta }_{\alpha }/n$ into Equation (28) as ${\dot{x}}_{\mathrm{o}\mathrm{u}\mathrm{t}}=-1$. Hence, the reflected velocity ${\dot{x}}_{\mathrm{o}\mathrm{u}\mathrm{t}}$ from the step barrier is the same as the incident velocity ${\dot{x}}_{\mathrm{i}\mathrm{n}}$, but in the opposite direction. The characteristics of the entire tunneling trajectory are summarized in Figure 7.

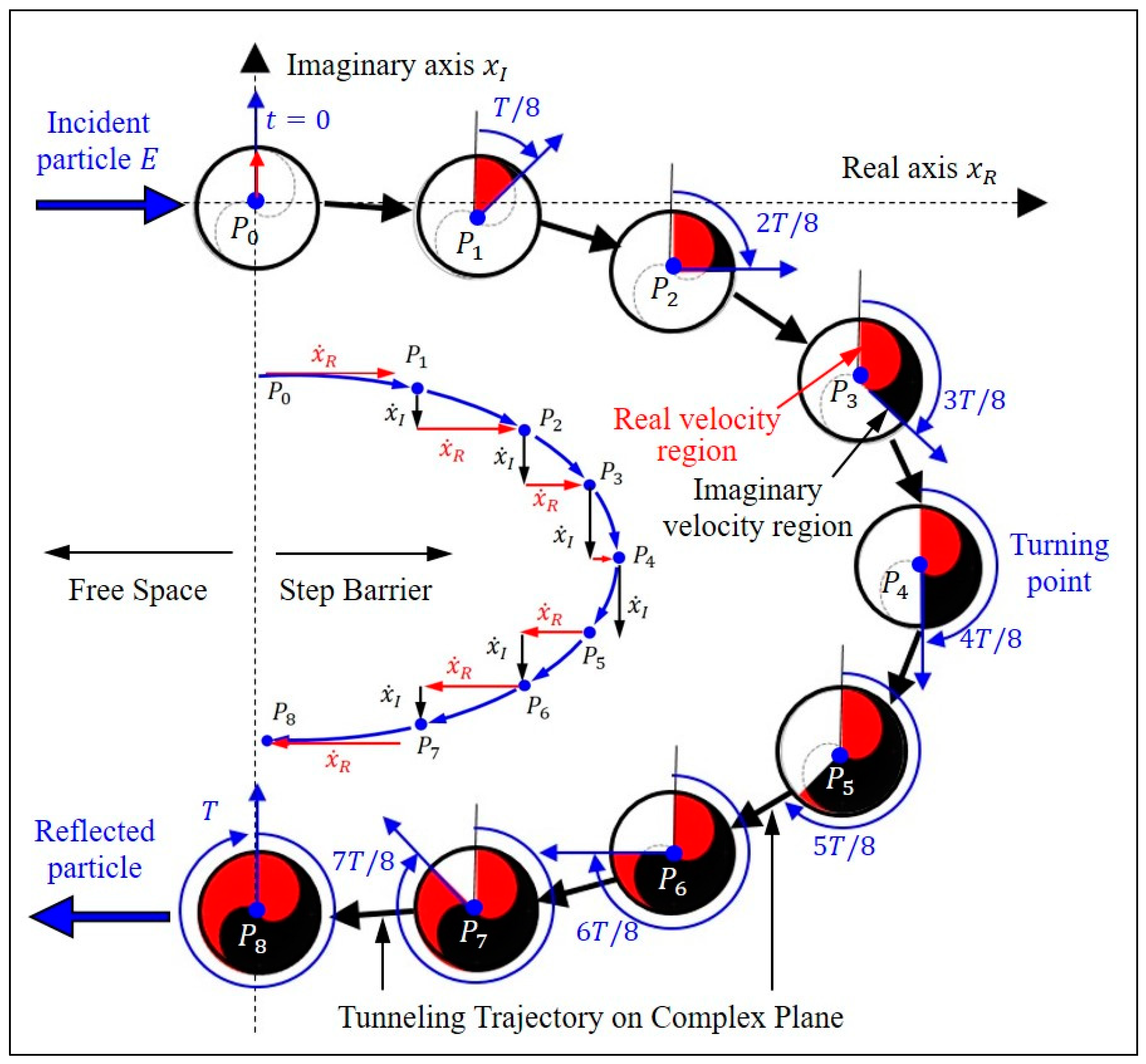
6. Time Evolution of Quantum YYD

The obtained tunneling-based YYD in Figure 6 is actually a graphical recorder of the particle’s tunneling dynamics, which stores the particle’s velocity at every moment so far. Figure 8 shows the time evolution of the YYD at nine moments, $t_0,t_1,\cdots ,t_8$, corresponding to nine trajectory points in Figure 6. When time increases from 0 to $T/2$, the real velocity of the particle (in red) decreases from the maximum value at $P_0^{\prime }$ to zero at $P_4^{\prime }$, while at the same time, the imaginary velocity of the particle (in black) increases from zero to the maximum value. In the time range of $T/2\le t<T$, one sees the opposite trend that the real velocity of the particle increases from zero at $P_4^{\prime }$ to the maximum value at $P_8^{\prime }$, and at the same time, the imaginary velocity decreases from the maximum value to zero. Only when the quantum tunneling process is completed one can see the complete quantum YYD, wherein the intertwined red and black pattern expresses the alternating changes of the real velocity and the imaginary velocity during the tunneling process.

Figure 9 shows the velocity distributions at nine trajectory points along the tunneling trajectory. It appears that the quantum YYD moves together with the particle, recording the velocity of the particle, and then presenting it graphically. The quantum YYD allows us to examine how the particle nature and the wave nature interchanges during the tunneling process. The imaginary velocity of a particle is a measure of its wave nature such that the greater the imaginary velocity of a particle is, the higher the uncertainty of its motion in the real space is, and the greater the wave nature it has [23]. As shown in Figure 9, when the particle continues to tunnel towards the barrier, the particle’s real velocity (in red) gradually decreases while its imaginary velocity (in black) increases. This means that as the particle tunnels deeper, its wave nature becomes larger. When the particle reaches the turning point $P_4$, its imaginary velocity reaches the maximum, while its real velocity is zero, which means that the particle behaves completely like a wave at the turning point. In the process of returning from point $P_4$ to the exit point $P_8$, the real velocity increases while the imaginary velocity decreases, indicating that the particle nature gradually recovers towards the exit, at which the imaginary velocity of the particle is zero and the wave nature of the particle disappears completely. After leaving the step potential, the particle returns to the free space, and its motion is again described by Equation (29) with $A=0$, which yields $\dot{x}=-1$ and indicates a classical motion along the negative real axis.

In quantum mechanics, the wave-like behavior of a tunneling particle is described by the probability density function ${\left|\psi \left(x\right)\right|}^2$ as shown in Figure 5a. As soon as the particle imaginary velocity is uniquely determined by ${\left|\psi \left(x\right)\right|}^2$, as derived below in this Section, the imaginary velocity serves as an alternative indicator of the particle’s wave behavior. The relation between the particle’s velocity $\dot{x}$ and the wavefunction $\psi \left(x\right)$ is given by Equation (16) as

$$p=m\dot{x}={\displaystyle \frac{\partial S}{\partial x}}={\displaystyle \frac{\hslash }{\mathrm{i}}}{\displaystyle \frac{\mathrm{d}\ln \psi \left(x\right)}{\mathrm{d}x}}={\displaystyle \frac{\hslash }{\mathrm{i}}}{\displaystyle \frac{\psi \prime \left(x\right)}{\psi \left(x\right)}}.$$

(44)

To separate the complex velocity $\dot{x}$ into its real part and imaginary part, let us express wavefunction $\psi \left(x\right)$ as $\psi \left(x\right)=\left|\psi \right|e^{i{\theta }_{\psi }}$, where ${\theta }_{\psi }\in \mathbb{R}$ is the phase of $\psi \left(x\right)$. Using this expression of $\psi \left(x\right)$ in Equation (44) yields

$$\dot{x}={\displaystyle \frac{\hslash }{m}}{\displaystyle \frac{\mathrm{d}{\theta }_{\psi }}{\mathrm{d}x}}+{\displaystyle \frac{\hslash }{2m\mathrm{i}}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}}\ln {\left|\psi \left(x\right)\right|}^2={\displaystyle \frac{\hslash }{m}}{\displaystyle \frac{\mathrm{d}{\theta }_{\psi }}{\mathrm{d}x}}+{\displaystyle \frac{\hslash }{m\mathrm{i}}}{\displaystyle \frac{1}{\left|\psi \left(x\right)\right|}}{\displaystyle \frac{\mathrm{d}\left|\psi \left(x\right)\right|}{\mathrm{d}x}}={\dot{x}}_R+\mathrm{i}{\dot{x}}_I.$$

(45)

from which the imaginary velocity is

$${\dot{x}}_I=-{\displaystyle \frac{\hslash }{2m}}{\displaystyle \frac{\mathrm{d}}{\mathrm{d}x}}\ln {\left|\psi \left(x\right)\right|}^2=-{\displaystyle \frac{\hslash }{m}}{\displaystyle \frac{1}{\left|\psi \left(x\right)\right|}}{\displaystyle \frac{\mathrm{d}\left|\psi \left(x\right)\right|}{\mathrm{d}x}}.$$

(46)

One can see that the imaginary velocity ${\dot{x}}_I$ is uniquely determined by the probability density function ${\left|\psi \left(x\right)\right|}^2$ and can be interpreted as the change rate of $\left|\psi \left(x\right)\right|$ per unit magnitude of $\left|\psi \left(x\right)\right|$. Therefore, when the particle’s imaginary velocity ${\dot{x}}_I$ reaches the maximum, it is the place where the wave magnitude $\left|\psi \left(x\right)\right|$ changes most drastically, that is, where the wave behavior of the particle is most significant. Corresponding to the quantum tunneling process, this is exactly where the particle reaches the turning point, as shown in Figure 9.

The driving force behind the tunneling dynamics comes from the total potential $V_{\mathrm{T}}=V_0+Q$, as shown by Equation (23). Since the applied potential $V_0$ is a constant, the quantum potential $Q$ is the dominant potential governing the particle’s tunneling motion. It is precisely because of the effect of quantum potential $Q$ that the particle is forced to turn back after penetrating the step barrier for a certain distance. The deeper the particle penetrates the step barrier, the greater resistance it encounters. The maximum depth to which a particle penetrates is where it tolerates the greatest resistance.

One determine the total potential $V_{\mathrm{T}}$ by substituting the wavefunction $\psi \left(x\right)$ from Equation (25) into Equation (21) to obtain the following result:

$${\overline{V}}_{\mathrm{T}}={\displaystyle \frac{Q\left(x\right)+V_0}{E}}=1+{\left({\displaystyle \frac{\mathrm{d}\ln \psi \left(x\right)}{\mathrm{d}x}}\right)}^2=1+n^2{\left({\displaystyle \frac{\alpha e^{nx}-e^{-nx}}{\alpha e^{nx}+e^{-nx}}}\right)}^2.$$

(47)

where $V_{\mathrm{T}}$ is expressed in a dimensionless form. Once the total potential is obtained, the quantum force exerted on the particle during the tunneling process can be found as

$${\overline{F}}_Q=-{\displaystyle \frac{\mathrm{d}{\overline{V}}_{\mathrm{T}}}{\mathrm{d}x}}=-2n^3\left({\displaystyle \frac{\alpha e^{nx}-e^{-nx}}{\alpha e^{nx}+e^{-nx}}}\right)\left[1-{\left({\displaystyle \frac{\alpha e^{nx}-e^{-nx}}{\alpha e^{nx}+e^{-nx}}}\right)}^2\right].$$

(48)

If expressed in terms of the particle’s velocity $\dot{x}$, ${\overline{F}}_Q$ can be rewritten in a simple form as

$${\overline{F}}_Q=-2\mathrm{i}\dot{x}\left(n^2+{\dot{x}}^2\right).$$

(49)

With the velocity ${\dot{x}}_{\mathrm{t}\mathrm{p}}$ (40), one can determine the quantum force exerted on the particle at the turning point as

$${\left({\overline{F}}_Q\right)}_{\mathrm{t}\mathrm{p}}=-{\displaystyle \frac{2n^3\left(n^2+1\right)}{{\left(n^2+2\right)}^{\frac{3}{2}}}}.$$

(50)

As expected, the quantum force experienced by the particle at the turning point is in the negative $x_R$ direction, preventing the particle from continuing to penetrate in the positive $x_R$ direction. Equation (50) shows that as $n=\sqrt{V_0/E-1}$ increases, the resistance encountered by the particle becomes greater, resulting in a smaller penetration depth (37).

From the perspective of probability, the higher the step barrier $V_0$ is, the lower the probability of tunneling is. The transition from the probability interpretation to the trajectory interpretation of the tunneling phenomenon requires the assistance of the quantum potential $Q\left(x\right)$. Figure 10 shows the complex trajectories of the particle moving over the total potential surface $V_T=Q\left(x\right)+V_0$ in the two cases of $n=1$ and $n=5$, indicating that when $n$ is larger, the total potential surface becomes steeper, and the depth that the particle can penetrate is shallower. The turning point $P_4$ is the place with the highest total potential in the overall tunneling trajectory, while the entry point $P_0$ and the exit point $P_8$ are the places with the lowest total potential.

7. Growth of Quantum YYD with Tunneling Intensity

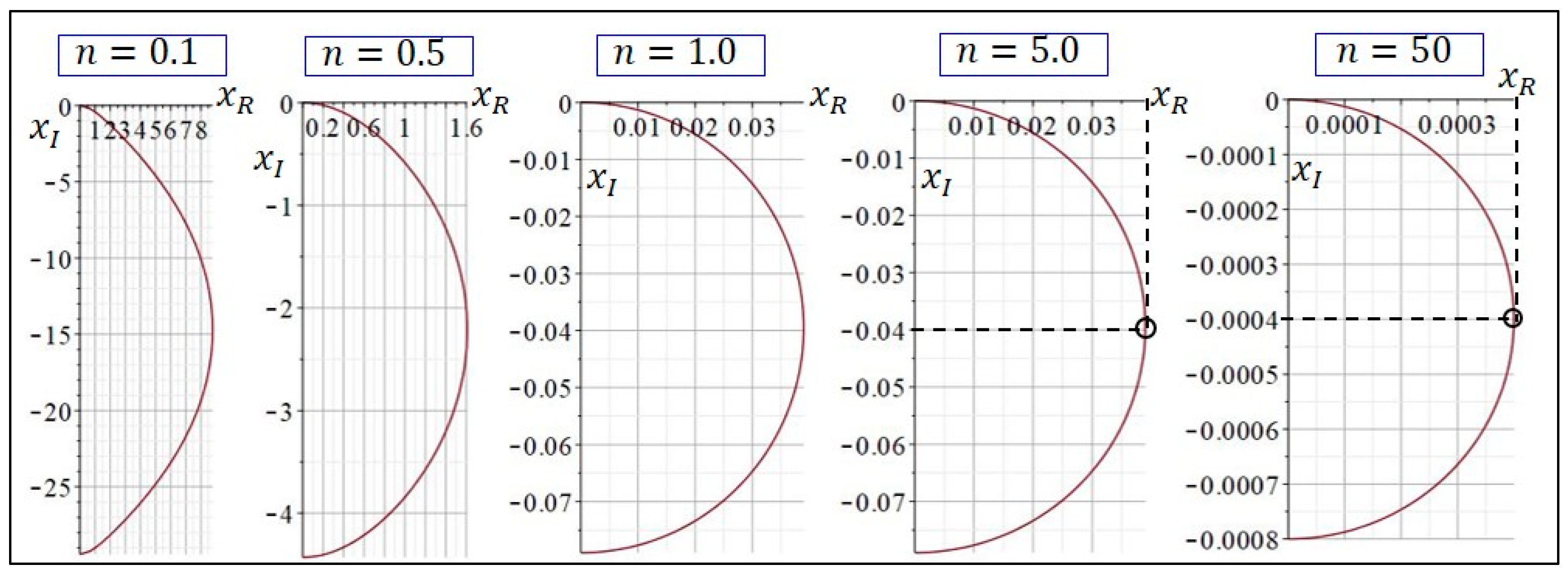
The quantum YYD based on tunneling velocity $\left(p_A,p_B\right)=\left({\dot{x}}_R^2,{\dot{x}}_I^2\right)$ is not always an ideal YYD, and its shape depends on the intensity of the quantum tunneling effect. It is found here that the stronger the quantum tunneling effect the clearer and more complete the quantum YYD is. Once the intensity of the tunneling effect approaches zero, the quantum YYD disappears. The intensity of the tunneling effect is related to the relative magnitude between the incident particle’s energy $E$ and the step barrier height, $V_0$. This relative magnitude is measured by the dimensionless parameter $n=\sqrt{V_0/E-1}$. The larger the value of $n$ is, the smaller the particle’s energy is compared to the barrier height, and a larger tunneling effect is required for the particle to penetrate the barrier.

What makes us curious is how the intensity of the tunneling effect affects the quantum YYD. Figure 11 shows the quantum YYDs corresponding to different values of $n$. One can see that the quantum YYD is born from $n=0$, initially like a melon seed, and gradually grows into a perfect appearance as n increases. As $n\gg 1$, the quantum YYD no longer changes, and the corresponding polar Equation (10) converges to

$$r=\left\{\begin{array}{cc}{\cos }^2\left(n^{2}t\right),& 0\le t<T/2\\ {\sin }^2\left(n^{2}t\right),& T/2\le t<T\end{array}\right.=\left\{\begin{array}{cc}\left(1+\cos \theta \right)/2,& 0\le \theta \le \pi ,\\ \left(1-\cos \theta \right)/2,& \pi \le \theta \le 2\pi ,\end{array}\right.$$

(51)

where $T=\pi /n^2$ is the dimensionless tunneling time. The satisfaction of the complementarity condition $p_A+p_B={\cos }^2\left(n^{2}t\right)+{\sin }^2\left(n^{2}t\right)=1$ and the continuity condition $p_A\left(\pi \right)=p_B\left(2\pi \right)=0$ show that the quantum YYD described by Equation (51) is an ideal YYD, whose inner curve is composed of two sections of cardioid. For small value of $n$, the corresponding YYDs as shown in Figure 11 are nonideal and only satisfy the condition of mutual exclusion, i.e., $p_A\left(\theta \right)+p_B\left(\theta \right)\le 1$. In this case, the pair $\left(p_A,p_B\right)=\left({\dot{x}}_R^2,{\dot{x}}_I^2\right)$ is only partially complementary, because the condition of complementarity $p_A\left(\theta \right)+p_B\left(\theta \right)=1$ is still satisfied for $\theta$ near $0$ and $2\pi$, but $p_A\left(\theta \right)+p_B\left(\theta \right)<1$ for other values of $\theta$.

Comparing Equation (51) with Equation (5), it was quite surprising to find that the ideal YYD generated by the tunneling motion resembles Bohr’s YYD designed in his coat of arms. If Bohr drew YYD based on Equation (51) instead of Equation (5), then the coat of arms he designed would completely reflect his principle of complementarity not only in image but also in theory.

Figure 11 shows that when the parameter $n=\sqrt{V_0/E-1}$ $\gg$ 1, the tunneling-based YYD converges to a steady-state pattern, known as the ideal YYD. Since the ideal YYD is drawn based on the particle’s tunneling trajectory, it is expected that the tunneling trajectory also converges to a steady-state pattern as $n\gg 1$. Let us verify that this steady-state trajectory is a semicircle on the complex plane.

Figure 12 shows the tunneling trajectories of the particle on the complex plane solved from Equation (28) under several different values of $n$. The main feature of this series of trajectories indicates that as the value of $n$ increases, the covering range of the particle’s position $x$ becomes narrower, as expressed by the relation $\left|nx\right|\approx 1/n$. Therefore, when $n$ is large, one obtains the result $\left|nx\right|\ll 1$. With this observation, the exponential function $e^{nx}$ can be estimated by its first-order expansion $1+nx$, which is then used in Equation (28) to yield the particle’s velocity for $n\gg 1$ as

$${\displaystyle \frac{dx}{dt}}={\displaystyle \frac{n}{\mathrm{i}}}{\displaystyle \frac{{\alpha }_2{e}^{nx}-e^{-nx}}{{\alpha }_2{e}^{nx}+e^{-nx}}}\approx {\displaystyle \frac{1-\mathrm{i}{n}^{2}x}{1+\mathrm{i}x}}\approx 1-\mathrm{i}{n}^{2}x,n\gg 1,$$

(52)

where note that $\left|nx\right|\ll 1$ and $1+\mathrm{i}x\approx 1$. With the initial condition $x\left(0\right)=0$, the solution of Equation (48) can be found readily as

$$x\left(t\right)={\displaystyle \frac{1}{n^2}}\sin \left(n^{2}t\right)-{\displaystyle \frac{\mathrm{i}}{n^2}}\left(1-\cos \left(n^{2}t\right)\right)=x_R\left(t\right)+\mathrm{i}{x}_I\left(t\right),n\gg 1,$$

(53)

From Equation (53), one can obtain the position, velocity, and time when the particle reaches the turning point and the exit point. These results are identical to those summarized in Figure 7, when $n$ is large. For example, the overall tunneling time $T$ is the time that the real coordinate $x_R\left(t\right)$ returns to zero, and from Equation (53), one has $T=\pi /n^2$, which is identical to Equation (43). In addition, the penetration depth ${\delta }_p$ is the maximum value of the real part of $x\left(t\right)$, which is equal to $1/n^2$ from Equation (53), and this result is identical to Equation (37) as $n$ is large.

The tunneling trajectory expressed by Equation (53) is a semicircle on the complex plane with radius $1/n^2$ and center $\left(0,-1/n^2\right)$:

$${\left(x_R\right)}^2+{\left(x_I+1/n^2\right)}^2={\displaystyle \frac{1}{n^4}},x_R\ge 0, n\gg 1.$$

(54)

It is based on this ideal tunneling trajectory that one can construct the ideal quantum YYD. Differentiating Equation (53) with respect to time, one obtains the real and imaginary velocities of the particle as

$${\dot{x}}_R\left(t\right)=\cos \left(n^{2}t\right), {\dot{x}}_I\left(t\right)=-\sin \left(n^{2}t\right),n\gg 1.$$

(55)

Using Equation (55) in Equation (10), one obtains the ideal YYD as given by Equation (51).

The YYD derived previously is based on the velocity distribution of a tunneling particle, so a natural question is whether the quantum YYD can also be constructed by the position distribution of a tunneling particle. The answer is yes, and surprisingly, when the value of $n$ is large, the YYDs obtained by these two different methods are the same. To search for the complementary pair $(A,B)$ for the position-based YYD, let us consider Equation (54), which under the coordinate transformation ${\overline{x}}_R=n^2{x}_R$ and ${\overline{x}}_I=n^2{x}_I+1$ can be expressed as ${\overline{x}}_R^2+{\overline{x}}_I^2=1$. Hence, the new pair $\left(A,B\right)=({\overline{x}}_R,{\overline{x}}_I)$ with the quantitative measures

$$p_A={\overline{x}}_I^2={\left(n^2{x}_I+1\right)}^2, p_B={\overline{x}}_R^2={\left(n^2{x}_R\right)}^2.$$

(56)

becomes complementary by noting $p_A+p_B={\overline{x}}_I^2+{\overline{x}}_R^2=1$. Therefore, the outer curve of the position-based YYD is $r=p_A+p_B=1$, which is a unit circle, and the corresponding inner curve defined by Equation (1) becomes

$$r=\left\{\begin{array}{cc}{\left(n^2{x}_I+1\right)}^2,& 0\le t<T/2\\ {\left(n^2{x}_R\right)}^2,& T/2\le t<T\end{array}=\right.\left\{\begin{array}{cc}{\cos }^2\left(n^{2}t\right),& 0\le t<T/2,\\ {\sin }^2\left(n^{2}t\right),& T/2\le t<T,\end{array}\right.$$

(57)

where $x_R\left(t\right)$ and $x_I\left(t\right)$ are given by Equation (53). Equation (51) and Equation (57) are equivalent, which implies that the velocity-based YYD and the position-based YYD become identical as $n\gg 1$.

For a general value of $n$ not satisfying $n\gg 1$, the symmetric center of the tunneling trajectory is not at $(x_R,x_I)=(0,-1/n^2)$, but at $(0,-(1/n\left){\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(1/n\right)\right)$, as can be seen from Figure 7. Hence, for a general position-based YYD, the quantitative measures $p_A$ and $p_B$ in Equation (56) are replaced by

$$p_A={\left(n^2{x}_I+n{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(1/n\right)\right)}^2, p_B={\left(n^2{x}_R\right)}^2,$$

(58)

where the time history of the complex position $x\left(t\right)=x_R\left(t\right)+\mathrm{i}{x}_I\left(t\right)$ is solved from Equation (28) for a general value of $n$.

Figure 13 shows how the position-based YYD evolves with the tunneling intensity $n$. The YYD emerges from the origin with $n=0$, initially resembling a walnut in appearance, and grows into an ideal YYD as $n$ increases. Regardless of whether the velocity or position data are used to construct the YYD, one finds that when the value of n is large, the two methods result in the same ideal YYDs, whose outer curve approaches a perfect circle, and whose inner curve approaches a cardioid.

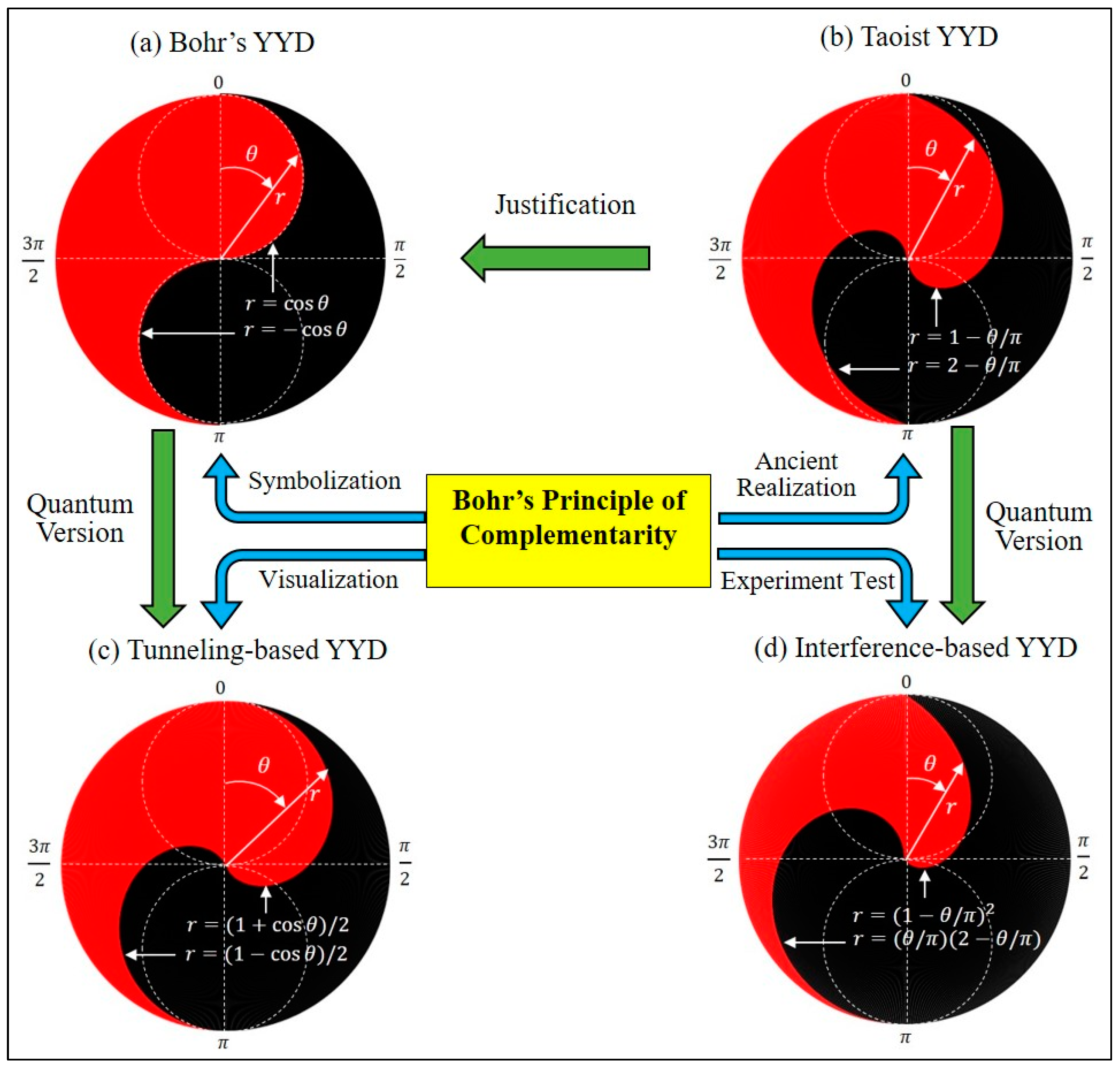
8. Conclusions

In this paper, it is found that Bohr’s YYD in quantum tunneling dynamics and discussed four special forms of YYD relating to BPC. Bohr’s YYD in his coat of arms is a popular YYD consisting of a unit circle and two inscribed circles, as shown in Figure 14a. Except for being like the tunneling-based YYD in appearance, this popular YYD has no link to physical systems. The second type of YYD is the traditional Taoist YYD, which is an ancient realization of BPC as shown in Figure 14b. The third type of YYD in Figure 14c visualizes a particle’s tunneling motion by displaying the time evolution of the particle’s position and velocity. The fourth type of YYD in Figure 14d is drawn based on the data of the two-path interference experiments for testing the wave–particle duality. Taoist YYD has been reproduced in this article by BPC, which, in turn, justifies Bohr’s use of Taoist YYD as the icon of his principle. The only pity is that the YYD designed by Bohr in his cost of arms is not Taoist YYD drawn based on his principle. However, Bohr did not need to borrow Taoist YYD to symbolize the wave–particle duality, because the wave–particle duality has its own representative YYDs, i.e., the tunneling-based YYD and the interference-based YYD, as revealed in this article. The investigation in this paper shows that Bohr’s YYD and its quantum version, the tunneling-based YYD, belong to the same category, while Taoist YYD and its quantum version, the interference-based YYD, belong to another category.

The types of YYD are not limited to those shown in Figure 14. Actually, every system in nature has its accompanying YYD that can be constructed according to Equation (1). Any complementary pair A and B in a system, whether classical or quantum, can be employed to construct the system’s YYD, if their quantitative measures $p_A$ and $p_B$ are available within a period. In ancient China, the complementary pair could be the daytime and nighttime in a day. In classical mechanics, the complementary pair could be the kinetic energy and the gravitational potential energy of a particle during vertical projectile motion or could be the kinetic energy and the elastic potential energy of a spring-mass system. In quantum mechanics, the complementary pair could be the particle nature and the wave nature of a photon in a two-path interference experiment or could be the real and imaginary velocities of a tunneling particle. If, as Bohr said, complementarity is a universal principle, the YYD constructed in this paper is a universal image found all over in nature.

When the complementary pair satisfies the conditions of continuity and complementarity, the obtained YYD turns out to be an ideal one, whose outer curve is a perfect circle with continuous inner curve. One can then judge the degree to which the system satisfies BPC based on the deviation of the system’s YYD from the ideal YYD.