1. Introduction
In this study, the evolution of an electrically charged matter distribution is investigated by treating it as an anisotropic fluid. It is quite widely accepted that different energy–momentum tensors can produce identical space-time configurations [
1,
2]. An illustrative example is in the framework of spherical symmetry, where viscosity can be considered to be a particular manifestation of anisotropy [
3]. Then, to demonstrate the proposed methodology and based on the derivation of dynamical models, free streaming is adopted as the underlying transport mechanism while employing a self-similar space-time description with the Schwarzschild coordinates for the interior region. This approach accommodates several gravitational collapse scenarios, including one previously documented [
4,
5,
6].
Spherically symmetric exact solutions play a crucial role in studying compact stellar objects within the framework of general relativity. In particular, the investigation of charged fluid spheres, characterized by self-gravitation and anisotropy, has been explored in a separate study [
7]. Several research endeavors have recently focused on compact star models in an electric field, using the Einstein–Maxwell system of equations. It is worth noting that the presence of charge can significantly impact essential stellar parameters such as redshift, radius, and maximum mass values [
8,
9,
10].
Incorporating electric charge into the analysis often requires researchers to make additional assumptions, such as defining an equation of state, introducing additional symmetries, or establishing relationships between metric variables [
7,
11]. The majority of studies in this field have focused on static conditions. For instance, in Ref. [
12], static-charged perfect fluid spheres in general relativity were extensively explored, while Ref. [
13], the effects of electric charge on compact stars and its implications for gravitational collapse were investigated. In Ref. [
14], charged fluid spheres in an Einstein–Maxwell spacetime were studied with the imposition of conformal symmetry.
Other investigations on electric charge have examined self-similar charged spherical distributions using diffusion approximation [
9,
11]. These studies have found that exact solutions can provide valuable information about the physical characteristics of collapsing stars [
4,
9,
15]. These analyses highlight the relevance of precise solutions within the framework of Einstein–Maxwell systems for describing highly dense astronomical objects, such as neutron stars and strange stars. In Ref. [
16], exact solutions of the Einstein–Maxwell systems were obtained for charged spheres with specific choices of electric field and gravitational potential.
In Ref. [
17], regular models of invariant conformal spheres exhibiting an anisotropic energy-momentum tensor were successfully identified. In this research, self-similar symmetry was proved to be a valuable tool for modeling dense relativistic stellar objects, representing a specific case of conformal symmetry. Furthermore, in Ref. [
18], it was proposed that the presence of electric fields in stellar bodies can give rise to pressure anisotropy.
In the current study, it is considered that electric charge can be seen as a form of anisotropy [
11], but not just any anisotropy, as is discussed. Within specific density ranges, local anisotropic pressure can be physically justified in self-gravitating systems since different physical phenomena that lead to local anisotropy can occur and relax the upper limits imposed on the maximum value of the surface gravitational potential.
We investigate self-gravitating spherical distribution of charged matter, which includes a dissipative fluid. Schwarzschild coordinates are used, following the method described in Refs. [
5,
11]. An additional symmetry (homothetic motion) is assumed to be present inside the sphere of viscous fluid induced by the electric charge, along with the radiation flux. The self-similar inner solution is found to match with the outer Reissner–Nordström–Vaidya solution.
The results of this paper demonstrate that electric charge produces local anisotropy in the same sense as viscosity. From this perspective, relevant physical information is obtained for spherically symmetric, self-similar, and electrically charged matter distributions under the free streaming approximation. Furthermore, the solutions are found to satisfy the Darmois–Lichnerowicz boundary conditions on the surface of the distribution and well match the inner self-similar solution with the outer Reissner–Nordström–Vaidya solution.
Section 2 presents the field equations for Bondian observers, showcasing how they demonstrate the influence of the electric charge in inducing anisotropy and establishing the connection with the Reissner–Nordström–Vaidya exterior solution. Additionally, this Section provides the corresponding surface equation for this analysis.
Section 3 presents a brief description of the numerical methods used in this study. This Section provides a summary description of application and implementation of the methods considered.
Section 4 illustrates self-similar solutions using non-adiabatic charged models with an emphasis of their significant and noteworthy implications within the research context. Finally,
Section 5 gives the conclusions and pertinent observations.
2. The Metric, Energy–Momentum Tensor, and Field Equations
2.1. Bondian Observers and Field Equations
The Einstein field equations are written using the line element in Schwarzschild coordinates [
6],
where
,
λ =
λ(
t,
r), and
t and
r are the temporal and radial coordinates, respectively. This matter exhibits spherical symmetry and comprises a charged fluid characterized by energy density,
, pressure,
p, electrical energy density,
, and non-polarized radiation flux,
, as follows [
5,
19]:
where
is the stress-energy tensor,
and
are the components of the 4-velocity and the 4-null vector, respectively, satisfying
and
, and
are the components of the electromagnetic energy–momentum tensor,
where
are the components of the Maxwell field tensor, which satisfies the Maxwell equations:
and
where the semicolon and the comma in the subscript denote, respectively, the covariant derivative and partial differentiation relative to the next indicated coordinate,
is the determinant of metric 4-tensor,
is electric current 4-vector,
σ is the electric conductivity, and the Greek letter indexes take 0 (time) and 1, 2, and 3 (space) values. Thanks to the spherical symmetry, only the radial electric field,
, is nonzero, with
On the other hand, the inhomogeneous Maxwell Equations (4) and (5) become [
11]
and
where
and
are, respectively, the temporal and radial components of the current 4-vector
. The function
is naturally interpreted as the electric charge within the radius
r at the time
t.
The conservation of charge inside a sphere moving with the fluid is expressed as
The conservation Equation (9) can be written in a form more suitable for numerical purposes as follows:
where the velocity of matter in the Schwarzschild coordinates is
with
, the radial direction velocity.
The contravariant components of the 4-velocity are
with
the Kronecker delta. Then, the field Equation (12) can be written as
2.2. Anisotropy Fluid and Electric Charge
To express the field equations in a form equivalent to that of an anisotropic fluid, the following definition is introduced:
where
and
is the mass distribution [
11]. Thus, the field Equations (17)–(20) read
where
and the conservative variables are
and
Generally, and , are referred to as effective density and effective pressure, respectively.
For an anisotropic fluid, Equations (18)–(21) are formally the same, with
,
,
, and the electric energy density
), and the local electric field strength being equal to
If
, which is defined as the degree of local anisotropy induced by the electric charge,
s; then, at any point, the electric charge determines the degree of local anisotropy. Once the metrics
and
are obtained, together with their derivatives, from the symmetry equations the physical variables
,
p,
ω, and
ε, and are determined in algebraic form from the field equations. In this framework, the electric charge becomes an integral part of the metric, manifesting as anisotropy within the fluid. The electric charge plays a significant role by contributing to the energy density and pressure. Adopting the Bondian observers’ [
5] approach to general relativity, which incorporates a moving reference frame, enhancing understanding of this perspective.
2.3. Junction Conditions and Surface Equations
The exterior spacetime is described by the Reissner–Nordström–Vaidya metric. The spherically symmetric charged distribution is considered to be bounded by the
a(
t) surface. Beyond this boundary, a Reissner–Nordström–Vaidya spacetime is assumed, as described in Refs. [
12,
13]:
where
is the total active gravitational mass,
is the total charge of the sphere, and
u is the time delay. The exterior and interior solutions are separated by the surface
. Darmois junction conditions [
9] ensure a smooth transition between both regions on this surface by demanding the continuity of the first fundamental form, resulting in
The quantity (27) is evaluated on the surface what is indicated by the subscript .
2.4. Surface Equations
The space in the matter distribution can be divided into the two distinct regions: the inner region, which is described by the line element (1), and the outer region, characterized by the Reissner–Nordström–Vaidya metric (23). These two regions are separated by the hypersurface located at r = a. Consequently, it is imperative to account for the interaction and connection between the solutions governing the inner and outer regions as dictated by the field Equations (17)–(20).
Furthermore, in order to obtain the evolution of the matter physical variables, such as the pressure p, the density , the electric charge s, the radiation flux ε, and the velocity ω, within the distribution, it is essential to establish a system of ordinary differential equations at the surface of the matter distribution.
Once a system of the equations is established, one obtains a system consisting of two ordinary differential equations. These equations involve three functions that vary with respect to time t: the radius of the distribution, the velocity ω at the distribution’s edge, and the mass function μ at the distribution’s surface.
Following the procedure outlined in Ref. [
9], the surface equations are written by evaluating Equations (11) and (20) on the surface of the distribution. The first and second surface equations then read:
where
and
Up to here, four field Equation (10) governing seven unknowns, which consist of two geometric variables, and , and five physical variables, p, , radiation flux ε, velocity ω, and electric charge s.
Here is the step-by-step solution algorithm:
Prior to this, solve the surface equations by utilizing a fourth-order Runge–Kutta method. This yields the surface variables, which are obtained by satisfying the coupling conditions.
Start by obtaining the geometric variables through the application of an additional homothetic (self-similar) symmetry. This means deriving these variables based on the equations of symmetry by considering the surface variables.
Determine the electric charge by numerically solving the charge conservation equation.
Once the geometric variables and the electric charge are determined, the physical variables of pressure, density, radiation flux, and velocity are determined in algebraic form from the field Equations (13)–(16).
3. Integration of the Conservative Equation
Once the equations are integrated on the surface, observation Equation (10) has to be integrated to obtain all the physical variables in the source. For this purpose, we introduce the dimensionless coordinate,
x = r/a. Thus, the conservation equation can be written as
which is integrated numerically using the Lax method with the appropriate Courant–Friedrichs–Levy (CFL) condition [
17]. The solution of the conservation Equation (32) is constrained by the evolution of the surface and was implemented as follows:
The superscript
n points to the hypersurface
u = nδu, and the subscript
j points to the position for a comoving observer with
. Typically, the time delay increments in
u = 10
−2 with the CFL condition of
. To integrate the conservation equation, one must specify the boundary and initial conditions. In this case, the boundary condition is
with the initial condition of
where the power p allows studying the sensitivity of the results to the initial conditions. We define the initial electric charge function in a manner that ensures it complies with the conservation Equation (32), particularly with respect to its radial dependence.
At this point, there are no limitations on exploring the interior of the distribution and tracking the temporal changes in the physical variables. To achieve this, it is essential to specify the charge function with regard to the radial coordinate r at time t = 0. While doing so, it is needed to take into account that the temporal evolution should not compromise the fulfillment of the physical prerequisites. By this consideration, one can readily derive the model.
4. Self-Similarity and Determination of the Metric
Covariant descriptions of self-similarity in the context of spherical matter distributions reveal that self-similar solutions can be categorized into two types based on their invariance or non-invariance to scale transformations. From a mathematical perspective, self-similarity is intriguing for two primary reasons: it first simplifies the field equations into a set of ordinary differential equations, and, secondly, it nullifies both the homothetic Killing symmetry and the conformal Killing symmetry [
20,
21,
22].
The presence of a homothetic Killing vector field serves as an invariant definition of self-similarity. In a specific coordinate system, self-similarity becomes evident through a straightforward scaling relation for the metric functions. Subsequently, an additional homothetic (self-similar) symmetry is imposed [
20,
23]:
where
is the metric tensor, and the homothetic generator,
ξ, is of the form
where
and ᴦ are the temporal and radial components of the homothetical vector, respectively, and
represents the Kronecker delta.
Equations (36) and (37) combined with Equation (1) lead to
Then, inserting the functions
and
into Equations (40) and (41) leads to
and
respectively, which can also be written as
As soon as Equations (44) and (45) are solved, it is possible to know the form of the metric variables μ and ν at all t and r.
Equations (46) and (47) have general solutions where .
Specific solutions of and are proposed, where A1, A2, k, and l are constants.
Therefore, the geometrical variables are
The case study involves a system consisting of a radiant fluid with an electric charge, made possible through the application of field equations describing the Einstein–Maxwell system. Solving these equations leads to two crucial outcomes. Firstly, it yields a set of physical properties, including density, pressure, fluid velocity, energy flow, and electric charge. Secondly, it furnishes insights into the structural characteristics of space-time.
From a theoretical perspective, this problem requires a more complete examination where it is taken into account that the matter distribution’s surface delineates two distinct space-time regions: the inner region, replete with matter and radiation, and the outer region beyond the surface, where radiation emanates unhindered into infinity. Thus, it becomes imperative to adequately define the geometry of both the inner and outer regions and delineate the nature of their energy and material constituents.
To facilitate the analysis, the sphere was partitioned into five layers, wherein the physical variables derived from the field equations were meticulously assessed. The collapse was imposed by imparting an initial velocity to the surface, allowing the surface’s evolution. The fourth-order Runge–Kutta method integrated the differential Equations (28) and (29) on the surface. In addition, the physical variables during integration are bounded within the physically acceptable values of > 0, , and −1 < ω < 1.
That is, at a density above zero, high pressure, and radial velocity in between −1 and 1, one avoids propagation at speeds exceeding the speed of light. The CFL sets a limit the latter not to happen.
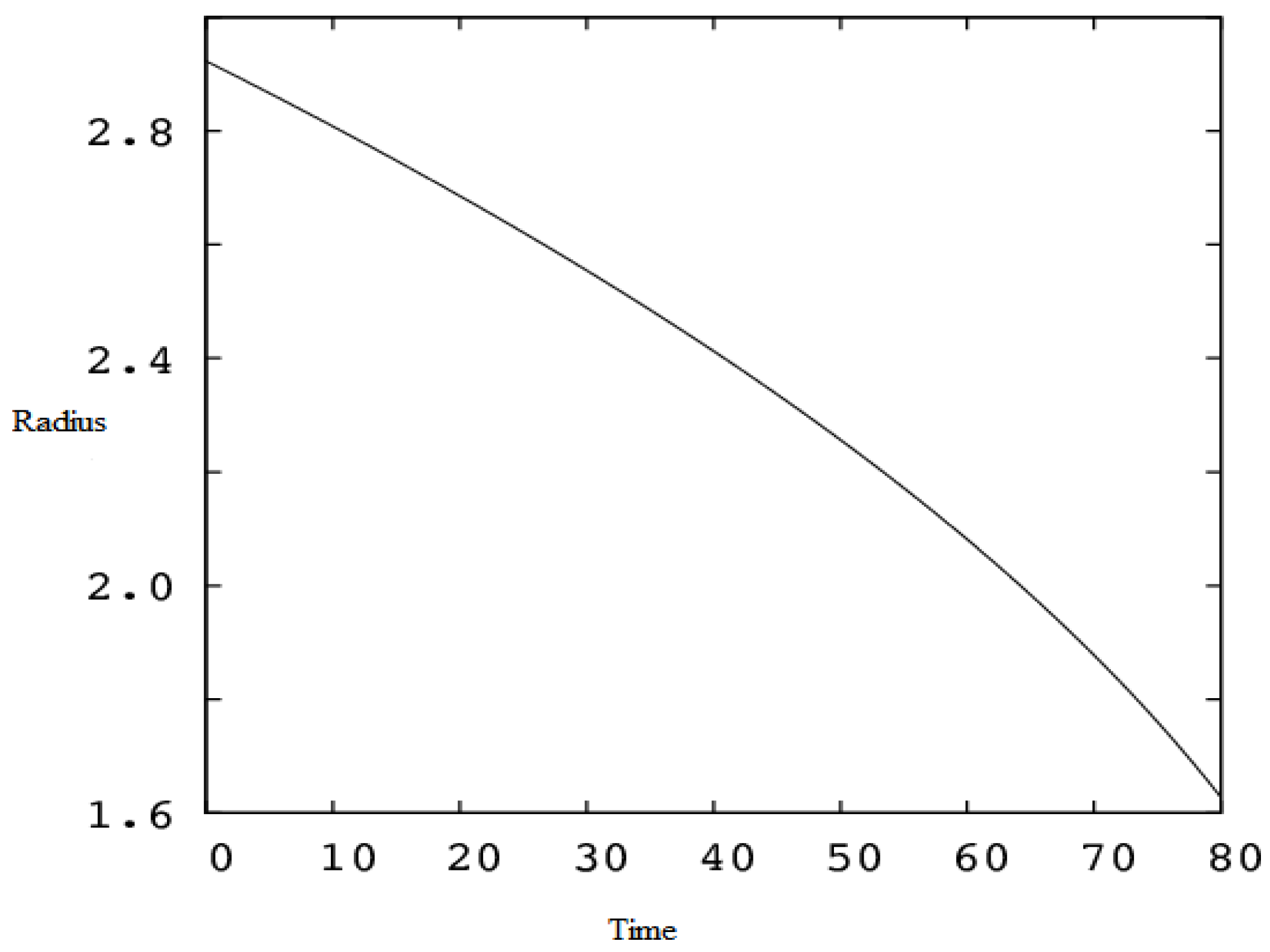
A crucial feature is the anisotropy index of
, where it is evident that the charge induces such anisotropy. When the charge is zero, the anisotropy index is also zero. The time evolution of the distribution radius and the variation of the physical variables are detailed in
Figure 1, with the radius of the distribution, which inevitably collapses, being illustrated.
5. Discussion
Initially, in the search for solutions for the Einstein–Maxwell system (17)–(20) proposed in this study, there were no limitations regarding the specification of the values of the constants
k, l, and the initial electric charge
C (25); see Equations (48)–(50). What was required is that the choice allows for physically acceptable behaviors, as discussed in
Section 4 above. Any choice of the parameters listed must be consistent with the condition of −1 <
< 1 and
M > 0 (defined in Equation (26)) in the initial light cone (surface of the matter distribution).
The evolution with time of the distribution radius in
Figure 1 shows that the matter distribution collapses inexorably. The parameters used in the simulation are
k = 0.25,
l = 0.30, and the initial data of the initial charge and the radius
s(0) = 0.75 and
a(0) = 0.23, respectively [
9,
24].
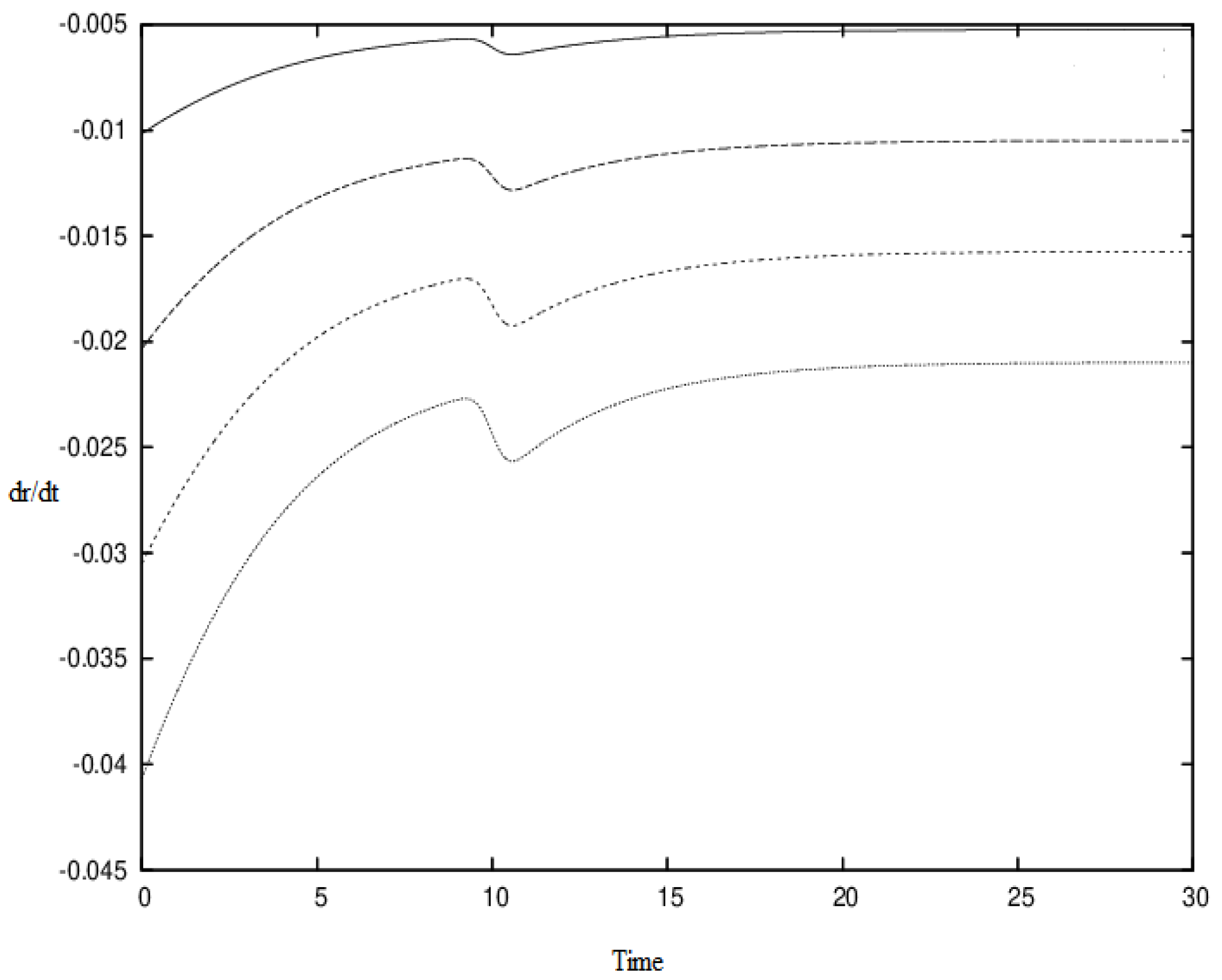
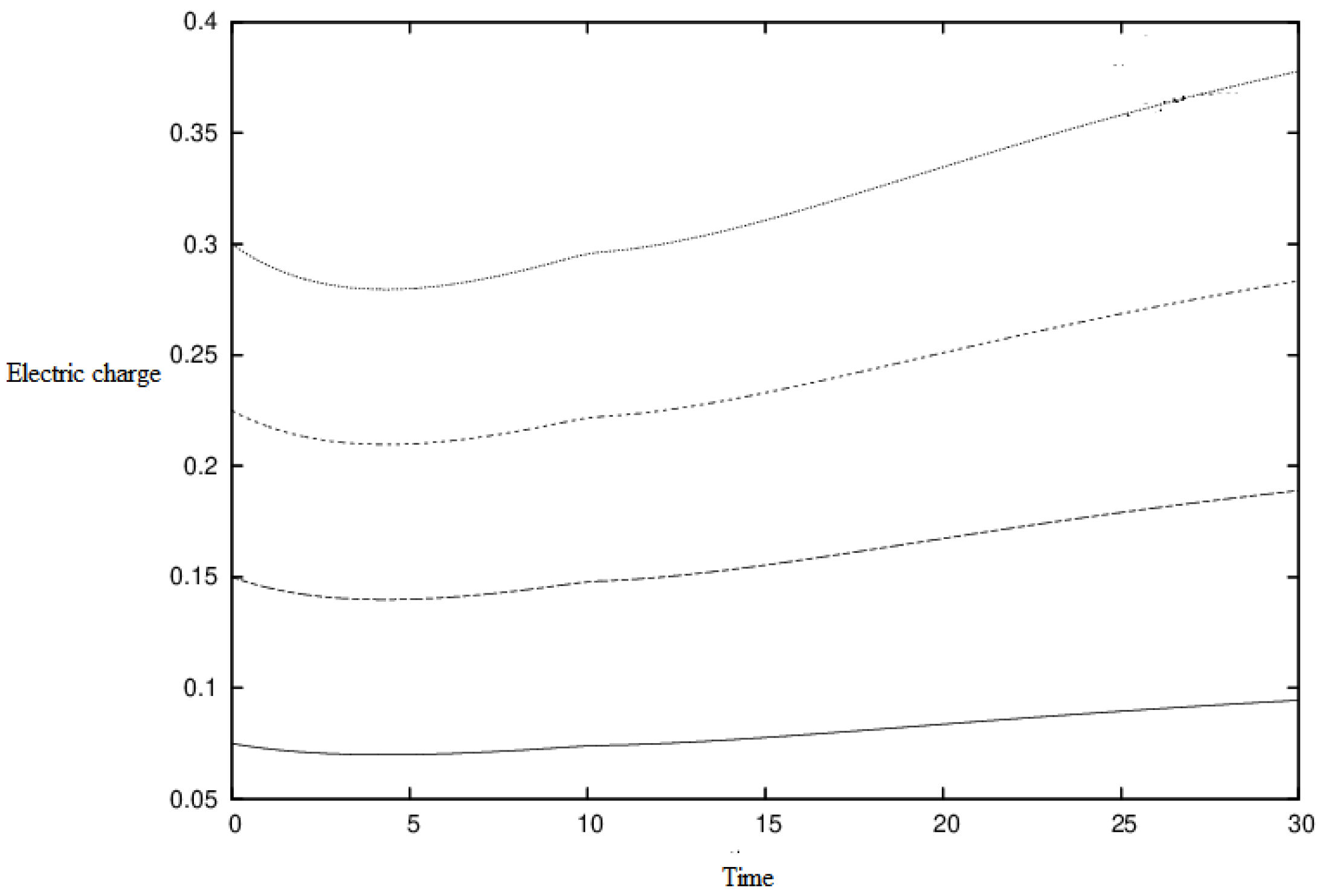
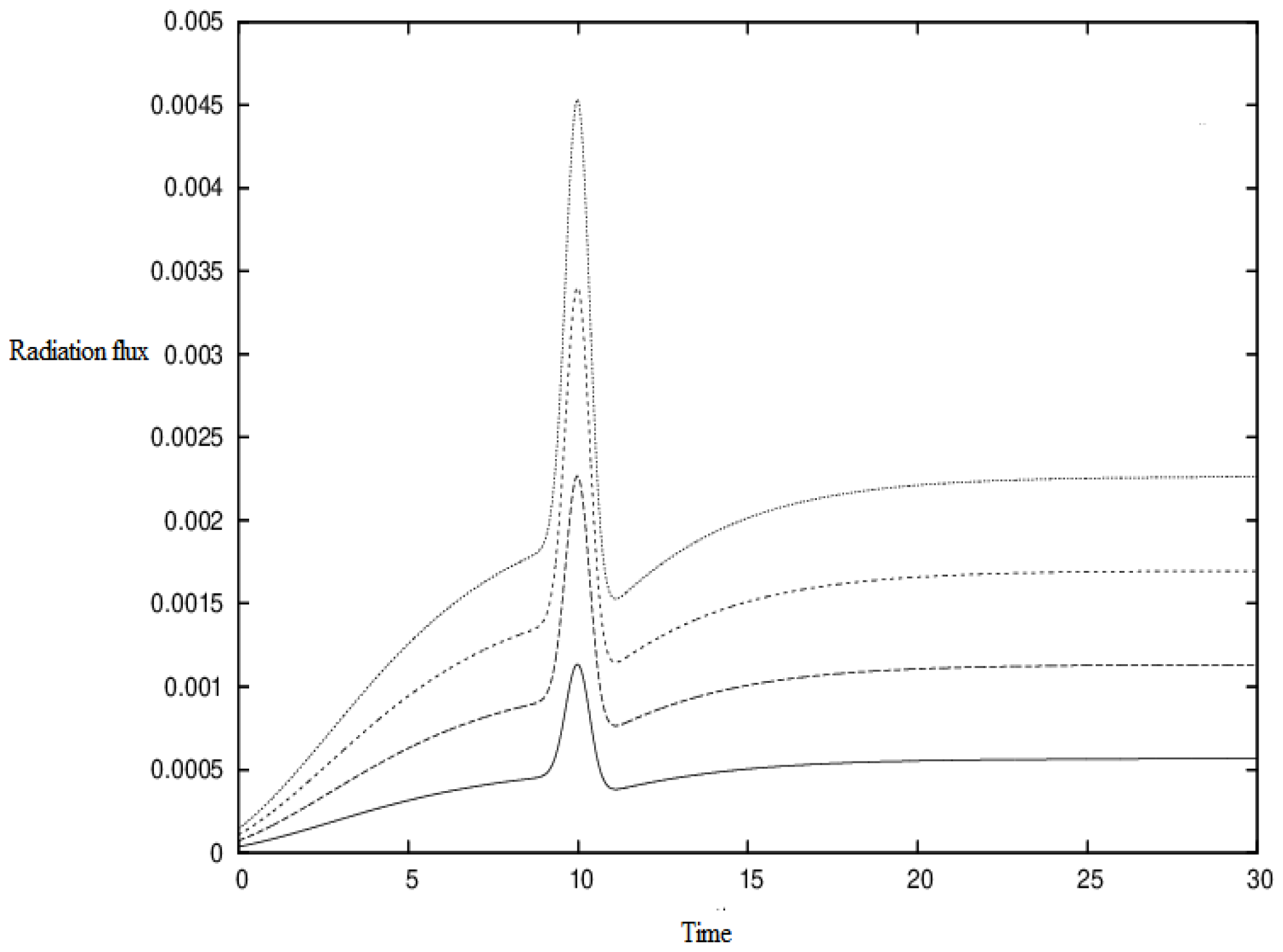
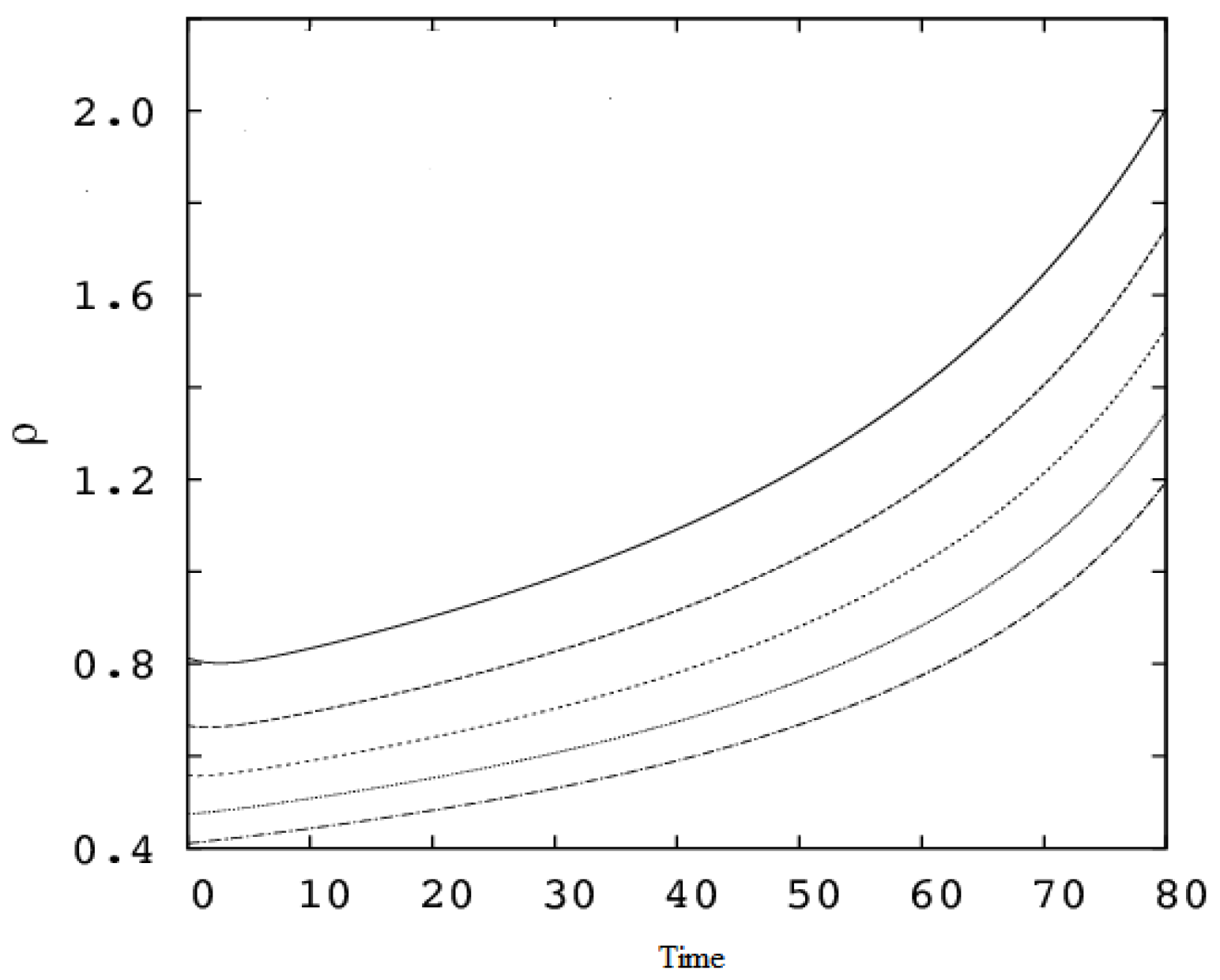
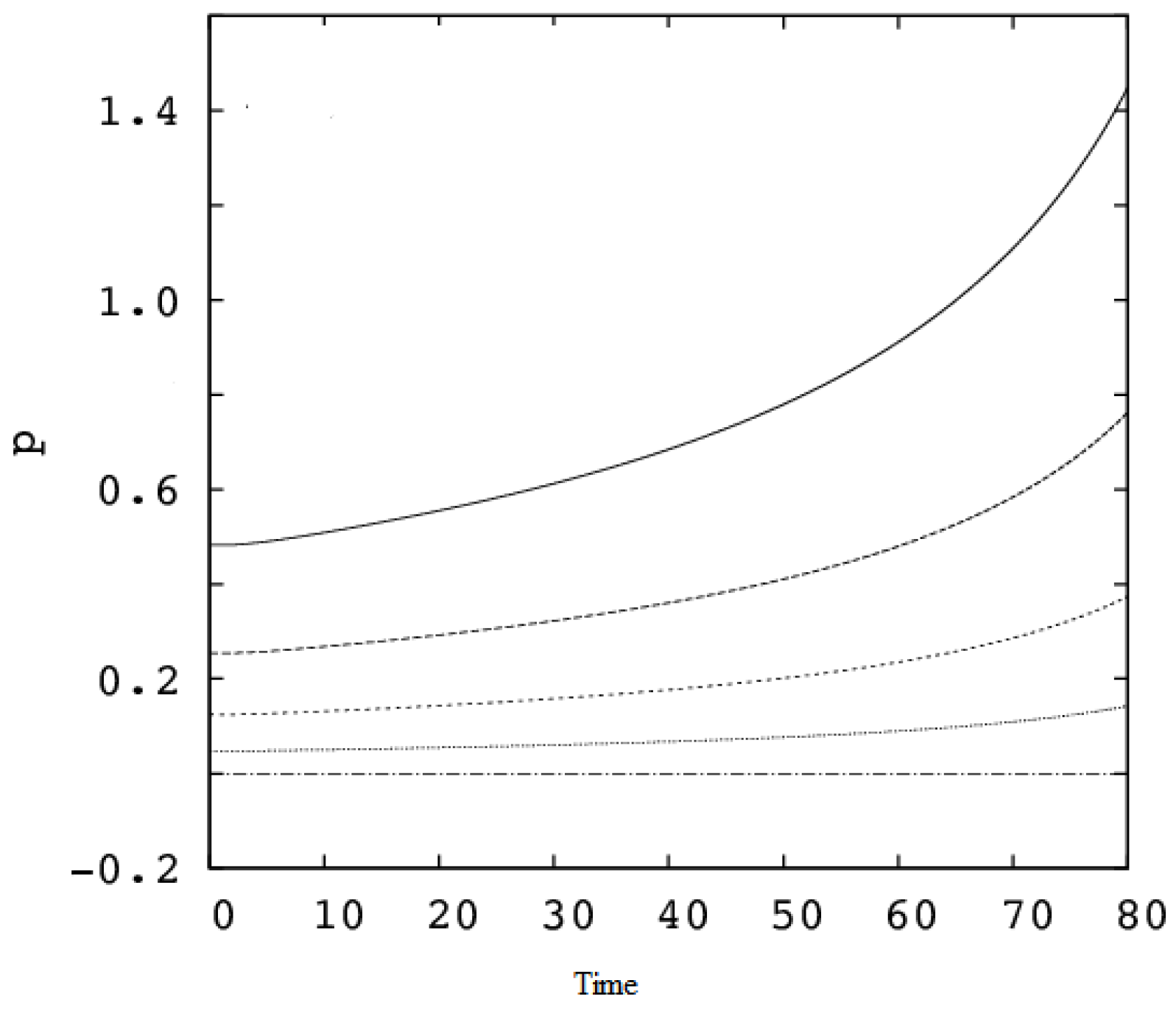
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6 show, respectively, the velocity
dr/dt (11), the charge function,
s, the radiation flux,
ε, the matter density,
and the pressure,
p for the set of initial conditions:
a(0) = 5,
M(0) = 1,
(0) = −
,
s(0) = 0.5, with
k = 0.35,
l = 0.5, and different
r/a values as indicated. From
Figure 3, it follows that at any time, the interior electric charge for any comoving space marker
is always less than the total electric charge enclosed by the boundary surface. Therefore, the electric charge for inner regions can, actually, increase.
Due to the effect of the repulsive force, the charged matter distribution is expected to exhibit a larger mass and radius than for the uncharged matter. This phenomenon resembles that which was observed in Refs. [
14,
25]. Notably, the presence of the electric field results in an increase in the gravitational redshift at the surface; consequently, an observer then perceives a more distant compact distribution compared to the no-charge scenario. This aspect was used to check the validity of the code.
It should be noted that
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6 represent a selection of various executions of the code with different initial conditions of the radius
a(0) and with different values of the self-similar variables
k, l, and total charge
C.
The primary motivation for this study was based on previous results employing the same system and solutions but with a different transport mechanism, i.e., the diffusion limit [
11]. The evolution of the distribution varies markedly due to heat flow: the presence of electric charge prevents collapse, resulting in a final state with oscillations. In this paper, the electric charge does not alter the fate of gravitational collapse.
In this study, the Einstein–Maxwell equations are resolved with the inclusion of the homothetic vector, resulting in the creation of realistic generalized exact models featuring charge and pressure anisotropy. A thorough physical analysis was conducted on this newly generated class of solutions to assess its physical viability. The examination revealed regularity of matter variables and gravitational potentials at the distribution center, satisfaction of energy conditions, and adherence to stability criteria. Notably, our generalized set of exact solutions builds upon earlier explorations [
9,
11,
26,
27,
28,
29,
30,
31,
32,
33].
A feature of great importance is the anisotropy factor. In Ref. [
32], similar results were obtained despite having carried it out with the Bondi metric, and this study has been undertaken with the Schwarzschild metric, straightforwardly showing that the charge induces anisotropy in both cases. When the charge is zero, the anisotropy factor also becomes zero. This observation was used to validate the code, given that results have been previously presented in the case of zero charge. It can be seen in
Figure 1 that the radius of distribution falls over time, with a further observation that the electric charge does not prevent the collapse, unlike in the study developed in Ref. [
11], where the determining factor to stop the collapse is the flow of heat.
6. Conclusions
In this investigation, we delved into a model of an anisotropic compact star endowed with electric charge. The exploration led to the obtaining of an exact solution within the framework of the Einstein–Maxwell equations, showcasing a self-similar symmetry. Specifically, the [fits better, the scrutiny cannot belong to someone] scrutiny extended here to instances where the parameters k and l deviate from zero. The analysis distinctly illustrates the commendable behavior of the metric variables and the metric potentials ν and μ across the entire distribution, signifying their stability and cohesiveness.
Our study focused on incorporating electric charge as a specific manifestation of anisotropy within spherical symmetry. Leveraging the free streaming approximation as a transport mechanism, we implemented a dynamic model, employing a self-similar spacetime for the interior region. Emphasis was placed on scrutinizing the final state of gravitational collapse, exploring the ramifications of dissipation through the free streaming of radiation and local anisotropy stemming from electric charge. The assumption of self-similarity facilitated the simplification of the problem into a system of ordinary differential equations, with boundary conditions dictated by matching to a Reissner–Nordström–Vaidya exterior solution.
With free streaming, the interior was found to evolve under a total charge surpassing the maximum allowable charge in the diffusion limit derived in prior studies [
11,
32]. The system deviates from equilibrium and undergoes collapse. The contribution of electric charge to the collapse parallels how anisotropy, with tangential pressure exceeding radial pressure, favors collapse, as elucidated in earlier studies [
25,
26]. A critical total electric charge (or anisotropy parameter) exists, defining the boundaries within which the system evolves according to the Einstein–Maxwell system of field equation constraints.
To ascertain the universality of the results presented in this paper exploring more general solutions of the symmetry equations is imperative. Nevertheless, the outcomes derived through the anisotropic approach align with those previously reported when the steady state is the final state [
27,
28].
To ascertain the universality of the results presented in this paper exploring more general solutions of the symmetry equations is imperative. Nevertheless, the outcomes derived through the anisotropic approach align with those previously reported when the steady state serves as the final state [
28,
29].