Complex Transitions of the Bounded Confidence Model from an Odd Number of Clusters to the Next

Abstract

The bounded confidence model assumes simple continuous opinion dynamics in which agents ignore opinions which are too far from their own. The two initial variants—Hegselmann–Krause (HK) and Deffuant–Weisbuch (DW)—of the model have attracted significant attention since the early 2000s. This paper revisits the version of the HK model applied to a probability distribution, earlier studied by Jan Lorenz. It shows that the bifurcation diagram depends on the parity of the size of the discretisation and that adding a small noise to the initial conditions leads to complex transitions involving several phases.

1. Introduction

The field of sociophysics produces a wide variety of models and invests a lot of effort into their study. These models are new conceptual objects lying at the boundary between mathematics, physics and computer science. From the early models of James Sakoda  [1] and Thomas Schelling  [2], the aim was to instantiate the complex interactions between individual and collective dynamics or between psychology and sociology [3], that physicists tend to call the interactions between micro and macro behaviours. Serge Galam illustrates this point with his extensive production of models about diverse social dynamics such as pyramidal vote, minority opinion diffusion, the diffusion of terrorist activities and the formation of coalitions and uses a variety of tools from physics to study them (for instance, see a review in Ref. [4]). The models used in the field indeed often require sustained theoretical efforts to fully formalise the micro–macro dynamics (see for instance the voter model [5,6] or the Axelrod model of culture [7,8] or the CODA opinion and action model [9]). This paper presents such an effort to understand the details of the collective dynamics emerging from specific models that can be related to sociophysics: bounded confidence models of opinions.

The idea the bounded confidence model, namely of agents that are influenced by others’ opinions only when these are close enough to their own, appeared almost simultaneously in two variants in the early 2000s. The Hegselmann–Krause (HK) variant [10], inaugurating the term bounded confidence to designate the model, was motivated by the dynamics of opinions within groups of experts, and assumes that the agents consider the opinions of all of the others when revising their own. The Deffuant–Weisbuch (DW) variant [11,12] was initially aimed at modelling exchanges among farmers and assumes that agents revise their attitude when discussing with a single randomly chosen other.

Running these models with agents that hold the same confidence bound leads to one or more separate clusters of opinions, depending on the value of the confidence bound. A number of papers are devoted to studying these models and their variants [13]. Early papers study the model in which all agents have the same confidence bound, showing the details of the bifurcation diagrams when model parameters change. Other researchers investigate populations with different confidence bounds. Several studies focus on including so-called extremists agents, whose opinion is at the border of the opinion interval [14,15,16]. Others consider agents with confidences drawn in a given interval [17]. Many papers assess the effect of different types of networks of interactions [18,19,20], and in some of them, the topology changes with rules depending on the opinion dynamics [21,22]. Introducing noise into these models also significantly modifies their qualitative behaviour [23,24,25]. Some reviews are fully or partly devoted to these models and their variations [13,26,27].

This paper focuses on a specific theoretical approach, initially proposed in Ref. [28] to study the DW variant and then by Jan Lorenz [29] to study the HK variant. The approach uses a probability distribution of the opinions instead of a discrete set of opinions. Therefore, it approximates the behaviour of the model starting from a perfectly uniform initial distribution and an infinity of agents. Reference [28] identifies several features of the model that were not well apparent when running it in its agent version. The main feature is the periodicity of the model which is made apparent by changing the commonly used variables of representation. Another feature is the systematic presence of smaller clusters, called minor or secondary clusters, in addition to the usual major or primary clusters.

Following Lorenz [29], this paper studies the HK bounded confidence in distribution. As discussed by Lorenz, the utility of a distribution version of the HK model is not straightforward as the discretised initial uniform probability distribution is equivalent to starting with initially equally spaced agents, a case which has been the subject of several papers [10,30]. Moreover, the discretisation introduces approximation errors, whereas a computation with rational numbers yields an exact result. However, the distribution approach is more efficient computationally, making systematic simulation studies easier. With this approach, Reference [29] shows that, with the HK model, the number of clusters does not change monotonously when the bound decreases. Indeed, generally, a central cluster reappears instead of two clusters equally distant from the center. Lorenz notices long convergence times, indicating metastable states in this case.

This study replicates the approach of Ref. [29] with several differences: first, this study uses the same axes of representation as in Ref. [28], in order to make more apparent a possible periodicity. Second, this study uses both odd and even size of discretisation of the opinion axis. The results indeed show a striking difference in the behaviour of the model when the parity of the discretisation size changes. Finally, this paper investigates the effect of adding a small noise to the initial distribution. This leads to complex transitions between an odd number of clusters and the next, involving different phases.

2. The Models and Their Approximation with Distributions

2.1. The Two Variants of the BC Model

Let us consider the initial models, assuming a total mixing of the agents all sharing the same confidence bound $ϵ$. The two variants of the Bounded Confidence model differ in the schedule they use for agents to update their opinions. In the HK variant, all the agents update their opinions simultaneously, considering all of the agents with close enough opinions (see Algorithm 1). Importantly, the HK variant is deterministic. By contract, in the DW variant, at each time step, a couple of agents’ opinions $(a_i,a_j)$ is randomly chosen, and if the distance between opinions is below the confidence bound $ϵ$, then the opinion $a_i$ is updated by its influence on $a_j$ (see Algorithm 2). Note that, in the original version [11], both agents update their opinions. This change is actually not much consequential, as it does not change the general behaviour of the model. In both cases, we assume that the opinions are updated until a convergence criterion is reached. Indeed, in both cases the agents ultimately form clusters that are at more than $ϵ$-distance one from another.

A noticeable difference between the algorithms is that an iteration of the HK model updates all the opinions while an iteration of the DW model updates only a randomly chosen couple of opinions.

Algorithm 1: runHK($[a_1,\cdots ,a_n]$ (initial opinions), $ϵ$ (confidence bound))

Algorithm 2: runDW($[a_1,\cdots ,a_n]$ (initial opinions), $ϵ$ (confidence bound))

2.2. Distribution Version

Let us consider a probability distribution of agents’ opinions of density $\rho$ on the opinion range $[0,1]$, or more conveniently $[-1,1]$. Theoretically this density is continuously defined over this range. Computers cannot manipulate such an object and we approximate the continuous density by a vector of size $n_g$ on a discrete subset of the opinion range. We start with a uniform distribution, hence all the values in the vector ${\rho }_0$ are equal to $1/n_g$.

In general, physicists determine the evolution of the distribution over time by writing a master equation, which expresses the balance between the density flows coming and leaving at each discrete location of the discrete grid. Here, I use a method (already used in Ref. [15]) that is equivalent but can be seen as more straightforward. Indeed, it applies the model directly on the discrete sites, stores all the results in a buffer vector $\Delta$ and once all the sites are completed, it updates distribution $\rho$ by adding $\Delta$ to it. Actually, in the end, $\Delta$ includes the results of the master equation at the considered time step. In the case of the HK model, instead of computing a difference, we directly compute the new distribution $\widehat{\rho }$ and then replace $\rho$ with $\widehat{\rho }$.

As the opinion axis is discretised, the method always produces some errors, particularly when the new opinion value coming from the interaction of opinions is not located exactly at a discrete value. In particular, with the DW version, the method should transfer amounts of density from site i on the axis to the theoretical position $(i+j)/2$. When an integer k exists, such that $i+j=2k$, the whole $\delta$ is transferred to site k. However, if $i+j=2k+1$, then it would be arbitrary to transfer the whole $\delta$ to site k or to site $k+1$. Therefore, $\delta /2$ is transferred to each site k and $k+1$. Generalised to the HK model, the method defines the new position a where the amount of density $\delta$ should be transferred as a weighted average that can be located anywhere in a segment $[k,k+1]$. Then the method affects $\delta$ to sites k and $k+1$ proportionally to the proximity of a to the site. $a-k$ is the proximity of a to site $k+1$ and $k+1-a$ is the proximity of a to site k. Lorenz uses the same approximation in his distribution version of the HK model [29].

Then the investigation process includes, for different values of the confidence bound $ϵ$, running the model approximation until the distribution stabilises and then determining the positions and amplitude of the final clusters. With the chosen approximation, the convergence is ensured when there are only either a single or a couple of isolated sites with non-zero density; isolated meaning that there is no other non-zero site at a distance lower than $n_{ϵ}$. Algorithms 3 and 4 display the pseudo code of the method for the two variants of the BC model.

As noticed in Ref. [28], it is convenient to use an opinion range $[-1,1]$ to vary $1/ϵ$ instead of $ϵ$ and $a/ϵ$ instead of the opinion a because the DW model then shows a periodic behaviour in the vicinity of $a/ϵ=0$. Taking this into account, and following [28], we also define $n_g$ as an integer close to $2n_{ϵ}/ϵ$ (number of discrete values describing the probability distribution ${\rho }_t$), where t is the number of iterations.

Algorithm 3: distributionRunDW($ϵ$ (confidence bound), $n_{ϵ}$ ($ϵ$ discretisation size))

Algorithm 4: distributionHK($ϵ$ (confidence bound), $n_{ϵ}$ ($ϵ$ discretisation size))

In order to evaluate the importance of a cluster, its mass (total distribution in the cluster) is divided by $2ϵ$. If the result is higher than 0.5, the cluster is major. If it is lower than 0.01, it is minor. Reference [28] explains the emergence of minor clusters in the DW model qualitatively. Their explanation suggests that the HK model should not produce minor clusters.

2.3. Dealing with Computational Instabilities: Forcing Symmetry and Adding Noise

Lorenz notices [29] cases of computational instabilities in the HK distribution model for some values of the parameters, which are revealed by asymmetric results. Indeed, as the initial state and the rules of change are all symmetric, these asymmetries necessarily come from computational errors.

This study deals with these potential computational instabilities in two ways. Firstly, the model runs on only half of the distribution and then it copies these results by symmetry to the other half. In this way, computational instabilities lead to different outcomes that are always symmetric. Secondly, in order to better understand the behaviour of the model in these zones of computational instability, I compare the results to the ones obtained when adding a small amount of noise to the initial distribution. In my tests, the initial mass $1/n_g$ of each discrete site in the distribution becomes $(1+\delta )/n_g$, where $\delta$ is uniformly drawn in $[-0.001,0.001]$. I only apply this noise in the segment $[-ϵ,ϵ]$, as the instabilities only occur in this part of the space.

3. Simulation Results

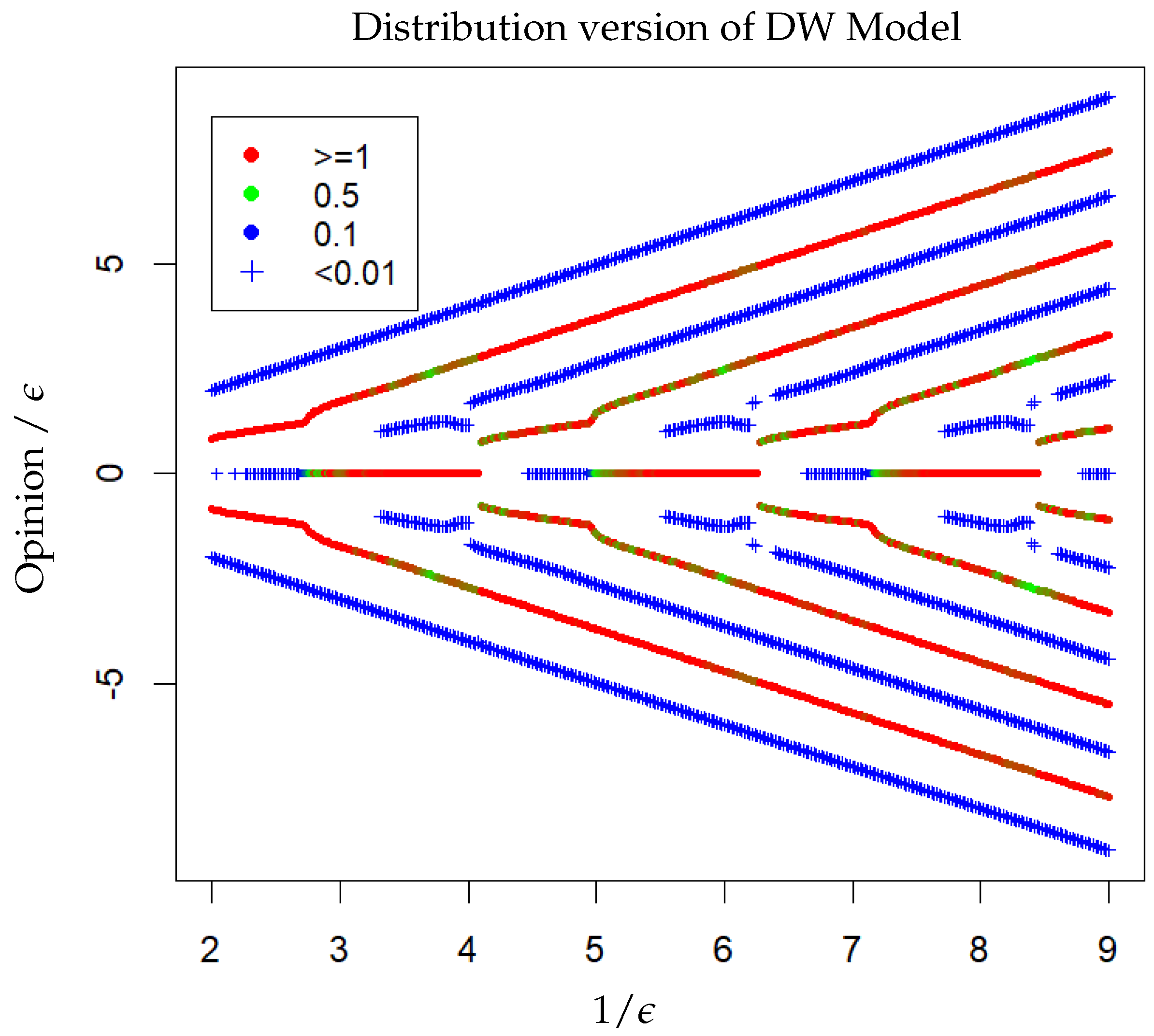
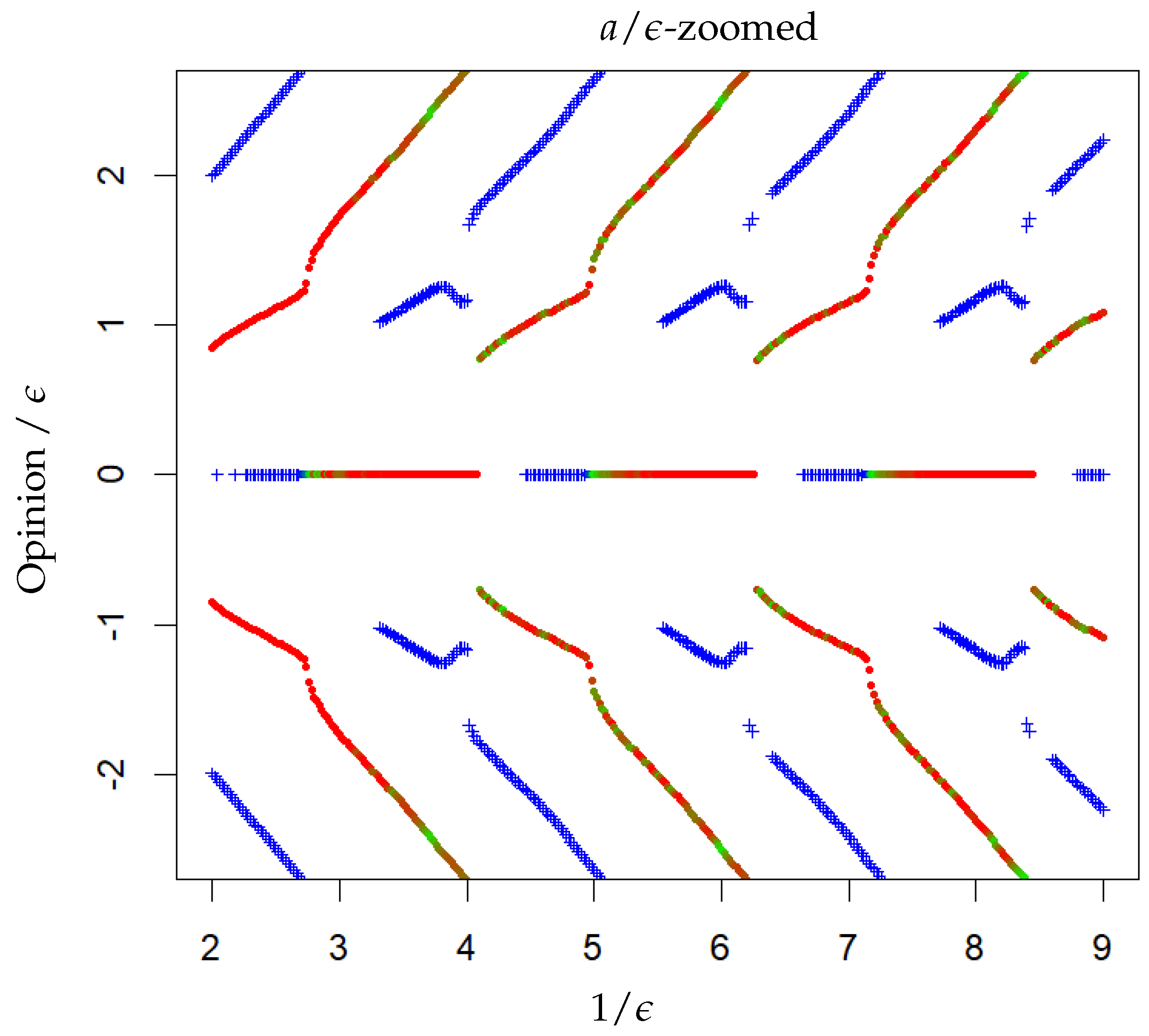
3.1. DW Model

Figure 1 shows the final clusters of the DW model for opinions in range $[-1,1]$ and $1/ϵ\in [2,9]$. The colour code of site i is determined by $\rho \left(i\right)/2ϵ$ where $\rho \left(i\right)$ is the mass at the site. For the major clusters, this value varies from 0.5 (green dots) to 1 and higher (red dots). The smaller values are represented as blue dots, shown by the plus symbols for quite low ones (lower than 0.01), representing the minor clusters.

Figure 1. Positions of the clusters ($a/ϵ$) in the full (upper) and zoomed (lower) $a/ϵ$ ranges for the opinion, a, range $[-1,1]$. The discretisation of $ϵ$ is $n_{ϵ}=101$. The colors and symbols represent the values of the total mass of the cluster divided by $2ϵ$ as indicated. See text for details.

Figure 1 replicates the results from Ref. [28] (also replicated by Lorenz [29], but not using the same axes) with systematic minor clusters and a clear periodicity. I find a discontinuity in the presence of the minor clusters that does not appear in Ref. [28], and their positions are slightly different. These differences are small and could come from a different convergence criterion (the simulations stop when the absolute value of the change vector is lower than ${10}^{-5}$).

Figure 1 was obtained with only odd values of $n_g$, the size of the total discretisation. However, taking even values instead yields exactly the same results. Let us recall these results in order to contrast them with the ones obtained with the HK model, which are the focus of this paper.

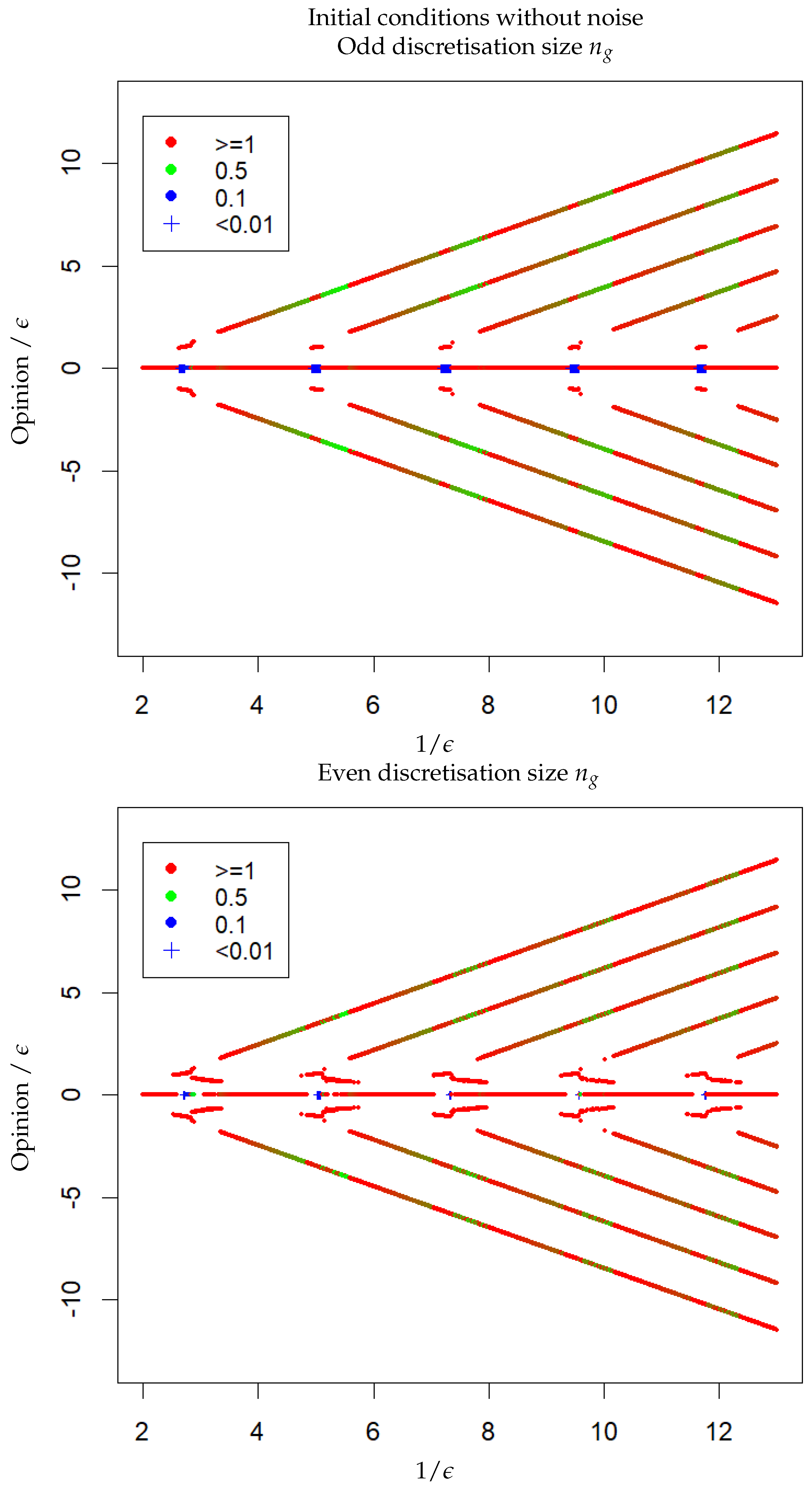
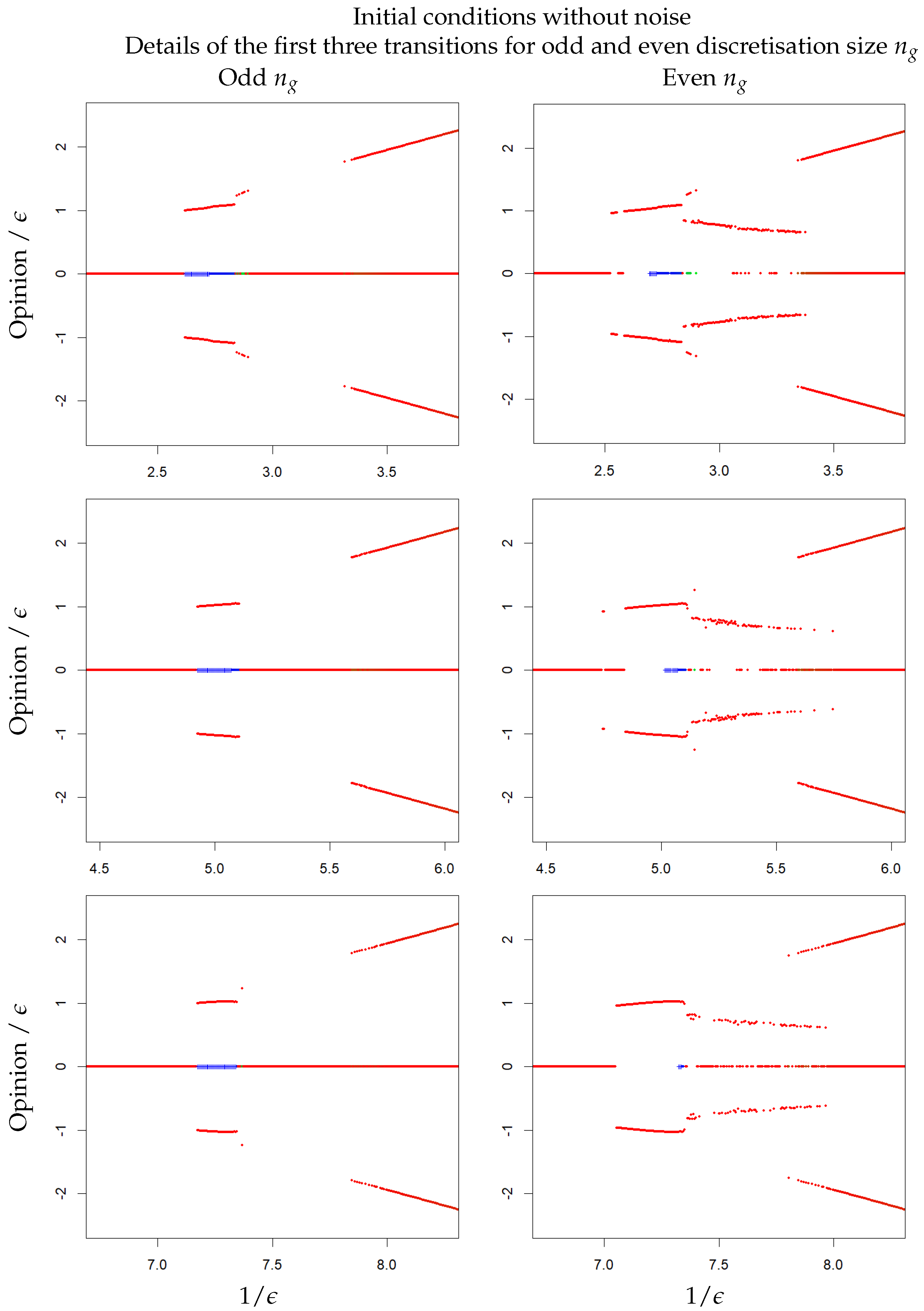
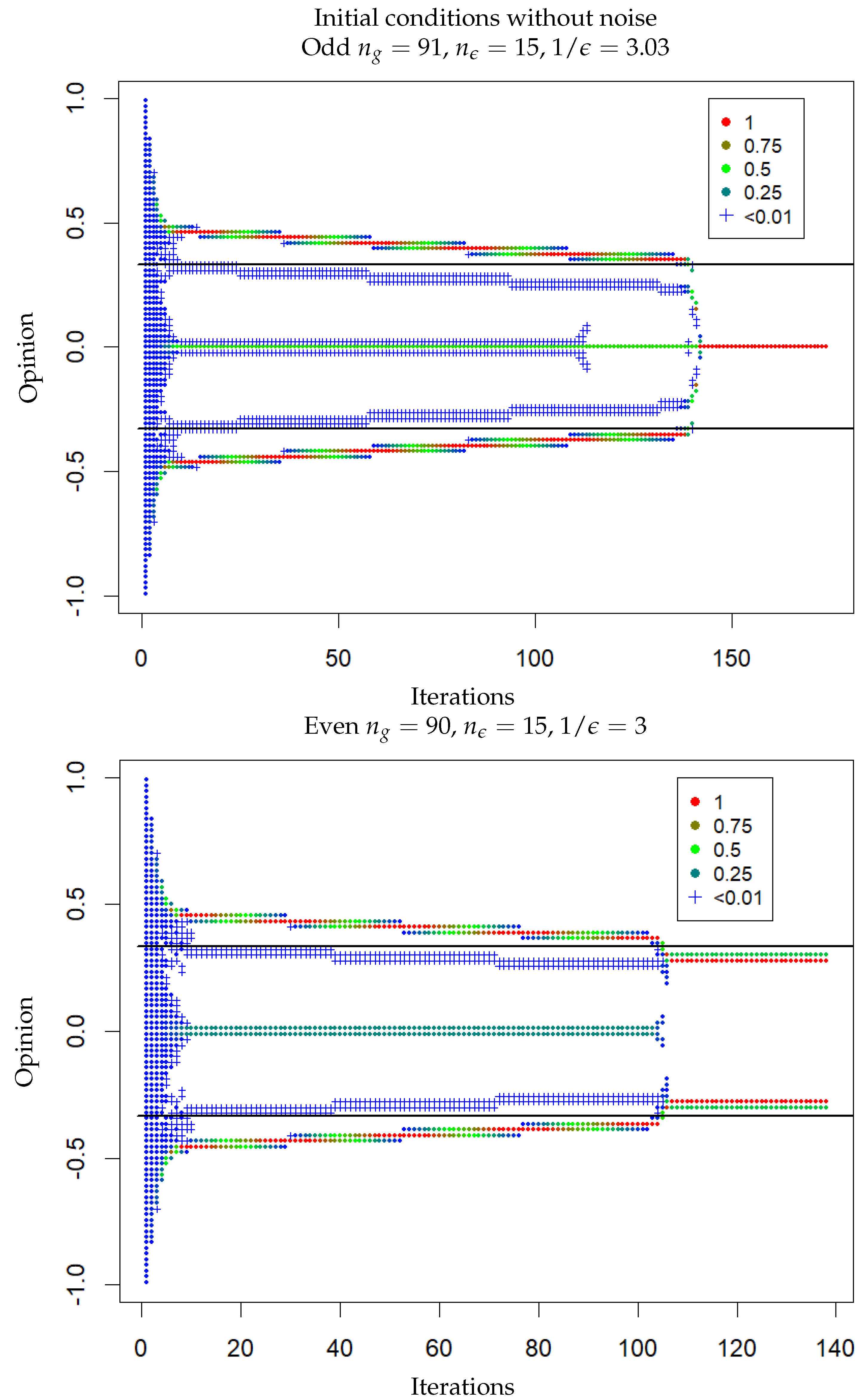
3.2. HK Model with Odd or Even Discretisation Size

Figure 2 shows the positions and types of clusters obtained with the HK distribution model, with $1/ϵ$ varying from 2 to 13 (with an opinion range of $[-1,1]$), with odd (top) and even (bottom) discretisation sizes $n_g$. In both cases, the discretisation of $ϵ$ is $n_{ϵ}=1001$. The results look periodic for both odd and even values of $n_g$, but they are quite different. Moreover, unlike the DW model, in which, periodically, one new central cluster or two new central clusters are created and remain stable, it looks that the HK model goes through periodic complex transitions with instabilities until two new major clusters stabilise, at about $2ϵ$ from the centre.

Figure 2. Positions of the clusters ($a/ϵ$) for the opinion range $[-1,1]$) for the odd (upper) and bottm (lower) opinion range discretisation, $n_g$. $ϵ$ discretisation size, $n_{ϵ}=1001$. The colors and symbols represent the values of the total mass of the cluster divided by $2ϵ$ as indicated.

In the case of odd values of $n_g$ (Figure 2, upper) in each transition, when $1/ϵ$ increases, two clusters around a minor cluster in the middle appear briefly, replacing a central major cluster, and then there is a central cluster which is alone again, and finally two clusters around the central one, at a distance of about $ϵ$. This phenomenon was already observed by Lorenz [29], and highlighted in the title of his paper (“consensus strikes back”). However, the periodicity was less apparent in Lorenz’s representation. The details of the three first transitions shown in Figure 3, left, suggest that this periodicity is not perfect. In the first and the third transitions, there are a few more values of $1/ϵ$ leading to a couple of major clusters around the centre, where the equivalent values lead to a central cluster in the second transition. Moreover, the slope of the positions of the clusters appearing at the beginning of the transition looks to be smaller in the second transition than in the first, and even smaller in the third.

Figure 3. A closer look at the first three transitions for odd (left) and even (right) opinion discretisation sizes shown in Figure 2.

In the case of even values of $n_g$ (Figure 2, lower), the transitions include more cases of convergence towards a couple of clusters around the centre. Moreover, the transitions are more complicated as can be seen in more details in Figure 3. The central cluster separates into two clusters which remain for more values of $1/ϵ$ than when $n_g$ is odd, and then the positions of these clusters move closer to the central cluster as $1/ϵ$ increases. Moreover, the results then look unstable as there are cases where the central cluster reappears. Again, the transitions are not exactly the same at each period and the instability of the results may not be sufficient to explain all the differences. Indeed, there looks to be significantly more convergences to the central cluster in the third transition.

The difference in behaviour between the odd and even discretization sizes is illustrated by examples of simulation with odd and even values of $n_g$ in Figure 4. The simulations use a smaller discretisation size, $n_{ϵ}=15$ of $ϵ$, for $1/ϵ=3$, which is in the first transition, in order to make all the sites in the distribution visible, with an odd $n_g=91$ in Figure 4, upper, and an even $n_g=90$ in Figure 4, lower.

Figure 4. Examples of runs of HK distribution model for $1/ϵ\approx 3$ and $n_{ϵ}=15$ when the total discretisation, $n_g$, is odd (upper) or even (lower). The two black lines are at $\pm ϵ$. The colors and symbols represent the values of the total mass of the cluster divided by $2n_{ϵ}$, as indicated.

In both cases, a central major cluster, two major clusters at positions larger than $\pm ϵ$ and two minor clusters located just below $\pm ϵ$ appear after a few iterations. Then, the minor clusters quite slowly attract the two major clusters towards the centre, until the major clusters arrive at $ϵ$ from the central cluster.

Then, the process depends on the parity of $n_g$. If $n_g$ is odd, the central cluster involves only one discrete site with a significant mass (with possibly very small residual masses in the sites just below and above). Then, the two major clusters at $\pm ϵ$ are both attracted by the central cluster, yielding a single major central cluster. If $n_g$ is even, the central cluster is made of two sites with a significant mass. Each of them is attracted by the closest of the two clusters situated at $\pm ϵ$ and the final result is two major clusters at the same distance, smaller than $ϵ$, from the centre.

These examples clarify why central clusters are more likely with odd $n_g$ and couples of clusters around the centre are more likely with even $n_g$.

It can be argued that a central cluster including only a one site with a significant mass is a better representation of the agent model (taking initially regularly spaced agents). Indeed, starting with two sites with significant masses defining the central cluster, the agent algorithm would progressively merge them. This justifies Lorenz’s choice to privilege the odd discretisation size.

However, the situation becomes more complicated than the two simple cases shown in Figure 4 suggest. Indeed, these cases hide potential instabilities that can take place, which are more likely when the discretisation size $n_g$ is larger. In order obtain a better view of these instabilities, let us now run the model when adding a small noise to the initial state.

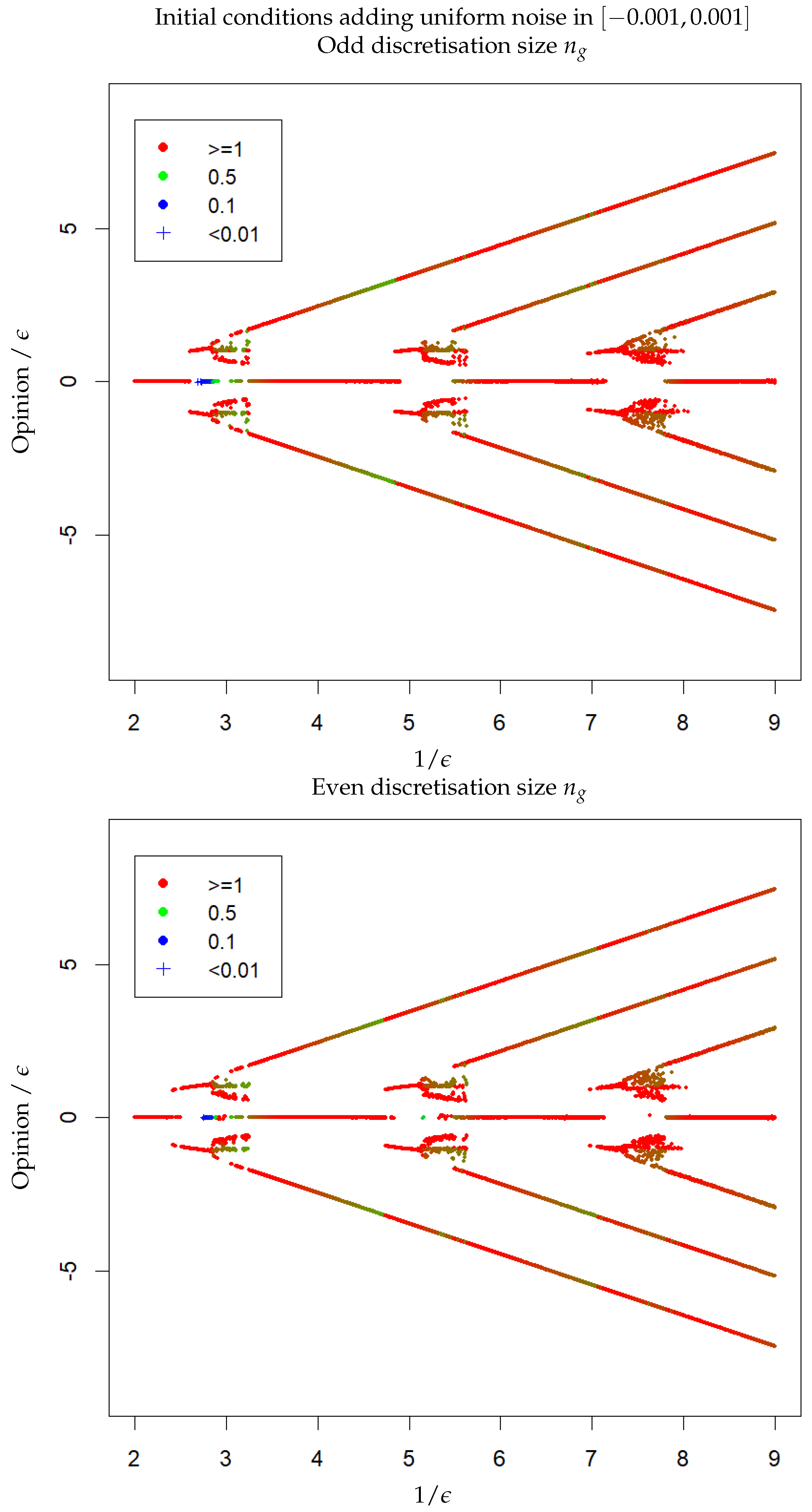
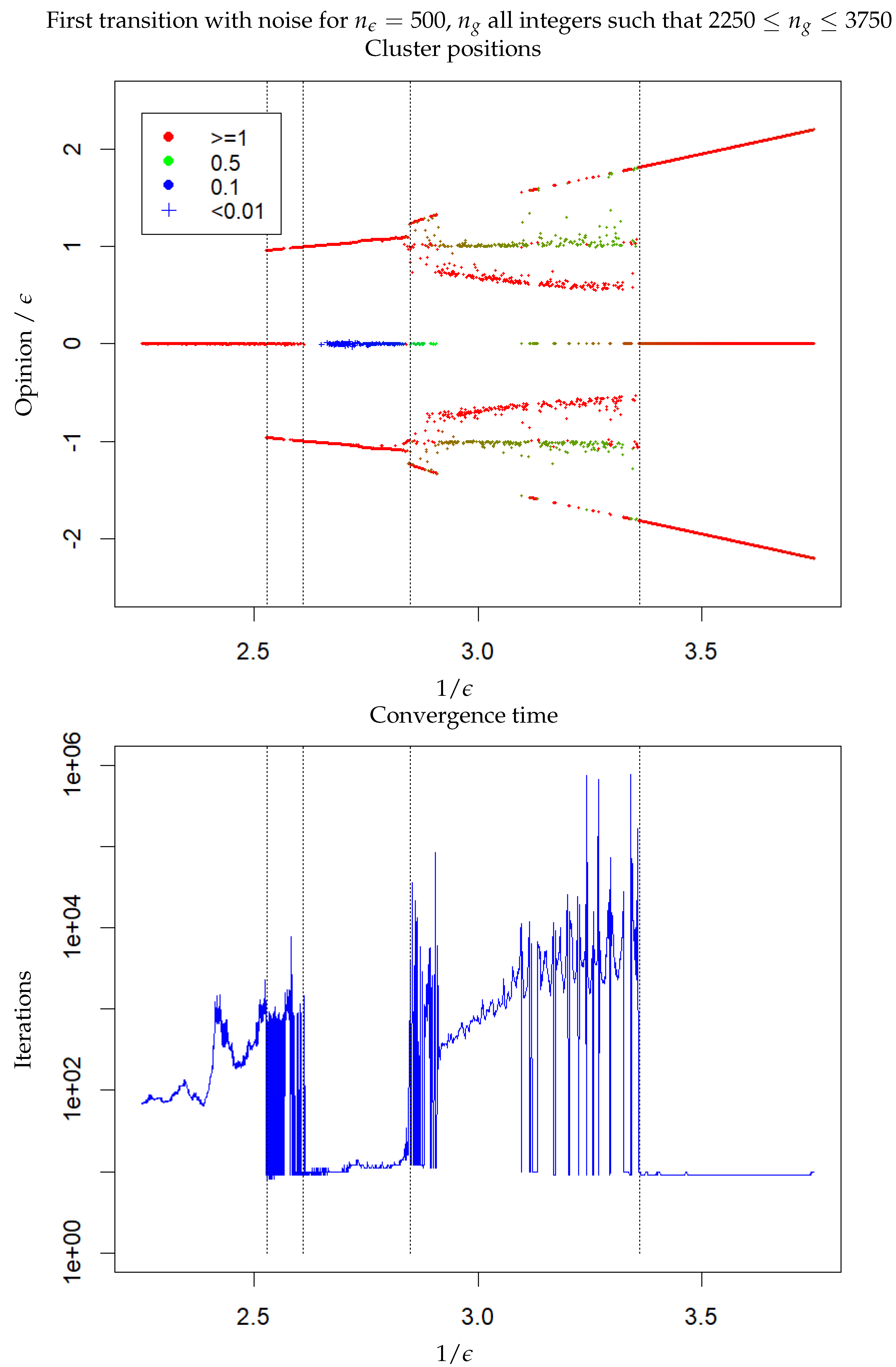
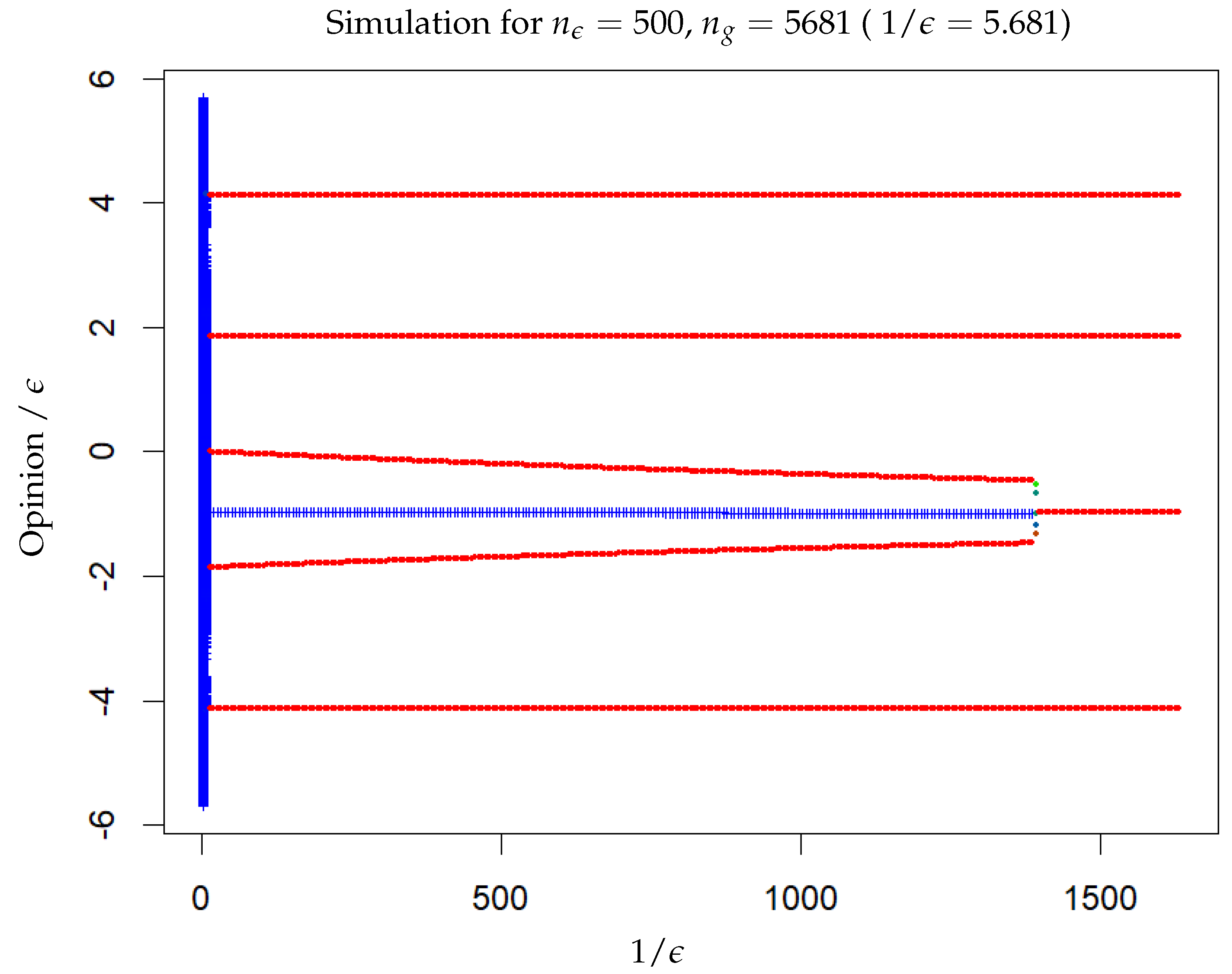
3.3. HK Model with Noise on the Initial Conditions

Figure 5 shows the results of the HK model in distribution when adding a small noise to the initial distribution, as specified in Section 2.3. In this case, the unstable part of the transition appears clearly. The odd (Figure 5, upper) and even (Figure 5, lower) discretisation sizes $n_g$ yield rather similar results.

Figure 5. Positions of the clusters ($a/ϵ$) (opinion range $[-1,1]$) for odd (upper) and even (lower) opinion range discretisation, $n_g$. $ϵ$ discretisation size $n_{ϵ}=101$. The colors and symbols represent the values of the total mass of the cluster divided by $2n_{ϵ}$, as indicated.

In order to obtain a more precise view of the model’s behaviour at the transition, I run the model for $n_{ϵ}=500$ for 1501 values of $1/ϵ\in [2.25,3.75]$, an interval in which the first transition takes place, and $n_g$ takes all of the integer values such that $2250\le n_g\le 3750$. The values of $n_g$ are thus alternatively odd and even. Indeed, in this case, the value the discretisation size $n_g$ is $1000/ϵ$. Figure 6 shows the results, with the cluster positions in Figure 6, upper, and the convergence times in Figure 6, bottom.

Figure 6. Positions of the clusters ($a/ϵ$) (upper) and convergence time (lower) (opinion range $[-1,1]$). Discretisation $n_g$ is odd or even. $ϵ$ discretisation size $n_{ϵ}=500$. Upper: the colors and symbols represent the values of the total mass of the cluster divided by $2ϵ$, as indicated.

One can identify three main phases in this transition (delimited by dotted lines on Figure 6):

• From $1/ϵ\approx 2.53$ to $1/ϵ\approx 2.62$, for an odd $n_g$, one central cluster is reached after a few hundred iterations, and for an even $n_g$, two clusters, at distance roughly $\pm ϵ$ from the centre (slowly increasing with $1/ϵ$), are reached after about 10 iterations.
• From $1/ϵ\approx 2.62$ to $1/ϵ\approx 2.85$, two clusters at a distance of roughly $\pm ϵ$ from the centre (slowly increasing with $1/ϵ$) with one minor cluster at the centre are reached after a dozen iterations,
• From $1/ϵ\approx 2.85$ to $1/ϵ\approx 3.35$, there are two clusters in asymmetric positions and of different masses. The cluster of smaller mass is located at $\pm ϵ$ and the one of bigger mass is closer to the centre on the other side, and moves slowly closer to the centre when $1/ϵ$ increases. The convergence is reached after a large number of iterations (several thousands), except at the beginning and in the second half the phase where some cases of fast convergence also appear.

Figure 7 shows two examples of simulations in the first phase of the transition, one for an odd discretisation size $n_g=2531$ ($1/ϵ=2.351$; Figure 7, top) the other for an even $n_g=2532$ ($1/ϵ=2.352$; Figure 7, middle), and one example in the third phase for $n_g=3001$ ($1/ϵ=3.001$; Figure 7, bottom).

Figure 7. Examples of runs with initial noise, for $n_{ϵ}=500$ and $n_g=1000/ϵ$ for the simulations in the first phase (top and middle) and in the third phase (bottom) of the transition. The colors and symbols are as in Figure 1.

In Figure 7, top, for $n_g=2531$, there is a quite small cluster remaining at the centre (blue plus symbols) which slowly attracts both clusters initially located at a bit less than $ϵ$ from the centre until they merge. In Figure 7, middle, for $n_g=2532$, the initial evolution of the distribution is quite similar, except that there is no minor cluster at the centre. Therefore, the two major clusters remain in their positions and the simulation converges in about ten iterations. In this first phase, the convergence is the same with or without noise.

Figure 7, bottom, represents an example of a simulation in the third phase of the transition. In this case, the noise strongly influences the result. The configuration emerging after a dozen time steps includes one major central cluster (in green), two minor clusters located at about $\pm ϵ$ (in blue) and two external major clusters symmetrically located a bit further (in red). Then, the minor clusters attract the two further major clusters and also move progressively closer to the centre. As a consequence of the noise, the configuration is slightly asymmetric. The major external cluster located on the positive side becomes closer than $ϵ$ to the central cluster before the other, and at this moment, it merges with the central cluster and the minor cluster into a major cluster which is closer than $ϵ$ to the centre. The other major external cluster merges with the minor cluster on its side and remains located quite close to $-ϵ$. Certainly, depending on the noise, the first major cluster to merge can also be the one located on the negative side.

This last example explains the shape of the cluster positions in Figure 6, upper, showing two main branches on each side of the centre: the one in red corresponds to the external cluster that arrives closer to the centre first and merges with the central cluster, the other in green is the one that arrives after and only merges with the minor cluster on its side, and remains close to $\pm ϵ$.

Note that, at the beginning and in the second half of the third phase, there are many cases where the minor clusters are located slightly further than $ϵ$ and they directly merge with the external major clusters, with the whole distribution converging to three clusters in a dozen iterations. This explains the frequent oscillations in the convergence time, at the beginning and in the second half of the third phase of the transition (these differences could also define more specific phases in the transition).

Figure 8 shows the positions of the clusters during the transition from three to five clusters (for $1/ϵ\in [4.5,6]$), focusing on opinions a such that $a/ϵ\in [-2.5,2.5]$, where the transition takes place.

Figure 8. Positions of the clusters ($a/ϵ$) (upper) and convergence time (lower) (opinion range $[-1,1]$). The vertical dotted lines delimit the phases of the transition. Upper: the colors and symbols represent the values of the total mass of the cluster divided by $2ϵ$, as indicated.

The second transition (between three and five clusters) is similar to first one (between one and three clusters). Three phases can also be identified as having broadly similar characteristics. Some differences are noticeable in the third phase though. Indeed, in the first transition, one underlines that, in the second half of the third phase, the results can be either an asymmetric configuration of two clusters or a symmetric configuration of three clusters. By contrast, during the whole third phase of the second transition, only the asymmetric configuration of two clusters takes place (here we omit to count the two symmetric clusters that are located further than $2.5ϵ$ and that do not appear in Figure 8, upper). Moreover, a fourth phase can then be identified, in which the results alternate between a new asymmetric configuration, with one major cluster around $\pm ϵ$ and the other around $\pm 2ϵ$, and the standard symmetric configuration of three clusters. The limits of the four phases appear as vertical dotted lines in Figure 8.

An example of a simulation yielding this new configuration is represented on Figure 9. In this case, there is a single minor cluster that is formed between the central major cluster and the first cluster located in its negative side. The minor cluster slowly attracts both major clusters which finally merge. In other simulations, the minor cluster can be formed between the central cluster and the first cluster on the positive side (located around $2ϵ$).

Figure 9. Example of simulation in the fourth phase of the second transition. The colors and symbols are as in Figure 1.

4. Discussion

Starting from a slightly noisy uniform distribution, the HK model of distribution shows surprisingly complex transitions from an odd number of clusters to the next, when the confidence bound, $ϵ$, decreases. Indeed, the first transition (from one to three clusters) includes three different phases. In the first phase, the result depends on the parity of the discretisation. In the third phase, the result is sensitive to small initial asymmetries, because of the presence of persisting minor clusters that slowly attract major clusters.

The second transition (from three to five clusters) shows strong similarities with the first one, but also striking differences. In particular, a fourth phase appears, in which a single persisting minor cluster appears between the central major and one of its neighbours, slowly attracting these clusters until they finally merge. Further investigations are necessary to explain why this fourth phase takes place in the second transition and not in the first one.

We did not investigate the third transition in detail, but strong differences with the two first transitions are clear. These observations suggest that, unlike the DW model, the HK model is not perfectly periodic. Indeed, the differences between the transitions look too systematic to be due to the noise only.

These results suggest that the HK version of the bounded confidence is more different from the DW version than suggested by the comparison made by Lorenz in 2006 [29]. Indeed, the DW version shows a clear periodicity and no sensitivity to the parity of the discretisation or to a small amount of initial noise.

However, before making definite conclusions, it is strongly advisable to closely compare the distribution version of the HK model with its agent version. Indeed, a distribution model is particularly relevant when it averages some randomness in the agent model. This is the case for the distribution version of the DW model, which averages the randomness of the pair interactions of the agent version. As the HK model is deterministic, the distribution version introduces approximations without averaging, hence its relevance is rather questionable. Moreover, as shown by Rainer Hegselmann [31], when starting from regularly spaced agents on the opinion axis, it is possible to compute the exact result of the HK model for a rational confidence bound $ϵ$ and to find all the values of $ϵ$ leading to different outcomes.

However, the results presented in this paper could promote new investigations into the agent model and new interpretations of its results. Therefore, the merit of the distribution version could simply be to provide a different perspective on the HK model, hopefully leading to a better understanding of its properties.

Overall, although the HK version looks simpler in its principle than the DW version, as it is deterministic, the collective behaviours that it generates in the case of initially regularly spaced agents do not look fully understood more than twenty years after its first publications [10,11] about this model. This looks to us a typical example of the general endeavour of sociophysics to understand precisely how collective regularities emerge from individual dynamics.