Abstract
The anisotropic flow of photons produced in relativistic nuclear collisions is known as a promising observable for studying the initial state and the subsequent evolution of the hot and dense medium formed in such collisions. The investigation of photon anisotropic flow coefficients, , has attracted high interest over the last decade, involving both theory and experiment. The thermal emission of photons and their anisotropic flow are found to be highly sensitive to the initial state of the fireball, where even slight modifications can lead to significant variations in the final state results. In contrast, the ratio of photon anisotropic flow stands out as a robust observable, exhibiting minimal sensitivity to the initial conditions. Here, we briefly review the studies of the individual elliptic and triangular flow parameters of photons as well as their ratios and how these parameters serve as valuable probes for investigating the intricacies of the initial state and addressing the challenges posed by the direct photon puzzle.
1. Introduction
Anisotropic flow provides some of the most compelling evidence of the existence of quark–gluon plasma (QGP) in relativistic heavy-ion collisions [1,2,3,4,5]. It serves as a response to the initial spatial anisotropy showing how efficiently this anisotropy is transformed into the final state momentum space anisotropy of the emitted particles [6,7,8,9,10,11].
Relativistic hydrodynamics is known as one of the most successful theoretical frameworks for explaining the observed large anisotropic flow of hadrons in relativistic heavy-ion collisions. The hydrodynamic framework treats the strongly interacting matter produced in these collisions as a ‘nearly perfect fluid’ characterized by its collective behavior and hydrodynamic flow properties [12,13,14,15,16,17,18,19].
Initially, it was believed that non-central collisions between two spherical nuclei or central collisions of two deformed nuclei (such as the collisions of uranium nuclei with a prolate shape) could lead to a substantial elliptic flow of charged particles. Higher order even flow coefficients were anticipated to be non-zero but significantly smaller compared to the elliptic flow of charged particles [12]. However, subsequent observations revealed that even the most central collisions of spherical nuclei could produce a non-zero elliptic flow of charged particles. This observation provided confirmation that event-by-event fluctuating initial density distributions can contribute significantly to the anisotropic flow of particles produced in heavy-ion collisions [20,21,22]. This also resulted in significantly large odd flow coefficients, particularly the triangular flow parameter [23,24].
The anisotropic flow coefficients, , are estimated by expanding the invariant particle number distribution in the transverse momentum plane using Fourier decomposition:
Here, denotes the transverse momentum, y denotes the rapidity and represents the azimuthal angle of the emitted particle. denotes the event plane angle for the nthflow coefficient. The event plane angle is a crucial quantity for the study of anisotropic flow as it provides a quantitative measure of the orientation of the anisotropy in each event. The anisotropic flow coefficients are extracted from experimental data and can be compared to theoretical models to understand the various properties of the QGP such as its viscosity, formation time, equation of state, etc. [5,25].
Photons produced in relativistic nuclear collisions have long been recognized as a highly sensitive and unique probe for studying the initial state and its evolution [12,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. They are also known as the thermometer of the produced matter from the initial days of heavy-ion collisions. Both real as well as virtual photons are emitted from every stage of the expanding fireball, suffer negligible re-scatterings with the hot and dense medium, and provide undistorted information about the medium produced [26,46,47,48,49,50].
The experimentally measured inclusive photon spectrum contains a large portion of the late-time decay photons originating mostly from the two- decay of and mesons. After successful subtraction of the decay background, one obtains the direct photon spectrum at different beam energies and collision centralities [25,35].
It was first shown by the PHENIX Collaboration that there is an excess of direct photon yield for 200A GeV AuAu collisions at RHIC (Relativistic Heavy Ion Collider) at different centrality bins over the properly normalized production of photons in proton-proton (pp) collisions [51]. The prompt photons produced in initial hard scatterings are the dominant source of direct photons for pp collisions, and it is considered that the thermal contribution is negligible for these collisions as there is no formation of QGP. Although some recent experiments suggest that the high multiplicity events in pp collisions show signatures of medium formation [52], in the context of direct photon production, the prompt photons in pp collisions were found to explain the data well without any thermal contribution. Hence, the observed excess for heavy-ion collisions over the scaled proton–proton results in the direct photon spectrum is attributed to thermal radiations produced in the interaction of the thermalized medium constituents. The excess production of photons has also been reported later at the LHC (Large Hadron Collider) for PbPb collisions at 2.76A TeV by the ALICE Collaboration [53].
To note is that a significant contribution to the direct photon spectrum also comes from the pre-equilibrium phase as well as the production of photons by the passing of high-energy jets through QGP; see Ref. [25] and references therein for details.
In the QGP phase, the quark–gluon Compton scatterings and quark anti-quark annihilation processes are the dominant ones to produce thermal photons. The different hadronic channels (involving mostly and mesons) take part in the photon production in the hot hadronic matter.
These thermal photons hold significant promise for characterizing the initial hot and dense state of the matter produced in heavy-ion collisions at relativistic energies using appropriate observables. To note also is that a number of large and small systems have been studied in recent times, especially at the RHIC energy, which show an evidence of thermal radiation in these collisions [54,55,56].
2. Anisotropic Flow of Photons
The anisotropic flow of photons serves as a valuable observable for studying thermal photons given that non-thermal contributions are not subjected to the collectivity of the produced medium [57,58,59,60,61,62,63]. The elliptic flow of thermal photons was estimated initially considering an ideal hydrodynamic evolution of the system in collisions of gold nuclei at RHIC and using the state-of-the-art rates [57,64,65].
The thermal photons produced in typical heavy-ion collisions dominate the direct photon spectrum in the region of 3–4 GeV. The majority of these thermal photons with GeV (high- region) are expected to originate from the QGP, and the hadronic contribution tends to populate the lower GeV region of the spectrum. However, understanding their individual contribution to the total anisotropic flow is complicated due to the competing contributions from these two sources.
Theoretical model calculations also show that the anisotropic flow of photons is larger for peripheral collisions than for central collisions [57]. The relative contribution of the photons produced in the hadronic medium as well as the initial spatial eccentricity (of the overlapping zone between the two incoming nuclei), increases towards peripheral collisions. These photons have a larger anisotropic flow compared to the photons produced in the QGP medium, which results in a larger total photon anisotropic flow for peripheral collisions than for central collisions. In addition, the -dependent behavior of elliptic flow and triangular flow is found to be similar on a qualitative scale. Both photon and rise with up to about 2 GeV and then drop as is increased further (see Figure 3 in Ref. [57]). The peak value of depends on the beam energy, initial conditions, as well on the centrality of the collisions.
The first experimental measurement of photon elliptic flow from AuAu collisions at RHIC shows that direct photon is consistent with zero above 4 GeV [66]. This confirms that the prompt photons are not subjected to collectivity, and as a result, their contribution to photon elliptic flow is negligible. In the region, 4 GeV, the elliptic flow of direct photons as a function of transverse momentum was found to be significantly large for mid-central AuAu collisions at RHIC.
Additionally, it was found that the elliptic flow of direct photons from experimental analysis shows a similar -dependent nature as predicted earlier by hydrodynamic model calculation. However, the theoretical results tend to underestimate the experimental data by a significant margin [66,67]. This was termed as a ‘direct photon puzzle’, where theoretical model calculations cannot simultaneously explain experimental data for the spectra and anisotropic flow of direct photons.
Several advancements were made in the last decade in theoretical model calculations in order to understand the discrepancy between experimental data and results from model calculation [37,38,39,68,69,70,71,72,73,74]. A recent study explored the influence of a weak magnetic field on direct photon production using a realistic (3+1)D (dimensional) hydrodynamic evolution containing a tilted fireball configuration [74]. This study is found to provide a good agreement of direct photon and with the experimental data at both the RHIC and the LHC energies. Directed flow () of photons from relativistic heavy-ion collisions has also been estimated using hydrodynamic model calculation [72]. Although the charged particle was estimated from heavy ion experiments, experimental determination of photon is yet to be conducted [75].
It has been shown that the inclusion of initial state nucleon shadowing in the Monte Carlo Glauber model provides a better description of the experimental data for hadronic observables [76]. This shadowing effect is also found to increase the elliptic flow of thermal photons from heavy-ion collisions at RHIC and LHC energies significantly [62]. Event-by-event hydrodynamic model calculations have revealed that the presence of fluctuations in the initial density distribution increases the elliptic flow in comparison to a scenario with a smooth initial density distribution [68,69]. Additionally, the incorporation of shear viscosity was identified as a factor that reduces elliptic flow significantly, particularly at larger values.
The inclusion of the photons from the pre-equilibrium phase has been shown to affect both the photon spectra and anisotropic flow parameters marginally [77]. Estimation of photon anisotropic flow calculation from collisions of small, deformed, and clustered nuclei has also been found to provide interesting new insight into the initial state produced in those collisions.
Nevertheless, achieving a simultaneous explanation of both the photon spectra and anisotropic flow through model calculations and experimental data, often referred to as the ‘direct photon puzzle’, is still a challenge.
It is also important to emphasize the pivotal role played by the initial conditions in model calculations when determining the anisotropic flow of photons [78]. Photon observables exhibit greater sensitivity to initial conditions, such as the formation time and initial temperature, in contrast to hadronic observables. A smaller initial time of QGP formation, , results in a larger initial temperature, , and a relatively greater contribution from the QGP phase compared to photons produced in the hadronic matter. This results in a larger relative contribution of the QGP photons in the anisotropic flow calculation. Theoretical model calculations show that the anisotropic flow of (only) QGP photons is significantly smaller than the photon from (only) hadronic matter. Consequently, this leads to a reduction in the (overall) photon anisotropic flow at higher [58]. Hence, there is a hope that photon anisotropic flow could serve as a valuable observable for precisely determining the thermalized time of the hot and dense QGP formed in relativistic heavy-ion collisions. However, the existing disparity between experimental data and photon calculations impedes the extraction of precise information regarding the initial formation time.
3. Ratio of Photon Anisotropic Flow
The anisotropic flow of direct photons is primarily driven by the competing contributions of thermal photons originating from the QGP and hot hadronic matter. The unique -dependent nature of photon is mainly determined by the QGP contribution. The expanding hot fireball, with time, produces anisotropic flow and the -dependent shape, which is a result of the convoluted emission of thermal photons. The high- thermal photons largely originate during the initial QGP dynamics and, therefore, have a lower anisotropy, whereas the magnitude of the photon is controlled by thermal photons originating from hot hadronic matter at the later part of the expansion, which is almost an order of magnitude larger compared to the photon anisotropy from the QGP phase [57]. However, it is important to note that the impact of non-thermal contributions, particularly from prompt photons, dilutes the anisotropic flow at larger -values. This dilution occurs as the non-thermal contributions introduce additional weight in the denominator of the photon anisotropic flow analysis.
In a recent study, it was shown that the ratio of photon and as a function of transverse momentum within a specific centrality bin could serve as a valuable parameter for gaining insights into the dynamics of heavy-ion collisions [79]. One can reduce uncertainties arising from non-thermal contributions in the estimation of direct photon by calculating the ratio of direct photon and .
An event-by-event ideal hydrodynamic framework has been used to study the evolution of matter produced in collisions involving heavy nuclei at relativistic energies [20]. The standard Woods–Saxon nuclear density distribution coupled with a Monte Carlo Glauber model is employed to determine the initial density distribution in the overlapping zone between the two colliding nuclei [59,69]. A two-dimensional Gaussian distribution function of the form
is used to distribute initial entropy/energy density around the source points. The position of the ith nucleon is denoted by () in the transverse plane, and the parameter denotes the granularity or the size of the initial density fluctuation. K is an overall normalization factor tuned to reproduce key observables, including charged particle multiplicity, spectra, and anisotropic flow parameters.
For AuAu (PbPb) collisions at RHIC (LHC), an initial formation time of about 0.17 (0.14) fm/c (with c the speed of light) is considered [80]. A lattice-based equation of state is used for transition from QGP to hot hadronic matter [81].
The state-of-the-art complete leading order, as well as next-to-leading-order rates of thermal photons production from QGP, has been available for quite some time now [64,82]. In the last couple of decades, there has been significant advancement in photon production from hadronic matter as well, which also includes the meson-meson and meson-baryon bremsstrahlung; see Ref. [25] and references therein for details.
Thermal photon rates are taken from Refs. [64,65,82] to calculate the anisotropic flow parameters at different centrality bins.
The total thermal emission is estimated by integrating the emission rates, , over the space-time four-volume:
where E and p denote the photon energy and momentum, respectively, and is the local temperature. = , where is the four-momentum of the photon, and is the local four-velocity of the flow field obtained using longitudinal boost invariant ideal hydrodynamic model evolution. The Greek letter indices take the values 0 for time and 1, 2 and 3 for space (x) components.
In event-by-event hydrodynamic model calculation, the event plane angle ( in Equation (1)) is often replaced by the participant plane angle (), which is obtained from the initial state participant distribution [20].
The initial eccentricities are estimated using the relation
Here, is the initial energy density and .
The participant plane angle is estimated as
The elliptic and triangular flows of thermal photons are calculated with respect to the participant plane angle. The anisotropic flow of direct photons can be estimated as follows:
where is the anisotropic flow of thermal photons and and are the yields of thermal and non-thermal contributions, respectively. The appears only in the denominator of Equation (6). Thus, the ratio of anisotropic flow parameters reflects only the thermal contribution by minimizing the non-thermal part. In this review, we calculate the ratio after taking an ensemble (event) average of individual anisotropic flow parameters (i.e., ) of thermal photons as follows:
The theoretical ratio of elliptic and triangular flow parameters of thermal photons from 200A GeV AuAu collisions is shown in Figure 1 as a function of transverse momentum. The ratio of to and obtained from the experimental direct photon data by the PHENIX experiment at RHIC is shown in the same plot for comparison (see Figure A1 in Appendix A for the estimate of the experimental error on the ratio).
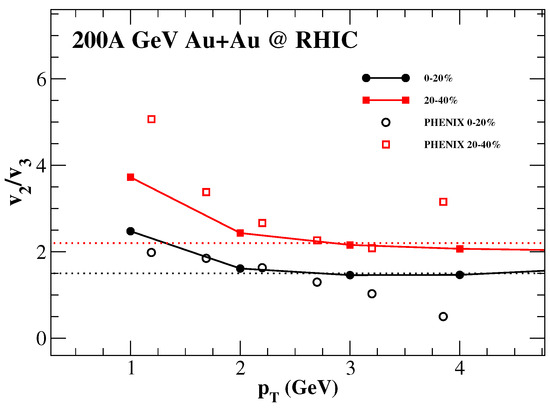
Figure 1.
The calculated ratio of to for thermal photons from 200A GeV AuAu collisions for centrality bins 0–20% and 20–40% [79] compared to the PHENIX Collaboration experimental data at RHIC [83] (see text for details). The dotted lines parallel to -axis show the approximate value of at which the ratio starts to saturate for each centrality bin.
The -dependent behavior of the ratio is found to be different from the individual anisotropic flow parameters. The ratio is larger for peripheral collisions than for central collisions, as the photon triangular flow shows less sensitivity to collision centrality compared to the elliptic flow parameter. The ratio shows stronger -dependence in the region 2 GeV compared to the larger- region where it remains almost invariant with respect to .
It was shown in Ref. [59] that the correlation between photon and is negligible for individual events. However, the event-averaged anisotropic flow parameters show similar -dependent behavior in the region 2 GeV. As a result, negligible variation with can be observed in that region for the ratio. In the lower- region, the photon elliptic flow shows stronger sensitivity to than the triangular flow parameter, and the ratio rises towards smaller values.
Although hydrodynamic model calculations tend to significantly underestimate individual and data, an interesting observation emerges in the comparison of the ratios. Both experimental data and model calculations reveal a remarkable proximity in the 2–4 GeV region. This specific range is believed to be dominated by the QGP radiation in the direct photon spectrum.
It has been shown in Ref. [84], that the -integrated ratio, , of thermal photon anisotropic flow as a function of collision centrality shows much stronger sensitivity to the shear viscosity of the QGP medium compared to the same ratio estimated for charged particles. It was shown that both the differential as well as the -integrated ratio of anisotropic flow can serve as a viscometer for the QGP phase.
The ratio of thermal photons at LHC energy has been shown for three different centrality bins of PbPb collisions at the LHC energy in Figure 2. The ratio is found to be marginally dependent on transverse momentum in a relatively larger- bin at the LHC energy compared to that ratio at RHIC. The lifetime, as well as temperature of the system produced at LHC, is expected to be larger than at RHIC, which resulted in significantly more production of thermal photons at LHC in the region 2 GeV. This might lead to a larger- range over which the ratio remains flat at LHC compared to RHIC. The photon data at LHC would be valuable to confirm this behavior.
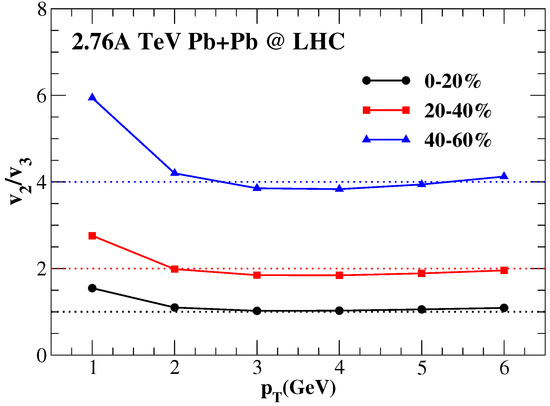
Figure 2.
The predicted ratio of to of thermal photons thermal photon and from 2.76A TeV PbPb collisions for three different centrality bins [59]. The dotted lines parallel to -axis show the approximate value of at which the ratio starts to saturate for each centrality bin.
The of thermal photons from smaller systems also show similar qualitative nature as observed for AuAu and PbPb collisions; see Figure 3. The ratio is found to be slightly smaller for smaller systems as the triangular flow parameter for smaller systems is found to be relatively larger due to the more pronounced presence of initial state fluctuations.
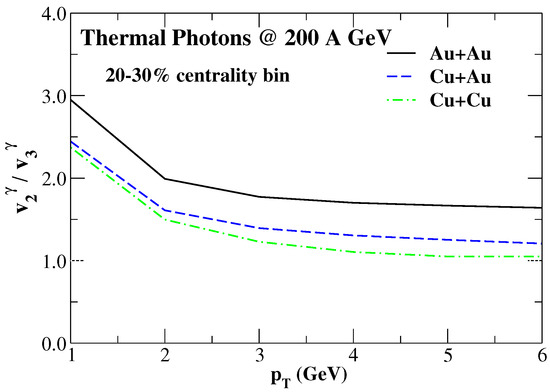
Figure 3.
The predicted ratio of to of thermal photons from 20–30% centrality collisions of AuAu, CuAu, and CuCu collisions at 200A GeV [79].
The ratio is also found to be a robust quantity compared to the individual anisotropic flow parameters when the initial parameters of the model calculation are varied slightly. The initial formation time, , of QGP is not known precisely, and the value ranging from 0.17 fm/c to 0.60 fm/c is considered mostly in different hydrodynamic model calculations to estimate the charged particle as well as photon production. The consideration of a fixed for central as well as peripheral collisions is also an assumption to simplify the model calculation for a typical set of heavy-ion collisions. One should expect a larger value of plasma formation time for peripheral collisions, as the produced initial temperatures as well as the initial energy densities are expected to be relatively smaller for the more glancing collisions.
Although the individual anisotropic flow parameters show a strong sensitivity to the initial formation time [58], particularly at larger values, due to the larger relative contribution in photon production from the hadronic phase, their -dependent ratio does not change significantly in the same region (see Figure 4 when the formation time is increased from 0.17 fm/c to 0.60 fm/c at RHIC).
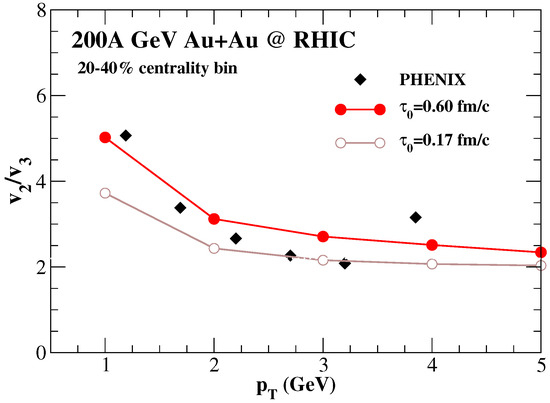
Figure 4.
The predicted ratio of to of thermal photons with the quark–gluon plasma formation time, , values 0.60 fm/c and 0.17 fm/c from AuAu collisions.
Additionally, a smaller value of the freeze-out temperature would result in a much larger contribution to from the hadronic phase and subsequently a significantly larger total for thermal photons [57]. However, it was observed that the ratio is a little sensitive to the value of kinetic freeze-out temperature. Even a significant drop in the value of from 160 MeV to 120 MeV changes the ratio only marginally, as shown in Figure 5.
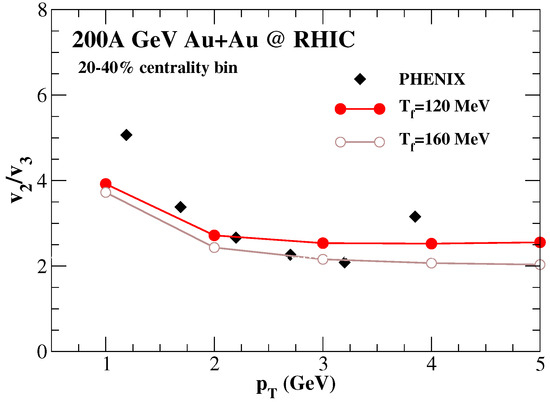
Figure 5.
The predicted ratio of to of thermal photons from 200A GeV AuAu collisions at two different kinetic freeze-out temperatures of 120 MeV and 160 MeV [79].
To note is that the directed flow of photons shows a different -dependent behavior than the elliptic or triangular flow parameters. The thermal photon , as calculated from hydrodynamic model calculations, is found to be negative for 2 GeV and becomes positive as increases. The directed flow shows stronger sensitivity to the QGP phase compared to elliptic and triangular flow of photons; see Figures 3 and 6 in Ref. [72]. Thus, the ratio of photon with the elliptic (or triangular) flow parameter is more sensitive to hydrodynamic parameters (such as freeze-out temperature) than the ratio is. Therefore, could be a potential parameter to understand more about photon observables and address the direct photon puzzle in relativistic nuclear collisions.
The final momentum anisotropies are considered to be a response of the initial geometry, and the correlation between and shows how efficiently the initial spatial anisotropy is converted into final [85]. Theoretical model calculations have shown that the correlation between and is stronger for hadrons than for thermal photons. The correlation has also been found to be stronger for and compared to and both for photons and hadrons [59]. The linear correlation coefficient, , between and is estimated using the relation,
The averages are taken over a sufficiently large number of random events. and are the standard deviations of the initial spatial and final momentum anisotropies of thermal photons, respectively. In addition, the event averages of the initial spatial anisotropies and the anisotropic flow parameters are calculated by taking weight factors of impact parameter and thermal photon yields, respectively, for the corresponding events.
The is found to be larger in the region 3 GeV for both RHIC and LHC (Figure 6). The correlation coefficient is found to be slightly larger at LHC than at RHIC. Probably the build-up of larger transverse flow velocity in the region 3 GeV might have resulted in a larger correlation strength in that region. Photons with relatively larger are mostly from the initial hot and dense state with smaller transverse flow velocity and show a weaker correlation between and .
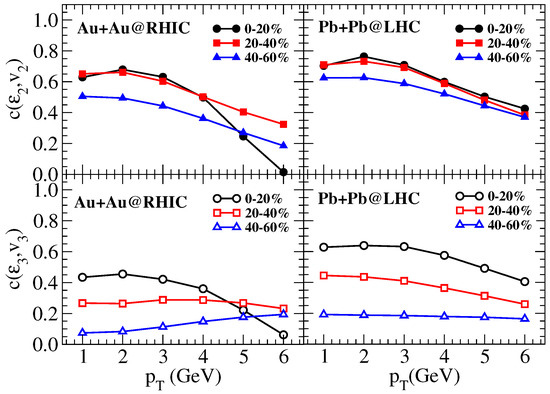
Figure 6.
The predicted correlation between initial spatial anisotropies, , and final momentum anisotropies, , of thermal photons at 200A GeV and at 2.76A TeV heavy-ion collisions for different centrality bins using relativistic ideal hydrodynamic model calculations [59].
The photon elliptic flow parameter shows much stronger sensitivity to the collision centrality compared to the triangular flow parameter. However, the correlation coefficient for both the elliptic and triangular flow parameters (with corresponding initial spatial eccentricities) show similar -dependent behavior.
To note is that the high- part of the photon spectrum as well as the anisotropic flow parameters is more sensitive to the change in initial formation time and freeze-out temperature. Thus, the correlation strength is also expected to be strongly dependent on the initial parameters of the model calculation, especially at larger values.
Interestingly, the larger- part of the ratio of elliptic and triangular flow parameters is found to be less sensitive to the value of as shown in Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5.
Thus, one can say that the correlation between and is stronger in the initial few fm time periods for high- photons. One can see from Figure 7 that the ratio of total for high- thermal photons saturates early and resembles the ratio of QGP contributions. In the later stage, with the strong build-up of transverse flow velocity, the relative change in elliptic flow is more than the triangular flow parameter resulting in a larger value of the ratio; see Figure 7.
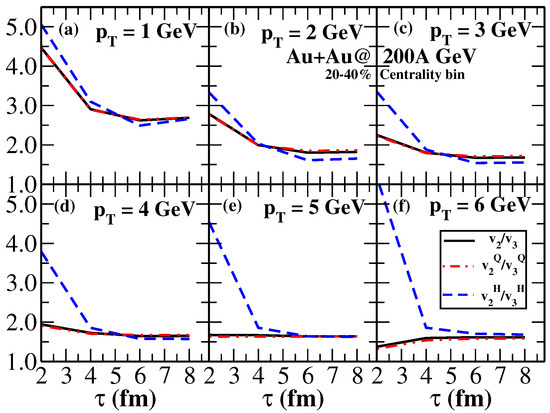
Figure 7.
Time evolution of normalized total photon at different [79].
Temporal evolution of the individual anisotropic flow parameters, as well as the correlation coefficient at different values, is expected to provide a more insight into the -dependent behavior of the ratio of photon anisotropic flow parameters.
4. Ratio of Anisotropic Flow in the Presence of Clustered Structure
In recent time, measurements with small collision systems such as pAu, dAu, and HeAu have shown evidence of medium formation with the significantly large anisotropic flow of hadrons [86,87,88] and the scaling behavior of direct photon production over the scaled prompt photon production from pp collisions [89]. Recent studies suggest that the presence of triangular alpha-clustered structures in light nuclei might result in significant spatial anisotropies in the initial state when collided with heavy nuclei at relativistic energies [90,91,92,93,94,95,96,97]. These initial spatial anisotropies, due to the cluster structure, can be studied efficiently from final state momentum anisotropies.
Significant qualitative as well as quantitative differences between observables have been shown when alpha-clustered structures are included in light nuclei (like C, O, …) compared to the collisions of light nuclei with uniform density distributions. It is assumed that the typical time scale of relativistic nuclear collisions is too small for any slower nuclear excitation to take place, and thus, the initial clustered structure of the incoming light nuclei remains unchanged in these collisions.
Electromagnetic radiation can be a useful probe to study clustered structures in light nuclei due to their strong sensitivity to the initial state [98,99].
It has been shown that different orientations of triangular alpha-clustered carbon can give rise to different initial geometry on the transverse plane in collision with gold nuclei and subsequently different values of the anisotropic flow parameters even for most central collisions [99]. On the other hand, thermal photon production is found to be independent of the orientation of the clustered light nuclei.
A more realistic event-by-event ideal hydrodynamic model calculation of -clustered carbons with gold at 200A GeV shows that the triangular flow of photons is significantly larger than the elliptic flow parameter [98]. This is contrary to the anisotropic flow results in heavy-ion collisions (such as AuAu, PbPb, …), where the elliptic flow is always larger than the triangular flow parameter. The event-averaged initial triangular eccentricities for most central collisions are found to be significantly larger than the elliptical eccentricities, which is reflected in the final flow results; see Figure 1 in Ref. [98].
The ratio of photon anisotropic flow from the collision of triangular -clustered carbon with gold at RHIC energy is shown in Figure 8. As the photon is larger than in such collisions, the ratio is found to be less than 1 in the region 1 GeV.
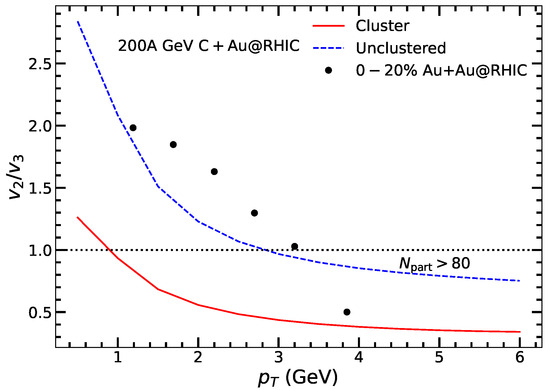
Figure 8.
The predicted ratio of to of thermal photons from collisions of alpha-clustered and unclustered carbon nuclei with gold at the RHIC energy [98]. The dotted line (parallel to -axis) shows the case.
Thus, the estimation of individual photon anisotropic flow and the ratio of the anisotropic flow parameters from light -clustered nuclei can be complementary to the results from typical symmetric heavy-ion collisions. These findings will not only shed light on the clustered structure within light nuclei but also contribute to our understanding of the direct photon puzzle. Recent proposals for collisions of oxygen nuclei at the LHC indicate the potential to experimentally validate the presence of alpha-clustered structures in light nuclei [100].
5. Summary and Conclusions
Direct photons originating from various stages of the evolving fireball in relativistic heavy-ion collisions dominate the differential photon spectrum in different regions. Meanwhile, the differential elliptic and triangular flow parameters are predominantly influenced by thermal radiations. The presence of non-thermal photons dilutes the photon anisotropic flow, introducing an additional weight factor in the denominator of the photon calculation.
The direct photon measurements at RHIC and LHC energies consistently fall below the theoretical model calculations indicating a significant under-prediction of anisotropic flow.
It has been demonstrated in this review that the ratio of the elliptic and triangular flow parameters of thermal photons as a function of exhibits intriguing characteristics. The ratio remains nearly independent of in the region GeV whereas it increases for smaller values of transverse momentum.
These findings straightforwardly indicate that the -dependent behavior of and closely resemble each other in the GeV region, dominated by radiation from the hot and dense plasma phase (although the prompt contribution starts to dominate the photon spectrum above 4 GeV, these photons are not contributing to the anisotropic flow directly). The ratio also explains the experimental data better in the 2–4 GeV -region dominated by thermal radiation. The high- ( GeV) thermal photons mostly originate from the initial stage of system evolution, during which the development of transverse flow velocity is anticipated to be minimal. This likely contributes to the relatively poor explanation of the data in that region. This ratio helps minimize the impact of non-thermal contributions and offers a more reliable measure of the anisotropic flow parameters associated with photon production.
By focusing on the ratio of photon to as a function of within specific centrality bins along with the individual photon anisotropic flow parameters, one aims to provide a robust and insightful characterization of collision dynamics.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
The estimatie of the error of the ratio of photon anisotropic flow parameters at each was calculated using the given experimental values [83] of individual total uncertainties (comprising both systematic and statistical uncertainties) on and . This calculation was performed as follows:
where denotes relative uncertainity.
The estimated error of photon ratio for 0–20% and 20–40% AuAu collisions at 200A GeV is shown in Table A1.
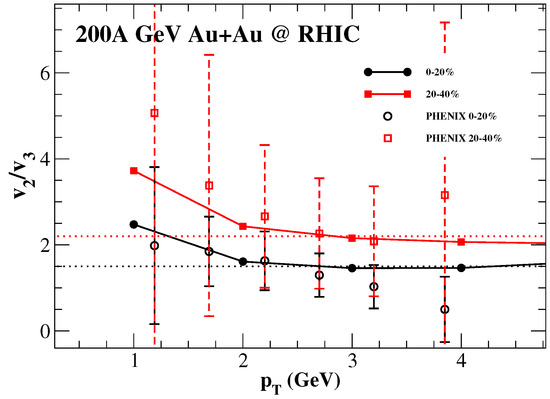
Figure A1.
The model ratio of thermal photon to from 200A AuAu collisions for centrality bins 0–20% and 20–40% [79] compared to the PHENIX Collaboration experimental data [83], the latter at RHIC shown with the estimated errors (see text for details).

Table A1.
Estimated (symmetric) error of the ratio of direct photon and in AuAu collisions at 200A GeV based on the experimental uncertainties of individual flow parameters.
Table A1.
Estimated (symmetric) error of the ratio of direct photon and in AuAu collisions at 200A GeV based on the experimental uncertainties of individual flow parameters.
| Centrality | (GeV) | Error Estimate | |
|---|---|---|---|
| 0–20% centrality | 1.19 | 1.9832 | 1.8354 |
| 1.69 | 1.8482 | 0.8103 | |
| 2.20 | 1.6303 | 0.6833 | |
| 2.70 | 1.2974 | 0.5053 | |
| 3.20 | 1.0289 | 0.5063 | |
| 3.85 | 0.5063 | 0.7587 | |
| 20–40% centrality | 1.19 | 5.0674 | 9.0235 |
| 1.69 | 3.3807 | 3.0394 | |
| 2.20 | 2.6640 | 1.6579 | |
| 2.70 | 2.2646 | 1.2841 | |
| 3.20 | 2.0832 | 1.2792 | |
| 3.85 | 3.1558 | 4.0156 |
Due to considerably large uncertainties present in both the direct photon and data, the relative uncertainty in the ratio is also estimated to be quite large, especially for more peripheral collisions. Disregard the large error bars, the mean values of the data appear to align closely with the ratio calculated from theoretical model framework, as Figure A1 shows.
References
- Harris, J.W.; Müller, B. The Search for the quark-gluon plasma. Annu. Rev. Nucl. Part. Sci. 1996, 46, 71–107. [Google Scholar] [CrossRef]
- Shuryak, E. Strongly coupled quark-gluon plasma in heavy ion collisions. Rev. Mod. Phys. 2017, 89, 035001. [Google Scholar] [CrossRef]
- Yagi, K.; Hatsuda, T.; Miake, Y. Quark-Gluon Plasma: From Big Bang to Little Bang; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Busza, W.; Rajagopal, K.; van der Schee, W. Heavy ion collisions: The big picture, and the big questions. Annu. Rev. Nucl. Part. Sci. 2018, 68, 339–376. [Google Scholar] [CrossRef]
- Kolb, P.F.; Heinz, U. Hydrodynamic description of ultrarelativistic heavy-ion collisions. In Quark–Gluon Plasma 3; Hwa, R.C., Wang, X.-N., Eds.; World Scientific Co., Ltd.: Singapore, 2004; pp. 634–714. [Google Scholar] [CrossRef]
- Adler, C. et al. [STAR Collaboration] Identified particle elliptic flow in Au + Au collisions at 130 GeV. Phys. Rev. Lett. 2001, 87, 182301. [Google Scholar] [CrossRef]
- Adler, S.S. et al. [PHENIX Collaboration] Elliptic flow of identified hadrons in Au + Au collisions at 200 GeV. Phys. Rev. Lett. 2003, 91, 182301. [Google Scholar] [CrossRef]
- Kolb, P.F.; Sollfrank, J.; Heinz, U.W. Anisotropic transverse flow and the quark hadron phase transition. Phys. Rev. C 2000, 62, 054909. [Google Scholar] [CrossRef]
- Teaney, D.; Lauret, J.; Shuryak, E.V. A hydrodynamic description of heavy ion collisions at the SPS and RHIC. arXiv 2001, arXiv:nucl-th/0110037. [Google Scholar]
- Huovinen, P.; Kolb, P.F.; Heinz, U.W.; Ruuskanen, P.V.; Voloshin, S.A. Radial and elliptic flow at RHIC: Further predictions. Phys. Lett. B 2001, 503, 58–64. [Google Scholar] [CrossRef]
- Heinz, U.; Snellings, R. Collective flow and viscosity in relativistic heavy-ion collisions. Annu. Rev. Nucl. Part. Sci. 2013, 63, 123–151. [Google Scholar] [CrossRef]
- Eskola, K.J.; Honkanen, H.; Niemi, H.; Ruuskanen, P.V.; Räsänen, S.S. Predictiions for low-pT and high-pT hadron spectra in nearly central Pb+Pb collisions at 5.5 TeV tested at 130 and 200 GeV. Phys. Rev. C 2005, 72, 044904. [Google Scholar] [CrossRef]
- Huovinen, P.; Ruuskanen, P.V. Hydrodynamic models for heavy ion collisions. Annu. Rev. Nucl. Part. Sci. 2006, 56, 163–206. [Google Scholar] [CrossRef]
- Nonaka, C.; Bass, S.A. Space-time evolution of bulk QCD matter. Phys. Rev. C 2007, 75, 014902. [Google Scholar] [CrossRef]
- Romatschke, P.; Romatschke, U. Viscosity information from relativistic nuclear collisions: How perfect is the fluid observed at RHIC? Phys. Rev. Lett. 2007, 99, 172301. [Google Scholar] [CrossRef]
- Gale, C.; Jeon, S.; Schenke, B. Hydrodynamic modeling of heavy-ion collisions. Int. J. Mod. Phys. A 2013, 28, 1340011. [Google Scholar] [CrossRef]
- Schenke, B.; Jeon, S.; Gale, C. Elliptic and triangular flow in event-by-event D = 3 + 1 viscous hydrodynamics. Phys. Rev. Lett. 2011, 106, 042301. [Google Scholar] [CrossRef]
- Hama, Y.; Kodama, T.; Socolowski, O., Jr. Topics on hydrodynamic model of nucleus-nucleus collisions. Braz. J. Phys. 2005, 35, 24–51. [Google Scholar] [CrossRef]
- Andrade, R.; Grassi, F.; Hama, Y.; Kodama, T.; Socolowski, O., Jr. On the necessity to include event-by-event fluctuations in experimental evaluation of elliptical flow. Phys. Rev. Lett. 2006, 97, 202302. [Google Scholar] [CrossRef] [PubMed]
- Holopainen, H.; Niemi, H.; Eskola, K.J. Event-by-event hydrodynamics and elliptic flow from fluctuating initial state. Phys. Rev. C 2011, 83, 034901. [Google Scholar] [CrossRef]
- Schenke, B.; Tribedy, P.; Venugopalan, R. Fluctuating Glasma initial conditions and flow in heavy ion collisions. Phys. Rev. Lett. 2012, 108, 252301. [Google Scholar] [CrossRef]
- Heinz, U.; Qiu, Z.; Shen, C. Fluctuating flow angles and anisotropic flow measurements. Phys. Rev. C 2013, 87, 034913. [Google Scholar] [CrossRef]
- Alver, B.; Roland, G. Collision-geometry fluctuations and triangular flow in heavy-ion collisions. Phys. Rev. C 2010, 81, 054905. [Google Scholar] [CrossRef]
- Qiu, Z.; Shen, C.; Heinz, U. Hydrodynamic elliptic and triangular flow in Pb–Pb collisions at 2.76ATeV. Phys. Lett. B 2012, 707, 151–155. [Google Scholar] [CrossRef]
- David, G. Direct real photons in relativistic heavy ion collisions. Rep. Prog. Phys. 2020, 83, 046301. [Google Scholar] [CrossRef] [PubMed]
- McLerran, L.D.; Toimela, T. Photon and dilepton emission from the quark-gluon plasma: Some general considerations. Phys. Rev. D 1985, 31, 545–563. [Google Scholar] [CrossRef] [PubMed]
- Alam, J.; Sinha, B.; Raha, S. Electromagnetic probes of quark gluon plasma. Phys. Rep. 1996, 273, 243–362. [Google Scholar] [CrossRef]
- Cassing, W.; Bratkovskaya, E.L. Hadronic and electromagnetic probes of hot and dense nuclear matter. Phys. Rep. 1999, 308, 65–233. [Google Scholar] [CrossRef]
- Peitzmann, T.; Thoma, M.H. Direct photons from relativistic heavy-ion collisions. Phys. Rep. 2002, 364, 175–246. [Google Scholar] [CrossRef]
- Stankus, P. Direct photon production in relativistic heavy-ion collisions. Annu. Rev. Nucl. Part. Sci. 2005, 55, 517–554. [Google Scholar] [CrossRef]
- Shen, C.; Heinz, U.W.; Paquet, J.-F.; Gale, C. Thermal photons as a quark-gluon plasma thermometer reexamined. Phys. Rev. C 2014, 89, 044910. [Google Scholar] [CrossRef]
- Paquet, J.-F. Probing the space-time evolution of heavy ion collisions with photons and dileptons. Nucl. Phys. A 2017, 967, 184–191. [Google Scholar] [CrossRef]
- Gale, C. Direct photon production in relativistic heavy-ion collisions—A theory update. PoS Proc. Sci. 2019, 320, 023. [Google Scholar] [CrossRef]
- Srivastava, D.K. Direct photons from relativistic heavy-ion collisions. J. Phys. G Nucl. Part. Phys. 2008, 35, 104026. [Google Scholar] [CrossRef]
- Chatterjee, R.; Bhattacharya, L.; Srivastava, D.K. Electromagnetic probes. In The Physics of the Quark-Gluon Plasma. Introductory Lectures; Sarkar, S., Satz, H., Sinha, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 219–264. [Google Scholar] [CrossRef]
- Chatterjee, R. Anisotropic flow of photons in relativistic heavy ion collisions. Pramana 2021, 95, 15. [Google Scholar] [CrossRef]
- Gale, C.; Hidaka, Y.; Jeon, S.; Lin, S.; Paquet, J.-F.; Pisarski, R.D.; Satow, D.; Skokov, V.V.; Vujanovic, G. Production and elliptic flow of dileptons and photons in a matrix model of the quark-gluon plasma. Phys. Rev. Lett. 2015, 114, 072301. [Google Scholar] [CrossRef]
- Monnai, A. Thermal photon v2 with slow quark chemical equilibration. Phys. Rev. C 2014, 90, 021901(R). [Google Scholar] [CrossRef]
- McLerran, L.; Schenke, B. The Glasma, photons and the implications of anisotropy. Nucl. Phys. A 2014, 929, 71–82. [Google Scholar] [CrossRef]
- Başar, G.; Kharzeev, D.E.; Skokov, V. Conformal anomaly as a source of soft photons in heavy ion collisions. Phys. Rev. Lett. 2012, 109, 202303. [Google Scholar] [CrossRef] [PubMed]
- Tuchin, K. Electromagnetic radiation by quark-gluon plasma in a magnetic field. Phys. Rev. C 2013, 87, 024912. [Google Scholar] [CrossRef]
- Zakharov, B.G. Effect of magnetic field on the photon radiation from quark-gluon plasma in heavy ion collisions. Eur. Phys. J. C 2016, 76, 609. [Google Scholar] [CrossRef]
- Vujanovic, G.; Paquet, J.-F.; Denicol, G.S.; Luzum, M.; Schenke, B.; Jeon, S.; Gale, C. Probing the early-time dynamics of relativistic heavy-ion collisions with electromagnetic radiation. Nucl. Phys. A 2014, 932, 230–234. [Google Scholar] [CrossRef][Green Version]
- Liu, F.-M.; Liu, S.-X. Quark-gluon plasma formation time and direct photons from heavy ion collisions. Phys. Rev. C 2014, 89, 034906. [Google Scholar] [CrossRef]
- Garcia-Montero, O.; Löher, N.; Mazeliauskas, A.; Berges, J.; Reygers, K. Probing the evolution of heavy-ion collisions using direct photon interferometry. Phys. Rev. C 2020, 102, 024915. [Google Scholar] [CrossRef]
- Ruuskanen, P.V. Electromagnetic probes of quark-gluon plasma in relativistic heavy-ion collisions. Nucl. Phys. A 1992, 544, 169–182. [Google Scholar] [CrossRef]
- Srivastava, D.K.; Kapusta, J.I. Photon interferometry of quark-gluon dynamics. Phys. Lett. B 1993, 307, 1–6. [Google Scholar] [CrossRef]
- Srivastava, D.K. Intensity interferometry of thermal photons from relativistic heavy-ion collisions. Phys. Rev. C 2005, 71, 034905. [Google Scholar] [CrossRef]
- Peressounko, D. Hanbury Brown–Twiss interferometry of direct photons in heavy ion collisions. Phys. Rev. C 2003, 67, 014905. [Google Scholar] [CrossRef]
- Frodermann, E.; Heinz, U. Photon Hanbury-Brown–Twiss interferometry for noncentral heavy-ion collisions. Phys. Rev. C 2009, 80, 044903. [Google Scholar] [CrossRef]
- Adare, A. et al. [PHENIX Collaboration] Centrality dependence of low-momentum direct-photon production in Au + Au collisions at 200 GeV. Phys. Rev. C 2015, 91, 064904. [Google Scholar] [CrossRef]
- Adam, J. et al. [ALICE Collaboration] Enhanced production of multi-strange hadrons in high-multiplicity proton–proton collisions. Nat. Phys. 2017, 13, 535–539. [Google Scholar] [CrossRef]
- Adam, J. et al. [ALICE Collaboration] Direct photon production in Pb–Pb collisions at 2.76 TeV. Phys. Lett. B 2016, 754, 235–248. [Google Scholar] [CrossRef]
- Chatterjee, R. Electroweak physics: Summary. PoS Proc. Sci. 2021, 387, 026. [Google Scholar] [CrossRef]
- Adare, A. et al. [PHENIX Collaboration] Low-momentum direct-photon measurement in Cu + Cu collisions at 200 GeV. Phys. Rev. C 2018, 98, 054902. [Google Scholar] [CrossRef]
- Adare, A. et al. [PHENIX Collaboration] Beam energy and centrality dependence of direct-photon emission from ultrarelativistic heavy-ion collisions. Phys. Rev. Lett. 2019, 123, 022301. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, R.; Frodermann, E.S.; Heinz, U.W.; Srivastava, D.K. Elliptic flow of thermal photons in relativistic nuclear collisions. Phys. Rev. Lett. 2006, 96, 202302. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, R.; Srivastava, D.K. Formation time of QGP from thermal photon elliptic flow. Nucl. Phys. A 2009, 830, 503c–506c. [Google Scholar] [CrossRef]
- Chatterjee, R.; Dasgupta, P.; Srivastava, D.K. Anisotropic flow of thermal photons at energies available at the BNL Relativistic Heavy Ion Collider and at the CERN Large Hadron Collider. Phys. Rev. C 2017, 96, 014911. [Google Scholar] [CrossRef]
- Chatterjee, R.; Srivastava, D.K.; Renk, T. Triangular flow of thermal photons from an event-by-event hydrodynamic model for 2.76A TeV Pb + Pb collisions at the CERN Large Hadron Collider. Phys. Rev. C 2016, 94, 014903. [Google Scholar] [CrossRef]
- Dasgupta, P.; Chatterjee, R.; Srivastava, D.K. Spectra and elliptic flow of thermal photons from full-overlap U+U collisions at energies available at the BNL Relativistic Heavy Ion Collider. Phys. Rev. C 2017, 95, 064907. [Google Scholar] [CrossRef]
- Dasgupta, P.; Chatterjee, R.; Singh, S.K.; Alam, J. Effects of initial-state nucleon shadowing on the elliptic flow of thermal photons. Phys. Rev. C 2018, 97, 034902. [Google Scholar] [CrossRef]
- Chatterjee, R.; Srivastava, D.K.; Heinz, U.; Gale, C. Elliptic flow of thermal dileptons in relativistic nuclear collisions. Phys. Rev. C 2007, 75, 054909. [Google Scholar] [CrossRef]
- Arnold, P.B.; Moore, G.D.; Yaffe, L.G. Photon emission from quark gluon plasma: Complete leading order results. J. High Energy Phys. 2001, 12, 009. [Google Scholar] [CrossRef]
- Turbide, S.; Rapp, R.; Gale, C. Hadronic production of thermal photons. Phys. Rev. C 2004, 69, 014903. [Google Scholar] [CrossRef]
- Adare, A. et al. [PHENIX Collaboration] Observation of direct-photon collective flow in Au + Au collisions at 200 GeV. Phys. Rev. Lett. 2012, 109, 122302. [Google Scholar] [CrossRef] [PubMed]
- Lohner, D.; ALICE Collaboration. Measurement of direct-photon elliptic flow in Pb–Pb collisions at 2.76 TeV. J. Phys. Conf. Ser. 2013, 446, 012028. [Google Scholar] [CrossRef]
- Chatterjee, R.; Holopainen, H.; Helenius, I.; Renk, T.; Eskola, K.J. Elliptic flow of thermal photons from event-by-event hydrodynamic model. Phys. Rev. C 2013, 88, 034901. [Google Scholar] [CrossRef]
- Chatterjee, R.; Holopainen, H.; Renk, T.; Eskola, K.J. Enhancement of thermal photon production in event-by-event hydrodynamics. Phys. Rev. C 2011, 83, 054908. [Google Scholar] [CrossRef]
- van Hees, H.; Gale, C.; Rapp, R. Thermal photons and collective flow at energies available at the BNL Relativistic Heavy-Ion Collider. Phys. Rev. C 2011, 84, 054906. [Google Scholar] [CrossRef]
- Linnyk, O.; Cassing, W.; Bratkovskaya, E.L. Centrality dependence of the direct photon yield and elliptic flow in heavy-ion collisions at 200 GeV. Phys. Rev. C 2014, 89, 034908. [Google Scholar] [CrossRef]
- Dasgupta, P.; Chatterjee, R.; Srivastava, D.K. Directed flow of photons in Cu+Au collisions at RHIC. J. Phys. G 2020, 47, 085101. [Google Scholar] [CrossRef]
- Dasgupta, P.; De, S.; Chatterjee, R.; Srivastava, D.K. Photon production from Pb + Pb collisions at 5.02 TeV at the CERN Large Hadron Collider and at 39 TeV at the proposed Future Circular Collider facility. Phys. Rev. C 2018, 98, 024911. [Google Scholar] [CrossRef]
- Sun, J.-A.; Yan, L. The effect of weak magnetic photon emission from quark-gluon plasma. arXiv 2023, arXiv:2302.07696. [Google Scholar]
- Adamczyk, L. et al. [STAR Collaboration] Charge-dependent directed flow in Cu + Au collisions at 200 GeV. Phys. Rev. Lett. 2017, 118, 012301. [Google Scholar] [CrossRef]
- Chatterjee, S.; Singh, S.K.; Ghosh, S.; Hasanujjaman, M.; Alam, J.; Sarkar, S. Initial condition from the shadowed Glauber model. Phys. Lett. B 2016, 758, 269–273. [Google Scholar] [CrossRef]
- Gale, C.; Paquet, J.-F.; Schenke, B.; Shen, C. Probing early-time dynamics and quark-gluon plasma transport properties with photons and hadrons. Nucl. Phys. A 2021, 1005, 121863. [Google Scholar] [CrossRef]
- Chatterjee, R.; Holopainen, H.; Renk, T.; Eskola, K.J. Collision centrality and τ0 dependence of the emission of thermal photons from fluctuating initial state in ideal hydrodynamic calculation. Phys. Rev. C 2012, 85, 064910. [Google Scholar] [CrossRef]
- Chatterjee, R.; Dasgupta, P. Ratio of photon anisotropic flow in relativistic heavy ion collisions. Phys. Rev. C 2021, 104, 064907. [Google Scholar] [CrossRef]
- Eskola, K.J.; Kajantie, K.; Ruuskanen, P.V.; Tuominen, K. Scaling of transverse energies and multiplicities with atomic number and energy in ultrarelativistic nuclear collisions. Nucl. Phys. B 2000, 570, 379–389. [Google Scholar] [CrossRef]
- Laine, M.; Schröder, Y. Quark mass thresholds in QCD thermodynamics. Phys. Rev. D 2006, 73, 085009. [Google Scholar] [CrossRef]
- Ghiglieri, J.; Hong, J.; Kurkela, A.; Lu, E.; Moore, G.D.; Teaney, D. Next-to-leading order thermal photon production in a weakly coupled quark-gluon plasma. J. High Energy Phys. 2013, 2013, 10. [Google Scholar] [CrossRef]
- Adare, A. et al. [PHENIX Collaboration] Azimuthally anisotropic emission of low-momentum direct photons in Au + Au collisions at 200 GeV. Phys. Rev. C 2016, 94, 064901. [Google Scholar] [CrossRef]
- Shen, C.; Heinz, U.; Paquet, J.-F.; Gale, C. Thermal photon anisotropic flow serves as a quark-gluon plasma viscometer. Nucl. Phys. A 2014, 932, 184–188. [Google Scholar] [CrossRef]
- Niemi, H.; Denicol, G.S.; Holopainen, H.; Huovinen, P. Event-by-event distributions of azimuthal asymmetries in ultrarelativistic heavy-ion collisions. Phys. Rev. C 2013, 87, 054901. [Google Scholar] [CrossRef]
- Aidala, C. et al. [PHENIX Collaboration] Creation of quark–gluon plasma droplets with three distinct geometries. Nat. Phys. 2019, 15, 214–220. [Google Scholar] [CrossRef]
- Aad, G. et al. [ATLAS Collaboration] Observation of long-range elliptic azimuthal anisotropies in 13 and 2.76 TeV pp collisions with the ATLAS detector. Phys. Rev. Lett. 2016, 116, 172301. [Google Scholar] [CrossRef] [PubMed]
- Chatrchyan, S. et al. [CMS Collaboration] Observation of long-range, near-side angular correlations in pPb collisions at the LHC. Phys. Lett. B 2013, 718, 795–814. [Google Scholar] [CrossRef]
- Khachatryan, V.; PHENIX Collaboration. Direct photon production and scaling properties in large and small system collisions. J. Phys. Conf. Ser. 2020, 1602, 012015. [Google Scholar] [CrossRef]
- Rybczyński, M.; Piotrowska, M.; Broniowski, W. Signatures of α clustering in ultrarelativistic collisions with light nuclei. Phys. Rev. C 2018, 97, 034912. [Google Scholar] [CrossRef]
- Bożek, P.; Broniowski, W.; Ruiz Arriola, E.; Rybczyński, M. α clusters and collective flow in ultrarelativistic carbon–heavy-nucleus collisions. Phys. Rev. C 2014, 90, 064902. [Google Scholar] [CrossRef]
- Behera, D.; Deb, S.; Singh, C.R.; Sahoo, R. Characterizing nuclear modification effects in high-energy O-O collisions at energies available at the CERN Large Hadron Collider: A transport model perspective. Phys. Rev. C 2024, 109, 014902. [Google Scholar] [CrossRef]
- Behera, D.; Mallick, N.; Tripathy, S.; Prasad, S.; Mishra, A.N.; Sahoo, R. Predictions on global properties in O+O collisions at the Large Hadron Collider using a multi-phase transport model. Eur. Phys. J. A 2022, 58, 175. [Google Scholar] [CrossRef]
- Li, Y.-A.; Zhang, S.; Ma, Y.-G. Signatures of α-clustering in 16O by using a multiphase transport model. Phys. Rev. C 2020, 102, 054907. [Google Scholar] [CrossRef]
- Zhang, S.; Ma, Y.G.; Chen, J.H.; He, W.B.; Zhong, C. Nuclear cluster structure effect on elliptic and triangular flows in heavy-ion collisions. Phys. Rev. C 2017, 95, 064904. [Google Scholar] [CrossRef]
- He, J.; He, W.-B.; Ma, Y.-G.; Zhang, S. Machine-learning-based identification for initial clustering structure in relativistic heavy-ion collisions. Phys. Rev. C 2021, 104, 044902. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, S.; Cao, B.; Xu, H.-j.; Song, H. Exploring the compactness of α cluster in the 16O nuclei with relativistic 16O+16O collisions. arXiv 2024. arXiv:2401.15723. [Google Scholar] [CrossRef]
- Dasgupta, P.; Chatterjee, R.; Ma, G.-L. Production and anisotropic flow of thermal photons in collisions of α-clustered carbon with heavy nuclei at relativistic energies. Phys. Rev. C 2023, 107, 044908. [Google Scholar] [CrossRef]
- Dasgupta, P.; Ma, G.-L.; Chatterjee, R.; Yan, L.; Zhang, S.; Ma, Y.-G. Thermal photons as a sensitive probe of α-cluster in C + Au collisions at the BNL Relativistic Heavy Ion Collider. Eur. Phys. J. A 2021, 57, 134. [Google Scholar] [CrossRef]
- Brewer, J.; Mazeliauskas, A.; van der Schee, W. Opportunities of OO and pO collisions at the LHC. arXiv 2021. arXiv:2103.01939. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).