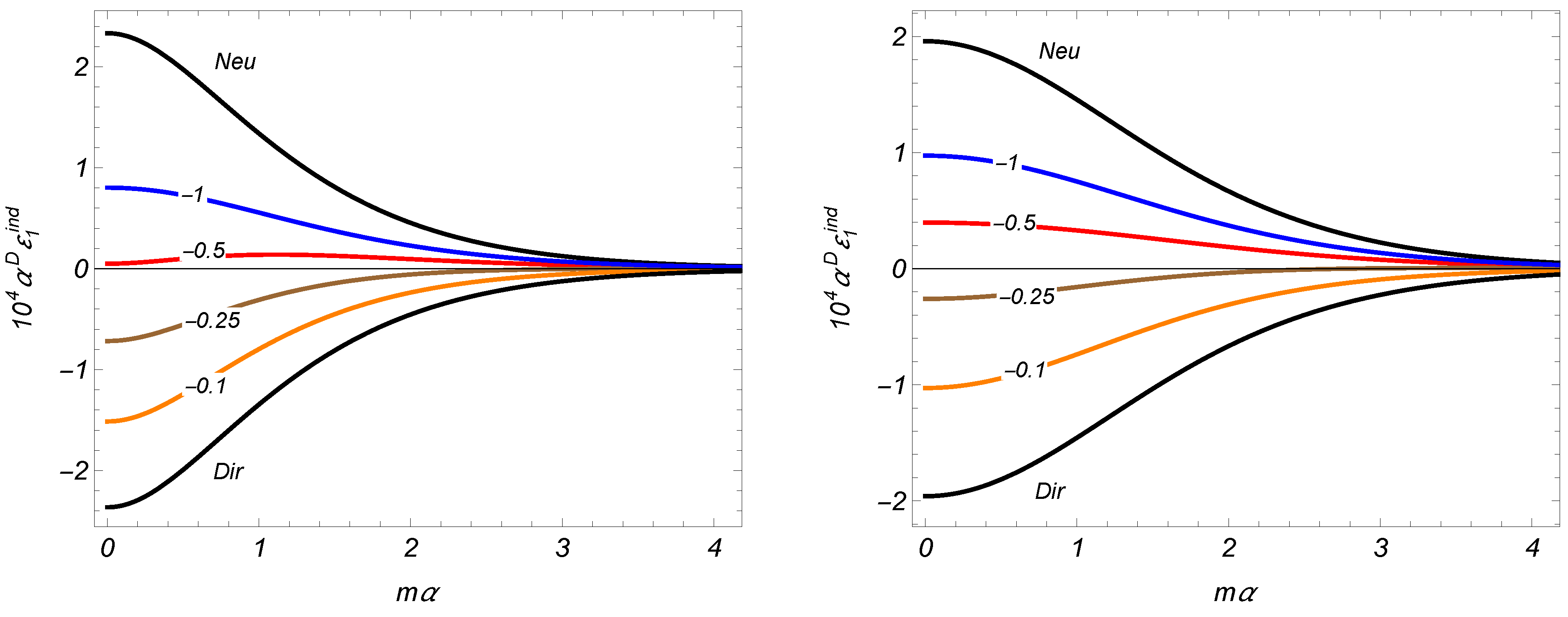1. Introduction
Among the interesting directions in the development of the Casimir effect theory (for a general introduction and applications, see, e.g., [
1,
2,
3,
4,
5,
6]) is the study of the dependence of expectation values of physical characteristics for quantum fields on the bulk and boundary geometries, as well as on the spatial topology. The interest is motivated by applications in gravitational physics, in cosmology, and in condensed matter physics. Exact analytic expressions for physical characteristics are obtained in geometries with a sufficient degree of symmetry. In particular, the corresponding background geometries include maximally symmetric spacetimes sourced by positive and negative cosmological constants. These geometries, referred as de Sitter (dS) and anti-de Sitter (AdS) spacetimes, respectively, are among the most popular bulks in quantum field theory on curved backgrounds.
The goal of this paper is to investigate the surface Casimir densities on two parallel branes for a scalar field in AdS spacetime. Quantum field theoretical effects on a fixed AdS background have been extensively studied in the literature. These investigations are important for several reasons. The AdS spacetime is a non-globally hyperbolic manifold with a timelike boundary at spatial infinity and the early interest in the formulation of quantum field theory in that geometry was related to principal questions of quantization [
7,
8,
9] (see also the references in Ref. [
10]). The necessity to control the information through the spatial infinity requires the imposition of boundary conditions on quantum fields (for a discussion of possible boundary conditions on the AdS boundary, see, e.g., [
11,
12]). The different boundary conditions correspond to physically different field theories. The AdS boundary at spatial infinity plays a central role in models of AdS/conformal field theory (AdS/CFT) correspondence [
13,
14,
15,
16]. The latter establishes duality between conformal field theory living on the boundary of AdS spacetime and supergravity or string theory on AdS bulk. This holographic correspondence between two different theories provides an efficient computational framework for non-perturbative effects, mapping them to the perturbative region of the dual theory. Within this approach interesting results have been obtained in high energy physics, in quantum chromodynamics, and in condensed matter physics [
14,
17,
18]. The braneworld models [
19] with large extra dimensions, both phenomenological- and string-theory-motivated, present another interesting setup where the properties of AdS spacetime play a crucial role. They provide a geometrical solution to the hierarchy problem between the electroweak and gravitational energy scales and serve as an interesting framework to discuss the problems in high energy physics, gravitation, and cosmology.
The braneworld models contain two types of field: fields propagating in the bulk and fields localized on the branes. In simplified models, the interaction between branes and bulk fields is reduced to boundary conditions on the branes. Those conditions modify the spectrum of vacuum fluctuations of bulk quantum fields and give rise to the Casimir-type contributions in the expectation values of physical observables, such as the ground state energy and the vacuum forces acting on the branes. The Casimir energy and forces in the geometry of branes parallel to the AdS boundary have been widely studied in the literature (see [
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34,
35] for early investigations and [
36] for a more complete list of references). The Casimir forces can be used as a possible mechanism for stabilization of the interbrane distance that is required to escape the variations in physical constants in the effective theory on the branes. The vacuum fluctuations of the bulk field may also provide a mechanism for the generation of the cosmological constant on branes. More detailed information on the properties of the vacuum state is contained in the expectation values of bilinear combinations of fields, such as the field squared and the energy–momentum tensor. In braneworld models on AdS bulk, those expectation values are considered in Refs. [
32,
37,
38,
39,
40,
41,
42,
43,
44,
45] for scalar, fermionic, and electromagnetic fields.
In the references cited above, the branes are parallel to the AdS boundary (Randall–Sundrum-type models [
46,
47]). In a number of recent developments in conformal field theories, additional boundaries are present (see, e.g., [
48] and references therein). In the context of AdS/CFT correspondence, the corresponding dual theory on the AdS bulk contains boundaries intersecting the AdS boundary (AdS/BCFT correspondence) [
49,
50]. Another interesting problem on AdS bulk with surfaces crossing its boundary is related to the evaluation of the entanglement entropy of a quantum system in conformal field theory with a boundary. In accordance with the procedure suggested in Refs. [
51,
52], the entanglement entropy in a bounded region from the CFT side on the AdS boundary is expressed in terms of the area of the minimal surface in the AdS bulk that asymptotes the boundary of CFT (see also [
53,
54] for reviews). Motivated by those developments, the influence of branes orthogonally intersecting the AdS boundary on the local properties of the scalar vacuum in a general number of spatial dimensions was studied in Refs. [
55,
56]. As local characteristics of the vacuum state, the expectation values of the field squared and of the energy–momentum tensor were considered. By using the corresponding vacuum stresses, the Casimir forces acting on the branes were investigated as well. It was shown that, in addition to the component perpendicular to the brane, those forces have a nonzero parallel component (shear force). In quantum field theory with boundaries, the expectation values of physical quantities may contain contributions localized on the boundary. The expression for the surface energy–momentum tensor of a scalar field with a general curvature coupling parameter, and for general bulk and boundary geometries, was derived in Ref. [
57] by using the standard variational procedure. The corresponding vacuum expectation value in the problem with branes parallel to the AdS boundary was investigated in Refs. [
58,
59]. The present paper considers the vacuum expectation value of the surface energy–momentum tensor (SEMT) for a scalar field in the problem with two parallel branes orthogonal to the AdS boundary.
The organization of the paper is as follows.
Section 2 describes the geometry of the problem and present the expression for the surface energy–momentum tensor. The corresponding vacuum expectation value (VEV) is investigated in
Section 3 by using the two-point function from [
56]. The surface energy density is decomposed into contributions corresponding to the self-energy of the brane when the second brane is absent and the part induced by the second brane. The renormalization is required only for the first contribution. In the limit of infinite curvature radius, the result for parallel plates in the Minkowski bulk is recovered. Another special case with conformal relation to the Casimir problem in Minkowski spacetime corresponds to a conformally coupled massless field. The behavior of the SEMT in asymptotic regions of the parameters is discussed in
Section 4. A numerical analysis for the induced surface energy density is presented as well. The main results of the paper are summarized in
Section 5. The regularization of the self-energy contribution, by using the generalized zeta function approach, is considered in
Appendix A. The finite part is separated on the basis of principal part prescription.
2. Geometry of the Problem
AdS spacetime is the maximally symmetric solution of the Einstein equations with a negative cosmological constant
as the only source of the gravitational field. In Poincaré coordinates
, with
t denoting the time,
the space coordinates with the spatial dimension
, the corresponding metric tensor,
, is given by
Here, the parameter determines the curvature radius of the background spacetime, for , and . The D-dimensional hypersurfaces and present the AdS boundary and horizon, respectively. The proper distance along the z-direction is measured by the coordinate , . In the coordinate system one has and , with being the metric tensor for Minkowski spacetime.
The aim is to investigate the surface Casimir densities induced by quantum fluctuations of a scalar field
on codimension one parallel branes located at
and
,
(see
Figure 1 for the geometry of the problem). Throught the paper, it is assumed that the field is prepared in the Poincaré vacuum state. For a scalar field with curvature coupling parameter
, the corresponding field equation reads
where
is the covariant d’Alembertian,
m is the mass, and
is the Ricci scalar for AdS spacetime. On the branes, the field operator is constrained by Robin boundary conditions,
where
is the normal to the brane at
pointing into the region under consideration. The branes divide the background space into three regions:
,
, and
. In the first and third regions, one has
and
, respectively, where
is the Kronecker symbol. For the region
, the normal in Equation (
3) is expressed as
. In the discussion below, the region between the branes is considered. The VEVs for the regions
and
are obtained in the limits
and
. For the sets of the coefficients
and
the constraints (
3) are reduced to Dirichlet and Neumann boundary conditions, respectively. For Robin boundary conditions, here the special case
is assumed, with
,
, being constants. For this choice, the boundary conditions (
3), written in terms of the coordinate
, take the form
where
.
The latter is the Robin boundary condition with constant coefficient
. This coefficient characterizes the properties of the brane and can be used to model the finite penetration length of quantum fluctuations. Note that the coordinate
in Equation (
4) measures the proper distance from the brane for a fixed
z.
For the scalar field modes in the region between the branes, the eigenvalues of the quantum number
, corresponding to the momentum along the direction
, are quantized by the boundary conditions (
4). Those eigenvalues are roots of the transcendental equation (see [
56])
where
. Depending on the values of the Robin coefficients, this equation, in addition to an infinite set of roots with real
, may have purely imaginary roots
(for the corresponding conditions, see [
60]). The energy of the scalar modes, with the momentum
,
,
, in the subspace with coordinates
, is expressed as
, where
is the quantum number corresponding to the
z-direction. The dependence of the mode functions on the coordinate
z is expressed in terms of the function
, with
being the Bessel function and
Note that, in contrast to the Minkowski bulk, the energy of the scalar modes with given momentum does not depend on the mass of the field quanta. The mass enters in the problem through the parameter
. Now, one can see that in the presence of imaginary roots
, for the scalar field modes with
, the energy becomes imaginary. This signals the instability of the vacuum state under consideration. In the discussion below, the values of the coefficients
and
, for which there are no imaginary roots of the eigenvalue Equation (
5), are assumed. The corresponding conditions read [
60]
For a general
-dimensional spacetime with a smooth boundary
, the SEMT
, localized on the boundary by the one-sided Dirac delta function
, is given by [
57]
Here,
is the induced metric on the boundary, with
being the inward-pointing unit normal vector for
, and
is the corresponding extrinsic curvature tensor. The expression (
8) was obtained in Ref. [
57] by using the standard variational procedure for the action of a scalar field with general curvature coupling parameter and with an appropriate boundary term localized on
. Denoting the vacuum state by
, the VEV of the SEMT is presented as
where the VEV
is written in terms of the Hadamard function
by the formula
The limit contains two types of divergences. The first type of the divergences is present already in the case when the point
x does not belong to the boundary. The corresponding divergent part is the same as that in the problem where the branes are absent and is removed by the subtraction from the Hadamard function in Equation (
10), the corresponding function in the brane-free geometry. The SEMT is absent in the latter geometry and the brane-free Hadamard function does not contribute to the VEV of the SEMT. The second type of divergences originates from the surface divergences in quantum field theory with boundaries and arises when the point
x belongs to the boundary.
4. Asymptotics and Numerical Analysis
In this Section, the behavior of the VEV for SEMT in asymptotic regions of the parameters is studied. Let us start with the asymptotics at relatively small and large separations between the branes. For a given
z, the proper separation between the branes is given by
. For quite small proper separations compared to the curvature radius, one has
and the integral in Equation (
22) is dominated by the contribution of the region with large enough values of the argument of the function
. By using the corresponding asymptotic [
55],
one can see that the relation
takes place, where
is given by Equation (
24) with
. In the limit under consideration, the main contribution to the SEMT comes from the zero-point fluctuations with wavelengths smaller than the curvature radius and the effect of the gravitational field is weak. The asymptotic (
29) is further simplified if the separation
a is smaller than the length scales determined by the boundary conditions,
,
. For Dirichlet boundary conditions on the brane
,
, the condition
is assumed. Under those conditions,
(
in the case
) for the region of
that dominates in the integral on the right-hand side of Equation (
24) (with
). In the leading order one obtains:
with
being the Riemann zeta function. Note that the asymptotic (
29) also describes the behavior of the SEMT near the AdS horizon. As is seen from Equation (
30), in the special cases of minimally (
) and conformally (
) coupled fields and for quite small separations between the branes, the energy density induced on the brane
by the second brane is positive for
and negative for
. For the Dirichlet boundary condition on the second brane (
), the sign of the induced energy density coincides with the sign of the product
.
In the opposite limit of considerably large proper separations compared with the curvature radius, one has
and the main contribution to the integral in Equation (
22) gives the region near the lower limit, corresponding to
. In the leading order, replacing the function
by
one obtains
This expression is further simplified for separations larger than the length scales in Robin boundary conditions. Assuming
,
, one can see that
for the region, giving the dominant contribution to the integral in Equation (
32). For the case of Neumann boundary conditions on the brane
, corresponding to the limit
, for separations
, one has
in the region with the dominant contribution to the integral. For the leading order term in the VEV of the SEMT and for non-Neumann (
) boundary conditions on the second brane, one finds:
For Neumann boundary conditions on the second brane, an additional factor
should be added to the right-hand side of Equation (
33). One can see that at considerably large distances between the branes the decay of the SEMT, as a function of the proper separation, is a power law for both massive and massless fields. This feature for massive fields is in contrast with the corresponding behavior for parallel plates in the Minkowski bulk, where the suppression is exponential, by the factor
. Let us note that the Formula (
32) also gives the asymptotic of the SEMT near the AdS boundary. As seen, for fixed
, the SEMT tends to zero on the AdS boundary, like
. The asymptotic estimate (
33) shows that for
, and for non-Neumann boundary conditions on the second brane (
), at quite large separations between the branes the induced energy density
is negative for minimally and conformally coupled fields.
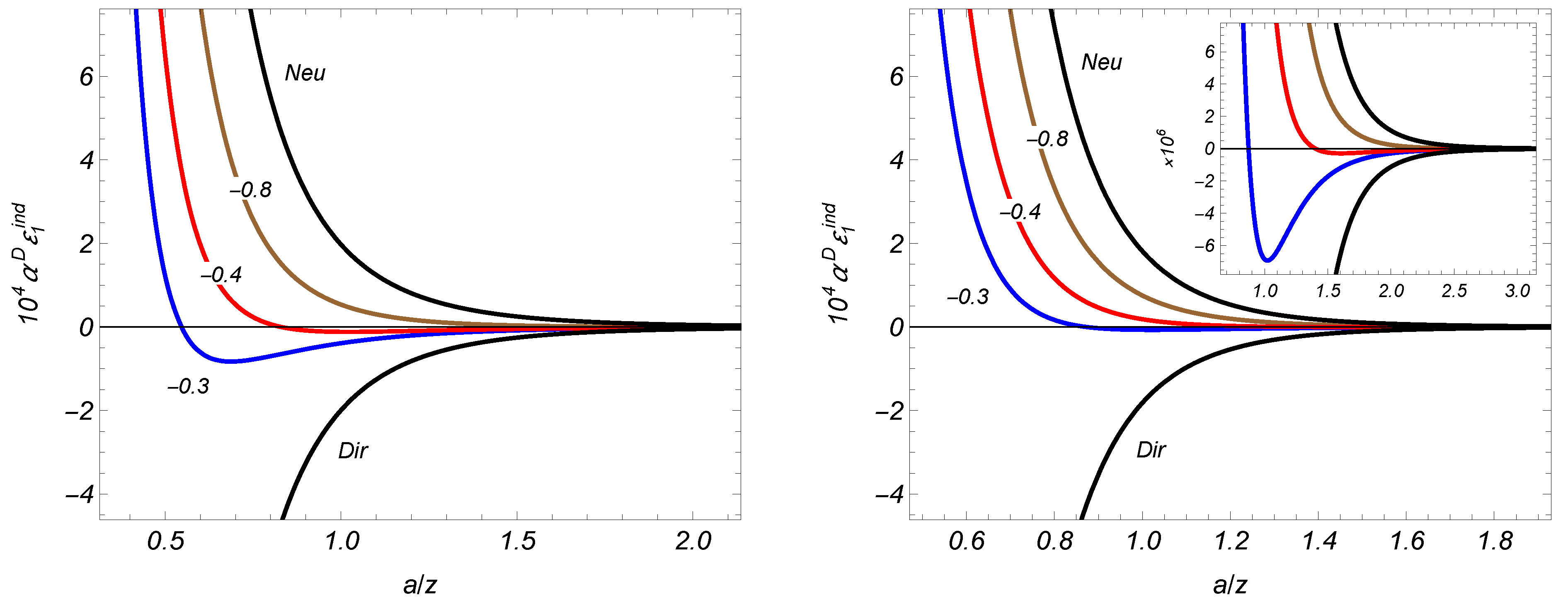
Figure 2 presents the VEV of the energy density, induced on the brane at
by the brane at
as a function of the proper separation between the branes
. The graphs are plotted for a scalar field in (4 + 1)-dimensional AdS spacetime (
), for the Robin boundary condition with
and with the mass corresponding to
. The dependence on the proper separation is displayed for different values of the ratio
(the numbers near the curves) and for Dirichlet and Neumann boundary conditions on the second brane.
Figure 2, left, and
Figure 2, right, correspond to conformally and minimally coupled fields, respectively. In accordance with the asymptotic analysis given above, for minimally and conformally coupled fields and at relatively small separations between the branes, the energy density, induced by the second brane, is positive (negative) for non-Dirichlet (Dirichlet) boundary conditions on the second brane. At considerably large separations, the energy density is negative for non-Neumann boundary conditions on the second brane and is positive for Neumann boundary conditions. The inset in
Figure 2, right, is given to emphasize the change in the sign of the surface energy density as a function of the separation between the branes.
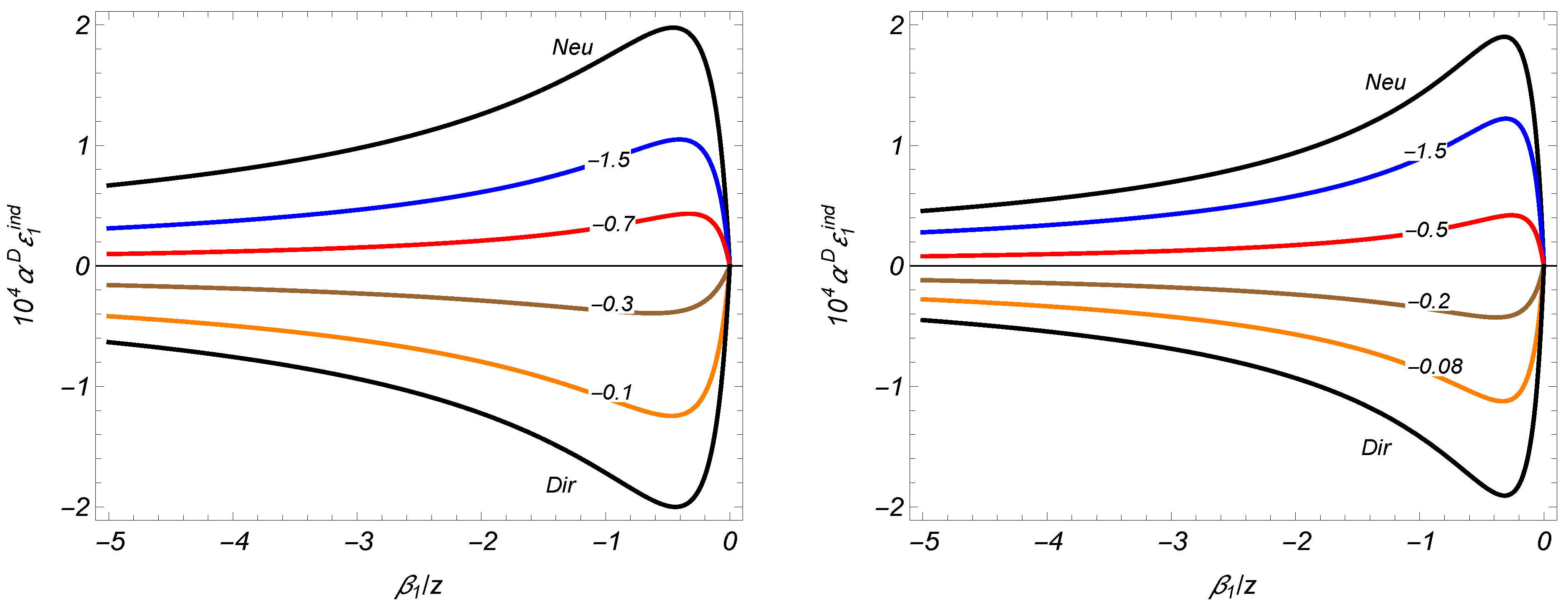
In
Figure 3, for conformally (
Figure 3, left) and minimally (
Figure 3, right) coupled scalar fields in
spatial dimensions, the dependence of the energy density
on the Robin coefficient
is plotted for different values of the Robin coefficient
(the numbers marking the curves) on the second brane and for Dirichlet and Neumann boundary conditions. The graphs are plotted for
and
.
The dependence of the surface energy density on the mass of the field (in units of
) is displayed in
Figure 4 for conformally (
Figure 4, left) and minimally (
Figure 4, right) coupled scalar fields in spatial dimensions
. The graphs are plotted for
,
, and for different values of the ratio
(the numbers marking the curves). The graphs corresponding to Robin boundary conditions,
, are located between the graphs corresponding to Neumann and Dirichlet boundary conditions on the second brane (
and
, respectively). As seen, the induced energy density, in general, is not a monotonic function of the field mass. In addition, for fixed values of the other parameters it may change the sign as a function of the mass. In particular, that is the case for a minimally coupled field with the boundary conditions corresponding to
and
(see
Figure 4, right).
5. Conclusions
For a scalar field with general curvature coupling, the VEV of the SEMT induced on branes in AdS spacetime orthogonal to its boundary has been studied. On the branes, the field operator is constrained by the boundary conditions (
3) or, equivalently, by the conditions (
4). To ensure the stability of the vacuum state, the values of the parameters in Robin boundary conditions are restricted by (
7). For the geometry of the branes under consideration, the extrinsic curvature tensor is zero and the general formula for the SEMT is simplified to Equation (
11). From the viewpoint of observers living on the branes this SEMT presents a gravitational source with the equation of state for a cosmological constant. In order to evaluate the corresponding VEV, the Hadamard function is used, obtained from the positive frequency Wightman function from Ref. [
56]. In the region between the branes, the Hadamard function is decomposed into single-brane and the second-brane-induced contributions. This allows the separation of the part generated by the second brane from the total VEV of the SEMT. The surface divergences are contained in the self-energy contributions on the branes and the renormalization is required for those parts only. In order to extract the finite parts in the corresponding VEVs, in
Appendix A, the regularization procedure based on the generalized zeta function approach is employed. The divergences, appearing in the form of simple poles, are absorbed by the renormalization of the corresponding parameters in the “classical” action localized on the branes. The finite part of the SEMT separated in this way contains renormalization ambiguities and additional conditions are required to obtain a unique result. This is fully similar to the case of the self-energy in the Casimir effect in the geometry of a single boundary (see, for example, the corresponding discussion in Ref. [
4]).
The part of the SEMT induced on the brane by the presence of the second brane is finite and uniquely defined. The induced SEMT on the brane
is given by the expression (
22). It vanishes for special cases of Dirichlet and Neumann boundary conditions on that brane. As a consequence of the maximal symmetry of AdS spacetime, for the general case of Robin boundary conditions, the dimensionless quantity
is completely determined by the dimensionless ratios
and
,
. The first one is the proper separation between the branes, measured by an observer with fixed
z in units of the curvature radius
. The VEV of the SEMT for Robin parallel plates in the Minkowski bulk is obtained from Equation (
22) in the limit
and is expressed as Equation (
24). The latter includes special cases previously discussed in the literature and coincides with the result obtained in Ref. [
58] as a limit
of the SEMT in the geometry of branes parallel to the AdS boundary. For a conformally coupled massless field, the problem in the AdS bulk is conformally related to the problem in Minkowski spacetime consisting of two parallel Robin plates perpendicularly intersected by a Dirichlet plate, the latter being the image of the AdS boundary. The VEV in the Minkowski counterpart is given by the Formula (
27), where the contribution of the Dirichlet plate comes from the term in the square brackets with the Bessel function.
At quite small separations between the branes, compared to the curvature radius and length scales determined by the Robin coefficients, the influence of the gravitational field on the SEMT is small enough and the leading term in the corresponding expansion is expressed by Equation (
30). In this limit, and for non-Dirichlet (Dirichlet) boundary conditions on the brane
, the sign of the surface energy density induced on the brane
coincides with the sign of the product
(
). The effects of the gravitational field are essential at proper separations between the branes of the order or larger than the curvature scale of the background geometry. Additionally, assuming that the separation is larger than the length scales fixed by the boundary conditions, the leading behavior of the induced SEMT is described by Equation (
33) for non-Neumann boundary conditions on the second brane. The sign of the energy density coincides with the sign of
. For Neumann conditions on the second brane, an additional factor
needs to be added on the right-hand side of Equation (
33) and the energy density at quite large distances has an opposite sign. An important feature of the large-distance behavior of the SEMT is the power law decay as a function of the proper separation. For parallel plates in Minkowski spacetime, the corresponding decay for massive fields is exponential. The induced surface energy density vanishes on the AdS boundary like
and behaves as
near the AdS horizon.
The investigations of the brane-induced effects on the properties of the scalar vacuum in AdS spacetime have discussed the branes parallel or perpendicular to the AdS boundary. An interesting generalization, that includes these special cases, would be the geometry of branes crossing the AdS boundary at an arbitrary angle. In this case, the dependence of the scalar mode functions on the coordinates parallel and perpendicular to the AdS boundary are not separable and the problem is more complicated. It is expected that for a general crossing angle, in addition the normal and shear Casimir forces, a rotational momentum to appear generated by the vacuum fluctuations.
The study of the boundary-induced effects on the fermionic and electromagnetic vacua for branes perpendicular to the AdS boundary is another direction for further research. The dependence of the mode functions on the coordinate
z is expressed in terms of the functions
for the fermionic field (with
m being the mass of the field) and in terms of the function
for the vector potential of the electromagnetic field. Similar to the case of a scalar field, it is expected that the equation determining the eigenvalues of the quantum number corresponding to the direction normal to the branes to be the same as that in the Minkowski bulk, with the same boundary conditions on planar boundaries. The summation over those eigenvalues in the corresponding mode sum for the VEV of the energy–momentum tensor can be achieved using the generalized Abel–Plana formula. This allows the explicit extraction of the brane-induced contribution. Note that previous investigations of the vacuum energy–momentum tensor for fermionic and electromagnetic fields have considered branes parallel to the AdS boundary (see [
41,
42,
43,
44,
45]). The bag boundary condition has been imposed for the fermionic field, and for the electromagnetic field, the perfect conductor and confining boundary conditions have been discussed.