Casimir Effect Invalidates the Drude Model for Transverse Electric Evanescent Waves
Abstract
1. Introduction
2. Formalisms of the Lifshitz Theory in Terms of Real or Pure Imaginary Frequencies
3. Calculation of the Casimir Pressure between Metalic Plates Using the Drude and Plasma Models
4. Comparison Studies of Contributions from the Propagating and Evanescent Waves
4.1. Transverse Magnetic Polarization
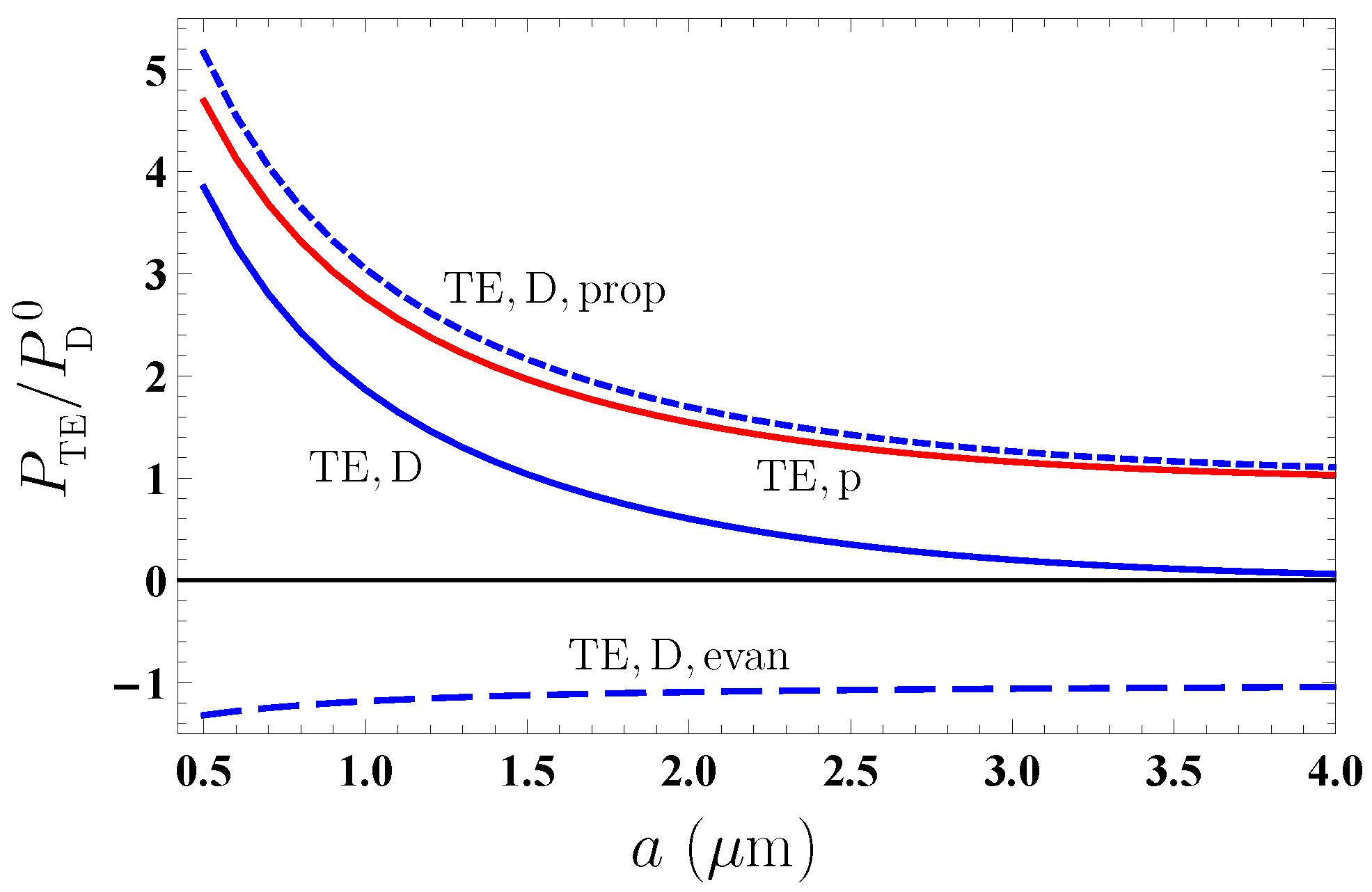
4.2. Transverse Electric Polarization
5. Discussion: Failure of the Drude Model for Transverse Electric Evanescent Waves, the Role of Dissipation, and Possibilities of Alternative Tests
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Casimir, H.B.G. On the attraction between two perfectly conducting plates. Proc. Kon. Ned. Akad. Wetensch. B 1948, 51, 793–795. Available online: https://dwc.knaw.nl/DL/publications/PU00018547.pdf (accessed on 26 August 2023).
- Lifshitz, E.M. The theory of molecular attractive forces between solids. Zh. Eksp. Teor. Fiz. 1955, 29, 94–110. (In Russian); English translation: Sov. Phys. JETP 1956, 2, 73–83. Available online: http://jetp.ras.ru/cgi-bin/e/index/e/2/1/p73?a=list (accessed on 26 August 2023).
- Mahanty, J.; Ninham, B.W. Dispersion Forces; Academic Press: London, UK, 1976. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces; Academic Press: San Diego, CA, USA; Elsevier: San Diego, CA, USA, 2011. [Google Scholar] [CrossRef]
- Milonni, P.W. The Quantum Vacuum. An Introduction to Quantum Electrodynamics; Academic Press, Inc.: San Diego, CA, USA, 1994. [Google Scholar] [CrossRef]
- Mostepanenko, V.M.; Trunov, N.N. The Casimir Effect and Its Applications; Clarendon Press/Oxford University Press, Inc.: Oxford, UK; New York, NY, USA, 1997. [Google Scholar]
- Milton, K.A. The Casimir Effect: Physical Manifestations of Zero-Point Energy; World Scientific: Singapore, 2001. [Google Scholar] [CrossRef]
- Parsegian, V.A. Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Buhmann, S.Y. Disperson Forces I: Macroscopic Quantum Electrodynamics and Ground-State Casimir, Casimir–Polder and van der Waals Forces; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Buhmann, S.Y. Disperson Forces II: Many-Body Effects, Excited Atoms, Finite Temperature and Quantum Friction; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Langbein, D. Theory of Van der Waals Attraction; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Bordag, M.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. Advances in the Casimir Effect; Oxford University Press Inc.: New York, NY, USA; Oxford, UK, 2015. [Google Scholar] [CrossRef]
- Sernelius, B.E. Fundamentals of van der Waals and Casimir Interactions; Springer Nature, Switzerland AG: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Lamoreaux, S.K. Demonstration of the Casimir Force in the 0.6 to 6 μm Range. Phys. Rev. Lett. 1997, 78, 5–8. [Google Scholar] [CrossRef]
- Speake, C.C.; Trenkel, C. Forces between conducting surfaces due to spatial variations of surface potential. Phys. Rev. Lett. 2003, 90, 160403. [Google Scholar] [CrossRef] [PubMed]
- Bezerra, V.B.; Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M.; Romero, C. Impact of surface imperfections on the Casimir force for lenses of centimeter-size curvature radii. Phys. Rev. B 2011, 83, 075417. [Google Scholar] [CrossRef]
- Mohideen, U.; Roy, A. Precision measurement of the Casimir force from 0.1 to 0.9 μm. Phys. Rev. Lett. 1998, 81, 4549–4552. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Krause, D.E. Measurement of the Casimir force between dissimilar metals. Phys. Rev. Lett. 2003, 91, 050402. [Google Scholar] [CrossRef]
- Decca, R.S.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; López, D.; Mostepanenko, V.M. Improved tests of extra-dimensional physics and thermal quantum field theory from new Casimir force measurements. Phys. Rev. D 2003, 68, 116003. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Precise comparison of theory and new experiment for the Casimir force leads to stronger constraints on thermal quantum effects and long-range interactions. Ann. Phys. 2005, 318, 37–80. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Tests of new physics from precise measurements of the Casimir pressure between two gold-coated plates. Phys. Rev. D 2007, 75, 077101. [Google Scholar] [CrossRef]
- Decca, R.S.; López, D.; Fischbach, E.; Klimchitskaya, G.L.; Krause, D.E.; Mostepanenko, V.M. Novel constraints on light elementary particles and extra-dimensional physics from the Casimir effect. Eur. Phys. J. C 2007, 51, 963–975. [Google Scholar] [CrossRef]
- Bimonte, G.; López, D.; Decca, R.S. Isoelectronic determination of the thermal Casimir force. Phys. Rev. B 2016, 93, 184434. [Google Scholar] [CrossRef]
- Bimonte, G.; Spreng, B.; Maia Neto, P.A.; Ingold, G.-L.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Decca, R.S. Measurement of the Casimir Force between 0.2 and 8 μm: Experimental Procedures and Comparison with Theory. Universe 2021, 7, 93. [Google Scholar] [CrossRef]
- Chang, C.-C.; Banishev, A.A.; Castillo-Garza, R.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Gradient of the Casimir force between Au surfaces of a sphere and a plate measured using an atomic force microscope in a frequency-shift technique. Phys. Rev. B 2012, 85, 165443. [Google Scholar] [CrossRef]
- Banishev, A.A.; Chang, C.-C.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Measurement of the gradient of the Casimir force between a nonmagnetic gold sphere and a magnetic nickel plate. Phys. Rev. B 2012, 85, 195422. [Google Scholar] [CrossRef]
- Banishev, A.A.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Demonstration of the Casimir force between ferromagnetic surfaces of a Ni-coated sphere and a Ni-coated plate. Phys. Rev. Lett. 2013, 110, 137401. [Google Scholar] [CrossRef]
- Banishev, A.A.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Casimir interaction between two magnetic metals in comparison with nonmagnetic test bodies. Phys. Rev. B 2013, 88, 155410. [Google Scholar] [CrossRef]
- Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Reducing detrimental electrostatic effects in Casimir-force measurements and Casimir-force-based microdevices. Phys. Rev. A 2018, 97, 032501. [Google Scholar] [CrossRef]
- Liu, M.; Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Examining the Casimir puzzle with an upgraded AFM-based technique and advanced surface cleaning. Phys. Rev. B 2019, 100, 081406. [Google Scholar] [CrossRef]
- Liu, M.; Xu, J.; Klimchitskaya, G.L.; Mostepanenko, V.M.; Mohideen, U. Precision measurements of the gradient of the Casimir force between ultraclean metallic surfaces at larger separations. Phys. Rev. A 2019, 100, 052511. [Google Scholar] [CrossRef]
- Sushkov, A.O.; Kim, W.J.; Dalvit, D.A.R.; Lamoreaux, S.K. Observation of the thermal Casimir force. Nat. Phys. 2011, 7, 230–233. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Bordag, M.; Mostepanenko, V.M. Comparison between experiment and theory for the thermal Casimir force. Int. J. Mod. Phys. A 2012, 27, 1260012. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Experiment and theory in the Casimir effect. Contemp. Phys. 2006, 47, 131–144. [Google Scholar] [CrossRef]
- Bimonte, G.; Emig, T.; Kardar, M.; Krüger, M. Nonequilibrium fluctuational quantum electrodynamics: Heat radiation, heat transfer, and force. Ann. Rev. Condens. Matter Phys. 2017, 8, 119–143. [Google Scholar] [CrossRef]
- Milton, K.A.; Li, Y.; Kalauni, P.; Parashar, P.; Guérout, P.; Ingold, G.-L.; Lambrecht, A.; Reynaud, S. Negative entropies in Casimir and Casimir-Polder interactions. Fortschr. Phys. 2017, 65, 1600047. [Google Scholar] [CrossRef]
- Svetovoy, V.B.; van Zwol, P.J.; Palasantzas, G.; De Hosson, J.T.M. Optical properties of gold films and the Casimir force. Phys. Rev. B 2008, 77, 035439. [Google Scholar] [CrossRef]
- Bimonte, G. Making precise predictions of the Casimir force between metallic plates via a weighted Kramers-Kronig transform. Phys. Rev. A 2011, 83, 042109. [Google Scholar] [CrossRef]
- Behunin, R.O.; Intravaia, F.; Dalvit, D.A.R.; Maia Neto, P.A.; Reynaud, S. Modeling electrostatic patch effects in Casimir force measurements. Phys. Rev. A 2012, 85, 012504. [Google Scholar] [CrossRef]
- van Zwol, P.J.; Palasantzas, G.; De Hosson, J.T.M. Influence of random roughness on the Casimir force at small separations. Phys. Rev. B 2008, 77, 075412. [Google Scholar] [CrossRef]
- Broer, W.; Palasantzas, G.; Knoester, J.; Svetovoy, V.B. Roughness correction to the Casimir force at short separations: Contact distance and extreme value statistics. Phys. Rev. B 2012, 85, 155410. [Google Scholar] [CrossRef]
- Maia Neto, P.A.; Lambrecht, A.; Reynaud, S. Casimir effect with rough metallic mirrors. Phys. Rev. A 2005, 72, 012115. [Google Scholar] [CrossRef]
- Canaguier-Durand, A.; Maia Neto, P.A.; Cavero-Pelaez, I.; Lambrecht, A.; Reynaud, S. Casimir interaction between plane and spherical metallic surfaces. Phys. Rev. Lett. 2009, 102, 230404. [Google Scholar] [CrossRef] [PubMed]
- Fosco, C.D.; Lombardo, F.C.; Mazzitelli, F.D. Proximity force approximation for the Casimir energy as a derivative expansion. Phys. Rev. D 2011, 84, 105031. [Google Scholar] [CrossRef]
- Bimonte, G.; Emig, T.; Jaffe, R.L.; Kardar, M. Casimir forces beyond the proximity force approximation. Europhys. Lett. (EPL) 2012, 97, 50001. [Google Scholar] [CrossRef]
- Teo, L.P. Material dependence of Casimir interaction between a sphere and a plate: First analytic correction beyond proximity force approximation. Phys. Rev. D 2013, 88, 045019. [Google Scholar] [CrossRef]
- Bimonte, G. Going beyond PFA: A precise formula for the sphere-plate Casimir force. Europhys. Lett. 2017, 118, 20002. [Google Scholar] [CrossRef]
- Hartmann, M.; Ingold, G.-L.; Maia Neto, P.A. Plasma versus Drude modeling of the Casimir force: Beyond the proximity force approximation. Phys. Rev. Lett. 2017, 119, 043901. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mohideen, U.; Mostepanenko, V.M. The Casimir force between real materials: Experiment and theory. Rev. Mod. Phys. 2009, 81, 1827–1885. [Google Scholar] [CrossRef]
- Mostepanenko, V.M. Casimir puzzle and conundrum: Discovery and search for resolution. Universe 2021, 7, 84. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Current status of the problem of thermal Casimir force. Int. J. Mod. Phys. A 2022, 37, 2241002. [Google Scholar] [CrossRef]
- Esquivel, R.; Svetovoy, V.B. Correction to the Casimir force due to the anomalous skin effect. Phys. Rev. A 2004, 69, 062102. [Google Scholar] [CrossRef]
- Svetovoy, V.B.; Esquivel, R. Nonlocal impedances and the Casimir entropy at low temperatures. Phys. Rev. E 2005, 72, 036113. [Google Scholar] [CrossRef] [PubMed]
- Sernelius, B.E. Effects of spatial dispersion on electromagnetic surface modes and on modes associated with a gap between two half spaces. Phys. Rev. B 2005, 71, 235114. [Google Scholar] [CrossRef]
- Torgerson, J.R.; Lamoreaux, S.K. Low-frequency character of the Casimir force between metallic films. Phys. Rev. E 2004, 70, 047102. [Google Scholar] [CrossRef]
- Bimonte, G. Comment on “Low-frequency character of the Casimir force between metallic films”. Phys. Rev. E 2006, 73, 048101. [Google Scholar] [CrossRef] [PubMed]
- Intravaia, F.; Henkel, C. Casimir interaction from magnetically coupled eddy currents. Phys. Rev. Lett. 2009, 103, 130405. [Google Scholar] [CrossRef] [PubMed]
- Intravaia, F.; Ellingsen, S.A.; Henkel, C. Casimir-Foucault interaction: Free energy and entropy at low temperature. Phys. Rev. A 2010, 82, 032504. [Google Scholar] [CrossRef]
- Svetovoy, V.B.; Esquivel, R. The Casimir free energy in high- and low-temperature limits. J. Phys. A Math. Gen. 2006, 39, 6777–6784. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Svetovoy, V.B. Experimentum crucis for electromagnetic response of metals to evanescent waves and the Casimir puzzle. Universe 2022, 8, 574. [Google Scholar] [CrossRef]
- Bordag, M. The Casimir effect for thin plasma sheets and the role of the surface plasmons. J. Phys. A Math. Gen. 2006, 39, 6173–6185. [Google Scholar] [CrossRef]
- Palik, E.D. (Ed.) Handbook of Optical Constants of Solids. Volume 1; Academic Press, Inc.: San Diego, CA, USA, 1985. [Google Scholar] [CrossRef]
- Boström, M.; Sernelius, B.E. Thermal effects on the Casimir force in the 0.1–5 μm range. Phys. Rev. Lett. 2000, 84, 4757–4760. [Google Scholar] [CrossRef] [PubMed]
- Bordag, M.; Geyer, B.; Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir force at both nonzero temperature and finite conductivity. Phys. Rev. Lett. 2000, 85, 503–506. [Google Scholar] [CrossRef] [PubMed]
- Greffet, J.-J.; Carminati, R. Image formation in near-field optics. Prog. Surf. Sci. 1997, 56, 133–237. [Google Scholar] [CrossRef]
- Törmä, P.; Barnes, W.L. Strong coupling between surface plasmon polaritons and emitters: A review. Rep. Progr. Phys. 2015, 78, 013901. [Google Scholar] [CrossRef]
- Culshaw, W.; Jones, D.S. Effect of a metal plate on total reflection. Proc. Phys. Soc. B 1953, 66, 859–864. [Google Scholar] [CrossRef][Green Version]
- Brady, J.J.; Brick, R.O.; Pearson, V.D. Penetration of microwaves into the rarer medium in total reflection. J. Opt. Soc. Am. 1960, 50, 1080–1084. [Google Scholar] [CrossRef]
- Zhu, S.; Yu, A.W.; Hawley, D.; Roy, R. Frustrated total internal reflection: A demonstration and review. Am. J. Phys. 1986, 54, 601–606. [Google Scholar] [CrossRef]
- Hsu, J.W.P. Near-field scanning optical microscopy studies of electronic and photonic materials and devices. Mater. Sci. Engin R Rep. 2001, 33, 1–50. [Google Scholar] [CrossRef]
- Aigouy, L.; Lahrech, A.; Grésillon, S.; Cory, H.; Boccara, A.C.; Rivoal, J.C. Polarization effects in apertureless scanning near-field optical microscopy: An experimental study. Opt. Lett. 1999, 24, 187–189. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M.; Svetovoy, V.B. Probing the response of metals to low-frequency s-polarized evanescent waves. Europhys. Lett. (EPL) 2022, 139, 66001. [Google Scholar] [CrossRef]
- Ulvr, M. Design of PCB search coils for AC magnetic flux density measurement. AIP Adv. 2018, 8, 047505. [Google Scholar] [CrossRef]
- Ramadan, Q.; Samper, V.; Poenar, D.; Yu, C. On-chip micro-electromagnets for magnetic-based bio-molecules separation. J. Magn. Magnet. Mater. 2004, 281, 150–172. [Google Scholar] [CrossRef]
- Wensink, H.; Benito-Lopez, F.; Hermes, D.C.; Verboom, W.; Gardeniers, H.J.G.E.; Reinhoudt, D.N.; van den Berg, A. Measuring reaction kinetics in a lab-on-a-chip by microcoil NMR. Lab Chip 2005, 5, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.-X.; Wang, B.; Kong, C.; Si, L.-G.; Xiong, H.; Wu, Y. A proposed method to measure weak magnetic field based on a hybrid optomechanical system. Sci. Rep. 2017, 7, 12521. [Google Scholar] [CrossRef]
- Murzin, D.; Mapps, D.J.; Levada, K.; Belyaev, V.; Omelyanchik, A.; Panina, L.; Rodionova, V. Ultrasensitive magnetic field Sensors for biomedical applications. Sensors 2020, 20, 1569. [Google Scholar] [CrossRef]
- Huang, J.-H.; Duan, X.-Y.; Wang, G.-J.; Hu, X.-Y. Enhancing the precision of detecting weak magnetic fields based on weak-value amplification. J. Opt. Soc. Amer. B 2022, 39, 1289. [Google Scholar] [CrossRef]
- Hannemann, M.; Wegner, G.; Henkel, C. No-slip boundary conditions for electron hydrodynamics and the thermal Casimir pressure. Universe 2021, 7, 108. [Google Scholar] [CrossRef]
- Brevik, I.; Shapiro, B. A critical discussion of different methods and models in Casimir effect. J. Phys. Commun. 2022, 6, 015005. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. An alternative response to the off-shell quantum fluctuations: A step forward in resolution of the Casimir puzzle. Eur. Phys. J. C 2020, 80, 900. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir effect for magnetic media: Spatially non-local response to the off-shell quantum fluctuations. Phys. Rev. D 2021, 104, 085001. [Google Scholar] [CrossRef]
- Klimchitskaya, G.L.; Mostepanenko, V.M. Theory-experiment comparison for the Casimir force between metallic test bodies: A spatially non-local dielectric response. Phys. Rev. A 2022, 105, 012805. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimchitskaya, G.L.; Mostepanenko, V.M. Casimir Effect Invalidates the Drude Model for Transverse Electric Evanescent Waves. Physics 2023, 5, 952-967. https://doi.org/10.3390/physics5040062
Klimchitskaya GL, Mostepanenko VM. Casimir Effect Invalidates the Drude Model for Transverse Electric Evanescent Waves. Physics. 2023; 5(4):952-967. https://doi.org/10.3390/physics5040062
Chicago/Turabian StyleKlimchitskaya, Galina L., and Vladimir M. Mostepanenko. 2023. "Casimir Effect Invalidates the Drude Model for Transverse Electric Evanescent Waves" Physics 5, no. 4: 952-967. https://doi.org/10.3390/physics5040062
APA StyleKlimchitskaya, G. L., & Mostepanenko, V. M. (2023). Casimir Effect Invalidates the Drude Model for Transverse Electric Evanescent Waves. Physics, 5(4), 952-967. https://doi.org/10.3390/physics5040062





