Is the Non-Pointness of the Electron Observable in
Abstract
1. Introduction
2. Theoretical Frameworks
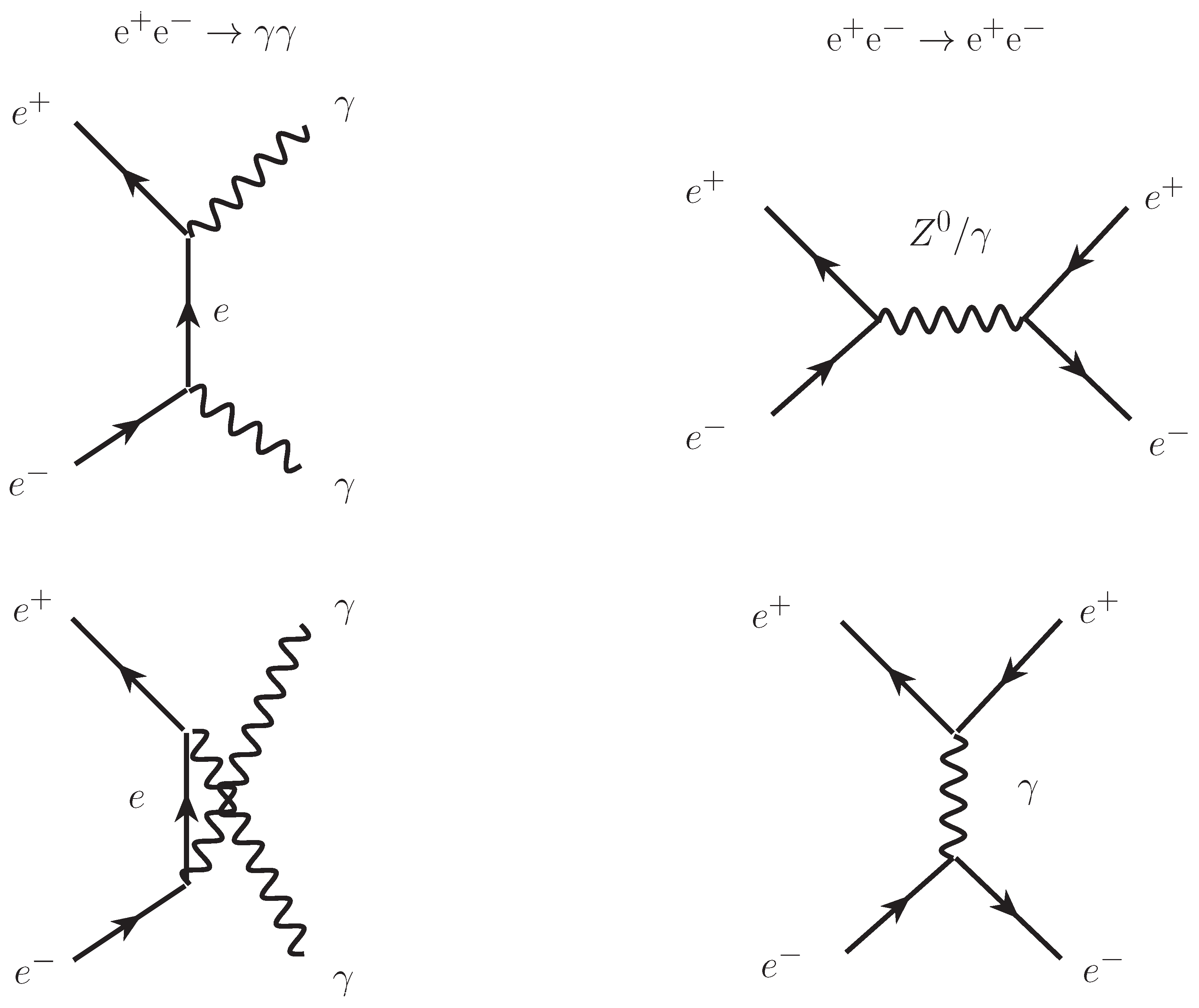
2.1. The Lowest Order Cross-Section of
2.2. Radiative Corrections
2.2.1. Virtual and Soft Radiative Corrections
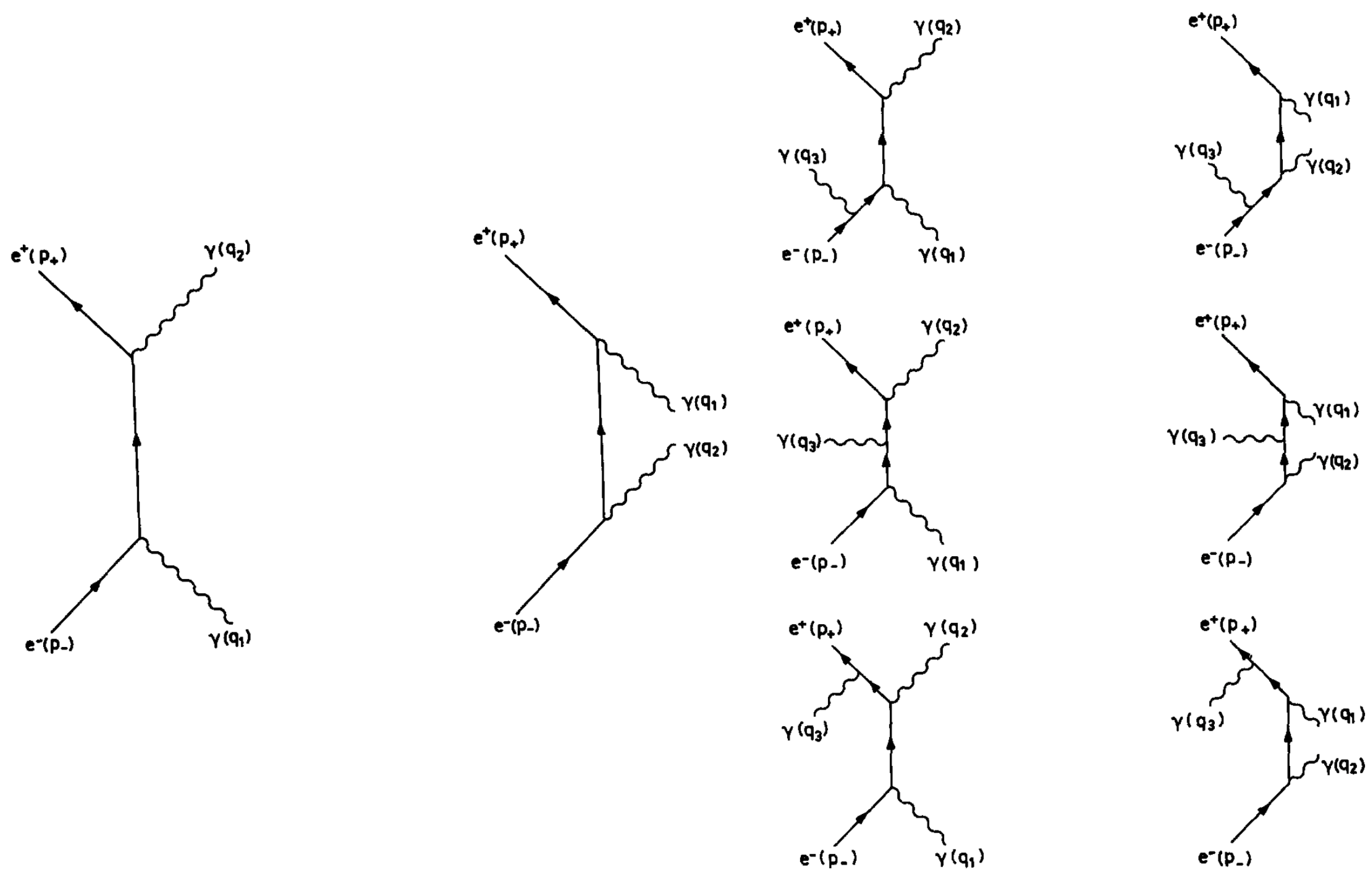
2.2.2. Hard Radiative Corrections
2.3. The Total Cross-Section in
2.4. The Numerical Calculation of the Differential Cross-Section
2.5. Deviations from QED
2.5.1. Heavy Electron Mass
2.5.2. Minimal Interaction Length and Non-Pointness of the Electron
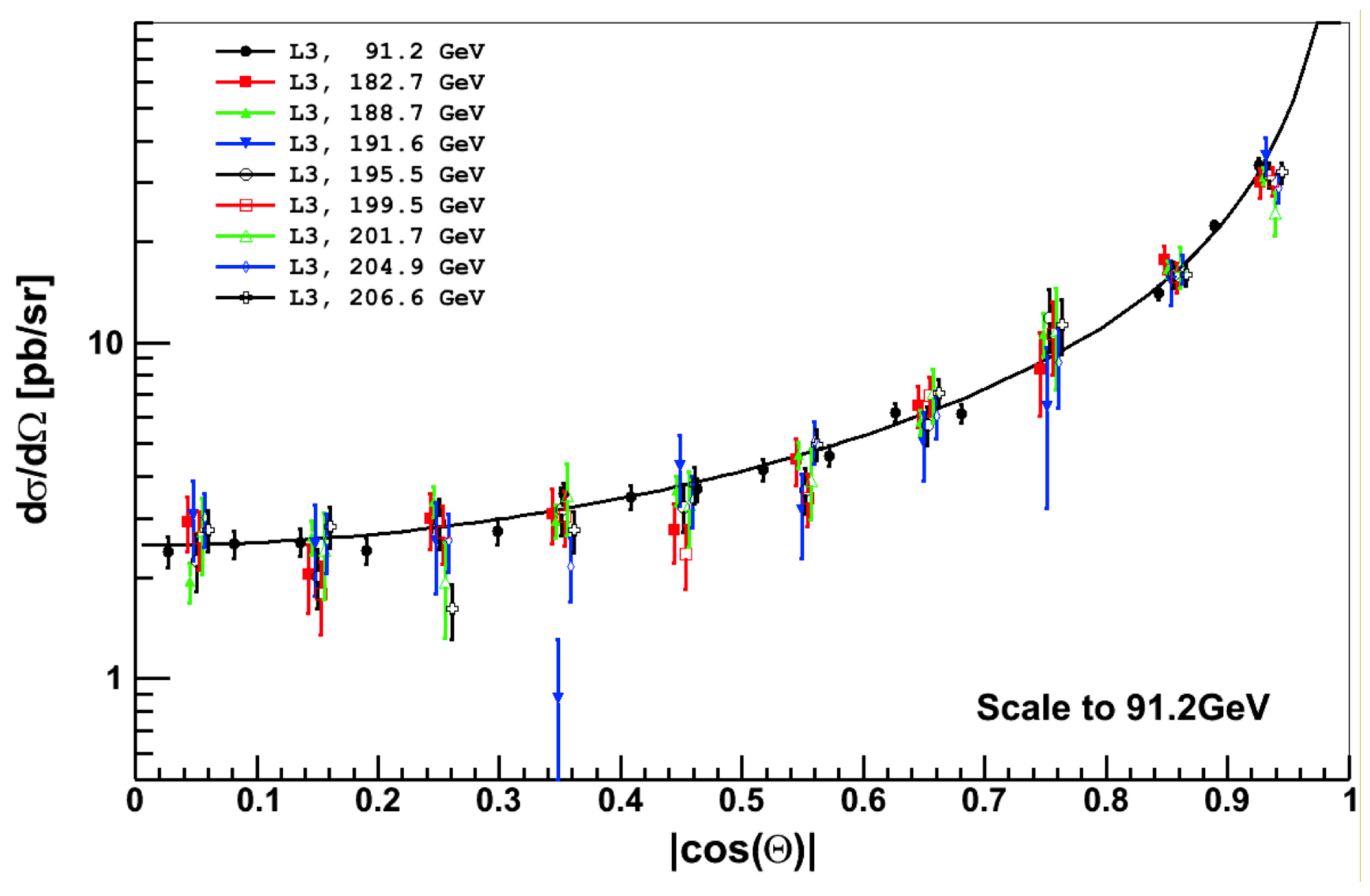
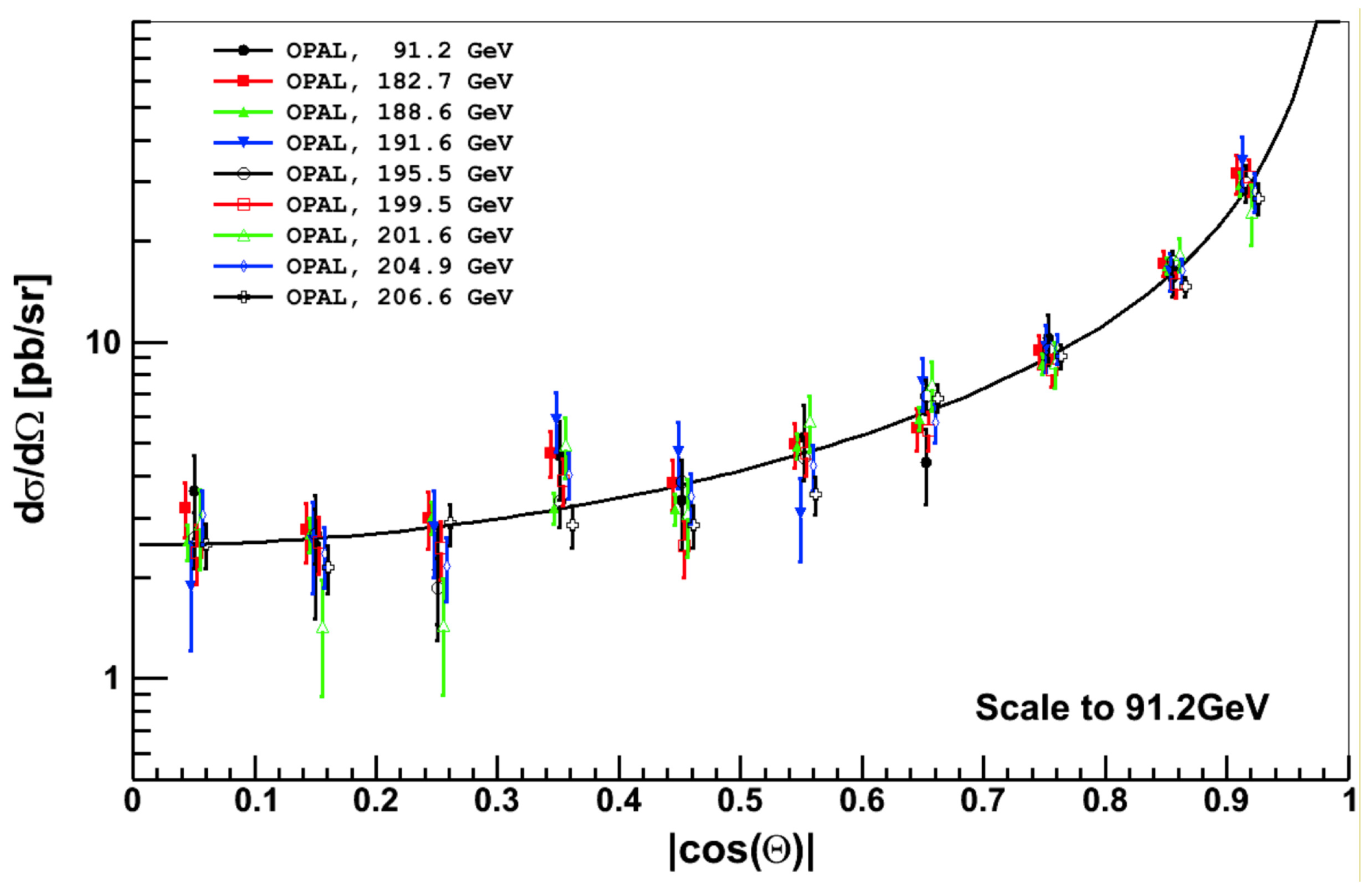
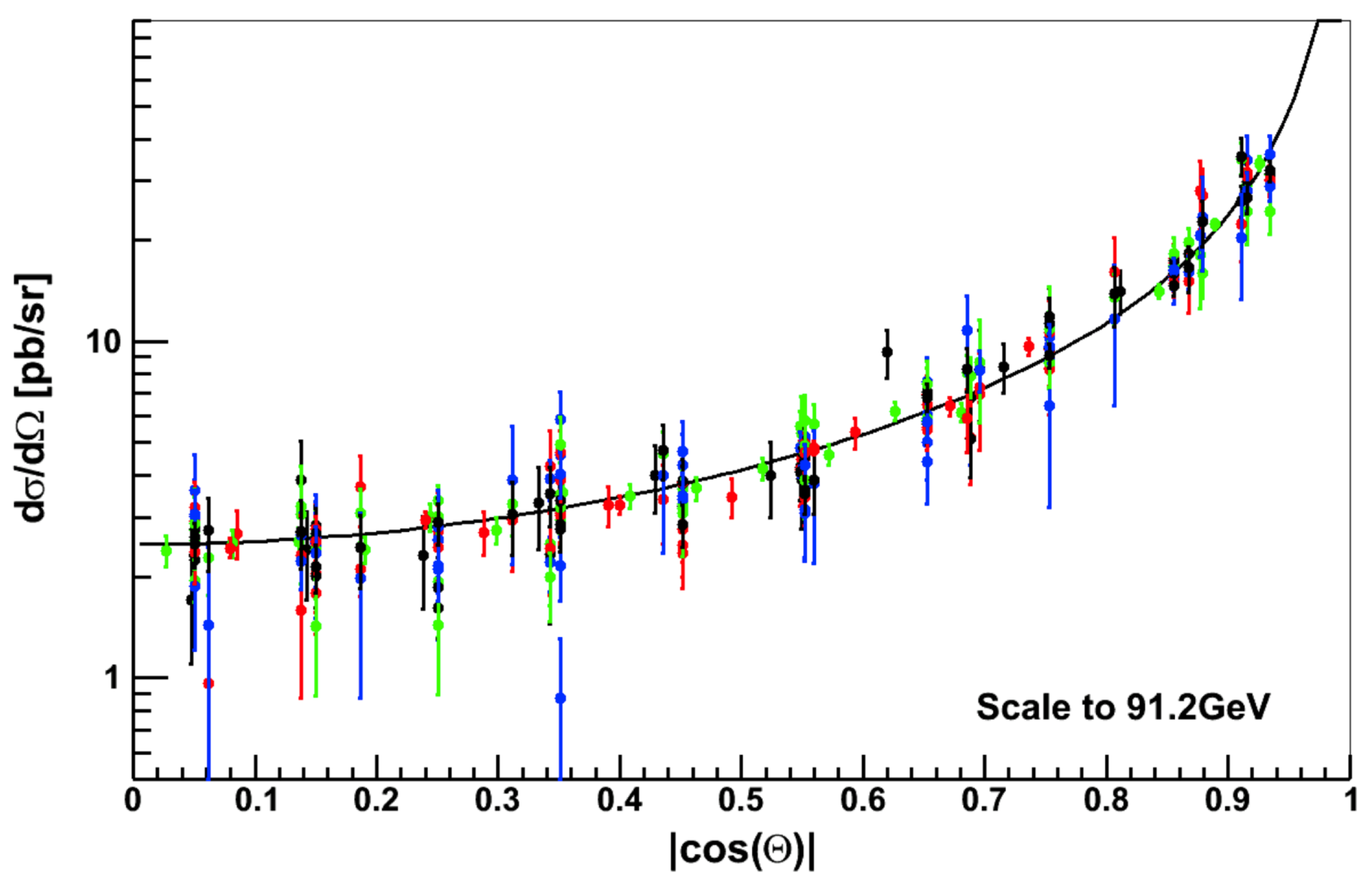
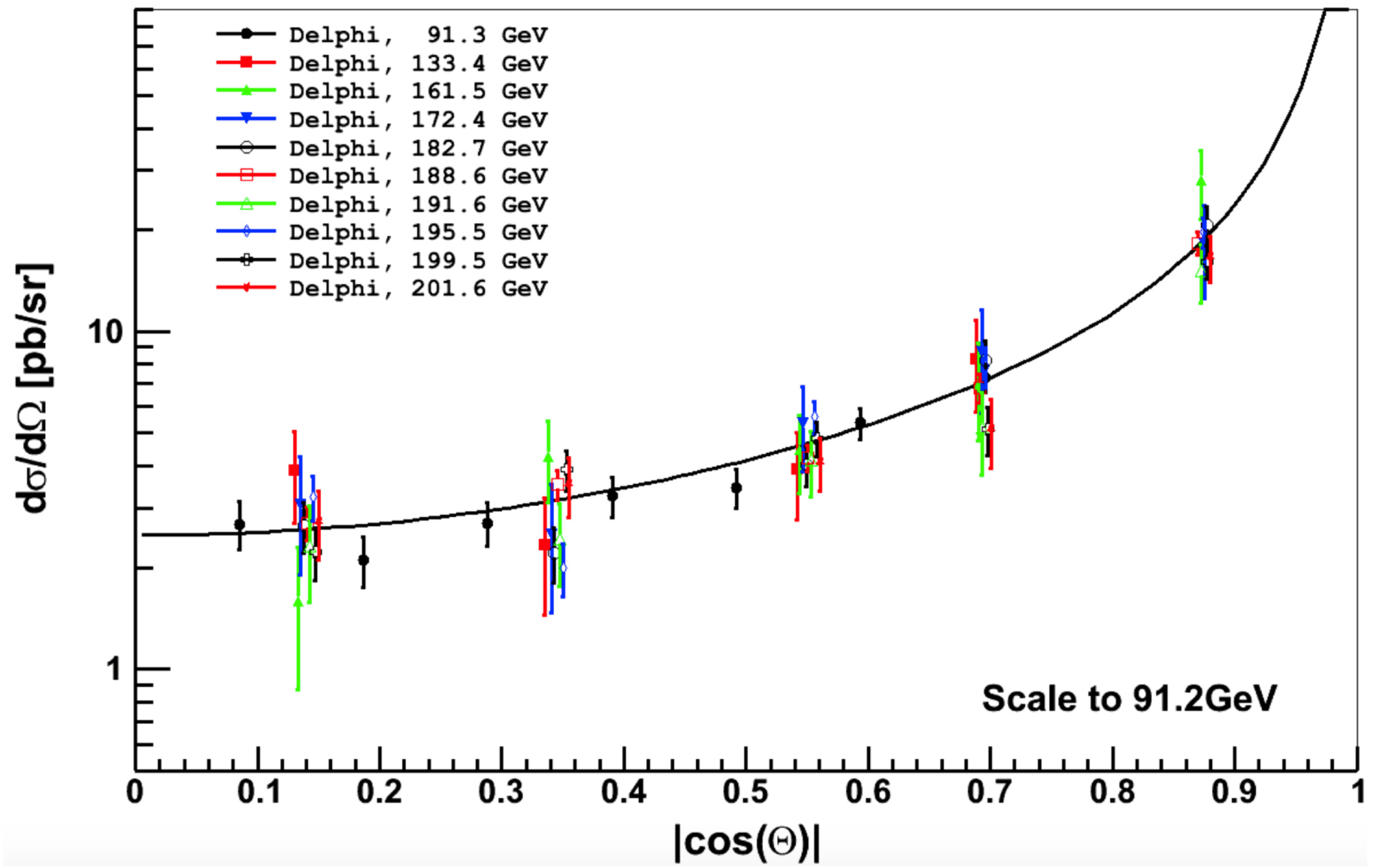
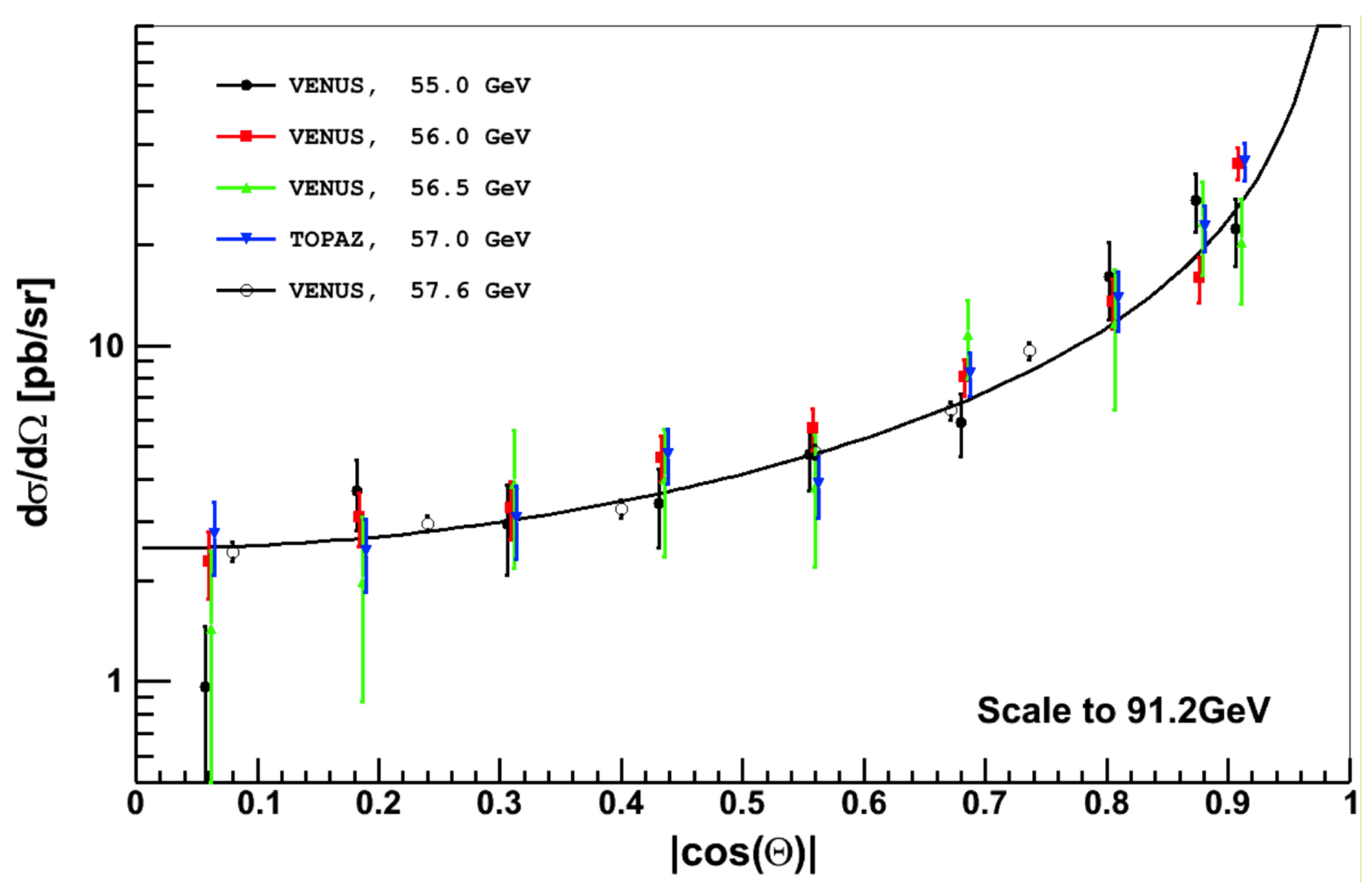
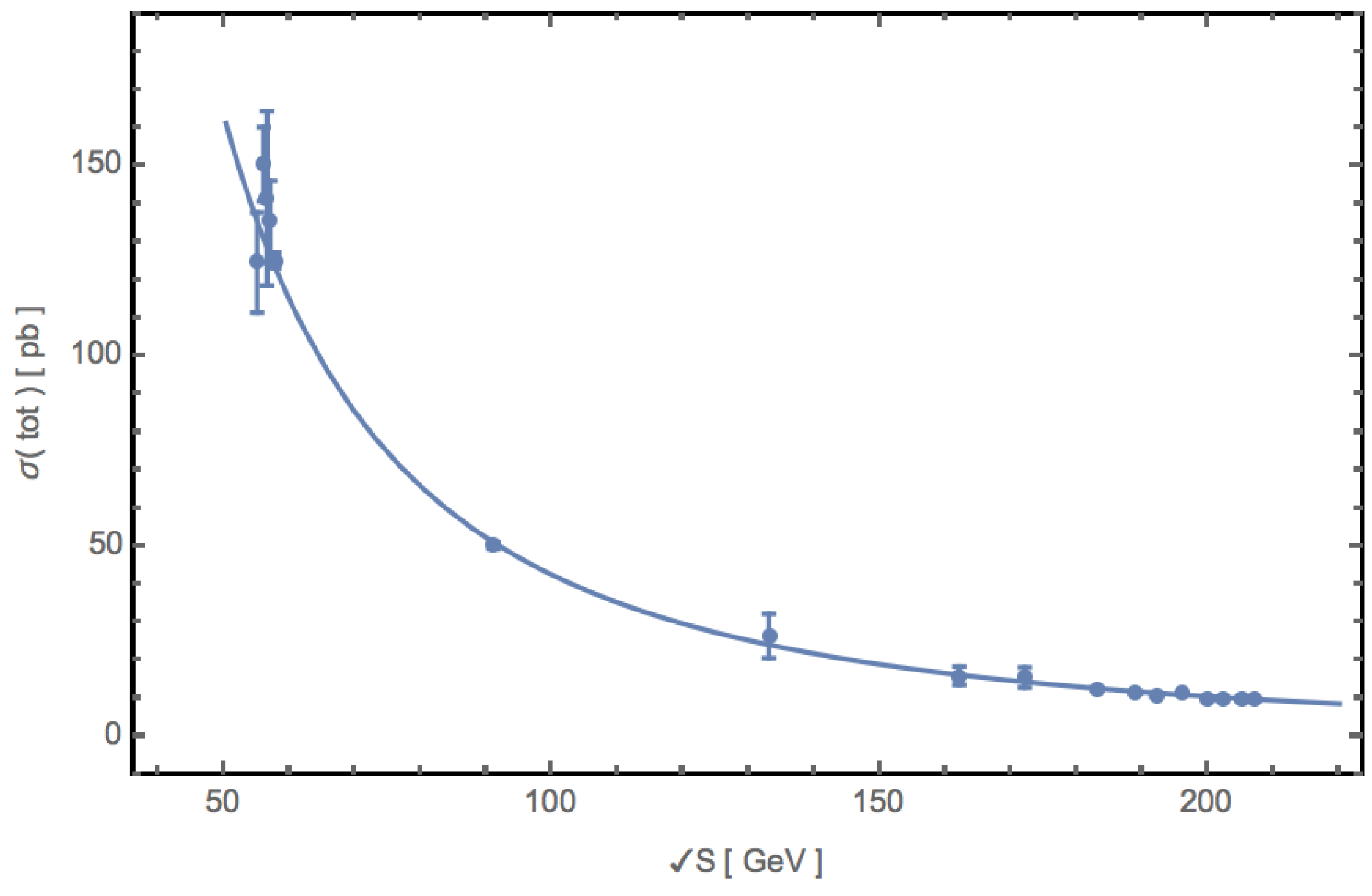
3. The Measurement of the Total and Differential Cross-Section
Differential Cross-Section Datasets
4. Global -Test of the Differential Cross-Section
4.1. Global -Test for Heavy Electron
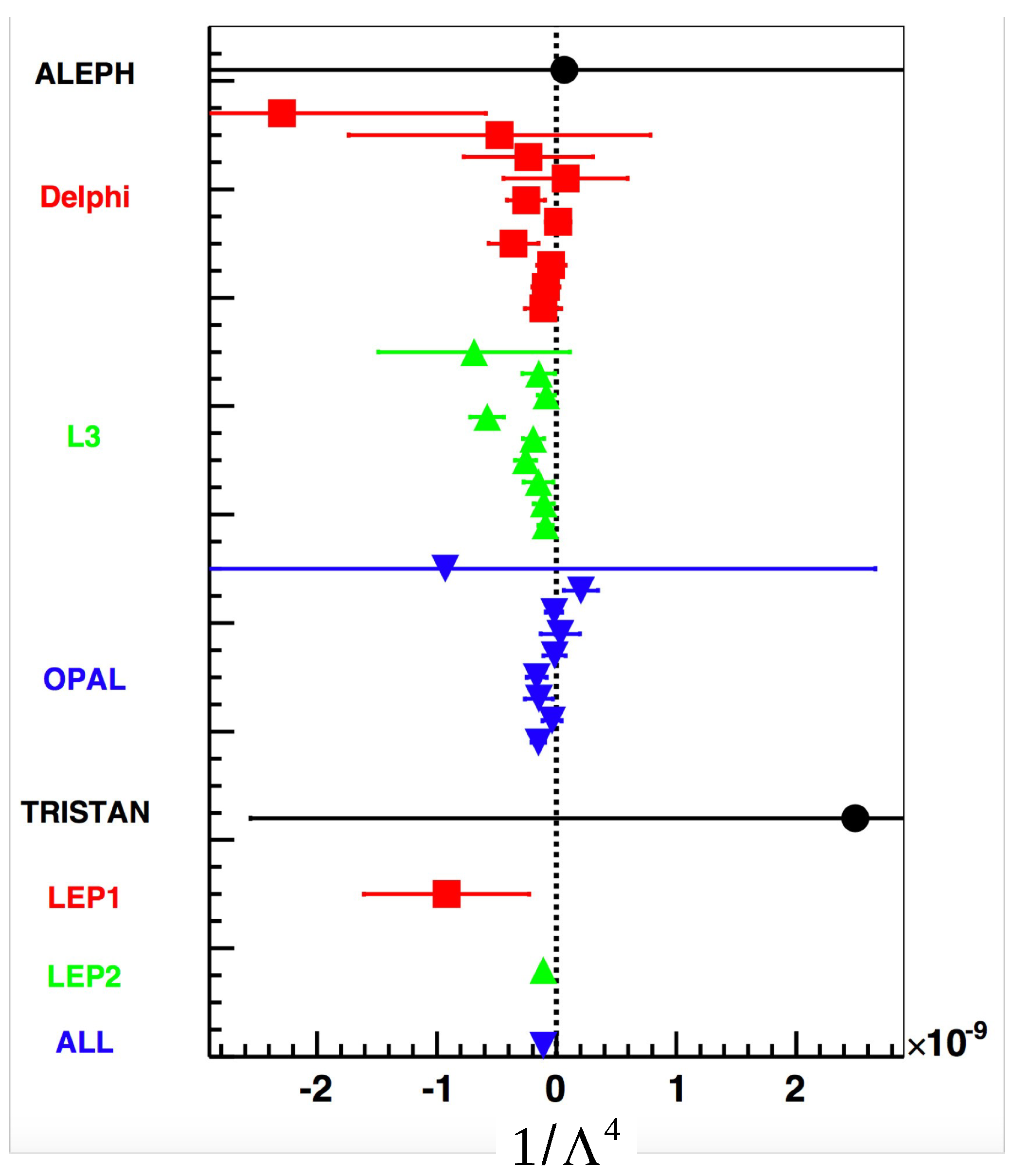
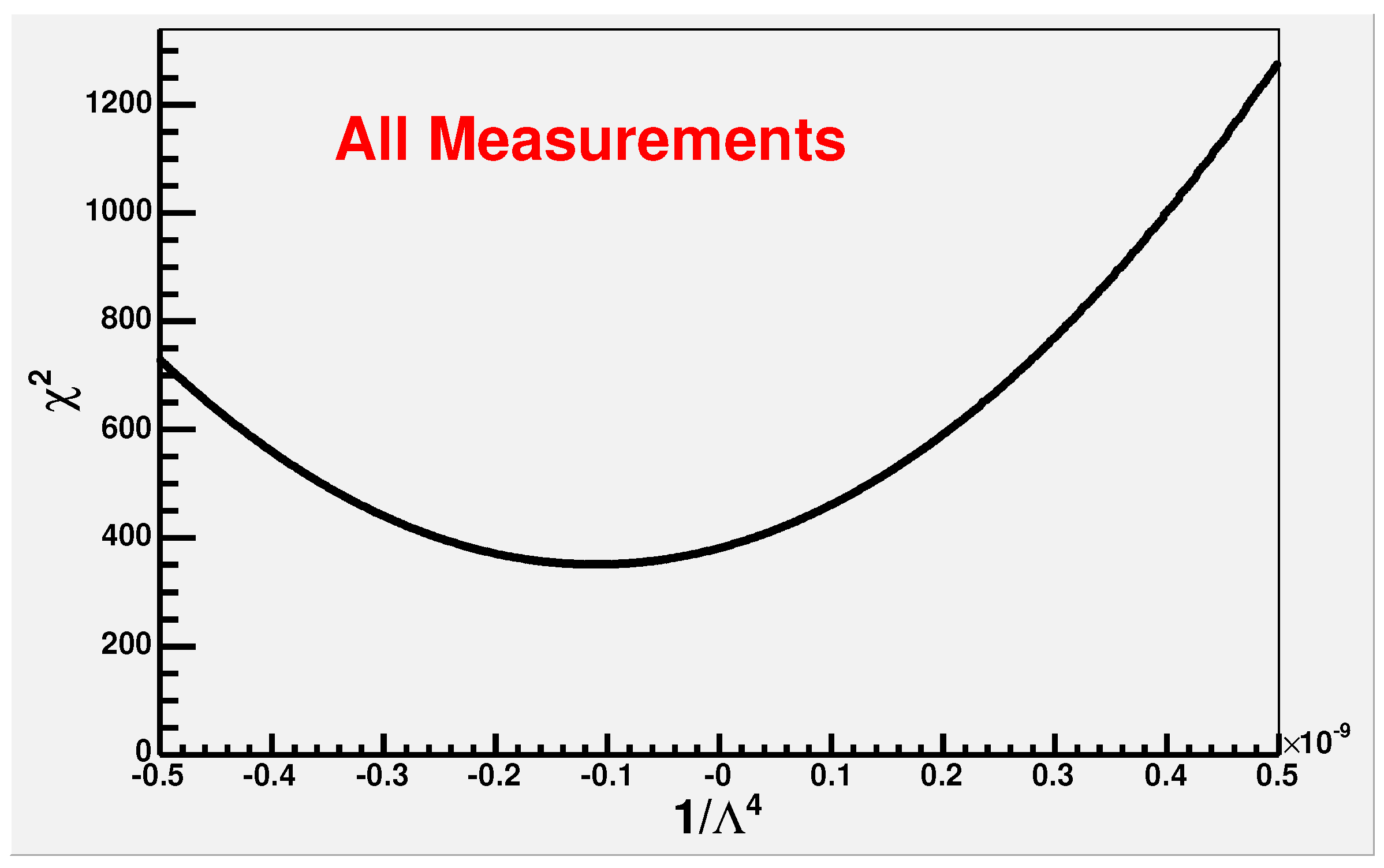
4.2. Global -Test for a Non-Pointness of the Electron
5. Indication of a Signal in the Total Cross-Section
6. Systematic Uncertainties
7. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References and Notes
- Coulomb, C.A. Premier mémoire sur l’électricité et le magnétisme. Mémoire l’Acad. Sci. 1785, 569–577, Reprinted in Coulomb, C.A. Mémoires sur L’électricité et le Magnétisme. Extraits des Mémoires de l’Académie Royale des Sciences de Paris, publiés dans le années 1785 à 1789, avec planches at tableaux. Bachelier, libraire: Paris, France, 1789. [Google Scholar]
- Coulomb, C.A. Second mémoire sur l’électricité et le magnétisme. Mémoire l’Acad. R. Sci. 1785, 578–611, Reprinted in Coulomb, C.A. Mémoires sur L’électricité et le Magnétisme. Extraits des Mémoires de l’Académie Royale des Sciences de Paris, publiés dans le années 1785 à 1789, avec planches at tableaux. Bachelier, libraire: Paris, France, 1789. [Google Scholar] [CrossRef]
- Whittaker, E.T. A History of the Theories of Aether and Electricity; Longman, Green, and Co.: London, UK; Hodges, Figgis & Co. Ltd.: Dublin, UK, 1910; Available online: https://archive.org/details/historyoftheorie00whitrich (accessed on 5 June 2023).
- Oersted, H.C. Experiments on the effect of a current of electricity on the magnetic needle. Ann. Philos. 1820, 16, 273–276. Available online: http://www.ampere.cnrs.fr/ice/ice_book_detail.php?lang=fr&type=role&bdd=koyre_ampere&table=ampere_text&bookId=5&typeofbookId=2&num=0 (accessed on 5 June 2023).
- Blondel, C. A.-M. Ampère et la Création de l’Électrodynamique, 1820–1827; Bibliothèque Nationale: Paris, France, 1982. [Google Scholar]
- Blundell, S.J. Magnetism: A Very Short Introduction; Oxford University Press: Oxford, UK, 2012; p. 31. [Google Scholar] [CrossRef]
- Tricker, R.A.R. Early Electrodynamics. The First Law of Circulation; Pergamon Press Ltd.: Oxford, UK, 1965; p. 23. [Google Scholar] [CrossRef]
- Biot, J.-B.; Savart, F. Note sur le magnétisme de la pile de Volta. Ann. Chem. Phys. 1820, 15, 222–223. Available online: http://www.ampere.cnrs.fr/ice/ice_book_detail.php?lang=fr&type=text&bdd=koyre_ampere&table=ampere_text&bookId=7&typeofbookId=2&num=0 (accessed on 5 June 2023).
- Martin, A. Cathode ray tubes for industrial and military applications. Adv. Electron. Electron Phys. 1986, 67, 183–328. [Google Scholar]
- Keithley, J.F. The Story of Electrical and Magnetic Measurements: From 500 B.C. to the 1940s; IEEE Press/Instituteof Electrical and Electronics Engineers, Inc.: New York, NY, USA, 1999; p. 205. Available online: https://www.scribd.com/document/424498727/The-Story-of-Electrical-and-Magnetic-Measurements-From-500-BC-to-the-1940s-pdf (accessed on 5 June 2023).
- Goldstein, E. Vorläufige Mittheilungen über elektrische Entladungen in verdünnten Gasen (Preliminary communications on electric discharges in rarefied gases). Monatsber. der Königl. Preuss. Akad. Wissensch. Berlin (Month. Rep. R. Pruss. Acad. Sci. Berlin) 1876, 4 May. 279–295, Quoting p. 286: “13. Das durch die Kathodenstrahlen in der Wand hervorgerufene Phosphorescenzlicht ist höchst selten von gleichförmiger Intensität auf der von ihm bedeckten Fläche, und zeigt oft sehr barocke Muster.” (13. The phosphorescent light that’s produced in the wall by the cathode rays is very rarely of uniform intensity on the surface that it covers and [it] often shows very baroque patterns). Available online: https://books.google.ch/books?id=7-caAAAAYAAJ&pg=PA279&redir_esc=y#v=onepage (accessed on 5 June 2023).
- Science History Institute. Education. Scientific Biographies. Joseph “J.J.” John Thomson. Available online: https://sciencehistory.org/education/scientific-biographies/joseph-john-j-j-thomson/ (accessed on 6 June 2023).
- Davis, E.A.; Falconer, I.J. J.J. Thompson and the Discovery of the Electron; CRC Press/Taylor & Francis Group: London, UK, 1997. [Google Scholar] [CrossRef]
- Thomson, J.J. XL. Cathode rays. London Edinburg Dublin Philos. Magaz. J. Sci. 1897, 44, 293–316. [Google Scholar] [CrossRef]
- The Nobel Prize in Physics 1923. Robert. A. Millikan. Nobel Lecture. Available online: https://www.nobelprize.org/prizes/physics/1923/millikan/lecture/ (accessed on 5 June 2023).
- NIST. Fundamental Physics Constants: Elementary Charge. In The NIST Reference on Constants, Units and Uncertainty; NIST: Gaithersburg, MD, USA, 2019. Available online: https://physics.nist.gov/cgi-bin/cuu/Value?e (accessed on 5 June 2023).
- Tessinga, E.; Mohr, P.J.; Taylor, B.N.; Newell, D.B. CODATA recommended values of the fundamental physics constants: 2018. J. Phys. Chem. Ref. Data 2021, 50, 033105. [Google Scholar] [CrossRef]
- Abraham, M. Prinzipien der Dynamik des Elektrons. Ann. Phys. 1903, 315. [Google Scholar] [CrossRef]
- Lorentz, H.A. Electromagnetic phenomena in a system moving with any velocity smaller than that of light. Proc. R. Netherl. Acad. Arts Sci. (KNAW) 1903–1904, 6, 809–831, Reprinted in Lorentz, H.A. Collected Papers. Volume V; Springer Science+Business Media, B.V.: Dordrecht, The Netherlands, 1937; 172–197. [Google Scholar] [CrossRef]
- Lorentz, H.A. Theory of Electrons and Its Applications to the Phenomena of Light and Radiant Heat; Dover Publications, Inc.: New York, NY, USA, 1952. [Google Scholar]
- Dirac, P.A.M. Classical theory of radiating electrons. Proc. R. Soc. Lond. A Math. Phys. Eng. 1938, 167, 148–169. [Google Scholar] [CrossRef]
- Compton, A.H. The magnetic electron. J. Frankl. Inst. 1921, 192, 145–155. [Google Scholar] [CrossRef]
- Enz, C.P. Heisenberg’s applications of quantum mechanics (1926-33) or the settling of the new land. Helv. Phys. Acta 1983, 56, 993–1001. [Google Scholar] [CrossRef]
- Gerlach, W.; Stern, O. Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld. Z. Phys. 1922, 9, 349–352. [Google Scholar] [CrossRef]
- Pauli, W. Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren. Z. Phys. 1925, 31, 765–783. [Google Scholar] [CrossRef]
- Schmor, P.W. A review of polarized ion sources. In Proceedings of the 1995 IEEE Conference on Particle Accelerator, Dallas, TX, USA, 1–5 May 1995; IEEE: New York, NY, USA, 1996; pp. 853–857. [Google Scholar] [CrossRef]
- Haeberli, W. Sources of polarized ions. Annu. Rev. Nucl. Sci. 1967, 17, 373–426. [Google Scholar] [CrossRef]
- Arnold, W.; Ulbricht, J.; Berg, H.; Keiner, P.; Krause, H.H.; Schmidt, R.; Clausnitzer, G. The Giessen polarization facility: II. 1.2 MeV tandem accelerator. Nucl. Instr. Meth. 1977, 143, 457–465. [Google Scholar] [CrossRef]
- Krause, H.H.; Stock, R.; Arnold, W.; Berg, H.; Huttel, E.; Ulbricht, J.; Clausnitzer, G. The Giesssen polarization facility: III. Multi-detector analyzing system. Nucl. Instr. Meth. 1977, 143, 467–471. [Google Scholar] [CrossRef]
- According to William Barletta, Director of USPAS, the US Particle Accelerator School; see Feder, T. Accelerator school travels university circuit. Phys. Today 2010, 63, 20–22. [Google Scholar] [CrossRef]
- Minehara, E.; Abe, S.; Yoshida, T.; Sato, Y.; Kanda, M.; Kobayashi, C.; Hanashima, S. On the production of the KrF− and XeF− ion beams for the tandem electrostatic accelerators. Nucl. Instrum. Meth. Phys. Res. B 1984, 5, 217–220. [Google Scholar] [CrossRef]
- Szczerba, D. Development of a Polarized Atomic Beam Source and Measurement of Spin Correlation Parameters. Ph.D. Thesis, Naturwissenschaften ETH Zürich, Zürich, Switzerland, 2001. [Google Scholar] [CrossRef]
- Nass, A.; Stancari, M.; Steffens, E. Studies on beam formation in an atomic beam source. AIP Conf. Proc. 2009, 1149, 863–867. [Google Scholar] [CrossRef]
- Clegg, T.B. Lamb-shift polarized ion sources—After 15 years. AIP Conf. Proc. 1982, 80, 21–37. [Google Scholar] [CrossRef]
- Arnold, W.; Berg, H.; Krause, H.H.; Ulbricht, J.; Clausnitzer, G. The Giessen poarization facility: I. Lambshift source. Nucl. Instr. Meth. 1977, 143, 441–455. [Google Scholar] [CrossRef]
- Ulbricht, J.; Arnold, W.; Berg, H.; Huttel, E.; Krause, H.H.; Clausnitzer, G. The polarised proton capture reaction 7Li(d, γ)8Be in the energy range from 380 to 960 keV. Nucl. Phys. A 1977, 287, 220–236. [Google Scholar] [CrossRef]
- Aruldhas, G. Quantum Mechanics, PHI Learning Private Limited: New Delhi, India, 2009; Ch. 15.15. Available online: https://www.scribd.com/document/397840888/G-Aruldhas-Quantum-Mechanics (accessed on 5 June 2023).
- Raymond, R.S. An Intense Source of Negative Polarized Hydrogen Ions. Ph.D. Thesis, University of Wisconsin–Madison, Madison, WI, USA, 1979; pp. 123–126. [Google Scholar]
- Schrödinger, E. Über die kräftefreie Bewegung in der relativistischen Quantenmechanik. Sitzunber. Preuss. Akad. Wiss. Phys.-Math. Kl. 1930, 24, 418–428. [Google Scholar]
- Weyssenhoff, J.; Raabe, A. Relativistic dynamics of spin-fluids and spin-particles. Acta Phys. Pol. 1947, 9, 7–18. Available online: Phttps://www.actaphys.uj.edu.pl/fulltext?series=T&vol=9&no=1&page=19 (accessed on 5 June 2023).
- Pryce, M.H.L. The mass-center in the restricted theory of relativity and its connexion with the quantum theory of elementary particles. Proc. R. Soc. A Math. Phys. Eng. Sci. 1948, 195, 62–81. [Google Scholar] [CrossRef]
- Fleming, C.N. Covariant position operators, spin and locality. Phys. Rev. B 1965, 137, 188–197. [Google Scholar] [CrossRef]
- Riewe, F. Generalized mechanics of a spinning particle. Lett. Nuovo Cim. 1971, 1, 807–808. [Google Scholar] [CrossRef]
- Barut, A.O.; Zanghi, N. Classical model of the Dirac electron. Phys. Rev. Lett. 1984, 52, 2009–2012. [Google Scholar] [CrossRef]
- Srednicki, M. Quantum Field Theory; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; CRC Press/Taylor & Francis Group LLC: Boca Raton, FL, USA, 1995. [Google Scholar] [CrossRef]
- Schwartz, M.D. Quantum Field Theory and the Standard Model; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Thomson, M. Modern Particle Physics; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar] [CrossRef]
- Itzykson, C.; Zuber, J.-B. Quantum Field Theory; McGraw-Hill, Inc.: New York, NY, USA, 1980. [Google Scholar]
- Frenkel, J. Die Elektrodynamik des rotierenden Elektrons. Z. Phys. 1926, 37, 243–262. [Google Scholar] [CrossRef]
- Mathisson, M. Neue Mechanik materieller Systeme. Acta Phys. Pol. 1937, 6, 163–200. Available online: https://www.actaphys.uj.edu.pl/fulltext?series=T&vol=6&no=3&page=163 (accessed on 5 June 2023).
- Kramers, L.H. Quantentheorie des Electron und der Strahlung; Akademische Verlagsgesellschaft: Leipzig, Germany, 1938. [Google Scholar]
- Hönl, H.; Papapetrou, A. Über die innere Bewegung des Elektrons. I. Z. Phys. 1939, 112, 512–540. [Google Scholar] [CrossRef]
- Bhabha, H.J.; Corben, A.C. General classical theory of spinning particles in a Maxwell field. Proc. R. Soc. A Math. Phys. Eng. 1941, 178, 273–314. [Google Scholar] [CrossRef]
- Bargman, V.; Michel, L.; Telegdi, V.L. Precession of the polarization of particles moving in a homogeneous electromagnetic field. Phys. Rev. Lett. 1959, 2, 435–436. [Google Scholar] [CrossRef]
- Nash, P.L. A Lagrangian theory of the classical spinning electron. J. Math. Phys. 1984, 25, 2104–2108. [Google Scholar] [CrossRef]
- Plyushchay, M.S. Relativistic massive particle with higher curvatures as a model for the description of bosons and fermions. Phys. Lett. B 1990, 235, 47–51. [Google Scholar] [CrossRef]
- Yee, K.; Bander, M. Equations of motion for spinning particles in external electromagnetic and gravitational fields. Phys. Rev. D 1993, 48, 2797–2799. [Google Scholar] [CrossRef]
- Bolte, J.; Keppeler, S. Semiclassical form factor for chaotic systems with spin. J. Phys. A Math. Gen. 1999, 32, 8863–8880. [Google Scholar] [CrossRef]
- Nesterenko, V.V. Singular Lagrangians with higher derivatives. J. Phys. A Math. Gen. 1989, 22, 1673–1687. [Google Scholar] [CrossRef]
- Rylov, Y.A. Spin and wave function as attributes of ideal fluid. J. Math. Phys. 1999, 40, 256–278. [Google Scholar] [CrossRef]
- Rivas, M.K. Kinematic Theory of Spinning Particles: Classical and Quantum Mechanical Formalism of Elementary Particles; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar] [CrossRef]
- Rivas, M. The dynamical equation of the spinning electron. J. Phys. A Math. Gen. 2003, 36, 4703–4716. [Google Scholar] [CrossRef]
- Newman, E.T.; Cough, E.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. Metric of a rotating, charged mass. J. Math. Phys. 1965, 6, 918–919. [Google Scholar] [CrossRef]
- Dymnikova, I. Image of the electron suggested by nonlinear electrodynamics coupled to gravity. Particles 2021, 4, 129–145. [Google Scholar] [CrossRef]
- De Sitter, W. On the relativity of inertia. Remarks concerning Einstein’s latest hypothesis. Proc. R. Netherl. Acad. Arts Sci. (KNAW) 1917, 19, 1217–1225. Available online: https://dwc.knaw.nl/DL/publications/PU00012455.pdf (accessed on 5 June 2023).
- De Sitter, W. On the curvature of space. Proc. R. Netherl. Acad. Arts Sci. (KNAW) 1918, 20, 229–243. Available online: https://dwc.knaw.nl/DL/publications/PU00012216.pdf (accessed on 5 June 2023).
- Dymnikova, I. De Sitter–Schwarzschild black hole: Its particlelike core and thermodynamical properties. Int. J. Mod. Phys. D 1996, 5, 529–540. [Google Scholar] [CrossRef]
- Terazawa, H.; Yasue, M.; Akama, K.; Hayashi, M. Observable effects of the possible substructure of leptons and quarks. Phys. Lett. B 1982, 112, 387–392. [Google Scholar] [CrossRef]
- Renard, F.M. Excited quarks and new hadronic states. Nuovo Cim. A 1983, 77, 1–20. [Google Scholar] [CrossRef]
- De Rujula, A.; Maiani, L.; Petronzio, R. Search for excited quarks. Phys. Lett. B 1984, 140, 253–258. [Google Scholar] [CrossRef]
- Eichten, E.; Lane, K.D.; Peskin, M.E. New tests for quark and lepton substructure. Phys. Rev. Lett. 1983, 50, 811–814. [Google Scholar] [CrossRef]
- Terazawa, H.; Chikashige, Y.; Akama, K. Unified model of the Nambu-Jona-Lasinio type for all elementary particle forces. Phys. Rev. D 1977, 15, 480–487. [Google Scholar] [CrossRef]
- Ne’eman, Y. Primitive particle model. Phys. Lett. B 1979, 82, 69–70. [Google Scholar] [CrossRef]
- Baur, U.; Spira, M.; Zerwas, P.M. Excited quark and lepton production at hadron colliders. Phys. Rev. D 1990, 42, 815–824. [Google Scholar] [CrossRef]
- Low, F.E. Heavy electrons and muons. Phys. Rev. Lett. 1965, 14, 238–239. [Google Scholar] [CrossRef]
- Boudjema, F. Substructure effects at LEP100. Int. J. Mod. Phys. A 1991, 6, 1–20. [Google Scholar] [CrossRef]
- Harari, H. Colored leptons. Phys. Lett. B 1985, 156, 250–254. [Google Scholar] [CrossRef]
- Abe, K. et al. [VENUS Collaboration]. Measurements of the differential cross-sections of e+e−→γγ and e+e−→γγγ at √s = 55, 56, 56.5 and 57 GeV. Z. Phys. C 1989, 45, 175–191. [Google Scholar] [CrossRef]
- Akrawy, M.Z. et al. [OPAL Collaboration]. Measurements of the cross-sections of the reaction e+e−→γγ and e+e−→γγγ at LEP. Phys. Lett. B 1991, 257, 531–540. [Google Scholar] [CrossRef]
- Shimozawa, K. et al. [TOPAZ Collaboration]. Studies of e+e−→γγ and e+e−→γγγ reaction. Phys. Lett. B 1992, 284, 144–150. [Google Scholar] [CrossRef]
- Decamp, D. et al. [The ALEPH Collaboration]. Search for new particles in Z decays using the ALEPH detector. Phys. Rep. 1992, 216, 253–340. [Google Scholar] [CrossRef]
- Abreu, P. et al. [DELPHI Collaboration]. Measurement of the e+e−→γγ(γ) cross-section at LEP energies. Phys. Lett. B 1994, 327, 386–396. [Google Scholar] [CrossRef]
- Abreu, P. et al. [DELPHI Collaboration]. Measurement of the e+e−→γγ(γ) cross-section at LEP energies. Phys. Lett. B 1998, 433, 429–440. [Google Scholar] [CrossRef]
- Abreu, P. et al. [DELPHI Collaboration]. Determination of the e+e−→γγ(γ) cross-section at center-of-mass energies ranging from 189 GeV to 202 GeV. Phys. Lett. B 2000, 491, 67–80. [Google Scholar] [CrossRef]
- Acciarri, M. et al. [L3 Collaboration]. Test of QED at LEP energies using e+e−→γγ(γ) and e+e−→l+l−γγ. Phys. Lett. B 1995, 353, 136–144. [Google Scholar] [CrossRef]
- Achard, P. et al. [L3 Collaboration]. Study of multiphoton final states and tests of QED in e+e− collisions at √s up to 209 GeV. Phys. Lett. B 2002, 531, 28–38. [Google Scholar] [CrossRef]
- Abbiendi, G. et al. [OPAL Collaboration]. Multi-photon production in e+e− collisions at √s = 181–209 GeV. Eur. Phys. J. C 2003, 26, 331–344. [Google Scholar] [CrossRef]
- Xe, J. Physics with γ Final States at the Z0 Energy Scale Using Electron-Positron Collision. Master’s Thesis, Chinese University of Science and Technology, Hefei, China, 1992. [Google Scholar]
- Wu, J. Tests of Quantum Electrodynamics at the Z0 Scale. Master’s Thesis, Chinese University of Science and Technology, Hefei, China, 1997. [Google Scholar]
- Zhao, J. Tests of QED using e+e−→γγ(γ) Reactions at LEP200 and Study of Inclusive Semileptonic D Meson Decays at BES. Master’s Thesis, Chinese University of Science and Technology, Hefei, China, 2001. [Google Scholar]
- Altarelli, G.; Kleiss, R.; Verzegnassi, C. (Eds.) Z Physics at LEP1. Volume 2: Higgs Search and New Physics; CERN: Geneva, Switzerland, 1989. [Google Scholar] [CrossRef]
- The ALEPH Collaboration; The DELPHI Collaboration; The L3 Collaboration; The OPAL Collaboration; The LEP Electroweak Working Group. Electroweak measurements in electron-positron collisions at W-boson-pair energies at LEP. Phys. Rep. 2013, 532, 119–244. [Google Scholar] [CrossRef]
- Dymnikova, I.; Sakharov, A.; Ulbricht, J. Appearance of a minimal length in e+e− annihilation. Adv. High Energy Phys. 2014, 2014, 707812. [Google Scholar] [CrossRef]
- Bajo, A.; Dymnikova, I.; Sakharov, A.; Sanchez, E.; Ulbricht, J.; Zhao, J. QED test at LEP200 energies in the reaction e+e−→γγ(γ). AIP Conf. Proc. 2001, 564, 255–562. [Google Scholar] [CrossRef]
- Dymnikova, I.G.; Hasan, A.; Ulbricht, J.; Zhao, J. Limits on the sizes of fundamental particles and gravitational mass of the Higgs particle. Gravit. Cosmol. 2001, 7, 122–130. [Google Scholar]
- Berends, F.A.; Kleiss, R. Distributions for electron-positron annihilation into two and three photons. Nucl. Phys. B 1981, 186, 22–34. [Google Scholar] [CrossRef]
- Berends, F.A. et al. [CALKUL Collaboration]. Multiple bremsstrahlung in gauge theories at high energies: (IV) The process e+e−→γγγγ. Nucl. Phys. B 1984, 239, 395–409. [Google Scholar] [CrossRef]
- Berends, F.A.; Gatsmans, R. Hard production corrections for e+e-→γγ. Nucl. Phys. B 1973, 61, 414–428. [Google Scholar] [CrossRef]
- Carloni Calame, C.M.; Montagna, G.; Nicrosini, O.; Piccinini, F. Status of the BabaYaga event generator. EPJ Web Conf. 2019, 218, 07004. [Google Scholar] [CrossRef]
- Maolinbay, M. Study of Reactions e+e−→γγ/γγγ at LEP Energies. Master’s Thesis, Eidgenössische Technische Hochschule, Zürich, Switzerland, 1995. [Google Scholar]
- Mandl, F.; Skyrme, T.H.R. The theory of the double Compton effect. Proc. R. Soc. A Math. Phys. Eng. 1952, 215, 497–507. [Google Scholar] [CrossRef]
- Litke, A.M. Experiments with Electron-Positron Colliding Beams. Master’s Thesis, Harvard University, Cambridge, MA, USA, 1970. [Google Scholar]
- Mery, P.; Perrottet, M.; Renard, F.M. Anomalous effects in e+e− annihilation into boson pairs. II. e+e-→ZZ, γZ, γγ. Z. Phys. C 1988, 38, 579–591. [Google Scholar] [CrossRef]
- King, S.F.; Sharpe, S.R. Exotic CERN events from exotic color states. Nucl. Phys. B 1985, 253, 1–13. [Google Scholar] [CrossRef]
- Leung, C.N.; Love, S.T.; Rao, S. Low-energy manifestations of a new interactions scale: Operator analysis. Z. Phys. C 1986, 31, 433–437. [Google Scholar] [CrossRef]
- Drell, S.D.; Parke, S.J. Constraints on radiative Z0 decays. Phys. Rev. Lett. 1984, 53, 1993–1995. [Google Scholar] [CrossRef]
- Dicus, D.A.; Tata, X. Anomalous photon interactions. Phys. Lett. B 1985, 155, 103–106. [Google Scholar] [CrossRef]
- Dicus, D.A. New interactions and neutrino counting. Phys. Rev. D 1985, 31, 2999–3001. [Google Scholar] [CrossRef]
- Éboli, O.J.P.; Natale, A.A.; Novaes, S.F. Bounds on effective interactions from the reaction e+e−→γγ at LEP. Phys. Lett. B 1991, 271, 274–276. [Google Scholar] [CrossRef]
- Kempf, A.; Mangano, G.; Mann, R.B. Hilbert space representation of the minimal length uncertainty relation. Phys. Rev. D 1995, 52, 1108–1118. [Google Scholar] [CrossRef]
- Kempf, A.; Mangano, G. Minimal length uncertainty relation and ultraviolet regularization. Phys. Rev. D 1997, 55, 7909–7920. [Google Scholar] [CrossRef]
- Kempf, A. Mode generating mechanism in inpation with a cutoff. Phys. Rev. D 2001, 63, 083514. [Google Scholar] [CrossRef]
- Khan Academy. Light: Electromagnetic Waves, the Electromagnetic Spectrum Photons. Available online: https://www.khanacademy.org/science/physics/light-waves/introduction-to-light-waves/a/light-and-the-electromagnetic-spectrum (accessed on 5 June 2023).
- Hossenfelder, S. Minimal length scale scenarios for quantum gravity. Living Rev. Relativ. 2013, 16, 2. [Google Scholar] [CrossRef] [PubMed]
- Bosso, P.; Das, S.; Todorinov, V. Quantum field theory with the generalized uncertainty principle II: Quantum electrodynamics. Ann. Phys. 2021, 424, 168350. [Google Scholar] [CrossRef]
- Luciano, G.G.; Petruzziello, L. Generalized uncertainty principle and its implications on geometric phases in quantum mechanics. Eur. Phys. J. Plus 2021, 136, 179. [Google Scholar] [CrossRef]
- Adriani, O. et al. [L3 Collaboration]. A test of quantum electrodynamics in the reaction e+e−→γγ(γ). Phys. Lett. B 1992, 288, 404–411. [Google Scholar] [CrossRef]
- Acciarri, M. et al. [L3 Collaboration]. Observation of multiple hard photon final states at √s = 130–140 GeV at LEP. Phys. Lett. B 1996, 384, 323–332. [Google Scholar] [CrossRef]
- Acciarri, M. et al. [L3 Collaboration]. Hard-photon production at √s = 161 and 172 GeV at LEP. Phys. Lett. B 1997, 413, 159–166. [Google Scholar] [CrossRef]
- Acciarri, M. et al. [L3 Collaboration]. Hard-photon production and tests of QED at LEP. Phys. Lett. B 2000, 475, 198–205. [Google Scholar] [CrossRef]
- James, F. MINUIT, Function Minimization and Error Analysis. Version 94.1; CERN: Geneva, Switzerland, 1994; Available online: https://root.cern.ch/download/minuit.pdf (accessed on 5 June 2023).
- James, F.; Roos, M. MINUIT: A system for function minimization and analysis of the parameter errors and corrections. Comput. Phys. Commun. 1975, 10, 343–367. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, M.; Ulbricht, J. Hint for a minimal interaction length in e+e−→γγ annihilation in total cross-section of center-of-mass energies 55–207 GeV. arXiv 2022, arXiv:2112.04767. [Google Scholar] [CrossRef]
- Isiksal, E. Test der Quantenelektrodynamik Bei LEP-Energien. Master’s Thesis, Eidgenössische Technische Hochschule, Zürich, Switzerland, 1991. [Google Scholar]
- Workman, R.L. et al. [Particle Data Group]. The Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01, see Chapter 91 “Searches for Quark and Lepton Compositeness”. [Google Scholar] [CrossRef]
- Bourilkov, D. Hint for axial-vector contact interactions in the data on e+e−→e+e−(γ) at center-of-mass energies 192–208 GeV. Phys. Rev. D 2001, 64, 071701(R). [Google Scholar] [CrossRef]
- Achard, P. et al. [L3 Collaboration]. Search for heavy neutral and charged leptons in e+e− annihilation at LEP. Phys. Lett. B 2001, 517, 75–85. [Google Scholar] [CrossRef]
- Abbiendi, G. et al. [OPAL Collaboration]. Search for stable and long-lived massive charged particles in e+e− collisions at s = 130 GeV–209 GeV. Phys. Lett. B 2003, 572, 8–20. [Google Scholar] [CrossRef]
- Abbiendi, G. et al. [The OPAL Collaboration]. Search for unstable heavy and excited leptons at LEP2. Eur. Phys. J. C. 2000, 14, 73–84. [Google Scholar] [CrossRef]
- Ahmed, T. et al. [H1 Collaboration]. A search for heavy leptons at HERA. Phys. Lett. B 1994, 340, 205–216. [Google Scholar] [CrossRef]
- Chatrchyan, S. et al. [CMS Collaboration]. Search for long-lived charged particle in pp collisions at √s = 7 and 8 TeV. J. High Energy Phys. 2013, 2013, 122. [Google Scholar] [CrossRef]
- Aaron, F.D. et al. [H1 Collaboration]. Search for excited electrons in ep collisions at HERA. Phys. Lett. B 2008, 666, 131–139. [Google Scholar] [CrossRef]
- Abazov, V.M. et al. [D0 Collaboration]. Search for excited electrons in pp¯ collisions at √s = 1.96 TeV. Phys. Rev. D 2008, 77, 091102. [Google Scholar] [CrossRef]
- Aad, G. et al. [ATLAS Collaboration]. Search for excited electrons and muons in √s=8 TeV proton-proton collisions with the ATLAS detector. New J. Phys. 2013, 15, 093011. [Google Scholar] [CrossRef]
- Khachatryan, V. et al. [The CMS Collaboration]. Search for excited leptons in proton-proton collisions at √s = 8 TeV. J. High Energy Phys. 2016, 2016, 125. [Google Scholar] [CrossRef]
- Aaboud, M. et al. [The ATLAS Collaboration]. Search for new high-mass phenomena in the dilepton final state using 36 fb−1 of proton-proton collision data at √s=13 TeV with the ATLAS detector. J. High Energy Phys. 2017, 2017, 182. [Google Scholar] [CrossRef]
- Sirunyan, A.M. et al. [The CMS Collaboration]. Search for contact interactions and large extra dimensions in the dilepton mass spectra from proton-proton collisions at √s= 13 TeV. J. High Energy Phys. 2019, 2019, 114. [Google Scholar] [CrossRef]
- Carloni Calame, C.M.; Chiesa, M.; Montagna, G.; Nicrosini, O.; Piccinini, F. Electroweak corrections to e+e−→γγ as a luminosity process at FCC-ee. Phys. Lett. B 2019, 798, 134976. [Google Scholar] [CrossRef]
- The CEPC Study Group. CEPC Conceptual Design Report. August 2018. Volume 1: Accelerator. arXiv 2018, arXiv:1809.00285. [Google Scholar] [CrossRef]
- Behnke, T.; Brau, J.E.; Foster, B.; Fuster, J.; Harrison, M.; Paterson, J.M.; Peskin, M.; Stanitzki, M.; Walker, N.; Yamamoto, H. (Eds.) The International Linear Collider Technical Design Report 2013. Volume 1: Executive Summary. arXiv 2013, arXiv:1306.6327. [Google Scholar] [CrossRef]
- Blondel, A.; Janot, P. Circular and linear e+e− colliders: Another story of complementarity. arXiv 2019, arXiv:1912.11871. [Google Scholar] [CrossRef]
- Pospelov, M.; Ritz, A. Electric dipole moments as probes of new physics. Ann. Phys. 2005, 318, 119–169. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Drell, S.D. The anomalous magnetic moment and limits on fermion substructure. Phys. Rev. D 1980, 22, 2236–2243. [Google Scholar] [CrossRef]
- Kinoshita, T.; Yennie, D.R. High precision tests of quantum electrodynamics: An Overview. Adv. Ser. Direct. High Energy Phys. 1990, 7, 1–14. [Google Scholar] [CrossRef]
- Gakh, G.I.; Konchatnij, M.I.; Merenkov, N.P.; Gakh, A.G. Effects of excited electron and contact eeγγ interaction in e+e−→γγ reaction. arXiv 2022, arXiv:2211.16306. [Google Scholar] [CrossRef]
- Bondarenko, S.; Dydyshka, Y.; Kalinovskaya, L.; Kampf, A.; Rumyantsev, L.; Sadykov, R.; Yermolchyk, V. One-loop radiative corrections to photon-pair production in polarized positron-electron annihilation. Phys. Rev. D 2023, 107, 073003. [Google Scholar] [CrossRef]
- Dymnikova, I. Spinning superconducting electrovacuum soliton. Phys. Lett. B 2006, 639, 368–372. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schriffer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Daintith, J.; Rennie, R. The Facts on File Dictionary of Physics; Infobase Publishing: New York, NY, USA, 2005; p. 238. [Google Scholar]
- Gallop, J.C. SQUIDs, the Josephson Effects and Superconducting Electronics; CRC Press/Taylor & Francis Group, LLC: New York, NY, USA, 1991; pp. 1, 20. [Google Scholar]
- Durrant, A. (Ed.) Quantum Physics of Matter; The Open University/Institute of Physics Publishing: Bristol, UK, 2000; pp. 102–103. [Google Scholar]
- Lin, C.-H.; Ulbricht, J.; Wu, J.; Zhao, J. Experimental and theoretical evidence for extended particle models. arXiv 2010, arXiv:1001.5374. [Google Scholar] [CrossRef]
- Ulbricht, J. Substructure of Fundamental Particles. Lecture at CICPI on 9 December 2019. Available online: http://cicpi.ustc.edu.cn/indico/conferenceDisplay.py?confId=5724 (accessed on 5 June 2023).
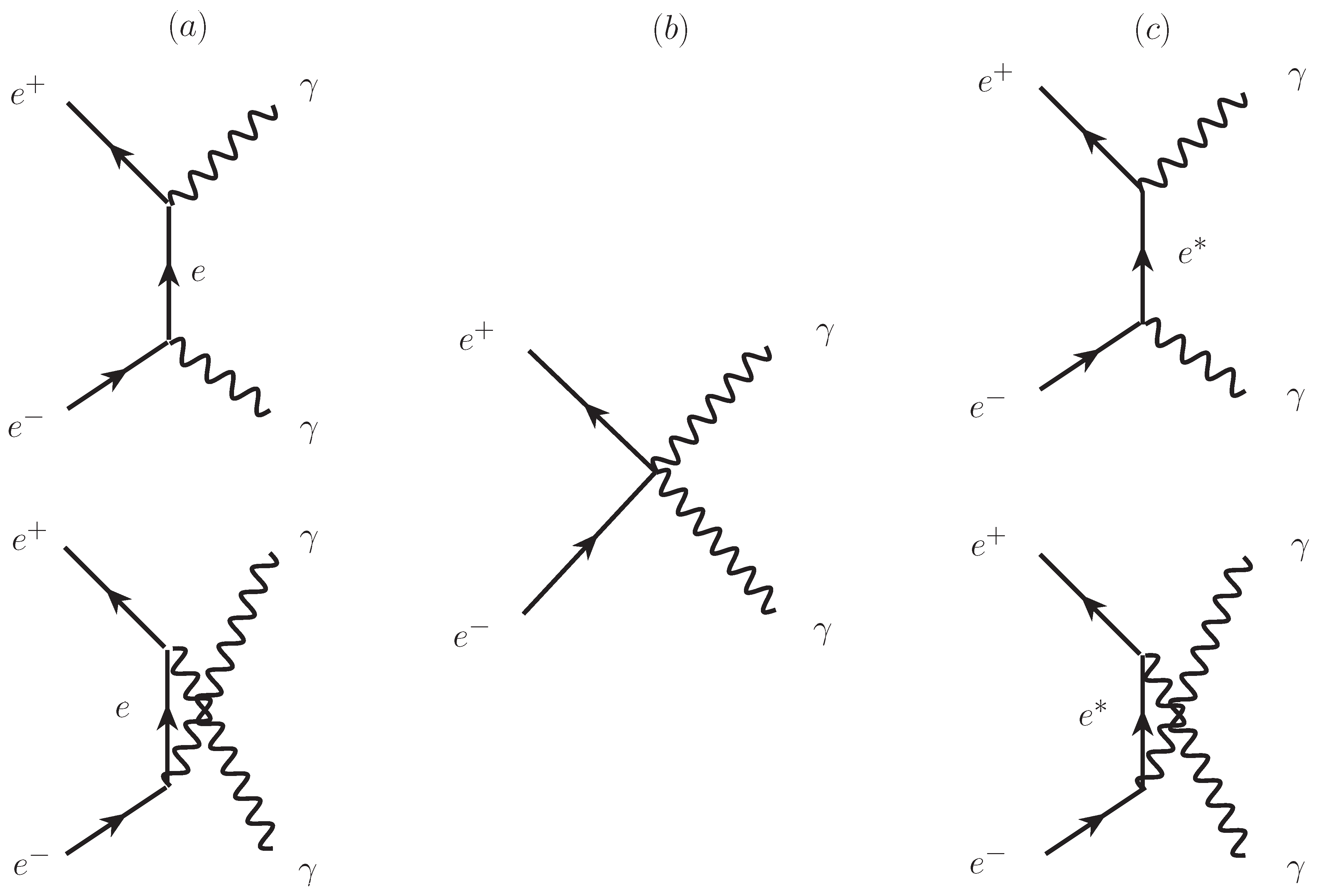



| , GeV | VENUS [79] | TOPAS [81] | ALEPH [82] | DELPHI [83] | L3 | OPAL |
|---|---|---|---|---|---|---|
| 55 | 2.34 pb | |||||
| 56 | 5.18 pb | |||||
| 0.86 pb | ||||||
| 57 | 3.70 pb | |||||
| 52.26 pb | ||||||
| 91 | 8.5 pb | 36.9 pb | 64.6 pb [86] | 7.2 pb [80] | ||
| 133 | 5.92 pb | |||||
| 162 | 9.58 pb | |||||
| 172 | 9.80 pb | |||||
| 183 | 52.9 pb | 54.8 pb [87] | 55.6 pb [88] | |||
| 189 | 151.9 pb | 175.3pb [87] | 181.1 pb [88] | |||
| 192 | 25.1pb | 28.8 pb [87] | 29.0 pb [88] | |||
| 196 | 76.1 pb | 82.4pb [87] | 75.9 pb [88] | |||
| 200 | 82.6 pb | 67.5 pb [87] | 78.2 pb [88] | |||
| 202 | 40.1 pb | 35.9 pb [87] | 36.8 pb [88] | |||
| 205 | 74.3 pb [87] | 79.2 pb [88] | ||||
| 207 | 138.1 pb [87] | 136.5 pb [88] |
| , GeV | ||||||
|---|---|---|---|---|---|---|
| 55 | ||||||
| 56 | ||||||
| 57 | ||||||
| 91 | ||||||
| 133 | ||||||
| 162 | ||||||
| 172 | ||||||
| 183 | ||||||
| 189 | ||||||
| 192 | ||||||
| 196 | ||||||
| 200 | ||||||
| 202 | ||||||
| 205 | ||||||
| 207 | ||||||
| Source | ||
|---|---|---|
| TRISTAN | ||
| LEP 1 | ||
| LEP 2 | ||
| All Data |
| Heavy Electron Mass, () | |
|---|---|
| Gev | GeV |
| Test () | |
|---|---|
| Gev | cm |
| , GeV | , pb | R(exp) |
|---|---|---|
| 55 | 124.746 ± 13.1736 | 0.92001 ± 0.09716 |
| 56 | 150.623 ± 9.7176 | 1.15000 ± 0.07419 |
| 56.5 | 141.633 ± 22.9310 | 1.10000 ± 0.17810 |
| 57 | 135.456 ± 10.7933 | 1.07000 ± 0.08526 |
| 57.6 | 125.311 ± 1.9970 | 1.01000 ± 0.01610 |
| 91 | 50.3103 ± 0.86517 | 0.98764 ± 0.01698 |
| 133 | 26.5472 ± 5.80853 | 1.09604 ± 0.23981 |
| 162 | 16.0640 ± 2.42633 | 0.98462 ± 0.14872 |
| 172 | 15.6375 ± 2.64851 | 1.08187 ± 0.18324 |
| 183 | 12.6404 ± 0.34388 | 0.99219 ± 0.02699 |
| 189 | 11.7626 ± 0.18843 | 0.98582 ± 0.01579 |
| 192 | 11.0253 ± 0.46129 | 0.95427 ± 0.03993 |
| 196 | 11.2978 ± 0.27689 | 1.02004 ± 0.02500 |
| 200 | 10.1373 ± 0.26604 | 0.95400 ± 0.02504 |
| 202 | 10.1199 ± 0.37855 | 0.97204 ± 0.03636 |
| 205 | 9.98539 ± 0.32275 | 0.98865 ± 0.03196 |
| 207 | 9.66178 ± 0.23860 | 0.97594 ± 0.02410 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Lin, C.-H.; Liu, M.; Sakharov, A.S.; Ulbricht, J.; Zhao, J.
Is the Non-Pointness of the Electron Observable in
Chen Y, Lin C-H, Liu M, Sakharov AS, Ulbricht J, Zhao J.
Is the Non-Pointness of the Electron Observable in
Chen, Yutao, Chih-Hsun Lin, Minghui Liu, Alexander S. Sakharov, Jürgen Ulbricht, and Jiawei Zhao.
2023. "Is the Non-Pointness of the Electron Observable in
Chen, Y., Lin, C.-H., Liu, M., Sakharov, A. S., Ulbricht, J., & Zhao, J.
(2023). Is the Non-Pointness of the Electron Observable in