Machine Learning Approach for Event Position Reconstruction in the DEAP-3600 Dark Matter Search Experiment
Abstract
1. Introduction
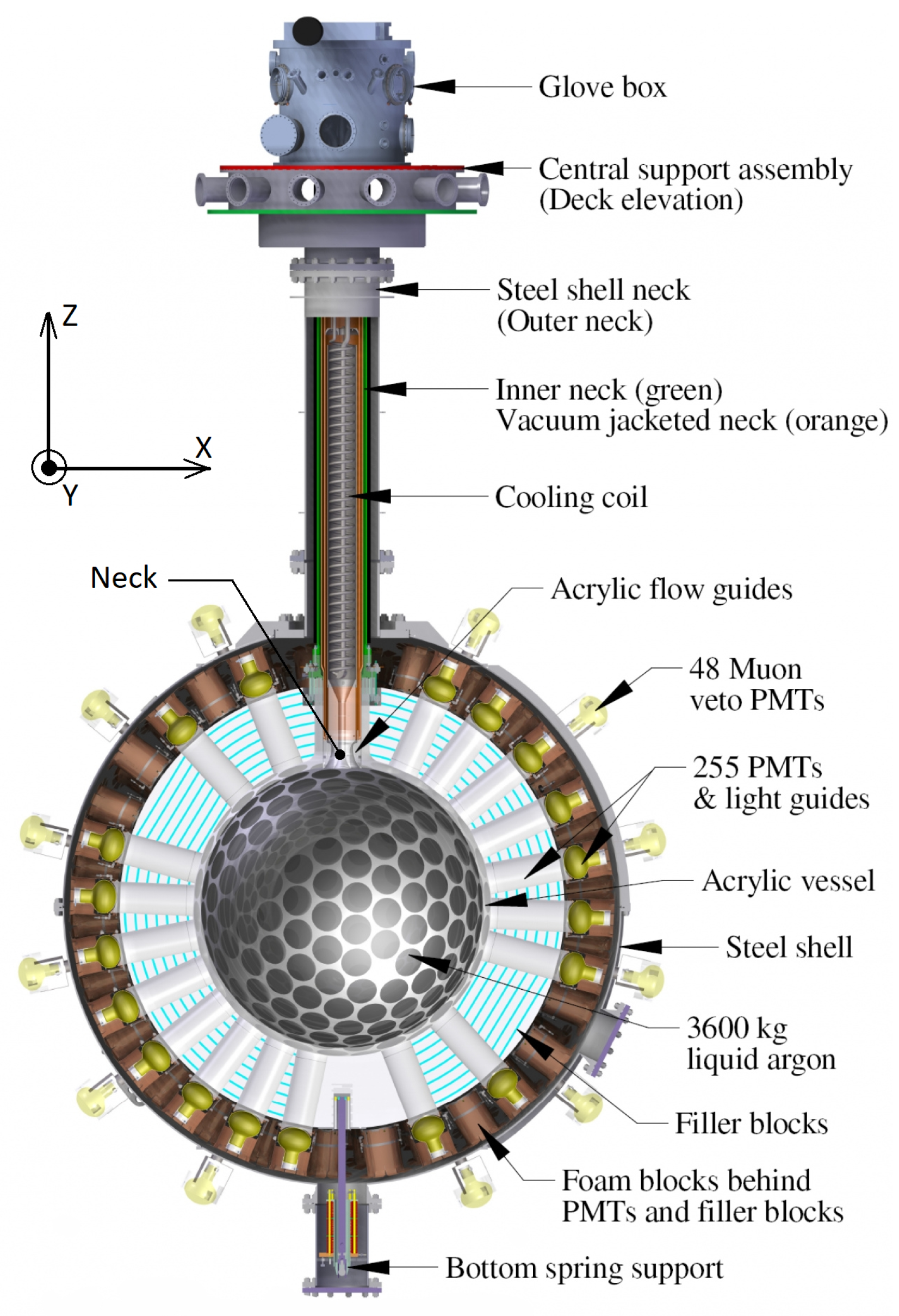
2. The Detector
3. Machine Learning Approach
3.1. Neural Network Algorithm
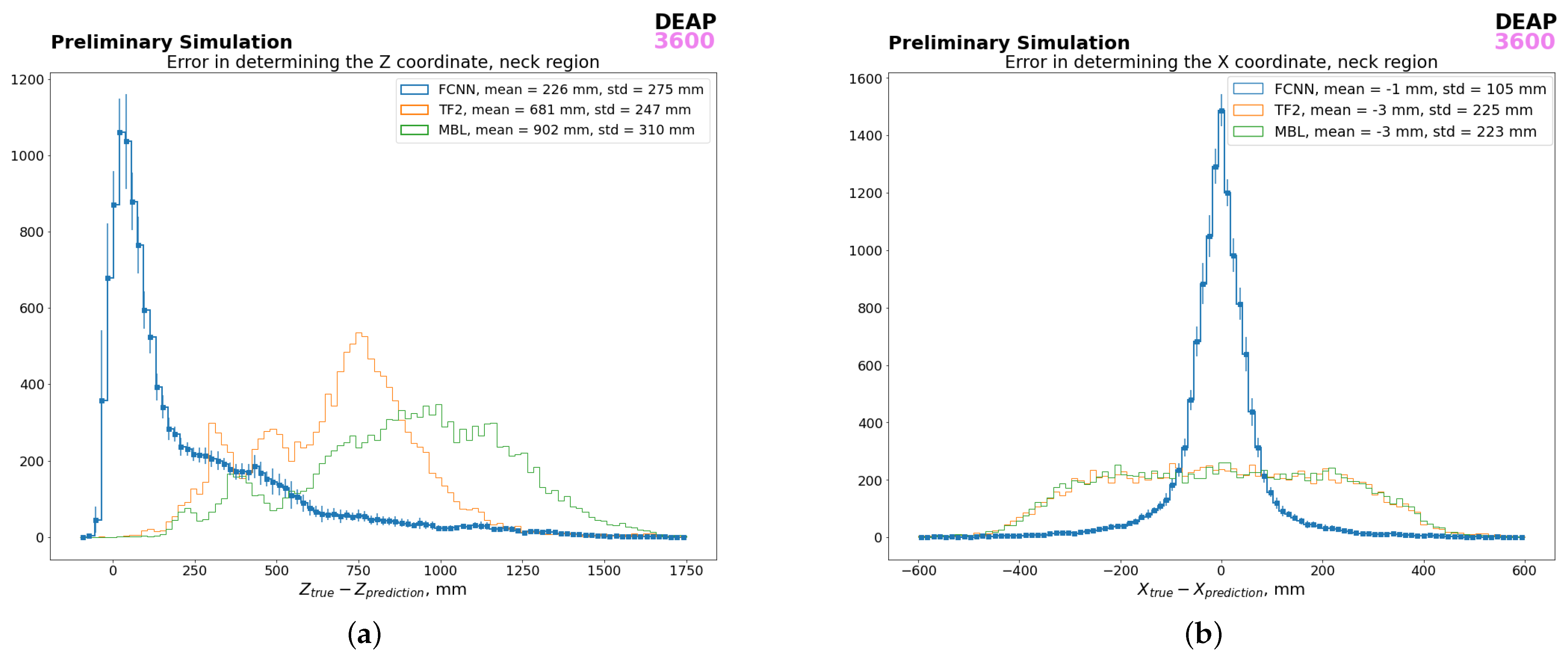
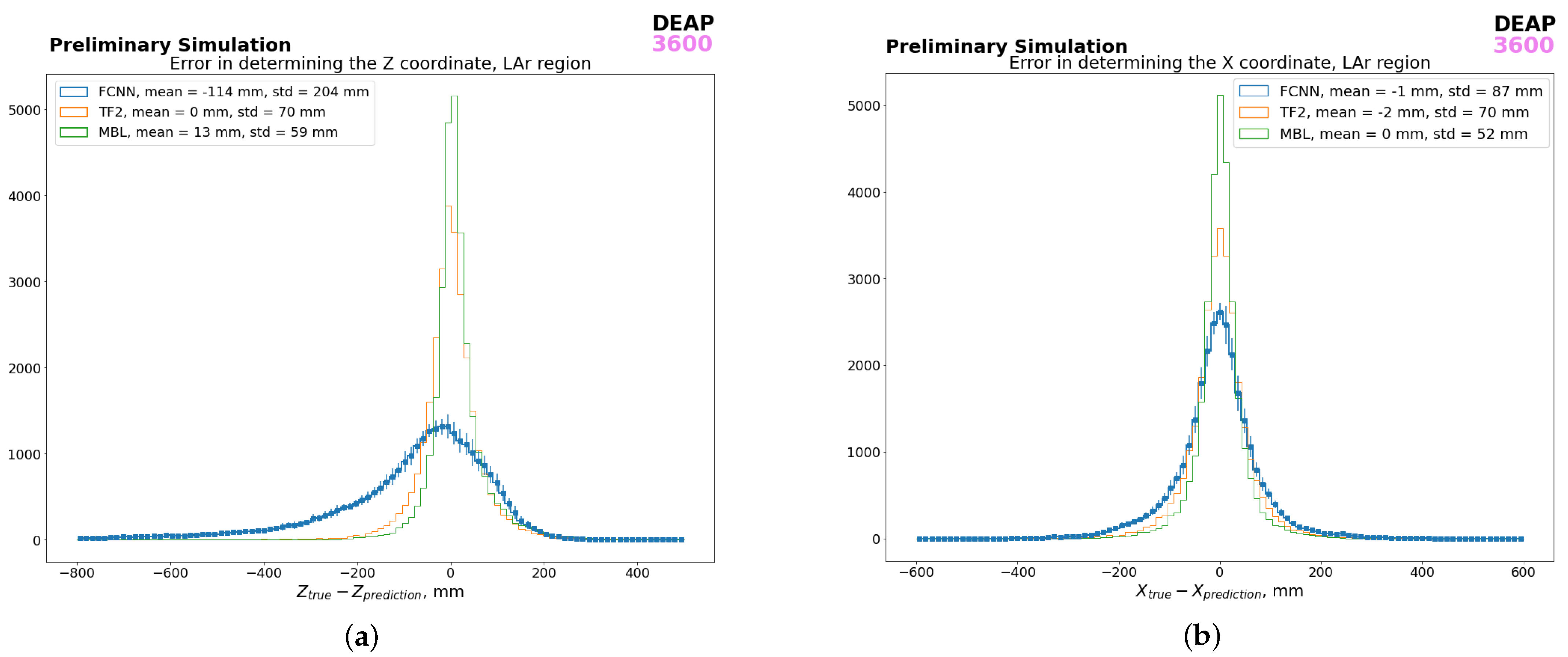
3.2. Results
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Membership of the DEAP Collaboration
Affiliations
- Department of Physics, University of Alberta, Edmonton, Alberta, T6G 2R3, Canada
- AstroCeNT, Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, Rektorska 4, 00-614 Warsaw, Poland
- Physics Department, Università degli Studi di Cagliari, Cagliari 09042, Italy
- Canadian Nuclear Laboratories, Chalk River, Ontario, K0J 1J0, Canada
- Department of Physics and Astronomy, University of California, Riverside, CA 92507, USA
- Department of Physics, Carleton University, Ottawa, Ontario, K1S 5B6, Canada
- Centro de Investigaciones Energéticas, Medioambientales y Tecnológicas, Madrid 28040, Spain
- Physics Department, Università degli Studi “Federico II” di Napoli, Napoli 80126, Italy
- Astronomical Observatory of Capodimonte, Salita Moiariello 16, I-80131 Napoli, Italy
- INFN Cagliari, Cagliari 09042, Italy
- INFN Laboratori Nazionali del Gran Sasso, Assergi (AQ) 67100, Italy
- INFN Napoli, Napoli 80126, Italy
- School of Natural Sciences, Laurentian University, Sudbury, Ontario, P3E 2C6, Canada
- Nuclear Science Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
- Instituto de Física, Universidad Nacional Autónoma de México, A.P. 20-364, Ciudad de México D. F. 01000, Mexico
- BP2, National Centre for Nuclear Research, ul. Pasteura 7, 02-093 Warsaw, Poland
- National Research Centre Kurchatov Institute, Moscow 123182, Russia
- National Research Nuclear University MEPhI, Moscow 115409, Russia
- Physics Department, Princeton University, Princeton, NJ 08544, USA
- PRISMA+ Cluster of Excellence and Institut für Kernphysik, Johannes Gutenberg-Universität Mainz, 55128 Mainz, Germany
- Department of Physics, Engineering Physics, and Astronomy, Queen’s University, Kingston, Ontario, K7L 3N6, Canada
- Royal Holloway University London, Egham Hill, Egham, Surrey TW20 0EX, United Kingdom
- Rutherford Appleton Laboratory, Harwell Oxford, Didcot OX11 0QX, United Kingdom
- SNOLAB, Lively, Ontario, P3Y 1M3, Canada
- University of Sussex, Sussex House, Brighton, East Sussex BN1 9RH, United Kingdom
- TRIUMF, Vancouver, British Columbia, V6T 2A3, Canada
- Department of Physics, Technische Universität München, 80333 Munich, Germany
- Arthur B. McDonald Canadian Astroparticle Physics Research Institute, Queen’s University, Kingston, ON, K7L 3N6, Canada
- Deceased
- Currently at SNOLAB, Lively, Ontario, P3Y 1M3, Canada
- Currently at Nikhef and the University of Amsterdam, Science Park, 1098XG Amsterdam, Netherlands
- *
- Correspondence: ilyasovaid@yandex.ru
References
- Ajaj, R. et al. [DEAP Collaboration] Search for dark matter with a 231-day exposure of liquid argon using DEAP-3600 at SNOLAB. Phys. Rev. D 2019, 100, 022004. [Google Scholar] [CrossRef]
- Aghanim, N. et al. [Planck Collaboration] Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Amaudruz, P.A. et al. [DEAP Collaboration] Design and construction of the DEAP-3600 dark matter detector. Astropart. Phys. 2019, 108, 1–23. [Google Scholar] [CrossRef]
- Amaudruz, P.A. et al. [DEAP Collaboration] In-Situ characterization of the Hamamatsu R5912-HQE photomultiplier tubes used in the DEAP-3600 experiment. Nucl. Instrum. Meth. Phys. Res. A 2019, 922, 373–384. [Google Scholar] [CrossRef]
- Francini, R.; Montereali, R.M.; Nichelatti, E.; Vincenti, M.A.; Canci, N.; Segreto, E.; Cavanna, F.; Di Pompeo, F.; Carbonara, F.; Fiorillo, G.; et al. Tetraphenyl-butadiene films: VUV-Vis optical characterization from room to liquid argon temperature. J. Instrum. 2013, 8, C09010. [Google Scholar] [CrossRef]
- Bhat, P.C. Multivariate analysis methods in particle physics. Annu. Rev. Nucl. Part. Sci. 2011, 61, 281–309. [Google Scholar] [CrossRef]
- Rosenblatt, F. Principles of Neurodynamics. Perceptrons and the Theory of Brain Mechanisms; Report No. VG-II96-G-8; Cornell Aeronautical Laboratory, Inc.; Cornell University: Buffalo, NY, USA, 1961; Available online: https://apps.dtic.mil/sti/citations/AD0256582 (accessed on 1 April 2023).
- Reed, R.D.; Marks, R.J., II. Neural Smithing: Supervised Learning in Feedforward Artificial Neural Networks; The MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; Chapman & Hall; CRC; Taylor & Francis Group, LLC: Boca Raton, FL, USA, 1984. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Peterson, C.; Rögnvaldsson, T. An introduction to artificial neural networks. In 1991 CERN School of Computing; Verkerk, C., Ed.; CERN: Geneva, Switzerland, 1992; pp. 113–170. [Google Scholar] [CrossRef]
- Barate, R. et al. [The ALEPH Collaboration] Determination of |Vub| from the measurement of the inclusive charmless semileptonic branching ratio of b hadrons. Eur. Phys. J. C 1999, 6, 555–574. [Google Scholar] [CrossRef]
- Akers, R. et al. [OPAL Collaboration] A measurement of the production of D*± mesons on the Z0 resonance. Z. Phys. C 1995, 67, 27–44. [Google Scholar] [CrossRef]
- Chiappetta, P.; Colangelo, P.; De Felice, P.; Nardulli, G.; Pasquariello, G. Higgs search by neural networks at LHC. Phys. Lett. B 1994, 322, 219–223. [Google Scholar] [CrossRef]
- Peterson, C.; Rögnvaldsson, T.; Lönnblad, L. JETNET 3.0—A versatile artificial neural network package. Comput. Phys. Commun. 1994, 81, 185–220. [Google Scholar] [CrossRef]
- Buskulic, D. et al. [ALEPH Collaboration] Measurement of the tau polarisation at the Z resonance. Z. Phys. C 1993, 59, 369–386. [Google Scholar] [CrossRef]
- Babbage, W.S.; Thompson, L.F. The use of neural networks in γ-π0 discrimination. Nucl. Instrum. Meth. Phys. Res. A 1993, 330, 482–486. [Google Scholar] [CrossRef]
- Lönnblad, L.; Peterson, C.; Rögnvalsson, T. Pattern recognition in high energy physics with artificial neural networks—JETNET 2.0. Comput. Phys. Commun. 1992, 70, 167–182. [Google Scholar] [CrossRef]
- Lönnblad, L.; Peterson, C.; Rögnvaldsson, T. Using neural networks to identify jets. Nucl. Phys. B 1991, 349, 675–702. [Google Scholar] [CrossRef]
- Lönnblad, L.; Peterson, C.; Rögnvaldsson, T. Finding gluon jets with a neural trigger. Phys. Rev. Lett. 1990, 65, 1321. [Google Scholar] [CrossRef]
- Denby, B. Neural networks and cellular automata in experimental high energy physics. Comput. Phys. Commun. 1988, 49, 429–448. [Google Scholar] [CrossRef]
- Roe, B.P.; Yang, H.J.; Zhu, J.; Liu, Y.; Stancu, I.; McGregor, G. Boosted decision trees as an alternative to artificial neural networks for particle identification. Nucl. Instrum. Meth. Phys. Res. A 2005, 543, 577–584. [Google Scholar] [CrossRef]
- Aad, G. et al. [ATLAS Collaboration] Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys. Lett. B 2012, 716, 1–29. [Google Scholar] [CrossRef]
- Chatrchyan, S. et al. [CMS Collaboration] Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Russakovsky, O.; Deng, J.; Su, H.; Krause, J.; Satheesh, S.; Ma, S.; Huang, Z.; Karpathy, A.; Khosla, A.; Bernstein, M.; et al. ImageNet Large Scale Visual Recognition Challenge. Int. J. Comput. Vis. 2015, 115, 211–252. [Google Scholar] [CrossRef]
- Radovic, A.; Williams, M.; Rousseau, D.; Kagan, M.; Bonacorsi, D.; Himmel, A.; Aurisano, A.; Terao, K.; Wongjirad, T. Machine learning at the energy and intensity frontiers of particle physics. Nature 2018, 560, 41–48. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- Brun, R.; Rademakers, F. ROOT: An object oriented data analysis framework. Nucl. Instrum. Meth. Phys. Res. A 1997, 389, 81–86. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—A simulation toolkit. Nucl. Instrum. Meth. Phys. Res. A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Bolton, T.; Gastler, D.; Klein, J.; Lippincott, H.; Mastbaum, A.; Nikkel, J.; Orebi Gann, G.; Akashi-Ronquest, M.; Seibert, S.; Sekula, S.; et al. RAT (Is an Analysis Tool) User’s Guide. 2018. Available online: https://rat.readthedocs.io/ (accessed on 1 April 2023).
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- McKinney, W. Data structures for statistical computing in Python. In Proceedings of the 9th Python in Science Conference (SciPy 2010), Austin, TX, USA, 28 – 30 June 2010; pp. 56–61. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-scale machine learning on heterogeneous systems. arXiv 2016, arXiv:1603.04467. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Collaboration, D. Machine Learning Approach for Event Position Reconstruction in the DEAP-3600 Dark Matter Search Experiment. Physics 2023, 5, 483-491. https://doi.org/10.3390/physics5020033
Collaboration D. Machine Learning Approach for Event Position Reconstruction in the DEAP-3600 Dark Matter Search Experiment. Physics. 2023; 5(2):483-491. https://doi.org/10.3390/physics5020033
Chicago/Turabian StyleCollaboration, DEAP. 2023. "Machine Learning Approach for Event Position Reconstruction in the DEAP-3600 Dark Matter Search Experiment" Physics 5, no. 2: 483-491. https://doi.org/10.3390/physics5020033
APA StyleCollaboration, D. (2023). Machine Learning Approach for Event Position Reconstruction in the DEAP-3600 Dark Matter Search Experiment. Physics, 5(2), 483-491. https://doi.org/10.3390/physics5020033



