The Abundance of the Species ^†

Abstract

I review the pioneering work of Jean Cleymans in establishing the statistical description of multihadron production in high energy strong interaction physics.

Jean Cleymans joined Physics Department of the University of Bielefeld, Germany, in the year 1975, coming to us from CERN (European Organization for Nuclear Research, Geneva, Switzerland). Physics at the newly founded University of Bielefeld was only four years old then, and to establish a new research center here required attracting bright and adventurous people from throughout the world—people open not only to a new university, but also to new physics. Jean definitely was one of these. He was instrumental in putting Bielefeld physics-wise onto the map and in his later career he did the same for Cape Town.

In his earlier years here, Jean worked a lot on lepton pair production, but around 1980 when QCD (quantum chromodynamics) entered the scene, he quickly turned to the quark gluon-plasma and its hadronization. The 1986 Physics Report [1] on “Quarks and gluons at high temperatures and densities”, written by Jean together with two other bright young international Bielefeld accessions, Rajiv Gavai and Esko Suhonen, quickly became the standard reference to the field and remained so for many years.

I had worked for some years on the statistical description of hadron production, and so Jean and I took this up as the mechanism for the hadronization of the quark-gluon plasma. In this paper, I elaborate a little on our joint work, which indeed turned out to be the beginning of a new approach to multi-hadron production. Much of this material is covered in Chapter 11 of Ref. [2], where more details can also be found.

1. Statistical Multihadron Production

Multiparticle production in high energy collisions of strongly interacting particles has fascinated physicists for well over half a century. As predicted by Heisenberg [3], the little bang of such collisions produce with increasing energy an ever growing number of mesons and baryons of different quantum states, and from the beginning, the large numbers were a challenge to describe these reactions by collective or statistical approaches. It was tempting to go even further, to imagine that what they produced were really droplets of strongly interacting matter, thus providing a means to access the thermodynamics of strong interaction physics in the laboratory.

The main features observed in high energy collisions are the multiplicity, i.e., the number of produced particles as a function of the collision energy, the momentum spectra of the particles, their correlations, and the relative abundances of the different species. These then are also the basic quantities which any theoretical framework has to provide.

The first statistical treatment was formulated by Fermi [4]. He assumed that the collision deposits a great amount of energy in a small spatial region around the colliding particles, and that the energy of this fireball is then distributed among the various observable degrees of freedom, the emitted mesons and nucleons, according to statistical laws. Thus, the description of the production process is determined by the grand canonical phase space volume $Q(E,V)$ of a gas of non-interacting hadrons; here, E denotes the collision energy in the center of mass of the colliding particles, and V the interaction volume. This phase space volume was to be calculated with whatever constraints are imposed by conservation laws (charge, baryon number, etc.).

The main features obtained from Fermi’s model are:

• A multiplicity $n\left(E\right)\sim E^{3/4}$, growing as a power of E;
• Isotropic production of secondary particles; and
• Average secondary momenta, $\langle \left|p\right|\rangle \sim E^{1/4}$, also increasing as a power of E.

Modified versions of the model [5,6] lead to slightly changed powers, but the basic features remain. The available collision energy is equidistributed among the isotropically emitted secondaries; any increase of E goes partially into making more secondaries and partially into making each constituent more energetic.

Experimental data showed that with increasing collision energy, this picture became untenable for two main reasons:

• In a nucleon-nucleon collision, the incident nucleons always retained a considerable fraction of the collision energy (“leading particle effect”);
• The secondaries were not emitted isotropically; their average transverse momenta (orthogonal to the collision axis) reached a constant value, independent of the incident energy, while the average longitudinal momenta increased with E.

Certainly, this meant that not all information about the initial state was lost in the collision; the reaction retained a memory both of the conserved quantum numbers of the incident particles and of the collision axis. Fermi had already suggested that the spatial volume, as seen in the overall center-of-mass system, should be Lorentz-contracted along the collison axis. However, as long as there is no interrelation between the momenta and the coordinates of the secondaries, this does not produce anisotropic particle production.

From another point of view, the combination of the anisotropic secondary momentum distributions and the leading particle effect seemed to indicate that at high energy the incident nucleons could not fully stop each other. Instead, they seemed to “pass through” one another, losing only part of their energy in the process. This “transparency” was subsequently explained by Gribov [7] as a consequence of hadronic size and the finite speed of information transmission.

It thus became evident that high-energy collisions could not be understood in terms of the the formation of just one fireball, in the sense of a single isotropic energy deposit into a small spatial volume. The collision instead seems more like the passage of an energetic charge through a medium, leaving behind a condensation trail of smaller fireballs superimposed along the collision axis. Each of these bubbles could now, in principle, have the phase space structure envisioned by Fermi, and if one attributes the conserved baryon numbers to the fastest bubbles in each direction, the scenario would also provide the leading particle effect.

While this does bring in the desired longitudinal momentum growth, the energy of each bubble could also still increase, and this in turn results in an energy dependence (albeit weaker) for the average transverse momenta. The basic puzzle of the field, or, looked at in a more positive way, the most important hint provided by nature, was the constancy of the average transverse momenta, $p_t$, of the secondaries. Making this even more tantalizing was the observation that while different species of secondaries led to different (energy-independent) transverse momentum distributions, the transverse energies, $m_t^i$, appeared to follow one universal pattern, with

$$\frac{d{N}_i}{d{m}_t^i}\sim exp\left(-\lambda m_t^i\right),m_t^i=\sqrt{{\left(p_t^i\right)}^2+m_i^2},$$

(1)

describing the functional form of the distribution of all species i of different masses, $m_i$, in terms of one universal parameter $\lambda$.

The first explanation of this universality was proposed by Hagedorn [8,9], based on the resonance structure governing the interaction of the different hadron species. Experiment had shown that multiparticle production with increasing energy did not just produce a shower of many pions, kaons and nucleons. Instead, it led to the production of more and different excited resonant states which decayed strongly into less excited states and finally into the ground state hadrons. Starting in the nineteen-sixties, an ever growing number of such hadronic resonances were discovered, and today the standard compilation [10] lists hundreds of them. It thus was necessary to obtain a scheme to determine how many states of each mass are produced in the collision, and Hagedorn’s statistical bootstrap model provided that in terms of a self-similar composition law, claiming that resonances consist of resonances and so on, with a universal composition equation. The number of states, $\rho \left(m\right)$, of a resonance of mass m, its “degeneracy”, is then given as the number of different composition patterns. This led to an exponential growth of $\rho \left(m\right)$,

$$\rho \left(m\right)\sim m^a{e}^{bm},$$

(2)

while the power a depends on the details of the partition problem, the coefficient b was expressed in terms of fundamental features of strong interaction physics, such as the hadronic size, the range of the strong force, or the Regge resonance pattern.

At this stage then, the experiment had shown several basic deviations from Fermi’s original fireball picture. The assumption of a completely random production process failed: the system retained some information of the initial state, secondary particle distributions were different in directions along and orthogonal to the collision axis, and there were leading particles carrying a baryon number. Moreover, the emitted pions, kaons and nucleons, had gone through some intermediate interactive stage, with resonance formation and decay as the dominant process. The first of these features, anisotropy and leading particles, could be accounted for through a superposition of fireballs, using initial state dynamical information as input.

To solve the resonance problem, Hagedorn invoked a result first obtained by Beth and Uhlenbeck [11] and subsequently generalized by Dashen, Ma and Bernstein [12]. They had argued that if the interaction of a gas of constituents is indeed dominated by resonance formation, then one can replace the interacting system of elementary particles with a non-interacting system of all possible resonances. The relevant phase space for the states of multiparticle production would thus be that of an ideal resonance gas, with an exponentially growing resonance mass spectrum, and contained in an interaction volume $V_0$.

The grand-canonical partition function $Z(T,V_0)$ of such a resonance gas diverges for

$$T>T_H=\frac{1}{b},$$

(3)

so $T_H$ becomes an upper bound on the temperature. Increasing the energy of such a system does not increase the momentum of the secondaries and hence its temperature; instead, it leads to more species of more massive hadrons. As a result, the momentum spectra now have the form (1); the experimentally observed universal transverse mass pattern with a parameter $\lambda$ is thus accounted for as the universal limiting temperature of an ideal resonance gas. This indeed agreed quite well with the observed transverse energy spectra. The energy-dependent and unbounded longitudinal momenta, on the other hand, arise from the superposition of an energy-dependent number of such Hagedorn-type fireballs. Conceptually, this provides the basis for the superposition of fireballs moving at different rapidities, as a phenomenological picture of high energy multihadron production.

2. The Abundance of the Species

For an ideal resonance gas, the hadronization temperature, $T_H$, determines not only the momentum spectra, but also the relative abundances of the different species. At a fixed temperature, a heavy meson is less likely to be present than a lighter one. In the case of heavy ion collisions, the overall baryon density in the clusters enters as still another factor, modifying the relation between baryon and antibaryon abundances. This is generally taken into account through a baryochemical potential, ${\mu }_B$; the overall relative abundance of species i in an ideal resonance gas is thus described in terms of two parameters, the temperature $T_H$ and the baryochemical potential $u_B$. The corresponding multiplicity of species i then given by

$$N_i=d_i\frac{VT{m}_i^2}{2{\pi }^2}{K}_2(m_i/T_H)exp(B{\mu }_B/T_H)$$

(4)

where $d_i$ specifies the degeneracy of species i, $K_2$ is the modified Bessel function of the second kind, V denotes the overall volume, and $B=0,\pm 1,\pm 2$ is the baryon number of the species. In other words, the ratio of the multiplicities of species i to j is predicted as the ratio of the corresponding phase space weights,

$$\frac{N_i}{N_j}=\left(\frac{d_i}{d_j}\right){\left(\frac{m_i}{m_j}\right)}^2\frac{K_2(m_i/T_H)}{K_2(m_j/T_H)}exp\left[(B_i{\mu }_i-B_j{\mu }_j)/T_H\right]$$

(5)

Hence, if high energy collision results are specified just by the pure phase space of a resonance gas, they should also lead to corresponding ideal resonance gas ratios of the form (5). Let us consider this in more detail.

The statistical hadronization model assumes that hadronization in high energy collisions is a universal process proceeding through the formation of multiple colorless massive clusters or fireballs of finite spacial extension at fixed temperature $T_H$ and baryochemical potential ${\mu }_B$. These clusters are assumed to decay into hadrons according to a purely statistical law: every multi-hadron state of the fireball phase space defined by its mass, volume and charges is equally probable. The mass distribution and the distribution of charges (electric, baryonic and strange) among the clusters and their (fluctuating) number are, however, in principle determined in the prior dynamical stage of the process, which determines how fireballs are emitted along the collision axis.

Hence, one would seem to need this dynamical information in order to make definite quantitative predictions to be compared with data. Nevertheless, for Lorentz-invariant quantities such as multiplicities, one can introduce a simplifying assumption and thereby obtain a simple analytical expression in terms of $T_H$ and ${\mu }_B$. The key point is to assume that the distribution of masses and charges among clusters is again purely statistical [13,14,15], so that, as far as the calculation of multiplicities is concerned, the set of many clusters becomes equivalent, on the average, to one large cluster (an equivalent global cluster) whose volume is the sum of the individual proper cluster volumes and whose charge is the sum of cluster charges (and thus the conserved charge of the initial colliding system). In such a framework, the global cluster can be hadronized on the basis of statistical equilibrium.

The primary multiplicity of a hadron species i due to fireball decay in the Boltzmann limit of phase space is then given by Equation (4), where V now is the production volume (the sum of all fireballs). In abundance ratios, V cancels out, so it is a parameter needed only for absolute multiplicities. Let $N_i$ denotes the observed multiplicity; since all heavier resonances will still decay into lighter ones, so that the actually observed multiplicities are obtained from (4) by

$$N_i=N_i^{\mathrm{primary}}+\sum _k{N}_k\mathrm{Br}(k\to i),$$

(6)

summing over the various branching ratios $Br$ as measured. The final pion multiplicity, for example, is in fact several times larger than the primary one.

The other species parameter in Equation (5), apart from the mass, is the degeneracy $d_i$. It had been noted above that self-similar resonance composition leads to a degeneracy $exp\left\{bm\right\}$ increasing exponentially in mass (see Equation (2)). Such an increase in turn leads to a critical point $T_H=1/b$, limiting hadron thermodynamics to $T\le T_H$. A more empirical alternative is the physical resonance gas, in which the resonance spectrum is taken to consist of the actually measured and tabulated resonances, with only their spin and isospin degeneracy taken into account. This approach is apparently limited in resonance mass since little is known about states above 2.5 to 3.0 GeV. With an upper limit in resonance mass, the partition function is analytic and hence there is no critical point; the energy density and all higher derivatives remain finite for all values to the temperature, and also those above a Hagedorn $T_H$. As far as the measurable abundances are concerned, the missing high mass states do not play a significant role: including all excited states up to 2.0 GeV covers almost all of the feed-down sources for pions, for example, since the higher mass states are strongly suppressed, for $m\gg T_H$. Studies comparing species abundances with cuts at 1.5 or 2.0 GeV thus show very little difference.

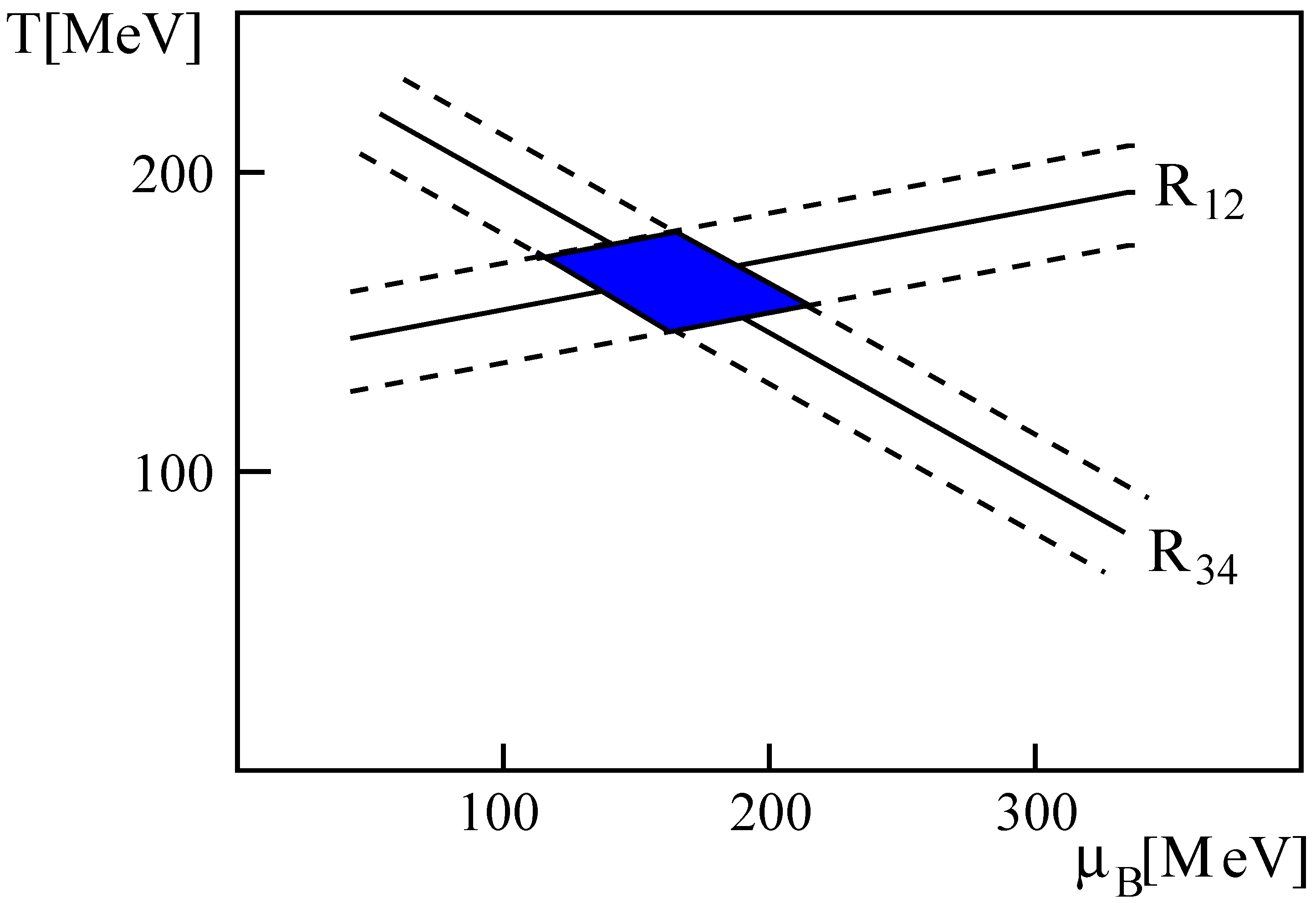
If the basic assumption of statistical hadronization—the equivalence of interacting hadron gas and ideal resonance gas—is indeed correct, the abundances of the species can thus be used to determine the hadronization temperature. In particular, the measured ratio of specific hadron abundances provides by Equations (4) and (6) an equation in terms of T and ${\mu }_B$ and thus leads to a line in the T–${\mu }_B$ plane. Consider the ratio of two hadron species abundances, $h_1$ and $h_2$,

$$R_{12}=\frac{N_1(T,{\mu }_B)}{N_2(T,{\mu }_B)}=a\pm \Delta a.$$

(7)

The crossing region of ratio $R_{12}$ and another ratio $R_{34}$ then specifies the thermal parameter values at hadronization; see Figure 1.

The ratios of further species abundances give different different lines and, if statistical hadronization is correct, all lines should cross at a common point, thus specifying the temperature and the baryon density of the medium at hadronization. This was proposed and first carried out in 1992 in a study by Jean and myself [16]. The essential point is that a variety of hadron species are measured, providing a comparatively large number of ratios, and these should all lead to the same hadronization temperature, if the model is correct. Given many ratios, the two parameters $T_H$ and ${\mu }_B$ are thus over-determined.

Our initial study involved heavy baryons, $\mathrm{\Lambda }$, $\mathrm{\Xi }$ and their anti-particles, the vector mesons $\rho$, $\omega$ and $\varphi$, and positive and negative kaons and pions—up to ten or more hadron species. The results were quite amazing: five ratios of heavy baryons and $\mathrm{\Lambda }/K$ led to a hadronization temperature of some 150–200 MeV, in good agreement to theoretical results both from lattice QCD and from statistical bootstrap considerations. This temperature was found to be slightly too high for the ratio ($\mathrm{\Lambda }$/all hadrons), and definitely too high for that of kaons to all hadrons. This was an early indication of what became known as strangeness suppression in hadronic collisions, and which led to the introduction of a third parameter [17], the relative strangeness abundance, ${\gamma }_s$, which was found to have values around 0.6 for the data available at that time.

To some surprise, this approach with the three parameters—$T_H,{\mu }_B$, and ${\gamma }_s$ has turned out to be correct far beyond all expectations. Over the past years, the resulting predictions were tested in a variety of collision configurations, from $e^{+}{e}^{-}$ annihilation [13,18,19,20] over $pp$/$p\overline{p}$ [21,22] to nucleus-nucleus collisions [16,23,24,25,26,27]. 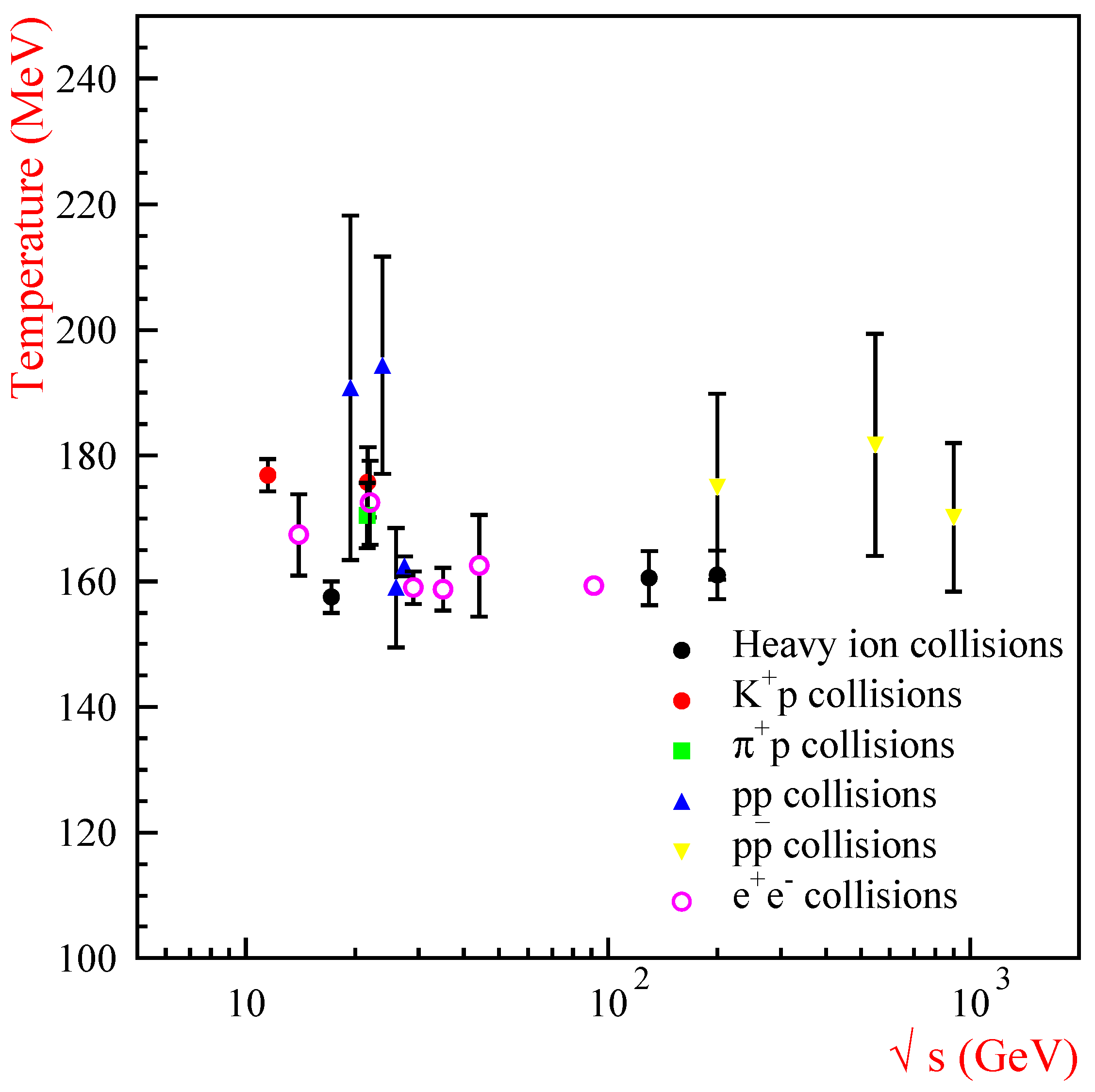With some caveats to be elaborated, they were found to provide a most remarkable account for what is observed, both of species abundances and, where applicable, of transverse momentum spectra [13]. Moreover, the temperature obtained for high energy experiments turned out to be quite universal, always lying around 160–180 MeV, i.e., in a range, which partitioning arguments as well as studies of critical phenomena in QCD had pre- and postdicted.

To illustrate, we compare in

Table 1. Fit results for a set of 12 long-lived particles in high energy $pp$, $AuAu$ and $e^{+}{e}^{-}$ collisions [22].

Collision	$\mathit{p}\mathit{p}$	${\mathit{e}}^{+}{\mathit{e}}^{-}$	$\mathit{A}\mathit{u}\mathit{A}\mathit{u}$
CMS Energy [GeV]	200	91.25	200
Temperature [MeV]	169.8 ± 4.2	164.7 ± 0.9	168.5 ± 4.0
Average relative deviation data vs. fit [%]	12.5	9.4	11.7
Strangeness Suppression, ${\gamma }_s$	0.57 ± 0.03	0.66 ± 0.01	0.93 ± 0.04

the results of $pp$ data to those from other initial state configurations ($e^{+}{e}^{-}$ and nucleus-nucleus, $AA$) at high collision energies [28,29,30,31,32,33]. To start from a comparable basis, the data set in all three reaction channels has been restricted as far as possible to the same 12 long-lived hadron species; the rates for short-lived and hence broader resonances are in general more difficult to measure. One can see that all channels indeed appear to converge to a hadronization temperature value of about 160–170 MeV. We also note that with increasing energy density for the collision, the strangeness suppression factor approaches unity, as predicted by a description in terms of hadronization volumes [34].

Combining the results for $e^{+}{e}^{-}$ annihilation, from elementary hadron-hadron interactions and from nucleus-nucleus collisions at different high energies leads to one of the truly striking observations in high energy strong interaction physics: the existence of a universal hadronization temperature $T_H$. An overall view of this result is given in Figure 2.

On the theoretical side, this suggests that there must be an underlying universal production mechanism, i.e., that the hadronization temperature is indeed determined by or closely related to the confinement/deconfinement transition of strongly interacting matter. On the experimental side, it leads to the remarkable prediction that the relative hadron abundances produced in high energy collisions become with increasing energy independent of the collision energy. One can thus predict such ratios with considerable confidence for the higher energy experiments at the CERN-LHC (Large Hadron Collider) [35].

Nevertheless, one important feature distinguishes elementary from nuclear interactions. It is seen in Table 1 that the strangeness suppression observed in elementary reactions has essentially disappeared in nucleus–nucleus collisions. This had been already mentioned above—the suppression factor ${\gamma }_s$ is now compatible with unity, and whatever deviations remain, can be understood as arising from “corona” interactions, i.e., collisions at the edge of the nuclei, which do not really experience the nuclear medium [36]. The fully thermal behavior of strange hadrons in the hot medium produced in central nuclear collisions is indeed a first indication for collective features present in such interactions. For its further understanding, it is expected that elementary $pp$ collisions at the very much higher energies of the CERN-LHC, with the much higher absolute strange hadron production rates, will also show a ${\gamma }_s$ approaching unity [35].

3. Conclusions

This success of the statistical hadronization model is undoubtedly one of the milestones in high energy multihadron production, and the pioneering contributions of Jean Cleymans have made it into an essential tool for the analysis of such studies. Jean continued his work in this direction and provided many further essential results [37].