Abstract
In this paper, the nuclear modification factors, , are investigated for pion production in small system collisions, measured by PHENIX experiment at RHIC (Relativistic Heavy Ion Collider). The theoretical framework is the parton transverse momentum -factorization formalism for hard processes at small momentum fraction, x. Evidence for collective expansion and thermal effects for pions, produced at equilibrium, is studied based on phenomenological parametrization of blast-wave type in the relaxation time approximation. The dependencies on the centrality and on the projectile species are discussed in terms of the behavior of Cronin peak and the suppression of at large transverse momentum, . The multiplicity of produced particles, which is sensitive to the soft sector of the spectra, is also included in the present analysis.
1. Introduction
The transverse momentum () spectra of charged and neutral particles have been experimentally studied in proton–proton (), proton–nucleus (), and nucleus–nucleus () collisions from different perspectives. First of all, the role played by this observable is highlighted as a measure of the partonic interactions in the perturbative quantum chromodynamics (pQCD) regime. One can extract from the particle spectra relevant information about the initial state dynamics of the colliding system. On the other hand, the spectrum has been used as a probe of the collective behavior developed by the hydrodynamic expansion of the hot environment created in heavy ion collisions. A key aspect of the problem is the emergence of thermal behavior observed even in small systems such as and collisions [1,2,3,4,5,6]. The nuclear effects are quantified by the nuclear modification factor, , which is obtained by the ratio between the multiplicity of produced particles in the collision of a projectile X off a nucleus A and the scaling on the number of binary collisions, , with being the yield in collisions. The latter is expected in the case of an absence of final state nuclear medium effects. From the experimental point of view, the nuclear modification factor for small systems presents a suppression in the small transverse momentum region (∼1 GeV), followed by an enhancement in the intermediate momentum region (∼2–5 GeV), and it finally goes to unity at large . This behavior is known as the Cronin effect [7], which has been explained by different theoretical models [8,9,10,11,12,13,14,15,16,17,18].
The scenario of hadron production from the decay of minijets described by -factorization formalism, where denotes the parton transverse momentum, considers that the cold matter nuclear (CNM) effects originate in the hard interaction of the nuclei at initial states of the collision. However, the particle production in those systems undergoes a hydrodynamics evolution to freeze-out, which modifies the corresponding spectrum. In [19,20,21], it is argued that the spectrum can be described by performing a temporal separation in the relaxation time approximation (RTA) of the Boltzmann transport equation [22]. The time separation corresponds to the hadrons produced in initial state hard collision and those produced in the equilibrium situation. Moreover, two-component models (thermal+hard) have been successful in describing experimental measurements [23,24,25]. In these approaches, the spectrum is decomposed into two parts: one related to the Boltzmann statistics and a second one characterized by the typical power-law behavior from pQCD. Nevertheless, the thermal nature of the spectrum has been posed in [26,27,28], where the two-component model takes into account a soft contribution coming from the longitudinal dissociation projectile-nucleus and a hard contribution due to the transverse production of jets. This seems to be enough to explain the data available without invoking collective flow. In a previous study [29], this approach has been considered to describe the spectra of produced pions in lead–lead () collisions at the Large Hadron Collider (LHC). It was shown that the thermal parametrization can be substantially modified by taking into account the nuclear effects present in the gluon distribution function.
In this paper, thermal effects are investigated in the nuclear modification factor, , for neutral pion production, which has been measured by the PHENIX Collaboration at the Relativistic Heavy Ion Collider (RHIC) [30], in small system collisions. A salient feature of in these systems is that the Cronin peak tends to grow for smaller projectiles, which is in contradiction to the expected behavior from pQCD. In particular, the interface between the hard process described within the QCD -factorization formalism and the thermal sector is investigated, which can play an important role in more central collisions. To this end, both the hard part of the spectrum and the multiplicity, , determined by the soft part, are studied. One important issue regards the separation region where the collective effects are needed for the spectrum description. In [31], an analysis of the high multiplicity distribution of particles in collisions was performed, and it was argued that the bulk part of spectra ( GeV) can be described by a distribution-like blast-wave. In [32], an approach based on a blast-wave parametrization that incorporates Tsallis statistics was also considered in order to study the collective flow effects in collisions as a function of the center-of-mass energy, . Evidence of collective expansion in high energies was shown. This suggests a dependence of the radial flow as the multiplicity or collision energy increase. Such effects also become important with the increasing number of constituents of a projectile/nuclear target. Therefore, it is fundamental to analyze the produced spectrum for distinct projectiles in order to relate the emergence of thermal behavior in terms of , and the geometric parameters of the colliding system such and , the number of participants.
This paper is organized as follows. In Section 2.1, the predictions of pQCD for the nuclear modification factor, , is discussed in different approaches. The main theoretical expressions for computing this observable are presented in the context of the pQCD -factorization formalism. The main physical input is the nuclear unintegrated gluon distribution (nUGD). Following [29], the Moriggi–Peccini–Machado (MPM) analytical parametrization for the nuclear UGD is considered. It describes correctly the spectra of particles produced in collisions, as well as the nuclear modification factors in collisions at the LHC. In Section 2.2, it is determined how the thermal corrections can be included in the spectrum is determined by using a blast–wave model. The focus is on pion production in , , , and collisions. It is demonstrated that the Cronin peak decreases for larger projectiles, in opposition to what is expected, as only cold nuclear matter effects are considered. It is verified that presents a behavior almost independent of projectile species at ∼10 GeV. The same occurs for the thermal parameters of the system, such as the relaxation time, , and temperature, T, which could suggest a correlation between the energy loss at large and the production of a thermal system of particles. These results and corresponding discussions are presented in Section 3. Conclusions are summarized in Section 4.
2. Theoretical Framework and Main Predictions
2.1. Nuclear Effects in the Gluon Distribution in a Nucleus
In the collinear factorization formalism of pQCD, the cross-section can be expressed as the convolution of the parton distribution functions (PDFs) of the small projectile (labeled here as X) and the nucleus A with the hard parton level cross-section. In this context, the nuclear modification factor is described in terms of the modification of the parton distribution within a nucleus compared to the ones in a free nucleon. These modifications give rise to the shadowing/anti-shadowing effects observed in the nuclear structure functions probed in deep-inelastic-scattering (DIS) events [33,34,35,36,37]. Moreover, the multiple interactions among nucleons can be described in the Glauber model, where the nuclear cross-section is expected to scale with . Corrections to the collinear factorization approach can take into account an intrinsic transverse momentum, , of partons at initial state. This effect increases with , which leads to an enhancement of with respect to centrality [8,38,39].
An important aspect that appears in RHIC data [30] is that the Cronin peak tends to increase for smaller projectiles species in agreement with the ordering . However, the collinear approach with cold nuclear matter effects predicts the following: . This prediction is in agreement with what is observed with respect to the nuclear structure functions. There, the shadowing/anti-shadowing contributions are intensified due to the atomic mass number, A. Another essential aspect presented by these data is that for more central collisions (0–5%), the factor presents a suppression that is not seen for smaller projectiles. Moreover, it is worth mentioning that increases for more peripheral collisions, while the factors decrease. In the multiple scattering model, it is expected that the average transverse momentum, , acquired by partons from the projectile as a result of interaction with the nuclear target is larger in more central collisions. Therefore, this effect raises the Cronin peak, and a decrease of is consequently anticipated in more peripheral reactions.
In the context of parton saturation approaches, like the color glass condensate (CGC) effective theory, the nuclear modification factor can be associated to the saturation of the nuclear UGD in the region of small . This saturation is more intense in more central collisions and for large nuclei (dense color system). In those approaches, through the Glauber–Mueller formalism [40,41], the multiple interactions of colored partons in the projectile with the color field of the nuclear target modifies the transverse momentum of the gluons in target, and the Cronin peak is reproduced. One can find that the evolution in the rapidity of the nUGD and the nuclear geometry should influence the behavior of in terms of [11,15,42]. The saturation approach has been used in different studies [43,44,45,46,47,48] in order to describe the -spectrum and the ratio for reaction at RHIC and ones at the LHC. In collisions, the saturation approach has been utilized in [49,50,51,52,53,54,55,56].
In this study, we consider the -factorization formalism in contrast to the collinear one. The main advantage is that the initial partons already present non-zero transverse momenta and the effects of parton saturation can be easily implemented. Now, the -spectrum is given by the convolution of the unintegrated gluon distributions of the colliding nuclei, , and the production cross-section at the parton level. The nUGD depends on the impact parameter, , of the reaction. In particular, the gluon production in collisions at very high energies is given by the following invariant cross section:
where are the longitudinal momentum fraction of incoming partons in projectile A and target B, respectively. The quantity is the transverse coordinate of the produced gluon. The strong coupling constant is , and is the QCD Casimir color factor with being the color number. Here, some remarks are in order. The processes initiated by quarks, and , are important in the fragmentation region and under large enough [57,58]. Here, g and denote the gluon and the fragmenting quark of flavour f, respectively. The data from PHENIX Collaboration [30] correspond to midrapidities () and not so large transverse momentum. This is the reason for disregarding the quark contribution in the numerical calculations here.
The unintegrated gluon distribution depends on the transverse momentum and longitudinal momentum fraction x. Here, in the numerical calculation, we use the MPM analytical parametrization [59] for the UGD. It is determined from the analysis of available data for light hadron production in collisions. It presents scaling on the variable , based on the geometric scaling property associated to the parton saturation formalism [60,61]. The characteristic momentum scale giving the transition between a dilute and a dense parton system is set by the saturation scale, . It is defined in terms of the longitudinal momentum fraction in the form . The MPM parametrization for a proton is written as follows:
where , and is fixed [62,63]. The parameters , , a, and b have been fitted from DESY-HERA (Deutsches Elektronen-Synchrotron, Hadron-Electron Ring Accelerator) data for proton structure function (see discussion in [59]). For central rapidity, y∼0, the x variable can be expressed as .
The incorporation of the nuclear effects in the gluon distribution is given by the Glauber–Gribov approach for multiple scattering. The main ingredients are the nuclear thickness function, , and the color dipole cross-section. The last quantity describes the multiple interactions of the leading Fock state of the projectile parton with the nucleons. The Woods–Saxon parametrization for the nuclear density has been considered for a large nucleus [64,65], and the thickness function has the normalization . For deuteron, the Hulthén form was used [66], and for helium, the parametrization, presented in [67], is considered. Following the previous study [29], the nuclear UGD is given as follows:
where is the Hankel transform of order 0. The quantity is the two-dimensional (2-D) Laplacian in momentum space. The key quantity is the dipole scattering matrix in configuration space, . It can be determined from the cross-section for dipole scattering off a proton, , in the following way:
where, the last line gives the corresponding expression for the dipole-proton cross-section in the MPM model. In particular, it scales with , as is usual in geometric-scaling-based models. Here, K is the modified Bessel function of second kind and is the Gamma function. The calculation is made straightforward by including any other phenomenological model for this quantity.
Considering only CNM effects, it is found that Equation (1) predicts only small changes in in collisions of gold nucleus with deuteron d or helium . Essentially, the nuclear modification is driven by the large nucleus in a similar way as occurs in the collinear factorization formalism. Namely, the nuclear effects in the gluon distribution for small nuclei is tiny. In Section 3, the need for corrections to the initial distribution is discussed once the experimental measurements present a large difference as the projectile changes. The nuclear modification factor, , based on the discussion above, can be determined by using the Glauber model:
where is obtained by using Equations (1), (3), and (4).
The nuclear gluon distribution in Equation (3) is characterized by two main quantities: the saturation scale, ∼, which determines the increasing of the spectrum in terms of the collision energy, ; and a power index that reproduces the power-like behavior on in the large transverse momentum limit. In Ref. [59], the investigation into the spectrum was restricted to the region, where geometric scaling is expected. For RHIC data at 200 GeV, this is valid only at small . In order to achieve a good description at large , in the present paper, the parameter was modified as , corresponding to the effective slope observed in the spectrum in collisions at RHIC. On the other hand, in order to keep the point of maximum in the UGD at the same place, the saturation scale has to be modified as . The fragmentation process is described in a simplified way by taking the hadron transverse momentum in the approximate form . Here, is the transverse momentum of the produced gluon, with . The spectrum determination contains uncertainties, such as the appropriated description of the fragmentation process, the contribution of processes initiated by quarks at large , and the determination of the mass of the gluon jet. However, in the ratio , these uncertainties are reasonably canceled, and the nuclear modification factor essentially provides the ratio of the UGDs in the nucleus and in the nucleon, , at a given centrality.
Having determined the basic parameters and the formalism to compute the unintegrated gluon distribution in both nucleons and nuclei in the initial hard process, in the next Section, we present how the thermal effects are incorporated in the analysis.
2.2. Collective Expansion and the Blast-Wave Model
In [19,20,21], it has been argued that the spectrum can be described by doing a time separation in the RTA of the Boltzmann transport equation [22]. In order to include the thermal corrections to the spectrum, predicted by Equation (1), We assume that the final state distribution can be expressed in the RTA,
where is the ratio of the freeze-out and relaxation times, with given by Equation (1) and being the equilibrium distribution of the thermal system.
One way of investigating the collective properties on the spectrum is based in phenomenological models of blast-wave type [68], developed in order to capture the essential aspects of the thermal and hydrodynamic description of collisions. These models have been applied to heavy-ion collisions at RHIC [69,70,71], LHC [72,73,74,75] and CERN/SPS (European Organizationfor Nuclear Research/Super Proton Synchrotron) [76]. The velocity profile of the expanding medium is parametrized in the following way:
where is the transverse expansion velocity, m is the velocity profile’s exponent, and is the transverse expansion velocity at the surface. The average speed is , r is the radial distance in the transverse plane from the centre of the fireball, and R is the fireballs radius. Here, a linear profile is considered, that is, . The spectrum of produced particles is given by the following:
where ard are the modified Bessel functions of the first and second kind, respectively, and T is the kinetic freeze-out temperature, , in the context of the Boltzmann-Gibbs blast-wave (BGBW) approach. In the RTA, considered here, is the temperature characterizing the Boltzmann local equilibrium distribution, . It has been shown in [21] that for a given centrality, the temperature is larger than the kinetic one. This is consistent with the idea that the temperature decreases with the evolution of the system from the local equilibrium to the kinetic freeze-out. The spectrum is determined by the parameters and T, which are adjusted from the experimental measurements.
As an exploratory study, the fitted parameters are presented in Table 1. A further study on possible constraints for the parameter ranges and discussion of data statistics is deserved. The expansion average velocity varies very little for the different systems. One obtains ∼0.55, which is closer to the values determined in paper [29] for pions in collisions in TeV at the LHC. It is also noticed that in [31], the obtained values are ∼0.65 in collisions, independently of the multiplicity. The temperature follows a trend similar to that observed for at large (i.e., almost independent of the projectile species). This could suggest a relation between the energy loss in the large transverse momentum region and the equilibrium temperature of the system.

Table 1.
Adjusted parameters’ equilibrium temperature, , which characterizes the Boltzmann local equilibrium distribution; the average speed, ; and the ratio of the freeze-out and relaxation times, . Results are presented for three classes of centrality.
3. Results and Discussions
Our analysis is restricted to more central collisions (0–5, 0–20, 20–40)%, where the nuclear effects are more prominent. The average values of geometric parameters such as and are calculated using a Glauber MC simulation, and they are explicitly presented in the PHENIX Collaboration papers (see Table II of [30] and page 6 of [77]). In Figure 1, the nuclear modification factor is shown for different systems, namely , , , and . For semi-central collisions such as (20–40)%, is close to unity at large . This indicates the absence of relevant nuclear effects, which is independent of the projectile species. On the other hand, for the most central collisions, (0–5)%, there exists a suppression of at large for all projectiles. This implies that the underlying mechanism of suppression does not depend on the colliding nucleus and has a strong dependence on centrality. In the figure, the lines represent the result obtained from Equations (6)–(9), including the thermal effects. In the relaxation time approximation, ∼, the initial distribution scales with . This indicates that the relaxation time diminishes for more central collisions for any projectile. This can be understood supposing that the time should be inversely proportional to the energy density, which varies little for different colliding systems. For more peripheral reactions, the predicted Cronin peak is larger than that experimentally observed in the collisions, which is related to the impact parameter dependence of the nuclear UGD. It decreases more slowly with the impact parameter than in case of the aluminium nucleus. In the small region, it is observed a suppression due to the nuclear shadowing in the nUGD, followed by an enhancement near the maximum of the nUGD. In the initial distribution, an enhancement in the peak and a stronger shadowing effect are expected for the nucleus. However, it was verified that the thermal contribution at small contributes to diminishing these effects. A similar phenomenon occurs in heavy-ion collisions, as the produced particles in thermal equilibrium compensate the expected suppression due to strong nuclear shadowing from the nuclear UGD. In the case of small systems that are investigated here, the contribution of this piece, , to the spectrum is found to be small, ∼. This contribution is made clear if one looks at Figure 2, where the small region of the spectrum is shown. There, the yield has been divided by and presented as a function of the transverse momentum. The dot-dashed lines represent the contribution of the particle produced in thermal equilibrium, and the solid line corresponds to the sum given by Equation (7). For less central collisions, where tends to unity at large , such a contribution is small, and it is higher in more central collisions.
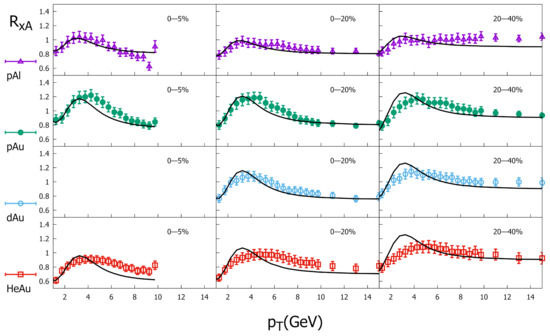
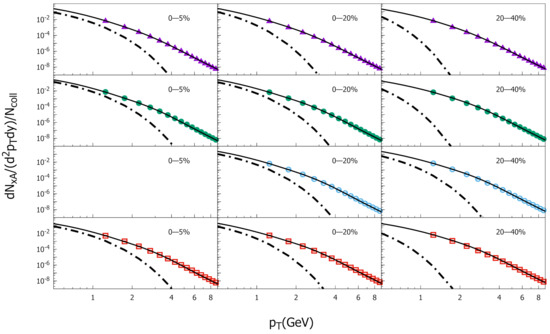
Figure 2.
The yield for collisions divided by the number of binary collisions, , as a function of transverse momentum. Data from PHENIX Collaboration [30] at small transverse momentum region. Different projectile species and three more central classes of centrality are presented. The dot-dashed lines represent the contribution of the particle produced in thermal equilibrium, and the solid lines correspond to the sum given by Equation (7). See text for details.
Each part of the spectrum has a distinct behavior in terms of the geometric parameter of the nuclear collision. The is analyzed in three different regions as a function of , as presented in Figure 3. At GeV, where , the dot-dashed lines correspond to the expected result by considering only , which is determined by the nuclear shadowing present in the nuclear UGD. We draw attention to the fact that the contribution to from presents fewer theoretical uncertainties compared to the absolute spectrum, as they are canceled in the ratio. In this limit, basically resembles the behavior of the ratio at a given centrality class. For , data present the expected behavior, with a stronger suppression for increasing . However, in the case of , the ratio is almost flat. For instance, in the case of , reaction increases for more central collisions compared to the peripheral ones. At GeV, near the Cronin peak, the expected behavior is peak enhancement as increases. However, for , the observed behavior is the opposite; namely, the peak diminishes as the number of collisions increases. An interesting case is the nuclear modification factor at large . The value GeV is considered, where ∼1 is expected due to the -scaling predicted by pQCD. However, the nuclear modification factor is substantially smaller than unity for the two more central classes of centrality. The most intriguing fact is that is independent of the projectile species and practically the same for each centrality. This suggests that in the large region is testing observables, which have a poor dependence on the projectile or collision geometry, such as the multiplicity or transverse energy density. In [78], it was demonstrated that the obtained temperature in the Tsallis-blast-wave model scales with for , , and collisions but presents an intense reliance on the size of the colliding system.
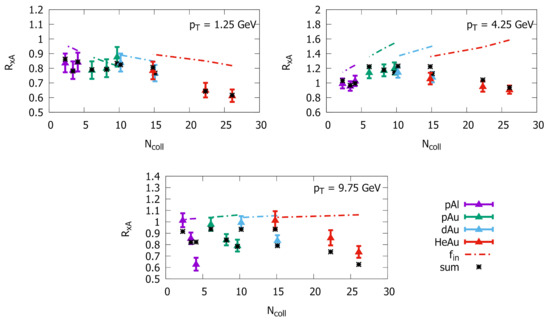
Figure 3.
Nuclear modification factor as a function of the number of binary collisions for three values of transverse momentum, . Dot-dashed lines represent the calculation without thermal effects by using only . The black “×” symbols correspond to the full calculation given by Equations (6)–(9). Data from PHENIX Collaboration [30].
Finally, the quantity is studied, assuming that the charged hadron multiplicity () is given predominantly by pions. Accordingly, the integrated pion spectra (after transformation ) can be compared to the measured multiplicities. A comparison between predictions and the PHENIX data [77] is presented in Figure 4. In the figures, the black “×” symbols represent the results, and for better viewing, the dot-dashed lines correspond to their linear regression for each projectile species. For , the ratio follows the same pattern observed for at small ; namely, there is a scaling that is less steep on . In the intermediate region, is practically constant in terms of . In [79], an analysis of the energy loss parameter, , for different systems in collisions at RHIC and LHC (200 GeV) demonstrates that the energy loss imposed by the nuclear medium does not scale with the geometric parameters of the system (, ), but scales with quantities related to the system energy density and the multiplicity .
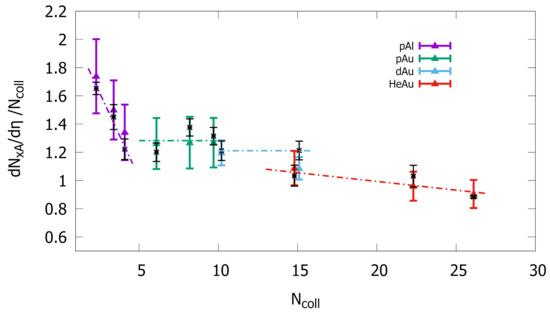
Figure 4.
Multiplicity of charged hadrons measured by PHENIX Collaboration [77] as a function of for different projectile species and centrality classes. The black “×” symbols represent the numerical results, and for better viewing, the dot-dashed lines correspond to their linear regression for each projectile species.
4. Summary and Conclusions
In this paper, the relevance of the thermal effects is investigated in collisions of small systems based on the analysis of the transverse momentum spectra of neutral pions measured at RHIC (Relativistice Heavy Ion Collider. The Boltzmann equation in the relaxation time approximation has been considered. It was shown that the hard part contribution attributed to an initial production computed within the -factorization formalism in pQCD (perturbative quantum chromodynamics) presents a different behavior from the one experimentally observed, even at large transverse momentum, . The deviation can be understood in terms of enhancement/suppression of particles produced in the collective expansion of the thermal system. In particular, the Cronin peak tends to decrease in the case of larger-size projectiles, in opposition to what is expected, due to considering cold nuclear matter effects only. It is verified that the nuclear modification factor, , at ∼10 GeV does not depend on the projectile species. The same occurs for the thermal parameters of the system such as the relaxation time, and temperature, T, which suggests a correlation between the energy loss at large and the production of a thermal system of particles.
Author Contributions
L.M. and M.M. have contributed to the study equally, starting from the conceptualization of the problem, to the methodology, paper writing, and review. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Brazilian National Council for Scientific and Technological Development (CNPq) under the contract number 306101/2018-1.
Data Availability Statement
The data used can be found in the corresponding references.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Bergauer, T.; Dragicevic, M.; Erö, J.; Fabjan, C.; Friedl, M.; Frühwirth, R.; et al. Observation of long-range near-side angular correlations in proton-proton collisions at the LHC. JHEP 2010, 9, 91. [Google Scholar] [CrossRef]
- Aad, G.; Abbott, B.; Abdallah, J.; Aben, R.; Abolins, M.; AbouZeid, O.S.; Abramowicz, H.; Abreu, H.; Abreu, R.; Abulaiti, Y.; et al. Observation of long-range elliptic azimuthal anisotropies in = 13 and 2.76 TeV pp collisions with the ATLAS Detector. Phys. Rev. Lett. 2016, 116, 172301. [Google Scholar] [CrossRef] [PubMed]
- Khachatryan, V.; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Evidence for collectivity in pp collisions at the LHC. Phys. Lett. B 2017, 765, 193–220. [Google Scholar] [CrossRef]
- Aaboud, M.; Aad, G.; Abbott, B.; Abeloos, B.; Abidi, S.H.; AbouZeid, O.S.; Abraham, N.L.; Abramowicz, H.; Abreu, H.; Abreu, R.; et al. Measurement of long-range multiparticle azimuthal correlations with the subevent cumulant method in pp and p + Pb collisions with the ATLAS detector at the CERN Large Hadron Collider. Phys. Rev. C 2018, 97, 024904. [Google Scholar] [CrossRef]
- Adam, J.; Adamova, D.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, S.; Ahn, S.U.; Aiola, S.; et al. Enhanced production of multi-strange hadrons in high-multiplicity proton-proton collisions. Nat. Phys. 2017, 13, 535–539. [Google Scholar] [CrossRef]
- Acharya, S.; Adamová, D.; Adhya, S.P.; Adler, A.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; et al. Multiplicity dependence of (multi-)strange hadron production in proton-proton collisions at = 13 TeV. Eur. Phys. J. C 2020, 80, 167. [Google Scholar] [CrossRef]
- Cronin, J.; Frisch, H.J.; Shochet, M.; Boymond, J.; Mermod, R.; Piroue, P.; Sumner, R.L. Production of hadrons with large transverse momentum at 200, 300, and 400 GeV. Phys. Rev. D 1975, 11, 3105–3123. [Google Scholar] [CrossRef]
- Wang, X.N. Systematic study of high pT hadron spectra in pp, pA and AA collisions from SPS to RHIC energies. Phys. Rev. C 2000, 61, 064910. [Google Scholar] [CrossRef]
- Kopeliovich, B.Z.; Nemchik, J.; Schafer, A.; Tarasov, A.V. Cronin effect in hadron production off nuclei. Phys. Rev. Lett. 2002, 88, 232303. [Google Scholar] [CrossRef]
- Vitev, I.; Gyulassy, M. High pT tomography of d + Au and Au + Au at SPS, RHIC, and LHC. Phys. Rev. Lett. 2002, 89, 252301. [Google Scholar] [CrossRef]
- Kharzeev, D.; Kovchegov, Y.V.; Tuchin, K. Cronin effect and high-pT suppression in pA collisions. Phys. Rev. 2003, D68, 094013. [Google Scholar] [CrossRef]
- Hwa, R.C.; Yang, C.B. Final state interaction as the origin of the Cronin effect. Phys. Rev. Lett. 2004, 93, 082302. [Google Scholar] [CrossRef]
- Gelis, F.; Jalilian-Marian, J. From DIS to proton nucleus collisions in the color glass condensate model. Phys. Rev. D 2003, 67, 074019. [Google Scholar] [CrossRef]
- Albacete, J.L.; Armesto, N.; Milhano, J.G.; Salgado, C.A.; Wiedemann, U.A. Numerical analysis of the Balitsky-Kovchegov equation with running coupling: Dependence of the saturation scale on nuclear size and rapidity. Phys. Rev. D 2005, 71, 014003. [Google Scholar] [CrossRef]
- Baier, R.; Kovner, A.; Wiedemann, U.A. Saturation and parton level Cronin effect: Enhancement versus suppression of gluon production in p-A and A-A collisions. Phys. Rev. D 2003, 68, 054009. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Gelis, F.; Venugopalan, R. High-energy pA collisions in the color glass condensate approach. 1. Gluon production and the Cronin effect. Nucl. Phys. A 2004, 743, 13–56. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Iancu, E. The Quark gluon plasma: Collective dynamics and hard thermal loops. Phys. Rep. 2002, 359, 355–528. [Google Scholar] [CrossRef]
- Jalilian-Marian, J.; Kovchegov, Y.V. Saturation physics and deuteron-gold collisions at RHIC. Prog. Part. Nucl. Phys. 2006, 56, 104–231. [Google Scholar] [CrossRef]
- Tripathy, S.; Bhattacharyya, T.; Garg, P.; Kumar, P.; Sahoo, R.; Cleymans, J. Nuclear modification factor using Tsallis non-extensive statistics. Eur. Phys. J. A 2016, 52, 289. [Google Scholar] [CrossRef]
- Tripathy, S.; Khuntia, A.; Tiwari, S.K.; Sahoo, R. Transverse momentum spectra and nuclear modification factor using Boltzmann transport equation with flow in Pb + Pb collisions at = 2.76 TeV. Eur. Phys. J. A 2017, 53, 99. [Google Scholar] [CrossRef]
- Qiao, L.; Che, G.; Gu, J.; Zheng, H.; Zhang, W. Nuclear modification factor in Pb–Pb and p-Pb collisions using Boltzmann transport equation. J. Phys. G Nucl. Part. Phys. 2020, 47, 075101. [Google Scholar] [CrossRef]
- Florkowski, W.; Ryblewski, R. Separation of elastic and inelastic processes in the relaxation-time approximation for the collision integral. Phys. Rev. C 2016, 93, 064903. [Google Scholar] [CrossRef]
- Bylinkin, A.; Chernyavskaya, N.; Rostovtsev, A. Two components in charged particle production in heavy-ion collisions. Nucl. Phys. B 2016, 903, 204–210. [Google Scholar] [CrossRef]
- Giannini, A.V.; Goncalves, V.P.; Silva, P.V.R.G. Thermal radiation and inclusive production in the running coupling kT-factorization approach. Eur. Phys. J. A 2021, 57, 43. [Google Scholar] [CrossRef]
- Urmossy, K.; Barnaföldi, G.G.; Harangozó, S.; Biró, T.S.; Xu, Z. A ‘soft + hard’ model for heavy-ion collisions. J. Phys. Conf. Ser. 2017, 805, 012010. [Google Scholar] [CrossRef]
- Adams, J.; Aggarwal, M.M.; Ahammed, Z.; Amonett, J.; Anderson, B.D.; Anderson, M.; Arkhipkin, D.; Averichev, G.S.; Bai, Y.; Balewski, J.; et al. The Multiplicity dependence of inclusive pt spectra from pp collisions at = 200-GeV. Phys. Rev. D 2006, 74, 032006. [Google Scholar] [CrossRef]
- Trainor, T.A. Centrality evolution of p(t) and y(t) spectra from Au-Au collisions at s(NN)**(1/2) = 200-GeV. Int. J. Mod. Phys. E 2008, 17, 1499–1540. [Google Scholar] [CrossRef]
- Trainor, T.A. A two-component model for identified-hadron pt spectra from 5 TeV p-Pb collisions. J. Phys. G 2020, 47, 045104. [Google Scholar] [CrossRef]
- Moriggi, L.S.; Peccini, G.M.; Machado, M.V.T. Role of nuclear gluon distribution on particle production in heavy ion collisions. Phys. Rev. D 2021, 103, 034025. [Google Scholar] [CrossRef]
- Acharya, U.A.; Adare, A.; Aidala, C.; Ajitan, N.N.; Akiba, Y.; Al-Bataineh, H.; Alexander, J.; Alfred, M.; Andrieux, V.; Angerami, A.; et al. Systematic study of nuclear effects in p + Al, p + Au, d + Au, and 3He+Au collisions at = 200 GeV using π0 production. Phys. Rev. C 2022, 105, 064902. [Google Scholar] [CrossRef]
- Rath, R.; Khuntia, A.; Sahoo, R.; Cleymans, J. Event multiplicity, transverse momentum and energy dependence of charged particle production, and system thermodynamics in pp collisions at the Large Hadron Collider. J. Phys. G 2020, 47, 055111. [Google Scholar] [CrossRef]
- Jiang, K.; Zhu, Y.; Liu, W.; Chen, H.; Li, C.; Ruan, L.; Tang, Z.; Xu, Z.; Xu, Z. Onset of radial flow in p+p collisions. Phys. Rev. C 2015, 91, 024910. [Google Scholar] [CrossRef]
- Eskola, K.J.; Honkanen, H. A Perturbative QCD analysis of charged particle distributions in hadronic and nuclear collisions. Nucl. Phys. 2003, A713, 167–187. [Google Scholar] [CrossRef][Green Version]
- Helenius, I.; Eskola, K.J.; Paukkunen, H. Centrality dependence of inclusive prompt photon production in d+Au, Au+Au, p+Pb, and Pb+Pb collisions. JHEP 2013, 5, 30. [Google Scholar] [CrossRef]
- Helenius, I.; Paukkunen, H.; Eskola, K.J. Nuclear PDF constraints from p+Pb collisions at the LHC. arXiv 2015, arXiv:1509.02798. [Google Scholar] [CrossRef]
- Kovarik, K.; Kusina, A.; Ježo, T.; Clark, D.B.; Keppel, C.; Lyonnet, F.; Morfín, J.G.; Olness, F.I.; Owens, J.F.; Schienbein, I.; et al. nCTEQ15—Global analysis of nuclear parton distributions with uncertainties in the CTEQ framework. Phys. Rev. D 2016, 93, 085037. [Google Scholar] [CrossRef]
- Abdul Khalek, R.; Ethier, J.J.; Rojo, J. Nuclear parton distributions from lepton-nucleus scattering and the impact of an electron-ion collider. Eur. Phys. J. C 2019, 79, 471. [Google Scholar] [CrossRef]
- Vitev, I.; Zhang, B.W. A Systematic study of direct photon production in heavy ion collisions. Phys. Lett. B 2008, 669, 337–344. [Google Scholar] [CrossRef]
- Zhang, Y.; Fai, G.I.; Papp, G.; Barnafoldi, G.G.; Levai, P. High pT pion and kaon production in relativistic nuclear collisions. Phys. Rev. C 2002, 65, 034903. [Google Scholar] [CrossRef]
- Glauber, R. Cross-sections in deuterium at high-energies. Phys. Rev. 1955, 100, 242–248. [Google Scholar] [CrossRef]
- Mueller, A.H. Small-x Behavior and Parton Saturation: A QCD Model. Nucl. Phys. B 1990, 335, 115–137. [Google Scholar] [CrossRef]
- Albacete, J.L.; Armesto, N.; Kovner, A.; Salgado, C.A.; Wiedemann, U.A. Energy dependence of the Cronin effect from nonlinear QCD evolution. Phys. Rev. Lett. 2004, 92, 082001. [Google Scholar] [CrossRef]
- Lappi, T.; Mäntysaari, H. Single inclusive particle production at high energy from HERA data to proton-nucleus collisions. Phys. Rev. D 2013, 88, 114020. [Google Scholar] [CrossRef]
- Dumitru, A.; Hayashigaki, A.; Jalilian-Marian, J. Geometric scaling violations in the central rapidity region of d + Au collisions at RHIC. Nucl. Phys. 2006, A770, 57–70. [Google Scholar] [CrossRef]
- Goncalves, V.P.; Kugeratski, M.S.; Machado, M.V.T.; Navarra, F.S. Saturation physics at HERA and RHIC: An nified description. Phys. Lett. 2006, B643, 273–278. [Google Scholar] [CrossRef]
- Boer, D.; Utermann, A.; Wessels, E. Geometric Scaling at RHIC and LHC. Phys. Rev. 2008, D77, 054014. [Google Scholar] [CrossRef]
- Rezaeian, A.H. CGC predictions for p+A collisions at the LHC and signature of QCD saturation. Phys. Lett. B 2013, 718, 1058–1069. [Google Scholar] [CrossRef]
- Kharzeev, D.; Kovchegov, Y.V.; Tuchin, K. Nuclear modification factor in d+Au collisions: Onset of suppression in the color glass condensate. Phys. Lett. B 2004, 599, 23–31. [Google Scholar] [CrossRef]
- Armesto, N.; Salgado, C.A.; Wiedemann, U.A. Relating high-energy lepton-hadron, proton-nucleus and nucleus-nucleus collisions through geometric scaling. Phys. Rev. Lett. 2005, 94, 022002. [Google Scholar] [CrossRef]
- Albacete, J.L.; Dumitru, A. A model for gluon production in heavy-ion collisions at the LHC with rcBK unintegrated gluon densities. arXiv 2010, arXiv:1011.5161. [Google Scholar] [CrossRef]
- Kharzeev, D.; Levin, E.; Nardi, M. Color glass condensate at the LHC: Hadron multiplicities in pp, pA and AA collisions. Nucl. Phys. 2005, A747, 609–629. [Google Scholar] [CrossRef]
- Tribedy, P.; Venugopalan, R. QCD saturation at the LHC: Comparisons of models to p+p and A+A data and predictions for p+Pb collisions. Phys. Lett. B 2012, 710, 125–133, Erratum in Phys. Lett. B 2013, 718, 1154–1154. [Google Scholar] [CrossRef]
- Lappi, T. Energy dependence of the saturation scale and the charged multiplicity in pp and AA collisions. Eur. Phys. J. C 2011, 71, 1699. [Google Scholar] [CrossRef]
- Levin, E.; Rezaeian, A.H. Gluon saturation and energy dependence of hadron multiplicity in pp and AA collisions at the LHC. Phys. Rev. D 2011, 83, 114001. [Google Scholar] [CrossRef]
- Albacete, J.L.; Marquet, C. Single inclusive hadron production at RHIC and the LHC from the color glass condensate. Phys. Lett. B 2010, 687, 174–179. [Google Scholar] [CrossRef]
- Durães, F.; Giannini, A.; Goncalves, V.; Navarra, F. Testing the running coupling kT-factorization formula for the inclusive gluon production. Phys. Rev. D 2016, 94, 054023. [Google Scholar] [CrossRef]
- Czech, M.; Szczurek, A. Unintegrated CCFM parton distributions and pion production in proton-proton collisions at high energies. Phys. Rev. C 2005, 72, 015202. [Google Scholar] [CrossRef]
- Czech, M.; Szczurek, A. Unintegrated parton distributions and pion production in pp collisions at RHIC’s energies. J. Phys. G 2006, 32, 1253–1268. [Google Scholar] [CrossRef][Green Version]
- Moriggi, L.; Peccini, G.; Machado, M. Investigating the inclusive transverse spectra in high-energy pp collisions in the context of geometric scaling framework. Phys. Rev. D 2020, 102, 034016. [Google Scholar] [CrossRef]
- McLerran, L.; Praszalowicz, M. Saturation and scaling of multiplicity, mean pT and pT distributions from 200 GeV ≤ ≤ 7 TeV. Acta Phys. Polon. B 2010, 41, 1917–1926. [Google Scholar]
- McLerran, L.; Praszalowicz, M. Saturation and scaling of multiplicity, mean pT and pT distributions from 200 GeV ≤ ≤ 7 TeV—Addendum. Acta Phys. Polon. B 2011, 42, 99–103. [Google Scholar] [CrossRef]
- Praszałowicz, M.; Francuz, A. Geometrical Scaling in Inelastic Inclusive Particle Production at the LHC. Phys. Rev. D 2015, 92, 074036. [Google Scholar] [CrossRef]
- Staśto, A.M.; Golec-Biernat, K.J.; Kwiecinski, J. Geometric scaling for the total γ*p cross section in the low x region. Phys. Rev. Lett. 2001, 86, 596–599. [Google Scholar] [CrossRef] [PubMed]
- De Jager, C.; De Vries, H.; De Vries, C. Nuclear charge and magnetization density distribution parameters from elastic electron scattering. Atom. Data Nucl. Data Tabl. 1974, 14, 479–508, Erratum in Atom. Data Nucl. Data Tabl. 1975, 16, 580–580. [Google Scholar] [CrossRef]
- De Vries, H.; De Jager, C.; De Vries, C. Nuclear charge-density-distribution parameters from elastic electron scattering. At. Data Nucl. Data Tables 1987, 36, 495–536. [Google Scholar] [CrossRef]
- Hulthén, L.; Sugawara, M. The two-nucleon problem. In Structure of Atomic Nuclei/Bau der Atomkerne; Springer: Berlin/Heidelberg, Germany, 1957; Volume 8/39, pp. 1–143. [Google Scholar] [CrossRef]
- McCarthy, J.S.; Sick, I.; Whitney, R.R. Electromagnetic structure of the helium isotopes. Phys. Rev. C 1977, 15, 1396–1414. [Google Scholar] [CrossRef]
- Schnedermann, E.; Sollfrank, J.; Heinz, U.W. Thermal phenomenology of hadrons from 200A GeV S+S collisions. Phys. Rev. C 1993, 48, 2462–2475. [Google Scholar] [CrossRef]
- Abelev, B.I.; Aggarwal, M.M.; Ahammed, Z.; Anderson, B.D.; Arkhipkin, D.; Averichev, G.S.; Bai, Y.; Balewski, J.; Barannikova, O.; Barnby, L.S.; et al. Systematic measurements of identified particle spectra in pp,d+ Au and Au+Au collisions from STAR. Phys. Rev. C 2009, 79, 034909. [Google Scholar] [CrossRef]
- Adams, J.; Adler, C.; Aggarwal, M.M.; Ahammed, Z.; Amonett, J.; Anderson, B.D.; Anderson, M.; Arkhipkin, D.; Averichev, G.S.; Badyal, S.K.; et al. Identified particle distributions in pp and Au+Au collisions at = 200 GeV. Phys. Rev. Lett. 2004, 92, 112301. [Google Scholar] [CrossRef]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Ajitan, N.N.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; Aparin, A.; et al. Bulk properties of the medium produced in relativistic heavy-ion collisions from the beam energy scan program. Phys. Rev. C 2017, 96, 044904. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Ahammed, Z.; et al. Centrality dependence of π, K, p production in Pb-Pb collisions at = 2.76 TeV. Phys. Rev. C 2013, 88, 044910. [Google Scholar] [CrossRef]
- Acharya, S.; Adamová, D.; Adhya, S.P.; Adler, A.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; et al. Production of charged pions, kaons, and (anti-)protons in Pb-Pb and inelastic pp collisions at = 5.02 TeV. Phys. Rev. C 2020, 101, 044907. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamová, D.; Adare, A.M.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Ahammed, Z.; et al. Multiplicity dependence of pion, kaon, proton and lambda production in p-Pb collisions at = 5.02 TeV. Phys. Lett. B 2014, 728, 25–38. [Google Scholar] [CrossRef]
- Acharya, S.; Adamová, D.; Adler, A.; Adolfsson, J.; Aggarwal, M.M.; Rinella, G.A.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahn, S.U.; et al. Multiplicity dependence of light-flavor hadron production in pp collisions at = 7 TeV. Phys. Rev. C 2019, 99, 024906. [Google Scholar] [CrossRef]
- Bearden, I.G.; Bøggild, H.; Boissevain, J.; Dodd, J.; Erazmus, B.; Esumi, S.; Fabjan, C.W.; Ferenc, D.; Fields, D.E.; Franz, A.; et al. Collective expansion in high-energy heavy ion collisions. Phys. Rev. Lett. 1997, 78, 2080–2083. [Google Scholar] [CrossRef]
- Adare, A.; Aidala, C.; Ajitan, N.N.; Akiba, Y.; Alfred, M.; Andrieux, V.; Aoki, K.; Apadula, N.; Asano, H.; Ayuso, C.E.; et al. Pseudorapidity dependence of particle production and elliptic flow in asymmetric nuclear collisions of p + Al, p + Au, d + Au, and 3He + Au at = 200 GeV. Phys. Rev. Lett. 2018, 121, 222301. [Google Scholar] [CrossRef]
- Gu, J.B.; Li, C.Y.; Wang, Q.; Zhang, W.C.; Zheng, H. Collective expansion in pp collisions using the Tsallis statistics. arXiv 2022, arXiv:2201.02091. [Google Scholar] [CrossRef]
- Adare, A.; Afanasiev, S.; Aidala, C.; Ajitan, N.N.; Akiba, Y.; Akimoto, R.; Al-Bataineh, H.; Alexander, J.; Alfred, M.; Al-Ta’ani, H.; et al. Scaling properties of fractional momentum loss of high-pT hadrons in nucleus-nucleus collisions at from 62.4 GeV to 2.76 TeV. Phys. Rev. C 2016, 93, 024911. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).