Abstract
In recent years, shell model studies have significantly contributed in improving the nuclear input, required in simulations of the dynamics of astrophysical objects and their associated nucleosynthesis. This review highlights a few examples such as electron capture rates and neutrino-nucleus cross sections, important for the evolution and nucleosynthesis of supernovae. For simulations of rapid neutron-capture (r-process) nucleosynthesis, shell model studies have contributed to an improved understanding of half lives of neutron-rich nuclei with magic neutron numbers and of the nuclear level densities and -strength functions that are both relevant for neutron capture rates.
1. Introduction
The interacting shell model, which takes in account correlations beyond mean field in a valence space, is generally considered as the method of choice to describe medium-mass nuclei [1,2,3]. Such nuclei play crucial roles for the dynamics of astrophysical objects and their associated nucleosynthesis. Unfortunately, a direct experimental determination of the required input is often prohibited due to the extreme conditions of the astrophysical environment in terms of temperature, density and also proton-to-neutron ratio; hence, the information has to be modeled. Here, the shell model has led to decisive progress in many cases in recent years, mainly due to its ability to account for the relevant correlations among nucleons and to accurately reproduce low-energy spectra and electromagnetic transitions [2,4,5].
This paper summarizes some of the progress achieved on the basis of shell model studies. Here, two different versions of the interacting shell model have been exploited: the diagonalization shell model [2] and the Shell Model Monte Carlo (SMMC) approach [6,7]. Diagonalization shell model calculations, which in contrast to SMMC allow for detailed spectroscopy, have been performed to derive rates for weak interaction processes of nuclei up to the iron-nickel mass range [8,9,10,11]. In particular, the shell model rates for electron captures on nuclei have significant impact on the presupernova core evolution of massive stars [12,13], the core evolution at the end of the hydrostatic evolution of medium-mass stars [11,14,15] and on the nucleosynthesis in thermonuclear supernovae [16].
The SMMC approach is based on a statistical description of the nucleus at finite temperature. In contrast to diagonalization, the shell model allows the derivation of nuclear properties at finite temperatures in extremely large model spaces by taking the relevant nuclear correlations into account [6,7]. SMMC has been the basis for deriving electron capture rates for heavier neutron-rich nuclei for which cross-shell correlations are essential in establishing the capture on nuclei as the main weak interaction process for the dynamics of the core collapse of a massive star [17,18,19].
Both varieties of the interacting shell model have improved the nuclear input required for simulations of rapid neutron-capture (r-process) nucleosynthesis. Diagonal shell model calculations have been used to derive half lives for neutron-rich nuclei with magic neutron numbers (called waiting points), which are crucial for the mass flow during the nucleosynthesis process [20,21,22]. Shell model calculations have also been used to study the general behavior of electromagnetic transitions, which are essential for modeling neutron capture rates, where an experimentally observed increase in the dipole’s strength function at low energies has drawn attention recently [23,24]. The nuclear level density is another important ingredient in modeling neutron capture rates. Here, SMMC calculations have allowed a microscopic derivation of level densities, also allowing the exploration of parameter dependencies, used in phenomenological approachesl (see, e.g., [25,26]).
2. Weak Interaction Processes in Supernovae
A massive star ends its life in a supernova explosion triggered by the gravitational collapse of its inner core that is no longer supported by energy released in charged-particle reactions [19,27]. Electron captures on nuclei have three important consequences during the collapse [4,28]: (i) electron captures reduce the number of electrons and hence the pressure with which the degenerate (relativistic) electron gas counteracts against the gravitational contraction; (ii) the neutrinos, generated by the capture process, leave the star mainly unhindered, carrying away energy and keeping the entropy in the core low such that heavy nuclei survive during collapse; (iii) electron capture changes a proton in the nucleus into a neutron, driving the core composition to be a more neutron-rich (and heavier) nuclei. In the late stage of the collapse, coherent scattering with nuclei and inelastic scattering with electrons are responsible for neutrinos becoming trapped and thermalized in what is called the homologous core [27]. Other neutrino–nucleus interactions are of minor importance during collapse; however, they play a role in the nucleosynthesis processes following supernova explosions and for the detection of supernova neutrinos.
2.1. Electron Capture on Nuclei
At the stellar conditions early in the collapse at which the core composition (described by nuclear statistical equilibrium) is dominated by nuclei from the iron-nickel mass range (-shell nuclei), electron capture is dominated by Gamow-Teller (GT) transitions. The subscript refers to the isospin component in the GT operator such that in GT transitions a proton is changed into a neutron, in GT transitions, which are relevant for decay of nuclei with neutron excess, a neutron is changed into a proton, and the GT strength, important for describing low-energy inelastic neutrino-nucleus scattering, refers to transitions between proton states and neutron states. It is now possible to derive converged low-energy spectra and transitions of -shell nuclei in the respective model space [2]. In fact, it turned out that, in addition to a constant renormalization of the Gamow–Teller operator [29,30], such highly correlated wave functions are required to describe the strong fragmentation and total value of GT strength [31], as experimentally determined by charge-exchange experiments [32,33].
The formalism for the calculation of electron capture rates has been introduced in ref. [34,35]. Note that the strong energy dependence of phase space as well as the fact that the electron Fermi energy is of the same order as the Q-value (the energy difference between initial and final nuclear states) of the abundant nuclei under presupernova conditions makes a detailed and accurate description of the GT distribution an important requirement for a reliable description of stellar electron capture during this phase of the collapse. That the diagonalization shell model is up to this task and indeed the method of choice to describe stellar weak-interaction rates during presupernova collapse has been demonstrated by Cole and collaborators [36]. In [36], the capture rates, derived from experimental GT data for all -shell nuclei for which data exist, are compared with rates calculated within the shell model using two different residual interactions. As shown in Figure 1, the agreement is quite satisfactory at the conditions at which these nuclei are abundant and relevant for the core dynamics. A tabulation of shell model capture rates for -shell nuclei has been made available based on large-scale studies using a variation of the Strasbourg–Madrid KB3 interaction [10]. More recent studies using an improved residual interaction basically confirmed prior calculations. These studies led to slight improvements for selected mid--shell nuclei; see Figure 1.
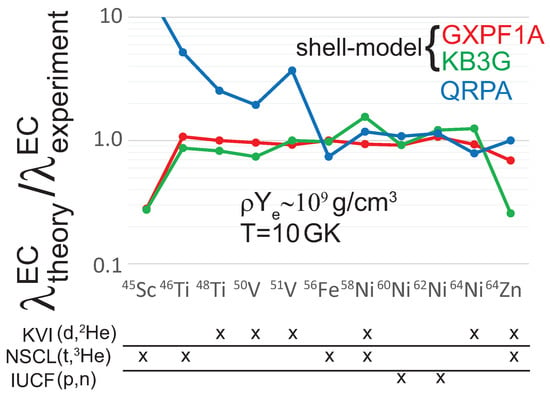
Figure 1.
Comparison of electron captures rates, calculated from experimental GT data and distributions, derived from the large-scale shell model calculations with two different interactions (KB3G [37] and GXPF1 [38]) and from a Quasiparticle Random Phase Approximation (QRPA) approach [36]. See text for details. The conditions correspond to the early stage of the collapse where the capture rates are sensitive to details of the GT distribution. The shell model rates have been quenched with typical factor of , as derived in [30]. and T denote the electron density and temperature, respectively. KVI, UCSL and IUCF stay for the laboratories at which the experiments were performed. Taken from [39] with permission.
Stars in the mass range of 8– ( denotes the Sun mass) received a lot of attention recently as they fill the gap between low-mass stars, which end their lives as white dwarfs and massive stars which, as discussed above, run through the full circle of hydrostatic burning stages ending finally as core-collapse supernovae. The intermediate mass stars are not massive enough to ignite all advanced hydrostatic burning stages and instead degenerate ONe or ONeMg cores. Electron captures are crucial for the final fate of the stars, where the most abundant nuclei, Mg and Ne, are of key importance together with selected Urca pairs, which reduce the temperature of the core. Shell model rates for -shell nuclei exist since several years [8]. The important capture rate on Mg has been recently updated, mainly due to improved experimental data [11]. The capture rate on Ne has also been updated with, however, two remarkable highlights. First, it has been pointed out that the rate at the relevant astrophysical conditions could be decisively altered due to the influence of the second forbidden transition between the Ne and F ground states [11]. Such a situation is a novum, as the electron capture process is usually dominated by permitted transitions and (first) forbidden transitions are contributed only in high-temperature, high-density environments. The transition was very recently measured in a dedicated experiment [15], and it was indeed confirmed that it increases the capture rate in the astrophysically relevant range by orders of magnitude (Figure 2). The measured transition strength also agrees with the value calculated within the shell model [40]. Secondly, the electron capture rate on Ne at the astrophysical conditions, relevant for the core evolution of intermediate-mass stars, is now completely determined experimentally [15,40]. The improved Ne electron capture rate has interesting consequences for the final core evolution as the faster electron capture supports the ignition of oxygen burning at slightly smaller densities and off-center. Simulations, exploiting the larger rate, indicate that some intermediate-mass stars might explode as thermonuclear rather than electron capture supernovae [40]. Final conclusions can, however, only been drawn after multidimensional simulations of the core evolution with improved treatments of convection becoming available [41,42]. Other nuclei, for which the electron capture rates are dominated by second forbidden transitions under astrophysical conditions, are Na and Al [43]. The latter is expected to play a minor role on the evolution of ONeMg cores. The former may trigger convectional instabilities that again require multidimensional modeling.
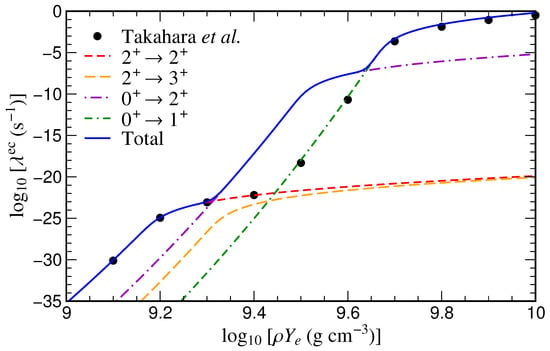
Figure 2.
Electron capture (ec) rate for Ne as function of density and for a specific temperature () relevant for the core evolution of intermediate-mass stars. The rate is broken down to the individual state-by-state contributions. In the density regime, particularly relevant for core evolution, the rate is dominated by the second-forbidden ground-state-to-ground-state transition. The rates labeled ’Takahara et al.’ are derived from allowed transitions calculated in the shell model [44]. Taken from [11].
In the later stage of the collapse of massive stars, the nuclei present in the core composition become heavier and more neutron-rich. The appropriate model space to describe electron capture for such nuclei is too large (requiring two major shells) to allow for shell model diagonalization calculations. The calculations are then based on the SMMC variant of the shell model [7], which allows the determination of nuclear properties at finite temperatures and in large multi-shell model spaces taking the relevant nuclear correlations into account. Such correlations are particularly important for nuclei with proton number below and neutron number, N, above an oscillator shell closure (such as ). In such states, GT transitions would be completely blocked by the Pauli principle in the Independent Particle Model (IPM) [45] suppressing electron capture on nuclei drastically. However, it has been shown in [17,46] that nuclear correlations induced by the residual interaction move nucleons across the shell gap, enabling GT transitions and making electron capture on nuclei the dominating weak interaction process during collapse [17,47]. Let us add two remarks. The unblocking of the GT strength across the shell closure has been experimentally confirmed for Se (with 34 protons and 42 neutrons) [48], in agreement with shell model studies [49]. Furthermore, shell model studies certainly show that the description of cross-shell correlations is a rather slowly converging process that requires the consideration of multi-particle multi-hole configurations [49,50,51].
Recently, it has been pointed out that the shell closure could serve as a severe obstacle for electron capture on the very neutron-rich nuclei encountered in the later stage of the collapse [52]. This finding was apparently confirmed by measurements of the GT strength in the nuclei Kr and Se, which showed basically the vanishing strength for the ground state [53,54]. However, the situation is decisively different at the high temperaures (about 1 MeV) present in the collapsing core when nuclei are abundantly present. Here, thermal excitations mix orbitals across the shell gap and unblock the GT transitions in this way. This was confirmed in two independent calculations for neutron-rich nuclei using a thermal Quasiparticle Random Phase Approximation (QRPA) approach [55,56], in agreement with the earlier results obtained within the SMMC studies [17,57].
Based on the diagonalization shell model and the SMMC results and assuming a nuclear statistical equilibrium distribution for the composition, electron capture rates have been tabulated for the range of astrophysical conditions encountered during collapse of massive stars [57]. These rates consider potential screening effects of the astrophysical surroundings. The rate tabulation of Ref. [57] is now incorporated in many of the leading supernova simulation codes. It turns out that the rates have significant impact on collapse simulations. In the presupernova phase ( g/cm), the captures proceed slower than assumed before, and for a short period during silicon burning, -decays can compete [12,13]. As a consequence, the core is cooler, more massive and less neutron rich before the final collapse. However, for a long time simulations of this final collapse assumed that electron captures on nuclei are prohibited by the Pauli blocking mechanism, as mentioned above (see, e.g., [27]). However, based on the SMMC calculations, it has been shown in [17] that capture on nuclei dominates over capture on free protons. The changes compared to the previous simulations are significant [17,18,19]. Importantly, the shock is now created at a smaller radius with more infalling material to traverse, but the density, temperature and entropy profiles are also strongly modified [18].
Finally, let us note that the shell model electron capture rates [10,58], which are noticeably slower than the pioneering rates of Fuller et al. (FFN) for -shell nuclei [34], have important consequences in nucleosynthesis studies for thermonuclear (type Ia) supernovae assuming the single-degenerate scenario as they result in a smaller reduction in the electron-to-nucleon ratio being the burning front [16]. As a consequence, very neutron-rich nuclei such as Ti and Cr are significantly suppressed compared to calculations, which use FFN rates [59]. In fact, in calculations using the shell-model rates, no nuclide is significantly overproduced compared to solar abundances [16].
2.2. Neutrino–Nucleus Scattering
At sufficiently high densities ( g cm), neutrinos become trapped and thermalized in the collapsing core by coherent scattering on nuclei and inelastic scattering on electrons. It had been suggested that de-excitation of thermally excited nuclei by neutrino pair emission [60] and inelastic neutrino–nucleus scattering [61] might be other modes contributing to neutrino thermalization. Although both processes have been found as rather unimportant cooling mechanisms [47,62], they have interesting impacts elsewhere. Neutrino pair emission has been identified as the major source of neutrino types other than electron neutrinos (produced overwhelmingly by electron capture) [47]. As the consequences of inelastic neutrino scattering are based on shell model calculations, the latter are briefly summarized. The formalism for the calculation of neutrino-nucleus reactions has been introduced in Ref. [63].
Supernova neutrinos have rather low energies (of order 10 MeV). Therefore, inelastic neutrino scattering of such neutrinos is dominated by allowed GT transitions. Unfortunately, no data about inelastic neutrino scattering on nuclei exist at such energies. Due to its success in describing GT (and GT) distributions, one can expect that the shell model will also reproduce the GT component quite well. Nevertheless, a validation of the shell model approach to inelastic neutrino-nucleus scattering is desired. This can be achieved by exploiting the fact that the GT strength is, in a rather good approximation, proportional to the M1 strength of spherical nuclei [64]. In fact, precision M1 data, obtained by inelastic electron scattering for such nuclei, are well reproduced by shell model calculations [64,65]. The same approaches can also be used to derive GT distributions for excited nuclear states, which can be thermally populated at finite supernova conditions [64,66]. At higher neutrino energies, forbidden transitions also contribute to the inelastic scattering cross section, which has been derived by RPA calculations. Supernova simulations that incorporate inelastic neutrino–nucleus scattering indicate that this mode has a noticeable effect on the early neutrino spectra emitted from supernova [62]. Here, nuclei act as obstacles for high-energy neutrinos which are down scattered in energy. This reduces significantly the tail of the neutrino spectra and, hence, also the predicted event rates for the observation of supernova neutrinos by earthbound detectors [62].
Charged-current and neutral-current neutrino–nucleus reactions are key to a specific nucleosynthesis process (called neutrino nucleosynthesis [67]), which are initiated by neutrinos emitted after core bounce in the supernova. Upon passing through the outer layers of the star, these neutrinos excite nuclei above particle thresholds so that the subsequent decay is by particle emission (mainly of protons or neutrons). Neutrino nucleosynthesis has been identified as the main or a strong source for the production of selected isotopes, B and F, from charged- and neutral-current reactions on the abundant isotopes C and Ne; La and Ta mainly by charged-current reactions on Ba and Ta isotopes, which had been previously been produced by the slow neutron-capture process (s-process) [67,68,69,70,71]. The partial neutrino–nucleus cross sections have been obtained by combining shell-model or RPA excitation functions with statistical model decay probabilities [72,73,74]. A particular interest in neutrino nucleosynthesis arises from the fact that the abundances of the produced nuclides depend on the spectra of those neutrino types ( and their antiparticles and ), which have likely not been observed from supernova 1987A.
In principle, neutrino–nucleus reactions also play a role in the process that operates in the neutrino-driven wind during cooling of the newborn proton–neutron star [75,76,77]. Simulations, however, show that the main neutrino reaction is the absorption of on protons that produce a continuous source of free neutrons, which drives the process and allows mass flow through long-lived waiting points such as Ge. The process is discussed as a potential source of isotopes such as Nb and Ru.
3. r-Process Nucleosynthesis
The r-process is the astrophysical origin of about half of the elements heavier than iron [78]. It occurs in an astrophysical environment with extreme neutron densities [79,80]. The r-process site has been a mystery for a long time until the observation of the neutron star merger event GW170817 by gravitational waves and its associated electromagnetic signal proved that heavy elements are produced by neutron star mergers [81,82]. The observed electromagnetic transient, called “kilonova,” agreed well with prior predictions [83].
r-process simulations show that the reaction path in the nuclear chart runs through nuclei with such large neutron excesses that most of them have yet not been made in the laboratory and their properties have to be modeled. The relevant nuclear properties are masses, half lives, fission rates and yields and neutron capture rates [80]. Shell model calculations improved the determination of half lives for the nuclei with magic neutron numbers, which with their relatively long half-lives, act as obstacles in the r-process flow. They have also demonstrated new methods to calculate electromagnetic strength functions and nuclear level densities, which are both required to calculate neutron capture rates within the framework of the statistical model. For a very recent review of the various astronomical, astrophysical, nuclear, and atomic aspects of r-process nucleosynthesis; see Ref. [84].
r-Process nucleosynthesis proceeds by successive neutron captures and beta decays, which increase the mass and charge numbers, respectively. Nuclear half lives decide the time required to produce the heaviest elements, beginning from free protons and neutrons that exist in the hot environment of merging neutron stars before matter is ejected and cooled allowing nuclei to form. Hence, nuclear beta decays compete with the time scales of the dynamical evolution of the ejected matter. There has been important progress made by measuring the half lives of some intermediate-mass nuclei on the r-process path [85,86]. However, most half lives still have to be modeled. Global sets of r-process half lives have been determined by QRPA calculations on the basis of phenomenological parametrizations [87,88] and more recently of microscopic Hartree-Fock-Bogoliubov (HFB) or density functional approaches [89,90,91,92,93].
Particularly important for the r-process mass flow are the waiting point nuclei at the magic neutron numbers N = 50, 82 and 126, which have rather long half lives due to their closed-shell configurations. For these nuclei, large-scale shell model calculations exist. Importantly, a few of these half lives could also been measured, showing good agreement with the shell model results: for Ni, an experiment done at the National Superconducting Cyclotron Laboratory (NSCL) experiment found a half life of ms [94], while the shell model predicted 127 ms [4]. Data and shell model results for the waiting points are compared in Figure 3. Unfortunately, no data exist yet for waiting points. For these nuclei, two independent shell model calculations have pointed to the importance of forbidden transitions induced by intruder states [21,22]. These forbidden transitions are predicted to shorten the half lives of the waiting points noticeably and enhanced the mass flow through these waiting points [95]. This implies more r-process material available for fission, thus affecting the abundances of the second r-process peak around atomic mass number, , which for very neutron-rich ejecta is built up by fission yields [95,96]. The enhanced mass flow also increase late-time -decays from the decaying r-process matter, which influence the kilonova signal [97].
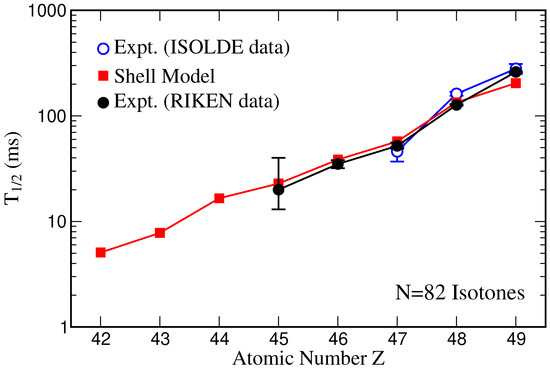
Figure 3.
Comparison of shell model half lives for neutron number r-process (rapid neutron-capture process) waiting point nuclei with data [86,98,99,100]. The GT strengths underlying the shell model results have been quenched with the standard factor of [30]. Taken from [84].
Neutron capture rates become relevant for r-process nucleosynthesis once the process drops out of equilibrium at temperatures below about 1 GK. Neutron capture rates are traditionally derived within the statistical Hauser–Feshbach model, although this approach might not always be justified for r-process nuclei; see discussion and references in [84]. Important ingredients in the Hauser–Feshbach approach are the nuclear level densities and the -strength functions [80]. Shell model calculations have provided a better understanding of both quantities.
A method has been presented to derive level densities within the SMMC approach by exploiting its ability to describe nuclei in extremely large model spaces and to account for the correlations among nucleons [25,26]. The method has been used to explore the effects of parity, angular-momentum and pairing on the level density [101,102,103]. Based on SMMC studies, Alhassid et al. [104] presented an approach in which a microscopically derived parity-dependence is incorporated into phenomenological level density formulas. This approach has been used to derive a large set of r-process nuclei by also employing a temperature-dependent parametrization of the pairing parameter modeled after SMMC calculations [105]. These improved level densities are now part of statistical model packages NON-SMOKER and SMARAGD, developed by Rauscher [106,107,108]. An alternative microscopic approach to level densities, built on the HFB model, has been derived by Goriely and collaborators [109,110,111].
Experimentally determined dipole -strength functions show an upbend of the strength towards low gamma energies [112,113], which can have important impacts on neutron capture rates [23,24,113,114,115,116]. The upbend in the M1 strength has been studied and reproduced in shell model calculations for -shell and heavier nuclei [117,118]. Similar studies have been used to calculate the M1 contribution to the neutron capture rate in a consistent state-by-state approach [119]. This study found that the rate will be dominated by a single resonance if this state happens to fall into the Gamow window of the reaction. Such a situation is difficult to describe within a statistical approach. The calculation also shows that the M1 scissors mode observed in deformed nuclei [120] can lead to a significant enhancement of the capture rate.
4. Summary
Due to the extreme densities, temperatures or neutron excesses encountered in astrophysical environments, the properties of nuclei cannot be measured directly in a laboratory and have to be modeled. If these properties are strongly influenced by nucleon correlations, the diagonalization shell model is the method of choice. In recent years, such studies have been performed to derive the electron capture rates and neutrino-induced cross sections for nuclei in the - and -shell advancing our understanding of the core evolution of intermediate-mass and massive stars. Another important application of the diagonalization shell model was the calculation of half-lives for rapid neutron-capture process (r-process) nuclei with magic neutron numbers, which serve as waiting points for the r-process’ mass flow. This example also shows the limitation of current shell model applications as such studies would be also very desirable for the other nuclei on the r-process path, but cannot be performed yet as the required model spaces exceed current computational possibilities. These limitations in model space can be overcome within the Shell Model Monte Carlo (SMMC) approach, which is an alternative formulation of the shell model. This approach describes nuclear properties at finite temperature, but is not capable of detailed spectroscopy. Thus, the SMMC cannot be used to calculate r-process half-lives, which need a state-by-state description of transition strength. However, the ability of the SMMC approach to describe nuclear properties at finite temperatures including correlations paves the way to determine electron capture rates of heavier nuclei, which are crucial for the fate of core-collapse supernovae. In particular, SMMC allows the evaluation of how the Pauli blocking of Gamow–Teller strength at closed shells is overcome by correlations. On the basis of these studies, it could be demonstrated that neither nor neutron shell closure serve as severe obstacles for electron capture on nuclei. It is now commonly accepted that electron capture proceeds on nuclei throughout the entire collapse.
Author Contributions
Writing—original draft preparation, K.L. and G.M.-P.; writing—review and editing, K.L. and G.M.-P.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), Project-ID 279384907, SFB 1245 Nuclei: From Fundamental Interactions to Structure and Stars, the Helmholtz Forschungsakademie Hessen für FAIR and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (ERC Advanced Grant KILONOVA No. 885281).
Data Availability Statement
Not applicable.
Acknowledgments
The authors are grateful for the long-term collaboration with the members of the Strasbourg-Madrid shell model group. We have learnt a lot from Etienne Caurier, Frederic Nowacki, Alfredo Poves and Andres Zuker. Our work has also benefited strongly from collaborations with many astrophysicists, most notably with Raphael Hix, Hans-Thomas Janka and Friedel Thielemann.
Conflicts of Interest
The authors declare no conflict of interest.
References
- The National Research Council. Nuclear Physics: Exploring the Heart of Matter; The National Academies Press: Washington, DC, USA, 2013; Available online: https://nap.nationalacademies.org/read/13438/ (accessed on 15 May 2022).
- Caurier, E.; Martinez-Pinedo, G.; Nowacki, F.; Poves, A.; Zuker, A.P. The shell model as a unified view of nuclear structure. Rev. Mod. Phys. 2005, 77, 427–488. [Google Scholar] [CrossRef] [Green Version]
- Coraggio, L.; Covello, A.; Gargano, A.; Itaco, N.; Kuo, T.T.S. Shell-model calculations and realistic effective interactions. Prog. Part. Nucl. Phys. 2009, 62, 135–182. [Google Scholar] [CrossRef] [Green Version]
- Langanke, K.; Martínez-Pinedo, G. Nuclear weak-interaction processes in stars. Rev. Mod. Phys. 2003, 75, 819–862. [Google Scholar] [CrossRef] [Green Version]
- Grawe, H.; Langanke, K.; Martinez-Pinedo, G. Nuclear structure and astrophysics. Rep. Prog. Phys. 2007, 70, 1525–1582. [Google Scholar] [CrossRef]
- Johnson, C.W.; Koonin, S.E.; Lang, G.H.; Ormand, W.E. Monte Carlo methods foer the nuclear shell model. Phys. Rev. Lett. 1992, 69, 3157–3160. [Google Scholar] [CrossRef] [Green Version]
- Koonin, S.E.; Dean, D.J.; Langanke, K. Shell model Monte Carlo methods. Phys. Rep. 1997, 278, 1–77. [Google Scholar] [CrossRef] [Green Version]
- Oda, T.; Hino, M.; Muto, K.; Takahara, T.; Sato, K. Rate tables for the weak processes of sd-shell nuclei in stellar matter. At. Data Nucl. Data Tables 1994, 56, 231–403. [Google Scholar] [CrossRef]
- Dean, D.J.; Langanke, K.; Chatterjee, L.; Radha, P.B.; Strayer, M.R. Electron capture on iron group nuclei. Phys. Rev. C 1998, 58, 536–544. [Google Scholar] [CrossRef] [Green Version]
- Langanke, K.; Martinez-Pinedo, G. Rate tables for the weak processes of pf-shell nuclei in stellar environments. At. Data Nucl. Data Tables 2001, 79, 1–46. [Google Scholar] [CrossRef]
- Martínez-Pinedo, G.; Lam, Y.H.; Langanke, K.; Zegers, R.G.T.; Sullivan, C. Astrophysical weak-interaction rates for selected A = 20 and A = 24 nuclei. Phys. Rev. C 2014, 89, 045806. [Google Scholar] [CrossRef] [Green Version]
- Heger, A.; Langanke, K.; Martinez-Pinedo, G.; Woosley, S.E. Presupernova collapse models with improved weak-interaction rates. Phys. Rev. Lett. 2001, 86, 1678–1681. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Heger, A.; Woosley, S.E.; Martinez-Pinedo, G.; Langanke, K. Presupernova evolution with improved rates for weak interactions. Astrophys. J. 2001, 560, 307–325. [Google Scholar] [CrossRef] [Green Version]
- Nomoto, K. Evolution of 8–10 M⊙ stars toward electron capture supernovale: II. Collapse of an O + Ne + Mg core. Astrophys. J. 1987, 322, 206–214. [Google Scholar] [CrossRef]
- Kirsebom, O.S.; Jones, S.; Strömberg, D.F.; Martínez-Pinedo, G.; Langake, K.; Röpke, F.K.; Brown, B.A.; Eronen, T.; Fynbo, H.O.U.; Hukkanen, M.; et al. Discovery of an exceptionally strong β-decay transition of 20F and the fate of intermediate-mass stars. Phys. Rev. Lett. 2019, 123, 262701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brachwitz, F.; Dean, D.J.; Hix, W.R.; Iwamoto, K.; Langanke, K.; Martinez-Pinedo, G.; Nomoto, F.; Strayer, M.R.; Thieleman, F.-K.; Umeda, H. The role of electron captures in Chandrasekhar-mass models for type Ia supernovae. Astrophys. J. 2000, 536, 934–947. [Google Scholar] [CrossRef] [Green Version]
- Langanke, K.; Martínez-Pinedo, G.; Sampaio, J.M.; Dean, D.J.; Hix, W.R.; Messer, O.E.B.; Mezzacappa, A.; Liebendörfer, M.; Janka, H.-T.; Rampp, M. Electron capture rates on nuclei and implications for stellar core collapse. Phys. Rev. Lett. 2003, 90, 241102. [Google Scholar] [CrossRef]
- Hix, W.R.; Messer, O.E.B.; Mezzacappa, A.; Liebendörfer, M.; Sampaio, J.; Langanke, K.; Dean, D.J.; Martínez-Pinedo, G. The consequences of nuclear electron capture in core collapse supernovae. Phys. Rev. Lett. 2003, 91, 210102. [Google Scholar] [CrossRef]
- Janka, H.-T.; Langanke, K.; Marek, A.; Martínez-Pinedo, G.; Mueller, B. Theory of core-collapse supernovae. Phys. Rep. 2007, 442, 38–74. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Pinedo, G.; Langanke, K. Shell-model half-lives for the N = 82 nuclei and their implications for the r-process. Phys. Rev. Lett. 1992, 83, 4502–4505. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, T.; Yoshida, T.; Kajino, T.; Otsuka, T. β decays of isotones with neutron magic number of N = 126 and r-process nucleosynthesis. Phys. Rev. C 2012, 85, 015802. [Google Scholar] [CrossRef] [Green Version]
- Zhi, Q.; Caurier, E.; Cuenca-García, J.J.; Langanke, K.; Martíz-Pinedo, G.; Sieja, K. Shell-model half-lives including first-forbidden contributions for r-process waiting-point nuclei. Phys. Rev. C 2013, 87, 025803. [Google Scholar] [CrossRef]
- Larsen, A.C.; Goriely, S.; Bernstein, L.A.; Bleuel, D.L.; Bracco, A.; Brown, B.A.; Camera, F.; Eriksen, T.K.; Frauendorf, S.; Giacoppo, F.; et al. Upbend and M1 scissors mode in neutron-rich nuclei—Consequences for r-process (n, γ) reaction rates. Acta Phys. Pol. B 2015, 46, 509–512. [Google Scholar] [CrossRef] [Green Version]
- Larsen, A.C.; Spyrou, A.; Liddick, S.N.; Guttormsen, M. Novel techniques for constraining neutron-capture rates relevant for r-process heavy-element nucleosynthesis. Prog. Part. Nucl. Phys. 2019, 107, 69–108. [Google Scholar] [CrossRef] [Green Version]
- Nakada, H.; Alhassid, Y. Total and parity-projected level densities of iron-region nuclei in the auxiliary fields Monte Carlo shell model. Phys. Rev. Lett. 1997, 79, 2939–2942. [Google Scholar] [CrossRef] [Green Version]
- Langanke, K. Shell model Monte Carlo level densities for nuclei around A ∼ 50. Phys. Lett. 1998, 438, 235–241. [Google Scholar] [CrossRef]
- Bethe, H.A. Supernova mechanisms. Rev. Mod. Phys. 1990, 62, 801–867. [Google Scholar] [CrossRef]
- Bethe, H.A.; Brown, G.E.; Applegate, J.; Lattimer, J.M. Equation of state in the gravitational collapse of stars. Nucl. Phys. A 1979, 324, 487–533. [Google Scholar] [CrossRef]
- Langanke, K.; Dean, D.J.; Radha, P.B.; Alhassid, Y.; Koonin, S.E. Shell model Monte Carlo studies of fp-shell nuclei. Phys. Rev. C 1995, 52, 718–725. [Google Scholar] [CrossRef] [Green Version]
- Martínez-Pinedo, G.; Poves, A.; Caurier, E.; Zuker, A.P. Effective gA in the pf-shell. Phys. Rev. C 1996, 53, R2602–R2605. [Google Scholar] [CrossRef] [Green Version]
- Caurier, E.; Langanke, K.; Martínez-Pinedo, G.; Nowacki, F. Shell-Model calculations of stellar weak interaction rates. I. Gamow-Teller distributions and spectra of nuclei in the mass range A = 45 − 65. Nucl. Phys. A 1999, 653, 439–452. [Google Scholar] [CrossRef] [Green Version]
- Vetterli, M.C.; Jackson, K.P.; Celler, A.; Engel, J.; Yen, S. The 70,72Ge(n, p)70,72Ga reactions: Suppression of Gamow–Teller strength near N = 40. Phys. Rev. C 1992, 45, 997–1004. [Google Scholar] [CrossRef] [PubMed]
- Frekers, D.; Alanssari, M. Charge-exchange reactions and the quest for resolution. Eur. Phys. J. A 2018, 54, 177. [Google Scholar] [CrossRef]
- Fuller, G.M.; Fowler, W.A.; Newman, M.J. Stellar weak-interaction rates for sd-shell nuclei. I. Nuclear matrix element systematics with application to 26Al and selected nuclei of importance to the supernova problem. Astrophys. J. Suppl. Ser. 1980, 42, 447–473. [Google Scholar] [CrossRef] [Green Version]
- Fuller, G.M.; Fowler, W.A.; Newman, M.J. Stellar weak interaction rates for intermediate mass nuclei. III. Rate tables for the free nucleons and nuclei with A = 21 to A = 60. Astrophys. J. Suppl. Ser. 1982, 48, 279–320. [Google Scholar] [CrossRef]
- Cole, A.L.; Anderson, T.S.; Zegers, R.G.T.; Sam, M.; Austin, B.; Brown, A.; Valdez, L.; Gupta, S.; Hitt, G.W.; Fawwaz, O. Gamow–Teller strengths and electron-capture rates for pf-shell nuclei of relevance for late stellar evolution. Phys. Rev. C. 2012, 86, 015809. [Google Scholar] [CrossRef] [Green Version]
- Poves, A.; Sánchez-Solano, J.; Caurier, E.; Nowacki, F. Shell model study of the isobaric chains A = 50, A = 51 and A = 52. Nucl. Phys. A. 2001, 694, 157–198. [Google Scholar] [CrossRef] [Green Version]
- Honma, M.; Otsuka, T.; Brown, B.A.; Mizusaki, T. New effective interaction for pf-shell nuclei and its implications for the stability of the N = Z = 28 closed core. Phys. Rev. C 2004, 69, 034335. [Google Scholar] [CrossRef] [Green Version]
- Langanke, K.; Martinez-Pinedo, G.; Zegers, R.M.T. Stellar electron capture. Rep. Prog. Phys. 2021, 84, 066301. [Google Scholar] [CrossRef]
- Kirsebom, O.S.; Hukkanen, M.; Kankainen, A.; Trzaska, W.H.; Ströberg, D.F.; Martínz-Pinedo, G.; Andersen, K.; Bodewits, E.; Canete, L.; Cederkäl, J. Measurement of the 2+→0+ ground-state transition in the β decay of 20F. Phys. Rev. C 2019, 100, 065805. [Google Scholar] [CrossRef] [Green Version]
- Jones, S.; Röpke, F.K.; Pakmor, R.; Seitenzahl, I.R.; Ohlmann, S.T.; Edelmann, P.V.F. Do electron-capture supernovae make neutron stars? First multidimensional hydrodynamic simulations of the oxygen deflagration. Astron. Astrophys. 2016, 593, A72. [Google Scholar] [CrossRef]
- Zha, S.; Leung, S.C.; Suzuki, T.; Nomoto, K. Evolution of ONeMg core in super-AGB stars toward electron-capture supernovae: Effects of updated electron-capture rate. Astrophys. J. 2019, 886, 22. [Google Scholar] [CrossRef]
- Strömberg, D.F.; Martínez-Pinedo, G.; Nowacki, F. Forbidden electron capture on 24Na and 27Al in degenerate oxygen-neon stellar cores. Phys. Rev. C 2022, 105, 025803. [Google Scholar] [CrossRef]
- Takahara, M.; Hino, M.; Oda, T.; Muto, K.; Wolters, A.A.; Glaudemans, P.W.M.; Sato, K. Microscopic calculation of the rates of electron captures which induce the collapse of the O+Ne+Mg cores. Nucl. Phys. A 1989, 504, 167–192. [Google Scholar] [CrossRef]
- Fuller, G.M. Neutron shell blocking of electron capture during gravitational collapse. Astrophys. J. 1982, 252, 741–764. [Google Scholar] [CrossRef]
- Langanke, K.; Kolbe, E.; Dean, D.J. Unblocking of the Gamow–Teller strength in stellar electron capture on neutron-rich germanium isotopes. Phys. Rev. C 2001, 63, 032801(R). [Google Scholar] [CrossRef] [Green Version]
- Fischer, T.; Langanke, K.; Martínez-Pinedo, G. Neutrino-pair emission from nuclear de-excitation in core-collapse supernova simulations. Phys. Rev. C 2013, 88, 065804. [Google Scholar] [CrossRef] [Green Version]
- Grewe, E.-W.; Bäumer, C.; Dohmann, H.; Frekers, D.; Harakeh, M.N.; Hollstein, S.; Johansson, H.; Popescu, L.; Rakers, S.; Savran, D.; et al. The (d,2He) reaction on 76Se and the double-β-decay matrix elements for A = 76. Phys. Rev. C 2008, 78, 044301. [Google Scholar] [CrossRef]
- Zhi, Q.; Langanke, K.; Martínez-Pinedo, G.; Nowacki, F.; Sieja, K. The 76Se Gamow–Teller strength distribution and its importance for stellar electron capture rates. Nucl. Phys. A 2011, 859, 172–184. [Google Scholar] [CrossRef]
- Dean, D.J.; Ressell, M.T.; Hjorth-Jensen, M.; Koonin, S.E.; Langake, K.; Zuker, A.P. Shell-model Monte Carlo studies of neutron-rich nuclei in the 1s-0d-1p-0f shells. Phys. Rev. C 1999, 59, 2474–2486. [Google Scholar] [CrossRef] [Green Version]
- Caurier, E.; Langanke, K.; Martínez-Pinedo, G.; Nowacki, F.; Vogel, P. Shell model description of isotope shifts in calcium. Phys. Lett. B 2001, 522, 240–244. [Google Scholar] [CrossRef] [Green Version]
- Sullivan, C.; Connor, E.O.; Zegers, R.G.T.; Grubb, T.; Austin, S.M. The sensitivity of core-collapse supernovae to nuclear electron capture. Astrophys. J. 2016, 816, 44. [Google Scholar] [CrossRef]
- Titus, R.; Ney, E.M.; Zegers, R.G.T.; Bazin, D.; Belarge, J.; Bender, P.C.; Brown, B.A.; Campbell, C.M.; Elman, B.; Engel, J.; et al. Constraints for stellar electron-capture rates on 86Kr via the 86Kr(t,3He + γ)86Br reaction and the implications for core-collapse supernovae. Phys. Rev. C 2019, 100, 045805. [Google Scholar] [CrossRef] [Green Version]
- Zamora, J.C.; Zegers, R.G.T.; Austin, S.M.; Bazin, D.; Brown, B.A.; Bender, P.C.; Crawford, H.L.; Engel, J.; Falduto, A.; Gade, A.; et al. Experimental constraint on stellar electron-capture rates from the 88Sr(t,3He + γ)88Rb reaction at 115 MeV/u. Phys. Rev. C 2019, 100, 032801. [Google Scholar] [CrossRef] [Green Version]
- Dzhioev, A.A.; Langanke, K.; Martínez-Pinedo, G.; Vdovin, A.I.; Stoyanov, C. Unblocking of stellar electron captures for neutron-rich N = 50 nuclei at finite temperatures. Phys. Rev. C 2020, 101, 025805. [Google Scholar] [CrossRef] [Green Version]
- Litvinova, E.; Robin, C. Impact of complex many-body correlations on electron capture in thermally excited nuclei around 78Ni. Phys. Rev. C 2021, 103, 024326. [Google Scholar] [CrossRef]
- Juodagalvis, A.; Langanke, K.; Hix, W.R.; Martínez-Pinedo, G.; Sampaio, J.M. Improved estimate of stellar electron capture rates on nuclei. Nucl. Phys. A 2010, 848, 454–478. [Google Scholar] [CrossRef] [Green Version]
- Langanke, K.; Martínez-Pinedo, G. Shell-model calculations of stellar weak interaction rates: II. Weak rates for nuclei in the mass range A = 45 − 65 in supernovae environments. Nucl. Phys. A 2000, 673, 481–508. [Google Scholar] [CrossRef] [Green Version]
- Iwamoto, K.; Brachwitz, F.; Nomoto, K.; Kishimoto, N.; Umeda, H.; Hix, W.R.; Thielemann, F.-K. Nucleosynthesis in Chandrasekhar mass models for type Ia supernovae and constraints on progenitor systems and burning-front propagation. Astrophys. J. Suppl. Ser. 1999, 125, 439–462. [Google Scholar] [CrossRef]
- Fuller, G.M.; Meyer, B.S. High-temperature neutrino-nucleus processes in stellar collapse. Astrophys. J. 1991, 376, 701–716. [Google Scholar] [CrossRef] [Green Version]
- Bruenn, S.W.; Haxton, W.C. Neutrino-nucleus interactions in core-collapse supernovae. Astrophys. J. 1991, 376, 678–700. [Google Scholar] [CrossRef]
- Langanke, K.; Martínez-Pinedo, G.; Müller, B.; Janka, H.-T.; Marek, A.; Hix, W.R.; Juodagalvis, A.; Sampaio, J.M. Effects of inelastic neutrino-nucleus scattering on supernova dynamics and radiated neutrino spectra. Phys. Rev. Lett. 2008, 100, 011101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donnelly, T.W.; Peccei, R.D. Neutral current effects in nuclei. Phys. Rep. 1979, 50, 1–85. [Google Scholar] [CrossRef]
- Langanke, K.; Martinez-Pinedo, G.; von Neumann-Cosel, P.; Richter, A. Supernova inelastic neutrino-nucleus cross sections from high-resolution electron scattering experiments and shell-model calculations". Phys. Rev. Lett. 2004, 93, 202501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Von Neumann-Cosel, P.; Poves, A.; Retamosa, J.; Richter, A. Magnetic dipole response in nuclei at the N = 28 shell closure: A new look. Phys. Lett. B 1998, 443, 1–6. [Google Scholar] [CrossRef]
- Juodagalvis, A.; Langanke, K.; Martínez-Pinedo, G.; Hix, W.R.; Dean, D.J.; Sampaioc, J.M. Neutral-current neutrino-nucleus cross sections for A ∼ 50–65 nuclei. Nucl. Phys. A 2005, 747, 87–108. [Google Scholar] [CrossRef] [Green Version]
- Woosley, S.E.; Hartmann, D.H.; Hofmann, R.D.; Haxton, W.C. The ν-process. Astrophys. J. 1990, 356, 272–301. [Google Scholar] [CrossRef]
- Heger, A.; Kolbe, E.; Haxton, W.C.; Langanke, K.; Martínez-Pinedo, G.; Woosley, S.E. Neutrino nucleosynthesis. Phys. Lett. B 2005, 606, 258–264. [Google Scholar] [CrossRef] [Green Version]
- Byelikov, A.; Adachi, T.; Fujita, H.; Fujita, K.; Fujita, Y.; Hatanaka, K.; Heger, A.; Kalmykov, Y.; Kawase, K.; Langanke, K. Gamov–Teller strength in the exotic, odd-odd nuclei 138La and 180Ta and its relevance for neutrino nucleosynthesis. Phys. Rev. Lett. 2007, 98, 082501. [Google Scholar] [CrossRef]
- Sieverding, A.; Martínez-Pinedo, G.; Huther, L.; Langanke, K.; Heger, A. The ν-process in the light of an improved understanding of supernova neutrino spectra. Astrophys. J. 2018, 865, 143. [Google Scholar] [CrossRef] [Green Version]
- Sieverding, A.; Langanke, K.; Martínez-Pinedo, G.; Bollig, R.; Janka, H.-T.; Heger, A. The ν-process with fully time-dependent supernova neutrino emission spectra. Astrophys. J. 2019, 876, 151. [Google Scholar] [CrossRef] [Green Version]
- Kolbe, E.; Langanke, K.; Thielemann, F.-K.; Vogel, P. Inclusive 12C(νμ, μ)12N reaction in the continuum random phase approximation. Phys. Rev C 1995, 52, 3437–3441. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kolbe, E.; Langanke, K.; Martínez-Pinedo, G.; Vogel, P. Neutrino–nucleus reactions and nuclear structure. J. Phys. G Nucl. Part. Phys. 2003, 29, 2569–2596. [Google Scholar] [CrossRef] [Green Version]
- Balasi, K.G.; Langanke, K.; Martínez-Pinedo, G. Neutrino–nucleus reactions and their role for supernova dynamics and nucleosynthesis. Prog. Part. Nucl. Phys. 2015, 85, 33–81. [Google Scholar] [CrossRef] [Green Version]
- Fröhlich, C.; Martínez-Pinedo, G.; Liebendörfer, M.; Thielemann, F.-K.; Bravo, E.; Hix, W.R.; Langanke, K.; Zinner, N.T. Neutrino-induced nucleosynthesis of A > 64 nuclei: The νp-process. Phys. Rev. Lett. 2006, 96, 142502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pruet, J.; Woosley, S.E.; Buras, R.; Janka, H.-T.; Hoffman, R.D. Nucleosynthesis in the hot convective bubble in core-collapse supernovae. Astrophys. J. 2006, 623, 325–336. [Google Scholar] [CrossRef] [Green Version]
- Wanajo, S. The rp-process in neutrino-driven winds. Astrophys. J. 2006, 647, 1323–1340. [Google Scholar] [CrossRef] [Green Version]
- Burbidge, E.M.; Burbidge, G.R.; Fowler, W.A.; Hoyle, F. Synthesis of the elements in stars. Rev. Mod. Phys. 1957, 29, 547–650. [Google Scholar] [CrossRef] [Green Version]
- Thielemann, F.-K.; Arcones, A.; Käppeli, R.; Liebendörfer, M.; Rauscher, T.; Winteler, C.; Fröhlich, C.; Dillmann, I.; Fischer, T.; Martinez-Pinedo, G.; et al. What are the astrophysical sites for the r-process and the production of heavy elements? Prog. Part. Nucl. Phys. 2011, 66, 346–353. [Google Scholar] [CrossRef]
- Cowan, J.J.; Thielemann, F.-K.; Truran, J.W. The R-process and nucleochronology. Phys. Rep. 1991, 208, 267–394. [Google Scholar] [CrossRef]
- Abbot, B.P.; et al. [LIGO Scientific Collaboration and Virgo Collaboration; Fermi GBM; INTEGRAL; IceCube Collaboration; AstroSat Cadmium ZincTelluride Imager Team; IPN Collaboration; The Insight-HXMT Collaboration; ANTARES Collaboration; The Swift Collaboration; AGILE Team; The 1M2H Team; The Dark Energy Camera GW-EM Collaboration and the DES Collaboration; The DLT40 Collaboration, GRAWITA: GRAvitational Wave Inaf TeAm; The Fermi Large Area Telescope Collaboration; ATCA: Australia Telescope CompactArray; ASKAP: Australian SKA Pathfinder; Las Cumbres Observatory Group; OzGrav; DWF(Deeper, Wider, Faster Program); AST3, and CAASTRO Collaborations; The VINROUGE Collaboration; MASTER Collaboration; J-GEM, GROWTH, JAGWAR, Caltech-NRAO, TTU-NRAO, and NuSTAR Collaborations; Pan-STARRS; TheMAXITeam; TZACConsortium; KU Collaboration; NordicOptical Telescope; ePESSTO; GROND; Texas Tech University; SALT Group; TOROS: Transient Robotic Observatory of the SouthCollaboration; The BOOTES Collaboration; MWA: Murchison Widefield Array; The CALET Collaboration; IKI-GW Follow-upCollaboration; H.E.S.S. Collaboration; LOFAR Collaboration; LWA: Long Wavelength Array; HAWC Collaboration; The Pierre Auger Collaboration; ALMA Collaboration; Euro VLBI Team; Pi of the Sky Collaboration; The Chandra Team at McGill University; DFN:Desert Fireball Network; ATLAS; High Time Resolution Universe Survey; RIMAS and RATIR; SKA South Africa/MeerKAT] Multi-messenger observations of a binary neutron star merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Cowperthwaite, P.S.; Berger, E.; Villar, V.A.; Metzger, B.D.; Nicholl, M.; Chornock, R.; Blanchard, P.K.; Fong, W.; Margutti, R.; Soares-Santos, M.; et al. The electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. II. UV, optical, and near-infrared light curves and comparison to kilonova models. Astrophys. J. Lett. 2017, 848, L17. [Google Scholar] [CrossRef]
- Metzger, B.D.; Martńez-Pinedo, G.; Darbha, S.; Quataert, E.; Arcones, A.; Kasen, D.; Thomas, R.; Nugent, P.; Panov, I.V.; Zinner, N.T. Electromagnetic counterparts of compact object mergers powered by the radioactive decay of r-process nuclei. Mon. Not. R. Astron. Soc. 2010, 406, 2650–2662. [Google Scholar] [CrossRef]
- Cowan, J.J.; Sneden, C.; Lawler, J.E.; Aprahamian, A.; Wiescher, M.; Langake, K.; Martínez-Pinedo, G.; Thielemann, F.-K. Origin of the heaviest elements: The rapid neutron-capture process. Process. Rev. Mod. Phys. 2021, 93, 015002. [Google Scholar] [CrossRef]
- Wu, J.; Nishimura, S.; Lorusso, G.; Möller, P.; Ideguchi, E.; Regan, P.-H.; Simpson, G.S.; Söderström, P.A.; Waller, P.M.; Watanable, H.; et al. 94 β-decay half-lives of neutron-rich 55Cs to 67Ho: Experimental feedback and evaluation of the r-process rare-earth peak formation. Phys. Rev. Lett. 2017, 118, 072701. [Google Scholar]
- Lorusso, G.; Nishimura, S.; Xu, Z.Y.; Jungclaus, A.; Shimizu, Y.; Simpson, G.S.; Söderström, P.-A.; Watanabe, H.; Browne, F.; Doornenbal, P.; et al. β-decay half-lives of 110 neutron-rich nuclei across the N = 82 shell gap: Implications for the mechanism and universality of the astrophysical r process. Phys. Rev. Lett. 2015, 114, 192501. [Google Scholar] [CrossRef] [Green Version]
- Möller, P.; Nix, J.R.; Kratz, K.-L. Nuclear properties for astrophysical and radioactive-ion-beam applications. At. Nucl. Data Tables 1997, 66, 131–343. [Google Scholar] [CrossRef] [Green Version]
- Borzov, I.N.; Goriely, S. Weak interaction rates of neutron-rich nuclei and the r-process nucleosynthesis. Phys. Rev. C 2000, 62, 035501. [Google Scholar] [CrossRef]
- Borzov, I.N. Gamow–Teller and first-forbidden decays near the r-process paths at N = 50, 82, and 126. Phys. Rev. C 2003, 67, 025802. [Google Scholar] [CrossRef]
- Marketin, T.; Huther, L.; Martinez-Pinedo, G. Large-scale evaluation of β-decay rates of r-process nuclei with the inclusion of first-forbidden transitions. Phys. Rev. C 2016, 93, 025805. [Google Scholar] [CrossRef] [Green Version]
- Mustonen, M.T.; Engel, G. Global description of β− decay in even-even nuclei with the axially-deformed Skyrme finite-amplitude method. Phys. Rev. C 2016, 93, 014304. [Google Scholar] [CrossRef] [Green Version]
- Shafer, T.; Engel, J.; Frölich, C.; Mclaughlin, G.C.; Mumpower, M.; Surman, R. β decay of deformed r-process nuclei near A = 80 and A = 160, including odd-A and odd-odd nuclei, with the Skyrme finite-amplitude method. Phys. Rev. C 2016, 94, 055802. [Google Scholar] [CrossRef] [Green Version]
- Ney, E.M.; Engel, J.; Li, T.; Schunck, N. Global description of β− decay with the axially deformed Skyrme finite-amplitude method: Extension to odd-mass and odd-odd nuclei. Phys. Rev. C 2020, 102, 034326. [Google Scholar] [CrossRef]
- Hosmer, P.T.; Schatz, H.; Aprahamian, A.; Arndt, O.; Clement, R.R.C.; Estrade, A.; Kratz, K.-L.; Liddick, S.N.; Mantica, P.F.; Mueller, W.F.; et al. Half-life of the doubly magic r-process nucleus 78Ni. Phys. Rev. Lett. 2005, 94, 112501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Jesús Mendoza-Temis, J.; Wu, M.-R.; Langanke, K.; Martínez-Pinedo, G.; Bauswein, A.; Janka, H.-T. Nuclear robustness of the r process in neutron-star mergers. Phys. Rev. C 2015, 92, 055805. [Google Scholar] [CrossRef] [Green Version]
- Petermann, I.; Langanke, K.; Martínez-Pinedo, G.; Panov, I.V.; Reinhard, P.-G.; Thielemann, F.-K. Have superheavy elements been produced in nature? Eur. Phys. J. A 2012, 48, 122. [Google Scholar] [CrossRef] [Green Version]
- Wu, M.-R.; Barnes, J.; Martínez-Pinedo, G.; Metzger, B.D. Fingerprints of heavy-element nucleosynthesis in the late-time lightcurves of kilonovae. Phys. Rev. Lett. 2019, 122, 062701. [Google Scholar] [CrossRef] [Green Version]
- Pfeiffer, B.; Kratz, K.-L.; Thielemann, F.-K.; Walters, W.B. Nuclear structure studies for the astrophysical r-process. Nucl. Phys. A 2001, 693, 282–324. [Google Scholar] [CrossRef]
- Dillmann, I.; Kratz, K.-L.; Wöhr, A.; Arndt, O.; Brown, B.A.; Hoff, P.; Hjorth-Jensen, M.; Köster, U.; Ostrowski, A.N.; Pfeiffer, D.; et al. N = 82 shell quenching of the classical r-process "waiting-point" nucleus 130Cd. Phys. Rev. Lett. 2003, 91, 162503. [Google Scholar] [CrossRef] [Green Version]
- Fogelberg, B.; Gausemel, H.; Mezilev, K.A.; Hoff, P.; Mach, H.; Sanchez-Vega, M.; Lindroth, A.; Ramström, E.; Genevey, J.; Pinston, J.A.; et al. Decays of 131In, 131Sn, and the position of the h11/2 neutron hole state. Phys. Rev. C 2004, 70, 034312. [Google Scholar] [CrossRef]
- Alhassid, Y.; Liu, S.; Nakada, H. Particle-number reprojection in the shell model Monte Carlo method: Application to nuclear level densities. Phys. Rev. Lett. 1999, 83, 4265–4268. [Google Scholar] [CrossRef] [Green Version]
- Alhassid, Y.; Liu, S.; Nakada, H. Spin projection in the shell model Monte Carlo method and the spin distribution of nuclear level densities. Phys. Rev. Lett. 2007, 99, 162504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Langanke, K. Shell Model Monte Carlo studies of pairing correlations and level densities in medium-mass nuclei. Nucl. Phys. A 2006, 778, 233–246. [Google Scholar] [CrossRef]
- Alhassid, Y.; Bertsch, G.F.; Liu, S.; Nakada, H. Parity dependence of nuclear level densities. Phys. Rev. Lett. 2000, 84, 4313–4316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mocelj, D.; Rauscher, T.; Martínez-Pinedo, G.; Langanke, K.; Pacearescu, L.; Faessler, A.; Thielemann, F.-K.; Alhassid, Y. Large-scale prediction of the parity distribution in the nuclear level density and application to astrophysical reaction rates. Phys. Rev. C 2007, 75, 045805. [Google Scholar] [CrossRef] [Green Version]
- Rauscher, T.; Thielemann, F.-K. Astrophysical reaction rates from statistical model calculations. At. Nucl. Data Tables 2000, 75, 1–351. [Google Scholar] [CrossRef] [Green Version]
- Rauscher, T.; Thielemann, F.-K. Tables of nuclear cross sections and reaction rates: An addendum to the paper “Astrophysical reaction rates from statistical model calculations”. At. Nucl. Data Tables 2001, 79, 47–64. [Google Scholar] [CrossRef] [Green Version]
- Rauscher, T. The path to improved reaction rates for astrophysics. Int. J. Mod. Phys. E 2011, 20, 1071–1169. [Google Scholar] [CrossRef] [Green Version]
- Goriely, S.; Hilaire, S.; Koning, A.J. Improved microscopic nuclear level densities within the Hartree-Fock-Bogoliubov plus combinatorial method. Phys. Rev. C 2008, 78, 064307. [Google Scholar] [CrossRef]
- Koning, A.J.; Hilaire, S.; Goriely, S. Global and local level density models. Nucl. Phys. A 2008, 810, 13–76. [Google Scholar] [CrossRef]
- Goriely, S.; Hilaire, S.; Girod, M. Latest development of the combinatorial model of nuclear level densities. J. Phys. Conf. Ser. 2012, 337, 012027. [Google Scholar] [CrossRef] [Green Version]
- Guttormsen, M.; Chankova, R.; Agvaanluvsan, U.; Algin, E.; Bernstein, L.A.; Ingebretsen, F.; Lönnroth, T.; Messelt, S.; Mitchell, G.E.; Rekstad, J.; et al. Radiative strength functions in 93–98Mo. Phys. Rev. C 2005, 71, 044307. [Google Scholar] [CrossRef] [Green Version]
- Larsen, A.C.; Chankova, R.; Guttormsen, M.; Ingebretsen, F.; Messelt, S.; Rekstad, J.; Siem, S.; Syed, N.U.H.; Øegård, S.W.; Lönnroth, T.; et al. Microcanonical entropies and radiative strength functions of 50,51V. Phys. Rev. C 2006, 73, 064301. [Google Scholar] [CrossRef] [Green Version]
- Goriely, S. Radiative neutron captures by neutron-rich nuclei and the r-process nucleosynthesis. Phys. Lett. B 1998, 436, 10–18. [Google Scholar] [CrossRef]
- Larsen, A.C.; Goriely, S. Impact of a low-energy enhancement in the γ-ray strength function on the neutron-capture cross section. Phys. Rev. C 2010, 82, 014318. [Google Scholar] [CrossRef] [Green Version]
- Litvinova, E.; Ring, P.; Tselyaev, V.; Langanke, K. Relativistic quasiparticle time blocking approximation. II. Pygmy dipole resonance in neutron-rich nuclei. Phys. Rev. C 2009, 79, 054312. [Google Scholar] [CrossRef] [Green Version]
- Sieja, K. Electric and magnetic dipole strength at low energy. Phys. Rev. Lett. 2017, 119, 052502. [Google Scholar] [CrossRef]
- Sieja, K. Shell-model study of the M1 dipole strength at low energy in the A > 100 nuclei. Phys. Rev. C 2018, 98, 064312. [Google Scholar] [CrossRef]
- Loens, H.P.; Langanke, K.; Martínez-Pinedo, G.; Sieja, K. M1 strength functions from large-scale shell model calculations and their effect on astrophysical neutron capture cross-sections. Eur. Phys. J. A 2012, 48, 34. [Google Scholar] [CrossRef]
- Bohle, D.; Richter, A.; Steffen, W.; Dieperink, A.E.L.; Lo Ludice, N.; Palumbo, F.; Scholten, O. New magnetic dipole excitation mode studied in the heavy deformed nucleus 156Gd by inelastic electron scattering. Phys. Lett. 1984, 137, 27–31. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).