Abstract
The basic characteristics of cylindrical as well as spherical solitary and shock waves in degenerate electron-nucleus plasmas are theoretically investigated. The electron species is assumed to be cold, ultra-relativistically degenerate, negatively charged gas, whereas the nucleus species is considered a cold, non-degenerate, positively charged, viscous fluid. The reductive perturbation technique is utilized in order to reduce the basic equations (governing the degenerate electron-nucleus plasmas under consideration) to the modified Korteweg-de Vries and Burgers equations. The latter are numerically solved and analyzed to detect the basic characteristics of solitary and shock waves in such electron-nucleus plasmas. The nonlinear nucleus-acoustic waves are found to be propagated in the form of solitary as well as shock waves in such degenerate electron-nucleus plasmas. Their basic properties as well as their time evolution are significantly modified by the effects of cylindrical as well as spherical geometries. The results of this study is expected to be applicable not only to astrophysical compact objects, but also to ultra-cold dense plasmas produced in laboratory.
1. Introduction
Recently, Mamun, Amina and Schlickeiser [1,2] have first used the name “nucleus-acoustic (NA) waves” for the study of NA shock waves in strongly coupled degenerate plasmas [1] as well as NA solitary waves in self-gravitating degenerate plasmas [2]. The NA waves (NAWs) are degenerate pressure driven acoustic type of waves. They are completely new since they exist in degenerate plasmas at absolute zero temperature, but they do not exist in non-degenerate plasmas at either absolute zero or finite temperature. The degenerate plasmas [3,4,5] containing negatively charged degenerate electron gas and positively charged nucleus or ion fluid have important applications not only in astrophysical compact objects [3,4,5,6,7], but also in ultra-cold dense plasmas produced in laboratory devices [8,9,10,11,12]. The degenerate electron gas is formed by increasing its pressure more and more so that it cannot be compressed anymore due to Pauli’s exclusion principle. This implies that there is no extra space in electron gas for more electrons to exist, and as a result, the space among electrons is infinitesimally small. This corresponds to an extremely high density electron gas with and , where and are the uncertainties in position and momentum, respectively. This generates an extremely high pressure because of Heisenberg’s uncertainty principle, , where ℏ is the reduced Planck constant. This pressure is called the electron degenerate pressure [3,4,5,6]. The latter is the function of only number density of the degenerate electron gas.
The electron degenerate pressure can be expressed as [3,4,5,6,13]
where is the number density of the degenerate electron gas, represents and represents at equilibrium, and are, respectively, for non-relativistically and cold ultra-relativistically degenerate electron (CUDE) gas, according to Chandrasekhar [3,4,5]. However, the CUDE pressure () is of the present interest. The CUDE pressures [5,6,13], and can, respectively, be expressed as
where , and c is the speed of light in vacuum. It is clear that the CUDE pressure depends only on and on its equilibrium value, .
On the basis of Mamun, Amina and Schlickeiser [1,2], a number of theoretical investigations [14,15,16,17,18,19,20,21,22] on nonlinear NAWs in degenerate quantum plasmas under different situations have been made during the last five years. However, in these studies the length scale, phase speed and dispersion properties of the NAWs are not defined. The dependent as well as independent variables are also not properly normalized. There are also some studies [13,14,22], where “ion-acoustic (IA) waves (IAWs)” are used instead of the NAWs. This is not correct, since at absolute zero temperature the degenerate electron gas does not allow the IAWs to exist, but does allow the NAWs to exist. This fact along with the concept of the IAWs [23,24] have lead Mamun [25] to introduce proper length scale as well as time scale of the NAWs for the study of the linear propagation of the latter. The linear dispersion relation for the NAWs [25], propagating in cold degenerate electron-nucleus plasmas (CDENPs), is given by
where is the angular frequency and k is the propagation constant of the NAWs; and are, respectively, the length scale and the time scale (inverse of the nucleus plasma frequency) of the NAWs; is the speed of the NAWs, in which is the nucleus mass density, is the equilibrium nucleus number density, and m () is the mass (charge state) of the nucleus species, and e is the charge of the proton.
The dispersion relation defined by Equation (4) for the long wavelength NAWs () becomes . There is an important issue on the basic differences between IAWs and NAWs since the form of their dispersion relations are identical. Their basic differences can be pinpointed as follows:
- The IAWs are driven by the electron thermal pressure depending on the electron temperature and number density, whereas the NAWs are driven by the electron degenerate pressure depending only on the electron number density.
- The non-degenerate plasmas at finite temperature allow the IAWs to exist, but do not allow the NAWs to exist.
- The degenerate plasmas at absolute zero temperature do not allow the IAWs to exist, but do allow the NAWs to exist.
- The NAWs and IAWs are completely different from the view of their length scale and phase speed.
The present paper is attempted to study the basic characteristics of cylindrical as well as spherical solitary and shock waves associated with the NAWs (defined by Equation (4)) in the CDENPs under consideration. The paper is structured as follows. The normalized basic equations describing the nonlinear dynamics of the NAWs in the CDENPs under consideration are provided in Section 2. To study cylindrical and spherical solitary waves, a modified Korteweg-de Vries (MK-dV) equation is obtained and properly examined in Section 3. To identify the basic features of the cylindrical and spherical shock waves, a modified Burgers (MBurgers) equation is also obtained and critically examined in Section 4. A brief discussion is given in Section 5.
2. Basic Equations
The CDENPs containing the CUDE gas [3,4,5,6,26,27] and the cold viscous fluid of any nucleus like or [3,4,5] or or or [6,26,27] are considered. The macroscopic state of such CDENPs is described in nonplanar geometry as
where and represent the cylindrical and spherical geometries, respectivel, is the nucleus fluid number density; is the nucleus fluid speed, is the electrostatic potential, m and are, respectively, the mass and charge of the nucleus species, T and R are the time and space variables, respectively, and is the coefficient of dynamic viscosity for the cold nucleus fluid. To note is that in Equation (5), the inertia of the CUDE gas is negligible compared to that of the viscous nucleus fluid, and that in Equation (7) the effects of the self-gravitational field and nucleus degeneracy are negligible in comparison with those of the electrostatic field and electron degeneracy, respectively.
To describe the equilibrium state of the CDENPs under consideration, it is reasonably assumed that , , and at equilibrium. Thus, the equilibrium state of the CDENPs under consideration is described by
where Equation (9) represents the equilibrium charge neutrality condition, and in Equation (10), is the integration constant, given by Equation (3).
To find the expression for the normalized ultra-relativistically degenerate electron number density in terms of the normalized electrostatic potential, , first, substitute Equation (2) and (where r is the normalized space variable) into Equation (5). Thus, Equation (5) reduces to
Next, integrating Equation (11), and obtaining the integration constant as 3 (since and at equilibrium), can finally be expressed as
3. MK-dV Equation
The MK-dV equation for the nonlinear propagation of the NAWs in the CDENPs is derived by the reductive perturbation technique (RPT) which requires first the stretching of the independent variables, r and t as [28]
and next the expansion of the dependent variables, n, u and as [28]
where is the normalized NAW phase speed, is normalized by , is normalized by , and is a smallness parameter satisfying .
Using Equations (16)–(20) in the system (13)–(15), taking the coefficients of from Equation (13) as well as from Equation (14), and the coefficients of from Equation (15), one obtains:
The relation (23), representing , is the linear dispersion relation for the long wavelength NAWs, which can also be obtained from Equation (4) for a long wavelength limit, . This means that the RPT, utilized here, is valid for the long wavelength NAWs, and that the phase speed of the long wavelength NAWs is directly proportional to the square root of the degenerate pressure of the CUDE gas, while inversely proportional to the square root of the mass density of cold nucleus fluid. Thus, in the NAWs, the pressure of the CUDE gas gives rise to the restoring force, and the mass density of the nucleus fluid gives rise to the inertia.
Again, using Equations (16)–(20) in Equations (13)–(15), keeping the coefficients of from Equation (13) as well as from Equation (14), and keeping the coefficients of from Equation (15), one obtains:
Now, using Equations (21)–(26), , and can be eliminated to obtain the MK-dV equation in the form:
where and are the nonlinear and dispersion coefficients, respectively.
Let us note that the second term of the MK-dV Equation (27) is due to the effect of cylindrical or spherical geometry, which disappears for a large value of . To examine the effects of cylindrical and spherical geometries on the NA solitary waves in the CDENPs under consideration, one has to solve the MK-dV Equation (27) numerically by using the stationary solitary wave solution [29] of Equation (27) with as an initial profile,
where , with and being normalized by and , respectively, and and are the normalized amplitude and width of the initial pulse, respectively.
The positive values of and along with Equation (28) (with , and ) indicate that the CDENPs under consideration support cylindrical as well as spherical solitary waves with . The MK-dV Equation (27) is numerically solved and analyzed for nonplanar ( and ) geometries. Let us notice that means that the solitary waves propagate inward the direction of the cylinder or sphere [30]. It is also used to converse the numerical solution of the MK-dV equation given by Equation (27). The results are displayed in Figure 1.
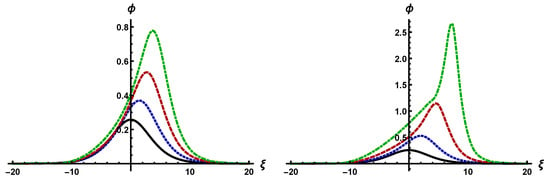
Figure 1.
Time evolution of (left panel) cylindrical () and (right panel) spherical () nucleus-acoustic (NA) solitary waves in the cold degenerate electron-nucleus plasmas (CDENPs) under consideration for , (solid line), (dotted line), (dashed line), and (dashed-dotted line). See text for details.
It shows that the time evolution of the solitary waves in the CDENPs under consideration are significantly modified by the effects of cylindrical and spherical geometries. It is observed from Figure 1 that the amplitude of the spherical solitary waves is approximately two times higher than that of the cylindrical ones, and that the time evolution of the spherical solitary waves is faster than that of the cylindrical ones.
4. MBurgers Equation
To derive the MBurgers equation for the nonlinear propagation of the NAWs, one can again employ the RPT [28], but exploit different stretching of the independent variables r and t as [31,32]
Now, using Equations (29), (30) and (18)–(20) in the system (13)–(15), and taking the coefficients of from Equations (13) and (14), and the coefficients of from Equation (15), a set of Equations (21)–(23) is obtained. However, using Equations (29), (30), (18)–(20) in Equations (13)–(15), and again taking the coefficients of from Equations (13) and (14), and the coefficients of from Equation (15), one obtains:
Using Equations (21)–(23) and (31)–(33), , and can be eliminated to obtain the MBurgers Equation (34) in the form:
where is the dissipation coefficient. One can also see that the second term of the MBurgers Equation (34) is due to the effect of cylindrical or spherical geometry, which disappears for a large value of .
To define shock wave solution clearly, first, consider in the MBurgers Equation (34). The latter (for ) can be expressed as:
which is the standard Burgers equation. To obtain the stationary shock wave solution of this standard Burgers equation, a frame moving (; ) with the constant speed , the steady state condition () and are assumed. These assumptions reduce Equation (35) to
where the integration constant is found to be zero, since and at . Now, skipping few steps of mathematics of undergraduate level, the shock wave solution of Equation (6) is given by [31]
where and are, respectively, the amplitude and thickness of the shock waves. Equation (37) represents the stationary shock wave solution of the MBurgers Equation (35).
The positive values of and along with Equation (37) imply that the CDENPs under consideration support cylindrical as well as spherical shock waves with .
To examine the effects of cylindrical and spherical geometries on the NA shock waves in the CDENPs under consideration, one has to solve the MBurgers Equation (34) numerically by using the stationary shock wave solution of Equation (34) with as the initial profile given by Equation (37). The MBurgers equation is numerically solved for cylindrical and spherical geometries. Let us again notice that means that the shock waves propagate inward direction of the cylinder and sphere [30], and that is used to converse its numerical solution. The results are shown in Figure 2.
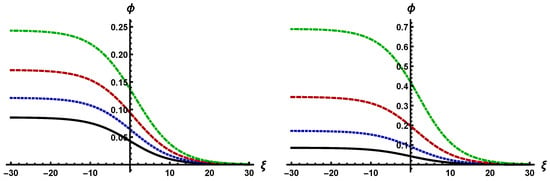
Figure 2.
Time evolution of (left panel) cylindrical () and (right panel) spherical () NA shock waves in the CDENPs under consideration for , , (solid line), (dotted line), (dashed line), and (dashed-dotted line). See text for details.
The numerical results, shown in Figure 2, point out that the time evolution of the NA shock waves in the CDENPs under consideration are significantly modified by the effects of the cylindrical and spherical geometries. The numerical results observed in Figure 2 indicate that the amplitude of the spherical shock waves is approximately two times higher than that of the cylindrical ones, and that the time evolution of the spherical shock waves is faster than that of the cylindrical ones.
The profiles represented by the analytic solution of the standard Burgers Equation (37) or those obtained from the numerical solutions of the MBurgers Equation (34) are known as shock waves. The latter are formed when the effect of this dissipation represented by the term containing is balanced by that of the nonlinearity represented by the term containing .
5. Discussion
The nonlinear propagation of the NAWs in the CDENPs composed of CUDE gas [3,4,5] and the viscous fluid of nucleus of any element like [3,4,5] or or or [6,26,27] has been considered to identify the characteristics of the nonlinear waves formed in the CDENPs under consideration. The results obtained from current study study are as follows:
- The phase speed of the NAWs is given bywhere Equation (3) is used, and is the inter-electron distance. This expression indicates that is inversely proportional to and the mass, m, of a nucleus species, but is directly proportional to the number of protons, , in the nucleus species. The phase speed does not depend on the temperature of the electron or nucleus species. This is an unique feature of the NAWs by which the NAWs appeared as new waves, and are completely different from the IAWs [23,24] which do not exist at absolute zero-temperature.
- The dimensional amplitudes of both types of nonlinear waves are determined by using Equations (3) and (38), and are expressed as:where is the dimensional speed of the frame of reference. These expressions imply that the amplitudes of the both types of nonlinear waves are directly proportional to , and to the square root of the mass of the nucleus species, , but inversely proportional to the square root of the inter-electron distance, , and the number of the proton, , in a nucleus species.
- The dimensional widths of both types of nonlinear waves are given byThese expressions imply that the width of the solitary waves is the order of a fraction of the length scale, , of the waves, since is a fraction of for the formation of the NA solitary waves. The width of the NA shock waves increases with the dynamical viscosity coefficient, , of the nucleus fluid, but decreases with the speed, .
- The amplitude (width) of the cylindrical NA solitary and shock waves is smaller (larger) than that of the spherical NA solitary and shock waves. The time evolution of the spherical solitary and shock waves is faster than that of the NA cylindrical solitary and shock waves.
- The amplitude (width) of the NA solitary waves is minimum (maximum) for a very large value of , which causes to neglect the effect of cylindrical and spherical geometries, and gives rise to one dimensional (1D) planar NA solitary and shock waves. Thus, for a large value of , 1D planar, cylindrical and spherical solitary and shock waves are found to be identical.
- The length scale as well as the phase speed, height, and thickness of the NA solitary and shock waves are completely independent of temperature. These are completely new linear and nonlinear features of the NAWs under consideration.
The exact analytical solutions of Equations (27) and (34) are difficult to be obtained because of the nonplanar term (containing ), where a singularity arises at . A class of analytical solutions of Equation (27) was obtained from the solution of the standard K-dV equation [33,34]. However, we are interested to find a solitary wave solution of Equation (27) with the standard boundary condition, viz., . Therefore, Equation (27) was solved numerically in order to find the spatiotemporal evolution of an initially imposed solitary profile at with the standard boundary conditions in () domain. It was also assumed that the solution along with its derivative tends to zero as . Further, the solutions of Equations (27) and (34) with as an initial profiles (i.e., for Equation (27) and for Equation (34)) were used. The finite difference method was used for numerical solutions. On the other hand, the traveling wave solutions [35] of combined K-dV-modified K-dV equations as well as complexly coupled-K-dV equation are obtained by utilizing the technique of the Bäcklund transformation.
Recently, the trace of nuclei of massive elements, such as , , , etc. in white dwarf and neutron stars has also been predicted [36,37]. The densities of the stars are small to neglect their roles in the formation of the NA solitary and shock waves in the CDENPs [3,4,5,6,26,27] under consideration.
Let us add here that the roles of magnetic field and rotation of neutron stars in the formation of the NA solitary and shock waves are also important problems, but those are beyond. the scope of the present study. However, the theory, presented here, is valid for the long wavelength electrostatic NAWs propagating along the magnetic lines of force of white dwarfs and non-rotating neutron stars.
Funding
This research received no external funding.
Acknowledgments
The work is dedicated to an eminent space and astrophysicist, Reinhard Schlickeiser, who supervised the author during his research stay at Ruhr Universität Bochum (Germany) as a Friedrich Wilhelm Bessel Research Awardee, on the occasion of his 70th Birth Anniversary. The author wishes him a very long active and cherished life on the same occasion.
Conflicts of Interest
The author declares no conflict of interest.
References
- Mamun, A.A.; Amina, M.; Schlickeiser, R. Nucleus-acoustic shock (waves in a strongly coupled self-gravitating degenerate quantum plasma. Phys. Plasmas 2016, 23, 094503. [Google Scholar] [CrossRef]
- Mamun, A.A.; Amina, M.; Schlickeiser, R. Heavy NA spherical solitons in self-gravitating super-dense plasmas. Phys. Plasmas 2017, 24, 042307. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The highly collapsed configurations of a stellar mass. Mon. Not. R. Astron. Soc. 1931, 91, 456–4566. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The maximum mass of ideal white dwarfs. Astrophys. J. 1931, 74, 81–82. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The pressure in the interior of a star. Mon. Not. R. Astron. Soc. 1936, 96, 644–646. [Google Scholar] [CrossRef]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects, 1st ed.; Wiley-VCH Verlag: Weinheim, Germany, 1983; pp. 15–375. [Google Scholar]
- Potekhin, A.Y.; Chabrier, G. Thermodynamic functions of dense plasmas: Analytic approximations for astrophysical applications. Contrib. Plasma Phys. 2010, 50, 82–87. [Google Scholar] [CrossRef] [Green Version]
- Fletcher, R.S.; Zhang, X.L.; Rolston, S.L. Observation of collective modes of ultracold plasmas. Phys. Rev. Lett. 2006, 96, 105003. [Google Scholar] [CrossRef] [Green Version]
- Glenzer, S.H.; Redmer, R. X-ray Thomson scattering in high energy density plasmas. Rev. Mod. Phys. 2009, 81, 1625. [Google Scholar] [CrossRef]
- Drake, R.P. Perspectives on high-energy-density physics. Phys. Plasmas 2009, 16, 055501. [Google Scholar] [CrossRef]
- Drake, R.P. High-energy-density physics. Phys. Today 2010, 63, 18. [Google Scholar] [CrossRef]
- Hu, S.X.; Collins, L.A.; Boehly, T.R.; Kress, J.D.; Goncharov, V.N.; Skupsky, S. First-principles thermal conductivity of warm-dense deuterium plasmas for inertial confinement fusion applications. Phys. Rev. E 2014, 89, 04105. [Google Scholar] [CrossRef]
- Shukla, P.K.; Mamun, A.A.; Mendis, D.A. Nonlinear ion modes in a dense plasma with strongly coupled ions and degenerate electron fluids. Phys. Rev. E 2011, 84, 026405. [Google Scholar] [CrossRef] [Green Version]
- Sultana, S.; Schlickeiser, R. Fully nonlinear heavy ion-acoustic solitary waves in astrophysical degenerate relativistic quantum plasmas. Astrophys. Space Sci. 2018, 363, 1–9. [Google Scholar] [CrossRef]
- Sultana, S.; Schlickeiser, R. Arbitrary amplitude nucleus-acoustic solitons in multi-ion quantum plasmas with relativistically degenerate electrons. Phys. Plasmas 2018, 25, 022110. [Google Scholar] [CrossRef]
- Sultana, S.; Islam, S.; Mamun, A.A.; Schlickeiser, R. Modulated heavy nucleus-acoustic waves and associated rogue waves in a degenerate relativistic quantum plasma system. Phys. Plasmas 2018, 25, 012113. [Google Scholar] [CrossRef]
- Chowdhury, N.A.; Hasan, M.M.; Mannan, A.; Mamun, A.A. Nucleus-acoustic envelope solitons and their modulational instability in a degenerate quantum plasma system. Vacuum 2018, 147, 31–37. [Google Scholar] [CrossRef] [Green Version]
- Karmakar, P.K.; Das, P. Nucleus-acoustic waves: Excitation, propagation, and stability. Phys. Plasmas 2018, 25, 082902. [Google Scholar] [CrossRef]
- Das, P.; Karmakar, P.K. Nonlinear nucleus-acoustic waves in strongly coupled degenerate quantum plasmas. Europhys. Lett. 2019, 126, 10001. [Google Scholar] [CrossRef]
- Mannan, A.; Sultana, S.; Mamun, A.A. Arbitrary amplitude heavy nucleus-acoustic solitary waves in thermally degenerate plasmas. IEEE Trans. Plasma Sci. 2020, 48, 4093–4102. [Google Scholar] [CrossRef]
- Kaur, R.; Singh, K.; Saini, N.S. Heavy-and light-nuclei acoustic dressed shock waves in white dwarfs. Chin. J. Phys. 2021, 72, 286–298. [Google Scholar] [CrossRef]
- Saini, N.S.; Kaur, R. Ion-acoustic solitary, breathers, and freak waves in a degenerate quantum plasma. Waves Random Complex Media 2021, 1–22. [Google Scholar] [CrossRef]
- Tonks, L.; Langmuir, I. Oscillations in ionized gases. Phys. Rev. 1929, 33, 95–210. [Google Scholar] [CrossRef]
- Revans, R.W. The transmission of waves through an ionized gas. Phys. Rev. 1933, 44, 798–902. [Google Scholar] [CrossRef]
- Mamun, A.A. Degenerate pressure driven modified nucleus-acoustic waves in degenerate plasmas. Phys. Plasmas 2018, 25, 024502. [Google Scholar] [CrossRef]
- Koester, D.; Chanmugam, G. Physics of white dwarf stars. Rep. Prog. Phys. 1990, 53, 837–915. [Google Scholar] [CrossRef]
- Koester, D. White dwarfs: Recent developments. Astron. Astrophys. Rev. 2002, 11, 33–66. [Google Scholar] [CrossRef]
- Washimi, H.; Taniuti, T. Propagation of ion-acoustic solitary waves of small amplitude. Phys. Rev. Lett. 1966, 17, 996–997. [Google Scholar] [CrossRef]
- Mamun, A.A.; Shukla, P.K. Effects of nonthermal distribution of electrons and polarity of net dust-charge number density on nonplanar dust-ion-acoustic solitary waves. Phys. Rev. E 2009, 80, 037401. [Google Scholar] [CrossRef] [PubMed]
- Maxon, S.; Viecelli, J. Spherical solitons. Phys. Rev. Lett. 1974, 32, 4–6. [Google Scholar] [CrossRef]
- Mamun, A.A.; Cairns, R.A. Dust-acoustic shock waves due to strong correlation among arbitrarily charged dust. Phys. Rev. E 2009, 79, 055401. [Google Scholar] [CrossRef]
- Mamun, A.A. On stretching of plasma parameters and related open issues for the study of dust-ion-acoustic and dust-acoustic shock waves in dusty plasmas. Phys. Plasmas 2019, 26, 084501. [Google Scholar] [CrossRef]
- Hirota, R. Exact solutions to the equation describing “cylindrical solitons”. Phys. Lett. A 1979, 71, 393–394. [Google Scholar] [CrossRef]
- Mannan, A.; Fedele, R.; Onorato, M.; De Nicola, S.; Jovanović, D. Ring-type multi-soliton dynamics in shallow water. Phys. Rev. E 2015, 91, 012921. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yokus, A.; Kaya, D. Comparison exact and numerical simulation of the traveling wave solution in nonlinear dynamics. Int. J. Modern Phys. B 2020, 34, 2050282. [Google Scholar] [CrossRef]
- Witze, A. Space-station science ramps up. Nature 2014, 510, 196–197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vanderburg, A.; Johnson, J.A.; Rappaport, S.; Bieryla, A.; Irwin, J.; Lewis, J.A.; Kipping, D.; Brown, W.R.; Dufour, P.; Ciardi, D.R.; et al. A disintegrating minor planet transiting a white dwarf. Nature 2015, 526, 546–549. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).