Log-Normal Superstatistics for Brownian Particles in a Heterogeneous Environment
Abstract
1. Introduction
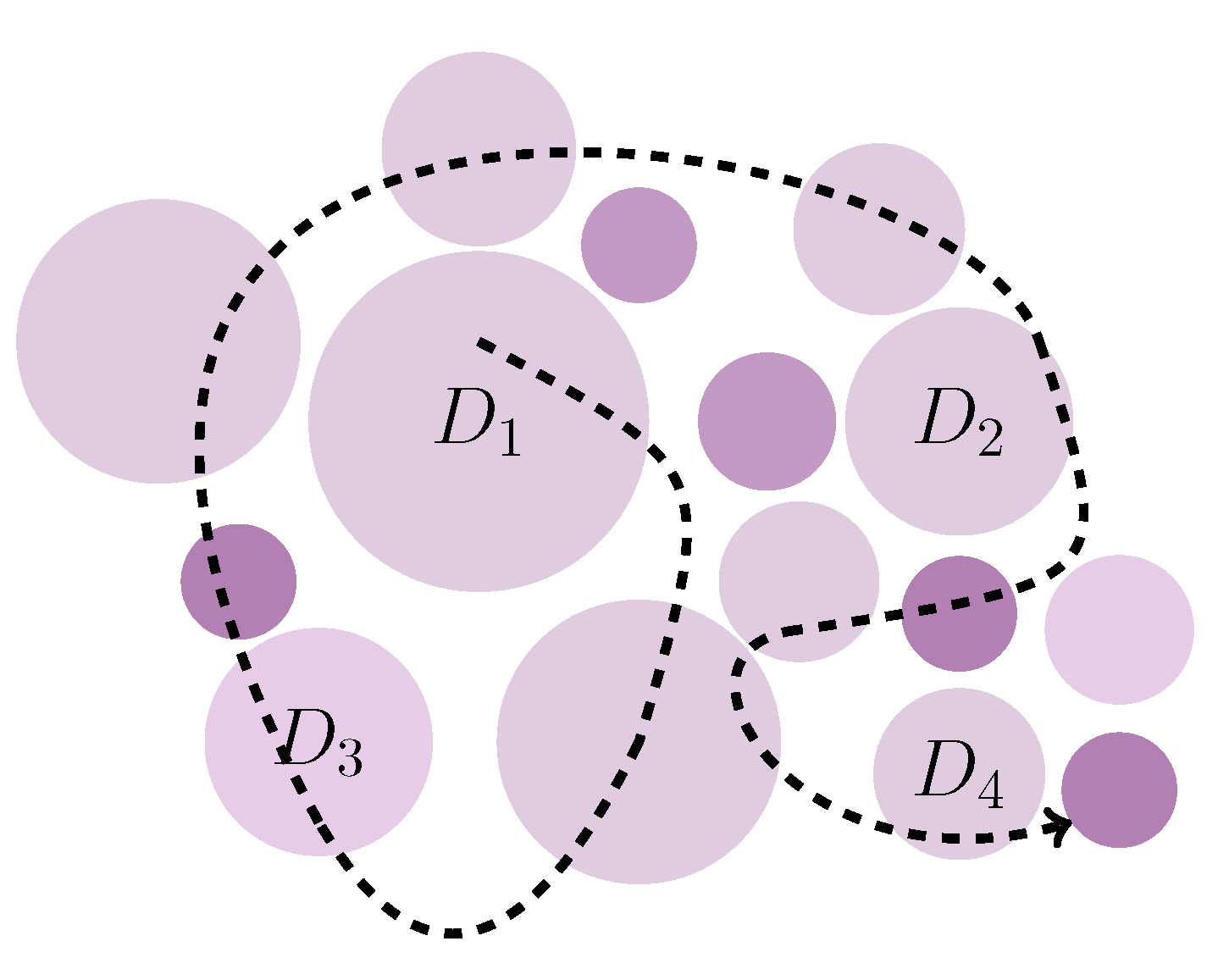
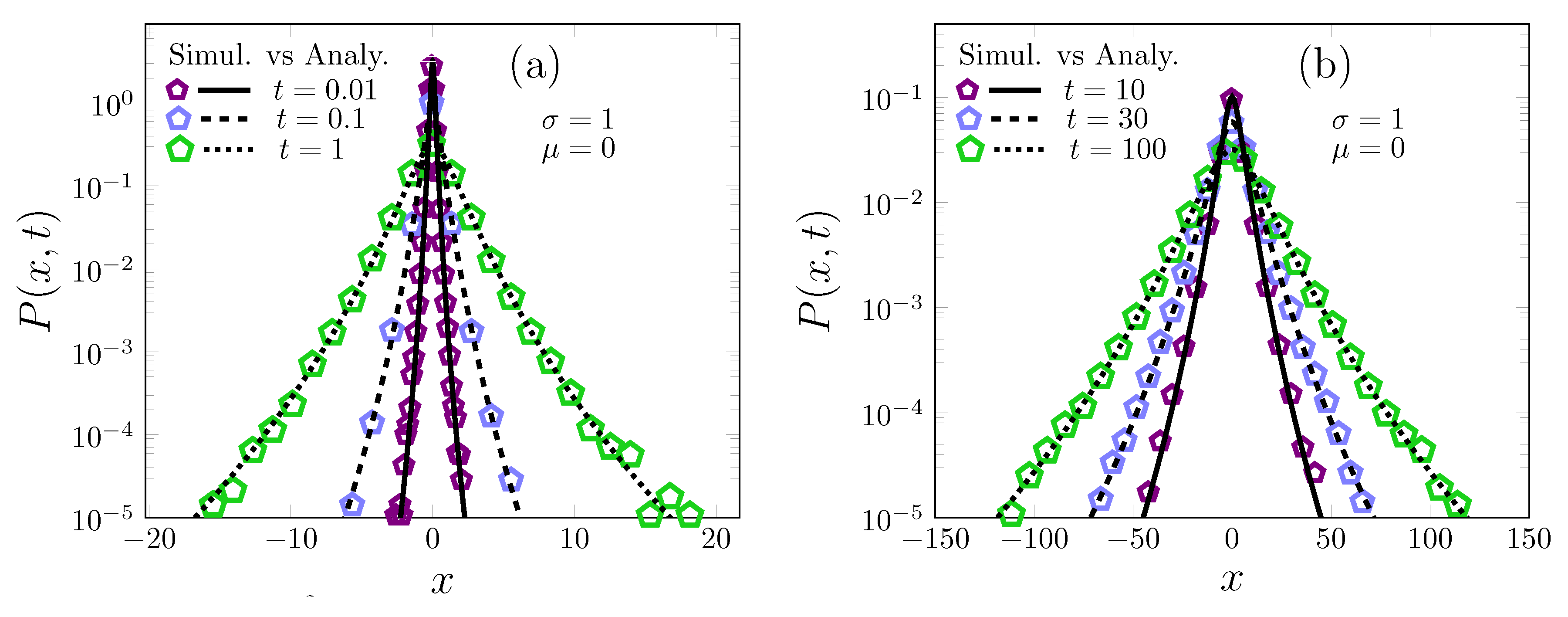
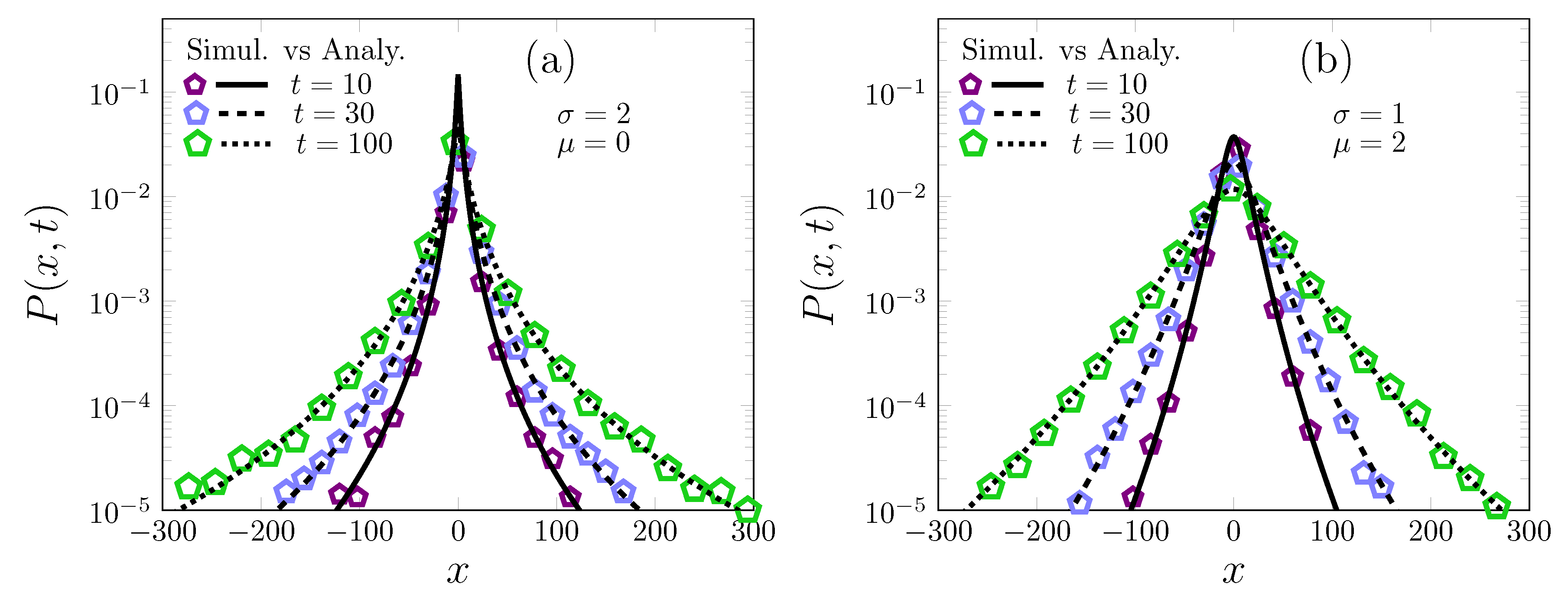
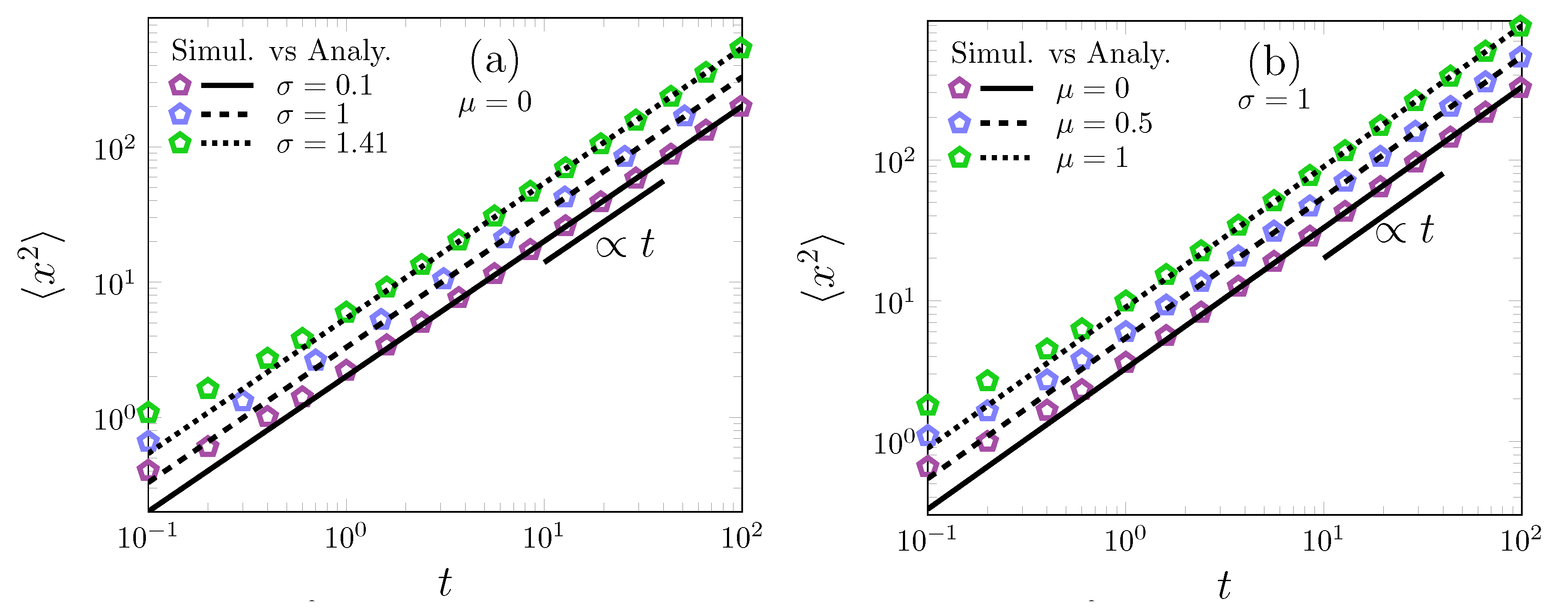
2. From Log-Normal Superstatistics to Brownian Yet Non-Gaussian Diffusion
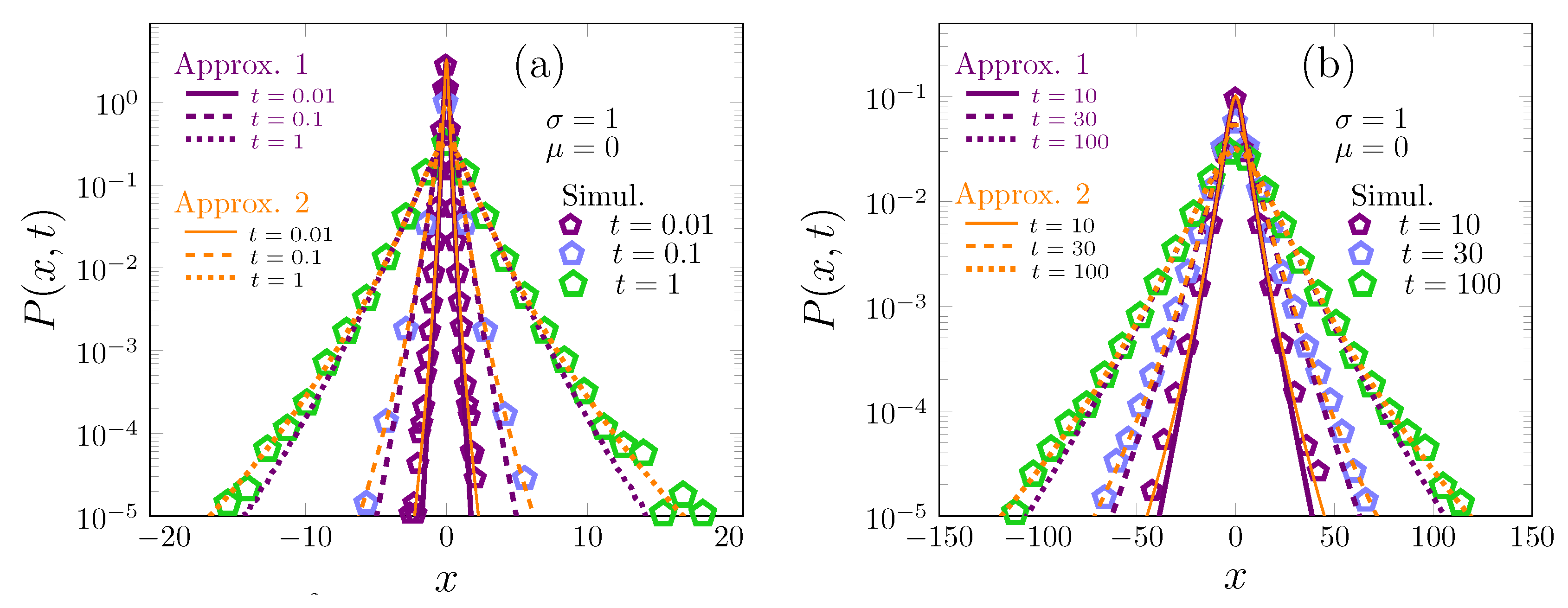
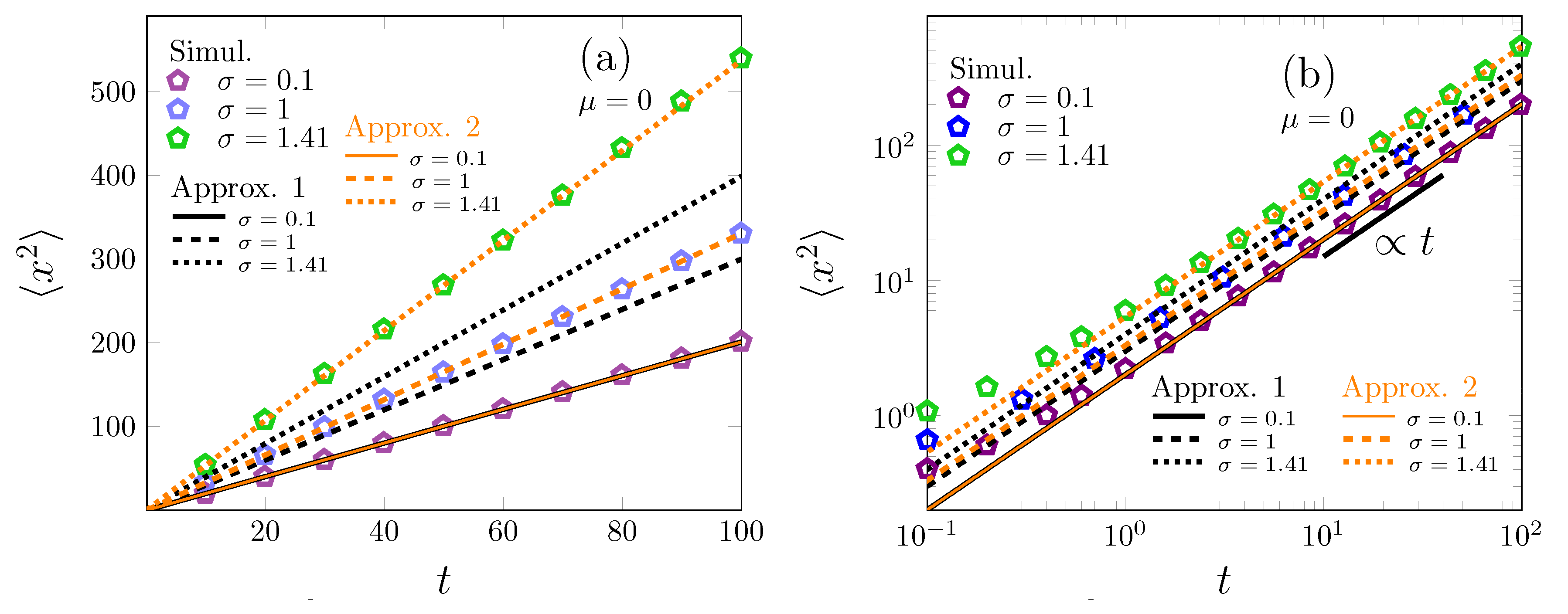
2.1. Two Approximations for Log-Normal Superstatistics of Brownian Particles in a Heterogeneous Environment
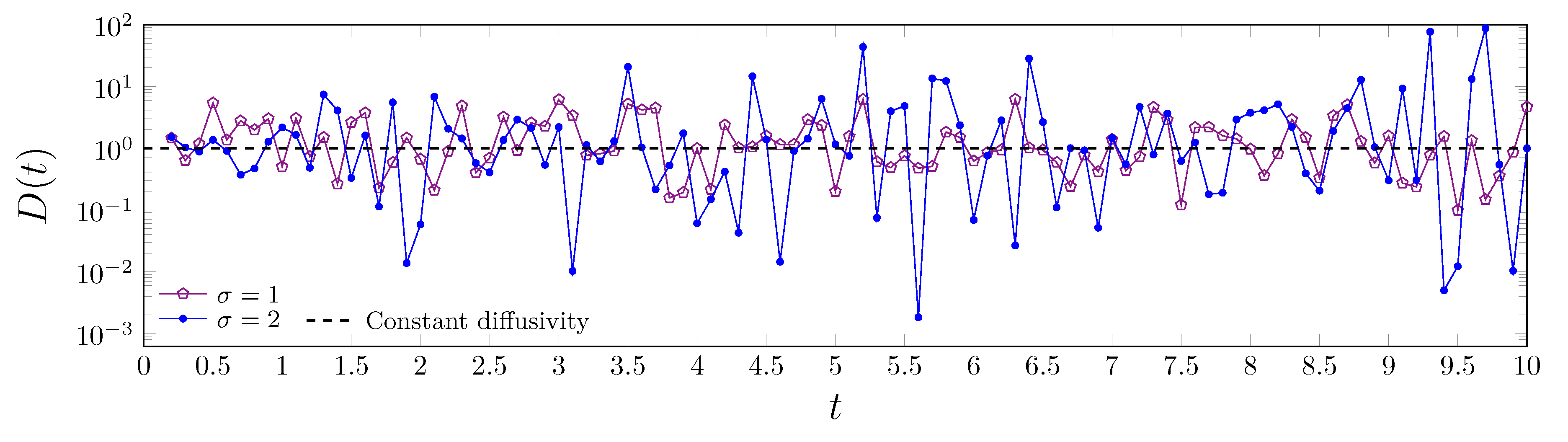
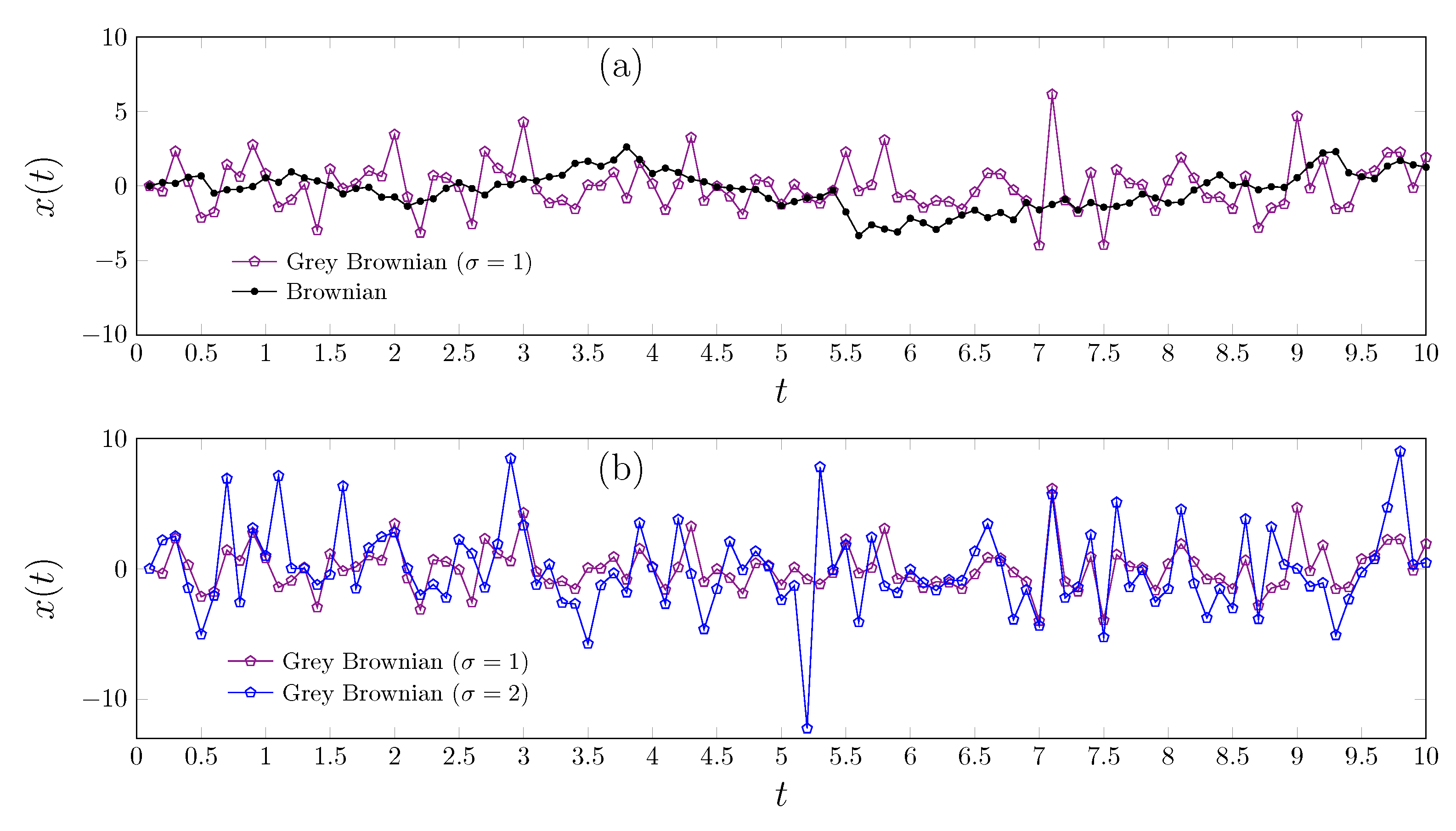
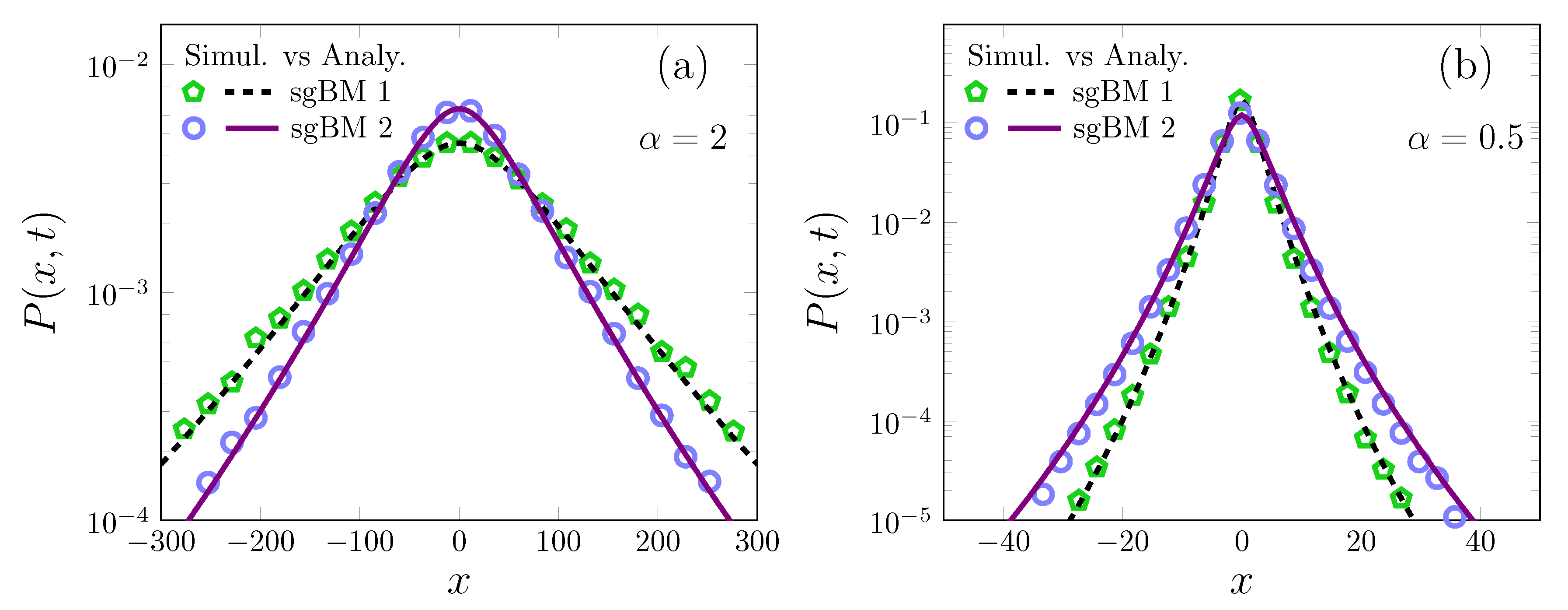
3. Two Models for Scaled Grey Brownian Motion: Log-Normal Superstatistics and Anomalous Diffusion
4. Conclusions
- The investigation of the sgBM models for different time-scale ( functions [73]).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Brown, R. Mikroskopische Beobachtungen über die im Pollen der Pflanzen enthaltenen Partikeln, und über das allgemeine Vorkommen activer Molecüle in organischen und unorganischen Körpern. Ann. Der Phys. 1828, 90, 294–313. [Google Scholar] [CrossRef]
- Einstein, A. On the theory of the Brownian movement. Ann. Phys. 1906, 19, 371–381. [Google Scholar] [CrossRef]
- Einstein, A. Investigations on the Theory of the Brownian Movement; MACourier Corporation: Chelmsford, UK, 1956. [Google Scholar]
- Sutherland, W. LXXV. A dynamical theory of diffusion for non-electrolytes and the molecular mass of albumin. Lond. Edinburgh Dublin Philos. Mag. J. Sci. 1905, 9, 781–785. [Google Scholar] [CrossRef]
- Langevin, P. Sur la théorie du mouvement brownien. Compt. Rendus 1908, 146, 530–533. [Google Scholar]
- Smoluchowski, M.v. Zur kinetischen Theorie der Brownschen Molekular Bewegung und der Suspensionen. Ann. Phys. 1906, 21, 756–780. [Google Scholar] [CrossRef]
- Smoluchowski, M.V. Über Brownsche Molekularbewegung unter Einwirkung äußerer Kräfte und deren Zusammenhang mit der verallgemeinerten Diffusionsgleichung. Ann. Phys. 1916, 353, 1103–1112. [Google Scholar] [CrossRef]
- Risken, H. Fokker-Planck Equation. In The Fokker-Planck Equation; Springer: Berlin/Heidelberg, Germany, 1996; pp. 63–95. [Google Scholar]
- Hänggi, P.; Marchesoni, F. Introduction: 100 years of Brownian motion. Chaos 2005, 15, 26101. [Google Scholar] [CrossRef]
- Richardson, L.F. Atmospheric diffusion shown on a distance-neighbour graph. Proc. R. Soc. Lond. Ser. A: Math. Phys. Eng. Sci. 1926, 110, 709–737. [Google Scholar] [CrossRef]
- Scher, H.; Montroll, E.W. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B 1975, 12, 2455. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- dos Santos, M.A.F. Analytic approaches of the anomalous diffusion: A review. Chaos Solitons Fractals 2019, 124, 86–96. [Google Scholar] [CrossRef]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef]
- Metzler, R. Gaussianity Fair: The Riddle of Anomalous yet Non-Gaussian Diffusion. Biophys. J. 2017, 112, 413–415. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Kuo, J.; Bae, S.C.; Granick, S. When Brownian diffusion is not Gaussian. Nat. Mater. 2012, 11, 481–485. [Google Scholar] [CrossRef] [PubMed]
- Chechkin, A.V.; Seno, F.; Metzler, R.; Sokolov, I.M. Brownian yet non-Gaussian diffusion: From superstatistics to subordination of diffusing diffusivities. Phys. Rev. X 2017, 7, 021002. [Google Scholar] [CrossRef]
- Wang, B.; Anthony, S.M.; Bae, S.C.; Granick, S. Anomalous yet brownian. Proc. Natl. Acad. Sci. USA 2009, 106, 15160–15164. [Google Scholar] [CrossRef]
- Leptos, K.C.; Guasto, J.S.; Gollub, J.P.; Pesci, A.I.; Goldstein, R.E. Dynamics of enhanced tracer diffusion in suspensions of swimming eukaryotic microorganisms. Phys. Rev. Lett. 2009, 103, 198103. [Google Scholar] [CrossRef]
- Ślęzak, J.; Burov, S. From diffusion in compartmentalized media to non-Gaussian random walks. arXiv 2019, arXiv:1909.11395. [Google Scholar]
- Dutta, S.; Chakrabarti, J. Anomalous dynamical responses in a driven system. Europhys. Lett. 2016, 116, 38001. [Google Scholar] [CrossRef]
- Wang, D.; Hu, R.; Skaug, M.J.; Schwartz, D.K. Temporally anticorrelated motion of nanoparticles at a liquid interface. J. Phys. Chem. Lett. 2015, 6, 54–59. [Google Scholar] [CrossRef]
- Lanoiselée, Y.; Grebenkov, D.S. Non-Gaussian diffusion of mixed origins. J. Phys. Math. Theor. 2019, 52, 304001. [Google Scholar] [CrossRef]
- Barkai, E.; Burov, S. Packets of Diffusing Particles Exhibit Universal Exponential Tails. Phys. Rev. Lett. 2020, 124, 060603. [Google Scholar] [CrossRef]
- Metzler, R. Superstatistics and non-Gaussian diffusion. Eur. Phys. J. Spec. Top. 2020, 229, 711–728. [Google Scholar] [CrossRef]
- Beck, C. Dynamical foundations of nonextensive statistical mechanics. Phys. Rev. Lett. 2001, 87, 180601. [Google Scholar] [CrossRef]
- Beck, C.; Cohen, E.G. Superstatistics. Physica A 2003, 322, 267–275. [Google Scholar] [CrossRef]
- Kärger, J. NMR self-diffusion studies in heterogeneous systems. Adv. Colloid Interface Sci. 1985, 23, 129–148. [Google Scholar] [CrossRef]
- Goldstein, H. Multilevel Statistical Models; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 922. [Google Scholar]
- Beck, C.; Cohen, E.G.; Swinney, H.L. From time series to superstatistics. Phys. Rev. E 2005, 72, 056133. [Google Scholar] [CrossRef] [PubMed]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Abul-Magd, A. Superstatistics in random matrix theory. Physica A 2006, 361, 41–54. [Google Scholar] [CrossRef][Green Version]
- Abul-Magd, A.; Dietz, B.; Friedrich, T.; Richter, A. Spectral fluctuations of billiards with mixed dynamics: From time series to superstatistics. Phys. Rev. E 2008, 77, 046202. [Google Scholar] [CrossRef]
- Beck, C. Superstatistics in hydrodynamic turbulence. Phys. D Nonlinear Phenom. 2004, 193, 195–207. [Google Scholar] [CrossRef]
- Beck, C. Lagrangian acceleration statistics in turbulent flows. Europhys. Lett. 2003, 64, 151. [Google Scholar] [CrossRef]
- Abe, S. Fluctuations of entropy and log-normal superstatistics. Phys. Rev. E 2010, 82, 011131. [Google Scholar] [CrossRef] [PubMed]
- Allen, A.P.; Li, B.L.; Charnov, E.L. Population fluctuations, power laws and mixtures of lognormal distributions. Ecol. Lett. 2001, 4, 1–3. [Google Scholar] [CrossRef]
- Yamamoto, E.; Akimoto, T.; Mitsutake, A.; Metzler, R. Universal relation between instantaneous diffusivity and radius of gyration of proteins in aqueous solution. arXiv 2020, arXiv:2009.06829. [Google Scholar]
- Miyaguchi, T.; Akimoto, T.; Yamamoto, E. Langevin equation with fluctuating diffusivity: A two-state model. Phys. Rev. E 2016, 94, 012109. [Google Scholar] [CrossRef] [PubMed]
- Uneyama, T.; Miyaguchi, T.; Akimoto, T. Relaxation functions of the Ornstein-Uhlenbeck process with fluctuating diffusivity. Phys. Rev. E 2019, 99, 032127. [Google Scholar] [CrossRef]
- Manzo, C.; Torreno-Pina, J.A.; Massignan, P.; Lapeyre, G.J., Jr.; Lewenstein, M.; Parajo, M.F.G. Weak ergodicity breaking of receptor motion in living cells stemming from random diffusivity. Phys. Rev. X 2015, 5, 011021. [Google Scholar] [CrossRef]
- Cherstvy, A.G.; Thapa, S.; Wagner, C.E.; Metzler, R. Non-Gaussian, non-ergodic, and non-Fickian diffusion of tracers in mucin hydrogels. Soft Matter 2019, 15, 2526–2551. [Google Scholar] [CrossRef]
- Lawley, S.D.; Miles, C.E. Diffusive search for diffusing targets with fluctuating diffusivity and gating. J. Nonlinear Sci. 2019, 29, 2955–2985. [Google Scholar] [CrossRef]
- Sposini, V.; Chechkin, A.V.; Seno, F.; Pagnini, G.; Metzler, R. Random diffusivity from stochastic equations: Comparison of two models for Brownian yet non-Gaussian diffusion. New J. Phys. 2018, 20, 043044. [Google Scholar] [CrossRef]
- Vitali, S.; Budimir, I.; Runfola, C.; Castellani, G. The role of the central limit theorem in the heterogeneous ensemble of Brownian particles approach. Mathematics 2019, 7, 1145. [Google Scholar] [CrossRef]
- Postnikov, E.B.; Chechkin, A.; Sokolov, I.M. Brownian yet non-Gaussian diffusion in heterogeneous media: From superstatistics to homogenization. New J. Phys. 2020, 22, 063046. [Google Scholar] [CrossRef]
- Lampo, T.J.; Stylianidou, S.; Backlund, M.P.; Wiggins, P.A.; Spakowitz, A.J. Cytoplasmic RNA-protein particles exhibit non-Gaussian subdiffusive behavior. Biophys. J. 2017, 112, 532–542. [Google Scholar] [CrossRef]
- Stuhrmann, B.; e Silva, M.S.; Depken, M.; MacKintosh, F.C.; Koenderink, G.H. Nonequilibrium fluctuations of a remodeling in vitro cytoskeleton. Phys. Rev. E 2012, 86, 020901. [Google Scholar] [CrossRef]
- Sabri, A.; Xu, X.; Krapf, D.; Weiss, M. Elucidating the origin of heterogeneous anomalous diffusion in the cytoplasm of mammalian cells. Phys. Rev. Lett. 2020, 125, 058101. [Google Scholar] [CrossRef] [PubMed]
- Hidalgo-Soria, M.; Barkai, E. Hitchhiker model for Laplace diffusion processes. Phys. Rev. E 2020, 102, 012109. [Google Scholar] [CrossRef]
- Rajesh, R.; Das, D.; Chakraborty, B.; Barma, M. Aggregate formation in a system of coagulating and fragmenting particles with mass-dependent diffusion rates. Phys. Rev. E 2002, 66, 056104. [Google Scholar] [CrossRef] [PubMed]
- Sliusarenko, O.Y.; Vitali, S.; Sposini, V.; Paradisi, P.; Chechkin, A.; Castellani, G.; Pagnini, G. Finite-energy Lévy-type motion through heterogeneous ensemble of Brownian particles. J. Phys. Math. Theor. 2019, 52, 095601. [Google Scholar] [CrossRef]
- Beck, C. Superstatistical Brownian motion. Prog. Theor. Phys. Suppl. 2006, 162, 29–36. [Google Scholar] [CrossRef]
- Hapca, S.; Crawford, J.W.; Young, I.M. Anomalous diffusion of heterogeneous populations characterized by normal diffusion at the individual level. J. R. Soc. Interface 2009, 6, 111–122. [Google Scholar] [CrossRef] [PubMed]
- Jeon, J.H.; Javanainen, M.; Martinez-Seara, H.; Metzler, R.; Vattulainen, I. Protein crowding in lipid bilayers gives rise to non-Gaussian anomalous lateral diffusion of phospholipids and proteins. Phys. Rev. X 2016, 6, 021006. [Google Scholar] [CrossRef]
- dos Santos, M.A.F. Mittag-Leffler functions in superstatistics. Chaos Solitons Fractals 2020, 131, 109484. [Google Scholar] [CrossRef]
- Sánchez, E. Burr type-XII as a superstatistical stationary distribution. Physica A 2019, 516, 443–446. [Google Scholar] [CrossRef]
- Mathai, A.; Haubold, H.J. Mittag-Leffler functions to pathway model to Tsallis statistics. Integral Transform. Spec. Funct. 2010, 21, 867–875. [Google Scholar] [CrossRef]
- Agahi, H.; Khalili, M. Truncated Mittag-Leffler distribution and superstatistics. Physica A 2020, 555, 124620. [Google Scholar] [CrossRef]
- Mura, A.; Taqqu, M.S.; Mainardi, F. Non-Markovian diffusion equations and processes: Analysis and simulations. Physica A 2008, 387, 5033–5064. [Google Scholar] [CrossRef]
- Mura, A.; Mainardi, F. A class of self-similar stochastic processes with stationary increments to model anomalous diffusion in physics. Integral Transform. Spec. Funct. 2009, 20, 185–198. [Google Scholar] [CrossRef]
- Pagnini, G. Erdélyi-Kober fractional diffusion. Fract. Calc. Appl. Anal. 2012, 15, 117–127. [Google Scholar] [CrossRef]
- Molina-García, D.; Pham, T.M.; Paradisi, P.; Manzo, C.; Pagnini, G. Fractional kinetics emerging from ergodicity breaking in random media. Phys. Rev. E 2016, 94, 052147. [Google Scholar] [CrossRef]
- Pagnini, G.; Paradisi, P. A stochastic solution with Gaussian stationary increments of the symmetric space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 2016, 19, 408–440. [Google Scholar] [CrossRef]
- Rojas-Nandayapa, L. Risk Probabilities: Asymptotics and Simulation. Ph.D. Thesis, Aarhus Universitetsforlag, Aarhus, Denmark, 2008. [Google Scholar]
- Asmussen, S.; Jensen, J.L.; Rojas-Nandayapa, L. On the Laplace transform of the lognormal distribution. Methodol. Comput. Appl. Probab. 2016, 18, 441–458. [Google Scholar] [CrossRef]
- Holgate, P. The lognormal characteristic function. Commun. Stat. Theory Methods 1989, 18, 4539–4548. [Google Scholar] [CrossRef]
- Touchette, H.; Beck, C. Asymptotics of superstatistics. Phys. Rev. E 2005, 71, 016131. [Google Scholar] [CrossRef] [PubMed]
- Rabassa, P.; Beck, C. Extreme value laws for superstatistics. Entropy 2014, 16, 5523–5536. [Google Scholar] [CrossRef]
- Butler, R.W. Saddlepoint Approximations with Applications; Cambridge University Press: Cambridge, MA, USA, 2007; Volume 22. [Google Scholar]
- Lim, S.; Muniandy, S. Self-similar Gaussian processes for modeling anomalous diffusion. Phys. Rev. E 2002, 66, 021114. [Google Scholar] [CrossRef]
- Bodrova, A.S.; Chechkin, A.V.; Sokolov, I.M. Scaled Brownian motion with renewal resetting. Phys. Rev. E 2019, 100, 012120. [Google Scholar] [CrossRef]
- Bodrova, A.S.; Chechkin, A.V.; Cherstvy, A.G.; Metzler, R. Ultraslow scaled Brownian motion. New J. Phys. 2015, 17, 063038. [Google Scholar] [CrossRef]
- Fuliński, A. Anomalous diffusion and weak nonergodicity. Phys. Rev. E 2011, 83, 061140. [Google Scholar] [CrossRef]
- Safdari, H.; Cherstvy, A.G.; Chechkin, A.V.; Thiel, F.; Sokolov, I.M.; Metzler, R. Quantifying the non-ergodicity of scaled Brownian motion. J. Phys. Math. Theor. 2015, 48, 375002. [Google Scholar] [CrossRef]
- Sposini, V.; Metzler, R.; Oshanin, G. Single-trajectory spectral analysis of scaled Brownian motion. New J. Phys. 2019, 21, 073043. [Google Scholar] [CrossRef]
- Mainardi, F.; Pagnini, G.; Gorenflo, R. Mellin transform and subordination laws in fractional diffusion processes. Fract. Calc. Appl. Anal. 2007, 6, 441. [Google Scholar]
- Saxton, M.J. Anomalous subdiffusion in fluorescence photobleaching recovery: A Monte Carlo study. Biophys. J. 2001, 81, 2226–2240. [Google Scholar] [CrossRef]
- Fieremans, E.; Burcaw, L.M.; Lee, H.H.; Lemberskiy, G.; Veraart, J.; Novikov, D.S. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. NeuroImage 2016, 129, 414–427. [Google Scholar] [CrossRef]
- Molini, A.; Talkner, P.; Katul, G.G.; Porporato, A. First passage time statistics of Brownian motion with purely time dependent drift and diffusion. Physica A 2011, 390, 1841–1852. [Google Scholar] [CrossRef]
- Metzler, R. Brownian motion and beyond: First-passage, power spectrum, non-Gaussianity, and anomalous diffusion. J. Stat. Mech. Theory Exp. 2019, 2019, 114003. [Google Scholar] [CrossRef]
- Chubynsky, M.V.; Slater, G.W. Diffusing diffusivity: A model for anomalous, yet Brownian, diffusion. Phys. Rev. Lett. 2014, 113, 098302. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Cherstvy, A.G.; Chechkin, A.V.; Thapa, S.; Seno, F.; Liu, X.; Metzler, R. Fractional Brownian motion with random diffusivity: Emerging residual nonergodicity below the correlation time. J. Phys. Math. Theor. 2020. [Google Scholar] [CrossRef]
- Wang, W.; Seno, F.; Sokolov, I.M.; Chechkin, A.V.; Metzler, R. Unexpected crossovers in correlated random-diffusivity processes. New J. Phys. 2020, 22, 083041. [Google Scholar] [CrossRef]
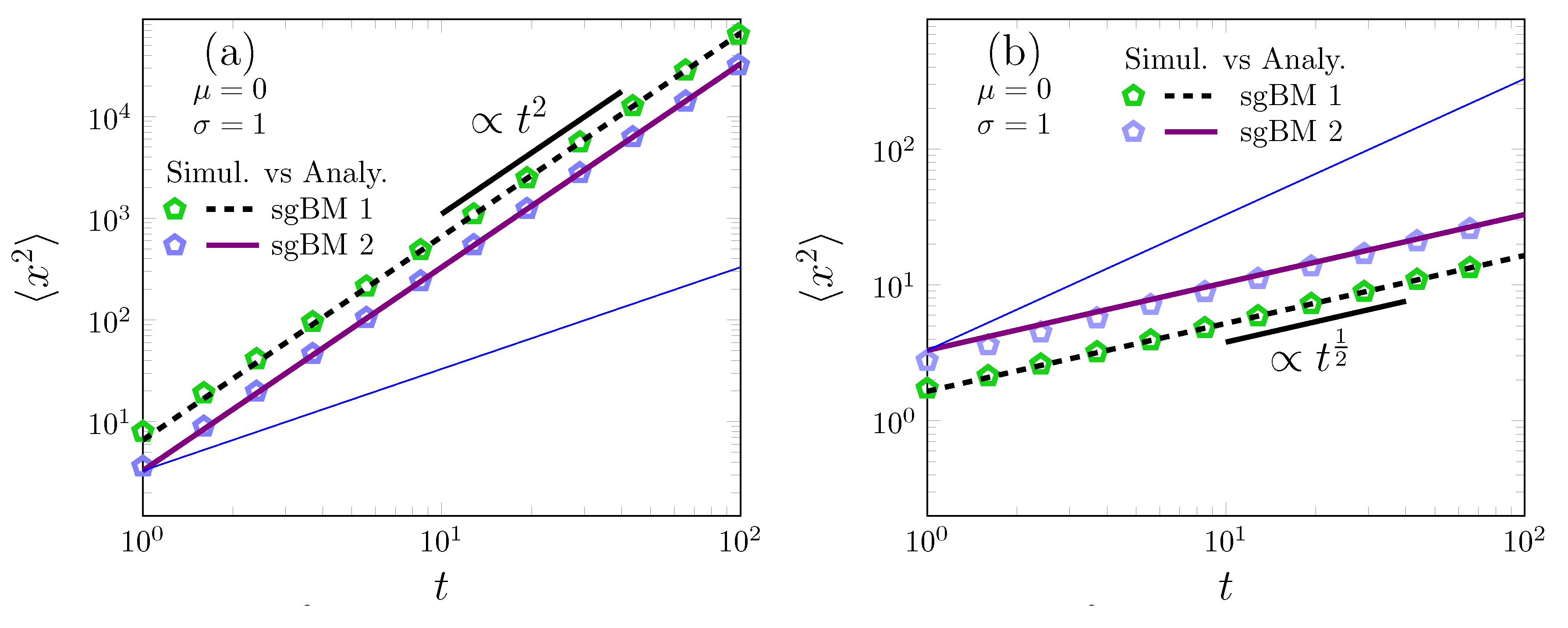
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
dos Santos, M.A.F.; Menon Junior, L. Log-Normal Superstatistics for Brownian Particles in a Heterogeneous Environment. Physics 2020, 2, 571-586. https://doi.org/10.3390/physics2040032
dos Santos MAF, Menon Junior L. Log-Normal Superstatistics for Brownian Particles in a Heterogeneous Environment. Physics. 2020; 2(4):571-586. https://doi.org/10.3390/physics2040032
Chicago/Turabian Styledos Santos, Maike Antonio Faustino, and Luiz Menon Junior. 2020. "Log-Normal Superstatistics for Brownian Particles in a Heterogeneous Environment" Physics 2, no. 4: 571-586. https://doi.org/10.3390/physics2040032
APA Styledos Santos, M. A. F., & Menon Junior, L. (2020). Log-Normal Superstatistics for Brownian Particles in a Heterogeneous Environment. Physics, 2(4), 571-586. https://doi.org/10.3390/physics2040032




