Photodetector Spectral Response Estimation Using Black Body Radiation
Abstract
1. Introduction
2. The Method
3. Generality of the Problem
4. Estimation with Basis Function
- Laguerre polynomials. The polynomials are defined as [14]:In this case one gets:The integral expression for the computation of the matrix elements reads:
- Hermite polynomials. These polynomials are defined as [14]:The integral expression for the computation of the matrix elements is:
- Sinc function. This function is defined as [14]:The resolution of the Fredholm equation requires some manipulations with the function. In a finite interval it can be considered a basis function,where:and h is the sample step. Then, the function, integrated in order to calculate the elements of the matrix , is:Considering the function , from its symmetry, the sum runs from to N:
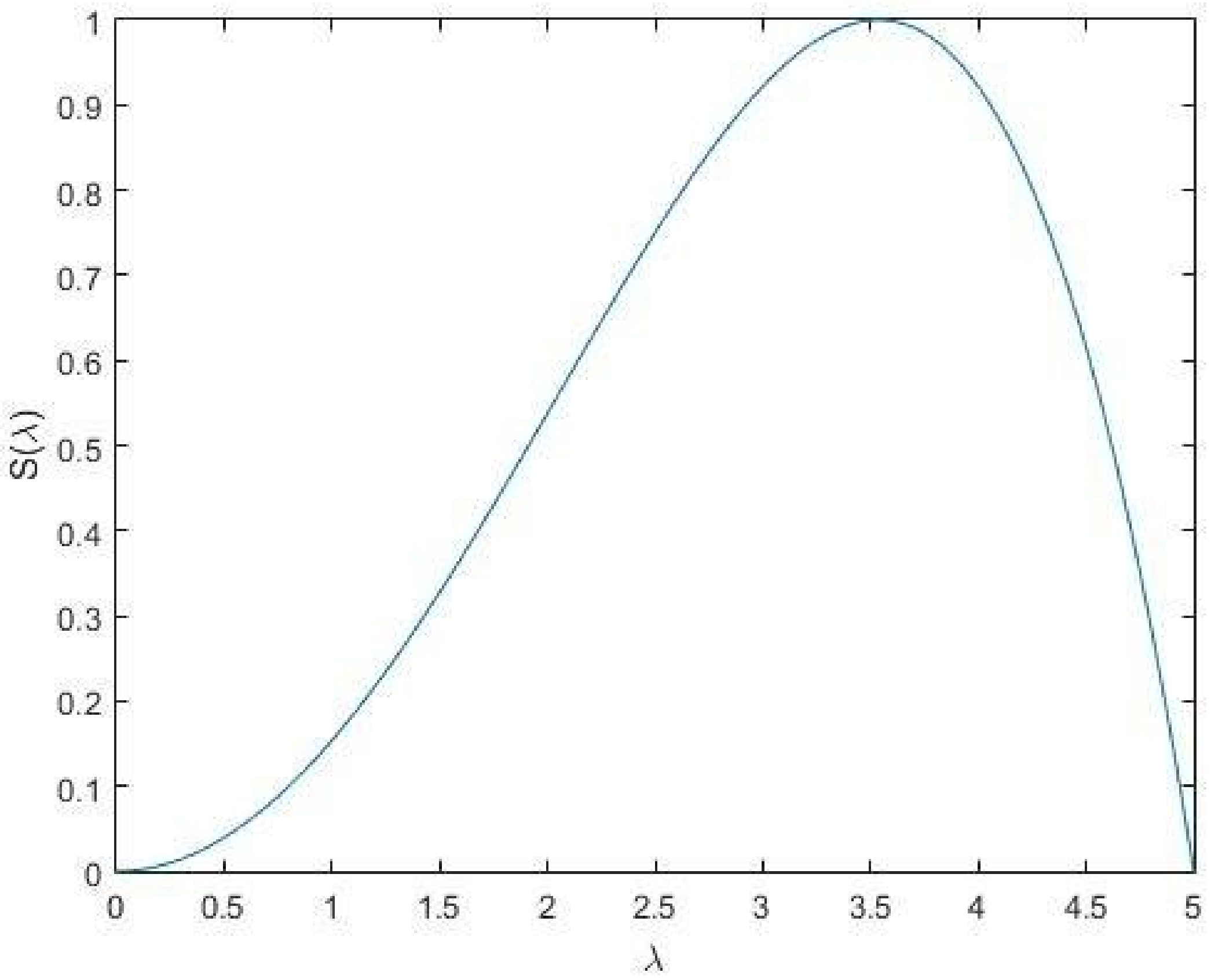
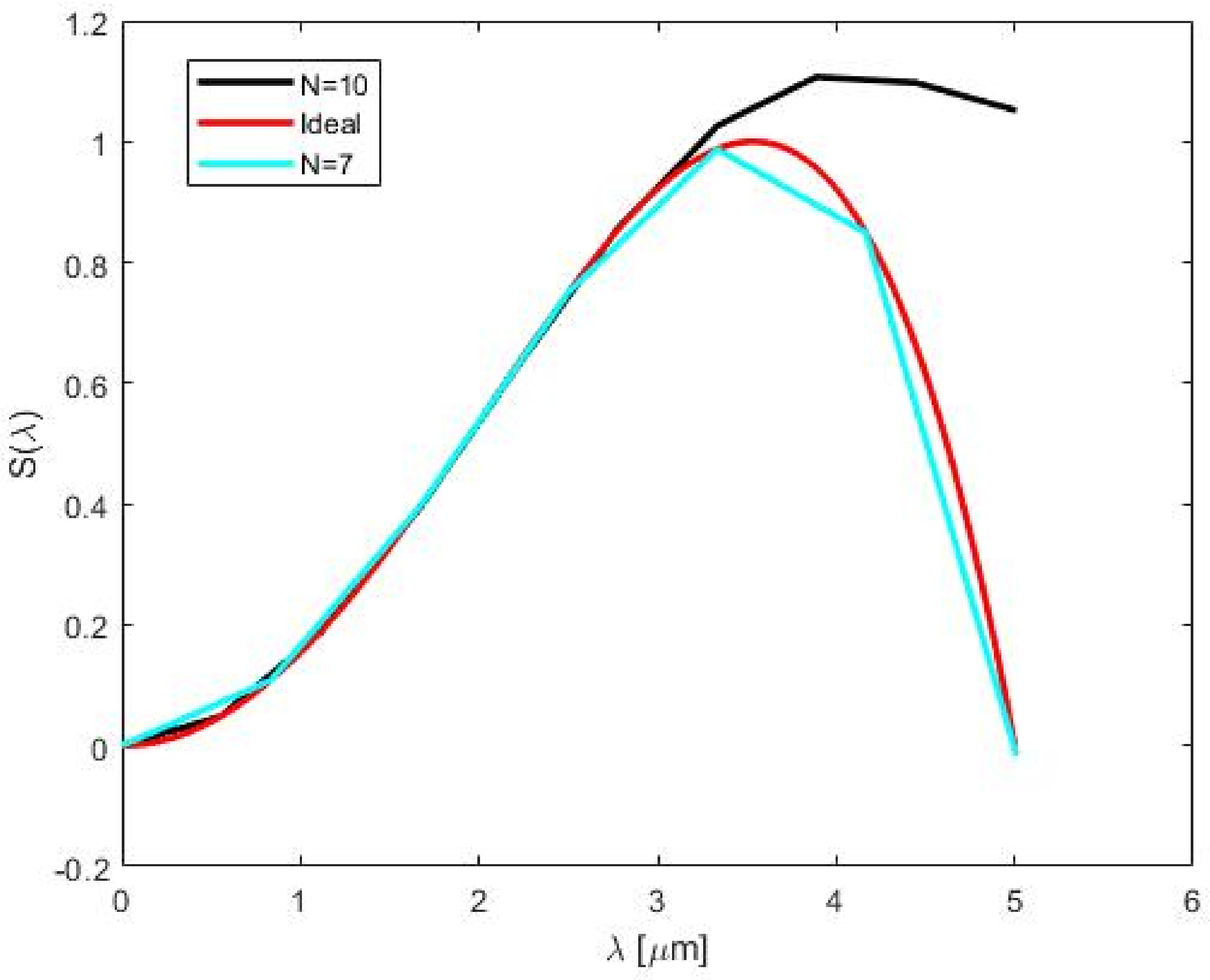
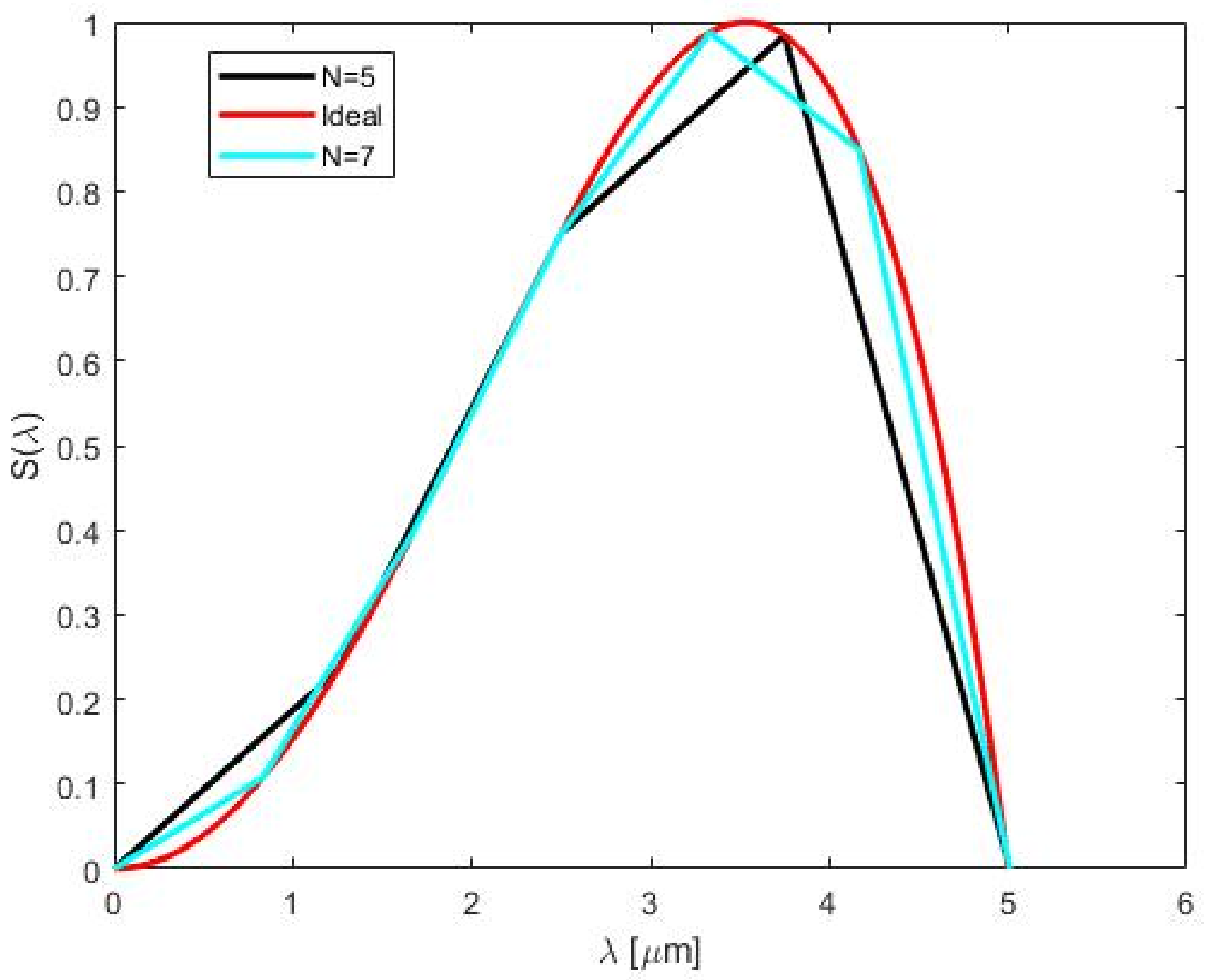
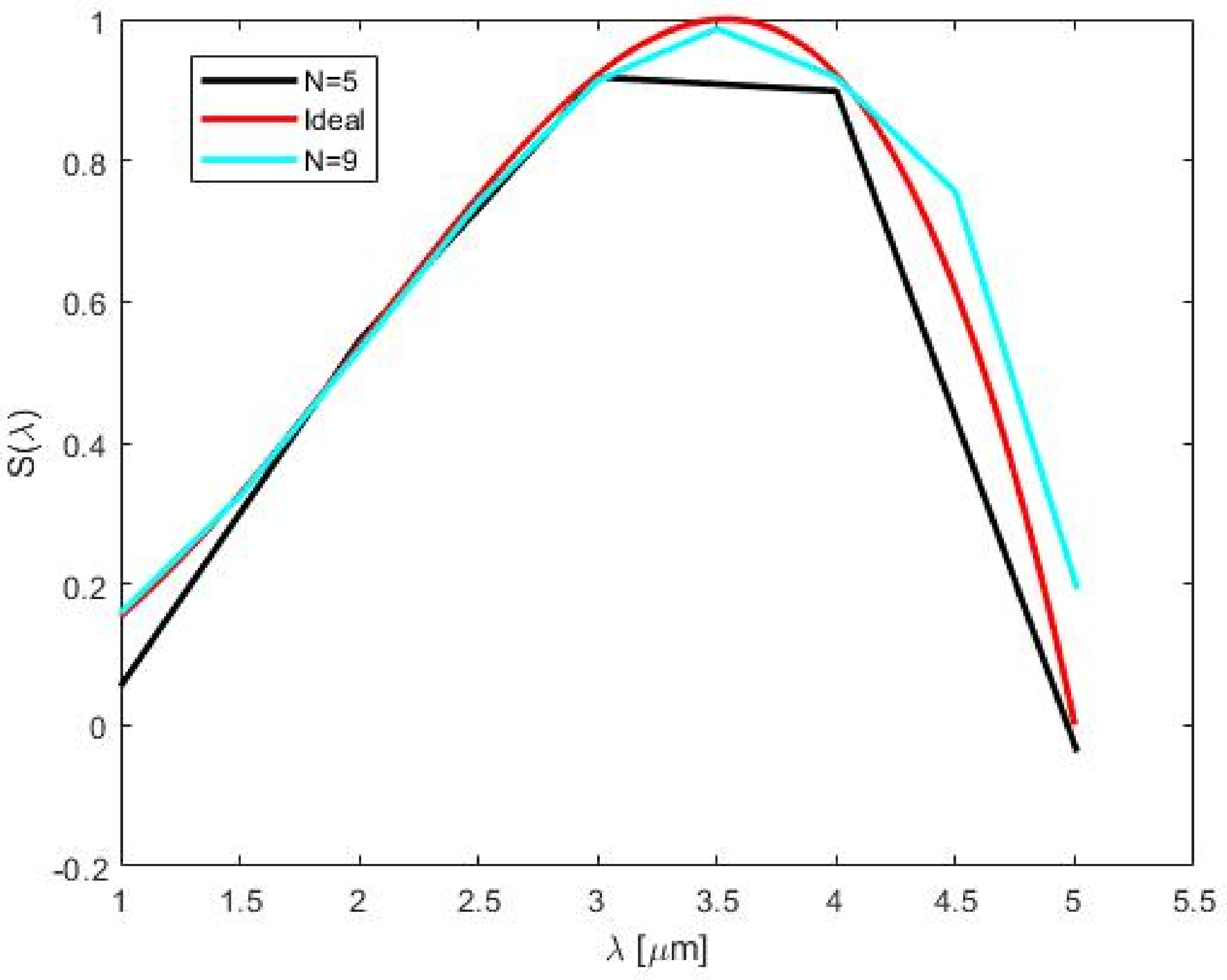
5. Results
5.1. Power Series Approximation
5.2. Laguerre Polynomials Approximation
5.3. Hermite Polynomials Approximation
5.4. Approximation with Sinc Functions
6. Conclusions
7. Patents
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NETD | Noise equivalent temperature difference |
Appendix A. Measurement Error Analysis
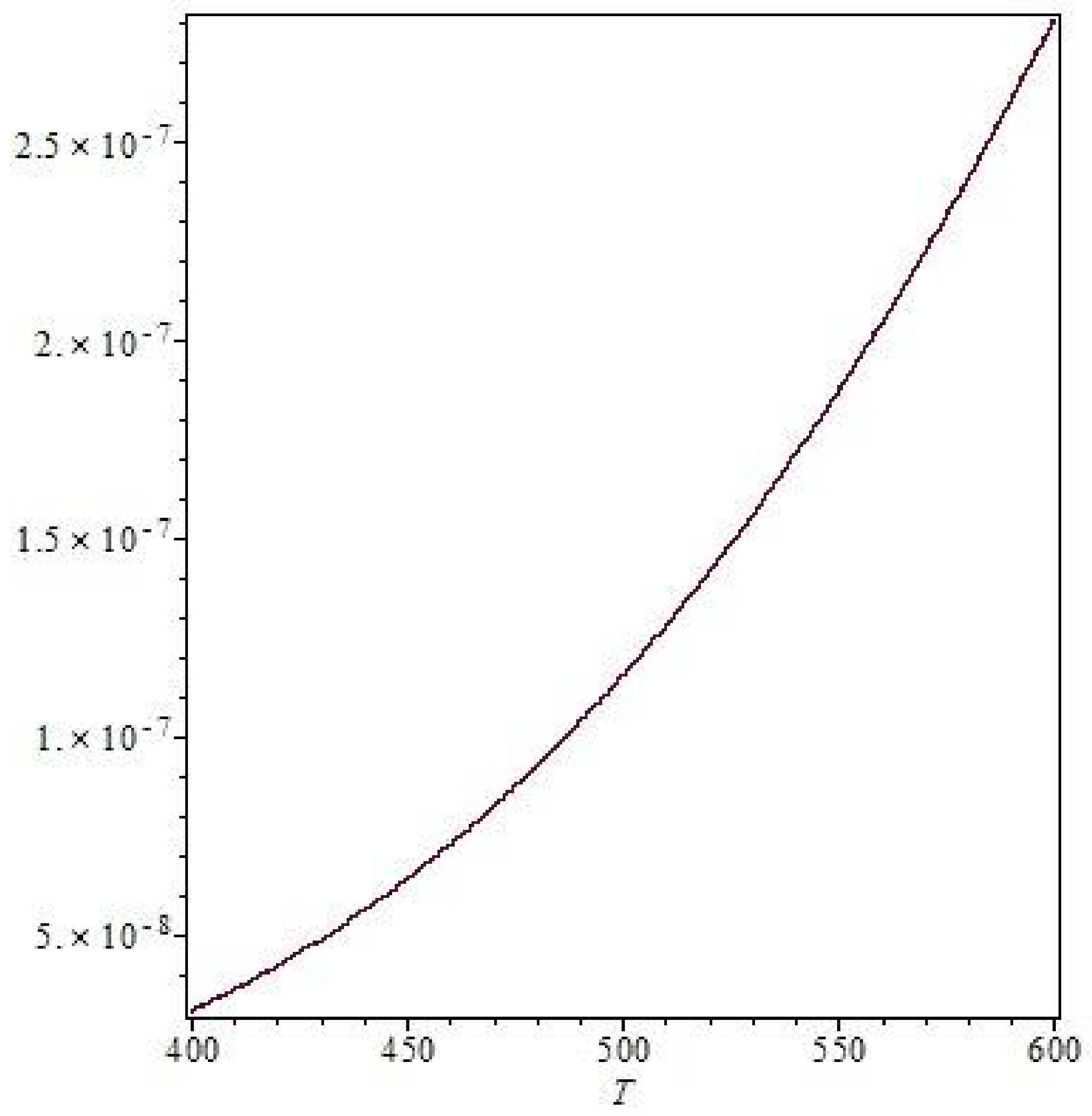
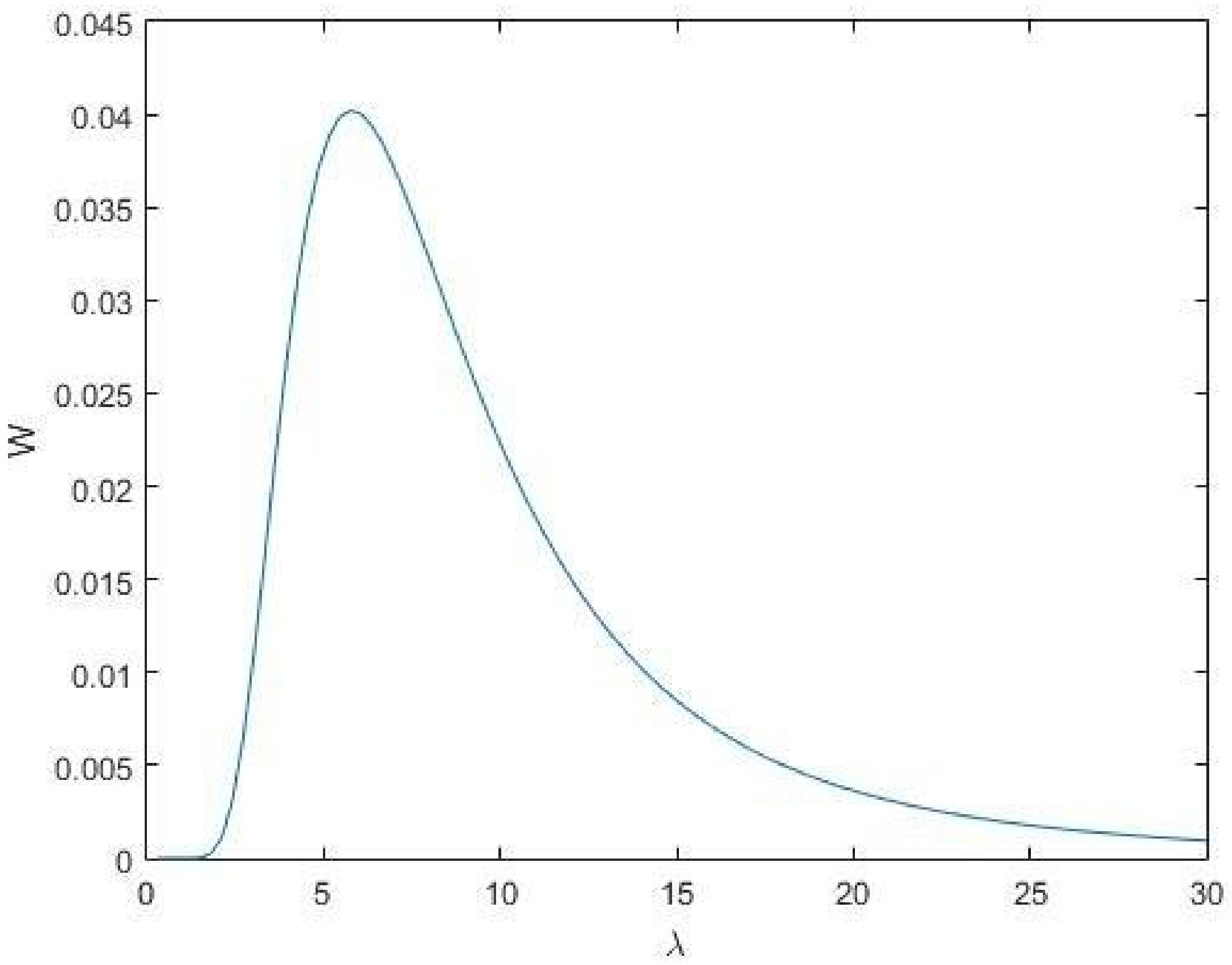
- Addressing the integral (Equation (2)) one can analyze the variation with respect to the temperature of the black body:considering a black body temperature of between 400 and 600 K; the derivative of the previous one is less than 1. It follows that using a perfectly calibrated black body, the error in the measurement of the temperature does not affect the integral (Figure A1).Figure A1. at according to the temperature of black-body.
- With regard to the error introduced in the voltage, one can write the equation (Equation (18)) in which the vector is given by the voltage measurements V:We assume that:The a coefficients can be written as:Resolving Equation (A4) with respect to one obtains:Then a small variation of V results in a small variation of a.
Appendix A.1. Power Series Approximation

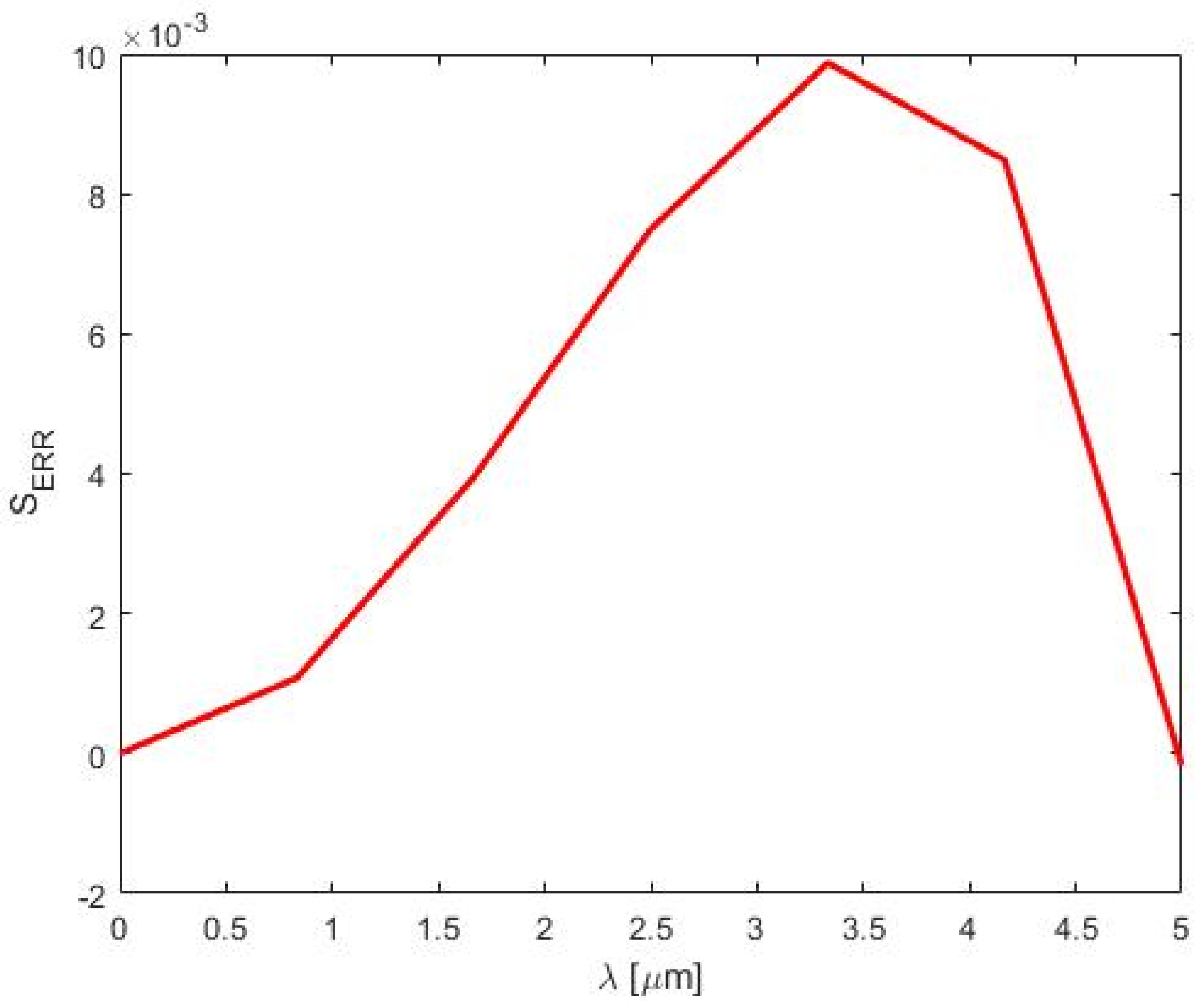
Appendix A.2. Laguerre Polynomials Approximation


Appendix A.3. Hermite Polynomials Approximation
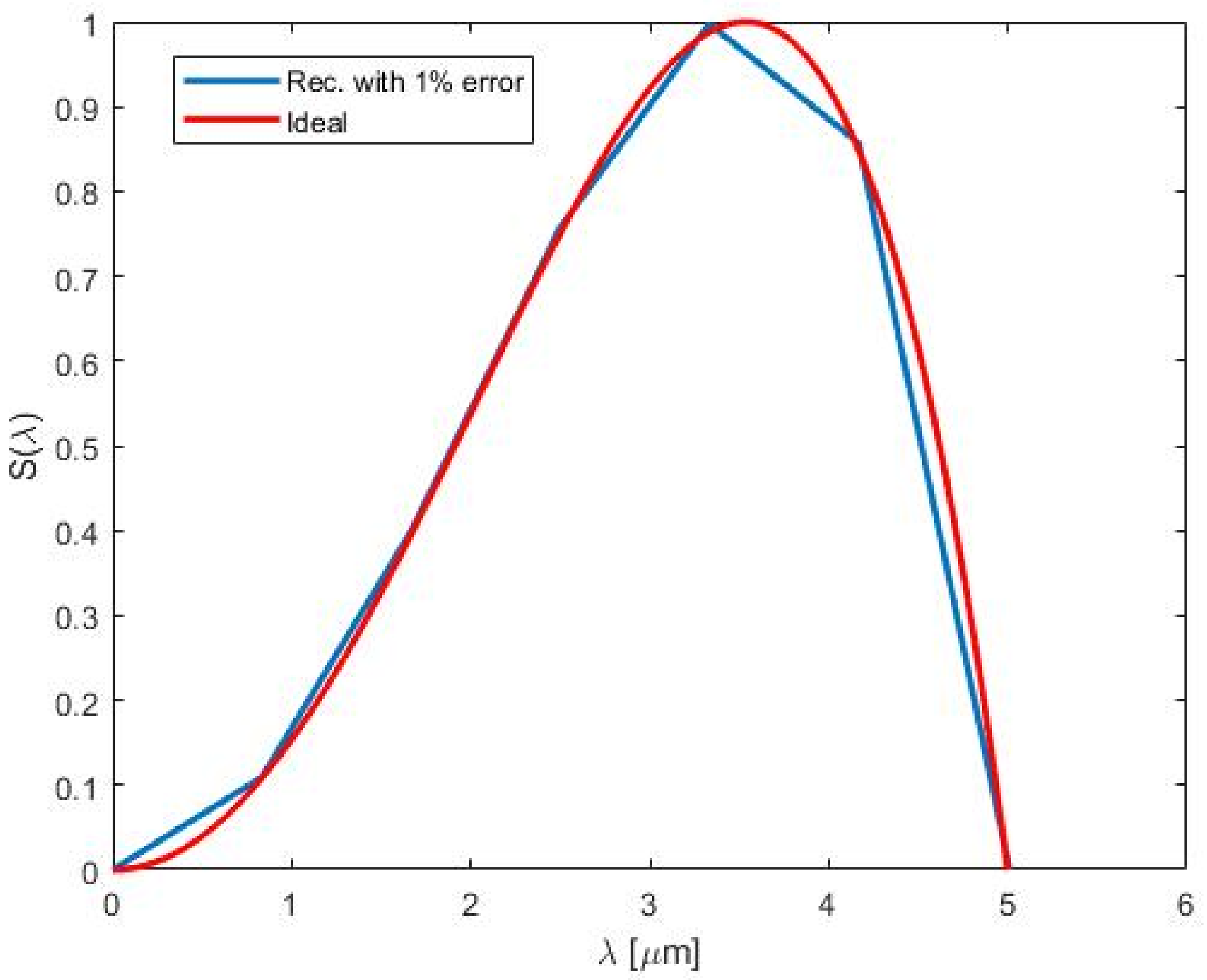

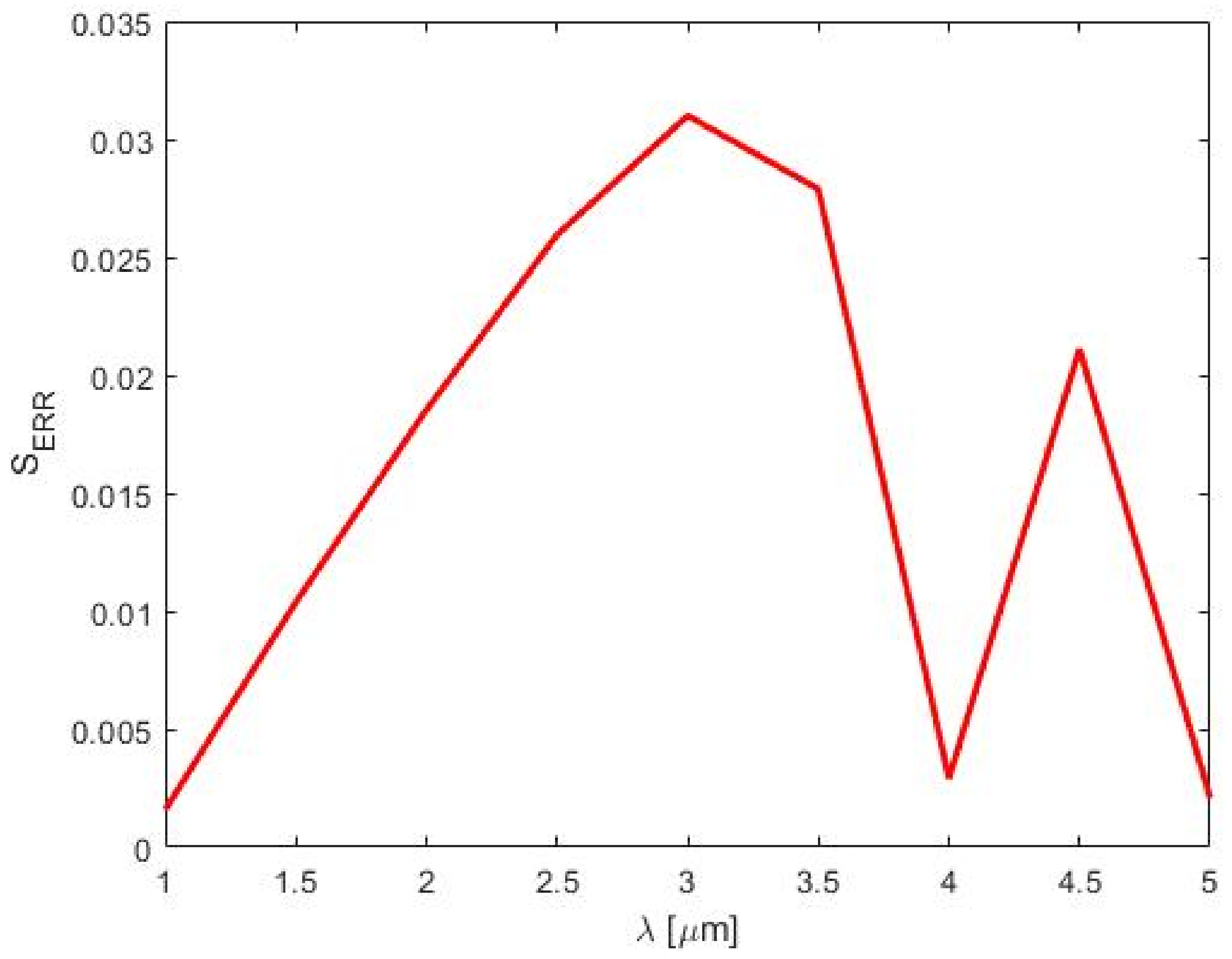
Appendix A.4. Approximation with Sinc Functions

References
- Jha, A.R. Infrared Tecnology: Applications to Electro-Optics, Photonics Devices and Sensors; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Vincent, J.D.; Hodges, S.E.; Vampola, J.; Stegall, M.; Pierce, G. Fundamentals of Infrared and Visible Detector Operation and Testing; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Vollemer, M.; Mollmann, K.P. Infrared Thermal Imaging: Fundamentals, Reserarch and Applications; WILEY-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2018. [Google Scholar]
- Richard, D.H., Jr. Infrared System Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Keyes, R.J. (Ed.) Optical and Infrared Detectors; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Miller, J.L.; Friedman, E. Photonics Rules of Thumb: Optics, Electro-Optics, Fiber Optics, and Lasers; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
- Ahmed, S. Physics and Engineering of Radiation Detection; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Riazimehr, S.; Bablich, A.; Schneider, D.; Kataria, S.; Passi, V.; Yim, C.; Duesberg, G.S.; Lemme, M.C. Spectral sensitivity of graphene/silicon heterojunction photodetectors. Solid-State Electron. 2016, 115, 207–212. [Google Scholar] [CrossRef]
- Faria, L.A.; Nohra, L.F.M.; Gomes, N.A.S.; Alves, F.D.P. A high-performance test-bed dedicated for responsivity measurements of infrared photodetectors in a wide band of low temperatures. Int. J. Optoelectron. Eng. 2012, 2, 12–17. [Google Scholar] [CrossRef]
- Willardson, R.K.; Beer, A.C. (Eds.) Semiconductors and Semimetals, Volume 12: Infrared Detectors II; Academic Press: Cambridge, MA, USA, 1977. [Google Scholar]
- Lloyd, J.M. Thermal Imaging Systems; Springer: New York, NY, USA, 1975. [Google Scholar]
- Kingston, R.H. Detection of Optical and Infrared Radiation; Springer: Berlin/Heidelberg, Germany, 1978. [Google Scholar]
- Arrasmith, W.W. System Engineering and Analysis of Electro-Optical and Infrared Systems; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Polyanin, A.D.; Manzhirov, A.V. Handbook of Integral Equations; Chapman and Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Wolfe, W.L. Infrared Design Examples; SPIE Press: Bellingham, WA, USA, 1999. [Google Scholar]
- Wolfe, W.L. Introduction to Infrared System Design; SPIE Press: Bellingham, WA, USA, 1996. [Google Scholar]
- Willers, C.J. Electro-Optical System Analysis and Design: A Radiometry Perspective; SPIE Press: Bellingham, WA, USA, 2013. [Google Scholar]
- Willardson, R.K.; Beer, A.C. (Eds.) Semiconductors and Semimetals, Volume 5: Infrared Detectors; Academic Press: Cambridge, MA, USA, 1970. [Google Scholar]
- Kinch, M.A. Fundamentals of Infrared Detector Materials; SPIE Press: Bellingham, WA, USA, 2007. [Google Scholar]
- Saxena, P.K. Infrared Photodetectors: Some Techiniques for Modeling and Simulation; LAP Lambert Academic Publishing: Saarbruecken, Germany, 2018. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liberati, R.M.; Del Paggio, A.; Rossi, M. Photodetector Spectral Response Estimation Using Black Body Radiation. Physics 2019, 1, 360-374. https://doi.org/10.3390/physics1030026
Liberati RM, Del Paggio A, Rossi M. Photodetector Spectral Response Estimation Using Black Body Radiation. Physics. 2019; 1(3):360-374. https://doi.org/10.3390/physics1030026
Chicago/Turabian StyleLiberati, Riccardo Maria, Alessio Del Paggio, and Massimiliano Rossi. 2019. "Photodetector Spectral Response Estimation Using Black Body Radiation" Physics 1, no. 3: 360-374. https://doi.org/10.3390/physics1030026
APA StyleLiberati, R. M., Del Paggio, A., & Rossi, M. (2019). Photodetector Spectral Response Estimation Using Black Body Radiation. Physics, 1(3), 360-374. https://doi.org/10.3390/physics1030026