Fractional Prabhakar Derivative in Diffusion Equation with Non-Static Stochastic Resetting
Abstract
:1. Introduction
2. Preliminary Concepts about Tempered Fractional Calculus
3. Non-Static Stochastic Resetting Theory
3.1. Non-Static Stochastic Resetting: Diffusion Equation
3.2. Non-Static Stochastic Resetting: Fractional Caputo Diffusion Equation
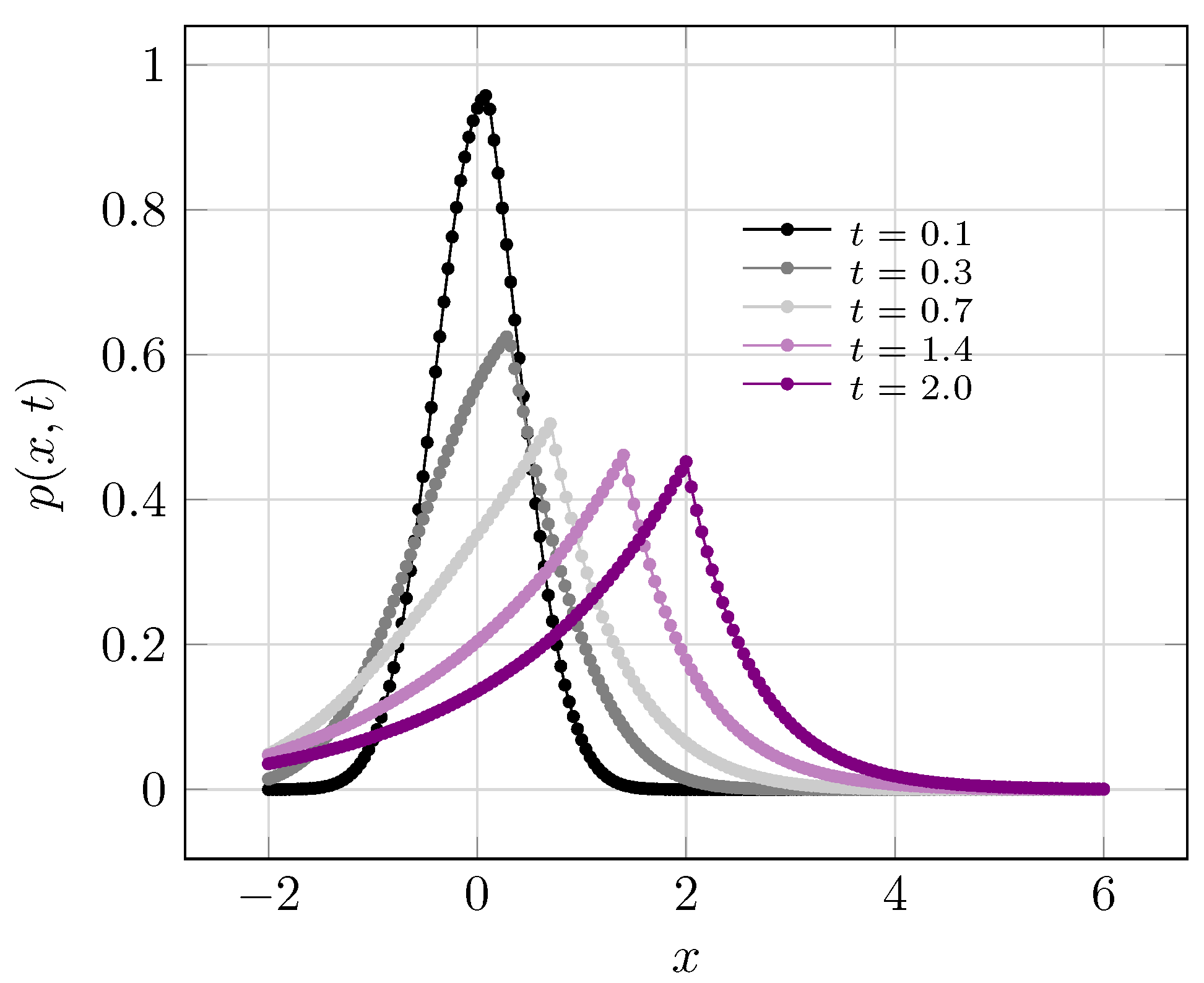
3.3. Non-Static Stochastic Resetting: Fractional Prabhakar Diffusion Equation
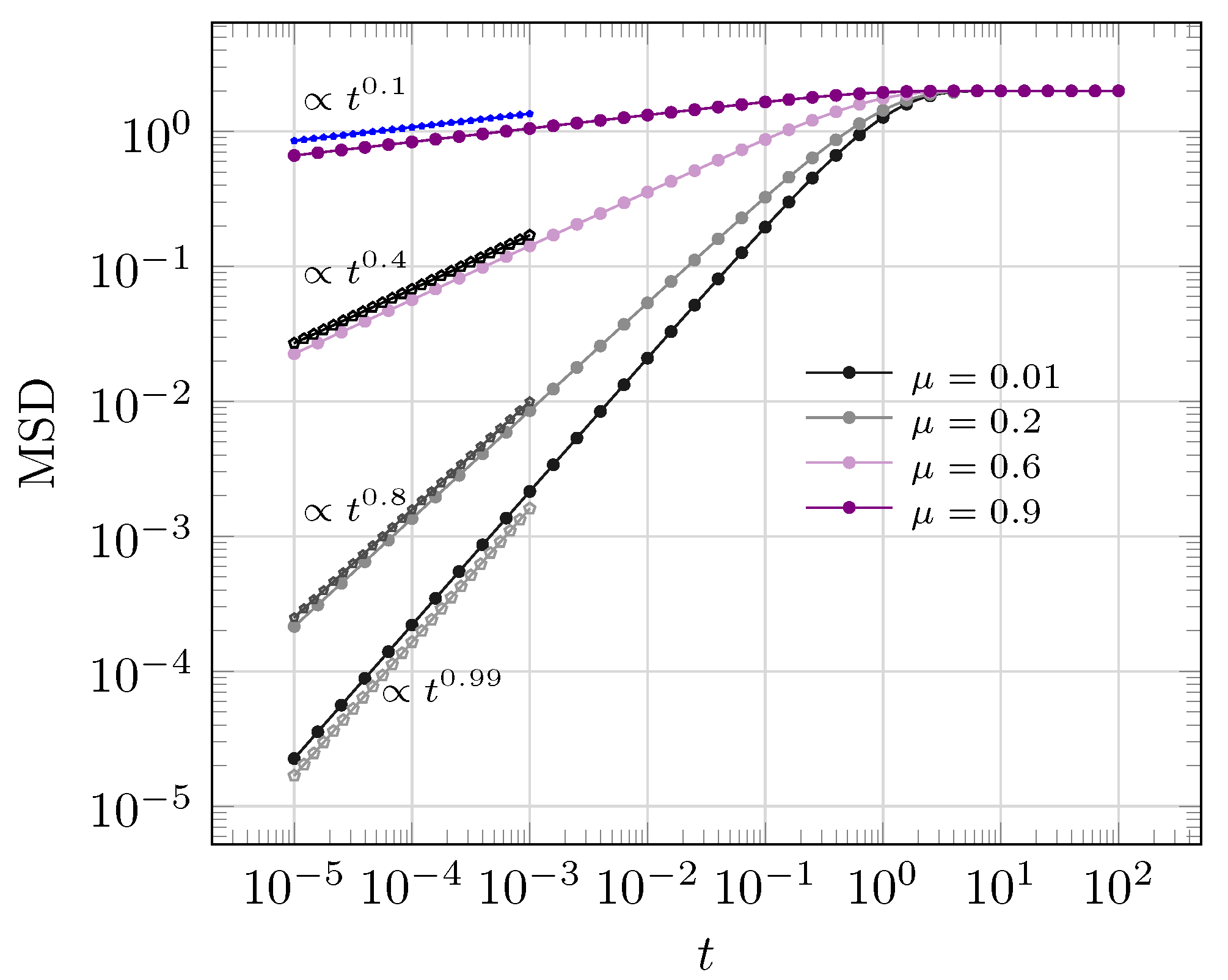
3.4. MSD and Anomalous Diffusion Phenomena
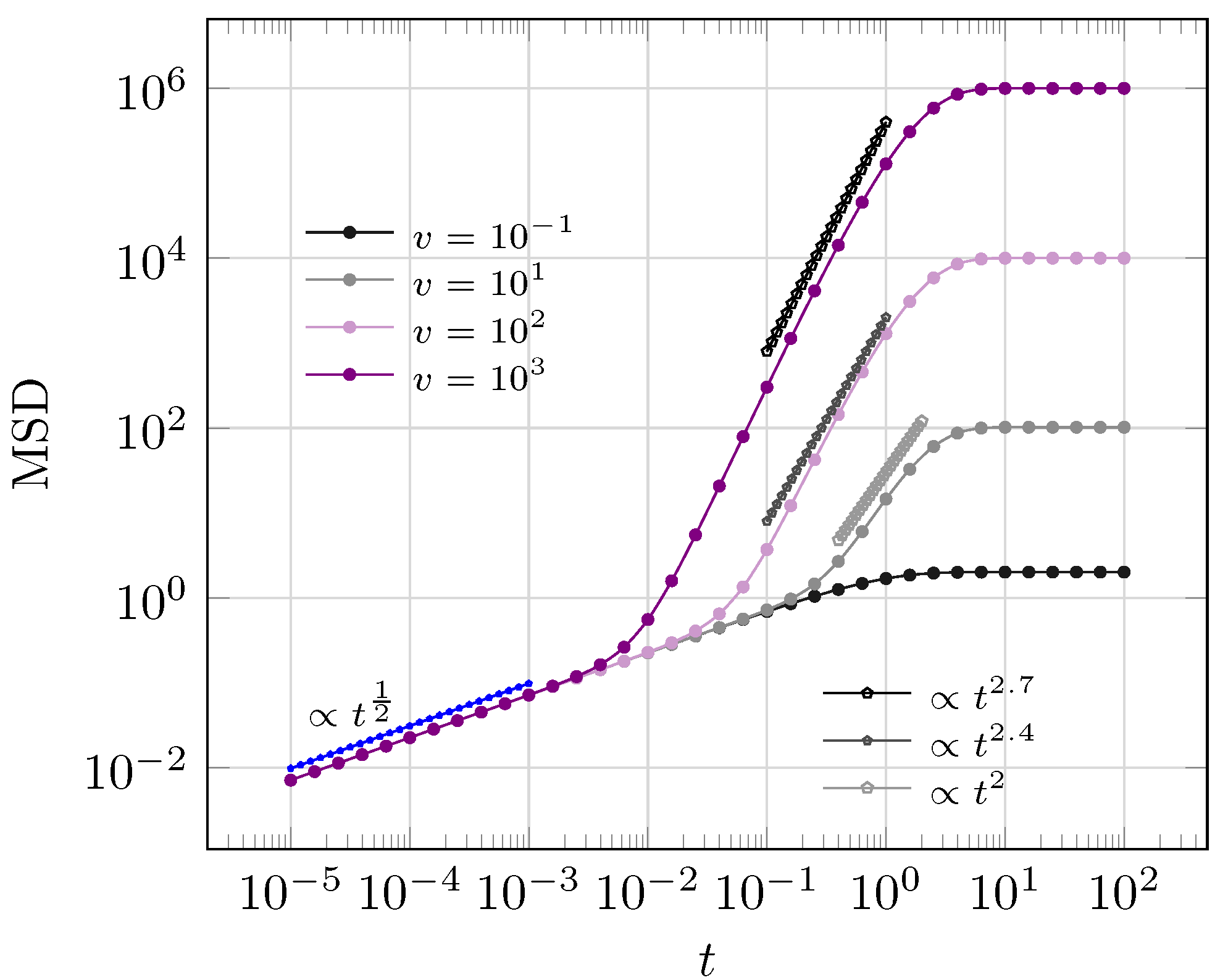
4. The Non-Static Stochastic Resetting Theory on Presence of Forces and Multiple Resetting Points
5. Conclusions
- Usual diffusion;
- Fractional Caputo diffusion;
- Fractional Prabhakar diffusion;
Funding
Acknowledgments
Conflicts of Interest
References
- Klages, R. Search for food of birds, fish and insects. In Diffusive Spreading in Nature, Technology and Society; Springer: Berlin, Germany, 2018; pp. 49–69. [Google Scholar]
- Noetel, J.; Freitas, V.; Macau, E.; Schimansky-Geier, L. Optimal noise in a stochastic model for local search. Phys. Rev. E 2018, 98, 022128. [Google Scholar] [CrossRef] [PubMed]
- Reuveni, S. Optimal stochastic restart renders fluctuations in first passage times universal. Phys. Rev. Lett. 2016, 116, 170601. [Google Scholar] [CrossRef] [PubMed]
- Pal, A.; Kundu, A.; Evans, M.R. Diffusion under time-dependent resetting. J. Phys. A Math. Theor. 2016, 49, 225001. [Google Scholar] [CrossRef] [Green Version]
- Belan, S. Restart could optimize the probability of success in a Bernoulli trial. Phys. Rev. Lett. 2018, 120, 080601. [Google Scholar] [CrossRef] [PubMed]
- Berg, O.G.; Winter, R.B.; Von Hippel, P.H. Diffusion-driven mechanisms of protein translocation on nucleic acids. 1. Models and theory. Biochemistry 1981, 20, 6929–6948. [Google Scholar] [CrossRef] [PubMed]
- Coppey, M.; Bénichou, O.; Voituriez, R.; Moreau, M. Kinetics of target site localization of a protein on DNA: A stochastic approach. Biophys. J. 2004, 87, 1640–1649. [Google Scholar] [CrossRef] [PubMed]
- Lomholt, M.A.; van den Broek, B.; Kalisch, S.M.J.; Wuite, G.J.; Metzler, R. Facilitated diffusion with DNA coiling. Proc. Natl. Acad. Sci. USA 2009, 106, 8204–8208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Evans, M.R.; Majumdar, S.N. Run and tumble particle under resetting: A renewal approach. J. Phys. A Math. Theor. 2018, 51, 475003. [Google Scholar] [CrossRef]
- Evans, M.R.; Majumdar, S.N. Diffusion with stochastic resetting. Phys. Rev. Lett. 2011, 106, 160601. [Google Scholar] [CrossRef] [PubMed]
- Majumdar, S.N.; Sabhapandit, S.; Schehr, G. Dynamical transition in the temporal relaxation of stochastic processes under resetting. Phys. Rev. E 2015, 91, 052131. [Google Scholar] [CrossRef] [PubMed]
- Durang, X.; Henkel, M.; Park, H. The statistical mechanics of the coagulation–diffusion process with a stochastic reset. J. Phys. A Math. Theor. 2014, 47, 045002. [Google Scholar] [CrossRef] [Green Version]
- Eule, S.; Metzger, J.J. Non-equilibrium steady states of stochastic processes with intermittent resetting. New J. Phys. 2016, 18, 033006. [Google Scholar] [CrossRef] [Green Version]
- Roldán, É.; Lisica, A.; Sánchez-Taltavull, D.; Grill, S.W. Stochastic resetting in backtrack recovery by RNA polymerases. Phys. Rev. E 2016, 93, 062411. [Google Scholar] [CrossRef] [PubMed]
- Risken, H. Fokker-Planck Equation; Springer: Berlin, Germany, 1996; pp. 63–95. [Google Scholar]
- Frank, T.D. Nonlinear Fokker-Planck Equations: Fundamentals and Applications; Springer Science & Business Media: Berlin, Germany, 2005. [Google Scholar]
- Tarasov, V.E. Fractional hydrodynamic equations for fractal media. Ann. Phys. 2005, 318, 286–307. [Google Scholar] [CrossRef] [Green Version]
- Metzler, R.; Barkai, E.; Klafter, J. Deriving fractional Fokker-Planck equations from a generalised master equation. EPL Europhys. Lett. 1999, 46, 431. [Google Scholar] [CrossRef]
- Metzler, R.; Barkai, E.; Klafter, J. Anomalous diffusion and relaxation close to thermal equilibrium: A fractional Fokker-Planck equation approach. Phys. Rev. Lett. 1999, 82, 3563. [Google Scholar] [CrossRef]
- Lua, R.C.; Grosberg, A.Y. First passage times and asymmetry of DNA translocation. Phys. Rev. E 2005, 72, 061918. [Google Scholar] [CrossRef] [PubMed]
- Dieterich, P.; Klages, R.; Preuss, R.; Schwab, A. Anomalous dynamics of cell migration. Proc. Natl. Acad. Sci. USA 2008, 105, 459–463. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lomholt, M.A.; Ambjörnsson, T.; Metzler, R. Optimal target search on a fast-folding polymer chain with volume exchange. Phys. Rev. Lett. 2005, 95, 260603. [Google Scholar] [CrossRef] [PubMed]
- Sokolov, I.M. Models of anomalous diffusion in crowded environments. Soft Matter 2012, 8, 9043–9052. [Google Scholar] [CrossRef]
- Barkai, E.; Metzler, R.; Klafter, J. From continuous time random walks to the fractional Fokker-Planck equation. Phys. Rev. E 2000, 61, 132. [Google Scholar] [CrossRef]
- Barkai, E. Fractional Fokker-Planck equation, solution, and application. Phys. Rev. E 2001, 63, 046118. [Google Scholar] [CrossRef] [PubMed]
- del Castillo-Negrete, D. Fractional diffusion models of nonlocal transport. Phys. Plasmas 2006, 13, 082308. [Google Scholar] [CrossRef]
- Hristov, J. Diffusion models with weakly singular kernels in the fading memories. Therm. Sci. 2015, 19, 947–957. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- dos Santos, M. Non-Gaussian Distributions to Random Walk in the Context of Memory Kernels. Fractal Fract. 2018, 2, 20. [Google Scholar] [CrossRef]
- Tomovski, Ž.; Sandev, T.; Metzler, R.; Dubbeldam, J. Generalized space–time fractional diffusion equation with composite fractional time derivative. Phys. A Stat. Mech. Appl. 2012, 391, 2527–2542. [Google Scholar] [CrossRef]
- Deng, W.; Barkai, E. Ergodic properties of fractional Brownian-Langevin motion. Phys. Rev. E 2009, 79, 011112. [Google Scholar] [CrossRef] [PubMed]
- Jeon, J.H.; Tejedor, V.; Burov, S.; Barkai, E.; Selhuber-Unkel, C.; Berg-Sørensen, K.; Oddershede, L.; Metzler, R. In vivo anomalous diffusion and weak ergodicity breaking of lipid granules. Phys. Rev. Lett. 2011, 106, 048103. [Google Scholar] [CrossRef] [PubMed]
- Richardson, L.F. Atmospheric diffusion shown on a distance-neighbour graph. Proc. R. Soc. Lond. A 1926, 110, 709–737. [Google Scholar] [CrossRef]
- Scher, H.; Montroll, E.W. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B 1975, 12, 2455. [Google Scholar] [CrossRef]
- Atangana, A.; Koca, I. Chaos in a simple nonlinear system with Atangana–Baleanu derivatives with fractional order. Chaos Solitons Fractals 2016, 89, 447–454. [Google Scholar] [CrossRef]
- dos Santos, M.A.F.; Gomez, I.S. A fractional Fokker–Planck equation for non-singular kernel operators. J. Stat. Mech. Theory Exp. 2018, 2018, 123205. [Google Scholar] [CrossRef]
- Longhi, S. Fractional Schrödinger equation in optics. Opt. Lett. 2015, 40, 1117–1120. [Google Scholar] [CrossRef] [PubMed]
- Giusti, A.; Colombaro, I. Prabhakar-like fractional viscoelasticity. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 138–143. [Google Scholar] [CrossRef] [Green Version]
- Sabzikar, F.; Meerschaert, M.M.; Chen, J. Tempered fractional calculus. J. Comput. Phys. 2015, 293, 14–28. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prabhakar, T.R. A singular integral equation with a generalized Mittag Leffler function in the kernel. Yokohama Math. J. 1971, 19, 7–15. [Google Scholar]
- Loverro, A. Fractional Calculus: History, Definitions and Applications for the Engineer; Rapport Technique; Univeristy of Notre Dame, Department of Aerospace and Mechanical Engineering: Notre Dame, IN, USA, 2004; pp. 1–28. [Google Scholar]
- Ross, B. The development of fractional calculus 1695–1900. Hist. Math. 1977, 4, 75–89. [Google Scholar] [CrossRef] [Green Version]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Gorenflo, R.; Kilbas, A. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin, Germany, 2014. [Google Scholar]
- Bouchaud, J.P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 1990, 195, 127–293. [Google Scholar] [CrossRef]
- Laskin, N. Fractional schrödinger equation. Phys. Rev. E 2002, 66, 056108. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Deng, W.; Barkai, E. Tempered fractional Feynman-Kac equation: Theory and examples. Phys. Rev. E 2016, 93, 032151. [Google Scholar] [CrossRef] [PubMed]
- Meerschaert, M.M.; Sabzikar, F. Tempered fractional Brownian motion. Stat. Probab. Lett. 2013, 83, 2269–2275. [Google Scholar] [CrossRef]
- Li, C.; Deng, W. High order schemes for the tempered fractional diffusion equations. Adv. Comput. Math. 2016, 42, 543–572. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Saigo, M.; Saxena, R.K. Generalized Mittag-Leffler function and generalized fractional calculus operators. Integr. Transform. Spec. Funct. 2004, 15, 31–49. [Google Scholar] [CrossRef]
- Garra, R.; Gorenflo, R.; Polito, F.; Tomovski, Ž. Hilfer–Prabhakar derivatives and some applications. Appl. Math. Comput. 2014, 242, 576–589. [Google Scholar] [CrossRef] [Green Version]
- Colombaro, I.; Giusti, A.; Vitali, S. Storage and dissipation of energy in Prabhakar viscoelasticity. Mathematics 2018, 6, 15. [Google Scholar] [CrossRef]
- Liang, X.; Yang, Y.G.; Gao, F.; Yang, X.J.; Xue, Y. Anomalous Advection-Dispersion Equations within General Fractional-Order Derivatives: Models and Series Solutions. Entropy 2018, 20, 78. [Google Scholar] [CrossRef]
- Sandev, T.; Deng, W.; Xu, P. Models for characterizing the transition among anomalous diffusions with different diffusion exponents. J. Phys. A Math. Theor. 2018, 51, 405002. [Google Scholar] [CrossRef]
- Stanislavsky, A.; Weron, A. Transient anomalous diffusion with Prabhakar-type memory. J. Chem. Phys. 2018, 149, 044107. [Google Scholar] [CrossRef] [PubMed]
- Liemert, A.; Sandev, T.; Kantz, H. Generalized Langevin equation with tempered memory kernel. Phys. A Stat. Mech. Appl. 2017, 466, 356–369. [Google Scholar] [CrossRef]
- Sandev, T. Generalized Langevin equation and the Prabhakar derivative. Mathematics 2017, 5, 66. [Google Scholar] [CrossRef]
- Fernandez, A.; Baleanu, D.; Srivastava, H. Series representations for fractional-calculus operators involving generalised Mittag-Leffler functions. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 517–527. [Google Scholar] [CrossRef]
- Agarwal, P.; Al-Mdallal, Q.; Cho, Y.J.; Jain, S. Fractional differential equations for the generalized Mittag-Leffler function. Adv. Differ. Equ. 2018, 2018, 58. [Google Scholar] [CrossRef] [Green Version]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and Application to Heat Transfer Model. arXiv, 2016; arXiv:1602.03408. [Google Scholar]
- Koca, I. Modelling the spread of Ebola virus with Atangana-Baleanu fractional operators. Eur. Phys. J. Plus 2018, 133, 100. [Google Scholar] [CrossRef]
- Avcı, D.; Yetim, A. Analytical solutions to the advection-diffusion equation with the Atangana-Baleanu derivative over a finite domain. Balıkesir Üniversitesi Fen Bilimleri Enstitüsü Dergisi 2018, 20, 382–395. [Google Scholar] [CrossRef]
- Majumdar, S.N.; Oshanin, G. Spectral content of fractional Brownian motion with stochastic reset. J. Phys. A Math. Theor. 2018, 51, 435001. [Google Scholar] [CrossRef]
- Boyer, D.; Evans, M.R.; Majumdar, S.N. Long time scaling behaviour for diffusion with resetting and memory. J. Stat. Mech. Theory Exp. 2017, 2017, 023208. [Google Scholar] [CrossRef] [Green Version]
- Evans, M.R.; Majumdar, S.N.; Mallick, K. Optimal diffusive search: Nonequilibrium resetting versus equilibrium dynamics. J. Phys. A Math. Theor. 2013, 46, 185001. [Google Scholar] [CrossRef]
- Pal, A.; Reuveni, S. First passage under restart. Phys. Rev. Lett. 2017, 118, 030603. [Google Scholar] [CrossRef] [PubMed]
- Masoliver, J. Telegraphic processes with stochastic resetting. Phys. Rev. E 2019, 99, 012121. [Google Scholar] [CrossRef] [PubMed]
- Villarroel, J.; Montero, M. Continuous-time ballistic process with random resets. J. Stat. Mech. Theory Exp. 2018, 2018, 123204. [Google Scholar] [CrossRef]
- Pal, A.; Rahav, S. Integral fluctuation theorems for stochastic resetting systems. Phys. Rev. E 2017, 96, 062135. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fuchs, J.; Goldt, S.; Seifert, U. Stochastic thermodynamics of resetting. EPL (Europhys. Lett.) 2016, 113, 60009. [Google Scholar] [CrossRef] [Green Version]
- Henry, B.I.; Wearne, S.L. Fractional reaction–diffusion. Phys. A Stat. Mech. Appl. 2000, 276, 448–455. [Google Scholar] [CrossRef] [Green Version]
- Rebenshtok, A.; Barkai, E. Weakly non-ergodic statistical physics. J. Stat. Phys. 2008, 133, 565–586. [Google Scholar] [CrossRef]
- Thiel, F.; Sokolov, I.M. Weak ergodicity breaking in an anomalous diffusion process of mixed origins. Phys. Rev. E 2014, 89, 012136. [Google Scholar] [CrossRef] [PubMed]
- Barkai, E.; Garini, Y.; Metzler, R. Strange kinetics of single molecules in living cells. Phys. Today 2012, 65, 29. [Google Scholar] [CrossRef]
- Metzler, R.; Schick, W.; Kilian, H.G.; Nonnenmacher, T.F. Relaxation in filled polymers: A fractional calculus approach. J. Chem. Phys. 1995, 103, 7180–7186. [Google Scholar] [CrossRef]
- Garra, R.; Garrappa, R. The Prabhakar or three parameter Mittag–Leffler function: Theory and application. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 314–329. [Google Scholar] [CrossRef] [Green Version]
- Giusti, A. A comment on some new definitions of fractional derivative. Nonlinear Dyn. 2018, 93, 1757–1763. [Google Scholar] [CrossRef] [Green Version]
- Mainardi, F.; Pagnini, G.; Saxena, R. Fox H functions in fractional diffusion. J. Comput. Appl. Math. 2005, 178, 321–331. [Google Scholar] [CrossRef] [Green Version]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Volume 4: Direct Laplace Transforms. Volume 5: Inverse Laplace Transforms. In Integrals and Series; CRC Press: Boca Raton, FL, USA, 1992. [Google Scholar]
- Pearson, K. The problem of the random walk. Nature 1905, 72, 342. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
dos Santos, M.A.F. Fractional Prabhakar Derivative in Diffusion Equation with Non-Static Stochastic Resetting. Physics 2019, 1, 40-58. https://doi.org/10.3390/physics1010005
dos Santos MAF. Fractional Prabhakar Derivative in Diffusion Equation with Non-Static Stochastic Resetting. Physics. 2019; 1(1):40-58. https://doi.org/10.3390/physics1010005
Chicago/Turabian Styledos Santos, Maike A. F. 2019. "Fractional Prabhakar Derivative in Diffusion Equation with Non-Static Stochastic Resetting" Physics 1, no. 1: 40-58. https://doi.org/10.3390/physics1010005
APA Styledos Santos, M. A. F. (2019). Fractional Prabhakar Derivative in Diffusion Equation with Non-Static Stochastic Resetting. Physics, 1(1), 40-58. https://doi.org/10.3390/physics1010005




