Hierarchical Multiparty Digital Signature for Distributed Systems: Application in Intelligent Vehicle Surveillance

Abstract

The rapid expansion of distributed systems such as the Internet of Things (IoT) has increased the need for robust authentication and data integrity mechanisms to ensure public security in dynamic environments. This article presents a hierarchical multiparty digital signature (HMPS) technique designed to address the unique challenges of resource-constrained and decentralized systems. By integrating a modified ElGamal-based individual signature with linear encryption and hierarchical aggregation, HMPS delivers enhanced security through collaborative and layered signing processes. A key application is demonstrated in intelligent vehicle surveillance, where the scheme ensures the authenticity and integrity of commands and data in multi-level communication scenarios. Comprehensive security analysis confirms resistance to forgery, single points of failure, and unauthorized access. HMPS exhibits superior computational efficiency, scalability, and energy efficiency, as evidenced by comparative performance evaluations with state-of-the-art techniques. These results highlight HMPS as a highly effective solution for secure, real-time IoT applications, providing a pathway to more resilient and trustworthy distributed systems.

1. Introduction

Digital signatures are a crucial component of secure communication systems, providing essential services such as authenticity, integrity, and non-repudiation. They enable the message receiver to verify the sender’s identity, ensure that the message has not been tampered with during transmission, and prevent the sender from denying the origin of the message. This trifecta of security measures is foundational for trust in digital communications [1]. Numerous digital signature techniques have been developed, leveraging advancements in cryptographic algorithms to provide practical and scalable security mechanisms. For instance, digital signatures are instrumental in enabling secure online banking transactions, protecting intellectual property through code signing, and safeguarding sensitive communications in government and healthcare systems.

Unlike physical signatures, which can be forged or altered with relative ease, digital signatures offer a significantly higher level of security. They are inherently resistant to tampering and duplication, as they rely on complex cryptographic operations that bind the signature to both the data being signed and the signer’s private key. Furthermore, digital signatures ensure that the signers cannot later repudiate their signatures due to the mathematical linkage between the private key and the signed message.

In asymmetric cryptography, digital signature techniques rely on private keys as a key element for their operation. The digital signature—uniquely derived from the data and the private key—serves as a tamper-proof identifier, ensuring that the data originate from the intended source and have not been altered during transmission. The signing process begins with the signer using their private key—a secret known only to them—to create the digital signature, which is then transmitted along with the signed data to the recipient. On the recipient’s side, verification leverages the signer’s public key, which is mathematically linked to the private key, thus making it computationally infeasible for an attacker to forge a signature without access to the private key.

In the increasingly interconnected world of the Internet of Things (IoT) and distributed systems, the need for secure and reliable methods of authentication and data integrity has become paramount [2,3,4]. These systems often involve vast networks of devices, sensors, and stakeholders, making them particularly vulnerable to cyber attacks and data breaches. Traditional digital signature schemes, typically designed for single entities, are inadequate for addressing the complexities and vulnerabilities inherent in such environments. They fail to accommodate the collaborative nature of distributed systems, where multiple parties work together to authenticate transactions, validate messages, or reach consensus on critical decisions.

Multiparty digital signature techniques have emerged as a robust solution to address these challenges. These schemes enable several participants to collaboratively generate a single, unified digital signature, which cryptographically secures the contributions and consent of all parties involved. This collaborative approach significantly enhances trust and accountability in distributed environments, as the resulting signature serves as a verifiable record of consensus among the stakeholders. By requiring the involvement of multiple parties, multiparty digital signatures provide an additional layer of security against unauthorized activities. Malicious entities would find it exceedingly difficult to forge or tamper with the signature without detection, as doing so would necessitate the compromising of multiple independent participants.

In contrast to simply appending individual signatures after the message, this article presents a hierarchical multiparty digital signature (HMPS) technique tailored to the unique demands of IoT and distributed systems for public security. This layered aggregation approach offers several distinct advantages including scalability and efficiency; rather than transmitting and verifying a long list of individual signatures, the hierarchical scheme aggregates these into a compact signature. This reduces communication overheads and allows for batch verification, thereby enhancing computational efficiency—an essential feature in resource-constrained IoT environments. This approach has enhanced security; by organizing the signing process into multiple layers, the hierarchical approach minimizes the risk of a single point of failure. Even if one layer is compromised, the structure ensures that the integrity of the overall signature remains intact. This layered defense mechanism provides stronger resistance against forgery and unauthorized modifications.

This approach improves the management of distributed trust; the hierarchical model naturally aligns with the multi-level communication and control structures found in modern distributed systems, such as intelligent vehicle surveillance networks. It facilitates more efficient key management and trust delegation among diverse stakeholders, ensuring that security is maintained even in complex, dynamic environments. Collectively, these advantages position the HMPS scheme as a highly effective solution for real-time IoT applications, delivering superior computational efficiency, scalability, and robustness compared to traditional approaches that merely append signatures.

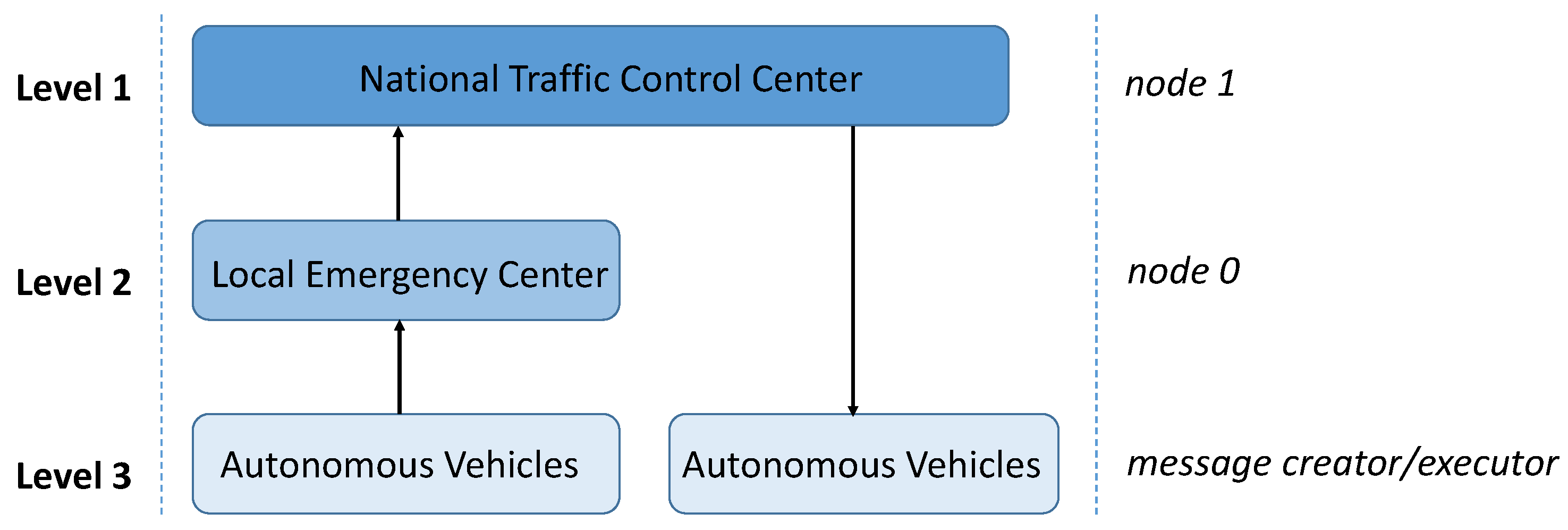
The use case described in this paper is collaborative issues detection in the surveillance of autonomous vehicle systems [5,6].

2. Related Work

Mohammed et al. [7] introduced enhancements to the ElGamal signature system, presenting a novel blind signature technique grounded in number theory operations and modular arithmetic operations. This approach offers enhanced participant anonymity by ensuring that multiple signatures of the same message yield distinct results.

The authors in [8] proposed the Shortened Complex Digital Signature Algorithm (SCDSA), leveraging short complex numbers for efficient signature and verification operations. SCDSA targets user-centric IoT devices [3], aiming to reduce communication and computational overhead on networks while ensuring secure communication.

In [9], Lavanya and Natarajan designed the Lightweight Digital Signature Algorithm (LWDSA) based on ECDSA [10] and cryptographic hash functions tailored for Wireless Sensor Networks (WSNs). However, the computational efficiency of the signature generation and verification processes remains unspecified, and validating the scheme’s efficacy in large-scale, dynamic WSN networks presents significant challenges.

The authors of [11] developed the Enhanced Digital Signature Algorithm (EDSA) to safeguard data integrity and secure access in cloud storage environments.

The authors of [12] introduced an attribute-based proxy signature scheme on lattices that is resistant to quantum attacks. This scheme combines attributes and proxy features, offering fine-grained access control. However, lattice-based methods often involve large matrix operations and storage, which can limit practical usability.

Zhou et al. [13] proposed a mixed private- and consortium-based blockchain system for secure storage of medical cyber–physical data. Their approach includes a blockchain-based threshold signature system for joint consultation, although it lacks support for multiparty signatures.

The authors of [14] introduce a solution that integrates functional signatures and multiparty ECDSA signatures to establish a multiparty functional signature tailored for private blockchains. This approach ensures verification of each transaction component, and in cases where the aggregate signature of the entire transaction cannot be verified, it identifies the specific part of the transaction that failed authentication without rejecting the entire transaction. However, its applicability remains limited to private blockchains.

In [15], the authors presented two practical protocols for multiparty EdDSA signatures, designed for both semi-honest and malicious settings. These protocols streamline operations by securely maintaining a global state, thereby eliminating the need for distributed hashing in EdDSA-based blockchains. Additionally, they enhanced the malicious protocol to withstand DoS attacks. Nonetheless, these protocols are specifically tailored for blockchain environments.

The aforementioned works suffer from many problems, such as high computational complexity, limited work environment, large data size, etc. Therefore, the proposed work aims to address these shortcomings.

3. Modified ElGamal-Based Individual Signature

The proposed technique for constructing an MPS is based on a new variant of ElGamal encryption system [16] to create the individual signature.

ElGamal is a widely adopted public key cryptographic system designed to secure digital communications [16]. Its security is based on the discrete logarithm, making it a fundamental element of modern encryption methods. ElGamal is commonly used for secure data transmission, digital signatures, and authentication protocols. The strength of its security is influenced by the size of the cryptographic keys, with larger keys providing stronger protection, though they require more computational resources. The ElGamal algorithm operates through key generation, encryption, and decryption processes, utilizing the mathematical properties of large prime numbers and modular arithmetic.

• Key Generation

Pick a prime number, p, select a private key, k, and calculate the public key, y, as illustrated in Equation (1).

$$y=g^{k}modp$$

(1)

where g is a generator.

2.

Signature

In our modified system, we put h and $h^{\prime }$ as presented in Equation (2).

$$h=Hash\left(m\right),h^{\prime }=Hash\left(h\right),$$

(2)

To sign the hash of a message, m, the signature function uses private and secret keys defined by the modified system as shown in Equations (3) and (4).

$$b=y^{r}modp$$

(3)

where r is a random number generated for each message.

$$a=k\times (h\times b-h^{\prime }\times r)mod(p-1)$$

(4)

3.

Verification

To verify a signature $\sigma =(a,b)$, Verf function uses Equation (5).

$$y^{h\times b}modp\stackrel{!}{=}{g}^a\times b^{h^{\prime }}modp$$

(5)

We have

$$\begin{array}{c}{g}^a\times b^{h^{\prime }}=g^{k\times (h\times b-h^{\prime }\times r)}\times y^{h^{\prime }\times r},\hfill \\ =g^{k\times h\times b-k\times h^{\prime }\times r}\times g^{k\times h^{\prime }\times r},\hfill \\ =g^{k\times h\times b}=y^{h\times b}.\hfill \end{array}$$

4. The Proposed HMPS Technique

The novelty of the proposed scheme is the creation of a hierarchical multiparty signing (MPS) that includes both the signature and the message in ciphertext linear computation, where this signature is calculated using the modified ElGamal cryptosystem. Our scheme adopts a symmetric-like structure where the system secret key, s, remains unknown to external entities and is shared only within the system. This structural modification enhances security by preventing external attackers from performing standard ElGamal cryptanalysis. Therefore, our scheme introduces an HMPS mechanism that integrates linear encryption to facilitate collaborative and efficient authentication in resource-constrained environments. Unlike traditional signatures, which rely on single-party signing and verification, our method leverages hierarchical aggregation to provide enhanced integrity, scalability, and resistance to forgery.

In addition to KeyGen function, the protocol has first encryption (FEnc), message encryption (Enc), decryption (Dec), individual signature (IndS), hierarchic verification (HSig), and last verification (LVerf) functions.

As illustrated in Algorithm 1, the individual signature IndS has inputs of plaintext m, private–public keys $k,y$, and public parameters $g,p$. IndS returns the pair $(a,b)$.

Algorithm 1 Individual signature.

Require: m, y, k, g, p 1: function  IndS 2:       $r\nleftarrow \mathbb{Z}$ 3:       $h\leftarrow Hash\left(m\right)$ 4:       $h^{\prime }\leftarrow Hash\left(h\right)$ 5:       $b\leftarrow y^{r}modp$ 6:       $a\leftarrow k\times (h\times b-h^{\prime }\times r)mod(p-1)$ 7:       return $a,b$ 8: end function

The creator uses the first encryption (FEnc) function, which has inputs of plaintext m, own private–public keys $k,y$, system secret key s, and public parameters $g,p$. FEnc uses the linear encryption scheme shown in Equation (6).

$$c=A\times s+m$$

(6)

where A is the first part of the computed signature by IndS. For each message $m_i$, $c_i=A_i\times s+m_i$. Algorithm 2 illustrates the first encryption function.

Algorithm 2 First encryption.

Require: s, m, y, k, g, p 1: function  FEnc 2:       $A,B\leftarrow IndS(m,y,k,g,p)$ 3:       $c\leftarrow A\times s+m$ 4:       $Y\leftarrow y^{B}modp$ 5:       return $c,B,Y$ 6: end function

Algorithm 3 illustrates the general encryption function.

Algorithm 3 Encryption.

Require: s, m, A 1: function  Enc 2:       $c\leftarrow A\times s+m$ 3:       return c 4: end function

The decryption (Dec) function has as inputs the ciphertext c and the secret key of the system s. Dec uses the linear decryption scheme shown in Algorithm 4.

Algorithm 4 Decryption.

Require: c, s 1: function  Dec 2:      $\begin{array}{ccc}m\leftarrow cmods& & \hfill ▹m \mathrm{must\; be\; less\; than} s\end{array}$ 3:      $A\leftarrow {\displaystyle \frac{(c-m)}{s}}$ 4:      return $A,m$ 5: end function

The hierarchic signature (HSig) function has as inputs the message m, the signature $\sigma =(A,B,Y)$ where A is contained in the cipher c, the private–public keys $k,y$, the public parameters $g,p$, and the system secret key s. HSig is illustrated in Algorithm 5.

Algorithm 5 Hierarchic signature.

Require: B, Y, c, s, k, y, g, p 1: function  HSig 2:       $A,m\leftarrow Dec(c,s)$ 3:       $h\leftarrow Hash\left(m\right)$ 4:       $h^{\prime }\leftarrow Hash\left(h\right)$ 5:       if $\begin{array}{ccc}{Y}^{h}modp=g^A\times B^{h^{\prime }}modp \mathbf{then}& & ▹\mathrm{accept\; previous\; signatures}\end{array}$ 6:             $a,b\leftarrow IndS(m,y,k,g,p)$ 7:             $A\leftarrow A+amod(p-1)$ 8:             $B\leftarrow B\times bmodp$ 9:             $Y\leftarrow Y\times y^{b}modp$ 10:            $c\leftarrow Enc(s,m,A)$ 11:            return $c,B,Y$ 12:       else 13:            return $\perp err$ 14:       end if 15: end function

Finally, if the entity is the last verifier, Algorithm 6 illustrates its process.

Algorithm 6 last verification

Require: B, Y, c, s, k, y, g, p 1: function  LVerf 2:       $A,m\leftarrow Dec(c,s)$ 3:       $h\leftarrow Hash\left(m\right)$ 4:       $h^{\prime }\leftarrow Hash\left(h\right)$ 5:       if $\begin{array}{ccc}{Y}^{h}modp=g^A\times B^{h^{\prime }}modp \mathbf{then}& & ▹\mathrm{accept\; previous\; signatures}\end{array}$ 6:             return 1 7:       else 8:             return $err$ 9:       end if 10: end function

The system works as follows: One of the nodes decides to create a message m, then signs and encrypts it (FEnc function), and sends the ciphertext to node number one in the group in order to start a collective signing process from the first node to the last nodes. Each node that receives this encrypted message extracts the original text m and the first part of the signature A, which is included there (Dec function). The next step for the message receiver j is to verify that all the nodes before it (i from 1 to $j-1$) have signed the message by using a single verification process. Then, the receiver j updates the signature, $\sigma$, by adding its own signature on the extracted signature (signature of signature), then they encrypt the message again using the new computed signature (HSig) and send the new data (ciphertext and signature $c,B,Y$) to the next node.

Following Algorithm 5 (hierarchical signature), the node extracts the message, m, by the $Dec(c,s)$ function—line 2; then, it verifies the signature validity and signs the same m by using their individual signature (line 6, $a,b\leftarrow IndS(m,y,k,g,p)$). After updating the aggregate signature A (line 7) and the aggregate public keys B and Y (lines 8 and 9), they encrypt the same message, m (line 10, $c\leftarrow Enc(s,m,A)$). The next node will extract the same message, m, from c by using $Dec(c,s)$—line 2. This continues on.

For a hierarchical model and respecting the order of signatures, we can replace the hash h by $h=Hash(m\Vert I{D}_0\Vert I{D}_1\cdots \Vert I{D}_j)$. Algorithm 7 displays the entire process flow for the proposed scheme.

Algorithm 7 System progress.

1: function  SP 2:       $c_0,B_0,Y_0\leftarrow FEnc(s,m,y_0,k_0,g,p)$ 3:       $c_1,B_1,Y_1\leftarrow HS(B_0,Y_0,c_0,s,k_1,y_1,g,p)$ 4:       $c_2,B_2,Y_2\leftarrow HS(B_1,Y_1,c_1,s,k_2,y_2,g,p)$ 5:       $...$ 6:       $x\leftarrow LastV(B_j,Y_j,c_j,s,g,p)$▹x is 1 or err 7: end function

5. Use Case: Collaborative Issues Detection in an Intelligent Vehicle Surveillance System

This use case illustrates the uses of the proposed HMPS in a practical and scalable manner, ensuring secure and trustworthy collaboration in distributed systems. The use case objectives are as follows: (1) ensuring data integrity and commands sent to vehicles have not been tampered with; (2) ensuring that commands are hierarchically authenticated; and (3) trust enhancement by building a tamper-proof system through the digital signature of each layer of the transmission chain.

5.1. Scenario

Autonomous cars in smart cities depend on signals transmitted from several sources, including local emergency centers (LECs) and national traffic control centers (NTCCs). These commands are intended to solve issues like dealing with emergency traffic, defining no-go zones, or rerouting automobile traffic. Multiparty hierarchical digital signatures are utilized to guarantee that these commands come from reliable sources and have not been altered.

In addition to higher security that prevents any forged or unauthenticated commands, the system handles these issues efficiently like providing better safety by reducing accidents and ensuring effective response of vehicles in emergency situations, and crowd management by redirecting vehicles intelligently to avoid crowded or dangerous areas.

Figure 1 depicts a hierarchical communication system for traffic management and autonomous vehicle operation. At Level 1, NTCC acts as the top-level decision maker, overseeing the entire network. At Level 2, the local emergency center serves as an intermediary node, facilitating communication between the national level and autonomous vehicles. Finally, at Level 3, the autonomous vehicles operate as both message creators and executors, sending messages to LECs or receiving directives from NTCCs. In general, an LEC represents node 0 in the implementation and an NTCC represents node 1, which delineates the interaction levels in the hierarchy. This structure ensures efficient message flow and execution for traffic regulation and emergency responses.

From bottom to top, the system is read as follows: The Lower Level (LL) creates messages, signs them, and sends them to the middle level, or validates the chain of signatures before executing the commands. The Middle Level (ML) validates the messages and adds its own signature. The Top Level (TL) sends general commands such as “close a certain area” or “change directions” after validating the ML and LL signatures.

5.2. The Operational Flow of Messages and Commands Illustration

As shown in Figure 2, when an autonomous vehicle, $V_i$, detects an issue on road 1 leading to the stadium, it creates a message stating that this road has certain issues, attaches the time and a captured image, and then $V_i$ sends this information to LEC. Upon receiving the information, LEC verifies the integrity of the message and the validity of its signature. If we want to add a layer of security in applications that do not require real-time processing, LEC also extracts the issue from the captured image using artificial intelligence tools to ensure the actual existence of the issue and that $V_i$ made the correct decision.

After extracting $V_i$’s signature embedded in the message, LEC signs this signature, i.e., an implicit signature of the original message, then sends the new ciphertext to NTCC. Upon receiving the ciphertext, NTCC extracts the information from it, which is the original message and signature, then verifies the integrity of the message and the signature validity, and signs it. Finally, NTCC sends the ciphertext which contains the original message of the creator and the aggregated signature (hierarchical signature); and also sends an order to all vehicles in the area surrounding the stadium to avoid road 1 and take other road options.

6. Security Analysis

The most crucial security concern of the signature techniques is the potential retrieval of the private key or the forgery of the signature process, which we will discuss below.

HMPS represents a complex approach to ensuring both message integrity and confidentiality by combining elements of ElGamal-based encryption with symmetric architecture.

The ciphertext is formed by the expression $c=a\times s+m$, where m is the plaintext message, and s is a symmetric encryption key known only to the communicating parties. This intricate combination of digital signatures and encrypted message handling introduces a multi-layered security scheme resistant to attacks from both external and internal adversaries.

A comprehensive analysis of the proposed HMPS requires examining its security guarantees against different types of attackers. This begins by considering an external attacker who has no privileged access to the system. Such an adversary’s primary objectives would likely include forging a valid signature, $\sigma$, and decrypting the ciphertext, c, to recover the message, m, or the key, s, or both.

First, the security of the signature generation process relies heavily on the computational infeasibility of solving the discrete logarithm problem. For a more secure protocol, the modulus, p, can be kept secret, so the attacker cannot obtain it. The signature, $\sigma$, computed by a; then, b binds the message, m, to the signer, ensuring both the authenticity and integrity of the message. Without knowledge of the private key, k, an attacker cannot generate a valid signature for any message, thus preventing forgery.

Moreover, the inclusion of a hash function in the signature computation ensures that the signature is uniquely tied to the specific content of the message. A cryptographically secure hash function possesses properties such as pre-image resistance, second pre-image resistance, and collision resistance. Pre-image resistance ensures that, given a hash output, it is computationally infeasible to determine the original input. Second pre-image resistance makes it difficult to find a different input that produces the same hash output. Collision resistance further ensures that it is unlikely to find two different messages producing the same hash value. These properties collectively ensure that, even if an attacker attempts to manipulate the message content, they cannot produce a valid signature for a modified message.

The confidentiality of the message, m, is protected by the ciphertext c. Here, s serves as a symmetric encryption key, adding an additional layer of security. Since the values of a, s, and m are all unknown to an external attacker, Equation (6) does not readily reveal m without solving for multiple unknowns simultaneously. The security of the symmetric key, s, is paramount; ensuring that it is securely generated and shared between the communicating parties without interception is critical for maintaining the confidentiality of the message.

Analyzing the level of security against brute force attacks, it is evident that the protocol leverages both the strength of the ElGamal system and the unpredictability introduced by the symmetric key encryption. The discrete logarithm problem for recovering k is computationally infeasible for sufficiently large values of p, or keeping p secret for more security. This property, coupled with the complexity of guessing a or deducing s from the ciphertext, makes a direct brute force approach impractical for an external attacker.

In considering chosen ciphertext attacks (CCAs) or other forms of adaptive attacks, the dependency of m on both a and s complicates the decryption process. Without access to the correct symmetric key, s, or signature, a, decryption attempts are unlikely to yield meaningful results. The integration of asymmetric and symmetric encryption components thus creates a robust security framework that resists such sophisticated attacks.

Next, let us turn to the threat posed by an internal attacker who has access to the secret key, s, but lacks knowledge of the private key, k. This attacker might attempt to forge a signature or craft a counterfeit message that is verified as authentic. However, the security properties inherent to the modified ElGamal signature mechanism effectively prevent these actions. Since the computation of k requires solving discrete logarithm, the inside attacker cannot generate a valid signature for any message.

Additionally, the hash function’s integrity ensures that the signature is specific to the content of the message. Thus, even if the internal attacker attempts to replay a previously signed message, m, or construct a similar message, $m^{\prime }$, the hash value will differ unless m is identical to $m^{\prime }$. This characteristic prevents successful replay or tampering attacks.

The combined use of ElGamal-based encryption signatures and symmetric encryption enhances the overall security posture of the protocol by addressing potential weaknesses in isolation. The digital signature ensures message integrity and authenticity, while the symmetric encryption protects the confidentiality of the message content. This hybrid approach benefits from the complementary strengths of both cryptographic techniques, making it challenging for an adversary to compromise the system.

Nevertheless, potential weaknesses must be acknowledged and mitigated to ensure comprehensive security. For instance, if either the signature, $\sigma$, or the symmetric key, s, is compromised, the confidentiality of the message, m, is at risk. Thus, secure key management practices are crucial to prevent key leakage or unauthorized access. One effective mitigation strategy is to use unique keys for each message exchange, thereby reducing the risk of key reuse and subsequent pattern recognition in the ciphertext.

Furthermore, ensuring that the hash function used in the signature generation process remains secure against emerging cryptographic attacks is essential. The selection of a hash function resistant to both classical and quantum computing attacks can future-proof the protocol against evolving threats. Key length considerations for ElGamal modulus, p, also play a critical role in maintaining the security of the signature scheme. As computational power increases, longer key lengths are necessary to ensure that obtaining k remains computationally infeasible, especially with hiding p.

It it important to avoid extracting secret information due to a pattern in encrypted messages; this can be illustrated as follows: If $c_1=a_1\times s+m_1$ and $c_2=a_2\times s+m_2$, by computing the difference $c_1-c_2$, the attacker can obtain a multiple of the secret key, s, if m has a pattern.

Since the security of this linear encryption is dependent on message randomness, we can modify the ciphertext calculation and add randomness not related to the message, m, as follows: $c=a\times s_1+m\times s_2+r$, where r is a random number for each message and the new secret key of the system is ($s_1,s_2$) instead of s.

$$c=a\times s_1+m\times s_2+r$$

(7)

By using Equation (7), $c_1-c_2$ would be equal to $x\times s_1+t\times s_2+r_3$, where x is a multiple of $s_1$, t is a pattern into m, and $r_3$ is a new random number with $r_3=(r_1-r_2)$. As a result, the decryption of c should be as follows: $a=c//s_1$, $m=(c-a\times s_1)//s_2$. Therefore, for a correct decryption, these two conditions must be satisfied: $m\times s_2+r<s_1$ and $r<s_2$.

To further enhance the robustness of the protocol, incorporating additional security measures such as nonce values or time stamps in the message structure can provide protection against replay attacks. These elements introduce freshness into each transaction, ensuring that messages cannot be reused or duplicated by an adversary.

Therefore, the proposed HMPS cryptographic protocol effectively combines asymmetric and symmetric cryptographic techniques to achieve a secure and robust communication framework. The ElGamal encryption-based signature ensures message authenticity and integrity, while the symmetric encryption scheme protects message confidentiality. By addressing potential threats and implementing best practices for key management and hash function selection, the protocol can offer strong security assurances against both external and internal adversaries. This comprehensive approach highlights the strength of leveraging multiple cryptographic primitives to achieve layered security and demonstrates the importance of meticulous protocol design in safeguarding sensitive information.

6.1. Attacks by Low-Level Network Members

Regarding the risk of substitution attacks by unscrupulous low-level network members. Our proposed HMPS technique incorporates several inherent mechanisms to counter such threats, detailed here.

Hierarchical verification: Each node in the signing chain is required to verify the signatures from all preceding nodes. This layered verification ensures that any alteration or substitution of the original message (or its associated signature) by a low-level node would immediately cause a mismatch in the verification process. If even a single signature is invalid or missing, the entire chain is rejected, effectively preventing the propagation of a tampered message.

Digital signature binding: By binding the signature to the message via cryptographic hash functions (as shown in Algorithms 1–5), any modification to the message or substitution of its components (including images) results in a hash mismatch. This binding provides a robust cryptographic guarantee that only the authentic, original message will yield the correct signature upon verification.

Integrated encryption: The encryption process (Enc and Dec functions) integrates the signature with the message. This integration means that any unauthorized substitution not only disrupts the signature chain but also affects the decryption process, thereby exposing any tampering attempts.

Supplementary tools: While the HMPS technique is primarily focused on ensuring integrity and authenticity, we recognize that in scenarios where the consequences of substitution attacks are particularly severe (e.g., affecting reputation, logistics, or financial markets), additional measures could be implemented. These may include the following:

Consensus: A safety layer can be added to the level of the message origin where it is not accepted by LEC unless it is signed by more than one source. For instance, when reporting an accident, the first vehicle sends a picture to the other vehicles that witnessed the same accident. If a number x of the vehicles agree to the validity of the accident presence, they all sign the notification message, and it is then sent to LEC. Watermarking for images: embedding robust, cryptographic watermarks within images to verify their authenticity. Redundancy and consensus protocols: Incorporating distributed consensus mechanisms where multiple independent verification instances are required before accepting a message or image as authentic. Secure time stamping: using trusted time stamping services to provide an immutable record of when a message was created and signed, further reducing the window for substitution attacks. Together, these mechanisms ensure that any attempt by a low-level node to substitute false messages or images would be detected and rejected during the hierarchical verification process, preserving the integrity and trustworthiness of the system.

6.2. Cryptographic Key Management

Protecting private keys in vehicle environments is indeed a crucial aspect of ensuring the overall security of the system. To prevent unauthorized access or theft of private keys, several well-established security mechanisms can be employed [17]. Hardware Security Modules (HSMs): HSMs are dedicated physical devices used to securely generate, store, and manage cryptographic keys. These modules ensure that keys never leave the secure hardware, preventing key extraction even if the system is compromised [18]. Trusted Platform Modules (TPMs): TPMs provide hardware-based security for key storage. They offer tamper-resistant storage of private keys and can provide secure cryptographic operations, making them a suitable choice for vehicle systems where physical security is paramount [19]. Secure Enclaves (e.g., Intel SGX, ARM TrustZone): These provide isolated, trusted execution environments within the vehicle’s processor, safeguarding keys and sensitive data from both software and physical attacks. They are designed to protect against memory dumps, side-channel attacks, and other vulnerabilities. Key Rotation and Management: To enhance the security of private keys, periodic key rotation can be implemented. This ensures that, even if keys are compromised, they are only usable for a limited time. Additionally, key management systems can provide centralized control over key distribution and revocation [20]. Physical Tamper Resistance: In environments such as vehicles, physical tampering with devices can be mitigated by incorporating tamper-resistant hardware. For instance, systems can detect unauthorized attempts to access cryptographic modules and trigger self-destruct or zeroization processes to wipe keys [21].

6.3. Performance Metrics

The performance of the proposed HMPS scheme was evaluated based on its computational efficiency and execution time. These metrics were calculated to capture the end-to-end process of signature generation, verification, and hierarchical aggregation. For the experiment, parameters were set as follows: message size $m=256$ bits, symmetric key $s=260$ bits, ElGamal prime numbers $p=264$ bits, the generator $g=32$, private keys k = 230 bits.

The execution time achieved by HMPS for three signers was recorded as 2.2 ms, including both signature generation and verification. This performance reflects the capability of HMPS to operate efficiently in real-time systems, providing robust security with minimal delay. The lightweight nature of HMPS underscores its potential in applications demanding high throughput and low latency, such as intelligent vehicle monitoring and IoT-based issue detection systems.

6.4. Energy Efficiency

The HMPS scheme has been designed with energy efficiency as a core consideration, making it particularly suitable for IoT environments where devices often operate with limited power resources [22]. Energy consumption was assessed during critical cryptographic operations, including signature generation, verification, and aggregation.

The results demonstrated that HMPS consumes significantly less energy compared to alternative techniques due to its lightweight cryptographic design. By optimizing computational requirements and reducing communication overhead, the scheme ensures minimal power usage without compromising security. This makes HMPS ideal for battery-powered devices in resource-constrained scenarios.

6.5. Experiment with Benchmark Datasets

To validate the reliability and adaptability of the HMPS scheme, experiments were conducted using benchmark datasets representative of real-world IoT environments. These datasets included:

• Synthetic data simulating vehicle-to-infrastructure communication in intelligent transportation systems.
• Anomalous event datasets are designed to test the system’s capability for secure issue detection.

In these experiments, the hierarchical signature mechanism demonstrated robust performance, successfully validating message authenticity and maintaining data integrity across various conditions. The use of hierarchical aggregation further enhanced the efficiency of the system, allowing it to process large volumes of data in real-time.

6.6. Comparison of Execution Time for Different Techniques

Several existing works have proposed digital signature schemes optimized for various environments, such as vehicular ad hoc networks (VANETs) and IoT. Notable techniques include:

• Zhou et al. (2023) [14] combined functional signatures and multiparty ECDSA signatures to create a multiparty functional signature for private blockchains. This paper used a personal computer (RedmiBook with AMD CPU Ryzen 5 5600H with Radeon Graphics @ 3.30 GHz with 16.0 GB RAM and Windows 10 Home OS) implementing the proposed scheme in Python 3.9.6. The number of nodes is 3.
• Tan et al. [23] designed a multiparty collaborative signature scheme based on SM2 digital signature algorithm in the standard “SM2 Elliptic Curve Public Key Cryptography”. The experimental PC operating system is win10 operating system, the processor is Intel(R) Core(TM) i7-5500U CPU @ 2.40 GHz 2.39 GHz, 8 G RAM; the large integer library gmp-6.2.0 is selected for implementation; the main programming language is C; the platform used to implement the algorithm is Visual Studio 2019. The number of nodes is 5.

Table 1. Comparison of execution time (ms) for different techniques.

Technique	Execution Time (ms)	Remarks
Proposed HMPS	2.2	Superior efficiency, includes signing and verifying.
Zhou et al. (2023) [14]	343	Using a smart contract, higher computation cost.
Tan et al. (2023) [23]	3200	SM2 digital signature without revealing the key, computationally intensive.

compares the execution times of these schemes with the proposed HMPS. The computer base used for the testing of our algorithm was CPU: Intel Core i7-10610U 2.30 GHz. RAM: 16 GB DDR4, and storage: SSD. Operating system: Windows 11, and programming language: Python 3.10. The number of nodes is 3. In these experiments, we adopted Equation (6) for encryption and not Equation (7).

The HMPS scheme outperforms these prior techniques in terms of execution time while maintaining robust security properties. Its hierarchical design and efficient aggregation process reduce computational and communication costs, making it an excellent choice for real-time, resource-constrained systems.

In the context of signature generation techniques, a crucial metric for evaluating performance is the execution time or computation cost. As shown in Table 1, HMPS demonstrates a significant advantage in terms of efficiency when compared to recent alternatives in the literature.

HMPS vs. Zhou et al. (2023): When compared to the technique presented by Zhou et al. [14], which has a computation cost of 343 ms, our proposed method is dramatically faster, by more than 5 times. This significant improvement in computation time highlights the potential of our approach for real-time or resource-constrained environments where efficiency is paramount.

The clear reduction in execution time shown by our proposed method indicates its suitability for applications requiring fast processing, such as in scenarios where multiparty signatures need to be generated or verified rapidly, while the other methods may provide additional functionalities or security benefits that come with a higher computational cost, the trade-off between efficiency and other features would need to be carefully considered based on specific application requirements.

7. Conclusions

In this article, we introduced a hierarchical multiparty digital signature technique specifically designed for IoT environments and distributed systems, with a focus on enhancing public security. By integrating cryptographic principles with collaborative and hierarchical computational strategies, the proposed technique ensures data integrity, authenticity, and non-repudiation across decentralized, resource-constrained networks.

The implementation of the hierarchical multiparty digital signature scheme demonstrates significant potential in a variety of real-world applications, including smart city surveillance, blockchain-based consensus mechanisms, and collaborative cloud computing. One of the main use cases our paper highlights is emergency traffic coordination. To ensure that these instructions are authentic and unaltered, multiparty hierarchical digital signatures are used. This practical example emphasizes how the technique enhances trust, security, and accountability in collaborative IoT systems.

Through comprehensive theoretical analysis and practical simulations, we showed that the proposed technique effectively mitigates risks such as single points of failure, unauthorized access, and collusion attacks, thereby improving system trustworthiness and resilience. The scalability and fault tolerance of the system make it particularly suitable for dynamic, heterogeneous environments like IoT networks.

Future work will aim to adapt the scheme to emerging challenges, such as ensuring its resilience against quantum computing threats, optimizing its performance for large-scale IoT deployments, and exploring its integration with AI-driven threat detection systems to further enhance the security of collaborative IoT applications.