New Semi-Prime Factorization and Application in Large RSA Key Attacks
Abstract
1. Introduction
- i.
- The novel semi-prime factorization method uses simple number theory uniquely for the first of its kind;
- ii.
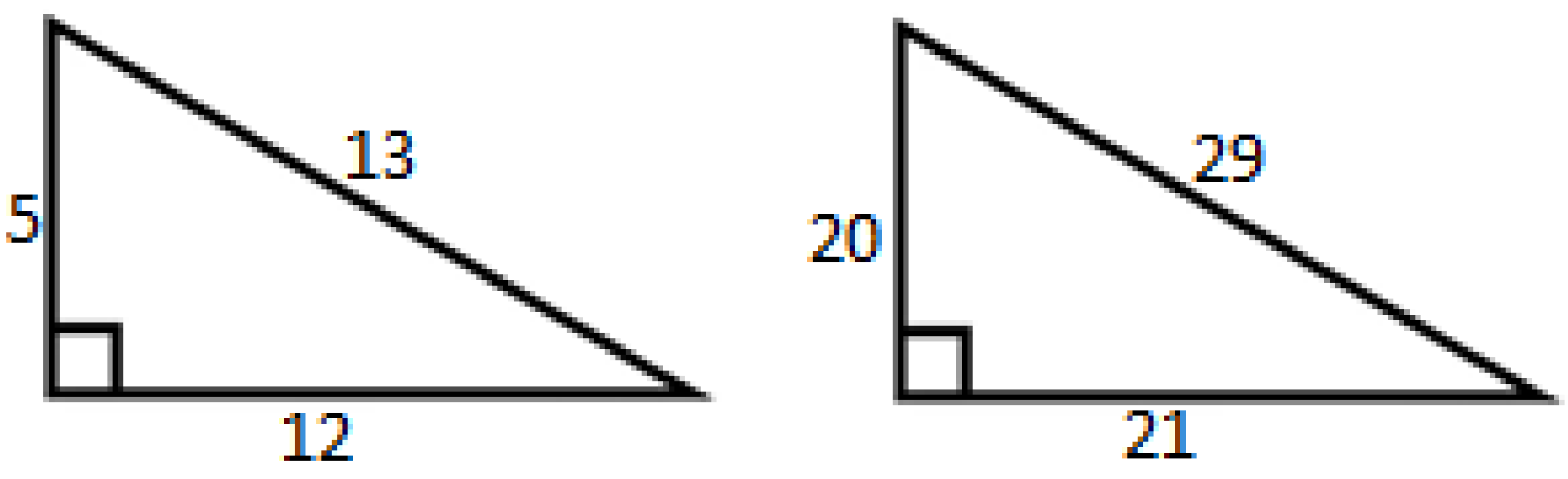
- The method applies new patterns of Pythagorean tuples and triples that are unexplored so far in literature;
- iii.
- By employing simple arithmetic operations, the semi-prime factorization algorithm assures a low order of computing cost;
- iv.
- The algorithm exhibits an enhanced solution space as compared to Fermat’s method.
2. Related Works
3. Background Theory
4. Proposed Method for Factoring Semi-Primes
4.1. Algorithm of Our Proposed Semi-Prime Factorization
4.2. Complexity, Comparison and Constraints of Our Algorithm
5. Case Study Examples Applied to RSA Key Factorization
- Pick two large prime numbers and ;
- Consider the semi-prime ;
- Consider ;
- Choose an integer such that and gcd(;
- Compute such that .
6. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Overmars, A.; Venkatraman, S. A Fast Factorisation of Semi-Primes Using Sum of Squares. Math. Comput. Appl. 2019, 24, 62. [Google Scholar] [CrossRef]
- Moreno, C.J.; Wagstaff, S.S. Sums of Squares of Integers, 1st ed.; Chapman and Hall/CRC Press: New York, NY, USA, 2005. [Google Scholar]
- Dunn, A.; Zaharescu, A. Sums of Kloosterman Sums Over Primes in an Arithmetic Progression. Q. J. Math. 2019, 70, 319–342. [Google Scholar] [CrossRef]
- Erdós, P. On the Normal Number of Prime Factors of P-1 and Some Related Problems Concerning Euler’s Ø-Function. Q. J. Math. 1935, os-6, 205–213. [Google Scholar] [CrossRef]
- Pollard, J. Theorems on factorization and primality testing. Proc. Camb. Philos. Soc. 1974, 76, 521–528. [Google Scholar] [CrossRef]
- Traversa, F.L.; di Ventra, M. Polynomial-time solution of prime factorization and NP-complete problems with digital memcomputing machines. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 023107. [Google Scholar] [CrossRef] [PubMed]
- Malapert, A.; Provillard, J. Puzzle—Solving the n-Fractions Puzzle as a Constraint Programming Problem. INFORMS Trans. Educ. 2018, 19, 48–55. [Google Scholar] [CrossRef]
- Rescorla, E. SSL and TLS: Designing and Building Secure Systems; Addison-Wesley Reading: London, UK, 2001. [Google Scholar]
- Schneier, B. Applied Cryptography, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Sun, H.-M.; Wu, M.-E.; Ting, W.-C.; Hinek, M. Dual RSA and Its Security Analysis. IEEE Trans. Inf. Theory 2007, 53, 2922–2933. [Google Scholar]
- McKee, J.F. Turning Euler’s Factoring Method into a Factoring Algorithm. Bull. Lond. Math. Soc. 1996, 28, 351–355. [Google Scholar] [CrossRef]
- Zagier, D. A One-Sentence Proof That Every Prime p ≡ 1 (mod 4) Is a Sum of Two Squares. Am. Math. Mon. 1990, 97, 144. [Google Scholar]
- Li, S. The Sum of Two Squares; Cornell University Press: New York, NY, USA, 2013. [Google Scholar]
- Agarwal, R.P. Pythagorean Triples before and after Pythagoras. Computation 2020, 8, 62. [Google Scholar] [CrossRef]
- Boneh, D. Twenty years of attacks on the RSA cryptosystem. Not. Am. Math. Soc. (AMS) 1999, 46, 203–213. [Google Scholar]
- Valenta, L.; Cohney, S.; Liao, A.; Fried, J.; Bodduluri, S.; Heninger, N. Factoring as a Service. In Financial Cryptography and Data Security. FC 2016. Lecture Notes in Computer Science; Grossklags, J., Preneel, B., Eds.; Springer: Berlin, Germany, 2017; Volume 9603. [Google Scholar]
- Durumeric, Z.; Kasten, J.; Bailey, M.; Halderman, J.A. Analysis of the HTTPS certificate ecosystem. In Proceedings of the 13th Internet Measurement Conference, Barcelona, Spain, 23–25 October 2013. [Google Scholar]
- Wiener, M. Cryptanalysis of short RSA secret exponents. IEEE Trans. Inf. Theory 1990, 160, 553–558. [Google Scholar] [CrossRef]
- Coppersmith, D. Solving homogeneous linear equations over GF(2) via block Wiedemann algorithm. Math. Comput. 1994, 62, 333–350. [Google Scholar] [CrossRef]
- Blömer, J.; May, A. New Partial Key Exposure Attacks on RSA. In Crypto 2003, LNCS; Springer: Berlin, Germany, 2003; pp. 27–43. [Google Scholar]
- Boneh, D.; Durfee, G. Cryptanalysis of RSA with Private Key D Less than N^0.292. In Proceedings of the International Conference on the Theory and Application of Cryptographic Techniques, Prague, Czech Republic, 2–6 May 1999; Springer: Berlin, Germany, 1999; Volume 1592, p. 111. [Google Scholar]
- Heninger, N.; Durumeric, Z.; Wustrow, E.; Halderman, J.A. Mining your Ps and Qs: Detection of widespread weak keys in network devices. In Proceedings of the 21st USENIX Security Symposium, Bellevue, WA, USA, 8–10 August 2012. [Google Scholar]
- Adrian, D.; Bhargavan, K.; Durumeric, Z.; Gaudry, P.; Green, M.; Halderman, J.A.; Heninger, N.; Springall, D.; Thomé, E.; Valenta, L.; et al. Imperfect forward secrecy: How Diffie-Hellman Fails in Practice. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, Denver, CO, USA, 12–16 October 2015; pp. 5–17. [Google Scholar]
- Nemec, M.; Sys, M.; Svenda, P.; Klinec, D.; Matyas, V. The Return of Coppersmith’s Attack: Practical Factorization of Widely Used RSA Moduli. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, CCS 2017, Dallas, TX, USA, 30 October–3 November 2017; pp. 1631–1648. [Google Scholar]
- Lehmer, D.H.; Powers, R.E. On Factoring Large Numbers. Bull. Am. Math. Soc. 1931, 37, 770–776. [Google Scholar] [CrossRef]
- Morrison, M.A.; Brillhart, J. A Method of Factoring and the Factorization of F7. Math. Comput. Am. Math. Soc. 1975, 29, 183–205. [Google Scholar]
- Pomerance, C.; Wagstaff, S.S. Implementation of the Continued Fraction Integer Factoring Algorithm. Congr. Numer. 1983, 37, 99–118. [Google Scholar]
- Pollard, J.M. A Monte Carlo method for factorization. In BIT Numerical Mathematics; Springer: Berlin, Germany, 1975; Volume 15, pp. 331–334. [Google Scholar]
- Pomerance, C. The Quadratic Sieve Factoring Algorithm. In Advances in Cryptology: EUROCRYPT’84; Springer: Berlin, Germany, 1985; pp. 169–182. [Google Scholar]
- Kameswari, P.A.; Jyotsna, L. An Attack Bound for Small Multiplicative Inverse of φ(N) mod e with a Composed Prime Sum p + q Using Sublattice Based Techniques. Cryptography 2018, 2, 36. [Google Scholar] [CrossRef]
- Kamel Ariffin, M.R.; Abubakar, S.I.; Yunos, F.; Asbullah, M.A. New Cryptanalytic Attack on RSA Modulus N = pq Using Small Prime Difference Method. Cryptography 2019, 3, 2. [Google Scholar] [CrossRef]
- Lenstra, A.K.; Lenstra Jr, H.W.; Manasse, M.S.; Pollard, J.M. The Number Field Sieve; Springer: Berlin, Germany, 1993. [Google Scholar]
- Cheng, Q. A New Special-Purpose Factorization Algorithm. Citeseer. 2002. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.8.9071&rep=rep1&type=pdf (accessed on 18 January 2021).
- Sedlacek, V.; Klinec, D.; Sys, M.; Svenda, P.; Matyas, V. I Want to Break Square-free: The 4p 1 Factorization Method and Its RSA Backdoor Viability. In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), Prague, Czech Republic, 26–28 July 2019; pp. 25–36. [Google Scholar]
- Grosswald, E. Representations of Integers as Sums of Squares; Springer: Berlin, Germany, 1985. [Google Scholar]
- Northshield, S. A Short Proof of Fermat’s Two-square Theorem. Am. Math. Mon. 2020, 127, 638. [Google Scholar]
- Jackson, T. From Polynomials to Sums of Squares; CRC Press: New York, NY, USA, 1995. [Google Scholar]
- Dickson, L.E. History of the Theory of Numbers: Diophantine Analysis, 2nd ed.; Dover Publications: New York, NY, USA, 2005. [Google Scholar]
- Roy, T.; Soni, F.J. A direct method to generate Pythagorean triples and its generalization to Pythagorean quadruples and n-tuples. arXiv 2012, arXiv:1201.2145. [Google Scholar]
- Christopher, A.D. A partition-theoretic proof of Fermat’s Two Squares Theorem. Discret. Math. 2016, 339, 1410–1411. [Google Scholar] [CrossRef]
- Knill, O. Some experiments in number theory. arXiv 2016, arXiv:1606.05971. [Google Scholar]
- Kostopoulos, G.L. An Original Numerical Factorization Algorithm. J. Inf. Assur. Cyber Secur. 2016, 2016, 775081. [Google Scholar] [CrossRef][Green Version]
- Kaddoura, I.; Abdul-Nabi, S.; Al-Akhrass, K. New Formulas for Semi-Primes. Testing, Counting and Identification of the nth and next Semi-Primes. arXiv 2016, arXiv:1608.05405. [Google Scholar]
- Hiary, G.A. A Deterministic Algorithm for Integer Factorization. Math. Comput. 2016, 85, 2065–2069. [Google Scholar] [CrossRef][Green Version]
- Overmars, A.; Venkatraman, S. Mathematical Attack of RSA by Extending the Sum of Squares of Primes to Factorize a Semi-Prime. Math. Comput. Appl. 2020, 25, 63. [Google Scholar] [CrossRef]
- McKee, J.F. Speeding Fermat’s factoring method. Math. Comput. 1999, 68, 1729–1737. [Google Scholar] [CrossRef][Green Version]
- Overmars, A.; Ntogramatzidis, L.; Venkatraman, S. A New approach to generate all Pythagorean triples. AIMS Math. 2019, 4, 242–253. [Google Scholar] [CrossRef]
- Boucard, J. Lagrange and the four-square theorem. Lett. Mat. 2014, 2, 59–66. [Google Scholar] [CrossRef][Green Version]
- Dickson, L.E. History of the Theory of Numbers; Carnegie Institute of Washington 1919; AMS Chelsea Publishing: Providence, RI, USA, 1992; Volume II, p. 15. [Google Scholar]
- Fenster, D.D. Leonard Dickson’s History of the theory of numbers: An historical study with mathematical implications. J. Hist. Math. 1999, 5, 159–179. [Google Scholar]
- Mitchell, D.W. An alternative characterisation of all Primitive Pythagorean Triples. Math. Gaz. 2001, 85, 273–275. [Google Scholar] [CrossRef]
- Venkatraman, S.; Overmars, A. New method of prime factorisation based attacks on RSA Authentication in IoT. Cryptography 2019, 3, 20. [Google Scholar] [CrossRef]
- Da Silva, J.C.L. Factoring Semi primes and Possible Implications. In Proceedings of the 26th IEEE Convention in Israel, Eliat, Israel, 17–20 November 2010; pp. 182–183. [Google Scholar]
- Bahig, H.M.; Mahdi, M.A.; Alutaibi, K.A.; AlGhadhban, A.; Bahig, H.M. Performance Analysis of Fermat Factorization Algorithms. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2020, 11, 340–352. [Google Scholar] [CrossRef]
- Baier, S.; Mazumder, D. Diophantine approximation with prime restriction in real quadratic number fields. Math. Z. 2021, 299, 699–750. [Google Scholar] [CrossRef]
- Pomerance, C. Analysis and Comparison of Some Integer Factoring Algorithms, in Computational Methods in Number Theory, Part 1; Lenstra, H.W., Jr., Tijdeman, R., Jr., Eds.; Math. Centre Tract 154: Amsterdam, The Netherlands, 1982; pp. 89–139. [Google Scholar]
- Hoffstein, J.; Pipher, J.; Silverman, J. An Introduction to Mathematical Cryptography, 1st ed.; Springer Publishing Company: Oakland, CA, USA, 2008; Incorporated. [Google Scholar]
- Stanoyevitch, A. Introduction to Cryptography with Mathematical Foundations and Computer Implementations, 1st ed.; Chapman & Hall/CRC: New York, NY, USA, 2010. [Google Scholar]
- Moreno, C.J.; Wagstaff, S.S. Sums of Squares of Integers. Discrete Mathematics and Its Applications; Chapman & Hall, CRC: Boca Raton, FL, USA, 2006; pp. 325–326. ISBN 978-1-58488-456-9. [Google Scholar]
- Kloster, K. Factoring a Semiprime n by Estimating φ(n). 2010. Available online: http://www.gregorybard.com/papers/phi_version_may_7.pdf (accessed on 30 September 2020).
- Cekerevac, Z.; Dvorak, Z.; Prigoda, L.; Cekerevac, P. Man in the Middle Attacks and the Internet of Things—Security and economic risks. FBIM Trans. 2017, 5, 25–35. [Google Scholar] [CrossRef]
- El-hajj, M.; Fadlallah, A.; Chamoun, M.; Serhrouchni, A. A Survey of Internet of Things (IoT) Authentication Schemes. Sensors 2019, 19, 1141. [Google Scholar] [CrossRef]
- Zhou, L.; Li, X.; Yeh, K.H.; Su, C.; Chiu, W. Lightweight IoT-based authentication scheme in cloud computing circumstance. Future Gen. Comput. Syst. 2019, 91, 244–251. [Google Scholar] [CrossRef]
- Yan, S.Y. Factoring Based Cryptography. In Cybercryptography: Applicable Cryptography for Cyberspace Security; Springer: Berlin/Heidelberg, Germany, 2018; pp. 217–286. [Google Scholar]
- Suárez-Albela, M.; Fraga-Lamas, P.; Fernández-Caramés, T.M. A Practical Evaluation on RSA and ECC-Based Cipher Suites for IoT High-Security Energy-Efficient Fog and Mist Computing Devices. Sensors 2018, 18, 3868. [Google Scholar] [CrossRef]
- Buhler, J.P.; Lenstra, H.W., Jr.; Pomerance, C. Factoring Integers with the Number Field Sieve; Lecture Notes in Mathematics; Springer: New York, NY, USA, 1993; Volume 1554, pp. 50–94. [Google Scholar]
- Pollard, J. Monte Carlo methods for index computation (mod p). Math. Comput. 1978, 32, 918–924. [Google Scholar] [CrossRef]
- Overmars, A.; Venkatraman, S. A New Method for Factorizing Semi-primes Using Simple Polynomials. In Proceedings of the 3rd International Conference on Research in Applied Science, Munich, Germany, 6–8 November 2020. [Google Scholar]
- Stillwell, J. Mathematics and Its History, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Vogel, D.; Onayemi, Y.; Murad, V. Integer Factorization Algorithms. 2016. Available online: http://maths.dk/teaching/courses/math357-spring2016/projects/factorization.pdf (accessed on 6 March 2021).
- Benedetto, R.; Ingram, P.; Jones, R.; Manes, M.; Silverman, J.H.; Tucker, T.J. Current Trends and Open Problems in Arithmetic Dynamics. Am. Math. Soc. 2019, 56, 611–685. [Google Scholar] [CrossRef]
- Wiśniewski, R.; Wisniewski, R. Representation of primes in the form p = 6·x ± 1 and its application to the RSA prime factorization. In AIP Conference Proceedings; AIP Publishing Center: New York, NY, USA, 2018; Volume 2040, p. 080006. [Google Scholar] [CrossRef]
- Wu, L.; Cai, H.J.; Gong, Z. The Integer Factorization Algorithm with Pisano Period. IEEE Access 2019, 7, 167250–167259. [Google Scholar] [CrossRef]
- Rutkowski, E.; Houghten, S. Cryptanalysis of RSA: Integer Prime Factorization Using Genetic Algorithms. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar]
| 123018668453011775513049495838496272077285356959533479219732245215 172640050726365751874520219978646938995647494277406384592519255732 630345373154826850791702612214291346167042921431160222124047927473 7794080665351419597459856902143413 | |
| 151335927879520346290803999457322598363508796074958341058717144380 245872835312747521375274637572332720319718269519140130366434717995 557448975805325285592901195789698493475842912499609903738365207236 511522080338199512854710820317535056362120218189196094883472059867 670273711218840191206761008283107936158558105422755888818703810974 813042919826949446811902964522404849739464632596646341875606194756 2985467999013006479462484696511372504488571635778058519793619288569 | |
| 122282464059209245992171436897658189706307595059665852419459721623 575268394641485120055721728993778585098737802795637062458727992772 215791535778942916633321748296084895133564298582155097077049551048 7891461504154220362780972595368188 | |
| 134384437923531027642685110944406395128150457221349204815473265992 860466317855675453545164265884545802321235838004890967990322730328 639778020385449818260083476767779296347341551505950443482805814798 593564305646242411389559844289235 | |
| 334780716989568987860441698482126908177047949837137685689124313889 82883793878002287614711652531743087737814467999489 | |
| 367460436667995904282446337996279526322791581643430876426760322838 15739666511279233373417143396810270092798736308917 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Overmars, A.; Venkatraman, S. New Semi-Prime Factorization and Application in Large RSA Key Attacks. J. Cybersecur. Priv. 2021, 1, 660-674. https://doi.org/10.3390/jcp1040033
Overmars A, Venkatraman S. New Semi-Prime Factorization and Application in Large RSA Key Attacks. Journal of Cybersecurity and Privacy. 2021; 1(4):660-674. https://doi.org/10.3390/jcp1040033
Chicago/Turabian StyleOvermars, Anthony, and Sitalakshmi Venkatraman. 2021. "New Semi-Prime Factorization and Application in Large RSA Key Attacks" Journal of Cybersecurity and Privacy 1, no. 4: 660-674. https://doi.org/10.3390/jcp1040033
APA StyleOvermars, A., & Venkatraman, S. (2021). New Semi-Prime Factorization and Application in Large RSA Key Attacks. Journal of Cybersecurity and Privacy, 1(4), 660-674. https://doi.org/10.3390/jcp1040033







