Non-Stationary Flood Discharge Frequency Analysis in West Africa
Abstract
1. Introduction
2. Materials and Methods
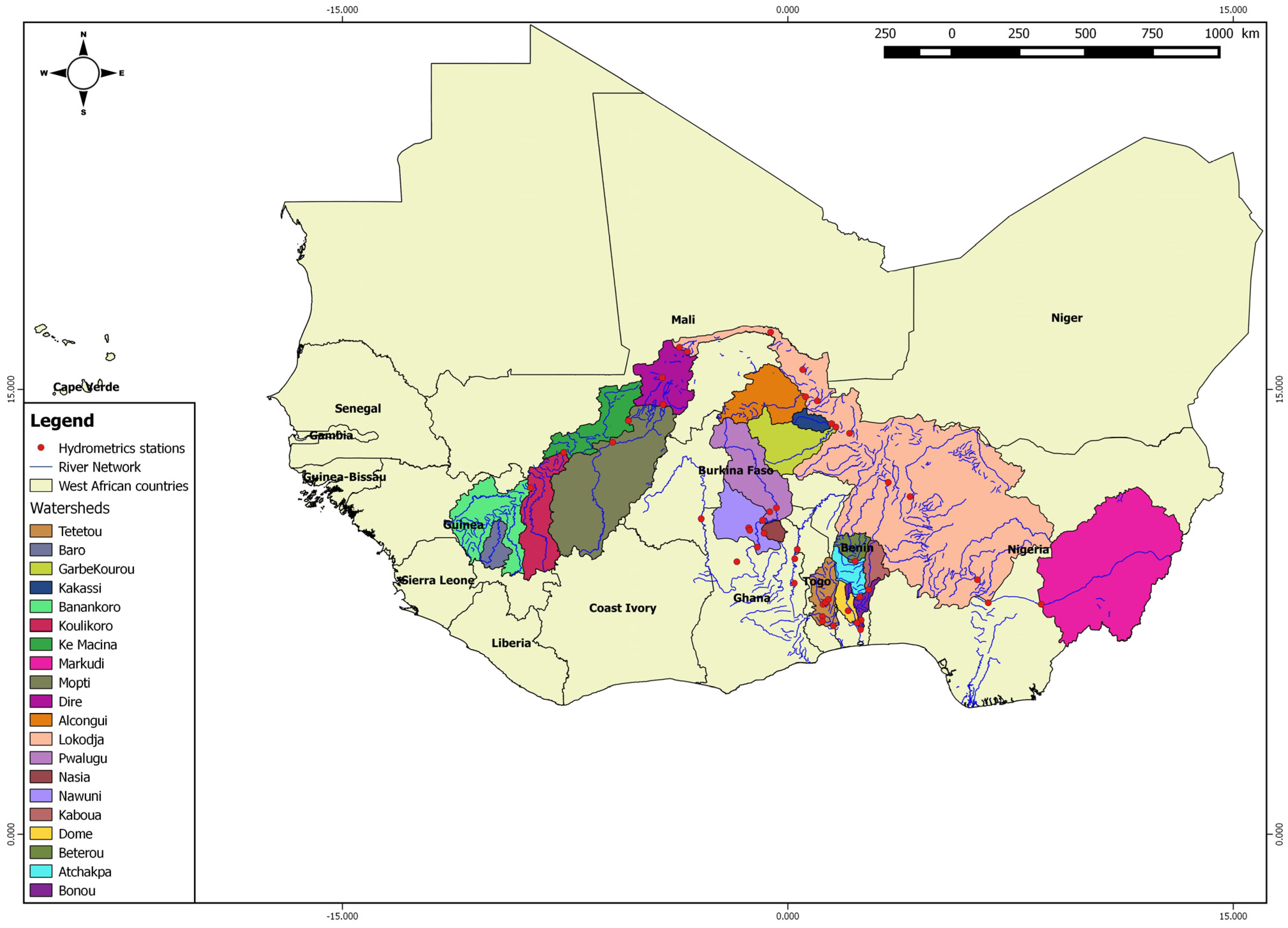
2.1. Description of the Study Area
- -
- The arid zone or Sahel Zone includes the Sahel or the Sahelian zone and has up to 750 mm of rainfall in a single short rainy season with an extended dry season of up to 10 months. The dry season sometimes extends into years causing severe droughts. This area includes parts of northern Senegal, parts of Mali, Burkina Faso, and Niger.
- -
- The semi-arid zone or Guinea Savanna Zone includes approximately the southern Sahel and covers the southern parts of Mali, Burkina Faso, Niger, Chad and the upper parts of Guinea-Bissau, Guinea, Togo, northern Benin, Nigeria, Cameroon, and the Central African Republic. The average annual rainfall, from 750 mm to 1250 mm, falls in one season followed by a 7- to 8-months-long dry season.
- -
- The subhumid zone or Equatorial Forest Zone includes southern Guinea-Bissau, the upper parts of Guinea, the southernmost parts of Mali and Burkina Faso and the southern parts of Ghana, Côte d’Ivoire, Cameroon, Sierra Leone, Benin, and the central parts of Nigeria. The average annual rainfall is between 1250 mm and 1500 mm in one season.
2.2. Data Collected
- -
- Tropical North Atlantic Index (TNAI) and TSAI (Tropical South Atlantic Index): These two indices are located in the tropical Atlantic. TNAI SSTs range from 5.5° N/23.5° N–15° W/57.5° W and TSAI from 0/20° S–10° E/30° W. These data are from the NOAA CPC archives [21]. These data downloaded are from 1948 to 2020 and are available on www.esrl.noaa.gov/psd/data/correlation/tna.data (accessed on 1 September 2021) and www.esrl.noaa.gov/psd/data/correlation/tsa.data (accessed on 1 September 2021).
- -
- Dipole Mode Index East (DMIE): The DMIE is located in the Indian Ocean in the range 10 S–10 N, 50 E–70 E [22]. These downloaded data are from 1870 to 2020 on https://psl.noaa.gov/gcos_wgsp/Timeseries/Data/dmieast.had.long.data (accessed on 1 September 2021).
- -
- Dipole Mode Index West (DMIW): The DMIW is located in the Indian Ocean in the range 10 S: 0.90 E–110 E [22]. These data downloaded are from 1870 to 2020 on https://psl.noaa.gov/gcos_wgsp/Timeseries/Data/dmiwest.had.long.data (accessed on 1 September 2021).
- -
- Dipole Mode Index (DMI): The DMI is calculated from the difference between the two East and Ouest indices located in the Indian Ocean [22]. The SSTs of the DMI are between the difference 10 S: 10 N, 50 E–70 E and 10 S: 0.90 E–110 E. It is available on https://psl.noaa.gov/gcos_wgsp/Timeseries/Data/dmi.had.long.data (accessed on 1 September 2021). These data downloaded are from 1870 to 2020.
- -
- MEI (Multivariate ENSO Index): It is calculated from the values of the six variables (surface pressure, zonal and meridian component of the surface wind, sea surface temperature, surface air temperature and cloud cover) [23]. Available on https://www.psl.noaa.gov/enso/mei (accessed on 1 September 2021), the MEI is part of the Pacific Ocean indices. This is a bimonthly index; these downloaded data are from 1979 to 2020.
- -
- ONI (Oceanic Nino Index): obtained on https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (accessed on 1 September 2021), this index is also part of the indices of the Pacific Ocean [21]. This trimonthly index was downloaded from 1950 to 2020.
2.3. Methods
2.3.1. Data Quality Assessment
- -
- delete stations with less than thirty (30) years of data available from at least 1980 to recent period.
- -
- determine the maximum flow values for each year at each station: the maximum per block (per year) approach is adopted [24]
- -
- delete the years whose maximum discharge value does not fall within the peak of rainy season (between June and November).
- -
- remove stations having less than twenty (20) years of continuous data.
- -
- remove outliers of annual maximum data obtained via the boxplot. By comparing the maximum values with the limit value corresponding to the station for the corresponding boxplot, we eliminated those below the limit value.
2.3.2. Data Processing
3. Results
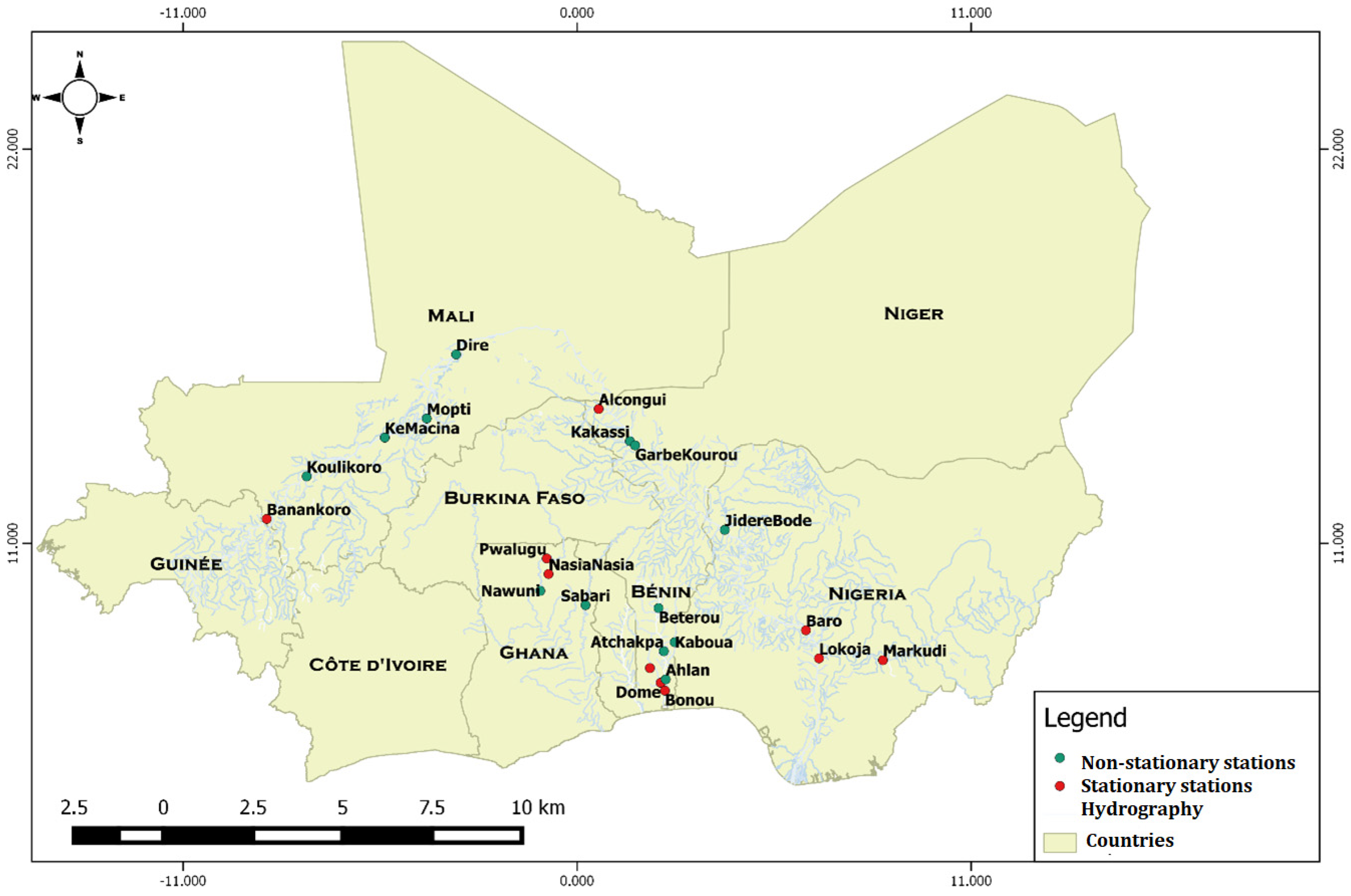
3.1. Homogeneity, Stationarity, and Independence of the Annual Maximum Flow Data in the Study Area
3.2. Identification of Climatic Covariates for AMD Indicating Non-Stationarity
3.3. Non-Stationary Frequency Analysis of Flows for Stations with Good Correlation with Climatic Covariates
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- GFDRR. Rapport D’évaluation des Besoins Post Catastrophes Préparé Par Le Gouvernement. 2020. Available online: https://www.gfdrr.org/sites/default/files/publication/pda-2011-benin-fr.pdf (accessed on 10 July 2021).
- Avahounlin, F.R.; Lawin, A.E.; Alamou, E.; Chabi, A.; Afouda, A. Analyse Fréquentielle Des Séries de Pluies et Débits Maximaux de L’ Ouémé et Estimation Des Débits de Pointe. Eur. J. Sci. Res. 2013, 107, 355–369. [Google Scholar]
- Komi, K.; Amisigo, B.A.; Diekkrüger, B.; Hountondji, F.C.C. Regional Flood Frequency Analysis in the Volta River Basin, West Africa. Hydrology 2016, 3, 5. [Google Scholar] [CrossRef]
- Nathanael, J.J.; Smithers, J.C.; Horan, M.J.C. Assessing the Performance of Regional Flood Frequency Analysis Methods in South Africa. Water SA 2018, 44, 387–398. [Google Scholar] [CrossRef]
- Singo, L.R.; Kundu, P.M.; Odiyo, J.O.; Mathivha, F.I.; Nkuna, T.R. Flood Frequency Analysis of Annual Maximum Stream Flows for Luvuvhu River Catchment, Limpopo Province, South Africa. 2012. Available online: https://univendspace.univen.ac.za/handle/11602/1262 (accessed on 10 July 2021).
- Mkhandi, S.H.; Kachroo, R.K.; Gunasekara, T.A.G. Analyse Frequentielle Des Crues En Afrique Australe, II Identification Des Distributions Régionales. Hydrol. Sci. J. 2000, 45, 449–464. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Hounkpè, J.; Diekkrüger, B.; Badou, D.; Afouda, A. Non-Stationary Flood Frequency Analysis in the Ouémé River Basin, Benin Republic. Hydrology 2015, 2, 210–229. [Google Scholar] [CrossRef]
- Johnson, K.; Smithers, J.; Schulze, R. A Review of Methods to Account for Impacts of Nonstationary Climate Data on Extreme Rainfalls for Design Rainfall Estimation in South Africa. J. S. Afr. Inst. Civ. Eng. 2021, 63, 55–61. [Google Scholar] [CrossRef]
- Cunderlik, J.M.; Burn, D.H. Non-Stationary Pooled Flood Frequency Analysis. J. Hydrol. 2003, 276, 210–223. [Google Scholar] [CrossRef]
- He, Y.; Bárdossy, A.; Brommundt, J. Non-Stationary Flood Frequency Analysis in Soutern Germany. In Proceedings of the 7th International Conference on HydroScience and Engineering, Philadelphia, PA, USA, 10–13 September 2006. [Google Scholar]
- Leclerc, M.; Ouarda, T.B.M.J. Non-Stationary Regional Flood Frequency Analysis at Ungauged Sites. J. Hydrol. 2007, 343, 254–265. [Google Scholar] [CrossRef]
- Seidou, O.; Ramsay, A.; Nistor, I. Climate Change Impacts on Extreme Floods II: Improving Flood Future Peaks Simulation Using Non-Stationary Frequency Analysis. Nat. Hazards 2012, 60, 715–726. [Google Scholar] [CrossRef]
- Seidou, O.; Ramsay, A.; Nistor, I. Climate Change Impacts on Extreme Floods I: Combining Imperfect Deterministic Simulations and Non-Stationary Frequency Analysis. Nat. Hazards 2012, 61, 647–659. [Google Scholar] [CrossRef]
- Mat Jan, N.A.; Shabri, A.; Samsudin, R. Handling Non-Stationary Flood Frequency Analysis Using TL-Moments Approach for Estimation Parameter. J. Water Clim. Chang. 2019, 1, 966–979. [Google Scholar] [CrossRef]
- Slater, L.J.; Anderson, B.; Buechel, M.; Dadson, S.; Han, S.; Harrigan, S.; Kelder, T.; Kowal, K.; Lees, T.; Matthews, T.; et al. Nonstationary Weather and Water Extremes: A Review of Methods for Their Detection, Attribution, and Management. Hydrol. Earth Syst. Sci. 2021, 25, 3897–3935. [Google Scholar] [CrossRef]
- Schneider, T.; Bischoff, T.; Haug, G.H. Migrations and Dynamics of the Intertropical Convergence Zone. Nature 2014, 513, 45–53. [Google Scholar] [CrossRef] [PubMed]
- USGS West Africa: Land Use and Land Cover Dynamics, Earth Resources observation and science (EROS) center science. 2023. Available online: https://pubs.usgs.gov/fs/2017/3004/fs20173004.pdf (accessed on 10 July 2021).
- FAO. FAO in Africa; FAO: Accra, Ghana, 2023; 35p. [Google Scholar]
- Global Runoff Data Centre(GRDC) Global Runoff Data Centre, Station Summary Statistics. 2019, pp. 1–28. Available online: https://www.bafg.de/GRDC/EN/01_GRDC/13_dtbse/database_node.html (accessed on 10 July 2021).
- NOAA Linear Correlations in Atmospheric Seasonal/Monthly Averages. Available online: https://psl.noaa.gov/data/correlation/tna.data. https://psl.noaa.gov/data/correlation/tsa.data (accessed on 1 October 2020).
- Smith, C. Dipole Mode Index (DMI). Available online: https://psl.noaa.gov/gcos_wgsp/Timeseries/DMI/ (accessed on 1 February 2021).
- ESRL/NOAA Multivariate ENSO Index Version 2 (MEI.V2). Available online: https://www.esrl.noaa.gov/psd/enso/mei/ (accessed on 15 February 2020).
- Nolet-gravel, É. Changements Projetés Des Précipitations Extrêmes Au Québec. Master’s Thesis, University of Montreal, Montreal, QC, Canada, 2019. [Google Scholar]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C.Y. Applicability of Prewhitening to Eliminate the Influence of Serial Correlation on the Mann-Kendall Test. Water Resour. Res. 2002, 38, 1068. [Google Scholar] [CrossRef]
- Friedman, J.H.; Rafsky, L.C. Multivariate Generalizations of the Wald-Wolfowitz and Smirnov Two-Sample Tests. Ann. Stat. 1979, 7, 697–717. [Google Scholar] [CrossRef]
- Hounkpè, J. Assessing the Climate and Land Use Changes Impact on Flood Hazard in Ouémé River Basin, Benin (West Africa). Ph.D. Thesis, University of Abomey, Calavi, Benin, 2016. [Google Scholar]
- Lüdecke, H.-J.; Müller-Plath, G.; Wallace, M.G.; Lüning, S. Decadal and multidecadal natural variability of African rainfall. J. Hydrol. Reg. Stud. 2021, 34, 100795. [Google Scholar] [CrossRef]
- Patra, J.P.; Kumar, R.; Mani, P.; Kumar, S. Impact of Non-Stationarity on Flood Frequency Estimates for a Himalayan Sub-Basin. 2020. Available online: https://www.iitr.ac.in/rwc2020/pdf/papers/RWC_66_Patra_et_al.pdf (accessed on 10 July 2021).

| Models | Parameters | ||
|---|---|---|---|
| Position | Scale | Shape | |
| GEV0 | |||
| GEV1 | |||
| GEV2 | |||
| GEV3 | |||
| GEV4 | |||
| GEV5 | |||
| GEV6 | |||
| GEV7 | |||
| GEV8 | |||
| GEV9 | |||
| GEV10 | |||
| GEV11 | |||
| GEV12 | |||
| GEV13 | |||
| GEV14 | |||
| GEV15 | |||
| Stations | Homogeneity | Stationarity Test | Independence | Conclusion | |||
|---|---|---|---|---|---|---|---|
| p-Value | Signifi. Level | p-Value | Signifi. Level | p-Value | Signifi. Level | ||
| Alcongui | 0.17 | 0.12 | 0.40 | Stationary | |||
| Banankoro | 0.19 | 0.57 | 0.08 | Non-stationary | |||
| Baro | 0.45 | 0.41 | 1.00 | Non-stationary | |||
| Dire | 0.0004 | *** | 1.0 × 10−4 | *** | 1.1 × 10−4 | *** | Stationary |
| Garbe Kourou | 0.007 | ** | 1.1 × 10−3 | ** | 0.01 | * | Stationary |
| Jidere Bode | 0.007 | ** | 9.44 × 10−15 | *** | 0.70 | Stationary | |
| Kakassi | 0.05 | * | 2.15 × 10−5 | *** | 0.04 | * | Non-stationary |
| Ke-Macina | 0.001 | ** | 9.2 × 10−3 | ** | 1.7 × 10−3 | ** | Stationary |
| Koulikoro | 0.001 | ** | 1.4 × 10−2 | * | 0.08 | Non-stationary | |
| Lokoja | 0.19 | 0.07 | 1.00 | Stationary | |||
| Makurdi | 0.18 | 0.19 | 0.69 | Non-stationary | |||
| Mopti | 0.002 | ** | 0.01 | * | 2.9 × 10−3 | ** | Non-stationary |
| Nasia Nasia | 0.08 | 0.14 | 0.66 | Non-stationary | |||
| Nawuni | 0.33 | 0.04 | * | 0.71 | Non-stationary | ||
| Ahlan | 0.03 | * | 0.02 | * | 0.14 | Non-stationary | |
| Atchakpa | 0.10 | 2.0 × 10−3 | ** | 0.49 | Non-stationary | ||
| Atcherigbe | 0.66 | 0.40 | 0.71 | Stationary | |||
| Beterou | 0.06 | 0.01 | ** | 0.51 | Stationary | ||
| Bonou | 0.79 | 0.56 | 1.00 | Non-stationary | |||
| Dome | 0.29 | 0.15 | 1.00 | Stationary | |||
| Kaboua | 0.21 | 0.04 | * | 0.42 | Non-stationary | ||
| Pwalugu | 0.64 | 0.96 | 0.19 | Stationary | |||
| Sabari Oti | 0.001 | ** | 9.94 × 10−5 | *** | 0.05 | Non-stationary | |
| Stations | Correlation | p-Value | Covariate |
|---|---|---|---|
| Ahlan | −0.63 | 0.00015 | MEI-AS |
| Atchakpa | 0.68 | 0.000011 | TSAI-M5 |
| Beterou | 0.55 | 0.00033 | TSAI-M5 |
| Dire | 0.65 | 0.0026 | TNAI-M9 |
| Garbe Kourou | −0.57 | 0.00078 | MEI-YY |
| Jidere Bode | 0.68 | 0.000048 | DMIW-M7 |
| Kaboua | 0.58 | 0.0014 | DMIW-M1 |
| Kakassi | 0.5 | 0.01 | DMIW-M1 |
| Ke-Macina | 0.36 | 0.04 | DMI-M3 |
| Koulikoro | 0.34 | 0.05 | DMI-M3 |
| Mopti | 0.48 | 0.0063 | DMI-M4 |
| Nawuni | 0.59 | 0.00067 | TSAI-M5 |
| Sabari Oti | 0.52 | 0.0042 | DMI-M3 |
| Stations | Models | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GEV0 | GEV1 | GEV2 | GEV3 | GEV4 | GEV5 | GEV6 | GEV7 | GEV8 | GEV9 | GEV10 | GEV11 | GEV12 | GEV13 | GEV14 | GEV15 | |
| Ahlan | 12 | 3 | 10 | ns | 11 | 1 | ns | 6 | 9 | 2 | 5 | ns | 4 | 8 | ns | 7 |
| Atchakpa | 12 | 3 | ns | 9 | 10 | 8 | ns | 5 | ns | 1 | 7 | 11 | 2 | 6 | ns | 4 |
| Beterou | 13 | 1 | ns | 7 | ns | 2 | ns | 3 | 8 | 5 | 4 | 11 | 6 | 9 | 12 | 10 |
| Dire | 14 | 4 | 12 | 10 | 13 | 2 | ns | 5 | 9 | 7 | 11 | 6 | 1 | ns | 8 | 3 |
| Garbe Kourou | 13 | 9 | ns | 3 | ns | 1 | ns | 7 | 8 | 2 | 10 | 6 | 4 | 12 | 11 | 5 |
| Jidere Bode | 6 | ns | 5 | 3 | ns | ns | ns | ns | ns | ns | ns | 4 | 2 | ns | ns | 1 |
| Kaboua | 10 | 2 | 9 | 7 | ns | 1 | ns | 3 | 8 | 5 | 4 | ns | 6 | ns | ns | ns |
| Kakassi | 11 | ns | 7 | 6 | ns | 10 | ns | 5 | 1 | 2 | ns | 8 | ns | 9 | 3 | 4 |
| Ke-Macina | 1 | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns |
| Koulikoro | 1 | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns |
| Mopti | 5 | ns | ns | 4 | ns | 1 | ns | ns | 2 | ns | 3 | ns | ns | ns | ns | ns |
| Nawuni | 1 | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns | ns |
| Sabari Oti | 6 | ns | ns | 1 | ns | 4 | ns | 3 | 5 | ns | ns | ns | ns | 2 | ns | ns |
| Stations | Parameters | Criterion (BIC) | ||
|---|---|---|---|---|
| Position | Log (Scale) | Shape | ||
| Alcongui | 191.12 | 4.56 | −0.39 | 306.16 |
| Atcherigbe | 311.44 | 5.26 | −0.37 | 435.49 |
| Banankoro | 2646.87 | 7.00 | −0.61 | 570.39 |
| Bar | 3762.53 | 7.57 | −0.17 | 444.40 |
| Bonou | 799.65 | 5.41 | −0.77 | 456.12 |
| Dome | 123.93 | 2.87 | −0.76 | 242.72 |
| Makurdi | 9865.04 | 2.02 | 0.00 | 4.6 × 10286 |
| Nasia Nasia | 126.19 | 3.84 | −0.04 | 246.80 |
| Pwalugu | 669.51 | 6.00 | −0.92 | 315.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bossa, A.Y.; Akpaca, J.d.D.; Hounkpè, J.; Yira, Y.; Badou, D.F. Non-Stationary Flood Discharge Frequency Analysis in West Africa. GeoHazards 2023, 4, 316-327. https://doi.org/10.3390/geohazards4030018
Bossa AY, Akpaca JdD, Hounkpè J, Yira Y, Badou DF. Non-Stationary Flood Discharge Frequency Analysis in West Africa. GeoHazards. 2023; 4(3):316-327. https://doi.org/10.3390/geohazards4030018
Chicago/Turabian StyleBossa, Aymar Yaovi, Jean de Dieu Akpaca, Jean Hounkpè, Yacouba Yira, and Djigbo Félicien Badou. 2023. "Non-Stationary Flood Discharge Frequency Analysis in West Africa" GeoHazards 4, no. 3: 316-327. https://doi.org/10.3390/geohazards4030018
APA StyleBossa, A. Y., Akpaca, J. d. D., Hounkpè, J., Yira, Y., & Badou, D. F. (2023). Non-Stationary Flood Discharge Frequency Analysis in West Africa. GeoHazards, 4(3), 316-327. https://doi.org/10.3390/geohazards4030018











