Abstract
Given the increasing occurrence of landslides worldwide, the improvement of predictive models for landslide mapping is needed. Despite the influence of geotechnical parameters on SHALSTAB model outputs, there is a lack of research on models’ performance when considering different variables. In particular, the role of geotechnical units (i.e., areas with common soil and lithology) is understudied. Indeed, the original SHALSTAB model considers that the whole basin has homogeneous soil. This can lead to the under-or-overestimation of landslide hazards. Therefore, in this study, we aimed to investigate the advantages of incorporating geotechnical units as a variable in contrast to the original model. By using locally sampled geotechnical data, 13 slope-instability scenarios were simulated for the Jaguar creek basin, Brazil. This allowed us to verify the sensitivity of the model to different input variables and assumptions. To evaluate the model performance, we used the Success Index, Error Index, ROC curve, and a new performance index: the Detective Performance Index of Unstable Areas. The best model performance was obtained in the scenario with discretized geotechnical units’ values and the largest sample size. Results indicate the importance of properly characterizing the geotechnical units when using SHALSTAB. Hence, future applications should consider this to improve models’ predictivity.
1. Introduction
Landslide disasters have increased significantly in the last decades, leading to economic disruption, damage to properties, and loss of lives. According to the EM-DAT database, landslides claimed the lives of 26,750 people worldwide from 1991 to 2020. In Brazil, 629 and 2502 fatalities were reported due to landslides and due to the combination of landslides and floods, respectively. Hence, Brazil is regarded as one of the countries with the highest annual mortality levels due to landslides [1]. To reduce the existing risk, public managers have long been adopting tools to subsidize decision-making by optimizing regional planning [2]. To this end, delineating landslide-prone areas is considered essential, as these assessments provide decision-makers with relevant information regarding landslide occurrences [3,4].
Overall, existing methods used for modeling landslide susceptibility can be classified into physically based models, statistical models, knowledge-driven (i.e., heuristic) models [4,5], and, more recently, machine learning models [2,6]. Among these approaches, physically based models such as the Shallow Landslide Stability Model (SHALSTAB) [7], Stability Index Mapping (SINMAP) [8], and Transient Rainfall Infiltration and Grid-based Regional (TRIGRS) [9,10] have been commonly adopted as effective tools for predicting areas susceptible to slope instability. These models currently deliver the highest prediction accuracy among all existing methods [6]. They are based on the Safety Factor (FS), which reduces the subjectivity of the model outcomes.
Among the aforementioned models, SHALSTAB stands out for its efficiency. It is worth mentioning that the SHALSTAB was conceptualized as a simple model to map shallow landslide potential [7]. Some studies demonstrate the better performance of SHALTAB, even when compared with accurate models such as TRIGRS [11,12,13], which incorporates varying hydrological parameters over time, and SINMAP, which follows a probabilistic approach [12,14]. Therefore, the frequent use of SHALTAB is associated with its high efficiency due to its deterministic aspect, easy access, availability of free software, and the small amount of data it requires.
Given its advantages, the SHALSTAB model has been applied in several countries: the USA [7,15]; Canada [16]; Argentina [15]; Portugal [17]; Italy [18,19,20]; Guatemala [21]; and Australia [22]. In Brazil, SHALSTAB has also been widely used [13,14,23,24,25,26,27,28,29,30,31]. In a recent systematic review, Melo et al. [32] highlighted aspects that should be considered to advance the SHALSTAB studies. Among the findings, the authors emphasized the importance of determining input parameters with local sampling. Indeed, it was found that, due to lack of resources, many studies in Brazil did not carry out field sampling to determine soil mechanical properties. Studies often use data obtained in other study areas which are pedologically similar [18,23,24,27,31,33,34]. Even when the studies sample data, these tend to have few data points. For instance, even though Kim et al. [35] characterized the soil by sampling it, they considered that the soil mechanical properties were homogeneous over the study area. This limitation is linked to the lack of resources and/or research time for collecting relevant information. This is the case in many developing countries such as Brazil, where data scarcity prevails.
The data required for applying SHALSTAB are related to topographic and physical characteristics of the soil for each terrain unit (i.e., pixel). These include variables such as the soil friction angle, cohesion, specific mass, and layer depth. In terms of topographic features, the counter length, the upstream contribution area, and the slope are variables often included. SHALSTAB also allows for customization. In Brazil, Michel et al. [25,26], inserted new variables (cohesion and root weight) and considered the spatially discretized characterization of the values of the geotechnical units into the model. Here, the geotechnical unit is defined as the area which has common soil type and lithology. Within one geotechnical unit, mechanical and hydraulic properties of soil are considered uniform. Therefore, a geotechnical unit can be determined with soil type and geological maps [36].
Concerning the model uncertainty and sensitivity, several studies highlight the influence of spatial resolution of digital terrain models (DTM) on the estimation of instability areas [37]. These studies demonstrated the importance of adopting more detailed spatial scales. This is relevant because, with more detail on the slope relief, it is possible to verify the degree of water concentration. The slope relief can also be used as an indication of failure predisposition. Based on a sensitivity analysis of SHALSTAB model outputs, Borga et al. [38] and Michel et al. [25,26] verified the most relevant parameters and demonstrated the strong sensitivity of SHALSTAB to the cohesion value.
The original SHALSTAB algorithm considers a single set of geotechnical values for a whole basin. However, for better performance, Michel et al. [25] modified the algorithm, inserting a spatial discretization of the geotechnical values of each unit into this model. Using the algorithm established by Michel et al. [25], Sbroglia et al. [28] considered spatially discretized geotechnical unit values. Although the consideration of these aspects enabled the generation of more realistic predictive maps, there are still many uncertainties of both the actual benefits as a consequence of the geotechnical-unit characterization and the inherent processes related to the spatialization as well as the amount of soil sample data required for this purpose. Hence, Michel et al. [26] and Sbroglia et al. [28] proposed a new technique for the discretization of geotechnical-unit characteristics. However, the effect of such discretization was not well investigated in detail.
Therefore, this study aimed at investigating the advantages of using the geotechnical-unit characterization as a variable in the slope stability calculation using SHALSTAB. To this end, several scenarios were proposed to represent distinct contexts of distribution and quantification of soil sampling points. To analyze the model performance, we used state-of-the-art techniques, such as the ROC (Receiver Operating Characteristic) curve [39], and the Success Index and Error Index [20]. Besides this, we also proposed a new metric which is termed Detective Performance Index of Unstable Areas (DPIUA).
2. Materials and Methods
2.1. An Overview of the SHALSTAB Model
SHALSTAB is a deterministic model directed to the identification of sites predisposed to shallow landslides. This model results from combining the infinite slope stability model and a hydrological model [7]. Thus, SHALSTAB determines the areas susceptible to landslides based on the ratio between recharge rate and soil transmissivity sufficient to cause a slope destabilization (Equation (1)). Here, soil transmissivity is defined as the product of saturated hydraulic conductivity and depth to a restrictive layer [40]. Detailed descriptions of the SHALSTAB model can be obtained in [7,41]
where q is the uniform recharge rate [mm]; T is the transmissivity of the soil [m2/day]; b is the contour length [m]; a is the upstream contribution area [m2]; θ is the slope [o]; ρs is the specific mass of the soil [kg/m3]; ρw is the specific mass of water [kg/m3]; ϕ is the angle of internal friction of the soil [°]; c is the soil cohesion [N/m2]; z is the depth of the soil [m]; and g is the gravitational acceleration [m/s2].
2.2. Study Area
To verify the applicability of the proposed approach, we considered the Jaguar creek basin (25 km2), located in the Rio Grande do Sul state, Brazil, as a case study (Figure 1). The altimetry in the basin varies from 78 m to 700 m. The mean slope is approximately 15°, and 8% of its area lies in slopes above 30°, which can be considered a reference angle of internal friction (ϕ) value. The predominant lithology types are acid volcanic rocks and sandstones (Flores et al., 2007). By considering the combination between the lithology and soil types, five geotechnical units can be observed (Table 1). Here, a geotechnical unit is defined as an area designated by the intersection between a given lithological unit and a given pedological unit. A detailed description of the lithology and soil types in the study area is provided by Coelho et al. [42].
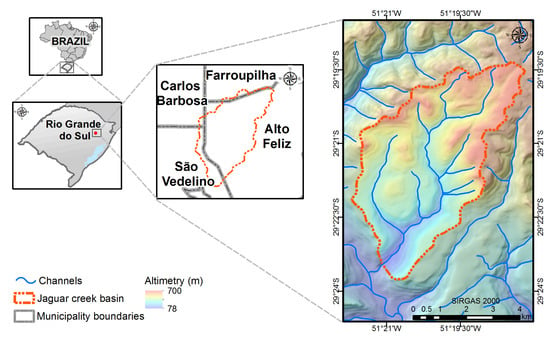
Figure 1.
Location and altimetry of Jaguar creek basin, southern Brazil.

Table 1.
Overview of the five geotechnical units present in the Jaguar creek basin.
Due to the aforementioned characteristics, the Jaguar creek is prone to landslides, and several occurrences have already been reported. Indeed, there are records of severe sediment-related disasters in 1982 and 2000 [43]. These disasters were characterized mainly by shallow landslides. In 2000, debris flow from two shallow landslides killed four people in the Böni basin, located in the Jaguar creek basin [44].
2.3. Data
The SHALSTAB model requires six variables for its application. The variables θ and a are the input data, obtained from the DTM with a spatial resolution of 2.5 m × 2.5 m provided by the Brazilian Geological Survey (CPRM). The DTM was generated by BRADAR by interferometry of Synthetic Aperture Radar data in the P band. The input parameters ϕ, c, and z were obtained from Michel [43], which carried out soil samplings and Borehole tests at 20 points distributed across the five geotechnical units (Figure 2). Note that the sampling depth for the borehole tests in Michel [43] was near the possible slipping plane. This was done because our interest was to have soil mechanical characteristics at the possible slipping depth, and we did not intend to characterize the entire soil layer profile.
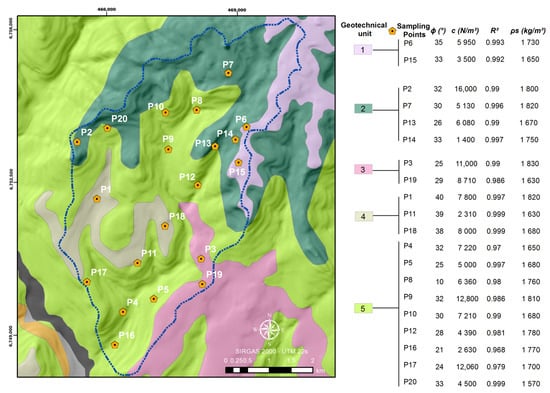
Figure 2.
Geotechnical map of the Jaguar creek basin and sampling points where the parameters ϕ, c, and z were estimated. R2 is the coefficient of determination and ρs is the wet soil bulk density. The values presented here characterize the mechanical properties of soil near this slipping plane.
To analyze the SHALSTAB model performance, we used available landslide inventory data. Michel [43] analyzed satellite images from the period after the landslide events that occurred in 2000 in the study area and constructed an inventory of landslide scars by considering preliminary data by Vanacôr and Rolim [45] and CPRM.
2.4. Application of the Modified SHALSTAB Model
The present work adopted the modified algorithm proposed by Michel et al. [25,26], which performs a spatial discretization of the geotechnical values of each unit. This modified version permits different values of soil characteristics such as c, ϕ, and z. Besides Michel et al. [25,26], Sbroglia et al. [28] also obtained a good performance when using this modified version.
Based on the values of 20 soil-sampling points (Figure 2) and the values proposed by the software default, 13 scenarios were elaborated and simulated for six different soil depths: 0.5 m, 0.75 m, 1 m, 1.5 m, 2 m, and 3 m. The mean soil depth of the whole basin is 0.75 m [43]. In addition to considering distinct soil depths, we also evaluated the effect of adopting different criteria for determining the variables such as mean values of all sampling points, sampling points only with the highest R2, among others (Figure 3).
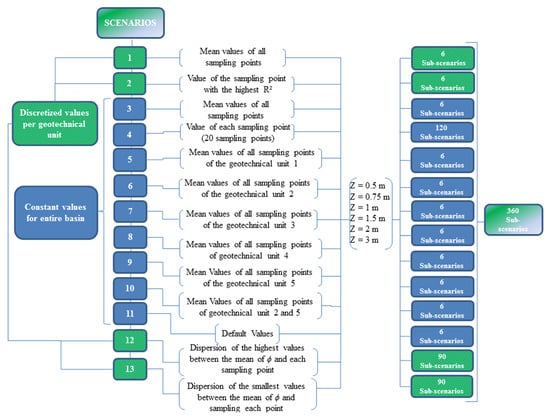
Figure 3.
Different scenarios elaborated for estimating the landslide susceptibility. Green boxes denote scenarios with discretized values per geotechnical unit, whereas blue boxes indicate scenarios in which constant values were adopted for the entire basin.
Scenario 1 considered all the 20 sampling points to calculate the mean value of each parameter (ϕ, c, and ρs) in each geotechnical unit. Conversely, Scenario 2 considered only one sampling point per geotechnical unit. To this end, the highest R2 of the shear envelope in each unit was adopted (Table 2). It should be noted that in geotechnical unit 4, the sampling points 11 and 18 obtained the same R2. In this case, the sampling point 18 was adopted given its central location. This consideration reduces possible uncertainties of values related to areas located between the boundaries of the geotechnical units.

Table 2.
SHALSTAB model input parameters in scenarios 1, 2, 3, and 11.
Scenario 3 used the mean values for the entire basin based on the average of the 20 sampling points (Table 2). Similarly, the geotechnical values for the whole basin were adopted in Scenario 4, but with the values obtained at each sampling point individually (Table 3). In Scenario 4, each set of parameter values of each sampling point was simulated at six different depths, resulting in 120 sub-scenarios. Since both Scenarios 3 and 4 considered constant values for the whole basin, their simulations were performed with the original SHALSTAB values.

Table 3.
SHALSTAB model input parameters in Scenario 4.
Still considering that the whole basin has a homogeneous soil, Scenarios 5 to 9 considered the mean set of the sampling points in each geotechnical unit. In Scenarios 5 to 9, the whole basin was characterized by the geotechnical units 1 to 5, respectively (Table 4). The number of the sampling points for each geotechnical unit was defined by prioritizing units with more landslide scars [43]. Hence, in Scenario 10 we considered the mean values of the sampling points contemplated by the geotechnical units 2 and 5 because the geotechnical units 2 and 5 possessed a larger number of sampling points. In Scenario 11, we adopted the values proposed by the SHALSTAB default (Table 2).

Table 4.
SHALSTAB model input parameters in Scenarios 5 to 10.
Scenarios 12 and 13 are based on the dispersion between the mean ϕ value of each geotechnical unit and the sampling points inserted within it. The criterion adopted in Scenario 12 admitted dispersion of the highest values to the lowest, i.e., the values with the highest dispersion compared to the average were gradually removed until only one point remained per geotechnical unit. This allowed the gradual withdrawal of values that presented greater dispersions until only one sampling point remained per geotechnical unit. Conversely, in Scenario 13, the criterion was inverted, with the progressive withdrawal of the values with smaller dispersions compared to the average (Table 5). In the case of identical dispersions between two points, if it was evident when there were only two sample points (geotechnical units 1 and 3) the criterion was the removal of the point with the worst R2 of the shear envelope. As Scenario 12 has 15 different values of ϕ with six different depths, the total number of sub-scenarios is 90. Likewise, the number of sub-scenarios for Scenario 13 is also 90.

Table 5.
SHALSTAB model input parameters in Scenarios 12 and 13.
2.5. Model Performance Assessment
The model performance was quantitatively evaluated by comparing simulation results with an existing inventory of landslide scars. The instability thresholds were altered according to the density of unstable cells within the inventory. In this study, we used the instability thresholds as in the original software [7]. SHALSTAB estimates the saturated proportion of soil thickness and originally classifies seven classes of instability, as shown in Table 6. From the value of q/T, the degree of instability for each cell in the study area is calculated. The model results are given on a logarithmic scale because of the very small values obtained for q/T.

Table 6.
Instability thresholds adopted in this study [7].
To evaluate our results, the performance evaluation methods proposed by Sorbino et al. [20] were used: the Success Index (SI) and the Error Index (EI). The SI (Equation (2)) is the percentage of the area considered as unstable (Ain) by the model that coincides within the area of the real occurrence of landslides (Aunstab). The EI (Equation (3)) is the percentage between the areas (Aout) considered as unstable by the model and not compatible with the inventory of scars and areas (Astab) of the basin that were not affected by landslides. It should be noted that the SI and EI indexes were calculated only for areas with slopes greater than 26.7°. This value represents the minimum slope angle with landslide scars in the Jaguar creek basin [43]. The obtained SI and EI were plotted on the ordinates axis and the abscissa axis, respectively. This graphical configuration enabled the evaluation of the performances given by representing the percentage proportionality of such indices.
In addition to the SI and EI indexes, the ROC curve [39] was also used to evaluate the model performance. This measure has been widely used [4,11,46,47]. Furthermore, we also used the methodology proposed by Dietrich et al. [48], in which a satisfactory performance is one that can detect the landslides in a smaller area classified as unstable in the basin. The lowest value of log q/T, detected within the sliding scar polygon, represents the least stable site, which categorizes the stability of the site that covers the scar.
Finally, we proposed a new metric for evaluating the model performance, termed Detective Performance Index of Unstable Areas (DPIUA) (Equation (4)). The DPIUA evaluates the performance through curves representing the number of grid cells in each log q/T category and the cumulative frequency resulting from the total area falling in each category. From these curves of cumulative areas in the basin and the scars of landslides, it is possible to verify the model performance in each category. The farther these curves are situated between themselves, the better is the performance.
where E is the percentage of the cumulative area of the landslides; A is the percentage of the cumulative area of the total area in the basin; and n is the number of classes. This index should be utilized together with SI, EI, and ROC.
3. Results
By considering 13 scenarios, 360 different simulations were executed, encompassing seven stability classes proposed by Montgomery and Dietrich [7]. To better visualize the outcomes, these classes are expressed in logarithmic scale. Two classes (unconditionally unstable and unconditionally stable) resulted from the topographical and pedological characteristics, being independent of the parameter q/T. The other classes are linked to the hydrological parameters relating to the parameter q/T. The lower values of log q/T (red areas in Figure 4, Figure 5 and Figure 6) represent areas that need less magnitude in the hydrological conditions for the area to become unstable. Therefore, they present higher instability.
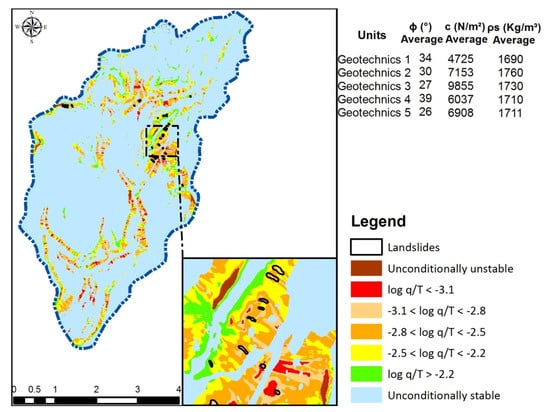
Figure 4.
Stability map of the Jaguar creek basin in Scenario 1.
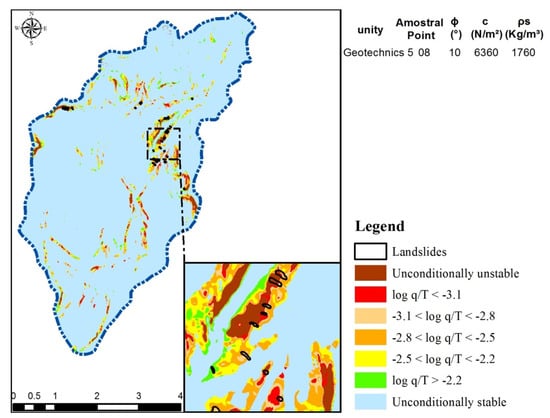
Figure 5.
Stability map of the Jaguar stream basin (Scenario 4, sampling point 08).
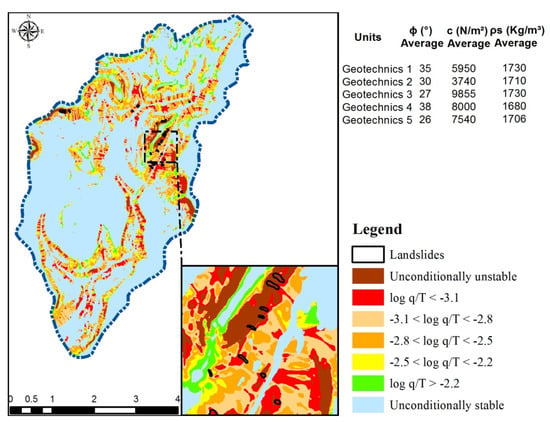
Figure 6.
Stability map of the Jaguar creek basin with Scenario 13 (13 sample points and z = 3 m).
The simulation results show that, in all scenarios, the instability classes increased as the soil layer depth increased. A reduction in unstable areas was also observed in places of lower soil depths, although they are located on steep slopes where the rate of surface erosion and the propensity for landslides are very high. When the instability threshold log q/T = −2.5 was adhered to, the best performance was obtained with Scenario 1 by considering z = 2 m, with an IA = 87% and IE = 10% (Figure 4 and Figure 7A).
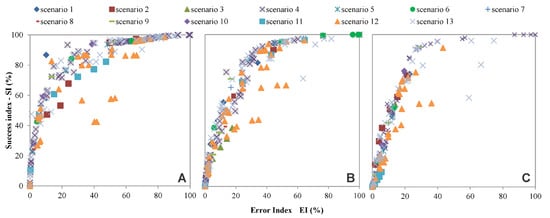
Figure 7.
ROC with the (A) threshold log q/T = −2.5. Scenario 1 presented the best performance; (B) threshold log q/T = −2.8. Scenario 4 presented the best performance; and (C) threshold log q/T = −3.1. Scenario 13 presented the best performance. The best scenarios are shown in the upper left corner of each graph.
By relating the stability classes and the cumulative percentage of the area and landslides in each class, 89% of the landslides fall into only 9% of the unstable areas in Scenario 1 when considering the threshold log q/T = −2.5. For this scenario, an area calculated between the curves of DPIUA = 55 was obtained (Figure 8A). The elaborated graphical presentation (Figure 8) presents two curves with values for each log q/T category: the first one is the “percentage of cumulative area”, and the second one is the “percentage of cumulative area of landslides”. The further these curves are, the higher the DPIUA is, and the better the performance of the SHALSTAB model.
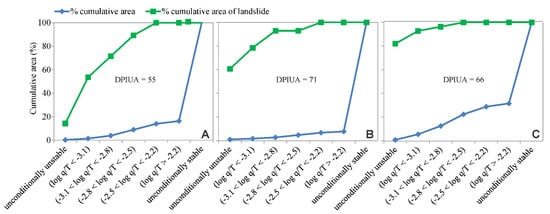
Figure 8.
DPIUA results for the scenarios with the best performance: (A) Scenario 1, (B) Scenario 4, and(C) Scenario 13.
When the instability threshold log q/T = −2.8 is adopted, the best performance was obtained with Scenario 4, where the values of the parameters of sample point 8, located in the geotechnical unit 5 and z = 1 m, were used (Figure 5). This result is observed in Figure 7B, where the values of SI and IE are 75% and 14%, respectively. Figure 8B shows the stability classes of the model and the cumulative percentage of the area and landslides in each class in Scenario 4 and the resulting area between such curves (DPIUA = 71). Thus, 93% of the landslides were classified in 3% of the unstable areas.
For the instability threshold log q/T = −3.1, the best performance was obtained with Scenario 13, which covered 13 sampling points and considered z = 3 m (Figure 6). The evaluation results corresponding to such a condition is shown in Figure 7C and Figure 8C, with SI and EI values of 90% and 26%, respectively and a DPIUA of 66. In this case, 93% of the landslides were encountered in 7% of the unstable area in the basin.
When considering instability thresholds of log q/T = −2.5 and log q/T = −3.1, the best results were obtained from the Scenarios that used the values of the discretized soil parameters per geotechnical unit. The DPIUA area in Figure 8 was larger in Scenario 13, which presented better performance when a threshold log q/T = −3.1 was adopted (DPIUA = 66). However, this result was obtained from the large value (82%) with the unconditionally unstable class, independent of the hydrologic parameters. Since rainfall is responsible for the landslides, this result can be considered incoherent.
Scenario 1, with z = 1 m, presented the best performance with the threshold q/T = −2.5, most parts of the scars from landslides (75%) were captured by this category, while 14% of landslides were captured by the unconditionally unstable category (q/T = −3.5). Observing the performances of Scenarios 13 and 1, the latter presents better coherence in the results due to a large part of the scars captured by the category associated with hydrological parameters. It is conjectured that the reduction in the c value of geotechnical unit 2, slightly more than 50%, caused an overestimation of unstable areas in the basin. Allied to this, the high soil thickness contributed to this result.
On the other hand, when the instability threshold log q/T = −2.8 is considered, the best performance was presented by Scenario 4, which adopted constant soil parameters for the whole basin. Thus, from the values of point 8 located in the geotechnical unit 5 and z = 1, 61% of the landslides were predominantly framed in the unconditionally unstable class. Meanwhile, 18% of the landslides were classified into the log q/T < −3.1 class. Similar to the aforementioned analysis associated with the log q/T = −3.1 threshold, we can assume that these results were influenced by values that are not consistent with the local reality. The low ϕ value (10°) for the whole basin probably contributed to the overestimation of unstable classes, setting the predominant classification of landslides in the unconditionally unstable class.
4. Discussion
Despite being widely used, the SHALSTAB model is often applied without considering the importance of in situ determination of geotechnical parameters and the necessity of spatial discretization of soil characteristics. Indeed, several applications tend to adopt values from other studies which investigated similar soils [18,23,27,33,34]. Michel et al. [25,26] and Sbroglia et al. [28], which used the modified algorithm of Michel et al. [25], proposed a useful procedure for discretizing soil characteristics. However, none of the previous studies quantified the effect of such discretization. To address this gap, here we analyzed it by considering different performance metrics: (1) SI and EI [20], (2) the ROC curve [39], and (3) a new index, the DPIUA (Figure 8).
Even though there are several uncertainties related to the effects of geotechnical-unit characterization, the evaluation of different instability thresholds, together with the different scenarios, showed that considering 20 sampling points to characterize the geotechnical units presented a better performance when compared to the original SHALSTAB model (Scenario 11). When considering the thresholds log q/T = −2.8 and log q/T = −3.1, the best performances had polarized results due to abrupt variation in soil resistance parameters. The importance of discretization of soil characteristics by using the geotechnical units confirms the necessity to carry out the field sampling at every unit. Hence, for improved performance, future studies should divide the study area (e.g., basins) into different geotechnical units through the use of existing data generated by other researchers or with similar soils, and, when possible, characterize them with in situ soil sampling.
The simulation results confirm the important role of soil depth in hillslope stability analysis. As demonstrated by Borga et al. [38] and Michel et al. [26], the increase in the soil depth reduces the safety factor of the hillslope. The results obtained here confirm this tendency. By analyzing the values of DPIUA, it can be said that soil depth of 2 m supported better performance in general. These results might imply that the mean depth in the basin could be 2 m. A condition with a steep hillslope and shallow soil layer can sustain the soil even in its saturated situation. Therefore, the soil layer thickness can be thought to influence hillslope failures significantly.
Although the present study showed the effect of geotechnical unit consideration on mapping performance with SHALSTAB, it did not investigate how uncertainties in parameter determination affect the reliability of the results. This theme should be investigated in more detail in future studies. How uncertainty affects results’ reliability is among the most central challenges in geosciences in general, including hydrology, geomorphology, and hydrogeomorphology [47,48]. The uncertainty depends on (i) the nature of each parameter (model input data), (ii) the methodological procedures used to collect data in the field and to analyze in the laboratory, (iii) the technical level of the involved researchers, and (iv) the adopted models, among other variables. Therefore, when feasible, uncertainty evaluations should be carried out together with sensitive analysis such as that in Michel et al. [26]. The results presented here advance this direction, showing how results vary when different assumptions are considered in each scenario.
5. Conclusions
The SHALSTAB model has been frequently applied to assess shallow-landslide susceptibility. In developing countries, where geotechnical-unit characterization is difficult due to lack of financial support, many studies measure the soil mechanical properties at few points or do not measure at all and use the data available in the SHALSTAB tutorial [32]. Therefore, the present study demonstrated the importance of considering the geotechnical-unit characterization on landslide mapping performance by considering the case of the Jaguar creek basin, southern Brazil.
In general, results showed that the use of geotechnical units characterized by several sampling points provides better results compared to the original SHALSTAB model. To evaluate the model performance, we proposed a new index called DPIUA, which allows evaluating the model robustness according to different instability thresholds (Table 6 and Figure 8). Through using several performance evaluation methods, the benefits generated by the characterization of the geotechnical units were verified. These advantages were evident as a result of the better performance of the scenarios in which the soil parameters were discretized into various geotechnical units.
Thus, future assessments should consider greater cartographic precision to obtain the variability of the geotechnical units in the application of the SHALSTAB model and also a sufficient amount of in situ soil sampling points to characterize these units. In this regard, it should be noted that the choice of the minimum number of sampling points requires careful consideration. This is one of the most critical issues for field workers who want to be time-efficient while at the same time achieving precise results. This number may depend on (i) soil types within an adopted soil classification, (ii) soil parameters for analysis, and (iii) other physical conditions such as soil covers (vegetation) and soil depth. In any case, adopting geotechnical units in future assessments will surely enable the generation of more reliable landslide-susceptibility maps.
Author Contributions
Conceptualization, M.K., G.P.M., C.M.M.; methodology, M.K., G.P.M., C.M.M.; validation, C.M.M., G.P.M. and M.K.; formal analysis, C.M.M.; investigation, C.M.M., M.K., G.P.M., M.M.d.B.; writing—original draft preparation, C.M.M., M.K.; writing—review and editing, M.M.d.B., C.M.M., M.K., G.P.M.; visualization, M.M.d.B., C.M.M.; supervision, M.K., G.P.M., M.M.d.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially supported by the Brazilian agencies CAPES and ANA (grant number 16/2017).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data is available upon request from the first author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hamza, O.; De Vargas, T.; Boff, F.E.; Hussain, Y.; Sian Davies-Vollum, K. Geohazard Assessment of Landslides in South Brazil: Case Study. Geotech. Geol. Eng. 2019, 38, 971–984. [Google Scholar] [CrossRef]
- Luo, X.; Lin, F.; Chen, Y.; Zhu, S.; Xu, Z.; Huo, Z.; Yu, M.; Peng, J. Coupling logistic model tree and random subspace to predict the landslide susceptibility areas with considering the uncertainty of environmental features. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef] [Green Version]
- De Brito, M.M.; Weber, E.J.; Krigger, V.S.; Leitzke, F.P. Análise dos Fatores Condicionantes de Movimentos de Massa No Município de Porto Alegre a Partir de Registros Históricos. Rev. Bras. Cartogr. 2016, 68, 1853–1872. [Google Scholar]
- De Brito, M.M.; Weber, E.J.; Pinto da Silva Filho, L.C. Multi-Criteria Analysis Applied to Landslide Susceptibility Mapping. Rev. Bras. Geomorfol. 2017, 18, 919–935. [Google Scholar] [CrossRef] [Green Version]
- De Brito, M.M.; Weber, E.J.; Carlos, L.; Filho, S. Revista Brasileira de Geomorfologia Multi-Criteria Analysis Applied to Landslide Susceptibility Mapping Análise Multi-Critério Aplicada ao Mapeamento da. Rev. Bras. Geomorfol. 2017, 4, 719–735. [Google Scholar]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Dietrich, W.E. A physically based model for the topographic control on shallow landsliding. Water Resour. Res. 1994, 30, 1153–1171. [Google Scholar] [CrossRef]
- Pack, R.; Tarboton, D.; Goodwin, C. SINMAP 2.0—A Stability Index Approach to Terrain Stability Hazard Mapping, User’s Manual; Utah State University: Logan, UT, USA, 1999. [Google Scholar]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef] [Green Version]
- Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS—A Fortran program for transient rainfall infiltration and grid-based regional slope-stability analysis. Open-File Rep. 2002, 424, 38. [Google Scholar] [CrossRef] [Green Version]
- Corominas, J.; van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F.; et al. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2014, 73, 209–263. [Google Scholar] [CrossRef]
- Zizioli, D.; Meisina, C.; Valentino, R.; Montrasio, L. Comparison between different approaches to modeling shallow landslide susceptibility: A case history in Oltrepo Pavese, Northern Italy. Nat. Hazards Earth Syst. Sci. 2013, 13, 559–573. [Google Scholar] [CrossRef] [Green Version]
- Vieira, B.C.; Fernandes, N.F.; Augusto Filho, O.; Martins, T.D.; Montgomery, D.R. Assessing shallow landslide hazards using the Trigrs and Shalstab models, Serra do Mar, Brazil. Environ. Earth Sci. 2018, 77, 1–15. [Google Scholar] [CrossRef]
- Michel, G.P.; Kobiyama, M.; Goerl, R.F. Comparative analysis of SHALSTAB and SINMAP for landslide susceptibility mapping in the Cunha River basin, southern Brazil. J. Soils Sediments 2014, 14, 1266–1277. [Google Scholar] [CrossRef]
- Rafaelli, S.G.; Montgomery, D.R.; Greenberg, H.M. A comparison of thematic mapping of erosional intensity to GIS-driven process models in an Andean drainage basin. J. Hydrol. 2001, 244, 33–42. [Google Scholar] [CrossRef]
- Goetz, J.N.; Guthrie, R.H.; Brenning, A. Integrating physical and empirical landslide susceptibility models using generalized additive models. Geomorphology 2011, 129, 376–386. [Google Scholar] [CrossRef]
- Teixeira, M.; Bateira, C.; Marques, F.; Vieira, B. Physically based shallow translational landslide susceptibility analysis in Tibo catchment, NW of Portugal. Landslides 2014, 12, 455–468. [Google Scholar] [CrossRef]
- Meisina, C.; Scarabelli, S. A comparative analysis of terrain stability models for predicting shallow landslides in colluvial soils. Geomorphology 2007, 87, 207–223. [Google Scholar] [CrossRef]
- Santini, M.; Grimaldi, S.; Nardi, F.; Petroselli, A.; Rulli, M.C. Pre-processing algorithms and landslide modelling on remotely sensed DEMs. Geomorphology 2009, 113, 110–125. [Google Scholar] [CrossRef]
- Sorbino, G.; Sica, C.; Cascini, L. Susceptibility analysis of shallow landslides source areas using physically based models. Nat. Hazards 2009, 53, 313–332. [Google Scholar] [CrossRef]
- Cando-Jácome, M.; Martínez-Graña, A. Determination of Primary and Secondary Lahar Flow Paths of the Fuego Volcano (Guatemala) Using Morphometric Parameters. Remote Sens. 2019, 11, 727. [Google Scholar] [CrossRef] [Green Version]
- Mazengarb, C. The Tasmanian Landslide Hazard Map Series: Methodology; Department of Infrastructure, Energy and Resources: Hobart, Australia, 2005. [Google Scholar]
- Guimaraes, R.F.; Montgomery, D.R.; Greenberg, H.M.; Fernandes, N.F.; Gomes, R.A.T.; de Carvalho Junior, O.A. Parameterization of soil properties for a model of topographic controls on shallow landsliding: Application to Rio de Janeiro. Eng. Geol. 2003, 69, 99–108. [Google Scholar] [CrossRef]
- Gomes, R.A.T.; Guimarães, R.F.; Osmar Abílio De Carvalho, J.; Fernandes, N.F.; Júnior, E.V.D.A. Combining Spatial Models for Shallow Landslides and Debris-Flows Prediction. Remote Sens. 2013, 5, 2219–2237. [Google Scholar] [CrossRef] [Green Version]
- Paulo Michel, G.; Kobiyama, M.; Fabris Goerl, R. Formulação do fator de segurança considerando a presença de vegetação. In Proceedings of the XX Brazilian Symposium on Water Resources, Bento Gonçalves, Brazil, 17–22 November 2013; Volume 8. (In Portuguese). [Google Scholar]
- Michel, G.P.; Kobiyama, M.; Goerl, R.F.; Zanandrea, F.; Paul, L.R.; Schwarz, H.; Cardozo, G.L. Efeitos da vegetação na modelagem de estabilidade de encostas na bacia hidrográfica do rio Cunha, Santa Catarina. Rev. Bras. Geomorfol. 2021, 22, 824–846. [Google Scholar] [CrossRef]
- Martins, T.D.; Vieira, B.C.; Fernandes, N.F.; Okafiori, C.; Montgomery, D.R. Application of the Shalstab model for the identification of areas susceptible to landslides: Brazilian case studies. Rev. Geomorfol. 2017, 19, 136–144. [Google Scholar] [CrossRef]
- Sbroglia, R.M.; Reginatto, G.M.P.; Higashi, R.A.R.; Guimarães, R.F. Mapping susceptible landslide areas using geotechnical homogeneous zones with different DEM resolutions in Ribeirão Baú basin, Ilhota/SC/Brazil. Landslides 2018, 15, 2093–2106. [Google Scholar] [CrossRef]
- Dos Santos, E.M.; Listo, F.D.L.R. Escorregamentos translacionais rasos no município de Camaragibe, região metropolitana do Recife: Uma análise preliminar a partir do modelo SHALSTAB. Rev. Geociências Nord. 2019, 5, 131–145. [Google Scholar] [CrossRef]
- Pacheco, T.C.K.F.; Kux, H.J.H.; Mendes, R.M. Identificação de Áreas de Suscetibilidade a Escorregamentos de Encosta Utilizando o Modelo Matemático Shalstab. Bol. Geogr. 2020, 37, 228–243. [Google Scholar] [CrossRef]
- Guimarães, R.F.; Machado, W.P.; De Carvalho, O.A.; Montgomery, D.R.; Gomes, R.A.T.; Greenberg, H.M.; Cataldi, M.; Mendonça, P.C. Determination of Areas Susceptible to Landsliding Using Spatial Patterns of Rainfall from Tropical Rainfall Measuring Mission Data, Rio de Janeiro, Brazil. ISPRS Int. J. Geo-Inf. 2017, 6, 289. [Google Scholar] [CrossRef] [Green Version]
- Melo, C.M.; Kobiyama, M. Aplicação do Modelo Shalstab No Estudo de Escorregamentos No Brasil: Revisão. Rev. Bras. Geomorfol. 2018, 19, 4. [Google Scholar] [CrossRef]
- Tarolli, P.; Borga, M.; Chang, K.T.; Chiang, S.H. Modeling shallow landsliding susceptibility by incorporating heavy rainfall statistical properties. Geomorphology 2011, 133, 199–211. [Google Scholar] [CrossRef]
- König, T.; Kux, H.J.H.; Mendes, R.M. Shalstab mathematical model and WorldView-2 satellite images to identification of landslide-susceptible areas. Nat. Hazards 2019, 97, 1127–1149. [Google Scholar] [CrossRef]
- Kim, M.S.; Onda, Y.; Uchida, T.; Kim, J.K. Effects of soil depth and subsurface flow along the subsurface topography on shallow landslide predictions at the site of a small granitic hillslope. Geomorphology 2016, 271, 40–54. [Google Scholar] [CrossRef]
- Dias, R.D. Proposta de metodologia de definição de carta geotécnica básica em regiões tropicais e subtropicais. Rev. Inst. Geológico 1995, 16, 51–55. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Montgomery, D.R. Digital elevation model grid size, landscape representation, and hydrologic simulations. Water Resour. Res. 1994, 30, 1019–1028. [Google Scholar] [CrossRef]
- Borga, M.; Fontana, G.D.; Gregoretti, C.; Marchi, L. Assessment of shallow landsliding by using a physically based model of hillslope stability. Hydrol. Process. 2002, 16, 2833–2851. [Google Scholar] [CrossRef]
- Zweig, M.H.; Campbell, G. Receiver-operating characteristic (ROC) plots: A fundamental evaluation tool in clinical medicine. Clin. Chem. 1993, 39, 561–577. [Google Scholar] [CrossRef] [PubMed]
- Giri, S.; Qiu, Z.; Prato, T.; Luo, B. An Integrated Approach for Targeting Critical Source Areas to Control Nonpoint Source Pollution in Watersheds. Water Resour. Manag. 2016, 30, 5087–5100. [Google Scholar] [CrossRef]
- Sarkar, S.; Roy, A.K.; Raha, P. Deterministic approach for susceptibility assessment of shallow debris slide in the Darjeeling Himalayas, India. CATENA 2016, 142, 36–46. [Google Scholar] [CrossRef]
- Coelho, F.F.; Giasson, E.; Campos, A.R.; de Oliveira e Silva, R.G.P.; Costa, J.J.F. Geographic object-based image analysis and artificial neural networks for digital soil mapping. CATENA 2021, 206, 105568. [Google Scholar] [CrossRef]
- Michel, G.P. Estimativa da Profundidade do Solo e Seu Efeito na Modelagem de Escorregamentos; Universidade Federal do Rio Grande do Sul: Porto Alegre, Brazil, 2015. [Google Scholar]
- Kobiyama, M.; Michel, R.D.L.; Paixão, M.A.; Michel, G.P. Small Fish-pond Design for Debris Flow Disaster Measure with Kanako-2D. In Proceedings of the Symposium Proceedings of the INTERPRAENENT 2018 in the Pacific Rim, Toyama, Japan, 1–4 October 2018; pp. 264–269. [Google Scholar]
- Vanacôr, R.N.; Rolim, S.B.A. Mapeamento da Suscetibilidade a Deslizamentos Usando Técnicas de Estatística Bivariada e Sistema de Informações Geográficas na Região Nordeste do Rio Grande do Sul. Rev. Bras. Geomorfol. 2012, 13, 1. [Google Scholar] [CrossRef] [Green Version]
- Van Den Eeckhaut, M.; Vanwalleghem, T.; Poesen, J.; Govers, G.; Verstraeten, G.; Vandekerckhove, L. Prediction of landslide susceptibility using rare events logistic regression: A case-study in the Flemish Ardennes (Belgium). Geomorphology 2006, 76, 392–410. [Google Scholar] [CrossRef]
- Beguería, S. Validation and Evaluation of Predictive Models in Hazard Assessment and Risk Management. Nat. Hazards 2006, 37, 315–329. [Google Scholar] [CrossRef] [Green Version]
- Dietrich, W.E.; Bellugi, D.; Real de Asua, R. Validation of the Shallow Landslide Model, SHALSTAB, for forest management. Water Sci. Appl. 2001, 2, 195–227. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).