CASPT2 Study of the Unimolecular Reactions of Nitromethane—A Look at the Roaming Reactions in the Decomposition of Nitromethane: An Exergonic Route at High Temperatures
Abstract
1. Introduction
2. Methods of Calculation
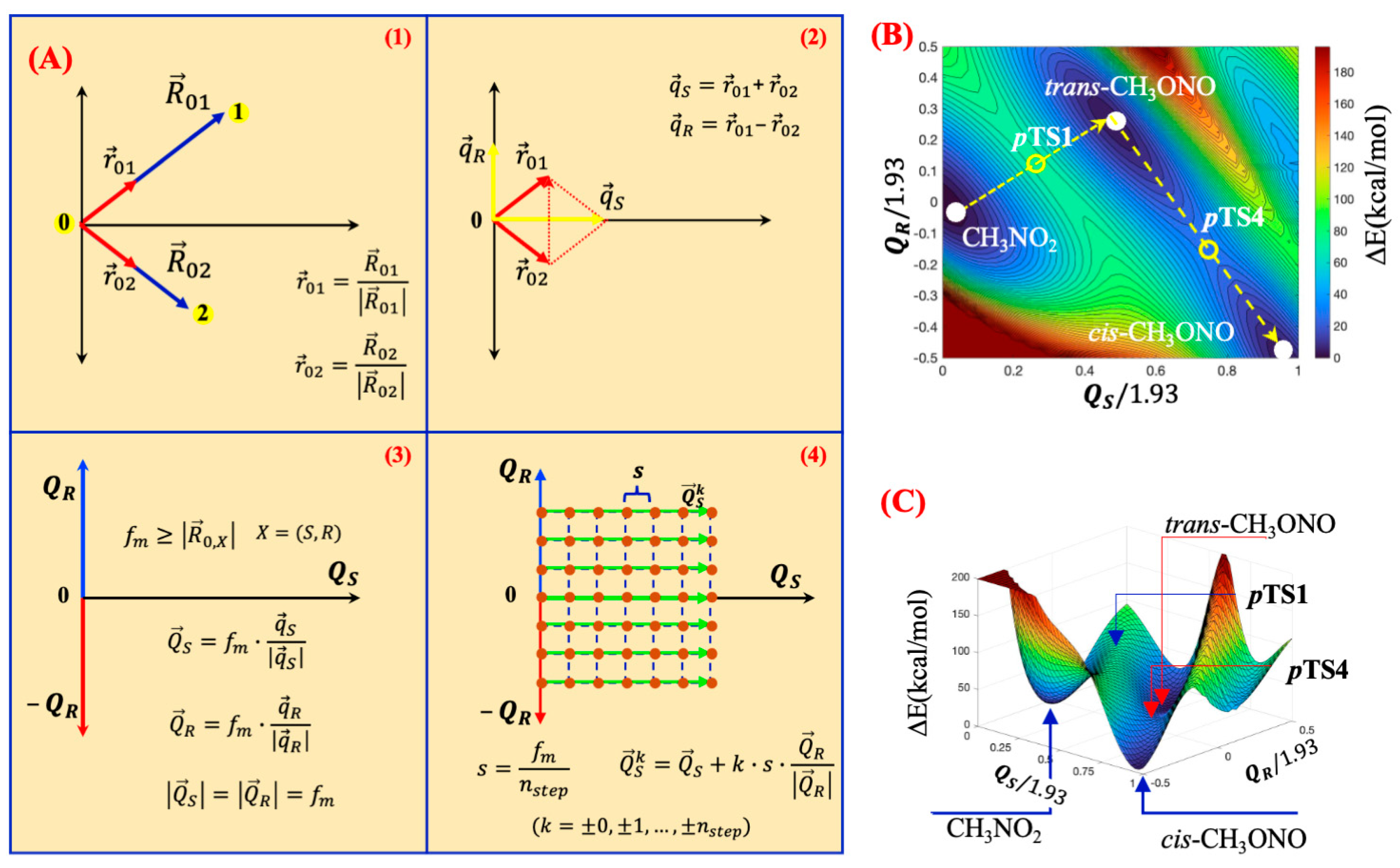
Mapping of 2D Potential Energy Surfaces
3. Results and Discussion
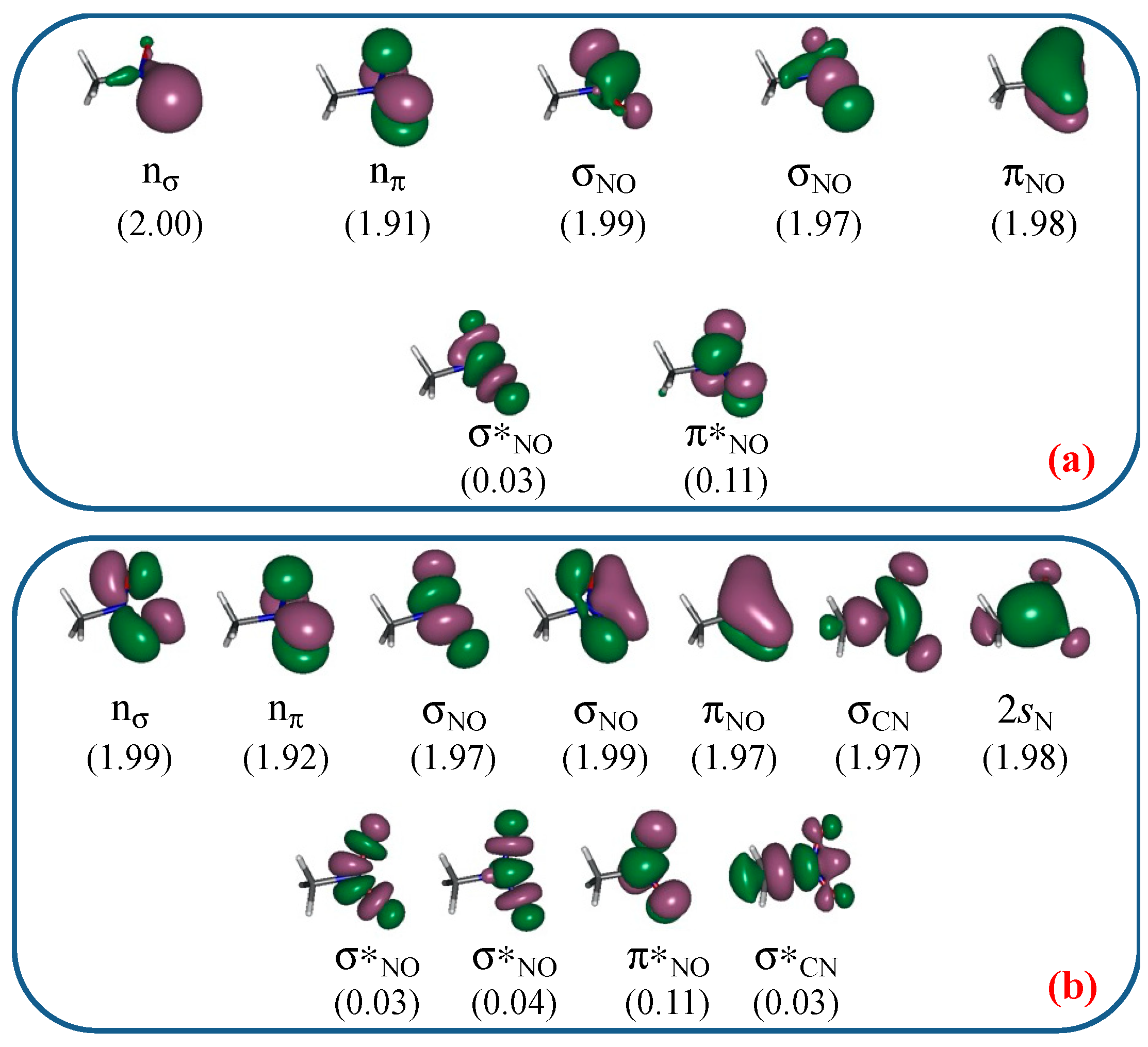
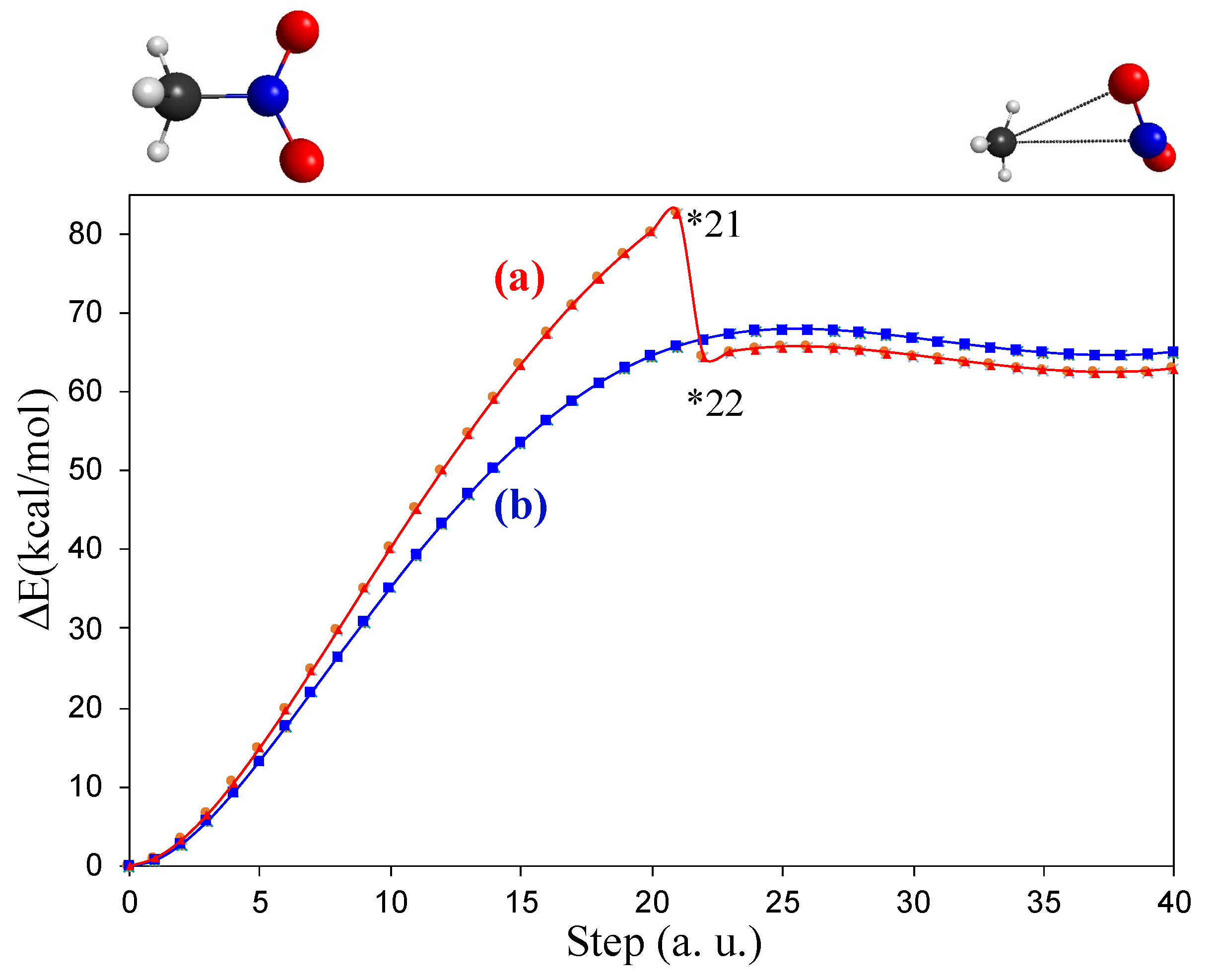
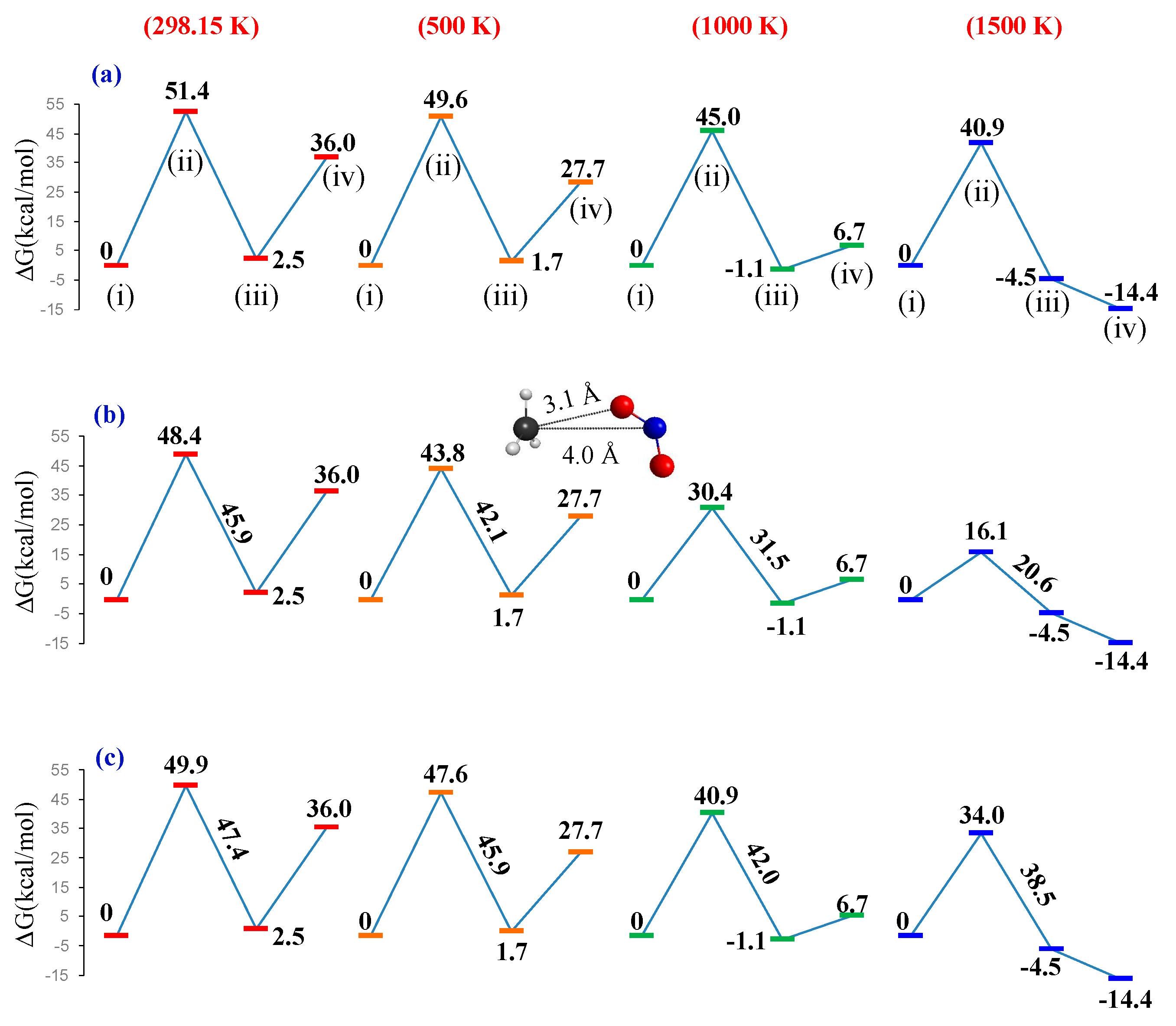
3.1. Unimolecular Reactions of Nitromethane and Methyl Nitrite
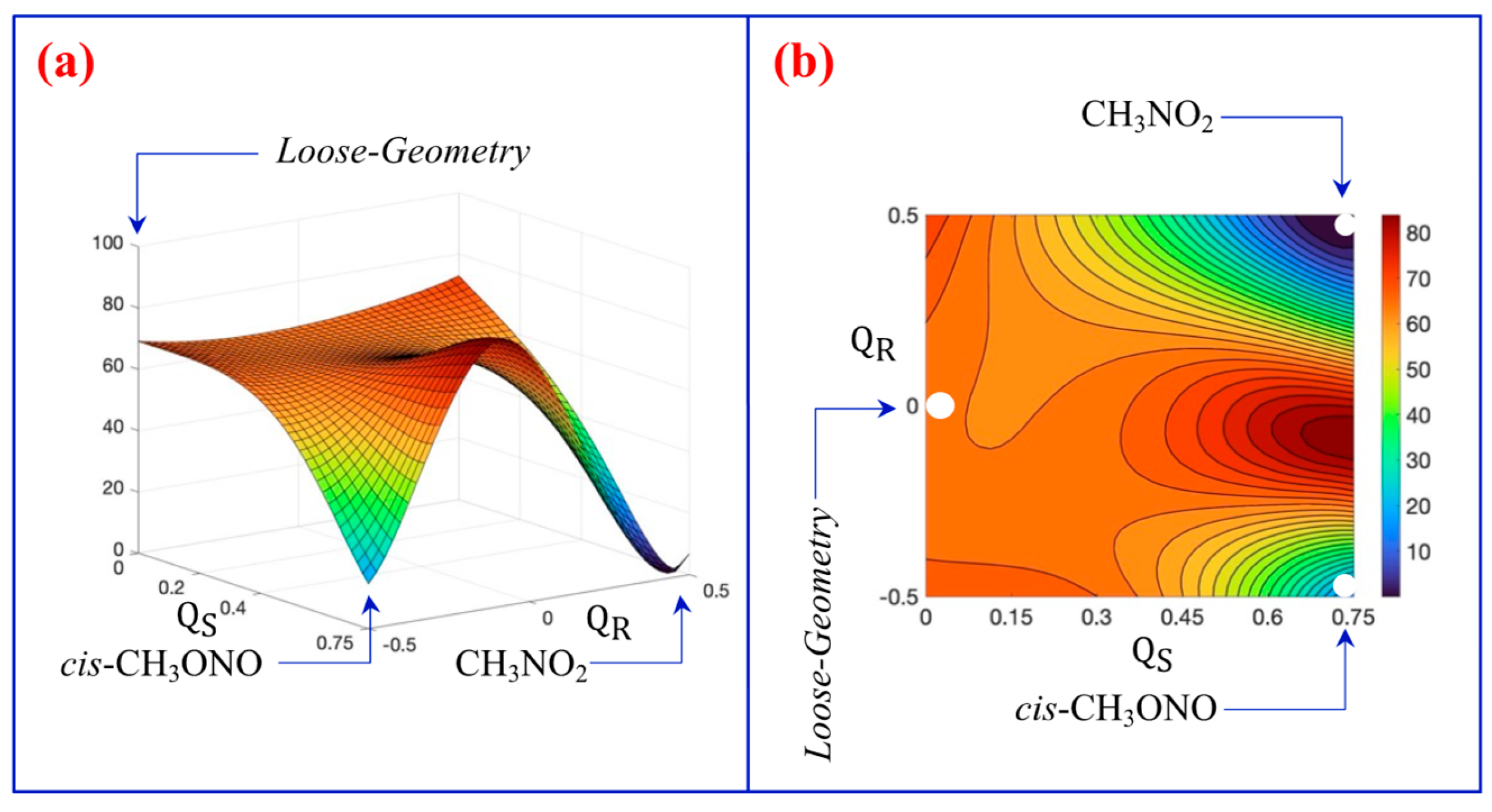
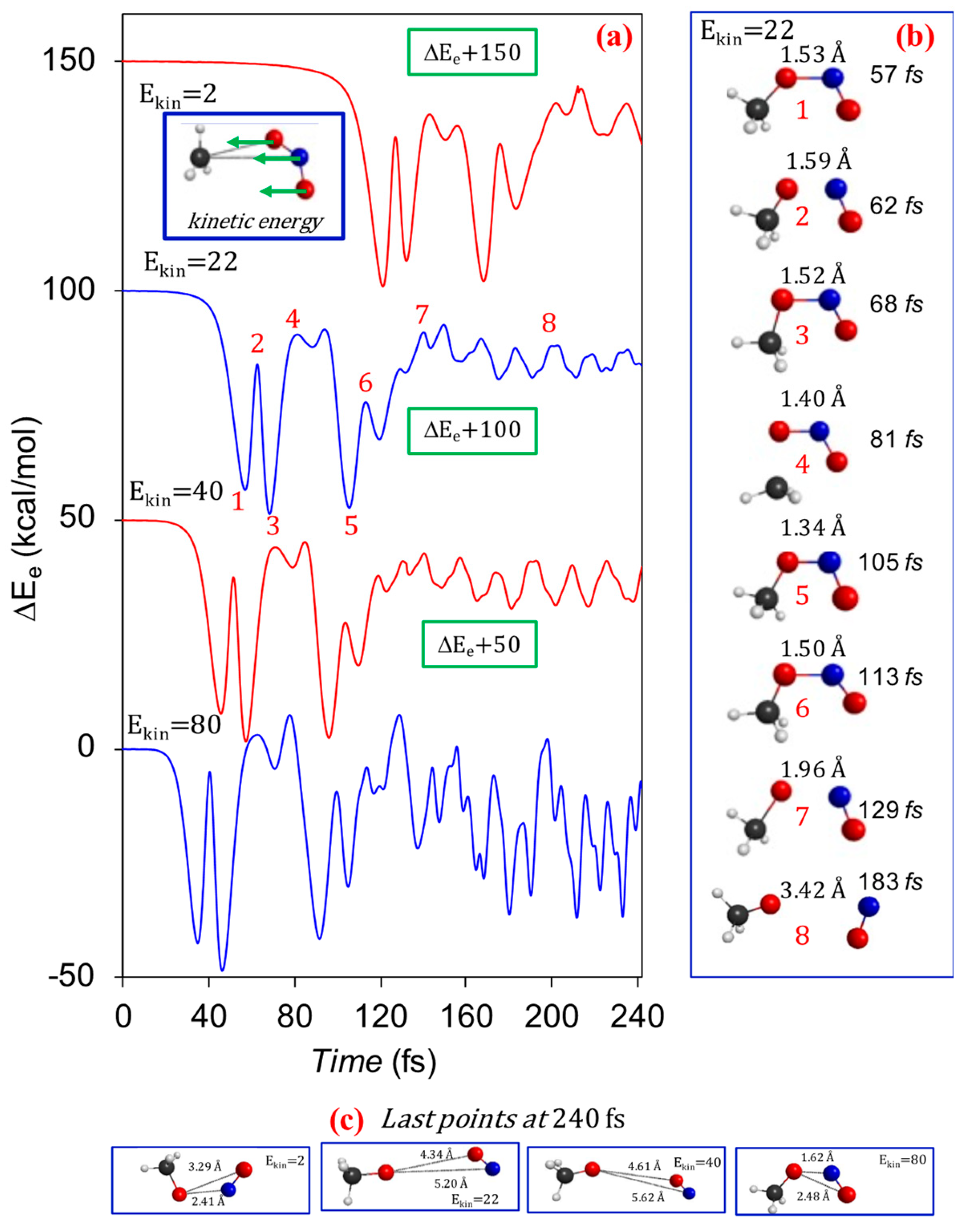
3.2. A Look at the So-Called Loose Transition State
4. Conclusions
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Word, M.D.; Lo, H.A.; Boateng, D.A.; McPherson, S.L.; Gutsev, G.L.; Gutsev, L.G.; Lao, K.U.; Tibbetts, K.M. Ultrafast dynamics of nitro–nitrite rearrangement and dissociation in nitromethane cation. J. Phys. Chem. A 2022, 126, 879–888. [Google Scholar] [CrossRef] [PubMed]
- Leyva, E.; Loredo-Carrillo, S.E.; Aguilar, J. Various techniques for the synthesis of 2-Nitrophenylamino-1,4-naphthoquinone derivatives. Reactions 2023, 4, 432–447. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, J.; Hu, D.; Lan, Z. Investigation of nonadiabatic dynamics in the photolysis of methyl nitrate (CH3ONO2) by on-the-fly surface hopping simulation. Phys. Chem. Chem. Phys. 2021, 23, 25597–25611. [Google Scholar] [CrossRef] [PubMed]
- McKee, M.L. MCSCF study of the rearrangement of nitromethane to methyl nitrite. J. Phys. Chem. 1989, 93, 7365–7369. [Google Scholar] [CrossRef]
- Saxon, R.P.; Yuoshimi, M. Theoretical study of nitro-nitrite rearrangement of CH3NO2. Can. J. Chem. 1992, 70, 572–579. [Google Scholar] [CrossRef]
- Chang, P.; Zhou, P.; Liu, J.; Yin, S. Theoretical study on autocatalytic reaction in thermal decomposition of nitromethane. Chem. Phys. Lett. 2022, 792, 139413. [Google Scholar] [CrossRef]
- Homayoon, Z.; Bowman, J.M. Quasiclassical trajectory study of CH3NO2 decomposition via roaming mediated isomerization using a global potential energy surface. J. Phys. Chem. A 2013, 117, 11665–11672. [Google Scholar] [CrossRef]
- Zhu, R.S.; Raghunath, P.; Lin, M.C. Effect of roaming transition states upon product branching in the thermal decomposition of CH3NO2. J. Phys. Chem. A 2013, 117, 7308–7313. [Google Scholar] [CrossRef]
- Zhu, R.S.; Lin, M.C. CH3NO2 decomposition/isomerization mechanism and product branching ratios: An ab initio chemical kinetic study. Chem. Phys. Lett. 2009, 478, 11–16. [Google Scholar] [CrossRef]
- Isegawa, M.; Liu, F.; Maeda, S.; Morokuma, K. Ab initio reaction pathways for photodissociation and isomerization of nitromethane on four singlet potential energy surfaces with three roaming paths. J. Chem. Phys. 2014, 140, 244310. [Google Scholar] [CrossRef]
- Arenas, J.F.; Otero, J.C.; Peláez, D.; Soto, J. Role of surface crossings in the photochemistry of nitromethane. J. Chem. Phys. 2005, 122, 084324. [Google Scholar] [CrossRef] [PubMed]
- Arenas, J.F.; Otero, J.C.; Peláez, D.; Soto, J. The ground and excited state potential energy surfaces of nitromethane related to its dissociation dynamics after excitation at 193 nm. J. Chem. Phys. 2003, 119, 7814–7823. [Google Scholar] [CrossRef]
- Sumida, M.; Kohge, Y.; Yamasaki, K.; Kohguchia, H. Multiple product pathways in photodissociation of nitromethane at 213 nm. J. Chem. Phys. 2016, 144, 064304. [Google Scholar] [CrossRef] [PubMed]
- Li, W.-G.; Liu, Q.-J.; Liu, F.-S.; Liu, Z.-T. Atomic mean square displacement study of the bond breaking mechanism of energetic materials before explosive initiation. Phys. Chem. Chem. Phys. 2023, 25, 5613–5618. [Google Scholar] [CrossRef]
- Zheng, W.; Liu, Q.-J.; Liu, F.-S.; Liu, Z.-T. Triggering the mechanism of the initial reaction of energetic materials under pressure based on Raman intensity analysis. Phys. Chem. Chem. Phys. 2023, 25, 5685–5693. [Google Scholar] [CrossRef]
- Rice, B.M.; Sahu, S.; Owens, F.J. Density functional calculations of bond dissociation energies for NO2 scission in some nitroaromatic molecules. J. Mol. Struct. (THEOCHEM) 2002, 583, 69–72. [Google Scholar] [CrossRef]
- Ford, J.; Seritan, S.; Zhu, X.; Sakano, M.N.; Islam, M.M.; Strachan, A.; Martínez, T.J. Nitromethane decomposition via automated reaction discovery and an ab initio corrected kinetic model. J. Phys. Chem. A 2021, 125, 1447–1460. [Google Scholar] [CrossRef]
- Nelson, T.; Bjorgaard, J.; Greenfield, M.; Bolme, C.; Brown, K.; McGrane, S.; Scharff, R.J.; Tretiak, S. Ultrafast photodissociation dynamics of nitromethane. J. Phys. Chem. A 2016, 120, 519–526. [Google Scholar] [CrossRef]
- Dey, A.; Fernando, R.; Abeysekera, C.; Homayoon, Z.; Bowman, J.M.; Suits, A.G. Photodissociation dynamics of nitromethane and methyl nitrite by infrared multiphoton dissociation imaging with quasiclassical trajectory calculations: Signatures of the roaming pathway. J. Chem. Phys. 2014, 140, 054305. [Google Scholar] [CrossRef]
- Annesley, C.J.; Randazzo, J.B.; Klippenstein, S.J.; Harding, L.B.; Jasper, A.W.; Georgievskii, Y.; Ruscic, B.; Tranter, R.S. Thermal dissociation and roaming isomerization of nitromethane: Experiment and theory. J. Phys. Chem. A 2015, 119, 7872–7893. [Google Scholar] [CrossRef]
- Wodtke, A.M.; Hintsa, E.J.; Lee, Y.T. Infrared Multiphoton Dissociation of Three Nitroalkanes. J. Phys. Chem. 1986, 90, 3549–3558. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Guo, Y.Q.; Bernstein, E.R. A comparison of the decomposition of electronically excited nitro-containing molecules with energetic moieties C-NO2, N-NO2, and O-NO2. J. Chem. Phys. 2012, 136, 024321. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.Q.; Bhattacharya, A.; Bernstein, E.R. Photodissociation dynamics of nitromethane at 226 and 271 nm at both nanosecond and femtosecond time scales. J. Phys. Chem. A 2009, 113, 85–96. [Google Scholar] [CrossRef] [PubMed]
- Matsugi, A.; Shiina, H. Thermal decomposition of nitromethane and reaction between CH3 and NO2. J. Phys. Chem. A 2017, 121, 4218–4224. [Google Scholar] [CrossRef]
- Townsend, D.; Lahankar, S.A.; Lee, S.K.; Chambreau, S.D.; Suits, A.G.; Zhang, X.; Rheinecker, J.; Harding, L.B.; Bowman, J.M. The roaming atom: Straying from the reaction path in formaldehyde decomposition. Science 2004, 306, 1158–1161. [Google Scholar] [CrossRef]
- Herath, N.; Suits, A.G. Roaming radical reactions. J. Phys. Chem. Lett. 2011, 2, 642–647. [Google Scholar] [CrossRef]
- Suits, A.G. Roaming reactions and dynamics in the van der Waals region. Annu. Rev. Phys. Chem. 2020, 71, 77–100. [Google Scholar] [CrossRef]
- Lopez, J.G.; Vayner, G.; Lourderaj, U.; Addepalli, S.V.; Kato, S.; Dejong, W.A.; Windus, T.L.; Hase, W.L. A direct dynamics trajectory study of F−+CH3OOH reactive collisions reveals a major non-IRC reaction path. J. Am. Chem. Soc. 2007, 129, 9976–9985. [Google Scholar] [CrossRef]
- Pomerantz, A.E.; Camden, J.P.; Chiou, A.S.; Ausfelder, F.; Chawla, N.; Hase, W.L.; Zare, R.N. Reaction products with internal energy beyond the kinematic limit result from trajectories far from the minimum energy path: An example from H + HBr → H2 + Br. J. Am. Chem. Soc. 2005, 127, 16368–16369. [Google Scholar] [CrossRef]
- Lourderaj, U.; Park, K.; Hase, W.L. Classical trajectory simulations of post-transition state dynamics. Int. Rev. Phys. Chem. 2008, 27, 361–403. [Google Scholar] [CrossRef]
- Suits, A.G. Roaming atoms and radicals: A new mechanism in molecular dissociation. Acc. Chem. Res. 2008, 41, 873–881. [Google Scholar] [CrossRef] [PubMed]
- Bowman, J.M.; Shepler, B.C. Roaming radicals. Annu. Rev. Phys. Chem. 2011, 62, 531–553. [Google Scholar] [CrossRef] [PubMed]
- Bowman, J.M.; Houston, P.L. Theories and simulations of roaming. Chem. Soc. Rev. 2017, 46, 7615–7624. [Google Scholar] [CrossRef] [PubMed]
- Houston, P.L.; Kable, S.H. Photodissociation of acetaldehyde as a second example of the roaming mechanism. Proc. Natl. Acad. Sci. USA 2006, 103, 16079–16082. [Google Scholar] [CrossRef]
- Harding, L.B.; Klippenstein, S.J.; Jasper, A.W. Ab initio methods for reactive potential surfaces. Phys. Chem. Chem. Phys. 2007, 9, 4055–4070. [Google Scholar] [CrossRef]
- Heazlewood, B.R.; Jordan, M.J.T.; Kable, S.H.; Selby, T.M.; Osborn, D.L.; Shepler, B.C.; Braams, B.J.; Bowman, J.M. Roaming is the dominant mechanism for molecular products in acetaldehyde photodissociation. Proc. Natl. Acad. Sci. USA 2008, 105, 12719–12724. [Google Scholar] [CrossRef]
- Roos, B.O. The Complete Active Space Self-Consistent Field Method and Its Applications in Electronic Structure Calculations. In Advances in Chemical Physics; Ab initio Methods in Quantum Chemistry II; Lawley, K.P., Ed.; John Wiley & Sons: Chichester, UK, 1987; Chapter 69; p. 399. [Google Scholar]
- Roos, B.O.; Taylor, P.R.; Siegbahn, P.E.M. A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys. 1980, 48, 157–173. [Google Scholar] [CrossRef]
- Roos, B.O. The complete active space scf method in a Fock-matrix-based super-CI formulation. Int. J. Quantum Chem. 1980, 18, 175–189. [Google Scholar] [CrossRef]
- Siegbahn, P.E.M.; Almlo, J.; Heiberg, A.; Roos, B.O. The complete active space scf (CASSCF) method in a Newton-Raphson formulation with application to the HNO molecule. J. Chem. Phys. 1981, 74, 2384–2396. [Google Scholar] [CrossRef]
- Werner, H.-J.; Meyer, W. A quadratically convergent multiconfiguration-self-consistent field method with simultaneous-optimization of orbitals and cl coefficients. J. Chem. Phys. 1980, 73, 2342–2356. [Google Scholar] [CrossRef]
- Werner, H.-J.; Meyer, W. A quadratically convergent MCSCF method for the simultaneous-optimization of several states. J. Chem. Phys. 1981, 74, 5794–5801. [Google Scholar] [CrossRef]
- Olsen, J. The CASSCF method: A perspective and commentary. Int. J. Quantum. Chem. 2011, 111, 3267–3272. [Google Scholar] [CrossRef]
- Roos, B.O.; Andersson, K.; Fu, M.P.; Malmqvist, P.Â.; Serrano-Andre, L.; Pierloot, K.; Mercha, M. Multiconfigurational perturbation theory: Applications in electronic spectroscopy. Adv. Chem. Phys. 1996, 93, 219–331. [Google Scholar]
- Finley, J.; Malmqvist, P.-Å.; Roos, B.O.; Serrano-Andrés, L. The multi-state CASPT2 method. Chem. Phys. Lett. 1998, 288, 299–306. [Google Scholar] [CrossRef]
- Veryazov, V.; Widmark, P.O.; Serrano-Andrés, L.; Lindh, R.; Roos, B.O. 2MOLCAS as a development platform for quantum chemistry software. Int. J. Quantum Chem. 2004, 100, 626–635. [Google Scholar] [CrossRef]
- Aquilante, F.; Autschbach, J.; Carlson, R.K.; Chibotaru, L.F.; Delcey, M.G.; De Vico, L.; Fdez. Galván, I.; Ferré, N.; Frutos, L.M.; Gagliardi, L. Molcas 8: New capabilities for multiconfigurational quantum chemical calculations across the periodic table. J. Comp. Chem. 2016, 37, 506–541. [Google Scholar] [CrossRef]
- Fdez Galván, I.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.J.; Bokarev, S.I.; Bogdanov, N.A.; Carlson, R.K.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef]
- Aquilante, F.; Autschbach, J.; Baiardi, A.; Battaglia, S.; Borin, V.A.; Chibotaru, L.F.; Conti, I.; De Vico, L.; Delcey, M.; Ferré, N.; et al. Modern quantum chemistry with [Open] Molcas. J. Chem. Phys. 2020, 152, 214117. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.-Å.; Veryazov, V.; Widmark, P.-O. Main group atoms and dimers studied with a new relativistic ANO basis set. J. Phys. Chem. A 2004, 108, 2851–2858. [Google Scholar] [CrossRef]
- Roos, B.O.; Lindh, R.; Malmqvist, P.-Å.; Veryazov, V.; Widmark, P.-O. New relativistic ANO basis sets for transition metal atoms. J. Phys. Chem. A 2005, 109, 6575–6579. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Frisch, M.E.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.; Cheeseman, J.R.; Scalmani, G.; Barone, V.P.G.A.; Petersson, G.A.; Nakatsuji, H.J.R.A.; et al. Gaussian 16, Revision C.02; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Soto, J.; Algarra, M. Electronic structure of nitrobenzene: A benchmark example of the accuracy of the multi-state CASPT2 theory. J. Phys. Chem. A 2021, 125, 9431–9437. [Google Scholar] [CrossRef] [PubMed]
- Arenas, J.F.; Otero, J.C.; Peláez, D.; Soto, J.; Serrano-Andrés, L. Multiconfigurational second-order perturbation study of the decomposition of the radical anion of nitromethane. J. Chem. Phys. 2004, 121, 4127–4132. [Google Scholar] [CrossRef]
- Arenas, J.F.; Otero, J.C.; Peláez, D.; Soto, J. Photodissociation mechanism of nitramide: A CAS-SCF and MS-CASPT2 study. J. Phys. Chem. A 2005, 109, 7172–7180. [Google Scholar] [CrossRef]
- Soto, J.; Peláez, D.; Otero, J.C.; Avila, F.J.; Arenas, J.F. Photodissociation mechanism of methyl nitrate. A study with the multistate second-order multiconfigurational perturbation theory. Phys. Chem. Chem. Phys. 2009, 11, 2631–2639. [Google Scholar] [CrossRef]
- Zhang, J.J.; Peng, J.W.; Zhu, Y.F.; Hu, D.P.; Lan, Z.G. Influence of mode-specific excitation on the nonadiabatic dynamics of methyl nitrate (CH3ONO2). J. Phys. Chem. Lett. 2023, 14, 6542–6549. [Google Scholar] [CrossRef]
- Zhang, J.J.; Peng, J.W.; Hu, D.P.; Xu, C.; Lan, Z.G. Understanding photolysis of CH3ONO2 with on-the-fly nonadiabatic dynamics simulation at the ADC(2) Level. Chin. J. Chem. Phys. 2022, 35, 451–460. [Google Scholar] [CrossRef]
- Verlet, L. Computer experiments on classical fluids. I. Thermodynamical properties of Lennard-Jones molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Swope, W.C.; Andersen, H.C.; Berens, P.H.; Wilson, K.R. A computer-simulation method for the calculation of equilibrium-constants for the formation of physical clusters of molecules-application to small water clusters. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Schaftenaar, G.; Noordik, J.H. Molden: A pre- and post-processing program for molecular and electronic structures. J. Comput. Aided Mol. Des. 2000, 14, 123–134. [Google Scholar] [CrossRef] [PubMed]
- Allouche, A.R. Gabedit-a graphical user interface for computational chemistry softwares. J. Comput. Chem. 2011, 32, 174–182. [Google Scholar] [CrossRef]
- BBode, M.; Gordon, M.S. MacMolPlt: A graphical user interface for GAMESS. J. Mol. Graphics Modell. 1998, 16, 133–138. [Google Scholar] [CrossRef]
- Soto, J.; Peláez, D.; Algarra, M. CASPT2 study of the electronic structure and photochemistry of protonated N-nitrosodimethylamine (NDMA-H+) at 453 nm. J. Chem. Phys. 2023, 158, 204301. [Google Scholar] [CrossRef]
- Aranda, D.; Avila, F.J.; López-Tocón, I.; Arenas, J.F.; Otero, J.C.; Soto, J. An MS-CASPT2 study of the photodecomposition of 4-methoxyphenyl azide: Role of internal conversion and intersystem crossing. Phys. Chem. Chem. Phys. 2018, 20, 7764–7771. [Google Scholar] [CrossRef]
- Soto, J.; Otero, J.C.; Avila, F.J.; Peláez, D. Conical intersections and intersystem crossings explain product formation in photochemical reactions of aryl azides. Phys. Chem. Chem. Phys. 2019, 21, 2389–2396. [Google Scholar] [CrossRef]
- Soto, J. Photochemistry of 1-phenyl-1-diazopropane and its Diazirine isomer: A CASSCF and MS-CASPT2 study. J. Phys. Chem. A 2022, 126, 8372–8379. [Google Scholar] [CrossRef]
- Peláez, D.; Arenas, J.F.; Otero, J.C.; Soto, J. A complete active space self-consistent field study of the photochemistry of nitrosamine. J. Chem. Phys. 2006, 125, 164311. [Google Scholar] [CrossRef]
- Soto, J.; Arenas, J.F.; Otero, J.C.; Peláez, D. Effect of an S1/S0 conical intersection on the chemistry of nitramide in its ground state. A comparative CASPT2 study of the nitro-nitrite isomerization reactions in nitramide and nitromethane. J. Phys. Chem. A 2006, 110, 8221–8226. [Google Scholar] [CrossRef] [PubMed]
- Arenas, J.F.; Centeno, S.P.; López-Tocón, I.; Peláez, D.; Soto, J. DFT and CASPT2 study of two thermal reactions of nitromethane: C-N bond cleavage and nitro-to-nitrite isomerization. An example of the inverse symmetry breaking deficiency in density functional calculations of an homolytic dissociation. J. Mol. Struct. (THEOCHEM) 2003, 630, 17–23. [Google Scholar] [CrossRef]
- Ruscic, B.; Pinzon, R.E.; Morton, M.L.; von Laszevski, G.; Bittner, S.J.; Nijsure, S.G.; Amin, K.A.; Minkoff, M.; Wagner, A.F. Introduction to active thermochemical tables: Several “key” enthalpies of formation revisited. J. Phys. Chem. A 2004, 108, 9979–9997. [Google Scholar] [CrossRef]
- Ruscic, B.; Pinzon, R.E.; von Laszewski, G.; Kodeboyina, D.; Burcat, A.; Leahy, D.; Montoy, D.; Wagner, A.F. Active Thermochemical Tables: Thermochemistry for the 21st century. J. Phys. Conf. Ser. 2005, 16, 561–570. [Google Scholar] [CrossRef]
- Ruscic, B.; Bross, D.H. Active Thermochemical Tables (ATcT), Values Based on Ver. 1.124 of the Thermochemical Network. 2022. Available online: https://atct.anl.gov/Thermochemical%20Data/version%201.124/index.php (accessed on 7 March 2025).
- Cox, A.P.; Waring, S. Microwave-spectrum and structure of nitromethane. J. Chem. Soc. Faraday Trans. II 1972, 68, 1060–1071. [Google Scholar] [CrossRef]
- Turner, P.H.; Corkill, M.J.; Cox, A.P. Microwave-spectra and structures of cis-methyl nitrite and trans-methyl nitrite-methyl barrier in trans-methyl nitrite. J. Phys. Chem. 1979, 83, 1473–1482. [Google Scholar] [CrossRef]
- Van der Veken, B.J.; Maas, R.; Guirgis, G.A.; Stidham, G.A.; Sheehan, T.G.; Durig, J.R. Infrared spectrum, ab initio calculations, barriers to internal-rotation, and structural parameters for methyl nitrite. J. Phys. Chem. 1990, 94, 4029–4039. [Google Scholar] [CrossRef]
- Turner, P.H.; Cox, A.P. Dipole Moment of Acetaldehyde. Microwave-spectrum, structure, dipole-moment and centrifugal-distortion of nitrosomethane-dipole-moment of acetaldehyde. J. Chem. Soc. Faraday Trans. II 1978, 74, 533–559. [Google Scholar] [CrossRef]
- Soto, J. Identification of the photoreactive species of protonated N-nitrosopiperidine in acid medium: A CASPT2 and DFT study. J. Phys. Chem. A 2023, 127, 9781–9786. [Google Scholar] [CrossRef]
- Soto, J.; Peláez, D.; Otero, J.C. A SA-CASSCF and MS-CASPT2 study on the electronic structure of nitrosobenzene and its relation to its dissociation dynamics. J. Chem. Phys. 2021, 154, 044307. [Google Scholar] [CrossRef]
- Liu, M.K.; Li, J.; Li, Q.S.; Li, Z.S. Theoretical insights into photo-induced isomerization mechanisms of phenylsulfinyl radical PhSO˙. Phys. Chem. Chem. Phys. 2022, 24, 6266–6273. [Google Scholar] [CrossRef] [PubMed]
- Mu, D.; Li, Q.S. A theoretical study on the photochemical generation of phenylborylene from phenyldiazidoborane. Phys. Chem. Chem. Phys. 2023, 25, 8074–8081. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.L.; Migani, A.; Li, Q.S.; Li, Z.S.; Blancafort, L. Theoretical study of non-Hammett vs. Hammett behaviour in the thermolysis and photolysis of arylchlorodiazirines. Phys. Chem. Chem. Phys. 2018, 20, 1181–1188. [Google Scholar] [CrossRef]
- Soto, J.; Algarra, M.; Peláez, D. Nitrene formation is the first step of the thermal and photochemical decomposition reactions of organic azides. Phys. Chem. Chem. Phys. 2022, 24, 5109–5115. [Google Scholar] [CrossRef]
- Arenas, J.F.; Marcos, J.I.; López-Tocón, I.; Otero, J.C.; Soto, J. Potential-energy surfaces related to the thermal decomposition of ethyl azide: The role of intersystem crossings. J. Chem. Phys. 2000, 113, 2282–2289. [Google Scholar] [CrossRef]
- Blahous, C.P., III; Yates, B.F.; Xie, Y.; Schaefer, H.F., III. Symmetry-breaking in the NO2 sigma-radical-construction of the 2A1-state and 2B2-state with Cs symmetry complete active space self-consistent-field wave-functions. J. Chem. Phys. 1990, 93, 8105–8109. [Google Scholar] [CrossRef]


| Reaction | Method | ΔdG a | ΔdEe b | ΔdH c | ΔdH d |
|---|---|---|---|---|---|
| CH3NO2(g) → CH3(g) + NO2(g) | CASPT2 | 65.95 | |||
| (0 K) | 58.76 | 58.76 | 59.16 | ||
| (298.15 K) | 50.83 | 60.10 | 61.00 | ||
| MP2/HF | 66.61 | ||||
| (0 K) | 63.71 | 63.71 | |||
| (298.15 K) | 56.70 | 65.06 | |||
| M062X | 67.93 | ||||
| (0 K) | 60.51 | 60.51 | |||
| (298.15 K) | 53.35 | 61.93 | |||
| t-CH3ONO(g) → CH3O(g)+NO(g) | CASPT2 | 46.48 | |||
| (0 K) | 42.60 | 42.60 | 41.11 | ||
| (298.15 K) | 33.13 | 43.99 | 42.32 | ||
| MP2/HF | 51.10 | ||||
| (0 K) | 49.28 | 49.28 | |||
| (298.15 K) | 39.79 | 50.69 | |||
| M062X | 42.63 | ||||
| (0 K) | 37.86 | 37.86 | |||
| (298.15 K) | 28.31 | 39.40 | |||
| CH3NO2(g) → CH3NO(g)+O(3P)(g) | CASPT2 | 99.53 | |||
| (0 K) | 95.32 | 95.32 | 92.83 | ||
| (298.15 K) | 88.19 | 96.47 | 94.35 | ||
| MP2/HF | 104.88 | ||||
| (0 K) | 100.44 | 100.44 | |||
| (298.15 K) | 93.46 | 101.57 | |||
| M062X | 96.82 | ||||
| (0 K) | 92.53 | 92.53 | |||
| (298.15 K) | 85.47 | 93.68 |
| Reaction | ΔaG a | ΔaEe b | ΔaH c | ΔrH d | ΔrH d | |
|---|---|---|---|---|---|---|
| CH3NO2(g) t-CH3ONO(g) | CASPT2 | 69.25 | ||||
| (0 K) | 66.31 | 66.31 | 2.55 | 1.99 | ||
| (298.15 K) | 66.66 | 66.42 | 2.66 | 2.45 | ||
| MP2 | 71.84 | |||||
| (0 K) | 69.19 | 69.19 | 6.10 | |||
| (298.15 K) | 69.91 | 69.12 | 5.91 | |||
| M062X | 73.15 | |||||
| (0 K) | 70.77 | 70.77 | 2.10 | |||
| (298.15 K) | 71.33 | 70.77 | 2.44 | |||
| CH3NO2(g) CH2N(O)OH(g) | CASPT2 | 66.54 | ||||
| (0 K) | 63.01 | 63.01 | 12.88 | |||
| (298.15 K) | 64.98 | 62.54 | 12.76 | |||
| MP2 | 66.35 | |||||
| (0 K) | 62.86 | 62.86 | 16.32 | |||
| (298.15 K) | 62.86 | 62.95 | 16.20 | |||
| M062X | 65.66 | |||||
| (0 K) | 62.19 | 62.19 | 12.52 | |||
| (298.15 K) | 63.25 | 61.77 | 12.33 | |||
| t-CH3ONO(g) CH2O(g) + HNO(g) | CASPT2 | 43.80 | ||||
| (0 K) | 38.76 | 38.76 | 14.34 | 13.62 | ||
| 14.85 | ||||||
| (298.15 K) | 38.90 | 38.68 | 15.97 | |||
| MP2 | 41.94 | |||||
| (0 K) | 37.69 | 37.69 | 13.42 | |||
| (298.15 K) | 37.27 | 37.99 | 15.06 | |||
| M062X | 49.92 | |||||
| (0 K) | 45.88 | 45.88 | 14.92 | |||
| (298.15 K) | 46.73 | 45.54 | 16.06 | |||
| t-CH3ONO(g) c-CH3ONO(g) | CASPT2 | 12.12 | ||||
| (0 K) | 11.62 | 11.62 | −0.86 | −0.74 | ||
| (298.15 K) | 11.47 | 12.28 | −0.60 | −0.70 | ||
| MP2 | 11.26 | |||||
| (0 K) | 10.63 | 10.63 | −1.11 | |||
| (298.15 K) | 10.42 | 10.75 | −0.94 | |||
| M062X | 10.95 | |||||
| (0 K) | 10.48 | 10.48 | −1.29 | |||
| (298.15 K) | 11.46 | 9.99 | −1.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soto, J. CASPT2 Study of the Unimolecular Reactions of Nitromethane—A Look at the Roaming Reactions in the Decomposition of Nitromethane: An Exergonic Route at High Temperatures. Reactions 2025, 6, 21. https://doi.org/10.3390/reactions6010021
Soto J. CASPT2 Study of the Unimolecular Reactions of Nitromethane—A Look at the Roaming Reactions in the Decomposition of Nitromethane: An Exergonic Route at High Temperatures. Reactions. 2025; 6(1):21. https://doi.org/10.3390/reactions6010021
Chicago/Turabian StyleSoto, Juan. 2025. "CASPT2 Study of the Unimolecular Reactions of Nitromethane—A Look at the Roaming Reactions in the Decomposition of Nitromethane: An Exergonic Route at High Temperatures" Reactions 6, no. 1: 21. https://doi.org/10.3390/reactions6010021
APA StyleSoto, J. (2025). CASPT2 Study of the Unimolecular Reactions of Nitromethane—A Look at the Roaming Reactions in the Decomposition of Nitromethane: An Exergonic Route at High Temperatures. Reactions, 6(1), 21. https://doi.org/10.3390/reactions6010021






