Modeling of the Anaerobic Digestion of Biomass Produced by Agricultural Residues in Greece
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Background and Improvements in ADM1
2.2. Experimental
2.3. Simulations
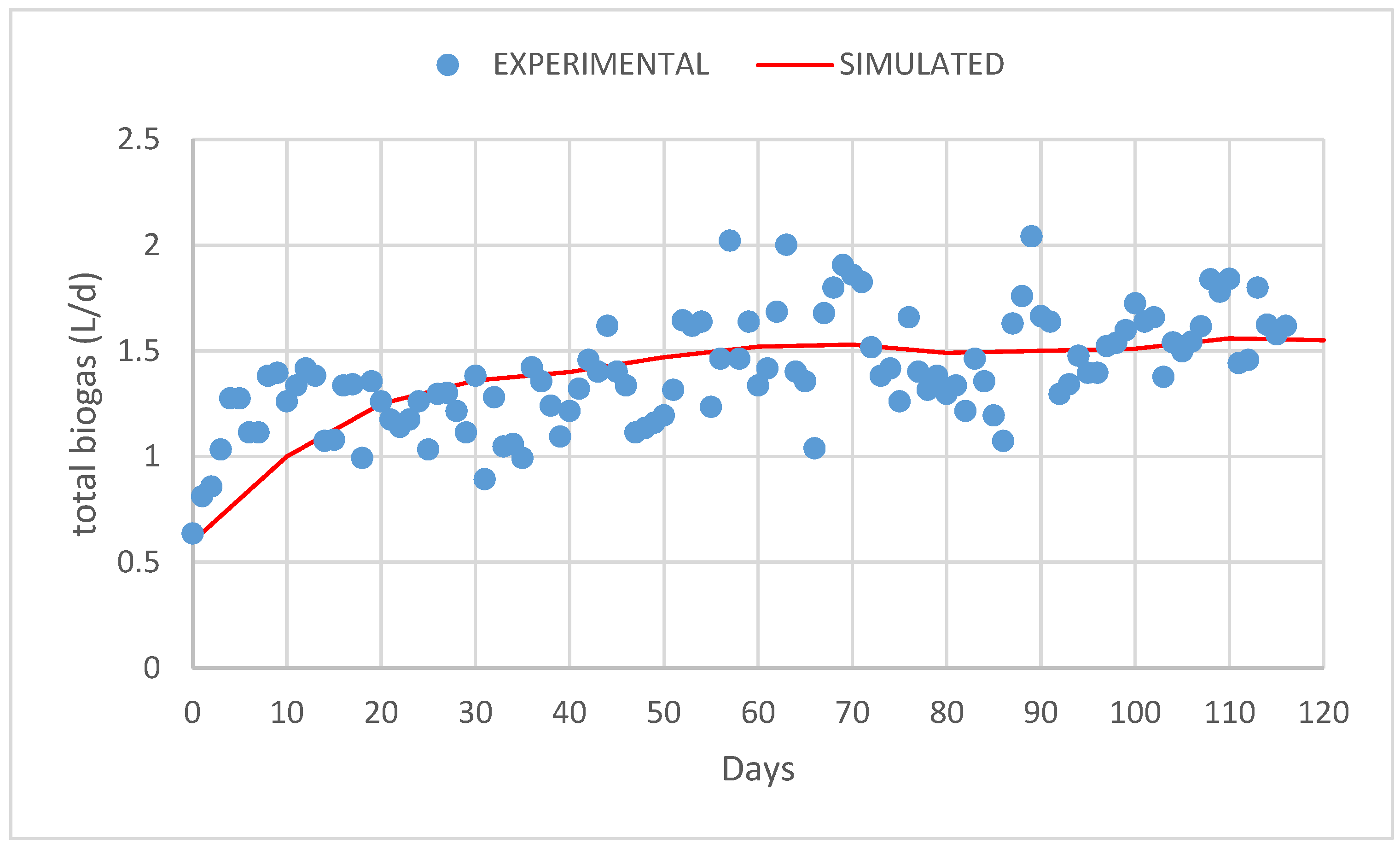
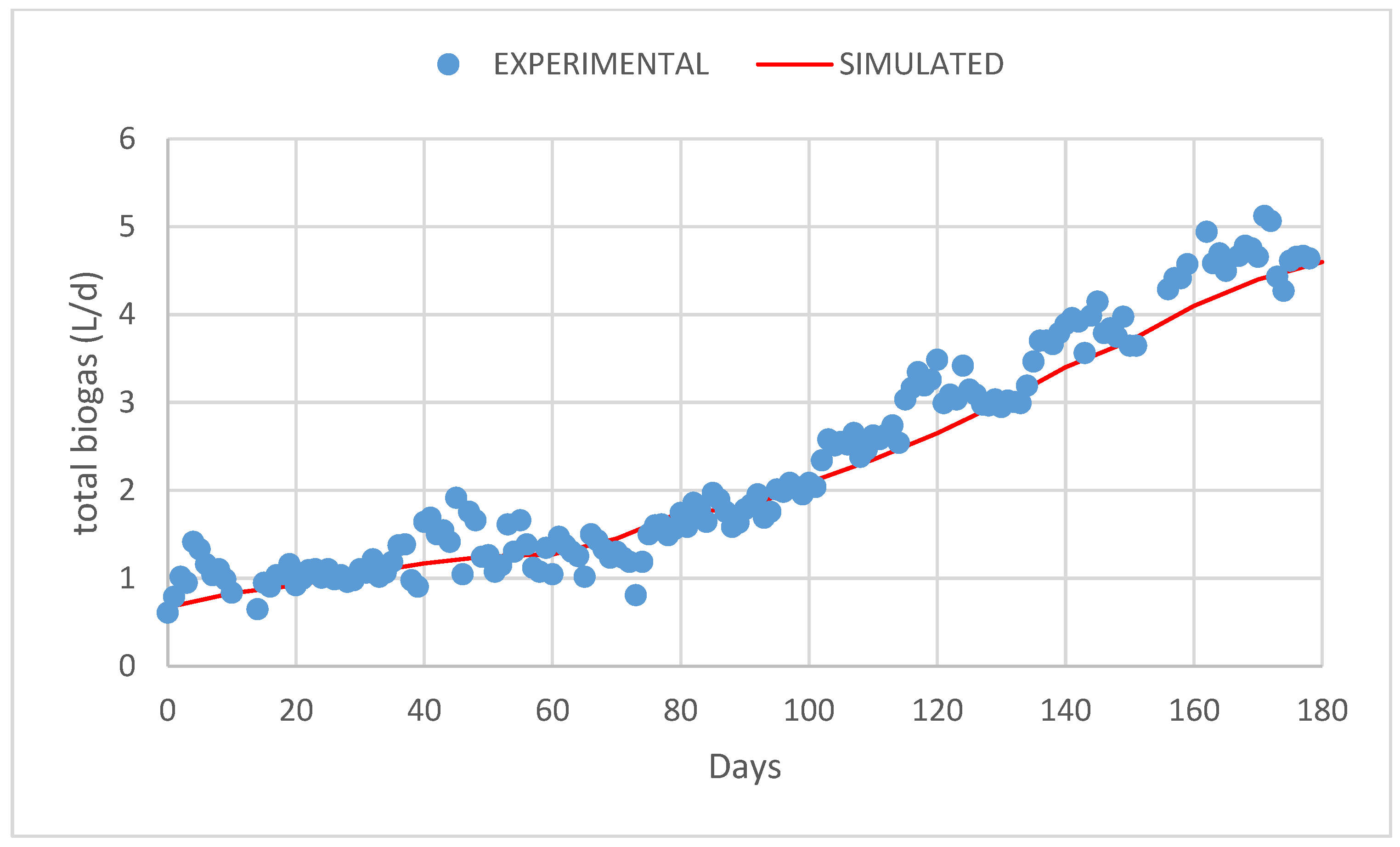
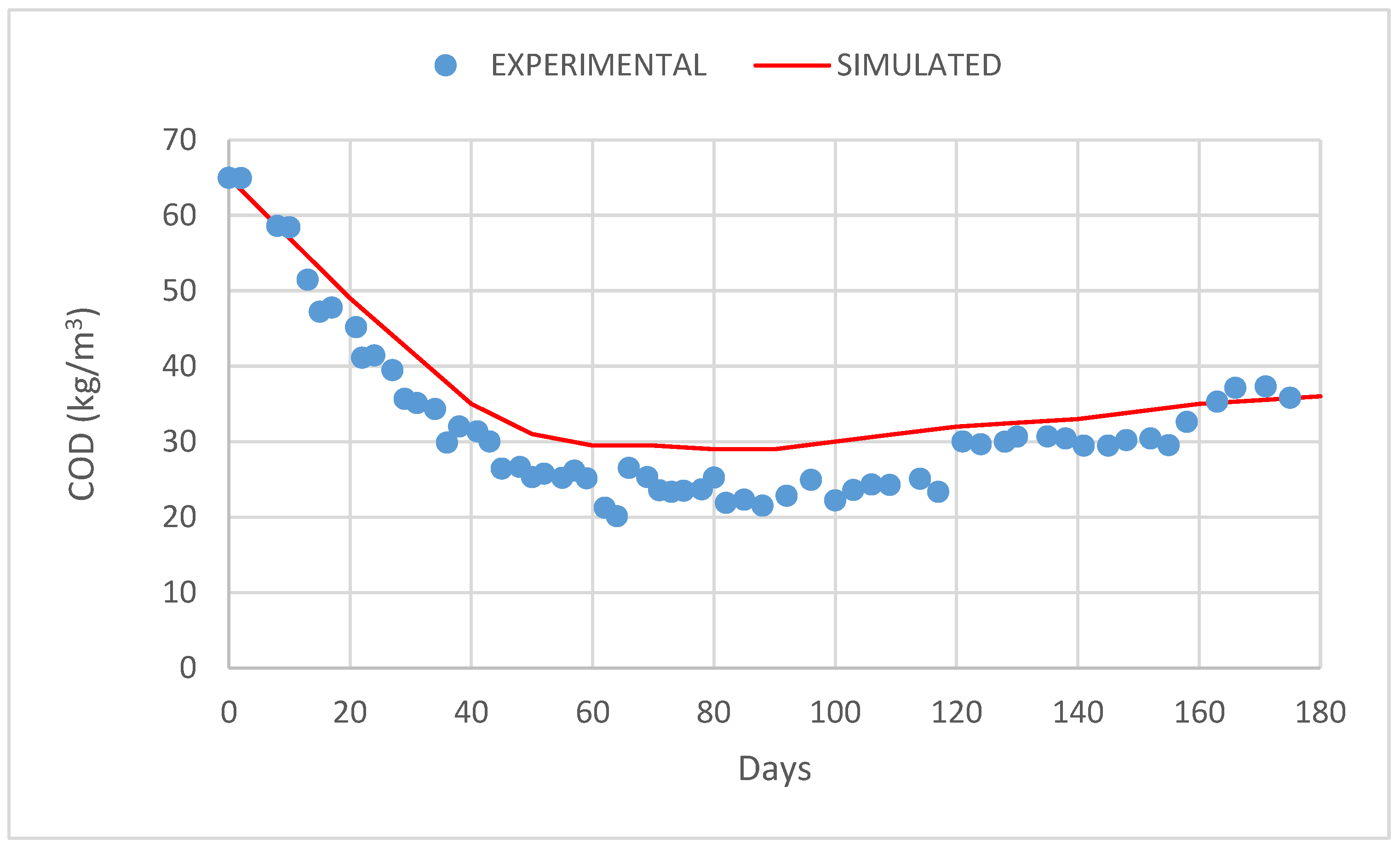
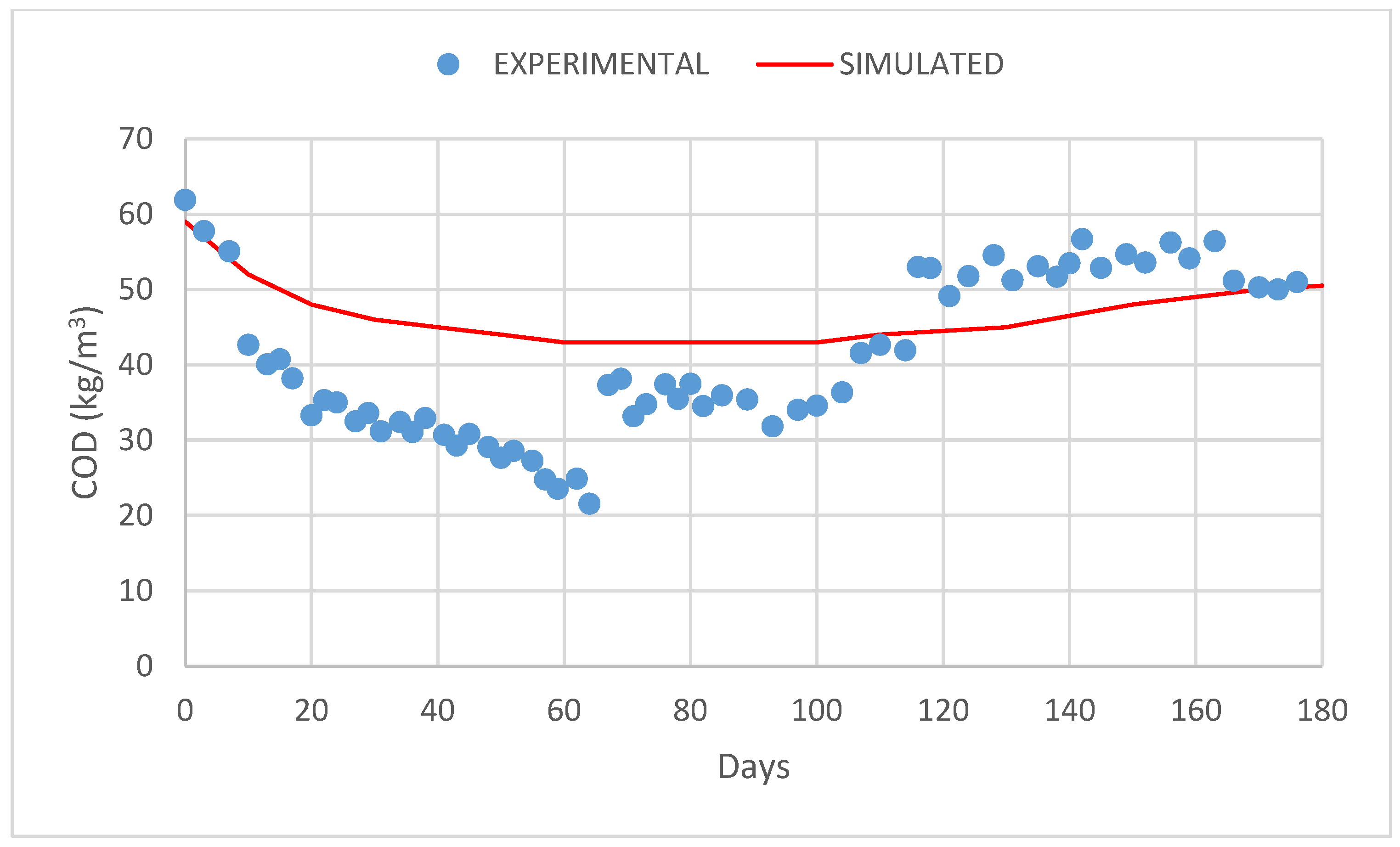
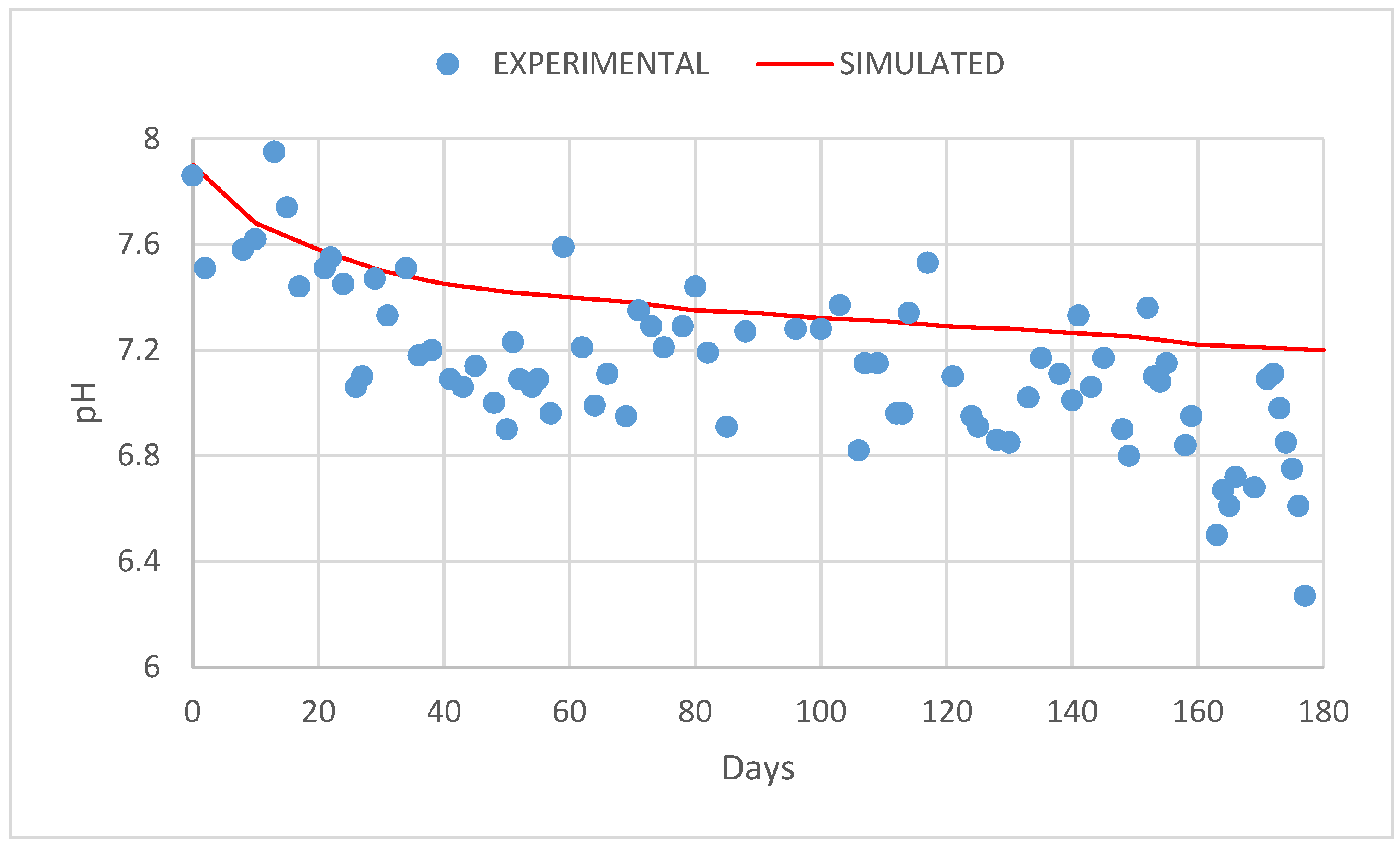
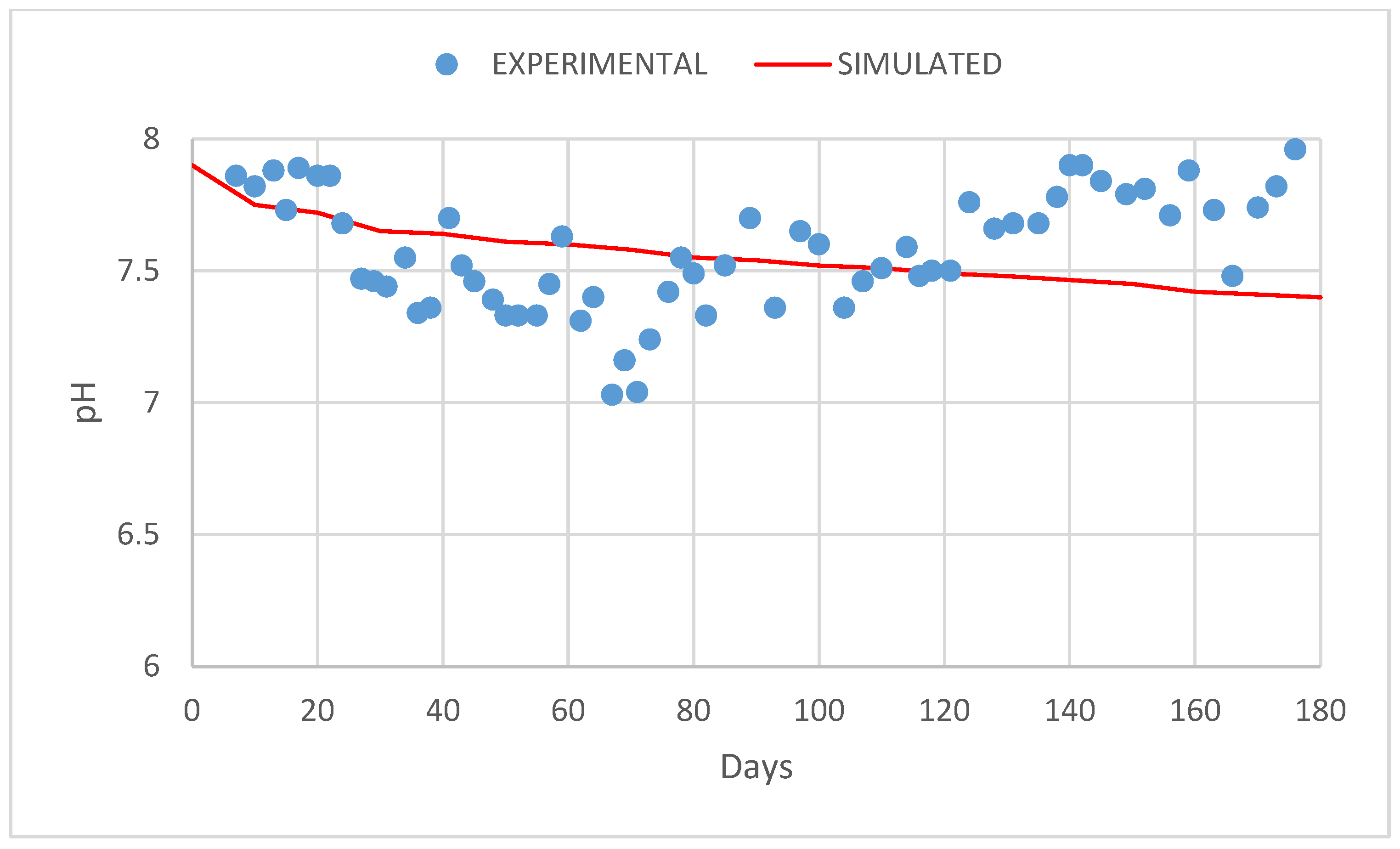
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moustakas, K.; Parmaxidou, P.; Vakalis, S. Anaerobic digestion for energy production from agricultural biomass waste in Greece: Capacity assessment for the region of Thessaly. Energy 2020, 191, 116556. [Google Scholar] [CrossRef]
- Kumar, D.J.P.; Mishra, R.P.; Chinnam, S.; Binnal, P.; Dwivedi, N. A comprehensive study on anaerobic digestion of organic solid waste: A review on configurations, operating parameters, techno-economic analysis and current trends. Biotechnol. Notes 2024, 5, 33–49. [Google Scholar] [CrossRef]
- Bong, C.P.C.; Lim, L.Y.; Lee, C.T.; Klemes, J.J.; Ho, C.S.; Ho, W.S. The characterization and treatment of food waste for improvement of biogas production during anaerobic digestion—A review. J. Clean. Prod. 2018, 172, 1545–1558. [Google Scholar] [CrossRef]
- González, R.; Carrillo Peña, D.; Gómez, X. Anaerobic Co-Digestion of Wastes: Reviewing Current Status and Approaches for Enhancing Biogas Production. Appl. Sci. 2022, 12, 8884. [Google Scholar] [CrossRef]
- Vasiliadou, I.A.; Gioulounta, K.; Stamatelatou, K. Production of biogas via anaerobic digestion. In Handbook of Biofuels Production, 3rd ed.; Woodhead Publishing: Sawston, UK, 2023; pp. 253–311. [Google Scholar]
- Weinrich, S.; Nelles, M. Systematic simplification of the anaerobic digestion model No. 1 (ADM1)—Model development and stoichiometric analysis. Bioresour. Technol. 2021, 333, 125124. [Google Scholar] [CrossRef] [PubMed]
- Reichert, P. AQUASIM—A tool for simulation and data analysis of aquatic systems. Water Sci. Technol. 1994, 30, 21–30. [Google Scholar] [CrossRef]
- Batstone, D.J.; Keller, J.; Angelidaki, I.; Kalyuzhnyi, S.V.; Pavlostathis, S.G.; Rozzi, A.; Sanders, W.T.; Siegrist, H.; Vavilin, V.A. The IWA Anaerobic Digestion Model No 1 (ADM1). Water Sci. Technol. 2002, 45, 65–73. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Coutu, A.; Mottelet, S.; Pauss, A.; Ribeiro, T. Overview of Numerical Simulation of Solid-State Anaerobic Digestion Considering Hydrodynamic Behaviors, Phenomena of Transfer, Biochemical Kinetics and Statistical Approaches. Energies 2023, 16, 1108. [Google Scholar] [CrossRef]
- Emebu, S.; Pecha, J.; Janacova, D. Review on anaerobic digestion models: Model classification & elaboration of process phenomena. Renew. Sustain. Energy Rev. 2022, 160, 112288. [Google Scholar]
- Aravani, V.; Tsigkou, K.; Papadakis, V.G.; Kornaros, M. Biochemical Μethane Potential of Most Promising Agricultural Residues in Northern and Southern Greece. Chemosphere 2022, 296, 133985. [Google Scholar] [CrossRef] [PubMed]
- Aravani, V.; Tsigkou, K.; Papadakis, V.G.; Wang, W.; Kornaros, M. Anaerobic Co-Digestion of Agricultural Residues Produced in Southern and Northern Greece. Fermentation 2023, 9, 131. [Google Scholar] [CrossRef]
- Parker, W.J. Application of the ADM1 model to advanced anaerobic digestion. Bioresour. Technol. 2005, 96, 1832–1842. [Google Scholar] [CrossRef] [PubMed]
- Fukuyama, Y.; Inoue, M.; Omae, K.; Yoshida, T.; Sako, Y. Chapter Three—Anaerobic and hydrogenogenic carbon monoxide-oxidizing prokaryotes: Versatile microbial conversion of a toxic gas into an available energy. In Advances in Applied Microbiology; Gadd, G.M., Sariaslani, S., Eds.; Academic Press: Cambridge, MA, USA, 2020; Volume 110, pp. 99–148. [Google Scholar]
- Waszkielis, K.; Białobrzewski, I.; Bułkowska, K. Application of anaerobic digestion model No. 1 for simulating fermentation of maize silage, pig manure, cattle manure and digestate in the full-scale biogas plant. Fuel 2022, 317, 123491. [Google Scholar] [CrossRef]
- Haugen, F.; Bakke, R.; Lie, B. Adapting dynamic mathematical models to a pilot anaerobic digestion reactor. Model. Identif. Control. 2013, 34, 35–54. [Google Scholar] [CrossRef]




| Type | Symbol | Value | Units | |
|---|---|---|---|---|
| Soluble | ||||
| Degradable COD * | Real list variable | Input_S_COD | ~18–33 | kg COD/m3 |
| Sugars * | Real list variable | Input_S_su_in | ~8–20 | kg COD/m3 |
| Inorganic carbon ** | Constant variable | Input_S_IC_in | 0.005 | kmol/m3 |
| Inorganic nitrogen ** | Constant variable | Input_S_IN_in | 0.065 | kmol/m3 |
| Particulate | ||||
| Degradable COD * | Real list variable | Input_X_COD | ~8–33 | kg COD/m3 |
| Carbohydrates * | Real list variable | Input_X_ch_in | ~11–41 | kg COD/m3 |
| Degradable pCOD * | Through equation | Input_X_I_in | =Input_×_COD-Input_×_ch_in | kg COD/m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papachristopoulos, E.; Prodromidis, G.N.; Mytakis, D.E.; Papadakis, V.G.; Coutelieris, F.A. Modeling of the Anaerobic Digestion of Biomass Produced by Agricultural Residues in Greece. Reactions 2024, 5, 338-349. https://doi.org/10.3390/reactions5020017
Papachristopoulos E, Prodromidis GN, Mytakis DE, Papadakis VG, Coutelieris FA. Modeling of the Anaerobic Digestion of Biomass Produced by Agricultural Residues in Greece. Reactions. 2024; 5(2):338-349. https://doi.org/10.3390/reactions5020017
Chicago/Turabian StylePapachristopoulos, Efstathios, George N. Prodromidis, Dennis E. Mytakis, Vagelis G. Papadakis, and Frank A. Coutelieris. 2024. "Modeling of the Anaerobic Digestion of Biomass Produced by Agricultural Residues in Greece" Reactions 5, no. 2: 338-349. https://doi.org/10.3390/reactions5020017
APA StylePapachristopoulos, E., Prodromidis, G. N., Mytakis, D. E., Papadakis, V. G., & Coutelieris, F. A. (2024). Modeling of the Anaerobic Digestion of Biomass Produced by Agricultural Residues in Greece. Reactions, 5(2), 338-349. https://doi.org/10.3390/reactions5020017







