Segmentation of Porous Structure in Carbonate Rocks with Applications in Agricultural Soil Management: A Hybrid Method Based on the UNet Network and Kriging Geostatistical Techniques
Abstract
1. Introduction
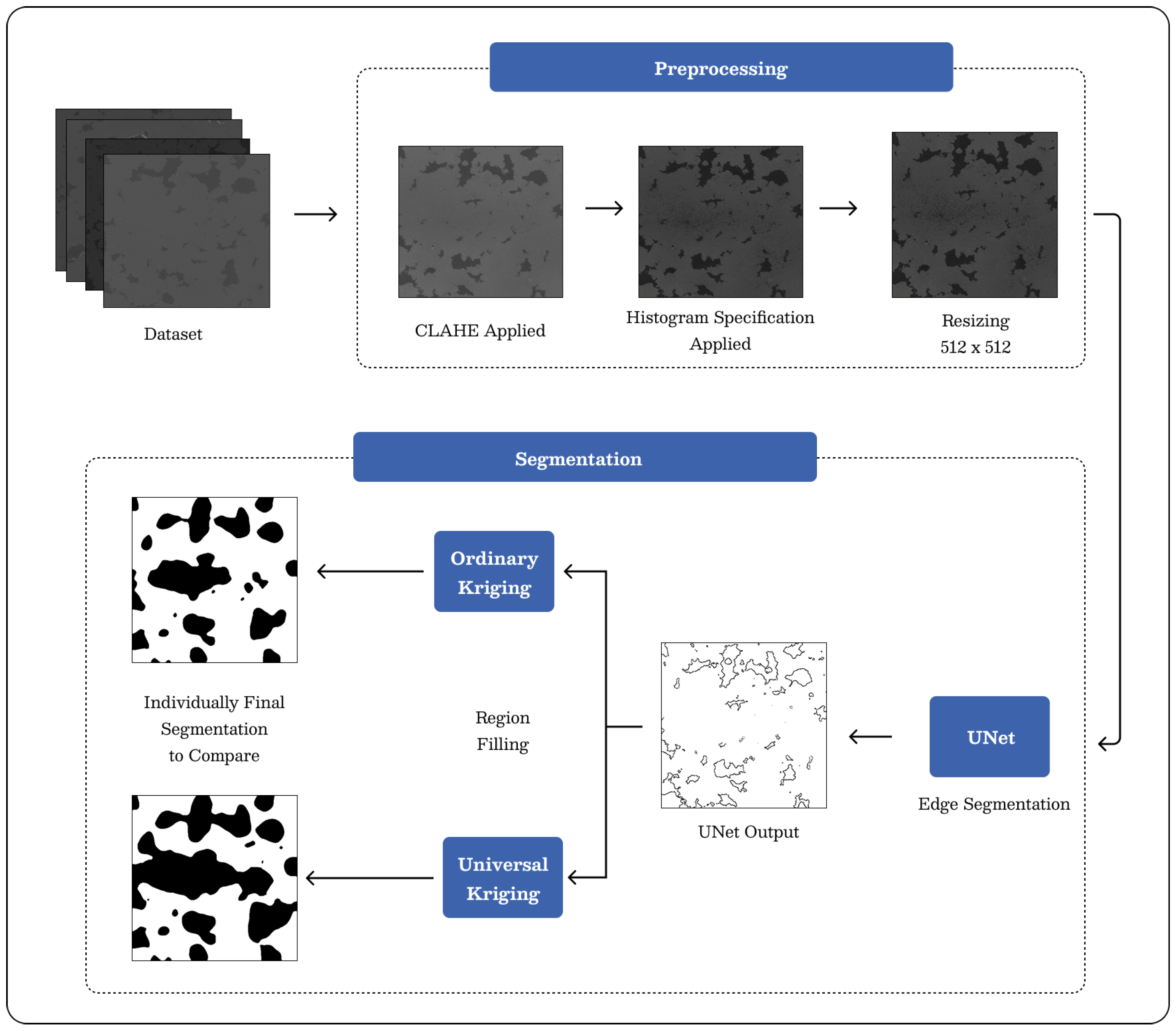
2. Proposed Method and Materials
2.1. Dataset
2.2. Preprocessing
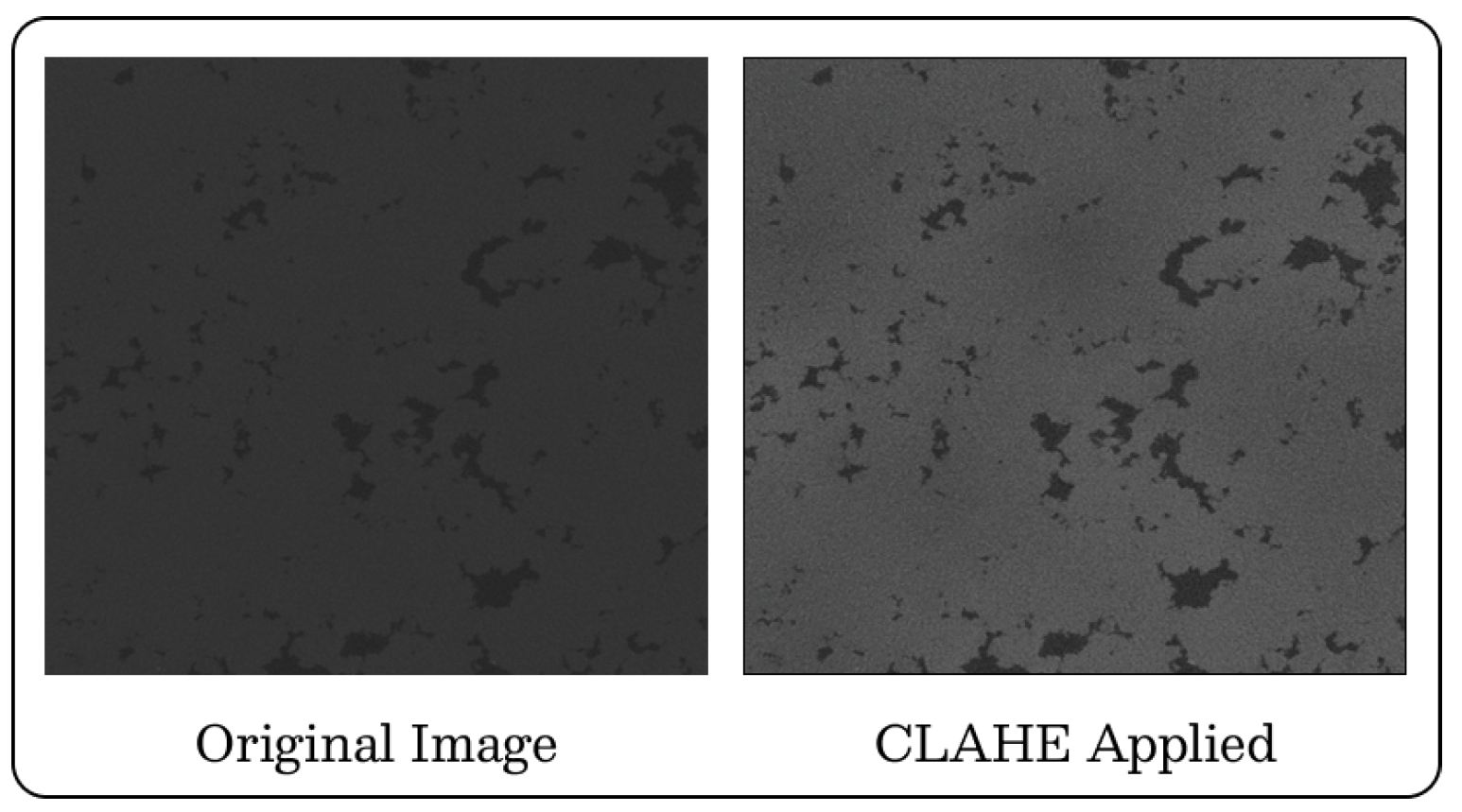
2.2.1. CLAHE
2.2.2. Histogram Specification
2.3. Segmentation
2.3.1. UNet
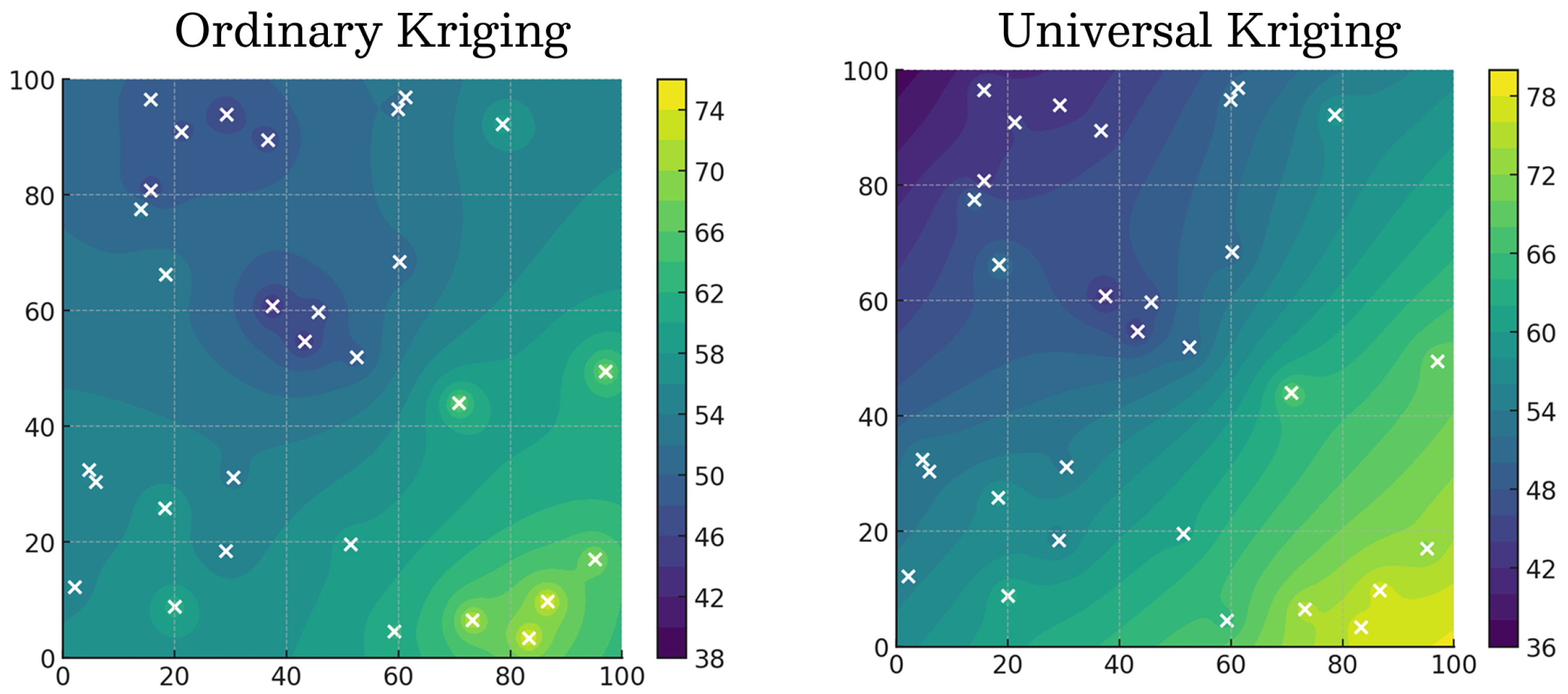
2.3.2. Ordinary Kriging and Universal Kriging
3. Experiments and Results
3.1. Results of Edge Segmentation with UNet
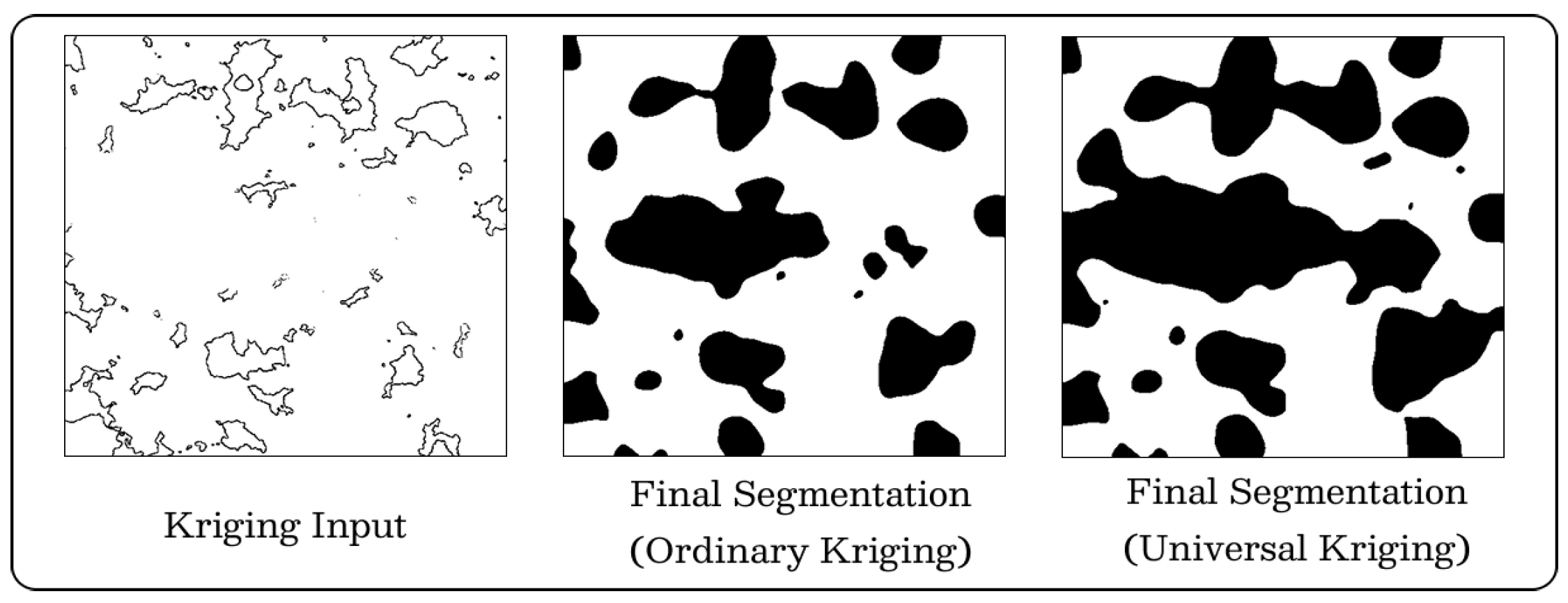
3.2. Final Segmentation Results
4. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goldscheider, N.; Chen, Z.; Auler, A.S.; Bakalowicz, M.; Broda, S.; Drew, D.; Hartmann, J.; Jiang, G.; Moosdorf, N.; Stevanovic, Z.; et al. Global distribution of carbonate rocks and karst water resources. Hydrogeol. J. 2020, 28, 1661–1677. [Google Scholar] [CrossRef]
- Tucker, M.E.; Wright, V.P. Carbonate Sedimentology; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Chen, Q.; Zhang, P.; Hu, Z.; Li, S.; Zhang, Y.; Hu, L.; Zhou, L.; Lin, B.; Li, X. Soil organic carbon and geochemical characteristics on different rocks and their significance for carbon cycles. Front. Environ. Sci. 2022, 9, 784868. [Google Scholar] [CrossRef]
- Houston, A.N.; Otten, W.; Falconer, R.; Monga, O.; Baveye, P.C.; Hapca, S.M. Quantification of the pore size distribution of soils: Assessment of existing software using tomographic and synthetic 3D images. Geoderma 2017, 299, 73–82. [Google Scholar] [CrossRef]
- Ivonin, D.; Kalnin, T.; Grachev, E.; Shein, E. Quantitative analysis of pore space structure in dry and wet soil by integral geometry methods. Geosciences 2020, 10, 365. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, T. Soil pore structure and its research methods: A review. Soil Water Res. 2024, 19, 1–24. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, T.; Ge, Z.; Man, T.; Huppert, H.E. Infiltration characteristics of slurries in porous media based on the coupled Lattice-Boltzmann discrete element method. Comput. Geotech. 2025, 177, 106865. [Google Scholar] [CrossRef]
- Mahdi, Z.A.; Farman, G.M. A review on models for evaluating rock petrophysical properties. Iraqi J. Chem. Pet. Eng. 2023, 24, 125–136. [Google Scholar] [CrossRef]
- Yang, Y.; Hakim, S.; Bruns, S.; Rogowska, M.; Boehnert, S.; Hammel, J.; Stipp, S.; Sørensen, H. Direct observation of coupled geochemical and geomechanical impacts on chalk microstructure evolution under elevated CO2 pressure. ACS Earth Space Chem. 2018, 2, 618–633. [Google Scholar] [CrossRef]
- Gonzalez, R.C. Digital Image Processing; Pearson education india, 2009. [Google Scholar]
- Jia, L.; Chen, M.; Jin, Y. 3D imaging of fractures in carbonate rocks using X-ray computed tomography technology. Carbonates Evaporites 2013, 29, 147–153. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; proceedings, part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Bressan, P.O.; Junior, J.M.; Martins, J.A.C.; Gonçalves, D.N.; Freitas, D.M.; Osco, L.P.; Silva, J.d.A.; Luo, Z.; Li, J.; Garcia, R.C.; et al. Semantic segmentation with labeling uncertainty and class imbalance. arXiv 2021, arXiv:2102.04566. [Google Scholar] [CrossRef]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. South. Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar]
- Wang, H. Application of Machine Learning and Deep Learning Methods in Geological Carbon Sequestration Across Multiple Spatial Scales. 2022. Available online: https://vtechworks.lib.vt.edu/items/c0fc3745-99b6-465a-881b-de15d08f2a99 (accessed on 4 September 2025).
- Vidal, A.; Menezes dos Anjos, C.E.; Medeiros, L.; Surmas, R.; Neta, A.; Evsukoff, A.; Vargas, J. 16 Brazilian Pre-Salt Carbonates: Multi-Resolution Micro-CT Images. 2025. Available online: https://www.doi.org/10.17612/xr50-s717 (accessed on 4 September 2025). [CrossRef]
- Zuiderveld, K. Contrast limited adaptive histogram equalization. In Graphics Gems IV; 1994; pp. 474–485. [Google Scholar]
- Khan, F.F.; Kim, J.H.; Park, C.S.; Kim, J.I.; Kwon, G.R. A Resource-Efficient 3D U-Net for Hippocampus Segmentation Using CLAHE and SCE-3DWT Techniques. IEEE Access 2025, 13, 3. [Google Scholar] [CrossRef]
- Moreira, J.M.M.; de Almeida, J.D.S.; Junior, G.B.; de Paiva, A.C. Detecçao de glaucoma usando redes em cápsula. In Proceedings of the Simpósio Brasileiro de Computação Aplicada à Saúde (SBCAS). SBC, online, 15–18 June 2021; pp. 188–199. [Google Scholar]
- Stimper, V.; Bauer, S.; Ernstorfer, R.; Schölkopf, B.; Xian, R.P. Multidimensional contrast limited adaptive histogram equalization. IEEE Access 2019, 7, 165437–165447. [Google Scholar] [CrossRef]
- Avanaki, A. Exact histogram specification optimized for structural similarity. arXiv 2008, arXiv:0901.0065. [Google Scholar] [CrossRef]
- Xu, Z.; Baojie, X.; Guoxin, W. Canny edge detection based on Open CV. In Proceedings of the 2017 13th IEEE international conference on electronic measurement & instruments (ICEMI), Yangzhou, China, 20–23 October 2017; pp. 53–56. [Google Scholar]
- Sobel, I. An isotropic 3 × 3 image gradient operater. In Machine Vision for Three-Dimensional Scenes; Elsevier: Amsterdam, The Netherlands, 1990; pp. 376–379. [Google Scholar]
- Chilès, J.P.; Desassis, N. Fifty years of kriging. In Handbook of Mathematical Geosciences: Fifty Years of IAMG; Springer International Publishing: Cham, Swtizerland, 2018; pp. 589–612. [Google Scholar]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246–1266. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Pyrcz, M.J.; Deutsch, C.V. Geostatistical Reservoir Modeling; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Cheng, B.; Girshick, R.; Dollár, P.; Berg, A.C.; Kirillov, A. Boundary IoU: Improving object-centric image segmentation evaluation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 15334–15342. [Google Scholar]
- Junior, C.R.P.; da Silva, R.C.; da Silva Neto, E.C.; de Azevedo, A.C.; do Nascimento, C.W.R.; Fontana, A.; de Souza Júnior, V.S.; dos Anjos, L.H.C.; Pereira, M.G. Influence of carbonate rocks on soil properties in the humid tropical climate of atlantic forest, Rio de Janeiro–Brazil. J. South Am. Earth Sci. 2021, 112, 103582. [Google Scholar] [CrossRef]








| Preprocessing | IoU | Precision | Recall | F1-Score |
|---|---|---|---|---|
| CLAHE | 0.056 ± 0.013 | 0.055 ± 0.015 | 0.049 ± 0.009 | 0.029 ± 0.017 |
| Specification + CLAHE | 0.5723 ± 0.012 | 0.4528 ± 0.014 | 0.4426± 0.018 | 0.4476 ± 0.017 |
| CLAHE + Specification | 0.9429 ± 0.022 | 0.9689 ± 0.034 | 0.9532 ± 0.023 | 0.9609 ± 0.021 |
| Ordinary Kriging (Thresholds) | IoU | PRC | REC | F1-Score |
|---|---|---|---|---|
| 50% | 0.127 ± 0.042 | 0.761 ± 0.031 | 0.101 ± 0.025 | 0.047 ± 0.045 |
| 60% | 0.792 ± 0.023 | 0.933 ± 0.036 | 0.817 ± 0.028 | 0.871 ± 0.012 |
| Universal Kriging | 0.616 ± 0.018 | 0.954 ± 0.028 | 0.596 ± 0.036 | 0.733 ± 0.043 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, M.P.; Silva, I.F.S.d.; Araújo, A.d.C.; Almeida, J.D.S.d.; Paiva, A.C.d.; Silva, A.C.; Roehl, D. Segmentation of Porous Structure in Carbonate Rocks with Applications in Agricultural Soil Management: A Hybrid Method Based on the UNet Network and Kriging Geostatistical Techniques. AgriEngineering 2025, 7, 294. https://doi.org/10.3390/agriengineering7090294
Silva MP, Silva IFSd, Araújo AdC, Almeida JDSd, Paiva ACd, Silva AC, Roehl D. Segmentation of Porous Structure in Carbonate Rocks with Applications in Agricultural Soil Management: A Hybrid Method Based on the UNet Network and Kriging Geostatistical Techniques. AgriEngineering. 2025; 7(9):294. https://doi.org/10.3390/agriengineering7090294
Chicago/Turabian StyleSilva, Maxwell Pires, Italo Francyles Santos da Silva, Alan de Carvalho Araújo, João Dallyson Sousa de Almeida, Anselmo Cardoso de Paiva, Aristófanes Corrêa Silva, and Deane Roehl. 2025. "Segmentation of Porous Structure in Carbonate Rocks with Applications in Agricultural Soil Management: A Hybrid Method Based on the UNet Network and Kriging Geostatistical Techniques" AgriEngineering 7, no. 9: 294. https://doi.org/10.3390/agriengineering7090294
APA StyleSilva, M. P., Silva, I. F. S. d., Araújo, A. d. C., Almeida, J. D. S. d., Paiva, A. C. d., Silva, A. C., & Roehl, D. (2025). Segmentation of Porous Structure in Carbonate Rocks with Applications in Agricultural Soil Management: A Hybrid Method Based on the UNet Network and Kriging Geostatistical Techniques. AgriEngineering, 7(9), 294. https://doi.org/10.3390/agriengineering7090294







