Impact of Drying Conditions on Soybean Quality: Mathematical Model Evaluation
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Collection and Preparation
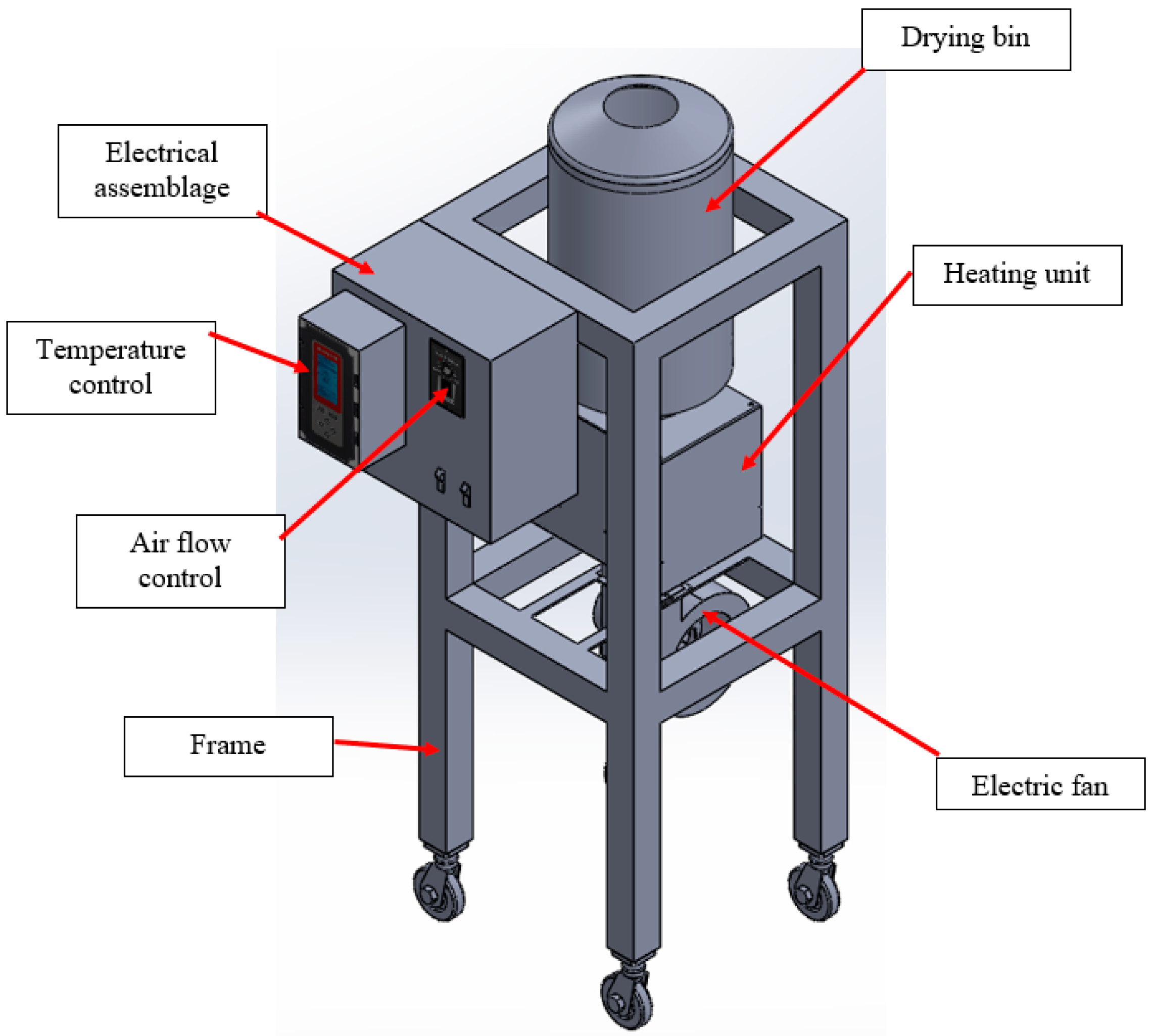
2.2. Drying Apparatus and Experiments
2.3. Mathematical Modeling of Drying Kinetics Using the Fractional Order Model
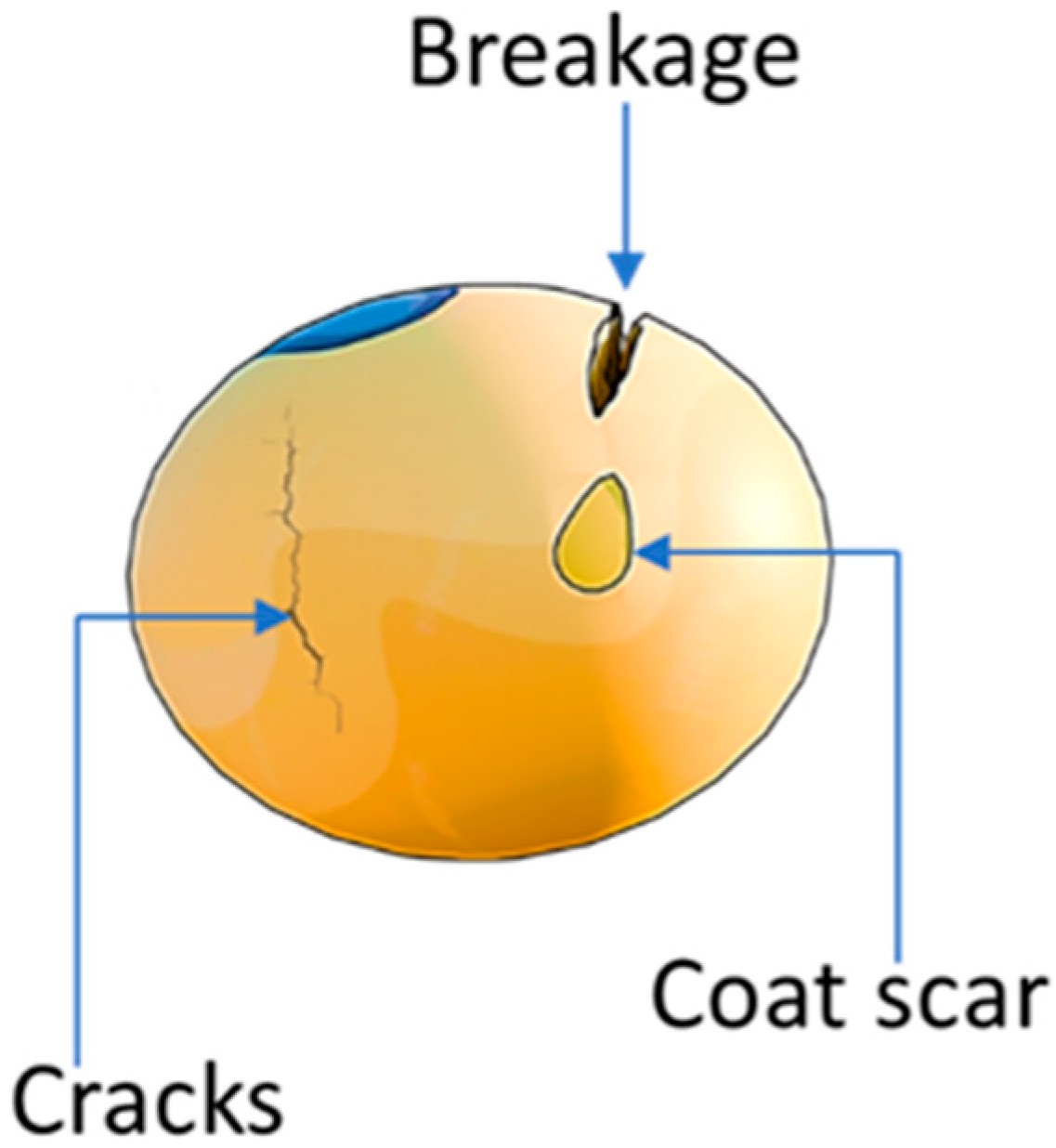
2.4. Determination of Breakage Quality Indices
2.5. Logistic Modeling of Breakage Quality Indices
2.6. Statistical Analysis
3. Results and Discussion
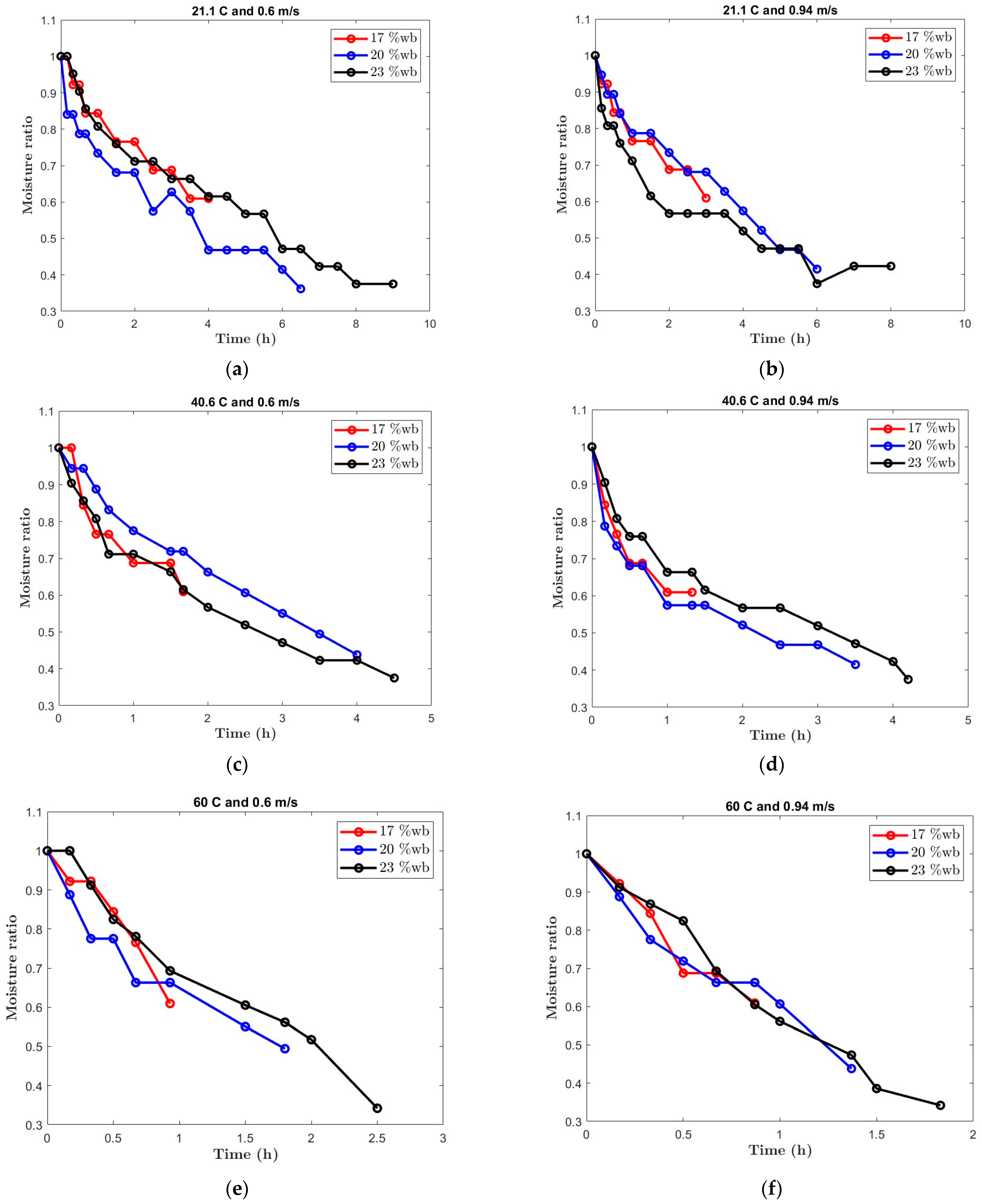
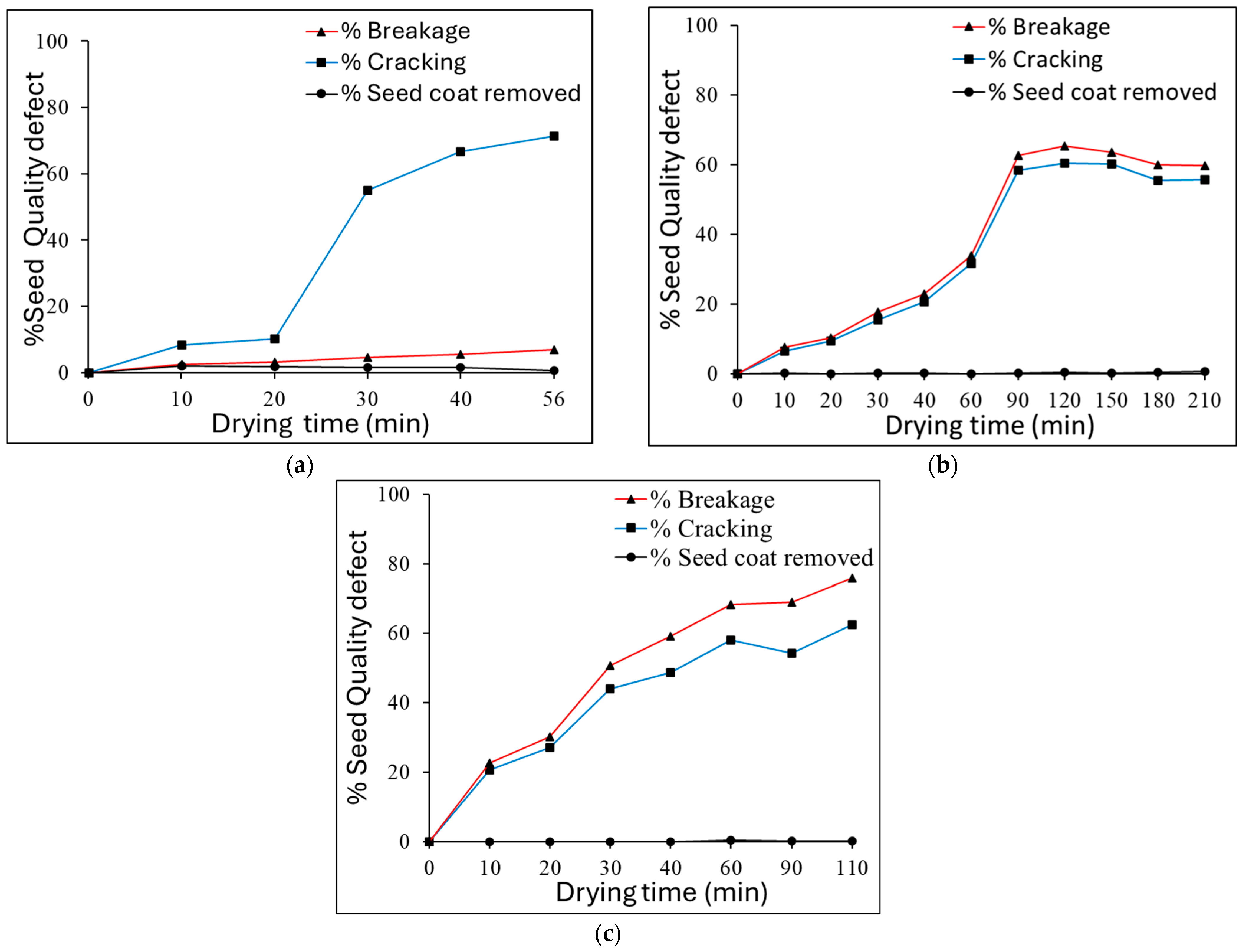
3.1. Drying Characteristics of Soybean Kernels
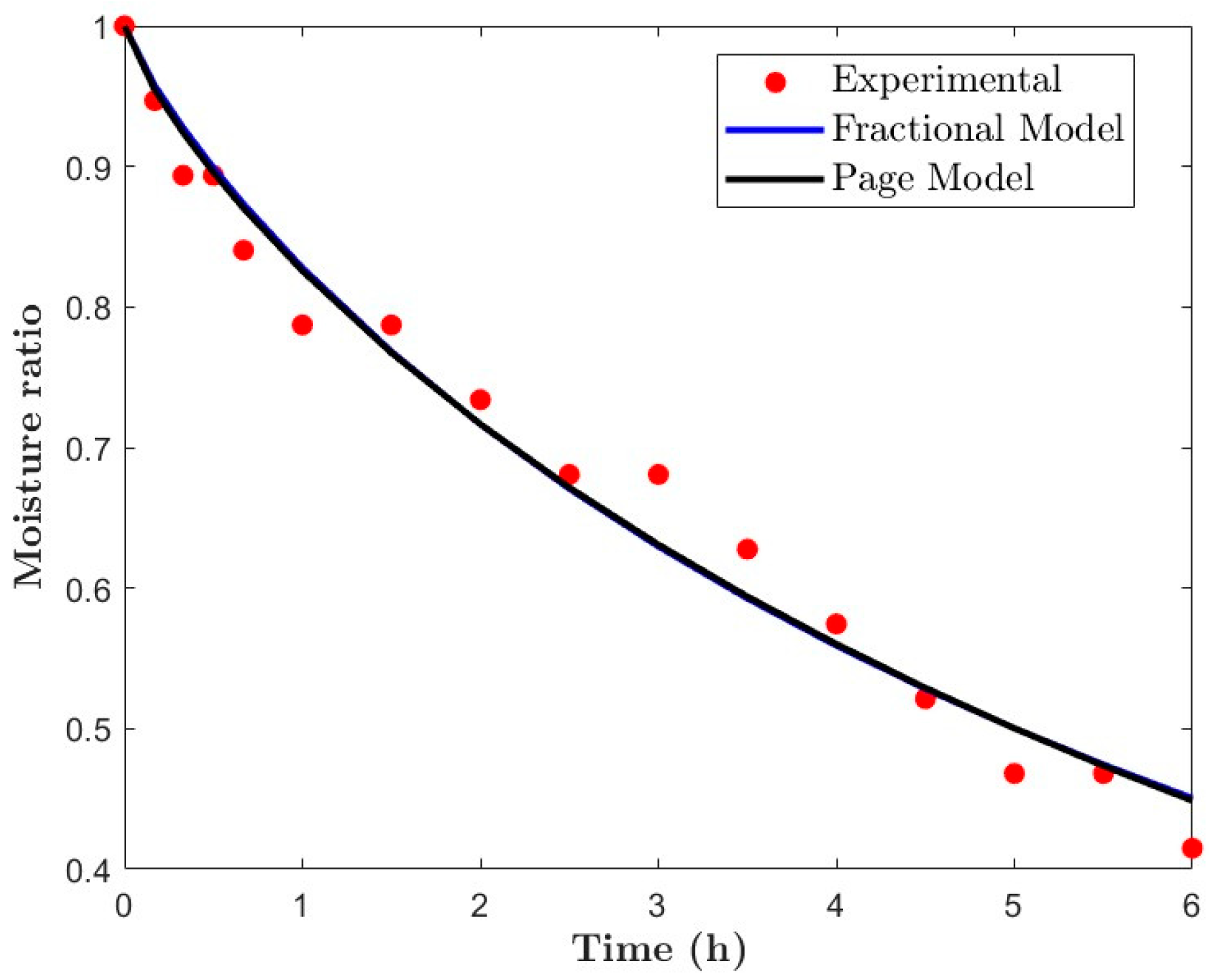
3.2. Mathematical Modeling of Drying Kinetics
3.2.1. Comparison of Fractional Order and Lumped Parameter Models
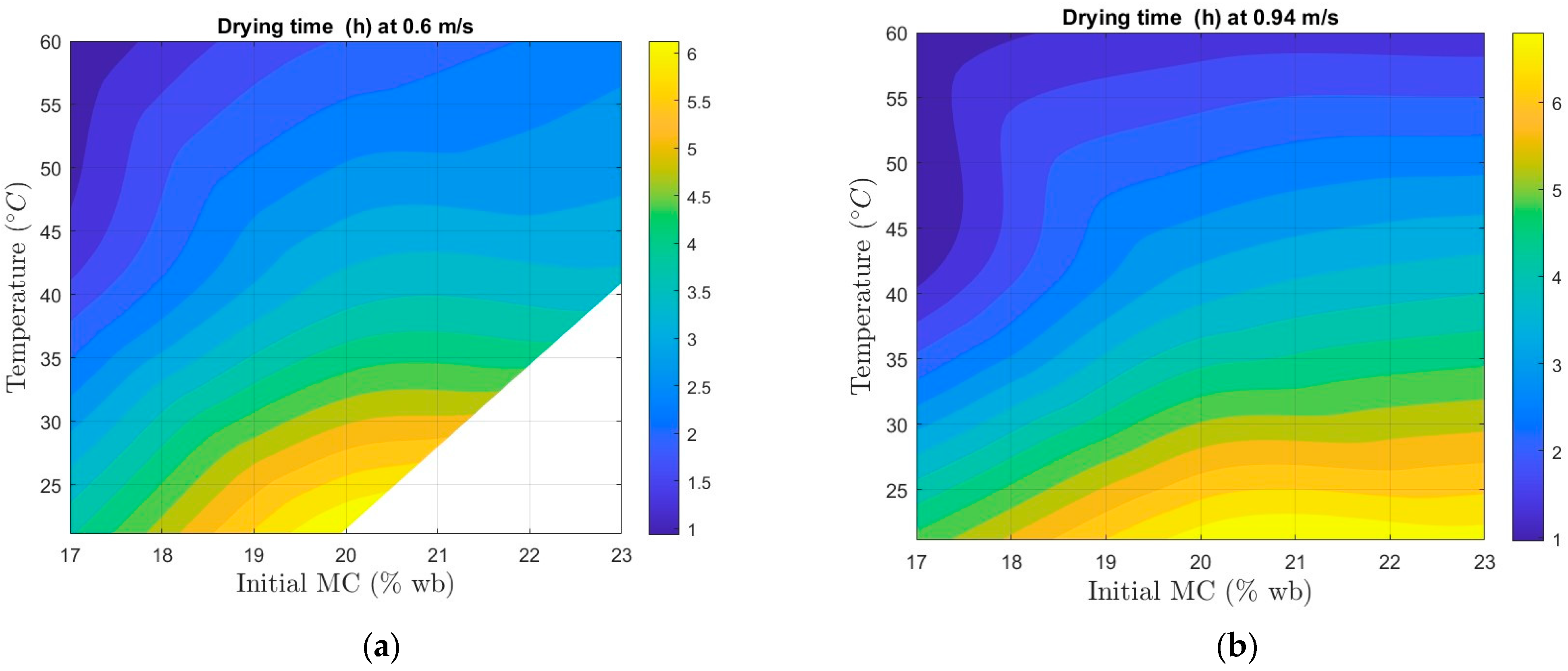
3.2.2. Effect of Drying Conditions on Model Parameters
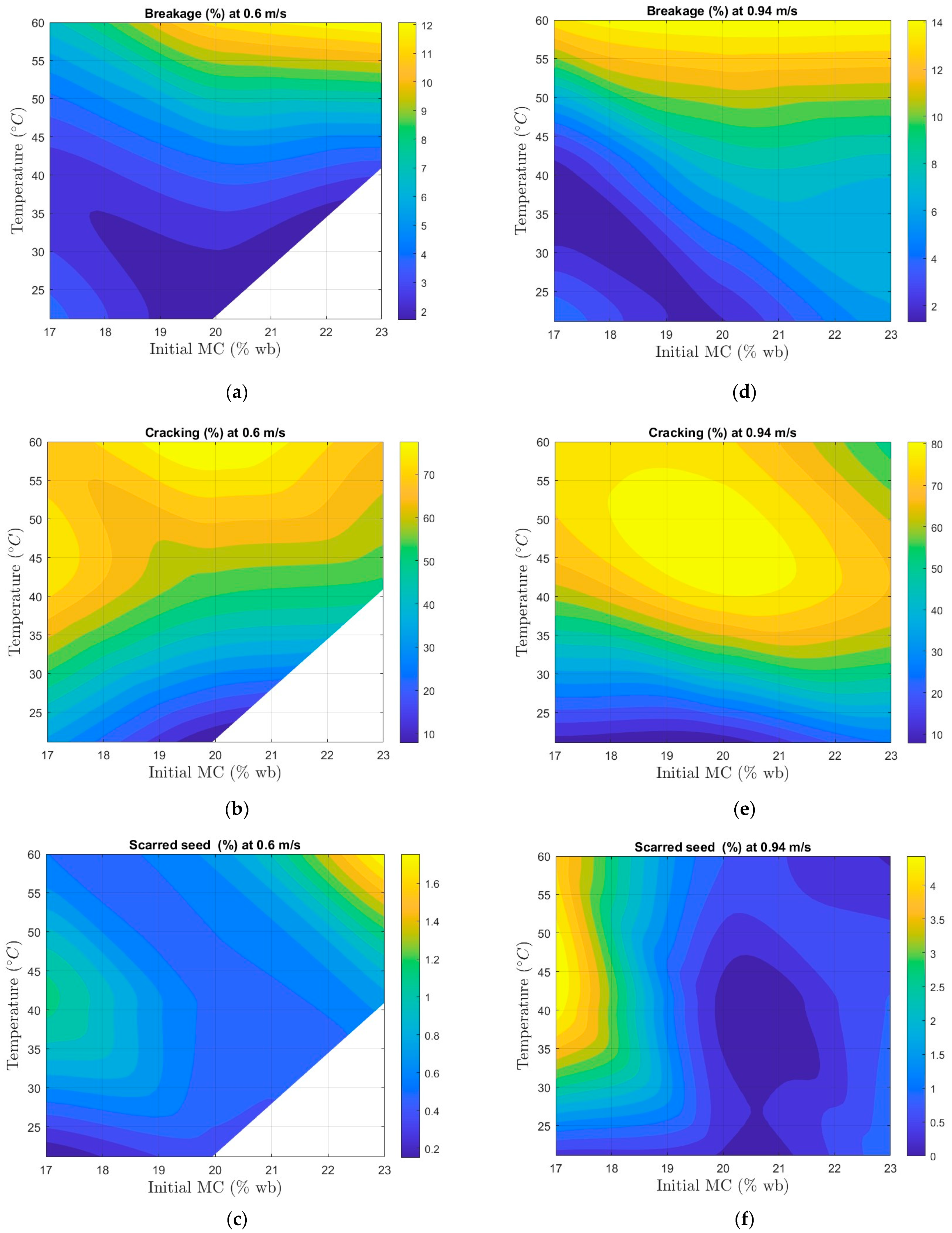
3.3. Effect of Drying Conditions on Soybean Quality
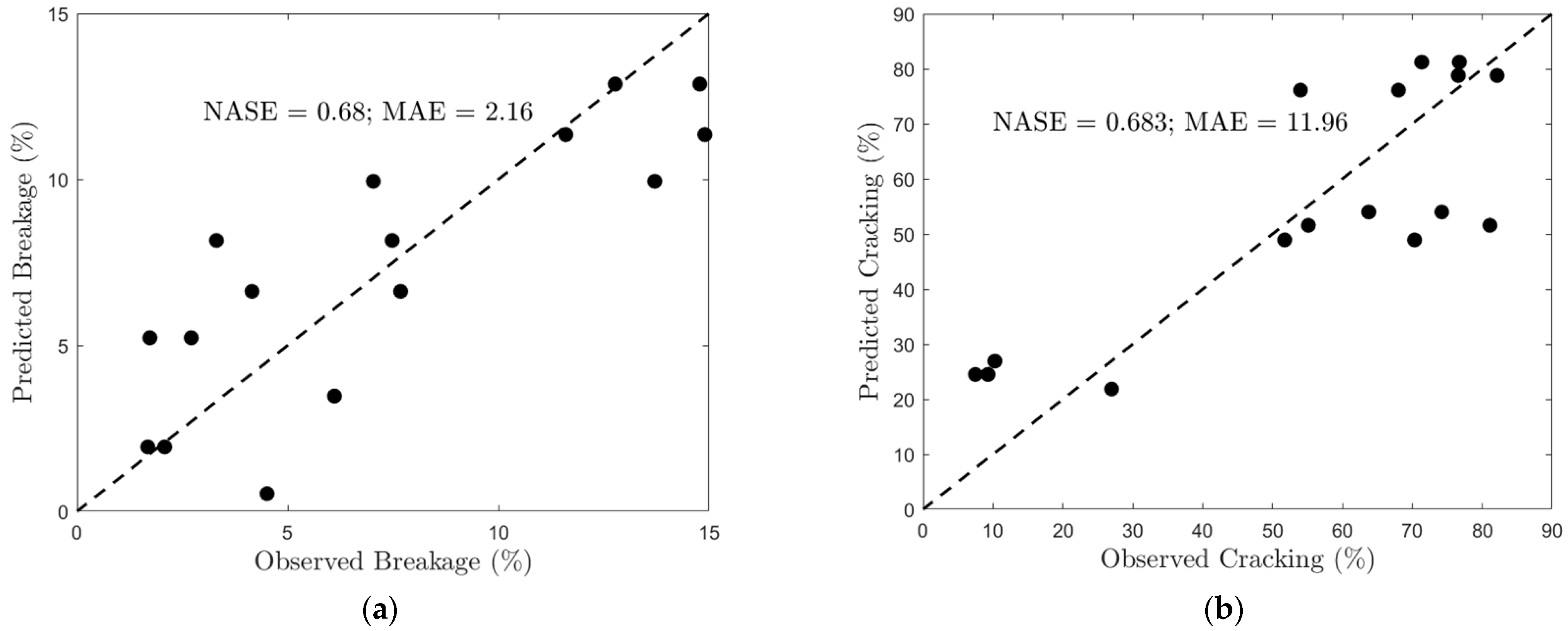
3.4. Logistic Modeling of Cracking and Breakage Indices
4. Conclusions
- (a)
- The fractional model provided significantly greater accuracy in predicting drying behavior, achieving performance improvement of 83.7% in RSME and 81.2% in MAE compared to the Page model. Notably, the fractional order model closely approximated the empirical Page model, suggesting a strong theoretical basis for its application.
- (b)
- Cracking and breakage increased with both rising drying temperature and higher initial moisture content. Drying temperature had a more pronounced effect on breakage quality than initial moisture content. The optimal drying conditions for minimizing quality deterioration were below 27 °C at 45% relative humidity and an initial moisture content of 19–20% (wb).
- (c)
- Logistic models demonstrated high predictive accuracy for both breakage and cracking indices, with stronger performance observed for breakage prediction. All logistic model parameters, except constant a, achieved excellent fit statistics (adjusted R2 > 0.98, RMSE and MAE < 1.5).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a, b, c | model constants expressed as function of initial moisture content and drying temperature |
| AI | Accuracy Improvement (%) |
| Br | percentage of broken kernels (%) |
| Cr | percentage of cracked kernels (%) |
| Eα | Mittag-Leffler function |
| j | number of terms of the series of the Mittag-Leffler function |
| k | kinetic constant (h−1) |
| k0, k1, k2 | constants |
| m | Caputo derivative constant |
| MAE | mean absolute error |
| Mc | initial weight of cleaned sample (g) |
| Me | equilibrium moisture content |
| Mf | final moisture content (%, db) |
| Mi | initial moisture content at t = 0 min (db) |
| MR | moisture ratio (dimensionless) |
| Mt | moisture content of soybean at any given time (db) |
| Mw | mass of water added (g) |
| n | reaction order (unitless) |
| R2 | coefficient of determination |
| RMSE | root mean square error |
| Sc | percentage of scarred kernels (%) |
| T | drying temperature (K) |
| t | drying time (h) |
| W1 | weight of wet sample (g) |
| W2 | weight of dried sample (g) |
| Wbr | weight of broken kernels (g) |
| Wc | initial moisture content of the cleaned sample (% wb) |
| Wcr | weight of the cracked kernels (g) |
| Wf | final desired moisture content of the sample (% wb) |
| Ws | weight of soybean sample (g) |
| Wsc | mass of scarred kernels (g) |
| X | model performance metric (such as MAE or RMSE) |
| Y | quality index such as Cr and Br |
| Yc | model constant such as a, b, and c |
| τ | dummy time derivative of Caputo derivative |
References
- Dai, H.; Wei, S.; Twardowska, I. Biofortification of soybean (Glycine max L.) with Se and Zn, and enhancing its physiological functions by spiking these elements to soil during flowering phase. Sci. Total Environ. 2020, 740, 139648. [Google Scholar] [CrossRef]
- Qin, P.; Wang, T.; Luo, Y.J.J.o.A.; Research, F. A review on plant-based proteins from soybean: Health benefits and soy product development. J. Agric. Food Res. 2022, 7, 100265. [Google Scholar] [CrossRef]
- CropProphet. US Soybean Production by State: Ranking the Top 11 [In 2024]. Available online: https://www.cropprophet.com/soybean-production-by-state-top-11/ (accessed on 26 July 2025).
- Lima, R.E.; Coradi, P.C.; Rodrigues, D.M.; Teodoro, P.E.; Teodoro, L.P.R.; de Oliveira, D.P. Monitoring and predicting the quality of soybeans for different drying and storage technologies on a real scale using sensors and Machine Learning models. J. Stored Prod. Res. 2024, 108, 102386. [Google Scholar] [CrossRef]
- Ting, K.; White, G.; Ross, I.; Loewer, O. Seed coat damage in deep-bed drying of soybeans. Trans. ASAE 1980, 23, 1293–1296. [Google Scholar] [CrossRef]
- Khoshtaghaza, M.H.; Darvishi, H.; Minaei, S. Effects of microwave-fluidized bed drying on quality, energy consumption and drying kinetics of soybean kernels. J. Food Sci. Technol. 2014, 52, 4749–4760. [Google Scholar] [CrossRef] [PubMed]
- Baidhe, E.; Clementson, C.L.; Hellevang, K.; Lin, Z. Comprehensive analysis of drying kinetics, heat and mass transfer, and thermaodynamic properties in high-temperature drying of high-moisture corn. J. Food Process Eng. 2025, 48, e70159. [Google Scholar] [CrossRef]
- Lima, R.E.; Coradi, P.C.; Nunes, M.T.; Bellochio, S.D.C.; da Silva Timm, N.; Nunes, C.F.; de Oliveira Carneiro, L.; Teodoro, P.E.; Campabadal, C. Mathematical modeling and multivariate analysis applied earliest soybean harvest associated drying and storage conditions and influences on physicochemical grain quality. Sci. Rep. 2021, 11, 23287. [Google Scholar] [CrossRef] [PubMed]
- Jung, H.; Yoon, W.B. The effect of intermittent drying on the cracking ratio of soybeans (Glycine max) at different relative humidity using reaction engineering approach modeling. Food Sci. Nutr. 2018, 6, 1492–1500. [Google Scholar] [CrossRef]
- Soponronnarit, S.; Swasdisevi, T.; Wetchacama, S.; Wutiwiwatchai, W. Fluidised bed drying of soybeans. J. Stored Prod. Res. 2001, 37, 133–151. [Google Scholar] [CrossRef]
- de Oliveira, D.E.C.; Resende, O.; Bessa, J.F.V.; Kester, A.N.; Smaniotto, T.A.S. Mathematical modeling and thermodynamic properties for drying soybean grains. Afr. J. Agric. Res. 2015, 10, 31–38. [Google Scholar] [CrossRef]
- Silva, L.P.; dos SANTOS, S.G.F.; Queiroz, J.S.; Rodovalho, R.S.; Buso, W.H.D. Drying kinetics of soybean grains. Científica 2020, 48, 99–106. [Google Scholar] [CrossRef]
- Nicolin, D.J.; Defendi, R.O.; Rossoni, D.F.; de Matos Jorge, L.M. Mathematical modeling of soybean drying by a fractional-order kinetic model. J. Food Process Eng. 2018, 41, e12655. [Google Scholar] [CrossRef]
- Aranha, A.C.R.; Ferrari, A.L.; Bissaro, C.A.; Matias, G.D.S.; Defendi, R.O.; Paschoal, S.M.; Jorge, L.M.D.M. Mathematical modelling of wheat drying by fractional order and assessment of transport properties. Can. J. Chem. Eng. 2024, 102, 996–1006. [Google Scholar] [CrossRef]
- Erenturk, K.; Kose, B.; Erenturk, S.J.F.S.; International, T. Fractional order calculus approach for drying modeling of eggplants. Food Sci. Technol. Int. 2020, 26, 379–387. [Google Scholar] [CrossRef]
- Ferrari, A.L.; Gomes, M.C.S.; Aranha, A.C.R.; Paschoal, S.M.; de Souza Matias, G.; de Matos Jorge, L.M.; Defendi, R.O. Mathematical modeling by fractional calculus applied to separation processes. Sep. Purif. Technol. 2024, 337, 126310. [Google Scholar] [CrossRef]
- Balasubramanian, D. Physical properties of raw cashew nut. J. Agric. Eng. Res. 2001, 78, 291–297. [Google Scholar] [CrossRef]
- Visvanathan, R.; Palanisamy, P.; Gothandapani, L.; Sreenarayanan, V. Physical properties of neem nut. J. Agric. Eng. Res. 1996, 63, 19–25. [Google Scholar] [CrossRef]
- ASAE S352.2 April 1988 (R2008); Moisture Measuremtn-Unground Grain and Seeds. ASABE: St. Joseph, MI, USA, 2008.
- Baidhe, E.; Clemenston, C.L.; Hellevang, K.; Lin, Z. Optimization of high-temperature drying conditions for enhanced quality of high-moisture corn. Smart Agric. Technol. 2025, 12, 101271. [Google Scholar] [CrossRef]
- He, C.; Wang, H.; Yang, Y.; Huang, Y.; Zhang, X.; Arowo, M.; Ye, J.; Zhang, N.; Xiao, M. Drying behavior and kinetics of drying process of plant-based enteric hard capsules. Pharmaceutics 2021, 13, 335. [Google Scholar] [CrossRef]
- Mondal, M.H.T.; Akhtaruzzaman, M.; Sarker, M.S.H. Modeling of dehydration and color degradation kinetics of maize grain for mixed flow dryer. J. Agric. Food Res. 2022, 9, 100359. [Google Scholar] [CrossRef]
- Agnew, J. Equilibrium Moisture Content Charts for Grain Storage Management; Prairie Agricultural Machinery Institute: Humboldt, SK, Cannda, 2017. [Google Scholar]
- Page, G.E. Factors Influencing the Maximum Rates of Air Drying Shelled Corn in Thin layers. Master’s Thesis, Purdue University, West Lafayette, IN, USA, 1949. [Google Scholar]
- ANSI/ASAE S448.2 SEP2014 (R2022); Thin-Layer Drying of Agricultural Crops. ASABE: St. Joseph, MI, USA, 2022.
- Dondee, S.; Meeso, N.; Soponronnarit, S.; Siriamornpun, S. Reducing cracking and breakage of soybean grains under combined near-infrared radiation and fluidized-bed drying. J. Food Eng. 2011, 104, 6–13. [Google Scholar] [CrossRef]
- Wiriyaumpaiwong, S.; Soponronnarit, S.; Prachayawarakorn, S. Effect of temperature on soybean quality using spouted bed technique. Kasetsart J. (Nat. Sci.) 2001, 35, 460–466. [Google Scholar]
- Hanoon, M.S.; Ammar, A.M.; Ahmed, A.N.; Razzaq, A.; Birima, A.H.; Kumar, P.; Sherif, M.; Sefelnasr, A.; El-Shafie, A. Application of soft computing in predicting groundwater quality parameters. Front. Environ. Sci. 2022, 10, 828251. [Google Scholar] [CrossRef]
- Eryani, I.; Jayantari, M.; Wijaya, I. Sensitivity analysis in parameter calibration of the WEAP Model for integrated water resources management in Unda watershed. Civ. Eng. Archit. 2022, 10, 455–469. [Google Scholar] [CrossRef]
- Golpour, I.; Guiné, R.P.; Poncet, S.; Golpour, H.; Amiri Chayjan, R.; Amiri Parian, J. Evaluating the heat and mass transfer effective coefficients during the convective drying process of paddy (Oryza sativa L.). J. Food Process Eng. 2021, 44, e13771. [Google Scholar] [CrossRef]
- Coradi, P.C.; Fernandes, C.H.; Helmich, J.C.; Goneli, A.L.J.E.A. Effects of drying air temperature and grain initial moisture content on soybean quality (Glycine max (L.) Merrill). Eng. Agrícola 2016, 36, 866–876. [Google Scholar] [CrossRef]
- Ferrari, A.L.; Aranha, A.C.R.; Nascimento, F.M.; Romansina, B.C.; de Matos Jorge, L.M.; Nicolin, D.J.; Gomes, M.C.S.; Defendi, R.O. Mathematical modeling of beans, corn and wheat drying by fractional calculus. J. Food Process Eng. 2023, 46, e14390. [Google Scholar] [CrossRef]
- Matias, G.S.; Lermen, F.H.; Matos, C.; Nicolin, D.J.; Fischer, C.; Rossoni, D.F.; Jorge, L.M. A model of distributed parameters for non-Fickian diffusion in grain drying based on the fractional calculus approach. Biosyst. Eng. 2023, 226, 16–26. [Google Scholar] [CrossRef]
- Sadaka, S. On-Farm Drying and Storage of Soybeans. In Arkansas Soybean Production Handbook; University of Arkansas Division of Agriculture: Little Rock, AR, USA, 2014. [Google Scholar]

| Airflow Velocity (m/s) | IMC (% wb) | Temp (°C) | Fractional Model | Page Model | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | R2 | Adj R2 | RMSE | MAE | R2 | Adj R2 | |||
| 0.6 | 17 | 60 | 0.0048 | 0.0038 | 0.914 | 0.857 | 0.0254 | 0.0146 | 0.973 | 0.967 |
| 20 | 60 | 0.0039 | 0.0033 | 0.981 | 0.973 | 0.0254 | 0.0184 | 0.98 | 0.977 | |
| 23 | 60 | 0.0074 | 0.0065 | 0.975 | 0.968 | 0.0366 | 0.0286 | 0.975 | 0.972 | |
| 0.94 | 17 | 60 | 0.0034 | 0.0026 | 0.964 | 0.939 | 0.0328 | 0.0202 | 0.964 | 0.955 |
| 20 | 60 | 0.0054 | 0.0042 | 0.964 | 0.95 | 0.0346 | 0.0237 | 0.966 | 0.96 | |
| 23 | 60 | 0.005 | 0.0043 | 0.989 | 0.987 | 0.0239 | 0.0185 | 0.99 | 0.989 | |
| 0.6 | 17 | 40.6 | 0.0053 | 0.0039 | 0.905 | 0.867 | 0.0485 | 0.0314 | 0.903 | 0.887 |
| 20 | 40.6 | 0.0026 | 0.0021 | 0.993 | 0.992 | 0.0154 | 0.0114 | 0.993 | 0.993 | |
| 23 | 40.6 | 0.0039 | 0.0025 | 0.989 | 0.988 | 0.02 | 0.0122 | 0.99 | 0.99 | |
| 0.94 | 17 | 40.6 | 0.0022 | 0.0018 | 0.982 | 0.973 | 0.0215 | 0.0145 | 0.98 | 0.977 |
| 20 | 40.6 | 0.003 | 0.0025 | 0.989 | 0.987 | 0.017 | 0.0121 | 0.99 | 0.989 | |
| 23 | 40.6 | 0.0049 | 0.0041 | 0.981 | 0.978 | 0.0247 | 0.0192 | 0.983 | 0.981 | |
| 0.6 | 17 | 21.1 | 0.0028 | 0.0024 | 0.973 | 0.967 | 0.0243 | 0.0105 | 0.972 | 0.97 |
| 20 | 21.1 | 0.0064 | 0.0048 | 0.962 | 0.957 | 0.0337 | 0.0243 | 0.967 | 0.965 | |
| 23 | 21.1 | 0.0058 | 0.0048 | 0.98 | 0.978 | 0.0284 | 0.0223 | 0.981 | 0.98 | |
| 0.94 | 17 | 21.1 | 0.0025 | 0.0022 | 0.972 | 0.964 | 0.0219 | 0.0179 | 0.972 | 0.969 |
| 20 | 21.1 | 0.0049 | 0.0041 | 0.978 | 0.974 | 0.027 | 0.0208 | 0.98 | 0.978 | |
| 23 | 21.1 | 0.0054 | 0.0042 | 0.977 | 0.973 | 0.0282 | 0.0202 | 0.976 | 0.974 | |
| Airflow Velocity (m/s) | Fractional Order Model | Page Model | ||
|---|---|---|---|---|
| k (h−α) | α | k (h−1) | n | |
| 0.6 | 0.306 ± 0.107 a | 0.828 ± 0.143 a | 0.324 ± 0.123 a | 0.862 ± 0.308 a |
| 0.94 | 0.423 ± 0.152 a | 0.748 ± 0.216 a | 0.423 ± 0.145 a | 0.718 ± 0.255 a |
| p-value | 0.08 | 0.373 | 0.138 | 0.297 |
| Quality Index | Constant Expressions | RMSE | MAE | R2 | Adj R2 |
|---|---|---|---|---|---|
| Cracking | 21.284 | 17.832 | 0.8595 | 0.8494 | |
| 0.838 | 0.705 | 0.9976 | 0.9973 | ||
| 1.307 | 1.099 | 0.9889 | 0.9871 | ||
| Breakage | 3.855 | 3.316 | 0.7803 | 0.7465 | |
| 0.429 | 0.361 | 0.9975 | 0.9971 | ||
| 0.251 | 0.205 | 0.9979 | 0.9976 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baidhe, E.; Clementson, C.L.; Ajayi-Banji, I.; Akatuhurira, W.; Monono, E.; Hellevang, K. Impact of Drying Conditions on Soybean Quality: Mathematical Model Evaluation. AgriEngineering 2025, 7, 273. https://doi.org/10.3390/agriengineering7090273
Baidhe E, Clementson CL, Ajayi-Banji I, Akatuhurira W, Monono E, Hellevang K. Impact of Drying Conditions on Soybean Quality: Mathematical Model Evaluation. AgriEngineering. 2025; 7(9):273. https://doi.org/10.3390/agriengineering7090273
Chicago/Turabian StyleBaidhe, Emmanuel, Clairmont L. Clementson, Ibukunoluwa Ajayi-Banji, Wilber Akatuhurira, Ewumbua Monono, and Kenneth Hellevang. 2025. "Impact of Drying Conditions on Soybean Quality: Mathematical Model Evaluation" AgriEngineering 7, no. 9: 273. https://doi.org/10.3390/agriengineering7090273
APA StyleBaidhe, E., Clementson, C. L., Ajayi-Banji, I., Akatuhurira, W., Monono, E., & Hellevang, K. (2025). Impact of Drying Conditions on Soybean Quality: Mathematical Model Evaluation. AgriEngineering, 7(9), 273. https://doi.org/10.3390/agriengineering7090273





