Crop Identification with Monte Carlo Simulations and Rotation Models from Sentinel-2 Data
Abstract
1. Introduction
1.1. Prior Work
1.1.1. Crop Identification Using Rotation Models
1.1.2. Monte Carlo Simulation in Agriculture Data
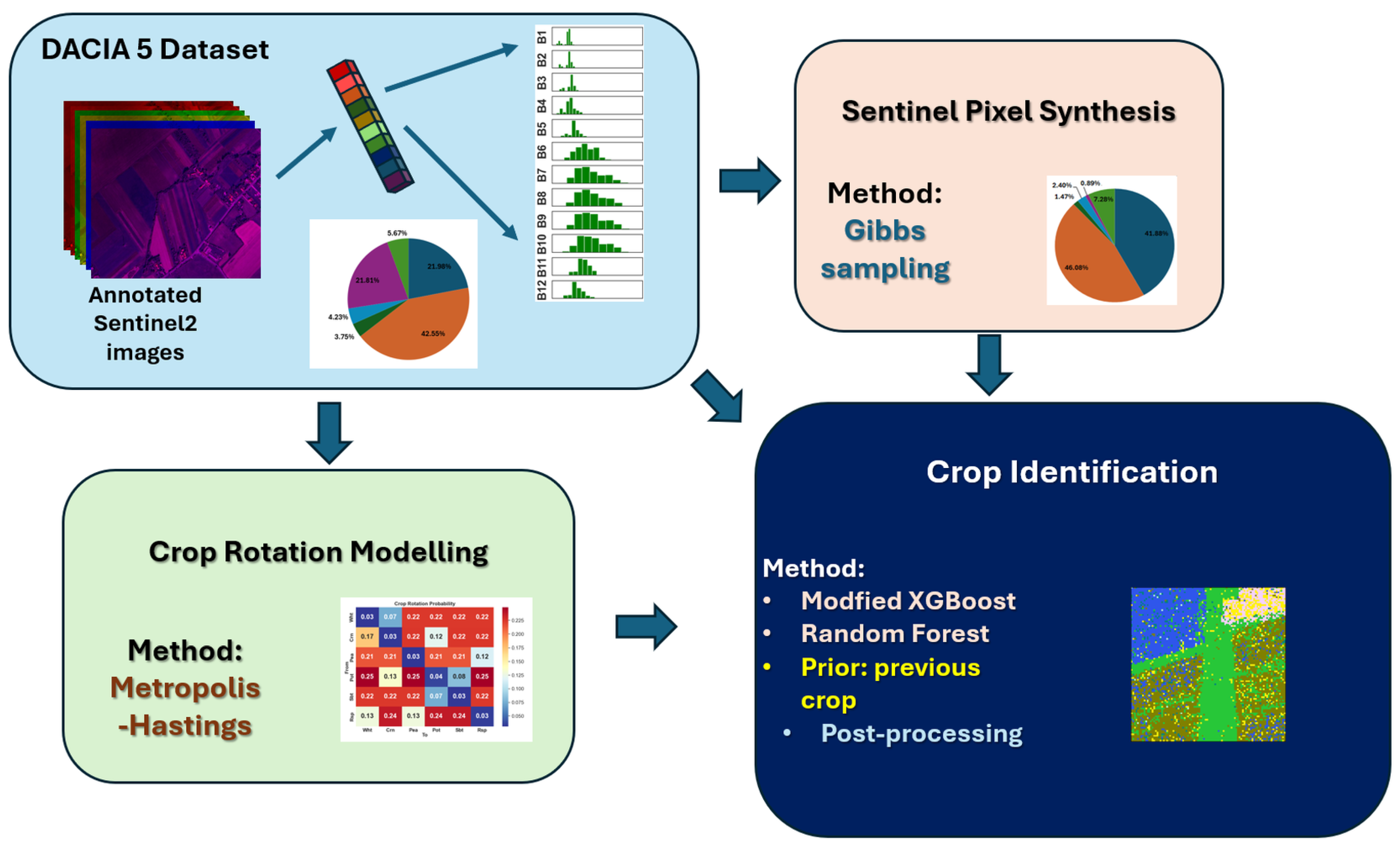
2. Materials and Methods
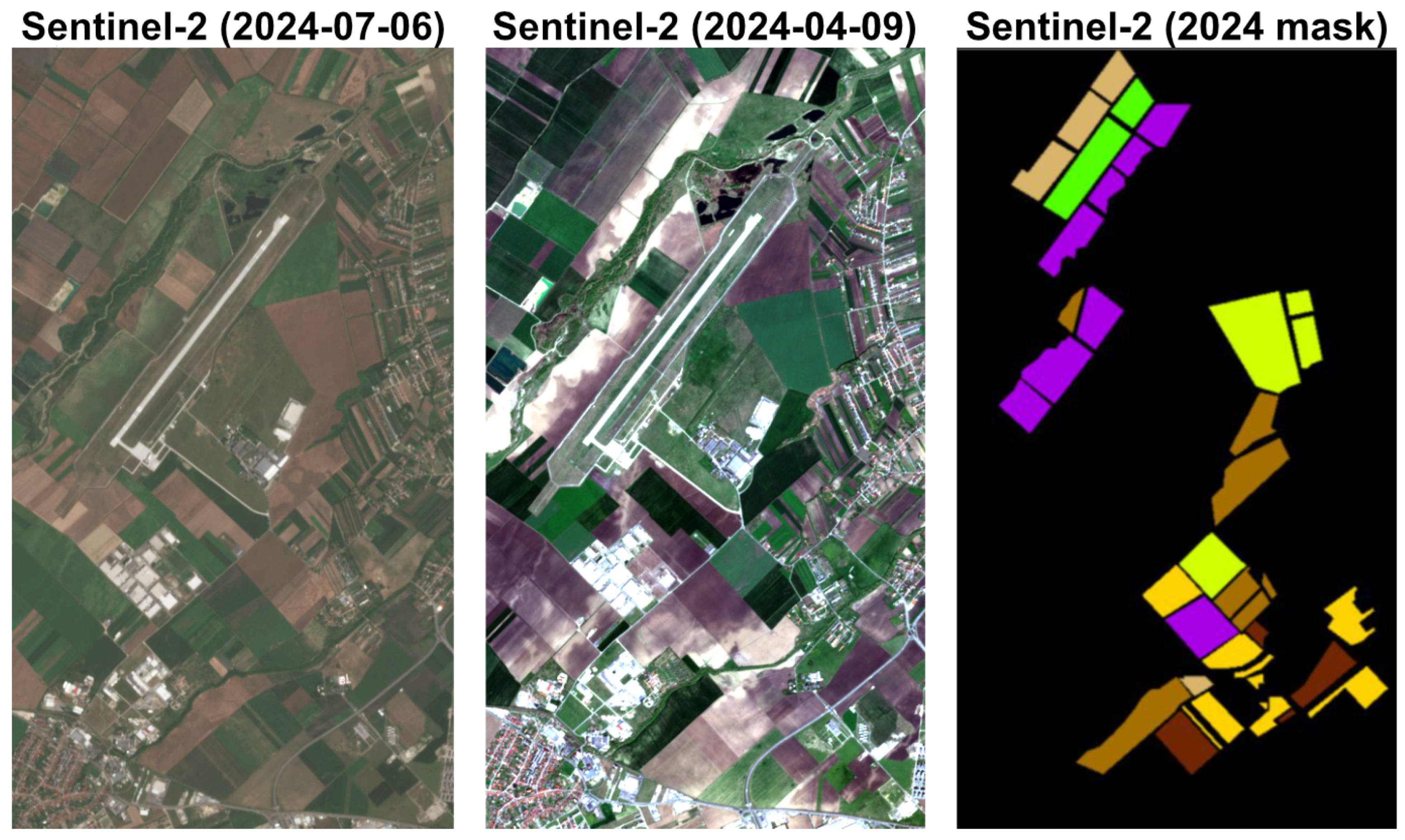
2.1. DACIA5 Dataset
- Sentinel-2 multispectral images (12 spectral bands), provided in GeoTIFF format and acquired between 2020 and 2024. Each annual image stack covers the study area at a spatial resolution of 10 m, with individual image tiles measuring 800 × 450 pixels.
- Ground truth data: crop type annotations.
- Crop history: crops from previous years in the same location.
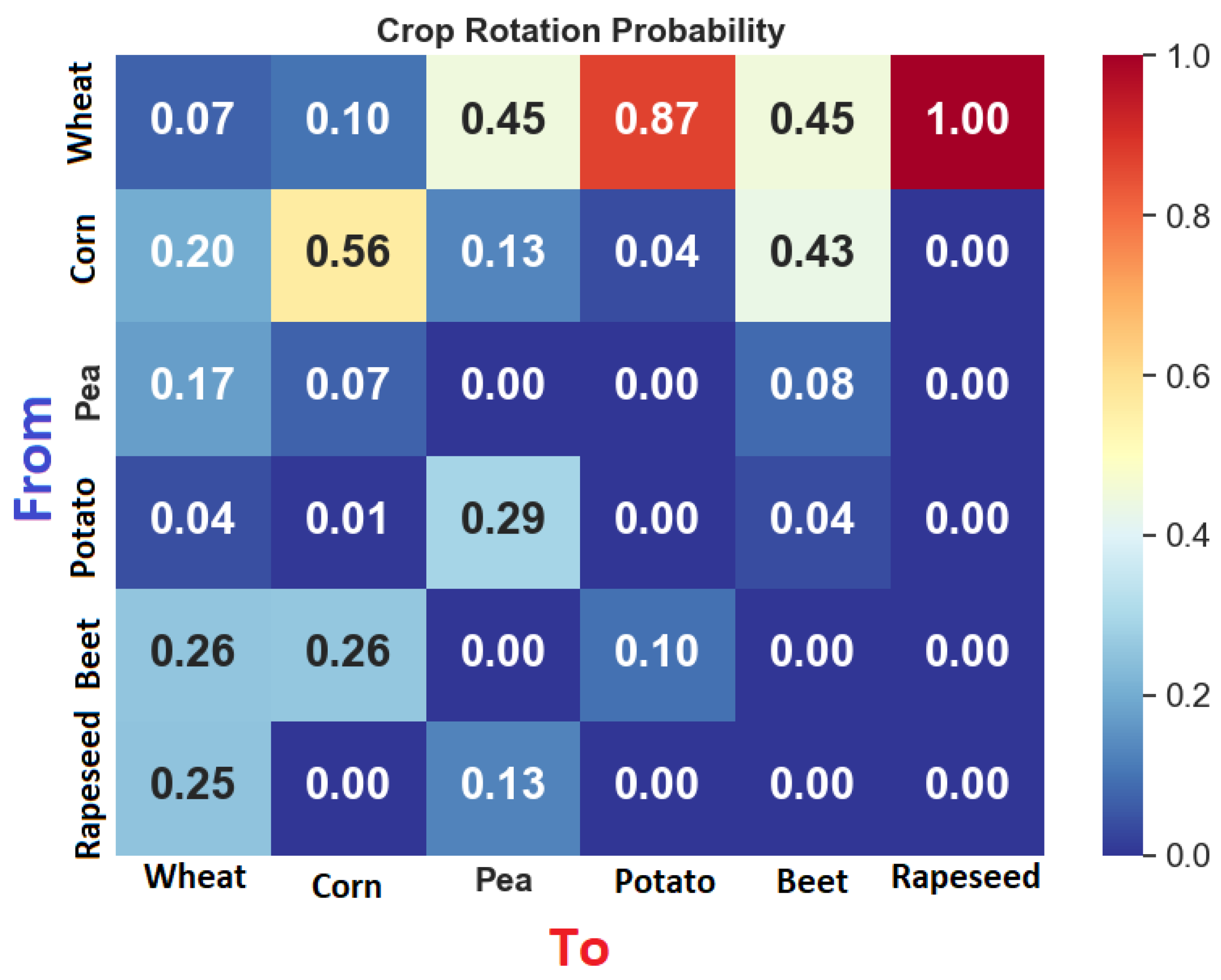
2.2. Principles of Crop Rotation
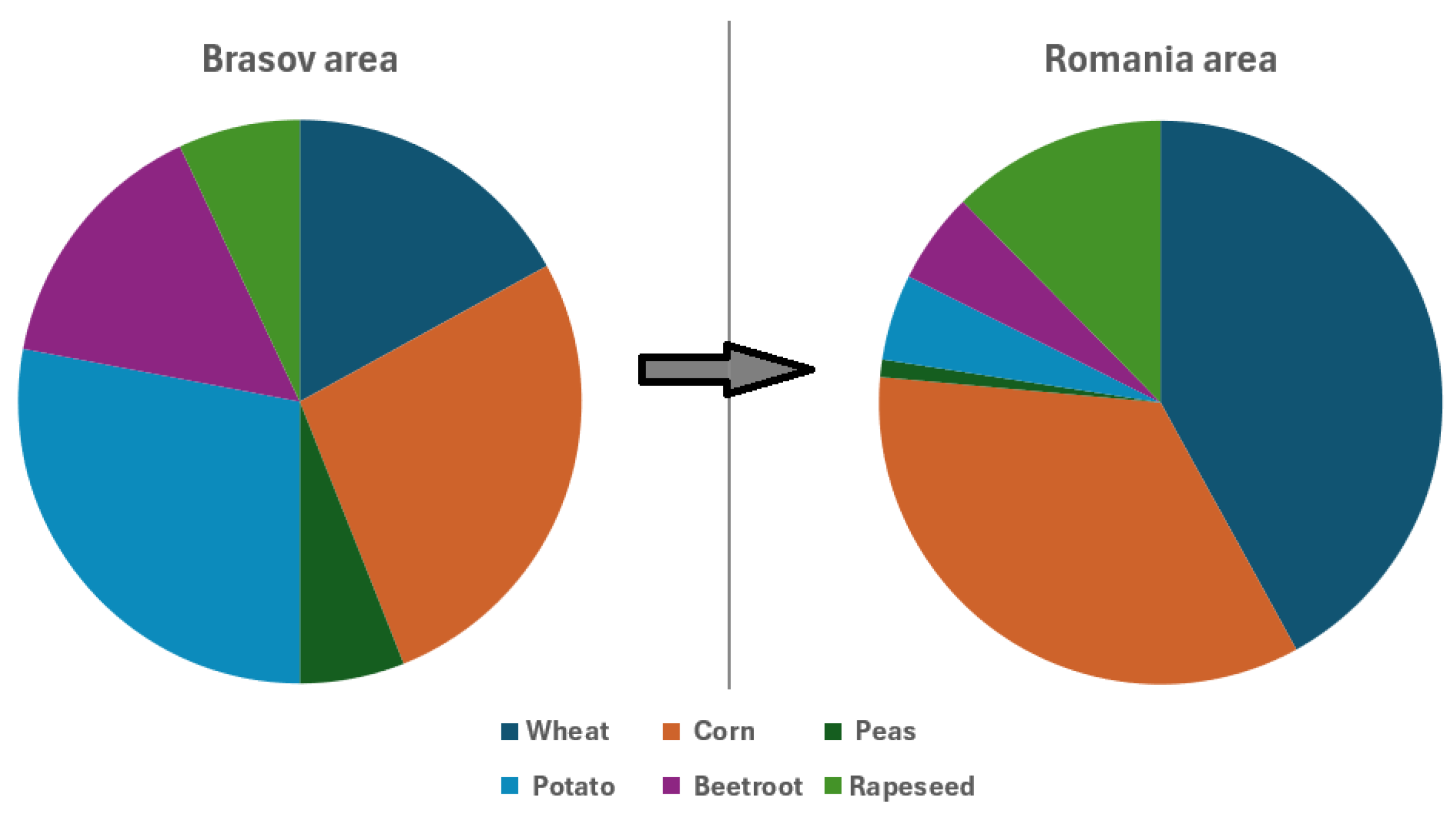
2.3. Romanian Crop Distribution
2.4. Sentinel-2 Pixel Simulation
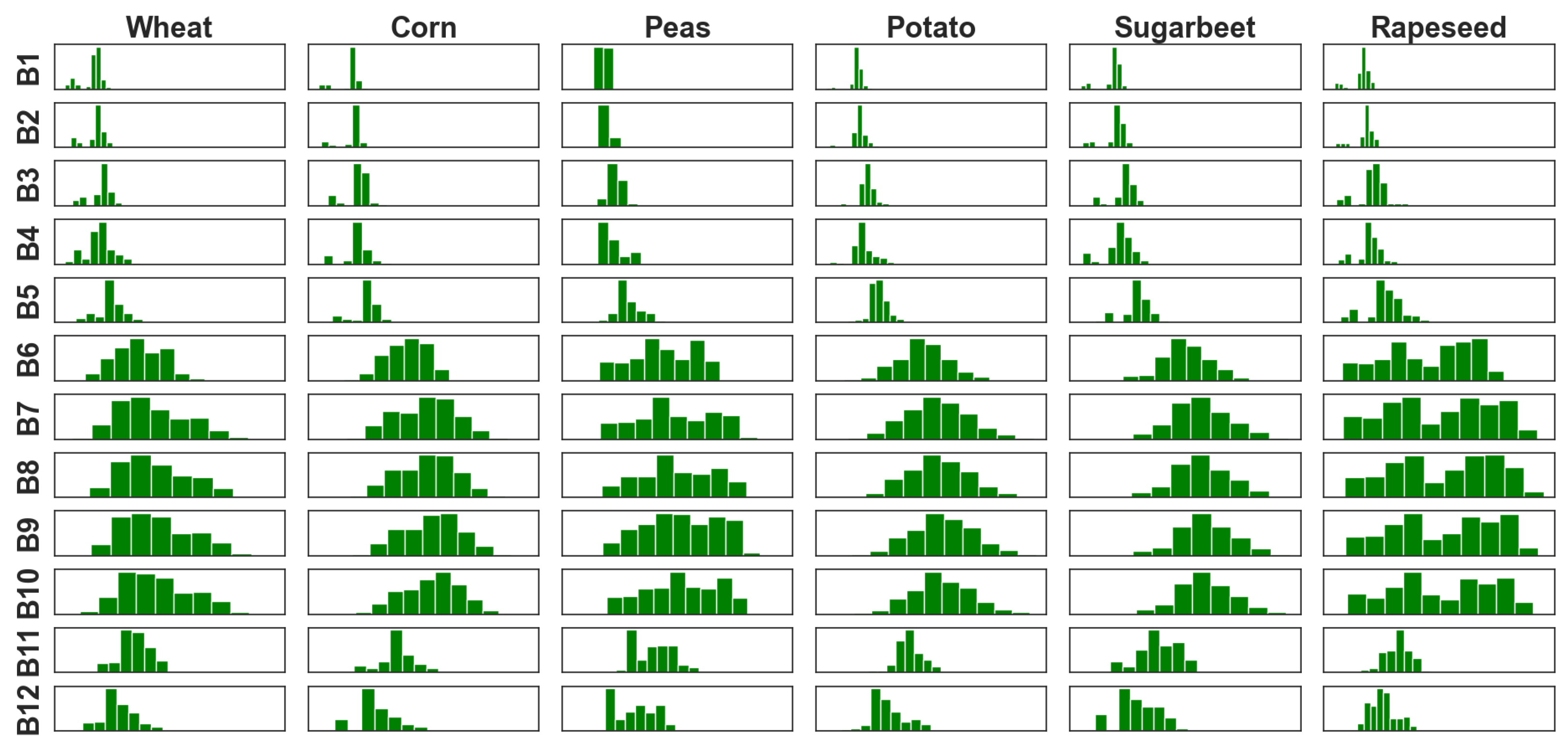
2.4.1. 12D Pixel Synthesis
| Algorithm 1 Gibbs Sampling for pair of dimensions correlation. |
|
| Algorithm 2 Metropolis–Hastings Algorithm |
|
2.4.2. Practical Details
- The histograms representing the pixel values distribution for each band within each agricultural crop, illustrated in Figure 5;
- The co-occurrence matrices representing the joint histograms between selected adjacent bands.
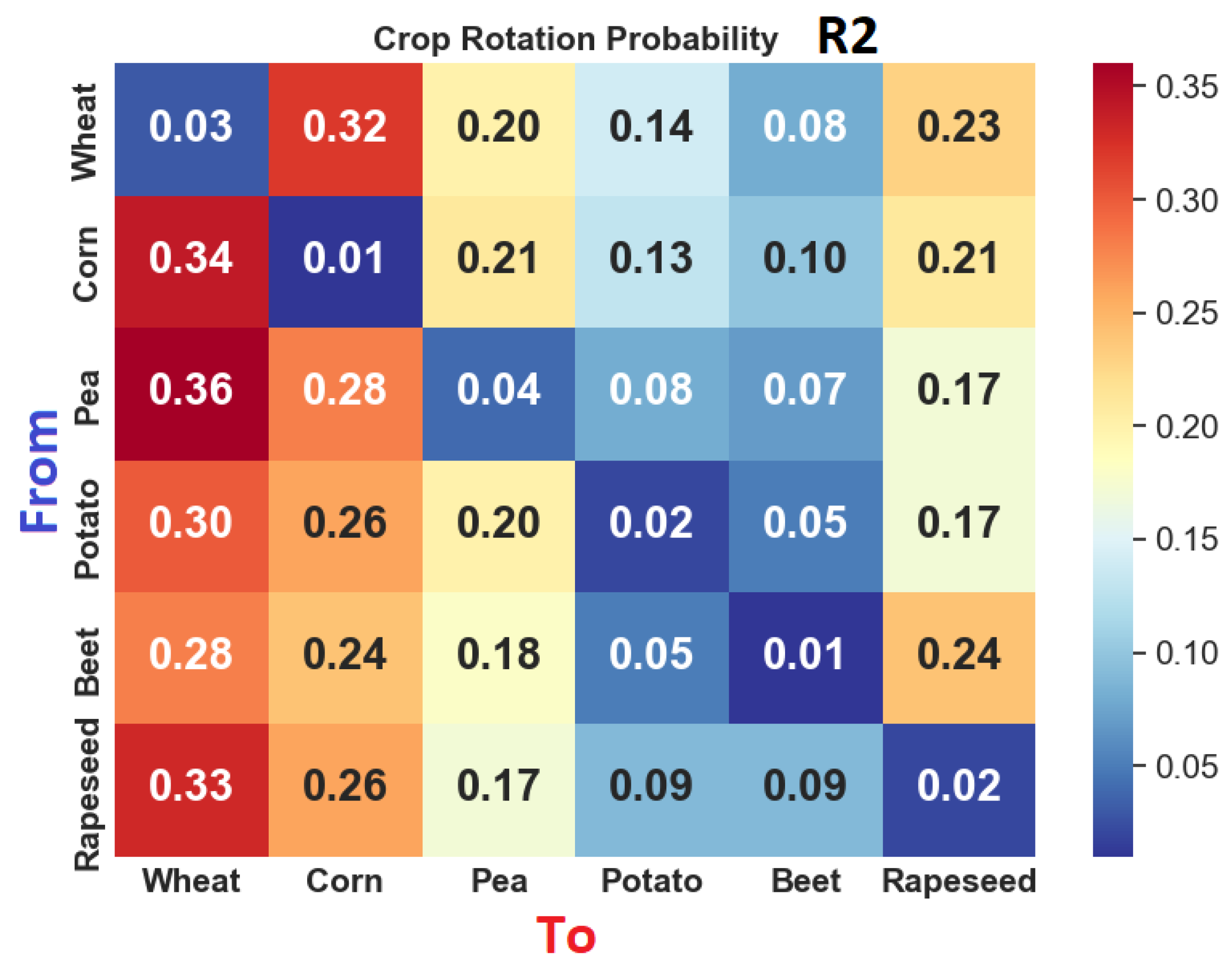
2.5. Crop Rotation Simulation
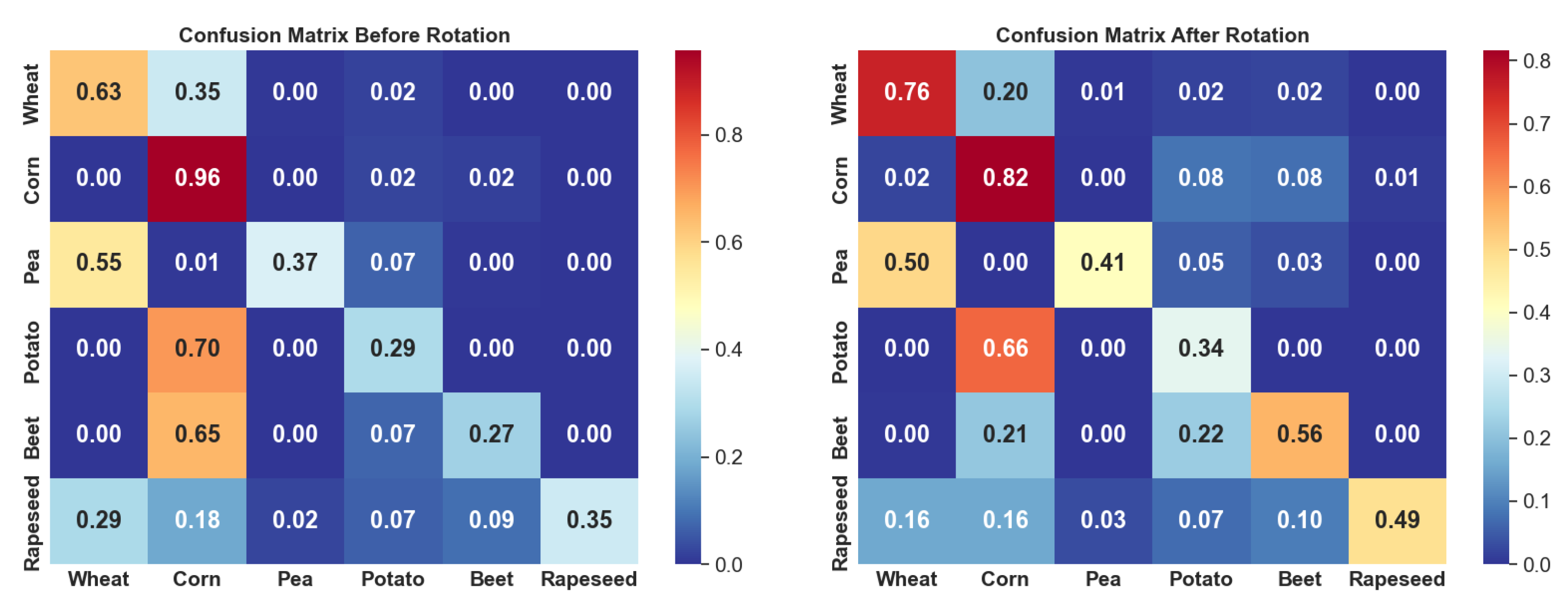
2.6. Crop Identification
- The loss residual error, , is not from , directly, but from . is the previous crop in the same location:where is the vector of rotation probabilities corresponding to the crop grown in the previous year at pixel i
- the gradient and the Hessian are penalized if a tree sets the same prediction as the previous (i.e., ): and, respectively, , where G and H are the gradient total magnitude and respective hessian magnitude for an entire tree. The constant is chosen to control the penalty. While values between to showed beneficial effect, the preferred value is .
Post-Prediction Processing with Crop Rotation Information
3. Results
3.1. Implementation
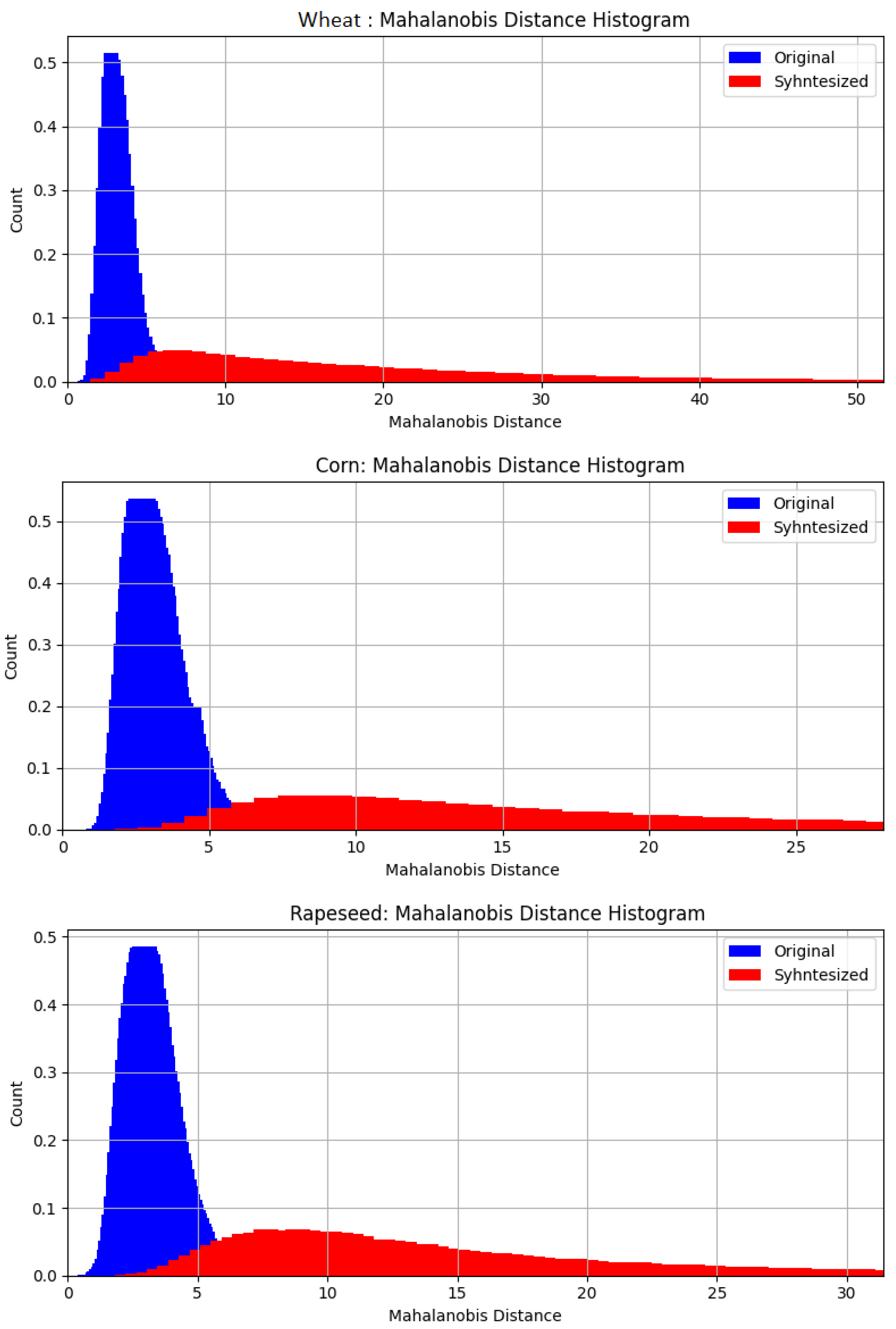
3.2. Sentinel-2 Pixel Simulation
- If the synthesized data is too similar to the original, it adds little value during the machine learning process, as it merely replicates existing patterns without expanding the feature space.
- If it is too different, it may introduce unrealistic crop representations, potentially confusing the classifier and degrading performance.
3.3. Crop Identification
3.3.1. DACIA5 Test
| Classifier | Rotation Model | Synthetic | Accuracy [%] |
|---|---|---|---|
| XGB | No | No | 65.64 |
| XGB | Post-R1 | No | 66.14 |
| XGB-loss | default | No | 68.15 |
| XGB-loss | def + post-R1 | No | 67.95 |
| XGB-loss | def + post-R1 | Yes | 70.15 |
| XGB-loss | def + post-R2 | No | 69.22 |
| XGB-loss | def + post-R2 | Yes | 71.14 |
| RF | No | No | 64.22 |
| RF | Post-R1 | No | 65.96 |
| RF | Post-R1 | Yes | 68.04 |
3.3.2. Romania Test
4. Discussion and Limitations
4.1. Rotation Model
4.2. Data Specificity
4.3. Synthesis by Monte Carlo
4.4. Machine Learning Perspective
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| CE | Cross-Entropy |
| GBM | Gradient Boosting Machine |
| INCDCSZ | National Institute of Research and Development for Potato and Sugar Beet |
| LPIS | Land Parcel Identification Systems |
| MC | Monte Carlo |
| MCMC | Markov Chain Monte Carlo |
| MD | Mahalanobis distance |
| NIR | Near Infrared |
| RF | Random Forest |
| RS | Remote Sensing |
| SAR | Synthetic Aperture Radar |
| XGBoost | eXtreme Gradient Boosting |
References
- Aijaz, N.; Lan, H.; Raza, T.; Yaqub, M.; Iqbal, R.; Pathan, M.S. Artificial intelligence in agriculture: Advancing crop productivity and sustainability. J. Agric. Food Res. 2025, 20, 101762. [Google Scholar] [CrossRef]
- Victor, B.; Nibali, A.; He, Z. A systematic review of the use of Deep Learning in Satellite Imagery for Agriculture. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 18, 2297–2316. [Google Scholar] [CrossRef]
- Wu, B.; Meng, J.; Li, Q.; Yan, N.; Du, X.; Zhang, M. Remote sensing-based global crop monitoring: Experiences with China’s CropWatch system. Int. J. Digit. Earth 2014, 7, 113–137. [Google Scholar] [CrossRef]
- Boryan, C.; Yang, Z.; Mueller, R.; Craig, M. Monitoring US agriculture: The US department of agriculture, national agricultural statistics service, cropland data layer program. Geocarto Int. 2011, 26, 341–358. [Google Scholar] [CrossRef]
- Schneider, M.; Schelte, T.; Schmitz, F.; Körner, M. EuroCrops: The Largest Harmonized Open Crop Dataset Across the European Union. Sci. Data 2023, 10, 612. [Google Scholar] [CrossRef]
- Blickensdörfer, L.; Schwieder, M.; Pflugmacher, D.; Nendel, C.; Erasmi, S.; Hostert, P. Mapping of crop types and crop sequences with combined time series of Sentinel-1, Sentinel-2 and Landsat 8 data for Germany. Remote Sens. Environ. 2022, 269, 112831. [Google Scholar] [CrossRef]
- Qiu, B.; Lin, D.; Chen, C.; Yang, P.; Tang, Z.; Jin, Z.; Ye, Z.; Zhu, X.; Duan, M.; Huang, H.; et al. From cropland to cropped field: A robust algorithm for national-scale mapping by fusing time series of Sentinel-1 and Sentinel-2. Int. J. Appl. Earth Obs. Geoinf. 2022, 113, 103006. [Google Scholar] [CrossRef]
- Băicoianu, A.; Plajer, I.; Debu, M.; Ștefan, F.M.; Ivanovici, M.; Florea, C.; Cațaron, A.; Coliban, R.M.; Popa, S.; Oprisescu, S.; et al. DACIA5: A Sentinel-1 and Sentinel-2 dataset for agricultural crop identification applications. Big Earth Data 2025, 1–32. [Google Scholar] [CrossRef]
- Wang, X.; Tang, Q.; Yang, K. Improving crop rotation classification using a random forest model incorporating spatial heterogeneity. Geocarto Int. 2024, 39, 2384473. [Google Scholar] [CrossRef]
- Yang, L.; Song, M.; Zhu, A.X.; Qin, C.; Zhou, C.; Qi, F.; Li, X.; Chen, Z.; Gao, B. Predicting soil organic carbon content in croplands using crop rotation and Fourier transform decomposed variables. Geoderma 2019, 340, 289–302. [Google Scholar] [CrossRef]
- Giordano, S.; Bailly, S.; Landrieu, L.; Chehata, N. Improved crop classification with rotation knowledge using Sentinel-1 and-2 time series. Photogramm. Eng. Remote Sens. 2020, 86, 431–441. [Google Scholar] [CrossRef]
- Quinton, F.; Landrieu, L. Crop rotation modeling for deep learning-based parcel classification from satellite time series. Remote Sens. 2021, 13, 4599. [Google Scholar] [CrossRef]
- Upcott, E.V.; Henrys, P.A.; Redhead, J.W.; Jarvis, S.G.; Pywell, R.F. A new approach to characterising and predicting crop rotations using national-scale annual crop maps. Sci. Total Environ. 2023, 860, 160471. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Q.; Zhou, Q.; Wang, C.; Bellingrath-Kimura, S.D.; Wu, W. Mapping the complex crop rotation systems in Southern China considering cropping intensity, crop diversity, and their seasonal dynamics. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 9584–9598. [Google Scholar] [CrossRef]
- Wang, P.; Xie, W.; Ding, L.; Zhuo, Y.; Gao, Y.; Li, J.; Zhao, L. Effects of maize–crop rotation on soil physicochemical properties, enzyme activities, microbial biomass and microbial community structure in Southwest China. Microorganisms 2023, 11, 2621. [Google Scholar] [CrossRef]
- Kussul, N.; Deininger, K.; Shumilo, L.; Lavreniuk, M.; Ali, D.A.; Nivievskyi, O. Biophysical impact of sunflower crop rotation on agricultural fields. Sustainability 2022, 14, 3965. [Google Scholar] [CrossRef]
- Xing, H.; Chen, B.; Lu, M. A sub-seasonal crop information identification framework for crop rotation mapping in smallholder farming areas with time series sentinel-2 imagery. Remote Sens. 2022, 14, 6280. [Google Scholar] [CrossRef]
- Barriere, V.; Claverie, M.; Schneider, M.; Lemoine, G.; d’Andrimont, R. Boosting crop classification by hierarchically fusing satellite, rotational, and contextual data. Remote Sens. Environ. 2024, 305, 114110. [Google Scholar] [CrossRef]
- Dong, Z.; Yao, L.; Bao, Y.; Zhang, J.; Yao, F.; Bai, L.; Zheng, P. Prediction of soil organic carbon content in complex vegetation areas based on CNN-LSTM model. Land 2024, 13, 915. [Google Scholar] [CrossRef]
- Chinembiri, T.S.; Mutanga, O.; Dube, T. A multi-source data approach to carbon stock prediction using Bayesian hierarchical geostatistical models in plantation forest ecosystems. GISci. Remote Sens. 2024, 61, 2303868. [Google Scholar] [CrossRef]
- Wu, Y.; Knudby, A.; Lapen, D. Topography-adjusted Monte Carlo simulation of the adjacency effect in remote sensing of coastal and inland waters. J. Quant. Spectrosc. Radiat. Transf. 2023, 303, 108589. [Google Scholar] [CrossRef]
- Radoux, J.; Chomé, G.; Jacques, D.C.; Waldner, F.; Bellemans, N.; Matton, N.; Lamarche, C.; d’Andrimont, R.; Defourny, P. Sentinel-2’s potential for sub-pixel landscape feature detection. Remote Sens. 2016, 8, 488. [Google Scholar] [CrossRef]
- Abdelmoula, H.; Kallel, A.; Roujean, J.L.; Gastellu-Etchegorry, J.P. Dynamic retrieval of olive tree properties using Bayesian model and Sentinel-2 images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9267–9286. [Google Scholar] [CrossRef]
- Makhloufi, A.; Kallel, A. Inversion of a new designed ANN-based 3-D-RTM emulator by continuous MCMC technique to monitor crop biophysical properties using sentinel-2 images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Weir, W.W. A Study of the Value of Crop Rotation in Relation to Soil Productivity; US Department of Agriculture: Washington, DC, USA, 1926; Volume 1377. [Google Scholar]
- Bullock, D.G. Crop rotation. Crit. Rev. Plant Sci. 1992, 11, 309–326. [Google Scholar] [CrossRef]
- Tanveer, A.; Ikram, R.M.; Ali, H.H. Crop rotation: Principles and practices. In Agronomic Crops: Volume 2: Management Practices; Springer: Singapore, 2019; pp. 1–12. [Google Scholar]
- Shah, K.K.; Modi, B.; Pandey, H.P.; Subedi, A.; Aryal, G.; Pandey, M.; Shrestha, J. Diversified crop rotation: An approach for sustainable agriculture production. Adv. Agric. 2021, 2021, 8924087. [Google Scholar] [CrossRef]
- Bowles, T.M.; Mooshammer, M.; Socolar, Y.; Calderón, F.; Cavigelli, M.A.; Culman, S.W.; Deen, W.; Drury, C.F.; y Garcia, A.G.; Gaudin, A.C.; et al. Long-term evidence shows that crop-rotation diversification increases agricultural resilience to adverse growing conditions in North America. One Earth 2020, 2, 284–293. [Google Scholar] [CrossRef]
- Mesfin, M.; Tekalign, A.; Fikre, A.; Yirga, C.; Jembere, T.; Getahun, T. Potentials of legumes rotation on yield and nitrogen uptake of subsequent wheat crop in northern Ethiopia. Heliyon 2023, 9, e16684. [Google Scholar] [CrossRef] [PubMed]
- Ridgman, W.J.; Walters, D.E. A comparison of growing wheat continuously with growing wheat in a four-course rotation. J. Agric. Sci. 1982, 99, 139–143. [Google Scholar] [CrossRef]
- Yuan, M.; Bi, Y.; Han, D.; Wang, L.; Wang, L.; Fan, C.; Zhang, D.; Wang, Z.; Liang, W.; Zhu, Z.; et al. Long-Term Corn–Soybean Rotation and Soil Fertilization: Impacts on Yield and Agronomic Traits. Agronomy 2022, 12, 2554. [Google Scholar] [CrossRef]
- Carrière, Y.; Brown, Z.; Aglasan, S.; Dutilleul, P.; Carroll, M.; Head, G.; Tabashnik, B.E.; Jørgensen, P.S.; Carroll, S.P. Crop rotation mitigates impacts of corn rootworm resistance to transgenic Bt corn. Proc. Natl. Acad. Sci. USA 2020, 117, 18385–18392. [Google Scholar] [CrossRef]
- Tejendra Chapagain, A.R. Barley—pea intercropping: Effects on land productivity, carbon and nitrogen transformations. Field Crops Res. 2014, 166, 18–25. [Google Scholar] [CrossRef]
- Petek, M.; Rotter, A.; Kogovsek, P.; Baebler, S.; Mithofer, A.; Gruden, K. Potato virus Y infection hinders potato defence response and renders plants more vulnerable to Colorado potato beetle attack. Mol. Ecol. 2014, 23, 5378–5391. [Google Scholar] [CrossRef]
- Dong, S.M.; Zhou, S.Q. Potato late blight caused by Phytophthora infestans: From molecular interactions to integrated management strategies. J. Integr. Agric. 2022, 21, 3456–3466. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, M.; Zhang, R.; Zhang, W.; Liu, Y.; Sun, D.; Wang, X.; Qin, S.; Kang, Y. Legume–potato rotations improve soil physicochemical properties, enzyme activity, and rhizosphere metabolism in continuous potato cropping. Chem. Biol. Technol. Agric. 2023, 10, 132. [Google Scholar] [CrossRef]
- Qin, J.; Bian, C.; Duan, S.; Wang, W.; Li, G.; Jin, L. Effects of different rotation cropping systems on potato yield, soil biochemical properties and microbial community. Front. Plant Sci. 2022, 13, 999730. [Google Scholar] [CrossRef] [PubMed]
- Koch, H.J.; Trimpler, K.; Jacobs, A.; Stockfisch, N. Crop rotational effects on yield formation in current sugar beet production–results from a farm survey and field trials. Front. Plant Sci. 2018, 9, 231. [Google Scholar] [CrossRef]
- Kahl, U.; Krüssel, S.; von Tiedemann, A. Development of a decision support system for managing Heterodera schachtii in sugar beet production. J. Nematol. 2019, 14, e2019-05. [Google Scholar]
- Derbyshire, M.C.; Denton-Giles, M.; Hegedus, D.D.; Ford, R.; Cullina, D.; Pena-Ramirez, Y.J.; Bolton, M.D. The control of sclerotinia stem rot on oilseed rape (Brassica napus): Current practices and future opportunities. Plant Pathol. 2016, 65, 1217–1231. [Google Scholar] [CrossRef]
- Paula, S.; Gheorghe, B.A.; Elena, S.; Elena, T.; Mihai, M.M.; Mihai, G.; Andreea, D.C.; Magdalena, I.A.; Adriana, C.I. Crop Rotation Practiced by Romanian Crop Farms before the Introduction of the “Environmentally Beneficial Practices Applicable to Arable Land” Eco-Scheme. Agronomy 2023, 13, 2086. [Google Scholar] [CrossRef]
- AGR108B—Suprafata Cultivata cu Principalele Culturi, pe Judete si Localitati. Available online: http://statistici.insse.ro:8077/tempo-online/#/pages/tables/insse-table (accessed on 2 June 2025).
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 6, 721–741. [Google Scholar] [CrossRef]
- Venugopal, D.; Gogate, V. Dynamic Blocking and Collapsing for Gibbs Sampling. In Proceedings of the Uncertainty in Artificial Intelligence, Bellevue, WA, USA, 11–15 July 2013; pp. 664–673. [Google Scholar]
- Wang, N.Y.; Wu, L. Convergence rate and concentration inequalities for Gibbs sampling in high dimension. arXiv 2014, arXiv:1410.4329. [Google Scholar] [CrossRef]
- Figueira, A.; Vaz, B. Survey on synthetic data generation, evaluation methods and GANs. Mathematics 2022, 10, 2733. [Google Scholar] [CrossRef]
- Pisanti, A.; Magrì, S.; Ferrando, I.; Federici, B. Sea Water Turbidity Analysis from Sentinel-2 Images: Atmospheric Correction and Bands Correlation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, XLVIII-4/W1-2022, 371–378. [Google Scholar] [CrossRef]
- Inglada, J.; Michel, J.; Hagolle, O. Assessment of the Usefulness of Spectral Bands for the Next Generation of Sentinel-2 Satellites by Reconstruction of Missing Bands. Remote Sens. 2022, 14, 2503. [Google Scholar] [CrossRef]
- Gascon, F. Sentinel-2 Products Data Quality and Evolutions; Technical Report; euroSDR: Stuttgart, Germany, 2015. [Google Scholar]
- Schlemmer, M.; Gitelson, A.A.; Schepers, J.S.; Ferguson, R.B.; Peng, Y.; Shanahan, J.F.; Rundquist, D.C. Estimation of nitrogen and chlorophyll content of maize leaves in the field using hyperspectral and multispectral data. Remote Sens. Environ. 2013, 128, 170–178. [Google Scholar]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. In The Annals of Statistics; Institute of Mathematical Statistics: Waite Hill, OH, USA, 2001; pp. 1189–1232. [Google Scholar]
- Feng, H.; Wang, T.; Osborne, S.L.; Kumar, S. Yield and economic performance of crop rotation systems in South Dakota. Agrosystems Geosci. Environ. 2021, 4, e20196. [Google Scholar] [CrossRef]
- Lasisi, A.; Liu, K. A global meta-analysis of pulse crop effect on yield, resource use, and soil organic carbon in cereal-and oilseed-based cropping systems. Field Crops Res. 2023, 294, 108857. [Google Scholar] [CrossRef]
- Agomoh, I.V.; Drury, C.F.; Phillips, L.A.; Reynolds, W.D.; Yang, X. Increasing crop diversity in wheat rotations increases yields but decreases soil health. Soil Sci. Soc. Am. J. 2020, 84, 170–181. [Google Scholar] [CrossRef]
- National Research Council. Committee on the Role of Alternative Farming Methods in Modern Production Agriculture. In Alternative Agriculture; National Academies Press: Washington, DC, USA, 1989. [Google Scholar]
- Zhong, L.; Hu, L.; Zhou, H. Deep learning based multi-temporal crop classification. Remote Sens. Environ. 2019, 221, 430–443. [Google Scholar] [CrossRef]
- Rußwurm, M.; Körner, M. Multi-temporal land cover classification with sequential recurrent encoders. ISPRS Int. J.-Geo-Inf. 2018, 7, 129. [Google Scholar] [CrossRef]
- Hegewald, H.; Wensch-Dorendorf, M.; Sieling, K.; Christen, O. Impacts of break crops and crop rotations on oilseed rape productivity: A review. Eur. J. Agron. 2015, 85, 1–8. [Google Scholar]
- Cai, Y.; Guan, K.; Peng, J.; Wang, S.; Seifert, C.; Wardlow, B.; Li, Z. A high-performance and in-season classification system of field-level crop types using time-series Landsat data and a machine learning approach. Remote Sens. Environ. 2018, 210, 35–47. [Google Scholar] [CrossRef]
- Farooq, M.; Bramley, H.; Palta, J.A.; Siddique, K.H. Heat stress in wheat during reproductive and grain-filling phases. Crit. Rev. Plant Sci. 2011, 30, 491–507. [Google Scholar] [CrossRef]
- Naawe, E.K.; Yavuz, C.; Demirel, U.; Çaliskan, M.E. Effects of Elevated Temperature on Agronomic, Morphological, Physiological and Biochemical Characteristics of Potato Genotypes: 2. Physiological and Biochemical Traits. Potato Res. 2024, 68, 2167–2204. [Google Scholar] [CrossRef]
- Ryo, M. Explainable artificial intelligence and interpretable machine learning for agricultural data analysis. Artif. Intell. Agric. 2022, 6, 257–265. [Google Scholar] [CrossRef]
- Gauriau, O.; Galárraga, L.; Brun, F.; Termier, A.; Davadan, L.; Joudelat, F. Comparing machine-learning models of different levels of complexity for crop protection: A look into the complexity-accuracy tradeoff. Smart Agric. Technol. 2024, 7, 100380. [Google Scholar] [CrossRef]

| To | Wheat | Corn | Pea | Potato | Sugar Beet | Rapeseed | |
|---|---|---|---|---|---|---|---|
| From | |||||||
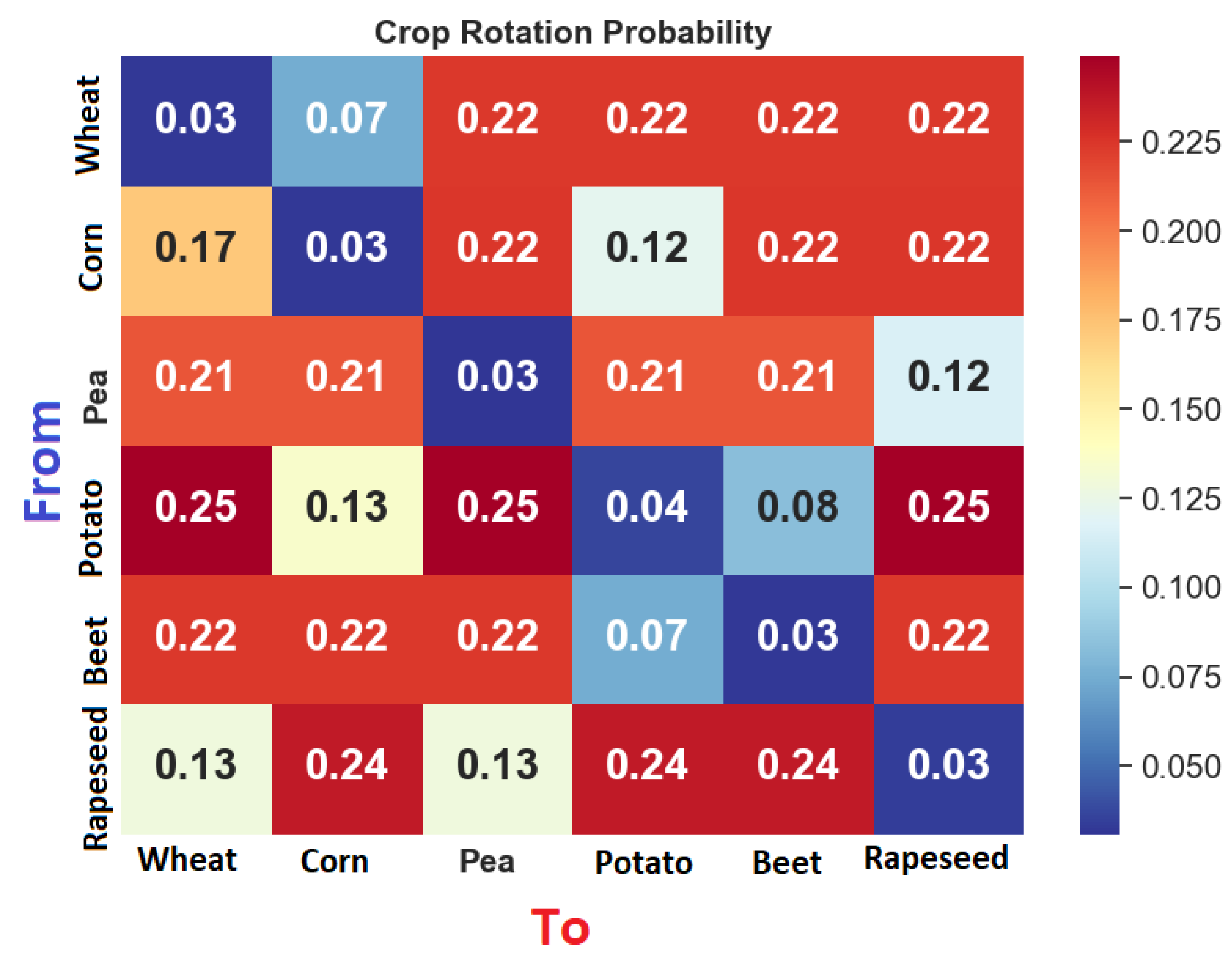
| Wheat | 5 | 4 | 1 | 1 | 1 | 1 | |
| Corn | 2 | 5 | 1 | 3 | 1 | 1 | |
| Pea | 1 | 1 | 5 | 1 | 1 | 3 | |
| Potato | 1 | 3 | 1 | 5 | 4 | 1 | |
| Sugar beet | 1 | 1 | 1 | 4 | 5 | 1 | |
| Rapeseed | 3 | 1 | 3 | 1 | 1 | 5 | |
| Classifier | Rotation Model | Synthetic | Accuracy [%] |
|---|---|---|---|
| XGB | No | No | 56.06 |
| XGB | Post-R0 | No | 55.68 |
| XGB | Post-R1 | No | 63.06 |
| XGB-loss | default | No | 58.54 |
| XGB-loss | def + post-R1 | No | 64.15 |
| XGB-loss | def + post-R1 | Yes | 66.61 |
| RF | No | No | 55.12 |
| RF | Post-R0 | No | 55.36 |
| RF | Post-R1 | No | 63.26 |
| Classifier | Rotation Model | Synthetic | Accuracy [%] |
|---|---|---|---|
| XGB | No | No | 58.25 |
| XGB | Post-R1 | No | 61.90 |
| XGB | Post-R2 | No | 63.26 |
| XGB-loss | default | No | 58.92 |
| XGB-loss | def + post-R2 | No | 61.75 |
| XGB-loss | def + post-R2 | Yes | 67.15 |
| RF | No | No | 58.25 |
| RF | Post-R1 | No | 61.94 |
| Setup/Year | Accuracy [%] | ||||
|---|---|---|---|---|---|
| 2020 | 2021 | 2022 | 2023 | 2024 | |
| Real pixels (no rotation) | 58.25 | 43.38 | 55.12 | 63.89 | 28.80 |
| Real pixels (with rotation) | 61.94 | 45.18 | 63.26 | 62.56 | 34.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Racoviteanu, A.; Nițu, A.; Florea, C.; Ivanovici, M. Crop Identification with Monte Carlo Simulations and Rotation Models from Sentinel-2 Data. AgriEngineering 2025, 7, 259. https://doi.org/10.3390/agriengineering7080259
Racoviteanu A, Nițu A, Florea C, Ivanovici M. Crop Identification with Monte Carlo Simulations and Rotation Models from Sentinel-2 Data. AgriEngineering. 2025; 7(8):259. https://doi.org/10.3390/agriengineering7080259
Chicago/Turabian StyleRacoviteanu, Andrei, Andreea Nițu, Corneliu Florea, and Mihai Ivanovici. 2025. "Crop Identification with Monte Carlo Simulations and Rotation Models from Sentinel-2 Data" AgriEngineering 7, no. 8: 259. https://doi.org/10.3390/agriengineering7080259
APA StyleRacoviteanu, A., Nițu, A., Florea, C., & Ivanovici, M. (2025). Crop Identification with Monte Carlo Simulations and Rotation Models from Sentinel-2 Data. AgriEngineering, 7(8), 259. https://doi.org/10.3390/agriengineering7080259








