Aerodynamic Optimization and Wind Field Characterization of a Quadrotor Fruit-Picking Drone Based on LBM-LES
Abstract
1. Introduction
- A novel approach for studying transient wind fields. We propose a new method for investigating transient wind fields based on LBM-LES. This approach enables more accurate simulation of both large-scale turbulent structures and the microscopic fluid motion, providing improved turbulence information.
- Interaction between drones and tree canopy. By designing a porous medium model to represent the tree canopy surface, we examine the interaction between the harvesting drone and the tree canopy. This interaction is essential for understanding the aerodynamic effects during the harvesting process.
- Experimental validation and aerodynamic optimization. We developed an experimental platform to validate the accuracy of our simulation algorithm. Furthermore, we explored the impact of rotor spacing and duct intake ratio on the drone’s transient wind field and conducted aerodynamic structural optimization for the harvesting drone.
2. Materials and Methods
2.1. Establishment of Drone Model
2.2. Establishment of Drone Wind Field Testing Platform
2.3. LES-LBM Numerical Simulation
2.4. Simulation Boundary Condition Setting
2.4.1. Simulation Parameter Setting
2.4.2. Boundary Setting for the Interaction Model Between the Drone and the Fruit Trees
3. Results and Discussion
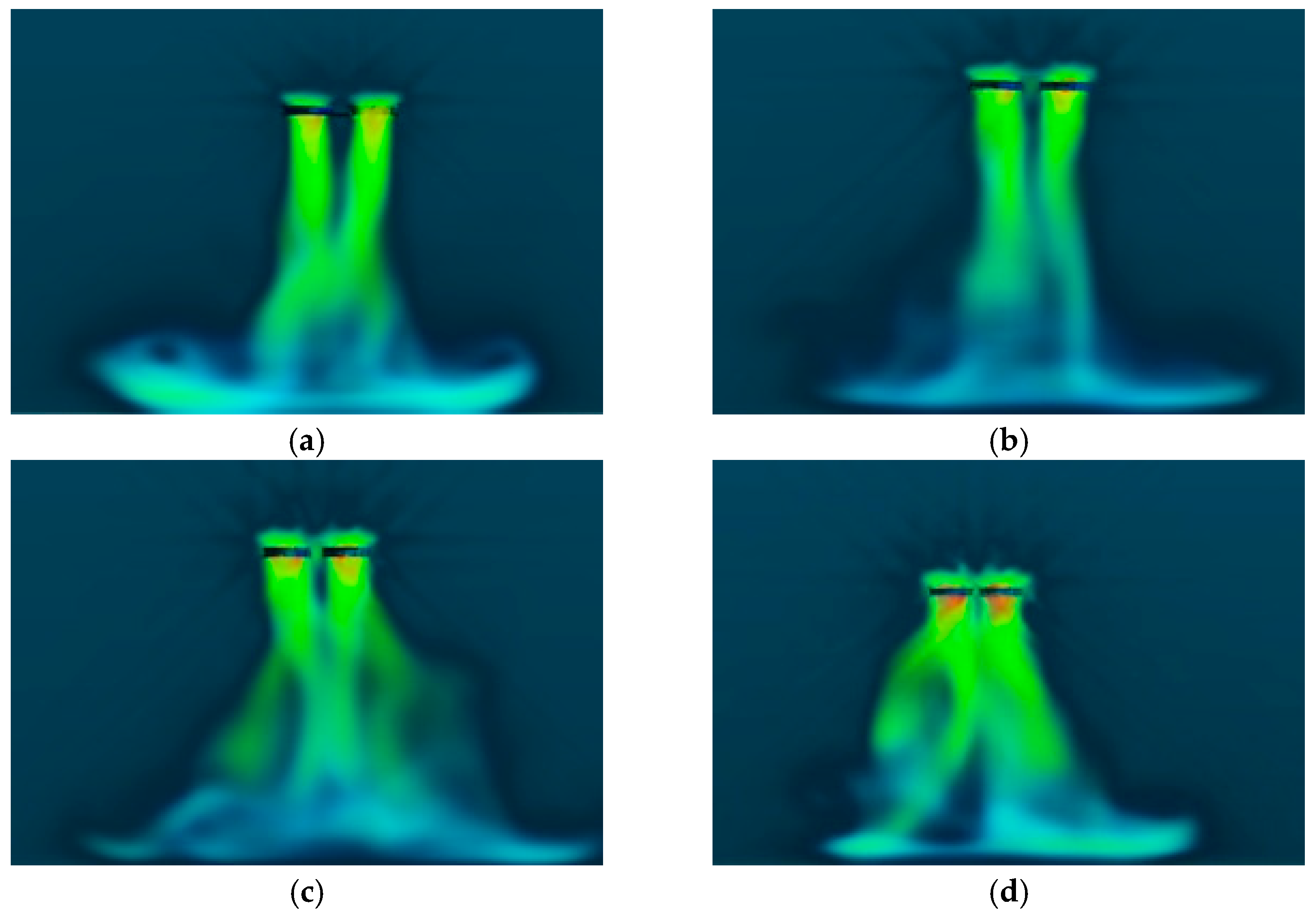
3.1. Interaction Between the Drone and the Canopy Wind Field at Different Distances
- When d = −30 cm, the foliage density is relatively high, causing the dense canopy to absorb part of the kinetic energy, thereby reducing the effective range of the rotor airflow. This leads to increased power consumption when the drone hovers or operates. At this position, the front downwash airflow column undergoes deformation, causing the rear rotor’s downwash airflow to disperse outward, while the front downwash airflow experiences the greatest energy absorption. Consequently, the drone exhibits poor stability and higher power consumption.
- When d = 0 cm, the foliage density decreases slightly, but at this position, the drone enters the vortex ring state. As the airflow interacts with the tree leaves, micro-scale vortices form within the boundary layer of the leaves, enhancing local turbulence intensity. This results in a reduction in lift force and compromises the drone’s stability, requiring continuous rotor speed adjustments to maintain balance.
- When d = 30 cm, the impact of the rotor airflow on the canopy becomes negligible. At this distance, the interaction between the drone’s rotor wind field and the tree canopy can be disregarded.

3.2. Transient Wind Field Simulation Results of the Harvesting Drone
3.3. Aerodynamic Characteristics of the Drone at Different Rotor Spacings
3.3.1. Characteristics of Hovering Downwash Flow Field at Different Rotor Spacings
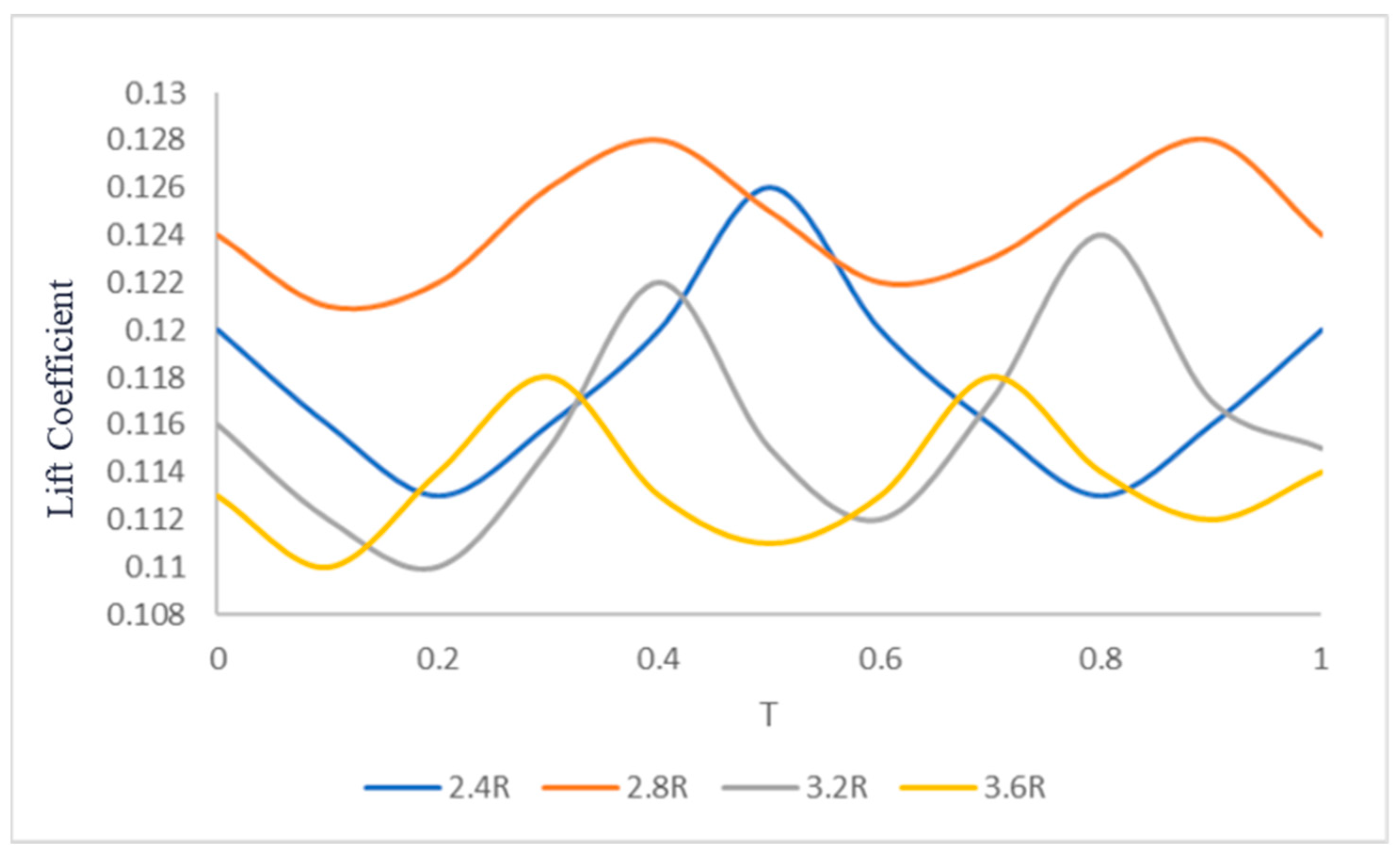
3.3.2. Lift Coefficient at Different Rotor Spacings
3.3.3. Transient Wind Field Analysis of the Drone at Different Rotor Spacings
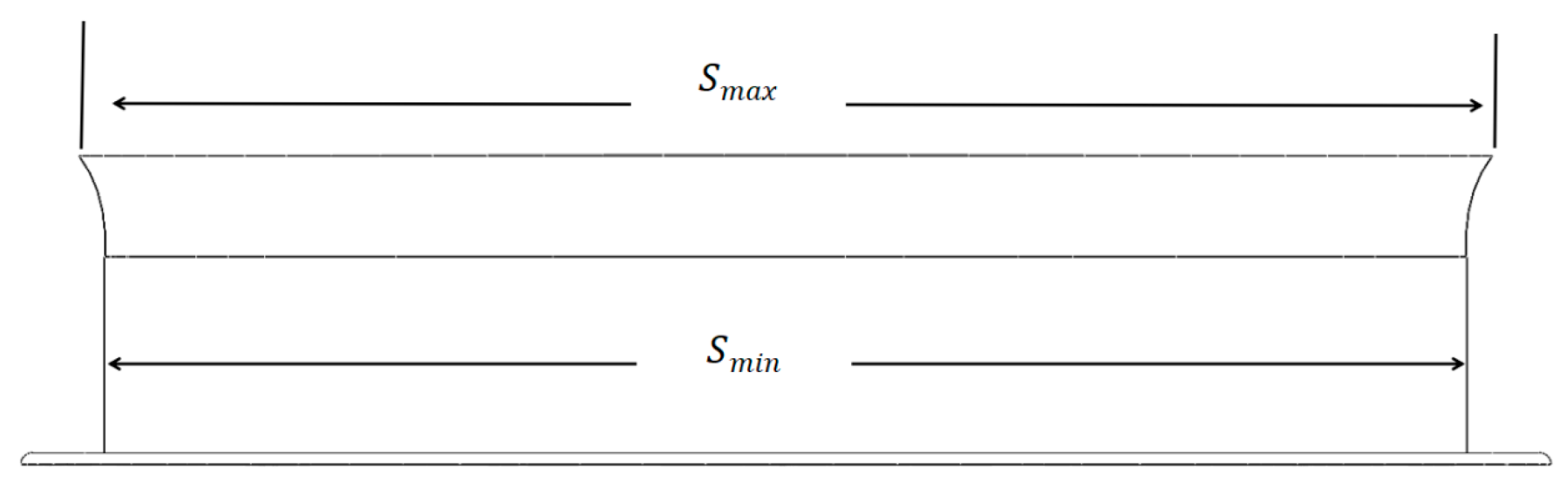
3.4. Aerodynamic Characteristics of Harvesting Drone Under Different Duct Ratios
3.4.1. Analysis of Transient Wind Fields in Harvesting Drone at Different Duct Ratios
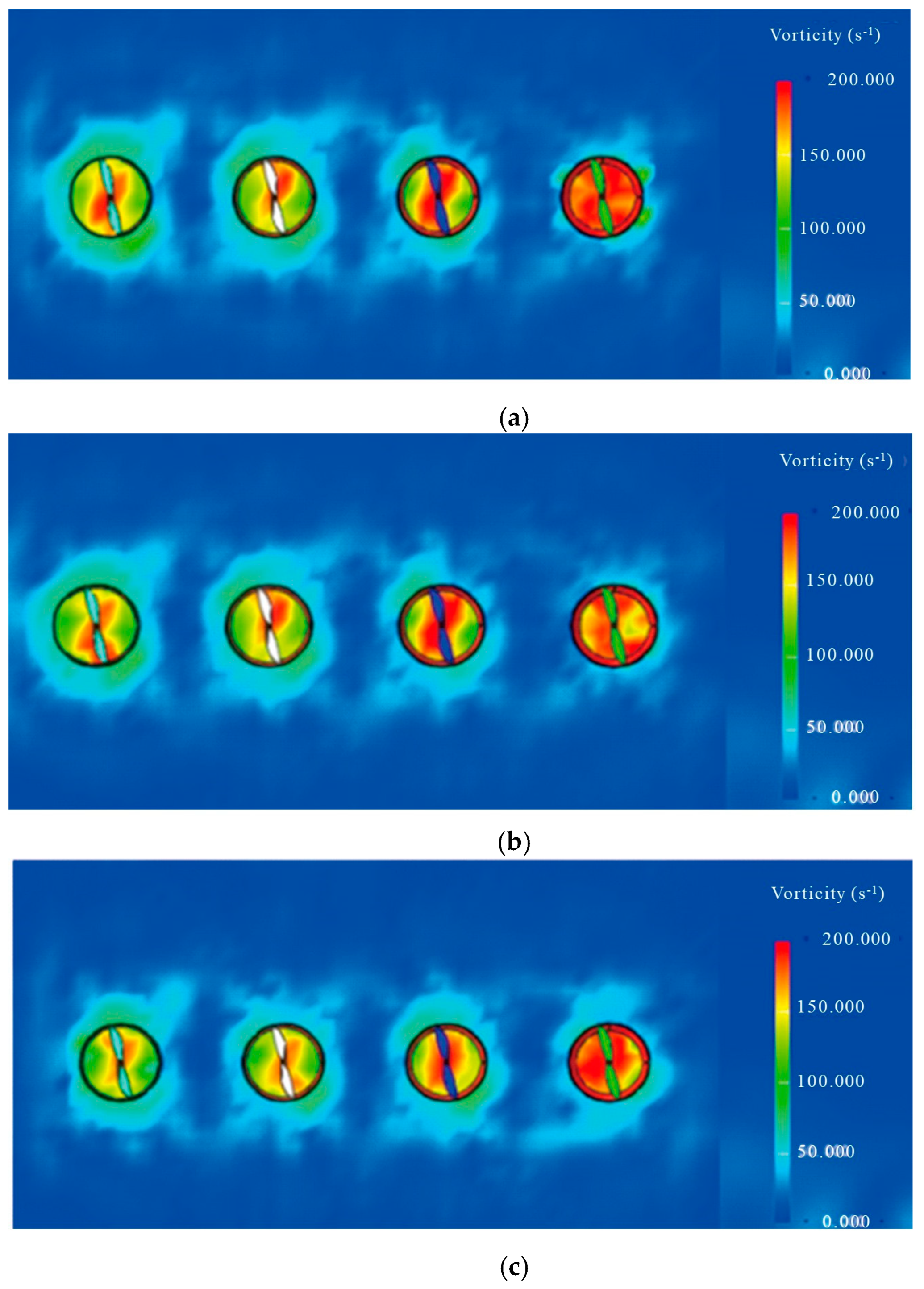
3.4.2. Vorticity Contour Plots of Harvesting Drone Under Different Duct Ratios
3.5. Optimal Structural Configuration of Harvesting Drone
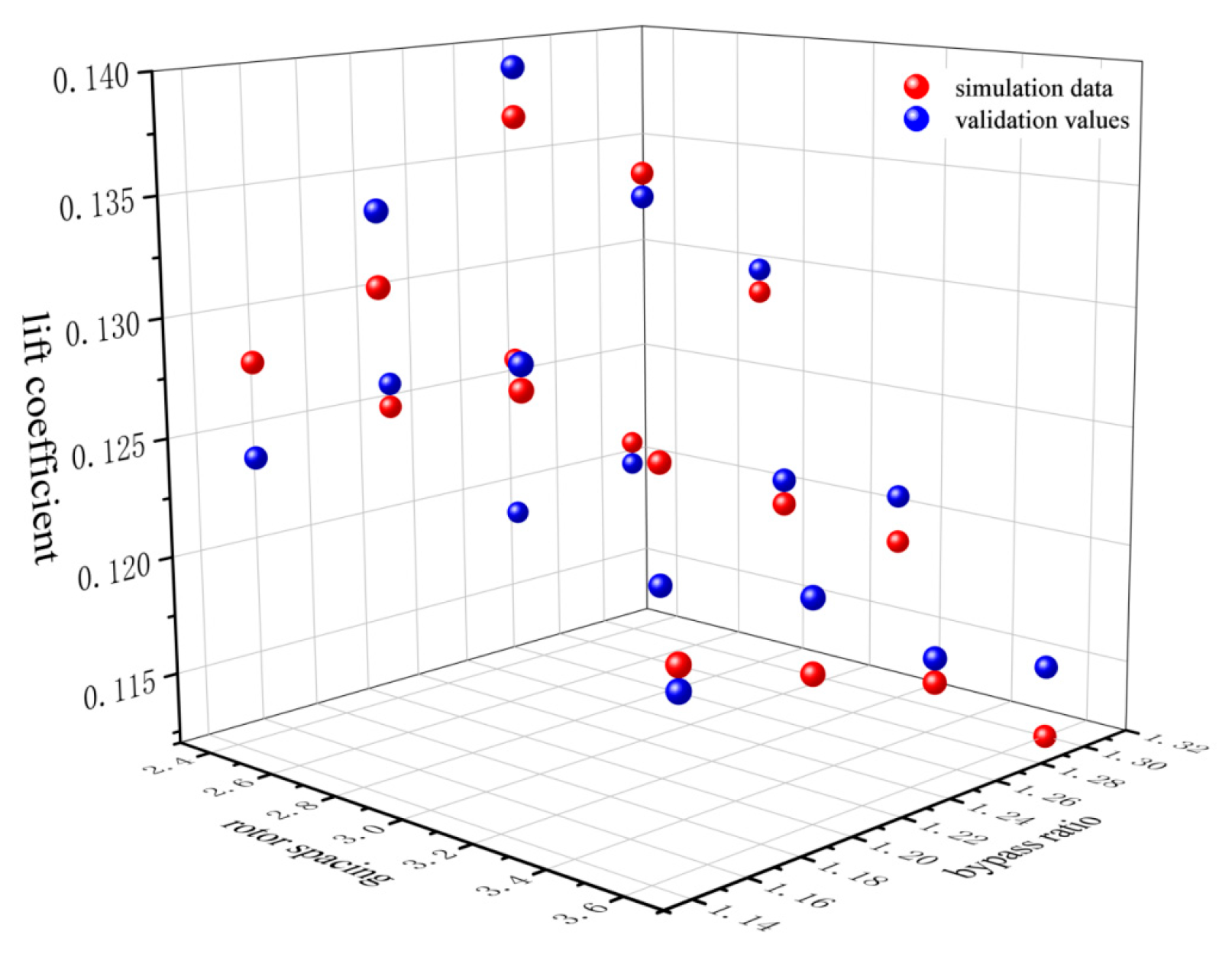
3.6. Experimental Results Validation
4. Conclusions
- The interaction between the harvesting drone and the fruit tree canopy is primarily influenced by the density of the foliage. When the foliage density is high, a significant portion of the airflow energy is dissipated, leading to increased power consumption and reduced flight stability. Upon initial contact between the rotor airflow and the canopy, microscale vortices in the boundary layer intensify local turbulence, causing a reduction in lift force and a degradation of drone stability. However, when the distance between the drone rotor and the canopy exceeds 30 cm, the interaction effect weakens, and the drone maintains better aerodynamic performance.
- Through LES-LBM simulations, it was observed that the transient wind field undergoes significant variations during the harvesting process. However, after the front and rear rotor airflows merge, the downwash flow stabilizes more rapidly. This suggests that adjusting the rotor spacing could enhance the aerodynamic stability of the harvesting drone. The simulation results indicate that when the rotor spacing is set to 2.8R, transient airflow diffusion is minimized, and the wind field stabilizes more efficiently. Furthermore, a comparison of lift coefficients under different rotor spacings revealed that at a rotor spacing of 2.8R, the periodic lift coefficient increases significantly, improving the overall aerodynamic performance of the drone.
- To further improve the aerodynamic stability of the harvesting drone, an optimized ducted rotor design was proposed by adjusting the duct ratio. Simulation experiments demonstrated that when the β = 1.20, the airflow acceleration effect is most pronounced, and the airflow remains more concentrated, indicating that this duct design effectively enhances airflow velocity. Additionally, during the recovery phase, the optimized duct exhibited better airflow retention, and after the drone returned to a horizontal state, the airflow stabilized more rapidly.
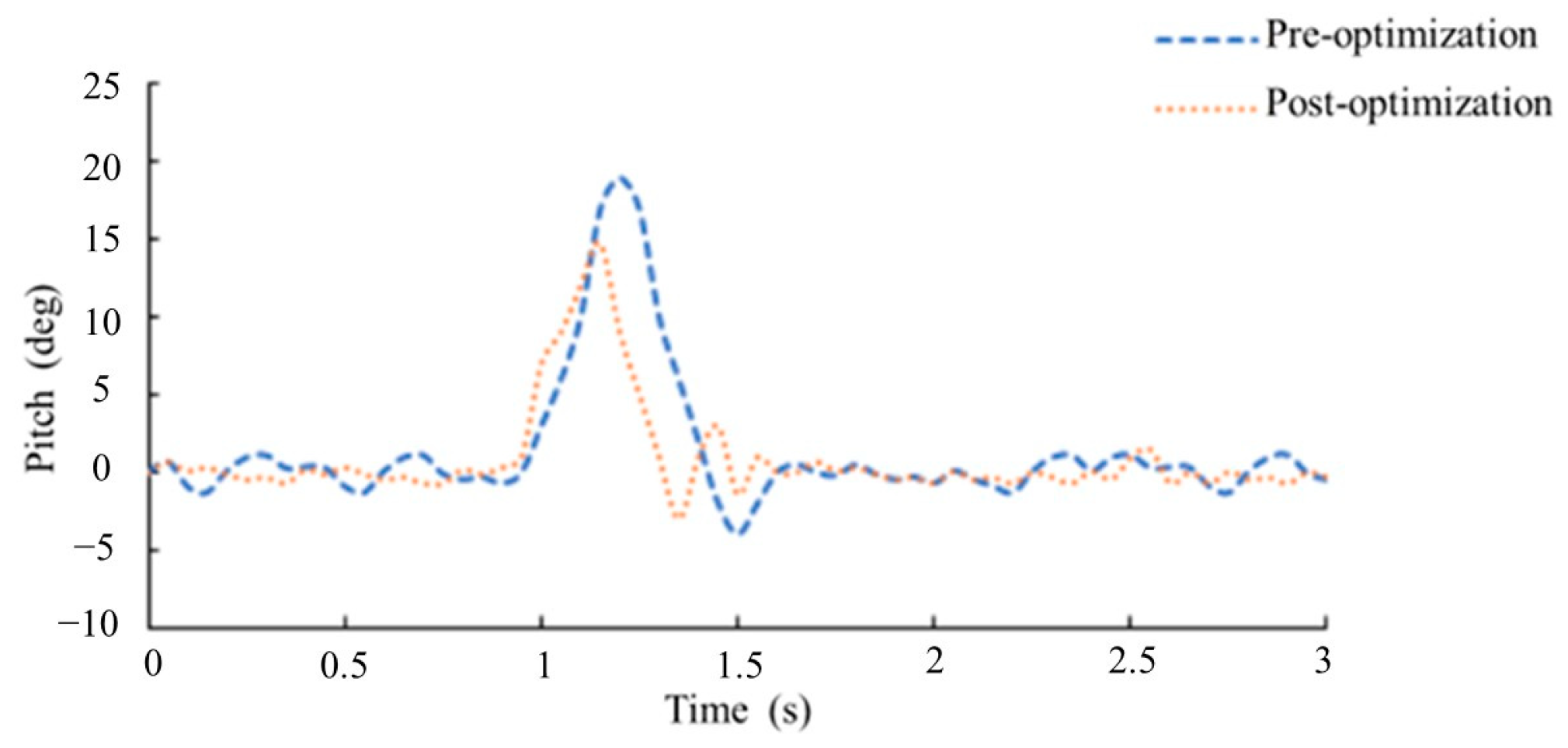
- Based on the optimal rotor spacing and duct ratio, the harvesting drone was reconstructed accordingly. Experimental validation using the harvesting test platform was conducted to compare the attitude function variations before and after optimization. The results showed that the optimized drone achieved a stable horizontal position 0.3 s faster, reduced the maximum pitch angle by 4°, and shortened the adjustment time by 0.4 s. These improvements indicate that the optimized drone can achieve stability more quickly, enhancing operational efficiency and flight performance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Abbreviation | Full Term |
|---|---|
| UAV | Unmanned Aerial Vehicle |
| LBM | Lattice Boltzmann Method |
| LES | Large Eddy Simulation |
| CFD | Computational Fluid Dynamics |
| RPM | Revolutions Per Minute |
| RANS | Reynolds-Averaged Navier-Stokes |
| CAD | Computer-Aided Design |
| XFlow | CFD Simulation Software |
References
- Chen, H.; Lan, Y.; Fritz, B.K.; Hoffmann, W.C.; Liu, S. Review of agricultural spraying technologies for plant protection using unmanned aerial vehicle (UAV). Int. J. Agric. Biol. Eng. 2021, 14, 38–49. [Google Scholar] [CrossRef]
- Yang, S.; Tang, Q.; Zheng, Y.; Liu, X.; Chen, J.; Li, X. Model migration for CFD and verification of a six-rotor UAV downwash. Int. J. Agric. Biol. Eng. 2020, 13, 10–18. [Google Scholar] [CrossRef]
- Carreño, R.M.; Scanavino, M.; D’Ambrosio, D.; Guglieri, G.; Vilardi, A. Experimental and numerical analysis of hovering multicopter performance in low-Reynolds number conditions. Aerosp. Sci. Technol 2022, 128, 107777. [Google Scholar] [CrossRef]
- Zhang, H.; Qi, L.; Wu, Y.; Musiu, E.M.; Cheng, Z.; Wang, P. Numerical simulation of airflow field from a six–rotor plant protection drone using lattice Boltzmann method. Biosyst. Eng 2020, 197, 336–351. [Google Scholar] [CrossRef]
- Wang, G.; Han, Y.; Li, X.; Andaloro, J.; Chen, P.; Hoffmann, W.C.; Han, X.; Chen, S.; Lan, Y. Field evaluation of spray drift and environmental impact using an agricultural unmanned aerial vehicle (UAV) sprayer. Sci. Total Environ. 2020, 737, 139793. [Google Scholar] [CrossRef]
- Guo, Q.W.; Zhu, Y.Z.; Tang, Y.; Hou, C.; He, Y.; Zhuang, J.; Zheng, Y.; Luo, S. CFD simulation and experimental verification of the spatial and temporal distributions of the downwash airflow of a quad-rotor agricultural UAV in hover. Comput. Electron. Agric. 2020, 172, 105343. [Google Scholar] [CrossRef]
- Wang, L.; Xu, M.; Hou, Q.; Wang, Z.; Lan, Y.; Wang, S. Numerical verification on influence of multi-feature parameters to the downwash airflow field and operation effect of a six-rotor agricultural UAV in flight. Comput. Electron. Agric. 2021, 190, 106425. [Google Scholar] [CrossRef]
- Shi, Q.; Liu, D.; Mao, H.; Shen, B.; Li, M. Wind-induced response of rice under the action of the downwash flow field of a multi-rotor UAV. Biosyst. Eng. 2021, 203, 60–69. [Google Scholar] [CrossRef]
- Tang, Q.; Zhang, R.; Chen, L.; Xu, G.; Deng, W.; Ding, C.; Xu, M.; Yi, T.; Wen, Y.; Li, L. High-accuracy, high-resolution downwash flow field measurements of an unmanned helicopter for precision agriculture. Comput. Electron. Agric. 2020, 173, 105390. [Google Scholar] [CrossRef]
- Zhu, Y.; Guo, Q.; Tang, Y.; Zhu, X.; He, Y.; Huang, H.; Luo, S. CFD simulation and measurement of the downwash airflow of a quadrotor plant protection UAV during operation. Comput. Electron. Agric. 2022, 201, 107286. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, R. Effect of wind disturbance on the aerodynamic performance of coaxial rotors during hovering. Meas. Control 2019, 52, 665–674. [Google Scholar] [CrossRef]
- Yao, L.; Wang, Q.; Yang, J.; Zhang, H.; Li, X.; Zhou, Y. UAV-Borne dual-band sensor method for monitoring physiological crop status. Sensors 2019, 19, 816. [Google Scholar] [CrossRef] [PubMed]
- Chang, K.; Chen, S.; Wang, M.; Liao, J.; Liu, J.; Lan, Y. Numerical Simulation and Experimental Verification of Rotor Airflow Field Based on Finite Volume Method and Lattice Boltzmann Method. Drones 2024, 8, 612. [Google Scholar] [CrossRef]
- Tang, Q.; Chen, L.P.; Zhang, R.R.; Xu, G.; Deng, W.; Ding, C. Effects of application height and crosswind on the crop spraying performance of unmanned helicopters. Comput. Electron. Agric. 2021, 181, 105961. [Google Scholar] [CrossRef]
- Zhan, Y.; Chen, P.; Xu, W.; Liu, X.; Li, X.; Wang, Z. Influence of the downwash airflow distribution characteristics of a plant protection UAV on spray deposit distribution. Biosyst. Eng. 2022, 216, 32–45. [Google Scholar]
- Zhang, H.; Qi, L.; Wan, J.; Cheng, Z.; Wang, P.; Li, X. Numerical simulation of downwash airflow distribution inside tree canopies of an apple orchard from a multirotor unmanned aerial vehicle (UAV) sprayer. Comput. Electron. Agric. 2022, 195, 106817. [Google Scholar]
- Haddadi, S.; Zarafshan, P.; Dehghani, M. A coaxial quadrotor flying robot: Design, analysis and control implementation. Aerosp. Sci. Technol. 2022, 120, 107260. [Google Scholar] [CrossRef]
- Del Cerro, J.; Cruz Ulloa, C.; Barrientos, A.; de León Rivas, J. Unmanned Aerial Vehicles in Agriculture: A Survey. Agronomy 2021, 11, 203. [Google Scholar] [CrossRef]
- Li, J.; Shi, Y.; Lan, Y.; Guo, S. Vertical distribution and vortex structure of rotor wind field under the influence of rice canopy. Comput. Electron. Agric. 2019, 159, 140–146. [Google Scholar] [CrossRef]
- Hu, H.; Yang, Y.; Liu, Y.; Liu, X.; Wang, Y. Aerodynamic and aeroacoustic investigations of multi-copter rotors with leading edge serrations during forward flight. Aerosp. Sci. Technol. 2021, 112, 106669. [Google Scholar]
- Tang, D.; Tang, B.; Shen, W.; Zhu, K.; Quan, Q.; Deng, Z. On genetic algorithm and artificial neural network combined optimization for a Mars rotorcraft blade. Acta Astronaut. 2023, 203, 78–87. [Google Scholar]
- Zhang, Z.; Ma, H. Application of Phase-Locked PIV Technique to the Measurements of Flow Field in a Turbine Stage. J. Therm. Sci. 2020, 29, 784–792. [Google Scholar]
- Tanabe, Y.; Sugawara, H.; Sunada, S.; Yonezawa, K.; Tokutake, H. Quadrotor Drone Hovering in Ground Effect. J. Robot. Mechatron 2021, 33, 339–347. [Google Scholar]
- Chatila, J.G.; Danageuzian, H.R. PIV and CFD investigation of paddle flocculation hydrodynamics at low rotational speeds. Sci. Rep. 2022, 12, 19742. [Google Scholar]
- Li, Y.; Yonezawa, K.; Liu, H. Effect of Ducted Multi-Propeller Configuration on Aerodynamic Performance in Quadrotor Drone. Drones 2021, 5, 101. [Google Scholar] [CrossRef]
- Kostic, I.; Tanovic, D.; Kostic, O.; Abubaker, A.A.I.; Simonovic, A. Initial development of tandem wing UAV aerodynamic configuration. Aircr. Eng. Aerosp. Technol. 2023, 95, 431–441. [Google Scholar]
- Cipolla, V.; Dine, A.; Viti, A.; Binante, V. MDAO and Aeroelastic Analyses of Small Solar-Powered UAVs with Box-Wing and Tandem-Wing Architectures. Aerospace 2023, 10, 105. [Google Scholar] [CrossRef]
- Zhang, Q.; Xue, R.; Li, H. Aerodynamic Exploration for Tandem Wings with Smooth or Corrugated Surfaces at Low Reynolds Number. Aerospace 2023, 10, 427. [Google Scholar] [CrossRef]
- Ventura Diaz, P.; Yoon, S. High-Fidelity Simulations of a Quadrotor Vehicle for Urban Air Mobility. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar]
- Chen, Q.; Zhang, J.; Zhang, C.; Zhou, H.; Jiang, X.; Yang, F.; Wang, Y. CFD Analysis and RBFNN-Based Optimization of Spraying System for a Six-Rotor Unmanned Aerial Vehicle (UAV) Sprayer. Crop Prot. 2023, 174, 106433. [Google Scholar]
- Wang, H.P.; Sun, W.H.; Zhao, C.L.; Zhang, S.J.; Han, J.D. Dynamic Modeling and Control for Tilt-Rotor UAV Based on 3D Flow Field Transient CFD. Drones 2022, 6, 338. [Google Scholar] [CrossRef]
- Paz, C.; Suárez, E.P.; Gil, C.; Vence, J. Assessment of the Methodology for the CFD Simulation of The Flight of a Quadcopter UAV. J. Wind Eng. Ind. Aerodyn. 2021, 218, 104776. [Google Scholar] [CrossRef]
- Abichandani, P.; Lobo, D.; Ford, G.; Bucci, D.; Kam, M. Wind Measurement and Simulation Techniques in Multi-Rotor Small Unmanned Aerial Vehicles. IEEE Access 2020, 8, 54910–54927. [Google Scholar]
- Chen, P.; Douzals, J.P.; Lan, Y.; Cotteux, E.; Delpuech, X.; Pouxviel, G.; Zhan, Y. Characteristics of unmanned aerial spraying systems and related spray drift: A review. Front. Plant Sci. 2022, 13, 870956. [Google Scholar]
- Ni, M.; Wang, H.J.; Liu, X.D.; Liao, Y.L.; Fu, L.; Wu, Q.Q.; Mu, J.; Chen, X.Y.; Li, J. Design of Variable Spray System for Plant Protection UAV Based on CFD Simulation and Regression Analysis. Sensors 2021, 21, 638. [Google Scholar] [CrossRef] [PubMed]
- Mohebbi, M.; Rezvani, M.A. Analysis of the effects of lateral wind on a high speed train on a double routed railway track with porous shelters. J. Wind. Eng. Ind. Aerodyn. 2019, 184, 116–127. [Google Scholar] [CrossRef]
- Dbouk, T.; Drikakis, D. Quadcopter Drones Swarm Aeroacoustics. Phys. Fluids 2021, 33, 057112. [Google Scholar]
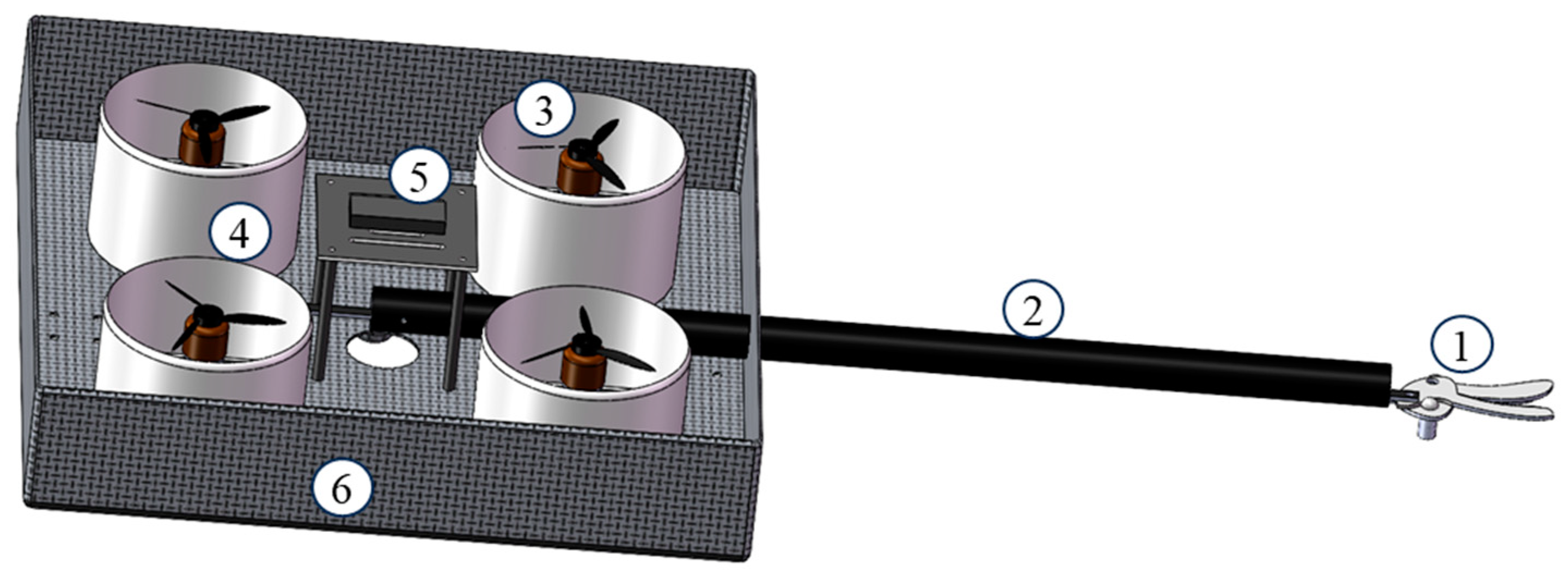
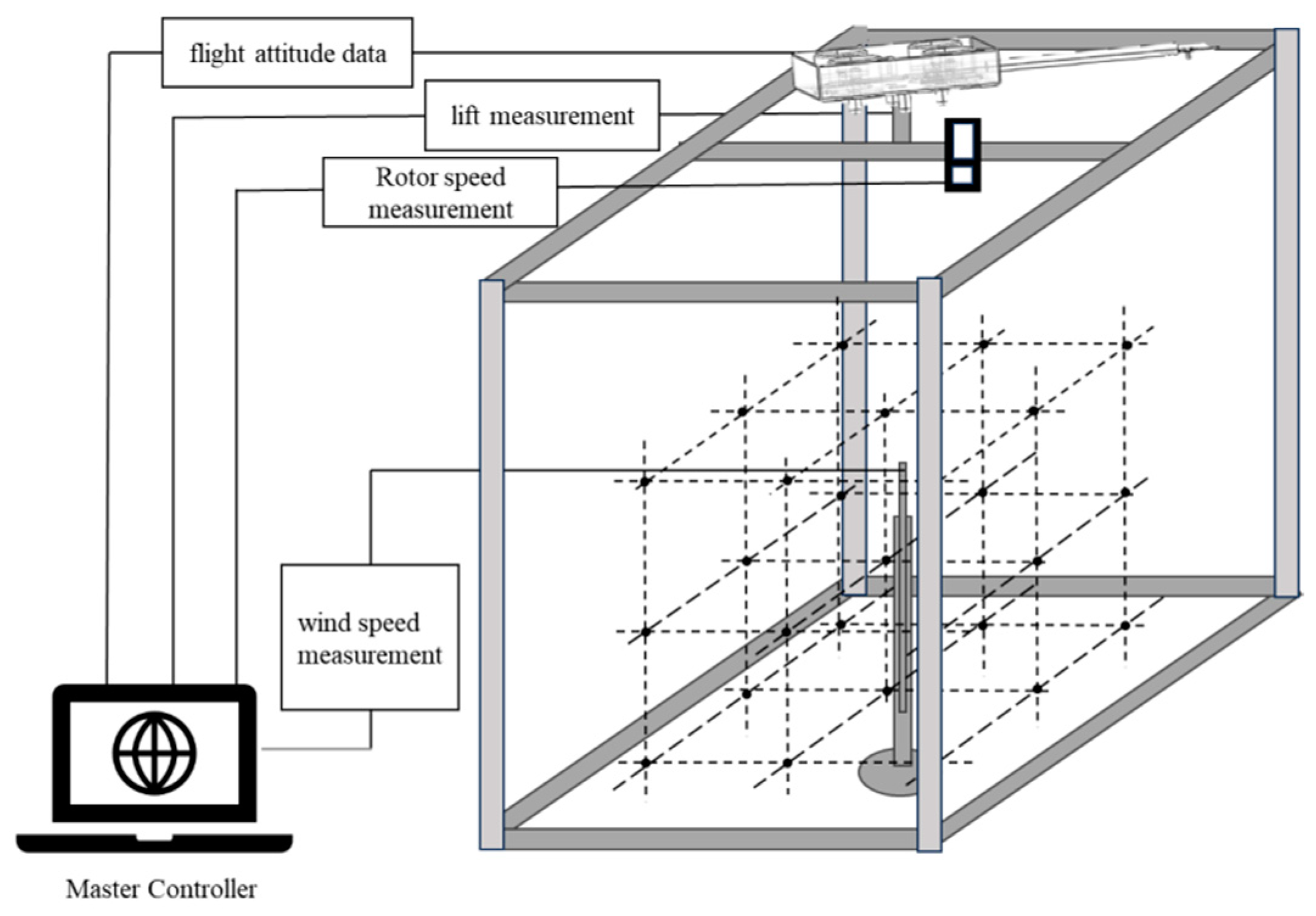
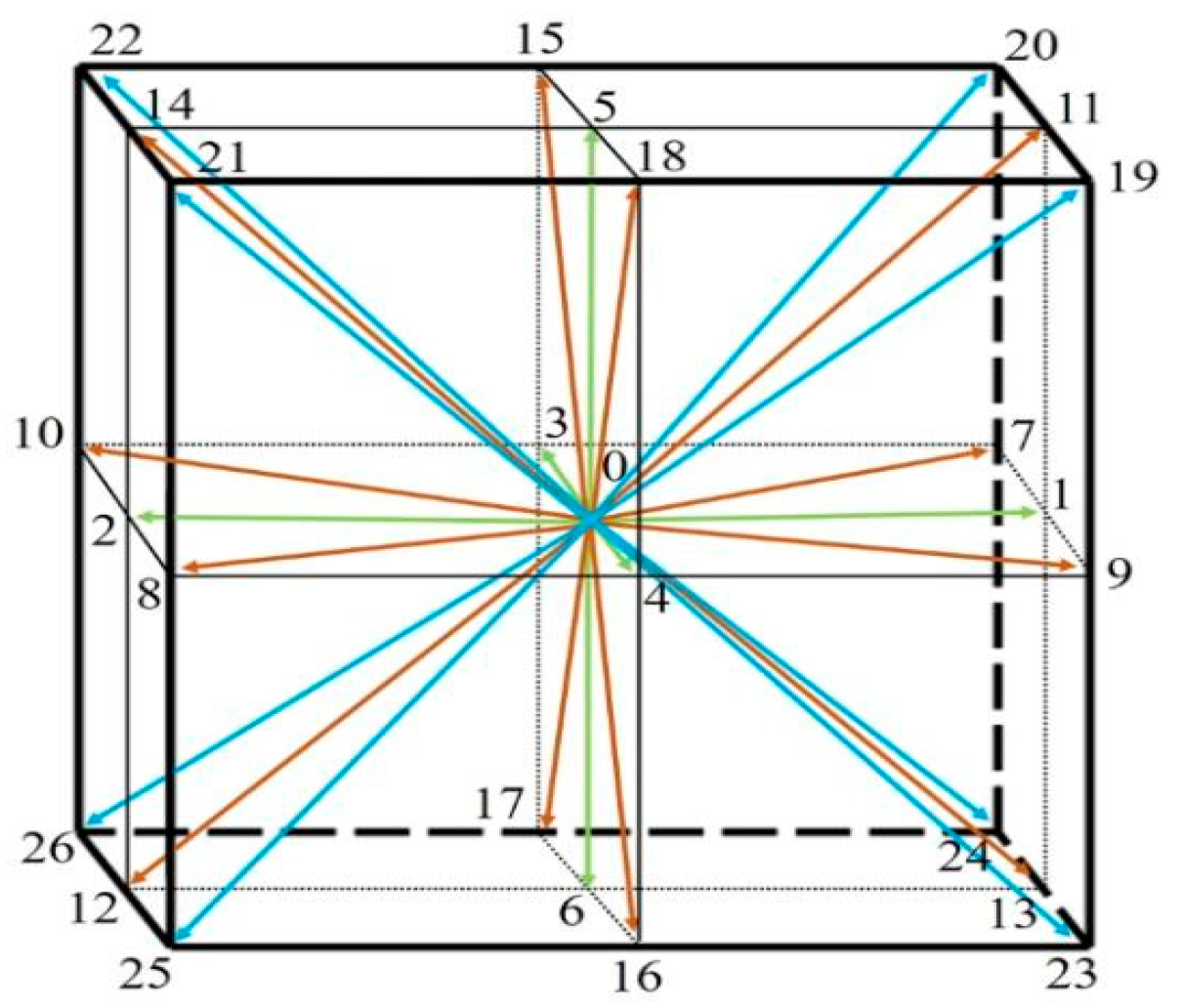









| Project Parameters | Value |
|---|---|
| Drone Weight | 2.38 kg |
| Fuselage Length | 610 mm |
| Fuselage Width | 670 mm |
| Harvesting Rod Extension Distance | 500 mm |
| Symmetrical Motor Spacing | 595 mm |
| Number of Rotors | 4 |
| Rotor Diameter | 337 mm |
| Measurement Device | Measurement Range | Resolution | Accuracy | Other Specifications |
|---|---|---|---|---|
| Tensile Sensor | 0–10 kg | 0.01 | 0.3% | Combined error: ≤±0.3%; Sensitivity: 1.0/2.0 ± 10% mV/V |
| Rotational Speed Measurement | 2.5–99,999 RPM | 0.01 | ±0.5% + 1 | Sampling rate: 0.5 sample/s Testing distance: 50–500 mm |
| Thermosensitive Anemometer Probe | 0.1–30.0 m/s 0–50 °C 0–9999 m3/min | 0.01 | ±0.5% + 1 | Measurement area: 0.999 ft2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Tan, Y.; Lin, Y.; Pan, Z.; Wang, L.; Liu, Z.; Yang, Y.; Chen, L.; Peng, X. Aerodynamic Optimization and Wind Field Characterization of a Quadrotor Fruit-Picking Drone Based on LBM-LES. AgriEngineering 2025, 7, 100. https://doi.org/10.3390/agriengineering7040100
Zhou Z, Tan Y, Lin Y, Pan Z, Wang L, Liu Z, Yang Y, Chen L, Peng X. Aerodynamic Optimization and Wind Field Characterization of a Quadrotor Fruit-Picking Drone Based on LBM-LES. AgriEngineering. 2025; 7(4):100. https://doi.org/10.3390/agriengineering7040100
Chicago/Turabian StyleZhou, Zhengqi, Yonghong Tan, Yongda Lin, Zhili Pan, Linhui Wang, Zhizhuang Liu, Yu Yang, Lizhi Chen, and Xuxiang Peng. 2025. "Aerodynamic Optimization and Wind Field Characterization of a Quadrotor Fruit-Picking Drone Based on LBM-LES" AgriEngineering 7, no. 4: 100. https://doi.org/10.3390/agriengineering7040100
APA StyleZhou, Z., Tan, Y., Lin, Y., Pan, Z., Wang, L., Liu, Z., Yang, Y., Chen, L., & Peng, X. (2025). Aerodynamic Optimization and Wind Field Characterization of a Quadrotor Fruit-Picking Drone Based on LBM-LES. AgriEngineering, 7(4), 100. https://doi.org/10.3390/agriengineering7040100







