Abstract
This paper presents research on the impact of vibrations on the hand–arm and body system of agricultural tractor operators as ergonomic indicators in relation to certain operational parameters. The measurements were conducted on a LANDINI POWERFARM 100 tractor on agricultural production areas and access roads of the Agricultural and Veterinary School in Osijek. The measurements followed the ISO 5008:2015 standard, which describes the creation of test tracks: a smooth track of 100 m in length and a rough track of 35 m in length. Body vibration measurements were conducted according to the prescribed standards HRN ISO 2631-1: 1999/A1:2019 and HRN ISO 2631-4:2010. Hand–arm system vibration measurements were performed according to the prescribed standards HRN ISO 5349-1:2008 and HRN ISO 5349-2:2008/A1:2015. After the measured data were processed, a three-factor analysis of variance was performed, where some operational parameters were designated as A—agrotechnical surfaces (6 types), B—tractor speed (6 speeds), and C—tire air pressure (3 pressures), along with multiple regression analysis and the AHP (analytical hierarchical process). This research determined that none of the measured hand–arm system vibrations exceeded the warning (2.5 ms−2) or limit (5 ms−2) values of daily exposure. Furthermore, vibrations affecting the operator’s body in the x-axis at higher speeds and pressures C2 and C3, in the y-axis at higher speeds and pressures C1 and C2, and in the z-axis at the highest speed and pressures C1 and C2 were found to exceed the daily exposure warning value of 0.5 ms−2. It was concluded that the operator’s health is at risk, and it is recommended that the seat’s air suspension system be inspected to prevent further complications in a timely manner.
1. Introduction
Every motion that repeats within a certain time frame is called a vibration. Vibrations in machines are those originating from the engine and transmitted to the machine [1]. The human body perceives and absorbs vibrations ranging from 1 to 1000 Hz [2]. Operators’ exposure to vibrations can be categorized into three groups: those causing fatigue and reducing work efficiency, those adversely affecting the worker’s health at a specific workplace, and those impairing comfort at the workplace [3,4]. Vibrations at the workstation of an agricultural tractor operator result from the interaction of motion, terrain, the operation of attached implements, and the tractor’s powertrain system [5,6,7]. Furthermore, the same vibrations are transmitted to the entire operator’s body via the steering wheel, control levers, pedals, seat, and cabin floor [8].
The levels of vibrations produced during tractor operation often exceed internationally accepted limits and can be classified as sinusoidal (indirect) and random (direct) vibrations (HRN ISO 2631-1:1999/A1:2019 [9]). Mechanical vibrations affecting tractor operators are divided into two groups: linear and rotational (or angular) vibrations [10]. General vibrations occur when the operator is in a vibrating environment, influencing the entire body. Linear vibrations (longitudinal, x; lateral, y; and vertical, z) are transmitted to the operator in the respective directions within a spatial coordinate system with its origin near the heart. Accordingly, vibrations are classified into three components: z, x, and y. Unlike general vibrations, which affect the whole body, localized vibrations act on specific body parts, with their direction determined by three axes. Vibrations impacting the hand–arm system are mostly caused by handheld electric or pneumatic tools, machine controls, and similar equipment [11].
According to the Croatian Health Insurance Fund, the most commonly diagnosed occupational diseases in Croatia include conditions caused by harmful vibrations [12]. Hand–Arm Vibration Syndrome (HAVS), also known as white finger syndrome, poses a serious health issue, with most professional forestry workers experiencing some consequences of vibration syndrome [13]. Intense low-frequency vibrations transmitted to the hands and arms can also lead to degenerative changes in the hand bones, finger joints, wrists, elbows, and shoulders. The most effective vibration dampers in the human body are the joints and air cavities; besides frequency characteristics, two additional parameters are crucial for assessing vibration exposure risks: vibration levels (intensity) and exposure duration [11,14].
Injuries to the hip, neck, buttocks, and spine in tractor operators are the result of exposure to vibrations transmitted to the operator’s torso and the unfavorable physiological posture adopted while sitting in the tractor during agricultural operations [15]. Vibrations transmitted to the operator’s torso occur when the body rests on a vibrating surface (e.g., when the operator sits on a vibrating seat, stands on a vibrating floor, or lies on a vibrating surface) [16]. The negative impact of mechanical vibrations at the workstation of an agricultural tractor operator is mitigated through seat and cabin suspension, as well as suspension of the tractor’s front axle. The most widespread method of protecting the operator from mechanical vibrations is through seat suspension, as this type of suspension offers advantages such as simpler construction, higher reliability, easier maintenance, and lower cost compared to the other aforementioned methods [16].
Modern tractors are often equipped with various components, such as vibration dampers, to reduce the vibrations transmitted to the operator [17,18,19]. The use of modern low-pressure tires positively affects vibration levels, as reducing air pressure in the tires decreases the level of vibrations.
Factors contributing to the occurrence of vibrations are directly related to the forces and moments generated in the engine during operation, the method of engine installation, and the transmission of vibrations from the engine through the transmission system and structure to the operator’s seat [20,21].
According to the Occupational Safety Ordinance (Official Gazette, 155/2008) [22], the limit and warning values of vibration exposure are as follows:
- Vibrations affecting the operator’s hand–arm system (the daily exposure limit value, normalized to an eight-hour reference period, is 5 ms−2, and the daily exposure warning value is 2.5 ms−2).
- Vibrations affecting the operator’s torso (the daily exposure limit value, normalized to an eight-hour reference period, is 1.15 ms−2, and the daily exposure warning value is 0.5 ms−2).
Deboli et al. [23] investigated vibrations generated by four tractors equipped with different tires while driving on three different surfaces (macadam, asphalt, and a combination of macadam and asphalt, where two wheels moved on macadam and the other two on asphalt). Regardless of tire type, all measured vibrations were lowest on asphalt. Servadio et al. [24] studied vibration levels transmitted to the operator’s body on asphalt while the tractor was in motion. Measurements were taken on tractors with two different types of tires at speeds of 11.1 and 13.9 ms−1. The measured values did not exceed the permissible limits. Vibration levels affecting the operator’s torso and the potential for vibration absorption were examined using a hydraulic system. Their results indicate that during operation with a tractor aggregated with mounted implements, vibration levels increased [25]. Langer et al. [26] observed that vibration levels increase or decrease depending on the terrain. Driving uphill and downhill with four-wheel drive caused the most significant increase in vibration levels compared to driving on flat terrain. In a study of vibration levels affecting operators on a cables tractor (manufactured in 1997) and a cab-equipped tractor (manufactured in 2014), it was concluded that vibration levels did not exceed the permissible limits for operator exposure [27]. In a study of vibrations affecting the operator’s torso and hand–arm system on tractors moving over various agricultural surfaces, it was reported that all measured vibration levels were below the allowed 1.15 ms−2 (body) and 5.0 ms−2 (hand–arm system) [28].
Studies were conducted on macadam with a two-wheel tractor at three speeds (1.11, 1.71, and 2.31 ms−1) during transportation and three speeds (0.30, 0.45, and 0.63 ms−1) during soil tillage, in all three axes. The vibration level reached 5.52 ms−2 during transportation and 8.07 ms−2 during soil tillage [29]. Investigating seat-transmitted vibrations, transmitted to the operator’s whole body from the seat, Dewangan et al. [30] noted lower vibration levels transmitted to the operator when using seats made of polyurethane foam compared to those with air suspension. In an analysis of vibrations on the operator’s hand–arm system during spraying and mulching, it was concluded that vibration levels did not exceed permissible values [31]. In measurements of torso vibrations during two agricultural operations, the 2017 measurements showed slight axis-specific differences (0.05 to 0.11 ms−2), unlike the subsequent year when vibration levels increased but still remained below the allowed limit of 1.15 ms−2 [32]. Scarlett et al. [33] researched vibrations acting on the operator’s whole body as a result of tractor operation during four agrotechnical operations and determined that vibrations were in the x-axis direction, most during the agrotechnical operation of transport.
Determining the impact of vibrations on the hand–arm system, [34,35] conducted research on two tractors with the same characteristics while moving on four agrotechnical surfaces, at two speeds (13 and 20 kmh−1) and two tire pressures (0.9 and 1.6 bar). The highest measured vibration values were recorded on a smooth test track at all speeds and tire pressures, while the lowest values were recorded on an asphalt surface. Comparing similar surfaces, such as a field road and a grassy surface, as well as asphalt and the test track, it is evident that higher vibration values were observed on the field road at a tire pressure of 1.6 bar (at all speeds) and at a pressure of 0.9 bar (at a speed of 13 kmh−1). Analyzing the surfaces or vibration levels when driving on a field road, grassy surface, and smooth test track, it is evident that they correlate with one another (excluding the asphalt surface). It is noticeable that the vibration level on all surfaces, at all tractor speeds and tire pressures, exceeded the permissible vibration value of 1.15 ms−2, except on the asphalt surface. Research was conducted to measure the level of vibrations affecting the operator’s body on three tractors with different power ratings, moving on different surfaces (grass surface, disked surface, asphalt surface, field road, and smooth test track) and at different speeds (10, 14, 30, and 41 kmh−1). The results indicate that none of the vibration values exceeded the permissible limit of 1.15 ms−2. The aim of this study was to establish that a smooth test track can simulate similar surfaces, i.e., vibration levels on the same surfaces [36]. Vallone et al. [37] examined the daily vibration exposure values for operators at their workplace. The study was conducted on six tractors and three locations. The results show that the vibrations on all tractors exceeded the daily operator exposure value (0.5 ms−2). For two tractors, the daily vibration exposure limit of 1.15 ms−2 was exceeded, regardless of soil type. The vibration that affects the hand–arm system during various agrotechnical operations (4) and tractor speeds (5) was measured, and it was in the range of 2.11 to 2.52 ms−2. The measured vibration levels affecting the operator’s body ranged from 0.54 to 0.82 ms−2. It was determined that the vibration levels did not exceed the permissible vibration limits of 5 ms−2 (hand–arm system of the operator) and 1.15 ms−2 (operator’s body) [37]. The issue of the impact of vibrations on the operator’s body and hand–arm system was researched on six operators during grass mowing. It was determined that the vibration value affecting the hand–arm system of one operator exceeded the permissible limit of 5 ms−2 by 0.06 ms−2. For other operators, the vibration levels were below the permissible limit. The vibration values affecting the operator’s body for all operators did not exceed the permissible limit of 1.15 ms−2 [38].
Researchers investigated the impact of seat suspension, agrotechnical surface, tractor speed, and tire pressure on the vibration levels affecting the operator’s body. The research was conducted on a tractor with pneumatic seat suspension, which moved across various agrotechnical surfaces (asphalt, disked surface, grass surface, and field road) with different tire pressures (0.9 and 1.6 bar) and at different tractor speeds (2.78 and 5.56 ms−1). The lowest measured vibration values affecting the operator’s body at a speed of 2.78 ms−1 and a tire pressure of 0.9 bar were on the asphalt surface in the x-axis direction (0.93 ms−2), y-axis direction (0.87 ms−2), and z-axis direction (0.42 ms−2). The highest vibration values were measured on the disked surface in the x-axis direction (1.60 ms−2) and z-axis direction (0.79 ms−2), with the y-axis direction reaching 1.42 ms−2, and these were observed on the field road. When measuring vibrations at the same tractor speed of 2.78 ms−1 and a tire pressure of 1.6 bar, the lowest values were again recorded on the asphalt surface in the x-axis direction (0.93 ms−2), y-axis direction (0.85 ms−2), and z-axis direction (0.59 ms−2), while the highest values were recorded on the disked surface in the x-axis direction (1.63 ms−2) and y-axis direction (1.38 ms−2), with the highest values on the field road in the z-axis direction (0.72 ms−2). At a tractor speed of 5.56 ms−1 and tire pressure of 1.6 bar, the lowest vibration levels were measured on the asphalt surface in the x-axis direction (1.37 ms−2), on the grass surface in the y-axis direction (1.48 ms−2), and on the disked surface in the z-axis direction (0.65 ms−2). The highest vibration levels at the same tractor speed were measured on the disked surface in the x-axis direction (2.40 ms−2), on the asphalt surface in the y-axis direction (1.96 ms−2), and on the field road in the z-axis direction (0.75 ms−2). Vibration values exceeded the permissible limit (1.15 ms−2) at all speeds, pressures, and surfaces, except at a tire pressure of 0.9 and 1.6 bar and a speed of 2.78 ms−1 on the asphalt surface in the x-axis and y-axis directions, as well as on all surfaces in the z-axis direction, and at a speed of 5.56 ms−1 on all surfaces in all three axes [39].
Yuan and Wu [40] researched how to create a vibration diagnostic optimization model for failures in all types of rotating machines using the Analytical Hierarchy Process (AHP). The machines were divided into two groups: group 1 (class 1—small machines with an electric motor of 15 kW; class 2—medium machines with an electric motor of 15—75 kW) and group 2 (class 3—large machines on rigid foundations; class 4—large machines on soft foundations). Furthermore, they tested two models on machines of the first and second classes (group 1) and the third and fourth classes (group 2). It was found that the most applicable models were the following: model 2 for group 1 machines and model 1 for group 2 machines.
In a study of workers exposed to vibrations for eight hours, and who produce tools with a risk to their health, the AHP was applied to the design of handheld machines with the aim of reducing vibrations. The aim of the study was to obtain an instrument that would help in the production of brushcutters, specifically, for an Italian company. The analysis showed that in order to reduce vibrations, it is necessary to perform the following [41]:
- Insertion of anti-vibration systems (with a ranking in percentage of 29.2%);
- Changes to the geometry and/or materials of the handles reaching 23.5%;
- Application of strategies for perfect repeatability of properties (20.2%);
- Changes to the expected conditions of use for workers (13.3%);
- Changes to other components (8.1%);
- Changes to the mechanics of the machine (5.7%).
The AHP is used to try to create a model for optimizing the occurrence of vibrations in the cabin of commercial vehicles with the aim of protecting the operator. Furthermore, it was determined that in order to successfully optimize the occurrence of vibrations, it is necessary to disassemble the vehicle into different or more subsystems and observe it in such a way that the transmission of vibrations to the operator is reduced to the smallest possible extent [42]. The application of AHP in this study confirmed this itself. There is an increasing number of studies where the application of the AHP in the field of ergonomics is significantly visible. Since the parameters that affect ergonomic factors are complex and non-parametric, the AHP method provides efficiency in grouping and deciding the importance of data [43,44].
The aim of this research is to determine the dependence of the investigated variables (operator’s body vibration and the hand–arm system vibration) and operational parameters (surface, tractor speed, and tire pressure of the agricultural tractor), and to develop a theoretical model for optimizing the tractor speed and tire pressure for specific investigated surfaces. The research hypothesis is that, at different operational parameters, the investigated variables will differ significantly, and that the measured values of the investigated variables will differ significantly from the values of the same variables under controlled conditions during testing on test tracks.
2. Materials and Methods
This research was conducted on the production of agricultural surfaces and access roads of the Agricultural and Veterinary School Osijek with the aim of measuring vibrations affecting the operator’s body and the hand–arm system of an agricultural tractor operator. The measurements were taken while the tractor moved over four agro-technical surfaces and two standardized test tracks (smooth and rough), in accordance with the HRN ISO 5008:2015 [45] standard. The tractor used for the measurements was the LANDINI POWERFARM 100 with a power output of 68 kW, which is used for tasks in production (arable farming, fruit growing, and viticulture). This tractor has suspension on the front part, specifically on the front axle, and a cabin suspension. The seat suspension is pneumatic. During the measurements, the tire pressure was set to the prescribed value (2.4 bar), lower than the prescribed value (1.9 bar), and higher than the prescribed value (2.9 bar). The tractor’s speed on the surfaces was selected according to the HRN ISO 5008:2015 [45] standard, with speeds of 6, 5, 4, 3, 2, and 1 kmh−1. Two test tracks were created according to HRN ISO 5008:2015 [45] a smooth track (100 m long) and a rough track (35 m long). The tracks were made for each wheel row separately, using rubber as the surface material and wooden slats to simulate unevenness. The slats were made and placed in accordance with the aforementioned standard.
Mechanical vibrations were measured using the MMF brand device, model VM30 (Figure 1), equipped with the appropriate sensors for measuring body vibrations of the operator and hand–arm system vibrations, which are transmitted through the tractor’s steering wheel to the operator’s hand–arm system (Table 1).

Figure 1.
Vibration measuring device (1.) with associated sensors for measuring vibrations of the whole body (2.) and the hand–arm system (3.).

Table 1.
Technical characteristics of the vibration measuring device MMF type VM30.
The measurement of body vibrations was carried out according to the prescribed standards HRN ISO 2631-1:1999/A1:2019 [9] and HRN ISO 2631-4:2010 [46]. The HRN ISO 2631-1:1999/A1:2019 [9] standard describes the vibrations that are measured in three areas of the operator using a vibration coordinate system in the x-axis, y-axis, and z-axis, and which weighting filter should be used during the measurement. The weighting filters used for measuring vibrations affecting the operator’s body in a seated position were Wd (measuring vibrations in the x-axis and y-axis) (Figure 2) and Wk (measuring vibrations in the z-axis) (Figure 3) (HRN ISO 2631-1:1999/A1:2019 [9]).
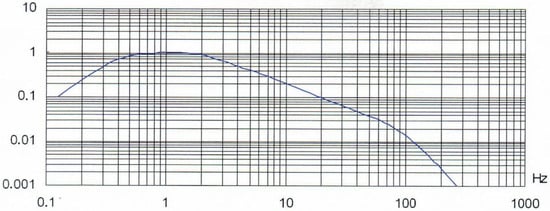
Figure 2.
Weighted filters for measuring vibrations affecting the operator’s whole body in the x and y directions (Wd) (source: HRN ISO 2631-1:1999/A1:2019 [9]).
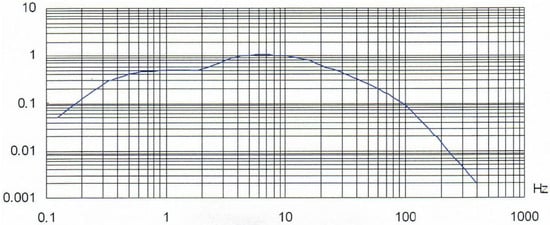
Figure 3.
Weighted filters for measuring vibrations affecting the operator’s whole body in the z-axis direction (Wk) (source: HRN ISO 2631-1:1999/A1:2019 [9]).
According to HRN ISO 2631-1:1999/A1:2019 [9] the R.M.S. method of measurement in motion takes into account intermittent impulse and transient vibrations using a short integration time constant. The vibration magnitude is defined as the maximum transient vibration value (MTVV), which is the maximum for (t0).
- (t)—current frequency of measured acceleration (ms−2);
- τ—integration time for continuous averaging;
- t—time (s);
- t0—observation time (s).
- MTVV—maximum transient vibration value (ms−2).
The HRN ISO 2631-4:2010 [46] standard provides guidelines for assessing the effects of vibration and rotational motion on passengers and operator comfort in a transport system. The standard specifies how to mount a torso vibration sensor on the seat (Figure 4), with the axes oriented as follows:

Figure 4.
Sensor installed to measure vibrations affecting the operator’s whole body.
- x-axis: longitudinal, in the direction of travel—forward (positive)/backward (negative);
- y-axis: lateral, at right angles to the direction of travel (left/right);
- z-axis: vertical, upwards perpendicular to the floor (positive)/downwards perpendicular to the floor (negative).
The measurement of vibrations in the hand–arm system was carried out according to the prescribed standards HRN ISO 5349-1:2008 [47] and HRN ISO 5349-2:2008/A1:2015 [48]. The HRN ISO 5349-1:2008 [47] standard specifies how to position the sensor on the steering wheel (Figure 5) and which weighting filter to choose. According to this standard, the weighting filter for measuring vibrations affecting the hand–arm system of the operator is Wh (Figure 6). The sensor was positioned so that the x-axis was aligned with the direction of tractor movement, the y-axis was perpendicular to the direction of movement, and the z-axis was vertical to the direction of tractor movement.

Figure 5.
A sensor has been installed to measure vibrations that affect the operator’s hand–arm system.
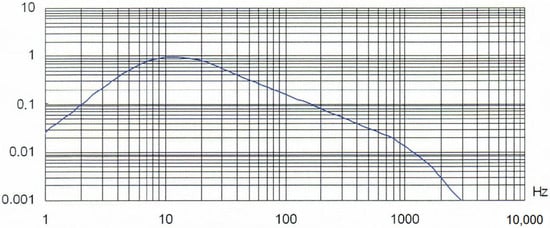
Figure 6.
Weight filter for measuring vibrations affecting the operator’s hand–arm system in the x-, y-, and z-axes (Wh) (source: HRN ISO 5349-1:2008 [47]).
According to HRN ISO 5349-2:2008/A1:2015 [48], the minimum duration for measuring vibrations affecting the hand–arm system of the operator is 1 min. If the measurement duration is shorter than one minute, it is necessary to take multiple samples so that the total duration reaches 1 min. The sensor is positioned closer to the hand grips and firmly attached to the steering wheel. In several cases, the daily exposure of the worker results from a series of operations. For each operation, the total vibration value, , and the exposure time to that source, Ti, must be measured. The daily vibration exposure A(8), in ms−2, is calculated as follows:
- T0 is the reference duration, 8 h (28,800 s).
- n is the number of operations.
In order to enable comparison between different operations and assess the individual contribution of each task to daily vibration exposure A(8), the calculation of partial exposure for each operation Ai (8) is as follows:
Daily vibration exposures are calculated as
The measurement range for measuring vibrations affecting the operator’s torso and the operator’s hand–arm system is 12 ms−2. This range was used to ensure that the obtained values were of sufficient precision (two decimal places). Data processing and transfer were carried out using a Microsoft Excel File that includes a Visual Basic Macro (MMF User’s Guide). The vibration measurements affecting the operator’s torso (Figure 7) and the hand–arm system (Figure 8) in a seated position for a specific part of the body were performed according to the coordinate system in the x-axis, y-axis, and z-axis.
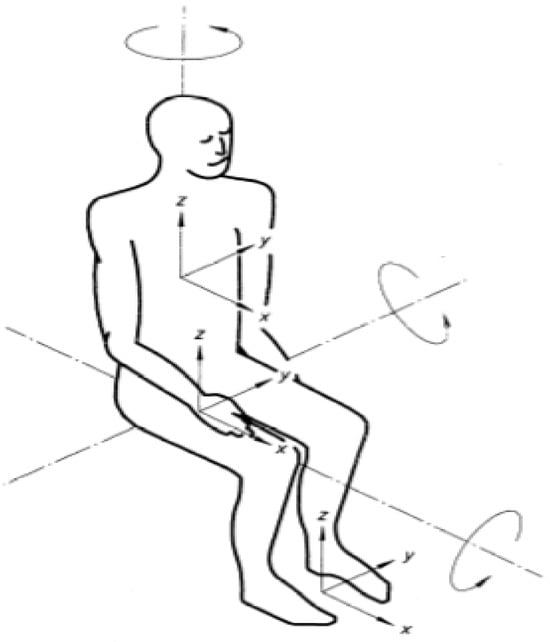
Figure 7.
Display of the coordinate system for a certain part of the vibrations of the whole body in the sitting position (source: HRN ISO 2631-1:1999/A1:2019 [9]).
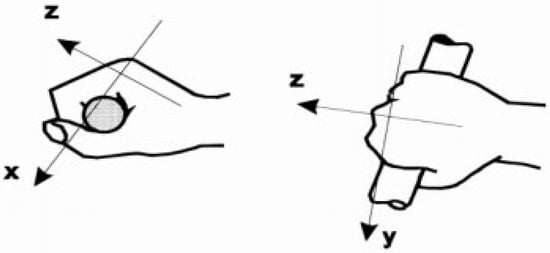
Figure 8.
Representation of the coordinate system for the hand–arm system (source: HRN ISO 5349-1:2008 [47]).
This study, when planning the experiment, was set up as a three-factorial design in which the main factors were A, surface (smooth (Figure 9) and rough (Figure 10) test tracks with other selected agrotechnical surfaces—(6)); B, speed of movement (6); and C, tire pressure (3).

Figure 9.
Smooth test track.

Figure 10.
Rough test track.
Since the dependent variable, the agrotechnical surface, is non-parametric (ordinal), hierarchical analysis was chosen and performed using the Analytical Hierarchy Process (AHP). The result of the hierarchical analysis is a dendrogram, which is essentially a condensed visualization of the diversity matrix. Data analysis was carried out using the SAS/STAT Software 9.4 (2014/2017). Statistical processing and interpretation of the results, including descriptive statistics, also included a two-factorial analysis of variance (ANOVA—BxC) with six repetitions—measurements. A multiple correlation test and regression analysis were conducted for the key relationships between the factors as independent variables and the vibrations as dependent variables.
2.1. Theoretical Model for Optimizing Tractor Speed and Tire Pressure
Considering that one of the aims was to create a theoretical model, the Theoretical Model for Optimizing Tractor Speed and Tire Pressure was created and presented below. It outlines an approach to optimizing tractor speed and tire pressure for specific surfaces using a theoretical model derived from experimental data. The independent variables are tractor speed (v) categorized into levels (e.g., 1–6 kmh−1), tire pressure (p) with levels such as low, prescribed, and high, and surface types grouped using the Analytic Hierarchy Process (AHP) into categories such as smooth, rough, asphalt, grass, etc. The dependent variables are the vibration levels affecting the hand–arm system and the whole body, measured in the x-axis, y-axis, and z-axis.
The methodology used in this theoretical model is the application of two-factor analysis of variance (ANOVA) to identify interactions between variables, grouping surfaces and other operating parameters using AHP and grouping similar vibration profiles. Furthermore, multiple regression analysis was applied to model the relationships and determine significant predictors of vibration levels. The optimization criteria are to reduce vibration levels below safety thresholds (e.g., 1.15 ms−2 for the body and 5 ms−2 for hand–arm systems) and to balance the speed of movement and tire pressure to maintain work efficiency without compromising the health of the operator. The mathematical representation is as follows:
General form:
Specific regression model forms may include interactions, e.g.,
where Vaxis represents vibration levels for each axis (x, y, z).
The optimization results indicate that an optimal combination of speed (v*) and tire pressure (p*) is required for each type of surface to ensure that vibrations remain within acceptable limits. A decision tree or AHP dendrograms that visualize grouped surfaces and conditions for quick reference are also required.
2.2. Formalized Theoretical Model
In order to formalize a theoretical model for optimizing tractor speed and tire pressure for specific surfaces based on the data obtained, detailed formulations of the relationship between vibration levels and operating parameters (speed, tire pressure, and type of surface) are included. The following is a structured and extended model:
The objective function of the model aims to minimize the vibration levels affecting both the hand–arm system (VHA) and the whole body system (VWB) while maintaining operational efficiency. The objective function can be expressed as
where the following definitions hold:
- VHA(v,p,s): vibration level for the hand–arm system.
- VWB(v,p,s): vibration level for the whole body.
- α, β: weights representing the relative importance of reducing vibrations for each system.
The independent variables are speed (v) (discrete levels, e.g., v ∈ {1,2,3,4,5,6} (kmh−1)), tire pressure (p) (categorical, e.g., p ∈ {C1,C2,C3} where C1, C2, and C3 correspond to low, prescribed, and high pressures), and surface type (s) [grouped via AHP into categories s ∈ {GL,GR}, (GL: smooth-like surfaces—e.g., asphalt, grass, smooth test track) and (GR: rough-like surfaces, e.g., field road, rough test track)].
The dependent variables are the vibration levels along each axis (x, y, and z):
For the regression models, using multiple regression analysis for each vibration metric, the functional forms are:
Here, the following definitions hold:
- β0: intercept.
- β1, β2, β3: coefficients for main effects (speed, pressure, surface).
- β12, β13: interaction coefficients between variables.
- ϵ: residual error.
Two types of constraints are “safety limits” (for vibration levels of VHA ≤ 5.0 ms−2 (hand–arm system) and VWB ≤ 1.15 ms−2 (whole body)) and “operational constraints” (speed range: 1 kmh−1 ≤ v ≤ 6 kmh−1 and tire pressure range: low (C1) to high (C3)). The outputs for optimal parameters are v*, the optimal speed for a specific surface s and pressure p, and p*, the optimal tire pressure for a specific surface s and speed v.
The predicted vibration levels are as follows: VHA(v*,p*,s), VWB(v*,p*,s).
2.3. General Recommendation Based on Theoretical and Formalized Theoretical Model for Optimizimg Tractor Speed and Tire Pressure
The main effects, vibrations affecting the hand–arm system (VHA) and the operator’s whole body (VWB), increase with tractor speed (v) and tire pressure (p). Furthermore, rough surfaces significantly increase vibrations compared to smooth surfaces. The interaction effects between tractor speed and tire pressure (v, p) can disproportionately increase vibrations (VHA and VWB) at high values. Observing the interaction between tractor speed and agrotechnical surfaces (v,⋅s) highlights the importance of speed control on uneven terrain. The practical utility of these models is that they allow for the prediction of vibrations for different operating conditions. They form the basis for optimization, allowing the identification of combinations of speed and pressure that minimize vibrations, which is very important.
3. Results
For the purposes of conducting the analysis using the Analytical Hierarchy Process, the agrotechnical surfaces were considered as independent variables, and the vibrations of the hand–arm system in all three axes and the vibrations of the body in all three axes were considered as dependent variables. Using the two-way grouping method (a statistical clustering technique that organizes items (agrotechnical surfaces in this study) into meaningful groups based on shared characteristics across multiple dimensions (vibration levels in this study)), the result is shown in Figure 11. It is evident that in the first level of grouping, there are two groups of agrotechnical surfaces (Macadam–Grass and Rough–Field Road) and two individual agrotechnical surfaces: Asphalt and Smooth. Since they are close to each other, in the second level of grouping, the individual Asphalt surface was grouped with the Macadam–Grass group. In the third level of grouping, the individual agrotechnical surface Smooth was added to the Macadam–Grass–Asphalt group, forming a smooth group of agrotechnical surfaces (GL). In contrast to the GL group, the Rough–Field Road group remains (rough group—GR).
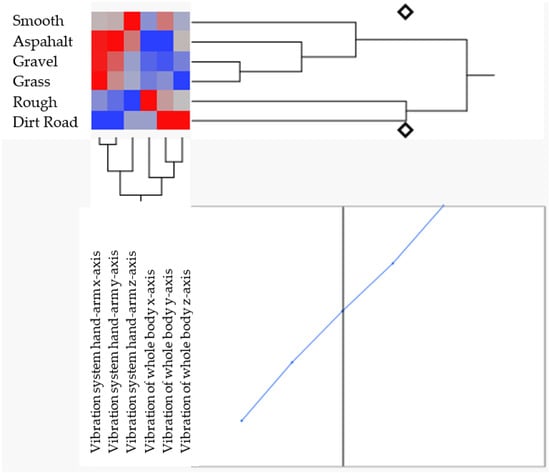
Figure 11.
Display of data grouping by AHP for hand–arm and whole body vibrations.
The one-way analysis of variance for the mean values of the dependent variables, according to the groups of independent variables determined by the hierarchical analysis (AHP), yielded results presented in Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7. The air pressure groups in the tires are marked with colors from lowest to highest in the following order: green for the lowest (C1), red for the prescribed (C2), and blue for the highest (C3).
3.1. Relationship Between Grouped Agrotechnical Surfaces and Other Independent Variables on Hand–Arm System Vibrations in the x-Axis Direction
Statistically significant differences were found between the mean values of hand–arm system vibrations in the x-axis direction and the groups determined by AHP, at both lower and prescribed air pressures in the tires, and for lower tractor movement speeds (1, 2, 3, and 4 kmh−1). For the lower air pressure, as the speed increases, the coefficient of determination decreases, and the mean vibration value decreases, while the coefficient of variation increases. The same was found for the prescribed air pressure in the tires, except at a movement speed of 3 kmh−1. Statistically significant differences were also found at higher air pressures in the tires for higher movement speeds (5 and 6 kmh−1), with a reversed dynamic change in the coefficient of determination, coefficient of variation, and mean values compared to the earlier described dynamics at lower speeds (Table 2).

Table 2.
Analysis of variance for hand–arm system vibrations in the x-axis direction.
Table 2.
Analysis of variance for hand–arm system vibrations in the x-axis direction.
| Variants | F | Pr > F | R2 | C.V. (%) | |
|---|---|---|---|---|---|
| B1C1 | 138.57 | <0.0001 | 0.802980 | 23.69865 | 1.248333 |
| B1C2 | 100.91 | <0.0001 | 0.747987 | 23.51933 | 1.023056 |
| B1C3 | 0.08 | 0.7838 | 0.002245 | 21.36400 | 1.116944 |
| B2C1 | 116.10 | <0.0001 | 0.773484 | 26.01350 | 1.110000 |
| B2C2 | 70.61 | <0.0001 | 0.674985 | 28.51435 | 0.945833 |
| B2C3 | 0.55 | 0.4627 | 0.015970 | 23.49500 | 1.114167 |
| B3C1 | 105.16 | <0.0001 | 0.755684 | 26.09971 | 0.995556 |
| B3C2 | 188.91 | <0.0001 | 0.847471 | 18.18881 | 0.908889 |
| B3C3 | 0.18 | 0.6749 | 0.005236 | 23.78212 | 0.972222 |
| B4C1 | 31.73 | <0.0001 | 0.482700 | 34.43180 | 1.059167 |
| B4C2 | 43.30 | <0.0001 | 0.560163 | 29.21920 | 0.896111 |
| B4C3 | 0.37 | 0.5450 | 0.010875 | 23.69694 | 1.033056 |
| B5C1 | 12.81 | 0.0011 | 0.273586 | 39.31974 | 1.094722 |
| B5C2 | 2.75 | 0.1066 | 0.074777 | 42.84920 | 0.983889 |
| B5C3 | 29.16 | <0.0001 | 0.461667 | 12.47938 | 1.093056 |
| B6C1 | 2.72 | 0.1081 | 0.074141 | 43.66584 | 1.143333 |
| B6C2 | 0.05 | 0.8328 | 0.001329 | 52.36972 | 1.068611 |
| B6C3 | 33.66 | <0.0001 | 0.497498 | 24.30758 | 1.200833 |
| B1 speed of movement 1 kmh−1 B2 speed of movement 2 kmh−1 B3 speed of movement 3 kmh−1 F; F-test value R2; coefficient of determination | B4 speed of movement 4 kmh−1 B5 speed of movement 5 kmh−1 B6 speed of movement 6 kmh−1 Pr > F; p-value (probability) C.V.; coefficient of variation | C1 tire pressure 1.9 bar C2 tire pressure 2.4 bar C3 tire pressure 2.9 bar ; mean value of hand–arm vibration in the x-axis direction, ms−2 | |||
3.2. Relationship Between Grouped Agrotechnical Surfaces and Other Independent Variables on Hand–Arm System Vibrations in the y-Axis Direction
The analysis of variance for the mean values of vibrations affecting the hand–arm system in the y-axis direction revealed, overall, the fewest statistically significant differences. These were observed for lower, prescribed, and higher air pressures in the tires, but only at movement speeds of 1 and 2 kmh−1. As the speed increased, the mean vibration values and the coefficient of variation decreased for lower and prescribed air pressures in the tires. The coefficient of determination for both air pressures in the tires increased as the tractor speed increased (Table 3).

Table 3.
Analysis of variance for hand–arm system vibrations in the y-axis direction.
Table 3.
Analysis of variance for hand–arm system vibrations in the y-axis direction.
| Variants | F | Pr > F | R2 | C.V. (%) | |
|---|---|---|---|---|---|
| B1C1 | 86.50 | <0.0001 | 0.717851 | 29.84622 | 0.433889 |
| B1C2 | 39.47 | <0.0001 | 0.537251 | 48.29240 | 0.412500 |
| B1C3 | 22.80 | <0.0001 | 0.401362 | 42.70676 | 0.479722 |
| B2C1 | 94.54 | <0.0001 | 0.735493 | 28.14218 | 0.396667 |
| B2C2 | 46.14 | <0.0001 | 0.575734 | 40.46236 | 0.392778 |
| B2C3 | 14.66 | 0.0005 | 0.301322 | 30.65624 | 0.483889 |
| B3C1 | 0.00 | 0.9964 | 0.000001 | 65.70610 | 0.391944 |
| B3C2 | 1.14 | 0.2932 | 0.032435 | 44.70775 | 0.466667 |
| B3C3 | 0.18 | 0.6749 | 0.005236 | 23.78212 | 0.972222 |
| B4C1 | 3.07 | 0.0890 | 0.082710 | 68.66542 | 0.611667 |
| B4C2 | 1.81 | 0.1873 | 0.050567 | 58.27954 | 0.616111 |
| B4C3 | 4.66 | 0.0380 | 0.120619 | 40.89716 | 0.632500 |
| B5C1 | 6.85 | 0.0132 | 0.167630 | 74.76111 | 0.781944 |
| B5C2 | 7.33 | 0.0105 | 0.177398 | 74.57970 | 0.815833 |
| B5C3 | 10.17 | 0.0031 | 0.230209 | 69.04360 | 0.792778 |
| B6C1 | 9.38 | 0.0043 | 0.216146 | 80.12540 | 0.905000 |
| B6C2 | 11.12 | 0.0021 | 0.246506 | 85.41954 | 0.903889 |
| B6C3 | 19.08 | 0.0001 | 0.359437 | 59.81058 | 1.022222 |
| B1 speed of movement 1 kmh−1 B2 speed of movement 2 kmh−1 B3 speed of movement 3 kmh−1 F: F-test value R2: coefficient of determination | B4 speed of movement 4 kmh−1 B5 speed of movement 5 kmh−1 B6 speed of movement 6 kmh−1 Pr > F: p-value (probability) C.V.: coefficient of variation | C1 tire pressure 1.9 bar C2 tire pressure 2.4 bar C3 tire pressure 2.9 bar : mean value of hand–arm vibration in the y-axis direction, ms−2 | |||
3.3. Relationship of Grouped Agrotechnical Surfaces and Other Independent Variables with Hand–Arm Vibrations in the z-Axis Direction
An analysis of the variance of the mean values of hand–arm system vibrations in the z-axis direction revealed significant differences for lower, prescribed, and higher tire pressures when the tractor was moving at speeds of 5 and 6 kmh−1. For these variants of the independent variables, the mean vibration value and the coefficient of variation increase with the increase in tractor speed. For lower and prescribed pressures, the coefficient of determination decreases with increasing tractor speed, while for higher pressures, it increases. In addition, statistically significant differences were found for the dependent variable at lower and prescribed tire pressures at speeds of 1 and 3 kmh−1. The highest recorded coefficient of determination, 70.24%, is at a tractor speed of 5 kmh−1 and the prescribed tire pressure (Table 4).

Table 4.
Analysis of the variance of hand–arm vibrations in the z-axis direction.
Table 4.
Analysis of the variance of hand–arm vibrations in the z-axis direction.
| Variants | F | Pr > F | R2 | C.V. (%) | |
|---|---|---|---|---|---|
| B1C1 | 30.66 | <0.0001 | 0.474159 | 21.18047 | 0.102500 |
| B1C2 | 52.22 | <0.0001 | 0.605673 | 23.91855 | 0.067500 |
| B1C3 | 13.41 | 0.0008 | 0.282796 | 53.27910 | 0.086389 |
| B2C1 | 2.96 | 0.0942 | 0.080185 | 30.54959 | 0.100833 |
| B2C2 | 2.82 | 0.1024 | 0.076540 | 30.42157 | 0.090000 |
| B2C3 | 3.29 | 0.0787 | 0.088129 | 22.44285 | 0.081111 |
| B3C1 | 65.54 | <0.0001 | 0.658436 | 25.87920 | 0.135000 |
| B3C2 | 48.19 | <0.0001 | 0.586334 | 34.71631 | 0.140833 |
| B3C3 | 14.76 | 0.0005 | 0.302715 | 20.98422 | 0.116944 |
| B4C1 | 6.15 | 0.0183 | 0.153162 | 44.18610 | 0.134444 |
| B4C2 | 5.88 | 0.0208 | 0.147353 | 42.71466 | 0.140000 |
| B4C3 | 10.03 | 0.0032 | 0.227848 | 22.32411 | 0.120000 |
| B5C1 | 63.27 | <0.0001 | 0.650448 | 54.48019 | 0.155833 |
| B5C2 | 80.26 | <0.0001 | 0.702426 | 56.26769 | 0.191944 |
| B5C3 | 19.92 | <0.0001 | 0.369466 | 83.60035 | 0.184444 |
| B6C1 | 45.66 | <0.0001 | 0.573213 | 68.68984 | 0.239167 |
| B6C2 | 53.03 | <0.0001 | 0.609342 | 78.16220 | 0.245556 |
| B6C3 | 23.69 | <0.0001 | 0.410690 | 119.6096 | 0.258889 |
| B1 speed of movement 1 kmh−1 B2 speed of movement 2 kmh−1 B3 speed of movement 3 kmh−1 F: F-test value R2: coefficient of determination | B4 speed of movement 4 kmh−1 B5 speed of movement 5 kmh−1 B6 speed of movement 6 kmh−1 Pr > F: p-value (probability) C.V.: coefficient of variation | C1 tire pressure 1.9 bar C2 tire pressure 2.4 bar C3 tire pressure 2.9 bar : mean value of hand–arm vibration in the z-axis direction, ms−2 | |||
3.4. The Relationship of Grouped Agrotechnical Surfaces and Other Independent Variables with Whole Body Vibrations in the x-Axis Direction
An analysis of the variance of the mean values of body vibrations in the x-axis direction between the AHP-determined groups revealed significant differences for all tractor speeds at the prescribed and higher tire pressures. As the tractor speed increases, the mean vibration value also increases, and it is significantly higher at higher pressure compared to the prescribed pressure. The highest recorded coefficient of determination occurs at a tractor speed of 3 kmh−1, and it decreases as the speed either decreases or increases, with the coefficients being more pronounced at higher speeds than at lower ones. The lowest coefficient of variation was also recorded at 3 kmh−1, but it increases as the speed either increases or decreases. The coefficient of variation is more pronounced at prescribed pressure compared to higher tire pressures (Table 5).

Table 5.
Analysis of whole body vibration variance in the x-axis direction.
Table 5.
Analysis of whole body vibration variance in the x-axis direction.
| Variants | F | Pr > F | R2 | C.V. (%) | |
|---|---|---|---|---|---|
| B1C1 | 31.32 | <0.0001 | 0.479488 | 46.69061 | 0.125833 |
| B1C2 | 34.03 | <0.0001 | 0.500195 | 108.4327 | 0.394444 |
| B1C3 | 28.60 | <0.0001 | 0.456843 | 115.1667 | 0.387500 |
| B2C1 | 16.07 | 0.0003 | 0.321013 | 85.85998 | 0.263611 |
| B2C2 | 140.81 | <0.0001 | 0.805503 | 49.98170 | 0.487222 |
| B2C3 | 151.39 | <0.0001 | 0.816601 | 47.78166 | 0.489722 |
| B3C1 | 16.48 | 0.0003 | 0.326489 | 94.73067 | 0.347500 |
| B3C2 | 585.27 | <0.0001 | 0.945097 | 23.22971 | 0.530556 |
| B3C3 | 653.96 | <0.0001 | 0.950578 | 20.41095 | 0.559722 |
| B4C1 | 16.69 | 0.0003 | 0.329266 | 97.97840 | 0.383333 |
| B4C2 | 389.76 | <0.0001 | 0.919765 | 25.91458 | 0.566667 |
| B4C3 | 503.17 | <0.0001 | 0.936705 | 22.26402 | 0.597500 |
| B5C1 | 17.28 | 0.0002 | 0.336956 | 89.83134 | 0.426389 |
| B5C2 | 386.60 | <0.0001 | 0.919164 | 25.23964 | 0.607222 |
| B5C3 | 397.56 | <0.0001 | 0.921216 | 23.21176 | 0.629722 |
| B6C1 | 19.09 | 0.0001 | 0.359622 | 91.55669 | 0.491944 |
| B6C2 | 226.57 | <0.0001 | 0.869519 | 32.07237 | 0.670833 |
| B6C3 | 300.76 | <0.0001 | 0.898436 | 26.50157 | 0.673611 |
| B1 speed of movement 1 kmh−1 B2 speed of movement 2 kmh−1 B3 speed of movement 3 kmh−1 F: F-test value R2: coefficient of determination | B4 speed of movement 4 kmh−1 B5 speed of movement 5 kmh−1 B6 speed of movement 6 kmh−1 Pr > F: p-value (probability) C.V.: coefficient of variation | C1 tire pressure 1.9 bar C2 tire pressure 2.4 bar C3 tire pressure 2.9 bar : mean value of whole body vibration in the x-axis direction, ms−2 | |||
3.5. Relationship of Grouped Agrotechnical Surfaces and Other Independent Variables with Whole Body Vibrations in the y-Axis Direction
Statistically significant differences were found between the mean values of body vibrations in the direction of the y-axis and the AHP-determined groups at the prescribed and higher tire pressures for all tractor movement speeds. The mean values of the measured vibrations increase with increasing speed and are higher at the prescribed pressure compared to higher tire pressure. The determination coefficients for the prescribed pressure range from 42.09% to 94.51%, and for higher pressure from 37.41% to 64.39% (Table 6).

Table 6.
Analysis of whole body vibration variance in the y-axis direction.
Table 6.
Analysis of whole body vibration variance in the y-axis direction.
| Variants | F | Pr > F | R2 | C.V. (%) | |
|---|---|---|---|---|---|
| B1C1 | 12.54 | 0.0012 | 0.269488 | 13.11371 | 0.093889 |
| B1C2 | 24.72 | <0.0001 | 0.420949 | 87.26454 | 0.172222 |
| B1C3 | 20.32 | <0.0001 | 0.374057 | 82.43183 | 0.131944 |
| B2C1 | 8.04 | 0.0076 | 0.191295 | 62.69665 | 0.133889 |
| B2C2 | 94.06 | <0.0001 | 0.734507 | 47.78531 | 0.207500 |
| B2C3 | 61.48 | <0.0001 | 0.643906 | 52.57738 | 0.176667 |
| B3C1 | 17.53 | 0.0002 | 0.340240 | 101.2328 | 0.321389 |
| B3C2 | 585.27 | <0.0001 | 0.945097 | 23.22971 | 0.530556 |
| B3C3 | 29.75 | <0.0001 | 0.466680 | 77.23342 | 0.275556 |
| B4C1 | 16.23 | 0.0003 | 0.323165 | 109.8494 | 0.540000 |
| B4C2 | 48.05 | <0.0001 | 0.585610 | 76.35622 | 0.503889 |
| B4C3 | 41.92 | <0.0001 | 0.552187 | 77.55695 | 0.458333 |
| B5C1 | 16.67 | 0.0003 | 0.329005 | 111.6145 | 0.670556 |
| B5C2 | 41.43 | <0.0001 | 0.549259 | 87.52851 | 0.652222 |
| B5C3 | 38.50 | <0.0001 | 0.531035 | 86.98481 | 0.611389 |
| B6C1 | 15.87 | 0.0003 | 0.318182 | 105.8862 | 0.758056 |
| B6C2 | 42.65 | <0.0001 | 0.556426 | 79.10860 | 0.768056 |
| B6C3 | 39.86 | <0.0001 | 0.539661 | 79.17441 | 0.748333 |
| B1 speed of movement 1 kmh−1 B2 speed of movement 2 kmh−1 B3 speed of movement 3 kmh−1 F: F-test value R2: coefficient of determination | B4 speed of movement 4 kmh−1 B5 speed of movement 5 kmh−1 B6 speed of movement 6 kmh−1 Pr > F: p-value (probability) C.V.: coefficient of variation | C1 tire pressure 1.9 bar C2 tire pressure 2.4 bar C3 tire pressure 2.9 bar : mean value of whole body vibration in the y-axis direction, ms−2 | |||
3.6. The Relationship of Grouped Agrotechnical Surfaces and Other Independent Variables with Whole Body Vibrations in the Direction of the z-Axis
Statistically significant differences were found between the mean values of body vibrations in the direction of the z-axis and the AHP-determined groups only at lower tire pressures for all tractor movement speeds except the highest. As the speed increases, the mean body vibration value increases, while the determination coefficients decrease. The highest determination coefficient was found at a speed of 1 kmh−1 and is 47.42%, while the lowest was at a speed of 5 kmh−1, at 38.24%. The coefficients of variation range from 21.18% to 71.16% and increase with speed (Table 7).

Table 7.
Analysis of whole body vibration variance in the z-axis direction.
Table 7.
Analysis of whole body vibration variance in the z-axis direction.
| Variants | F | Pr > F | R2 | C.V. (%) | |
|---|---|---|---|---|---|
| B1C1 | 30.66 | <0.0001 | 0.474159 | 21.18047 | 0.102500 |
| B1C2 | 0.88 | 0.3550 | 0.025212 | 49.39178 | 0.063611 |
| B1C3 | 2.84 | 0.1009 | 0.077168 | 28.83101 | 0.080000 |
| B2C1 | 28.70 | <0.0001 | 0.457731 | 44.92170 | 0.198333 |
| B2C2 | 4.08 | 0.0513 | 0.107155 | 66.13250 | 0.175556 |
| B2C3 | 0.02 | 0.9006 | 0.000465 | 58.13911 | 0.177222 |
| B3C1 | 23.42 | <0.0001 | 0.407871 | 63.11796 | 0.293611 |
| B3C2 | 7.09 | 0.0118 | 0.172541 | 71.81273 | 0.261944 |
| B3C3 | 3.10 | 0.0873 | 0.083529 | 60.70315 | 0.260278 |
| B4C1 | 23.68 | <0.0001 | 0.410537 | 65.85860 | 0.310000 |
| B4C2 | 8.35 | 0.0067 | 0.197170 | 83.87689 | 0.280556 |
| B4C3 | 2.41 | 0.1300 | 0.066139 | 71.29949 | 0.276944 |
| B5C1 | 21.05 | <0.0001 | 0.382357 | 71.16268 | 0.366389 |
| B5C2 | 7.09 | 0.0118 | 0.172511 | 94.98799 | 0.325278 |
| B5C3 | 5.63 | 0.0235 | 0.142058 | 78.92956 | 0.376944 |
| B6C1 | 16.92 | 0.0002 | 0.332351 | 75.12901 | 0.510556 |
| B6C2 | 12.26 | 0.0013 | 0.265058 | 102.3807 | 0.507222 |
| B6C3 | 9.43 | 0.0042 | 0.217198 | 89.91699 | 0.483056 |
| B1 speed of movement 1 kmh−1 B2 speed of movement 2 kmh−1 B3 speed of movement 3 kmh−1 F: F-test value R2: coefficient of determination | B4 speed of movement 4 kmh−1 B5 speed of movement 5 kmh−1 B6 speed of movement 6 kmh−1 Pr > F: p-value (probability) C.V.: coefficient of variation | C1 tire pressure 1.9 bar C2 tire pressure 2.4 bar C3 tire pressure 2.9 bar : mean value of whole body vibration in the z-axis direction, ms−2 | |||
3.7. Summary of Results
- Hand–Arm Vibration (VHA)
Statistically significant differences in vibration in the x-axis direction were found for lower (C1) and prescribed (C2) pressures at lower speeds (1–4 kmh−1). Furthermore, as speed increases, the coefficient of determination (R2) decreases, while the coefficient of variation (CV) increases, showing greater variability at higher speeds. The least significant differences in vibration in the y-axis direction were found for lower (C1) and prescribed (C2) tyre pressures at speeds of 1–2 kmh−1. They generally decrease with increasing speed for C1 and C2 pressures. Significant differences in vibration in the z-axis direction were found for higher speeds (5–6 kmh−1) and higher pressures (C3). Furthermore, the mean vibration levels and variability increase with tractor speed.
- Whole Body Vibration (VWB)
Significant differences in vibration in the x-axis direction were found for all speeds at the prescribed (C2) and higher (C3) pressures. They increase with speed, with the highest values observed at v = 3 kmh−1. More significant differences in vibration in the y-axis direction were found at the prescribed tire pressures. The mean values increase with speed and are generally higher at C2 pressure compared to C3 pressure. Statistically significant differences in vibration in the z-axis direction were found at lower tire pressures at speeds of 1–5 kmh−1. Vibrations increase with speed, but the coefficients of determination (R2) decrease.
Surface grouping using AHP resulted in two groups: smooth surface (GL) which includes asphalt, smooth test track and grass surface, and rough surface (GR) which includes field road and rough test track. Regression analysis (VHA and VWB) found that higher speeds and tire pressures were significantly associated with increased vibration. Rough surfaces increased vibration in all axes compared to smooth surfaces.
Hand–arm vibration levels did not exceed the safety alert (2.5 ms−2) or limit (5 ms−2) values, indicating that there were no direct health risks to the operator. Whole body vibration levels exceeded the Daily Exposure Alert Threshold (0.5 ms−2) in several combinations, especially at higher speeds and tire pressures.
4. Discussion
A study was conducted on the impact of vibrations on the tractor operator’s body using test tracks (according to HRN ISO 5008:2015 [45]) and moving at different tractor speeds. Scarlett et al. [33] found that the levels of vibration affecting the operator’s body increased proportionally with the speed of travel, regardless of the type of suspension system of the tractors tested. When traveling on a 35 m uneven test track, the levels of vibration affecting the operator’s body in the x- and y-axes were similar, regardless of the type of tractor suspension, but significantly higher compared to the vibration levels measured in the z-axis. This is due to the roughness of the test track and the inability of the tractor’s suspension system (be it the seat, cab, or axle) to dampen the vibration levels in the x-axis and y-axis.
In the results of this study where the test tractor was moving in a straight line, the test track generated lower vertical vibrations (z-axis), while the lateral acceleration was significantly higher. This is in line with the findings of [33]. Similar results were obtained when the tractor was moving on a smooth track of 100 m. In this case, significantly lower levels of vibration affecting the operator’s body were measured, which is consistent with the results in this study when the tractor was moving on a smooth track.
Scarlett et al. [49] measured vibrations when the tractor moved on test tracks and during various agricultural operations (plowing, transporting a plow, cultivating, applying pesticides, and transporting with a trailer), comparing these measurements to assess the application of measured vibrations generated during tractor movement on test tracks to possible vibration levels during operational use. This comparison proved to be impossible. A comparison of vibration levels caused by tractor movement on test tracks with those generated during specific agricultural operations was not fully feasible. There were differences in vehicle mass, weight distribution, tire pressures, and the impact of external forces. For this reason, this study compared the vibrations generated by the tractor moving on different agrotechnical surfaces, which was confirmed by the AHP analysis as correct. In this way, the agrotechnical surfaces were statistically grouped into similar categories, and together around the rough or smooth test track. This avoided the issue of differences in mass, weight distribution, and external forces.
Deboli et al. [23] determined the impact of the transfer of vibrations to the tractor operator’s body from agricultural tractors equipped with different radial tires. In their study, they tested four different types of tires at three different air pressures (1.6, 1.2, and 0.8 bar), driving the tractor on three different surfaces at two different speeds, with three repetitions. The study enabled the selection of the optimal tire type depending on the surface the tractor is moving on. It was found that in all variations of the study, lower movement speed and lower tire pressure resulted in lower vibrations, regardless of the surface and tire characteristics. It was concluded that no statistically significant differences in vibrations in the horizontal x-axis and y-axis were found in relation to the type of tire, while significant differences in vibrations in the z-axis were observed depending on the type of tire.
The values of vibrations affecting the operator’s body in this study show that there are no statistically significant differences in terms of vibrations in the z-axis, except at a pressure of 1.9 bar, which is consistent with research [22]. Vibrations increase with tractor speed. For horizontal vibrations (x-axis and y-axis), statistically significant differences were found between the rough and smooth surface groups in all variants, except at a tire pressure of 1.9 bar. In the horizontal direction, vibrations increase with increasing tractor speed and tire pressure.
Similar results to this study were obtained by Deboli et al. [39,44], who investigated the vibration values affecting the body of a tractor operator. The study was conducted on two tractors of the same power, load capacity, and weight, but equipped with different tires. The same was performed at two different tractor speeds, on five agrotechnical surfaces (including a smooth test track). The vibration results measured on the standard test track were significantly higher (at all pressures and speeds) compared to the measurements obtained when the tractor was moving on other surfaces. The results of the study indicate a large variability for individual agrotechnical surfaces (dirt road, grass surface, and field road). The vibration results for the remaining two surfaces (asphalt surface and smooth test track) were more consistent. Higher tire pressure (1.6 bar) and higher speed (20 kmh−1) resulted in higher vibrations.
The issue of the impact of vibrations on the operator of agricultural tractors was addressed in the study by Deboli et al. [36] with respect to the tractor category, agrotechnical surface, and standard smooth test tracks. The results of the study indicate that the vibrations acting in the horizontal axes (x-axis and y-axis) on a smooth test track are higher than those measured on other agrotechnical surfaces. In this study, the tractor was not connected to the attachment, which caused low vibration values on asphalt and field roads. Vibrations on the smooth test track and other agrotechnical surfaces along the y-axis were very similar to the values measured along the x-axis. The measured values of vertical vibrations (z-axis), when the tractor was moving on the test track, indicate that they are very similar to the vibrations measured on other agrotechnical surfaces.
As shown in the dendrogram (Figure 11), two groups of agrotechnical surfaces were formed. The asphalt surface, gravel, and grass surfaces were grouped around the smooth test track, while the field road was grouped with the rough test track. From this, it can be concluded that the surfaces grouped around a particular test track can be simulated under specific vibration conditions by moving the tractor on just one of the test tracks (rough or smooth). The measured vibration values affecting the hand–arm system in this study indicate significantly higher vibrations in the x-axis and y-axis (0.89–1.24 ms−2 for the x-axis and 0.39–0.47 ms−2 for the y-axis) compared to vibrations in the z-axis (0.06–0.25 ms−2). Similar results were found while investigating vibrations affecting the hand–arm system during different agrotechnical operations (mulching and spraying). Higher vibration levels in all three axes were established during mulcher operation. Horizontal vibrations (x = 0.59 ms−2 and y = 0.20 ms−2) were several times higher than vertical vibrations (z = 0.03 ms−2) [31]. Similar findings were reported by [29], who determined the vibration levels affecting the hand–arm system in all three axes. For this purpose, they conducted research with a single-axle tractor moving on a gravel surface at three movement speeds (4, 6, and 8 kmh−1) during transport and three movement speeds (1, 1.5, and 2 kmh−1) during soil tillage. The highest vibration levels were measured during soil tillage (8.07 ms−2). Overall, the highest measured vibrations were in the x-axis and y-axis, followed by the z-axis, which is consistent with the analysis of variance, showing a significant impact of vibrations transmitted to the hand–arm system during both agrotechnical operations. Research on the impact of different agrotechnical surfaces on the vibrations affecting the tractor operator’s hand–arm system determined that different agrotechnical surfaces generate vibrations of varying intensity that affect the hand–arm system. The highest values were measured on the asphalt surface (x-axis 0.079 ms−2; y-axis 0.071 ms−2; z-axis 0.069 ms−2), and the lowest on the grass surface (x-axis 0.020 ms−2; y-axis 0.069 ms−2; z-axis 0.040 ms−2), while the tractor was moving at 7.5 kmh−1. This research, excluding the test tracks, showed that the highest levels of vibrations affecting the hand–arm system in the x-axis and y-axis were recorded on the asphalt surface. The lowest vibrations affecting the hand–arm system were measured on the grass surface in the y- and z-axes [28].
The impact of vibrations on the hand–arm system during the operation of the IMT 539 tractor under different agrotechnical operations and at different movement speeds was researched. The measured vibration values were significantly higher in all three axes during the operation of the side rotary harrow compared to other observed agrotechnical operations. The lowest vibration values were measured during the operation of the sprayer. An analysis of variance revealed significant differences between the mean values in all three axes. The effect of the independent variable movement speed in the y-axis and the independent variable agrotechnical operation in the x-axis, y-axis, and z-axis was highly significant, as was the interaction. After research measuring the vibrations affecting the hand–arm system of the agricultural tractor operator in the y-axis was conducted, significance was found at the tractor speeds B1 (1 kmh−1) and B2 (2 kmh−1) for all air pressures in the tires [50]. Table 8 summarizes the results obtained in the Results section and compares them with the findings from previous studies as reported in the Discussion section. Furthermore, it provides specific comparisons from the values of the investigated vibrations in the direction of all three axes (as dependent variables) to the influence of the independent variables (speed, tire pressure, agrotechnical surfaces).

Table 8.
Comparative summary of results: current findings and previous studies.
5. Conclusions
Significant differences between the mean values of vibrations affecting the hand–arm system in the x-axis and certain groups were identified at tire pressure levels C1 and C2 for lower tractor speeds (1, 2, 3, and 4 kmh−1). For lower tire air pressure, as the tractor speed increases, the coefficient of determination and the mean vibration value decrease, while the coefficient of variation increases. The same was found for tire pressure levels C2, except at speed B3. A significant difference was also found for tire pressure levels C3 at higher tractor speeds (5 and 6 kmh−1) with the opposite dynamics of change for the mentioned coefficients and mean values compared to lower speeds.
The lowest number of significant differences in the mean vibration values affecting the hand–arm system in the y-axis was found at tire pressure levels C1, C2, and C3, but only at tractor speeds of 1 and 2 kmh−1. As the tractor speed increases, the mean vibration value and the coefficient of variation decrease at tire pressure levels C1 and C2. The coefficient of determination for both of these pressures increases as speed increases.
Significant differences in the mean values of vibrations affecting the hand–arm system in the z-axis were identified for tire pressure levels C1, C2, and C3 at tractor speeds of 5 and 6 kmh−1. For these variants of independent variables, the mean vibration value and the coefficient of variation increase with an increase in tractor speed. For tire pressure levels C1 and C2, the coefficient of determination decreases with an increase in speed, while for higher tire air pressure, it increases as speed increases. In addition, statistically significant differences were found for the dependent variable for tire pressure levels C1 and C2 at tractor speeds of 1 and 3 kmh−1. The highest recorded coefficient of determination was for speed B5 and C2 tire air pressure, at 70.24%.
Significance was found between the mean vibration values affecting the tractor operator’s body in the x-axis between certain groups for all tractor speeds at tire pressure levels C2 and C3. As the tractor speed increases, the vibration also increases, and it is significantly higher at C3 tire air pressure compared to tire pressure level C2. The highest coefficient of determination was found at a tractor speed of B3, and it decreases as the speed decreases or increases, with higher values at higher speeds. The lowest coefficient of variation was also recorded at speed B3, but it increases with a decrease or increase in tractor speed. The coefficient of variation was more pronounced at C2 tire air pressure compared to tire pressure level C3.
Statistically significant differences between the mean values of vibrations affecting the tractor operator’s body in the y-axis and certain groups were identified at tire pressure levels C2 and C3 for all movement speeds. The mean vibration values increase with an increase in speed and are higher at tire pressure level C2 compared to tire pressure level C3. The coefficients of determination for tire pressure level C2 range over a larger span compared to higher pressures.
Significant differences between the mean values of vibrations affecting the tractor operator’s body in the z-axis and certain groups were found only at C1 tire pressure level for all movement speeds except the highest. As speed increases, the mean vibration values affecting the tractor operator’s body also increase. The coefficient of determination values decrease in this case. The highest coefficient of determination was found at a speed of B1, with a value of 47.42%. The lowest was at speed B5, with a value of 38.24%.
For vibrations affecting the hand–arm system, it was found that no measured data exceeded the warning (2.5 ms−2) or the threshold (5 ms−2) daily exposure values. Therefore, the operator’s health is not at risk, and they can perform tasks without using personal protective equipment (gloves).
Measured vibration data affecting the tractor operator’s body in the x-axis at higher tractor speeds and tire pressure levels C2 and C3, in the y-axis at higher speeds and tire pressure levels C1 and C2, and in the z-axis at the highest speed and tire pressure levels C1 and C2 were found to exceed the warning daily exposure value of 0.5 ms−2. It is recommended that the operator’s health be assessed and the air suspension of the seat be checked to prevent potential complications from starting. Despite this, the measured data do not exceed the threshold daily exposure value of 1.15 ms−2.
Reasonable improvement measures include the optimization of operating parameters in such a way as to use lower speeds (1–2 kmh−1) and reduced tire pressures (20% below the prescribed value) on rough terrains to minimize vibrations and then employ moderate speeds (3–4 kmh−1) and prescribed tire pressures on smooth terrains for a balance between efficiency and safety while avoiding high speeds (5–6 kmh−1) and overinflated tires, as they significantly increase vibration levels, especially along the z-axis.
In the future, it would be good to introduce automatic tire inflation and deflation systems that adjust tire pressure in real time based on terrain type and operational requirements, improving ground adhesion and reducing vibrations, and then develop guidelines for specific terrains (e.g., rough, field roads, smooth surfaces) with tailored operational parameters such as optimal speed and tire pressure and educate operators on these guidelines to improve adherence to best practices and provide feedback to operators through visual or auditory alerts when vibration levels exceed safety thresholds. Of course, it is suggested to conduct long-term studies on the cumulative effects of vibration exposure on operators and explore the role of additional operational factors, such as load weight and attachment type, in influencing vibration levels.
Author Contributions
Conceptualization, Ž.B. and I.P.; methodology, Ž.B. and I.P.; software, Ž.B. and I.P.; validation, Ž.B., I.P., T.J. and M.M.; formal analysis, Ž.B.; investigation, Ž.B.; resources, Ž.B.; data curation, Ž.B.; writing—original draft preparation, Ž.B. and I.P.; writing—review and editing, Ž.B., I.P., T.J. and M.M.; visualization, Ž.B.; supervision, T.J.; project administration, M.M.; funding acquisition, Ž.B., I.P., T.J. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Grubišić, A.; Guljaš, I. Uzajamni utjecaj aktivnosti ljudi i vibracija međukatnih konstrukcija. Elektron. Časopis Građev. Fak. Osijek 2010, 1, 67–79. [Google Scholar] [CrossRef] [PubMed]
- Anđelović, M.; Jovanović, J. Medicina Rada; Medicine Faculty in Niš, University of Niš: Niš, Serbia, 2009; ISBN 86-80599-52-2. [Google Scholar]
- Griffin, M.J. Handbook of Human Vibration; Academic Press: Cambridge, MA, USA, 1996; ISBN 978-0-12-303041-2. [Google Scholar]
- Rački, Z. The relationship between white fingers, cold-test and digital plethysmography in loggers working with different motor saws. Arh. Hig. Rada Toksikol. 1984, 35, 343–353. [Google Scholar] [PubMed]
- Brunetti, J.; D’Ambrogio, W.; Fregolent, A. Analysis of the Vibrations of Operators’ Seats in Agricultural Machinery Using Dynamic Substructuring. Appl. Sci. 2021, 11, 4749. [Google Scholar] [CrossRef]
- Mehta, C.R.; Shyam, M.; Singh, P.; Verma, R.N. Ride Vibration on Tractor-Implement System. Appl. Ergon. 2000, 31, 323–328. [Google Scholar] [CrossRef]
- Lines, J.; Stiles, M.; Whyte, R. Whole Body Vibration During Tractor Driving. J. Low Freq. Noise Vib. Act. Control. 1995, 14, 87–104. [Google Scholar] [CrossRef]
- Barač, Ž.; Marković, M.; Heffer, G.; Jurišić, M.; Duvnjak, V.; Jurić, T.; Plaščak, I.; Baličević, P. Influence of an Uneven Surface on the Vibration Occurrence Affecting the Tractor Operator. Teh. Glas. 2019, 13, 192–196. [Google Scholar] [CrossRef]
- HRN ISO 2631-1:1999/A1:2019/Hrvatski Normativni Dokument/HRN4You—Hrvatski Zavod Za Norme. Available online: https://repozitorij.hzn.hr/norm/HRN+ISO+2631-1%3A1999%2FA1%3A2019 (accessed on 10 December 2022).
- Sanders, M.S.; McCormick, E.J. Human Factors in Engineering and Design; McGraw-Hill: New York, NY, USA, 1987; ISBN 13-9780070449039. Available online: https://www.abebooks.com/9780070449039/Human-Factors-Engineering-Design-Sanders-0070449031/plp (accessed on 27 November 2024).
- Neugebauer, G.; Jancurova, L.; Martin, J.; Manek, T. Opasnosti Od Vibracija Koje Se Prenose Na Cijelo Tijelo i Na Šake-Ruke; International Social Security Association: Geneva, Switzerland, 2010; ISBN 978-3-941441-52-1. [Google Scholar]
- HZZO. Ozljede na Radu i Profesionalne Bolesti, Specifična Zdravstvena Zaštita. Available online: http://hzzo.hr/ozljede-na-radu-i-profesionalne-bolesti-specificna-zdravstvena-zastita (accessed on 27 November 2024).
- Poplašen, D.; Kerner, I. Vibracije koje se prenose na šake i ruke. Sigur. Časopis Za Sigur. U Radn. Životn. Okolini 2013, 55, 389–392. [Google Scholar]
- Goglia, V.; Suchomel, J.; Žgela, J. Izloženost vibracijama šumarskih radnika u svjetlu directive 2002/44/EC. Šumar. List 2012, 5–6, 283–289. [Google Scholar]
- Singh, G.K. Effect of Whole-Body Vibration on Vehicle Operators: A Review. Int. J. Sci. Res. (IJSR) 2012, 3, 320–323. [Google Scholar]
- Fahy, F.; Thompson, D. (Eds.) Fundamentals of Sound and Vibration, 2nd ed.; CRC Press: London, UK, 2016; ISBN 978-0-429-17647-0. [Google Scholar]
- Gomez-Gil, J.; Gomez-Gil, F.J.; Martin-de-Leon, R. The Influence of Tractor-Seat Height above the Ground on Lateral Vibrations. Sensors 2014, 14, 19713–19730. [Google Scholar] [CrossRef]
- Pobedin, A.V.; Dolotov, A.A.; Shekhovtsov, V.V. Decrease of the Vibration Load Level on the Tractor Operator Working Place by Means of Using of Vibrations Dynamic Dampers in the Cabin Suspension. Procedia Eng. 2016, 150, 1252–1257. [Google Scholar] [CrossRef]
- Shinde, A.; Jadhav, S.G. Vibration Measurement and Vibration Reduction of Steering Wheel of an Agricultural Tractor. Int. J. Sci. Res. (IJSR) 2013, 5, 44–48. [Google Scholar]
- Petrović, P.; Bracanović, Z.; Vukas, S. Oscillatory Appearance on Agricultural of Tractors. Poljopr. Teh. 2005, 30, 15–23. [Google Scholar]
- Beheshti, M.H.; Ghandhari, P. Assessment of Noise Exposure in Operator Cultivator Tiller. Int. J. Occup. Hyg. 2015, 7, 197–201. [Google Scholar]
- Ministarstvo Gospodarstva, Rada I Poduzetništva. Pravilnik o Zaštiti Radnika Od Rizika Zbog Izloženosti Vibracijama Na Radu. Available online: https://narodne-novine.nn.hr/clanci/sluzbeni/2008_12_155_4248.html (accessed on 10 January 2025).
- Deboli, R.; Calvo, A.; Preti, C. The Use of a Capacitive Sensor Matrix to Determine the Grip Forces Applied to the Olive Hand Held Harvesters. In Proceedings of the International Conference “Innovation Technology to Empower Safety, Health and Welfare in Agriculture and Agro-food Systems”, Ragusa, Italy, 15–17 September 2008. [Google Scholar]
- Servadio, P.; Marsili, A.; Belfiore, N.P. Analysis of Driving Seat Vibrations in High Forward Speed Tractors. Biosyst. Eng. 2007, 97, 171–180. [Google Scholar] [CrossRef]
- Cheng, J.; Chi, R.; Mao, E. Influence of Hanging Farm Implement on Vibration of Tractor with Electro-Hydraulic Hitch System. Trans. Chin. Soc. Agric. Eng. 2015, 31, 24–32. [Google Scholar] [CrossRef]
- Langer, T.H.; Ebbesen, M.K.; Kordestani, A. Experimental Analysis of Occupational Whole-Body Vibration Exposure of Agricultural Tractor with Large Square Baler. Int. J. Ind. Ergon. 2015, 47, 79–83. [Google Scholar] [CrossRef]
- De Almeida, S.V.; Sperotto, F.C.S.; Doimo, L.d.S.; Correia, T.P.d.S.; dos Santos, J.E.G.; Silva, P.R.A. Analysis of Vibration Levels in Agricultural Tractor with and without Cabin. Afr. J. Agric. Res. 2015, 10, 4945–4949. [Google Scholar] [CrossRef]
- Barač, Ž.; Plaščak, I.; Jurić, T.; Jurišić, M.; Heffer, G.; Nikolić, A. Proizvedena Razina Traktorskih Vibracija Pri Različitim Agrotehničkim Podlogama Koje Utječu Na Trup Rukovatelja. In Proceedings of the 9th International Scientific/Professional Conference Agriculture in Nature and Environment Protection, Vukovar, Croatia, 6–8 June 2016; pp. 82–85. [Google Scholar]
- Barač, Ž.; Plaščak, I.; Jurišić, M.; Zimmer, D.; Vidaković, I.; Laslo, J. Utjecaj Različitih Agrotehničkih Podloga Na Proizvedene Vibracije Koje Utječu Na Sustav Ruka-Šaka Rukovatelja. In Proceedings of the 10th International Scientific/Professional Conference Agriculture in Nature and Environment Protection, Vukovar, Croatia, 5–7 June 2017; pp. 187–190. [Google Scholar]
- Dewangan, K.N.; Tewari, V.K. Characteristics of Hand-Transmitted Vibration of a Hand Tractor Used in Three Operational Modes. Int. J. Ind. Ergon. 2009, 39, 239–245. [Google Scholar] [CrossRef]
- Dewangan, K.N.; Rakheja, S.; Marcotte, P.; Shahmir, A. Effects of Elastic Seats on Seated Body Apparent Mass Responses to Vertical Whole Body Vibration. Ergonomics 2015, 58, 1175–1190. [Google Scholar] [CrossRef]
- Barač, Ž.; Vidaković, I.; Zimmer, D.; Ermenić, V. Odnos Agrotehničkih Zahvata Na Proizvedenu Razinu Vibracija Te Njihov Utjecaj Na Sustav Ruka-Šaka Rukovatelja Traktora. In Proceedings of the 52. Hrvatskog i 12. Međunarodnog Simpozija Agronoma, Dubrovnik, Croatia, 12–17 February 2017. [Google Scholar]
- Barač, Ž.; Plaščak, I.; Jurišić, M.; Heffer, G.; Vidaković, I.; Marković, M.; Zimmer, D. The impact of vibration on operator whole body at agrotehnical operations. Glas. Zašt. Bilja 2017, 40, 8–14. [Google Scholar] [CrossRef]
- Scarlett, A.J.; Price, J.S.; Stayner, R.M. Whole-Body Vibration: Evaluation of Emission and Exposure Levels Arising from Agricultural Tractors. J. Terramech. 2007, 44, 65–73. [Google Scholar] [CrossRef]
- Cutini, M.; Brambilla, M.; Bisaglia, C. Whole-Body Vibration in Farming: Background Document for Creating a Simplified Procedure to Determine Agricultural Tractor Vibration Comfort. Agriculture 2017, 7, 84. [Google Scholar] [CrossRef]
- Deboli, R.; Calvo, A.; Preti, C. Comparison between ISO 5008 and Field Whole Body Vibration Tractor Values. J. Agric. Eng. 2012, 43, e8. [Google Scholar] [CrossRef]
- Vallone, M.; Bono, F.; Quendler, E.; Febo, P.; Catania, P. Risk Exposure to Vibration and Noise in the Use of Agricultural Track-Laying Tractors. Ann. Agric. Environ. Med. AAEM 2016, 23, 591–597. [Google Scholar] [CrossRef]
- Tewari, V.K.; Vidhu, K.P.; Arudra, A.K.; Kumari, S. Reduction of Hand Transmitted and Whole Body Vibrations Experienced by Tractor Operators by Using Piezo Crystal Material. Agric. Eng. Int. CIGR J. 2013, 15, 209–220. [Google Scholar]
- Calvo, A.; Deboli, R.; Preti, C. Operators’ Exposure to Noise and Vibration in the Grass Cut Tasks: Comparison between Private and Public Yards. Agric. Eng. Int. CIGR J. 2016, 18, 213–225. [Google Scholar]
- Deboli, R.; Calvo, A.; Preti, C. Whole-Body Vibration: Measurement of Horizontal and Vertical Transmissibility of an Agricultural Tractor Seat. Int. J. Ind. Ergon. 2017, 58, 69–78. [Google Scholar] [CrossRef]
- Yuan, X.; Wu, W. The WASPAS and AHP Optimization Methods Applied on Vibro-Diagnostic Models for Rotational Machines. Eng. Comput. 2022, 38, 2389–2406. [Google Scholar] [CrossRef]
- Carra, S.; Monica, L.; Vignali, G. Reduction of Workers’ Hand-Arm Vibration Exposure through Optimal Machine Design: AHP Methodology Applied to a Case Study. Saf. Sci. 2019, 120, 706–727. [Google Scholar] [CrossRef]
- He, S.; Tang, T.; Ye, M.; Xu, E.; Deng, J.; Tang, R. A Domain Association Hierarchical Decomposition Optimization Method for Cab Vibration Control of Commercial Vehicles. Measurement 2019, 138, 497–513. [Google Scholar] [CrossRef]
- Som, S.; Singh, L.P. Evaluation of Ergonomic Assessment Tools Using Fuzzy AHP. In Proceedings of the Recent Advances in Operations Management and Optimization, Jalandhar, India, 10–12 March 2023; Sachdeva, A., Goyal, K.K., Garg, R.K., Davim, J.P., Eds.; Springer Nature: Singapore, 2024; pp. 213–219. [Google Scholar]
- HRN ISO 5008:2015/Hrvatski Normativni Dokument/HRN4You—Hrvatski Zavod Za Norme. Available online: https://repozitorij.hzn.hr/norm/HRN+ISO+5008%3A2015 (accessed on 10 December 2022).
- HRN ISO 2631-4:2010/Hrvatski Normativni Dokument/HRN4You—Hrvatski Zavod Za Norme. Available online: https://repozitorij.hzn.hr/norm/HRN+ISO+2631-4%3A2010 (accessed on 10 December 2022).
- HRN EN ISO 5349-1:2008/Hrvatski Normativni Dokument/HRN4You—Hrvatski Zavod Za Norme. Available online: https://repozitorij.hzn.hr/norm/HRN+EN+ISO+5349-1%3A2008 (accessed on 10 December 2022).
- HRN EN ISO 5349-2:2008/A1:2015/Hrvatski Normativni Dokument/HRN4You—Hrvatski Zavod Za Norme. Available online: https://repozitorij.hzn.hr/norm/HRN+EN+ISO+5349-2%3A2008%2FA1%3A2015 (accessed on 10 December 2022).
- Deboli, R.; Calvo, A.; Preti, C. Whole Body Vibration (WBV): Comparison among Fied Dana and Standard Test Track (ISO 5008) in Different Operative Conditions. In Proceedings of the 33 CIOSTA—CIGR V Conference Technology and Management to Ensure Sustainable Agriculture, Agro-System, Forestry and Safety, Reggio Calabria, Italy, 17–19 June 2009; pp. 1–10. [Google Scholar]
- Barač, Ž.; Plaščak, I.; Jurić, T.; Jurišić, M.; Heffer, G.; Zimmer, D.; Vidaković, I.; Radočaj, D.; Majstorović, S. Utjecaj Vibracija Na Sustav Ruka-Šaka Pri Radu Traktora IMT 539. In Proceedings of the 12th International Scientific/Professional Conference Agriculture in Nature and Environment Protection, Osijek, Croatia, 27–29 May 2019; pp. 295–299. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).