Optimization of Liquid Manure Injector Designs for Cover Crop Systems Using Discrete Element Modeling and Soil Bin Evaluation

Abstract

This study integrates Discrete Element Method (DEM) simulations, soil bin experiments, and multi-objective optimization to develop an energy-efficient manure injector shank. Eighteen geometries were first screened using DEM, reducing the set to six designs (S_1–S_6) based on draft force–rupture area performance. The selected designs, varying in rake angle (30°, 45°, 60°), thickness (25 and 30 mm), and width (102, 110, and 118 mm), were tested in a soil bin to measure draft, trench width, spoil cross-sectional area, and soil rupture. Statistical analysis revealed significant differences among designs (p < 0.05), confirming that rake angle, width, and thickness have a strong influence on the soil–tool interaction. A multi-objective optimization framework was then used to minimize draft, trench width, and spoil area while maximizing rupture, with performance quantified through overall desirability values (0–1). Shank S_3 (45° rake, 25 mm thickness, 110 mm width) achieved the highest desirability (0.6676), representing the best trade-off between energy efficiency, minimal surface disturbance, and effective subsurface loosening. This integrated DEM–experimental–optimization approach demonstrates a reliable, data-driven workflow for implement design, reducing reliance on extensive field trials. However, future studies should validate the performance of S_3 and other candidate designs under diverse soil types, moisture levels, and operating conditions to confirm their agronomic and environmental benefits.

1. Introduction

Wisconsin’s $52.8 billion dairy industry supports over 120,700 jobs and nearly 45% of the state’s agricultural revenue [1]. Each year, around 6 billion gallons of manure are applied to fields, often by custom operators. However, poor manure management has led to environmental issues, such as nitrate contamination and harmful algal blooms, resulting in over a billion dollars in mitigation costs. Cover crops, typically planted after corn harvests, coincide with manure application periods, creating scheduling and field management challenges. Applying manure before planting delays cover crop growth; while applying it afterward can smother young plants. Although manure injections could improve nutrient use, current methods are too invasive for newly established cover crops. An innovative solution is needed to align manure land application with cover cropping practices for sustainable agriculture. The integration of cover crops into agricultural systems has garnered significant attention due to their role in enhancing soil health, reducing erosion, and improving nutrient management [2,3]. Cover crops have been proposed as a potential solution to mitigate nitrogen losses by absorbing and temporarily immobilizing nitrogen through plant uptake [4] and mineralization [5]. However, applying liquid manure in cover crop systems presents challenges, particularly in balancing effective nutrient incorporation with minimal soil disturbance.

Traditional manure application methods often disrupt soil structure and diminish the benefits of cover crops, prompting the use of injection techniques that place liquid manure below the soil surface to reduce odors, nitrogen emissions, and nutrient losses by runoff [6,7,8]. The design of injection tools, including chisels, knives, discs, and sweeps, strongly influences manure distribution and soil disturbance. Chisel injectors cut deep slots that channel manure downward, but they demand high energy and may lack sufficient holding capacity [9,10]. In contrast, disc injectors mix manure with surface soil through a rolling action, which compacts the soil and reduces infiltration [11,12,13]. Sweep injectors, by contrast, distribute manure in wide horizontal bands at shallow depths, lifting the soil and allowing it to settle back over the manure [14]. However, this pattern has been linked to higher nitrate levels compared to knife injectors, due to greater soil–manure contact, which enhances nitrogen mineralization [15]. Soil bin studies have been widely used to evaluate manure application equipment, providing controlled conditions to isolate the effects of tool geometry and operating parameters. Nyord et al. [16] optimized the slurry injector design through soil bin experiments, demonstrating that double discs at a 40 mm depth, combined with a tine at a 100 mm depth and a 40° rake angle, minimizing draft forces and crop damage, emphasizing the importance of precise component alignment [16]. McLaughlin et al. [17] also employed soil bins to compare draft requirements of single-disc, sweep, and chisel-sweep injectors, finding that soil condition and tool design strongly influenced energy demand, with sweep-based systems performing more efficiently than single-disc designs [17]. Rahman et al. [18] introduced a manure distribution index in soil bin testing of disc, furrower, and sweep injectors, showing that discs concentrated manure vertically. At the same time, furrowers achieved a lateral spread of up to 1.4 times their tool width, demonstrating higher efficiency relative to their size. Collectively, these soil bin studies reveal how injector depth, rake angle, travel speed, and cutting width govern draft force, soil disturbance, and manure placement [19,20], while also highlighting the resource-intensive nature of prototype-based testing.

The Discrete Element Method (DEM) is a computational modeling technique used to simulate the mechanical behavior of systems composed of many individual particles or discrete elements. In DEM, each particle is treated as an independent entity with its mass, position, and velocity, and interactions between particles are governed by contact mechanics that account for normal and tangential forces, including friction, damping, and sometimes cohesion. This method is particularly well-suited for analyzing granular materials, such as soils, powders, seeds, or aggregates, where particle-level interactions significantly influence bulk behavior. DEM has emerged as a powerful computational tool for analyzing soil-tool interactions in agricultural engineering. It enables modeling individual soil particles and their interactions with tool surfaces, allowing for visualization and quantification of dynamic soil displacement. DEM captures soil’s discontinuous and heterogeneous nature, making it suitable for evaluating liquid manure injection tools in varying soil conditions. DEM has been effectively used to simulate draft force, soil disturbance, and flow behavior, enabling rapid screening of multiple tool geometries under various soil conditions [21,22,23]. These simulations reduce the need for extensive field trials and support performance-driven design decisions. Studies such as Sedara et al. [24] have demonstrated that combining DEM with similitude principles can enhance prediction accuracy and identify efficient tool geometries for cohesive-frictional soils. Following DEM-based screening, soil bin experiments are critical for validating tool performance under controlled conditions. These tests enable the precise measurement of key parameters, such as draft force and above- and below-ground soil disturbance, with data collection supported by load cells, imaging systems, and standardized soil preparation methods [20,25]. Integrating simulation and experimental data has paved the way for systematic optimization strategies, often employing multi-objective frameworks to balance energy demand and minimal soil disruption. Combining DEM simulations, soil bin validation, and iterative optimization provides a powerful approach to developing next-generation manure injector tools.

This study focuses on developing an improved liquid manure injector tool that requires minimal draft force and causes minimal soil disturbance, maintaining soil structure and preserving cover crops. DEM offers a powerful computational approach for simulating soil-tool interactions, allowing for virtual testing and evaluation of various tool geometries, thereby reducing the time and cost associated with physical prototyping. The goal is to develop a liquid manure injector that minimizes draft force and soil disturbance.

The specific objectives of the research are to:

• Develop a diverse set of liquid manure injector geometries incorporating variations in rake angle, thickness, and width to capture a broad design space.
• Utilize Discrete Element Method (DEM) simulations to evaluate injector geometries for optimal soil–tool interaction.
• Experimentally evaluate selected injector designs in a controlled soil bin to quantify draft force, above-ground soil disturbance, and below-ground rupture characteristics.
• Apply multi-objective optimization techniques to identify the injector configuration that balances minimal energy demand with minimal surface disturbance and maximum subsoil manure placement.

2. Materials and Methods

2.1. Liquid Manure Injector CAD Design

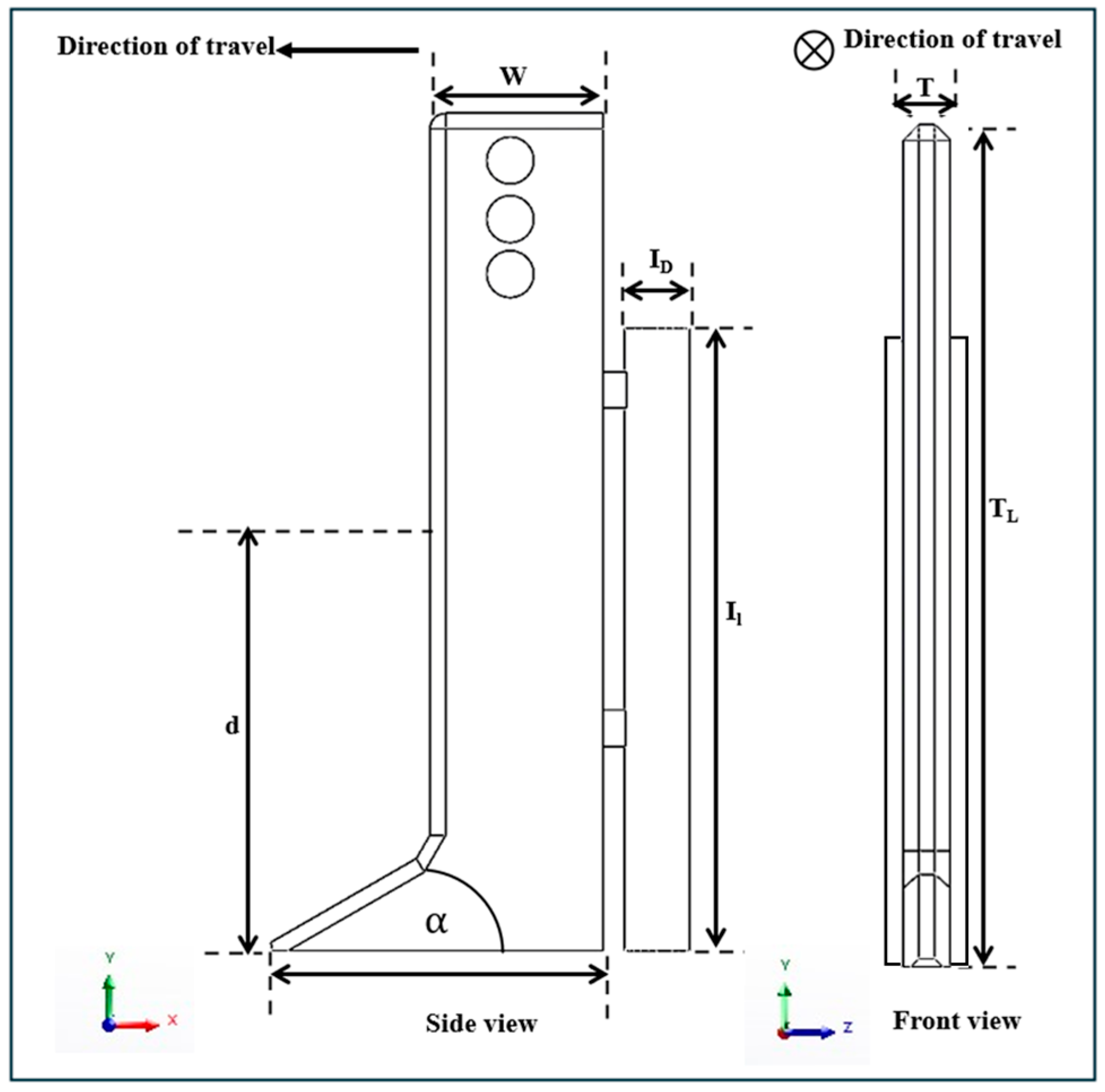
A comprehensive literature review was conducted on existing liquid manure injectors (shank-based) used in cover crop manure applications. Insights from this review informed the development of a new injector design, which focuses on minimizing draft force and soil disturbance. To systematically analyze different design configurations, 3D CAD models of eighteen liquid manure injectors were created using SolidWorks 2024. The injector designs incorporated variations in rake angle (30°, 45°, and 60°), tool thickness (25 and 30 mm), and tool width (102, 110, and 118 mm) (

Table 1. Design features of the eighteen liquid manure injectors as shown in Figure 1.

DI *	Rake Angle (α) (°)	Tool Thickness (T) (mm)	Tool Width (w) (mm)
1	30	25	102
2	30	25	110
3	30	25	118
4	30	30	102
5	30	30	110
6	30	30	118
7	45	25	102
8	45	25	110
9	45	25	118
10	45	30	102
11	45	30	110
12	45	30	118
13	60	25	102
14	60	25	110
15	60	25	118
16	60	30	102
17	60	30	110
18	60	30	118

* DI is the injector design.

). These geometric configurations were selected to assess their impact on injector performance. A schematic diagram of the modeled injectors is presented in Figure 1. The design includes side and front views, with features like rake angle (α), tool width (W), tool thickness (T), tool total length (T_L), injection tube length (I_L), and injector tube diameter (I_D), providing a detailed understanding of the tool’s structural properties. The injector design (ID) tools were labeled ID_1–ID_18. The rake angle of a shank tool plays a critical role because it enables the soil to flow more smoothly over the tool surface, thereby decreasing resistance and making it easier to pull the tool through the soil [26]. The tool width is related to side friction and soil compaction along the tool’s edges during soil engagement. Tool width also helps determine the size of the cross-sectional area of the soil that the tool engages. Tool thickness is related to structural strength, which affects the frontal surface area facing the direction of motion, thereby increasing soil-tool contact and friction.

2.2. DEM Screen Soil-to-Tool Simulation Setup

The DEM screening model was developed using soil mechanical parameters reported in the literature [27,28,29,30] for soils, which reliably capture soil rupture patterns and relative draft force trends in soil–tool interaction simulations in ALTAIR-EDEM (2024) software. Because many DEM input parameters, such as particle stiffness, friction, and cohesion, are material-property based and transferable across studies, their use from validated sources ensures consistency with accepted modeling practices [31]. Thus, the DEM setup provides a reliable approach for screening injector designs, reducing experimental costs while maintaining confidence in comparative outcomes. A similar method was successfully applied by Sedara et al. [24] for screening scaled shank designs.

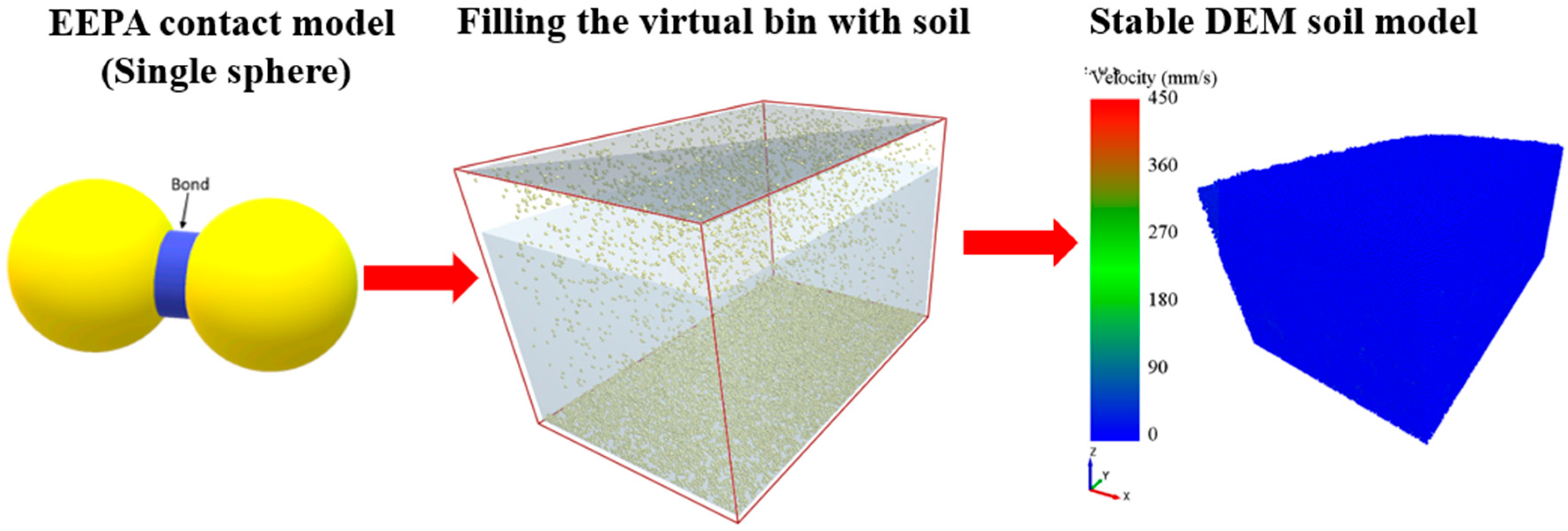
Figure 2 shows the development of a stable DEM soil model using the Edinburgh Elasto-Plastic Adhesive (EEPA) contact model. In this method, soil particles are modeled as bonded spheres that interact through elastic, plastic, and adhesive forces, capturing the cohesive behavior of real soil. A virtual soil bin (1140 × 1010 × 580 mm) is filled with spherical particles (Pd = 3 mm) using a controlled filling procedure, after which the soil settles under gravity until particle velocities stabilize. The blue region in the velocity map indicates that the particles have reached equilibrium, confirming a mechanically stable soil bed suitable for simulating soil–tool interactions and deformation behavior.

The DEM was employed to simulate soil-to-injector shank interactions, screening and evaluating the performance of eighteen initial shank designs, which ultimately yielded six design shanks for the subsequent soil bin experiment study. The screening focused on two key DEM-predicted parameters, draft force and soil rupture area, enabling comparison of design features based on performance efficiency. This DEM-based pre-screening approach aimed to significantly reduce the need for physical prototyping and experimental testing, which are often time-consuming and costly [32]. The Edinburgh Elasto-Plastic Adhesive (EEPA) contact model in EDEM software [33] was selected for the constitutive modeling of contact forces and displacements between particles and between soil and tool surfaces. The EEPA model captures elasto-plastic behavior during loading and unloading cycles, incorporating a stress-dependent cohesion mechanism, which makes it suitable for modeling the mechanical response of agricultural soils. For the DEM simulations, soil particles were represented as single spheres with a diameter of 3 mm. All relevant material and interaction properties (Poisson’s ratio, shear modulus, particle density, and frictional coefficients) were based on values reported in previous DEM soil-tool interaction studies [34,35].

Table 2. Initial DEM parameters for screening the initial eighteen designs.

DEM Parameters	Value	Source
Soil particle
Single sphere particle diameter (mm)	3	Assumed
Soil parameters
Poisson’s ratio	0.32	[34]
Steel parameters
Poisson’s ratio	0.30	[33]
Shear modulus (Pa)	1.0 × 106	[33]
Solid density (kg/m3)	7800	[33]
Soil-to-Soil interaction
Coefficient of Restitution	0.01	[34]
Soil-to-Tool (steel) interaction
Coefficient of Restitution	0.01	[34]
Coefficient of Static friction	0.31	[35]
Coefficient of Rolling friction	0.13	[34]
Edinburgh elastic plastic adhesion (EEPA) contact model
Contact plasticity ratio	0.926	[37]
Slope exp	1.5	[33]
Tensile exp	1.5	[33]
Tangential stiff multiplier	0.66667	[33]

and

Table 3. DEM simulation setup and operating parameters.

Parameter	Description/Value	Unit/Notes
Virtual soil bin dimensions	1140 × 1010 × 580	mm (Length × Width × Height)
Number of particles	809,943	—
Particle diameter (Pd)	3	mm
Software used	ALTAIR-EDEM (2024)	—
Time step (Δt)	5.07 × 10−5	s (3% Rayleigh criterion)
Solver	GPU CUDA + 22 CPU cores	—
Hardware configuration	Dell Intel® Core™ Ultra 9 185H, 2.30 GHz, 64 GB RAM	High-performance system
Forward speed	440	mm/s
Working depth	200	mm
Simulation duration	0.5	s
Sampling rate	100	Hz
Measured outputs	Draft force, soil rupture area	In tool travel direction

summarize the parameters and simulation setup used for soil-to-soil and soil-to-geometry interactions, including coefficients of restitution, static friction, and rolling friction based on the Hertz-Mindlin contact law. The EEPA model’s parameters, such as surface energy, contact plasticity ratio, pull-off force, slope exponent, tensile exponent, and tangential stiffness multiplier, were also configured according to EDEM documentation [33,36].

2.3. Soil Bin Design of Experiment

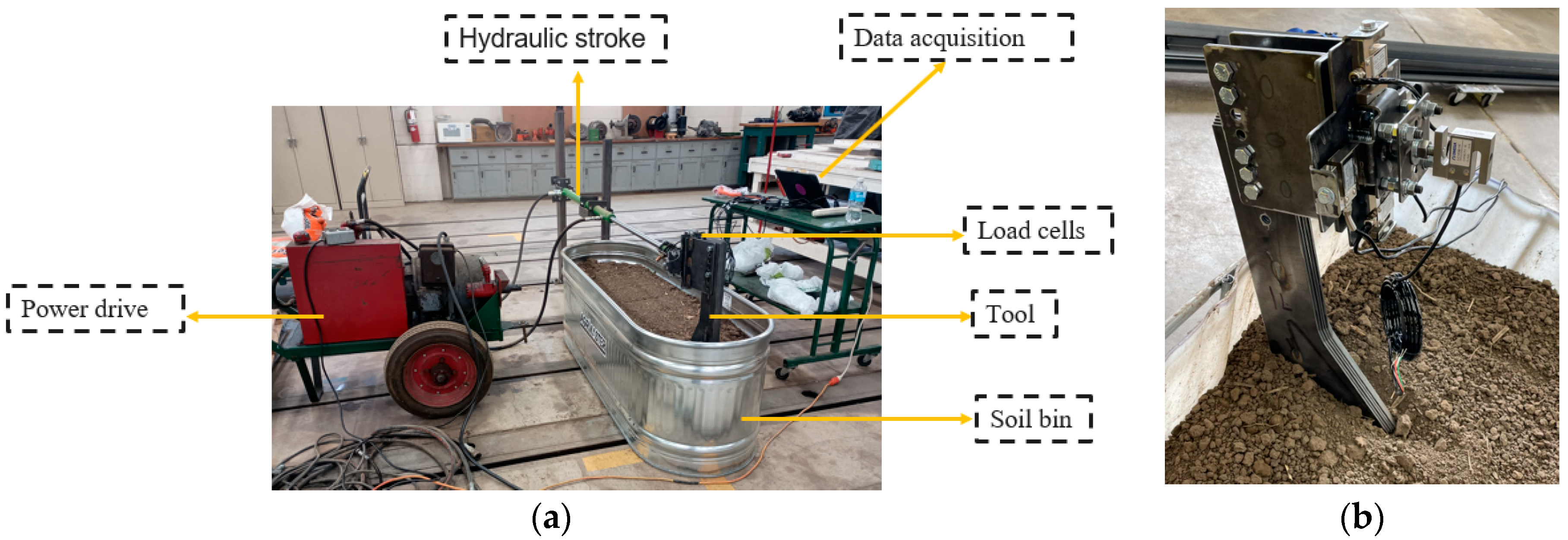
The soil bin used in this study measured 1140 mm in length, 1010 mm in width, and 580 mm in height (Figure 3). The soil was filled to a consistent soil height of 460 mm, creating a controlled environment to evaluate the soil–tool interaction of different manure injector shank designs. A hydraulic actuation system drove the movement of the liquid manure tool through the soil. A 1220 mm stroke hydraulic cylinder, powered by a portable hydraulic power unit, provided the pulling force. A flow control valve regulated the hydraulic flow, allowing a consistent tool travel nominal speed of 440 mm/s. This speed was selected to simulate typical field conditions and was maintained uniformly across all trials. The operating depth of the tools was precisely maintained at 200 mm using an adjustable mounting system. The hydraulic cylinder mounts allowed vertical adjustment, and both the tools and mounting brackets were fabricated with 25.4 mm (1-inch) spaced holes, enabling fine depth control. These settings ensured consistent tool alignment and depth across all treatments.

The soil used in the experiment was sourced from the West Madison Agricultural Research Station in Verona of Wisconsin, USA (Bayer sandy loam (Coarse-loamy, mixed, semiactive, mesic Typic Hapludalfs)), consisting of 45% sand, 32% silt, and 16% clay, and allowed to air-dry for one week before use. After drying, large clumps and shafts were manually removed to ensure a uniform soil texture suitable for controlled testing. Between replications, the soil was reconditioned to ensure consistency across trials. Reconditioning involves using a pulverizer machine (Max LiIon Cultivator/Tiller, Black & Decker, New Britain, CT, USA) to loosen and break up the soil, thereby eliminating clumps. After loosening, the soil was leveled using a flat wooden plate to create a smooth and even surface. A 10 × 10-inch tamper (Yard Works, Charleston, SC, USA) was then used to achieve the desired bulk density of 1340 kg/m³ using the core sampling method, for each run (core volume = 252.88 cm³)), ensuring consistent soil compaction across the entire bin. This systematic approach helped standardize soil conditions for each trial, thereby improving the reliability and repeatability of the experimental results.

A completely randomized design (CRD) was employed, with six different shank designs evaluated across three replications. Each replication consisted of a separately prepared soil bed. The shank designs were randomly assigned to minimize bias due to potential soil variability. Therefore, the objective was to identify a shank configuration that delivers effective subsoil fracturing with minimal energy input and surface disturbance, aligning with conservation tillage and sustainable manure management practices.

2.4. Soil Draft Forces and Soil Disturbance Measurement

The soil bin experimental setup and measurement parameters used are presented in

Table 4. Summary of Soil Bin Test Parameters.

Parameter	Description/Value	Details/Source
Measured variable	Draft forces (horizontal forces, Fx)	Acting on liquid manure tools
Force sensor	CALT S-Type Load Cell (Model: DYLY-103l)	SHANGHAI QIYI Co., Ltd., Baoshan District, Shanghai, China
Rated capacity	0–500 N
Sensitivity	2.0 mV/V
Number of tool prototypes tested	6	Selected for soil bin tests
Data acquisition system	DEWSoft KRYPTON	Dewesoft LLC, Whitehouse, OH, USA
System resolution	24-bit
Bandwidth	0.49 fs
Voltage ranges	±100 mV, ±10 mV
Tool travel speed	440 mm/s (constant nominal speed)
Working depth	200 mm
Sampling rate	100 Hz	Load cells recording frequency

, which outlines the instrumentation specifications, operating conditions, and data acquisition details employed to measure the draft forces acting on the liquid manure injector tools.

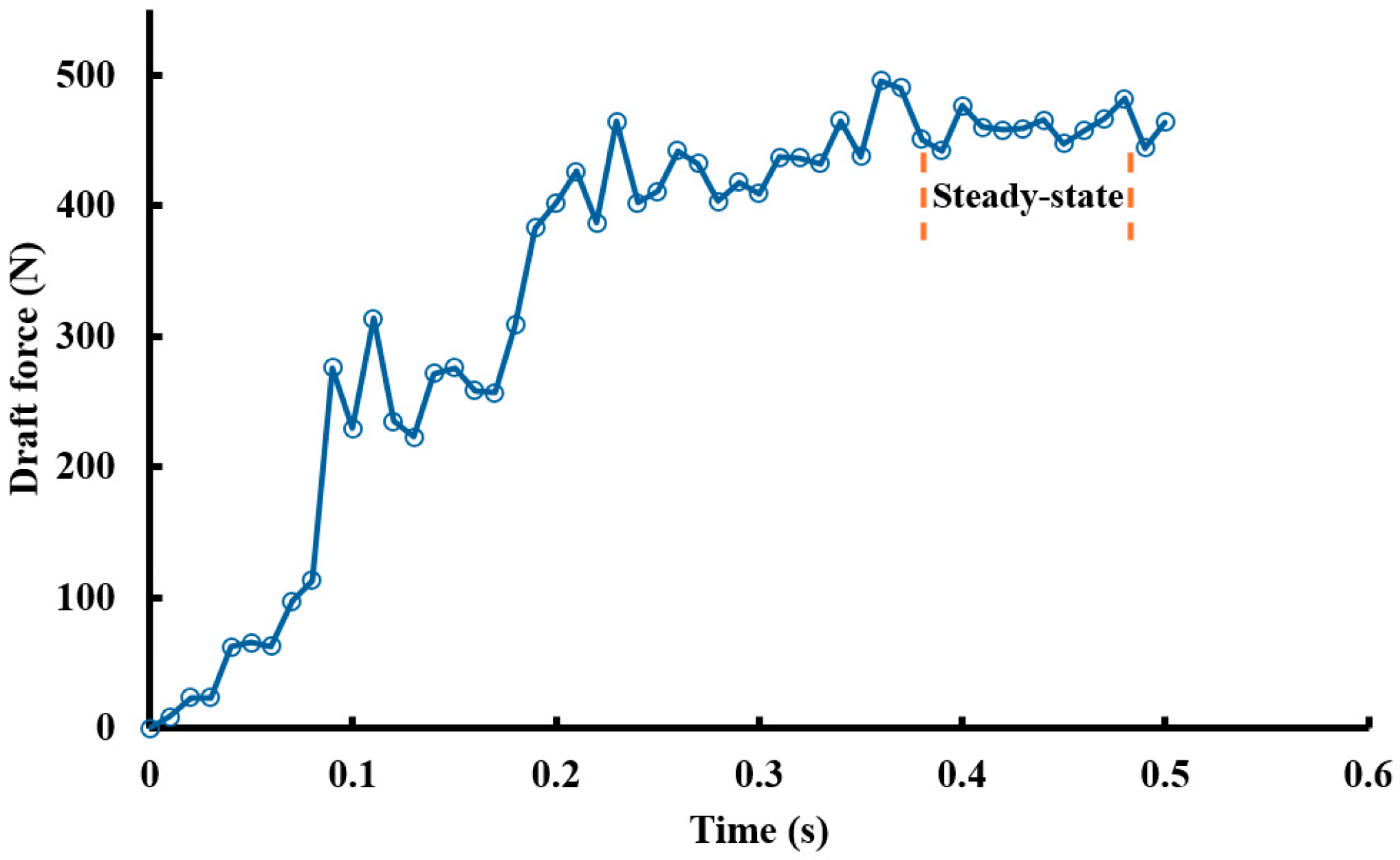
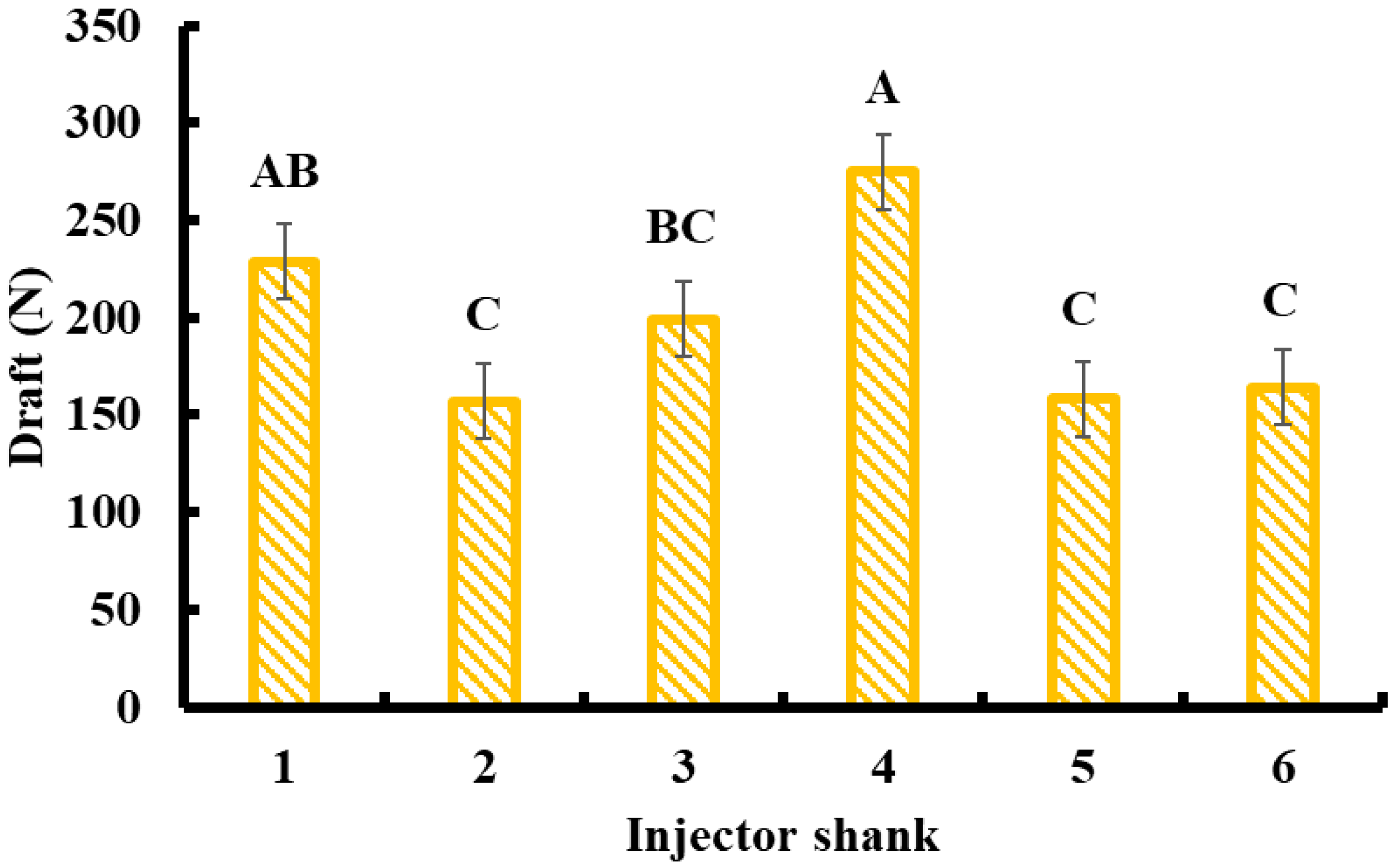
During the soil bin tests, the draft forces (horizontal forces, Fx) acting on the liquid manure tools were measured using CALT S-Type Load Cells DYLY-103l (rated capacity: 0–500 N, sensitivity: 2.0 mV/V; SHANGHAI QIYI Co., Ltd., Baoshan District, Shanghai, China). Draft force data were collected for six selected tool prototypes as they traveled along the soil bin. The data acquisition system used was the DEWSoft KRYPTON (resolution: 24-bit, bandwidth: 0.49 fs, voltage ranges: ±100 mV, ±10 mV; Dewesoft LLC, Whitehouse, OH, USA). Each tool traveled at a constant nominal speed of 440 mm/s and at a tool working depth of 200 mm. The load cells recorded force data at a sampling rate of 100 Hz.

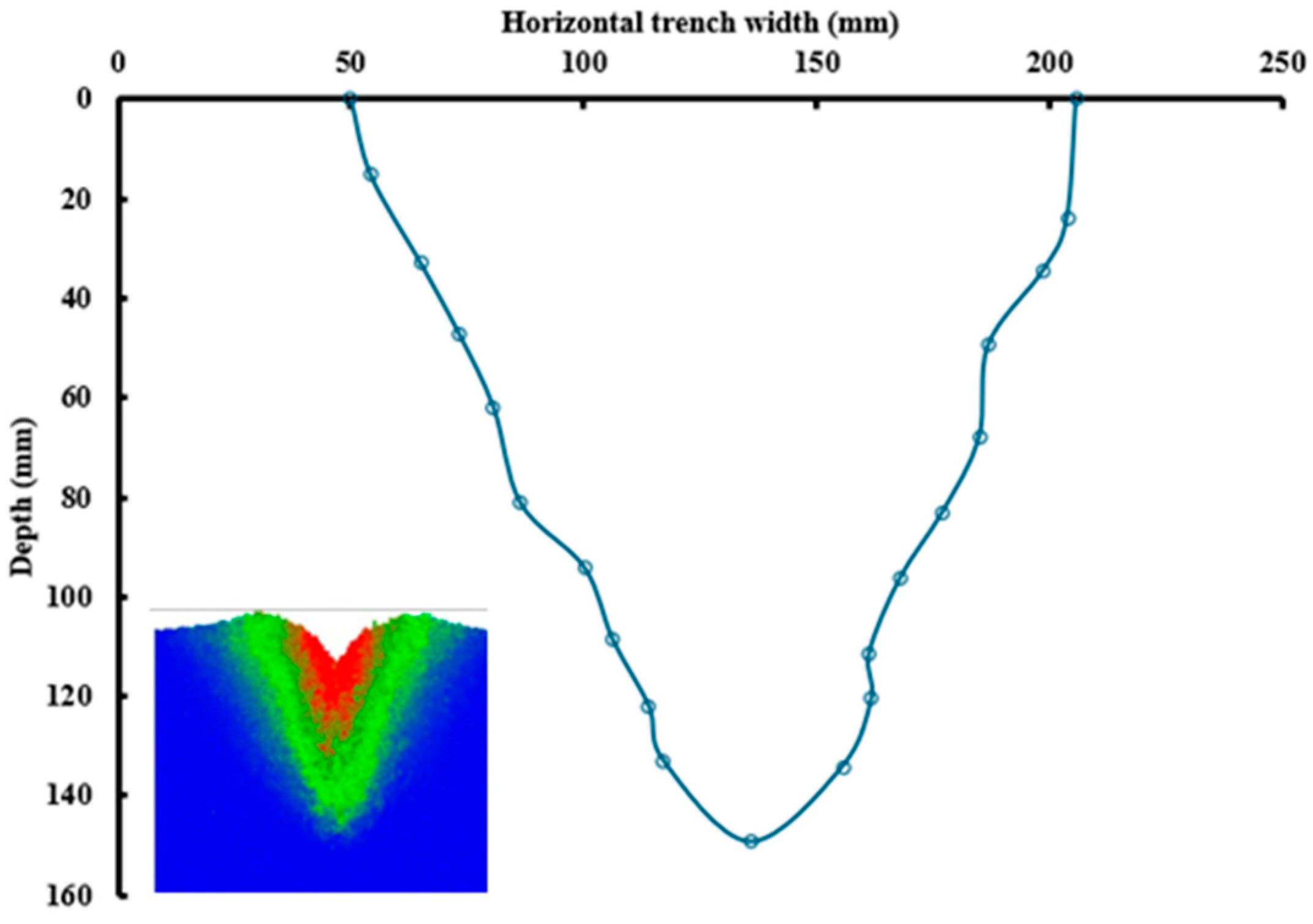
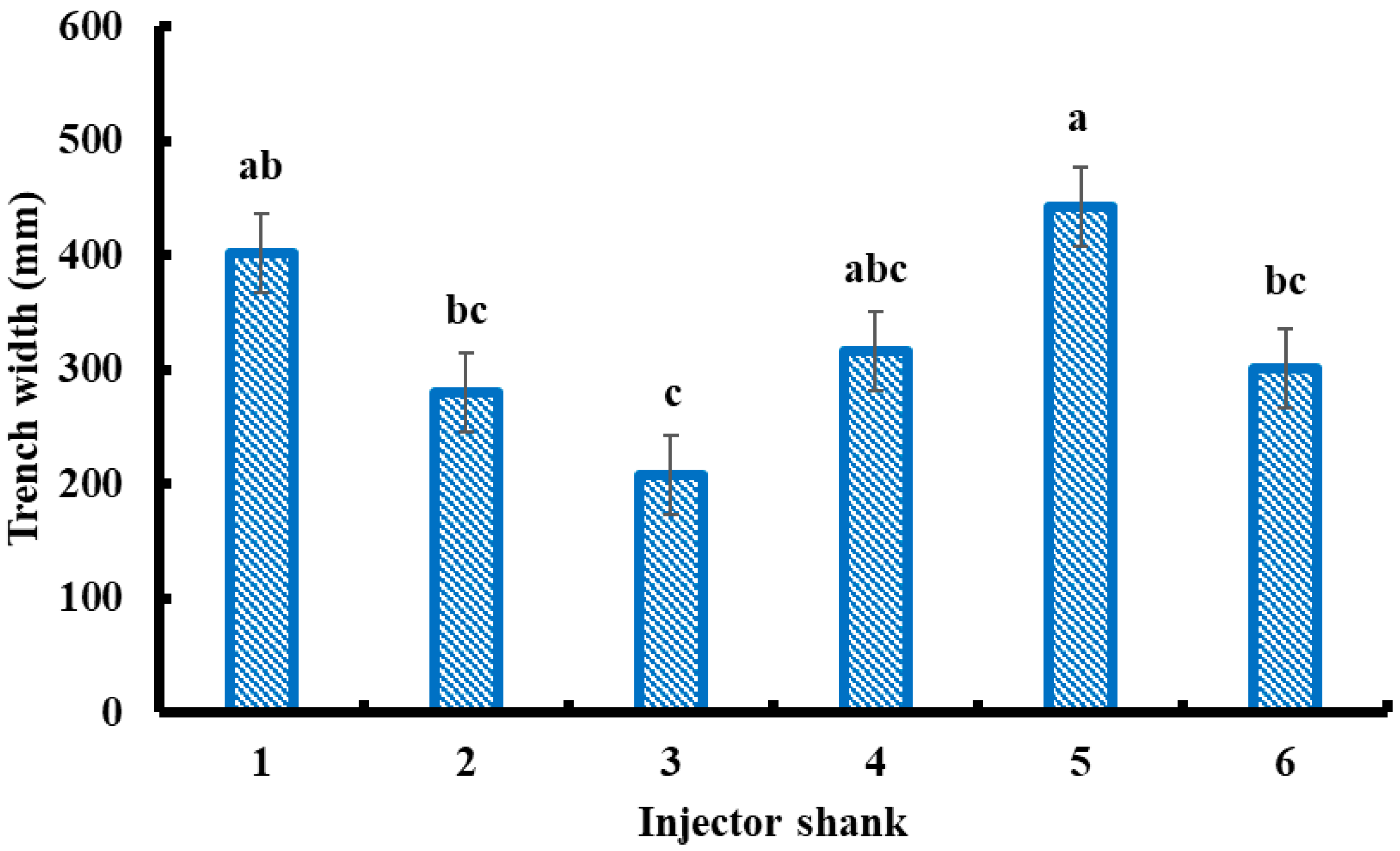
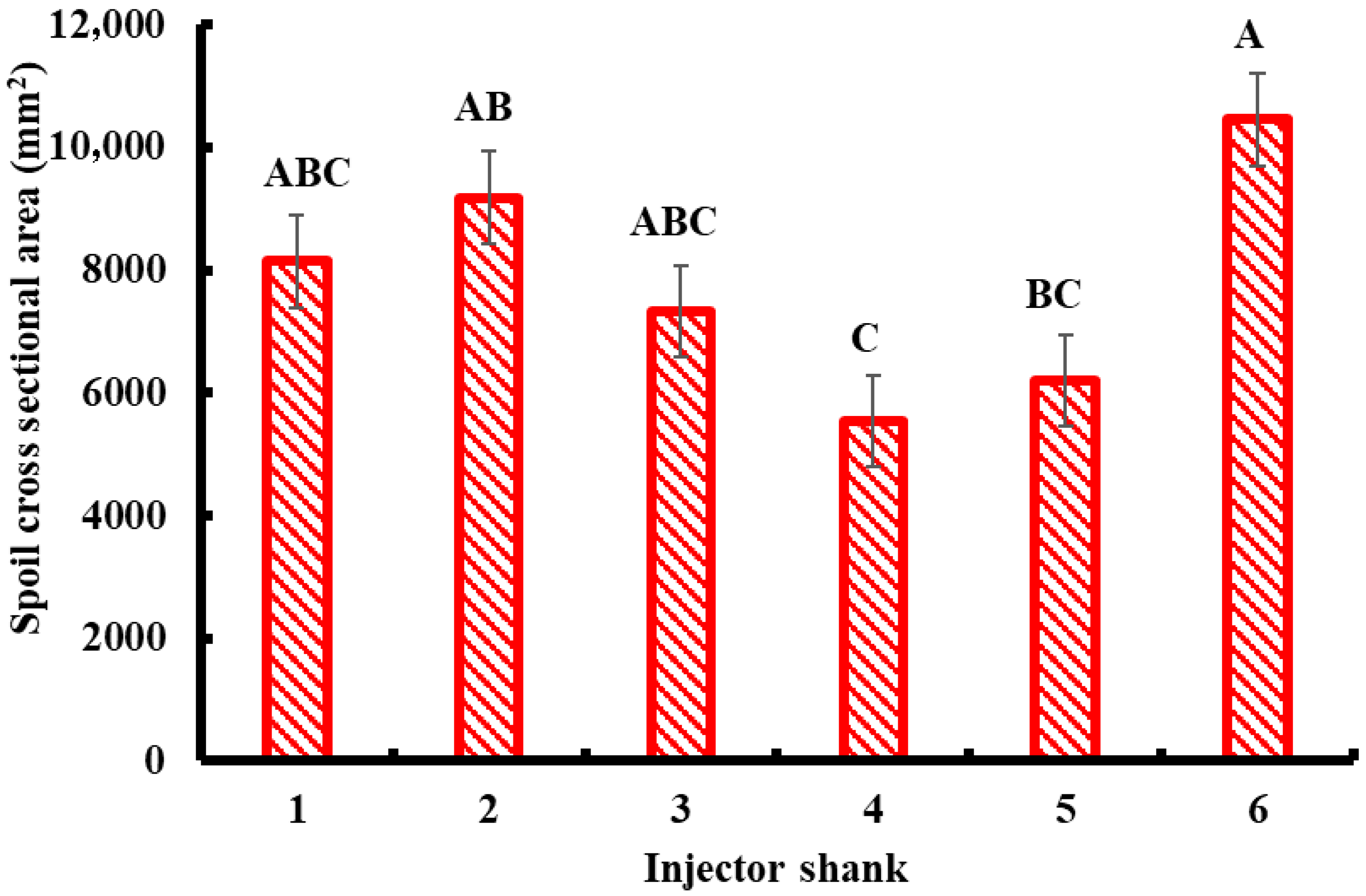
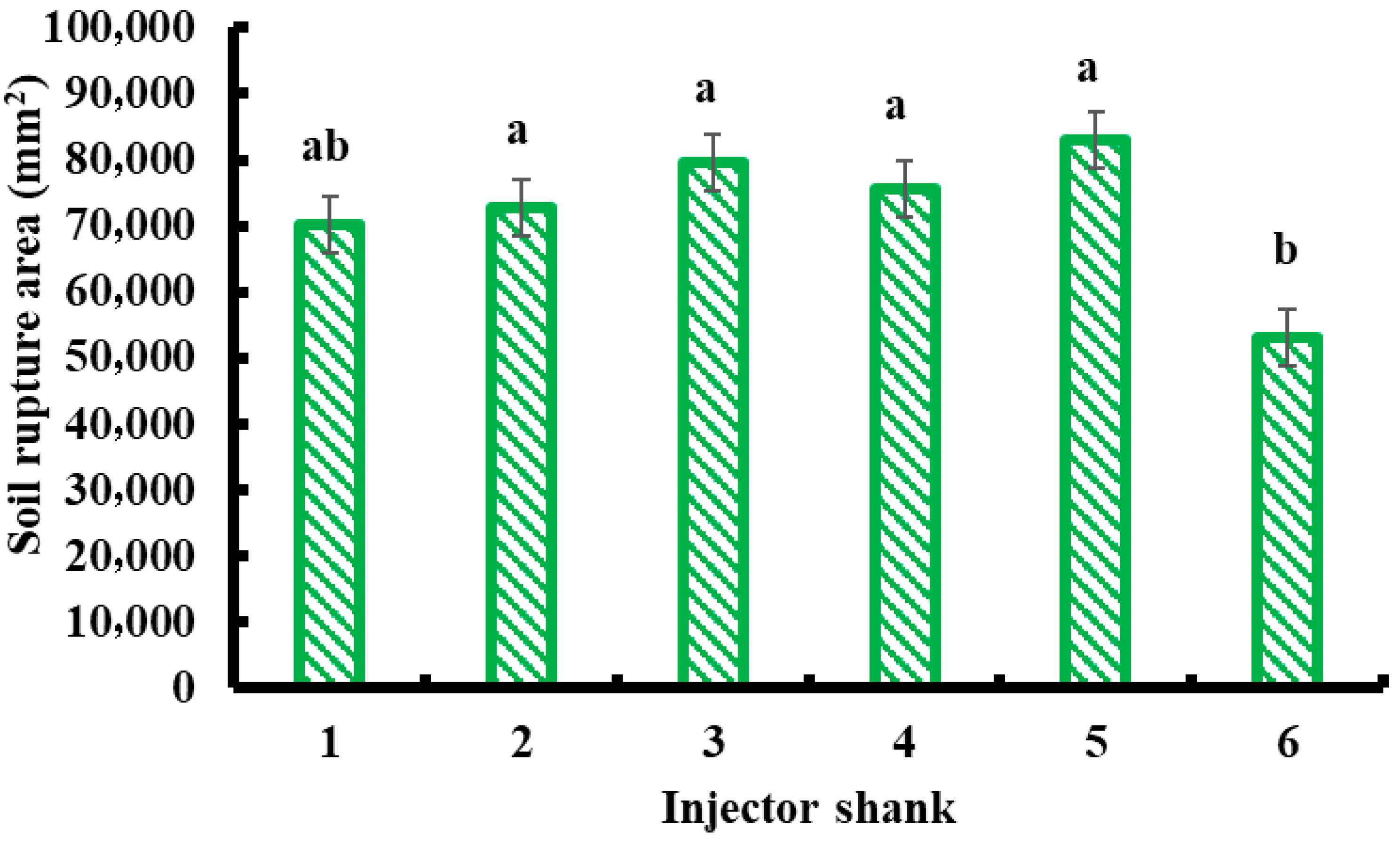
The liquid manure injector prototypes were also evaluated for their impact on both below-ground and above-ground soil disturbance. Above-ground disturbance was assessed by measuring trench width and spoil cross-sectional area (Equation (1)), while below-ground disturbance was quantified by determining the soil rupture area.

$$S_{CA}={MR}_H\times T_W$$

(1)

where $S_{CA}$ is Spoil cross-sectional area, ${MR}_H$ is mean ridge height, and $T_W$ is trench width.

Trench width and ridge height (left and right) were measured using a Wixey Remote Planer Readout Device (Barry Wixey Development, Seattle, WA, USA; resolution: 0.1 mm) (Figure 4b), with measurements referenced to the undisturbed soil surface after each test. The spoil cross-sectional area was calculated by multiplying the trench width by the vertical soil displacement (ridge height) (Figure 4c). To measure below-ground soil disturbance, loosened soil in the affected regions was carefully removed by hand to expose the soil rupture area. Vertical distances (y-axis) were measured using a Bosch GLM 50–27 CG Professional laser measurement device (Bosch, Gerlingen, Germany) (Figure 4a). In contrast, lateral distances (x-axis) were recorded using the Wixey Remote Planer Readout Device. Images of the exposed soil rupture areas were captured using a Canon G7X camera (Canon Inc., Tokyo, Japan) for image processing. The Canon G7 X, featuring a 25.4 mm sensor (13.2 × 8.8 mm) and a resolution of 5472 × 3648 pixels, has a pixel pitch of 2.41 µm. Its spatial resolution depends on the focal length and distance: at an 8.8 mm focal length, the resolution was 0.137 mm/pixel at 0.5 m, while at a 36.8 mm focal length, it improved to 0.0327 mm/pixel at the same distance. Thus, closer distances and longer focal lengths of 50 mm yield finer pixel resolution, making the setup adaptable to the resolution needs for soil rupture pictures, which were recorded at 30 frames per second (fps). Selected high-quality images were then analyzed using the open-source software ImageJ 1.54p [38]. In ImageJ, the disturbed and undisturbed soil sections were distinguished, and a profile line was drawn across the lateral extent of the disturbed soil to generate a graph showing horizontal distance versus depth (in pixels), which was then converted to millimeters. The soil rupture area was estimated from these profiles using the trapezoidal rule for calculating area under the curve in MATLAB (R2022b; MathWorks Inc., Natick, MA, USA) and reported as a numerical estimate [39]. These results were compared with the direct measurement approach to validate the consistency and reliability of the DEM model predictions.

2.5. Data Analysis and Optimization

All data were statistically analyzed to evaluate variability and trends across the six tool prototypes. Graphical analyses were conducted to compare minimum, maximum, and mean values for each response variable, including draft force and soil disturbance metrics. To assess whether the differences among tool designs were statistically significant, a one-way analysis of variance (ANOVA) was performed. When significant differences were detected, post hoc comparisons were conducted using Tukey’s HSD test with a significance level of 0.05. All statistical analyses were carried out using JMP Pro 11.0.0 (JMP Statistical Software, SAS Institute Inc., Cary, NC, USA).

A multi-response optimization was performed using the Optimization Profiler in JMP Pro to determine the optimal configuration of the liquid manure injector design. This analysis aimed to maximize overall desirability by simultaneously considering multiple performance criteria, specifically minimizing draft force and soil surface disturbance while maximizing subsurface soil rupture. The response variables included draft force, trench width, spoil cross-sectional area, and soil rupture area. The optimization was based on the desirability function methodology developed by [40], which enables the integration of multiple, potentially conflicting objectives into a single composite desirability score. Individual desirability functions were developed for each response by transforming the measured values of draft force, trench width, spoil cross-sectional area, and soil rupture area into a unitless scale from 0 (undesirable) to 1 (ideal). The optimization framework assigned weights based on the design objectives: minimizing draft force, trench width, and spoil area, while maximizing soil rupture. Draft force received the highest weight (0.40), reflecting its central role in reducing energy demand. Trench width (0.25) and spoil cross-sectional area (0.25) were given moderate weights to balance surface disturbance considerations. The soil rupture area was positively weighted (0.10), but at a lower level than the draft force, recognizing its importance for subsurface loosening, while ensuring energy efficiency remained the dominant criterion. By integrating these objectives, the optimization profiler identified the optimal combination of key design parameters, rake angle, tool width, and tool thickness that provided the best trade-off between reduced energy requirements and effective soil disturbance. The resulting optimized tool design enhances soil–tool interactions, leading to improved manure injection performance and operational efficiency.

3. Results and Discussions

3.1. DEM Screening Result for the Reduction in the Numbers of Shanks from Eighteen to Six

Figure 5 shows the variation in draft force (N) over time (s) during the operation of a soil-engaging tool. After around 0.4 s, the draft force levels off and enters a relatively steady range near 500 N, as indicated by the marked steady-state region. This steady-state period suggests the tool has reached a consistent working condition where soil resistance and tool motion stabilize. Figure 6 illustrates a cross-sectional profile of soil disturbance below the ground, showing depth (mm) on the vertical axis and horizontal trench width (mm) on the horizontal axis. The profile represents the shape of the soil rupture zone created by the tool. The V-shaped profile indicates the tool caused substantial vertical and lateral soil movement. The product of draft force to soil rupture area was calculated and used as a selection criterion, with a lower value indicating minimized soil disruption and draft force. A threshold was established using the product value of 63,000, and designs with values below this threshold were selected for production and experimented in a soil bin.

The criterion values (draft force x rupture area) ranged from 42,792 N·cm² (Shank 8) to 81,099 N·cm² (Shank 11) (

Table 5. Results from the DEM simulation of soil–shank interaction for the initial eighteen injector shank designs, showing soil draft force, soil rupture area (R), D*R, and selection criteria.

DI	Rake Angle	Tool Thickness	Tool Width	Draft Force (D)	Soil Rupture Area (S)	Criteria	Selected (<63,000)
	(°)	(mm)	(mm)	(N)	(cm2)	(D*S)
1	30	25	102	437.0	137.8	60,231.5	Selected
2	30	25	110	443.8	148.7	65,992.7
3	30	25	118	444.3	154.6	68,698.8
4	30	30	102	443.6	153.2	67,937.3
5	30	30	110	450.9	162.8	73,391.1
6	30	30	118	439.0	148.7	65,290.5
7	45	25	102	433.7	129.0	55,953.3	Selected
8	45	25	110	432.0	99.1	42,792.2	Selected
9	45	25	118	438.9	163.1	71,591.5
10	45	30	102	447.4	176.0	78,715.2
11	45	30	110	431.1	187.8	80,969.6
12	45	30	118	444.9	140.9	62,682.8	Selected
13	60	25	102	433.9	149.8	65,010.7
14	60	25	110	430.0	154.2	66,314.6
15	60	25	118	448.4	177.9	79,768.2
16	60	30	102	456.1	130.4	59,486.8	Selected
17	60	30	110	436.2	137.8	60,113.5	Selected
18	60	30	118	457.1	158.2	72,303.8

). Applying a selection threshold of D*R < 63,000, six designs (D1 (30° rake angle, 25 mm thickness, 102 mm width), D7 (45° rake angle, 25 mm thickness, 102 mm width), D8 (45° rake angle, 25 mm thickness, 110 mm width), D12 (45° rake angle, 30 mm thickness, 118 mm width), D16 (60° rake angle, 30 mm thickness, 102 mm width), and D17 (60° rake angle, 30 mm thickness, 110 mm width)) were identified as the most promising. Among these, D8 (45° rake angle, 25 mm thickness, 110 mm width) recorded the lowest value, indicating the most efficient combination of low draft requirement and adequate soil rupture. The selected injector shanks were re-labelled (

Table 6. Six selected CAD liquid manure injectors from DEM screening.

DI	Relabeled (S_)	Rake Angle (α) (°)	Tool Thickness (T) (mm)	Tool Width (w) (mm)
1	1	30	25	102
7	2	45	25	102
8	3	45	25	110
12	4	45	30	118
16	5	60	30	102
17	6	60	30	110

) (S_1 = Shank 1) as S_1 (30° rake angle, 25 mm thickness, 102 mm width), S_2 (45° rake angle, 25 mm thickness, 102 mm width), S_3 (45° rake angle, 25 mm thickness, 110 mm width), S_4 (45° rake angle, 30 mm thickness, 118 mm width), S_5 (60° rake angle, 30 mm thickness, 102 mm width), and S_6 (60° rake angle, 30 mm thickness, 110 mm width)). The DEM-based screening process provided substantial advantages over conventional trial-and-error prototyping. It enabled the rapid and repeatable evaluation of multiple configurations under controlled virtual soil conditions, significantly reducing the time, cost, and material requirements of fabricating and testing all initial designs. The six selected shanks were subsequently fabricated for validation in a soil bin experiment. This combined simulation–experimental approach offers a robust methodology for optimizing tillage tool design while minimizing development costs and improving design efficiency.

3.2. Effect of Injector Shank on the Draft and Above-Ground Soil Disturbance

Table 7. Draft forces acting on the six injector shanks with confidence intervals for lower and upper value.

			Draft (N)
Shank	Draft (N)	SD(N)	95% CI Upper Value	95% CI Lower Value
1	228.8	47.2	282.2	175.4
2	157.0	33.6	195.0	119.0
3	199.2	10.3	210.9	187.5
4	274.9	44.7	325.4	224.3
5	158.1	19.6	180.2	135.9
6	163.9	19.3	185.8	142.1

presents the mean draft forces, standard deviations (SD), and 95% confidence intervals (CI) for the six injector shank designs. The SD and CI indicate variability in the measurements. The results showed variation in draft requirements among the designs, with the widest CI observed for S_4 (224.3–325.4 N) and S_1 (175.4–282.2 N), reflecting higher variability in their draft force measurements. This variability may be attributed to the rake angle of the shank geometry to deflection in soil resistance. In contrast, S_3 exhibited the narrowest CI (187.5–210.9 N), indicating more consistent performance under the tested conditions. Lower draft force was observed for S_2, S_5 (158.1 N), and S_6 (163.9 N), which could offer potential energy savings.

Figure 7 shows the measured mean draft forces for the six selected injector shanks during soil bin testing. Draft forces range from 157 N to 280 N, with the injector shanks significantly affecting the draft with a p-value of 0.0323. The comparison analysis showed significant differences (p < 0.05) among the designs, as indicated by the different letters above the error bars. S_4 recorded the highest draft force (274.9 N), significantly greater than S_2, S_5, and S_6, which exhibited the lowest values (157–163.9 N). S_1 and S_3 showed intermediate performance, not significantly different from each other but differing from the highest- and lowest-draft designs. The variation in draft force among shanks can be attributed to differences in rake angle, tool thickness, and tool width, which influence soil failure patterns and the amount of displaced soil. Higher draft values, such as those observed for S_4, may indicate increased soil engagement or greater penetration resistance.

In contrast, lower values, as in S_2, S_5, and S_6, suggest more efficient soil cutting and reduced energy demand. Similar results have been reported by [26,41], who found that intermediate rake angles (45°) reduce draft without significantly compromising soil break-up. Additionally, the observed increase in draft with greater soil–tool contact width supports the findings of [42,43].

3.3. Above-Ground Soil Disturbance Response to Injector Shank Designs

Soil trench width measured was the horizontal distance across the loosened soil zone at the surface formed by the passage of a tool, which is a key indicator of above-ground soil disturbance. The mean trench width obtained for the six injector shanks are presented in

Table 8. Trench width caused by soil-tool interaction of the six injector shanks with confidence intervals for lower and upper value.

			Trench Width (mm)
Shank	Trench Width (mm)	SD (mm)	95% CI Upper Value	95% CI Lower Value
1	402.5	52.5	461.9	343.1
2	280.5	64.9	354.0	207.1
3	207.6	56.1	271.1	144.0
4	316.8	25.9	346.1	287.5
5	442.6	151.9	614.5	270.7
6	301.1	63.2	372.6	229.5

. It was observed that S_5 produced the widest trench (442.6 mm), followed closely by S_1 (402.5 mm), while S_3 recorded the smallest width (207.6 mm). The statistical grouping in Figure 8 reveals significant differences (p < 0.05) between shanks, with S_5 being significantly different from S_3 and partially overlapping with other shanks in groupings.

The variations in mean trench width can be attributed to differences in shank geometry, including rake angle, thickness, and width, which influence soil failure patterns and the extent of lateral soil throw. Shanks with greater width and aggressive geometry tend to increase the loosened zone due to higher soil displacement, as observed in S_5. These findings are consistent with previous studies. Ref. [44] reported that wider and more aggressive tine designs generate larger trench widths due to enhanced lateral soil fracture. Similarly, Ref. [45] observed that increasing the tool rake angle and working width leads to greater surface disturbance. However, narrower shanks, such as S_3 in this study, minimize lateral soil movement, which could be advantageous in manure injection, where reduced disturbance is desirable.

The spoil cross-sectional area varied significantly among the six injector shank designs (

Table 9. Spoil cross-sectional area caused by soil-tool interaction of the six injector shanks with confidence intervals for lower and upper value.

			Soil Cross-Sectional Area (mm2)
Shank	Soil Cross-Sectional Area (mm2)	SD (mm2)	95% CI Upper Value	95% CI Lower Value
1	8142.0	3129.1	11,682.9	4601.1
2	9179.5	1474.0	10,847.5	7511.5
3	7325.5	1949.2	9531.2	5119.8
4	5545.6	508.8	6121.3	4969.8
5	6202.5	1489.1	7887.5	4517.5
6	10,457.7	717.6	11,269.8	9645.7

). S_6 produced the maximum mean spoil disturbance (10,458 mm²), followed by S_2 (9179.5 mm²) and S_1 (8142.0 mm²), whereas S_4 recorded the smallest disturbance (5545.6 mm²). Statistical grouping showed that S_6 (group A) differed significantly (p < 0.05) from S_4 (group C), while Shanks 1–3 fell into intermediate groups (AB/ABC) (Figure 9). S_1 exhibited the highest variability (SD = 3129.1 mm²), and S_4 displayed the most consistent performance (SD = 508.8 mm²). The 95% CI confirmed these trends, with S_6 showing a broader and higher range (9645.7–11,269.8 mm²) compared with S_4 (4969.8–6121.3 mm²).

Low-disturbance knife injectors have been reported to preserve surface residue, reduce phosphorus runoff, and maintain soil structure [46]. While these outcomes were not directly measured in this study, the relatively narrow trench width and low spoil disturbance observed for S_4 suggests that it shares geometric characteristics with low disturbance knives and may therefore support similar conservation outcomes under field conditions. Conversely, more aggressive designs, such as S_6 and S_2, produce greater soil loosening but may increase the risk of erosion [47]. Literature also notes that while subsurface manure injections can reduce ammonia volatilization and nutrient losses, excessive disturbance may elevate nitrous oxide emissions [48,49]. Therefore, selecting an injector shank design should balance soil loosening requirements with minimizing environmental impacts, particularly under conservation tillage and cover-crop systems.

3.4. Effect of Injector Shank on Below-Ground Soil Disturbance (Soil Rupture Area)

The measured below-ground soil rupture area varied among the six injector shank designs (

Table 10. Below-ground soil rupture area caused by soil-tool interaction of the six injector shanks with confidence intervals for lower and upper value.

			Soil Rupture Area (mm2)
Shank	Soil Rupture Area (mm2)	SD (mm2)	95% CI Upper Value	95% CI Lower Value
1	70,284.0	2717.7	73,359.3	67,208.7
2	72,609.9	9406.8	83,254.5	61,965.3
3	79,511.5	3084.1	83,001.4	76,021.6
4	75,660.8	16,864.1	94,744.0	56,577.6
5	83,092.6	14,560.9	99,569.5	66,615.7
6	53,196.5	3923.2	57,635.9	48,757.1

). S_5 produced the maximum mean rupture area (83,092.6 mm²), followed closely by S_3 (79,511.5 mm²) and S_4 (75,660.8 mm²). The minimum mean soil rupture area was observed for S_6 (53,196.5 mm²), which was statistically different (p < 0.05) from all other designs except S_1 (70,284.0 mm²). Error bars in Figure 9 indicate variability between replicates, with SD ranging from 2717.7 mm² (S_1) to 16,864.1 mm² (S_4). The statistical grouping (letters a–b in Figure 10) indicates that Shanks 2, 3, 4, and 5 were similar in soil rupture area (group a), while Shank 6 consistently produced significantly lower values (group b). This suggests that geometric features of S_6, such as narrower width and less rake angle, may have limited its soil–tool interaction efficiency. The soil rupture areas obtained in this study are consistent with the range reported by [50], who found that subsoiler shanks produced 70,000–85,000 mm² rupture zones under similar loamy soil conditions. Similarly, Ref. [10] observed that increasing shank rake angle and wing width enhanced rupture area by 15–25%, which aligns with the superior performance of Shanks 3, 4, and 5 in the present study. However, our results show slightly higher variability than [51], potentially due to differences in soil moisture and compaction level.

The below-ground mean soil rupture profiles, obtained from three replicates, were generated using the six injector shank designs (Figure 11). These profiles display a characteristic V-shaped disturbance zone, with the rupture depth increasing towards the tool centerline and tapering laterally to undisturbed soil. Across all designs, the maximum rupture depth ranged between approximately 420 and 480 mm, with variations in trench width and side slope evident between shanks. Designs S_1, S_3, and S_5 exhibited broader lateral spread at shallower depths, while S_2, S_4, and S_6 produced narrower trenches with steeper side walls. These differences suggest that minimal geometric variations in the shank structure can significantly alter the propagation of soil failure, thereby directly impacting soil disturbance intensity and nutrient band placement during manure injection.

The observed rupture geometries align with previous experimental studies, which show that the shank rake angle, width, and tip shape influence the depth and lateral extent of soil disturbance [44]. Similar V-shaped failure patterns were reported in evaluations of subsoilers and manure injectors, where narrow-point designs reduced surface disruption and lateral crack propagation [52]. Field trials by [53] demonstrated that narrower rupture profiles preserve soil structure and reduce erosion risk, while wider profiles improve residue mixing but increase surface disturbance. The soil rupture areas quantified using ImageJ showed close agreement (5% relative error) with those obtained from laser measurements, providing a reliable and repeatable method for capturing such differences, which complement standard soil disturbance measurements used in tillage tool evaluation. These results reinforce the notion that selecting an injector design should strike a balance between manure incorporation effectiveness and minimal disturbance to soil cover and structure.

3.5. Multi-Objective Optimization of Six Injector Shanks Design Evaluated from Soil Bin Testing

The multi-objective optimization of six injector shank designs was carried out using soil bin testing results (

Table 11. Multiple objectives optimization for the sis injector shanks based on energy and soil disturbance responses.

Parameter	Response	Objective
Draft (N)	Energy	Minimize
Trench width (mm)	Above-ground soil disturbance	Minimize
Spoil cross-sectional area (mm2)	Above-ground soil disturbance	Minimize
Soil rupture area (mm2)	Below-ground soil disturbance	Maximize

), with the selection of the optimal design based on the overall desirability value ranging from 0 to 1, where values closer to 1 indicate superior performance. Draft force, expressed in newtons, represents the energy demand during operation and was targeted for minimization to reduce fuel consumption and tractor power requirements. Above-ground soil disturbance was assessed using trench width and spoil cross-sectional area, with both parameters minimized to preserve surface soil integrity, reduce damage to cover crops, and limit the need for post-operation leveling. Conversely, below-ground soil disturbance, quantified by the soil rupture area, was maximized to enhance the deep placement of liquid manure and for proper soil covering to prevent environmental odor. This optimization inherently involves trade-offs; for instance, shank geometries that increase rupture area may also increase draft force or above-ground disturbance.

The multi-objective optimization results in

Table 12. Results of the multiple objective optimizations for the six injector shanks based on the set objectives.

				Desirability 1
				Energy	Above-Ground		Below-Ground
Shank	Rake Angle	Tool Thickness	Tool Width	Draft	Trench Width	Spoil Cross-Sectional Area	Soil Rupture Area	Overall Desirability
	(°)	(mm)	(mm)	(N)	(mm)	(mm2)	(mm2)
1	30	25	102	0.4656	0.4465	0.4838	0.4595	0.4639
2	45	25	102	0.8202	0.6997	0.3687	0.5006	0.5973
3	45	25	110	0.6078	0.8578	0.5783	0.6265	0.6676 *
4	45	30	118	0.2573	0.6222	0.7934	0.5555	0.5571
5	60	30	102	0.8148	0.3681	0.7131	0.6938	0.6475
6	60	30	110	0.7850	0.6557	0.2313	0.1713	0.4608

¹ Individual desirability values were calculated by linearly rescaling each response between the observed minimum (1.0) and maximum (0.0) across the six shank designs, with draft force, trench width, and spoil area minimized and soil rupture area maximized. The overall desirability is the average of the individual desirability of the responses. * The selected optimal shank design in terms of the highest overall desirability.

show that the overall desirability values for the six injector shank designs ranged from 0.4608 to 0.6676, with values closer to 1 indicating superior performance according to the defined optimization objectives. Each performance parameter, draft force (energy), trench width, spoil cross-sectional area (above-ground disturbance), and soil rupture area (below-ground disturbance), was iterated into a scaled desirability function between 0 and 1, where higher values represent a closer match to the ideal target. The overall desirability for each design was then determined as the average of these individual desirability values, allowing for simultaneous consideration of all objectives within a single metric.

Among the tested configurations, S_3 (rake angle 45°, tool thickness 25 mm, tool width 110 mm) achieved the highest overall desirability value of 0.6676, making it the most effective design in balancing energy efficiency, minimal above-ground soil disturbance, and maximum subsoil rupture. This design demonstrated an optimal compromise by maintaining relatively low draft requirements and surface disturbance while producing a high soil rupture area conducive to improved liquid manure placement. S_5 (0.6475) and S_2 (0.5973) also performed well but exhibited slightly less favorable trade-offs compared to S_3 in terms of soil rupture area and spoil cross-sectional area. These findings highlight the effectiveness of the desirability value approach in providing a quantitative and systematic framework for selecting an injector shank design that meets the often-conflicting demands of reduced energy use, preserved surface integrity, and enhanced subsurface soil improvement, in alignment with conservation tillage and precision agriculture principles.

4. Conclusions

This study demonstrated a combined framework of DEM simulation, soil bin testing, and multi-objective optimization for evaluating liquid manure injector shank designs. DEM-based screening efficiently reduced eighteen initial designs to six prototypes, which were then assessed under controlled soil bin conditions. Significant differences in draft force, trench width, spoil cross-sectional area, and soil rupture area were observed, confirming that rake angle, tool width, and tool thickness strongly influence soil–tool interaction. Using a multi-objective desirability approach, Shank S_3 (45° rake, 25 mm thickness, 110 mm width) achieved the highest overall score, representing the most promising trade-off among the tested designs between energy efficiency, minimal surface disturbance, and maximal subsurface loosening. These findings demonstrate the utility of simulation–experiment–optimization workflows for implement design, reducing reliance on extensive field prototyping and enabling data-driven decision-making. From an application standpoint, the results suggest that manufacturers can adopt DEM-assisted design and optimization to refine tool geometries before fabrication, thereby shortening development cycles and improving product performance. Likewise, farmers and equipment operators may select injector shanks with moderate rake angles (around 45°) and optimized dimensions to achieve efficient manure placement with reduced soil disturbance and energy consumption. However, the results are limited to one soil type, moisture, bulk density, and test speed under controlled conditions. Future work should validate the performance of S_3 and other candidate designs under variable soil textures, moisture contents, and real-world operating environments to confirm their agronomic and environmental benefits.