Combining Artificial Intelligence and Remote Sensing to Enhance the Estimation of Peanut Pod Maturity
Abstract
1. Introduction
2. Materials and Methods
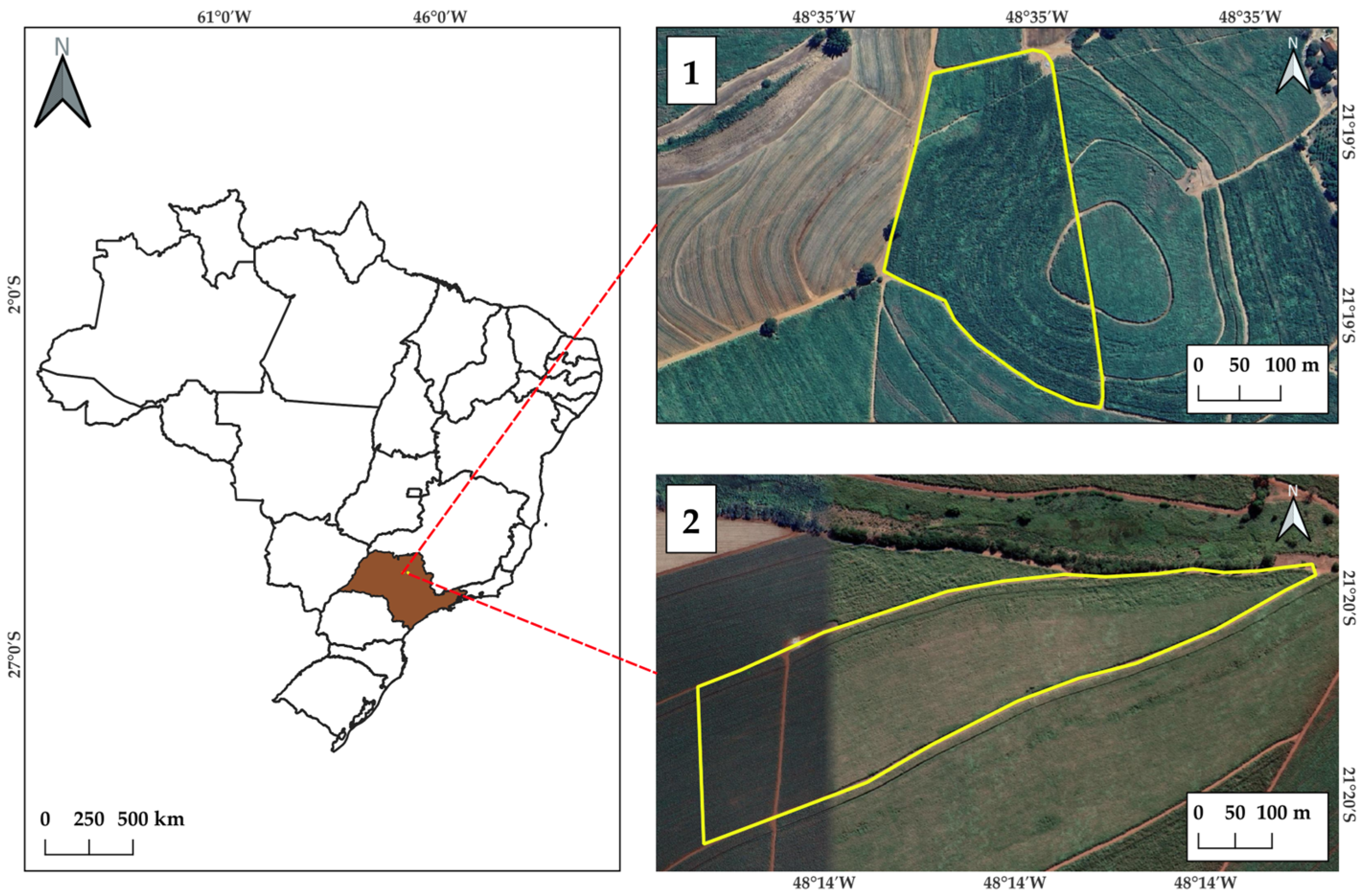
2.1. Experimental Area
2.2. Field Data Acquisition
2.3. Acquisition of Orbital Images
2.4. Vegetation and Topographic Indices
2.5. Climatic Variables
2.6. Data Analysis
2.7. Input Variables
2.7.1. Database Filtering
2.7.2. Variable Selection Analysis (Stepwise)
2.8. Description of Artificial Neural Networks
2.8.1. Multilayer Perceptron (MLP)
2.8.2. Radial Basis Function (RBF)
2.9. Model Performance
2.10. Theoretical Flowchart
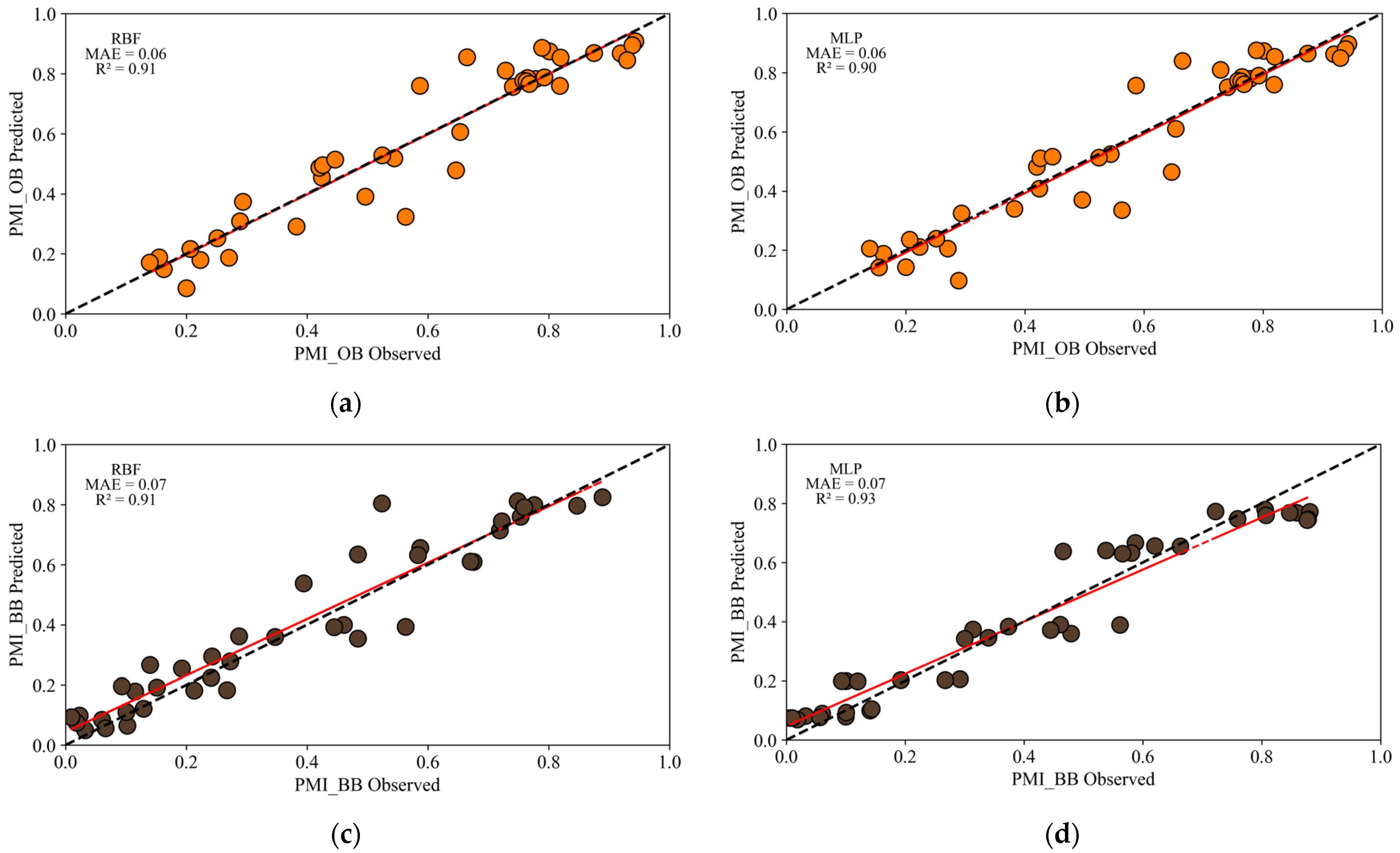
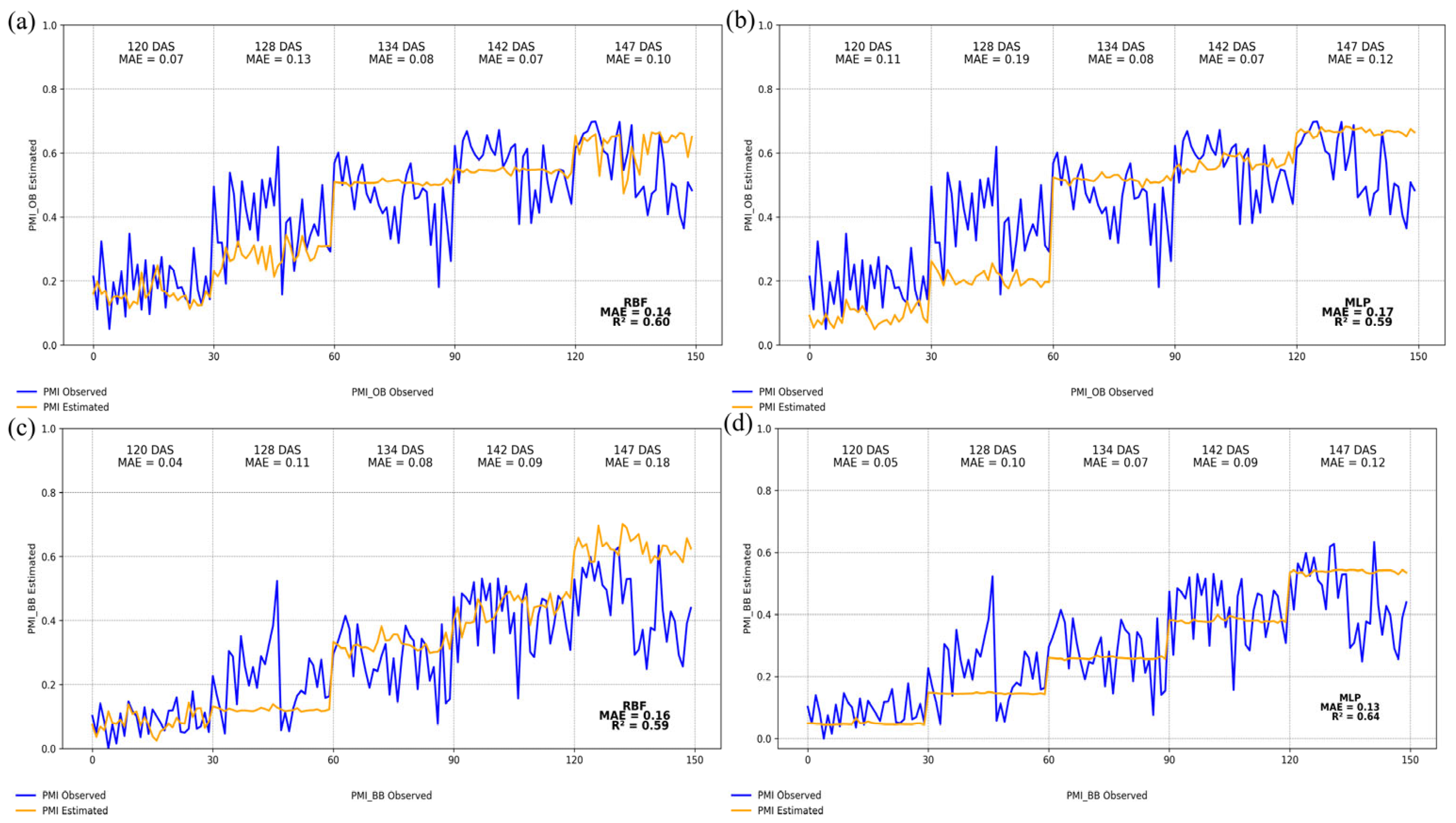
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- USDA. United States Department of Agriculture. Available online: https://ipad.fas.usda.gov/cropexplorer/cropview/commodityView.aspx?cropid=2221000 (accessed on 6 June 2024).
- Companhia Nacional de Abastecimento (CONAB). Acompanhamento da Safra Brasileira: Grãos, Safra 2023/2024, Sétimo Levantamento: Abril/2024; CONAB: Brasília, Brazil, 2024. Available online: https://www.conab.gov.br/info-agro/safras/graos/boletim-da-safra-de-graos?limitstart=0 (accessed on 6 June 2024).
- Shoko, M.D.; Tagwira, F. Benefits of soyabeans as a break crop in sugarcane production systems in the South Eastern Lowveld of Zimbabwe. Sugar J. 2007, 70, 18–22. [Google Scholar]
- Park, S.E.; Webster, T.J.; Horan, H.L.; James, A.T.; Thorburn, P.J. A legume rotation crop lessens the need for nitrogen fertiliser throughout the sugarcane cropping cycle. Field Crops Res. 2010, 119, 331–341. [Google Scholar] [CrossRef]
- Paungfoo-Lonhienne, C.; Wang, W.; Yeoh, Y.K.; Halpin, N. Legume crop rotation suppressed nitrifying microbial community in a sugarcane cropping soil. Sci. Rep. 2017, 7, 16707. [Google Scholar] [CrossRef]
- Zerbato, C.; Furlani, C.E.; Silva, R.P.; Voltarelli, M.A.; Santos, A.F. Statistical control of processes applied for peanut mechanical digging in soil textural classes. Eng. Agríc. 2017, 37, 315–322. [Google Scholar] [CrossRef]
- Michelotto, M.D.; Bolonhezi, D.; Freitas, R.S.; Santos, J.F.; Godoy, I.J.; Schwertner, C.F. Population dynamics, vertical distribution and damage characterization of burrower bug in peanut. Sci. Agric. 2022, 80, e20210161. [Google Scholar] [CrossRef]
- Santos, A.F.; Corrêa, L.N.; Lacerda, L.N.; Tedesco-Oliveira, D.; Pilon, C.; Vellidis, G.; Silva, R.P. High-resolution satellite image to predict peanut maturity variability in commercial fields. Precis. Agric. 2021, 22, 1464–1478. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, G.; Wang, J.; Zhang, P.; Wang, B.; Hu, Z. Adaptabilities of different harvesters to peanut plants after cutting stalks. Int. J. Agric. Biol. Eng. 2022, 15, 93–100. [Google Scholar] [CrossRef]
- Santos, E.P.; Silva, R.P.; Bertonha, R.S.; Noronha, R.H.; Zerbato, C. Produtividade e perdas de amendoim em cinco diferentes datas de arranquio. Rev. Ciênc. Agron. 2013, 44, 695–702. [Google Scholar] [CrossRef][Green Version]
- Bindlish, E.; Abbott, A.L.; Balota, M. Assessment of peanut pod maturity. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 688–696. [Google Scholar] [CrossRef]
- Moctezuma, E. The peanut gynophore: A developmental and physiological perspective. Can. J. Bot. 2003, 81, 183–190. [Google Scholar] [CrossRef]
- Santos, A.F.; Lacerda, L.N.; Gobbo, S.; Tofannin, A.; Silva, R.P.; Vellidis, G. Using remote sensing to map in-field variability of peanut maturity. In Precision Agriculture’19; Wageningen Academic: Wageningen, The Netherlands, 2019; pp. 605–611. [Google Scholar] [CrossRef]
- Abd-El Monsef, H.; Smith, S.E.; Rowland, D.L.; Abd El Rasol, N. Using multispectral imagery to extract a pure spectral canopy signature for predicting peanut maturity. Comput. Electron. Agric. 2019, 162, 561–572. [Google Scholar] [CrossRef]
- Song, Y.; Rowland, D.L.; Tillman, B.L.; Wilson, C.H.; Sarnoski, P.J.; Zurweller, B.A. Impact of seed maturity on season-long physiological performance and offspring seed quality in peanut (Arachis hypogaea L.). Field Crops Res. 2022, 288, 108674. [Google Scholar] [CrossRef]
- Williams, E.J.; Drexler, J.S. A non-destructive method for determining peanut pod maturity. Peanut Sci. 1981, 8, 134–141. [Google Scholar] [CrossRef]
- Rowland, D.L.; Sorensen, R.B.; Butts, C.L.; Faircloth, W.H. Determination of maturity and degree day indices and their success in predicting peanut maturity. Peanut Sci. 2006, 33, 125–136. [Google Scholar] [CrossRef]
- Colvin, B.C.; Rowland, D.L.; Ferrell, J.A.; Faircloth, W.H. Development of a digital analysis system to evaluate peanut maturity. Peanut Sci. 2014, 41, 8–16. [Google Scholar] [CrossRef]
- Souza, J.B.C.; Almeida, S.L.H.; Filho Brito, A.L.; Carneiro, M.F.; Santos, A.F.; Silva, R.P. Unmanned aerial system and satellite: Which one is a better platform for monitoring of the peanut crops? Agron. J. 2023, 115, 1146–1160. [Google Scholar] [CrossRef]
- Souza, J.B.C.; Almeida, S.L.H.; Oliveira, M.F.; Santos, A.F.; Filho Brito, A.L.; Meneses, M.D.; Silva, R.P. Integrating satellite and UAV data to predict peanut maturity upon artificial neural networks. Agronomy 2022, 12, 1512. [Google Scholar] [CrossRef]
- Santos, A.F.; Lacerda, L.N.; Rossi, C.; Moreno, L.A.; Oliveira, M.F.; Pilon, C.; Vellidis, G. Using UAV and multispectral images to estimate peanut maturity variability on irrigated and rainfed fields applying linear models and artificial neural networks. Remote Sens. 2021, 14, 93. [Google Scholar] [CrossRef]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; de Gonçalves, J.L.M.; Sparovek, G. Köppen’s climate classification map for Brazil. Meteorol. Z. 2014, 22, 711–728. [Google Scholar] [CrossRef]
- Planet. Understanding PlanetScope Instruments. Available online: https://developers.planet.com/docs/apis/data/sensors/ (accessed on 30 March 2023).
- Oliveira, M.F.; Souza, J.B.C.; Ortiz, B.V.; Bao, Y.; Sanz-Saez, A.; Silva, R.P. Integrating artificial neural networks and remote sensing for prediction of peanut maturity as a function of management zones. In Precision Agriculture’23; Wageningen Academic: Wageningen, The Netherlands, 2023; pp. 1083–1089. [Google Scholar] [CrossRef]
- Rouse, J.W.; Deering, D. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Goel, N.S.; Qin, W. Influences of canopy architecture on relationships between various vegetation indices and LAI and FPAR: A computer simulation. Remote Sens. Rev. 1994, 10, 309–347. [Google Scholar] [CrossRef]
- Fitzgerald, G.; Rodriguez, D.; O’Leary, G. Measuring and predicting canopy nitrogen nutrition in wheat using a spectral index—The canopy chlorophyll content index (CCCI). Field Crops Res. 2010, 116, 318–324. [Google Scholar] [CrossRef]
- Justice, C.O.; Vermote, E.; Townshend, J.R.; DeFries, R.; Roy, D.P.; Hall, D.K.; Barnsley, M.J. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Gong, P.; Pu, R.; Biging, G.S.; Larrieu, M.R. Estimation of forest leaf area index using vegetation indices derived from Hyperion hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1355–1362. [Google Scholar] [CrossRef]
- Boegh, E.; Soegaard, H.; Broge, N.; Hasager, C.; Jensen, N.; Schelde, K.; Thomsen, A. Airborne multi-spectral data for quantifying leaf area index, nitrogen concentration and photosynthetic efficiency in agriculture. Remote Sens. Environ. 2002, 81, 179–193. [Google Scholar] [CrossRef]
- Jordan, C.F. Derivation of leaf-area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar] [CrossRef]
- Mieza, M.S.; Cravero, W.R.; Kovac, F.D.; Bargiano, P.G. Delineation of site-specific management units for operational applications using the topographic position index in La Pampa, Argentina. Comput. Electron. Agric. 2016, 127, 158–167. [Google Scholar] [CrossRef]
- Meles, M.B.; Younger, S.E.; Jackson, C.R.; Du, E.; Drover, D. Wetness index based on landscape position and topography (WILT): Modifying TWI to reflect landscape position. J. Environ. Manag. 2020, 255, 109863. [Google Scholar] [CrossRef] [PubMed]
- Prediction of Worldwide Energy Resources (POWER) Project. POWER Data Access Viewer. NASA Langley Research Center, NASA. Available online: https://power.larc.nasa.gov/data-access-viewer/ (accessed on 21 August 2024).
- Barboza, T.O.C.; Ferraz, M.A.J.; Pilon, C.; Vellidis, G.; Valeriano, T.T.B.; Santos, A.F. Advanced farming strategies using NASA POWER data in peanut-producing regions without surface meteorological stations. AgriEngineering 2024, 6, 438–454. [Google Scholar] [CrossRef]
- Royston, P. Remark AS R94: A remark on Algorithm AS 181: The W-test for normality. J. R. Stat. Soc. Ser. C Appl. Stat. 1995, 44, 547–551. [Google Scholar] [CrossRef]
- Kaiser, H.F. The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23, 187–200. [Google Scholar] [CrossRef]
- Kujawa, S.; Niedbała, G. Artificial neural networks in agriculture. Agriculture 2021, 11, 497. [Google Scholar] [CrossRef]
- Silva, I.N.; Spatti, D.H.; Flauzino, R.A. Redes Neurais Artificiais: Para Engenharias e Ciências Aplicadas; Artliber: São Paulo, Brazil, 2016. [Google Scholar]
- Miao, Y.; Mulla, D.J.; Robert, P.C. Identifying important factors influencing corn yield and grain quality variability using artificial neural networks. Precis. Agric. 2006, 7, 117–135. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, K.; Zhong, Y.; Li, P. Um novo algoritmo de mapeamento de subpixel baseado em uma rede neural BP com um modelo de observação. Neurocomputing 2008, 71, 2046–2054. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation, 2nd ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Vishnuprabha, R.S.; Viswanathan, P.L.; Manonmani, S.; Rajendran, L.; Selvakumar, T. Genetic diversity in groundnut (Arachis hypogaea L.) genotypes varying in maturity duration. Vegetos 2023, 36, 1550–1556. [Google Scholar] [CrossRef]
- Janila, P.; Manohar, S.S.; Patne, N.; Variath, M.T.; Nigam, S.N. Genotype × environment interactions for oil content in peanut and stable high-oil-yielding sources. Crop Sci. 2016, 56, 2506–2515. [Google Scholar] [CrossRef]
- Arioglu, H.; Bakal, H.; Gulluoglu, L.; Onat, B.; Kurt, C. The effect of harvesting dates on some agronomic and quality characteristics of peanut (Arachis hypogaea L.) varieties grown as a main crop in Mediterranean region (Turkey). Turk. J. Field Crops 2018, 23, 27–37. [Google Scholar] [CrossRef]
- Rowland, D.L.; Sorensen, R.B.; Butts, C.L.; Faircloth, W.H.; Sullivan, D.G. Canopy characteristics and their ability to predict peanut maturity. Peanut Sci. 2008, 35, 43–54. [Google Scholar] [CrossRef]
- Mayranti, F.P.; Saputro, A.H.; Handayani, W. Chlorophyll A and B content measurement system of velvet apple leaf in hyperspectral imaging. In Proceedings of the 2019 3rd International Conference on Informatics and Computational Sciences (ICICoS), Semarang, Indonesia, 29–30 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Clevers, J.G.; Kooistra, L.; van den Brande, M.M. Using Sentinel-2 data for retrieving LAI and leaf and canopy chlorophyll content of a potato crop. Remote Sens. 2017, 9, 405. [Google Scholar] [CrossRef]
- Zhao, D.; Huang, L.; Li, J.; Qi, J. A comparative analysis of broadband and narrowband derived vegetation indices in predicting LAI and CCD of a cotton canopy. ISPRS J. Photogramm. Remote Sens. 2007, 62, 25–33. [Google Scholar] [CrossRef]
- Robson, A.J.; Wright, G.; Phinn, S. Using field spectroscopy and QuickBird imagery for the assessment of peanut crop maturity and aflatoxin. J. Spat. Sci. 2006, 51, 151–162. [Google Scholar] [CrossRef]
- Oliveira, M.F.; Carneiro, F.M.; Ortiz, B.V.; Thurmond, M.; Oliveira, L.P.; Bao, Y.; Tedesco, D. Predicting below and above-ground peanut biomass and maturity using multi-target regression. Comput. Electron. Agric. 2024, 218, 108647. [Google Scholar] [CrossRef]
- Souza, J.B.C.; Almeida, S.L.H.; Oliveira, M.F.; Carreira, V.S.; Brito Filho, A.L.; Santos, A.F.; Silva, R.P. Generalization of peanut yield prediction models using artificial neural networks and vegetation indices. Smart Agric. Technol. 2025, 11, 100873. [Google Scholar] [CrossRef]
- Barbosa Júnior, M.R.; Moreira, B.R.A.; Oliveira, R.P.; Shiratsuchi, L.S.; Silva, R.P. UAV imagery data and machine learning: A driving merger for predictive analysis of qualitative yield in sugarcane. Front. Plant Sci. 2023, 14, 1114852. [Google Scholar] [CrossRef]
- Chea, C.; Saengpachatanarug, K.; Posom, J.; Saikaew, K.; Wongphati, M.; Taira, E. Optimal models under multiple resource types for Brix content prediction in sugarcane fields using machine learning. Remote Sens. Appl. Soc. Environ. 2022, 26, 100718. [Google Scholar] [CrossRef]
- Alface, A.B.; Pereira, S.B.; Filgueiras, R.; Cunha, F.F. Monitoramento espaço-temporal da cana-de-açúcar e estimativa do coeficiente de cultivo por meio do NDVI. Rev. Bras. Eng. Agríc. Ambient. 2019, 23, 330–335. [Google Scholar] [CrossRef]
- Almeida, S.L.H.; Souza, J.B.C.; Pilon, C.; Castro Teixeira, A.H.; Santos, A.F.; Sysskind, M.N.; Silva, R.P. Performance of the SAFER model in estimating peanut maturation. Eur. J. Agron. 2023, 147, 126844. [Google Scholar] [CrossRef]





| Band | Name | Central Wavelength (nm) |
|---|---|---|
| 2 | Blue | 472 |
| 3 | Green 1 | 531 |
| 4 | Green | 565 |
| 5 | Yellow | 680 |
| 6 | Red | 665 |
| 7 | Red Edge | 750 |
| 8 | NIR | 865 |
| DAS | Field Sampling Date | Orbital Imagery Date |
|---|---|---|
| 122 | 24 February 2023 | 24 February 2023 |
| 129 | 3 March 2023 | 4 March 2023 |
| 136 | 10 March 2023 | 10 March 2023 |
| 144 | 18 March 2023 | 18 March 2023 |
| 150 | 24 March 2023 | 23 March 2023 |
| VIs | Equations | References |
|---|---|---|
| NDVI | [25] | |
| GNDVI | ) | [26] |
| NLI | [27] | |
| NDRE | [28] | |
| EVI | [29] | |
| SAVI | (1 + L) × (NIR − Red)/(L + NIR + Red) | [30] |
| MNLI | + Red + L) | [31] |
| LAI | 3618 × EVI − 0.118 | [32] |
| SR | [33] |
| Class | Architecture | Input Variables | Hidden Layers | Output |
|---|---|---|---|---|
| PMI_BB | RBF | Green band, SAVI, ADD | 1 layer, 20 neurons | PMI_BB |
| PMI_BB | MLP | Green band, MNLI, ADD | 2 layers (20, 14 neurons) | PMI_BB |
| PMI_OB | RBF | Green band, MNLI, ADD | 1 layer, 20 neurons | PMI_OB |
| PMI_OB | MLP | Green band, MNLI, ADD | 2 layers (20, 6 neurons) | PMI_OB |
| Output Variables | Input Variables | R2 | MSEP |
|---|---|---|---|
| PMI_BB | Green band; NDVI; SAVI; ADD | 0.87 | 2.61 |
| PMI_OB | Green band; MNLI; SAVI; ADD | 0.86 | 2.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, T.C.M.; Souza, J.B.C.; Almeida, S.L.H.d.; Filho, A.L.d.B.; Silva, R.H.d.S.; Carneiro, F.M.; da Silva, R.P. Combining Artificial Intelligence and Remote Sensing to Enhance the Estimation of Peanut Pod Maturity. AgriEngineering 2025, 7, 368. https://doi.org/10.3390/agriengineering7110368
Oliveira TCM, Souza JBC, Almeida SLHd, Filho ALdB, Silva RHdS, Carneiro FM, da Silva RP. Combining Artificial Intelligence and Remote Sensing to Enhance the Estimation of Peanut Pod Maturity. AgriEngineering. 2025; 7(11):368. https://doi.org/10.3390/agriengineering7110368
Chicago/Turabian StyleOliveira, Thiago Caio Moura, Jarlyson Brunno Costa Souza, Samira Luns Hatum de Almeida, Armando Lopes de Brito Filho, Rafael Henrique de Souza Silva, Franciele Morlin Carneiro, and Rouverson Pereira da Silva. 2025. "Combining Artificial Intelligence and Remote Sensing to Enhance the Estimation of Peanut Pod Maturity" AgriEngineering 7, no. 11: 368. https://doi.org/10.3390/agriengineering7110368
APA StyleOliveira, T. C. M., Souza, J. B. C., Almeida, S. L. H. d., Filho, A. L. d. B., Silva, R. H. d. S., Carneiro, F. M., & da Silva, R. P. (2025). Combining Artificial Intelligence and Remote Sensing to Enhance the Estimation of Peanut Pod Maturity. AgriEngineering, 7(11), 368. https://doi.org/10.3390/agriengineering7110368








