Bioenergy Potential of Anaerobic Co-Digestion of Aquaponics Effluent and Cattle Manure

Abstract

Mathematical modeling is a key tool for describing and predicting the dynamic behavior of anaerobic digestion. Studies combining the co-digestion of aquaponics effluent (AE) and cattle manure (CM) with kinetic modeling remain scarce, particularly regarding the estimation of the apparent kinetic constant of hydrolysis constants and energy conversion indicators. Accordingly, this study aimed to evaluate the bioenergy potential of co-digesting aquaponics effluent (AE) and cattle manure (CM), with an emphasis on kinetic modeling and energy conversion. The experiments were carried out in a bench-scale Indian-type anaerobic biodigester. Different AE, CM, and water (W) (0:1, 1:0, 1:1, 1:3, 3:1 W:CM, and 1:1, 1:3, and 3:1 AE:CM) ratios were tested to identify the most efficient substrate combination for biogas production. The 1:3 AE:CM ratio achieved the best performance, with the Gompertz model providing the best fit for cumulative production and the first-order model accurately estimating k. This ratio yielded the highest cumulative biogas production (72.2 L kg⁻¹ substrate), shorter lag phase, higher production rate, and greater energy conversion efficiency. Comparative analysis revealed that 1:3 AE:CM outperformed both 1:3 A:CM and CM alone, highlighting the positive influence of aquaponics effluent on microbial activity and process stability. These results demonstrate that anaerobic co-digestion of AE and CM, particularly at the 1:3 ratio, is a viable and efficient strategy for renewable energy generation in rural areas, while promoting waste valorization and enhancing environmental and energy sustainability.

1. Introduction

Biogas, produced through the anaerobic digestion process, is primarily composed of methane (CH₄), carbon dioxide (CO₂), hydrogen (H₂), nitrogen (N₂), hydrogen sulfide (H₂S), and oxygen (O₂), with its composition directly depending on the substrates used [1]. As a renewable biofuel, biogas can replace fossil sources such as natural gas, oil, and coal in the generation of electricity and heat [2,3]. Furthermore, its use contributes to reducing deforestation for firewood production, thereby decreasing pressure on forest resources and mitigating greenhouse gas emissions [4]. Biogas accounts for approximately 3% of global renewable energy generation, and its expansion potential is particularly significant in countries with strong agricultural and livestock production, such as Brazil, India, and China [5].

The valorization of biogas also promotes the sustainable use of organic waste, supporting the treatment of effluents and agro-industrial residues, and fostering sustainability initiatives with positive impacts on the socio-economic development of rural communities [6]. In addition to biogas, the anaerobic digestion process generates nutrient-rich digestate, which can be used as an organic fertilizer, thereby closing the nutrient cycle and aligning with the principles of the circular economy [7].

Aquaponics effluent (AE), resulting from the integration of aquaculture and hydroponic crop production, presents a high organic load and nutrient content, including nitrogen and phosphorus, as well as a carbon-to-nitrogen (C/N) ratio favorable for microbial activity [8]. These characteristics make it a promising co-substrate for anaerobic digestion when combined with cattle manure, which, in turn, has a high content of volatile solids and biodegradable organic matter. Previous studies have already indicated that the integration of aquaponics and anaerobic digestion can enhance biogas production and promote resource circularity in rural properties [9,10,11].

The efficiency of biogas production is associated with physicochemical factors such as substrate composition, hydrogen potential (pH), and temperature [12]. Variations in these conditions can result in distinct biogas production potential profiles, making it essential to employ tools that aid in understanding and predicting process behavior over time. In this context, mathematical modeling stands out as an important resource for representing the dynamic behavior of anaerobic digestion and estimating biogas production [13].

Nonlinear models have been widely used for this purpose, with the Gompertz, Logistic, and Boltzmann models being the most common for describing the kinetics of biogas production potential. Originally developed for microbial growth studies, these models have been adapted to estimate parameters such as accumulated production potential, lag phase (latency time), and maximum production rate, which respectively represent the total generation capacity, the process’s maximum rate, and the initial time required for production to intensify [14,15,16,17]. Such information is essential for anaerobic biodigester sizing, optimization of hydraulic retention time, and prediction of process yield at rural and industrial scales. Accordingly, mathematical modeling of anaerobic digestion supports the optimization of operating conditions, scenario prediction, reduction of experimental costs, and monitoring of critical parameters (e.g., temperature and pH), thereby strengthening decision-making [18].

The international literature underscores the value of kinetic modeling to describe anaerobic digestion and guide operations; for predictive models, it is important to select an appropriate formulation and cite original sources, since different variants serve distinct analytical aims [14]. In parallel, artificial intelligence (AI) approaches—such as artificial neural networks (ANN) and adaptive network–fuzzy inference systems (ANFIS)—have forecast biogas production under mesophilic conditions with performance competitive to kinetic models and with promising scale-up potential [15]. However, these AI models lack direct physico-biological interpretability. Kinetic models, in turn, yield process-meaningful parameters (maximum production, rate, lag phase) that enable substrate comparison, identification of operational windows, and translation of performance into energy metrics. Thus, adopting sigmoidal kinetics and complementing them with statistical diagnostics and sensitivity analyses aligns with the recognized kinetic tradition [14] while constructively engaging with AI-based prediction, preserving interpretability for operational planning and energy assessment of the evaluated scenarios [15]. Beyond engineering, this approach has been applied in various fields of knowledge, including health, biology, industrial applications, and environmental studies [19,20,21].

Each model has specific limitations related to parameter reliability, microbial diversity in the substrates, and the need for proper calibration and validation [22,23]. Therefore, selecting the most appropriate model should take into account both simplicity and the ability to accurately represent the biological phenomena involved. Despite its identified potential, there is a scarcity of studies evaluating the co-digestion of aquaponics effluent and cattle manure based on detailed kinetic analysis and energy conversion estimates, thus highlighting the relevance of the integrated aquaponics–anaerobic digestion system in rural properties.

In this scenario, the present study aimed to evaluate biogas production from the anaerobic digestion of AE, cattle manure (CM), and water (W) by fitting kinetic models, focusing on the estimation of accumulated production potential, analysis of the apparent kinetic constant of hydrolysis, and energy conversion.

2. Materials and Methods

The anaerobic digestion system, which included both mono-anaerobic digestion (MoAD) and co-anaerobic digestion (CoAD) processes, was carried out at the Multiuser Research Laboratories of the Renewable and Alternative Rural Energy Group (LabGERAR) of the Institute of Technology/Department of Engineering at the Federal Rural University of Rio de Janeiro (UFRRJ), Seropédica campus, Rio de Janeiro, Brazil (22°45′33″ S and 43°41′51″ W). The region’s climate is classified as Aw according to the Köppen classification, with an average annual temperature of 24.5 °C. The experimental work was conducted in collaboration with the Fishing Institute Foundation of the State of Rio de Janeiro (FIPERJ), ensuring the technical and logistical support required for AE sample acquisition.

This study reused the experimental setup (bench-scale Indian-type biodigester, mesophilic regime, feeding mode, AE:CM and W:CM ratios, and number of replicates) and the weekly time series of Biogas Yield (L kg⁻¹) during the anaerobic digestion period (week) exactly as described by Lobo Paes et al. [9].

To ensure reproducibility and cross-study comparison, the complete baseline physico-chemical characterization of the substrates—moisture content (MC), total solids (TS), total volatile solids (TVS), pH (without prior correction), electrical conductivity (EC), total alkalinity (TA), volatile fatty acids (VFA), chemical oxygen demand (COD), nitrate nitrogen (NO₃⁻–N), and total organic carbon (TOC)—was reproduced in the Supplementary Material (Table S1 and Figure S1) under the Creative Commons Attribution (CC BY) license, with proper attribution to the original source Lobo Paes et al. [9].

Anaerobic digestion was conducted in a bench-scale Indian-type anaerobic digester, consisting of an anaerobic digestion chamber, a containment chamber with a water seal, a gasometer, and a U-tube manometer containing water as the manometric fluid. Substrate homogenization inside the digesters was achieved by an aluminum spiral spring attached to the gasometer [9].

Anaerobic digesters were fed in a batch system with 1.7 kg of substrate composed of CM, AE, and W for MoAD in the 0:1 (only CM), 1:0 (only AE), 1:1, 1:3, and 3:1 W:CM, and for CoAD in the 1:1, 1:3, and 3:1 AE:CM ratio. Experiments were performed in triplicate. The process took place under mesophilic conditions, with an internal digestion temperature ranging from 25 to 35 °C, 29.4 ± 0.20 °C for the biogas, and 29.8 ± 0.66 °C for the ambient temperature [9].

The Accumulated Production Potential (APP) was obtained by summing the previous week’s Biogas Yield with that recorded in the current data collection week. Only APP values obtained after confirming the presence of methane in the biogas—verified through the flammability test—were considered valid. The values were expressed in liters of gas per kilogram of substrate (L kg⁻¹) [9]. Based on the APP data, the analyses, included modeling cumulative biogas production using sigmoidal models, evaluating statistical goodness-of-fit, kinetic modeling to estimate the apparent kinetic constant of hydrolysis, determining operational and temporal indicators, and estimating the conversion of biogas into different energy end-uses and the associated financial savings.

The methodological sequence adopted allowed not only the kinetic description of biogas production but also its applied interpretation, considering the technological and energy feasibility of using different substrate ratios in anaerobic digesters (Figure 1).

2.1. Sigmoidal Models (Boltzmann, Logistic, and Modified Gompertz)

The experimental APP data as a function of the anaerobic digestion period were fitted to nonlinear regression models for the estimation of kinetic parameters [16,24,25,26], as presented in

Table 1. Nonlinear sigmoidal models for Accumulated Production Potential (APP) as a function of anaerobic digestion period.

Model	Equation
Boltzmann	${\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{n}}={\mathrm{A}\mathrm{P}\mathrm{P}}_0+{\displaystyle \frac{\left({\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{s}}-{\mathrm{A}\mathrm{P}\mathrm{P}}_0\right)}{1+{\mathrm{e}\mathrm{x}\mathrm{p}}^{\left[\frac{4{\mathrm{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{\left({\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{s}}-{\mathrm{A}\mathrm{P}\mathrm{P}}_0\right)}\left(\mathsf{\lambda }-\mathrm{x}\right)\right]}}}$	(1)
Logistic	${\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{n}}={\displaystyle \frac{{\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{s}}}{1+{\mathrm{e}\mathrm{x}\mathrm{p}}^{\left(\frac{4\times {\mathrm{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\times \left(\mathsf{\lambda }-\mathrm{x}\right)}{{\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{s}}}+2\right)}}}$	(2)
Modified Gompertz	${\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{n}}={\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{S}}\times {\mathrm{e}\mathrm{x}\mathrm{p}}^{\left\{-{\mathrm{e}\mathrm{x}\mathrm{p}}^{\left[{\displaystyle \frac{-{\mathrm{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\times \mathrm{e}}{{\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{S}}}}\times \left(\mathsf{\lambda }-\mathrm{x}\right)+1\right]}\right\}}$	(3)

where APP_n—Accumulated Production Potential at week n (L kg⁻¹), APP₀—Accumulated Production Potential at the time of installation (L kg⁻¹), APP_S—Accumulated Production Potential Superior (L kg⁻¹), n—1,…, i, i—number of measurements of accumulated biogas, x—anaerobic digestion period (weeks), R_max—maximum specific production rate (L kg⁻¹ week⁻¹), λ—lag phase duration (weeks), and e—Euler’s number (2.71828).

.

2.2. Apparent Kinetic Constant of Hydrolysis

The data from the MoAD and CoAD ratio that exhibited the highest APP values were fitted to classical first-order (Equation (4)) and second-order (Equation (5)) kinetic models, with the aim of estimating the apparent kinetic constant of hydrolysis (k), expressed in week⁻¹ (

Table 2. Fitting of first- and second-order kinetic models for estimation of apparent kinetic constant of hydrolysis (k) from Accumulated Production Potential (APP).

Order	Equation
1	${\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{n}}={\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{S}}\times \left(1-{\mathrm{e}\mathrm{x}\mathrm{p}}^{-\mathrm{k}\mathrm{x}}\right)$	(4)
2	${\displaystyle \frac{1}{{\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{n}}}}={\displaystyle \frac{1}{{\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{S}}}}-\mathrm{k}\mathrm{x}$	(5)

) [16,18,24,25,26].

Kinetic models (Table 2) were applied to describe the initial phase of organic matter degradation (hydrolysis), which governs the methane release rate. To avoid bias in parameter estimation, the initial phase with no biogas production (APP = 0)—associated with the microbial lag—was excluded from the fit, as biochemical transformations may occur in this interval without yet being reflected in measurable methane. In this study, k was treated as the apparent kinetic constant of hydrolysis, estimated by first- and second-order models fitted to APP time series. Thus, k represented an aggregated operational parameter rather than a direct measurement of the isolated hydrolysis step.

2.3. Time Indicators

Based on the best-fitting sigmoidal model, operational indicators were determined, including the time to reach 90% of accumulated production (T₉₀) and the effective production time (T_ef). These parameters were calculated using Equations (6) and (7), respectively.

$${\mathrm{T}}_{90}=\mathsf{\lambda }+3.25\times {\displaystyle \frac{{\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{s}}}{{\mathrm{R}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\times \mathrm{e}}}$$

(6)

$${\mathrm{T}}_{\mathrm{e}\mathrm{f}}={\mathrm{T}}_{90}-\mathsf{\lambda }$$

(7)

2.4. Evaluation of Fit Quality

The selection of the most representative model for accumulated production potential, as well as for the apparent kinetic constant of hydrolysis, was based on residual analysis and statistical criteria. The indicators used included the adjusted coefficient of determination (R²adj), standard error of the estimate (SE), relative mean error (RME), root mean square deviation (RMSD), and Akaike information criterion (AIC) [16,18,24,25,26]. Additionally, the Shapiro–Wilk (normality) and Breusch–Pagan (homoscedasticity) tests were applied to assess the statistical validity of the models. In all cases, both normality and homoscedasticity were confirmed at the 95% confidence level [27]. The fitting of mathematical models and statistical analyses were performed in R software (version 4.0; R Foundation for Statistical Computing, Vienna, Austria) within RStudio (version 1.4.1106; Posit Software, PBC, Boston, MA, USA) [28]. Sigmoidal model parameters were estimated by nonlinear least squares in R (stats package, nls function), using the default Gauss–Newton algorithm with convergence settings tol = 1 × 10⁻⁶, minFactor = 1/1024, and maxiter = 500. No box constraints were applied (unconstrained fit). Data-driven initial values were set as follows: APP₀ = minimum observed production, APP_S = maximum observed production, R_max = 70 (technical/prior reference), and λ = 10. Parameter 95% confidence intervals were computed using profile likelihood (confint.nls). Model adequacy/selection was assessed using AIC, R²/R²-adjusted, and residual diagnostics (Shapiro–Wilk, and Breusch–Pagan).

A robustness and sensitivity analysis were applied when necessary. Parameters were estimated in R (v. 4.x) using nlsLM (Levenberg–Marquardt) with multi-start/jitter, positivity constraints on APP_S and R_max, and a maximum of 200 iterations. Initial values were heuristic: APP_S equal to the observed maximum APP, R_max equal to the largest weekly increment, and λ set to the week following the largest increment or to the median time when no clear peak was present. In the presence of heteroscedasticity, models were re-fitted by weighted least squares (WLS) with weights derived from a power-of-the-mean variance–mean relationship and, additionally, by generalized least squares (GLS) with a varPower variance function in gnls. Uncertainty was quantified by 95% confidence intervals (CI95%) for APP_S, R_max, and λ, prioritizing nonparametric bias-corrected and accelerated (BCa) bootstrap with resampling of pairs (week, APP) and 5000 replicates. When BCa did not converge, percentile intervals via nlsBoot (2.5–97.5%) were used; if issues persisted, Wald intervals were reported as a fallback. For GLS (varPower), Wald intervals obtained via intervals() were combined with parametric bootstrap consistent with the varPower structure. Phase sensitivity was examined through refits excluding the first and/or last week, preserving initialization and constraints, and model comparison relied on AIC and Akaike Information Criterion difference (ΔAIC). Model adequacy was assessed by graphical diagnostics—residuals versus fitted values and Q–Q plots comparing the sample quantiles of the residuals with the theoretical quantiles of standard normality and homoscedasticity tests (Shapiro–Wilk and Breusch–Pagan). Figures and summary tables were produced in ggplot2 using the minpack.lm, nlme, nlstools, and boot packages (R—v. 4.0).

2.5. Energy Conversion Estimate and Financial Savings

Energy conversion (EC) was calculated based on the highest APP values obtained for MoAD and CoAD, considering a herd of 200 dairy cows with an average production of 105 kg of animal waste per cow per week [29], resulting in 21,000 kg of substrate per week.

Gross biogas production (GP) was determined according to Equation (8).

$$\mathrm{G}\mathrm{P}\left(\mathrm{L}\right)={\mathrm{A}\mathrm{P}\mathrm{P}}_{\mathrm{S}}\left(\mathrm{L}{\mathrm{k}\mathrm{g}}^{-1}\right)\times \mathrm{21,000}\left(\mathrm{k}\mathrm{g}{\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{k}}^{-1}\right)$$

(8)

GP was corrected for methane content to obtain GP_CH4, using the CH₄ fraction reported by Lobo Paes et al. [9] for the selected ratio; the correction followed Equation (9). The CH₄ data were reproduced in the Supplementary Material (Table S2) under a Creative Commons Attribution (CC BY) license, with proper attribution to Lobo Paes et al. [9].

$${\mathrm{G}\mathrm{P}}_{{\mathrm{C}\mathrm{H}}_4}\left(\mathrm{L}\right)=\mathrm{G}\mathrm{P}\times {\mathrm{C}\mathrm{H}}_4\left(\mathrm{d}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{l}\right)$$

(9)

Useful Energy (UE) was calculated based on the Lower Heating Value (LHV) of methane of 38.0 MJ m⁻³ [30], according to Equation (10).

$$\mathrm{U}\mathrm{E}\left(\mathrm{M}\mathrm{J}\right)={\mathrm{G}\mathrm{P}}_{{\mathrm{C}\mathrm{H}}_4}\times {\displaystyle \frac{38.0}{1000}}$$

(10)

After calculating the daily biogas production, energy conversion estimates were performed, considering the energy equivalence (EQB) between 1 m³ of biogas and various fossil fuels and energy sources, based on their calorific value and combustion efficiency.

Table 3. Energy equivalence of biogas (EQB) for different fuels and current average market values (USD), as of August 2025.

Fuel	EQB	Source	Average Price (USD)	Source
Electricity (kWh)	1.428	[29]	4.15	[31]
Gasoline (L)	0.613		34.11	[32]
Hydrated Ethanol (L)	0.790		22.81
Firewood (kg)	1.536		N/A
Kerosene (L)	0.579		N/A
Diesel Oil (L)	0.553	[33]	33.28	[32]
Cooking Gas (kg)	0.454		47.53

where N/A—not applicable

presents these equivalences and the current average market values (as of August 2025), which were used to calculate the estimated financial savings from replacing these fuels with biogas.

In the specific case of domestic kerosene (intended for residential use, lighting, and heating) and firewood, the National Agency of Petroleum, Natural Gas, and Biofuels (ANP) does not provide weekly or monthly average price data. It should be noted that domestic kerosene differs from aviation kerosene (Jet A-1), and neither fuel is explicitly covered in the annual series, the ANP Dynamic Price Panel, or the weekly bulletins. Due to the absence of updated official information (as of August 2025) from a government source, only the energy equivalence of biogas (EQB) was calculated for these fuels, without monetary conversion, in order to maintain methodological standardization and the reliability of the results presented.

The energy conversion of biogas into each fuel was estimated using Equation (11).

$$\mathrm{E}\mathrm{C}={\mathrm{G}\mathrm{P}}_{{\mathrm{C}\mathrm{H}}_4}\times \mathrm{E}\mathrm{Q}\mathrm{B}$$

(11)

To estimate financial savings, the obtained EC values were multiplied by the current average market prices (R$ per unit) of each fuel (Table 3). The commercial exchange rate used was R$ 5.47 per USD, according to the quotation provided by the Central Bank of Brazil in August 2025 [34].

3. Results and Discussion

Analysis of the residual assumptions indicated that the combinations CM and 1:1, 1:3, and 3:1 W:CM simultaneously met the requirements for normality and homoscedasticity for all tested models, confirming the reliability of the kinetic parameters obtained for these ratios (

Table 4. Results of the Shapiro–Wilk (normality) and Breusch–Pagan (homoscedasticity) tests applied to the residuals of the Boltzmann, Logistic, and Modified Gompertz sigmoid models for the different ratio of aquaponics effluent (AE), water (W), and cattle manure (CM).

Ratio	Hypothesis Testing	Boltzmann	Logistic	Modified Gompertz
CM	Shapiro–Wilk	0.1524	0.6081	0.7203
	Breusch–Pagan	0.3137	0.2092	0.3266
AE	Shapiro–Wilk	0.0122	0.0122	0.0122
	Breusch–Pagan	0.0422	0.0422	0.0422
1:1 AE:CM	Shapiro–Wilk	0.7807	0.8085	0.5151
	Breusch–Pagan	0.0335	0.0260	0.0744
1:3 AE:CM	Shapiro–Wilk	0.9885	0.8960	0.3364
	Breusch–Pagan	0.0064	0.0339	0.0303
3:1 AE:CM	Shapiro–Wilk	0.5153	0.2271	0.3279
	Breusch–Pagan	0.0126	0.1230	0.0788
1:1 W:CM	Shapiro–Wilk	0.9271	0.7351	0.8439
	Breusch–Pagan	0.1203	0.0901	0.2460
1:3 W:CM	Shapiro–Wilk	0.3813	0.7123	0.8049
	Breusch–Pagan	0.1834	0.1287	0.1676
3:1 W:CM	Shapiro–Wilk	0.0723	0.7233	0.2316
	Breusch–Pagan	0.1690	0.1325	0.1170

). This behavior suggests a stable anaerobic process and consistent biogas production patterns over time, a condition essential for accurate predictions and system scaling [27].

For the CoAD, the residual normality assumptions (Table 4), verified by the Shapiro–Wilk test, indicated the presence of normally distributed residuals for all models (p > 0.05). In the homoscedasticity (Breusch–Pagan) test, the 1:1 AE:CM ratio was homoscedastic only under the Modified Gompertz model (Table 4). For 1:3 AE:CM, all models exhibited heteroscedastic residuals (Table 4). For 3:1 AE:CM, homoscedasticity held for the Logistic and Modified Gompertz models, whereas the Boltzmann model still indicated heteroscedasticity (Table 4). The heteroscedasticity observed in the other ratios, particularly pronounced across all three models for the 1:3 AE:CM condition, indicates non-constant residual variance, likely stemming from greater fluctuations in microbial activity and substrate-degradation rates over the course of digestion [35]. This instability may be related to the higher content of soluble nutrients in the aquaponics effluent [9], which tends to accelerate initial biogas production and increase variation in the subsequent phase of the process.

As expected, due to the absence of biogas production, the 1:0 AE:CM ratio showed p < 0.05 in both the Shapiro–Wilk and Breusch–Pagan tests, indicating a violation of statistical assumptions, i.e., the presence of non-normal and/or heteroscedastic residuals (Table 4). Therefore, none of the models were considered suitable for this ratio, and subsequent kinetic analyses were not justified. From a chemical–biological standpoint, the failure of AE under mono-digestion can be attributed to its very low solids and organic load (high moisture, low TS/TVS and COD; Table S1), which provide insufficient fermentable carbon to sustain acidogenesis and methanogenesis. In addition, the nitrogen speciation typical of aquaponics effluents (notably oxidized forms such as NO₃⁻–N) introduces strong electron acceptors that favor denitrification pathways, diverting reducing equivalents away from methanogenesis and raising the redox potential—both of which suppress methanogenic activity. Biologically, the endogenous microbiota in AE alone is unlikely to provide a robust, well-balanced methanogenic consortium or the full set of trace nutrients required for the syntrophic steps leading to CH₄. Combined with limited buffering (lower alkalinity relative to manure-based feeds), these factors hinder the establishment of stable anaerobic conditions and explain the persistent absence of methane and the resulting zero APP across the 19-week run. Consequently, model fitting was not applicable for the 1:0 AE:CM ratio [9]. It is worth noting that, although heteroscedasticity was observed in the 1:3 AE:CM ratio, the study by Lobo Paes et al. [9] reported that this ratio showed promising results, including consistent weekly biogas production, high methane content, and high efficiency in the removal of TS, TVS (Table S1) and COD (Figure S1). Therefore, its analysis regarding kinetic modeling is justified, especially considering that the p-values were very close to the 5% significance threshold.

The evaluation of statistical model selection criteria, through R²aj, RME, SE, RMSD, and AIC (

Table 5. Statistical model selection criteria (adjusted coefficient of determination (R²aj), standard error of the estimate (SE), mean relative error (RME), root mean square deviation (RMSD), and Akaike Information Criterion (AIC)) obtained for the Boltzmann, Logistic, and Modified Gompertz sigmoid models.

Ratio	Model	Selection Criteria
		R2aj	RME	SE	RMSD	AIC
CM	Boltzmann	0.9959	3.63	1.41	1.26	75.94
	Logistic	0.9941	4.72	1.70	1.57	82.71
	Modified Gompertz	0.9972	3.91	1.17	1.08	67.70
1:1 AE:CM	Boltzmann	0.9940	7.31	1.61	1.44	81.30
	Logistic	0.9889	9.16	2.19	2.02	92.87
	Modified Gompertz	0.9936	7.28	1.65	1.52	81.84
1:3 AE:CM	Boltzmann	0.9981	7.08	1.13	1.02	67.39
	Logistic	0.9948	11.07	1.88	1.72	86.71
	Modified Gompertz	0.9987	4.39	0.95	0.88	59.50
3:1 AE:CM	Boltzmann	0.9943	4.79	0.91	0.80	58.53
	Logistic	0.9909	5.84	1.15	1.05	67.25
	Gompertz Modified	0.9980	2.90	0.51	0.47	35.48
1:1 W:CM	Boltzmann	0.9950	4.01	1.31	1.17	73.47
	Logistic	0.9937	4.41	1.50	1.39	77.82
	Modified Gompertz	0.9947	5.40	1.36	1.24	73.79
1:3 W:CM	Boltzmann	0.9950	3.40	1.11	1.00	66.91
	Logistic	0.9933	3.76	1.31	1.21	72.33
	Gompertz	0.9953	4.93	1.07	0.99	64.75
3:1 W:CM	Boltzmann	0.9955	3.24	0.79	0.72	53.55
	Logistic	0.9913	4.90	1.11	1.04	66.20
	Modified Gompertz	0.9975	2.45	0.61	0.55	41.57

), allowed the identification of differences in the predictive performance of the Boltzmann, Logistic, and Modified Gompertz sigmoid functions for estimating APP_S, R_max, and λ across the different ratio based on the quality of their adjustment and simplicity in describing the phenomenon [25].

Overall, all models exhibited high adjusted R² values (greater than 0.98), indicating good agreement with the experimental data. However, comparison of the parameters revealed that the Modified Gompertz model performed best in most ratios, characterized by lower SE, RMSD, and AIC values (Table 5).

The evaluation of the selection criteria demonstrated that the Modified Gompertz model consistently presented the lowest AIC values across all substrate ratios (Table 5), confirming its superior adequacy for describing the cumulative biogas production process. The AIC estimates the relative quality of each model by balancing the trade-off between model fit and complexity, penalizing the inclusion of unnecessary parameters in relation to the available data. In this context, the systematically lower AIC values obtained for the Gompertz model indicate that it provided the best compromise between explanatory power and parsimony, ensuring reliable estimates of kinetic parameters without overfitting [25]. This result is consistent with previous studies that highlight its robustness in describing the kinetics of cumulative biogas production in batch systems [18,26].

Although the Boltzmann model showed competitive performance in the 1:1 AE:CM and 1:1 W:CM ratios, the combined analysis of statistical criteria (Table 4 and Table 5) and the representativeness of the phenomenon indicated that the Modified Gompertz model was the most suitable for describing cumulative biogas production over time and was therefore adopted for modeling anaerobic digestion in both MoAD and CoAD.

These results reinforce the biological plausibility of the Modified Gompertz model for anaerobic digestion systems. Its structure inherently captures the sigmoidal behavior of microbial growth, encompassing the lag phase, the exponential biogas production period, and the subsequent stabilization stage. This characteristic explains its better statistical and predictive performance compared to the Boltzmann and Logistic models, which either oversimplify or inadequately represent the dynamic phases of the digestion process.

Furthermore, the superiority of the Modified Gompertz model across all tested ratios highlights its robustness and flexibility, regardless of the substrate composition. This aspect is particularly relevant for the co-digestion scenarios (AE:CM and W:CM), where substrate heterogeneity and interactions between organic matter fractions could compromise the performance of simpler models. The alignment of the Gompertz model with both statistical indicators (lowest AIC values) and biological processes underscores its suitability as the primary tool for kinetic modeling in this study.

Based on the results obtained from the residual analysis (Table 4) and the statistical fit criteria (Table 5), it was found that the Logistic model performed worse compared to the Boltzmann and Modified Gompertz models and was therefore excluded from subsequent analyses.

For mono-digestion with CM, the Modified Gompertz model yielded the lowest AIC (67.70) and SE (1.17), indicating greater accuracy. In the 1:1 AE:CM ratio, Boltzmann and Modified Gompertz showed similar performance, although Boltzmann presented slightly lower error values. In the 1:3 AE:CM ratio, considered the most efficient in terms of bioenergy yield, Gompertz outperformed with the lowest RMS (4.39%), SE (0.95), and AIC (59.50), demonstrating superior fitting capability.

In the 3:1 AE:CM ratio, the Modified Gompertz model was again the most efficient, with an AIC of 35.48 (the lowest among all evaluated ratios) and an SE of only 0.51, suggesting that the model more accurately captured both the initial and stabilization phases of biogas production. For the ratio with water addition (W:CM), performance was more balanced between Gompertz and Boltzmann, with a slight advantage for Modified Gompertz in the 1:3 W:CM and 3:1 W:CM ratios, reinforcing observations by Lobo Paes et al. [9] regarding the model’s versatility across different substrate compositions.

The predominance of Modified Gompertz as the best-fitting model may be related to its ability to flexibly adjust the lag phase and maximum production rate, which is particularly important in co-digestion systems with varying biodegradability profiles [18].

Analysis of the kinetic parameters estimated by the Modified Gompertz model (

Table 6. Parameters estimated by the Modified Gompertz model for the maximum biogas production potential (APP_S), maximum biogas production rate (R_max), and lag phase (λ) during anaerobic digestion of different ratios of aquaponics effluent (AE), water (W), and cattle manure (CM).

Estimated Parameters	CM	1:1 AE:CM	1:3 AE:CM	3:1 AE:CM	1:1 W:CM	1:3 W:CM	3:1 W:CM
APPS (L kg−1)	64.02	60.19	72.20	31.94	51.04	43.06	32.57
Rmax (L kg−1 week−1)	6.02	5.52	7.47	5.77	5.53	4.74	3.73
λ (Week)	5.64	2.52	3.29	2.43	4.44	4.57	3.28

) revealed that the 1:3 AE:CM ratio exhibited the highest potential for maximum biogas production (APP_S = 72.20 L kg⁻¹) and the highest maximum production rate (R_max = 7.47 L kg⁻¹ week⁻¹), indicating high microbial activity and process efficiency. Although this ratio did not show the shortest lag phase (λ = 3.29 weeks), the observed latency period is considered moderate and compatible with systems in which gradual adaptation of the methanogenic microbiota occurs [36,37]. The lag phase observed for the 1:3 AE:CM ratio may be associated with the high organic load present, requiring an additional period for microbial community adaptation to the reaction medium. This behavior is corroborated by comparison with another ratio, in which an increased ratio of CM resulted in a longer initial period before biogas production intensified (Table 6).

In the overall comparison, the MoAD with CM showed intermediate performance, while CoAD with water (1:1 W:CM and 1:3 W:CM) resulted in lower yields (Table 6), highlighting the positive contribution of aquaponics effluent to improving anaerobic digestion performance. The 3:1 AE:CM ratio, although exhibiting a relatively high R_max (5.77 L kg⁻¹ week⁻¹) and a shorter lag phase (λ = 2.43 weeks), showed the lowest APPS among the ratio (Table 6), suggesting limitations in balanced nutrient availability and/or inhibitory effects from specific compounds, as well as indicating that the initial acceleration did not translate into higher final production. These results reinforce that the 1:3 AE:CM ratio stands out as the most promising, combining high bioenergy potential with a favorable biogas production rate for practical applications.

In particular, when assessing the robustness and sensitivity of the 1:3 AE:CM ratio to confirm the Modified Gompertz model, the WLS estimates were very close (APP_S = 72.11; R_max = 7.49; λ = 3.30; AIC = 59.79), and the GLS varPower fit yielded essentially coincident values (APPS = 72.21; R_max = 7.46; λ = 3.29), albeit with a higher AIC (61.49). These results indicated convergence across methods and robustness of the parameters, with only minor differences in parsimony.

The CI95% obtained via BCa bootstrap showed narrow and coherent uncertainty for the Base fit: APPS 71.31–73.86, R_max 7.08–7.87, and λ 3.06–3.58. For WLS, the CI95% (BCa) broadly overlapped with the Base, reinforcing the stability of the estimates. The phase sensitivity analysis (refits removing the first and/or last week) reduced AIC relative to the Base fit: TrimBoth = 56.20; TrimTail = 57.86; TrimHead = 57.89. This evidence suggested that initial transients and tail segments influenced part of the deviations and that trimming those segments improved parsimony without materially altering the kinetic interpretation.

Residual diagnostics supported the overall adequacy of the models. It can be seen in Figure 2 that the residuals indicated overall adequacy to normality, with slight deviations in the upper tail. In the Base fit (Figure 2a), the points followed the reference line across most of the domain, departing only at the highest quantiles, suggesting a slightly right-heavier distribution. The WLS fit (Figure 2b) and the GLS fit (Figure 2c) with a varPower variance function showed a similar pattern, without substantial correction in the tail, which was consistent with the Shapiro–Wilk results. Thus, residual normality was considered acceptable for inference, with the caveat of minor asymmetry at high response levels.

The Breusch–Pagan test indicates heteroscedasticity in the current export, suggesting a slight increase in dispersion at higher APP levels (Figure 3). Under these conditions, WLS (Figure 3b) and GLS varPower (Figure 3c) operated as robustness checks: point estimates remained virtually unchanged, and the AIC ranking kept the Base Gompertz fit competitive, with additional gains when phase sensitivity was considered.

Overall, it is inferred that the residual diagnostics (residuals versus fitted and Q–Q plots) for the Base, WLS, and GLS–varPower fits exhibited virtually identical patterns, with residual tests (Shapiro–Wilk and Breusch–Pagan) showing no significant deviations between them. Figure 2 and Figure 3 were retained to highlight the obtained results.

From a technological standpoint, the 1:3 AE:CM ratio showed high accumulated potential and an early maximum production rate, with λ around the third week, indicating accelerated onset and sustained growth (Table 6). Agreement among Base, WLS, and GLS, together with narrow CI95% and improved AIC under trims, supported the reliability of the estimates and the consistency of kinetic behavior under this configuration. Finally, the empirical evidence of mild variance heterogeneity did not change the main conclusions, because the robustness methods confirmed the results and the sensitivity analysis clarified the role of the initial and final segments of the series in model fit quality.

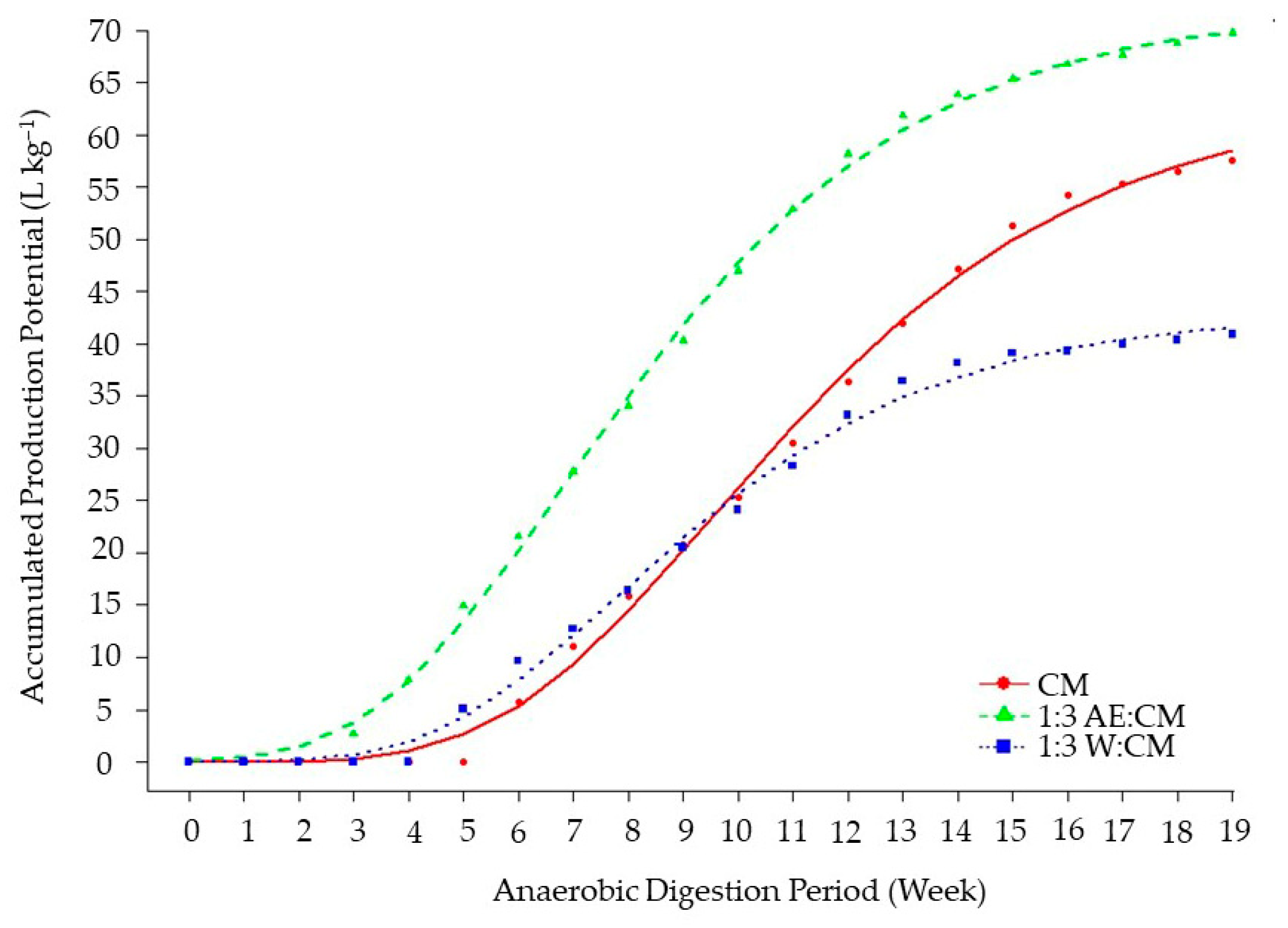
It was possible to observe an overall good agreement between all models and the experimental data (Figure 4). The Modified Gompertz model has a solid historical foundation and multiple reparameterizations, including modified versions capable of capturing maximum production and maximum rate, which underpins its wide application in bioproduction processes such as methane and hydrogen [14].

The kinetic behavior evidenced in Figure 4 demonstrates that CoAD with AE promoted a faster and more sustained increase in biogas production, with a reduced lag phase and a more pronounced inflection point, reflecting a steeper production rate compared to MoAD. Such performance can be attributed to the balanced C/N ratio, the presence of essential micronutrients, and the dilution of inhibitory compounds, conditions that favor microbial metabolism and process stability [8].

It can be observed in Figure 4 that the curve for the 1:3 AE:CM ratio surpasses the accumulated production of the other combinations throughout the entire experimental period, confirming its superior bioenergy potential for practical applications. For CM to reach values similar to those obtained by 1:3 W:CM, approximately 10 weeks of digestion were required, including a latency period of nearly six weeks.

The Modified Gompertz model fit was satisfactory for describing the APP (Figure 4), which is corroborated by the strong agreement between observed and estimated values (Figure 5). This proximity confirms the robustness of the model in describing the anaerobic digestion kinetics of the tested substrates. Similar results were reported by Sumardiono et al. (2021) [38], who observed high accuracy of the Gompertz model in predicting accumulated biogas production under different CoAD conditions.

The apparent hydrolysis kinetics were evaluated by fitting first- and second-order models, based on biogas production data for the three most representative ratios from CM, 1:3 AE:CM, and 1:3 W:CM. The selection of the most appropriate model simultaneously considered the magnitude of the adjusted R² (R²aj), the lowest values of SE, P, and RMSD, and the physico-biological coherence of the obtained parameters (

Table 7. Statistical performance of first- and second-order kinetic models in determining apparent kinetic constant of hydrolysis (k) for anaerobic digestion of cattle manure (CM), co-digestion of aquaponics effluent and cattle manure (1:3 AE:CM), and co-digestion of water and cattle manure (1:3 W:CM).

Ratio	Order	k	R2aj	SE	RME	RMSD
CM	1	0.06	0.9854	2.01	5.47	3.80
	2	0.03	0.9843	2.09	5.62	4.08
1:3 AE:CM	1	0.10	0.9855	2.33	5.75	5.15
	2	0.07	0.9807	2.69	6.65	6.87
1:3 W:CM	1	0.16	0.9753	1.62	6.10	2.44
	2	0.12	0.9694	1.81	6.61	3.03

where R²aj—adjusted coefficient of determination, SE—standard error of the estimate, RME—mean relative error, and RMSD—root mean square deviation.

).

The results indicated that the first-order model exhibited the best overall performance for the three studied ratios, with R²aj ranging from 0.9753 to 0.9855, along with lower SE, RME, and RMSD values compared to the second-order model (Table 7). These results align with the literature [16,18,24,26], which highlights the suitability of the first-order model for substrates with heterogeneous composition, where the hydrolysis rate was proportional to the amount of biodegradable organic matter available [39,40]. The second-order model presented metrics close to those of the first-order model but without significant improvements in fit, indicating that increased complexity did not substantially enhance prediction accuracy (Table 7).

The 1:3 AE:CM ratio stood out for having the highest apparent kinetic constant of hydrolysis in the first-order model (k = 0.10 week⁻¹), associated with a high R²aj (0.9855) and low statistical errors (SE = 2.33; RME = 5.75%; RMSD = 5.15). Furthermore, it exhibited the shortest T₉₀ (11.29 weeks) and T_ef (10.97 weeks), indicating that 90% of cumulative production was achieved and effective biogas production was maintained in less time than the other ratios. These results suggest that the presence of aquaponics effluent favored the hydrolytic stage, likely due to greater availability of soluble nutrients and lower recalcitrance of organic matter, promoting more efficient degradation of the substrate’s solid fraction. These results were consistent with those reported by Lobo Paes et al. [9]. On the other hand, mono-digestion of cattle manure exhibited T₉₀ of 14.44 weeks and T_ef of 12.07 weeks, suggesting a slower process, likely due to a higher fraction of lignocellulosic material [26]. The 1:3 W:CM ratio showed intermediate values for T₉₀ (11.96 weeks) and T_ef (10.31 weeks), reflecting kinetic performance superior to CM alone but inferior to that achieved with aquaponics effluent.

Table 8. Estimated weekly financial savings achieved through biogas substitution, considering current average prices (August 2025) in U.S. dollars (USD).

Ratio	Energy (MJ)	Electricity		Gasoline		Hydrated Ethanol		Diesel Oil		LPG		Firewood	Domestic Kerosene
		kWh	USD	L	USD	L	USD	L	USD	kg	USD	kg	L
CM	39,082	1469	6102	630	21,503	813	18,534	569	18,928	467	21,352	1.580	595
1:3 AE:CM	44,652	1678	6010	720	24,567	928	21,176	650	21,626	533	24,395	1.805	680
1:3 W:CM	26,630	1001	3584	430	14,652	554	12,629	388	12,898	318	14,549	1.076	406

presents the estimated weekly financial savings for different substrate ratios in the anaerobic digestion process, expressed as monetary values equivalent to the replacement of various conventional energy sources. It can be observed that the 1:3 AE:CM ratio exhibits the highest available energy (44,652 MJ) and the greatest weekly financial savings, followed by mono-digestion of CM and the 1:3 W:CM ratio (Table 8).

The data analysis reveals that anaerobic co-digestion with a higher ratio of AE to CM, at a 1:3 ratio, provides an energy increase of approximately 14% compared to pure CM, resulting in greater weekly financial savings across all evaluated energy sources. This increase can be attributed to the synergy between the substrates, which enhances biogas production, highlighting the efficiency of co-digestion in optimizing energy generation [41].

Furthermore, the reduction in the consumption of fossil fuels and firewood represents economic and environmental benefits, aligning with global targets for the mitigation of greenhouse gas emissions and the sustainable use of natural resources [4]. In addition to the economic aspect, the reduction in the consumption of fossil fuels and traditional biomass, such as firewood, represents an important environmental benefit, contributing to the mitigation of greenhouse gas emissions and aligning with global sustainability targets and the rational use of natural resources, as pointed out by the EEA (2025) [42]. On the other hand, the 1:3 W:CM ratio shows a weekly financial saving approximately 31.8% lower than pure CM, indicating lower energy efficiency for this specific combination of substrates.

These results show that the proper choice of substrate ratio in anaerobic digestion was fundamental to maximizing the financial savings provided by biogas, with co-digestion being a promising strategy to economically enable energy production from agro-industrial residues and effluents.

4. Conclusions

It was concluded that the 1:3 AE:CM ratio was the most efficient for anaerobic digestion systems aimed at biogas production in rural contexts, presenting high accumulated production, an optimized maximum production rate, and an adequate lag phase. The Gompertz kinetic model proved to be the most suitable for most treatments, especially those with a higher proportion of cattle manure, due to its greater explanatory capacity and lower error, enabling accurate estimates of key parameters (maximum production, lag time, and production rate). The statistical results supported these conclusions, normality (Shapiro–Wilk) and homoscedasticity (Breusch–Pagan), together with residuals-versus-fitted and Q–Q plots, corroborated the fits. When indications of non-constant variance arose, WLS and GLS with a varPower variance function, as well as phase-based sensitivity analysis, kept parameter estimates stable and increased parsimony. Uncertainty in APPS, R_max, and λ remained well bounded (95% confidence intervals by BCa bootstrap, with alternatives when necessary), and comparisons by AIC and ΔAIC indicated that minor violations—such as a slight increase in dispersion at higher APP levels—did not alter the conclusions or the kinetic interpretation. Therefore, the study ended with convergent evidence of inferential validity and application-oriented relevance, providing a reliable basis for the energy and economic interpretation of the evaluated scenarios.

Regarding the estimation of the apparent kinetic constant of hydrolysis, the first-order kinetic model showed better statistical performance and consistency with the characteristic times of the process, confirming its suitability for describing the hydrolytic stage in the anaerobic digestion of these substrates.

Scientifically, this study quantified kinetic behavior and process stability (APPS, R_max, λ, and formal residual diagnostics); practically, these parameters were translated into energy yields and illustrative cost savings, thereby clarifying how the kinetic evidence underpins economic and energy feasibility.

From an economic perspective, the 1:3 AE:CM co-digestion ratio showed the best cost–benefit relationship, with the potential to replace conventional energy sources and contribute to economic and environmental sustainability in rural areas. Thus, optimizing the substrate ratio in the biodigester proved essential to maximize the benefits of biogas, consolidating its strategic role in the rural energy matrix. It was acknowledged, however, that the study was conducted at bench scale under a batch regime, focusing on small installations and without claiming direct transfer to continuous or industrial reactors. Accordingly, the external validity of the parameters requires recalibration with continuous-operation data and/or the use of alternative metrics (e.g., time to production fractions or specific rates under fixed organic loading rate, OLR). As a continuation, it was proposed to integrate mechanistic/semi-continuous modeling and to carry out external validation in industrial reactors, clearly delineating the scope of the present study and its path toward real-scale application.