Glyphosate Pattern Recognition Using Microwave-Interdigitated Sensors and Principal Component Analysis

Abstract

Glyphosate is an herbicide used worldwide with harmful health effects, and efforts are currently being made to develop sensors capable of detecting its presence. In this work, an array of four interdigitated microwave sensors was used together with the multivariate statistical technique of principal component analysis, which allowed a well-defined pattern to be found that characterized waters for agricultural use extracted from the Bustillos lagoon. The variability due to differences between the samples was explained by the first principal component, amounting to 86.3% of the total variance, while the variability attributed to the measurements and sensors was explained through the second principal component, amounting to 13.2% of the total variance. The time evolution of measurements showed a clustering of data points as time passed, which was related to microwave–sample interaction, varied with the fluctuating dynamical structure of each sample, and tended to have a stable mean value.

1. Introduction

Glyphosate [(N-phosphonomethyl) glycine] (GLY) is a broad-spectrum, non-selective herbicide and is the most herbicide widely used worldwide [1,2]. Since the introduction of genetically modified GLY-resistant crops at the end of the twentieth century, their use has increased dramatically [3]. Glyphosate is considered toxicologically harmful and presents a potential association with human carcinogenesis and other chronic diseases, including mental and reproductive behaviors [4]. The conventional approach to glyphosate pollution water tests applies various chemical, physical, and microbiological methods, and most methods, such as this demand, specialized laboratories equipped with expensive and sophisticated scientific devices and also highly qualified personnel. Therefore, the current challenge is to develop cheap and portable sensors for use outside the laboratory [5,6]. In this regard, microwave-interdigitated sensors are a noninvasive, low-cost alternative with portability and rapid measurement options [7,8].

However, given the complex composition of the waters used in agriculture (they contain, besides glyphosate, other agricultural chemicals), together with the complexity of the interaction of these chemicals with the sensors, it is advisable to develop either glyphosate-specific sensors to determine its presence and concentration, or selective sensor arrays to recognize patterns, characteristic of samples containing glyphosate [9]. A sensor is specific when it reacts to a particular analyte, and no other analytes are present. In immunology, antibodies act as specific key-and-lock sensors for a particular antigen. A bio-enzyme can also act as a specific sensor by accelerating only the reaction of its corresponding substrate. A sensor array is selective, and it performs well when it comes to sensing the whole sample, not just its individual components. [10,11,12]. Microwave-interdigitated sensors provide us with a unique spectrum for different analytes, and in some cases, it might be sufficient to determine the analyte present in some media. The frequency spectra of microwave-interdigitated sensors have a significant number of resonant peaks available, which indicates that the various sensing elements each influence the obtained spectrum [13,14,15,16].

An interdigitated direct current sensor is a capacitive sensor that changes its capacitance when the dielectric constant of the material under test varies [17]. The operating principle of interdigitated direct current sensors can be understood starting with a simple parallel plate capacitor in a vacuum. Figure 1a shows the electric field force lines of the parallel plate capacitor that are parallel except for the so-called fringe effect on its edges. This fringe effect can be neglected when the distance between the plates is very small compared to their linear dimensions. If an acute angle is formed between the capacitor plates, as shown in Figure 1b, the electric field force lines are curved. Figure 1c shows the electric field force lines when both plates are in the same plane. This last configuration corresponds to the electric field above the two consecutive electrodes (two digits) of the interdigitated sensor. Finally, Figure 1d displays the equivalent circuit of the capacitive interdigitated sensor connected to a voltage source, with an applied voltage VDC and a known resistance R in series. By depositing the material under test in the electric field region above the fingers, the dielectric properties of that material produce a variation ΔC in sensor capacitance, and this, in turn, causes a variation Δi in the circuit current, which is measured as a voltage variation ΔV across the known resistance R. This voltage variation is the effect of the sample on the sensor output.

Interdigitated sensors have frequently been used at low frequencies, in which case, they can be represented by a capacitor-resistance equivalent circuit [4]. When an alternating excitation is used to excite the sensor instead of a direct current, the sensor’s conductive fingers acquire inductance. Then, the sensor’s capacitance and inductance produce resonance peaks whose frequencies depend on the sensor characteristics and on the sample dielectric properties. At higher frequencies in the RF and microwave ranges, when the wavelength λ of the applied signal is small compared to the linear dimensions of the sensor, it is necessary to use wave concepts (reflection coefficient) instead of circuit concepts (voltage). The design of an interdigital capacitive sensor requires the use of closed-form expressions for the computation of capacitance based on the sensor geometry and on the substrate dielectric properties [18]. Using complex-variable conformal mapping methods such as the Schwarz–Christoffel transformation and the partial capacitance method [19], it is possible to reduce the more complex calculation of the capacitance of an interdigitated sensor to a simpler one of a parallel-plate capacitor. Furthermore, when using microwaves, it is necessary to take into account that, at these higher frequencies, the analysis of interdigitated sensors becomes more complicated because the capacitances, inductances, and resistances are now distributed throughout the sensor [20].

Regarding the operating principle of an array of microwave-interdigitated sensors, this is based on the different responses of array sensors in the presence of the same material under test. These different responses are achieved by constructing the sensors with different geometric dimensions (finger length, width, and distance between fingers) and also by varying the dielectric constant of the substrate on which the sensor electrodes are deposited. The sensor’s different electrical responses are the original variables used in principal component analysis. The more measurements that are made, the greater the total variance in the set of studied samples, and the better the sensor array recognizes the sample pattern.

Principal component analysis is an unsupervised machine learning algorithm in which several correlated variables are transformed into a smaller set of new uncorrelated variables [21]. The “new variables” derived from the original variables by principal component analysis are simply linear combinations of the original variables. Principal component analysis is helpful for the reduction and interpretation of data, revealing internal relationships between data and also discovering previously unsuspected patterns between related substances [22]. The first principal component maximally discriminates among the samples, and its sample variance is as large as possible. The second principal component follows the first principal component by the amount it explains of the total variance, and its scores are uncorrelated with the scores on the first principal component. This process is continued for the remaining principal components. If the original variables are highly interrelated, it turns out that the first principal components account for a very high percentage of the variation in the original variables so that each subject’s scores on the remaining principal components can be ignored with very little loss of information [23].

Most of the relaxation phenomena of water molecules occur in the radiofrequency and microwave regions of the electromagnetic spectrum. Water is a polar molecule that forms tetrahedral structures with hydrogen bonds that are continually formed and destroyed because the hydrogen bond formation energy is of the order of average thermal energy at room temperature [24,25]. Currently, the most accepted dynamical model of water is the “wait and switch” model. This model describes the changes in water molecule orientation through a big jump. According to the “wait and switch” model, the water molecule waits until the appropriate defect conditions are created to make large jumps in the orientation of the molecule. When solutes are added to water, new hydration structures appear around the dissolved ions, and the water behavior is altered depending on the properties of the solutes, such as the polar or nonpolar behavior and the weak or strong character of acid (basis) dissolved in water [26,27,28,29].

The purpose of this work is to develop an array of microwave-interdigitated sensors and apply the multivariate statistical method of principal component analysis with the aim of determining patterns characteristic of glyphosate-containing water samples collected at different points in Bustillos lagoon. This lagoon is an internationally recognized sanctuary for migratory birds located in the state of Chihuahua, Mexico. Bustillos lagoon is contaminated with agrochemicals (GLY and other chemicals that are used in different crops in the region), solid waste, and urban wastewater [30].

2. Materials and Methods

Seven water samples from the Bustillos lagoon (S1, S2, S3, S4, S5, S6, S7) were studied. For comparison, samples of distilled water (DTW), deionized water (DIW), and commercial GLY were included in this study. GLY is a chemical used in crops in the region. Figure 2 is an aerial photograph showing the points from which the water samples from the Bustillos lagoon were extracted.

In total, 16 interdigitated sensors with different geometries (different size parameters) were constructed. The response of each sensor was measured in the presence of deionized water. For the sensor array, the four sensors with the greatest differences in their responses were selected. Finally, an array of sensors with 3, 6, 9, and 12 fingers (3F, 6F, 9F, 12F) was used in the experiments. Figure 3 shows, as an example, the 3F interdigitated sensor design scheme, and

Table 1. Sensor dimensions.

	A (mm)	B (mm)	C (mm)	G (mm)	W (mm)
3F	4.71	0.45	3.49	0.38	0.38
6F	4.71	0.45	3.49	0.29	0.29
9F	4.71	0.45	3.49	0.29	0.29
12F	4.71	0.45	3.49	0.19	0.19

displays the geometrical dimensions of the four interdigitated sensors. From Table 1, it can be observed that the dimensions A, B, and C are the same for the four sensors, while differences in dimensions appear in the dimensions G and W.

The interdigitated sensors were made on 50.8 μm thick flexible polyamide dielectric substrates, with a relative permittivity of 3.2, coated with a 35 μm thick copper layer from DuPontTM, and the model Pyralux^® AG, using optical lithography equipment with direct laser writing, model MicroWriter ML3, from Durham Magneto Optics Ltd., Cambridge, UK. With this MicroWriter ML3 equipment, four different minimum feature sizes (0.6 µm, 1 µm, 2 µm, and 5 µm) were selected automatically via software. This allows non-critical parts of the exposure to be performed rapidly while retaining high-resolution writing for critical parts. The substrates were cut into 2.5 cm × 4 cm rectangles using a wire saw model 850, brand South Bay Technology, Inc., San Clemente, CA, USA, and a diamond-impregnated wire blade, and then they were cleaned in isopropyl alcohol for 10 min using an ultrasonic cleaner, brand Branson Ultrasonics Corpotation, Brookfield, CT, USA, model 2510. After that, 4 mL of adhesion-enhanced positive photosensitive resin, model AR-P-3120, from Allresist, Strausberg, Alemania with a resolution of 0.4 μm, was deposited on each substrate, and a GmbH spin coater from APT Automation, Bienenbüttel, Germany, model SPIN150, APTwas used at 4500 rpm for 120 s to obtain a homogeneous layer of photosensitive resin with a thickness of 3 µm. The substrate with photosensitive resin was cured on a heating plate at 120 °C for 60 s to remove solvents and promote the cross-linking of the photosensitive resin, improving its adhesion to the substrate. For exposure of the interdigitated electrode patterns on the photosensitive resin coating, the substrates were placed inside photolithography equipment, MicroWriter ML3. This equipment projects the pattern of the designed interdigitated electrodes on the photoresin-coated substrates, scanning the surface with a laser beam with a spot diameter of 2 µm and a wavelength of 385 nm, applying an exposure dose of 60 mJ/cm² on the photo resin. The exposed substrates were immersed for 40 s in the Allresist developer, model AR-300-26, leaving the unwanted copper areas exposed and protecting only the pattern of interdigitated electrodes. The exposed areas were removed by immersing the substrates in a ferric chloride bath for 20 min or until it was clearly observed that the lines of the fingers and contacts did not present any residues. The photoresin protecting the interdigitated cooper electrodes was removed by immersing the substrates in acetone under ultrasound for 3 min. Lastly, a 50 Ω SMA-type connector for high frequency, model 73251-1150, Molex brand, Lisle, IL, USA, was soldered to each interdigitated sensor. This connector was coupled to the 50 Ω coaxial line, which, in turn, was connected to the vector network analyzer.

For microwave measurements, a vector network analyzer, Keysight, Santa Rosa, CA, USA, model, ENA E5063A (100 kHz–14 GHz), was used. This vector network analyzer is a versatile 2-port, 50 Ohm S-parameter test set. Vector network analyzer calibration was carried out using a Keysight N7553A (DC-14 GHz, 2-port) ECAL electronic calibration fixture, electronically connecting the following three calibration standards: short circuit, open circuit, and 50 Ω load. The dispersion parameter S₁₁ was measured through port 1 of the vector network analyzer. The vector network analyzer generates a microwave of known amplitude, phase, and frequency, and this microwave signal propagates from port 1 towards the sensor. The reflected wave is detected by the same port 1. This reflected wave carries valuable information about the interaction of the sensor with the liquid sample. The reflection scattering parameter ${\mathrm{S}}_{11}$ is defined by the formula ${\mathrm{S}}_{11}=20{\log }_{10}\mathrm{R}$, where ${\mathrm{R}=\mathrm{A}}_{\mathrm{r}\mathrm{e}\mathrm{f}}/{\mathrm{A}}_{\mathrm{i}\mathrm{n}\mathrm{c}}$ is the reflection coefficient, and ${\mathrm{A}}_{\mathrm{i}\mathrm{n}\mathrm{c}}$ and ${\mathrm{A}}_{\mathrm{r}\mathrm{e}\mathrm{f}}$ are the amplitudes of the incident and reflected waves, respectively. Using the vector network analyzer, a total of 10 samples were measured, and for each sample and sensor, 50 measurements of the ${\mathrm{S}}_{11}$ parameter were made at 100 MHz, one measurement every minute, keeping the microwave signal on during the whole measuring time. This means that a total of 2000 measurements of the S₁₁ scattering parameter were made. The data set measured by each of the four sensors contains the scores of each of the four correlated original variables, which were input into the software of principal component analysis.

Figure 4a shows one of the microwave-interdigitated sensors connected to the vector network analyzer using a 50 Ω coaxial cable, and Figure 4b shows an enlarged photo of the microwave-interdigitated sensor submerged in a beaker with water and connected to the coaxial cable through an SMA connector.

To determine the patterns that characterize the glyphosate-containing samples, the multivariate statistical technique of the principal component was used based on the software OriginPro 9.1.0. The principal component analysis was performed for the sample set (S1, S2, S3, S4, S5, S6, S7) using arrays of four and three sensors. For comparison, samples of distilled water (DTW), deionized water (DIW), and commercial glyphosate (GLY) were also included in this analysis.

3. Results and Discussion

In

Table 2. Eigenvalues of the correlation matrix.

	Eigenvalues	Percentage of Variance	Cumulative
1	3.45011	86.3%	86.3%
2	0.52631	13.2%	99.5%
3	0.0233	0.49%	99.99%
4	2.79 × 10−4	0.01%	100.00%

, the first column shows the eigenvalues associated with each of the four principal components, the second column shows the percentage of the total variance explained by each of the four principal components, and the third column shows the cumulative percentage of the variance. From this principal component analysis, it turns out that the first principal component amounts to 86.3% of the total variance, while the second principal component amounts to 13.2% of the total variance, i.e., together, they explain 99.5% of the total variance of the original data. The remaining two principal components amount only to 0.5% of the total variance and, therefore, are not considered in the following results.

The principal components are linear combinations of the original variables, and

Table 3. Extracted eigenvectors.

	Coefficients of CP1	Coefficients of CP2
3F	0.53418	0.01968
6F	0.52568	−0.29619
9F	0.51091	−0.42185
12F	0.42105	0.8567

shows the coefficients of the extracted eigenvectors associated with the two first principal components. Only these two eigenvectors were extracted from principal component analysis because the two last principal components account only for 0.5% of the total variance (see Table 1).

From these two extracted eigenvectors, it is now possible to represent the linear relations between the principal components and the original variables (parameters S₁₁ for the sensors), namely,

$$\begin{array}{c}CP1=0.53418\left(3\mathrm{F}\right)+0.52568\left(6\mathrm{F}\right)+0.51091\left(9\mathrm{F}\right)+0.42105\left(12\mathrm{F}\right)\\ CP2=0.01968\left(3\mathrm{F}\right)-0.29619\left(6\mathrm{F}\right)-0.42185\left(9\mathrm{F}\right)+0.8567\left(12\mathrm{F}\right)\end{array}$$

In these relationships, the following are observed: (a) the four sensors contribute to the first principal component with similar coefficients, while the sensor (12F) is the one that contributes the most to the second principal component, followed by the sensor (9F) with a contribution that opposes that of the sensor (12F); (b) for the first principal component, the contributions of the four sensors always appear in the same direction, while for the second principal component, the contributions of the sensors (6F) and (9F) appear in the opposite direction to the contributions from sensors (3F) and (12F).

Figure 5 is a component plot showing ten component scores: (S1, S2, S3, S4, S5, S6, S7, DIW, DTW, and GLY). In this plot, (S1, S2, S3, S4, S5, S6, S7) samples cluster together in a defined pattern in the upper left corner with similar scores for the first principal component. GLY has a score of the first principal component that is not very different from the scores of the (S1, S2, S3, S4, S5, S6, S7) samples. On the other hand, the scores of DIW and DTW samples for the first principal component are very different from the previously mentioned scores. From these observations, it is concluded that the first principal component strongly relates to the clustering of (S1, S2, S3, S4, S5, S6, S7) samples of the Bustillos lagoon with the commercial glyphosate GLY that is used in crops. On the other hand, the scores of (S1, S2, S3, S4, S5, S6, S7) samples for the second principal component are different from GLY scores for the second principal component, which is mainly attributed to the variability in measurements and the sensors.

Principal components using both the covariance matrix and the correlation matrix convey the same amount of information, and the choice of which one to use is strictly a matter of the use to which it is being applied [8]. In this work, principal component analysis was performed using both the covariance matrix and correlation matrix, obtaining very similar results. According to [8], there is no one-to-one correspondence between the principal component analysis using the correlation matrix and the principal component analysis using the covariance matrix, and the more heterogeneous the variances are, the greater the difference between the two types of principal component analysis. From these arguments and the very similar results mentioned above, it can be concluded that the variances of our samples are rather homogeneous. Therefore, from now on, only correlation matrix results are presented.

Figure 6a,b show the component plots of the first two principal components calculated using the correlation matrix and the covariance matrix, respectively. The relative locations of Bustillos lagoon samples (upper left corner) with respect to commercial glyphosate (lower left corner) and with respect to deionized and distilled water (upper right corner) are similar in both plots. It can be seen that using the correlation matrix, the first principal component explains 83.6% of the total variance of the samples, while using the covariance matrix, it explains 79.0% of the total variance of the samples. On the other hand, using the correlation matrix, the second principal component explains 13.2% of the total variance of the samples while using the covariance matrix explains 20.4% of the total variance of the samples.

An interesting dynamic effect is discussed below, using, as an example, the GLY sample. In the insert of Figure 5, an ellipse is drawn that encloses the 50 data points for GLY, with the measurement time as a parameter. The rightmost (leftmost) data point corresponds to the measurement made at time t = 1 min (t = 50 min), respectively. It is observed that the data points are further apart at the beginning of the measurements, and they become closer as the measurement time increases. This time evolution is explained by the interaction of the microwave signal with the sample. The greater agglomeration of the data points at the end of the measurement time indicates that a sort of stable state is reached. 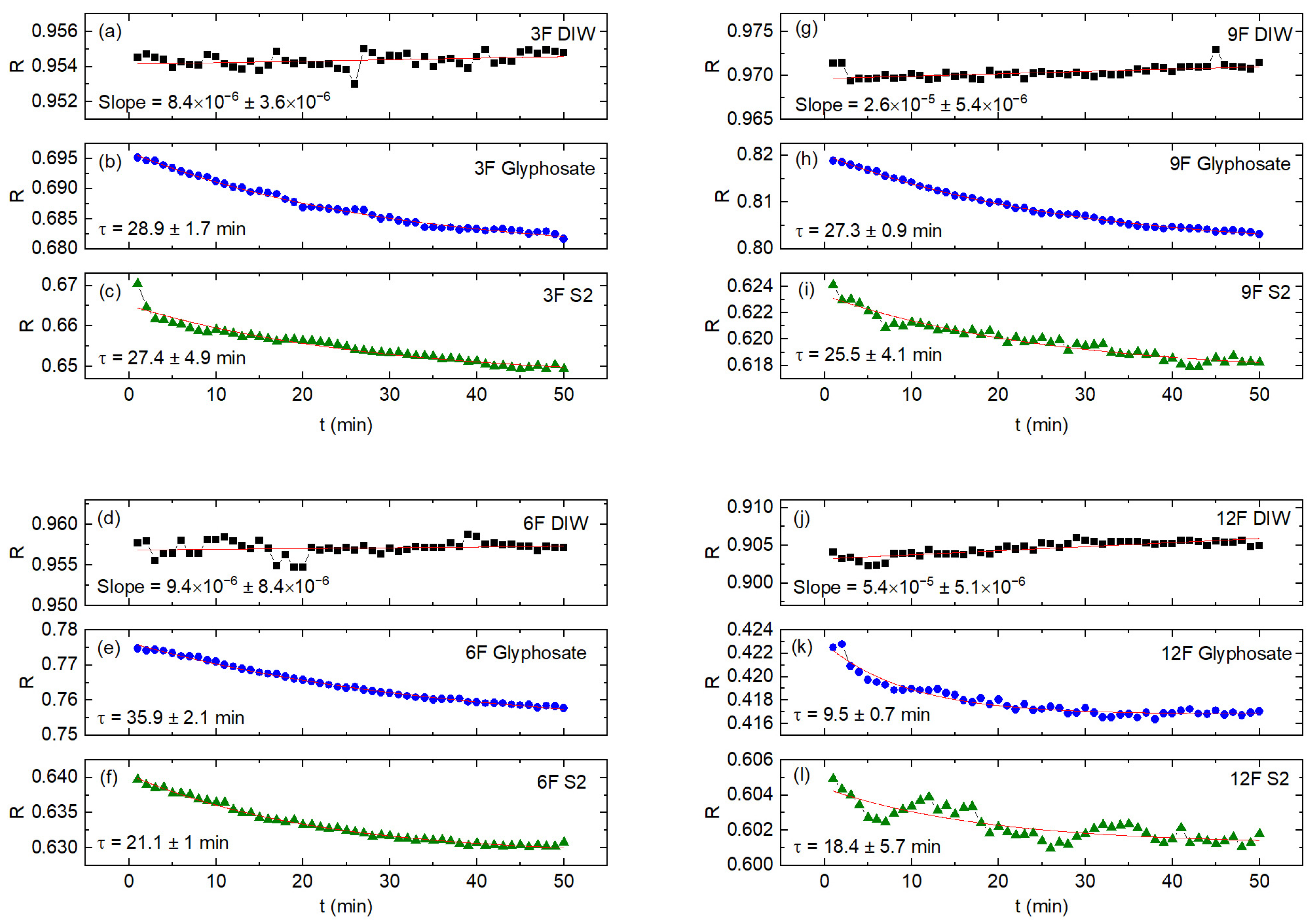In this same regard, Figure 7 shows the dynamical evolution of the reflection coefficient, R, of (DIW, GLY, S2) samples as a function of the measuring time for each sensor. It is noted that the curves for the DIW sample show only small variations in R, with data points randomly distributed around almost horizontal fitting lines, which indicates that this sample evolved at the beginning of the measurements towards a stable state. On the other hand, both the GLY curves and the S2 curves show a decrease in R over time. Data points for (GLY, S2) samples were fitted to decreasing exponential curves with a sort of “relaxation time τ”. This suggests that the DIW sample reacts more rapidly to the microwave signal, stabilizing the R value practically from the beginning of the measurements, while for (GLY, S2) samples with a more complex dynamic structure, it takes a longer time to stabilize the R values. It can also be observed that, for the same sample (GLY or S2), there are differences between the relaxation times obtained for different sensors, which indicates that these relaxation times are determined not only by the sample itself but also by the different responses of each sensor. Finally, it is important to note that for the sake of clarity and simplicity, only the curves of sample S2 are included in Figure 7. This decision was made because the remaining samples from Bustillos lagoon exhibit similar behavior.

Figure 8 shows the R curves for the (S1, S2, S3, S4, S5, S6, S7, DIW, DTW) samples as a function of R for GLY, where the measuring time is an implicit parameter; each graph corresponds to one different sensor. It is observed that the 12F sensor (Figure 5d) has a response markedly different from the remaining sensors, and it has the largest separation between the curves of the different samples. For each curve, the measurement at a time equal to 1 min (50 min) corresponds to the rightmost (leftmost) data point. The rightmost data points are more separated while the leftmost data points are closer; it suggests that the interaction of microwaves with samples tends to stabilize with the measurement time, which is a confirmation of a similar conclusion stated when the insert of Figure 5 was discussed. The important point here is that, in general, all curves are practically horizontal, meaning that the measurement time has only a minor effect on the R values. In fact, a simple calculation shows that the absolute values of the reflection coefficients of each sample only varied by 1–2% during the entire measurement time of 50 min. For this reason, large errors are not incurred by taking the R values as almost constant throughout the measurement range.

When applying principal component analysis to the measurements performed with an array of interdigitated sensors, an important issue is to determine the minimum number of needed non-redundant sensors in the sensor array. In this regard, a principal component analysis using arrays with three sensors instead of four was performed. Figure 9 shows component plots using arrays with only three sensors instead of the array with four sensors. Here, the component plots for the arrays (3F, 6F, 12F), (3F, 9F, 12F) and (6F, 9F, 12F) are very similar to each other, and it can be observed that the (S1, S2, S3, S4, S5, S6, S7) samples cluster together in the upper left corner of each plot, while the (DIW, DTW) samples are close to each other and are located towards the upper right corner of each graph. The GLY sample is also located very similarly in these three component plots. On the other hand, the component plot using the (3F, 6F, 9F) sensor array shows a pattern that is different from the three patterns aforementioned above, i.e., any combination of three sensors that includes the 12F sensor shows similar component plots. To better understand the behavior of the different arrays with three sensors, it is useful to analyze the correlation matrix obtained by principal component analysis for the original four-sensor array shown in

Table 4. Correlation matrix.

	3F	6F	9F	12F
3F	1	0.96371	0.92794	0.77924
6F	0.96371	1	0.99345	0.63082
9F	0.92794	0.99345	1	0.55541
12F	0.77924	0.63082	0.55541	1

. In this table, the diagonal elements are all equal to one, which corresponds to the definition of the correlation matrix, while the off-diagonal elements indicate the correlations between each pair of interdigitated sensors. This table shows that sensors 3F, 6F, and 9F are highly correlated with each other, with correlation values above 0.9, while sensor 12F is less correlated with 3F, 6F, and 9F sensors, with correlation values below 0.78; this means that the 12F sensor has less collinearity with the other sensors.

4. Conclusions

Seven (S1, S2, S3, S4, S5, S6, S7) glyphosate-containing water samples extracted from Bustillos lagoon showed similar behavior when they were measured with microwave radiation using an array of four interdigitated sensors, and they were subsequently analyzed by the unsupervised multivariate statistical method of principal component analysis. For comparison, samples of distilled water (DTW), deionized water (DIW), and commercial GLY were included in the study. The similar values of the first principal component score of the commercial glyphosate sample with respect to the scores of the seven glyphosate-containing water samples are indicative of their common content. In the principal component analysis of the (S1, S2, S3, S4, S5, S6, S7, DTW, DIW, and GLY) sample set, the first two principal components account for 99.5% of the total variance. The first principal component explains the variability of the samples, while the second principal component explains the variability due to measurements and sensors, respectively. The response signals of the four interdigitated microwave sensors contribute linearly with similar positive coefficients to the first principal component, while their contributions to the second principal component are different and of various signs. Component plots obtained using an array of only three sensors give the same results as component plots using an array of four sensors whenever the 12F sensor was included. This indicates that of the four sensors used initially in the sensor array, one would appear to be redundant; from the correlation matrix obtained from the principal component analysis, it was found that sensors 3F, 6F, and 9F were highly correlated and the 12F sensor had less collinearity with them. The component plots for the scores of all samples obtained by the covariance matrix and the correlation matrix have rather similar values; therefore, from the principal component theory, it can be concluded that the variances of our samples were rather homogeneous. An exponentially decreasing variation in the data scores with the measurement time was observed in the component plots for the (S1, S2, S3, S4, S5, S6, S7, GLY) samples, but no such variation was observed for the (DTW, DIW) samples; this would indicate that pure waters react faster to the applied microwave field. The curves of the reflection coefficient R of the samples as a function of the reflection coefficient of GLY also show a time variation, but this variation in measurements with time is small and amounts to only 1–2% of their absolute values; therefore, this variation has little influence on the absolute values of the reflection coefficients. These variations with time seem to be related to the evolution of the short-range fluctuating structures of liquid samples.