A Machine Learning Approach for the Estimation of Alfalfa Hay Crop Yield in Northern Nevada
Abstract
:1. Introduction
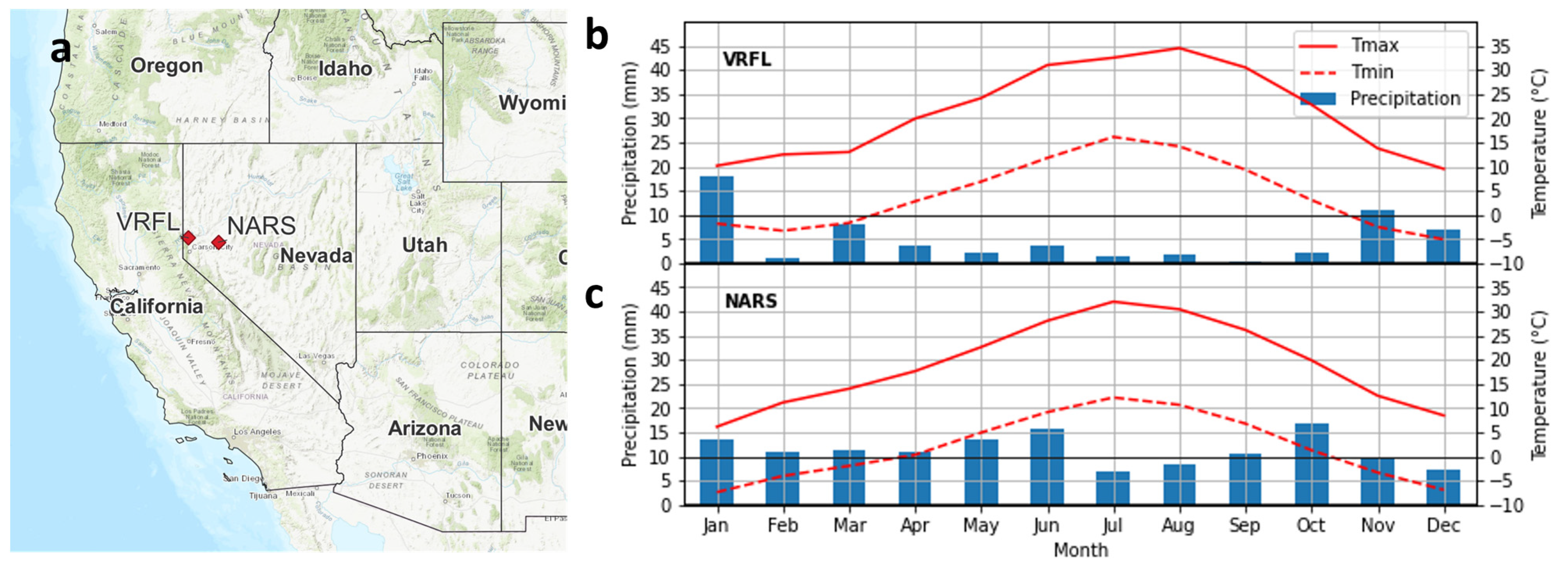
2. Materials and Methods
3. Results
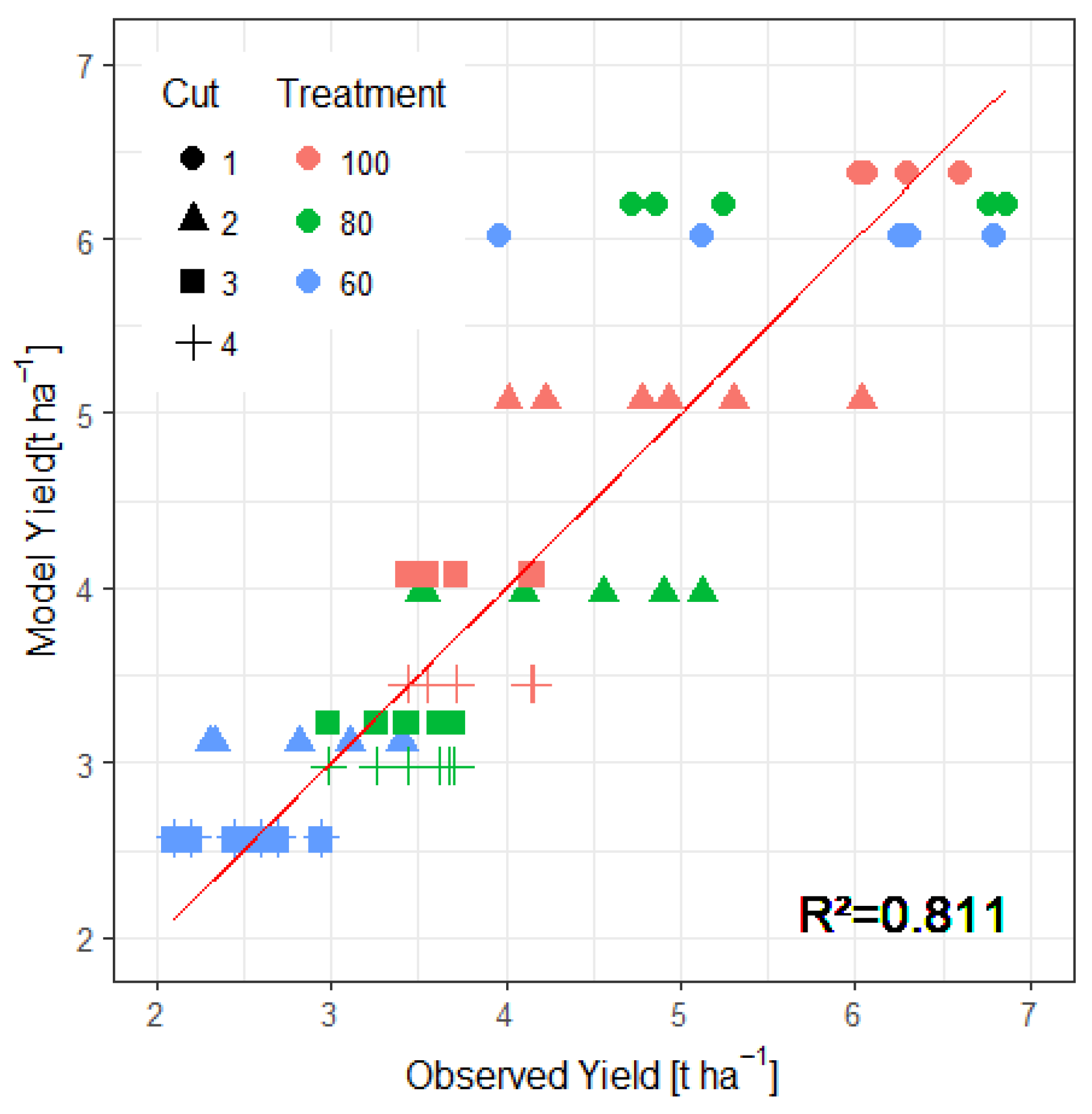
3.1. Linear Regression Model
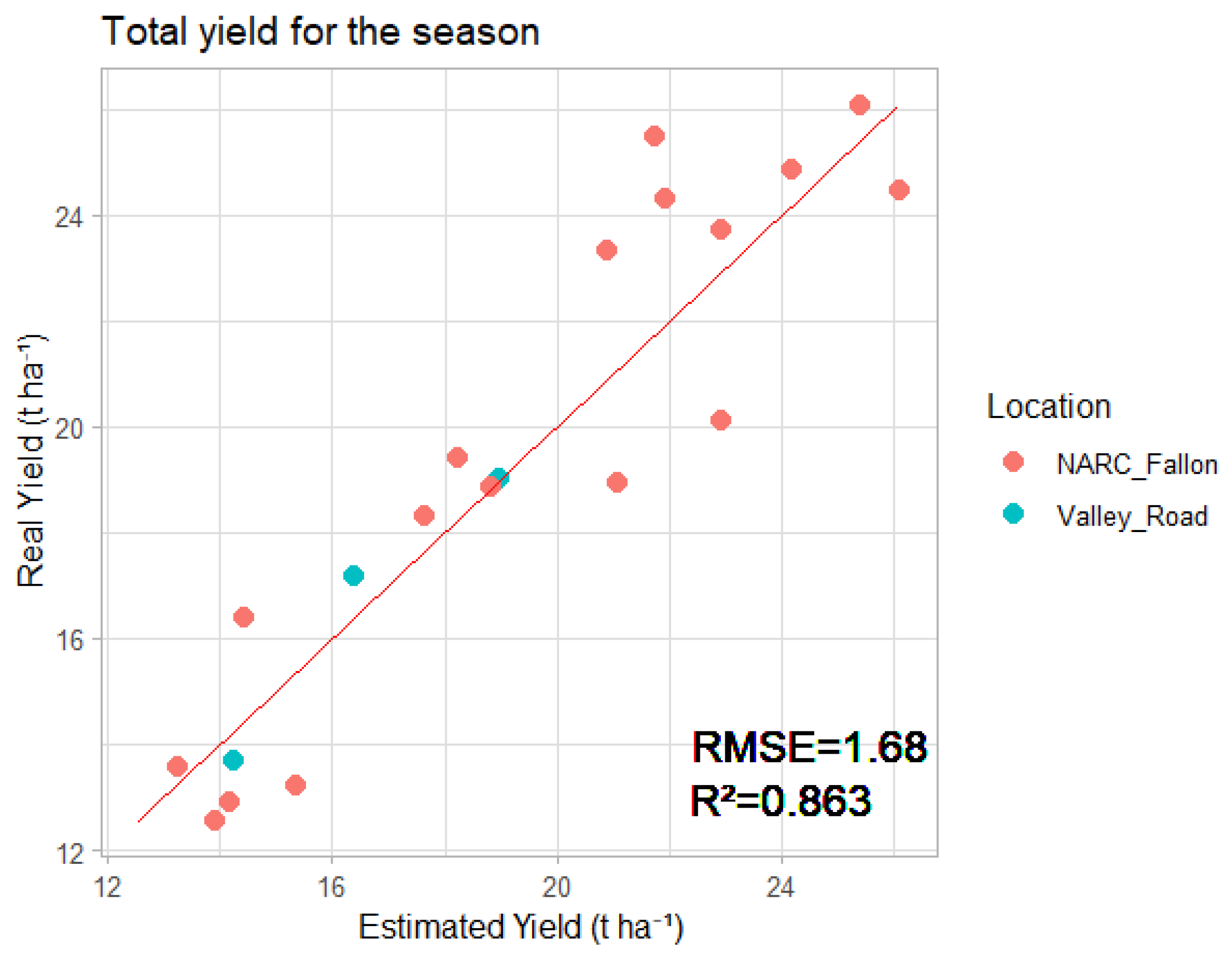
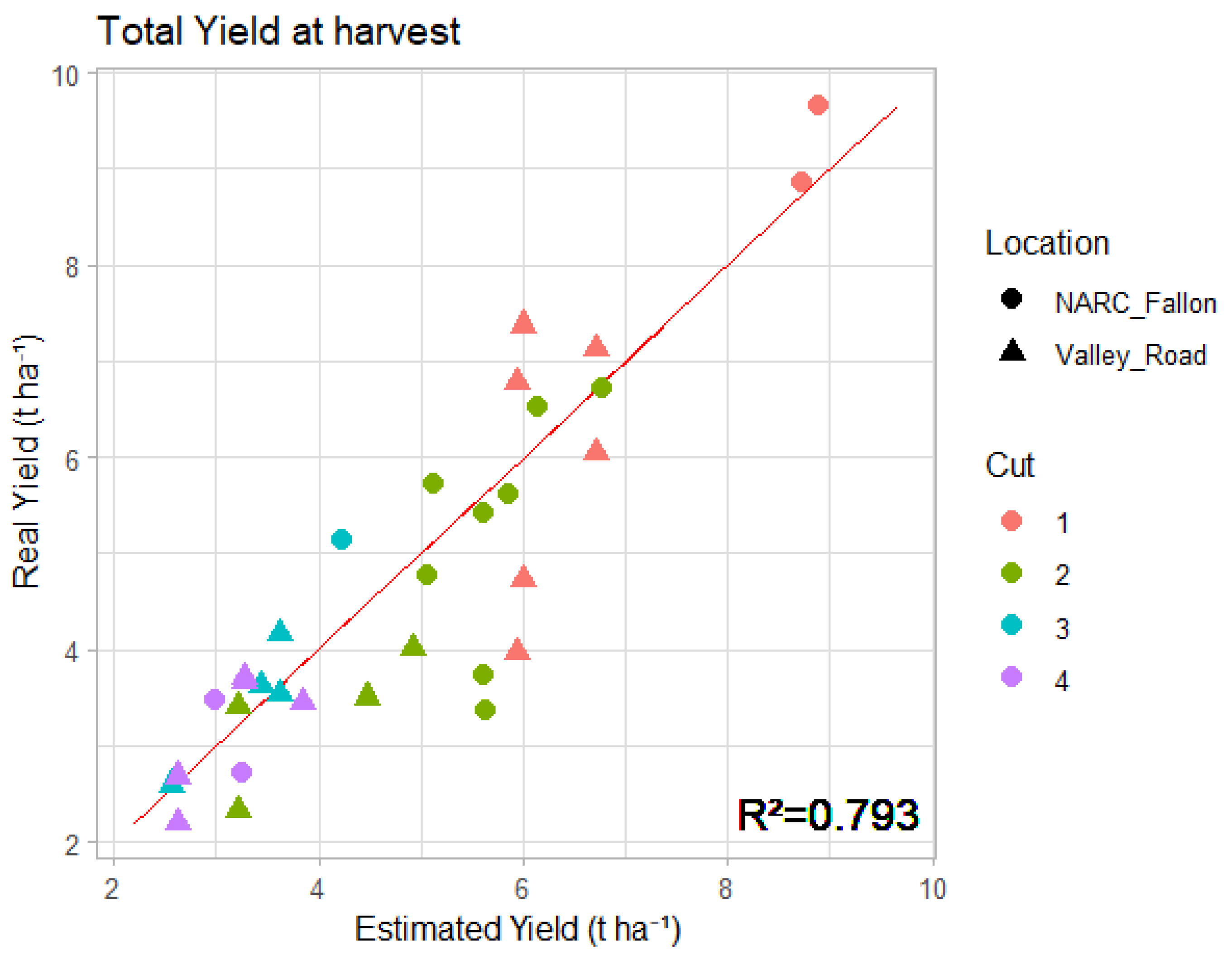
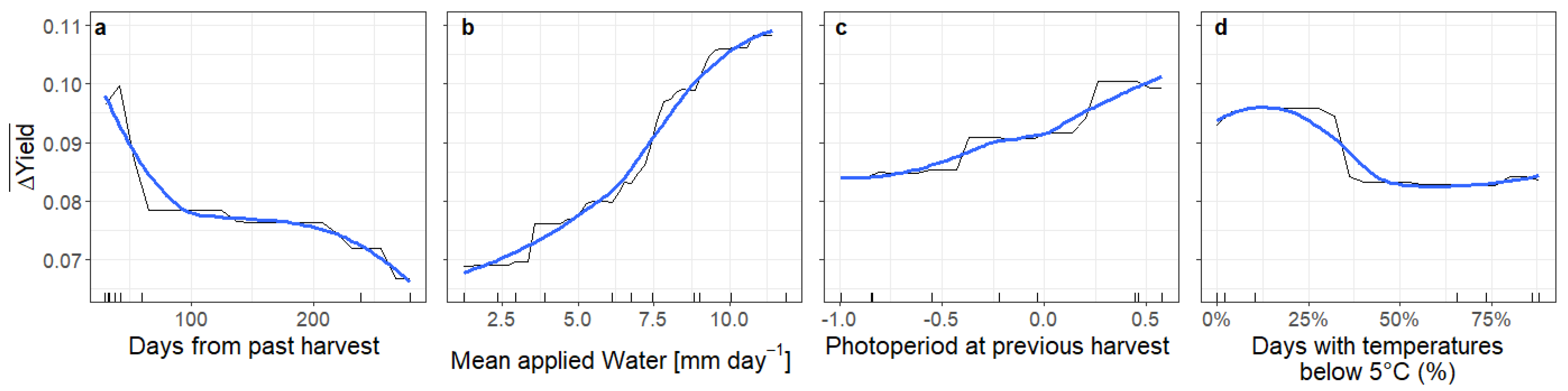
3.2. Random Forest Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rumberg, S. Nevada Agricultural Statistics Annual Bulletin 2016 Crop Year. 2016. Available online: https://www.nass.usda.gov/Statistics_by_State/Nevada/Publications/Annual_Statistical_Bulletin/2010s/NVANNBUL_update_Dec14.pdf (accessed on 13 May 2022).
- Graeff, S.; Link, J.; Binder, J.; Claupei, W. Crop Models as Decision Support Systems in Crop Production. In Crop Production Technologies; InTech: Rijeka, Croatia, 2012. [Google Scholar] [CrossRef]
- Teh, C.B.S. Introduction to Mathematical Modeling of Crop Growth: How the Equations are Derived and Assembled into a Computer Model; Brown Walker Press: Irvine, CA, USA, 2006. [Google Scholar]
- Boogaard, H.L.; De Wit, A.J.W.; Te Roller, J.A.; Van Diepen, C.A. Wofost Control Centre 2.1; User’s Guide for the Wofost Control Centre 2.1 and the Crop Growth Simulation Model Wofost 7.1.7; Alterra, Wageningen University & Research Centre: Wageningen, The Netherlands, 2014. [Google Scholar]
- Shi, W.; Tao, F.; Zhang, Z. A review on statistical models for identifying climate contributions to crop yields. J. Geogr. Sci. 2013, 23, 567–576. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.; Santra, G.H. Applications of Machine Learning Techniques in Agricultural Crop Production: A Review Paper. Indian J. Sci. Technol. 2016, 9, 1–4. [Google Scholar] [CrossRef]
- Sharma, A.; Jain, A.; Gupta, P.; Chowdary, V. Machine Learning Applications for Precision Agriculture: A Comprehensive Review. IEEE Access 2021, 9, 4843–4873. [Google Scholar] [CrossRef]
- Everingham, Y.; Sexton, J.; Skocaj, D.; Inman-Bamber, G. Accurate prediction of sugarcane yield using a random forest algorithm. Agron. Sustain. Dev. 2016, 36, 1–9. [Google Scholar] [CrossRef]
- Ghazvinei, P.T.; Darvishi, H.H.; Mosavi, A.; Yusof, K.; Bin, W.; Alizamir, M.; Shamshirband, S.; Chau, K. Sugarcane growth prediction based on meteorological parameters using extreme learning machine and artificial neural network. Eng. Appl. Comput. Fluid Mech. 2018, 12, 738–749. [Google Scholar] [CrossRef]
- Nantasaksiri, K.; Chareon-amornkitt, P. Comparison of Multiple Regression Analyses for Napier Grass Dry Matter Yield Prediction. JCREN 2015. Available online: https://www.researchgate.net/profile/Patcharawat-Charoen-Amornkitt/publication/287992611_Comparison_of_Multiple_Regression_Analyses_for_Napier_Grass_Dry_Matter_Yield_Prediction/links/567b5cd808aebccc4dfd9411/Comparison-of-Multiple-Regression-Analyses-for-Napier-Grass-Dry-Matter-Yield-Prediction.pdf (accessed on 16 May 2022).
- Whitmire, C.D.; Vance, J.M.; Rasheed, H.K.; Missaoui, A.; Rasheed, K.M.; Maier, F.W. Using Machine Learning and Feature Selection for Alfalfa Yield Prediction. AI 2021, 2, 71–88. [Google Scholar] [CrossRef]
- Moraffah, R.; Karami, M.; Guo, R.; Raglin, A.; Liu, H. Causal Interpretability for Machine Learning—Problems, Methods and Evaluation. ACM SIGKDD Explor. Newsl. 2020, 22, 18–33. [Google Scholar] [CrossRef]
- Qi, Y. Random Forest for Bioinformatics. Ensemble Mach. Learn. 2012, 307–323. [Google Scholar] [CrossRef]
- Luan, J.; Zhang, C.; Xu, B.; Xue, Y.; Ren, Y. The predictive performances of random forest models with limited sample size and different species traits. Fish. Res. 2020, 227, 105534. [Google Scholar] [CrossRef]
- Rashedi, N. Evapotranspiration Crop Coefficients for Alfalfa at Fallon, Nevada; University of Nevada: Reno, Nevada, 1983. [Google Scholar]
- Cholula, U.; Quintero-Puentes, D.; Andrade, M.; Solomon, J. Effects of Deficit Irrigation on Yield and Water Productivity of Alfalfa in Northern Nevada. In Proceedings of the 2022 ASABE Annual International Meeting, Houston, TX, USA, 17–20 July 2022. [Google Scholar]
- NOAA. Climate Data Online: Web Services Documentation. Available online: https://www.ncdc.noaa.gov/cdo-web/webservices/v2 (accessed on 13 October 2021).
- WRCC. RAWS USA Climate Archive. Available online: Https://Raws.Dri.Edu/ (accessed on 13 October 2021).
- World Meteorological Organization. Guidelines on Surface Station Data Quality Control and Quality Assurance for Climate Applications. WMO-No. 1269. 2021. Available online: https://library.wmo.int/records/item/57727-guidelines-on-surface-station-data-quality-control-and-quality-assurance-for-climate-applications (accessed on 18 October 2023).
- NOAA/OAR/ESRL. 20th Century Reanalysis Data. Available online: https://www.psl.noaa.gov/data/gridded/data.20thC_ReanV3.html. (accessed on 13 October 2021).
- Moot, D.J.; Yang, X.; Ta, H.T.; Brown, H.E.; Teixeira, E.I.; Sim, R.E.; Mills, A. Simplified methods for on-farm prediction of yield potential of grazed lucerne crops in New Zealand. New Zealand J. Agric. Res. 2021, 65, 252–270. [Google Scholar] [CrossRef]
- Kallenbach, R.L.; Nelson, C.J.; Coutts, J.H. Yield, Quality, and Persistence of Grazing- and Hay-Type Alfalfa under Three Harvest Frequencies. Agron. J. 2002, 94, 1094–1103. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. 2021. Available online: https://www.r-project.org/ (accessed on 13 October 2021).
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. Available online: https://cran.r-project.org/doc/Rnews/ (accessed on 18 October 2023).
- Greenwell, B.M. pdp: An R Package for Constructing Partial Dependence Plots. R.J. 2017, 9, 421–436. Available online: https://journal.r-project.org/archive/2017/RJ-2017-016/index.html (accessed on 18 October 2023). [CrossRef]
- Probst, P.; Wright, M.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. WIREs Data Mining Knowl. Discov. 2019, 9, e1301. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.C.; Fereres, E.; Raes, D. Crop Yield Response To Water. Food and agriculture organization of the united nations. 2012. Available online: https://www.researchgate.net/profile/Nageswara-Rao-V/publication/236894273_Suhas_P_Wani_Rossella_Albrizio_V_Nageswara_Rao_2012_Sorghum_In_Crop_Yield_response_to_Water_FAO_Irrigation_and_Drainage_Paper_66_Eds_Pasquale_Steduto_Theodore_C_Hsiao_Elias_Fereres_and_Dirk_RaesPages_/links/0deec51a01ddf96cca000000/Suhas-P-Wani-Rossella-Albrizio-V-Nageswara-Rao-2012-Sorghum-In-Crop-Yield-response-to-Water-FAO-Irrigation-and-Drainage-Paper-66-Eds-Pasquale-Steduto-Theodore-C-Hsiao-Elias-Fereres-and-Dirk-RaesP.pdf (accessed on 13 October 2021).
- Berengena, J.; Gavilán, P. Reference Evapotranspiration Estimation in a Highly Advective Semiarid Environment. J. Irrig. Drain. Eng. 2005, 131, 147–163. [Google Scholar] [CrossRef]
- Evett, S.R.; Howell, T.A.; Schneider, A.D.; Copeland, K.S.; Dusek, D.A.; Brauer, D.K.; Tolk, J.A.; Marek, G.W.; Thomas, M.; Gowda, P.H. The Bushland weighing lysimeters: A quarter century of crop ET investigations to advance sustainable irrigation 7004(November). Trans. ASABE. 2016, 59, 163–179. [Google Scholar]
- Stavi, I.; Thevs, N.; Priori, S. Soil salinity and Sodicity in drylands: A review of causes, effects, monitoring, and restoration measures. Front. Environ. Sci. 2021, 9, 330. [Google Scholar] [CrossRef]
- Abuelgasim, A.; Ammad, R. Mapping soil salinity in arid and semi-arid regions using Landsat 8 Oli Satellite Data. Remote Sens. Appl. Soc. Environ. 2019, 13, 415–425. [Google Scholar] [CrossRef]
- Claflin, L.E.; Stuteville, D.L.; Armbrust, D.V. Wind-Blown Soil in the Epidemiology of Bacterial Leaf Spot of Alfalfa and Common Blight of Bean. Phytopathology 1973, 63, 1417–1419. [Google Scholar] [CrossRef]
- Wassie, M.; Zhang, W.; Zhang, Q.; Ji, K.; Chen, L. Effect of Heat Stress on Growth and Physiological Traits of Alfalfa (Medicago sativa L.) and a Comprehensive Evaluation for Heat Tolerance. Agronomy 2019, 9, 597. [Google Scholar] [CrossRef]
- Zhu, R.Y.; Lei, J.Y.; Qu, L.; Chen, Y.; Jin, J. Metabolic responses of alfalfa (Medicago Sativa L.) leaves to low and high temperature induced stresses. Afr. J. Biotechnol. 2013, 10, 1117–1124. [Google Scholar]
- Goodrich, M. Dormant Season Evapotranspiration in Alfalfa; University of Nevada, Reno: Reno, Nevada, 1986. [Google Scholar]
- Villegas, D.; Alfaro, C.; Ammar, K.; Cátedra, M.M.; Crossa, J.; García del Moral, L.F.; Royo, C. Daylength, temperature and solar radiation effects on the phenology and yield formation of spring durum wheat. J. Agron. Crop Sci. 2015, 202, 203–216. [Google Scholar] [CrossRef]
- Ferrante, A.; Mariani, L. Agronomic management for enhancing plant tolerance to abiotic stresses: High and low values of temperature, light intensity, and relative humidity. Horticulturae 2018, 4, 21. [Google Scholar] [CrossRef]
- Liu, M.; Wang, Z.; Mu, L.; Xu, R.; Yang, H. Effect of regulated deficit irrigation on alfalfa performance under two irrigation systems in the inland arid area of midwestern China. Agric. Water Manag. 2021, 248, 106764. [Google Scholar] [CrossRef]


| Indicator | Description |
|---|---|
| Photoperiod of current harvest = , where is the Julian day of the current harvest. | |
| Photoperiod of previous harvest = , where is the Julian day of the previous harvest. | |
| Average of the total rain and irrigation input during the yield formation period (YFP). | |
| Daily mean solar radiation during YFP. | |
| Total growing degree days during YFP. | |
| Average daily wind speed during YFP. | |
| Fraction of days during YFP with minimum daily temperature below 5 °C. | |
| Fraction of days during YFP with maximum daily temperature below 5 °C. | |
| Fraction of days during YFP with minimum daily temperatures above 20 °C. | |
| Fraction of days during YFP with maximum daily temperatures above 30 °C. | |
| Days since the last harvest. | |
| Number of harvests (cut) in that season. E.g., 1 for the first harvest, 2 for the second, and so on. |
| Coefficient | Estimate | Pr (<|t|) |
|---|---|---|
| −3.207 | 0.000 | |
| +0.313 | 0.000 | |
| −0.161 | 0.000 | |
| −0.396 | 0.011 | |
| −1.261 | 0.001 | |
| −0.482 | 0.034 | |
| +0.358 | 0.000 | |
| +0.015 | 0.858 | |
| +0.021 | 0.477 | |
| −0.842 | 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quintero, D.; Andrade, M.A.; Cholula, U.; Solomon, J.K.Q. A Machine Learning Approach for the Estimation of Alfalfa Hay Crop Yield in Northern Nevada. AgriEngineering 2023, 5, 1943-1954. https://doi.org/10.3390/agriengineering5040119
Quintero D, Andrade MA, Cholula U, Solomon JKQ. A Machine Learning Approach for the Estimation of Alfalfa Hay Crop Yield in Northern Nevada. AgriEngineering. 2023; 5(4):1943-1954. https://doi.org/10.3390/agriengineering5040119
Chicago/Turabian StyleQuintero, Diego, Manuel A. Andrade, Uriel Cholula, and Juan K. Q. Solomon. 2023. "A Machine Learning Approach for the Estimation of Alfalfa Hay Crop Yield in Northern Nevada" AgriEngineering 5, no. 4: 1943-1954. https://doi.org/10.3390/agriengineering5040119
APA StyleQuintero, D., Andrade, M. A., Cholula, U., & Solomon, J. K. Q. (2023). A Machine Learning Approach for the Estimation of Alfalfa Hay Crop Yield in Northern Nevada. AgriEngineering, 5(4), 1943-1954. https://doi.org/10.3390/agriengineering5040119






