Traffic Flow Prediction via a Hybrid CPO-CNN-LSTM-Attention Architecture

Highlights

What are the main findings?

• This paper designs a traffic flow prediction model that integrates machine learning and deep learning to improve the efficiency of traffic flow prediction, alleviate road congestion, and further contribute to the development of smart cities.
• The combined model demonstrated excellent traffic flow prediction performance, achieving an RMSE of 17.35–19.83 and an MAE of 13.98–14.04 in the prediction results.

What is the implication of the main finding?

• An effective traffic flow prediction method for intelligent transportation systems, improving road services and management, is provided.
• The incorporation of cutting-edge machine learning and deep learning frameworks provides a basis for upcoming smart city programs.

Abstract

Spatiotemporal modeling and prediction of road network traffic flow are essential components of intelligent transport systems (ITS), aimed at effectively enhancing road service levels. Sustainable and reliable traffic management in smart cities requires the use of modern algorithms based on a comprehensive analysis of a significant number of dynamically changing factors. This paper designs a Crested Porcupine Optimizer (CPO)-CNN-LSTM-Attention time series prediction model, which integrates machine learning and deep learning to improve the efficiency of traffic flow forecasting in the condition of urban roads. Based on historical traffic patterns observed on Paris’s roads, a traffic flow prediction model was formulated and subsequently verified for effectiveness. The CPO algorithm combined with multiple neural network models performed well in predicting traffic flow, surpassing other models with a root-mean-square error (RMSE) of 17.35–19.83, a mean absolute error (MAE) of 13.98–14.04, and a mean absolute percentage error (MAPE) of 5.97–6.62%. Therefore, the model proposed in this paper can predict traffic flow more accurately, providing a solution for enhancing urban traffic management in intelligent transportation systems, and thus offering a research direction for the future development of smart city construction.

1. Introduction

The prediction of traffic flow, serving as a cornerstone of intelligent transportation systems (ITS), has consistently attracted researchers’ interest and is progressively significant for route planning and traffic administration [1]. Traffic participants can effectively avoid traffic congestion by using intelligent transportation systems, which can save travel time and reduce certain transportation costs [2]. In addition, effective traffic flow forecasting can provide sufficient decision-making support for traffic management departments and improve management quality [3]. In the process of traffic management, combined with ITS, the work tasks are reasonably assigned according to the characteristics of the road to achieve efficient supervision. Once congestion or accidents occur on urban roads, they can be handled quickly [4].

Existing research techniques for predicting traffic flow primarily involve methods derived from classical statistical theory, prediction methods employing nonlinear theory, and related approaches. At the same time, many machine learning methods have been proposed for traffic flow prediction problems, such as Support Vector Machine (SVM), Random Forest (RF), Gradient Boosting Decision Tree (GBDT), etc. Although these traditional machine learning methods have good nonlinear fitting capabilities, they cannot capture the variable temporal characteristics of traffic flow well [5]. Therefore, some research works have begun to use neural network models to predict traffic flow parameters [6,7]. These models generally use graph structures to model the spatial relationship of traffic flow, and use attention mechanisms, recurrent neural networks (RNNs) or convolutional neural networks (CNNs) to model the temporal relationship of traffic flow [8,9]. A single neural network model can perform time series-based predictions, but traffic networks are usually dynamically changing, so using only a simple neural network model usually cannot achieve the desired results [10,11].

Considering the dynamic characteristics of traffic flow and the problem of noisy data, some studies have begun to combine machine learning with neural network models for traffic flow prediction [12,13]. For example, using random forests and support vector machines to select important features in traffic flow data (such as weather, time, historical traffic, etc.), and then input these features into LSTM and CNN models for traffic prediction [14,15] can achieve excellent results. This method gets rid of the neural network model’s dependence on traffic flow data and reduces the difficulty of using the model [16]. However, these integrated models demand a significant quantity of traffic flow data to achieve optimal performance through training, which is unavailable within the timeframe required for predictive data [17]. Therefore, in practical applications, the model cannot be flexible and real-time, especially in scenarios where data collection is incomplete or data updates are delayed. For example, when a road section is subject to traffic control or a traffic jam, the spatial relationship between the adjacent sections of this section and this section will change, and these combined models will not be able to perform the prediction task [18].

The authors [19] note the importance of long-term traffic forecasting, since vital communications, such as health care, law enforcement, and other professional resources, depend on the proper organization of traffic. For this purpose, a traffic forecasting method is proposed that uses k-means clustering, a neural network with long short-term memory (LSTM), and a Fourier transform (FT) for long-term traffic forecasting. However, the application of the proposed algorithms for traffic optimization is limited.

Traffic recognition and forecasting based on machine learning [20,21,22] in combination with Internet of Things sensors [23] allows for the design of smart systems and further improvement of intelligent transport systems. The authors tested predictive algorithms suitable for processing complex and spatio-temporal parameters of urban traffic flow. It is noted that the stochastic nature of traffic significantly changes the traffic picture and requires consideration in each specific case.

The application of smart city algorithms in Polish cities is considered in [24] to support the activities of logistics companies. The authors note that in the cities under study, logistics companies can manage the flow of vehicles passing through the city by changing the traffic intensity in the city. At the same time, the authors emphasize that the proposed methodology cannot be extended to other cities, and simple scaling can lead to negative consequences. Lin et al. used the gravitational search algorithm and the Kolmogorov–Arnold network, an architecture that combines optimization algorithms and deep learning, to improve the accuracy of traffic flow prediction by about 5% [25]. Cai et al. successfully captured the spatial and temporal characteristics of traffic flow by integrating a dynamic graph structure with a neural network model [26]. This demonstrates that combining neural networks with optimization algorithms or gating mechanisms can significantly improve prediction efficiency.

To meet the needs of real-time and efficient traffic flow prediction, this paper proposes a CNN-LSTM model that integrates an attention mechanism and CPO. This model effectively handles noise in traffic flow data and captures temporal patterns in traffic behavior. It can be used to predict urban road traffic flow and thus alleviate urban congestion.

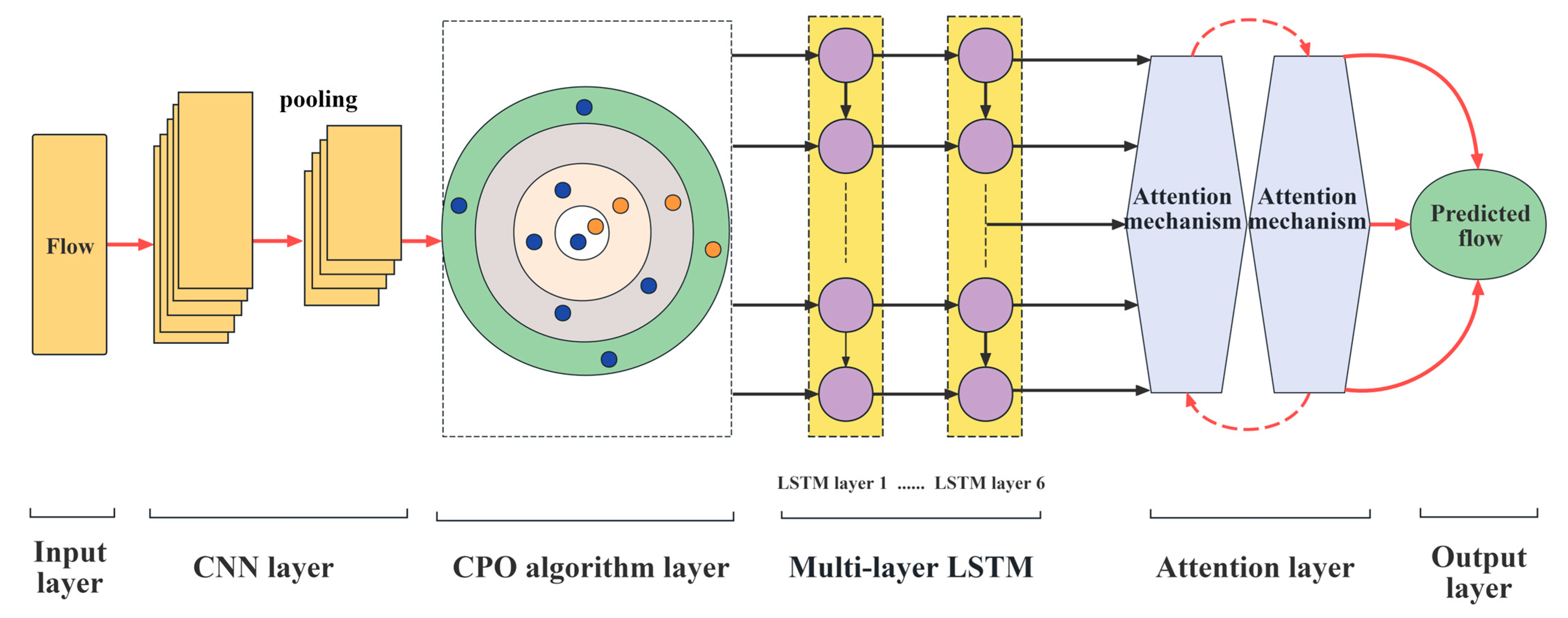
2. Proposed Method and Modeling

Figure 1 shows the overall architecture of the hybrid model, which mainly consists of a signal input layer, a CNN layer, a pooling layer, multiple LSTM layers, a classification output layer, a CPO optimization algorithm, and two attention mechanism components.

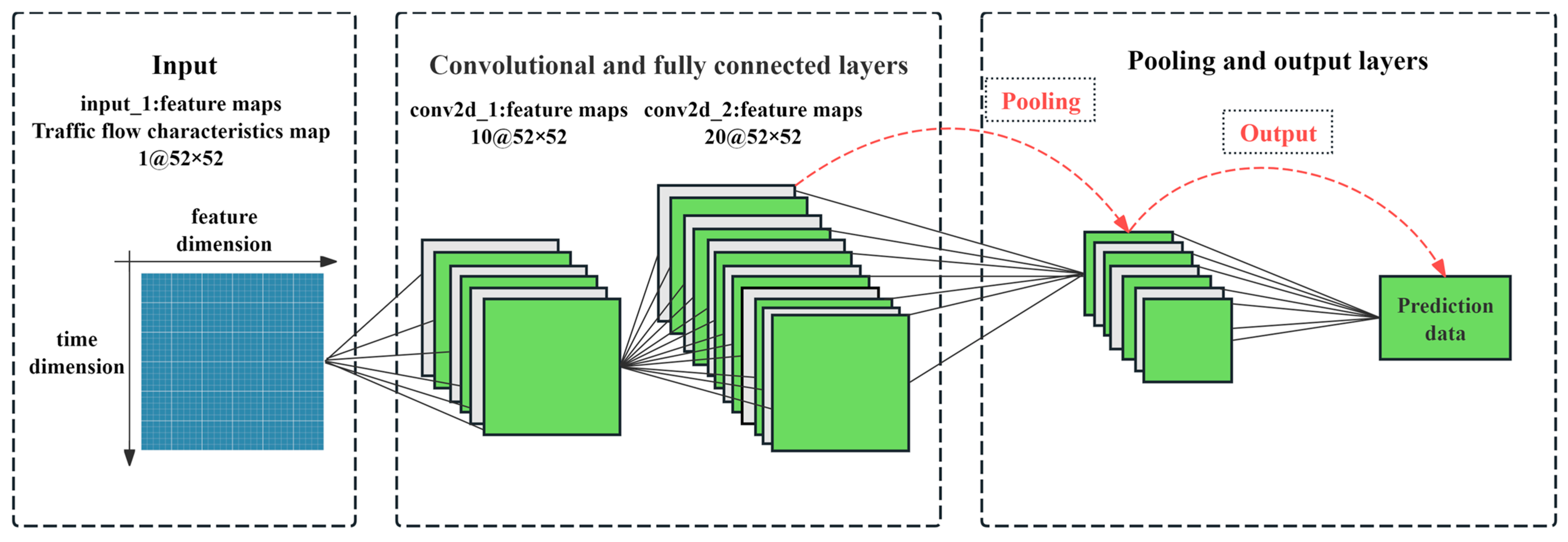
2.1. CNN Model Construction

The CNN primarily consists of a convolutional layer (employed for traffic flow feature extraction) and an activation function. A pooling layer (to reduce the dimensionality of the traffic flow data), a fully connected layer (to integrate the traffic flow characteristics), and an output layer (to generate the predicted data). Parameter optimization through minimizing the loss function is how the urban traffic flow prediction task is ultimately achieved. The convolutional neural network model structure used for modeling is shown in Figure 2.

Convolution operation is the core of CNN, and its purpose is to accurately extract local features of input data. Then, by stacking multiple convolution layers, CNN gradually extracts deeper traffic flow features [27,28]. The convolution operation used to extract local features of the input traffic flow data is denoted as Equation (1):

$$S\left(i,j\right)={\displaystyle \sum _{m=1}^M{\displaystyle \sum _{n=1}^{N}I\left(i+m,j+n\right)}}\cdot K\left(m,n\right)+b,$$

(1)

where $I$ denotes the input traffic flow characteristics and M is the length of the feature map; N represents the feature map width; K is the convolution kernel, of size M × N, $S\left(i,j\right)$ represents the element at the $\left(i,j\right)$ position of the output traffic flow features map; b is the bias term, and i and j are the spatial location indices of the output traffic flow feature map.

The next step is to select the activation function ReLU. The activation function can introduce nonlinear factors to CNN, allowing the network to learn and simulate real and complex traffic flow data. The activation function for the nonlinearity introduced by the CNN is shown in (2):

$$f\left(x\right)=\max \left(\mu x,x\right),$$

(2)

where x denotes the traffic flow output from the convolution operation, and $\mu$ denotes a constant, with a value of 0.01.

The pooling operation serves to reduce the dimensions of the traffic flow feature map, while maintaining key traffic flow feature information. The pooling layer is expressed as in (3):

$$P\left(i,j\right)=\underset{m,n\in R}{\max }I\left(x_{i,j}\right),$$

(3)

where P(i, j) denotes the output traffic flow after pooling; R denotes the pooling window and $x_{i,j}$ denotes the coordinate of the input data.

After the pooling operation is completed, the traffic flow data will be output to the fully connected layer, which integrates the traffic flow features extracted by the previous operation and prepares to output the final result. The fully connected layer runs in the form shown in (4):

$$y=W\cdot x+b,$$

(4)

where y denotes the output traffic flow; W denotes the model parameter matrix; x denotes the data sample; and b denotes the bias.

Since the error of the prediction results needs to be quantified, it is necessary to introduce a loss function into the CNN model. And the loss function can make the model self-adjust parameters to enhance forecast accuracy. The loss function is shown in Equation (5):

$$L=-{\displaystyle \sum _i{y}_i}\log \left({\widehat{y}}_i\right),$$

(5)

where $y_i$ denotes the real traffic flow data label; ${\widehat{y}}_i$ denotes the prediction probability.

After the loss function is introduced, the CNN technique is established. After a trial run in MATLAB, the next step is to combine the CPO optimization algorithm with the CNN technique.

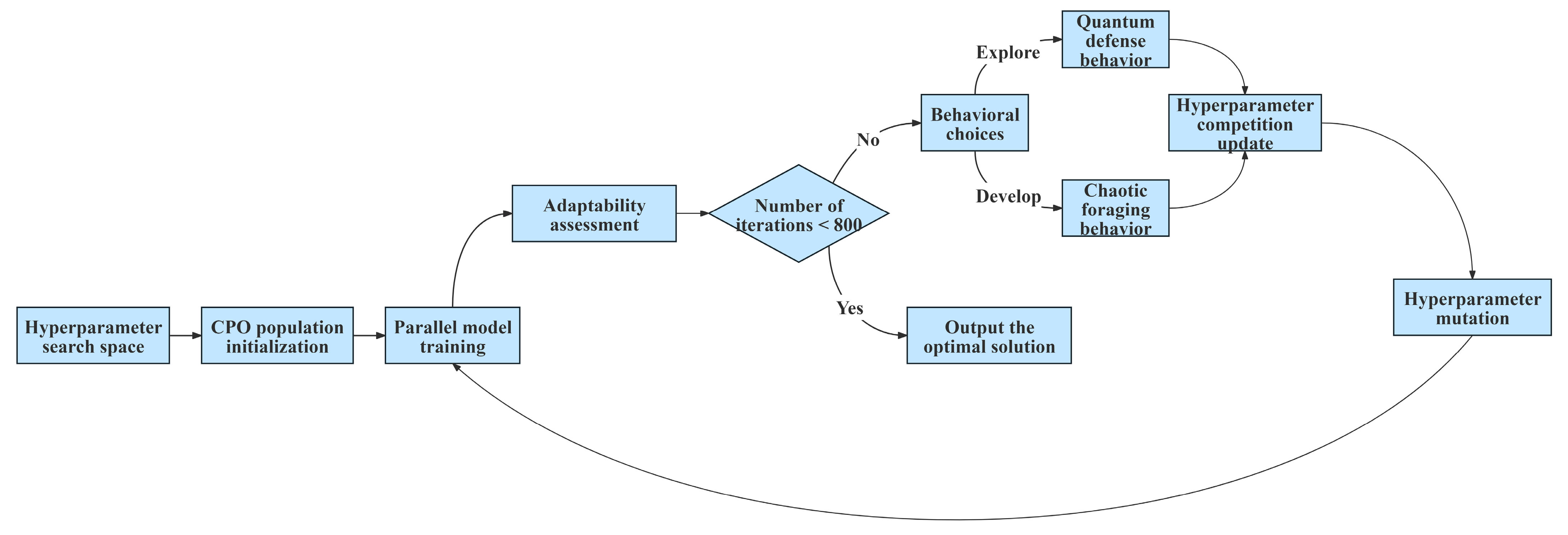
2.2. CPO Algorithm Modeling

The Crested Porcupine Optimizer (CPO) constitutes a heuristic optimization algorithm which emulates the observed daily behavior of crested porcupines in their natural habitat [29,30]. The CPO algorithm can perform a global search for traffic flow characteristics by simulating the scattered search and random exploration of animals, which can effectively reduce the risk of an insufficient search for traffic flow characteristics. Therefore, CPO needs to search for the optimal data in the dataset to complete the front-end prediction task. The expression for randomly initializing the traffic flow position is shown in Equation (6):

$$X_i=X_{\min }+rand\cdot \left(X_{\max }-X_{\min }\right),$$

(6)

where X is the location of the i-th data; $X_{\min }$ and $X_{\max }$ are the lower and upper bounds of the search space; and $rand$ denotes a stochastic value in the range [0.5, 0.8].

To identify the optimal solution for traffic flow, continuous updates to the location of stochastic traffic flow data are required. The expression for location update is shown in Equation (7):

$$X_i^{t+1}=X_i^t+\alpha \cdot rand\cdot \left(X_{best}-X_i^t\right),$$

(7)

where $X_i^{t+1}$ denotes the position of the i-th traffic flow data at the moment $t+1$; $X_i^t$ denotes the position of the i-th traffic flow data at the moment $t$; $\alpha$ denotes the step factor, which is used to control the exploration range; $X_{best}$ denotes the location of the optimal data.

To verify whether the input data is suitable for the prediction task, the fitness of each data is calculated. Each data adaptation value is expressed as Equation (8):

$$f_i=f\left(X_i\right),$$

(8)

where $f_i$ is the fitness value of the i-th data; $f\left(X_i\right)$ is the function of the objective value at location $X_i$.

To ensure the accuracy of the prediction, the global optimal solution must be changed in each iteration. The expression for updating the global optimal solution is shown in Equation (9):

$$X_{best}=\arg \underset{X_i}{\min }f\left(X_i\right),$$

(9)

After the traffic flow position update and fitness calculation functions are modeled, the CPO algorithm is basically modeled. Combine the CPO algorithm with the CNN model to test run the model, in preparation for adding the LSTM model in the next step.

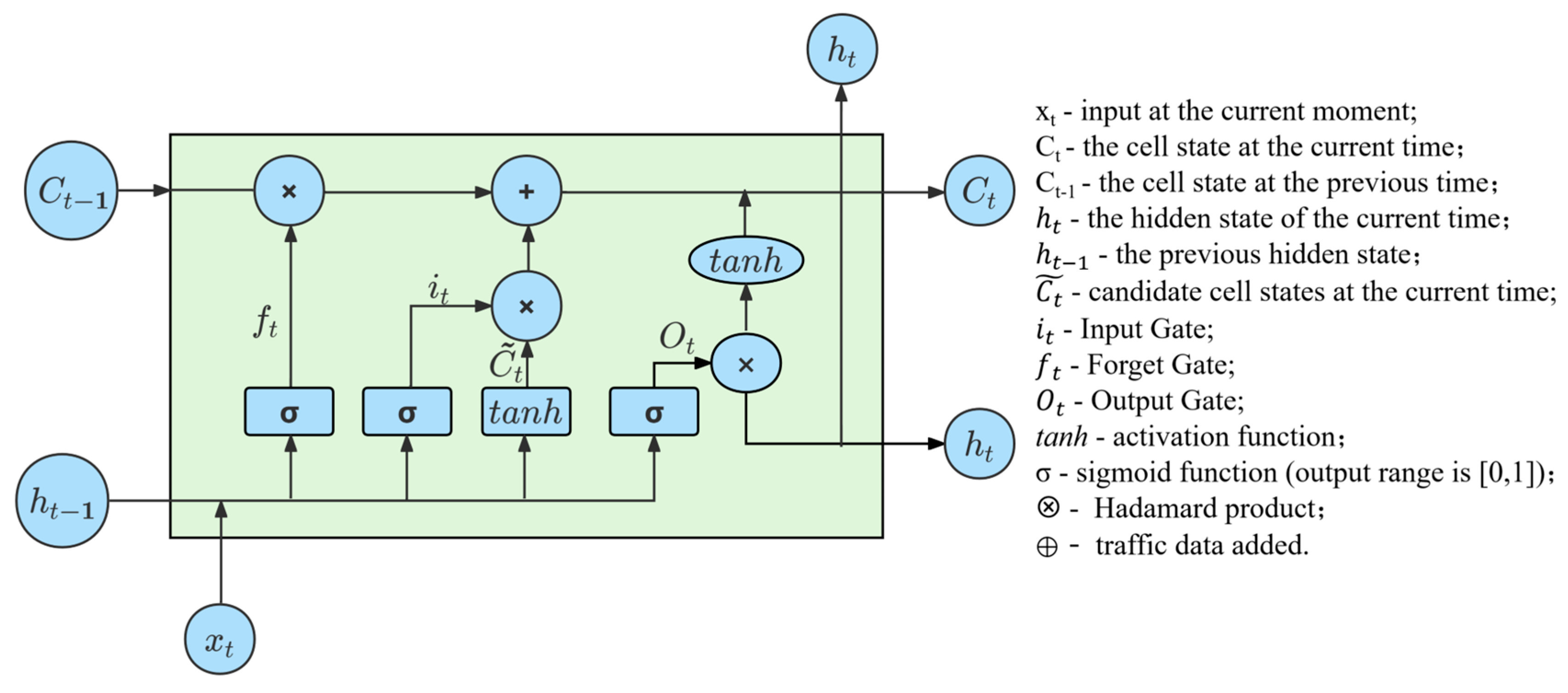
2.3. LSTM—Attention Model Construction

Traffic flow data has obvious time dependence and usually has significant fluctuations within a day, such as morning peak and evening peak. In response to dynamically changing traffic flows, LSTM can dynamically adjust the internal state of the algorithm to adapt to data modifications and can maintain high prediction accuracy in different time periods [31,32]. A single LSTM neural network unit is demonstrated in Figure 3.

LSTM introduces a forget function, input and output gates to solve the gradient vanishing task of data and can obtain the characteristics in time series data. The LSTM model forget gate is expressed as Equation (10):

$$f_t=\left(W_f\cdot x_t+U_f{h}_{t-1}+b_f\right)\cdot Sigmoid,$$

(10)

where $W_f$ denotes the parameter matrix of the forget function; $x_t$ denotes the input vector at time t; $U_f$ denotes the trainable weight matrix; $h_{t-1}$ denotes the trainable weight matrix $b_f$ denotes the bias of the forget function; Sigmoid denotes the activation function, which takes data in the range [0, 1].

The decision regarding what new data is stored in the LSTM model’s cell state is determined by the input gate. Equation (11) provides the input gate expression:

$$i_t=\left(W_i\cdot x_t+U_f\cdot h_{t-1}\right)\cdot Sigmoid,$$

(11)

where $W_i$ is the input gate parameter matrix.

In generating new information for the present predictive time frame, the candidate state functions in conjunction with the input gate, which then supplements the cell state. Formulate an expression that represents the candidate cell state at the present step, following the form in Equation (12).

$${\tilde{C}}_t=tanh\left(W_C\cdot x_t+U_C\cdot h_{t-1}\right),,$$

(12)

where tanh is the activation function; $W_C$ is the weight of the candidate cell state; $U_C$ is the trainable weight matrix of the candidate cell.

The cell state is dynamically updated by controlling the forgetting function and the input gate to decide whether to retain or discard certain information and avoid the vanishing gradient problem that occurs in experimental data. The expression of cell states is shown in (13):

$$C_t=f_t\cdot C_{t-1}+i_t\cdot {\tilde{C}}_t,$$

(13)

where $C_t$ is the previous cell state; ${\tilde{C}}_t$ is the current cell state.

LSTM outputs information from the cell state to the hidden state through the output gate. The expression for the output gate is shown in Equation (14):

$$o_t=\left(W_o\cdot x_t+U_o\cdot h_{t-1}\right)\cdot Sigmoid,,$$

(14)

where $W_o$ is the output gate weight; $U_o$ is the output gate trainable weight matrix.

The hidden state of LSTM works together with the cell state to transmit and output prediction information. And the hidden state carries important information at the current moment, which can help the model convey traffic flow characteristics in time series prediction. The expression for the hidden state is shown in (15):

$$h_t=o_t\cdot tanh\left(C_t\right),$$

(15)

In the current step, the output gate creates a hidden state and passes data information to the subsequent step. By using these equations together, the LSTM model is then able to effectively capture the long-term dependencies and features in the traffic flow data.

The attention mechanism constitutes an important technology in the field of deep learning and finds extensive use in computer technology and speech recognition [33,34]. Its function is to enable the prediction model to dynamically identify the characteristics of the input data, thereby enhancing the prediction model accuracy. By employing the attention mechanism, the CPO algorithm achieves improved multimodal information integration, thereby boosting prediction task performance. This relationship added to the hybrid model is expressed by (16):

$$Attention=Softmax\left({\displaystyle \frac{Q{K}^T}{\sqrt{d_k}}}\right)\cdot V,$$

(16)

where Q, K, and V denote matrices of different modes; Softmax denotes the activation function, which serves to transform real numbers into probability distributions; and $\sqrt{d_k}$ denotes the scaling factor.

Softmax as a commonly used activation function, is given by the expression in Equation (17):

$$Softmax\left(u_i\right)={\displaystyle \frac{e^{u_i}}{{\displaystyle {\sum }_{j=1}^n{e}^{u_j}}}},$$

(17)

where $u_i$ denotes the u-th component of the input vector; $e^{u_i}$ denotes the index of $u_i$; and ${\displaystyle {\sum }_{j=1}^n{e}^{u_j}}$ denotes the sum of the indexes of all elements.

In the process of combining models, the CPO optimization algorithm and attention mechanism are introduced to dynamically fuse the outputs of the CNN and LSTM techniques. The hyperparameter optimization process for the CPO algorithm is illustrated in Figure 4.

CPO automatically searches for and extracts spatial features of the road network and determines the optimal convolution kernel size for the CNN. For the LSTM model’s hyperparameters, CPO balances long-term memory with short-term fluctuations to prevent overfitting. It also works with the attention mechanism to determine how far back in history the most effective for future predictions. For historical data in the context of traffic accidents, this hybrid model allows the attention mechanism to dynamically focus on the most relevant historical information at the current moment. The model focuses on short-term, recent data points around the time of the accident, capturing trends leading up to the accident rather than fitting old data features to new circumstances. Therefore, the fusion of CPO and the attention mechanism yield a time-series prediction model that more accurately captures the periodic and random nature of traffic flow.

3. Results and Discussion

The Paris urban road traffic flow dataset in France (Research datasets [35]) was the source of the experimental data utilized in this paper. The dataset mainly includes measurements from loop detectors, which record vehicle flow and occupancy every 5 min. Paris’s road network structure means that traffic flows are highly correlated in space and exhibit distinct multi-periodic characteristics in time. This dataset greatly facilitates the validation of the model’s ability to capture complex spatiotemporal dependencies. Raw traffic flow data usually contains noise, missing values, and redundant information. Directly using the data set will lead to a decline in the model or even failure to run the model properly. Thus, data preprocessing is essential to enhance the caliber of data, empowering the model to more effectively discern traffic flow attributes, consequently boosting predictive precision and efficacy.

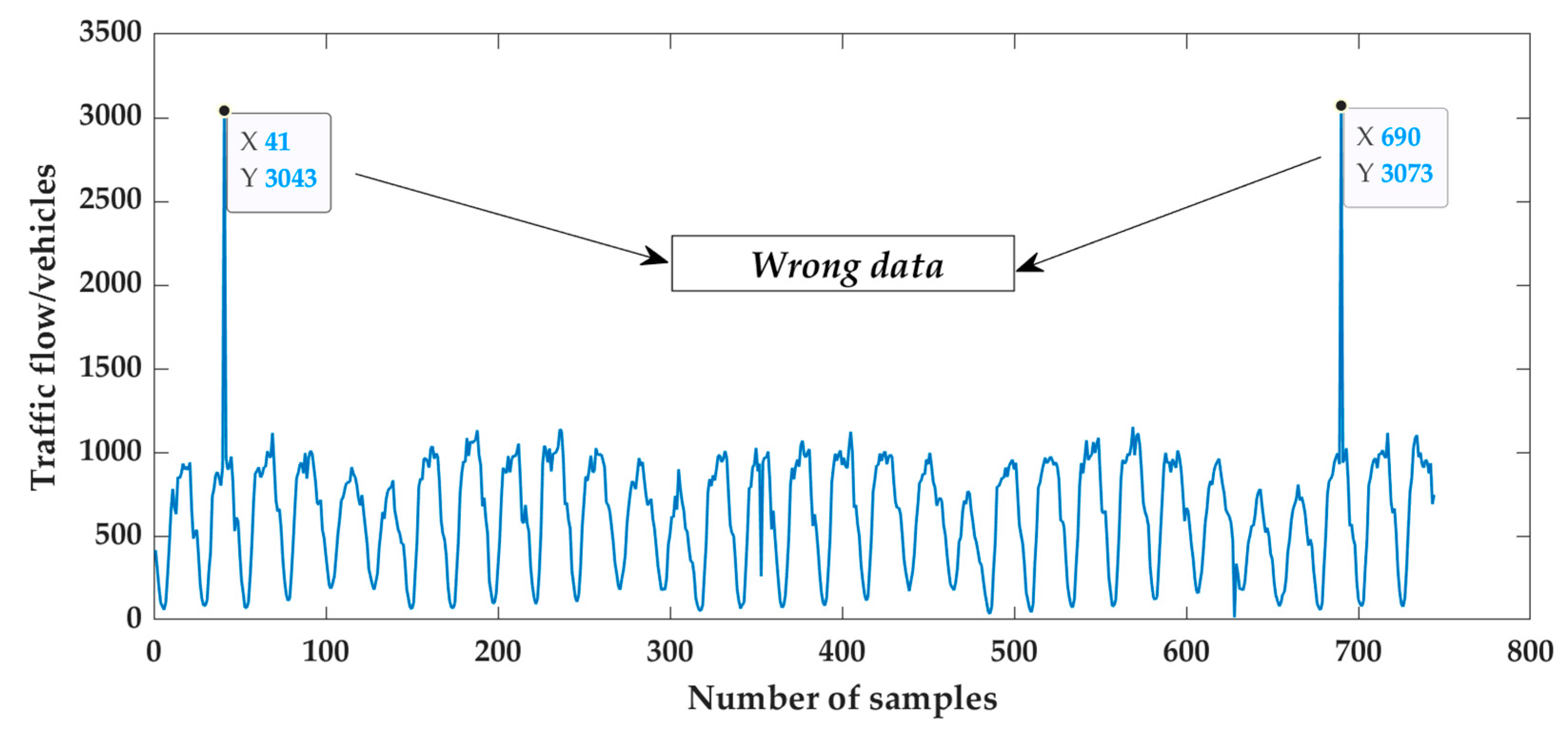
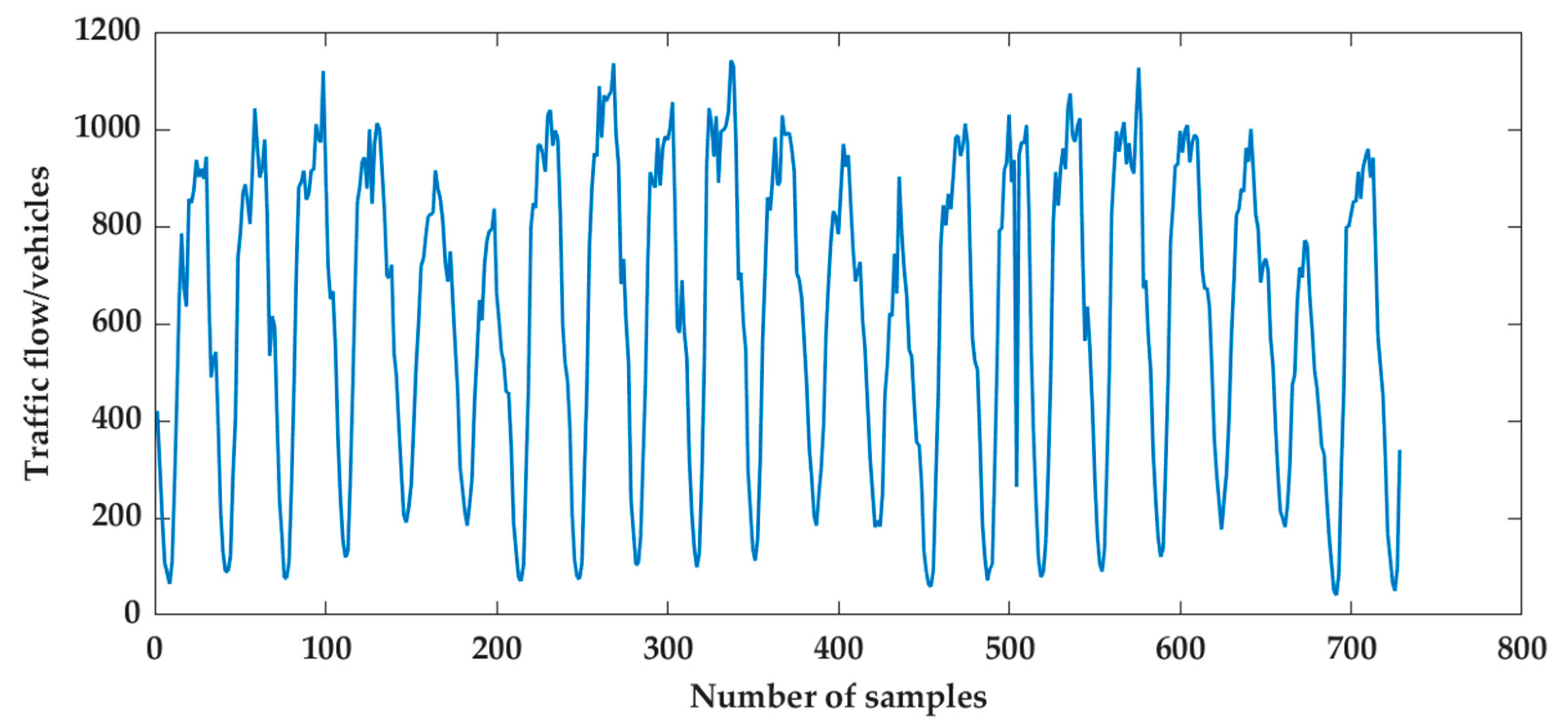
3.1. Data Processing

Road detectors may fail due to hardware aging, environmental interference, and other issues, so erroneous data may appear in the dataset. The raw traffic flow data without preprocessing (data collection time: March 2016) is demonstrated in Figure 5.

The maximum traffic flow on a road depends on several factors, including road type, number of lanes, speed, vehicle type, and traffic signal controls. On an ideal urban road, the interval between vehicles is about 1.5 s and the theoretical maximum flow is given by 2400 vehicles per hour. Exceeding the maximum traffic flow will lead to traffic congestion and dangerous accidents. So, it needs to clean and normalize the traffic flow data in the preliminary stage of prediction experiments. To ensure the accuracy and reliability of the data, erroneous values were deleted and filled with mean, median and fixed values. The traffic flow data after data cleaning and standardization is shown in Figure 6.

Through the refinement of traffic flow data, both accuracy and reliability are improved, thereby establishing a basis for ensuing data analysis and traffic forecasting.

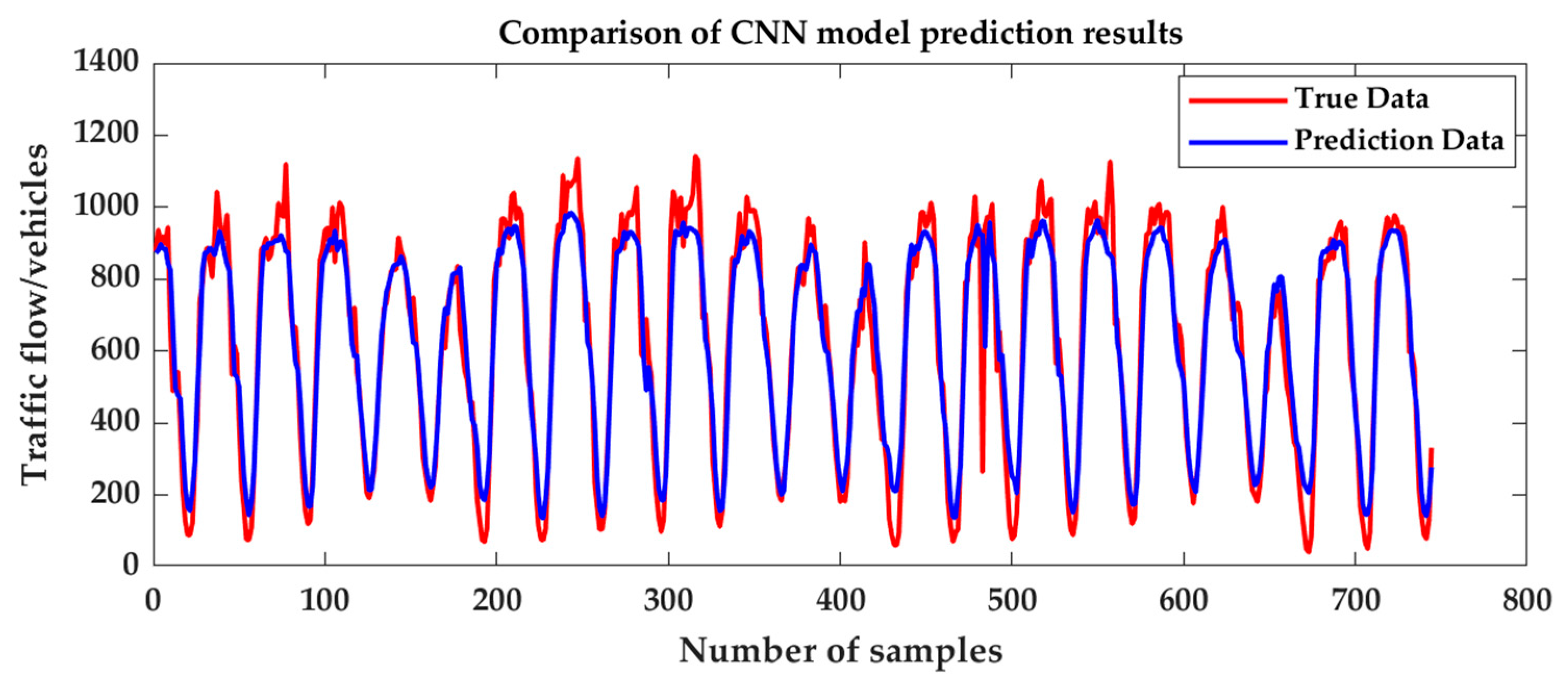
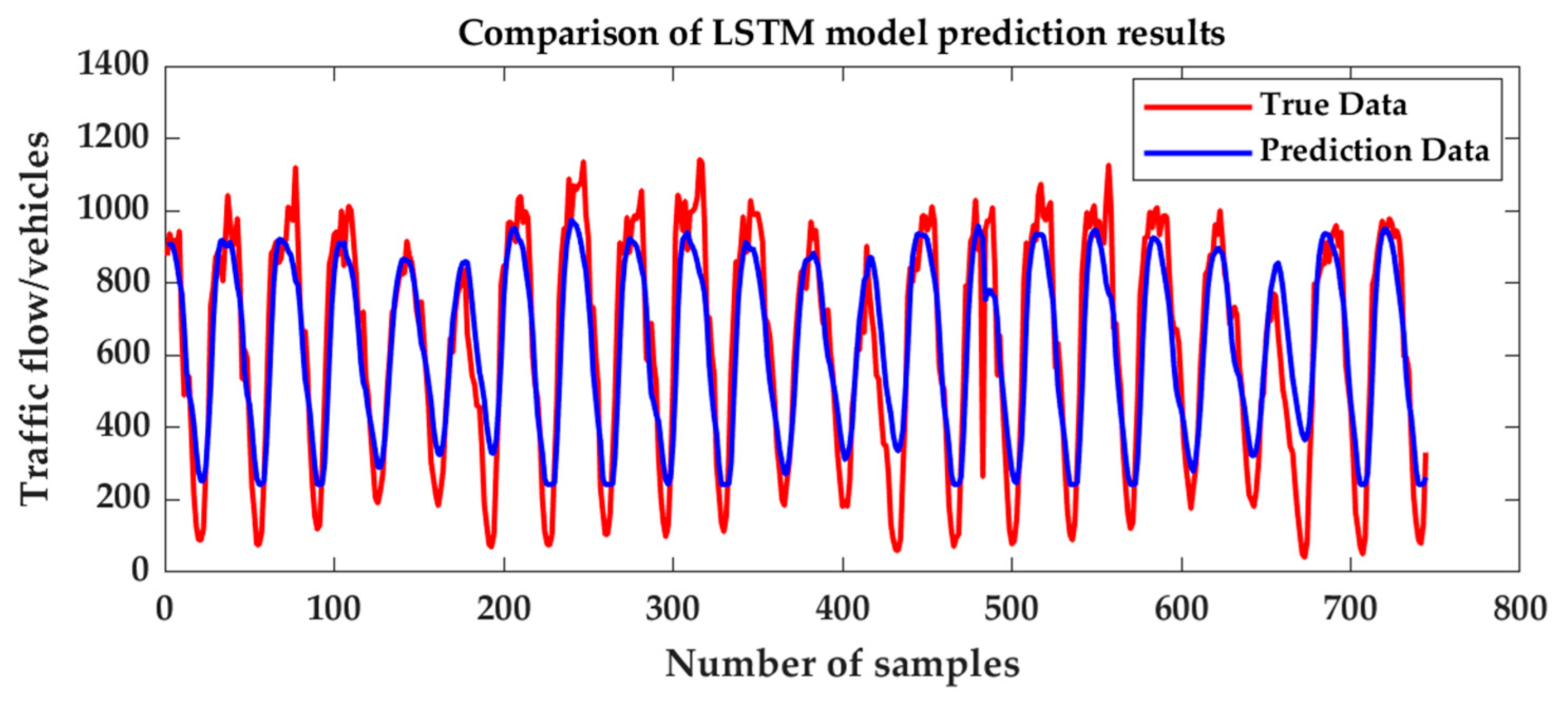
3.2. Single Model Prediction

The data for March was separately input into the CNN and LSTM algorithms for processing. Subsequently, the hyperparameters of both models were adjusted, including the learning rate, batch size, number of neurons, and other relevant parameters. The models were implemented using MATLAB v.R2025a, and the prediction results generated by the CNN model are presented in Figure 7, while those produced by the LSTM approach are displayed in Figure 8.

The prediction results of the CNN and LSTM models reveal the limited effectiveness of single neural network models in traffic flow prediction. This limitation arises from the fact that a singular neural network model typically captures only a single dependency in either time or space, making a concurrent analysis of traffic flow’s spatiotemporal characteristics challenging. To enhance predictive accuracy, the implementation of a hybrid model is necessary, along with an increase in data capacity and the volume of training data.

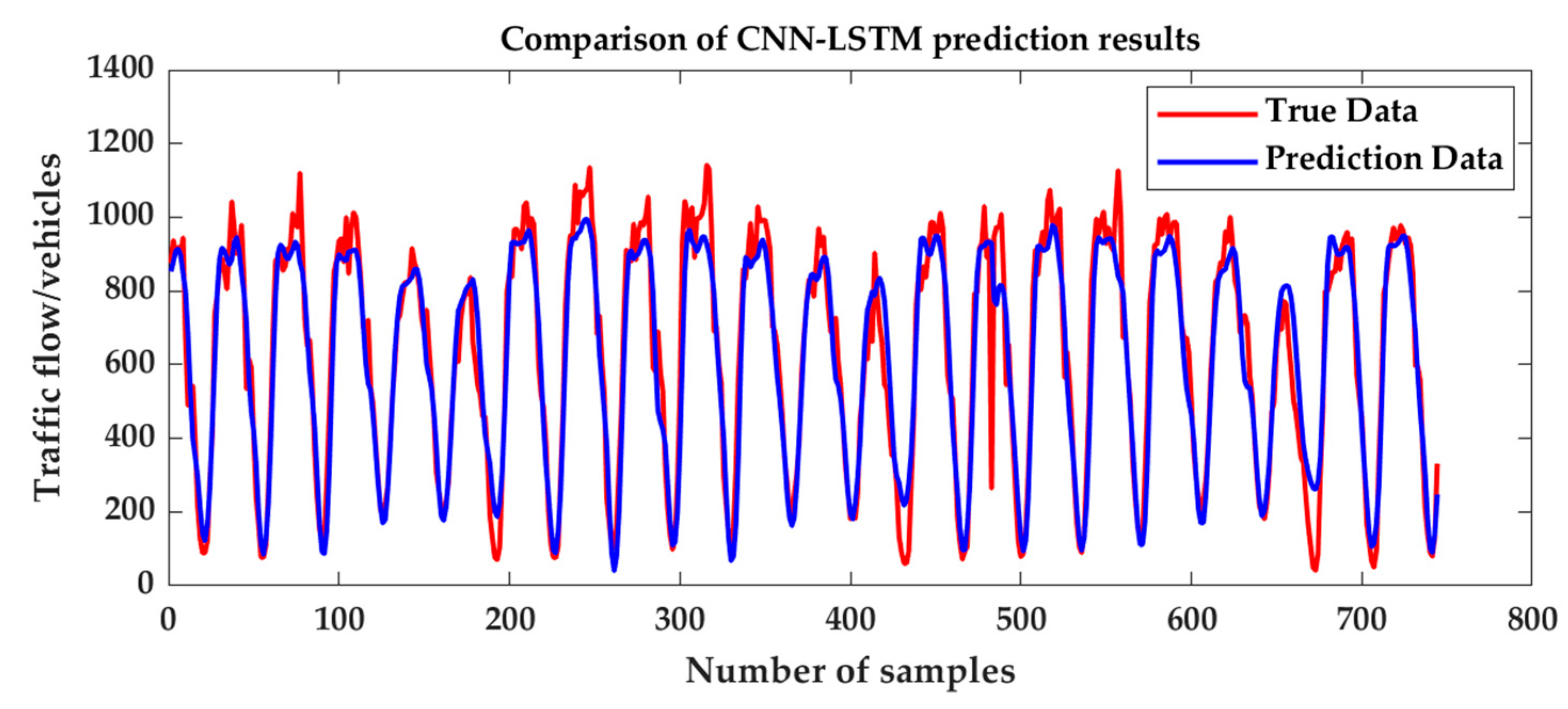
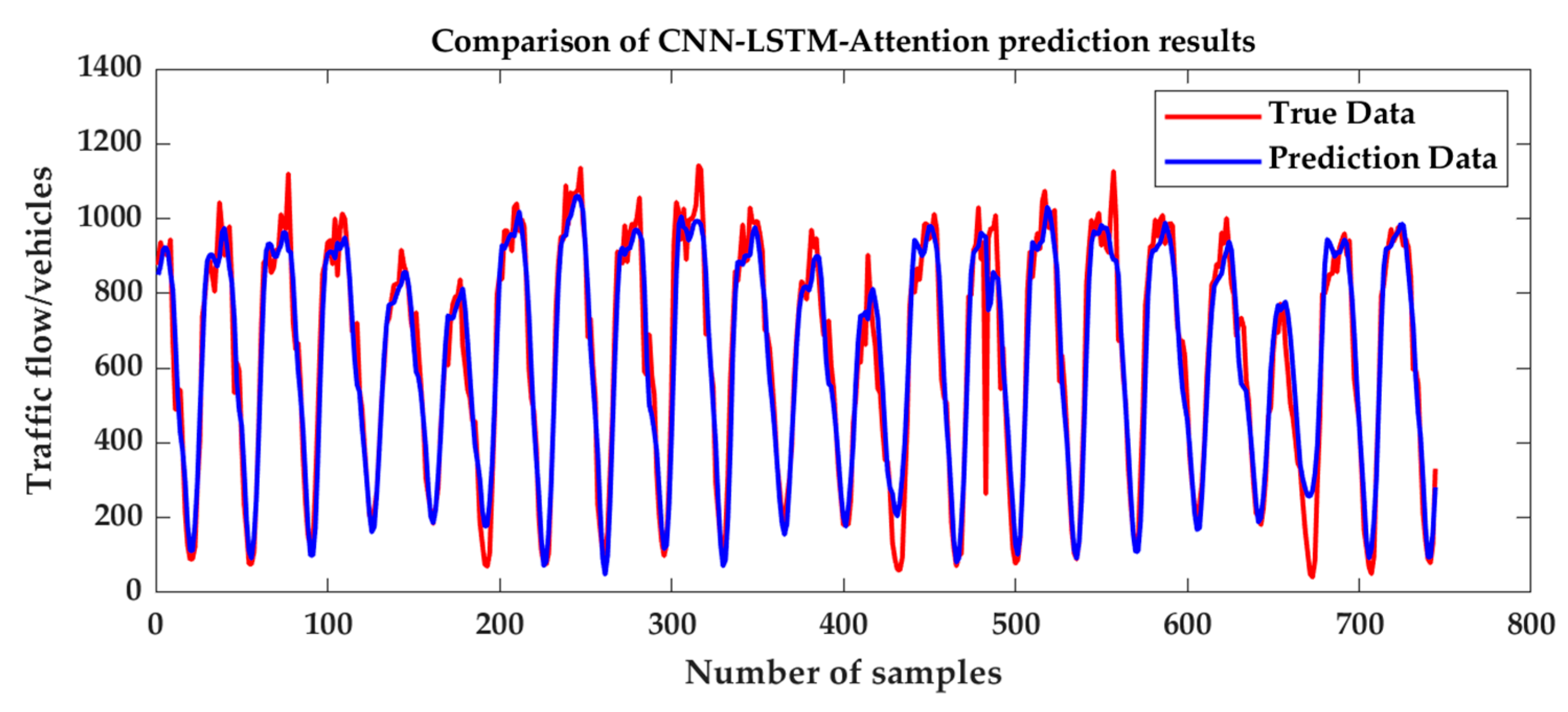
3.3. Hybrid Model Prediction

The hybrid neural network model is characterized by its ability to simultaneously capture the spatiotemporal dependencies of traffic flow and its flow characteristics, improving prediction accuracy. The neural network model with the addition of optimization algorithm can improve the efficiency of traffic flow prediction by accelerating convergence and automatically adjusting parameters. Therefore, it is necessary to use a hybrid model with optimization algorithms and a neural network combination model to perform prediction tasks and verify their effectiveness. The experiment also uses the data from March for prediction. The prediction results of the CNN-LSTM model are shown in Figure 9.

Based on the data presented in Figure 9, the hybrid CNN-LSTM model demonstrates a notably improved fit for predicted traffic flow results relative to the single neural network model. For the purpose of validating the optimization algorithm’s effectiveness, the CNN-LSTM model was augmented with the attention mechanism and CPO optimization algorithm in the experiment. Figure 10 illustrates the results of the model prediction following the integration of the attention mechanism. Figure 11 illustrates the predicted outcomes following the integration of the CPO optimization algorithm.

It can be seen from Figure 10 and Figure 11 that the fitting degree of the CNN-LSTM model with any optimization algorithm has converged, so the traffic flow prediction effect has also been improved.

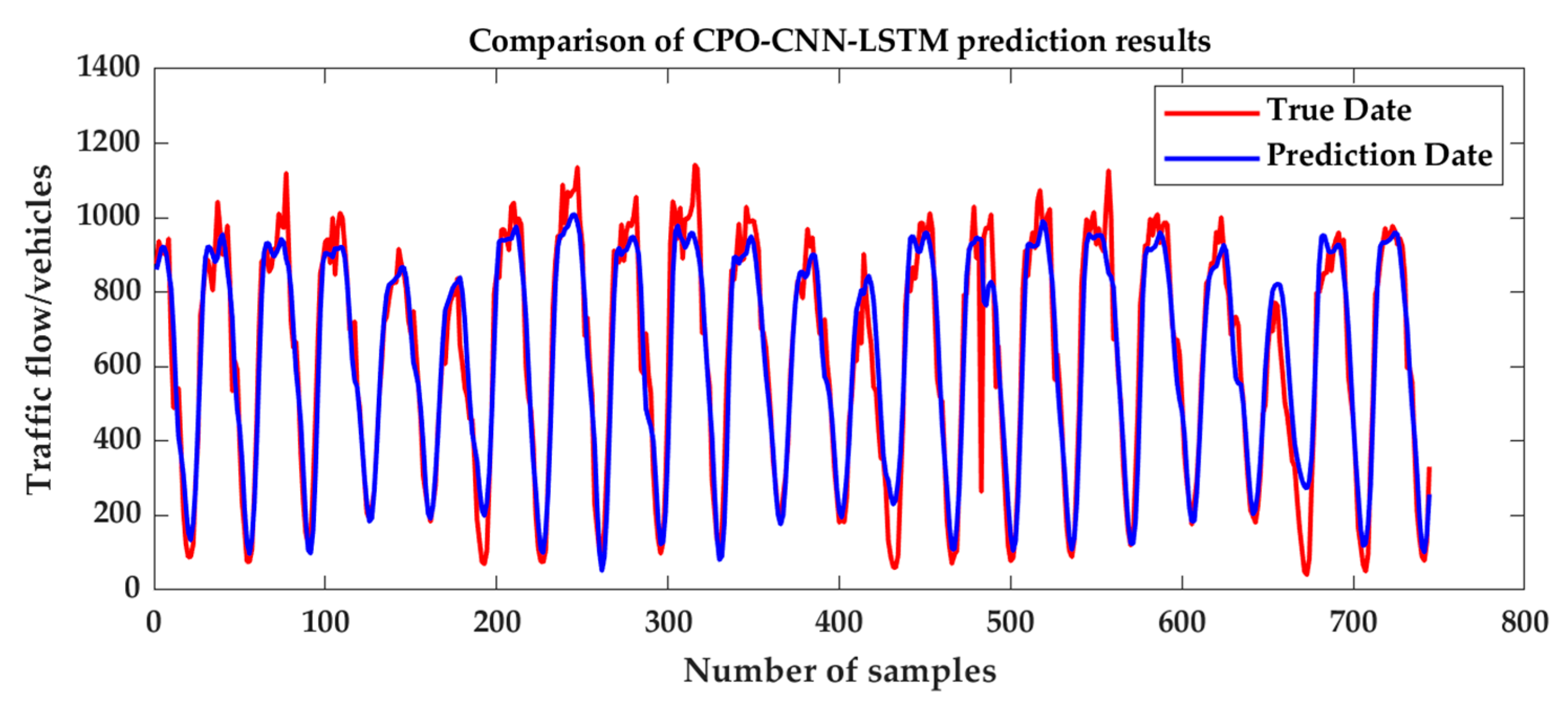
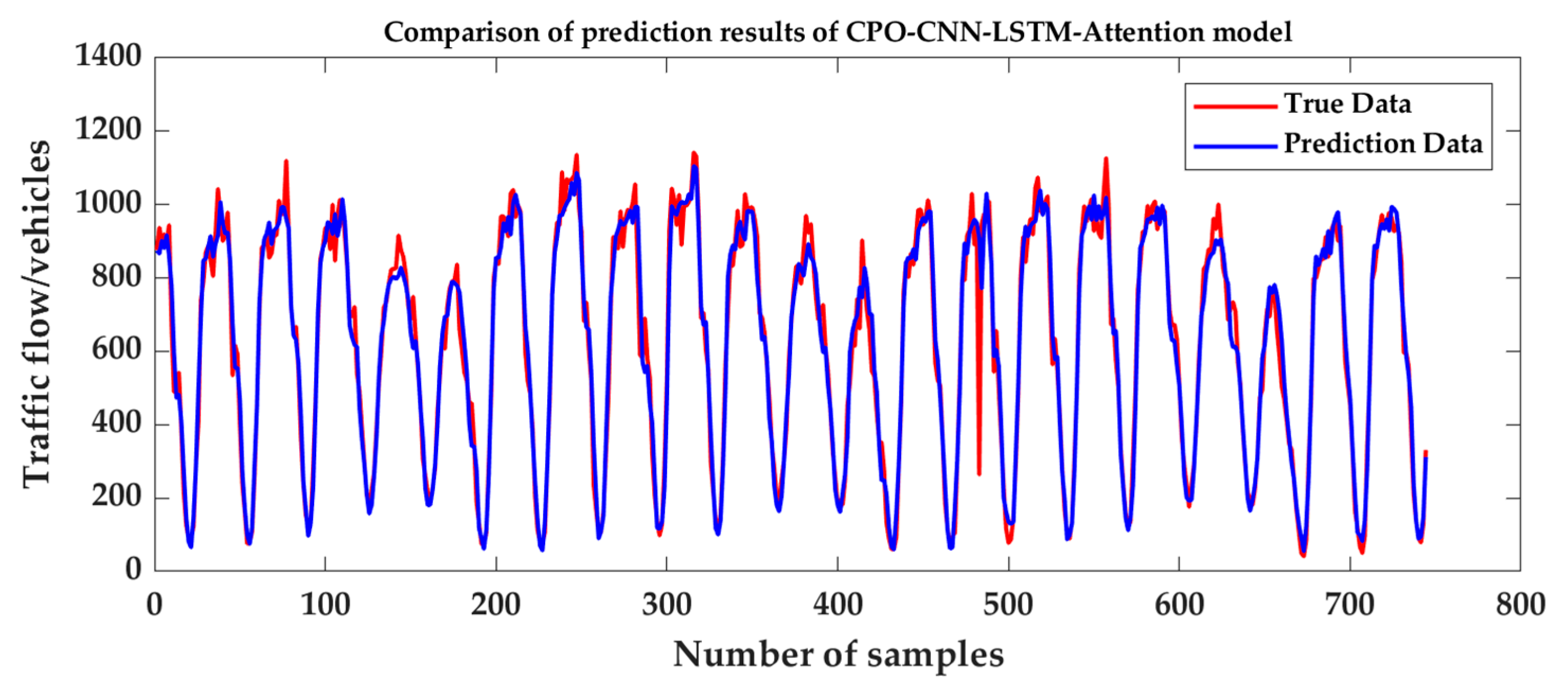
3.4. CPO-CNN-LSTM-Attention Model Prediction

The same method is used to import the data from March into the CPO-CNN-LSTM-attention model. The prediction results are shown in Figure 12.

As depicted in Figure 12, the CNN-LSTM neural network model, incorporating the two optimization algorithms, exhibits a superior fit in its prediction results compared to alternative models. This proves that CPO can significantly improve the convergence speed, stability and fit of predictions through global and local self-optimization methods.

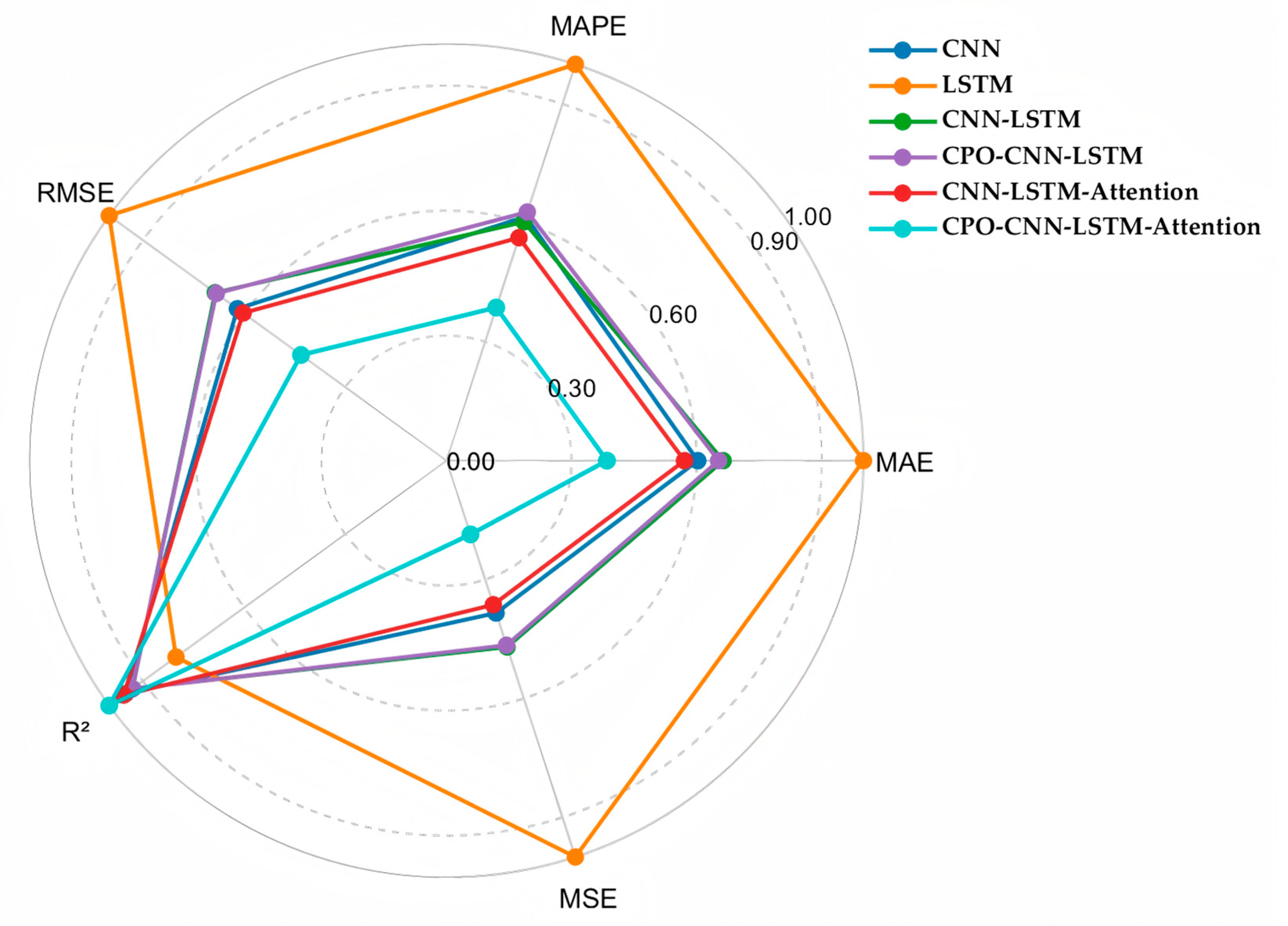
3.5. Simulation Result Analysis

To demonstrate the effectiveness of the hybrid CPO-CNN-LSTM-Attention model in traffic flow prediction, we used traffic flow data from the 48th detector in March and ran multiple neural network models in MATLAB. The running time and depth training time of each model are shown in

Table 1. Prediction time of the prediction model.

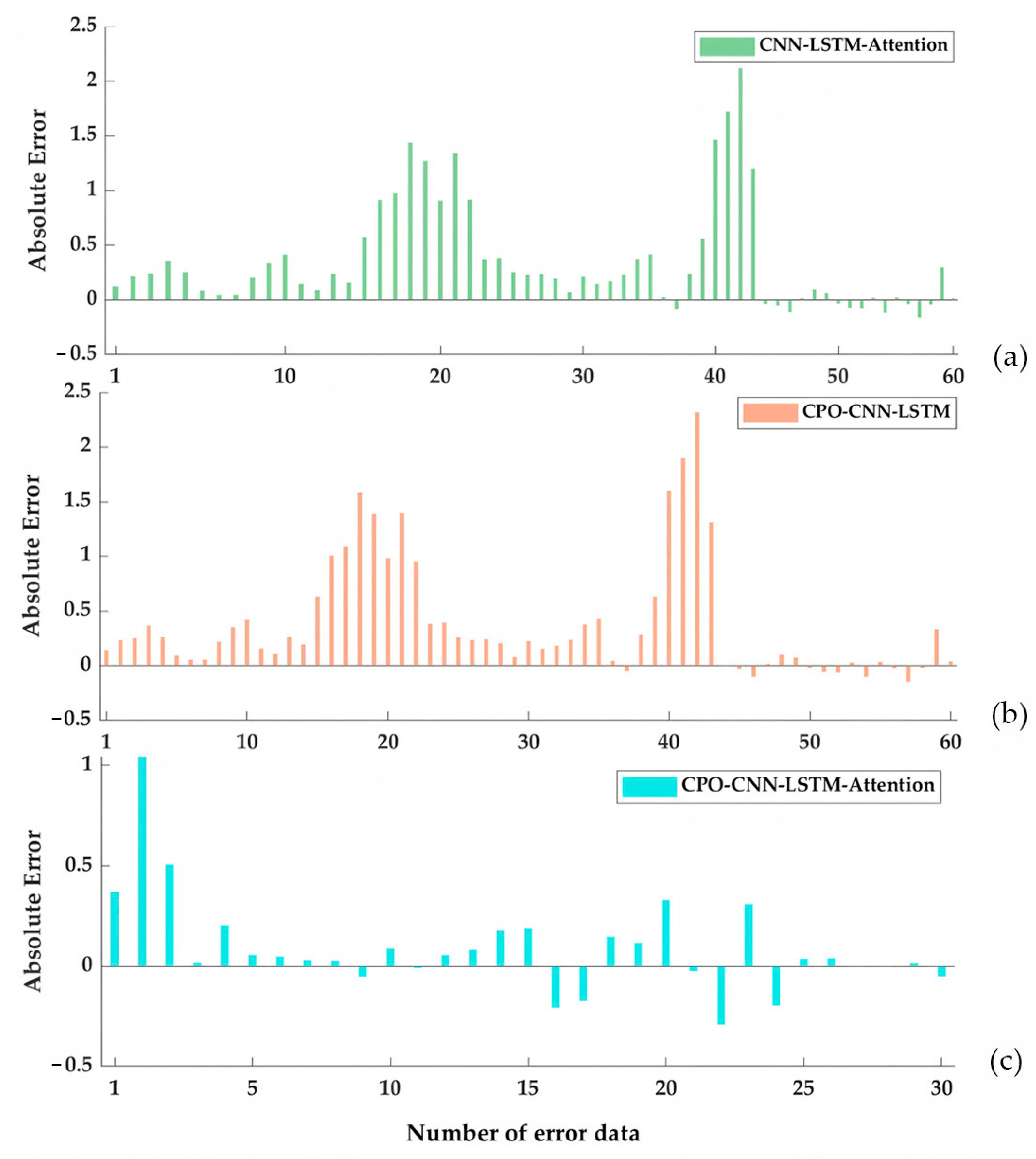
Model	Prediction Times (s)
CNN	5.42
LSTM	5.87
CNN-LSTM	6.43
CNN-LSTM-Attention	12.15
CPO-CNN-LSTM	15.33
CPO-CNN-LSTM-Attention	19.75

.

Table 1 shows that the training and prediction times for these six models are similar, indicating that models using optimized algorithms do not affect prediction efficiency. While the single CNN, LSTM, and CNN-LSTM models have shorter runtimes, their prediction results are poorly fitted and therefore inadequate for the prediction task.

To accurately analyze the discrepancies between the predicted data and the true data of the remaining models, absolute error is used to analyze the degree of data deviation. The absolute error of the error data for each model is shown in Figure 13.

As shown in Figure 13, the hybrid model exhibits the smallest amount of error among the three models, and its error data shows little deviation from the original data. Therefore, using this hybrid model for prediction can improve data accuracy.

To further verify the accuracy of each model, five key indicators (Equations (18)–(22)) including MAE, mean square error (MSE), RMSE, MAPE, and coefficient of determination (R²), were used to evaluate the model.

$$MAE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|y_i-\widehat{y}\right|}$$

(18)

$$MSE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{\left(y_i-\widehat{y}\right)}^2}$$

(19)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{\left(y_i-\widehat{y}\right)}^2}}$$

(20)

$$MAPE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|\frac{y_i-{\widehat{y}}_i}{{\widehat{y}}_i}\right|\times 100}$$

(21)

$$R^2=1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}}{{\displaystyle \sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}},$$

(22)

where $y_i$ is the experimental data; ${\widehat{y}}_i$—predicted data.

The indicator results obtained by running each model are shown in Figure 14.

R² evaluates the degree of fit between data. The better the model fit, the larger the R² value. MAPE calculates the average absolute percent error, considering magnitude and time series length. Smaller MAPE implies better predictive accuracy for the suggested model. RMSE is the square root of the average squared difference between predicted and actual values. Lower RMSE values mean the model is more accurate [33]. MAE and MSE both indicate the gap between prediction and actual value. A closer match between predicted and actual data is associated with lower MAE and MSE [34]. The CPO-CNN-LSTM-Attention model shows superior results than other models in all evaluation metrics, as shown in Figure 14.

To enhance the rigor and reliability of the model evaluation, it is imperative to replicate the validation experiment utilizing traffic flow data from April and May. This approach ensures a more comprehensive assessment of the model’s generalizability and strengthens the credibility of the prediction outcomes. The performance indicators for the prediction data from March to May are shown in

Table 2. Comparison of performance indicators from March to May.

Performance Indicators	Model	March	April	May
R2	CNN	0.8635	0.8701	0.8744
	LSTM	0.8415	0.8580	0.8500
	CNN-LSTM	0.8682	0.8607	0.8741
	CNN-LSTM-Attention	0.8951	0.8873	0.8972
	CPO-CNN-LSTM	0.9011	0.8901	0.9109
	CPO-CNN-LSTM-Attention	0.9207	0.9133	0.9290
RMSE	CNN	36.91	36.15	39.91
	LSTM	47.39	42.60	45.16
	CNN-LSTM	33.76	30.01	31.88
	CNN-LSTM-Attention	27.50	27.90	27.33
	CPO-CNN-LSTM	23.99	23.15	23.84
	CPO-CNN-LSTM-Attention	19.83	17.35	19.81
MAE	CNN	26.98	25.33	29.14
	LSTM	30.15	29.80	32.30
	CNN-LSTM	23.22	23.10	24.27
	CNN-LSTM-Attention	21.04	21.91	21.17
	CPO-CNN-LSTM	19.52	18.27	18.87
	CPO-CNN-LSTM-Attention	14.04	13.98	14.00
MAPE	CNN	26.33%	25.18%	26.00%
	LSTM	27.85%	25.57%	27.01%
	CNN-LSTM	18.09%	17.94%	18.11%
	CNN-LSTM-Attention	12.15%	11.27%	12.43%
	CPO-CNN-LSTM	10.99%	9.07%	9.94%
	CPO-CNN-LSTM-Attention	6.62%	5.97%	6.53%

.

In order to demonstrate the advantages of the CPO-CNN-LSTM-Attention model in capturing complex spatiotemporal dependencies and generalization capabilities, and to avoid false accuracy when compared with baseline models, this study should also use advanced prediction models in recent years for comparison to further verify the prediction efficiency and accuracy of the CPO-CNN-LSTM-Attention model. Furthermore, the experiment also incorporated open-source Spatio-Temporal Graph Convolutional Networks (STGCN) and Diffusion Convolutional Recurrent Neural Network (DCRNN) models for validation. DCRNN combines spatiotemporal modeling with graph diffusion to improve prediction stability, while STGCN uses graph convolution and temporal convolution to efficiently capture spatiotemporal dependencies and improve prediction accuracy. Both models have achieved promising results in numerous studies. The validation tests utilized data from July 2016, which exhibited significant fluctuations due to severe weather conditions, making them particularly suitable for evaluating the model’s stability and accuracy under unexpected scenarios. The results of the validation experiments are presented in

Table 3. Validation experiment results.

Model	R2	RMSE	MAE	MAPE
STGCN	0.8704	24.92	17.90	12.74%
DCRNN	0.8620	26.79	19.22	13.55%
CPO-CNN-LSTM-Attention	0.8815	21.07	16.13	10.18%

.

Table 3 shows that the CPO-CNN-LSTM-Attention model trained on historical normal data has a reduced prediction accuracy when faced with severe weather conditions. This is because the historical data contains few emergency event samples, and the prediction results tend to be closer to normal traffic flow. Although bad weather has an impact on the prediction accuracy, the hybrid model still achieves slightly higher accuracy than the DCRNN and STGCN models, demonstrating the robustness of the model.

4. Conclusions

The CPO-CNN-LSTM-Attention model proposed in this paper achieved RMSE values ranging from 17.35 to 19.83, MAE values ranging from 13.98 to 14.04, and MAPE values ranging from 5.97% to 6.62%. All evaluation metrics were within acceptable ranges, and R² values for all experimental models remained between 0.84 and 0.93, indicating good interpretability of the predicted data. The RMSE value of the CPO-CNN-LSTM-Attention model proposed in this paper ranges from 17.35 to 19.83, the MAE value ranges from 13.98 to 14.04, and the MAPE value ranges from 5.97% to 6.62%. The values for all three indicators of performance are within the acceptable range.

Under the condition that the required time for traffic flow prediction across various neural network models is relatively similar, the CPO-CNN-LSTM-Attention model demonstrates outstanding capabilities in traffic flow prediction, with a 14.51–26.33% improvement in goodness-of-fit and a 4.9–6.5% increase in accuracy compared to baseline models. Recent research has shown that the CNN-LSTM model can comprehensively capture traffic flow characteristics [36]. The LSTM model based on the attention mechanism significantly reduces prediction time by dynamically adjusting model parameters [37]. Our model, based on both the CNN-LSTM and LSTM-Attention models and combined with the CPO algorithm, can reduce average prediction time by approximately 15%. Under stable conditions with traffic flow of no more than 1400 vehicles per hour, the real-time control efficiency of ITS is expected to increase by approximately 7%. Furthermore, the model generates highly accurate short-term traffic flow predictions that can be transmitted to the traffic control platform via a standardized interface. Based on these predictions, the decision-making system within the ITS can dynamically optimize traffic signal timing, issue warnings, or recommend detour routes. This allows for guidance and control before congestion occurs, ultimately improving overall transportation efficiency within the road network.

Because the traffic flow dataset used in this paper only includes data under severe weather conditions, excluding holidays and emergencies, and the dataset contains relatively little noise data, future research should focus on traffic flow prediction under conditions of sudden traffic accidents and holiday congestion, further validate the model using datasets from different roads, and ultimately, conduct simulations and predictions using software such as Aimsun v. 24, combined with the travel characteristics of specific urban populations, to further improve the model’s reliability.