Intelligent Rebar Optimization Framework for Urban Transit Infrastructure: A Case Study of a Diaphragm Wall in a Singapore Mass Rapid Transit Station
Abstract
Highlights
- Development of an intelligent, AI-assisted framework that integrates BIM perspective and metaheuristic algorithms for rebar optimization in diaphragm wall construction.
- Demonstrated reductions in rebar usage, cutting waste, embodied carbon, and costs, while enhancing constructability through intelligent allocation of special-length rebars and coupler placement.
- Promotes intelligent, resource-efficient construction for urban transit infrastructure in dense city environments.
- Advances smart city goals by enabling digitalized, sustainability-driven practices in civil engineering.
Abstract
1. Introduction
- Strategic placement of mechanical couplers where splicing is infeasible or inefficient, based on special-length rebar optimization;
- Application of a hybrid metaheuristic algorithm that leverages special-length rebar to solve the rebar cutting stock problem, aiming to minimize waste and reduce offcuts.
2. Literature Review
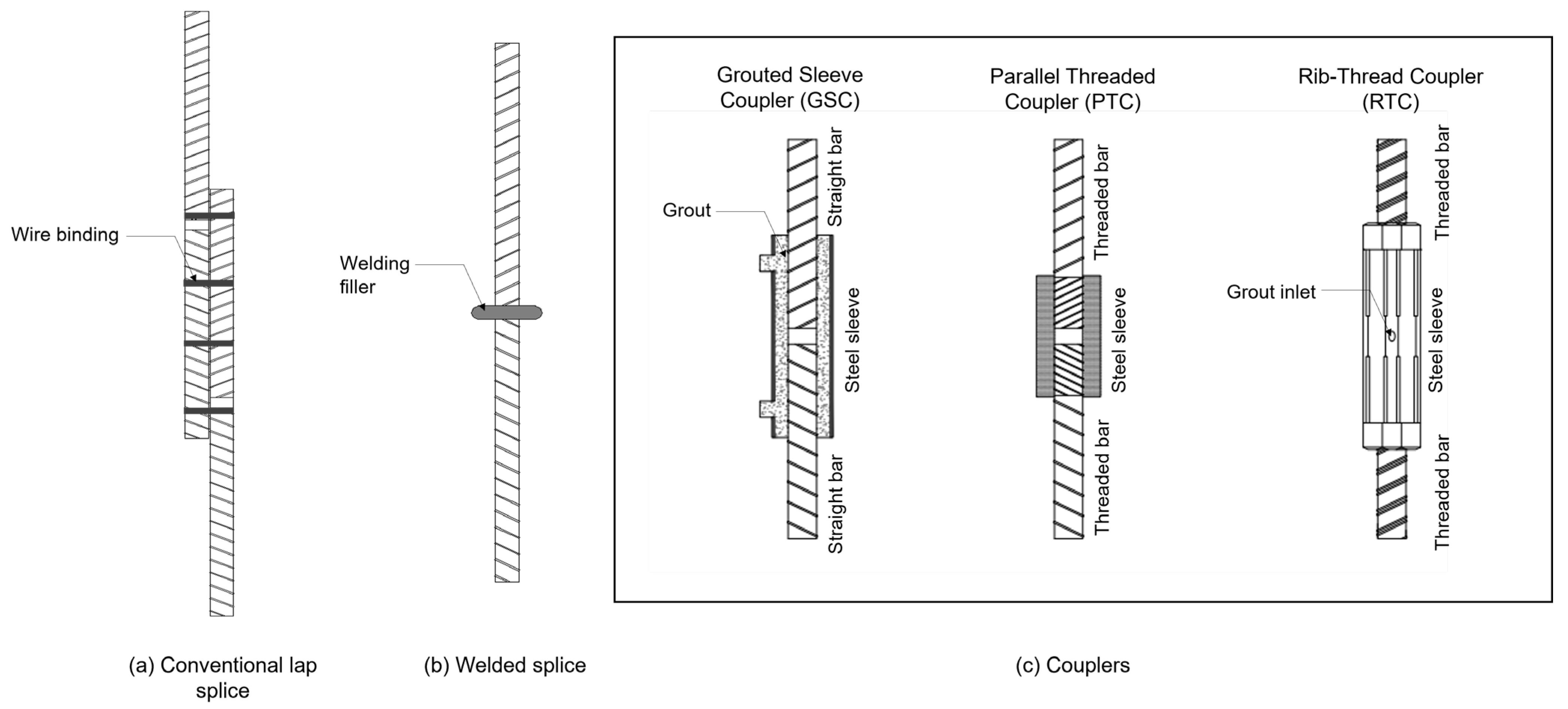
2.1. Rebar Connections: Lap Splices vs. Mechanical Couplers
2.2. BIM for Rebar Work and Digital Integration
2.3. AI and Metaheuristic Algorithms for Rebar Optimization
3. Overview of Diaphragm Walls: Design, Construction, and Reinforcement Characteristics
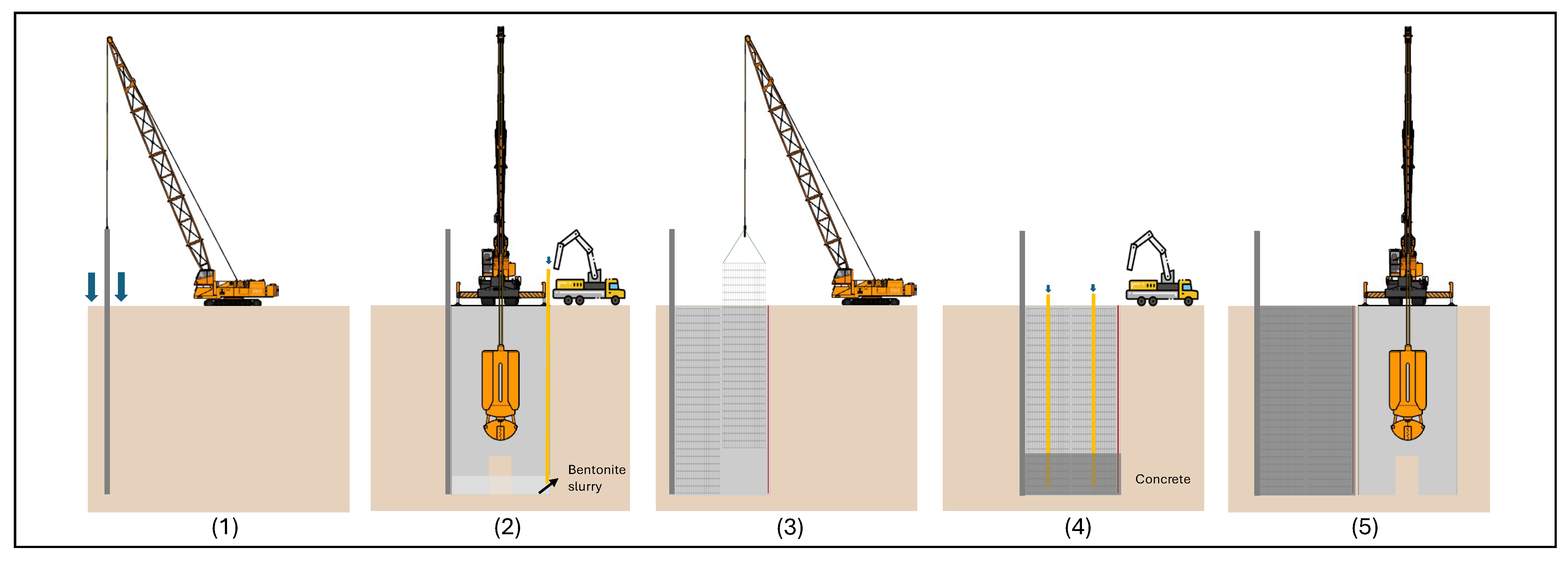
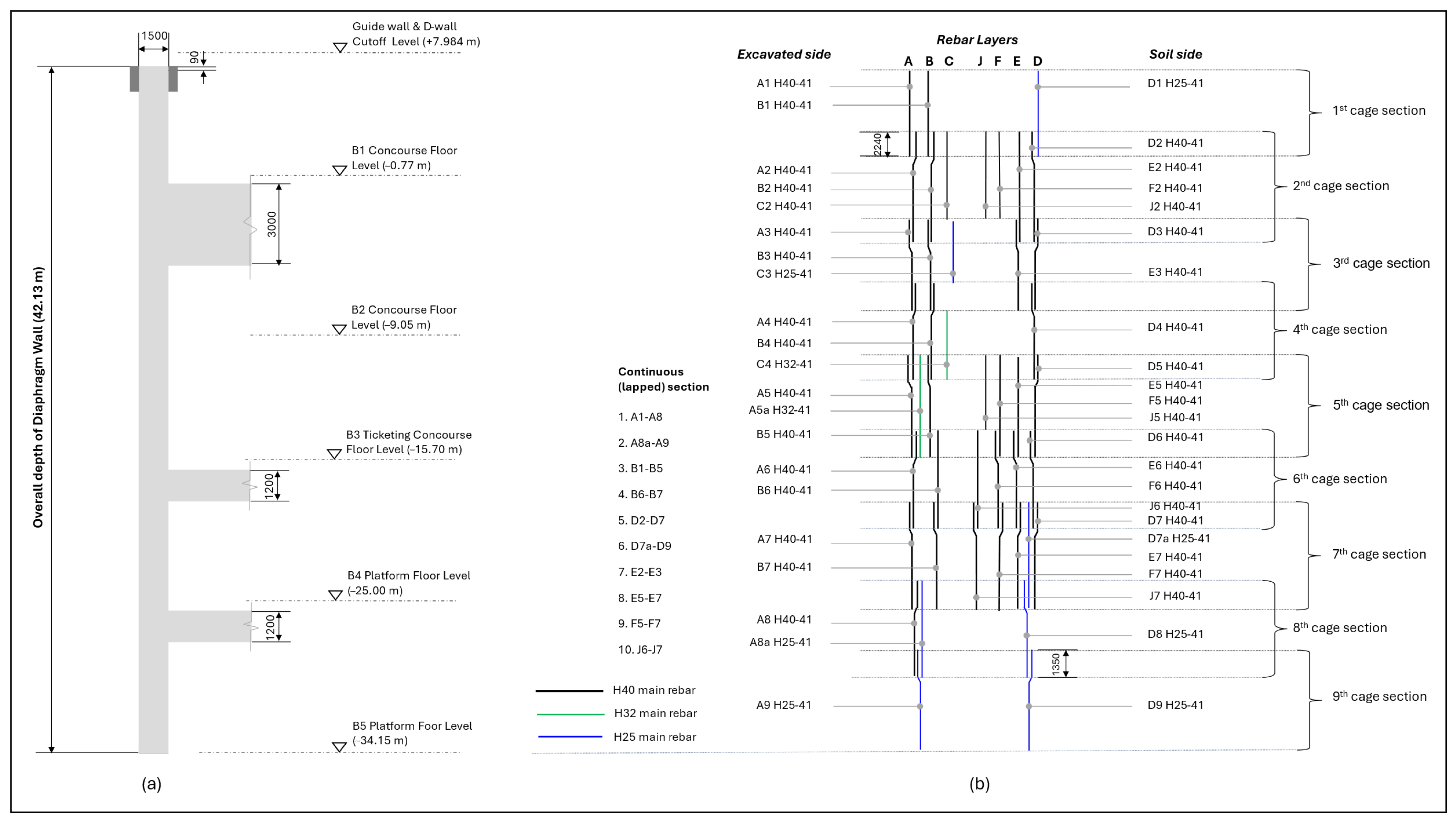
3.1. Design and Construction of Diaphragm Walls
- Guide wall construction: Shallow guide walls define alignment and support trench excavation.
- Deep trench excavation: Trenches are excavated and stabilized using bentonite slurry to prevent collapse.
- Rebar cage installation: Prefabricated rebar cages are lowered into the slurry-filled trench.
- In-situ concrete placement: Concrete is poured and cast using a tremie pipe from the bottom upward.
- Soil excavation around the panel: Hardened panels are exposed by excavating the surrounding soil to prepare for subsequent construction stages (station).
- Wall monitoring and additional reinforcement: Stability and deformation are monitored, and reinforcement is added as needed.
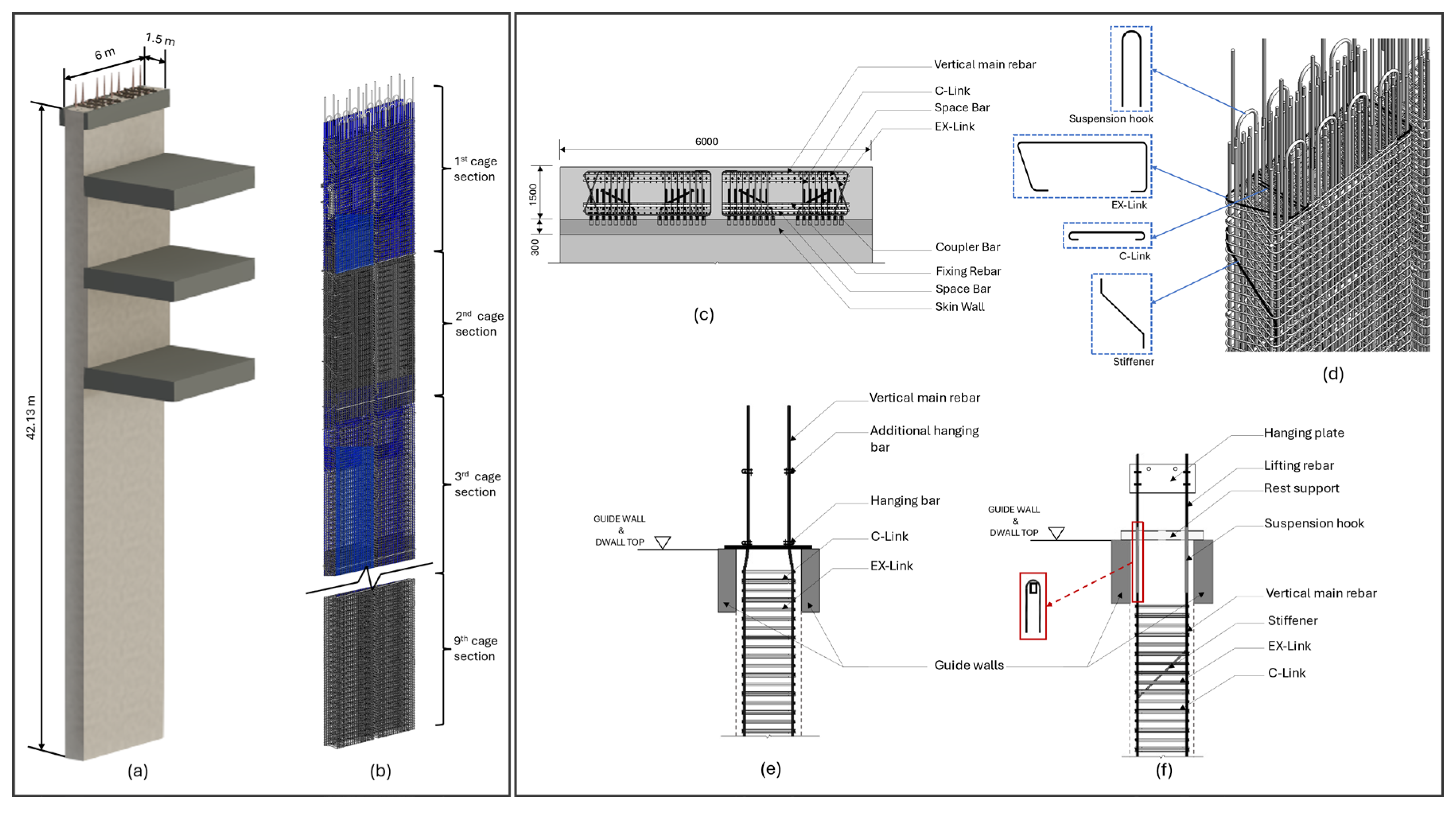
3.2. Structural Requirements, Reinforcement, and Connection Characteristics
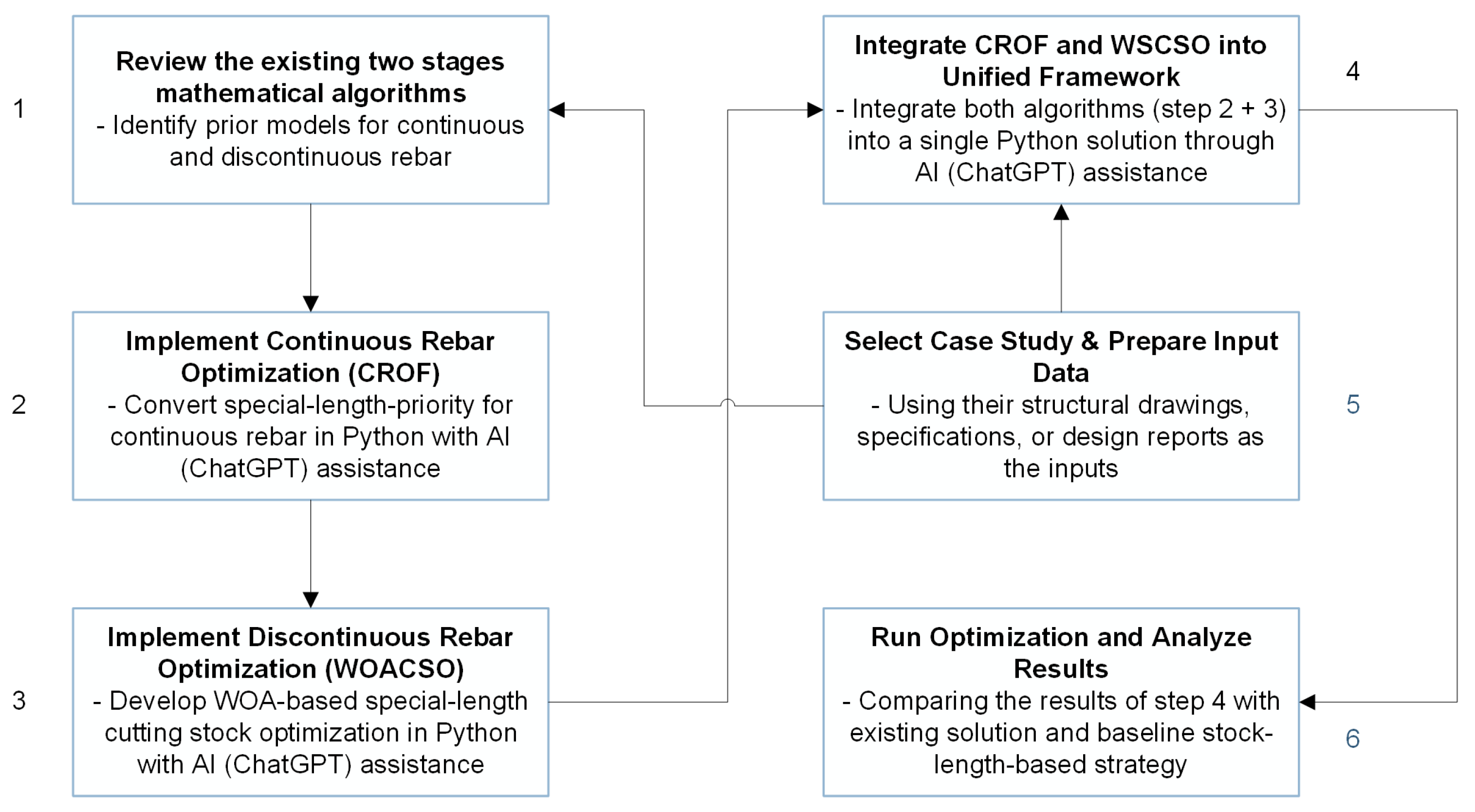
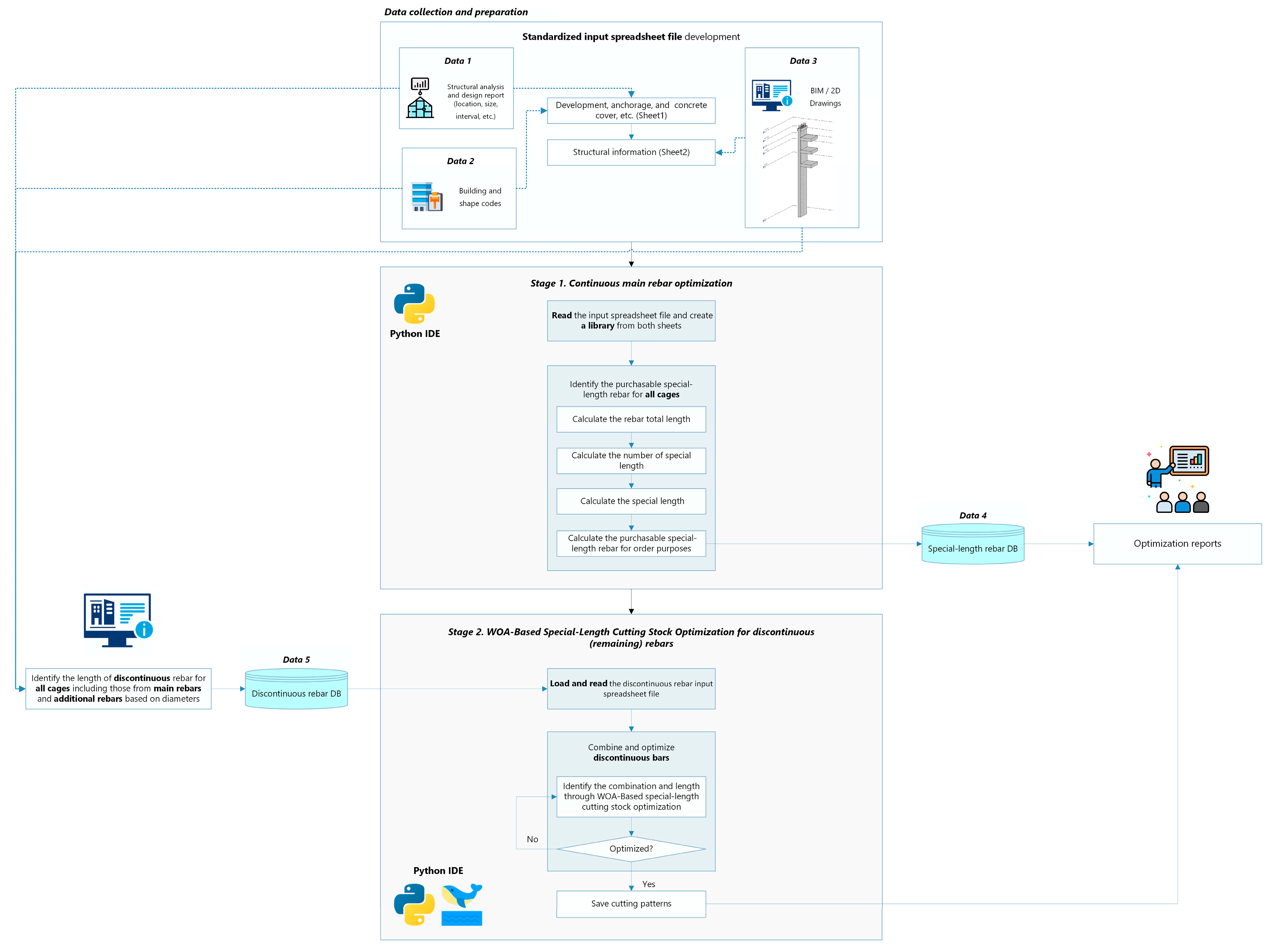
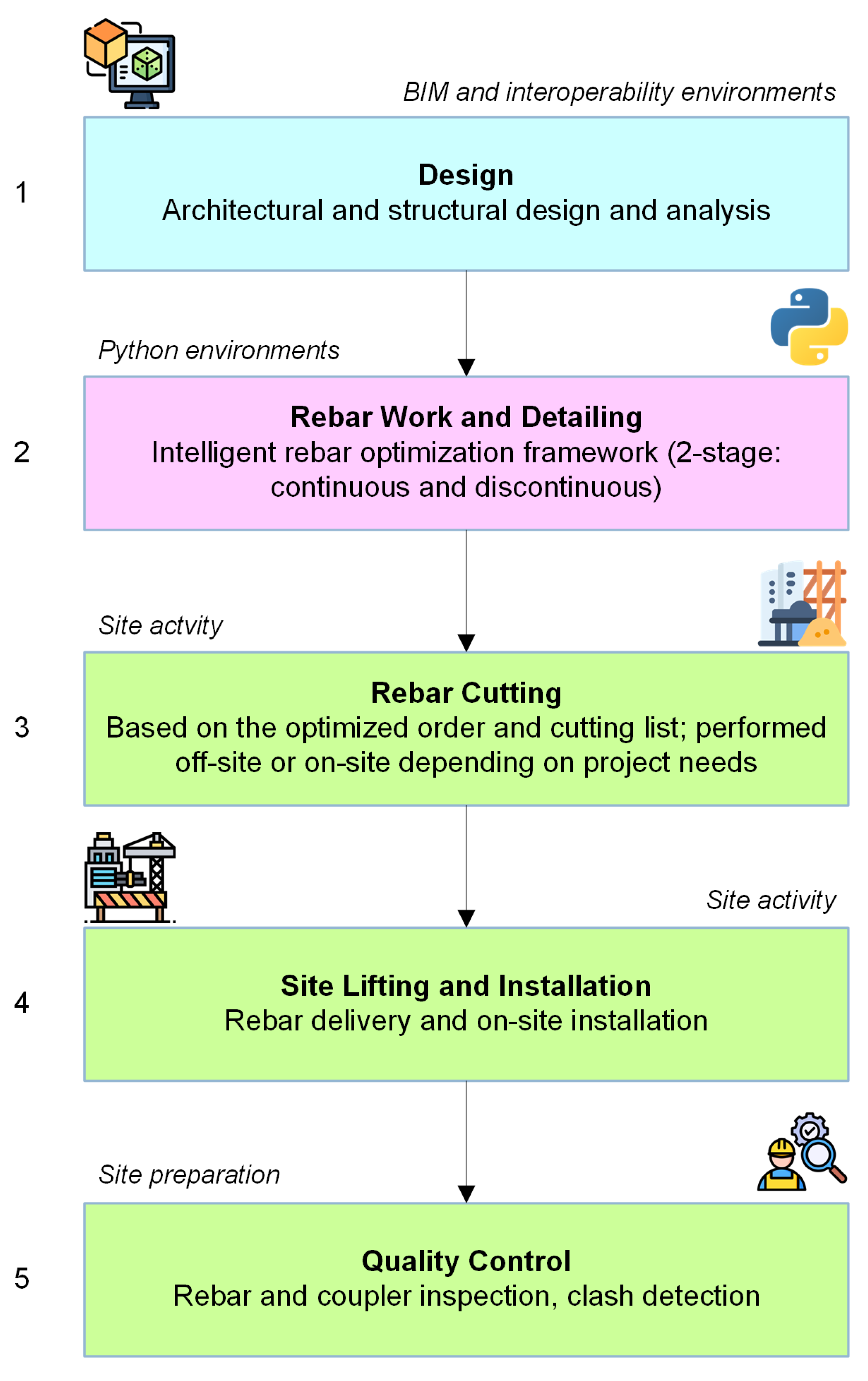
4. Development of Intelligent Rebar Optimization Framework
4.1. Existing Two-Stage Optimization Framework
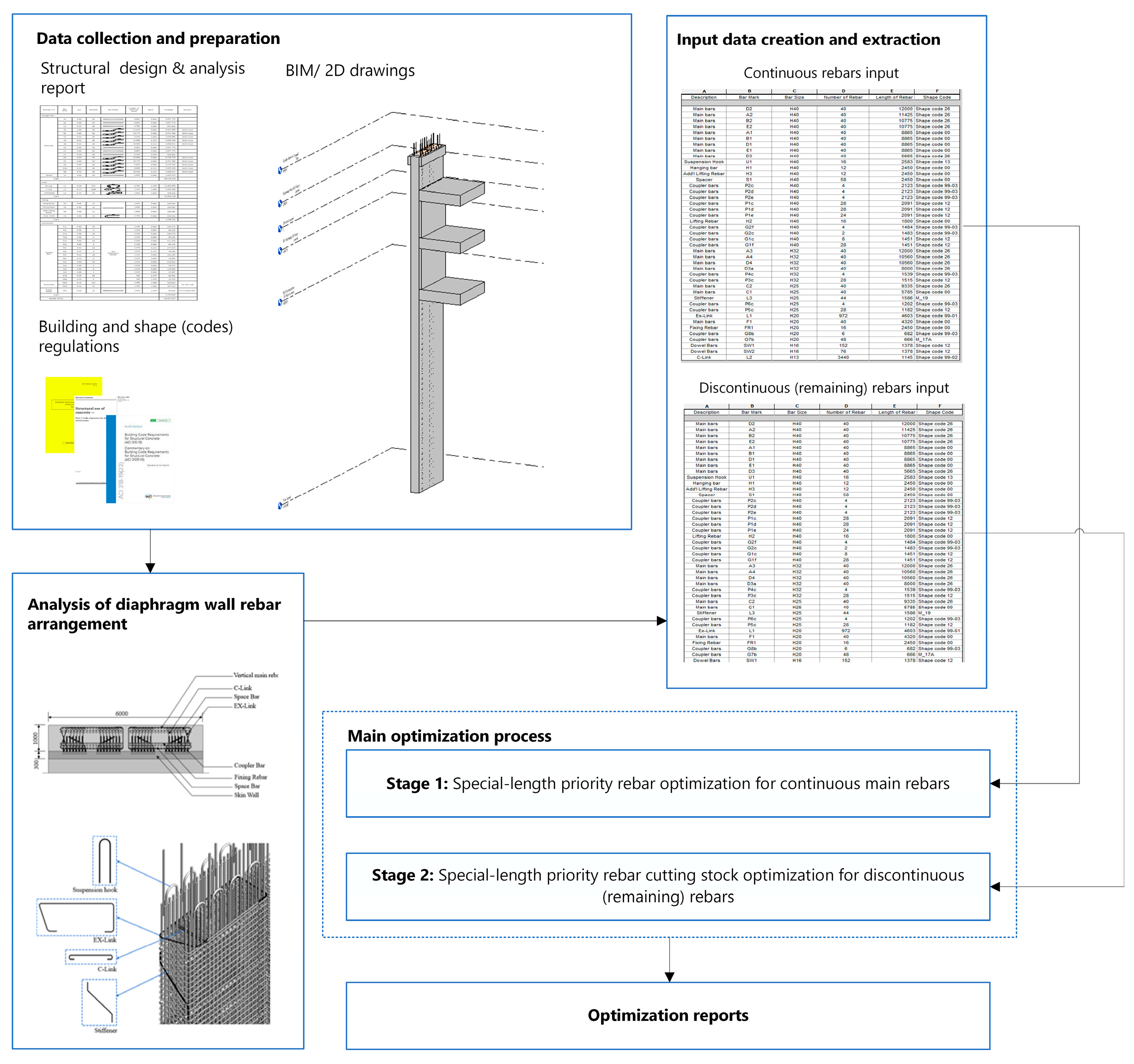
- Data Preparation: Retrieve all relevant input data, including basic rebar information from the structural analysis report (e.g., location, size, number, spacing), detailing requirements from applicable building codes (e.g., coupler inner gap, anchorage length, concrete cover), and geometric information of standard diaphragm walls (e.g., dimensions and location) from BIM models or 2D drawings.
- Using the input data, calculate the total continuous-reinforcement length required for the main reinforcement of a standard diaphragm wall, as described by Equation (1). The total reinforcement length () is determined by summing the lengths of rebars in each layer sharing the same diameter. In diaphragm wall construction, rebar cages typically consist of multiple layers with varying diameters, where smaller diameter rebars are generally used in deeper sections of the wall.where is the length of rebar , and is the upper limit of the summation, which is the total number of rebars considered in the total length calculation.
- The special length () that can be purchased is calculated by applying the total length calculated in Equation (1) following these equations.
- (1)
- Calculate the number of special lengths using Equation (2).where denotes the maximum rebar length that can be purchased.
- (2)
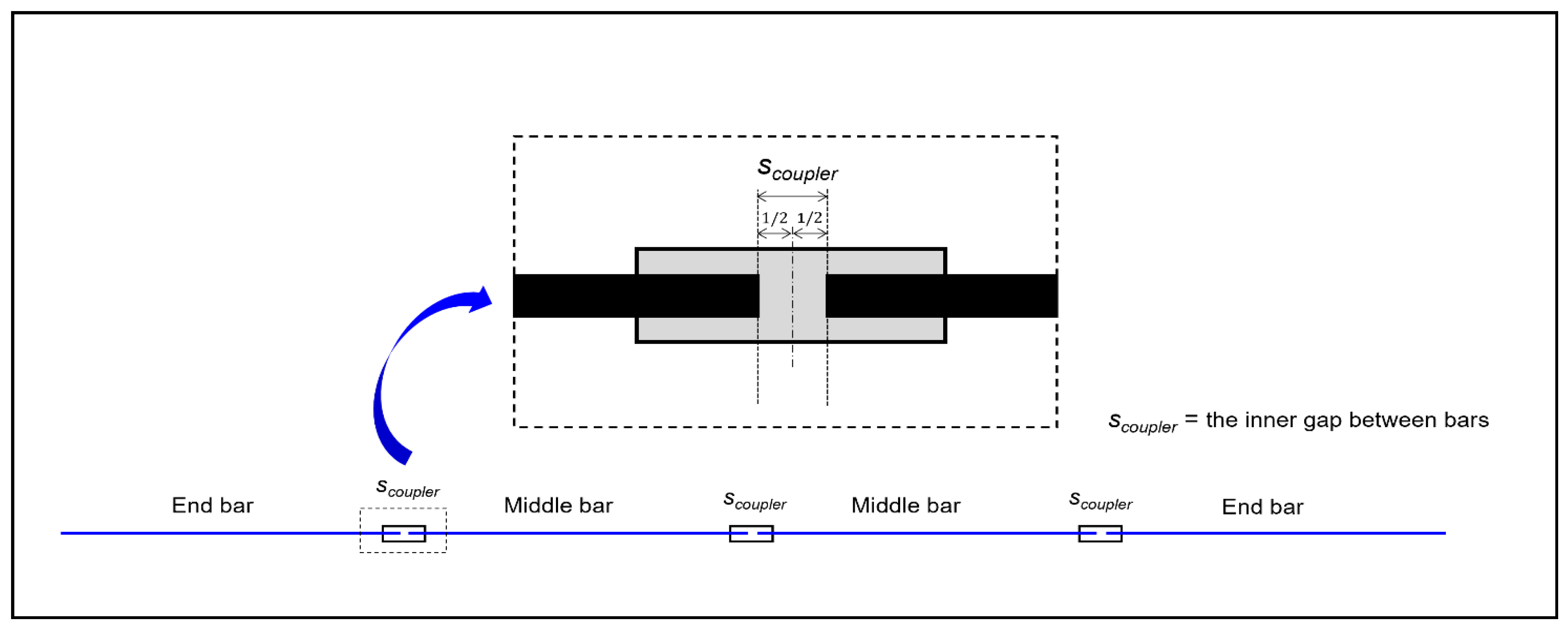
- Special bar lengths () are determined by incorporating the coupler’s inner installation gap, which influences both bar classification and length adjustment. As shown in Figure 6, a threaded coupler provides clearance for thread misalignment and grouting; half of this gap is deducted from an end bar, whereas the full gap is deducted from a middle bar. The resulting special lengths are calculated with Equation (3) for end bars and Equation (4) for middle bars.where, denotes the inner gap of the coupler.
- (3)
- The purchasable special length () is calculated using Equation (5), selecting the larger of the two values generated from the previous step, represented by Equations (3) and (4).
4.2. 1st Stage: Continuous Rebar Optimization Framework (CROF) in Python
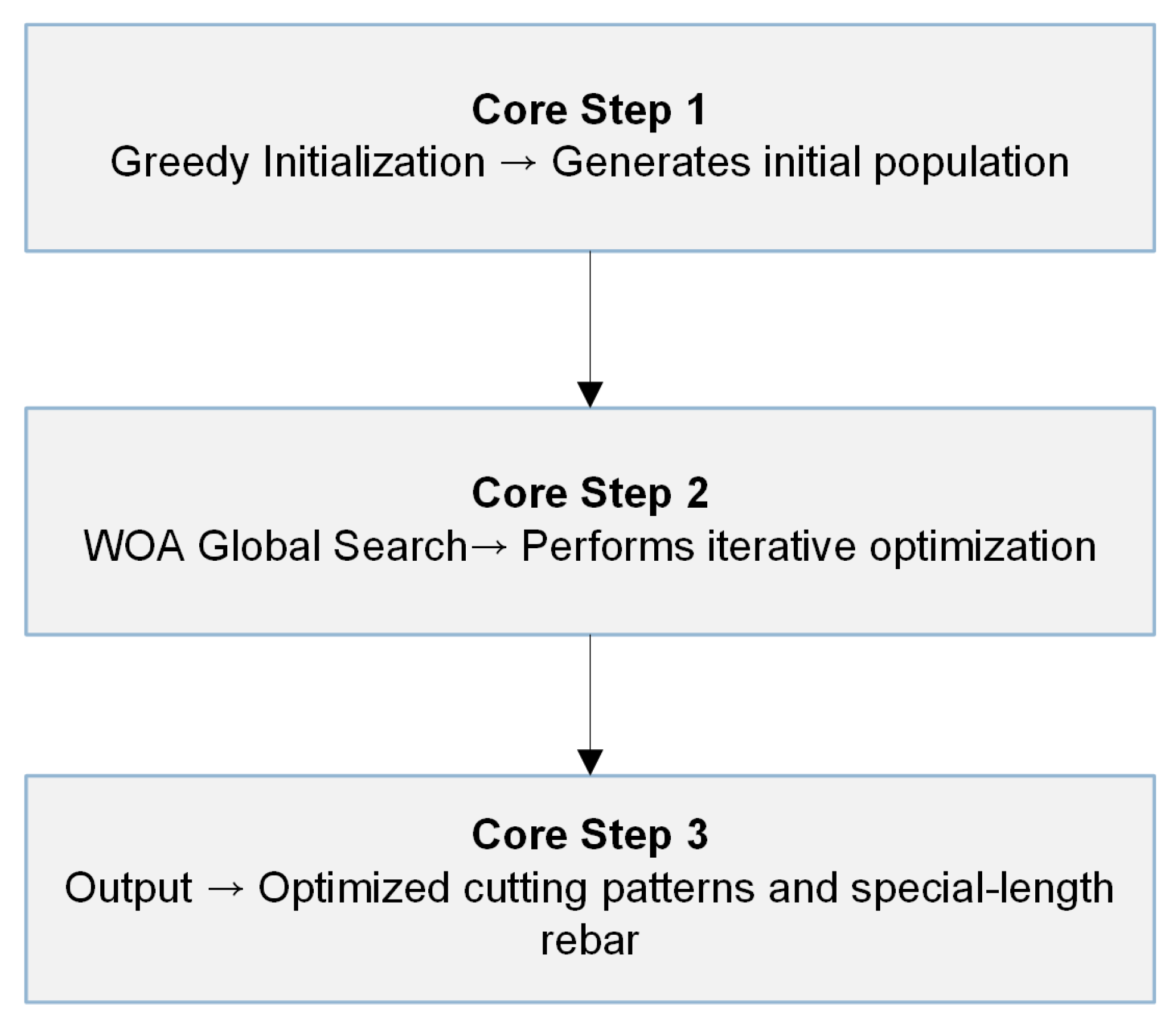
4.3. 2nd Stage: WOA-Based Special-Length Rebar Cutting Stock Optimizer (WOACSO) in Python
4.4. Integrated Intelligent Rebar Optimization Framework for Diaphragm Wall
5. Case Application and Validation
5.1. Case Study Selection and Preliminary Settings
5.2. Intelligent Rebar Optimization Framework Application
5.3. Verification, Validation, and Result Analysis
5.3.1. Verification
5.3.2. Validation and Result Analysis
- Rebar Usage, Waste, and Computational Time
- b.
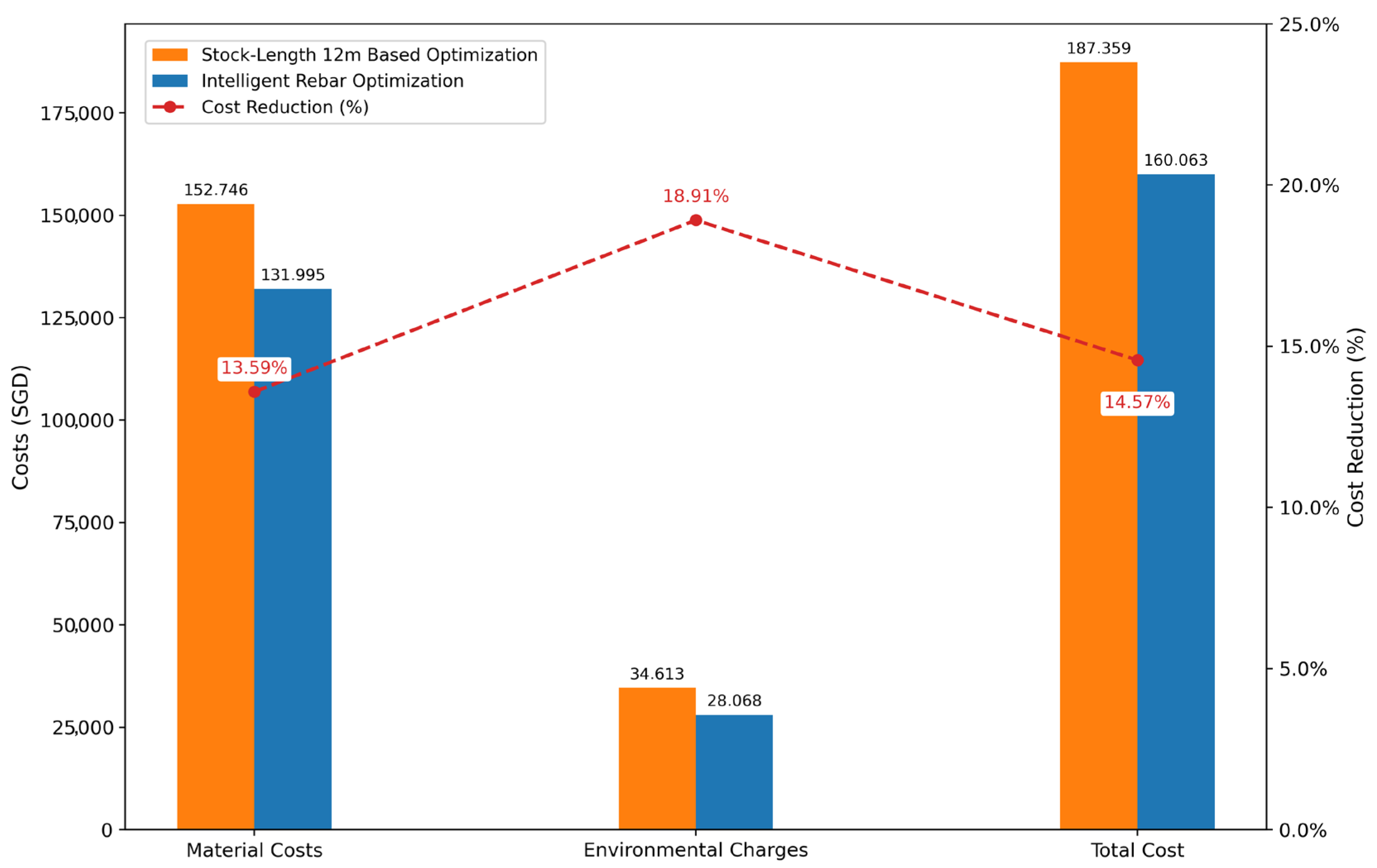
- Associated Carbon Emissions and Costs
6. Discussions
7. Conclusions
- AI large language model (LLM) tools, such as ChatGPT, effectively and efficiently assisted the framework’s code conversion, improvement, and development through structured task-specific prompts under close user oversight.
- The conventional stock-length rebar optimization approach that relies on fixed rebar length and lap splicing entails an excessive amount of rebar required, rebar used, and waste generated. In contrast, the proposed intelligent framework incorporating special-length rebar allocation and strategic coupler placement achieved a 19.76% reduction in rebar usage and an 84.57% reduction in cutting waste.
- These material savings translated into a 17.4% reduction in associated carbon emissions (equivalent to 136 tons of CO2-eq) and a 14.57% reduction in total costs (equivalent to SGD 27,296). As these results were derived from a single panel, wider application across all diaphragm wall panels could yield an even greater impact.
- The framework also significantly outperformed the conventional optimization in computational efficiency, converging to feasible solutions in under 20 s, representing a reduction of over 90% in computation time. This improvement reinforces the framework’s scalability and applicability to large-scale infrastructure projects.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| RC | Reinforced concrete |
| BIM | Building information modeling |
| LAI | Artificial intelligence |
| IPD | Integrated project delivery |
| WOA | Whale optimization algorithm |
| CROF | Continuous Rebar Optimization Framework |
| WOACSO | WOA-based special-length cutting stock optimizer |
Appendix A
| Pseudocode A1: Continuous Rebar Optimization |
| Load rebar specifications from Sheet 1 Load rebar layout and quantities from Sheet 2 For each rebar section: Retrieve total rebar length, diameter, and bundle quantity Determine maximum allowable rebar length Calculate number of required special-length bars Select appropriate coupler gap based on diameter Estimate end and middle bar lengths with gap adjustment Identify the required special length (max of end/middle) Round up to nearest 100 mm for purchasable length Retrieve unit rebar weight based on diameter Calculate total number of special-length bars and couplers Estimate total required and purchased weight for the section Aggregate results across all layers: - Total rebar quantities and weights - Total number of couplers - Estimated rebar waste rate Export results to spreadsheet |
| Pseudocode A2: WOA-Based Cutting Stock Optimization |
| Initialize the whales population Xi (i = 1, 2, …, n) within [lmin, lmax] Load required rebar lengths and quantities from an input Spreadsheet file Calculate the fitness of each search agent:
while (t < maximum number of iterations) for each search agent Update a, A, C, l, and p if1 (p<0.5) if2 (|A|< 1) Update the position of the current search agent else if2 (|A|≥ 1) Select a random search agent (Xrand) Update the position of the current search agent end if2 else if1 (p≥0.5) Update the position of the current search end if1 Ensure the updated position is within [lmin, lmax] and round to the nearest 0.1m Calculate the fitness of the updated search agent:
Update X* with the new best solution end if end for t=t+1 end while Calculate the final cutting pattern based on X* Compute and display total waste, total bars needed, and cutting details Save the optimized cutting pattern to a Spreadsheet file return X* (optimal rebar special length) |
| Input | ||||
| Length (m) | Quantity (pcs) | |||
| 5.665 | 41 | |||
| 5.780 | 16 | |||
| 5.950 | 41 | |||
| Results | ||||
| Strategy | Rebar Length Type | Number of bars needed (pcs) | Waste (m) | Waste (%) |
| Greedy only | Fixed (12 m) | 49 | 19.305 | 3.28 |
| WOACSO | Special (6–12 m). Identified: 11.7 m | 49 | 4.605 | 0.8 |
Appendix B
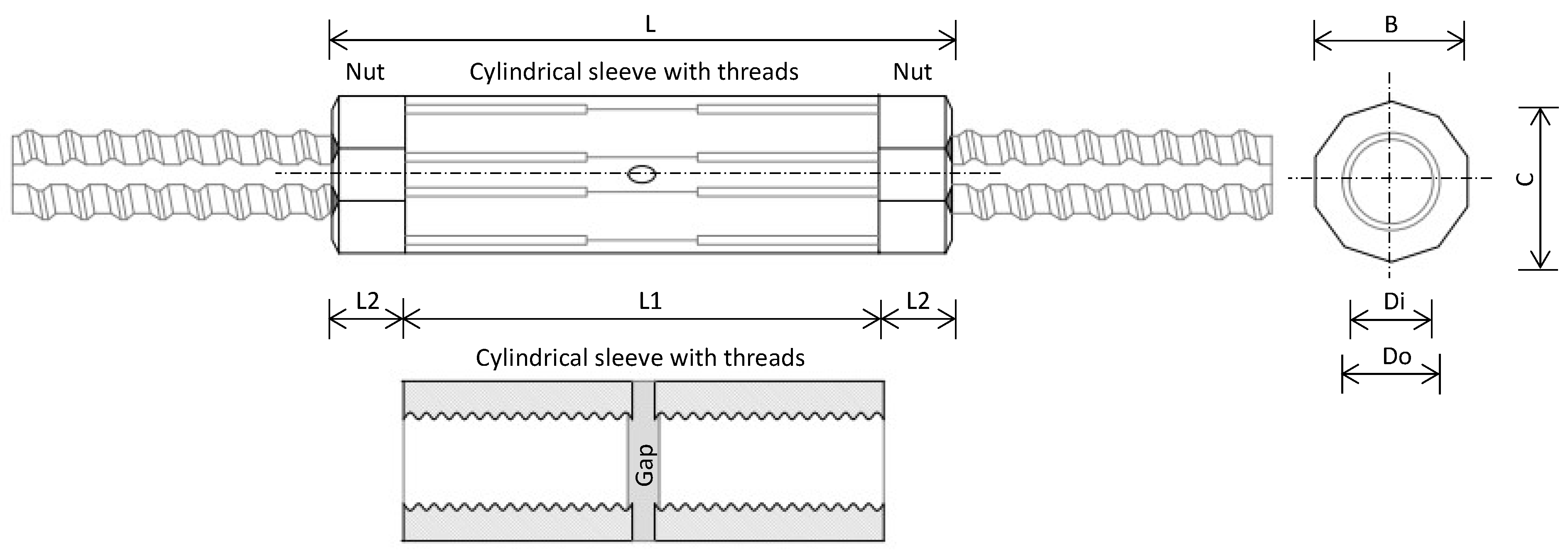
| Bar Size | Outside Diameter of Coupler | Length | Dimension of Thread | |||||
|---|---|---|---|---|---|---|---|---|
| Coupler | Nut | Total | Pitch | Inside Diameter | Root Diameter | |||
| B | C | L1 | L2 | L | P | Di | Do | |
| 19 | 29 | 30 | 100 | 20 | 140 | 8 | 18.9 | 22.3 |
| 22 | 34 | 35 | 110 | 20 | 150 | 9 | 21.8 | 25.6 |
| 25 | 38 | 39 | 120 | 20 | 160 | 10 | 24.8 | 29.0 |
| 29 | 43 | 44 | 135 | 20 | 175 | 12 | 28.2 | 33.0 |
| 32 | 48 | 49 | 160 | 20 | 200 | 13 | 31.4 | 36.6 |
| Serial No. | Description | Bar Mark | Size | No. of Rebar | Length (mm) |
|---|---|---|---|---|---|
| 1 | 1st rebar cage | A1 | H40 | 41 | 6674 |
| 2 | B1 | H40 | 41 | 5290 | |
| 3 | D1 | H25 | 41 | 6384 | |
| 4 | 2nd rebar cage | A2 | H40 | 41 | 9760 |
| 5 | B2 | H40 | 41 | 9760 | |
| 6 | C2 | H40 | 41 | 8500 | |
| 7 | D2 | H40 | 41 | 9110 | |
| 8 | E2 | H40 | 41 | 10,050 | |
| 9 | F2 | H40 | 41 | 10,550 | |
| 10 | J2 | H40 | 41 | 10,550 | |
| 11 | 3rd rebar cage | A3 | H40 | 41 | 5950 |
| 12 | B3 | H40 | 41 | 5950 | |
| 13 | C3 | H25 | 41 | 5950 | |
| 14 | D3 | H40 | 41 | 5950 | |
| 15 | E3 | H40 | 41 | 3950 | |
| 16 | 4th rebar cage | A4 | H40 | 41 | 8240 |
| 17 | B4 | H40 | 41 | 8240 | |
| 18 | C4 | H32 | 41 | 9300 | |
| 19 | D4 | H40 | 41 | 8240 | |
| 20 | 5th rebar cage | A5 | H40 | 41 | 2260 |
| 21 | A5a | H32 | 41 | 5665 | |
| 22 | B5 | H40 | 41 | 2260 | |
| 23 | D5 | H40 | 41 | 6835 | |
| 24 | E5 | H40 | 41 | 9075 | |
| 25 | F5 | H40 | 41 | 9075 | |
| 26 | J5 | H40 | 41 | 9500 | |
| 27 | 6th rebar cage | A6 | H40 | 41 | 9760 |
| 28 | B6 | H40 | 41 | 9760 | |
| 29 | D6 | H40 | 41 | 9760 | |
| 30 | E6 | H40 | 41 | 9760 | |
| 31 | F6 | H40 | 41 | 9760 | |
| 32 | J6 | H40 | 41 | 6835 | |
| 33 | 7th rebar cage | A7 | H40 | 41 | 8365 |
| 34 | B7 | H40 | 41 | 8365 | |
| 35 | D7 | H40 | 41 | 5465 | |
| 36 | D7a | H25 | 41 | 4200 | |
| 37 | E7 | H40 | 41 | 5665 | |
| 38 | F7 | H40 | 41 | 4165 | |
| 39 | J7 | H40 | 41 | 4165 | |
| 40 | 8th rebar cage | A8 | H40 | 41 | 3600 |
| 41 | A8a | H25 | 41 | 6650 | |
| 42 | D8 | H25 | 41 | 8900 | |
| 43 | 9th rebar cage | A9 | H25 | 41 | 10,650 |
| 44 | D9 | H25 | 41 | 10,650 | |
| 45 | Spacers | S1 | H40 | 58 | 2570 |
| 46 | S2 | H40 | 58 | 2465 | |
| 47 | Ex-Link | L1 | H20 | 376 | 5800 |
| 48 | L1a | H21 | 376 | 4480 | |
| 49 | L1b | H22 | 754 | 4550 | |
| 50 | C-Link | L2 | H13 | 3630 | 1704 |
| 51 | L2a | H16 | 6020 | 1729 | |
| 52 | L2b | H16 | 160 | 2453 | |
| 53 | Stiffener | L3 | H25 | 60 | 2505 |
| 54 | Couplers | G1 | H40 | 97 | 1587 |
| 55 | G1a | H40 | 68 | 1587 | |
| 56 | G1c | H40 | 180 | 1587 | |
| 57 | G1d | H40 | 71 | 1587 | |
| 58 | G1e | H40 | 71 | 1587 | |
| 59 | G1f | H40 | 88 | 1587 | |
| 60 | G2 | H40 | 22 | 1587 | |
| 61 | G2a | H40 | 15 | 1587 | |
| 62 | G2c | H40 | 39 | 1587 | |
| 63 | G2d | H40 | 16 | 1587 | |
| 64 | G2e | H40 | 16 | 1587 | |
| 65 | G2f | H40 | 16 | 1587 | |
| 66 | G3d | H32 | 52 | 1195 | |
| 67 | G4d | H32 | 14 | 1195 | |
| 68 | G5 | H25 | 40 | 957 | |
| 69 | G6 | H25 | 8 | 957 | |
| 70 | G7 | H20 | 2 | 786 | |
| 71 | Dowel Bars | SW1 | H13 | 1488 | 1125 |
| 72 | SW2 | H13 | 372 | 1125 | |
| 73 | Fixing Bars | FR1 | H20 | 19 | 1170 |
| 74 | FR2 | H20 | 19 | 1290 | |
| 75 | FR3 | H20 | 21 | 1175 | |
| 76 | FR4 | H20 | 30 | 1135 | |
| 77 | Hanging Bars | H1 | H40 | 32 | 2570 |
| 78 | Support Bars | SB1 | H25 | 36 | 1320 |
| 79 | Suspension Hook | U1 | H32 | 16 | 5780 |
| 80 | Lifting Hook | U1a | H32 | 16 | 1700 |
References
- Xie, Z.F.; Shen, S.L.; Arulrajah, A.; Horpibulsuk, S. Environmentally sustainable groundwater control during dewatering with barriers: A case study in Shanghai. Undergr. Space 2021, 6, 12–23. [Google Scholar] [CrossRef]
- Qiu, T.; Sun, X.; Chen, X.; Su, D.; Zhang, J.; Xu, Z.; Song, R.; Wang, X. Experimental study and resilience modeling for prefabricated hollow diaphragm walls of full-assembled underground stations under urban multi-disturbance conditions. Tunn. Undergr. Space Technol. 2023, 135, 105044. [Google Scholar] [CrossRef]
- Tong, L.; Guo, Q.; Che, H.; Zhang, M.; Pan, H.; Li, H. Investigation of rebar exposure issues of diaphragm wall and influencing factors analysis. KSCE J. Civ. Eng. 2019, 23, 1522–1536. [Google Scholar] [CrossRef]
- Liu, C.; Lee, Y.T.; Sung, S.P.; Tsai, Y.Y.; Lin, H.T. Design of Protection Measures for Deep Excavation of A New Underground Station Closely Adjacent to Viaduct of MRT System in Operation. In Proceedings of the HKIE Geotechnical Division 41st Annual Seminar—Adapt to Challenges, Create to Thrive, Hong Kong, 18 May 2021. [Google Scholar] [CrossRef]
- Liu, T.Y.; Chou, N.N.; Lin, S.J.; Tzou, H.K.; Chen, P.H. Challenges and sustainability-based solutions of Diaphragm Wall Construction for LG06 Underground Station in Taipei MRT. Transp. Infrastruct. Geotech. 2023, 10, 17–40. [Google Scholar] [CrossRef]
- Lasvaux, S.; Habert, G.; Peuportier, B.; Chevalier, J. Comparison of Generic and Product-Specific Life Cycle Assessment Databases: Application to Construction Materials Used in Building LCA Studies. Int. J. Life Cycle Assess. 2015, 20, 1473–1490. [Google Scholar] [CrossRef]
- Chen, L.; Huang, L.; Hua, J.; Chen, Z.; Wei, L.; Osman, A.I.; Fawzy, S.; Rooney, D.W.; Dong, L.; Yap, P.-S. Green Construction for Low-Carbon Cities: A Review. Environ. Chem. Lett. 2023, 21, 1627–1657. [Google Scholar] [CrossRef]
- Widjaja, D.D.; Khant, L.P.; Kim, S.; Kim, K.Y. Optimization of Rebar Usage and Sustainability Based on Special-Length Priority: A Case Study of Mechanical Couplers in Diaphragm Walls. Sustainability 2024, 16, 1213. [Google Scholar] [CrossRef]
- Widjaja, D.D.; Rachmawati, T.S.N.; Kim, S. Minimizing Rebar Consumption: A Decarbonization Strategy for the Civil and Construction Industry. Sustainability 2025, 17, 1172. [Google Scholar] [CrossRef]
- Widjaja, D.D.; Rachmawati, T.S.N.; Kim, S. A BIM-based intelligent approach to rebar layout optimization for reinforced concrete columns. J. Build. Eng. 2025, 99, 111604. [Google Scholar] [CrossRef]
- Widjaja, D.D. Algorithms for Optimal Rebar Work in Buildings Using BIM and AI Under an Integrated Project Delivery Concept. Ph.D. Thesis, Kyung Hee University, Seoul, Republic of Korea, August 2025. [Google Scholar]
- Sugianto, A.; Tung, Y.I. Bi-objective Optimization for Rebar Cutting Plan Using Symbiotic Organisms Search. Dimens. Utama Tek. Sipil 2022, 9, 1–17. [Google Scholar] [CrossRef]
- Güvel, S.T.; Karatas, I. A novel special length rebar order approach based on AI optimization techniques for reduction of rebar cutting waste. J. Constr. Eng. Manag. Innov. 2023, 6, 285–296. Available online: https://www.researchgate.net/profile/Sahin-Guevel/publication/376966051_A_novel_special_length_rebar_order_approach_based_on_AI_optimization_techniques_for_reduction_of_rebar_cutting_waste/links/665b2e1e22a7f16b4f685d8e/A-novel-special-length-rebar-order-approach-based-on-AI-optimization-techniques-for-reduction-of-rebar-cutting-waste.pdf (accessed on 23 June 2025). [CrossRef]
- Ren, K.; Jia, L.; Huang, J.; Wu, M. Research on cutting stock optimization of rebar engineering based on building information modeling and an improved particle swarm optimization algorithm. Dev. Built. Environ. 2023, 13, 100121. [Google Scholar] [CrossRef]
- Wang, Z.; Jia, L.; Lv, J.; Huang, J. Minimization of Rebar Cutting Waste Using BIM and Cutting Pattern-Oriented Multiobjective Optimization. J. Constr. Eng. Manag. 2024, 150, 04024166. [Google Scholar] [CrossRef]
- Dabiri, H.; Kheyroddin, A.; Dall’Asta, A. Splice Methods Used for Reinforcement Steel Bars: A State-of-the-Art Review. Constr. Build. Mater. 2022, 320, 126198. [Google Scholar] [CrossRef]
- Lim, J.; Kim, S. Data-driven Approach for Selecting Mechanical Rebar Couplers Based on the Shape and Structural Characteristics of Reinforcing Bars for Sustainable Built Environment. Sustainability 2024, 16, 4016. [Google Scholar] [CrossRef]
- Kim, S.; Rarasati, A.D.; Rachmawati, T.S.N.; Widjaja, D.D. Optimization Algorithm on Rebar Waste Reduction in Mechanical Coupler Applications on Diaphragm Wall Structures. In Proceedings of the 9th International Conference in Civil Engineering (ICOCE), Singapore, 22–24 March 2025. [Google Scholar] [CrossRef]
- Porwal, A.; Hewage, K.N. Building information modeling–based analysis to minimize waste rate of structural reinforcement. J. Constr. Eng. Manag. 2012, 138, 943–954. [Google Scholar] [CrossRef]
- Chen, Y.H.; Yang, T.K. Lapping pattern, stock length, and shop drawing of beam reinforcements of an RC building. J. Comput. Civ. Eng. 2015, 29, 04014028. [Google Scholar] [CrossRef]
- Nadoushani, Z.S.M.; Hammad, A.W.; Xiao, J.; Akbarnezhad, A. Minimizing cutting wastes of reinforcing steel bars through optimizing lap splicing within reinforced concrete elements. Constr. Build. Mater. 2018, 185, 600–608. [Google Scholar] [CrossRef]
- Khondoker, M.T.H. Automated reinforcement trim waste optimization in RC frame structures using building information modeling and mixed-integer linear programming. Autom. Constr. 2021, 124, 103599. [Google Scholar] [CrossRef]
- Mangal, M.; Cheng, J.C. Automated optimization of steel reinforcement in RC building frames using building information modeling and hybrid genetic algorithm. Autom. Constr. 2018, 90, 39–57. [Google Scholar] [CrossRef]
- Liu, J.; Xu, C.; Wu, Z.; Chen, Y.F. Intelligent rebar layout in RC building frames using artificial potential field. Autom. Constr. 2020, 114, 103172. [Google Scholar] [CrossRef]
- Liu, J.; Li, S.; Xu, C.; Wu, Z.; Ao, N.; Chen, Y.F. Automatic and optimal rebar layout in reinforced concrete structure by decomposed optimization algorithms. Autom. Constr. 2021, 126, 103655. [Google Scholar] [CrossRef]
- Wang, D.; Hu, Y. Research on the Intelligent Construction of the Rebar Project Based on BIM. Appl. Sci. 2022, 12, 5596. [Google Scholar] [CrossRef]
- Xu, C.; Liu, J.; Wu, Z.; Chen, Y.F. Automated steel reinforcement detailing in reinforced concrete frames using evolutionary optimization and artificial potential field. Autom. Constr. 2022, 138, 104224. [Google Scholar] [CrossRef]
- Li, S.; Shi, Y.; Hu, J.; Li, S.; Li, H.; Chen, A.; Xie, W. Application of BIM to Rebar Modeling of a Variable Section Column. Buildings 2023, 13, 1234. [Google Scholar] [CrossRef]
- Rachmawati, T.S.N. BIM—Based Optimization Model to Achieve Near-Zero Rebar Cutting Waste. Ph.D. Thesis, Kyung Hee University, Seoul, Republic of Korea, 2024. [Google Scholar]
- Ghaemifard, S.; Ghannadiasl, A. Usages of metaheuristic algorithms in investigating civil infrastructure optimization models; a review. AI Civ. Eng. 2024, 3, 17. [Google Scholar] [CrossRef]
- Houssein, E.H.; Hossam Abdel Gafar, M.; Fawzy, N.; Sayed, A.Y. Recent metaheuristic algorithms for solving some civil engineering optimization problems. Sci. Rep. 2025, 15, 7929. [Google Scholar] [CrossRef]
- NYU School of Professional Studies. What Is Metaheuristic Algorithms in AI? Available online: https://www.aimasterclass.com/glossary/metaheuristic-algorithms-in-ai (accessed on 23 June 2025).
- Tomar, V.; Bansal, M.; Singh, P. Metaheuristic algorithms for optimization: A brief review. Eng. Proc. 2024, 59, 238. [Google Scholar] [CrossRef]
- Lee, D.; Son, S.; Kim, D.; Kim, S. Special-length-priority algorithm to minimize reinforcing bar-cutting waste for sustainable construction. Sustainability 2020, 12, 5950. [Google Scholar] [CrossRef]
- Asadi, I.; Shpak, A.; Jacobsen, S. Analysis of Concrete Air Voids: Comparing OpenAI-Generated Python Code with MATLAB Scripts and Enhancing 2D Image Processing Using 3D CT Scan Data. Buildings 2024, 14, 3712. [Google Scholar] [CrossRef]
- OpenAI. Introducing ChatGPT. Available online: https://openai.com/index/chatgpt/ (accessed on 1 August 2025).
- Dong, Y.; Jiang, X.; Jin, Z.; Li, G. Self-collaboration code generation via chatgpt. ACM Trans. Softw. Eng. Methodol. 2024, 33, 1–38. [Google Scholar] [CrossRef]
- Feng, Y.; Vanam, S.; Cherukupally, M.; Zheng, W.; Qiu, M.; Chen, H. Investigating code generation performance of ChatGPT with crowdsourcing social data. In Proceedings of the 2023 IEEE 47th Annual Computers, Software, and Applications Conference (COMPSAC), Turino, Italy, 26–30 June 2023. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, Y.; Luo, X.; Zhou, Y.; Zhang, L.F. No need to lift a finger anymore? Assessing the quality of code generation by chatgpt. IEEE Trans. Softw. Eng. 2024, 50, 1548–1584. [Google Scholar] [CrossRef]
- Sakib, F.A.; Khan, S.H.; Karim, A.R. Extending the frontier of chatgpt: Code generation and debugging. In Proceedings of the 2024 International Conference on Electrical, Computer and Energy Technologies (ICECET), Sydney, Australia, 25–27 July 2024. [Google Scholar] [CrossRef]
- James, A.; Kurian, B. Design specifications for diaphragm wall: State of the art. Indian Geotech. J. 2020, 50, 838–847. [Google Scholar] [CrossRef]
- Rachmawati, T.S.N.; Khant, L.P.; Lim, J.; Lee, J.; Kim, S. Optimization of lap splice positions for near-zero rebar cutting waste in diaphragm walls using special-length-priority algorithms. J. Asian Archit. Build. Eng. 2024, 23, 1933–1950. [Google Scholar] [CrossRef]
- Widjaja, D.D.; Rachmawati, T.S.N.; Kwon, K.; Kim, S. Investigating Structural Stability and Constructability of Buildings Relative to the Lap Splice Position of Reinforcing Bars. J. Korea Inst. Build. Constr. 2023, 23, 315–326. [Google Scholar] [CrossRef]
- Khalifa, Y.; Salem, O.; Shahin, A. Cutting stock waste reduction using genetic algorithms. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, Seattle, WA, USA, 8–12 July 2006; pp. 1675–1680. [Google Scholar] [CrossRef]
- Widjaja, D.D.; Kim, S. Sustainable rebar cutting stock optimization using whale optimization algorithm (WOA). In Proceedings of the International Conference on Project Innovation, Management, and Enterprise (ICPRIME), Bandung, Indonesia, 14–15 May 2025. (in press).
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Ghaemifard, S.; Ghannadiasl, A. A Comparison of Metaheuristic Algorithms for Structural Optimization: Performance and Efficiency Analysis. Adv. Civ. Eng. 2024, 2024, 2054173. [Google Scholar] [CrossRef]
- Hasnaoui, A.; Omari, A.; Azzouz, Z.E.; Danoune, M.B.; Arini, N.R. Optimization and Management of Residential Energy Load Using PSO and WOA. In Proceedings of the 2022 International Electronics Symposium (IES), Surabaya, Indonesia, 9–11 August 2022. [Google Scholar] [CrossRef]
- Kumar, V.; Agarwal, R.; Shikha, D. PSO and WOA Algorithm Based Optimal Control for Photovoltaic Solar System. In Proceedings of the 2023 3rd International Conference on Emerging Frontiers in Electrical and Electronic Technologies (ICEFEET), Patna, India, 21–22 December 2023. [Google Scholar] [CrossRef]
- Mohammed, H.M.; Umar, S.U.; Rashid, T.A. A systematic and meta-analysis survey of whale optimization algorithm. Comput. Intell. Neurosci. 2019, 2019, 8718571. [Google Scholar] [CrossRef]
- Land Transport Authority (LTA). Cross Island Line. Available online: https://www.lta.gov.sg/content/ltagov/en/upcoming_projects/rail_expansion/cross_island_line.html (accessed on 23 June 2025).
- Tokyo Tekko Company Ltd. Threaded Rebar Joint, ACE-Joint. Available online: https://www.tokyotekko.co.jp/ko/prd/tekko/nsts/nsts04/main/04/teaserItems1/00/linkList/0/link/01.Ace%20Joint.pdf (accessed on 23 June 2025).
- Tokyo Tekko Company Ltd. Neji-Testu-Con (Hot Rolled Threaded Rebar). Available online: https://www.tokyotekko.co.jp/ko/prd/tekko/tc/tc01/main/04/teaserItems1/00/linkList/0/link/00.Threaded%20Bar.pdf (accessed on 23 June 2025).
- Ghayeb, H.H.; Razak, H.A.; Sulong, N.H.R. Evaluation of the CO2 emissions of an innovative composite precast concrete structure building frame. J. Clean. Prod. 2020, 242, 118567. [Google Scholar] [CrossRef]
- National Climate Change Secretariat Singapore. Carbon Tax. Available online: https://www.nccs.gov.sg/singapores-climate-action/mitigation-efforts/carbontax/#:~:text=Carbon%20Tax%20in%20Singapore%20from,period%20for%20emitters%20to%20adjust (accessed on 23 June 2025).
- Ministry of Sustainability and the Environment Singapore. Carbon Pricing Act. Available online: https://www.mse.gov.sg/policies/climate-change/carbon-pricing-act (accessed on 23 June 2025).
- Chen, X.; Yi, W.; Yuan, H.; Wu, W. Construction and demolition waste disposal charging scheme design. Comput. Aided Civ. Infrastruct. Eng. 2024, 39, 222–241. [Google Scholar] [CrossRef]
- Hong Kong and Shanghai Banking Corporation (HSBC). Exchange Rate Calculator. Available online: https://www.hsbc.com.hk/investments/currency-exchange-rate-calculator/ (accessed on 27 June 2025).
- Building and Construction Authority (BCA). Construction Demand, Tender Price Index & Construction Materials. Available online: https://www1.bca.gov.sg/docs/default-source/docs-corp-form/free_stats.pdf?sfvrsn=4d68fbe4_150 (accessed on 27 June 2025).
- DBS Singapore. DBS Currency Converter. Available online: https://www.dbs.com.sg/personal/rates-online/foreign-currency-foreign-exchange.page (accessed on 27 June 2025).
- United Nations Development Programme. The SDGs in Action. Available online: https://www.undp.org/sustainable-development-goals (accessed on 27 June 2025).

| Algorithm(s) | Characteristic(s) |
|---|---|
| Symbiotic Organism Search (SOS) [12] |
|
| Fuzzy Genetic Algorithms (GA) [13] |
|
| Greedy Adaptive Particle Swarm Optimization (PSO) [14] |
|
| Hybrid Particle Swarm Optimization (PSO) [15] |
|
| Whale Optimization Algorithm (WOA) [11] |
|
| Parameter | Description |
|---|---|
| Number of iterations (num_iterations) | 50 |
| Number of whales (num_whales) | 30 |
| Control modifier a | [0, 2] |
| Spiral parameter l, random | [−1, 1] |
| Minimum available rebar length () | 6 m |
| Maximum available rebar length () | 12 m |
| Description | Contents |
|---|---|
| Larger rebar diameter | 40 mm |
| Smaller rebar diameter | 25 mm |
| Concrete strength | 24 MPa |
| Rebar yield strength | 500 MPa |
| Concrete cover | 50 mm |
| Maximum rebar length | 12,000 mm |
| Rebar unit weight H40 | 9.854 kg/m |
| Rebar unit weight H25 | 3.854 kg/m |
| Inner gap of coupler > H32 | 30 mm |
| Inner gap of coupler < H32 | 20 mm |
| Layer | Diameter (mm) | Number of Rebar in Bundle (pcs) | Total Bar Length (mm) |
|---|---|---|---|
| A1-8 | 40 | 41 | 54,609 |
| A8-9 | 25 | 41 | 17,300 |
| B1-5 | 40 | 41 | 31,500 |
| D2-7 | 40 | 41 | 45,360 |
| D7-9 | 25 | 41 | 23,750 |
| E2-3 | 40 | 41 | 14,000 |
| E5-7 | 40 | 41 | 24,500 |
| F5-7 | 40 | 41 | 23,000 |
| J6-7 | 40 | 41 | 11,000 |
| Layer | Diameter (mm) | Purchasable Special-Length (m) | Total Number of Special Lengths (pcs) | Total Number of Coupler (pcs) | Total Required Quantity (ton) | Total Purchased Quantity (ton) |
|---|---|---|---|---|---|---|
| A1-8 | H40 | 11 | 205 | 164 | 22.01432 | 22.22077 |
| A8-9 | H25 | 8.7 | 82 | 41 | 2.73048 | 2.74944 |
| B1-5 | H40 | 10.5 | 123 | 82 | 12.7022 | 12.72644 |
| D2-7 | H40 | 11.4 | 164 | 123 | 18.28971 | 18.42304 |
| D7-9 | H25 | 11.9 | 82 | 41 | 3.74967 | 3.76073 |
| E2-3 | H40 | 7 | 82 | 41 | 5.64408 | 5.6562 |
| E5-7 | H40 | 8.2 | 123 | 82 | 9.8741 | 9.93874 |
| F5-7 | H40 | 11.5 | 82 | 41 | 9.2802 | 9.29232 |
| J6-7 | H40 | 11 | 41 | 0 | 4.44415 | 4.44415 |
| Total | 984 | 615 | 88.729 | 89.212 | ||
| Diameter (mm) | Purchasable Special-Length (m) | Number of Bars Needed (pcs) | Total Waste (m) | Total Required Quantity (ton) | Total Purchased Quantity (ton) | Total Waste (ton) |
|---|---|---|---|---|---|---|
| H40 | 11.2 | 285 | 105.317 | 30.41617 | 31.45397 | 1.03779 |
| H32 | 11.7 | 59 | 15.535 | 4.25979 | 4.35786 | 0.9807 |
| H25 | 10.3 | 87 | 9.3 | 3.41773 | 3.45357 | 0.3584 |
| H20 | 10.3 | 756 | 383.783 | 18.28545 | 19.23340 | 0.94794 |
| H16 | 10.4 | 1044 | 56.54 | 17.06567 | 17.15501 | 0.08933 |
| H13 | 11.4 | 731 | 55.38 | 8.60914 | 8.66674 | 0.05760 |
| Total (ton) | 82.054 | 84.320 | 2.266 | |||
| Diameter (mm) | Stock-Length (m) | Number of Bars Needed (pcs) | Total Required Quantity (ton) | Total Purchased Quantity (ton) | Total Waste (ton) | Number of Splices (pcs) |
|---|---|---|---|---|---|---|
| H40 | 12 | 1292 | 142.71954 | 152.77642 | 10.05687 | 943 |
| H32 | 12 | 33 | 2.32745 | 2.49995 | 0.17250 | 0 |
| H25 | 12 | 226 | 9.43556 | 10.45205 | 1.01649 | 123 |
| H20 | 12 | 753 | 18.28545 | 22.31892 | 4.03347 | 0 |
| H16 | 12 | 1030 | 17.06567 | 19.52880 | 2.46313 | 0 |
| H13 | 12 | 696 | 8.60914 | 8.68608 | 0.07694 | 0 |
| Total (ton) | 198.443 | 216.262 | 17.819 | 1066 | ||
| Approach/Framework | Number of Splices/Coupler (pcs) | Rebar Usage (ton) | Carbon Emissions (ton CO2-eq) |
|---|---|---|---|
| Stock-length-based optimization | 1066 | 216.262 | 758 |
| Intelligent optimization | 615 | 173.532 | 622 |
| Reduction | 42.73 | 136 | |
| Reduction rate (%) | 19.76 | 17.4 | |
| Cost Component | Unit Cost (SGD) |
|---|---|
| Rebar each ton | 706.3 [59] |
| Coupler H40; H25 each piece * | 15.88; 7.89 [8,60] |
| Disposal charge per ton | 28.23 |
| Carbon tax per ton | 45 [55,56] |
| Studies | Characteristic(s) |
|---|---|
| Conventional stock-length approaches [12,13,14,15] |
|
| Author’s previous work (unified two-stage lap splice position adjustment-based framework) [42] |
|
| Author’s previous work (unified two-stage coupler integration framework) [8] |
|
| This study (intelligent unified two-stage coupler integration framework) |
|
| Algorithm(s) | Population Size | Number of Iterations | Crossover Rate | Mutation Rate | Inertia Weight (w) | Cognitive Weight (c1) | Social Weight (c2) |
|---|---|---|---|---|---|---|---|
| GA | 30 | 50 | 0.8 | 0.15 | - | - | - |
| PSO | 30 | 50 | - | - | 0.7 | 1.5 | 1.5 |
| WOACSO | 30 | 50 | - | - | - | - | - |
| Diameter (mm) | GA | PSO | WOACSO | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Bar Length (m) | Quantity (pcs) | Waste (m) | Bar Length (m) | Quantity (pcs) | Waste (m) | Bar Length (m) | Quantity (pcs) | Waste (m) | |
| H40 | 12 | 279 | 261.32 | 12 | 279 | 261.32 | 11.2 | 285 | 105.32 |
| Waste rate (%) | 7.81 | 7.81 | 3.41 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Widjaja, D.D.; Kim, S. Intelligent Rebar Optimization Framework for Urban Transit Infrastructure: A Case Study of a Diaphragm Wall in a Singapore Mass Rapid Transit Station. Smart Cities 2025, 8, 130. https://doi.org/10.3390/smartcities8040130
Widjaja DD, Kim S. Intelligent Rebar Optimization Framework for Urban Transit Infrastructure: A Case Study of a Diaphragm Wall in a Singapore Mass Rapid Transit Station. Smart Cities. 2025; 8(4):130. https://doi.org/10.3390/smartcities8040130
Chicago/Turabian StyleWidjaja, Daniel Darma, and Sunkuk Kim. 2025. "Intelligent Rebar Optimization Framework for Urban Transit Infrastructure: A Case Study of a Diaphragm Wall in a Singapore Mass Rapid Transit Station" Smart Cities 8, no. 4: 130. https://doi.org/10.3390/smartcities8040130
APA StyleWidjaja, D. D., & Kim, S. (2025). Intelligent Rebar Optimization Framework for Urban Transit Infrastructure: A Case Study of a Diaphragm Wall in a Singapore Mass Rapid Transit Station. Smart Cities, 8(4), 130. https://doi.org/10.3390/smartcities8040130








