Mitigation of Voltage Magnitude Profiles Under High-Penetration-Level Fast-Charging Stations Using Optimal Capacitor Placement Integrated with Renewable Energy Resources in Unbalanced Distribution Networks
Abstract
Highlights
- An improved capacitor placement method using IGWO with zone-based control optimizes voltage profiles, minimizes power losses and CO2 emissions in unbalanced distribution systems.
- The best case involved placing unbalanced capacitors and PV systems using a distributed, zone-based control strategy to handle high EV fast-charging demand.
- Coordinated zone-based placement of renewable energy and reactive power devices enhance grid resilience and operational efficiency in EV-dominated smart city networks.
- The proposed method provides a practical and scalable approach for planners to support sustainable electrification, reduce environmental impact and improve power quality in modern distribution systems.
Abstract
1. Introduction
2. Overviews of Capacitor Placement in Power Systems
2.1. Type of Capacitor
2.2. Possible Installation Positions for Capacitors in Distribution Systems
3. Literature Reviews
4. Summary of Major Contributions
- It develops an optimization framework based on improved gray wolf optimization (IGWO) for the optimal placement and sizing of capacitors under both balanced and unbalanced network conditions, incorporating renewable energy sources to enhance voltage performance and system efficiency.
- A comprehensive voltage resilience analysis is carried out under high-penetration fast-charging electric vehicle stations (FCSs), addressing the voltage fluctuations and quality issues associated with increased EV load demands.
- This study implements a hybrid objective optimization model designed to minimize real and reactive power losses, capacitor installation costs, cumulative voltage deviations (CVDs), the voltage unbalance index (), and the total QuadTerm and ensure voltage average compliance (), providing a holistic view of system performance.
- Validation is carried out using the unbalanced IEEE 123-bus distribution system, demonstrating the robustness and applicability of the proposed IGWO-based framework under realistic network conditions with varying control strategies and renewable integrations.
5. Problem Formulation of the Proposal
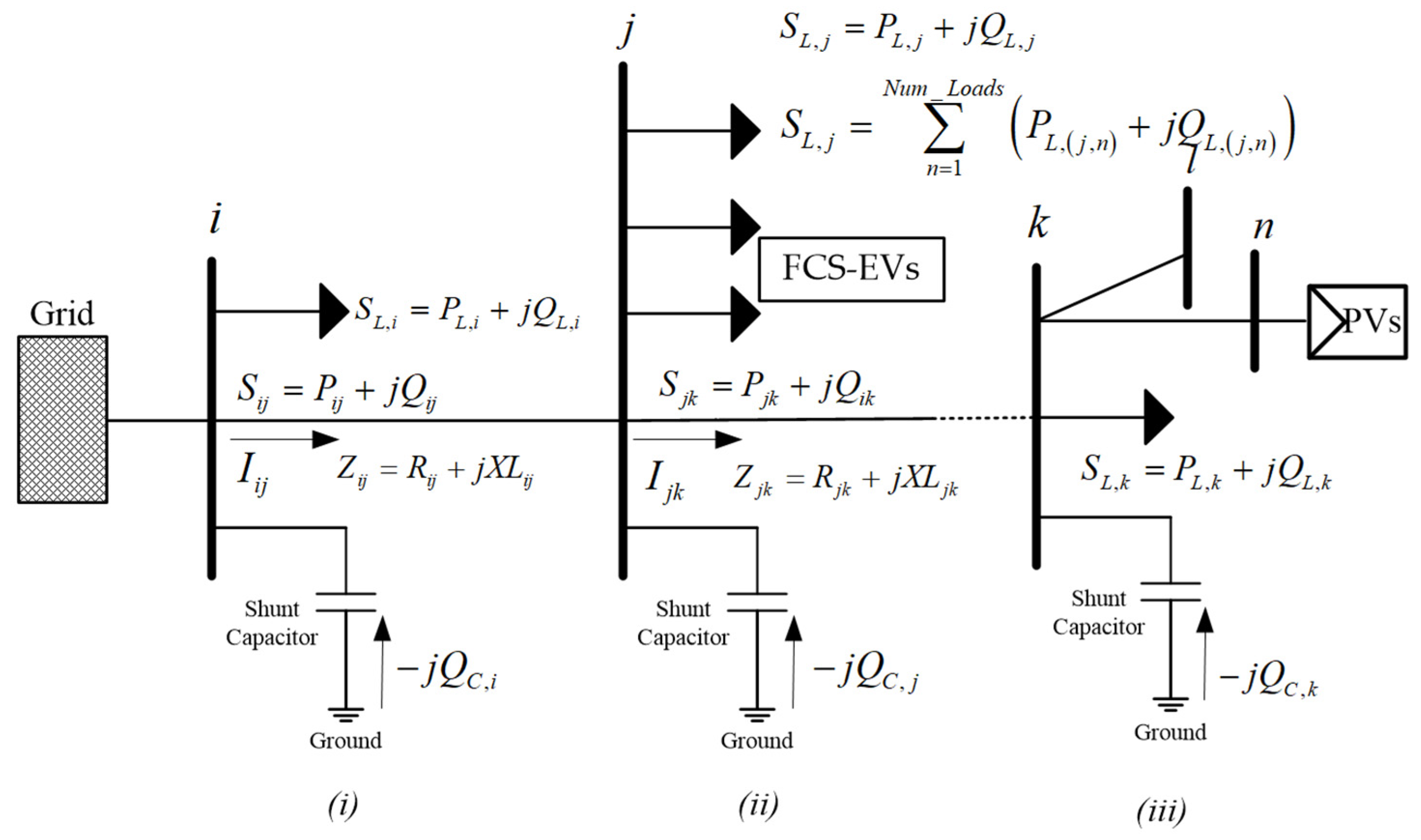
5.1. Unbalanced Power Flow Methodology
5.1.1. Total Power Loss and Reactive Power Loss
5.1.2. Commutative Voltage Deviation (CVD)
5.1.3. Total Quadratic Term (Total QuadTerm) of Control Voltage Tolerance
5.1.4. Voltage Average
5.1.5. Voltage Unbalance Index (VUI)
5.1.6. Environmental Performance Indices (EPIs)
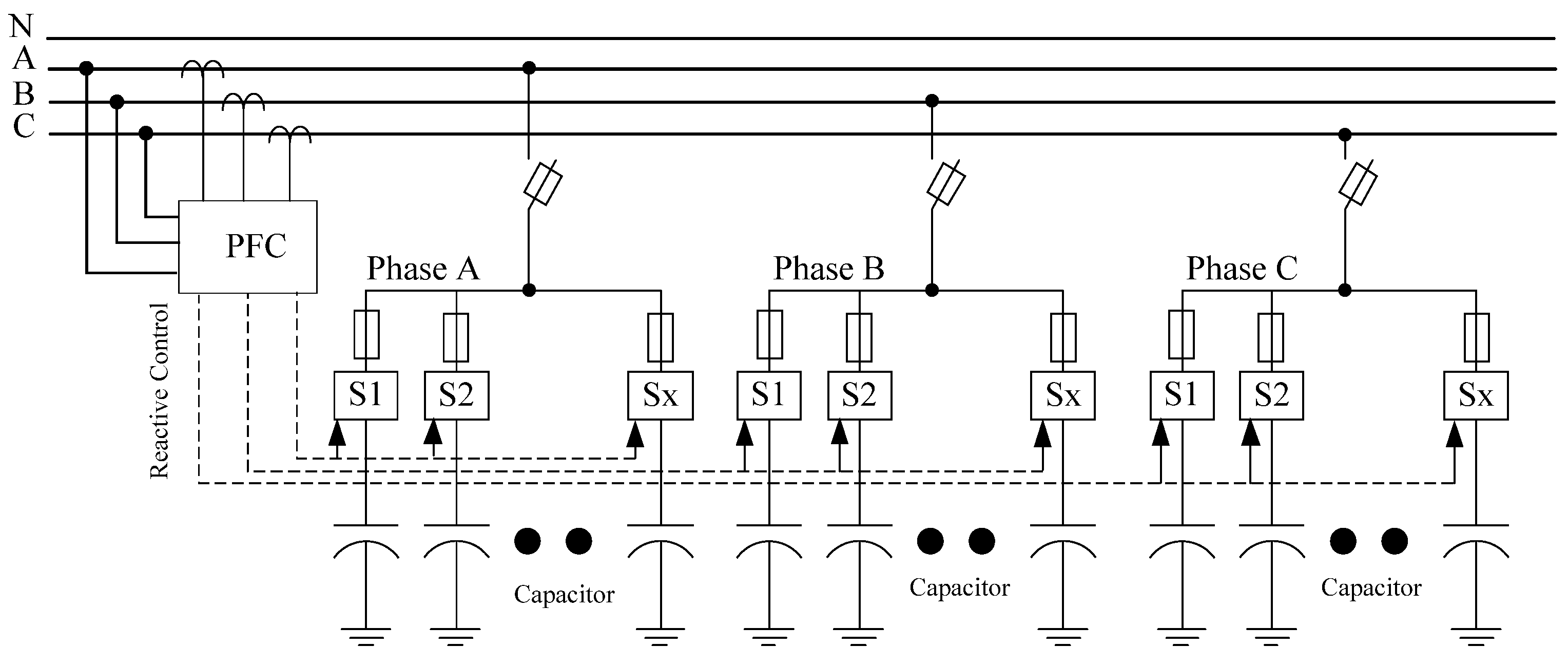
5.2. Unbalanced Control of Capacitor Steps
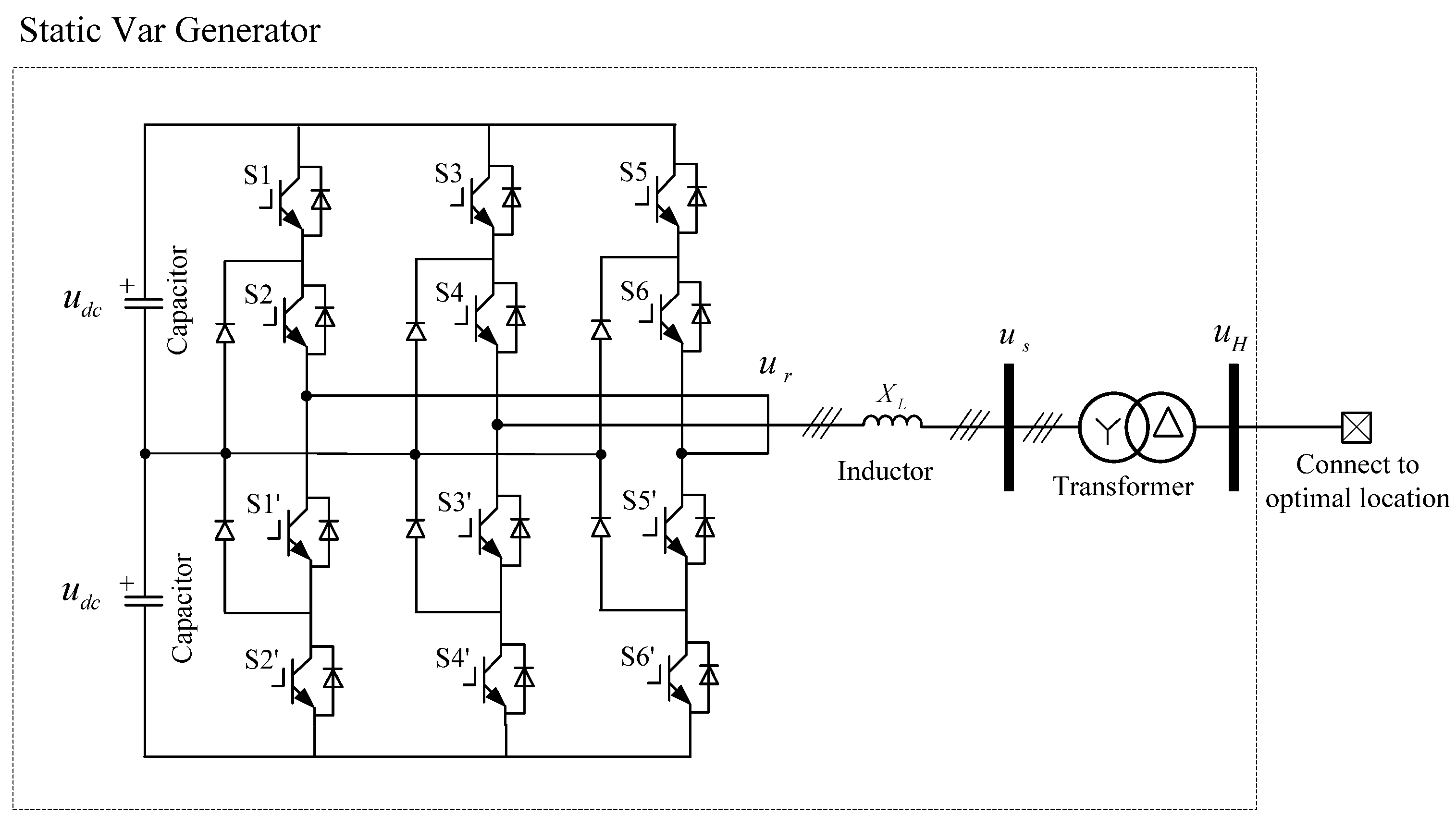
5.3. Static Var Generator (SVG)
5.4. Photovoltaic System Modeling
5.5. Fast-Charging Station for Electric Vehicles (FCS-EV)
5.6. Improved Gray Wolf Optimization
| Algorithm 1 Improved Gray Wolf Optimization | |
| Input: f(x), N, dim, Iteration, LB, UB | |
| Output: nvar, Fbest | |
| 1: | Begin |
| 2: | Initializing (Randomly N wolves in program and calculated of fitness function) |
| 3: | For iter = 2 to Iteration |
| 4: | |
| 5: | For i = 1 to N |
| 6: | , , |
| 7: | by using Equation (39) |
| 8: | by using Equation (41) |
| 9: | with radius |
| 10: | For d = 1 to dim |
| 11: | by using Equation (42) |
| 12: | End for |
| 13: | , ) |
| 14: | Updating population |
| 15: | End for |
| 16: | End for |
| 17: | Return nvar, Fbest |
| 18: | End |
6. Methodology
6.1. Hybrid Objective Function for Optimization Techniques
6.2. Inequality Constraint and Limits
6.2.1. The Voltage Magnitude at the Bus Must Remain Within Permissible Limits
6.2.2. Load Line Limit
6.2.3. FCS-EV and Capacitors
6.2.4. The Power Balance of the Grid Is Considered Relative to the Load Power Demand, the Power Demand of FCS-EV, and the Active Power Output of PV. It Is Described Using Equations (50) and (51)
6.2.5. Power Factor (PF) Constraints: The PF of DG Must Remain Within Its Operational Limits as Follows
6.2.6. Renewable Power Output Constraints: The Power Generated by PV Systems Must Re-Spect Resource Availability, Which Is Described as Follows
6.3. Simulation Parameters
6.4. Modified IEEE 123-Bus Testing System
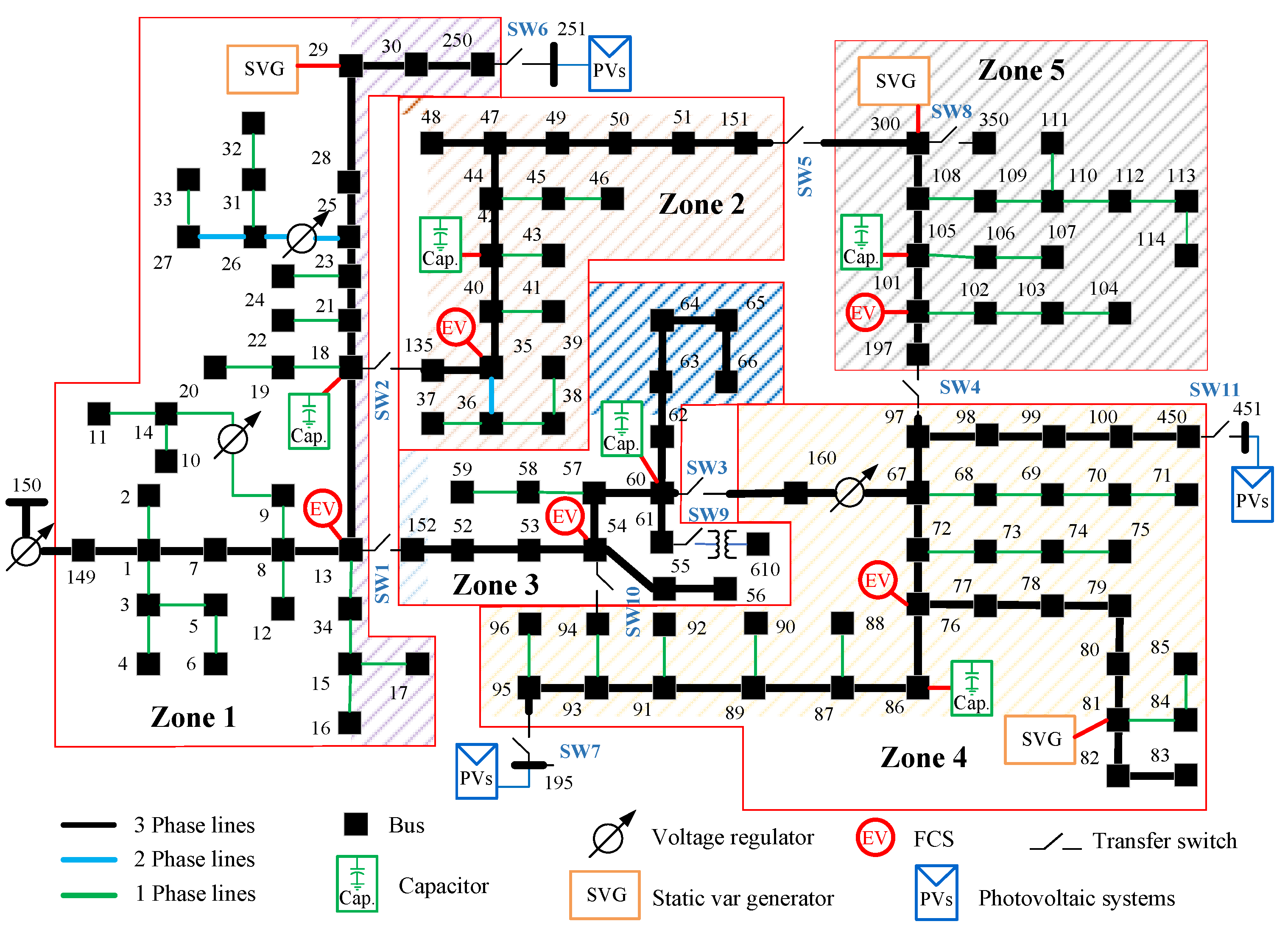
- Many researchers modified the IEEE 123-bus system by dividing the system into zones to solve issues [45,46,47]. Therefore, this research study was defined in accordance with an analysis zone named the All-Zone (AZ) (as shown in Figure 6), which was further divided into 5 zones (Zs) (as shown in Table 3).
- Previous research focuses on the reactive power compensation using capacitors that are balanced [15,48,49]. Thus, this scenario defined the balanced-phase capacitors with initial values set to 15 to 300 kVar (balanced static var generator, BSVG) using 6-step configurations: 75, 150, 225, 300, and 450 kVar (balanced step capacitor, BSC). The capacitor’s sizing steps (25, 50, and 75 kVar) were selected based on the commonly available standard ratings of practical distribution systems. This ensures that the optimization results are more applicable in the real world.
- Unbalanced-phase capacitors were set to 5 to 100 kVar per phase (unbalanced static var generator for reactive compensation, USVG) with 6-step configurations: 25, 50, 75, 100, 125, and 150 kVar (unbalanced step capacitor, USC).
- FCS-EV (EV) power levels were set at 22, 50, 125, 200, and 300 kW. Each FCS-EV installation is unique and not repeated, with different power capacities allocated to distinct zones based on spatial availability and operational requirements.
- PV locations were assigned to buses 195, 251, and 451 with the following configurations: single-phase PV (PV1P): 30 to 500 kVA with PF = 0.85; and three-phase PV (PV3P) at 100–1500 kVA with PF = 0.85.
- Capacitors, EV, and PV were only installed on three-phase buses, with the condition that each can only occupy one bus.
- The automatic voltage regulators (AVRs) for all transformers were uncontrolled relative to tap adjustments, and existing capacitors were disconnected from the system.
6.5. Definition of the Case Study
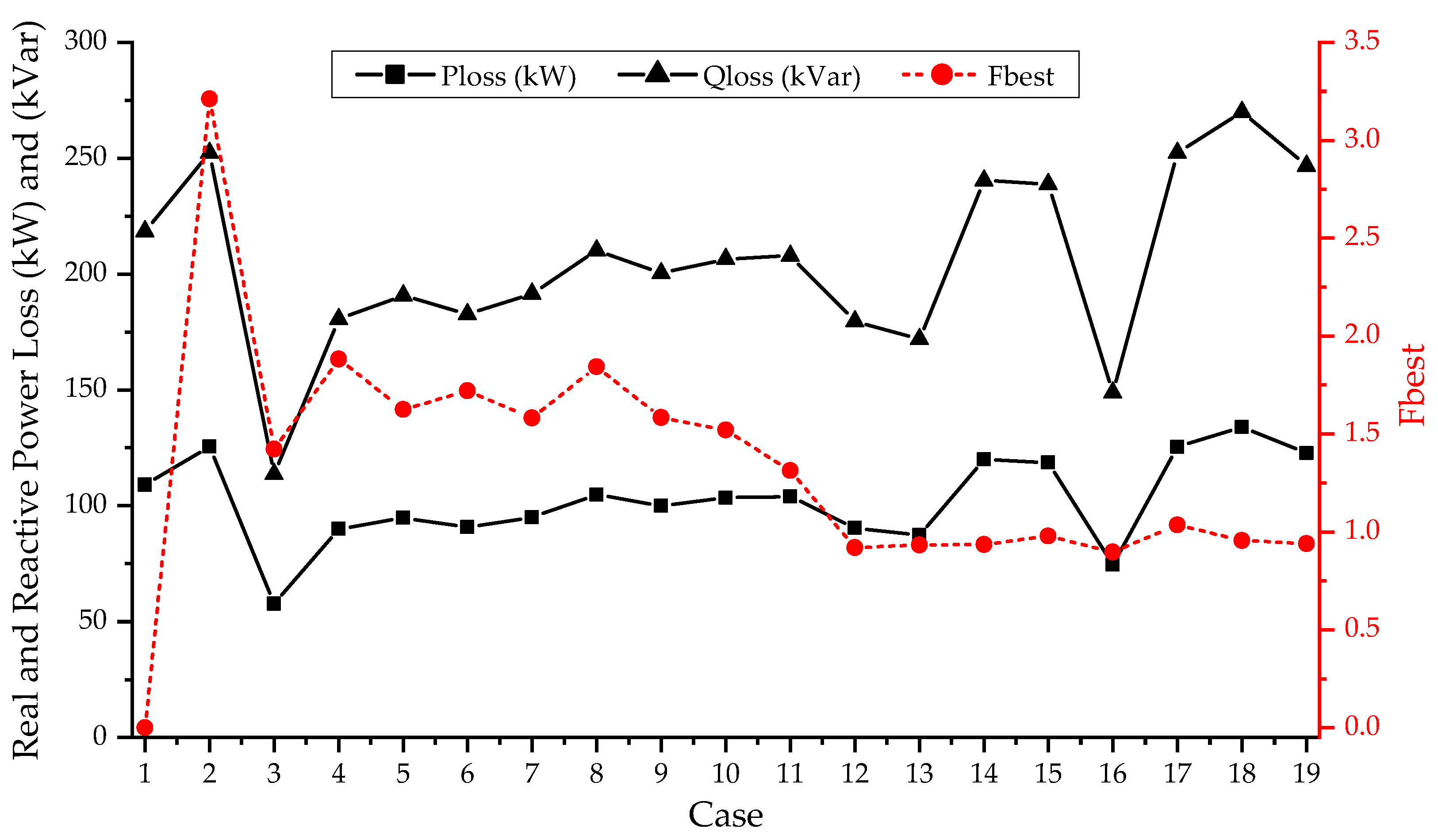
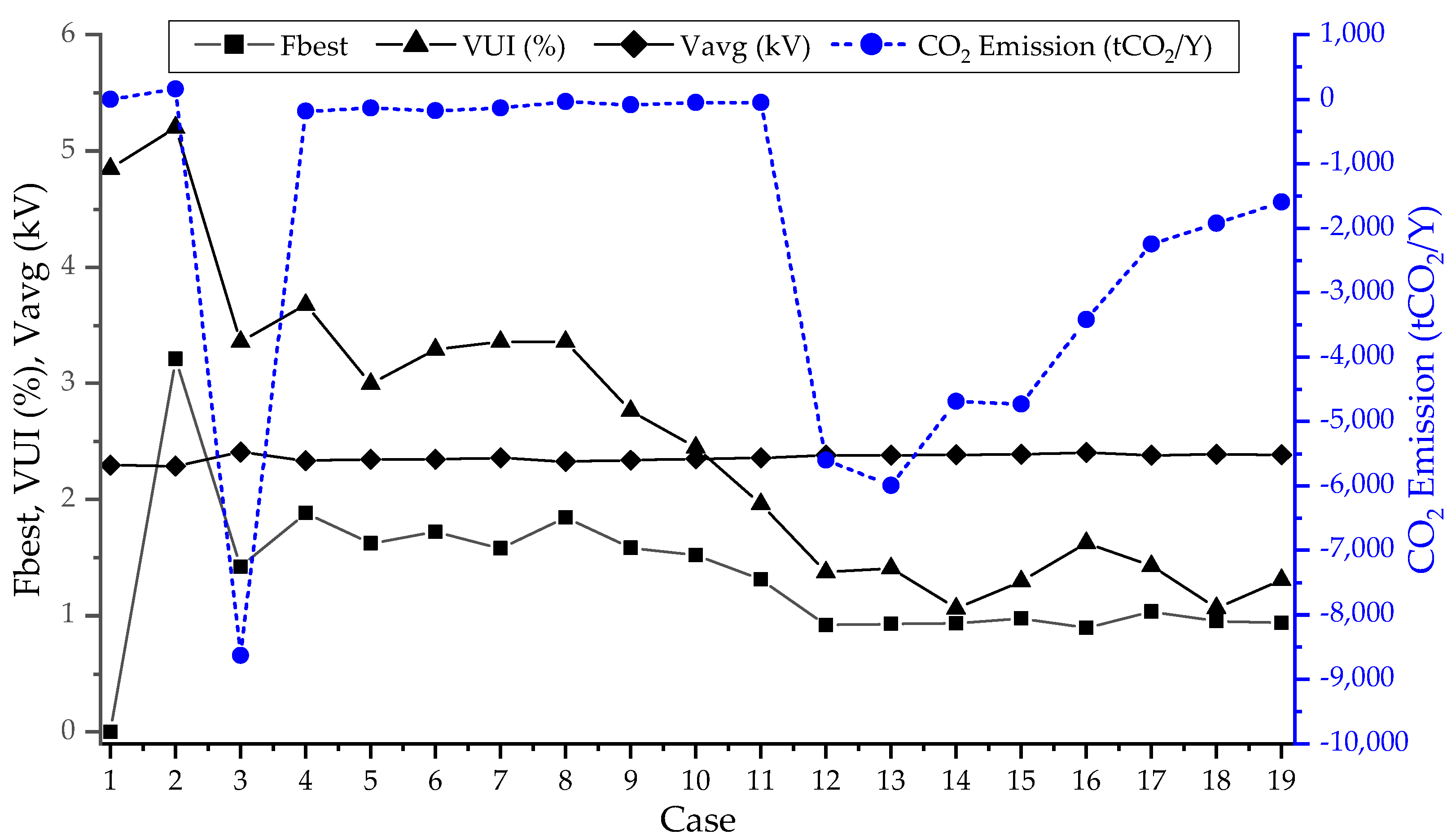
7. Simulation Results and Discussion
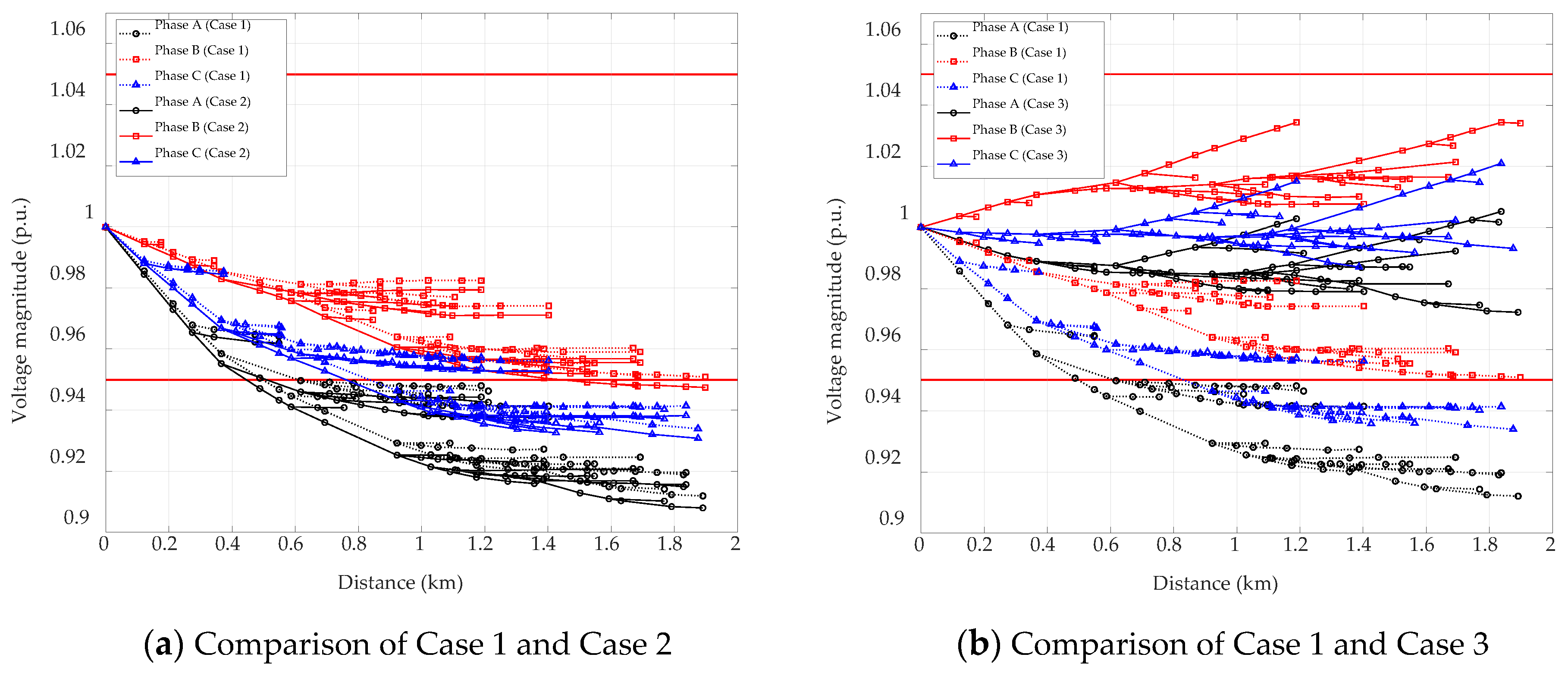
7.1. Simulation Model 1 (Case 1 to Case 3)
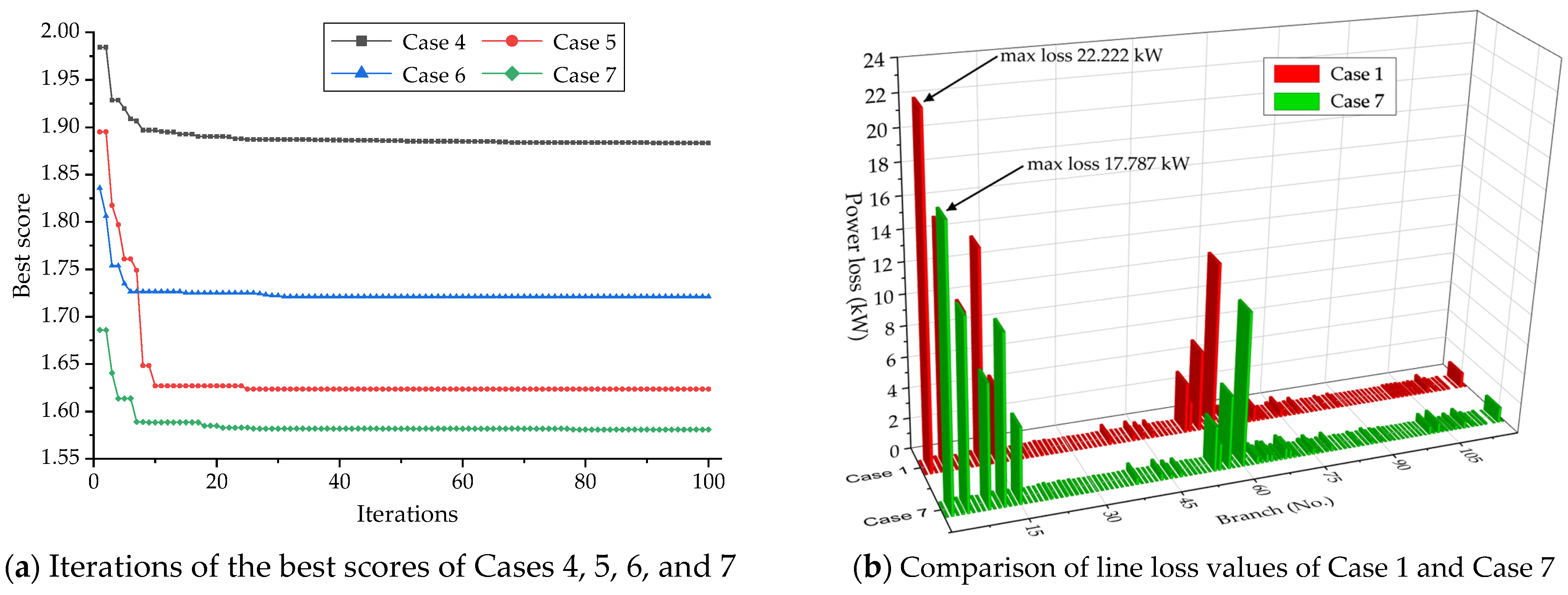
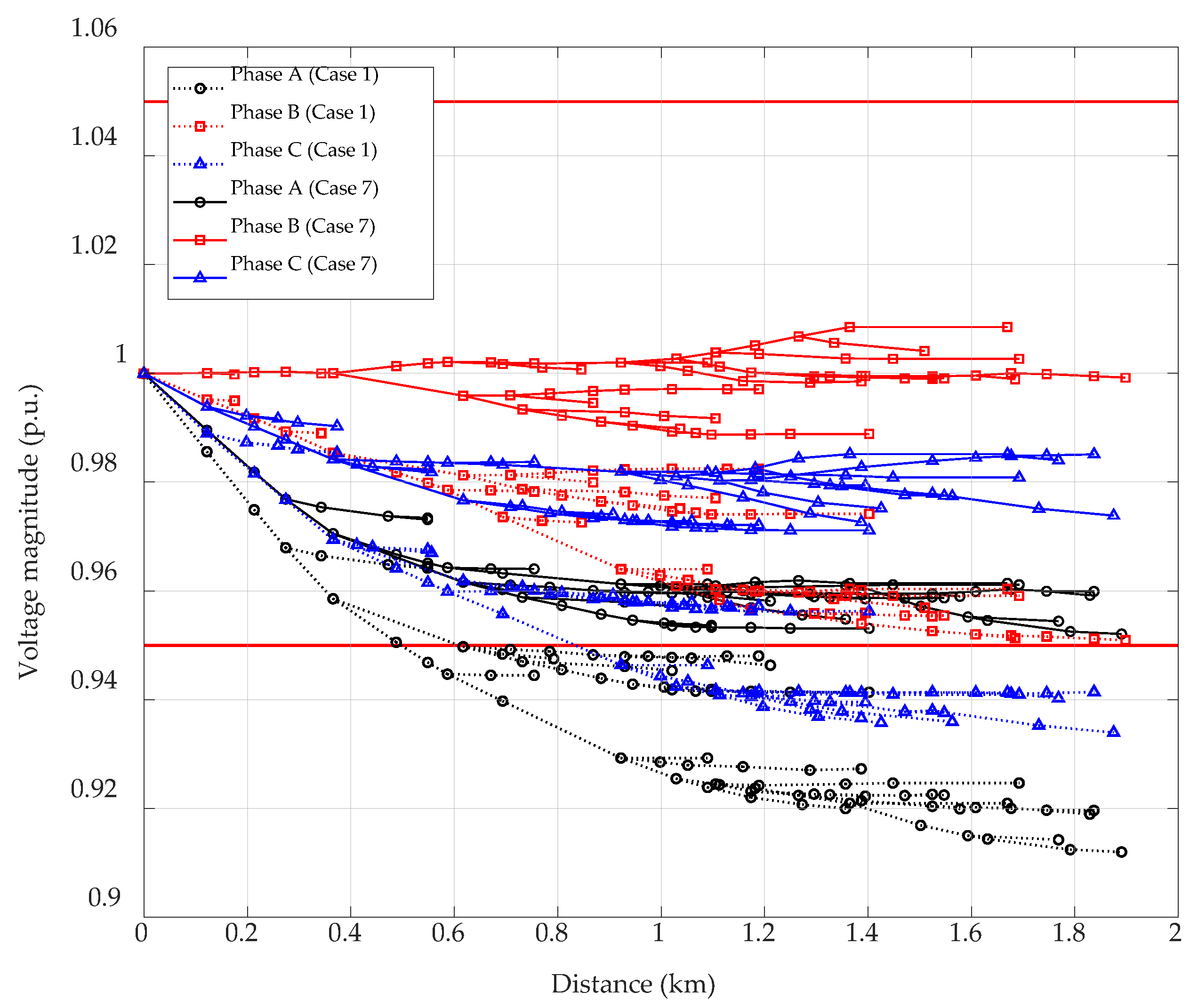
7.2. Simulation Model 2 (Case 4 to Case 7)
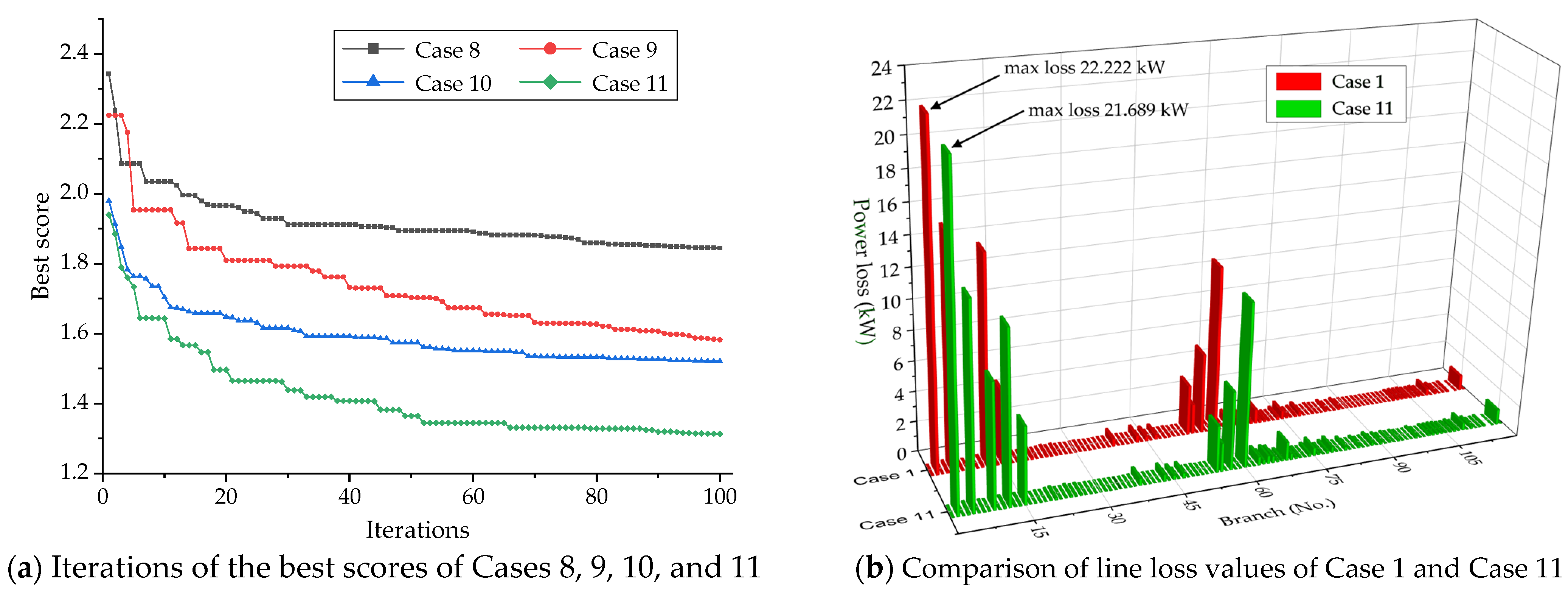
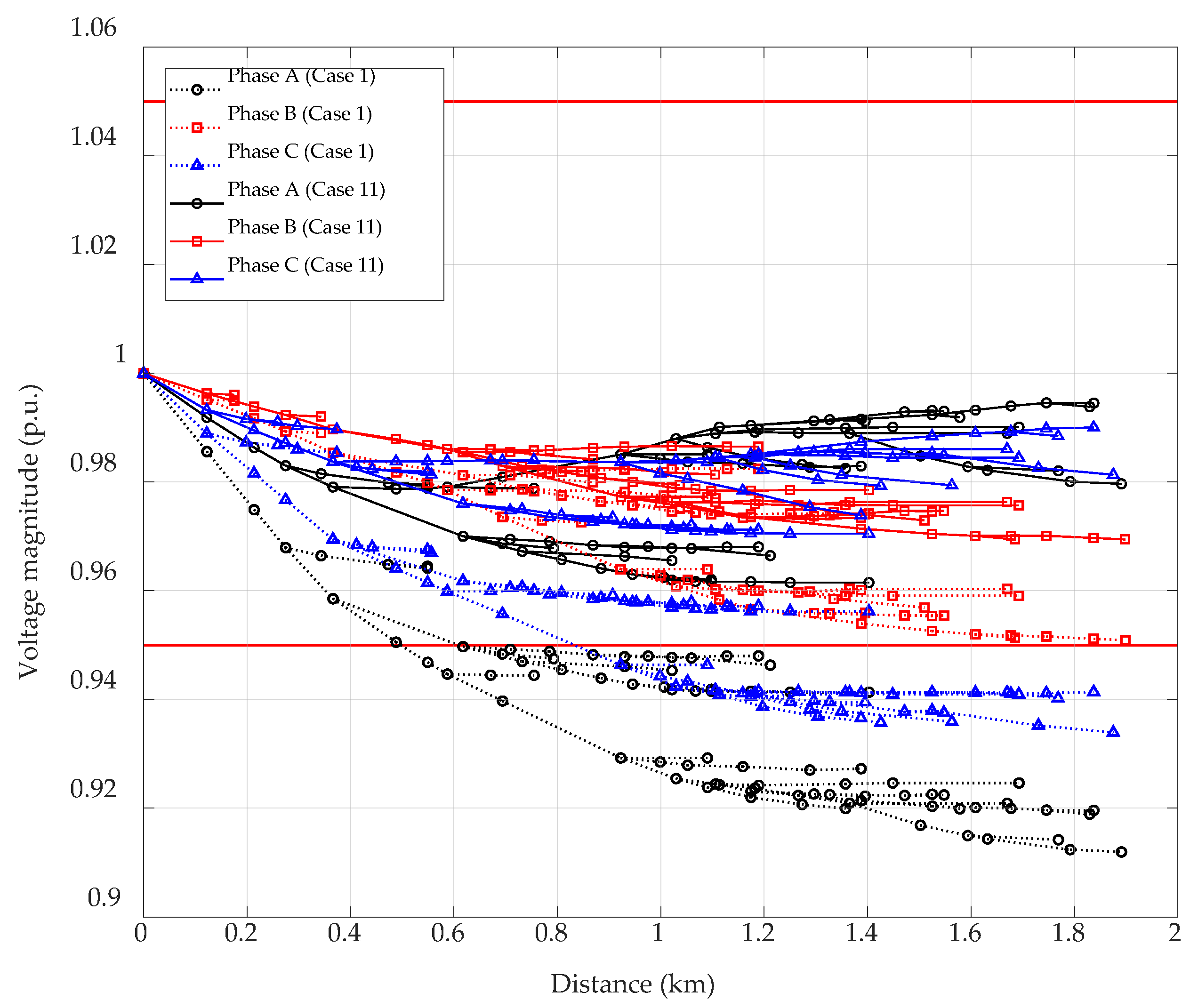
7.3. Simulation Model 3 (Case 8 to Case 11)
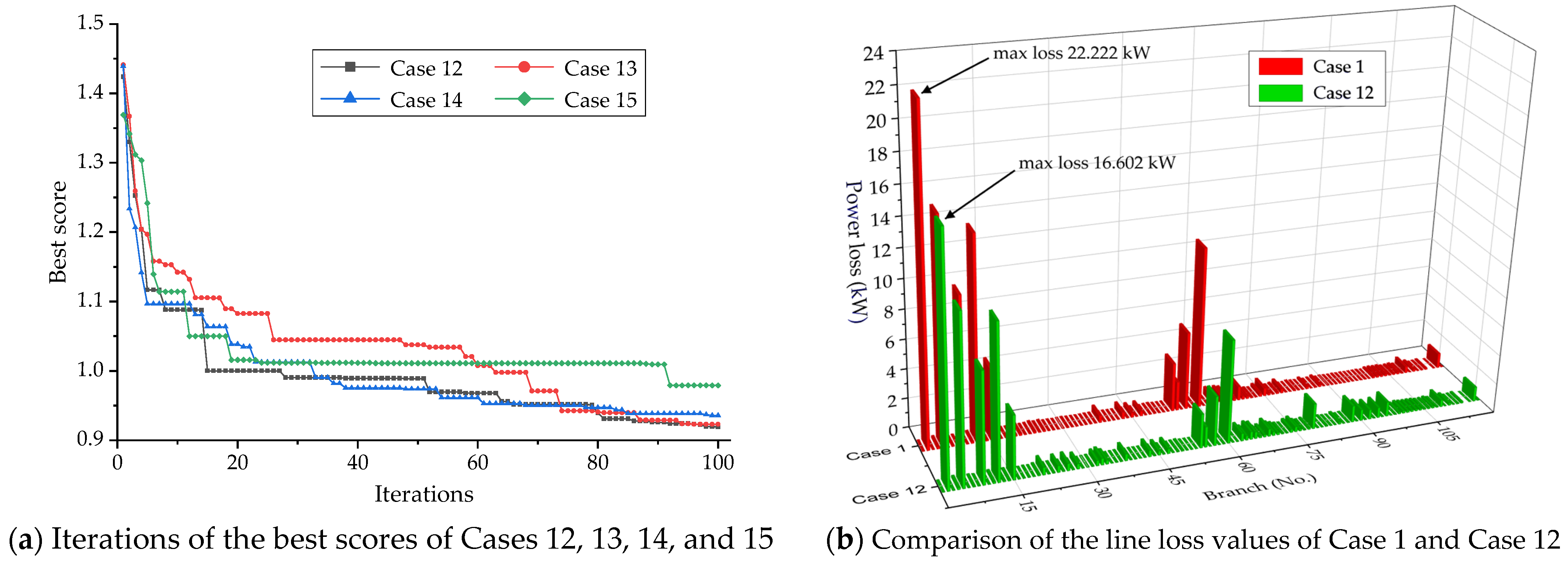
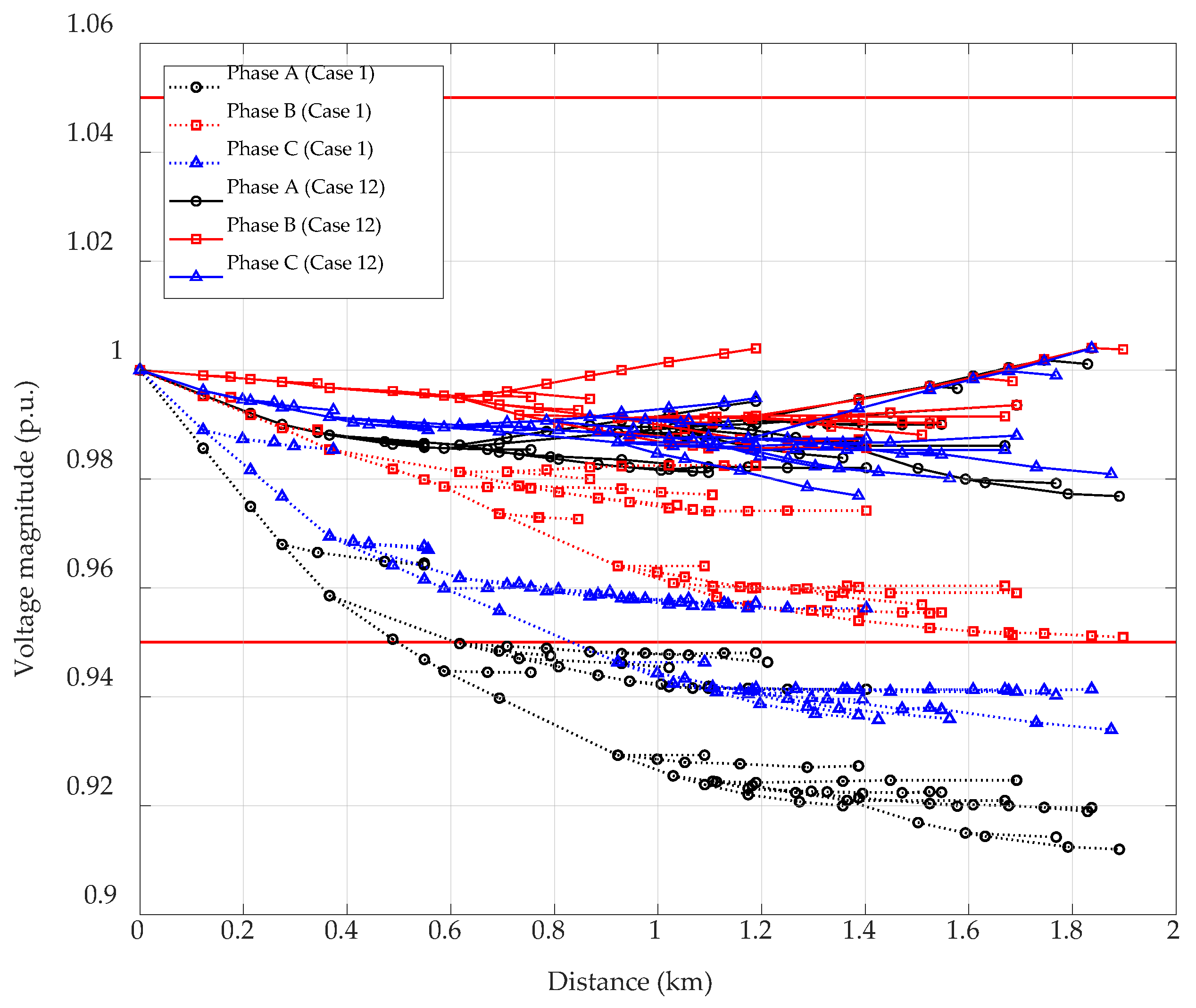
7.4. Simulation 4 Model 4 (Case 12 to Case 15)
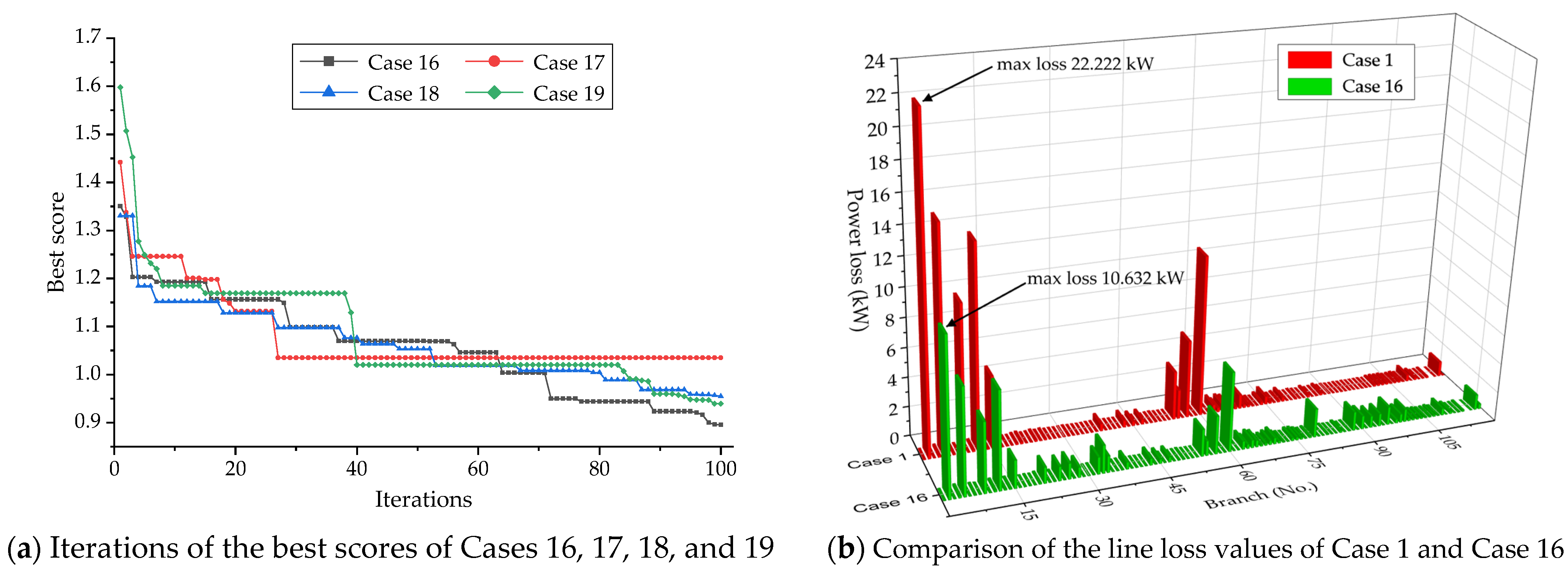
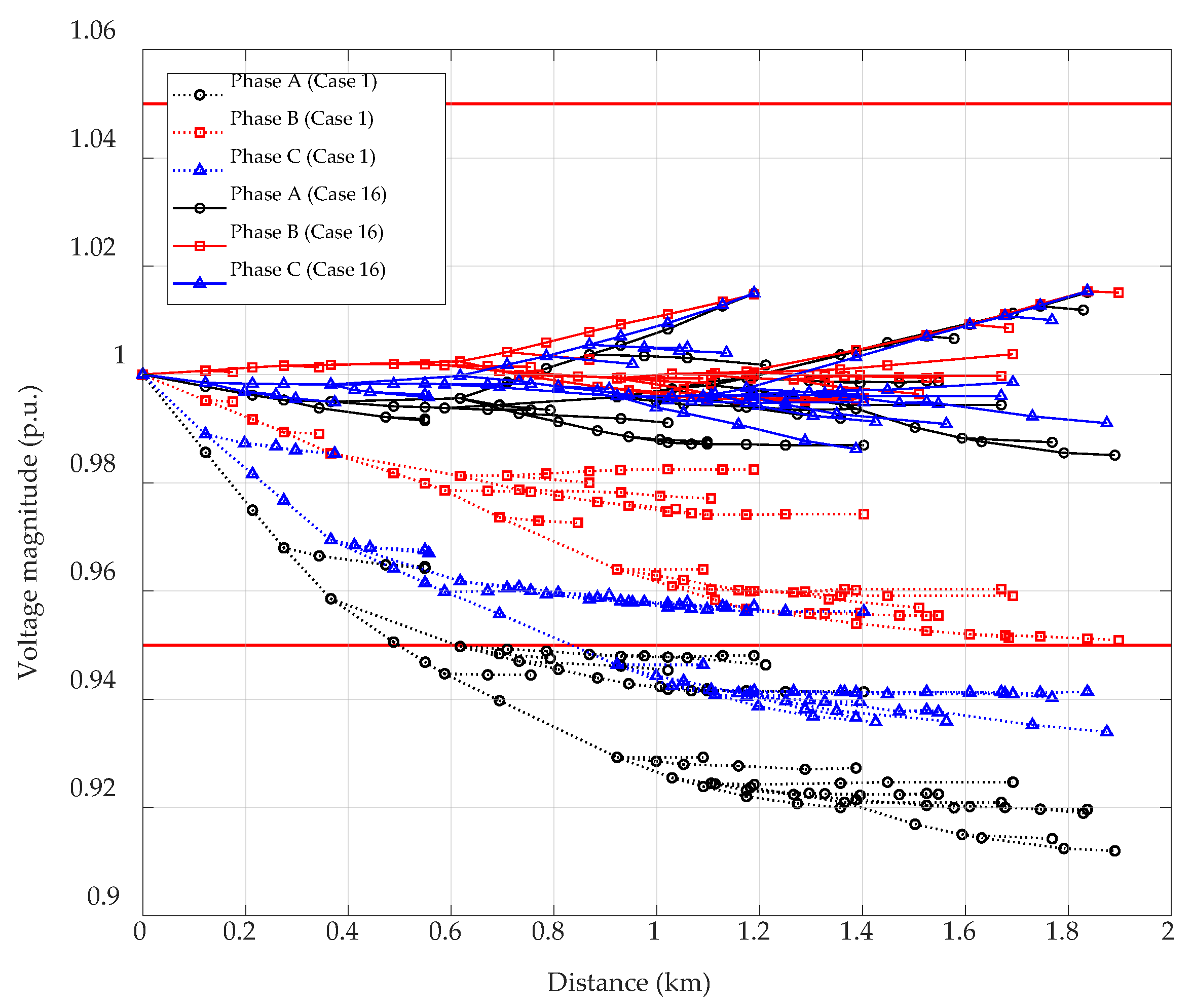
7.5. Simulation 5 Model 5 (Case 16 to Case 19)
7.6. Comparison of Economic Analysis Results
7.7. Discussion of Simulations
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CO2 | Carbon dioxide |
| IEA | International Energy Agency |
| DG | Distribution generator |
| FCS | Fast-charging stations |
| EVs | Electric vehicles |
| Active power | |
| Reactive power | |
| Buses | |
| A | |
| Rea | |
| Reactive power of capacitors at bus | |
| PV | Photovoltaic |
| SVG | Static var generator |
| IPSO | Improved particle swarm optimization |
| PSO | Particle swarm optimization |
| IGWO | Improved gray wolf optimization |
| Commutative voltage deviation | |
| Voltage unbalance index | |
| Unbalanced power flow | |
| Complex power at bus | |
| Active power at bus | |
| Reactive power at bus | |
| Voltage at bus | |
| The admittance matrix element between phase of bus and phase of bus | |
| Number of buses in the system | |
| Conductance of the admittance matrix | |
| Susceptance of the admittance matrix | |
| Real power is delivered to bus | |
| Reactive power is delivered to bus | |
| Load active power at bus in phase | |
| Reactive power at bus in phase | |
| Buses | |
| Current in phase of the line between buses and | |
| Resistance of phase lines | |
| Reactance of phase lines | |
| Admittance matrix | |
| Total real power loss | |
| Total reactive power loss | |
| Voltage reference | |
| Voltage bus | |
| Min control voltage range | |
| Max control voltage range | |
| Voltage average | |
| EPI | Environmental performance indices |
| Time of the peak sun | |
| Time of the capacitor’s operation | |
| Emission factor of the Thailand voluntary emission reduction program (T-VER) | |
| Reduced power loss | |
| Reactive power of phase A | |
| Reactive power of phase B | |
| Reactive power of phase C | |
| Set 1 | |
| Set 2 | |
| Set x | |
| Reactive power of capacitor set 1 of phases | |
| Reactive power of capacitor set 2 of phases | |
| Reactive power of capacitor set x of phases | |
| Connection inductor | |
| Output voltage magnitude of the SVG | |
| Voltage magnitude at a common connection point | |
| Real power of SVG | |
| Reactive power of SVG | |
| Power angle | |
| Inductive resistance value | |
| DERs | Distributed energy resources |
| Active power generated by the PV system | |
| Solar irradiance | |
| Total area of PV panels | |
| Overall efficiency of the PV system | |
| Module efficiency at standard test conditions | |
| Temperature coefficient of power | |
| Cell temperature | |
| Standard test condition temperature | |
| Ambient temperature | |
| Reference irradiance | |
| Nominal operating cell temperature | |
| PCC | The point of common coupling |
| Reactive power generated by the PV system | |
| Apparent power capacity of the PV system | |
| Power factor | |
| FCS-EV | Fast-charging-station electric vehicle |
| AC | Alternating current |
| DC | Direct current |
| Active power consumed by FCS-EVs at bus | |
| Size of FCS | |
| Reactive power consumed by FCS-EVs at bus | |
| GWO | Gray wolf optimizer |
| N | Number of search agents |
| Number of variables | |
| LB | Lower bound |
| UB | Upper bound |
| AVRs | Automatic voltage regulators |
| AZ | All-zone |
| Z | Zone |
| BC | Base case |
| BSVG | Balanced static var generator |
| BSC | Balanced step capacitor |
| USVG | Unbalanced static var generator |
| USC | Unbalanced step capacitor |
| PV3P | Three-phase photovoltaic |
| PV1P | Single-phase photovoltaic |
| Global best | |
| Active power loss of system | |
| Reactive power loss of system |
References
- IEA. Electricity Market Report 2023; IEA: Paris, France, 2023. [Google Scholar]
- Rezapour, H.; Fathnia, F.; Fiuzy, M.; Falaghi, H.; Lopes, A.M. Enhancing power quality and loss optimization in distorted distribution networks utilizing capacitors and active power filters: A simultaneous approach. Int. J. Electr. Power Energy Syst. 2024, 155, 109590. [Google Scholar] [CrossRef]
- Poshtyafteh, M.; Barati, H.; Falehi, A.D. Optimal placement of distribution network-connected microgrids on multi-objective energy management with uncertainty using the modified Harris Hawk optimization algorithm. IET Gener. Transm. Distrib. 2024, 18, 809–833. [Google Scholar] [CrossRef]
- Pamuk, N.; Uzun, U.E. Optimal Allocation of Distributed Generations and Capacitor Banks in Distribution Systems Using Arithmetic Optimization Algorithm. Appl. Sci. 2024, 14, 831. [Google Scholar] [CrossRef]
- Mohanad Muneer, Y.; Ali Nasser, H.; Wathiq Rafa, A.; Daniel Augusto, P. Power Loss Reduction and Reliability Improvement of Radial Distribution Systems Using Optimal Capacitor Placement Technique. J. Technol. 2024, 6, 1–9. [Google Scholar] [CrossRef]
- Lanjewar, S.F.; Jain, S. Power System Sustainability Enhancement Through Capacitor Placement. Process Integr. Optim. Sustain. 2024, 8, 631–654. [Google Scholar] [CrossRef]
- Elseify, M.A.; Hashim, F.A.; Hussien, A.G.; Kamel, S. Single and multi-objectives based on an improved golden jackal optimization algorithm for simultaneous integration of multiple capacitors and multi-type DGs in distribution systems. Appl. Energy 2024, 353, 122054. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, S.; Luo, W.; Wu, L. Intrusion-Detector-Dependent Distributed Economic Model Predictive Control for Load Frequency Regulation With PEVs Under Cyber Attacks. IEEE Trans. Circuits Syst. I. Regul. Pap. 2021, 68, 3857–3868. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, S.; Wu, L. Credibility-based distributed frequency estimation for plug-in electric vehicles participating in load frequency control. Int. J. Electr. Power Energy Syst. 2021, 130, 106997. [Google Scholar] [CrossRef]
- Ayub, M.A.; Hussan, U.; Rasheed, H.; Liu, Y.; Peng, J. Optimal energy management of MG for cost-effective operations and battery scheduling using BWO. Energy Rep. 2024, 12, 294–304. [Google Scholar] [CrossRef]
- Hu, Z.; Su, R.; Zhang, K.; Xu, Z.; Ma, R. Resilient Event-Triggered Model Predictive Control for Adaptive Cruise Control Under Sensor Attacks. IEEE/CAA J. Autom. Sin. 2023, 10, 807–809. [Google Scholar] [CrossRef]
- Hu, Z.; Su, R.; Veerasamy, V.; Huang, L.; Ma, R. Resilient Frequency Regulation for Microgrids Under Phasor Measurement Unit Faults and Communication Intermittency. IEEE Trans. Ind. Inform. 2025, 21, 1941–1949. [Google Scholar] [CrossRef]
- IEEE 18-2012; IEEE Standard for Shunt Power Capacitors. IEEE: Piscataway, NJ, USA, 2013. [CrossRef]
- Chitgreeyan, N.; Pilalum, P.; Kongjeen, Y.; Kongnok, R.; Buayai, K.; Kerdchuen, K. Modified MATPOWER for Multi-Period Power Flow Analysis with PV Integration. GMSARN Int. J. 2025, 19, 165–174. [Google Scholar]
- Falaghi, H.; Ramezani, M.; Elyasi, H.; Farhadi, M.; Estebsari, A. Risk-Based Capacitor Placement in Distribution Networks. Electronics 2022, 11, 3145. [Google Scholar] [CrossRef]
- Zanganeh, M.; Moghaddam, M.S.; Azarfar, A.; Vahedi, M.; Salehi, N. Multi-area distribution grids optimization using D-FACTS devices by M-PSO algorithm. Energy Rep. 2023, 9, 133–147. [Google Scholar] [CrossRef]
- Parvaneh, M.H.; Moradi, M.H.; Azimi, S.M. The advantages of capacitor bank placement and demand response program execution on the optimal operation of isolated microgrids. Electr. Power Syst. Res. 2023, 220, 109345. [Google Scholar] [CrossRef]
- Mohamed El-Saeed, M.A.E.; Abdel-Gwaad, A.F.; Farahat, M.A. Solving the capacitor placement problem in radial distribution networks. Results Eng. 2023, 17, 100870. [Google Scholar] [CrossRef]
- Masood, N.A.; Jawad, A.; Ahmed, K.T.; Islam, S.R.; Islam, M.A. Optimal capacitor placement in northern region of Bangladesh transmission network for voltage profile improvement. Energy Rep. 2023, 9, 1896–1909. [Google Scholar] [CrossRef]
- Jones, E.S.; Jewell, N.; Liao, Y.; Ionel, D.M. Optimal Capacitor Placement and Rating for Large-Scale Utility Power Distribution Systems Employing Load-Tap-Changing Transformer Control. IEEE Access 2023, 11, 19324–19338. [Google Scholar] [CrossRef]
- Peprah, F.; Gyamfi, S.; Effah-Donyina, E.; Amo-Boateng, M. Evaluation of reactive power support in solar PV prosumer grid. E-Prime—Adv. Electr. Eng. Electron. Energy 2022, 2, 100057. [Google Scholar] [CrossRef]
- Mouwafi, M.T.; El-Sehiemy, R.A.; El-Ela, A.A.A. A two-stage method for optimal placement of distributed generation units and capacitors in distribution systems. Appl. Energy 2022, 307, 118188. [Google Scholar] [CrossRef]
- Jayabarathi, T.; Raghunathan, T.; Sanjay, R.; Jha, A.; Mirjalili, S.; Cherukuri, S.H.C. Hybrid Grey Wolf Optimizer Based Optimal Capacitor Placement in Radial Distribution Systems. Electr. Power Compon. Syst. 2022, 50, 413–425. [Google Scholar] [CrossRef]
- Gupta, S.; Yadav, V.K.; Singh, M. Optimal Allocation of Capacitors in Radial Distribution Networks Using Shannon’s Entropy. IEEE Trans. Power Deliv. 2022, 37, 2245–2255. [Google Scholar] [CrossRef]
- Gallego, L.A.; López-Lezama, J.M.; Carmona, O.G. A Mixed-Integer Linear Programming Model for Simultaneous Optimal Reconfiguration and Optimal Placement of Capacitor Banks in Distribution Networks. IEEE Access 2022, 10, 52655–52673. [Google Scholar] [CrossRef]
- Nguyen, T.P.; Nguyen, T.A.; Phan, T.V.-H.; Vo, D.N. A comprehensive analysis for multi-objective distributed generations and capacitor banks placement in radial distribution networks using hybrid neural network algorithm. Knowl.-Based Syst. 2021, 231, 107387. [Google Scholar] [CrossRef]
- Mtonga, T.P.M.; Kaberere, K.K.; Irungu, G.K. Optimal Shunt Capacitors’ Placement and Sizing in Radial Distribution Systems Using Multiverse Optimizer. IEEE Can. J. Electr. Comput. Eng. 2021, 44, 10–21. [Google Scholar] [CrossRef]
- Martins, A.S.C.; Costa, F.R.M.d.S.; de Araujo, L.R.; Penido, D.R.R. Capacitor Allocation in Unbalanced Systems Using a Three-Level Optimization Framework. IEEE Lat. Am. Trans. 2021, 19, 1599–1607. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, H.; Zhao, Q.; Nan, D.; Li, W. Research and Application of Combined Reactive Power Compensation Device Based on SVG+SC in Wind Power Gathering Area. Appl. Sci. 2022, 12, 10906. [Google Scholar] [CrossRef]
- Tian, S.; Jia, Q.; Xue, S.; Yu, H.; Qu, Z.; Gu, T. Collaborative optimization allocation of VDAPFs and SVGs for simultaneous mitigation of voltage harmonic and deviation in distribution networks. Int. J. Electr. Power Energy Syst. 2020, 120, 106034. [Google Scholar] [CrossRef]
- Mehmood, A.; Yang, F.; Dong, J.; Luo, Z.; Yi, L.; Wu, T. Modeling and Load Flow Analysis for Three phase Unbalanced Distribution System. In Proceedings of the 2021 4th International Conference on Energy, Electrical and Power Engineering (CEEPE), Chongqing, China, 23–25 April 2021; pp. 44–48. [Google Scholar]
- Yu, Y.; Jin, Z.-x.; Li, J.-z.; Jia, L. Research on the Impact of Carbon Tax on CO2 Emissions of China’s Power Industry. J. Chem. 2020, 2020, 3182928. [Google Scholar] [CrossRef]
- Xu, W. Grid-connected inductor design of static var generator for photovoltaic system. J. Phys. Conf. Ser. 2023, 2450, 012008. [Google Scholar] [CrossRef]
- Ai, Y.; Du, M.; Pan, Z.; Li, G. The optimization of reactive power for distribution network with PV generation based on NSGA-III. CPSS Trans. Power Electron. Appl. 2021, 6, 193–200. [Google Scholar] [CrossRef]
- Chitgreeyan, N.; Kongjeen, Y.; Buayai, K.; Kerdchuen, K. Impact of Voltage Unbalance System on Modern Microgrid System under High Penetration of Fast Charging Station. GMSARN Int. J. 2021, 15, 353–359. [Google Scholar]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert. Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- PES Distribution System Analysis Subcommittee. feeder123.zip. IEEE Power & Energy Society. 2017. Available online: https://cmte.ieee.org/pes-testfeeders/wp-content/uploads/sites/167/2017/08/feeder123.zip (accessed on 21 June 2025).
- IEEE 1036-2010; IEEE Guide for the Application of Shunt Power Capacitors. IEEE: Piscataway, NJ, USA, 2011. [CrossRef]
- IEEE 1547-2018; IEEE Standard for Interconnection and Interoperability of Distributed Energy Resources with Associated Electric Power Systems Interfaces. IEEE: Piscataway, NJ, USA, 2018. [CrossRef]
- Dugan, R.C.; Montenegro, D. The Open Distribution System Simulator (OpenDSS) Reference Guide; EPRI: Palo Alto, CA, USA, 2020. [Google Scholar]
- Kongjeen, Y.; Bhumkittipich, K.; Mithulananthan, N. Optimal DG Sizing and Location in Modern Power Grids using PEVs Load Demand Probability. ECTI Trans. Electr. Eng. Electron. Commun. 2019, 17, 51–59. [Google Scholar] [CrossRef]
- Baek, S.; Lim, B.; Han, C.; Yoo, Y. A Study on Real-Time OLTC Control in PV-Integrated Distribution Systems Using Machine Learning. In Proceedings of the 2025 IEEE International Conference on Consumer Electronics (ICCE), Osaka, Japan, 11–14 January 2025; pp. 1–6. [Google Scholar]
- Alshehri, M.; Yang, J.; Lou, C.; Min, L. Optimal Operation in Active Distribution Networks Using Soft Open Point Integrated with Energy Storage. In Proceedings of the 2025 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 10–11 February 2025; pp. 1–6. [Google Scholar]
- Pandey, S.; Sasane, S.; Paul, S. Data-Driven Power Flow Solutions for Distribution Networks with Solar Energy Resources. In Proceedings of the 2025 3rd IEEE International Conference on Industrial Electronics: Developments & Applications (ICIDeA), Bhubaneswar, India, 21–22 February 2025; pp. 1–6. [Google Scholar]
- Xiao, M.; Wang, S.; Ullah, Z.; Li, Y.; Arghandeh, R. Topology detection in power distribution system using kernel-node-map deep networks. IET Gener. Transm. Distrib. 2020, 14, 4033–4041. [Google Scholar] [CrossRef]
- Li, P.; Wu, Z.; Meng, K.; Chen, G.; Dong, Z.Y. Decentralized Optimal Reactive Power Dispatch of Optimally Partitioned Distribution Networks. IEEE Access 2018, 6, 74051–74060. [Google Scholar] [CrossRef]
- Arce Polanco, L.; Osman, I.; Ren, B.; Zhong, Q.-C.; Bayne, S. Large-Scale Adoption of Self-Synchronized Universal Droop Controller-Based Inverters to Enable Ancillary Services for Different Modes of Distribution System Operations. In Proceedings of the 2020 5th IEEE Workshop on the Electronic Grid (eGRID), Aachen, Germany, 2–4 November 2020; pp. 1–6. [Google Scholar]
- Jahromi, M.H.M.; Dehghanian, P.; Khademi, M.R.M.; Jahromi, M.Z. Reactive Power Compensation and Power Loss Reduction using Optimal Capacitor Placement. In Proceedings of the 2021 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 2–5 February 2021; pp. 1–6. [Google Scholar]
- Mondal, S.; De, M. Optimal Capacitor Placement for Unbalanced Distribution System using Graph Theory. IETE J. Res. 2023, 69, 6512–6519. [Google Scholar] [CrossRef]
- ZDDQ Electric. High Voltage Static Var Generator HV SVG STATCOM Outdoor Container. Available online: https://www.zddqelectric.com/high-voltage-static-var-generator-hv-svg-statcom-outdoor-container_p21.html. (accessed on 10 May 2025).
- Sanhe Electric. Medium Voltage Advanced Static Var Generator. Available online: https://www.sanhenergy.com/Medium-Voltage-Advanced-Static-Var-Generator-pd599741798.html (accessed on 10 May 2025).
- Northeast Power Systems, Inc. (NEPSI). Cost per kvar for Medium Voltage Capacitors. Available online: https://nepsi.com/resource/Cost%20per%20kvar.pdf (accessed on 10 May 2025).
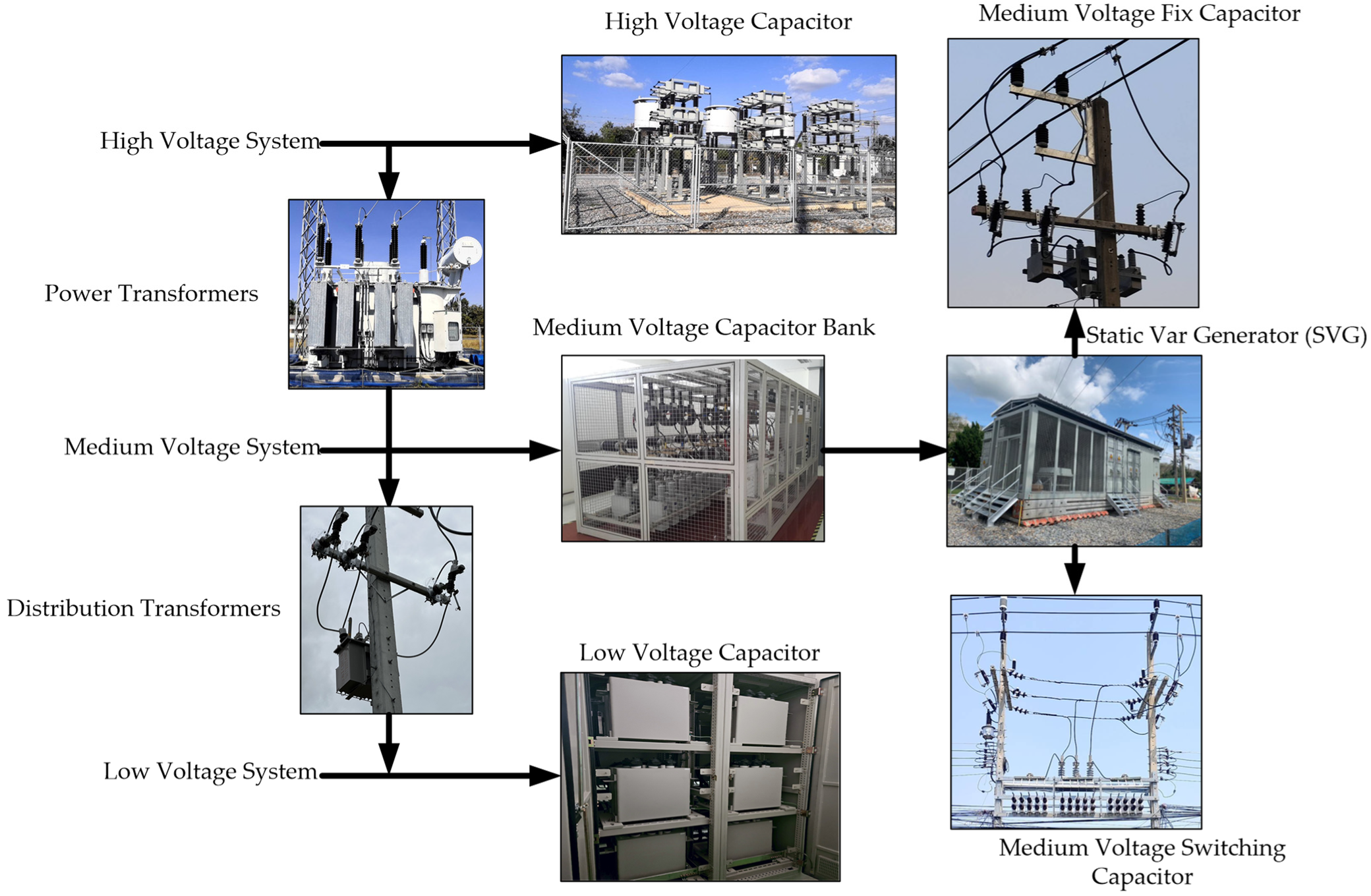



| Highlights and Brief Details | SVG | UC | RC | FC | CO | PS | VS | TL | VI | EL | AV | UF | SP | MP | CM | OB | OPT | PM | Ref. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Economic savings of USD 7000 per year | - | - | ✓ | ✓ | ✓ | - | - | ✓ | ✓ | ✓ | - | - | ✓ | - | CC | MO+MS | NSGA-II | BP | [15] |
| - | - | - | - | ✓ | ✓ | - | - | - | ✓ | ✓ | - | - | - | ✓ | HC | MO+MS | MPSO | BP | [16] |
| Reduces power losses from 86.6 kW to 32.1 kW; improved voltage from 0.967 to 0.987 p.u. | - | - | ✓ | - | - | - | - | - | ✓ | ✓ | - | - | - | ✓ | CC | MO+MS | HSA | BP | [17] |
| Reduces power losses by 32.37% (33-bus) and 31.10% (94-bus); economic savings from USD 23,612 to USD 23,131 (33-bus). | - | - | - | ✓ | ✓ | - | ✓ | - | - | - | - | - | ✓ | - | CC | MO+MS | NSGA-II | BP | [18] |
| Reduces power losses by 90 MVAR; improved voltage | - | - | ✓ | - | - | - | - | - | ✓ | ✓ | - | - | ✓ | - | CC | SO | MILP | BP | [19] |
| - | - | - | ✓ | - | - | - | - | - | ✓ | ✓ | ✓ | - | ✓ | - | CC | MO+MS | NSGA-III | BP | [20] |
| Reduces power losses from 76.52% to 34.04%; improved voltage from 0.97 to 0.98 p.u. | - | - | - | ✓ | - | ✓ | - | - | ✓ | ✓ | ✓ | ✓ | - | DC | MS | FBM | UP | [21] | |
| Improved average voltage from 0.9884 to 0.9925 p.u. | - | - | ✓ | - | - | - | ✓ | - | ✓ | ✓ | - | - | ✓ | - | DC | MS | CBA | BP | [22] |
| Reduces power losses from 158.57 to 157.53 kW | - | - | ✓ | - | ✓ | - | - | - | ✓ | ✓ | - | - | ✓ | - | DC | MS | HGWO | BP | [23] |
| - | - | - | ✓ | - | ✓ | - | - | - | ✓ | ✓ | - | - | ✓ | - | DC | MS | SE-IM+ PSO | BP | [24] |
| Improved voltage to 0.9729 p.u.; economic savings of USD 85,876 | - | - | ✓ | - | ✓ | - | - | - | ✓ | ✓ | - | - | ✓ | - | DC | MS | MILP | BP | [25] |
| - | - | - | ✓ | - | ✓ | - | ✓ | - | ✓ | ✓ | - | - | ✓ | - | DC | MO | SOS-NNA | BP | [26] |
| Reduces power losses to 224.89 kW; normalized bus voltages to 0.95 | - | - | ✓ | - | ✓ | - | - | - | - | ✓ | - | - | ✓ | - | DC | MS | MVA | BP | [27] |
| - | - | - | - | - | - | - | - | - | ✓ | - | - | - | ✓ | DC | MS | GA | UP | [28] | |
| Improved voltage to 0.032 p.u. | ✓ | - | ✓ | - | ✓ | - | ✓ | - | - | - | - | - | ✓ | - | CC | MS | IPSO | BP | [29] |
| - | ✓ | - | - | - | - | - | - | ✓ | - | - | - | - | ✓ | - | DC | SO | PSO | BP | [30] |
| - | ✓ | ✓ | ✓ | - | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | HC | HO | IGWO | UP | Proposed |
| Description | Parameters | Value/Range |
|---|---|---|
| Capacitors: | ||
| Possible position of capacitor | Cap. Pos. | All buses of three phases |
| Size of capacitors | Cap. Step Cap. Size | 6 steps 25, 50, 75, 100, 125, 150 kVar |
| Static Var Generator (SVG): | ||
| Pos. | All buses of three phases | |
| Voltage set point | Vset. | 1 p.u. |
| Electric Vehicle Fast-Charging Station: | ||
| Fast-charging station capacity | FCS Cap. | 22, 50, 125, 150, 300 kW |
| Possible position of FCS-EVs | FCS Pos. | All buses of three phases |
| Power factor of FCS-EVs | PF | 0.95 |
| Photovoltaic System: | ||
| PV power plant capacity | PVs Cap. | |
| Position of PV power plant | PVs Pos. | bus No. 195, 251, 451 |
| Power factor of PV | PF | 0.85 |
| Optimization Algorithm: | ||
| Solving the problem limit range | Iteration | 100 |
| Improve gray wolf optimization (IGWO): | ||
| Number of wolves | N | 100 |
| Zone | Bus (Number) |
|---|---|
| 1 | 149, 1, 7, 8, 13, 18, 21, 23, 25, 28, 29, 30, 250 |
| 2 | 135, 35, 40, 42, 44, 47, 48, 49, 50, 51, 151 |
| 3 | 152, 52, 53, 54, 55, 56, 57, 60, 62, 63, 64, 65, 66 |
| 4 | 160, 67, 97, 98, 99, 100, 450, 72, 72, 76, 77, 78, 79, 80, 81, 82, 83, 86, 87, 89, 91, 93, 95 |
| 5 | 197, 101, 105, 108, 300 |
| Simulation Model | Case | Case Configuration | Case Descriptions | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base Case (BC) | FCS-EV | PV1P | PV3P | BSVG | USVG | BSC | USC | Zone (Z) | All-Zone (AZ) | |||
| 1 | 1 | ✓ | Find values to assess the impact of the base case | |||||||||
| 2 | ✓ | ✓ | ✓ | Randomize EV values to assess impact | ||||||||
| 3 | ✓ | ✓ | Randomize PV3P values to assess impact | |||||||||
| 2 | 4 | ✓ | ✓ | ✓ | Randomize BSVG within each zone with CC method | |||||||
| 5 | ✓ | ✓ | ✓ | Randomize BSVG across all zones with DC method | ||||||||
| 6 | ✓ | ✓ | ✓ | Randomize BSC within each zone | ||||||||
| 7 | ✓ | ✓ | ✓ | Randomize BSC across all zones with DC method | ||||||||
| 3 | 8 | ✓ | ✓ | ✓ | ✓ | Randomize USVG and EV within each zone with CC method | ||||||
| 9 | ✓ | ✓ | ✓ | ✓ | Randomize USVG and EV across all zones with DC method | |||||||
| 10 | ✓ | ✓ | ✓ | ✓ | Randomize USC and EV within each zone with CC method | |||||||
| 11 | ✓ | ✓ | ✓ | ✓ | Randomize USC and EV across all zones with DC method | |||||||
| 4 | 12 | ✓ | ✓ | ✓ | ✓ | ✓ | Randomize USVG, EV, and PV3P within each zone with CC method | |||||
| 13 | ✓ | ✓ | ✓ | ✓ | ✓ | Randomize USVG, EV, and PV3P across all zones with DC method | ||||||
| 14 | ✓ | ✓ | ✓ | ✓ | ✓ | Randomize USC, EV, and PV3P within each zone with CC method | ||||||
| 15 | ✓ | ✓ | ✓ | ✓ | ✓ | Randomize USC, EV, and PV3P across all zones with DC method | ||||||
| 5 | 16 | ✓ | ✓ | ✓ | ✓ | ✓ | Randomize USVG, EV, and PV1P within each zone with CC method | |||||
| 17 | ✓ | ✓ | ✓ | ✓ | ✓ | Randomize USVG, EV, and PV1P across all zones with DC method | ||||||
| 18 | ✓ | ✓ | ✓ | ✓ | ✓ | Randomize USC, EV, and PV1P within each zone | ||||||
| 19 | ✓ | ✓ | ✓ | ✓ | ✓ | Randomize USC, EV, and PV1P across all zones with DC method | ||||||
| Case | Variable No. X1 to Xn | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Zone 1 | Zone 2 | Zone 3 | Zone 4 | Zone 5 | FCS-EVs | PV-Size Bus 195 | PV-Size Bus 251 | PV-Size Bus 451 | |||||||||||
| Cap. Bus | Phase ABC | EVs Bus | Cap. Bus | Phase ABC | EVs Bus | Cap. Bus | Phase ABC | EV Bus | Cap. Bus | Phase ABC | EVs Bus | Cap. Bus | Phase ABC | EVs Bus | Size | Phase ABC | Phase ABC | Phase ABC | |
| 1 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| 2 | - | - | X1 | - | - | X2 | - | - | X3 | - | - | X4 | - | - | X5 | X6 | - | - | |
| 3 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | X1 | X2 | X3 |
| 4 | X1 | X2 | - | X3 | X4 | - | X5 | X6 | - | X7 | X8 | - | X9 | X10 | - | - | - | - | |
| 5 | X1 | X2 | - | X3 | X4 | - | X5 | X6 | - | X7 | X8 | - | X9 | X10 | - | - | - | - | |
| 6 | X1 | X2 | - | X3 | X4 | - | X5 | X6 | - | X7 | X8 | - | X9 | X10 | - | - | - | - | |
| 7 | X1 | X2 | - | X3 | X4 | - | X5 | X6 | - | X7 | X8 | - | X9 | X10 | - | - | - | - | |
| 8 | X1 | X2–X4 | X5 | X6 | X7–X9 | X10 | X11 | X12–X14 | X15 | X16 | X17–X19 | X20 | X21 | X22–X24 | X25 | X26 | - | - | |
| 9 | X1 | X2–X4 | X5 | X6 | X7–X9 | X10 | X11 | X12–X14 | X15 | X16 | X17–X19 | X20 | X21 | X22–X24 | X25 | X26 | - | - | |
| 10 | X1 | X2–X4 | X5 | X6 | X7–X9 | X10 | X11 | X12–X14 | X15 | X16 | X17–X19 | X20 | X21 | X22–X24 | X25 | X26 | - | - | |
| 11 | X1 | X2–X4 | X5 | X6 | X7–X9 | X10 | X11 | X12–X14 | X15 | X16 | X17–X19 | X20 | X21 | X22–X24 | X25 | X26 | - | - | |
| 12 | X1 | X2–X4 | X5 | X6 | X7–X9 | X10 | X11 | X12–X14 | X15 | X16 | X17–X19 | X20 | X21 | X22–X24 | X25 | X26 | X27 | X28 | X29 |
| 13 | X1 | X2–X4 | X5 | X6 | X7–X9 | X10 | X11 | X12–X14 | X15 | X16 | X17–X19 | X20 | X21 | X22–X24 | X25 | X26 | X27 | X28 | X29 |
| 14 | X1 | X2–X4 | X5 | X6 | X7–X9 | X10 | X11 | X12–X14 | X15 | X16 | X17–X19 | X20 | X21 | X22–X24 | X25 | X26 | X27 | X28 | X29 |
| 15 | X1 | X2–X4 | X5 | X6 | X7–X9 | X10 | X11 | X12–X14 | X15 | X16 | X17–X19 | X20 | X21 | X22–X24 | X25 | X26 | X27 | X28 | X29 |
| 16 | X1 | X2–X4 | X5 | X6 | X7–X9 | X10 | X11 | X12–X14 | X15 | X16 | X17–X19 | X20 | X21 | X22–X24 | X25 | X26 | X27–X29 | X30–X32 | X33–X35 |
| 17 | X1 | X2–X4 | X5 | X6 | X7–X9 | X10 | X11 | X12–X14 | X15 | X16 | X17–X19 | X20 | X21 | X22–X24 | X25 | X26 | X27–X29 | X30–X32 | X33–X35 |
| 18 | X1 | X2–X4 | X5 | X6 | X7–X9 | X10 | X11 | X12–X14 | X15 | X16 | X17–X19 | X20 | X21 | X22–X24 | X25 | X26 | X27–X29 | X30–X32 | X33–X35 |
| 19 | X1 | X2–X4 | X5 | X6 | X7–X9 | X10 | X11 | X12–X14 | X15 | X16 | X17–X19 | X20 | X21 | X22–X24 | X25 | X26 | X27–X29 | X30–X32 | X33–X35 |
| Simulation | IGWO | HGWO | ||
|---|---|---|---|---|
| Case | Time (s) | Time (s) | ||
| 6 | 1.721 | 383.329 | 1.721 | 453.022 |
| 7 | 1.581 | 381.077 | 1.581 | 635.709 |
| 16 | 0.896 | 387.340 | 1.013 | 447.863 |
| 17 | 1.035 | 397.383 | 0.953 | 478.438 |
| Case | CO2 | FCS-EVs | PV Size (kVA) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (%) | (kV) | (kW) | (kVar) | (tCO2/Y) | Bus | Size (kW) | Bus 195 | Bus 251 | Bus 451 | ||
| 1 | - | 4.850 | 2.295 | 109.118 | 218.429 | - | - | - | - | - | - |
| 2 | 3.212 | 5.202 | 2.287 | 125.600 | 252.400 | 158 | 149, 135, 152, 160, 197 | 300, 125, 200, 50, 22 | - | - | - |
| 3 | 1.423 | 3.358 | 2.408 | 57.670 | 113.740 | −8632 | - | - | 1333 | 1356 | 480 |
| Case | CO2 | Capacitors | ||||||
|---|---|---|---|---|---|---|---|---|
| (%) | (kV) | (kW) | (kVar) | (tCO2/Y) | Bus | Size (kVar) | ||
| 4 | 1.883 | 3.679 | 2.336 | 89.958 | 180.610 | −184 | 13, 135, 60, 97, 108 | 300, 265, 300, 300, 300 |
| 5 | 1.624 | 2.998 | 2.348 | 94.903 | 190.820 | −136 | 300, 100, 105, 108, 95 | 295, 275, 297, 296, 300 |
| 6 | 1.721 | 3.292 | 2.348 | 90.799 | 182.650 | −176 | 13, 135, 60, 97, 108 | 225, 125, 450, 450, 450 |
| 7 | 1.581 | 3.357 | 2.359 | 95.071 | 191.610 | −135 | 105, 91, 108, 72, 62 | 450, 375, 450, 125, 375 |
| Case | CO2 | Capacitor | FCS-EVs | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (%) | (kV) | (kW) | (kVar) | (tCO2/Y) | Bus | Size (kVar)A-B-C | Bus | Size (kW) | ||
| 8 | 1.844 | 3.357 | 2.328 | 104.900 | 210.280 | −40 | 29 | 98-99-100 | 149 | 300 |
| 47 | 100-97-99 | 135 | 200 | |||||||
| 63 | 100-9-99 | 152 | 50 | |||||||
| 91 | 100-83-99 | 160 | 22 | |||||||
| 300 | 100-92-98 | 197 | 125 | |||||||
| 9 | 1.583 | 2.763 | 2.341 | 99.962 | 200.440 | −88 | 82 | 100-84-85 | 149 | 300 |
| 77 | 100-99-96 | 28 | 22 | |||||||
| 108 | 100-59-91 | 1 | 200 | |||||||
| 89 | 100-82-92 | 7 | 125 | |||||||
| 78 | 99-91-95 | 152 | 50 | |||||||
| 10 | 1.521 | 2.448 | 2.349 | 103.380 | 206.530 | −55 | 25 | 150-125-150 | 149 | 300 |
| 47 | 150-100-150 | 135 | 200 | |||||||
| 64 | 150-125-150 | 152 | 125 | |||||||
| 93 | 150-150-150 | 160 | 22 | |||||||
| 108 | 150-25-150 | 101 | 50 | |||||||
| 11 | 1.314 | 1.962 | 2.360 | 103.970 | 207.900 | −49 | 80 | 150-125-150 | 149 | 300 |
| 72 | 150-50-125 | 30 | 22 | |||||||
| 98 | 150-125-150 | 7 | 125 | |||||||
| 93 | 150-75-125 | 152 | 50 | |||||||
| 108 | 150-50-125 | 1 | 200 | |||||||
| Case | CO2 | Capacitor | FCS-EV | PV Size (kVA) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (%) | (kV) | (kW) | (kVar) | (tCO2/Y) | Pos. | Size (kVar) A-B-C | Pos. | Size (kW) | Pos. 195 | Pos. 251 | Pos. 451 | ||
| 12 | 0.919 | 1.376 | 2.383 | 90.366 | 179.53 | −5602 | 28 | 75-6-70 | 149 | 200 | 1242 | 623 | 246 |
| 49 | 96-6-92 | 48 | 50 | ||||||||||
| 62 | 90-12-63 | 54 | 125 | ||||||||||
| 97 | 89-15-38 | 95 | 300 | ||||||||||
| 197 | 52-8-32 | 105 | 22 | ||||||||||
| 13 | 0.932 | 1.41 | 2.383 | 87.368 | 171.97 | −5992 | 63 | 59-18-81 | 95 | 300 | 1374 | 549 | 329 |
| 135 | 95-9-85 | 93 | 200 | ||||||||||
| 62 | 87-7-13 | 35 | 50 | ||||||||||
| 49 | 88-9-66 | 23 | 22 | ||||||||||
| 66 | 100-11-50 | 53 | 125 | ||||||||||
| 14 | 0.936 | 1.063 | 2.384 | 120.05 | 240.34 | −4688 | 25 | 125-25-125 | 149 | 300 | 745 | 558 | 563 |
| 40 | 150-25-100 | 135 | 125 | ||||||||||
| 55 | 75-25-50 | 52 | 200 | ||||||||||
| 67 | 100-25-100 | 100 | 22 | ||||||||||
| 108 | 125-25-75 | 197 | 50 | ||||||||||
| 15 | 0.979 | 1.297 | 2.391 | 118.75 | 238.92 | −4734 | 50 | 50-25-75 | 135 | 50 | 715 | 365 | 799 |
| 80 | 125-25-125 | 152 | 125 | ||||||||||
| 35 | 100-25-25 | 149 | 200 | ||||||||||
| 81 | 125-50-75 | 1 | 300 | ||||||||||
| 49 | 125-50-12 | 40 | 22 | ||||||||||
| Case | CO2 | Capacitor | FCS-EV | PV Size (kVA) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (%) | (kV) | (kW) | (kVar) | (tCO2/Y) | Pos. | Size (kVar) A-B-C | Pos. | Size (kW) | Pos.195 A-B-C | Pos.251 A-B-C | Pos.451 A-B-C | ||
| 16 | 0.896 | 1.626 | 2.404 | 74.599 | 148.86 | −3418 | 25 | 48-16-57 | 29 | 200 | 475-482-462 | 497-406-385 | 230-70-75 |
| 51 | 6-11-15 | 50 | 22 | ||||||||||
| 53 | 73-39-82 | 55 | 50 | ||||||||||
| 450 | 19-69-75 | 95 | 300 | ||||||||||
| 101 | 30-12-77 | 101 | 125 | ||||||||||
| 17 | 1.035 | 1.428 | 2.383 | 125.31 | 252.39 | −2249 | 13 | 52-75-28 | 152 | 300 | 291-252-227 | 378-288-345 | 267-191-232 |
| 72 | 40-57-93 | 149 | 22 | ||||||||||
| 149 | 64-64-15 | 250 | 200 | ||||||||||
| 135 | 89-40-61 | 1 | 50 | ||||||||||
| 108 | 83-6-39 | 47 | 125 | ||||||||||
| 18 | 0.955 | 1.067 | 2.39 | 134.08 | 270.09 | −1926 | 18 | 25-50-125 | 7 | 200 | 257-223-230 | 357-209-276 | 22-192-253 |
| 47 | 100-50-75 | 42 | 125 | ||||||||||
| 55 | 75-50-125 | 52 | 300 | ||||||||||
| 76 | 75-75-75 | 78 | 22 | ||||||||||
| 108 | 150-50-50 | 101 | 50 | ||||||||||
| 19 | 0.94 | 1.309 | 2.385 | 122.78 | 246.69 | −1598 | 66 | 50-75-50 | 14,940 | 300 | 209-239-220 | 280-65-262 | 148-121-218 |
| 51 | 125-50-75 | 99 | 50 | ||||||||||
| 97 | 125-125-75 | 25 | 125 | ||||||||||
| 108 | 150-50-75 | 81 | 200 | ||||||||||
| 48 | 50-50-100 | 14,940 | 22 | ||||||||||
| Simulation Model | Case | Total Reactive Power (kVar) | Cost of Investment (USD) |
|---|---|---|---|
| 1 | 1 | - | - |
| 2 | - | - | |
| 3 | - | - | |
| 2 | 4 (SVG) | 1464.400 | 15,127.252 |
| 5 (SVG) | 1462.700 | 15,109.691 | |
| 6 | 1700.000 | 10,200.000 | |
| 7 | 1775.000 | 10,650.000 | |
| 3 | 8 (SVG) | 1371.700 | 14,169.661 |
| 9 (SVG) | 1370.600 | 14,158.298 | |
| 10 | 2025.000 | 12,150.000 | |
| 11 | 1850.000 | 11,100.000 | |
| 4 | 12 (SVG) | 742.080 | 7665.6864 |
| 13 (SVG) | 778.222 | 7782.220 | |
| 14 | 1150.000 | 6900.000 | |
| 15 | 1125.000 | 6750.000 | |
| 5 | 16 (SVG) | 630.136 | 6509.305 |
| 17 (SVG) | 806.000 | 10,650.000 | |
| 18 | 1150.000 | 6900.000 | |
| 19 | 1225.000 | 7350.000 |
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Case | Iterations | Case | Iterations | Case | Iterations | Case | Iterations | Case | Iterations |
| 2 | 17 | 4 | 82 | 8 | 96 | 12 | 98 | 16 | 99 |
| 3 | 78 | 5 | 25 | 9 | 100 | 13 | 94 | 17 | 27 |
| 6 | 31 | 10 | 92 | 14 | 98 | 18 | 100 | ||
| 7 | 78 | 11 | 94 | 15 | 92 | 19 | 99 | ||
| Avg. | 47.50 | 54.00 | 95.50 | 95.50 | 81.25 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pilalum, P.; Taksana, R.; Chitgreeyan, N.; Sa-nga-ngam, W.; Marsong, S.; Buayai, K.; Kerdchuen, K.; Kongjeen, Y.; Bhumkittipich, K. Mitigation of Voltage Magnitude Profiles Under High-Penetration-Level Fast-Charging Stations Using Optimal Capacitor Placement Integrated with Renewable Energy Resources in Unbalanced Distribution Networks. Smart Cities 2025, 8, 102. https://doi.org/10.3390/smartcities8040102
Pilalum P, Taksana R, Chitgreeyan N, Sa-nga-ngam W, Marsong S, Buayai K, Kerdchuen K, Kongjeen Y, Bhumkittipich K. Mitigation of Voltage Magnitude Profiles Under High-Penetration-Level Fast-Charging Stations Using Optimal Capacitor Placement Integrated with Renewable Energy Resources in Unbalanced Distribution Networks. Smart Cities. 2025; 8(4):102. https://doi.org/10.3390/smartcities8040102
Chicago/Turabian StylePilalum, Pongsuk, Radomboon Taksana, Noppanut Chitgreeyan, Wutthichai Sa-nga-ngam, Supapradit Marsong, Krittidet Buayai, Kaan Kerdchuen, Yuttana Kongjeen, and Krischonme Bhumkittipich. 2025. "Mitigation of Voltage Magnitude Profiles Under High-Penetration-Level Fast-Charging Stations Using Optimal Capacitor Placement Integrated with Renewable Energy Resources in Unbalanced Distribution Networks" Smart Cities 8, no. 4: 102. https://doi.org/10.3390/smartcities8040102
APA StylePilalum, P., Taksana, R., Chitgreeyan, N., Sa-nga-ngam, W., Marsong, S., Buayai, K., Kerdchuen, K., Kongjeen, Y., & Bhumkittipich, K. (2025). Mitigation of Voltage Magnitude Profiles Under High-Penetration-Level Fast-Charging Stations Using Optimal Capacitor Placement Integrated with Renewable Energy Resources in Unbalanced Distribution Networks. Smart Cities, 8(4), 102. https://doi.org/10.3390/smartcities8040102









